Inferring whole-genome histories in large population datasets

Abstract

Inferring the full genealogical history of a set of DNA sequences is a core problem in evolutionary biology as it encodes information about the events and forces that have influenced a species. However, current methods are limited, with the most accurate able to process no more than a hundred samples. With data sets consisting of millions of genomes being collected, there is a need for scalable and efficient inference methods to fully utilise these resources. We introduce an algorithm to infer whole-genome histories with comparable accuracy to the state-of-the-art but able to process four orders of magnitude more sequences. The approach also provides an “evolutionary encoding” of the data, enabling efficient calculation of relevant statistics. We apply the method to human data from the 1000 Genomes Project, Simons Genome Diversity Project and UK Biobank, showing that the inferred genealogies are rich in biological signal and efficient to process.

Introduction

Trees are fundamental to evolutionary biology. From Darwin’s speculative sketches¹ and Haeckel’s phylogenetic imagery² to modern syntheses encompassing all species of life³, trees elegantly encode and summarise the outcomes of evolutionary processes. A large number of methods now exist to infer evolutionary trees⁴, which are used as input in many downstream applications⁵. However, a tree can only be used to describe the ancestry of a set of DNA sequences if they are transmitted across generations as a single unit. Any process that causes different parts of a sequence to have different ancestors results in a history that cannot be described by a single tree, but instead requires a network⁶. This presents difficulties when inferring ancestry within a sexually reproducing species, where DNA is inherited from both mother and father through recombination.

The need for structures more general than trees to describe ancestry has long been understood⁷. Multiple representations of such “phylogenetic networks” exist which model non-vertical transmission of genetic information arising from horizontal gene transfer and hybridisation⁶. The Ancestral Recombination Graph (ARG)^8,9 models the network arising from inheritance within sexually reproducing species, encoding the recombination and common ancestor events in the history of a sample. In principle, ARGs contain all knowable information about genetic history, hence are central to population genetics^10,11,12,13; however, practical applications have been limited by the prohibitive computational cost of inferring them. The problem of finding an ARG with the minimum number of recombination events required to explain a set of sample sequences is NP-hard^14,15,16,17 and, while there exist non-minimal polynomial time algorithms^18,19 and various techniques to reduce search space^9,20,21, in practice these are too slow to apply to even moderately sized data sets. Several heuristic methods for inferring ARGs have been developed^{10,22,23,24,25}, though most are limited to tens of samples and a few thousand variant sites. The ARGweaver program¹³ is the current state-of-the-art and a substantial advance over earlier methods, as it performs statistically rigorous inference of ARGs over tens of thousands of variant sites. However, computational time grows rapidly with the number of samples, limiting use to a few tens of samples. The widespread use of ARGs is also hindered by the lack of interchange standards and community toolkits, despite several efforts to standardise^26,27. Consequently, the ARG remains a structure that is known to be fundamental to our understanding of the ancestry of populations, but one that is practically never used.

Here we introduce a method, tsinfer, that removes these barriers to the adoption of ARGs in the analysis of genome variation data. Crucially, tsinfer vastly expands the scale over which ancestry can be inferred, simultaneously increasing the number of variant sites and sample genomes by several orders of magnitude, with accuracy comparable to the state-of-the-art. Moreover, we show that the data structure produced by tsinfer, the succinct tree sequence (or tree sequence, for brevity)^28,29 has the potential to store genetic data for entire populations, using a fraction of the space that would be required by present-day methods. As an encoding of the data based on the evolutionary history of the samples, many statistics of importance in evolutionary biology and statistical genetics can be computed efficiently using this structure. The tree sequence toolkit (or tskit) is a free and open source library providing access to these efficient algorithms. Thus, the two main practical obstacles to using ARGs (the lack of efficient inference methods and software to process the output) have been removed. We demonstrate utility by applying tsinfer to three large-scale human data sets (1000 Genomes³⁰, the Simons Genomes Diversity Project³¹ and the UK Biobank³²) and show how biological signals can be easily inferred from the resulting genealogical representation.

Results

Succinct tree sequences

The tangled web of ancestry describing the genetic history of recombining organisms is conventionally encoded via common ancestor and recombination events in an ARG. The result of this process is a sequence of marginal trees, each encoding the genealogy for a particular segment of DNA¹⁶. Moving along a chromosome, recombination events alter the trees in a well-defined way¹⁷, with adjacent trees tending to be highly correlated. The succinct tree sequence is an encoding for recombinant ancestry that takes advantage of this correlation structure by storing each edge shared by multiple adjacent trees exactly once^28,29. This simple device captures shared structure among trees and leads to efficient processing algorithms²⁸. The ARG, which encodes the events that occurred in the history of a sample, is formally distinct from the succinct tree sequence, which encodes the outcome of those events, although we note that it is possible to augment a tree sequence to contain all information in an ARG.

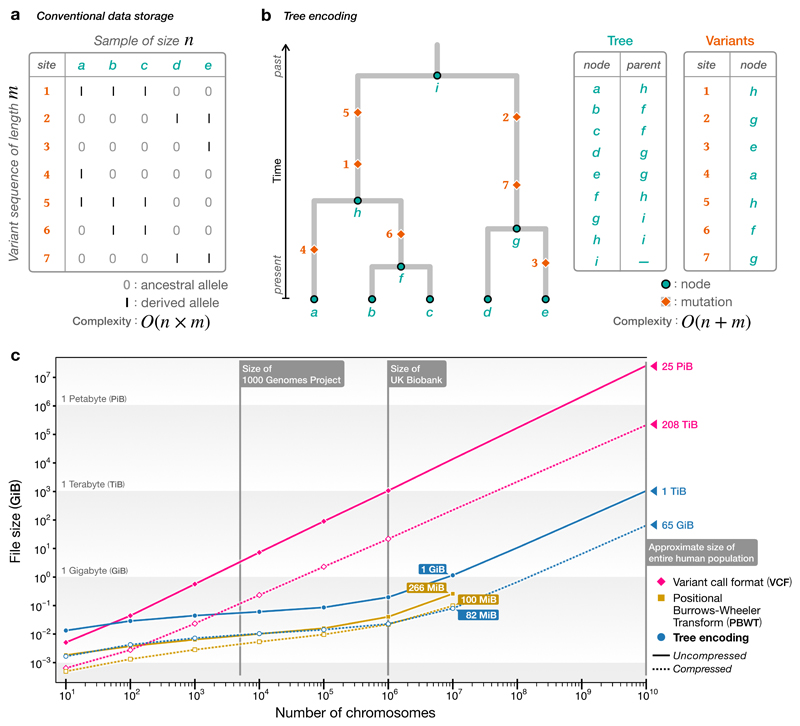
The succinct tree sequence has the potential to dramatically reduce the space required to store genomic variation data. Such information is usually encoded as a matrix, with columns representing samples and rows corresponding to sites along the genome at which variation is observed (Fig 1a). For n samples and m sites we need O(nm) space to store the matrix. Studies such as the UK Biobank³² contain hundreds of thousands of samples, and such large datasets are expected to become increasingly common³³. As many species have millions of variant sites per chromosome, storing and processing such huge matrices is a major burden. Tree sequences provide an efficient alternative. The variation that we observe is the result of mutations that occurred in the ancestors of our samples. If we know the genealogy at a particular site, we can fully describe genetic variation by recording where in the ancestry these mutations arose³⁴(Fig. 1b); multiple mutations at a given site are rare, and each site therefore requires O(1) storage space rather than O(n). Fig. 1c shows the space required to store variation data for simulations of up to 10 million human-like chromosomes, extrapolated out to 10 billion. In this idealised case, storing the genotype data in the most widely used format (VCF³⁵) would require 25PiB (i.e., approximately 25,000 1TiB hard disks) whereas the tree sequence encoding would require only around 1TiB. Thus, if we were able to store variation data using the tree sequence encoding we could store and process any conceivable data set on a present-day laptop. Existing specialised methods can also achieve much better compression levels than compressed VCF; in particular, the Positional Burrows Wheeler Transform (PBWT) is an extremely concise method of storing genotype matrices which supports efficient exact haplotype matching³⁶. Notably, Figure 1 shows that even though the compressed tree encoding also stores the full genealogy at every site (and therefore the haplotypes of every genetic ancestor), it is competitive with PBWT and even smaller at the largest scales.

Figure 1.

Comparison of tree sequences with standard methods for storing genetic variation data. a). The variant matrix underlying conventional storage methods for genetic variation data. b). A genealogical encoding for data; if we know the tree we can store each variant site in constant space. c). Estimated sizes of files required to store the genetic variation data for a simulated human-like chromosome (100 megabases) for up to 10 billion haploid (5 billion diploid) samples. Simulations were run for 10¹ up to 10⁷ haplotypes using msprime ²⁸, and the sizes of the resulting files plotted (points). In each case we show the original tree sequence file uncompressed and compressed using tszip (retaining only topological information needed to represent genotypes using the --variants-only option). We also show the corresponding variation data encoded in the VCF³⁵ and PBWT³⁶ formats, along with their gzip-compressed equivalents. The VCF files for 10⁷ samples were too large and time-consuming to process. The projected file sizes for VCF/compressed VCF are based on fitting a simple exponential model. Projected files sizes for tree sequences are based on fitting a model based on the theoretical growth of tree sequences²⁸. Where we have extrapolated, the largest data point was withheld from fitting to assess the model fit. We do not extrapolate for the PBWT files as there is no theoretical model to predict their size.

Converting data into a highly compressed form usually requires costly decompression before use. A great advantage of the tree sequence encoding is that we can compute many statistics directly from the trees without decoding the genotypes. For example, computing the frequency of specific variants within subsets is a key building-block of many genetic statistics. The algorithm for recovering trees from the encoded tree sequence representation allows us to compute allele frequencies far more efficiently than is possible when working with a raw matrix representation of the data²⁸. Consider, for example, the largest tree sequence simulated in Figure 1, which represents the ancestry of 10⁷ chromosomes, each 100 megabases long. It takes about 2.2 seconds to load this 1.2GiB tree sequence; about 7.5 seconds to iterate over all 650K trees; and about 17 seconds to compute allele frequencies within an arbitrary subset of 10⁶ samples at all 670K sites. In contrast, just decompressing and decoding the corresponding 6.1 TiB of genotype data from BCF (a more efficient binary encoding of VCF) would require an estimated 1.8 hours (based on extracting the first 10K variants using cyvcf2 ³⁷). Moreover, BCF and other existing formats for storing variant data do not consider ancestry in any way. If we wished to store the actual trees from this simulation of 10⁷ samples using the most efficient and popular interchange format (Newick), we would need approximately 256 TiB of space and it would take an estimated 5.3 CPU years to parse (based on BioPython’s³⁸ Newick parser—one of the most efficient available—taking about 262 seconds per tree).

Inference algorithm

DNA sequences can be considered mosaics of sequence fragments that have been inherited from recent ancestors via an error-prone copying process. Likewise, these ancestors are themselves mosaics, copied imperfectly from yet older ancestors. Further back in time these ancestral sequence fragments (or haplotypes) become shorter, as recombination breaks up the contributions of different ancestors over the generations. Our inference method is based on the premise that if these ancestral haplotypes were known it would be possible to infer a plausible copying history for large numbers of input DNA sequences. Critically, this approach means that we do not need to compare sample haplotypes with each other, avoiding the resulting quadratic time complexity.

We do not usually know these ancestral haplotypes, but we can attempt to infer them. If we assume that the contemporary variation we observe at each site on the genome is the result of a single mutation, we know that every sample haplotype that has the mutated (or derived) state at this site must have inherited it from a single ancestor. Moreover, these samples will also have inherited some fragment of the ancestral haplotype around the focal site. For mutations that arose recently, the shared haplotype will tend to be long, as recombination will not have had time to break it up. Conversely, for ancient mutations the shared ancestral haplotype will tend to be short (Fig. 2).

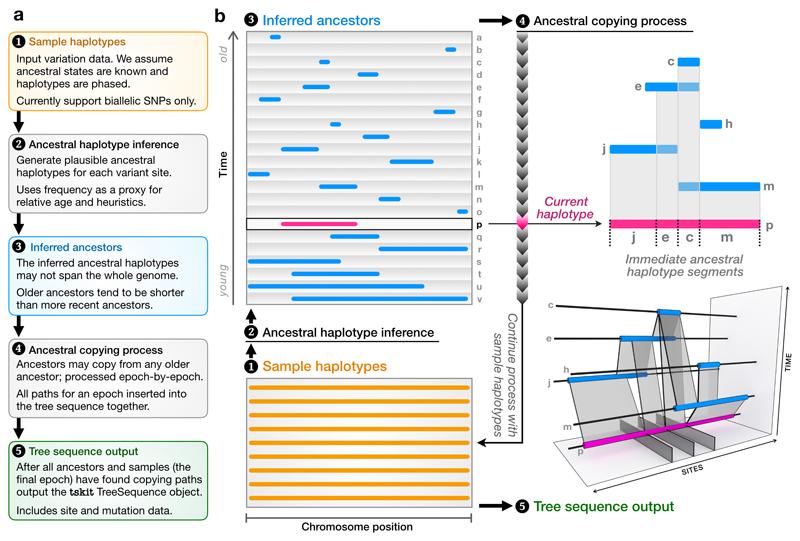
Figure 2.

A schematic of the major steps of the inference algorithm. Starting from a set of sample haplotypes extending over the genome (1), we use the ancestral haplotype inference method (2) to reconstruct fragments of ancestral sequence (3), then infer copying paths among these ancestors (4). The ancestral copying process is shown on the right, using an arbitrary haplotype (p) for illustration. As we move from left to right along p we infer that it has most recently copied from j, e, c and then m. Incorporating the copying history of all older haplotypes (for example, m copied partly from c and partly from h), partial coalescent trees emerge in the bottom-right panel. Once copying paths have been found for all ancestors and samples, we output a tskit tree sequence (5).

The first step in our algorithm is to infer ancestral haplotypes based on the variation present in the sample sequences, for which we use a simple heuristic. Briefly, we first use the frequency of the derived state at each site as an approximation of the relative age of the corresponding ancestor (Supplementary Figure 1). Then, for each ancestor we work outwards from the focal site taking a consensus value among samples carrying the derived state at the focal site (see Supplementary Figure 2 and Methods for details). Although heuristic, this method is reasonably accurate and robust to errors (Supplementary Figure 3).

After estimating ancestral haplotypes we then infer how they relate to each other using a variation of the Li and Stephens (LS) model³⁹, which regards a haplotype as an imperfect mosaic of the haplotypes in some reference panel. For a given ancestral haplotype, our reference panel consists of all older ancestral haplotypes. Because our reference haplotypes are ancestral rather than contemporary, we make a slight modification to the standard LS process: alongside the usual 0/1 states, a third haplotypic state is used to represent non-ancestral material from which copying can never occur. Computing the most likely path under the LS model allows us to estimate the immediate ancestor for each segment of DNA in the focal haplotype. Figure 2B shows an example of such a copying path for a focal haplotype and how it copies from different ancestors along its length. Once we have found copying paths for all ancestors and input sample haplotypes, we are guaranteed to have complete genealogical trees for every position along the genome, albeit ones that may contain nonbinary nodes (“polytomies”). Furthermore, these copying paths correspond to ‘edges’ in the tree sequence formulation²⁹, and so the copying process directly generates a succinct tree sequence. Representing the ancestral haplotypes as a tree sequence lends significant flexibility, as it allows us to combine information from diverse sources; for example, we can use a tree sequence estimated from one data set as ancestors for another (see Applications). Encoding the inferred ancestors as an incrementally-updated tree sequence also allows us to find copying paths under the LS model far more efficiently than is possible using existing approaches (see Methods).

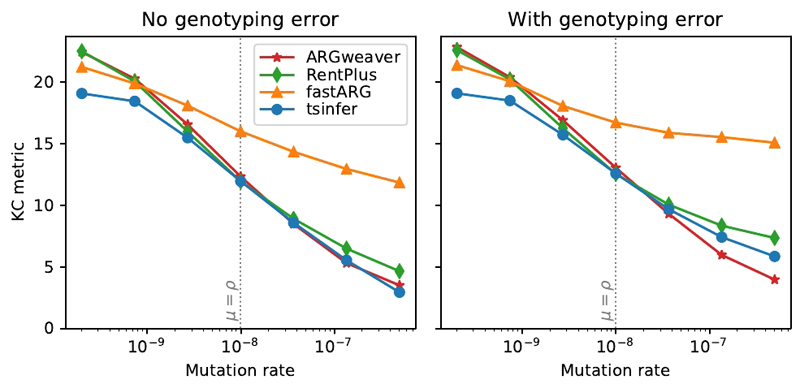
We evaluated tsinfer for accuracy and scalability using population genetic simulations to generate ground-truth data, and compare against three other tools for ancestry inference: ARGweaver ¹³, Rent+ ²⁵ and fastARG (https://github.com/lh3/fastARG). Fig. 3 compares the accuracy of inferred ancestral topologies; we use the Kendall-Colijn tree distance metric⁴⁰, as it is more sensitive than alternative metrics (Supplementary Figure 4) and is robust to the presence of nonbinary nodes in trees (see Methods). We find that tsinfer is consistently more accurate than fastARG and Rent+ and has similar accuracy to ARGweaver under a range of different models of error and demography (Supplementary Figures 5–7), while scaling to vastly larger input sizes (Supplementary Figures 8 and 9). In particular, Supplementary Figure 7 shows that tsinfer’s accuracy is substantially higher than ARGweaver’s in the presence of a selective sweep, suggesting that our nonparametric approach is more robust to departures from the assumptions of the neutral coalescent model. See the Methods for details of how these comparisons were performed.

Figure 3.

Accuracy of ancestry inference under different methods (lower values indicate greater accuracy). Coalescent simulations for 16 sample haplotypes of 1Mb in length under human-like parameters (N_e = 5000, with recombination rate ρ = 10⁻⁸ per base per generation) and an infinite sites model of mutation were simulated using msprime ²⁸. The reported tree topology distance is the Kendall-Colijn metric, weighted by the genomic distance spanned by each tree. Each point is the average of 100 independent replicates at a given mutation rate. The point where mutation rate equals recombination rate (similar to humans) is marked with a vertical dotted line. Standard errors are smaller than the plotted symbols in all cases.

Applications

To evaluate tsinfer’s performance on empirical data we inferred tree sequences for three data sets on human chromosome 20: the 1000 Genomes Project (TGP), consisting of low-coverage whole genome sequencing data from 2504 individuals across 26 worldwide populations³⁰; the Simons Genome Diversity Project (SGDP), consisting of high coverage sequencing data from 278 individuals from 142 worldwide populations³¹; and the UK Biobank (UKB), consisting of SNP array data from 487,327 individuals within the UK³². Table 1 summarises input data, inferred tree sequences and computing resources required. For UKB, we considered multiple strategies, augmenting the data with ancestors inferred from TGP and subsets of haplotypes from the UKB itself as potential ancestors. For each data set we used statistically inferred haplotypes as input.

Table 1.

Summary of input data, output tree sequences and computing resources required for TGP, SGDP and UKB chromosome 20. Input sizes reported are of tsinfer’s input .samples files, which uses the Zarr library (https://zarr.readthedocs.io/) to achieve similar compression levels to BCF. File sizes are reported using binary multipliers (i.e., 1M = 2²⁰ bytes); all other values use decimal multipliers (i.e., 1M = 10⁶). The times reported are the total wall clock time required to produce the output tree sequence from the .samples file on a server with two Xeon Gold 6148 CPUs (40 cores in total; no hyperthreading) and 187GiB of RAM. For SGDP, TGP and UKB we used the standard tsinfer inference pipeline. In UKB+TGP, we matched the UKB samples to the inferred TGP tree sequence (time reported is just for sample matching phase). In UKB+UKB we incrementally added samples from UKB to the ancestors inferred from UKB (see text).

	Input			Output				Resources
	n	sites	size	nodes	edges	trees	size	time	RAM
SGDP	277	348K	15M	236K	1.7M	196K	83M	5m	3.6G
TGP	2504	860K	135M	735K	7.3M	550K	296M	2h	11G
UKB	487K	15.8K	1.6G	1.9M	484M	15.8K	14.5G	3h	160G
UKB+TGP	487K	15.6K	1.6G	5.5M	185M	15.6K	5.8G	15h	66G
UKB+UKB	487K	15.8K	1.6G	2.0M	62M	15.8K	2.1G	50h	40G

Across chromosome 20, the TGP data consisted of 860K sites after filtering (see Methods for details). After inferring ancestors and matching sample haplotypes to these ancestors, we obtained a 297MiB tree sequence (46MiB compressed, compared to the 141MiB BCF encoding of the same genotypes). Under the standard neutral model we expect the number of distinct trees to be roughly equal to the number of variable sites within human data, and the number of edges to be roughly four times the number of trees^28,29. We observe similar numbers of distinct trees (550K) as filtered sites (860K, from 1.8M unfiltered), but the number of edges is 7.3M, which is greater than expected and suggests that the differences between adjacent inferred trees are larger than expected under idealised conditions. Loading the tree sequence required c. 3 seconds; iterating over all 550K trees c. 0.6 seconds; and decoding all genotypes c. 9 seconds. In comparison, decoding the same genotypes from BCF required c. 15 seconds using cyvcf2. The SGDP data consisted of 348K sites after filtering, and this resulted in an 83MiB tree sequence (11MiB compressed, compared to the 11MiB BCF encoding of the same genotypes). Loading the tree sequence required c. 1.6 seconds; iterating over all 196K trees c. 0.1 seconds; and decoding all genotypes c. 1.8 seconds. These results demonstrate the feasibility of representing existing data sets through tree sequences, with file sizes comparable to current standards and excellent analytical accessibility.

To assess the validity of the inferred tree sequences we computed a series of metrics summarising reconstructed ancestral relationships. We first calculated the number of edges for each sample, which measures the extent to which an individual’s genome can be compressed against the inferred ancestors. In TGP, samples have an average of 648 edges (with a median length of 44kb and an average N50 of 236kb), with those of African ancestry having a greater number (750) than those of European (551) or Asian (665) ancestry (Supplementary Figure 10a and Supplementary Figure 11). These findings are likely to primarily reflect known differences in the long-term effective population size, though will also be affected by sampling strategy and error modes. We find higher values in SGDP reflecting the lower sample sizes (overall average: 1113 edges, African ancestry: 2178, European ancestry: 803 and Asian ancestry: 879; Supplementary Figure 10b and Supplementary Figure 12). In both data sets we identified a few outlier samples with very high edge counts, suggesting error (see Supplementary Note).

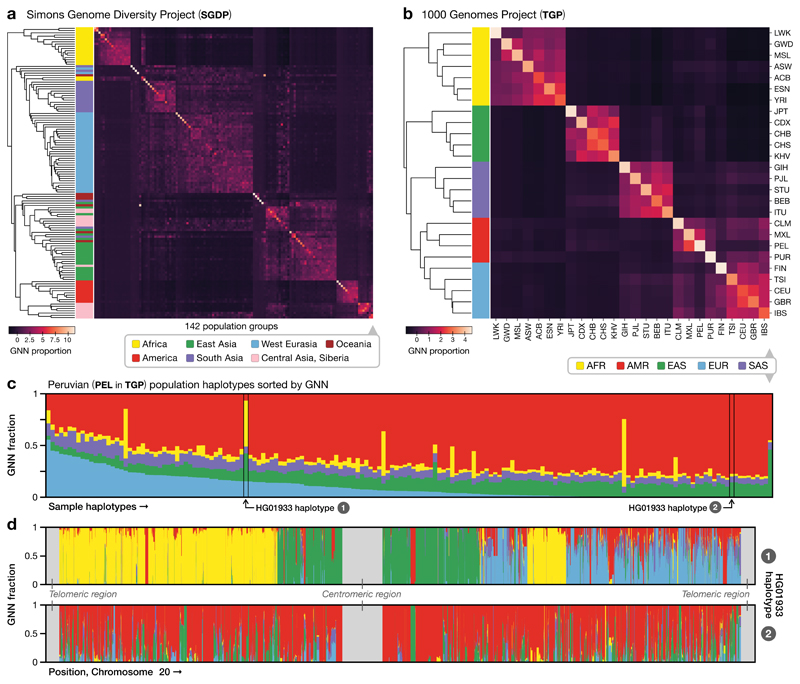
We next considered whether the inferred tree sequences could be used to characterise ancestral relationships in TGP and SGDP by computing, for each individual, the population distribution of their genealogical nearest neighbours (GNN). Given K sets of reference nodes (e.g., the samples for each of the 26 TGP populations), the GNN statistic for a specific node is a K-vector describing the proportion of its immediate neighbours within the tree from each of these reference sets (see Methods). We find that, despite the noise generated by uncertainty in tree reconstruction (manifest as polytomies), the chance nature of the genealogical process and data error, the tree sequences can characterise global population structure (Fig. 4a,b), within-population relatedness (Fig. 4c) and identify regions of differential ancestry within an individual (Fig. 4d). These analyses demonstrate the potential of interrogating the inferred genealogical structure at different resolutions to describe both broad and fine-scale patterns in contemporary human genomic diversity.

Figure 4.

Tree sequence characterisation of global genome diversity. a). Z-score normalised GNN proportions for SGDP by population (n = 278 individuals). The GNN matrix was first z-score normalised by column and the rows then hierarchically clustered. See Supplementary Figure 16 for a larger version with population labels. b). As for (a), but for the TGP data (n = 2504 individuals). c). Average GNN proportions for all individuals within the PEL population in TGP. Colours indicate continental-level groupings. d). The GNN proportions across the chromosome for the two haplotypes of HG01933, from the PEL population in TGP. HG01933 was chosen as an example of an individual showing evidence of very recent admixture from multiple source populations. We note that apparent short tracts of different ancestry most likely do not reflect true changes in recent ancestry, but arise through the stochastic nature of genealogical processes and errors in inference.

Finally, to assess the performance of tsinfer on vast data sets we analysed the ~500K individuals within UK Biobank. The sparsity of variant sites and inherent lack of rare variants in the UKB SNP array data is insufficient for accurate ancestor inference directly. However, we considered two alternative strategies: using ancestors estimated from other data and using subsets of the sample to act as proxies for ancestors. In the first approach, we matched the UKB haplotypes to the tree sequence inferred for TGP, generating a 5.8GiB tree sequence (740MiB compressed). Supplementary Figure 13 shows the self-reported ancestry in UKB tallies with TGP GNN values and adds granularity. Furthermore, by analysing the copying patterns in this tree sequence, we found 9 individuals that are likely to be in both the TGP and UKB data sets (see Supplementary Note).

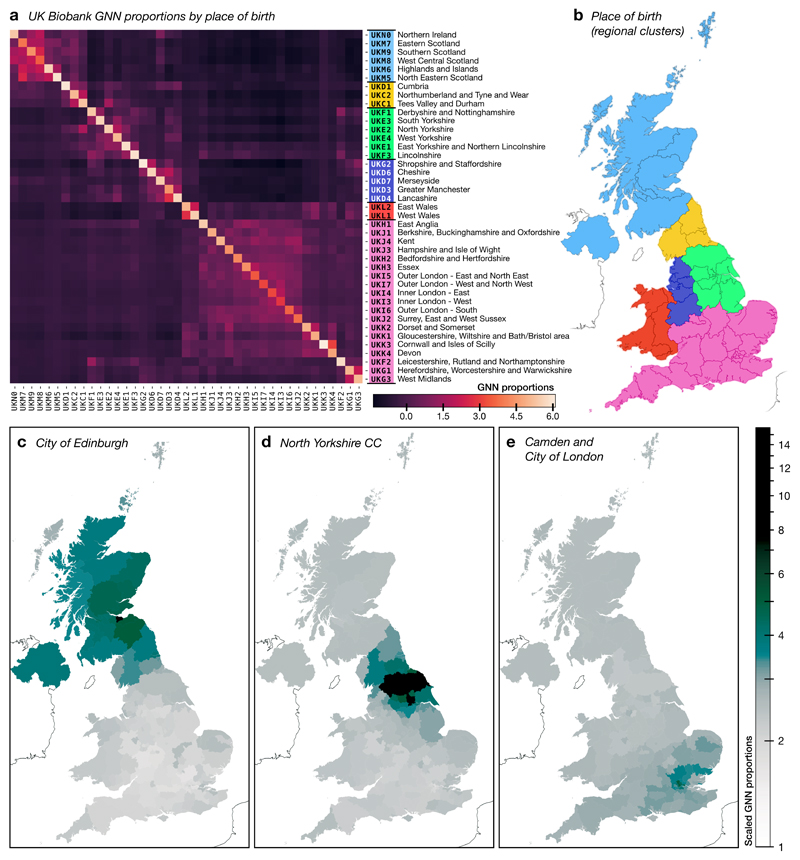
Our second strategy for improving ancestor inference involves sequentially adding subsets of the sample itself as potential ancestors. By iteratively adding samples, the approach of generating putative ancestors from shared recombination breakpoints (“path compression”; see Methods) constructs many more ancestors that would be possible if all samples were added simultaneously. Thus, we began by updating the ancestor’s tree sequence with the paths for two arbitrarily chosen samples; then updating the resulting tree sequence with the paths taken for four other samples; and then again for eight; and so on up to 131,072. After matching all 1M sample haplotypes against these augmented ancestors we obtained a 2.1GiB tree sequence (318MiB compressed, compared to the equivalent 1.4GiB BCF file). Loading this tree sequence required c. 9 seconds and iterating over all 15.8K trees c. 11 seconds. Decoding genotypes for the first 1000 sites required 9.5 seconds; in comparison, decoding the genotypes for the first 1000 sites in the original BGEN file using the bgen C library required 49 seconds. Analysis of the GNN structure of the tree sequence (Fig 5) demonstrates strong geographical clustering of relatedness at this level of resolution, with connections between birth locations reflecting geographical proximity. Although signals of population structure are evident here, further work is required to understand the implications for statistical analysis of association and other applications.

Figure 5.

Tree sequence characterisation of the UK Biobank data. a). Normalised GNN proportions for 628,651 haplotypes self-reported as born in Britain or Northern Ireland (the 262,136 sample haplotypes used for ancestor augmentation were removed from this analysis) calculated relative to birth location (grouped according to NUTS 2018, level 2; see Methods), i.e., reporting the fraction of each sample’s genealogical nearest neighbours who were born in a given geographical area. The columns in the GNN matrix were z-score normalised before the rows were hierarchically clustered. b). Geographical areas colour-coded by group clustering. The 6 areas correspond to the first 6 clusters obtained by hierarchical clustering of the 41 birth locations in (a). c, d and e). GNN proportions computed for specific NUTS level 3 areas: c) City of Edinburgh (n = 7571 individuals); d) North Yorkshire CC (n = 3416 individuals); e) Camden and City of London (n = 4726 individuals). For each area, the GNN proportions were computed over 170 geographical areas (169 NUTS-3 areas and Northern Ireland). The z-scored proportions were translated and log-normalised. The tree sequence constructed by iteratively augmenting ancestors (see text) was used as the basis for plots (a)–(e).

Discussion

Inferring genealogical relationships from patterns of genomic variation is a long-standing problem in evolutionary biology that connects to the fundamental forces and events shaping a species. However, our ability to infer such histories has, to date, been limited by the computational complexity of the problem. The work presented here represents a major advance by providing a principled, yet scalable approach that can be applied to data sets of unprecedented size. While the algorithms presented are both heuristic and deterministic, the approach of breaking down the problem into inferring relative variant age, ancestral haplotypes and the genealogical relationships between these ancestors results in a modular framework that scales to vast sample sizes (Supplementary Figure 9). Moreover, each component can be improved independently, potentially accommodating uncertainty through stochastic approaches.

Nevertheless, the method does make a number of fundamental assumptions. First, we assume that each variant in a population has a single mutational origin. While this is unlikely to be true in practice (particularly in large samples), our ancestor estimation method is likely to find the dominant ancestral haplotype. Recurrent and back mutations will therefore not be handled well by the current algorithm, though in principle could be addressed by iterative approaches. Second, we assume that frequency is a proxy for relative variant age. Importantly, our algorithms only require accuracy about relative age within genealogically connected parts of the tree sequence. Under simple demographic models, we estimate that relative frequency indicates relative age for roughly 90% of closely located pairs of variants (Supplementary Figure 1). In theory, methods for dating genomic variants could be used to improve ancestor estimation and also assign dates to nodes within the tree sequence, though these remain open problems. Third, we assume that the ratio of mutation to recombination is sufficiently high to use mutations as the starting point for ancestor inference. However, the path compression approach used here (see Methods) identifies additional ancestors through shared recombination events and, within the SNP array analysis on UKB, performs well, compensating for the low variant density and lack of rare variants. Finally, the current methodology works well for low error rates, but its performance is degraded (typically characterised by an excess of edges) by genotyping and, in particular, haplotype phasing error. In the future, population-scale high coverage and routine long-read genome sequencing will reduce the source of such errors and it may be feasible to construct steps of the algorithm that are more robust than those currently implemented. Our method does not estimate the times of internal tree nodes beyond a simple ordering, which is a significant limitation in terms of evolutionary analyses. Inferring nodes times conditioned on a tree sequence topology—at scale—is therefore an important goal for future work.

Tree sequences have many potential applications. The most obvious is as an efficient lossless storage format for population-scale data sets. While compression performance on simulated data (Supplementary Figures 14 and 15) is close to the theoretical possibilities shown in Fig. 1, tsinfer’s compression of real data does not currently fulfil this potential. More careful modelling of the complexities of genetic data—in particular the various error modes—will likely be required to effectively compress millions of whole genomes. Nonetheless, compression performance is comparable to existing formats while providing exceptional analytical accessibility. Recent, unpublished work on data compression using a genealogically-informed PBWT⁴¹ also offers a related and promising approach to genome-scale inference of tree sequence topologies. The integration of genealogical relationships with genomic variation data has value beyond population and personal genetics, for example in potentially correcting for the differential geographical confounding of rare and common variants in genetic association, and, as Speidel et al.⁴² have shown, enables powerful inference of underlying evolutionary events, processes and parameters, such as mutation age, natural selection and ancient contacts between populations. Moreover, our combined analysis of the UKB and TGP data sets demonstrates the potential of also using tree sequences to integrate data sources and, more generally, to build a reference tree sequence structure for human genomic variation that can be updated as new variants are discovered. Such a structure, coupled with efficient algorithms that make use of the tree sequence could enable (and make optimally powerful) diverse statistical genetic operations including genotype refinement, genotype imputation and haplotype phasing. It could also be used to share data effectively and in a manner that preserves privacy, by describing data sets in terms of inferred ancestors rather than individual samples.

Online Methods

Age of alleles

The first step in our algorithm is to estimate the relative time at which the mutation for each variant arose (we are assuming a single origin for each mutation). Classical results in population genetics provide a theoretical expectation for the age of an allele based on its frequency^43,44. There are several existing methods for estimating allele age, but are either computationally expensive or require detailed knowledge about historical population processes^45,46,47, although a more efficient non-parametric method has recently been introduced⁴⁸.

If we are interested in estimating topologies, however, we do not need precise esimates of allele age: all we require is the order in which nodes occur. The frequency of alleles provides a computationally inexpensive way of ordering allele ages, which is surprisingly accurate for our purposes (Supplementary Figure 1), as we only need the relative age ordering of alleles to be locally accurate. If variants on opposite ends of a chromosome are incorrectly ordered it makes little difference to the outcome of our algorithms, since the ancestral haplotypes involved are unlikely to overlap. By default tsinfer uses frequency as a proxy for relative allele age, but we also allow external sources of allele age to be provided as input.

Inferring ancestral haplotypes

Once we have assigned an age order to sites, the next step in our inference process is to generate a set of putative ancestral haplotypes. We assume that there are two alleles at every site: the ‘ancestral state’, which was inherited from the ancestor of the entire population and the ‘derived state’ which is the result of a mutation that occurred on the ancestor of the samples carrying this allele. We assume that these ancestral and derived states have been identified via existing methods⁴⁹. Each variant site is therefore the result of a mutation that occurred on an ancestor: samples that inherit from this ancestor have the derived state, and the rest carry the ancestral state. By definition this ancestor carries the derived state at the site in question; our task then is to reconstruct the state of the ancestor around this focal site.

For a given focal site ℓ let S be the set of samples that carry the derived state. We are attempting to reconstruct the ancestral haplotype a on which the mutation occurred, and so we begin by setting a_ℓ = 1, following the usual convention of labelling the ancestral state for a site 0 and the derived state 1. For all other sites 1 ≤ k ≤ m, k ≠ ℓ we set a_k = −1, indicating non-ancestral material that cannot be copied from; these non-ancestral values will be overwritten for sites around ℓ where we can estimate the state of the ancestor. We then work leftwards and rightwards from ℓ independently, computing the state of the ancestor at each site. The set S initially contains the samples that we believe descend from the current ancestor (assuming infinite sites and no error), and we use this set to compute a plausible state at other sites. As recombination modifies the tree topology, we update S to remove samples that are no longer in the clade induced by the focal site. We stop moving left or right from the focal site when we judge that we no longer have sufficient information to construct the ancestral haplotype. We use heuristics to determine when to remove a particular sample from S and when to end the ancestral haplotype.

Supplementary Figure 2 illustrates a simplified example of this process, showing the ancestral haplotype estimated at the focal site 8. We begin by setting S = {e, f, g, h}, i.e. the set of samples that carry the derived allele at site 8. We then proceed rightwards, considering each site in turn. For younger sites, the corresponding mutation cannot have occurred yet by definition, and so we always set the ancestor to 0 at these sites (e.g. 9 and 10). When we reach a site that is older than the focal one, we compute a plausible value for our ancestor by taking the consensus among the samples in S. For example, at site 11 the estimated value for the ancestor is 1 because all haplotypes in S carry 1; similarly, at site 13, three of four samples in S carry 1, and so the consensus is 1 (the consensus can also be 0, as in site 4). We interpret disagreement with the consensus value as evidence that the samples in question have recombined away to another part of the tree. Thus, after we have computed the ancestor’s state at a site, we remove (or “evict”) any samples from S that conflict with this consensus (but see below for a slight modification used in practice). In the example, we therefore evict h at site 13 and g at site 17. We continue rightwards in this way until we determine that we have insufficient information to accurately estimate ancestors. The heuristic we have chosen is to stop when the size of S is ≤ half of its original size. After completing the rightwards scan, we then repeat the process independently leftwards.

Variants with an age equal to the focal mutation are considered to be younger than the focal site (and hence always assigned the ancestral state) except in one special case. If several sites exist with precisely equal distribution of genotypes, we assume that these all arose on a single branch of the tree and that no recombination occurred between these sites. We therefore compute consensus values for older sites between these identical focal sites in the usual way, but we do not update S when conflicts occur (assuming these to be caused by error). Once outside of the region enclosed by the identical sites, the process outlined above resumes and we update S in the usual way.

Although this method is approximate and heuristic, it generates surprisingly accurate ancestors. Supplementary Figure 3 shows a plot of the lengths of the estimated vs true ancestors from simulations, colour-coded by the accuracy of the estimated states. We see that there is a strong bias towards ancestral haplotypes being longer than the truth; this is by design, as long haplotypes can be compensated for by the copying process, but short haplotypes cannot. Inferred haplotypes are also quite accurate, with many ancestors being inferred perfectly. Genotyping errors can result in many generated ancestors being too short, as errors often lead to samples being prematurely evicted from S. To add some resilience to this, we include a slight “dampening” to our eviction rule: we remove a sample from S only if it disagrees with the consensus at two consecutive older sites. Supplementary Figure 3 shows that this slightly more complex heuristic used in practice is reasonably robust to genotyping error.

Copying process

The Li and Stephens (LS) model³⁹ is central to many techniques in population genomics⁵⁰. Given an input haplotype with m sites and a reference panel of n haplotypes, the most likely copying path under the LS model is found using the Viterbi algorithm, which proceeds iteratively over sites. At each site, we compute the maximum likelihood that the input haplotype has copied from a particular reference haplotype given their states and the maximum likelihood values at the previous site; the particular form of the LS model allows this to be done in O(n) time. Once the last site is reached, the most likely reference haplotype at the end of the sequence is identified, then the algorithm traces back through sites, switching to other haplotypes where required. The overall time complexity is therefore O(nm) to find a copying path for an input haplotype, since we must compare with all n reference haplotypes at each of the m sites. In tsinfer the reference panel is the set of inferred ancestral haplotypes. Because there may be a different ancestor for every site, n ≈ m, hence the time complexity of finding a copying path is O(m ²). Modern sequencing data sets contain millions of variant sites, thus standard LS methods are not feasible. Moreover, in tsinfer, haplotypes can only copy from older haplotypes and the reference panel must be updated dynamically; algorithms that require a linear-time preprocessing step⁵⁰ are therefore also not feasible.

To solve this problem we use the LS model on the tree sequence directly. Each copying path generated is equivalent to a set of edges in a tree sequence²⁹, where the child is the focal haplotype and the parents are ancestors. Forwards in time (i.e. towards the present) we are therefore incrementally building a tree sequence. We use this partially built tree sequence as the substrate for computing LS copying paths for subsequent ancestors. The computational properties of the tree sequence data structure allow us to find exact copying paths far more efficiently than using standard methods.

The algorithm for computing Viterbi paths using a tree sequence works in the same way as the standard method. We proceed iteratively over sites, computing the maximum likelihood when copying from each ancestor at each site and recording the locations of potential recombination events. Once the last site is reached, trace-back proceeds as before, resolving a full copying path. The difference when using tree sequences is that we avoid needing to compute and store a likelihood for each reference haplotype by using the tree sequence to compress the associated likelihoods. Each ancestor corresponds to a node in the marginal tree at a given site, thus we compress the likelihoods by marking any node that has the same likelihood as its parent with a special value. Because the likelihood values are driven by the underlying tree structure of the data, they tend to cluster on the partially inferred trees and therefore compress well. Updating the likelihoods at a given site is then straightforward. We compute the likelihood for each node by reasoning about the state of the input haplotype and the location of the site’s mutation in the tree. Having updated the likelihoods for the nodes corresponding to the compressed subtrees, we then recompress to take into account the new likelihood values, and proceed to the next site. In many cases, moving to the next site will also involve a change in the tree topology, hence we redistribute the compressed likelihoods accordingly using logic common to other tree sequence algorithms^28,29. For simplicity, the current implementation only allows for exact haplotype matching. Under this assumption, we need only five discrete values to encode the node likelihoods in the LS Viterbi algorithm, simplifying the logic considerably. Methods to incorporate mismatch and integration with tskit are currently underway.

To validate the correctness of our implementation of the copying process, we devised a strong test, referred to as ‘perfect inference’, under which the correct tree sequence should be inferred. We begin with a simulated tree sequence with no mutations and derive the true ancestral segments from it. We then add a specific pattern of mutations that are designed to precisely identify the endpoints of each ancestor and use the resulting ancestral haplotypes as input to tsinfer. We then find copying paths for these ancestors and samples in the usual way. Using this method we are able to reproduce the input tree sequence topology perfectly, recovering every marginal tree and recombination breakpoint exactly for arbitrarily large inputs. Indeed, the numerical tables²⁹ representing the input and output tree sequences are byte-for-byte identical. Although not a formal proof, this identity holds for all tested inputs. It also strongly suggests that the key areas for further research are better ways to infer ancestral haplotypes and demarcate their endpoints.

Path compression

The algorithm for inferring ancestors discussed above is primarily based on signal arising from shared mutation events, and is only weakly informed by recombination. However, we can also derive information about ancestors from shared recombination events. If we assume that each recombination event is unique, i.e., that all samples that inherit the local haplotype resulting from a breakpoint did so from a single ancestor, we can then estimate the state of this ancestor. Note that this is equivalent to assuming an ‘infinite-sites’ like model for recombination events, an idea with a long history⁵¹. We use this signal of shared recombination breakpoints in a specific way, which we refer to as ‘path compression’.

When generating copying paths for successive ancestors, we often find that subsets of two or more paths are identical. Such identical path subsets is evidence for the existence of a single ancestor that consisted of the concatenation of the corresponding haplotype segments. We therefore add this ‘synthetic’ ancestor, and adjust the original identical path subsets to copy from the newly inserted ancestor. Ancestors corresponding to a given allele age are inserted at the same time, and path compression is run at the end of each of these time slices. Supplementary Figure 17 shows an illustrative example of this process.

Inference accuracy

To compare the accuracy of tsinfer to other inference methods we used simulation to generate known topologies. We assessed the effect of genotyping errors on inference accuracy by simulating errors on the haplotypes using an empirically determined genotyping error profile⁴⁸. We then provided the corresponding haplotypes (with and without simulated genotyping errors) to the various tools, and measured the difference between the estimated and true tree topologies using tree distance metrics. We considered four tools: tsinfer, ARGweaver, Rent+ and fastARG. ARGweaver requires several parameters to be specified: in all cases we used the known simulation values for mutation rate, recombination rate and effective population size parameters, and used the default number of timesteps for time discretisation (20) sampling 10 ARGs for each simulation (one every 20 MCMC cycles, after a burn-in period of 1000 cycles).

Although the succinct tree sequence data structure can fully represent node timing (and hence branch length) information, tsinfer does not currently attempt to infer the precise times of ancestors. Therefore, we limited our investigation of the accuracy of inference to assessing the quality of the inferred topologies using tree distance metrics. For each replicate simulation we computed the average distance between pairs of true and inferred trees along the sequence, weighted by the distance along the sequence that these trees persist. We report the average distance over replicate simulations. Metrics were calculated using the R packages treespace ⁵² and phangorn ⁵³. Some metrics (such as Robinson-Foulds) are undefined for trees that contain nonbinary nodes (“polytomies”), which indicate uncertainty in tsinfer and therefore occur frequently. We therefore also show results where tsinfer trees have been randomly resolved into fully bifurcating trees (averaged over 10 replicates). The Kendall-Colijn (KC) metric⁴⁰ provides the greatest discrimination (Supplementary Figure 4) and is well-defined for all tree topologies, hence was used exclusively in subsequent analyses. At low mutation rates, the KC metric shows a notable difference between the accuracy of tsinfer’s inferred trees before versus after random resolution of polytomies. This is because there is little information available to resolve the nodes, and generating a random binary subtree on average results in something further from the truth than the original polytomy. Thus, tsinfer’s innate strategy of using polytomies to indicate uncertainty in a principled and systematic way has a significant advantage over methods that always fully resolve trees.

To evaluate the sensitivity of tsinfer to changes in the underlying simulation model, we also tested accuracy on more complex simulations. In Supplementary Figure 6 we show results of simulations of a three population Out-of-Africa model of human demography⁵⁴. In this case, tsinfer does not seem to be affected by the underlying population structure and is a little more accurate than ARGweaver (although ARGweaver is less affected by error). In Supplementary Figure 7 we show inference accuracy on a simulated selective sweep, where we performed forward time simulations using SLiM ^55,56. In this case, once the advantageous mutation has swept to a reasonable frequency tsinfer becomes substantially more accurate than the other tools and continues to be so for many generations after fixation. In Supplementary Figure 18 we show the effect of running inference on a subset of the available haplotypes on tsinfer’s accuracy. We see that, in the absence of error, having extra samples has little effect on the accuracy of inference, but that larger samples can potentially help to correct for the presence of genotyping errors.

To evaluate the computational performance of the different inference methods we measured the total user time and maximum memory usage (taking the mean over replicates). All experiments were run on a server with two Xeon E5-2680 CPUs and 256GiB of RAM. Supplementary Figure 8 shows the CPU time required for all four tools for varying sample sizes. The disparity in the running times is too large to show on a single scale, and tsinfer and fastARG are many times faster than ARGweaver and Rent+. Supplementary Figure 9 compares tsinfer and fastARG at a much larger scale, where tsinfer shows far better scaling in terms of CPU time and memory when increasing both sequence length and sample size. Empirically, tsinfer’s running time grows approximately linearly with sample size and super-linearly with sequence length on simulated data (Supplementary Figure 9).

All code for running the evaluations, including the precise version of each tool used, is included in the accompanying GitHub repository (https://github.com/mcveanlab/treeseq-inference/).

Genealogical nearest neighbours

We use Genealogical Nearest Neighbours (GNN), a statistic based on the topological properties of trees and defined with respect to a collection of reference sets, to summarise the identity of nearest neighbours (Supplementary Figure 19). For a given tree and focal node u, GNN values are computed by traversing upwards from u until we find a target node v that has one or more descendants (not including u) present in any of the reference sets. The GNNs are then the proportions of each reference set among the descendants of v, not including u.

More formally, let R be a list of K sets of “reference nodes”, and let $C_{v,k}^t$ be the number of nodes descending from (and including) v in tree t from the set R_k, with $C_v^t={\displaystyle {\sum }_{k=1}^K{C}_{v,k}^t}.$ For a given focal node u and tree t, the GNN statistic is then defined as

$$G_{u,k}^t=\frac{C_{v,k}^t-[u\in R_k]}{C_v^t-\delta (u)}$$

where [x] is an Iversonian condition such that [x] = 0 if x is false and [x] = 1 otherwise; $\delta (u)=[u\in {\cup }_{j=1}^K{R}_j];$ and v is the first node on the path from u to root in t such that $C_v^t>\delta (u).$

The average GNN along a tree sequence 𝕋 is

$$G_{u,k}=\frac{1}{L}{\displaystyle \sum _{t\in \text{𝕋}}{L}^t{G}_{u,k}^t,}$$

where each tree t ∈ 𝕋 covers a span of L^t units of genetic sequence and L = ∑_t∈𝕋 L^t. Thus, the average GNNs are equal to the treewise GNN values weighted by each tree’s genomic span.

Note that if the reference sets do not include all leaf nodes in a tree, the sister clade to a leaf u may not contain any individuals in a reference set. In this case we will ascend to an older target node v, higher in the tree, and the GNN statistic will represent a more distant relationship.

Data visualisation

Data processing was performed using the Python data science stack including numpy ⁵⁷, pandas ⁵⁸, matplotlib ⁵⁹ and seaborn (https://doi.org/10.5281/zenodo.1313201).

Figure 5 shows patterns of genetic relatedness in UK Biobank on a map of Britain and Ireland. We grouped birth locations for individuals according to the NUTS 2018⁶⁰ classification. Reverse-geocoding of birth locations was performed for all 444,848 UKB participants with recorded birth coordinates using bng_latlon (https://pypi.org/project/bng-latlon/) and Shapely (https://pypi.org/project/Shapely/). 8315 samples, whose NUTS-2 birth locations were not found or did not tally with their reported country of birth, were removed. A different GNN matrix was computed for the NUTS-2 (Figure 5 A,B) and NUTS-3 (Figure 5 C,D,E) mappings. Maps were drawn with cartopy (http://scitools.org.uk/cartopy) using publicly available vector shape data. Shape data for NUTS areas was provided by the Office for National Statistics (https://data.gov.uk/) under the Open Government License. Shape data for the coastal outline of Ireland was downloaded from the Database of Global Administrative Areas, which is free to use for academic publishing (https://gadm.org/license.html).

Data Availability

The TGP³⁰, SGDP³¹ and UKB³² datasets used here are detailed in the relevant publications. Tree sequences inferred for all TGP (https://doi.org/10.5281/zenodo.3052359) and SGDP (https://doi.org/10.5281/zenodo.3052359) autosomes have been deposited on Zenodo. Tree sequences were compressed using the tszip utility; see the documentation at https://tzip.readthedocs.io/ for further details.

Code Availability

Tsinfer is freely available under the terms of the GNU GPL; see the documentation at https://tsinfer.readthedocs.io/ for further details. All code used to process data and run evaluations is available at https://github.com/mcveanlab/treeseq-inference.