Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Mar 19;141(14):6006–6012. doi: 10.1021/jacs.9b01204

Chiral Inversion of Thiolate-Protected Gold Nanoclusters via Core Reconstruction without Breaking a Au–S Bond

Sami Malola 1, Hannu Häkkinen 1,*
PMCID: PMC6727375  PMID: 30889350

Abstract

graphic file with name ja-2019-012048_0006.jpg

On the basis of density functional theory computations of the well-known chiral Au38(SR)24 nanocluster and its Pd- and Ag-doped derivatives, we propose here a mechanism for chiral inversion that does not require the breaking of a metal–sulfur bond at the metal–ligand interface but features a collective rotation of the gold core. The calculated energy barriers for this mechanism for Au38 and Pd-doped Au38 are in the range of 1–1.5 eV, significantly lower than barriers involving the breakage of Au–S bonds (2.5 eV). For Ag-doped Au38, barriers for both mechanisms are similar (1.3–1.5 eV). Inversion barriers for a larger chiral Au144(SR)60 are much higher (2.5−2.8 eV). Our computed barriers are in good agreement with racemization barriers estimated from existing experiments for bare and doped Au38. These results highlight the sensitivity of chiral inversion to the size, structure, and metal composition of the metal core and sensitivity to the detailed structure of the metal–thiolate interface. Our work also predicts that enantiopure Au144(SR)60 clusters would be promising materials for applications requiring high resistance to chiral inversion.

Introduction

Chirality is instrumental to many functions and processes of biomolecules, surface reactions, and organic catalysis, to name a few. In recent years, several structurally characterized metal nanoclusters protected by organic surface ligands (the so-called monolayer-protected clusters, MPCs) have been found chiral at various levels as a result of the metal core, ligand layer, or metal–ligand interface structures.1−3 The first structurally resolved members of gold-based MPCs emerged in 2007, after which the research field has been rapidly growing.1,4,5

The unique intrinsic chirality of molecules and nanoclusters is a basis for many interesting applications of sensing and catalysis utilizing the rich chiroptical properties. Challenges are usually related to achieving good enantioselectivity and resistance to racemization at elevated temperatures. Experimental work on chiral MPCs has successfully surveyed the separation of chiral enantiomers during and after synthesis,6−10 properties affecting chiral activity, and thermal stability against chiral inversion.6,11−16 One of the most extensively studied clusters in this perspective is the prolate, bi-icosahedral Au38(SR)24 and its derivatives afforded by doping or ligand exchange. For this cluster, relatively low activation barriers (0.8–1.3 eV) have been reported experimentally for the racemization that doping and ligand exchange affect.11−14 Surprisingly, the reported barriers are much too low for reactions including breaking Au–S bonds on the cluster surface,1b which would be the most obvious way to rearrange the Au–S interface structure into the opposite chirality.

Two possible mechanisms for the chiral inversion of Au38(SR)24 have been introduced previously: (i) an SN2 type of mechanism for protecting unit rearrangement and (ii) an S atom “sliding” mechanism.11 Both mechanisms require simultaneous Au–S bond breaking and formation. Despite the proposed mechanisms, the experimental observations have remained unexplained. In contradiction to Au38(SR)24, there are examples of other MPCs that are much more stable against racemization under heating, which raises unanswered questions about the uniqueness of the racemization mechanism with respect to the specific cluster type.6

In this work, we have computationally investigated detailed mechanisms and energy barriers for MPC racemization concentrating first on Au38(SR)24 and its doped derivatives. The findings for the plausible racemization mechanisms are generalized for another larger, well-known chiral MPC, Au144(SR)60. With the proposed mechanisms, we can explain experimental observations of racemization in detail and show that the racemization of MPCs is indeed unique for each individual cluster depending critically on the specific structure of the metal–ligand interface and especially on the structure of the metal core. These results will deepen our knowledge of the stability of MPCs against different structural reconstructions that can be crucial for explaining, for instance, metal atom exchange in cluster–cluster interactions or structural reconstructions during ligand exchange.17−26 Our main result is that metal–sulfur bond breaking is not needed for the full racemization of Au38(SR)24, not even as an associative SN2 type of process in which metal–sulfur bonds break and form simultaneously. The low-energy mechanism of Au38(SR)24 racemization includes only a reconstruction of the metal core, for which the activation barrier is much lower than for the studied Au–S bond-breaking reactions. Additionally, we show that in the small icosahedral MPCs Au25(SR)18 this kind of reconstruction may exist with comparably low activation energies leading to isomer structures different from the known measured structures. These rather low-energy isomers exhibit a more sterically open ligand shell allowing possible cluster–cluster interactions.

Computational Method

We used the numerical implementation of the density functional theory (DFT) in code-package GPAW.27 A real-space grid with 0.2 Å grid spacing, a PBE xc-functional,28 and 0.05 eV/Å criterion for the residual forces on atoms was used for the structural relaxation. The initial structures of Au38(SR)24, Pd2Au36(SR)24, Ag9Au29(SR)24, and Au25(SR)18– clusters were based on the experimentally reported structures and their most probable Pd/Ag doping sites.29,30 The initial structure for Au144(SR)60 was based on the theoretical prediction by Lopez-Acevedo et al.,31 which was very recently shown to be the correct one by the single-crystal X-ray structure of Jin and Wu’s group.32 Methylthiolate (SCH3) was used as a simple model ligand to reduce the computational cost for Au25, Au38, Pd2Au36, and Ag9Au29, and SH was used as the ligand for Au144. Atomic visualizations of the starting structures of Au25, Au38, and Au144 clusters are shown in Figure 1.

Figure 1.

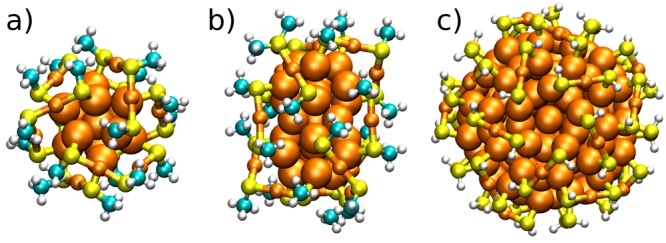
Figure 1

Open in a new tab

Atomic structures of the computational models for (a) Au25(SCH3)18–, (b) Au38(SCH3)24, and (c) Au144(SH)60. The structures in (a) and (b) are based on the respective experimental crystal structures (refs (30) and (29)a). The structure in panel c is from ref (31). Colors: H (white), C (cyan), S (yellow), and Au (orange).

Two mechanisms of chiral inversion were investigated using constrained structural relaxation. (See the schematics in Figure S1.) In the first mechanism, a number of core metal atoms were selected for rotational transformation applied around the principal symmetry axis (three atoms around C3 for Au38 and its derivatives as well as for Au25 and five atoms around C5 for Au144). The rotations were done in steps of 5 to 6°. In the second mechanism, sliding transformations of S atoms were applied linearly between the initial and final binding sites in 0.2 Å steps by keeping the minimum metal–sulfur distance equal to the initial bond distance. A constraint of fixing two atomic distances was applied for the atoms responsible of the transformations. In the case of rotational transformation, distances to two other metal core atoms were fixed for each active metal atom. For the S atom sliding transformations, distances to the initial and final metal atom binding positions were fixed for each active sulfur atom. Both of the mentioned constraints were obligatory in order to drive the system over the transition state. Further constrained relaxations were carried out (if necessary) starting from the optimized structures of the first constrained relaxation in order to increase the accuracy of the calculated energy barriers. For these follow-up relaxations carried out for Au38 and its derivatives, 3 metal atoms on both ends of the 23 atom metal core were fixed, but the rest of the atoms were free. The selected approach ensures that the nonrelevant strain accumulated in the structure gets released. In total for all systems, about 700 relaxations to a local-energy minimum were performed.

Results and Discussion

Au38 and Its Derivatives

We first investigated two different mechanisms for the racemization of Au38(SR)24, Pd2Au36(SR)24, and Ag9Au29(SR)24 clusters: S atom sliding between two adjacent Au-atom binding sites and the rotational transformation of selected metal atoms of the core. The first mechanism requires simultaneous Au–S bond breaking and formation, whereas the second is about reconstructing the metal core without Au–S bond breaking. In both cases, the rearrangement of the three long protecting units into the opposite chirality around the principal symmetry axis follows from the driven structural changes. Transformations were conducted simultaneously for all of the selected active atoms and for one end of the bi-icosahedral cluster in time. In general, transformation at one end is enough to estimate the activation energy reliably for the whole mechanism because it leads to an intermediate structure that is symmetric between the left- and right-handed enantiomers. The complete chirality inversion was modeled only for the Au38(SR)24 cluster.

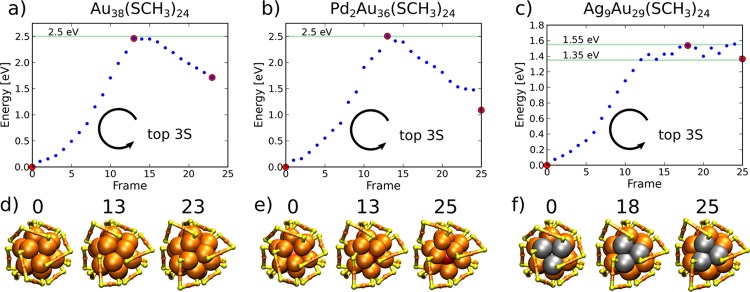
As a starting point, we modeled the previously suggested mechanism of S atom sliding between their adjacent binding sites around the principal symmetry axis.11 The rate-determining step of that mechanism is the jump in S atoms between their binding sites, which must be conducted twice at both icosahedral ends for the full chiral inversion process. Hence, to estimate if the suggested mechanism can provide an explanation of the experimentally measured results, the first jump in S atom sliding was modeled for each of the studied clusters Au38(SR)24, Pd2Au36(SR)24, and Ag9Au29(SR)24. During the mechanism, the metal core atoms’ rotation is slightly correlated with the S atom sliding, but the exchange between the binding sites remains a rate-determining step defining the transition state. This is confirmed by the energy behavior as a function of the relaxation step and the relaxed structures of the selected frames that are shown in Figure 2. (See also the animation of the mechanism in SI video 1.)

Figure 2.

Figure 2

Open in a new tab

Inversion energy profiles and selected configurations of (a, d) Au38(SCH3)24, (b, e) Pd2Au36(SCH3)24, and (c, f) Ag9Au29(SCH3)24 clusters by the sliding of three S atoms to their neighboring binding site. Three selected snapshots (frames) labeled by red dots in a–c are visualized below each panel. Only the gold–sulfur framework is shown for clarity. Arrows denote the direction of sliding of the three S atoms of the outermost core layer closest to principal symmetry axis C3 at both ends. Au, orange; S, yellow; Ag, gray; and Pd, red.

Calculated energy barriers for the S atom sliding were 2.5 eV for Au38(SR)24 and Pd2Au36(SR)24 clusters but only 1.55 eV for the Ag9Au29(SR)24 cluster. The barrier of Au38(SR)24 and Pd2Au36(SR)24 clusters is in agreement with the strength of the Au–S bond. The flexibility of Ag atom binding properties with thiolates compared to that of Au atoms explains the difference in the Ag-doped cluster. For example, metal–sulfur coordination of the silver atoms on known MPCs can vary between 2 and 4, and it is 2 for the surface Au atoms. The energy barriers of the sliding mechanism of Au38(SR)24 and Pd2Au36(SR)24 clusters are 1.2 and 1.6 eV higher, respectively, compared to experimentally measured results of 1.3 and 0.9 eV.11,14 Therefore, S atom sliding can possibly exist only during chiral inversion of the measured AgxAu38–x(SR)24 clusters, for which the experimentally measured activation energy is 0.9 eV.13 It is of interest to remark that one of the high-energy conformations at 2.5 eV shows the detachment of one of the core gold atoms out from the core surface as visualized for the Pd2Au36(SR)24 cluster in frame 13 of Figure 2b,e. This observation indicates that also other more complex mechanism affecting the conformation of the protecting units by simultaneous Au–S bond breaking and formation can be excluded.

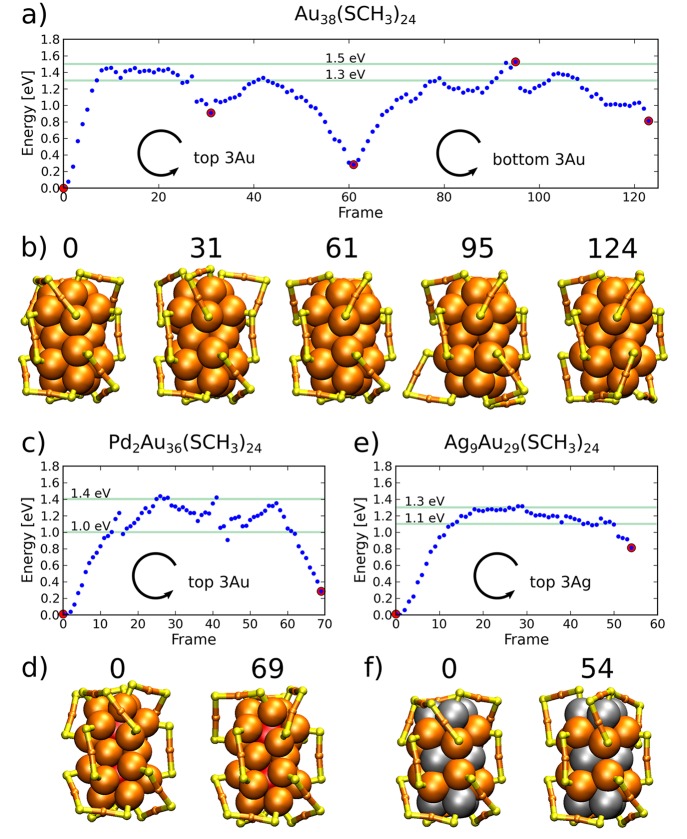
Because of the discrepancy between the calculated and experimental results, we proceeded to study other possible mechanisms. Metal clusters may transform by the rearrangement of atomic layers or changing the packing of atoms. These transformations may include, for example, the sliding of atomic layers with respect to each other. In the case of the Au38(SR)24 cluster and its doped derivatives, there exists a simple metal core transformation mechanism that leads to the full chiral inversion. By rotating the three outermost Au atoms of the metal core close to both of the poles of the principal C3 symmetry axis of the cluster, the protecting units can be rearranged automatically into the opposite handedness without any Au–S bond breaking. Thus, reconstruction of the metal core is solely responsible for the inversion.

The results for the rotational transformation mechanism of the Au core are shown in Figure 3 for Au38(SR)24, Pd2Au36(SR)24, and Ag9Au29(SR)24 clusters. (See also the animation in SI videos 2, 3, and 4.) The full chiral inversion is modeled for the Au38(SR)24 cluster, whereas only the first half of the process is modeled for the Pd2Au36(SR)24 and Ag9Au29(SR)24 clusters. Remarkably, the energy barriers for both Au38(SR)24 and Pd2Au36(SR)24 drop below 1.5 eV as compared to barriers of the S atom sliding mechanism. Considering the fluctuations in energy close to the top of the barriers, the calculated barrier heights lie in the range of 1.3–1.5 eV for Au38(SR)24, 1.0–1.4 eV for Pd2Au36(SR)24, and 1.1–1.3 eV for the Ag9Au29(SR)24 cluster.

Figure 3.

Figure 3

Open in a new tab

Inversion energy profiles and selected configurations of (a, b) Au38(SCH3)24, (c, d) Pd2Au36(SCH3)24, and (e, f) Ag9Au29(SCH3)24 clusters by rotation of the core Au and Ag atoms. Selected configurations labeled by red dots in the energy curves are visualized below each panel. Only the metal–sulfur framework is shown for clarity. Arrows denote the direction of the rotation of three Au or Ag atoms closest to the principal symmetry axis at both ends of the cluster core. Colors are the same as in Figure 2.

Detailed structural analysis of the rotational transformation mechanism reveals that the active end of the metal core transforms first from icosahedral symmetry more into FCC- or HCP-packed atomic layers resembling cuboctahedral symmetry, after which it transforms back to icosahedral symmetry when approaching the achiral intermediate conformation. The cuboctahedral arrangement is seen as a local minimum-energy structure along the reaction path as pointed out, for example, in frame 31 of Figure 3a). (See also the corresponding part of the SI video 2.) The Au2(SR)3 protecting units protruded out from the core surface during the transformation, which is also observed in the intermediate local minimum-energy structure.

The general observation based on the calculated results is that doping of the cluster with Pd or Ag atoms decreases the energy barrier of reconstructing the metal core. The result is contrary to the previous assumptions that the doping increases the stability of the cluster, especially regarding the metal core. However, our finding is in very good agreement with the experimentally measured results on racemization, which were thought to be explained by the decreased strength of Au–S bonds.11−14 Experimentally measured activation energies for Pd- and Ag-doped clusters, Pd2Au36(SR)24 and AgxAu38–x(SR)24, are reported to be around 0.9 eV with no major differences between the two systems, whereas for the Au38(SR)24 cluster the barrier is close to 1.3 eV.11−14 A similar trend can be seen in the calculated results despite the minor systematic overestimation in the energy barriers. After all, the reconstruction of the metal core by rotational transformation perfectly explains the experimental observation of rather low activation energies and effects of that by doping. Our interpretation is that the energy landscape for the isomerization of the metal core is more shallow for the doped clusters than for the pure gold MPCs. Our results indicate that the metal core reconstruction is mainly responsible for the racemization in all of the studied systems. For the Ag9Au29(SR)24 cluster, the S atom sliding type of SN2 mechanisms may also be important, which could explain the measured differences in the reaction entropy between AgxAu38–x(SR)24 and Au38(SR)24 clusters.

Chiral Inversion of Au144

The studied rotational reconstruction mechanism of the metal core can also be generalized to other chiral MPCs. For example, the Au144(SR)60 cluster was first predicted,31 and recently confirmed,32 to be chiral because of the binding and overall conformation of the short protecting RS-Au-SR units on the surface. The outermost anti-Mackay atomic layer of the three-layer icosahedral metal core and the highly symmetric Au–S interface allow a similar type of rotational transformation of the metal core as in Au38(SR)24. By rotating the five Au atoms of the outermost core layer, closest to each of the C5 symmetry axes, the chirality of the cluster becomes the inverse without any Au–S bond breaking. The results of rotational transformation of the first five atoms around one of the C5 axes are shown in Figure 4. (See also the animation in SI video 5.) The energy barrier for the mechanism is 2.8 eV, which is slightly larger than the Au–S bond strength and the energy barrier of the S atom sliding mechanism in Au38(SR)24 but much higher than the barrier of metal core transformation in Au38(SR)24. These results indicate that Au144(SR)60 is much more stable against racemization as compared to Au38(SR)24 or its doped derivatives. It also suggests that the S atom sliding mechanism may be relevant to chiral inversion of the larger clusters. This implies that the racemization mechanism and stability strongly depend on the size, core structure, and details of the metal–ligand interface.

Figure 4.

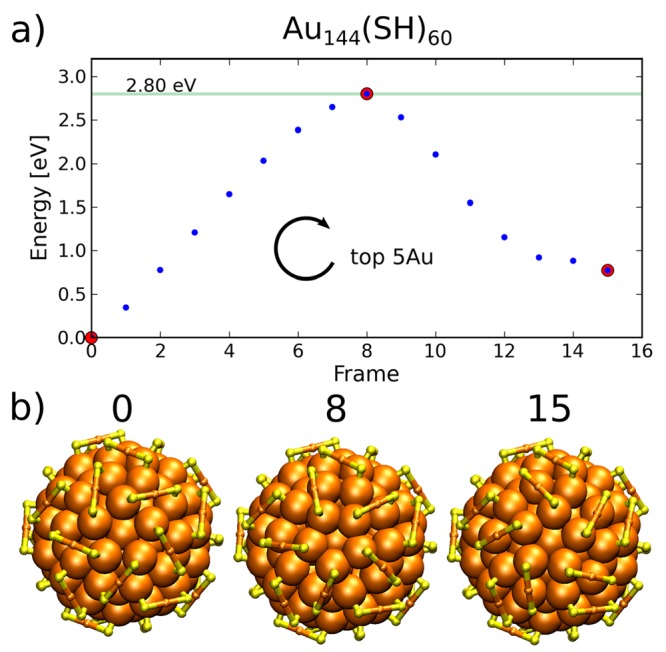
Figure 4

Open in a new tab

Inversion energy profile and selected configurations of Au144(SH)60 by rotation of the five core Au atoms closest to the C5 symmetry axis parallel to the top view direction. Behavior of the energy as a function of reaction frame is given in panel a, and selected frames are shown in panel b, corresponding to red data points in panel a. Only the gold–sulfur framework is shown for clarity. The arrow in panel a denotes the direction of the rotation.

Core Reconstruction of Au25

Finally, we broadened the idea of the metal core transformation to one more MPC, Au25(SR)18–, that also has an icosahedral core but consists of only one Au13 icosahedron instead of the face-fused bi-icosahedron of Au38(SR)24. The arrangement of the protecting units is partially analogous to the arrangement of the Au38(SR)24 cluster, and the same rotational reconstruction mechanism can be applied to one side of the Au core as in Au38(SR)24. (See the animation in SI video 6.) The calculated energy barrier of 1.30 eV for Au25(SR)18 is in line with the results for Au38(SR)24, as shown in Figure 5. This indicates that for small icosahedral MPCs the energy barrier for the Au-core reconstruction is of the same order, in general, considerably low.

Figure 5.

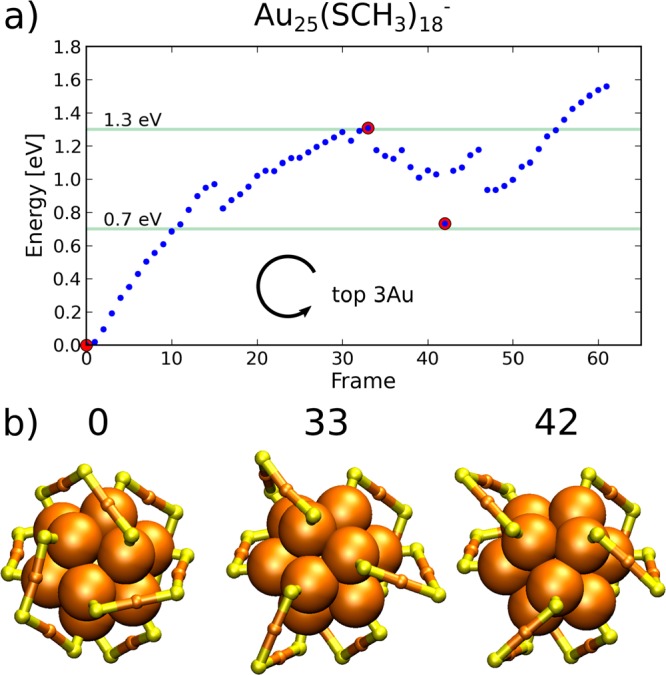
Figure 5

Open in a new tab

Transformation of [Au25(SCH3)18]− by rotation of the three core Au atoms closest to the C3 symmetry axis. (a) Energy profile and (b) selected structures corresponding to red data points in panel a. Only the gold–sulfur framework is shown for clarity. The arrow in panel a denotes the direction of the rotation.

Au25(SR)18– is not chiral, so the calculated energy barrier is not relevant to racemization. However, it is very interesting that a new local energy minimum configuration is found only 0.70 eV higher in energy as a consequence of the studied rotational reconstruction with a rather low formation barrier (frame 42 in Figure 5). Compared to the initial structure, this intermediate configuration has a more open surface structure due to three protruding long protecting units. We believe that this kind of isomeric structure could provide new insights for explaining other previously reported low-energy reactions and processes between MPCs such as the metal atom exchange that is expected to happen between the core metal atoms of two different clusters.17−22 Hence, under the same experimental conditions that racemize the Au38(SR)24 cluster, the Au25(SR)18– cluster should also be easily reconstructed by its core. These small icosahedral MPCs may be more prone to cluster–cluster interactions and atomic exchange exactly due to these special low-energy metal core reconstructions that can spatially reveal part of the surface. Interestingly, the reports on these experiments have also heavily concentrated on small icosahedral clusters such as Au25(SR)18 and Au38(SR)24 and their Ag-doped derivatives or protected silver clusters. In general, pure silver and silver-doped MPCs are more vulnerable to reconstruction as a result of the flexibility of Ag–S coordination as the results of this study have already shown. Therefore, selecting small icosahedral gold MPCs for a counterpart in cluster–cluster reactions may be the most important key behind the results because of low-energy metal core reconstructions. Our results here rationalize further why many MPCs easily undergo metal core reconstructions during ligand-exchange experiments in which the energy barriers for the metal core reconstructions are of the same order of magnitude or even remarkably lower compared to the reactions of Au–S bond breaking.24−26

Conclusions

We have studied computationally possible mechanisms for the chiral inversion of the Au38(SR)24 cluster and its Pd- and Ag-doped derivatives. The results show that the chiral inversion of the cluster can occur energy optimally without any Au–S bond breaking through a rotational reconstruction of the metal core. Furthermore, doping of the cluster core with Pd- or Ag-atoms decreases the energy barrier for the inversion. All of the calculated results match very well with the previously reported experimental results and rationalize the observations for which no explanation has been given before. The suggested metal core transformation can also be generalized for other monolayer-protected metal clusters such as Au144(SR)60 and Au25(SR)18–. In general, it is known from experiments on gold MPCs that gold–gold vibrational modes are softer than gold–sulfur modes at the metal–ligand interface,35 and we expect the collective soft core rotational modes to induce the suggested core reconstructions leading to chiral inversion. In general, the interactions in the ligand layer between the ligand molecules are distinctly weaker, which leads to a very dynamic layer even at room temperature. (See, for example, Figure 3 and accompanying animation of the simulated ligand dynamics of pMBA ligands in Au102(pMBA)44 in ref (36) and an early DFT molecular dynamics study of Au25(SH)18– in ref (37) about the gold–ligand interface dynamics.) These weaker interactions can thus be expected to adjust to core transformations, except for special cases in which bidentate ligands are used to stabilize the ligand layer.12

Our work suggests that the stability against chiral inversion is a unique property of each individual MPC depending on the metal–ligand interface and especially the metal core structure. These results are believed to be important to the development of sustainable applications using the intriguing chiroptical properties of MPCs by a better understanding of the effects of chiral stability. Our work also implies that if enantiopure samples of Au144(SR)60 clusters could be made, those materials would resist chiral inversion at elevated temperatures. This is particularly interesting in light of the recent calculation showing a very strong chiral dichroism (CD) signal from one of the enantiomers of Au144(SR)60.38 Furthermore, these results may provide new insights for explaining other interesting observations on MPCs such as cluster–cluster interactions, metal atom exchange, and cluster transformations, also seen at rather low temperatures.

Acknowledgments

We acknowledge funding from the Academy of Finland (projects 294217 and 315549 and H.H’s Academy Professorship) as well as generous CPU resources from the CSC supercomputer center in Espoo, Finland, and from the Barcelona Supercomputing Center, Spain, in PRACE project NANOMETALS.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.9b01204.

  • Schematics of S atom sliding and the core rotational mechanism for chiral inversion (PDF)

  • SI video 1: Au38(SR)24 S-atom sliding (AVI)

  • SI video 2: Au38(SR)24 core reconstruction (AVI)

  • SI video 3: Pd2Au36(SR)24 core reconstruction (AVI)

  • SI video 4: Ag9Au29(SR)24 core reconstruction (AVI)

  • SI video 5: Au144(SR)60 core reconstruction (AVI)

  • SI video 6: Au25(SR)18− core reconstruction (AVI)

The authors declare no competing financial interest.

Supplementary Material

ja9b01204_si_001.pdf (271.8KB, pdf)
ja9b01204_si_002.avi (1.2MB, avi)
ja9b01204_si_003.avi (1.5MB, avi)
ja9b01204_si_004.avi (3.3MB, avi)
ja9b01204_si_005.avi (609.5KB, avi)
ja9b01204_si_006.avi (1.5MB, avi)
ja9b01204_si_007.avi (739.8KB, avi)

References

  1. a Tsukuda T.; Häkkinen H.. Protected Metal Clusters: From Fundamentals to Applications; Elsevier: Amsterdam, 2015. [Google Scholar]; b Häkkinen H. The Gold-Sulfur Interface at the Nanoscale. Nat. Chem. 2012, 4, 443–455. 10.1038/nchem.1352. [DOI] [PubMed] [Google Scholar]; c Fernando A.; Weerawardene K. L. D. M.; Karimova N. V.; Aikens C. M. Quantum Mechanical Studies of Large Metal, Metal Oxide, and Metal Chalcogenide Nanoparticles and Clusters. Chem. Rev. 2015, 115, 6112–6216. 10.1021/cr500506r. [DOI] [PubMed] [Google Scholar]
  2. a Gautier C.; Burgi T. Chiral Gold Nanoparticles. ChemPhysChem 2009, 10, 483–492. 10.1002/cphc.200800709. [DOI] [PubMed] [Google Scholar]; b Knoppe S.; Burgi T. Chirality in Thiolate-Protected Gold Clusters. Acc. Chem. Res. 2014, 47, 1318–1326. 10.1021/ar400295d. [DOI] [PubMed] [Google Scholar]
  3. Knoppe S.Chirality in Ligand-Stabilized Metal Clusters. Encyclopedia of Interfacial Chemistry; Elsevier: Oxford, 2018; pp 406–416. [Google Scholar]
  4. Jadzinsky P. D.; Calero G.; Ackerson C. J.; Bushnell D. A.; Kornberg R. D. Structure of a Thiol Monolayer-Protected Gold Nanoparticle at 1.1 Angstrom Resolution. Science 2007, 318, 430–433. 10.1126/science.1148624. [DOI] [PubMed] [Google Scholar]
  5. Walter M.; Akola J.; Lopez-Acevedo O.; Jadzinsky P. D.; Calero G.; Ackerson C. J.; Whetten R. L.; Grönbeck H.; Häkkinen H. A Unified View of Ligand-Protected Gold Clusters as Superatom Complexes. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 9157–9162. 10.1073/pnas.0801001105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Deng G.; Malola S.; Yan J.; Han Y.; Yuan P.; Zhao C.; Yuan X.; Lin S.; Tang Z.; Teo B. K.; Häkkinen H.; Zheng N. From Symmetry Breaking to Unraveling the Origin of the Chirality of Ligated Au13Cu2 Nanoclusters. Angew. Chem., Int. Ed. 2018, 57, 3421. 10.1002/anie.201800327. [DOI] [PubMed] [Google Scholar]
  7. Yan J.; Su H.; Yang H.; Hu C.; Malola S.; Lin S.; Teo B. K.; Häkkinen H.; Zheng N. Asymmetric Synthesis of Chiral Bimetallic [Ag28Cu12(SR)24]4– Nanoclusters via Ion Pairing. J. Am. Chem. Soc. 2016, 138, 12751–12754. 10.1021/jacs.6b08100. [DOI] [PubMed] [Google Scholar]
  8. Knoppe S.; Wong O. A.; Malola S.; Häkkinen H.; Bürgi T.; Verbiest T.; Ackerson C. J. Chiral Phase Transfer and Enantioenrichment of Thiolate-Protected Au102 Clusters. J. Am. Chem. Soc. 2014, 136, 4129–4132. 10.1021/ja500809p. [DOI] [PubMed] [Google Scholar]
  9. Dolamic I.; Knoppe S.; Dass A.; Burgi T. First Enantioseparation and Circular Dichroism Spectra of Au38 Clusters Protected by Achiral Ligands. Nat. Commun. 2012, 3, 798. 10.1038/ncomms1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Yang H.; Yan J.; Wang Y.; Deng G.; Su H.; Zhao X.; Xu C.; Teo B. K.; Zheng N. From Racemic Metal Nanoparticles to Optically Pure Enantiomers in One Pot. J. Am. Chem. Soc. 2017, 139, 16113–16116. 10.1021/jacs.7b10448. [DOI] [PubMed] [Google Scholar]
  11. Knoppe S.; Dolamic I.; Burgi T. Racemization of a Chiral Nanoparticle Evidences the Flexibility of the Gold-Thiolate Interface. J. Am. Chem. Soc. 2012, 134, 13114–13120. 10.1021/ja3053865. [DOI] [PubMed] [Google Scholar]
  12. Knoppe S.; Michalet S.; Burgi T. Stabilization of Thiolate-Protected Gold Clusters Against Thermal Inversion: Diastereomeric Au38(SCH2CH2Ph)24–2x(R-BINAS)x. J. Phys. Chem. C 2013, 117, 15354–15361. 10.1021/jp4040908. [DOI] [Google Scholar]
  13. Zhang B.; Burgi T. Doping Silver Increases the Au38(SR)24 Cluster Surface Flexibility. J. Phys. Chem. C 2016, 120, 4660–4666. 10.1021/acs.jpcc.5b12690. [DOI] [Google Scholar]
  14. Barrabes N.; Zhang B.; Burgi T. Racemization of Chiral Pd2Au36(SCH2CH2Ph)24: Doping Increases the Flexibility of the Cluster Surface. J. Am. Chem. Soc. 2014, 136, 14361–14364. 10.1021/ja507189v. [DOI] [PubMed] [Google Scholar]
  15. Knoppe S.; Dolamic I.; Dass A.; Bürgi T. Separation of Enantiomers and CD Spectra of Au40(SCH2CH2Ph)24: Spectroscopic Evidence for Intrinsic Chirality. Angew. Chem., Int. Ed. 2012, 51, 7589–7591. 10.1002/anie.201202369. [DOI] [PubMed] [Google Scholar]
  16. Malola S.; Lehtovaara L.; Knoppe S.; Hu K.-J.; Palmer R. E.; Bürgi T.; Häkkinen H. Au-40(SR)(24) Cluster as a Chiral Dimer of 8-Electron Superatoms: Structure and Optical Properties. J. Am. Chem. Soc. 2012, 134, 19560–19563. 10.1021/ja309619n. [DOI] [PubMed] [Google Scholar]
  17. Krishnadas K. R.; Baksi A.; Ghosh A.; Natarajan G.; Pradeep T. Structure-Conserving Spontaneous Transformations Between Nanoparticles. Nat. Commun. 2016, 7, 13447. 10.1038/ncomms13447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Krishnadas K. R.; Baksi A.; Ghosh A.; Natarajan G.; Som A.; Pradeep T. Interparticle Reactions: An Emerging Direction in Nanomaterials Chemistry. Acc. Chem. Res. 2017, 50, 1988–1996. 10.1021/acs.accounts.7b00224. [DOI] [PubMed] [Google Scholar]
  19. Krishnadas K. R.; Ghosh A.; Baksi A.; Chakraborty I.; Natarajan G.; Pradeep T. Intercluster Reactions Between Au25(SR)18 and Ag44(SR)30. J. Am. Chem. Soc. 2016, 138, 140–148. 10.1021/jacs.5b09401. [DOI] [PubMed] [Google Scholar]
  20. Krishnadas K. R.; Ghosh D.; Ghosh A.; Natarajan G.; Pradeep T. Structure–Reactivity Correlations in Metal Atom Substitutions of Monolayer-Protected Noble Metal Alloy Clusters. J. Phys. Chem. C 2017, 121, 23224–23232. 10.1021/acs.jpcc.7b07605. [DOI] [Google Scholar]
  21. Zhang B.; Safonova O. V.; Pollitt S.; Salassa G.; Sels A.; Kazan R.; Wang Y.; Rupprechter G.; Barrabés N.; Bürgi T. On the Mechanism of Rapid Metal Exchange Between Thiolate-Protected Gold and Gold/Silver Clusters: A Time-Resolved in situ XAFS study. Phys. Chem. Chem. Phys. 2018, 20, 5312–5318. 10.1039/C7CP08272J. [DOI] [PubMed] [Google Scholar]
  22. Zhang B.; Salassa G.; Bürgi T. Silver Migration Between Au38(SC2H4Ph)24 and doped AgxAu38–x(SC2H4Ph)24 Nanoclusters. Chem. Commun. 2016, 52, 9205–9207. 10.1039/C6CC04469G. [DOI] [PubMed] [Google Scholar]
  23. Salassa G.; Sels A.; Mancin F.; Bürgi T. Dynamic Nature of Thiolate Monolayer in Au25(SR)18 Nanoclusters. ACS Nano 2017, 11, 12609–12614. 10.1021/acsnano.7b06999. [DOI] [PubMed] [Google Scholar]
  24. Zeng C.; Liu C.; Pei Y.; Jin R. Thiol Ligand-Induced Transformation of Au38(SC2H4Ph)24 to Au36(SPh-t-Bu)24. ACS Nano 2013, 7, 6138–6145. 10.1021/nn401971g. [DOI] [PubMed] [Google Scholar]
  25. Nimmala P. R.; Theivendran S.; Barcaro G.; Sementa L.; Kumara C.; Jupally V. R.; Apra E.; Stener M.; Fortunelli A.; Dass A. Transformation of Au144(SCH2CH2Ph)60 to Au133(SPh-tBu)52 Nanomolecules: Theoretical and Experimental Study. J. Phys. Chem. Lett. 2015, 6, 2134–2139. 10.1021/acs.jpclett.5b00780. [DOI] [PubMed] [Google Scholar]
  26. Dass A.; Theivendran S.; Nimmala P. R.; Kumara C.; Jupally V. R.; Fortunelli A.; Sementa L.; Barcaro G.; Zuo X.; Noll G. Au133(SPh-tBu)52 Nanomolecules: X-ray Crystallography, Optical, Electrochemical, and Theoretical Analysis. J. Am. Chem. Soc. 2015, 137, 4610–4613. 10.1021/ja513152h. [DOI] [PubMed] [Google Scholar]
  27. Enkovaara J.; Rostgaard C.; Mortensen J. J.; Chen J.; Dulak M.; Ferrighi L.; Gavnholt J.; Glinsvad C.; Haikola V.; Hansen H. A.; Kristoffersen H. H.; Kuisma M.; Larsen A. H.; Lehtovaara L.; Ljungberg M.; Lopez-Acevedo O.; Moses P. G.; Ojanen J.; Olsen T.; Petzold V.; Romero N. A.; Stausholm J.; Strange M.; Tritsaris G. A.; Vanin M.; Walter M.; Hammer B.; Häkkinen H.; Madsen G. K. H.; Nieminen R. M.; Norskov J. K.; Puska M.; Rantala T. T.; Schiotz J.; Thygesen K. S.; Jacobsen K. W. Electronic Structure Calculations with GPAW: A Real-Space Implementation of the Projector Augmented-Wave Method. J. Phys.: Condens. Matter 2010, 22, 253202. 10.1088/0953-8984/22/25/253202. [DOI] [PubMed] [Google Scholar]
  28. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  29. a Qian H.; Eckenhoff W. T.; Zhu Y.; Pintauer T.; Jin R. Total Structure Determination of Thiolate-Protected Au38 Nanoparticles. J. Am. Chem. Soc. 2010, 132, 8280–8281. 10.1021/ja103592z. [DOI] [PubMed] [Google Scholar]; b Zhang B.; Kaziz S.; Li H.; Wodka D.; Malola M.; Safonova O.; Nachtegaal M.; Mazet C.; Dolamic I.; Llorca J.; Kalenius E.; Daku L. M. L.; Häkkinen H.; Bürgi T.; Barrabés N. Pd2Au36(SR)24 Cluster: Structure Studies. Nanoscale 2015, 7, 17012–17019. 10.1039/C5NR04324G. [DOI] [PubMed] [Google Scholar]; c Kumara C.; Gagnon K. J.; Dass A. X-ray Crystal Structure of Au38–xAgx(SCH2CH2Ph)24 Alloy Nanomolecules. J. Phys. Chem. Lett. 2015, 6, 1223–1228. 10.1021/acs.jpclett.5b00270. [DOI] [PubMed] [Google Scholar]
  30. a Heaven M. W.; Dass A.; White P. S.; Holt K. M.; Murray R. W. Crystal Structure of the Gold Nanoparticle [N(C8H17)4][Au25(SCH2CH2Ph)18]. J. Am. Chem. Soc. 2008, 130, 3754–3755. 10.1021/ja800561b. [DOI] [PubMed] [Google Scholar]; b Zhu M.; Aikens C. M.; Hollander F. J.; Schatz G. C.; Jin R. Correlating the Crystal Structure of A Thiol-Protected Au25 Cluster and Optical Properties. J. Am. Chem. Soc. 2008, 130, 5883–5885. 10.1021/ja801173r. [DOI] [PubMed] [Google Scholar]
  31. Lopez-Acevedo O.; Akola J.; Whetten R. L.; Grönbeck H.; Häkkinen H. Structure and Bonding in the Ubiquitous Icosahedral Metallic Gold Cluster Au144(SR)60. J. Phys. Chem. C 2009, 113, 5035–5038. 10.1021/jp8115098. [DOI] [Google Scholar]
  32. Yan N.; Xia X.; Liao L.; Zhu M.; Jin M.; Jin R.; Wu Z. Unravelling the Long-Pursued Au144 Structure by X-ray Crystallography. Sci. Adv. 2018, 4, eaat7259. 10.1126/sciadv.aat7259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Yamazoe S.; Takano S.; Kurashige W.; Yokoyama T.; Nitta K.; Negishi Y.; Tsukuda T. Hierarchy of Bond Stiffnesses within Icosahedral-Based Gold Clusters Protected by Thiolates. Nat. Commun. 2016, 7, 10414–10414. 10.1038/ncomms10414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Salorinne K.; Malola S.; Wong O. A.; Rithner C. D.; Chen X.; Ackerson C. J.; Häkkinen H. Conformation and Dynamics of the Ligand Shell of a Water-Soluble Au102 Nanoparticle. Nat. Commun. 2016, 7, 10401. 10.1038/ncomms10401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mäkinen V.; Häkkinen H. Density Functional Theory Molecular Dynamics Study of the Au25(SH)18– Cluster. Eur. Phys. J. D 2012, 66, 310. 10.1140/epjd/e2012-30485-5. [DOI] [Google Scholar]
  36. Malola S.; Kaappa S.; Häkkinen H.. From Molecular to Metallic Gold Nanoparticles: The Role of Nanocrystal Symmetry in the Crossover Region. Preprint (2018) at https://arxiv.org/abs/1809.04411.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja9b01204_si_001.pdf (271.8KB, pdf)
ja9b01204_si_002.avi (1.2MB, avi)
ja9b01204_si_003.avi (1.5MB, avi)
ja9b01204_si_004.avi (3.3MB, avi)
ja9b01204_si_005.avi (609.5KB, avi)
ja9b01204_si_006.avi (1.5MB, avi)
ja9b01204_si_007.avi (739.8KB, avi)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES