Unraveling the Arrangement of Al and Fe within the Framework Explains the Magnetism of Mixed-Metal MIL-100(Al,Fe)

Abstract

Properties of mixed-metal MOFs depend on the distribution of different metals within their frameworks. Determination of this distribution is often very challenging. Using an example of aluminum- and iron-containing MIL-100, we demonstrate that ²⁷Al NMR spectroscopy, when combined with first-principles calculations and magnetic, X-band electron paramagnetic resonance, Fe K-edge extended X-ray absorption fine structure, and Mössbauer measurements, enables one to accurately determine the arrangement of Al and Fe within the metal trimers, which are the basic building units of MIL-100. In this particular material, the incorporation of Fe and Al on the framework metal sites is random. Crucial for deciphering the arrangement is detecting NMR signals, shifted because of the strong hyperfine interaction between the ²⁷Al nuclei and the unpaired electronic spins of Fe³⁺ ions, assigning the shifted signals aided by first-principles calculations of hyperfine couplings, and quantitatively evaluating the NMR intensities and the measured effective magnetic moment.

Metal–organic framework materials (MOFs), composed of metal-oxo vertices and organic linkers, exhibit immense structural and physicochemical variety. The main properties and topologies of these materials are determined by the coordination preferences of the metal ions and by the nature of the linkers included in the frameworks. In addition, the MOF’s properties can be fine-tuned by preparing mixed-linker and mixed-metal MOFs, which comprise the linkers or metal centers of two or more different types.¹⁻⁵ As has been shown recently, mixed-metal MOFs can exhibit very interesting magnetic, optical, and catalytic properties.⁶⁻⁹

Although syntheses of mixed-metal MOFs are becoming quite successful, characterizing the arrangement of different metal ions within the frameworks is still very challenging.¹⁰ Because ions of different metals in a mixed-metal MOF typically occupy crystallographically equivalent positions, diffraction techniques are able to provide only limited insight into the distribution of the metals within the framework. Spectroscopic methods that rely on local probes tend to be more informative. In the case of MOFs that comprises iron as one of the metals, Mössbauer, electron paramagnetic resonance (EPR), and Fe K-edge X-ray absorption near-edge structure (XANES), and extended X-ray absorption fine structure (EXAFS) spectroscopies have been employed thus far.⁸ EPR is particularly insightful, as it is able to distinguish the signal of isolated Fe³⁺ ions from the signal of iron dimers or clusters. In this work, we show that quickly accessible and easily readable information about the arrangement of Fe³⁺ and Al³⁺ ions is also offered by NMR spectroscopy. Complemented by first-principles calculations, EPR and EXAFS spectroscopy, and magnetometry, NMR spectroscopy also enables one to understand the complex magnetism within mixed-metal MIL-100(Al,Fe).

MIL-100 is composed of trimers of metal-oxo octahedra, which through benzene-1,3,5-tricarboxylate (BTC) anions are linked into a porous framework with MTN topology (Scheme 1).¹¹ MIL-100 materials have been prepared with Cr, Fe, Al, and Sc metal centers. Iron-based MIL-100 exhibits a very large capacity for adsorption of water and CO₂ and possesses a significant number of accessible Lewis acid sites.^12,13 These important properties of this material might be additionally fine-tuned by the controlled synthesis of mixed-metal MIL-100. In this work, we prepared mixed-metal MIL-100(Al,Fe) with empirical formula Al_1.3Fe_1.7O(OH)(H₂O)₂[BTC]₂·nH₂O and two reference single-metal counterparts, MIL-100(Al) and MIL-100(Fe). For deciphering the distribution of Al and Fe, we used complementary NMR, Fe K-edge XANES and EXAFS, Mössbauer, and EPR spectroscopies. These spectroscopies are sensitive to the local environment of the selected probe nuclei or ions and thus should be able to elucidate the nature of the trimers present within MIL-100(Al,Fe). In principle, within this mixed-metal material one can expect to find four basic types of metal-oxo trimers, which can, according to their composition, be denoted as 3Fe, 2Fe1Al, 1Fe2Al, and 3Al trimers. Fe K-edge XANES and EXAFS, Mössbauer, and EPR spectroscopies can detect and inspect the first three types, whereas ²⁷Al NMR can detect the last three types of trimers.

Scheme 1. Structure of Single-Metal MIL-100.

(A) Schematic presentation of the MTN framework, composed of vertex-sharing tetrahedra, and (B) unit cell of MIL-100. The framework is composed of super-tetrahedra, in which metal-oxo trimers are connected to one another through the BTC linkers (C).

Fe K-edge XANES and EXAFS, Mössbauer, and X-band EPR spectra of MIL-100(Al,Fe) and MIL-100(Fe) are shown in Figure 1. K-edge positions in the Fe XANES spectra clearly show that the single- and mixed-metal materials comprise only Fe³⁺ ions. Fe K-edge EXFAS measurements indicate that in the average metal-oxo trimer of MIL-100(Al,Fe), two Fe cations and one Al cation are positioned in the vertexes of an isosceles triangle with two shorter sides and one longer side (for details, see Table S1 in the Supporting Information). This result, which agrees well with the stoichiometry of MIL-100(Al,Fe) (Al_1.3Fe_1.7O(OH)(H₂O)₂[BTC]₂), suggests that the sample is neither a simple mixture of single-metal MIL-100(Al) and MIL-100(Fe) crystals nor a composite of large Fe-rich and Al-rich domains but instead could be a homogeneous mixture of 3Fe, 2Fe1Al, 1Fe2Al, and 3Al trimers.

Figure 1.

(A) Fe K-edge XANES spectra of MIL-100(Fe) and MIL-100(Al,Fe) samples and reference iron oxide compounds with iron valence states between Fe²⁺ and Fe³⁺ [Fe²⁺: FeSO₄·7H₂O; Fe^2.67+: Fe₃O₄; Fe³⁺: Fe₂O₃ (hematite), α-FeOOH (goethite)]. The spectra are shifted vertically for clarity. The vertical dashed line is plotted at the Fe K-edge position of 7125 eV to facilitate the comparison of the Fe K-edge energy positions in different Fe compounds. (B) Fourier transform magnitude of k³-weighted Fe EXAFS spectra of MIL-100(Fe) and MIL-100(Al,Fe) samples, calculated in the k range of 3–14 Å^–1. Experiment, circles; best-fit EXAFS models in the R range from 1.0–3.3 Å, solid lines. (C) Fe Mössbauer spectra of MIL-100(Fe) and MIL-100(Al,Fe) can be modeled well by at least three contributions. Three equally intense individual components, comprising the fit of the spectrum of MIL-100(Fe), are shown. The three components can be assigned to three crystallographically slightly different Fe sites within the 3Fe trimers. (D) X-band EPR spectra of MIL-100(Fe) (red bullets) and MIL-100(Al,Fe) (blue circles) recorded at 295 and 30 K. The thin black lines are the fits of the spectra (see the Supporting Information). The positions of the resonances with g = 2.09 and g = 4.3 are marked with vertical lines. The narrow signal indicated by a star is due to the dielectric resonator. The spectra are vertically shifted for clarity.

The Mössbauer spectrum (Figure 1C) confirms that iron within both iron-containing samples is octahedrally coordinated and that its oxidation state is the anticipated 3+. Spectra of both samples exhibit very similar doublets and no components exhibiting a magnetic hyperfine structure. It was shown in the literature that the isomer shift and quadrupole splitting for iron within a 3Fe trimer of MIL-100(Fe) differ considerably for an Fe³⁺ ion bonded to F^– or OH^– and an Fe³⁺ ion coordinated with a water molecule.¹⁴ If various neighbors in the first coordination sphere of iron are combined with various trimers within the mixed-metal sample (3Fe, 2Fe1Al, and 1Fe2Al), then the number of relevant models and the number of free parameters quickly become too large to allow one to obtain reliable information about the abundance of the different trimers from the Mössbauer spectra.

X-band EPR measurements on MIL-100(Al,Fe) suggest that the sample comprises magnetically coupled Fe dimers and/or trimers, as well as isolated octahedrally coordinated Fe³⁺ ions. Thus, the spectra demonstrate that in addition to 3Fe and/or 2Fe1Al units, 1Fe2Al units are present in this material. More specifically, the spectrum of MIL-100(Al,Fe) recorded at room temperature is dominated by broad resonance at g = 2.09 but also hints at the presence of another, much weaker component that peaks at around g_eff = 4.3 (Figure 1D). This latter signal becomes much more pronounced in the low-temperature spectrum, whereas the main broad component at g ≈ 2 at low temperatures broadens, shifts to slightly higher g-factor values, and loses its intensity. The room-temperature spectrum of MIL-100(Fe) similarly shows the dominance of the broad g = 2.09 line but exhibits an almost negligible component with g_eff = 4.3. EPR spectra of MIL-100(Al,Fe) resemble the spectrum of MIL-53(Al,Fe) in which the g_eff = 4.3 signal is assigned to isolated Fe³⁺ ions in the high-spin S = 5/2 state, and the broad g ≈ 2 signal is attributed to magnetically coupled dimers or polymers of Fe³⁺ ions.⁸ Such assignment is also fully corroborated by the data fitting where we assumed two EPR active species (for details, see the Supporting Information). The apparent decrease in the relative intensity of the g ≈ 2 signal with decreasing temperature suggests that the Fe³⁺ ions within the 3Fe and 2Fe1Al trimers are antiferromagnetically coupled.

In principle, ²⁷Al NMR spectroscopy can detect contributions of mixed 1Fe2Al and 2Fe1Al trimers, as well as of single-metal 3Al trimers, and thus is expected to complement the three other spectroscopic techniques. As shown in Figure 2, ²⁷Al NMR spectroscopy offers convincing and easily readable information. In contrast to a single narrow signal within the spectrum of MIL-100(Al), the spectra of MIL-100(Al,Fe) recorded in the temperature range between 263 and 358 K exhibit two strong contributions, one resonating between −150 and 250 ppm and one extending between 400 and 1100 ppm. The first one, although five times broader than the signal of the diamagnetic MIL-100(Al), has a peak maximum close to 0 ppm and is tentatively assigned to the 6-coordinated Al nuclei within the 3Al trimers. The second, substantially broader, contribution might be ascribed to nuclei within the 1Fe2Al and/or 2Fe1Al trimers. In fact (vide infra), a more correct statement is that the former contribution probably belongs to the Al nuclei within the trimers with a total spin of zero, whereas the latter belongs to Al nuclei within the trimers with a total spin different from zero. The conclusion that the broad peak between 400 and 1100 ppm belongs to Al nuclei, significantly affected by unpaired electronic spins, is nicely supported by its temperature-dependent resonance frequency.

Figure 2.

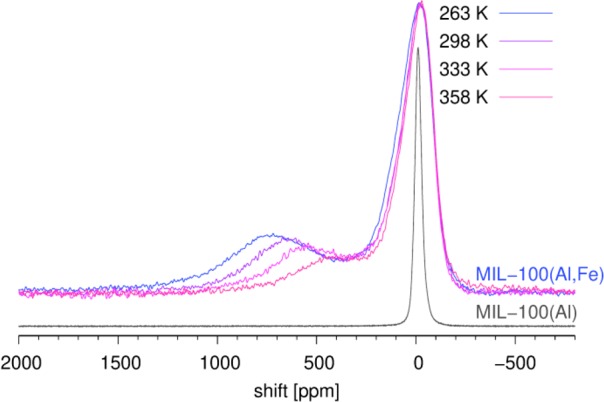
Static ²⁷Al NMR spectra of MIL-100(Al,Fe) (recorded in the temperature range between 263 and 358 K) and MIL-100(Al) (recorded at 298 K). They are scaled vertically so that the highest peaks close to 0 ppm are equally high in all the spectra.

NMR spectroscopy is a quantitative technique: The peak intensity is proportional to the number of nuclei contributing to the peak. To obtain insight into the abundance of different types of trimers within MIL-100(Al,Fe) based on its ²⁷Al NMR spectrum, we need reliable assignment of the different peaks in this spectrum. In other words, we need to answer the question whether the signal extending between 400 and 1100 ppm belongs to 1Fe2Al, to 2Fe/1Al, or to both. A possible method for obtaining this answer is via first-principles calculations of the isotropic shifts for each type of the trimer. Researchers, mostly intrigued by the NMR spectra of various battery materials, have started to tackle the prediction of isotropic shifts induced by paramagnetic centers only recently. Therefore, a relatively small number of successfully calculated paramagnetic shifts of ^6,7Li, ²⁹Si, ³¹P, and ⁵¹V nuclei exist, which were carried out using different approaches with different levels of accuracy.¹⁵ In addition, only very recently was the first example of a calculation of ¹H and ¹³C paramagnetic shifts within the Cr-MIL-101 metal–organic framework demonstrated.¹⁶ In the mixed-metal MIL-100(Al,Fe), the calculations are expected to be more demanding because of the presence of various Al/Fe arrangements within the metal-oxo trimers.

Generally, calculating the isotropic shift for nuclei that are close to paramagnetic centers requires calculating the orbital contribution, hyperfine coupling constant, electronic g-tensor, and dipolar tensor (the last one describes the through-space dipolar couplings between the nuclear spins and the spins of the unpaired electrons; for a more complete discussion, see refs (16−18)). In the case of MIL-100(Al,Fe), we can consider some simplifications. First, the orbital contribution to the isotropic shift of the Al nuclei within the mixed-metal trimers will be very similar to the orbital shift of the Al nuclei within the 3Al trimers and within the purely diamagnetic sample of MIL-100(Al). Therefore, there is no need to calculate it. Second, as was recently shown, materials with Fe³⁺ centers typically exhibit no anisotropy of the g-tensor;¹⁸ thus, we can also skip the calculation of this tensor (our successful simulation of X-band EPR data with the isotropic g-tensor confirms that Fe³⁺ centers with S = 5/2 are L = 0 centers). Third, if the g-tensor is isotropic, then the isotropic contributions that depend on the dipolar tensor also vanish. Thus, for the ²⁷Al nuclei of MIL-100(Al,Fe), predicting the isotropic paramagnetic shifts involves only first-principles calculation of the hyperfine coupling constants. Because far-reaching dipolar couplings do not contribute to the isotropic shifts, we can even avoid expensive calculations on the entire crystallographic unit cell with periodic boundary conditions and can limit the present study to calculations on relatively small clusters of atoms around selected ²⁷Al nuclei.

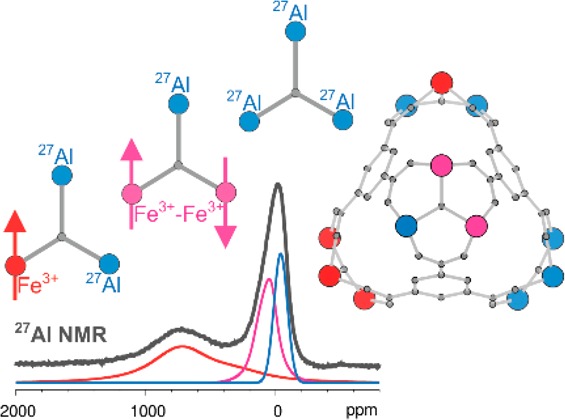
Scheme 2 shows the model clusters for which ground-state energies, spin densities, and hyperfine-coupling constants were calculated. The calculations are carried out within the frame of density functional theory, using a hybrid PBE0 exchange–correlation functional (incorporating 25% Hartree–Fock exchange) and a flexible def2-QZVPP basis set; for more details about the calculations, see the Supporting Information. As summarized in Table 1, the hyperfine coupling constants on the ²⁷Al nuclei, calculated in the 2Fe1Al and 1Fe2Al trimers, are similar. More than by the number of neighboring Fe³⁺ ions, hyperfine coupling constants are affected by the presence of either OH^– or H₂O within the first coordination sphere of Al. This is understandable; a bond with an electronegative OH^– affects the electron and spin density on Al quite differently from a coordination bond with a neutral (although polar) water molecule.

Scheme 2. Clusters of Atoms for Which Ground-State Energies, Spin Densities, and Hyperfine Coupling Constants Were Calculated.

Clusters represent simplified models of the 3Fe, 2Fe1Al, 1Fe2Al, and 3Al trimers that are expected to be found in MIL-100(Al,Fe). (Fe, orange; Al, blue; O, red; C, brown; H, white; for better distinction between the coordinated H₂O molecules and bonded OH^– groups, oxygen atoms of the latter are presented in violet).

Table 1. Hyperfine Coupling Constants A_HF Calculated within the DFT Frame for Simple 2Fe1Al and 1Fe2Al Model Clusters.

type of trimer	2Fe1Al	2Fe1Al	1Fe2Al	1Fe2Al
Al environment	Al–H2O	Al–OH	Al–H2O, Al–H2O	Al–H2O, Al–OH
AHF [MHz]	2.0	0.9	1.6, 1.7	1.8 (1.7), 0.9 (1.2)a

^aValues in parentheses list the hyperfine coupling constants calculated for an extended 1Fe2Al cluster, in which the terminating methyl groups of the simple model cluster are replaced by phenyl groups, better resembling the BTC linkers of MIL-100.

Practical calculations of paramagnetic shifts are carried out with a ferromagnetic arrangement of the electronic spins. In this arrangement, all the unpaired spins are collinear as the time-averaged spins within the paramagnetic phase are expected to be, on average, such that the spins point in the direction opposite from the direction of the magnetic field. The paramagnetic shift is given by the following expression:

1

in which the hyperfine coupling constant, A_HF, obtained with the DFT calculations, is multiplied by a factor, which scales the hyperfine coupling of the ferromagnetic state at 0 K to the residual coupling within a paramagnetic phase at a finite temperature. In eq 1, χ(T) is the volume magnetic susceptibility, N the number of paramagnetic centers per unit volume, g the electron g-factor, μ_B the Bohr magneton, and γ_n the nuclear gyromagnetic ratio for ²⁷Al nuclei. We measured the magnetic susceptibility of MIL-100(Al,Fe) (and of MIL-100(Fe) for comparison) with a superconducting quantum interference device (SQUID). As suggested by the EPR analysis, the magnetic susceptibility of the two samples is apparently the sum of several contributions, and even at the relatively high temperature of 300 K, neither MIL-100(Al,Fe) nor MIL-100(Fe) can be described as a paramagnetic phase comprising only independent paramagnetic Fe³⁺ centers (Figure 3). In other words, the temperature dependence of magnetic susceptibility does not follow the Curie or Curie–Weiss expression and confirms that a significant intramolecular antiferromagnetic coupling is present between Fe³⁺ ions sharing the same trimers. Additional DFT calculations show that the energy of the 2Fe1Al trimer with an antiparallel arrangement of the spins of the two Fe³⁺ centers is by 150 meV (3 meV/atom) lower than the energy of the same trimer with parallel alignment of the two spins, and that exchange coupling constant, J, can be estimated to be −6 meV (−50 cm^–1). Thus, it is not surprising that significant antiferromagnetic coupling is felt among the spins within the 2Fe1Al (and 3Fe) trimers even at 300 K.

Figure 3.

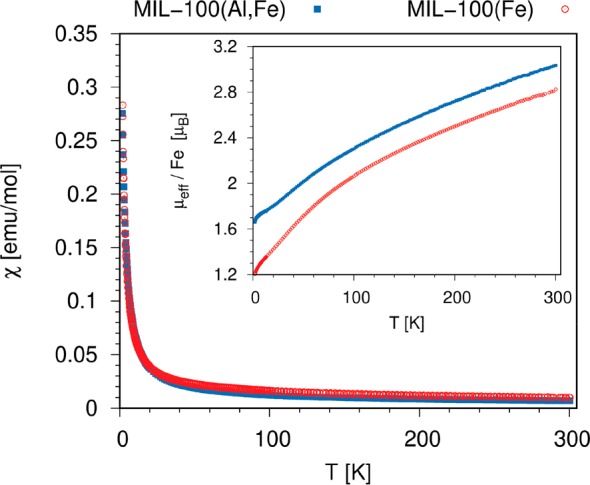
Magnetic susceptibility of MIL-100(Fe) and MIL-100(Al,Fe) and comparison of average effective magnetic moments (inset) as functions of temperature. The values of the average magnetic moments below 5.9 μ_B and their strong temperature dependence show that significant spin-coupling among Fe³⁺ ions is present in both materials throughout the examined temperature range.

According to the discussion above, the magnetic susceptibility of MIL-100(Al,Fe) can be described as the sum of at least three contributions: a contribution of antiferromagnetically coupled Fe³⁺ spins of the 3Fe trimer, a contribution of antiferromagnetically coupled Fe³⁺ spins of the 2Fe1Al trimers, and a contribution of the isolated paramagnetic centers of the 1Fe2Al trimers. The measurement actually shows one more contribution: a relatively strong temperature-independent paramagnetic (TIP) contribution. Non-negligible exchange coupling among the Fe³⁺ centers makes the prediction of isotropic shifts due to hyperfine interaction between electronic and nuclear spins in MIL-100(Al,Fe) difficult. Because NMR is a spectroscopic technique sensitive to the local environment, the calculation of the isotropic shift should take into account local susceptibility or local effective magnetic moments rather than the bulk quantities. If we assume that the Fe³⁺ ions within the 1Fe2Al trimers behave as independent paramagnetic centers, then the isotropic shift of the ²⁷Al nuclei for such trimers can be calculated by inserting

2

into eq 1. In the Curie relation above, the effective magnetic moment per isolated Fe³⁺ site μ_eff = 5.9 μ_B; k is the Boltzmann’s constant, and T is the temperature of the sample. The 200–430 ppm shifts (calculated at 263 K for A_HF ranging between 0.9 and 2.0 MHz) compare moderately well with the measured peak position of 650 ppm. The discrepancy between the calculated and measured isotropic shifts could partly be due to the inherent limited accuracy of the selected DFT approach and basis set, and partly due to the difference between the simplified structural models and the true structure of the powdered material.

Although excellent agreement between the calculated and observed isotropic shifts is not achieved, the results of the spectroscopic measurements and calculations allow us to conclude that the ²⁷Al NMR signal with the largest isotropic shift should be assigned to the aluminum within the 1Fe2Al trimers. It is also clear that the aluminum from the 3Al trimers will resonate close to 0 ppm. Thus, we need to find out only where the ²⁷Al NMR signal of the 2Fe1Al trimers appears. Neglecting the possible weak coupling of Fe³⁺ spins with the spins from the neighboring trimers, the susceptibility of the antiferromagnetically coupled pairs of spins 5/2 can be expressed as¹⁹

3

By inserting the value of J, as calculated with DFT, into eq 3, we can compare the predicted susceptibility of the Fe³⁺ pairs to the susceptibility of the isolated Fe³⁺ centers. We can see that in the temperature range between 260 and 360 K the former is 2–3 times smaller than the latter and that the former has much less pronounced temperature dependence (Figure S6). Thus, we can expect that the ²⁷Al NMR signal of aluminum from the 2Fe1Al trimers is significantly less shifted than that from the 1Fe2Al trimers and that this shift is much less temperature-dependent.

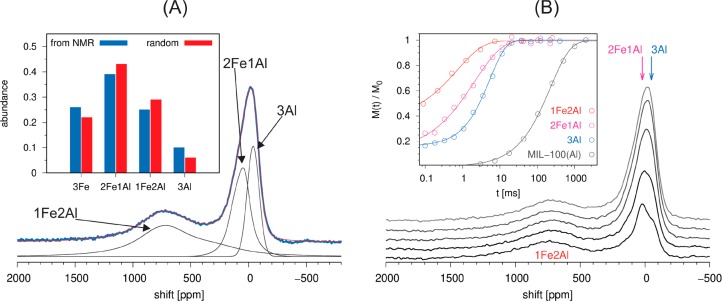
Closer inspection of the ²⁷Al NMR spectrum (Figure 4A), recorded at 263 K (the best resolved spectrum in the series), shows that neither the signal extending between 400 and 1100 ppm nor the signal resonating between −150 and 250 ppm is symmetric. For the broad paramagnetically shifted signal, this result is expected: The through-space dipolar coupling between the ²⁷Al nuclei and the unpaired electrons of the Fe³⁺ ion should lead to signal broadening which resembles broadening due to chemical shielding anisotropy (CSA). For the signal of the 3Al trimers, anisotropy is not necessarily expected. The nearest unpaired electrons are already quite distant from these aluminum nuclei, and they broaden the NMR signal mainly through accelerated relaxation. Although the ²⁷Al nuclei are quadrupolar, the spectrum of the diamagnetic MIL-100(Al) shows that the quadrupolar broadening of the ²⁷Al central transition is negligible compared to the broadening induced by the unpaired electrons. Thus, the asymmetry of the signal between −150 and 250 ppm suggests that this signal might be composed of more than one contribution; in other words, the signal could be composed of the contribution of the 3Al trimers and the contribution of the 2Fe1Al trimers. This hypothesis is strongly supported by the spin–lattice relaxation time measurements, which show that the ²⁷Al NMR spectrum is composed of at least three contributions and that these contributions have significantly different spin–lattice relaxation times (1Fe2Al, T₁ = 0.7 ms; 2Fe1Al, T₁ = 2.1 ms; 3Al, T₁ = 5.4 ms; see Figure 4B).

Figure 4.

(A) Decomposition of the ²⁷Al NMR spectrum of MIL-100(Al,Fe) into three contributions, presumably belonging to the 2Fe1Al, 1Fe2Al, and 3Al trimers. From the intensities of these contributions, the abundancies of individual trimers within MIL-100(Al,Fe) can be determined. In the inset, these abundancies are compared with those expected for the random incorporation of Fe and Al into the trimers. (B) ²⁷Al spin–lattice relaxation time analysis of MIL-100(Al,Fe). The spectra recorded with different relaxation delays clearly indicate that the contribution resonating between −150 and 250 ppm is composed of at least two signals. The inset shows that the three partly resolved signals have significantly different spin–lattice relaxation rates, all substantially higher than the relaxation rate of the diamagnetic MIL-100(Al).

Decomposition of the ²⁷Al NMR spectrum of MIL-100(Al,Fe) into three contributions, two of them described by CSA-like signals and one by a Gaussian signal, yields relative intensities of 0.46 (1Fe2Al), 0.30 (2Fe1Al), and 0.24 (3Al). Because of the significant overlap between the signals, the extracted relative intensities are not very reliable. Nevertheless, we used them to estimate the abundancies of four different types of trimers. These estimated abundancies match quite well the predicted probabilities of finding the different trimers (Figure 4A), as calculated by assuming that aluminum and iron are randomly incorporated in the trimers. This result is interesting and gives credence to the decomposition of the spectrum. The results of the decomposition are further confirmed when the abundancies of the 3Fe, 2Fe1Al, and 1Fe2Al trimers are used to predict the average effective magnetic moment of bulk MIL-100(Al,Fe). We may assume that at a sufficiently low temperature the effective magnetic moment per one Fe³⁺ ion is 5.9 μ_B in the 1Fe2Al trimers, zero in the 2Fe1Al trimers, and 5.9/3 μ_B in the 3Fe trimers. With such an assumption and with the abundancies obtained from the decomposition of the NMR spectrum, we get that 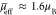, which is close to the experimental value (Figure 3B) at the lowest temperature of 2 K.

In conclusion, ²⁷Al NMR spectroscopy, X-band EPR spectroscopy, and magnetometry, supported by the first-principles calculations of hyperfine and spin-exchange interactions and by Fe K-edge EXAFS and Mössbauer spectroscopy, explain the magnetism of mixed-metal MIL-100(Al,Fe). These methods provide evidence that the framework of this material is composed of 3Fe, 2Fe1Al, 1Fe2Al, and 3Al trimers and that aluminum and iron randomly occupy the metal sites within the trimers. The results also suggest that NMR can, even more generally, offer relatively easily accessible and very informative insight into the distribution of different metals within mixed-metal materials. Crucial for a successful analysis is the ability to detect the NMR signals of the nuclei, which are strongly affected by their interaction with unpaired electronic spins. DFT-based evaluation of such interactions is also an important part of the analysis of mixed-metal materials.

Experimental and Computational Methods

Fe K-edge XANES and EXAFS spectra were measured at the XAFS beamline of the Elettra synchrotron radiation facilities in transmission detection mode. The samples and the reference Fe compounds were prepared in the form of homogeneous pellets, pressed from micronized powder mixed with BN. Mössbauer spectra were recorded using a constant acceleration Wissel spectrometer, in transmission mode with ⁵⁷Co source embedded in Rh matrix. X-band EPR spectra were recorded on a Bruker E580 spectrometer between 295 and 30 K. NMR measurements were carried under static conditions on a 600 MHz Varian NMR spectrometer equipped with a 3.2 mm Varian MAS probe. Teflon tubes, free of ²⁷Al background, were used as sample holders. Magnetic properties of polycrystalline samples were investigated by a Quantum Design MPMS-XL-5 SQUID magnetometer in the temperature range between 2 and 300 K in three magnetic fields (0.1, 1, and 5 T). First-principles calculations of hyperfine-coupling and J-coupling constants were carried out within the DFT frame as implemented in Orca.^20,21 More experimental and computational details are provided in the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b00341.

• Experimental and computational details, XRD powder patterns, detailed analysis of XAS and EPR measurements, additional computational results, and comparison of magnetic susceptibilities for independent spin-5/2 ions and for antiferromagnetically coupled pairs of spin-5/2 ions (PDF)

The authors declare no competing financial interest.