Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Feb 14;123(10):2325–2334. doi: 10.1021/acs.jpcb.9b01117

Protonation of the Biliverdin IXα Chromophore in the Red and Far-Red Photoactive States of a Bacteriophytochrome

Vaibhav Modi †, Serena Donnini ‡, Gerrit Groenhof †, Dmitry Morozov †,*
PMCID: PMC6727380  PMID: 30762368

Abstract

graphic file with name jp-2019-01117r_0007.jpg

The tetrapyrrole chromophore biliverdin IXα (BV) in the bacteriophytochrome from Deinococcus radiodurans (DrBphP) is usually assumed to be fully protonated, but this assumption has not been systematically validated by experiments or extensive computations. Here, we use force field molecular dynamics simulations and quantum mechanics/molecular mechanics calculations with density functional theory and XMCQDPT2 methods to investigate the effect of the five most probable protonation forms of BV on structural stability, binding pocket interactions, and absorption spectra in the two photochromic states of DrBphP. While agreement with X-ray structural data and measured UV/vis spectra suggest that in both states the protonated form of the chromophore dominates, we also find that a minor population with a deprotonated D-ring could contribute to the red-shifted tail in the absorption spectra.

Introduction

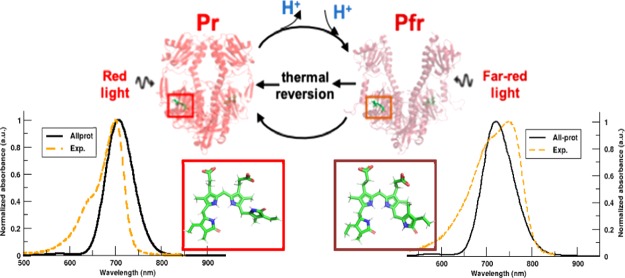
Light-sensitive signaling cascades in various plants, fungi, and bacteria are controlled by a photochemical mechanism involving photoactive proteins.1,2 Phytochromes belong to the class of photoreceptors that exist in nature with the ability to reversibly interconvert on the timescale of μs to ms between two structurally distinct states: Pr-dark and Pfr-illuminated. These states respond to red light (Pr) and far-red light (Pfr) and regulate numerous cellular functions, such as photomorphogenesis, flowering, shade avoidance in plants, and pigment synthesis in bacteria.3,4 The red/far-red light family of phytochromes exist as dimers. Upon red light (700 nm) absorption, the Pr state undergoes large conformational changes to photoconvert via various intermediate states into the Pfr state. The reverse photoconversion to Pr from the Pfr state is initiated either by far-red light (750 nm) absorption or by dark thermal relaxation.5 There are also bacterial phytochromes, for which the Pr-to-Pfr photoconversion occurs in darkness.6,7 These phytochromes with the reversed dark thermal relaxation mechanism are termed as bathy phytochromes.

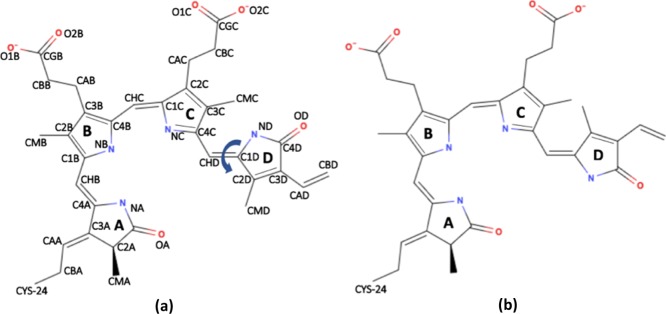
Recently, X-ray structures of the photosensory unit of phytochromes from Deinococcus radiodurans (DrBphP) have become available,5,8,9 which are of great help in beginning to understand the molecular mechanism responsible for the photoresponse of this protein. The structural unit of the core module consists of PAS (period, aryl hydrocarbon receptor nuclear translocator, and single-minded protein), GAF (cGMP-specific phosphodiesterase, adenylate cyclase, and Fhl proteins), and PHY (photochromic phytochrome) domains, while the full length phytochrome has also a histidine kinase (HK) domain attached to the PHY domain at the C-terminal end. The phytochromes can be classified based on the type and site of the covalently bound tetrapyrrole bilin chromophore that varies between organisms: phycocyanobilin (PΦB) in cyanobacterial phytochromes and phytochromobilin (PCB) in plant phytochromes have a covalent bond between the C31 atom (CAA atom in Figure 1a) and cysteine residue Cys259 in the GAF domain,4,10,11 while biliverdin IXα (BV) found in bacteriophytochromes is bound to the protein via the C32 carbon atom (CBA atom in Figure 1a) to cysteine residue Cys24 in the PAS domain.8,12

Figure 1.

Figure 1

Open in a new tab

Schematic representation of the BV IXα chromophore in the dark (left) and the illuminated state (right) phytochrome found in D. radiodurans (DrBphP). The atom naming scheme in (a) is used throughout the text. The figures were generated using MolView v2.2.

In DrBphP, the chromophore is located in the PAS-GAF domain cavity and bound to the protein via a thioether linkage with Cys24 and a hydrogen-bonding network involving residues Asp207, Arg254, His260, Ser272, Ser274, and His290 (the residue numbering is similar to the PDB structures 4O01 and 4O0P).5 In the red light-absorbing Pr state of DrBphP, the chromophore adopts a ZZZssa geometry, while in the far-red light-absorbing Pfr state, it adopts a ZZEssa geometry with an E, anticonformation for the isomerized D-ring (Figure 1b). Because of these differences in the chromophore conformation, it is widely assumed that photon absorption triggers photoisomerization of the D-ring along the CHD=C1D methyl bridge.4,13,14 In contrast, nonadiabatic QM dynamics simulations15 and calculations with different quantum chemical methods suggest that without protein environment, the BV isomerization can occur around the CHC=C1C methyl bridge between the B and C rings.16,17

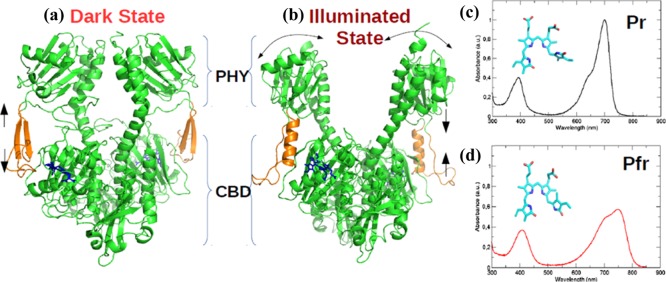
Biliverdin photoisomerization is followed by a series of structural changes in the chromophore binding pocket that ultimately lead to larger structural changes in the protein complex. These major changes include: (i) a secondary structure transformation from an anti-parallel β-sheet to an α-helix in the tongue region (residue range 461–490) between the GAF and PHY domains; and (ii) a large opening of more than ∼3 nm between the two PHY domains of the dimer in the Pfr state (Figure 2b).5 The light-induced changes in the PHY domains are speculated to reposition the HK domain as well as the phosphate-accepting histidine residues in the ATP-binding site within that HK domain.18 These structural rearrangements would eventually promote a phosphotransfer process within the phytochrome dimer and thereby regulate the downstream signal transmission.19

Figure 2.

Figure 2

Open in a new tab

Cartoon representation for the crystal structure of PAS-GAF-PHY domains of DrBphP in the (a) Pr-dark state (PDB: 4O0P(5)) that absorbs red light (700 nm) to trigger the secondary structure rearrangement from β-sheets to α-helix (orange) and a PHY domain opening to form the (b) Pfr-illuminated state (PDB: 4O01(5)) that absorbs far-red light (750 nm) to revert back to the Pr state; (c,d) experimental UV/vis absorption spectrum reported by Takala et al., which exhibits the Q-band and Soret band for Pr and Pfr states, respectively.5

The Pr and Pfr X-ray structures (Figure 2a,b) provide glimpses of structural changes that follow photoexcitation but do not address the crucial question of how the protein achieves high signaling efficiency. In addition, there is as yet no consensus about the precise sequence of events in what is essentially a dynamic process. To better understand the molecular mechanisms that drive this reversible photoactivation pathway, experimental data should be complemented with excited state molecular dynamics (MD) simulation, as in previous work on photoreceptors.20−22 However, performing such simulations requires an accurate structural model with detailed information about the electrostatic interactions in the chromophore binding pocket, and hence the protonation form of BV.

Various authors have proposed a fully protonated BV in Pr and Pfr states based on H-bond analysis from X-ray crystallography data,8,9 NMR experiments,23,24 and RR spectra.25,26 In contrast, others have shown that the Pr → Pfr photoactivation includes proton release/uptake9,27−33 by the chromophore in the intermediate states with a higher amplitude for the proton release than uptake.27,31−33 Although resonance Raman studies that are sensitive to N–H in-plane vibrations in BV have suggested that the C pyrrole ring nitrogen remains protonated in both Pr and Pfr states of plant and cyanobacterial phytochromes,25,34,35 ambiguity remains as to which of the other rings could be involved in these protonation changes. Nevertheless, these observations suggest that in addition to the photoisomerization, protonation changes may be relevant for photoactivation. Furthermore, because phytochromes from different species vary in (i) their chromophore linkage sites, (ii) orientation of pyrrole rings A/D in both Pr and Pfr state, and (iii) isomerization direction of the CHD=C1D double bond,36 it remains challenging to reconcile the aforementioned experimental findings into a consistent picture that is valid for phytochromes in general and DrBphP in particular.

To resolve the chromophore protonation state for DrBphP and prepare an accurate atomistic model for computationally costly excited state MD simulations,37 we have used classical MD simulations in combination with quantum chemistry and hybrid quantum mechanics/molecular mechanics (QM/MM) calculations to systematically investigate the effect of the chromophore protonation state on the structural and spectroscopic characteristics of the DrBphP photosensory domain in both Pr and Pfr conformations. Only the five most probable protonation patterns were investigated:

  • (1)

    all nitrogen atoms protonated (all-prot);

  • (2)

    nitrogen in ring A deprotonated and rings B, C, and D protonated (deprot-A);

  • (3)

    nitrogen in ring B deprotonated and rings A, C, and D protonated (deprot-B);

  • (4)

    nitrogen in ring C deprotonated and rings A, B, and D protonated (deprot-C);

  • (5)

    nitrogen in ring D deprotonated and rings A, B, and C protonated (deprot-D).

To the best of our knowledge, this is the first study to incorporate the PHY domain along with CBD in MD simulations and QM/MM calculations of DrBphP, aimed at systematically exploring the effects of the chromophore protonation state on the stability and absorptivity of this protein in solution.

In addition, we also assessed the accuracy with which various density functional theory (DFT) functionals predict the absorption maxima by comparing the DFT spectra to spectra computed at the correlated multiconfigurational level of ab initio theory. In line with the assumptions in previous computational studies,37−44 our results support a fully protonated biliverdin chromophore in both Pr and Pfr states of DrBphP, but also suggest that a very minor population, in which the D-ring is deprotonated, might be responsible for a long red tail in the absorption spectrum of this protein.

Methods

Protein Structures

The atomic coordinates of the core photosensory module (PAS-GAF-PHY: 523 amino acids) in dark and illuminated state of the photoreceptor protein reported by Takala et al., were taken from PDB models 4O0P and 4O01, with resolutions of 3.80 and 3.24 Å, respectively.5 Residues missing from these refined X-ray structures (see Table S1 in the Supporting Information for an overview of missing residues) were added based on the ab initio loop-modeling approach in the MODELLER program45,46 that finds the optimal structural model based on a potential energy function. We used the Dowser program to place internal water molecules inside hydrophobic cavities of the protein using protein–water and water–water interaction energy algorithms.47 With a probe radius of 0.2 Å and new DOWSER parameters for the BV chromophore molecule (Table S2), water molecules were inserted inside protein cavities, in which the interaction energy of the water was below a threshold value of −12 kcal/mol (Figure S1).

The protonation states and tautomeric forms of amino acids with ionizable side chains were determined by pKa estimation with H++ Server48 and PROPKA 3.149,50 at pH = 7. The rotameric states of these residues were inspected and modified to a new rotamer if that would increase the number of hydrogen bonds. For amino acids with nonionizable side chains, the H-atoms were added using force field parameters corresponding to their protonation form at pH = 7. As in previous works,38−41 we assume the same protonation state of the protein residues for all protonation states of the chromophore. While a change in protonation of the chromophore might affect the pKa’s of the surrounding protein residues, the number of possible states that would need to be sampled is too large to handle with standard MD simulations and was therefore not attempted here. The structural protein models of the Pr and Pfr states after equilibration are available in the Supporting Information (Pr.pdb and Pfr.pdb).

Force Field Model

The AMBER03 force field was used to model interactions between the atoms in our simulations.51 To model the intra- and intermolecular interactions of the chromophore, we derived force field parameters by means of ab initio calculations for a QM model that consisted of BV and the covalently attached side chain of Cys24. For all protonation states, the geometry of the QM model was optimized in the gas phase at the CAMB3LYP/6-31G(dp) level of DFT theory. The partial charges for the different protonation forms of BV were estimated by performing a two-stage restricted electrostatic potential (RESP) fit to the electron density obtained at the HF/6-31G(d) level of theory, using constraints on symmetry-related atoms in the second step (Tables S4 and S5).52 The atomic charges on the main chain of Cys24 were described following the approach proposed by Altun and co-workers (Tables S6 and S7).53 Additional atom types were created specifically for the chromophore to define new dihedrals and improve structural description. The complete force field for use with the Gromacs MD program54−56 is available in the Supporting Information. The DFT and ab initio calculations for the RESP fit were carried out with the Gaussian09 program,57 while the actual RESP fittings were performed with the AmberTools15 package.58

Classical MD Simulation

For MD simulations, the protein was solvated in a cubic periodic box (Pr: 12 × 12 × 12 nm and Pfr: 13 × 13 × 13 nm), which was filled with TIP3P water molecules.59 The large ∼3 nm opening of the PHY domain in the Pfr state necessitated the larger box size for this system. The total charge on the protein systems was neutralized by replacing solvent water molecules with Na+ and Cl– ions until a physiological salt concentration of 0.15 M was reached. The neutral solvated model contained 81 water molecules added by DOWSER (Figure S1) and another 50 454 and 68 294 water molecules in the Pr and Pfr models, respectively.

The short-range attractive and repulsive dispersive interactions were described by a Lennard-Jones potential with a cut off of 1.0 nm. Electrostatic interactions were calculated at each time step using the particle mesh Ewald method60 with a grid spacing of 0.12 nm. The LINCS algorithm was used to constrain bond lengths in the protein,61 while SETTLE62 was used to constrain the internal degrees of freedom of the TIP3P water molecules. These constraints allowed us to perform simulations with a time step of 2 fs.

The 10 phytochrome systems were initially subjected to an energy minimization for 10 000 steps using the steepest descent algorithm, followed by multiple equilibration steps: 200 ps simulation with position restrains on all protein atoms and two 500 ps simulations on the position-restrained system using NVT and NPT ensembles for temperature (300 K) and pressure (1 bar) equilibration, respectively. After minimization and equilibration, all phytochrome systems were simulated for 100 ns. All classical MD simulations were performed with the GROMACS 4.6.5 MD package.54−56

Spectra Calculations

For each chromophore protonation state, a snapshot was taken at every nanosecond from the 100 ns trajectories. Single-point vertical excitation energies were calculated for these 100 structures at the QM/MM level and superposed into a spectrum.86,87 For these QMMM calculations, a smaller BV chromophore QM subsystem (QM-small, Figure S3) was selected, in which the methyl groups of rings A, B, and D and the propionate side chains were replaced by H atoms, and the Cys24 attachment was excluded by truncating the chromophore system at the CAA-CBA bond (Figure 1a). The rest of the system was described at the AMBER03 force field level.51 In these calculations, electrostatic interactions with the rest of the chromophore, protein, and solvent were added to account for the polarization of the QM region by the environment. The choice for a QM subsystem that is smaller than the actual chromophore was validated by comparing the spectra computed for this small QM subsystem to those computed with the complete chromophore plus pyrrole water molecule inside the QM subsystem (Supporting Information, Figure S6).

The excitation energies (ΔEi) of the snapshots i were computed both at the level of time-dependent DFT (TD-DFT)63−69 and at the correlated multiconfigurational level of ab initio theory with the extended multiconfiguration quasidegenerate perturbation theory (XMCQDPT2) method.70 For the TD-DFT method, we used various functionals (BLYP,71,72 B3LYP,73−75 PBE0,76 and CAMB3LYP77) and the 6-31G(d,p) basis set. In the XMCQDPT2 computations, a complete active space self-consistent field (CASSCF) wave function78 based on an active space of 12 electrons in 12 orbitals, averaged over first 5 singlet states and expanded in the cc-pVDZ basis set,79 was used as a reference for the second-order perturbation theory calculation (i.e., XMCQDPT2/SA(5)-CASSCF(12,12)/cc-pVDZ). The active space orbitals used in these calculations are shown in Figure S10 of the Supporting Information. The selection of this active space was a trade-off between accuracy and computational efficiency and validated by computing energy profiles for the most relevant chromophore distortions (Figure S11).

The excitation energies were converted into a spectrum by convoluting the energy gaps with Gaussians

graphic file with name jp-2019-01117r_m001.jpg

where I is the intensity as a function of excitation energy (E), me is the electron mass, M is the number of snapshots included in the analysis, ΔEi is the excitation energy in snapshot i, and μi is the transition dipole moment of that excitation. A width of σ = 0.02 eV was chosen for the convolution. The QM calculations were performed with the Gaussian09 package57 (DFT and HF) and Firefly80 (XMCQDPT2).

We note that a similar approach has recently been used by Polyakov et al.42 However, the major difference between their work and ours is that we have computed absorption spectra of ensembles of the protein in solution at room temperature which can account for possible heterogeneities that may affect the interpretation of the spectra. In addition, while they focused on the fully protonated chromophore, we also investigated alternative protonation states.

Results and Discussion

MD Simulation

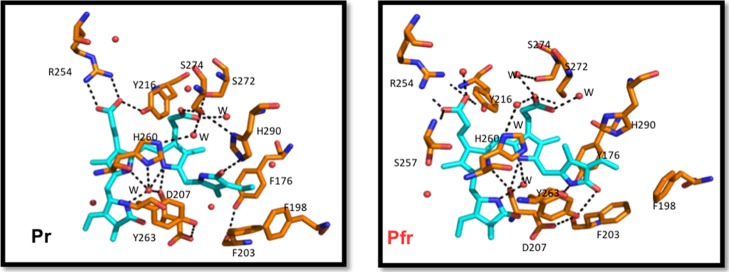
The stability of the chromophore pocket with different protonation forms of BV was assessed by analyzing the network of non-covalent interactions between the chromophore and the rest of the system in the MD trajectories and comparing these interactions to those in the X-ray structures (Figure 3).

Figure 3.

Figure 3

Open in a new tab

Stick representation of the conserved residues and the H-bonding network surrounding BV. Carbon atoms are colored in cyan and orange for BV and protein, respectively, with nitrogen in blue, oxygen in red, and water molecules as red spheres. The hydrogen bonding network for both models of DrBphP is shown as black dashed lines.

Pr—Dark State Simulations

The His260 residue stacked below the plane of the BV B-ring and C-ring is a stable H-bond acceptor for the pyrrole ring N–H atoms in the all-prot and deprot-D models. In contrast, in the deprot-A, deprot-B, and deprot-C models, this interaction breaks off within 25 ns and does not reform again (Figure S4). Furthermore, the absence of a proton on the A, B, or C ring of the chromophore disrupts the electrostatic interaction network involving the BV pyrrole N-atoms, Asp207 backbone carbonyl, and pyrrole water.

The distance distribution of the salt bridge between the Asp207–Arg466 side-chains (Figure S5) shows least disruptions over 100 ns in the all-prot and deprot-D models. In the deprot-A, deprot-B, and deprot-C Pr models, this salt bridge ruptures within the initial 20 ns and does not reform in the remainder of the 100 ns simulation time.

Hydrophobic residues Phe203, Tyr176, and Tyr263 form a pocket around the D-ring of BV, which allows the D-ring to isomerize without steric clashes between the residue side chains and methyl group on the D-ring.5,8,29 Altering the interactions involving Tyr176 and Tyr263 causes photobleaching in proteins where these amino acids are mutated.30 In our Pr simulations with A-ring, B-ring, or C-ring deprotonated, the rapid loss of the aforementioned salt bridge between Asp207 and Arg466 also disrupts the hydrogen bond between Asp207 and Tyr263 (Figure S5). This rupture causes Tyr263 to move away from Tyr176 and Phe203 and thus destabilizes the whole hydrophobic cavity. In contrast, the cavity remains intact in simulations where the chromophore is fully protonated (all-prot) and deprotonated at the D-ring (deprot-D).

The chromophore B-ring propionate side-chain is stabilized through a salt bridge with Arg254 and accepts a hydrogen bond from the Tyr216 hydroxyl group. The C-ring propionate side-chain makes polar contacts with S274 and a water-mediated contact with His260.4,5,8 These propionate side-chain interactions remain intact for all Pr models which suggests a negligible impact of the chromophore protonation on the side-chain interactions (Figure S5).

Pfr—Illuminated State Simulations

In the illuminated state, the residue configuration inside the chromophore binding pocket changes because of (i) photoisomerization, (ii) secondary structure changes in the conserved tongue region in contact with the chromophore, and (iii) a global opening of the PHY domain.5

The His260, D207, pyrrole water, and pyrrole N-atoms of BV form a polar contact network similar to the Pr state in all simulations. H260 maintains a stable contact with BV pyrrole-ring N-atoms by either acting as a hydrogen bond acceptor (all-prot and deprot-D) or donor (deprot-A, deprot-B, and deprot-C). However, the conserved interactions of Asp207-BV pyrrole N-atoms, Asp207–Ser468 and Ser468–Tyr263, are lost (Figures S6 and S7) in the Pfr state with BV deprotonated at the A, B, or C ring. Instead of re-establishing these hydrogen bonds later in the simulation, Asp207 moves out of the chromophore-binding pocket to form new interactions with the solvent molecules. In contrast, when the chromophore is fully protonated or deprotonated at the D-ring, the hydrogen bonds involving Asp207, Ser468, and Tyr263 remain intact. These observations support both a fully protonated chromophore and a chromophore with a deprotonated D ring, rather than the other chromophore protonation states, in which the hydrogen bonds are less stable.

Similar to the Pr state simulations, the B-ring and C-ring propionate side-chain interactions with residues Arg254, Tyr216, and Ser274 are stable in Pfr models regardless of the BV protonation state (Figure S7).

On the basis of the analysis of the conserved interactions between the chromophore and the protein in our MD simulations, we inferred that the A-ring, B-ring, and C-ring are protonated in Pr and Pfr but could not determine whether the D-ring is also protonated, as the chromophore binding pocket was stable in both situations (all-prot and D-deprot models). To differentiate further between these states, we also computed absorption spectra that can be directly compared to experiment.

Spectra Calculations

Effect of DFT Functional

In Figure 4, we compare the UV/vis spectra for Pr with an all-protonated chromophore, calculated at various levels of theory. Whereas the TD-DFT spectra contain the Soret band around 400 nm and the Q-band around 700 nm, the XMCQDPT2 spectrum lacks a clear Soret band. The latter is due to the limited number of states (nstates = 5) in the CASSCF calculations. With 10 states, the Soret band is predicted (Figure S8, Supporting Information), but this is computationally too expensive and also not needed as the Q-band absorption near 700 nm is much more sensitive to the structural changes associated with photoactivation from Pr to Pfr.4,5,9

Figure 4.

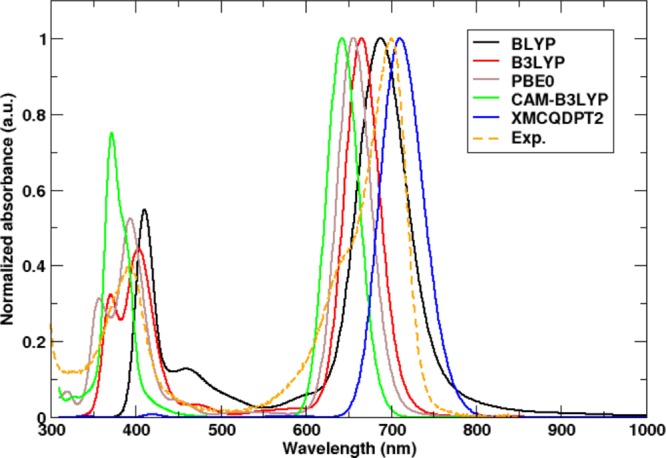
Figure 4

Open in a new tab

QM/MM UV/vis-absorption spectra of DrBphP evaluated at the TDDFT level with various DFT functionals and at the XMCQDPT2 level of theory in the Pr state. The experimental spectrum is shown in dashed orange lines, with a Q-band peak at 700 nm. The best agreement is obtained with the BLYP functional and XMCQDPT2 method with an absorption maxima at 692 nm (black line) and 708 nm (blue line), respectively.

Compared to the experimental spectrum with a maximum of the Q-band at 700 nm in the Pr state,5 the TDDFT spectra are blue-shifted, while the XMCQDPT2 spectrum is red-shifted. The hybrid functionals with 20–25% exact exchange, B3LYP and PBE0, deviated by 35 nm (0.09 eV) and 43 nm (0.116 eV), respectively, while the long-range-corrected metahybrid CAMB3LYP functional, which was developed to yield more accurate results for charge-transfer excitations, shows the largest blue shift of 56 nm (0.154 eV). While hybrid functionals and metahybrid functionals normally improve the accuracy of electronic excitations involving Rydberg or charge-transfer states, we here observe that the absorption maximum (692 nm/1.79 eV) obtained with the Generalized Gradient Approximation (GGA) BLYP functional is closest to both the experiment (700 nm/1.77 eV) and the XMCQDPT2 result (708 nm/1.75 eV). The performance of the different DFT functionals for the CBD-PHY dimer is in line with the results of a recent benchmark study on the CBD monomer.40 Because of the better agreement of the TD-BLYP/6-31G(d) and the XMCQDPT2/cc-pVDZ results for Pr, we only consider these methods in what follows.

TDDFT/MM Spectra of Various Protonation States

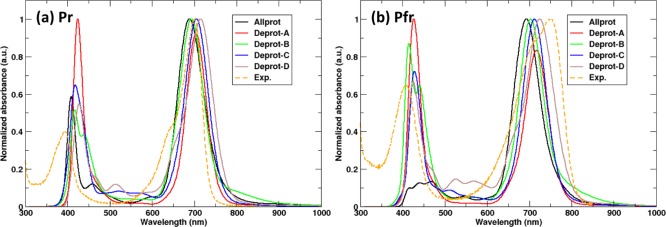
On the basis of the analysis of the conserved interactions between the chromophore and the protein in our MD simulations, we inferred that the A-ring, B-ring, and C-ring are protonated, but could not determine whether also the D-ring is protonated, as the chromophore binding pocket was stable in both situations (all-prot and D-deprot models). Therefore, we compare the computed absorption spectra of the five chromophore protonation states to experiments. Figure 5 shows these absorption spectra for both Pr and Pfr protein conformations. While in experiments the photoactivation of DrBphP is accompanied by a red shift in the Q-band absorption of 0.12 eV (from 700 to 750 nm), our TD-DFT/MM calculations show much smaller red shifts (Table 1). The largest red shift (0.04 eV) was obtained when the chromophore D-ring is deprotonated, in which case the absorption maximum changes from 714 nm in Pr to 731 nm in Pfr. With the fully protonated chromophore, the red shift is much smaller: only 8 nm or 0.02 eV. The maximum shift, however, is obtained if we assume that somewhere along the Pr to Pfr transition, the D ring becomes deprotonated. In this scenario, the Q-band absorption maximum moves from 688 nm in the Pr state to 731 nm in the Pfr state, which corresponds to a red shift of 0.11 eV (43 nm), in reasonable agreement with the experiment. Previously, such loss of a proton has been suggested to occur during the Pr-to-Pfr conversion in cyanobacterial phytochrome Cph1 and bacterial phytochrome Agp1 on the basis of flash-induced transient absorption measurements and pH dependence of the absorption spectra.27−30,33,34 On the basis of the MD snapshot in Figure S13, which highlights a proton wire from the chromophore to solvent, we speculate that the proton could leave the pyrrole D-ring of BV via that wire. Alternatively, also His260 might be involved, as it could potentially shuttle the proton onto the pyrrole water molecule, which exchanges frequently with bulk solvent in both Pr and Pfr simulations.

Figure 5.

Figure 5

Open in a new tab

Computed UV/Vis absorption spectra of the photoactive state models Pr and Pfr with different protonation forms of the BV chromophore computed using the TD-DFT method, BLYP/6-31G(d,p).

Table 1. Q-Band and Soret Band Peak Computed from Single-Point Excited State Energies Using BLYP/6-31G(d,p) for Five Different Protonation Forms of BV in Both Pr and Pfr States.
  Pr—dark state (nm)
 Pfr—illuminated state (nm)
BV protonation form Q-band Soret band Q-band Soret band
all-prot 696 409 704 476
deprot-A 708 421 720 433
deprot-B 696 439 708 413
deprot-C 712 416 716 424
deprot-D 716 430 742 423
Exp. 700 394 750 409
Open in a new tab

At this point, the combined MD simulations and TDDFT/MM calculations suggest a protonated chromophore in the Pr state of DrBphP and a chromophore that is deprotonated at the D-ring in the Pfr state. However, because the systematic error in TDDFT of about 0.25 eV81 is beyond the measurable red-shift, further confirmation is essential. We therefore also computed the absorption spectra at the correlated XMCQDPT2 level of theory, which has a higher accuracy with an error of about 0.1 eV.70

XMCQDPT2 Spectra

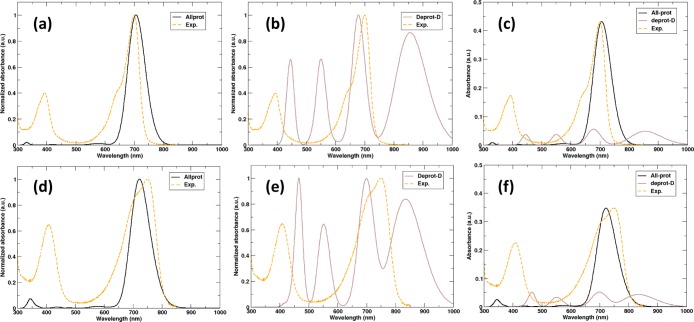
In previous works, the effect of deprotonation at the A, B, and C rings on the optical response of the chromophore has been computed,14,37,41,43 but not at the D-ring. Because, we rule out deprotonation of the A, B, and C rings in both the Pr and Pfr states of the photosensory domain based on the MD simulations, we have not computed the excitation spectra for these species at XMCQDPT2 level of theory. The XMCQDPT2/SA (5)-CASSCF(12,12)/cc-pVDZ//Amber03 QM/MM spectra are shown in Figure 6. While for the fully protonated chromophore, the spectra agree reasonably with the TD-BLYP results (Figures 5 and 6), the spectrum of the protein with a chromophore that is deprotonated at the D-ring, shows additional peaks. In particular, there is a broad optical transition beyond 800 nm that was not seen in the TD-DFT computations. Inspection of the molecular orbitals involved in these excitations reveals that the lowest energy S0–S1 transition in the deprotonated chromophore at 850 nm corresponds to a single-electron highest occupied molecular orbital–lowest unoccupied molecular orbital (HOMO-LUMO) transition, while the excitation around 700 nm is a two-electron or double excitation. Because of the adiabatic approximation in the exchange–correlation response kernel (ALDA), these double excitations are notoriously difficult to describe with TD-DFT, which is why they are missing here. The apparent agreement between the TD-DFT results and experiment must thus have been fortuitous and therefore cannot be used to support that the D-ring of the chromophore is deprotonated in either Pfr or Pr. Consistent with the TD-DFT results, the red shift between the Pr and Pfr states with the fully protonated chromophore is underestimated also at the XMCQDPT2/cc-pVDZ level (0.032 eV), but the deviation with respect to the experimental absorption maximum (0.12 eV) is closer to the anticipated error of the method (∼0.1 eV).70

Figure 6.

Figure 6

Open in a new tab

Calculated UV/vis absorption spectra for the fully protonated BV model [(a)-Pr, (d)-Pfr] and model with the D-ring deprotonated [(b)-Pr, (e)-Pfr] of DrBphP at the correlated XMCQDPT2 level of theory. Plots (c,f) represent the unnormalized spectra for the Pr and Pfr states, respectively, where the experimental spectra were scaled to the peak of the fully protonated BV model for better comparison.

However, before concluding that the chromophore is fully protonated in both Pr and Pfr states of the protein, we notice that because of the much lower oscillator strength of the chromophore with the deprotonated D-ring (Figure 6), the spectrum would be dominated by absorption of the protonated chromophore, masking the deprotonated species. Furthermore, the spectra available in the literature for this protein were only recorded up until 850 nm and sometimes even baseline corrected.4−7 Therefore, we speculate that, in particular, the red tail of the absorption might contain a minor contribution from proteins, in which the D-ring is not protonated. An indication in support of our speculation is the spectra of phytochromes with covalently modified biliverdin chromophores, which show a weak but a visible rise in absorption beyond 850 nm.82−84 Nevertheless, to experimentally verify whether the deprotonated chromophore indeed absorbs beyond 850 nm, we suggest recording the spectra over a larger range of wavelengths and pH values.

Conclusions

We have performed MD simulations of the photosensory domain of the D. radiodurans phytochrome protein with five different biliverdin protonation states in an attempt to determine the most likely protonation state. An analysis of the trajectories in terms of chromophore–protein interactions as well as absorption spectra suggests that the biliverdin chromophore in DrBphP is fully protonated, in line with previous assumptions. However, on the basis of the QM/MM spectra calculations at the correlated level of theory, we cannot rule out a minor population of proteins containing a chromophore with the deprotonated D-ring. Therefore, in our follow-up work, aimed at unraveling the photoisomerization mechanism, we will not only perform excited state dynamics simulations of the protein with a fully protonated chromophore, but also include simulations in which the D-ring of the chromophore is deprotonated. Because we found that the optical S0–S1 transition of the latter has a double excitation character, we will need a suitable multiconfigurational method rather than a TD-DFT model.

Acknowledgments

We want to thank Janne Ihalainen, Heli Lehtivuori, Jessica Rumsfeld, Heikki Takala, and Sebastian Westenhof for fruitful discussions. We thank Heikki Takala for sharing the absorption spectra and Alex Bjorling for sharing the details of their phytochrome simulations. We also acknowledge the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533), the CSC-IT center in Espoo, Finland, and PRACE (DECI-13) for awarding us access to resources at Cartesius in Dutch facility SURFsara. Molecular structure figures were generated using MolView v2.4 and PyMOL.85

Glossary

Abbreviations

TD-DFT

time-dependent density functional theory

XMCQDPT2

extended multiconfigurational quasidegenerate perturbation theory

DrBphP

Deinococcus radiodurans phytochrome

BV

biliverdin

MD

molecular dynamics

QM/MM

quantum mechanics/molecular mechanics

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.9b01117.

  • Additional data and figures including the molecular modeling parameters, force field parameterization of the BV chromophore, distance distribution analysis of MD simulations based on noncovalent interactions, Soret band peaks computed using the XMCQDPT2 method, comparison of different sizes of the QM subsystem, CASSCF(12,12) active-space orbitals generated for the XMCQDPT2 excited state energy calculations, excited-state relaxed energy scans of the most important biliverdin torsions, proton release/uptake pathway, and the effect of including range-separation on the chromophore force field parameters (PDF)

  • Equilibrated structure models of the Pr state for MD simulations (PDB)

  • Equilibrated structure models of the Pfr state for MD simulations (PDB)

  • GROMACS 4.6.5 compatible AMBER03 force field parameter files for 10 different BV chromophore models as a separate archive (ZIP)

Author Contributions

The manuscript was written through contributions of all the authors. All the authors have given approval to the final version of the manuscript.

This work was funded by the Academy of Finland (grant 304455 to G.G. and V.M., grant 285481 to D.M., and grant 266274 to S.D.).

The authors declare no competing financial interest.

Supplementary Material

jp9b01117_si_001.pdf (2MB, pdf)
jp9b01117_si_002.pdb (12.7MB, pdb)
jp9b01117_si_003.pdb (16.7MB, pdb)
jp9b01117_si_004.zip (3.6MB, zip)

References

  1. Sineshchekov V. A. Photobiophysics and Photobiochemistry of the Heterogeneous Phytochrome system. Biochim. Biophys. Acta, Bioenerg. 1995, 1228, 125–164. 10.1016/0005-2728(94)00173-3. [DOI] [Google Scholar]
  2. Davis S. J.; Vener A. V.; Vierstra R. D. Bacteriophytochromes: Phytochrome-Like Photoreceptors from Nonphotosynthetic Eubacteria. Science 1999, 286, 2517–2520. 10.1126/science.286.5449.2517. [DOI] [PubMed] [Google Scholar]
  3. Quail P. H. Phytochrome Photosensory Signalling Networks. Nat. Rev. Mol. Cell Biol. 2002, 3, 85–93. 10.1038/nrm728. [DOI] [PubMed] [Google Scholar]
  4. Rockwell N. C.; Su Y.-S.; Lagarias J. C. Phytochrome Structure and Signaling Mechanisms. Annu. Rev. Plant Biol. 2006, 57, 837–858. 10.1146/annurev.arplant.56.032604.144208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Takala H.; Björling A.; Berntsson O.; Lehtivuori H.; Niebling S.; Hoernke M.; Kosheleva I.; Henning R.; Menzel A.; Ihalainen J. A.; et al. Signal Amplification and Transduction in Phytochrome Photosensors. Nature 2014, 509, 245–248. 10.1038/nature13310. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Giraud E.; Fardoux J.; Fourrier N.; Hannibal L.; Genty B.; Bouyer P.; Dreyfus B.; Verméglio A. Bacteriophytochrome Controls Photosystem Synthesis in Anoxygenic Bacteria. Nature 2002, 417, 202–205. 10.1038/417202a. [DOI] [PubMed] [Google Scholar]
  7. Tasler R.; Moises T.; Frankenberg-Dinkel N. Biochemical and Spectroscopic Characterization of the Bacterial Phytochrome of Pseudomonas aeruginosa. FEBS J. 2005, 272, 1927–1936. 10.1111/j.1742-4658.2005.04623.x. [DOI] [PubMed] [Google Scholar]
  8. Wagner J. R.; Brunzelle J. S.; Forest K. T.; Vierstra R. D. A Light-Sensing Knot Revealed by the Structure of the Chromophore-Binding Domain of Phytochrome. Nature 2005, 438, 325–331. 10.1038/nature04118. [DOI] [PubMed] [Google Scholar]
  9. Burgie E. S.; Zhang J.; Vierstra R. D. Crystal Structure of Deinococcus Phytochrome in the Photoactivated State Reveals a Cascade of Structural Rearrangements During Photoconversion. Structure 2016, 24, 448–457. 10.1016/j.str.2016.01.001. [DOI] [PubMed] [Google Scholar]
  10. Rockwell N. C.; Njuguna S. L.; Roberts L.; Castillo E.; Parson V. L.; Dwojak S.; Lagarias J. C.; Spiller S. C. A Second Conserved GAF Domain Cysteine is Required for the Blue/Green Photoreversibility of Cyanobacteria Tlr0924 from Thermosynechoccus elongatus. Biochemistry 2008, 47, 7304–7316. 10.1021/bi800088t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Essen L.-O.; Mailliet J.; Hughes J. The Structure of a Complete Phytochrome Sensory Module in the Pr Ground State. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 14709–14714. 10.1073/pnas.0806477105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lamparter T. Evolution of Cyanobacterial and Plant Phytochromes. FEBS Lett. 2004, 573, 1–5. 10.1016/j.febslet.2004.07.050. [DOI] [PubMed] [Google Scholar]
  13. Vierstra R. D.; Karniol B. In Handbook of Photosensory Receptors; Briggs W., Spudich J., Eds.; Wiley-VCH Press: Weinheim, Germany, 2005; pp 171–196. [Google Scholar]
  14. Falklöf O.; Durbeej B. Steric Effects Govern the Photoactivation of Phytochromes. ChemPhysChem 2016, 17, 954–957. 10.1002/cphc.201501080. [DOI] [PubMed] [Google Scholar]
  15. Zhuang X.; Wang J.; Lan Z. Tracking of the Molecular Motion in the Primary Event of Photoinduced Reactions of a Phytochromobilin Model. J. Phys. Chem. B 2013, 117, 15976–15986. 10.1021/jp408799b. [DOI] [PubMed] [Google Scholar]
  16. Durbeej B. On the Primary Event of Phytochrome: Quantum Chemical Comparison of Photoreactions at C4, C10 and C15. Phys. Chem. Chem. Phys. 2009, 11, 1354–1361. 10.1039/b811813b. [DOI] [PubMed] [Google Scholar]
  17. Strambi A.; Durbeej B. Initial Excited-State Relaxation of the Bilin Chromophores of Phytochromes: A Computational Study. Photochem. Photobiol. Sci. 2011, 10, 569–579. 10.1039/c0pp00307g. [DOI] [PubMed] [Google Scholar]
  18. Björling A.; Berntsson O.; Lehtivuori H.; Takala H.; Hughes A. J.; Panman M.; Hoernke M.; Niebling S.; Henry L.; Henning R.; et al. Structural Photoactivation of a Full-Length Bacterial Phytochrome. Sci. Adv. 2016, 2, e1600920 10.1126/sciadv.1600920. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Li H.; Zhang J.; Vierstra R. D.; Li H. Quaternary Organization of a Phytochrome Dimer as Revealed by Cryoelectron Microscopy. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 10872–10877. 10.1073/pnas.1001908107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Pande K.; Hutchison C. D. M.; Groenhof G.; Aquila A.; Robinson J. S.; Tenboer J.; Basu S.; Boutet S.; DePonte D. P.; Liang M.; et al. Femtosecond Structural Dynamics Drives the trans/cis Isomerization in Photoactive Yellow Protein. Science 2016, 352, 725–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Polli D.; Altoè P.; Weingart O.; Spillane K. M.; Manzoni C.; Brida D.; Tomasello G.; Orlandi G.; Kukura P.; Mathies R. A.; Garavelli M. Conical Intersection Dynamics of the Primary Photoisomerization Event in Vision. Nature 2010, 467, 440. 10.1038/nature09346. [DOI] [PubMed] [Google Scholar]
  22. Gozem S.; Luk H. L.; Schapiro I.; Olivucci M. Theory and Simulation of the Ultrafast Double-Bond Isomerization of Biological Chromophores. Chem. Rev. 2017, 117, 13502–13565. 10.1021/acs.chemrev.7b00177. [DOI] [PubMed] [Google Scholar]
  23. Strauss H. M.; Hughes J.; Schmieder P. Heteronuclear Solution-State NMR Studies of the Chromophore in Cyanobacterial Phytochrome Cph1. Biochemistry 2005, 44, 8244–8250. 10.1021/bi050457r. [DOI] [PubMed] [Google Scholar]
  24. Rohmer T.; Strauss H.; Hughes J.; De Groot H.; Gärtner W.; Schmieder P.; Matysik J. 15N MAS NMR Studies of Cph1 Phytochrome: Chromophore Dynamics and Intramolecular Signal Transduction. J. Phys. Chem. B 2006, 110, 20580–20585. 10.1021/jp062454+. [DOI] [PubMed] [Google Scholar]
  25. Kneip C.; Hildebrandt P.; Németh K.; Mark F.; Schaffner K. Interpretation of the resonance Raman Spectra of Linear Tetrapyrroles Based on DFT Calculations. Chem. Phys. Lett. 1999, 311, 479–484. 10.1016/s0009-2614(99)00868-4. [DOI] [Google Scholar]
  26. Von Stetten D.; Günther M.; Scheerer P.; Murgida D. H.; Mroginski M. A.; Krauß N.; Lamparter T.; Zhang J.; Anstrom D. M.; Vierstra R. D.; Forest K. T.; Hildebrandt P. Chromophore Heterogeneity and Photoconversion in Phytochrome Crystals and Solution Studied by Resonance Raman Spectroscopy. Angew. Chem., Int. Ed. 2008, 47, 4753–4755. 10.1002/anie.200705716. [DOI] [PubMed] [Google Scholar]
  27. Van Thor J. J.; Borucki B.; Crielaard W.; Otto H.; Lamparter T.; Hughes J.; Hellingwerf K. J.; Heyn M. P. Light-Induced Proton Release and Proton Uptake Reactions in the Cyanobacterial Phytochrome Cph1. Biochemistry 2001, 40, 11460–11471. 10.1021/bi002651d. [DOI] [PubMed] [Google Scholar]
  28. Borucki B.; Von Stetten D.; Seibeck S.; Lamparter T.; Michael N.; Mroginski M. A.; Otto H.; Murgida D. H.; Heyn M. P.; Hildebrandt P. Light-Induced Proton Release of Phytochrome is Coupled to the Transient Deprotonation of the Tetrapyrrole Chromophore. J. Biol. Chem. 2005, 280, 34358–34364. 10.1074/jbc.m505493200. [DOI] [PubMed] [Google Scholar]
  29. Von Stetten D.; Seibeck S.; Michael N.; Scheerer P.; Mroginski M. A.; Murgida D. H.; Krauss N.; Heyn M. P.; Hildebrandt P.; Borucki B.; Lamparter T. Highly Conserved Residues Asp-197 and His-250 in Agp1 Phytochrome Control the Proton Affinity of the Chromophore and Pfr Formation. J. Biol. Chem. 2007, 282, 2116–2123. 10.1074/jbc.m608878200. [DOI] [PubMed] [Google Scholar]
  30. Wagner J. R.; Zhang J.; Von Stetten D.; Günther M.; Murgida D. H.; Mroginski M. A.; Walker J. M.; Forest K. T.; Hildebrandt P.; Vierstra R. D. Mutational Analysis of Deinococcus radiodurans Bacteriophytochrome Reveals Key Amino Acids Necessary for the Phtotochromicity and Proton Exchange Cycles of Phytochrome. J. Biol. Chem. 2008, 283, 12212–12226. 10.1074/jbc.m709355200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Borucki B.; Seibeck S.; Heyn M. P.; Lamparter T. Characterization of the Covalent and Noncovalent Adducts of Agp1 Phytochrome Assembled With Biliverdin and Phycocyanobilin by Circular Dichroism and Flash Photolysis. Biochemistry 2009, 48, 6305–6317. 10.1021/bi900436v. [DOI] [PubMed] [Google Scholar]
  32. Escobar F. V.; Piwowarski P.; Salewski J.; Michael N.; Lopez M. F.; Rupp A.; Qureshi B. M.; Scheerer P.; Bartl F.; Frankenberg-Dinkel N.; Siebert F. A Protonation-Coupled Feedback Mechanism Controls the Signalling Process in Bathy Phytochromes. Nat. Chem. 2015, 7, 423–430. 10.1038/nchem.2225. [DOI] [PubMed] [Google Scholar]
  33. Escobar F. V.; Lang C.; Takiden A.; Schneider C.; Balke J.; Hughes J.; Alexiev U.; Hildebrandt P.; Mroginski M. A. Protonation-Dependent Structural Heterogeneity in the Chromophore Binding Site of Cyanobacterial Phytochrome Cph1. J. Phys. Chem. B 2016, 121, 47–57. 10.1021/acs.jpcb.6b09600. [DOI] [PubMed] [Google Scholar]
  34. Matysik J.; Hildebrandt P.; Schlamann W.; Braslavsky S. E.; Schaffner K. Fourier-Transform Resonance Raman Spectroscopy of Intermediates of the Phytochrome Photocycle. Biochemistry 1995, 34, 10497–10507. 10.1021/bi00033a023. [DOI] [PubMed] [Google Scholar]
  35. Kneip C.; Hildebrandt P.; Schlamann W.; Braslavsky S. E.; Mark F.; Schaffner K. Protonation State and Structural Changes of the Tetrapyrrole Chromophore During the Pr→ Pfr Phototransformation of Phytochrome: A Resonance Raman Spectroscopic Study. Biochemistry 1999, 38, 15185–15192. 10.1021/bi990688w. [DOI] [PubMed] [Google Scholar]
  36. Rockwell N. C.; Shang L.; Martin S. S.; Lagarias J. C. Distinct Classes of Red/Far-red Photochemistry Within the Phytochrome Superfamily. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 6123–6127. 10.1073/pnas.0902370106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Boggio-Pasqua M.; Burmeister C. F.; Robb M. A.; Groenhof G. Photochemical Reactions in Biological Systems: Probing the Effect of the Environment by Means of Hybrid Quantum Chemistry/Molecular Mechanics Simulations. Phys. Chem. Chem. Phys. 2012, 14, 7912–7928. 10.1039/c2cp23628a. [DOI] [PubMed] [Google Scholar]
  38. Durbeej B.; Borg O. A.; Eriksson L. A. Computational Evidence in Favor of a Protonated Chromophore in the Photoactivation of Phytochrome. Chem. Phys. Lett. 2005, 416, 83–88. 10.1016/j.cplett.2005.09.050. [DOI] [Google Scholar]
  39. Matute R. A.; Contreras R.; González L. Time-dependent DFT on Phytochrome Chromophores: A Way to the Right Conformer. J. Phys. Chem. Lett. 2010, 1, 796–801. 10.1021/jz900432m. [DOI] [Google Scholar]
  40. Falklöf O.; Durbeej B. Modeling of Phytochrome Absorption Spectra. J. Comput. Chem. 2013, 34, 1363–1374. 10.1002/jcc.23265. [DOI] [PubMed] [Google Scholar]
  41. Falklöf O.; Durbeej B. Computational Identification of Pyrrole Ring C as the Preferred Donor for Excited-State Proton Transfer in Bacteriophytochromes. ChemPhotoChem 2018, 2, 453–457. 10.1002/cptc.201800014. [DOI] [Google Scholar]
  42. Polyakov I. V.; Grigorenko B. L.; Mironov V. A.; Nemukhin A. V. Modeling Structure and Excitation of Biliverdin-Binding Domains in Infrared Fluorescent Proteins. Chem. Phys. Lett. 2018, 710, 59–63. 10.1016/j.cplett.2018.08.068. [DOI] [Google Scholar]
  43. Feliks M.; Lafaye C.; Shu X.; Royant A.; Field M. Structural Determinants of Improved Fluorescence in a Family of Bacteriophytochrome-Based Infrared Fluorescent Proteins: Insights from Continuum Electrostatic Calculations and Molecular Dynamics Simulations. Biochemistry 2016, 55, 4263–4274. 10.1021/acs.biochem.6b00295. [DOI] [PubMed] [Google Scholar]
  44. Hasegawa J.-y.; Isshiki M.; Fujimoto K.; Nakatsuji H. Structure of Phytochromobilin in the Pr and Pfr Forms: SAC-CI Theoretical Study. Chem. Phys. Lett. 2005, 410, 90–93. 10.1016/j.cplett.2005.05.040. [DOI] [Google Scholar]
  45. Šali A.; Blundell T. L. Comparative Protein Modelling by Satisfaction of Spatial Restraints. J. Mol. Biol. 1993, 234, 779–815. 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
  46. Fiser A.; Do R. K. G.; Šali A. Modelling of Loops in Protein Structures. Protein Sci. 2000, 9, 1753–1773. 10.1110/ps.9.9.1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Zhang L.; Hermans J. Hydrophilicity of Cavities in Proteins. Proteins: Struct., Funct., Bioinf. 1996, 24, 433–438. . [DOI] [PubMed] [Google Scholar]
  48. Anandakrishnan R.; Aguilar B.; Onufriev A. V. H++ 3.0: Automating pK Prediction and the Preparation of Biomolecular Structures for Atomistic Molecular Modeling and Simulations. Nucleic Acids Res. 2012, 40, W537–W541. 10.1093/nar/gks375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Søndergaard C. R.; Olsson M. H. M.; Rostkowski M.; Jensen J. H. Improved Treatment of Ligands and Coupling Effects in Empirical Calculation and Rationalization of pKa Values. J. Chem. Theory Comput. 2011, 7, 2284–2295. 10.1021/ct200133y. [DOI] [PubMed] [Google Scholar]
  50. Olsson M. H. M.; Søndergaard C. R.; Rostkowski M.; Jensen J. H. PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions. J. Chem. Theory Comput. 2011, 7, 525–537. 10.1021/ct100578z. [DOI] [PubMed] [Google Scholar]
  51. Duan Y.; Wu C.; Chowdhury S.; Lee M. C.; Xiong G.; Zhang W.; Yang R.; Cieplak P.; Luo R.; Lee T. A Point-Charge Force Field for Molecular Mechanics Simulations of Proteins Based on Condensed-Phase Quantum Mechanical Calculations. J. Comput. Chem. 2003, 24, 1999–2012. 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
  52. Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: the RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
  53. Altun A.; Yokoyama S.; Morokuma K. Spectral Tuning in Visual Pigments: An ONIOM (QM: MM) Study on Bovine Rhodopsin and its Mutants. J. Phys. Chem. B 2008, 112, 6814–6827. 10.1021/jp709730b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Lighly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
  55. Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; Hess B. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Van Der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
  57. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford CT, 2009. [Google Scholar]
  58. Case D. A.; Berryman J. T.; Betz R. M.; Cerutti D. S.; Cheatham T. E.; Darden T. A. III; Duke R. E.; Giese T. J.; Gohlke H.; Goetz A. W.; et al. AMBER 2015; University of California: San Francisco, 2015. [Google Scholar]
  59. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  60. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  61. Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
  62. Miyamoto S.; Kollman P. A. SETTLE: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
  63. Schäfer L. V.; Groenhof G.; Klingen A. R.; Ullmann G. M.; Boggio-Pasqua M.; Robb M. A.; Grubmüller H. Photoswitching of the Fluorescent Protein asFP595: Mechanism, Proton Pathway, and Absorption Spectra. Angew. Chem., Int. Ed. 2007, 46, 530–536. 10.1002/anie.200602315. [DOI] [PubMed] [Google Scholar]
  64. Wiebeler C.; Rao A. G.; Gärtner W.; Schapiro I. The Effective Conjugation Length is Responsible for the Red/Green Spectral Tuning in the Cyanobacteriochrome Slr1393g3. Angew. Chem., Int. Ed. 2019, 58, 1934–1938. 10.1002/anie.201810266. [DOI] [PubMed] [Google Scholar]
  65. Bauernschmitt R.; Ahlrichs R. Treatment of Electronic Excitations Within the Adiabatic Approximation of Time Dependent Density Functional Theory. Chem. Phys. Lett. 1996, 256, 454–464. 10.1016/0009-2614(96)00440-x. [DOI] [Google Scholar]
  66. Casida M. E.; Jamorski C.; Casida K. C.; Salahub D. R. Molecular Excitation Energies to High-Lying Bound States from Time-Dependent Density-Functional Response Theory: Characterization and Correction of the Time-Dependent Local Density Approximation Ionization Threshold. J. Chem. Phys. 1998, 108, 4439–4449. 10.1063/1.475855. [DOI] [Google Scholar]
  67. Stratmann R. E.; Scuseria G. E.; Frisch M. J. An Efficient Implementation of Time-Dependent Density-Functional Theory for the Calculation of Excitation Energies of Large Molecules. J. Chem. Phys. 1998, 109, 8218–8224. 10.1063/1.477483. [DOI] [Google Scholar]
  68. Furche F.; Ahlrichs R. Adiabatic Time-Dependent Density Functional Methods for Excited State Properties. J. Chem. Phys. 2002, 117, 7433–7447. 10.1063/1.1508368. [DOI] [Google Scholar]
  69. Casida M. E. Time-Dependent Density-Functional Theory for Molecules and Molecular Solids. J. Mol. Struct.: THEOCHEM 2009, 914, 3–18. 10.1016/j.theochem.2009.08.018. [DOI] [Google Scholar]
  70. Adamo C.; Jacquemin D. The Calculations of Excited-State Properties with Time-Dependent Density Functional Theory. Chem. Soc. Rev. 2013, 42, 845–856. 10.1039/c2cs35394f. [DOI] [PubMed] [Google Scholar]
  71. Dreuw A.; Head-Gordon M. Single-Reference Ab initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 2005, 105, 4009–4037. 10.1021/cr0505627. [DOI] [PubMed] [Google Scholar]
  72. Granovsky A. A. Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory. J. Chem. Phys. 2011, 134, 214113. 10.1063/1.3596699. [DOI] [PubMed] [Google Scholar]
  73. Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098. 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
  74. Lee C.; Yang W.; Parr R. G. Development of Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
  75. Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact eEchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  76. Vosko S. H.; Wilk L.; Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
  77. Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
  78. Adamo C.; Barone V. Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  79. Yanai T.; Tew D. P.; Handy N. C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  80. Roos B. O.; Taylor P. R. A Complete Active Space SCF Method (CASSCF) Using a Density Matrix Formulated Super-CI Approach. Chem. Phys. 1980, 48, 157–173. 10.1016/0301-0104(80)80045-0. [DOI] [Google Scholar]
  81. Dunning T. H. Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  82. Granovsky A. A.Firefly version 8.2. Available at: http://classic.chem.msu.su/gran/firefly/index.html. Accessed Sept 20, 2017.
  83. Jacquemin D.; Wathelet V.; Perpète E. A.; Adamo C. Extensive TD-DFT Benchmark: Singlet-Excited States of Organic Molecules. J. Chem. Theory Comput. 2009, 5, 2420–2435. 10.1021/ct900298e. [DOI] [PubMed] [Google Scholar]
  84. Inomata K.; Hammam M. A. S.; Kinoshita H.; Murata Y.; Khawn H.; Noack S.; Michael N.; Lamparter T. Sterically Locked Synthetic Bilin Derivatives and Phytochrome Agp1 fromAgrobacterium tumefaciensForm Photoinsensitive Pr- and Pfr-like Adducts. J. Biol. Chem. 2005, 280, 24491–24497. 10.1074/jbc.m504710200. [DOI] [PubMed] [Google Scholar]
  85. Rockwell N. C.; Lagarias J. C. The Structure of Phytochrome: A Picture is Worth a Thousand Spectra. Plant Cell 2006, 18, 4–14. 10.1105/tpc.105.038513. [DOI] [PMC free article] [PubMed] [Google Scholar]
  86. Ihalainen J. A.; Gustavsson E.; Schroeder L.; Donnini S.; Lehtivuori H.; Isaksson L.; Thöing C.; Modi V.; Berntsson O.; Stucki-Buchli B.; Liukkonen A.; Kalenius E.; Westenhoff S.; Kottke T. Chromophore-Protein Interplay during the Phytochrome Photocycle Revealed by Step-Scan FTIR Spectroscopy. J. Am. Chem. Soc. 2018, 140, 12396–12404. 10.1021/jacs.8b04659. [DOI] [PubMed] [Google Scholar]
  87. DeLano W. L.The PyMOL Molecular Graphics System, version 2.0.6; Schrödinger, LLC, 2002; https://pymol.org/2/.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp9b01117_si_001.pdf (2MB, pdf)
jp9b01117_si_002.pdb (12.7MB, pdb)
jp9b01117_si_003.pdb (16.7MB, pdb)
jp9b01117_si_004.zip (3.6MB, zip)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES