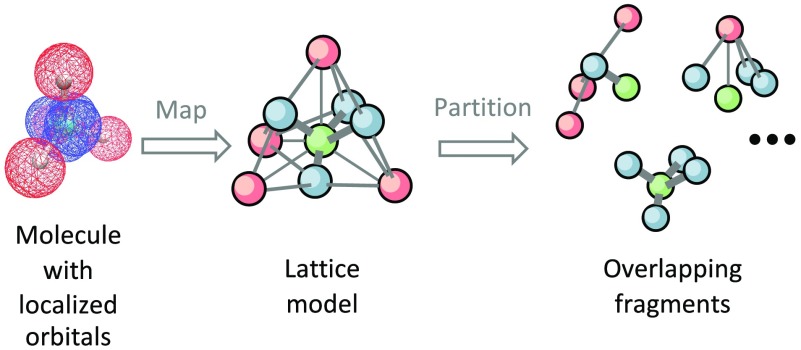
Abstract
Fragment embedding is one way to circumvent the high computational scaling of accurate electron correlation methods. The challenge of applying fragment embedding to molecular systems primarily lies in the strong entanglement and correlation that prevent accurate fragmentation across chemical bonds. Recently, Schmidt decomposition has been shown effective for embedding fragments that are strongly coupled to a bath in several model systems. In this work, we extend a recently developed quantum embedding scheme, bootstrap embedding (BE), to molecular systems. The resulting method utilizes the matching conditions naturally arising from using overlapping fragments to optimize the embedding. Numerical simulation suggests that the accuracy of the embedding improves rapidly with fragment size for small molecules, whereas larger fragments that include orbitals from different atoms may be needed for larger molecules. BE scales linearly with system size (apart from an integral transform) and hence can potentially be useful for large-scale calculations.
1. Introduction
When applying standard electronic structure methods to study realistic systems, one usually needs to compromise between cost and accuracy. On the one hand, lower-level, mean-field approximations such as Hartree–Fock1,2 (HF) have modest computational scaling but are insufficiently accurate due to lack of electron correlation. On the other hand, higher-level, correlated wave function methods such as coupled cluster3,4 (CC), density matrix renormalization group5−8 (DMRG), and full configuration interaction2 (FCI) are capable of making reasonable predictions related to experiments9−16 but are limited to small systems owing to their high computational cost.
One way to circumvent the steep computational scaling of accurate electron correlation methods is fragment embedding. The main motivation of fragment embedding is that electron correlation is local; hence, it is possible to treat the full system in a divide-and-conquer approach. Specifically, the full system is partitioned into smaller fragments, each made to interact with an effective bath constructed to approximate the rest of the system (i.e., the environment). Computationally involved, high-level theories are required only for each individual fragment but never for the full system, which leads to reduced computational scaling. Different research groups have successfully developed and applied fragmentation methods in various contexts, each focusing on a different embedding variable, including localized orbitals,17−20 electron density,21−26 density matrix,27−29 and Green’s function,30−35 to name a few.
Applying fragment embedding to a general molecular system is not a trivial problem. The main difficulty lies in proper description of the strong entanglement and correlation between fragments and baths arising from cutting chemical bonds. Schmidt decomposition36−39 has recently been used for embedding fragments that are strongly coupled to a bath. The central idea of Schmidt decomposition is to project the environment associated with a fragment to a small set of local states that have nonvanishing entanglement with that fragment. This projection naturally preserves the entanglement between fragments and baths and reduces the dimension of the problem simultaneously.
Although the general formulation has been known for a long time (especially in the quantum information community40−42), it was not until recently that Knizia and Chan recognized Schmidt decomposition as a key ingredient in fragment embedding in their method called density matrix embedding theory43,44 (DMET). In DMET, the fragment is embedded in a mean-field bath constructed by Schmidt decomposing the HF wave function of the full system. The embedded fragment and bath, which are a small subspace of the full system, are then solved using the aforementioned high-level theories. In order to optimize the mean-field bath, the fragment–fragment block of the one-particle density matrix (1PDM) of the mean-field bath is made to match that of the high-level calculation by a self-consistently determined one-electron effective potential. Good performance has been reported for model Hamiltonians43,45,46 and atomic rings/chains.44 DMET was originally proposed as a simplification to the more complicated dynamical mean-field theory30−32 (DMFT) but was soon recognized by the community as a new wave function-in-wave function embedding theory. Extensions of the original DMET include modified matching conditions,47−51 use of more accurate baths45,52,53 and other impurity solvers,54 time-dependent formulation55,56 and low-lying excited states,57 as well as application to simple solids.48
One of the main problems with DMET—as with many other fragment embedding methods—is the need to divide the system into fixed nonoverlapping fragments.58 This prescription leads to the inaccurate description of the edges (surface) of the fragment and their interaction with the bath. To that end, Welborn et al. propose an alternative to DMET called bootstrap embedding59 (BE) that explores the matching conditions arising from using overlapping fragments to reduce the surface error. When fragments overlap, the overlapping region will be more accurately described in some fragment than in others if it is the center (i.e., most embedded region) as opposed to the edge (i.e., least embedded region) of that fragment. BE improves the description of the edge sites of a fragment by requiring their density matrix elements to match the fragments where those sites are center. These matching conditions provide an internally consistent formulation of fragment embedding and hence lead to faster convergence compared to DMET on the Hubbard model.59
The application of BE to molecules is still challenging. In simple model systems such as the 1D Hubbard model,60 the intersite connectivity is clear, along with the distinction between edge and center sites for a given fragment. This is not the case, however, for the ab initio Hamiltonian of a general chemical system. As demonstrated by Ricke and co-workers in the context of the 2D Hubbard model with long-range interaction, the optimal choice of the center and edge sites is not always intuitive.61 Other attempts have also been made recently by Ye et al. in incremental embedding (IE), where the calculations of all fragments of certain size are combined carefully through an incremental scheme;62 fast convergence with fragment size is observed for small molecules but at the price of higher computational scaling.62
In this paper, we present an extension of BE to arbitrary molecular systems. Here, the key idea is to properly define the connectivity between orbitals and generalize the BE matching conditions to arbitrary connectivity. We present proof-of-concept calculations for several molecules using atom-centered Gaussian orbitals. Numerical results suggest that BE shows good convergence with fragment size for the correlation energy of small molecules at equilibrium geometry and also delivers smooth energy curves for dissociating single and double covalent bonds. For large molecules, we observe that BE converges slowly with fragment size and overestimates the all-electron correlation energy for the largest fragment size that we are able to test. This is attributed to the lack of interatomic fragment overlapping based on an active-space calculation on the same set of molecules. Nevertheless, the computation time of BE scales linearly with system size (apart from an integral transform) and hence is a promising method for large systems.
This paper is organized as follows. In section 2, we briefly review the theory of BE and then present how it can be generalized to treat arbitrary Hamiltonians. In section 3, we present the computational details. In section 4, we present numerical results and discussion on several molecules as a proof of concept. In section 5, we conclude this work by pointing out several future directions.
2. Theory
In this section, we first give a brief review of Schmidt decomposition as well as BE in the context of lattice models, with an emphasis on the matching conditions that naturally arise from using overlapping fragments. Then, we present how BE can be generalized to an arbitrary Hamiltonian assuming that we know the connectivity between sites. Finally, we end this section by introducing a heuristic scheme of determining the intersite connectivity for molecules.
Throughout this work, we assume that our system is described by the following second-quantized Hamiltonian
| 1 |
in some discrete basis of size Nbasis.
2.1. Schmidt Decomposition
The general theory of Schmidt decomposition can be found in the literature.38,39 Here, we review its application in DMET-related fragment embedding methods.
Suppose we partition our system into two parts, the
fragment (which we assume to be of smaller size) and the environment,
such that the Hilbert space observes the same decomposition, 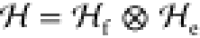 . Then, any state
. Then, any state 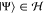 has the following
tensor factorization
has the following
tensor factorization
| 2 |
where 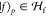 are the fragment states and
are the fragment states and 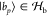 are the entangled bath states.
Note that
there are only
are the entangled bath states.
Note that
there are only 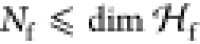 states in the
environment that have nonzero
entanglement with the fragments. If we further restrict Ψ to
be the ground state of the full-system Hamiltonian Ĥ, then the embedding Hamiltonian obtained by projecting Ĥ onto the Schmidt space
states in the
environment that have nonzero
entanglement with the fragments. If we further restrict Ψ to
be the ground state of the full-system Hamiltonian Ĥ, then the embedding Hamiltonian obtained by projecting Ĥ onto the Schmidt space
| 3 |
shares the same ground state as Ĥ.
For a general state |Ψ⟩, the computational cost of performing the tensor factorization in eq 2 grows exponentially with system size. In addition, Ĥemb contains many-body interactions that are not suitable for standard quantum chemistry methods even if Ĥ has only one- and two-body terms. The key approximation made by Knizia and Chan in DMET is to replace |Ψ⟩ with a single-determinant (i.e., HF) state |Φ⟩, which allows the otherwise complicated many-body decomposition to be performed at mean-field cost.43,44 The resulting fragment and bath states are single-particle states (i.e., sites), rendering Ĥemb a simple two-body Hamiltonian
| 4 |
where h̃ and Ṽ are obtained by projecting h and V in eq 1 using the 2Nf fragment and entangled bath sites (h̃ also includes the contribution from partially tracing V with the unentangled bath). Due to this simplicity, almost all Schmidt decomposition-based fragment embedding methods use a HF bath, with only a few exceptions.52,53 The differences among DMET, its different variants, and BE lie in the use of (1) different high-level theories to solve the embedding Hamiltonian and (2) different matching conditions to optimize the embedding. BE, among others, provides an internally consistent approach to optimizing the embedding.
2.2. Bootstrap Embedding
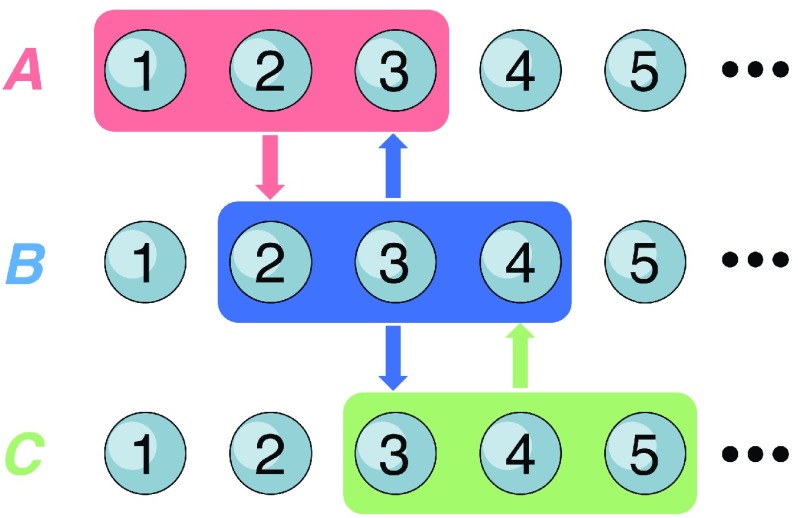
In this section, we use a 1D lattice chain to illustrate the idea of BE. As shown in Figure 1, there are three different ways to partition the system into fragments of three adjacent sites. The key assumption of BE is that the wave function on the central sites is more accurate than the wave function on the edge sites; hence, one can improve the description of the edge sites by constraining the edge site wave function on one fragment to match the central site wave function on another fragment.59 For example, in Figure 1, site 3 is the central site in B but the edge site in A and C. Hence, we require the following two constraints
| 5 |
to be satisfied when solving ĤembA and Ĥemb (blue arrows in Figure 1). Similar constraints can be imposed for sites 2 and 4, respectively.
Figure 1.
Schematic illustration of the BE matching conditions on a 1D lattice model. Site 3 is the center of fragment B and the edge of fragments A and C, which gives rise to the matching conditions in eq 5 (blue arrows). Similar matching conditions exist for sites 2 (red arrow) and 4 (green arrow).
The specific example shown above can be made general as follows.
Let fragments A and B be two overlapping
fragments, and assume that the set of the central sites of B (which we label 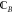 ) has nonzero intersection
with the set
of the edge sites of A (which we label
) has nonzero intersection
with the set
of the edge sites of A (which we label 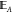 ), i.e.,
), i.e., 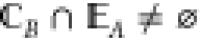 . Then, according to our assumption, we
require the 1PDM of fragment A to match that of fragment B in the overlapping region,
. Then, according to our assumption, we
require the 1PDM of fragment A to match that of fragment B in the overlapping region, 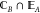 . Mathematically,
this can be formulated
as a constrained optimization for fragment A
. Mathematically,
this can be formulated
as a constrained optimization for fragment A
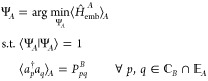 |
6 |
where ⟨···⟩A is short for ⟨ΨA|···| ΨA⟩, and we include the normalization condition of ΨA for completeness. Equation 6 can be turned into an unconstrained optimization by introducing the following Lagrangian
| 7 |
whose stationary points are given by an eigenvalue equation
| 8 |
where the Lagrange multipliers for the matching conditions appear as an effective potential
| 9 |
Given {PpqB} for
all 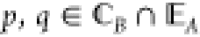 , the effective potential
λ̂A is determined by repeatedly
solving eq 8 until the
matching conditions
in eq 6 are satisfied.
As shown by Ricke et al.,61 the BE optimization
problem is numerically stable because the Hessian of
, the effective potential
λ̂A is determined by repeatedly
solving eq 8 until the
matching conditions
in eq 6 are satisfied.
As shown by Ricke et al.,61 the BE optimization
problem is numerically stable because the Hessian of 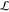 is negative
semidefinite, similar to the
direct optimization method used in density functional theory.63−65 This feature makes BE’s matching conditions different from
those in DMET because the exact satisfiability of the latter is not
guaranteed: there are known cases where DMET’s matching conditions
cannot be satisfied exactly.52
is negative
semidefinite, similar to the
direct optimization method used in density functional theory.63−65 This feature makes BE’s matching conditions different from
those in DMET because the exact satisfiability of the latter is not
guaranteed: there are known cases where DMET’s matching conditions
cannot be satisfied exactly.52
The equation presented above for matching the edges of fragment A to the centers of fragment B can be generalized to an arbitrary number of overlapping fragments, as long as a clear definition of edges and centers exists for all fragments (which is the case for simple lattice models). If the centers of all fragments are further constructed to be nonoverlapping but fully partition the system, i.e.
| 10 |
and
| 11 |
where 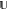 is
the set of all sites, any physical quantity
of the full system can be computed unambiguously as a sum of local
contributions from the center of each fragment. Specifically, we require
that the number of electrons on each fragment center sums up to the
correct total number of electrons, N. This can be
done by introducing a global chemical potential, μ, and optimizing
the full-system Lagrangian
is
the set of all sites, any physical quantity
of the full system can be computed unambiguously as a sum of local
contributions from the center of each fragment. Specifically, we require
that the number of electrons on each fragment center sums up to the
correct total number of electrons, N. This can be
done by introducing a global chemical potential, μ, and optimizing
the full-system Lagrangian
| 12 |
As a result, the effective potential for each fragment A defined in eq 9 needs to be modified to include (i) the matching between A and all other fragments and (ii) the global chemical potential
| 13 |
Note that now all fragment calculations are coupled through both the matching conditions and μ.
In practice, we turn the problem of simultaneously determining {λA} and μ into two uncoupled problems that are solved alternatively until the BE matching error
| 14 |
is below some preset threshold value, τ, where Ncons is the total number of constraints. An algorithm is outlined in Algorithm 1.
We note that while the convergence of density matching in each BE iteration is guaranteed as mentioned above, the convergence of Algorithm 1 (which uses a simple fixed-point method) is not. In principle, the BE iterations could oscillate or even diverge—just like the self-consistent field (SCF) algorithm of HF.66 In practice, however, we have never encountered such situations. An example demonstrating the convergence of the BE iteration algorithm is displayed in Figure S1 in the Supporting Information.
In the subsequent sections, we will see that the general framework of BE described above remains unchanged when applied to molecular systems. The major task is to generalize the algorithmic choice of fragments and central and edge sites.
2.3. BE for Molecules
For molecules, localized atomic orbitals (LAOs) such as those obtained by the Forster–Boys scheme67 are usually used as the site basis.53,54,58,62 Hence, the formalism presented above in the context of lattice models is in principle applicable to molecules too. The challenge here is two-fold: (i) how to measure the interorbital connectivity and (ii) how to partition the molecules into overlapping fragments that have well-defined centers and edges based on a well-defined connectivity. In the subsequent section, we will present an interaction-based metric for determining interorbital connectivity. Here, we tackle the second problem, assuming that we have such a metric.
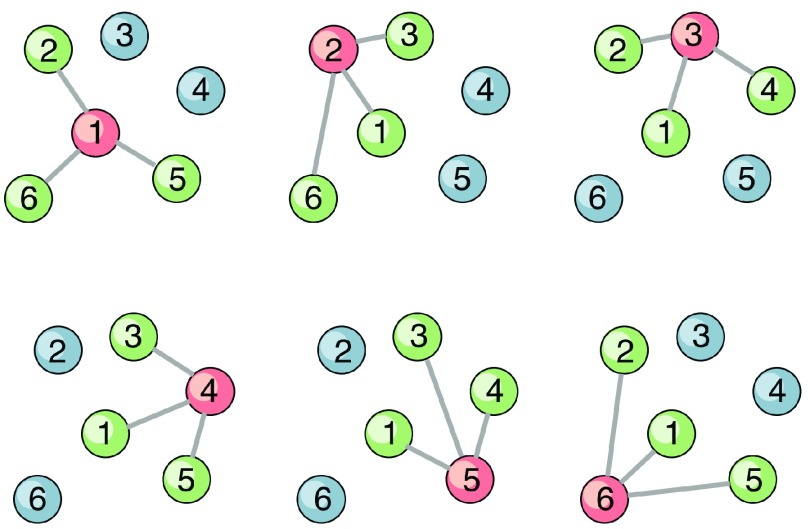
Suppose that we have a measure for the strength of connectivity (referred hereafter as “distance”) between any pair of orbitals. Then for each orbital p, we can construct an Nf-orbital fragment by including p and the Nf – 1 orbitals that are closest to p (see Figure 2 for a schematic illustration). By construction, p can be deemed the unique center of that fragment, while all other Nf – 1 orbitals are edges. Thus, for a molecule described by Nbasis LAOs (eq 1), we can construct Nbasis overlapping fragments, each of size Nf and centering on one LAO. Because the Nf – 1 edge orbitals of each fragment are centers in other fragments, we require the population of each edge orbital to match that of the corresponding center orbital, giving rise to Nf – 1 matching conditions for each fragment. Moreover, the Nbasis fragment centers satisfy eqs 10 and 11, and hence, we can compute full-system observables by summing all orbital contributions.
Figure 2.
Schematic illustration of distance-based fragmentation for arbitrary orbital connectivity. Each fragment has one unique center (red) and Nf – 1 edge (green) orbitals (here Nf = 4). The total number of fragments is equal to the total number of orbitals.
Formally, this one-center-per-fragment partition scheme is similar to orbital-specific virtual local correlation methods.68,69 In OSVMP2, for example, each (localized) occupied orbital is correlated to only a small set of (localized) virtual orbitals that are selected by either direct optimization or tensor factorization.68 In BE, each LAO is also correlated with only a small set of orbitals consisting of two parts: (i) the edge orbitals, which are selected by the distance measure, and (ii) the entangled bath orbitals, which are generated by Schmidt decomposition. However, we note that the difference in the orbital bases used by the two methods is in fact a significant one. For instance, concepts like frontier orbitals are less obvious in LAOs than in (localized) molecular orbitals (MOs). We will see the effect of this difference in section 4.2.
Despite the simplicity of the above partition scheme, we note here two potential problems. First, ties may arise when selecting edge orbitals from groups of nearly degenerate orbitals. In this work, we use fragments of fixed size and hence break the ties arbitrarily, which may break the molecule’s point group symmetry and lead to unphysical behaviors in some cases. Alternatively, one can include all degenerate orbitals at a time whenever one of them is selected as an edge orbital by a fragment. We will not, however, explore this scheme here because it usually leads to fragments whose sizes are beyond the ability of our high-level solver (i.e., FCI). Second, the one-center-per-fragment feature allows one to match only on-site properties (e.g., population) for overlapping fragments, even if the overlapping region may consist of more than one orbital. Multicenter fragments are needed for matching interorbital properties (e.g., coherences), which we will explore in future works.
2.4. Normalized Coulomb Metric
The most straightforward candidate for measuring the distance between orbitals is a real-space metric, e.g., the Euclidean distance between the average positions of two orbitals
| 15 |
Though simple, this metric is not ideal. First, it does not reflect the symmetry and spatial extension of orbitals, especially those with high angular momentum and/or a long diffuse tail. Second, it correlates with the interaction between orbitals only indirectly, which is not aligned with our purpose of recovering electron correlation.
To that end, we propose an interaction-based metric, the normalized Coulomb metric
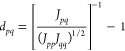 |
16 |
where Jpq = ⟨pq|pq⟩ is the bare Coulomb interaction between orbitals p and q. We choose the Coulomb interaction for several reasons. First, it is non-negative for all orbital pairs and decays as r–1 for remotely separated orbitals. Second, it does not vanish even for two orbitals of different symmetries (which could have vanishing one-electron interactions). The normalization in eq 16 is important because it not only renders dpq non-negative but also removes the bias arising from the orbital shape (e.g., Jpq tends to have a higher value for orbitals that are more s-like).
2.5. Computational Scaling
We end this section by briefly discussing the computational scaling of BE. Three of the algorithmic steps are most time-consuming. First, electron repulsion integrals (ERIs) generated in the AO basis (of size Nbasis) need to be transformed into the Schmidt basis (of size 2Nf) for each of the Nbasis fragments. The transformation for each fragment formally takes O(Nbasis4Nf) time, hence scaling as O(Nbasis) in total. Second, according to Algorithm 1, each BE iteration requires determination of both the effective potentials, {λA}, and the global chemical potential, μ. Both steps scale linearly with the number of fragments and hence the system size, while determining {λA} also scales linearly with Nf due to the O(Nf) matching conditions per fragment (section 2.3). The prefactor of these linear-scaling steps comes primarily from solving Ĥemb using the high-level method and hence also has some polynomial or even exponential dependence on Nf depending on the method. Overall, for a fixed fragment size, the ERI transform is currently the computational bottleneck for large systems. The fifth-power formal scaling could potentially be reduced in the future by various techniques established for electron correlation methods.70−75 We also note that the ERI transform needs to be performed only once, and the transformed integrals can then be stored on disk for later use. We will present timing data from numerical calculations in section 4.3.
3. Computational Details
In the following computational works, we examine the performance of BE using several molecular systems with atom-centered Gaussian bases. The structures of all molecules as optimized at the B3LYP76/cc-pVDZ77 level (available in the Supporting Information) as well as the needed atomic integrals are obtained in Q-Chem.78 Forster–Boys67 LAOs generated by Q-Chem are used for all molecules except for the active-space calculations on polyacene chains, in which case we adopt the symmetrically orthogonalized orbitals. The BE calculations are performed in frankenstein(79) using spin-restricted Hartree–Fock (RHF) as the bath and FCI as the high-level solver. The mean-field bath is kept fixed in this work. The entangled bath orbitals for a given fragment are obtained by following the prescription described in ref (47). The interacting bath formulation58 is adopted to construct the embedding Hamiltonian in eq 4. We note that currently the code is not integral-direct, which limits the size of the molecules to ∼200 basis functions.
BE calculations using fragments composed of Nf orbitals are denoted by BE(Nf). We restrict Nf ⩽ 5 in this work due to the use of FCI as a high-level solver. In the BE iteration algorithm (Algorithm 1), the density matching (step 2) and the determination of μ (step 3) are performed using Newton–Raphson and secant algorithms,80 respectively, which typically converge in several iterations. As discussed in section 2.2, the convergence of Algorithm 1 (which uses a simple fixed-point method) is not guaranteed in principle. However, for all molecules studied in this work, it often requires less than 10 iterations to convergence (τ = 10–6 is used in this work). As an illustration, we show the convergence for hexacene in the Supporting Information (Figure S1). Unless otherwise specified, we match the population (i.e., diagonal elements of 1PDM) for overlapping fragments.
For all molecules tested below except polyacenes, exact numerical solutions via DMRG (as obtained in Block(7,8,81−83)) are available and will be used as benchmark; for polyacenes, we benchmark our results against the CCSD(T) solution from Q-Chem. For the study of covalent bond dissociation, we also compare BE with complete active space configuration interaction84 (CASCI) performed using frankenstein. Results for DMET are presented with only one orbital per fragment and zero correlation potential [which is equivalent to BE(1) and will be denoted by BE(1) below] due to the difficulty in both obtaining unambiguous fragments and optimizing the correlation potential47,50,51,54 for molecules.
4. Results and Discussion
4.1. Correlation Energy at Equilibrium Geometry
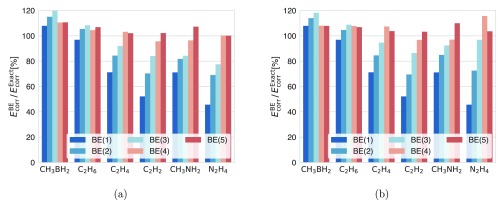
We first examine the performance of BE in terms of the correlation energy recovered for a set of small molecules at their equilibrium geometries. The results with the STO-3G basis85 are shown in Figure 3, both with and without the matching conditions.
Figure 3.
Correlation energies of several small molecules at equilibrium geometry computed by BE with increasing fragment size, (a) with or (b) without matching conditions. All calculations are performed using the STO-3G basis.
Overall, BE converges relatively fast and recovers most of the correlation energy with fragments of four or five orbitals. The rate of convergence is fastest for C2H6 and becomes slower when introducing either unsaturated bonds or heteroatoms. This pattern is similar to what has been reported in previous works62 and can be attributed to the half-filling nature of the embedding space generated from Schmidt decomposition (i.e., 2Nf electrons in 2Nf orbitals). Due to the RHF density being very good for these small molecules in the minimal basis, not much is improved by imposing the BE matching conditions.
4.2. Homolytic Cleavage of Covalent Bonds
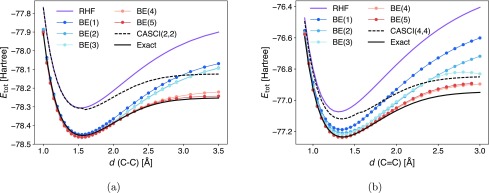
The second example that we study is covalent bond dissociation. Because our metric for determining orbital connectivity is structure-dependent, the partitioning of the molecules determined at different geometries may differ. Due to its discrete nature, the change in fragmentation is abrupt when the geometry changes, which usually leads to discontinuous potential energy curves even though the molecular structure itself varies smoothly. To that end, we use the fragments determined at equilibrium geometries for all subsequent calculations. The results of dissociating the carbon–carbon bonds of C2H6 and C2H4 in the STO-3G basis are shown in Figure 4. CASCI with a minimum active space is also included for comparison.
Figure 4.
Energy curves of homolytic cleavage of (a) the C–C single bond in C2H6 and (b) the C=C double bond in C2H4 computed by BE. For both molecules, fragments determined at their respective equilibrium geometries are used for all bond lengths. CASCI results obtained using a minimum active space are also included for comparison (small kinks arise from frontier orbitals changing order when varying the geometry). All calculations are performed using the STO-3G basis. Note that BE(3) does not improve over BE(2) for both molecules and most geometries (see the main text for discussion).
With fixed fragments, BE delivers smooth energy curves for both molecules and different sizes of fragments. Overall, the accuracy of embedding increases for larger fragments. Near equilibrium geometries, BE recovers most of the correlation energy even at the BE(2) level and improves drastically over CASCI. However, as both molecules dissociate, a gap emerges between BE(3) and BE(4), and the energy of BE(3) is even higher than that of CASCI at large bond lengths. The poor performance of BE(3) in these regimes suggests that the frontier orbitals (i.e., HOMO and LUMO for C2H6 and HOMO–1 to LUMO+1 for C2H4), which are crucial to the description of bond dissociation, are not accurately spanned by the fragment and entangled bath orbitals. As mentioned in section 2.3, this is not surprising because the embedding calculation is performed in a localized orbital basis instead of the canonical MO basis. Nevertheless, the problem is mitigated by adopting a larger fragment size, as can be seen from the curves of BE(4) and BE(5).
To examine the effect of density matching, we repeat the calculations in Figure 4 without the matching conditions. The results are displayed in Figure S2. As in previous examples, the effect of density matching is not significant for both equilibrium geometry and intermediate bond length. However, at large separation, imposing the matching conditions consistently worsens the results for small fragments, while bringing only little improvement to the largest fragment size. These results might be attributed to the small size of the fragments, an effect we will discuss in details in the next example.
4.3. Polyacene Chains
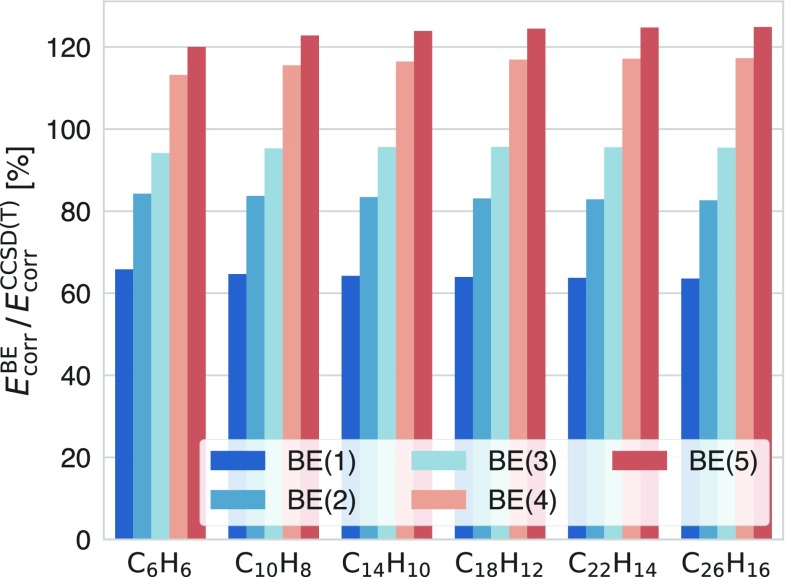
The last example that we study is polyacene chains. This example represents an important application of fragment embedding methods because the full-system calculations are beyond the capability of FCI/DMRG. The large conjugate π-systems in polyacenes lead to strong electron correlation86−88 and hence can be challenging for fragment embedding methods. The performance of BE for the first six polyacene chains in the STO-3G basis is shown in Figure 5.
Figure 5.
Fraction of CCSD(T) correlation energy recovered by BE with increasing fragment size for polyacene chains (from benzene to hexacene) at equilibrium geometry. All calculations are performed using the STO-3G basis.
For all six molecules, ∼95% of the correlation energy is recovered by using three-orbital fragments. Unlike previous examples, however, the convergence with fragment size is not monotonic: BE(4) and BE(5) seriously overestimate the correlation energy by ∼20%. An inspection of the calculations suggests that, even for fragments of five orbitals, most of the fragments generated by our metric are localized on one carbon atom. This is because the interaction of orbitals on the same atom is usually greater than the interaction of those on different atoms. As a consequence, fragments overlapping and matching conditions are only explored at the intra-atomic level, and the pertinent interatomic information (e.g., coherences between adjacent atoms) is thus missing in these calculations.
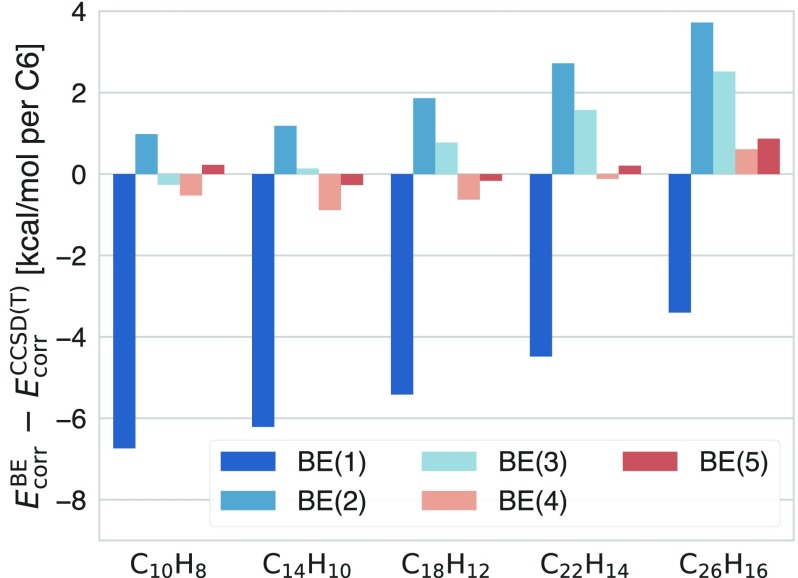
To illustrate this point, we repeat the calculations in Figure 5 using an active space consisting of the π orbitals from each molecule. By doing so, each carbon atom is described by only one pz orbital, and we are able to perform embedding calculations using up to five atoms per fragment. The results are displayed in Figure 6. As one can see, using one atom per fragment [i.e., BE(1)] overestimates the correlation energy in a way that is similar to what BE(4) and BE(5) do in Figure 5. Including the nearest neighbors of each atom [i.e., BE(4)], however, drastically reduces the error. Despite a slow growth of the error with molecular size for small fragments, the largest fragment size tested here [i.e., BE(5)] consistently delivers accurate correlation energy (normalized error < 1 kcal/mol) for all molecules. In addition, some improvements are observed by imposing the density matching (see Figure S3 in the Supporting Information for the results without matching conditions), although the effect is still very small because even BE(1) is very accurate for these molecules. These observations emphasize the importance of using fragments composed of orbitals from neighboring atoms, which we will explore in a more systematic manner in future works.
Figure 6.
Error of active-space correlation energy (normalized to six carbons) computed by BE with increasing fragment size compared to CCSD(T) for polyacene chains (from naphthalene to hexacene) at equilibrium geometry. The active space consists of symmetrically orthogonalized pz orbitals from all carbon atoms. All calculations are performed using the STO-3G basis. Note that benzene (C6H6) is not included as it has only six orbitals and BE becomes exact for three-atom fragments.
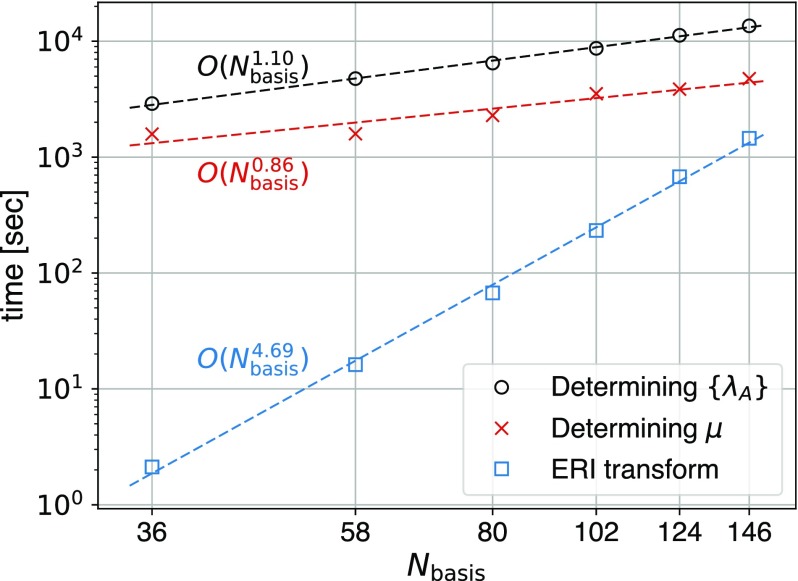
Despite the potential problem of overcorrelation, BE shows a favorable computational scaling and hence is promising for large-scale calculations. In Figure 7, the CPU time as a function of basis size for the three primary steps in a BE(5) calculation is plotted for the six polyacene molecules studied above (Figure 5). Exponential fit suggests that the determination of both {λA} and μ scales linearly with system size (the prefactor is large owing to our pilot implementation), while the ERI transform scales slightly less than the fifth power of Nbasis. These observations are consistent with our analyses in section 2.5.
Figure 7.
CPU time as a function of basis size for three primary steps in BE(5) calculations of the six polyacene chains in Figure 5. Times for the determination of both {λA} and μ are reported per BE iteration (ERI transform needs to be performed only once). Dashed lines are exponential fit, with the scalings indicated to the side.
5. Conclusions
To summarize, we extended bootstrap embedding (BE) to molecular systems by generalizing the definition of overlapping fragments from lattice models to generic ab initio Hamiltonians. A heuristic interaction-based metric for determining interorbial connectivity is proposed and tested in several molecules. Numerical results suggest that BE converges fast with fragment size for small molecules at both equilibrium geometry and bond dissociation. For large molecules, the lack of interatomic fragment overlapping plagues the convergence with fragment size and results in overcorrelation for fragments of four and five orbitals. Calculations on polyacene chains using an active space composed of only π orbitals, however, show fast convergence with fragment size, highlighting the important role of interatomic fragment overlapping. Nevertheless, BE exhibits linear computational scaling (apart from an integral transform) and hence is promising for large-scale calculations.
In the future, BE could be improved in several directions. First, in this work, the use of FCI as high-level solver restricts us to small fragments. Larger fragments that include orbitals from different atoms will be available if we adopt a less expensive high-level solver. In addition, the use of large fragments also enables alternative approaches to generating fragments such as including edge orbitals by their symmetry group and atom-based fragmentation.48,53,54,58,89 Last but not least, currently we explore only the matching of on-site population (i.e., diagonal elements of 1PDM). Future works will also include the matching of interorbital coherences (i.e., off-diagonal of 1PDM), which have been reported to be important for correlation energy.59
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.9b00529.
Supplementary figures showing the variation of the BE matching error with the number of iterations, energy curves of homolytic cleavage, and errors of the active-space correlation energy computed by BE and structures of the molecules studied here (PDF)
This work was funded by a grant from the NSF (Grant No. CHE-1464804). T.V. is a David and Lucille Packard Foundation Fellow.
The authors declare no competing financial interest.
Supplementary Material
References
- Roothaan C. C. J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. 10.1103/RevModPhys.23.69. [DOI] [Google Scholar]
- Szabo A.; Ostlund N. S.. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory; Dover Publications Inc.: Mineola, NY, 1996. [Google Scholar]
- Purvis G. D.; Bartlett R. J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. 10.1063/1.443164. [DOI] [Google Scholar]
- Ahlrichs R.; Scharf P. In Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry; Lawley K. P., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, 1987; Vol. 67. [Google Scholar]
- White S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. 10.1103/PhysRevLett.69.2863. [DOI] [PubMed] [Google Scholar]
- Verstraete F.; Murg V.; Cirac J. I. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv. Phys. 2008, 57, 143–224. 10.1080/14789940801912366. [DOI] [Google Scholar]
- Chan G. K.-L.; Head-Gordon M. Highly correlated calculations with a polynomial cost algorithm: A study of the density matrix renormalization group. J. Chem. Phys. 2002, 116, 4462–4476. 10.1063/1.1449459. [DOI] [Google Scholar]
- Chan G. K.-L. An algorithm for large scale density matrix renormalization group calculations. J. Chem. Phys. 2004, 120, 3172–3178. 10.1063/1.1638734. [DOI] [PubMed] [Google Scholar]
- Scheiner A. C.; Scuseria G. E.; Rice J. E.; Lee T. J.; Schaefer H. F. Analytic evaluation of energy gradients for the single and double excitation coupled cluster (CCSD) wave function: Theory and application. J. Chem. Phys. 1987, 87, 5361–5373. 10.1063/1.453655. [DOI] [Google Scholar]
- Theis M. L.; Candian A.; Tielens A. G. G. M.; Lee T. J.; Fortenberry R. C. Electronically Excited States of Anisotropically Extended Singly-Deprotonated PAH Anions. J. Phys. Chem. A 2015, 119, 13048–13054. 10.1021/acs.jpca.5b10421. [DOI] [PubMed] [Google Scholar]
- Fortenberry R. C.; Novak C. M.; Layfield J. P.; Matito E.; Lee T. J. Overcoming the Failure of Correlation for Outof-Plane Motions in a Simple Aromatic: Rovibrational Quantum Chemical Analysis of c–C3H2. J. Chem. Theory Comput. 2018, 14, 2155–2164. 10.1021/acs.jctc.8b00164. [DOI] [PubMed] [Google Scholar]
- Fortenberry R. C. The ArNH2+ noble gas molecule: Stability, vibrational frequencies, and spectroscopic constants. J. Mol. Spectrosc. 2019, 357, 4–8. 10.1016/j.jms.2019.02.001. [DOI] [Google Scholar]
- Mabrouk N.; Berriche H. Theoretical study of the NaLi molecule: potential energy curves, spectroscopic constants, dipole moments and radiative lifetimes. J. Phys. B: At., Mol. Opt. Phys. 2008, 41, 155101. 10.1088/0953-4075/41/15/155101. [DOI] [Google Scholar]
- Taffet E. J.; Scholes G. D. The Ag+ state falls below 3Ag– at carotenoid-relevant conjugation lengths. Chem. Phys. 2018, 515, 757–767. 10.1016/j.chemphys.2017.12.008. [DOI] [Google Scholar]
- Roemelt M.; Pantazis D. A. Multireference Approaches to Spin-State Energetics of Transition Metal Complexes Utilizing the Density Matrix Renormalization Group. Adv. Theory Simul. 2019, 2, 1800201. 10.1002/adts.201800201. [DOI] [Google Scholar]
- Pantazis D. A. Meeting the Challenge of Magnetic Coupling in a TriplyBridged Chromium Dimer: Complementary Broken-Symmetry Density Functional Theory and Multireference Density Matrix Renormalization Group Perspectives. J. Chem. Theory Comput. 2019, 15, 938–948. 10.1021/acs.jctc.8b00969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitaura K.; Ikeo E.; Asada T.; Nakano T.; Uebayasi M. Fragment molecular orbital method: an approximate computational method for large molecules. Chem. Phys. Lett. 1999, 313, 701–706. 10.1016/S0009-2614(99)00874-X. [DOI] [Google Scholar]
- Fedorov D. G.; Kitaura K. The importance of three-body terms in the fragment molecular orbital method. J. Chem. Phys. 2004, 120, 6832–6840. 10.1063/1.1687334. [DOI] [PubMed] [Google Scholar]
- Khaliullin R. Z.; Head-Gordon M.; Bell A. T. An efficient self-consistent field method for large systems of weakly interacting components. J. Chem. Phys. 2006, 124, 204105. 10.1063/1.2191500. [DOI] [PubMed] [Google Scholar]
- Fedorov D. G.; Kitaura K. Extendingthe Power of Quantum Chemistry to Large Systems with the Fragment Molecular Orbital Method. J. Phys. Chem. A 2007, 111, 6904–6914. 10.1021/jp0716740. [DOI] [PubMed] [Google Scholar]
- Senatore G.; Subbaswamy K. R. Density dependence of the dielectric constant of rare-gas crystals. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 34, 5754–5757. 10.1103/PhysRevB.34.5754. [DOI] [PubMed] [Google Scholar]
- Johnson M. D.; Subbaswamy K. R.; Senatore G. Hyperpolarizabilities of alkali halide crystals using the local-density approximation. Phys. Rev. B: Condens. Matter Mater. Phys. 1987, 36, 9202–9211. 10.1103/PhysRevB.36.9202. [DOI] [PubMed] [Google Scholar]
- Jacob C. R.; Neugebauer J. Subsystem density-functional theory. WIREs. Comput. Mol. Sci. 2014, 4, 325–362. 10.1002/wcms.1175. [DOI] [Google Scholar]
- Huang C.; Carter E. A. Potentialfunctionalembeddingtheoryformolecules and materials. J. Chem. Phys. 2011, 135, 194104. 10.1063/1.3659293. [DOI] [PubMed] [Google Scholar]
- Huang C.; Pavone M.; Carter E. A. Quantum mechanical embedding theory based on a unique embedding potential. J. Chem. Phys. 2011, 134, 154110. 10.1063/1.3577516. [DOI] [PubMed] [Google Scholar]
- Yu K.; Libisch F.; Carter E. A. Implementation of density functional embedding theory within the projectoraugmented-wave method and applications to semiconductor defect states. J. Chem. Phys. 2015, 143, 102806. 10.1063/1.4922260. [DOI] [PubMed] [Google Scholar]
- Manby F. R.; Stella M.; Goodpaster J. D.; Miller T. F. A Simple, ExactDensity-Functional-TheoryEmbedding Scheme. J. Chem. Theory Comput. 2012, 8, 2564–2568. 10.1021/ct300544e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chulhai D. V.; Goodpaster J. D. Projection-Based Correlated Wave FunctioninDensityFunctionalTheoryEmbedding for Periodic Systems. J. Chem. Theory Comput. 2018, 14, 1928–1942. 10.1021/acs.jctc.7b01154. [DOI] [PubMed] [Google Scholar]
- Yu K.; Carter E. A. Extending density functional embedding theory for covalently bonded systems. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E10861–E10870. 10.1073/pnas.1712611114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzner W.; Vollhardt D. Correlated Lattice Fermions in d = ∞ Dimensions. Phys. Rev. Lett. 1989, 62, 324–327. 10.1103/PhysRevLett.62.324. [DOI] [PubMed] [Google Scholar]
- Georges A.; Krauth W. Numerical solution of the d = ∞ Hubbard model: Evidence for a Mott transition. Phys. Rev. Lett. 1992, 69, 1240–1243. 10.1103/PhysRevLett.69.1240. [DOI] [PubMed] [Google Scholar]
- Georges A.; Kotliar G.; Krauth W.; Rozenberg M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. 10.1103/RevModPhys.68.13. [DOI] [Google Scholar]
- Lan T. N.; Kananenka A. A.; Zgid D. Communication: Towards ab initio selfenergy embedding theory in quantum chemistry. J. Chem. Phys. 2015, 143, 241102. 10.1063/1.4938562. [DOI] [PubMed] [Google Scholar]
- Lan T. N.; Zgid D. Generalized Self Energy Embedding Theory. J. Phys. Chem. Lett. 2017, 8, 2200–2205. 10.1021/acs.jpclett.7b00689. [DOI] [PubMed] [Google Scholar]
- Zhu T.; Jimenez-Hoyos C. A.; McClain J.; Berkelbach T. C.; Chan G. K.-L.. Coupled-cluster impurity solvers for dynamical mean-field theory. arXiv:1905.12050v1; 2019. [Google Scholar]
- Ekert A.; Knight P. L. Entangled quantum systems and the Schmidt decomposition. Am. J. Phys. 1995, 63, 415–423. 10.1119/1.17904. [DOI] [Google Scholar]
- Klich I. Lower entropy bounds and particle number fluctuations in a Fermi sea. J. Phys. A: Math. Gen. 2006, 39, L85. 10.1088/0305-4470/39/4/L02. [DOI] [Google Scholar]
- Peschel I.; Eisler V. Reduceddensitymatrices and entanglement entropy in free lattice models. J. Phys. A: Math. Theor. 2009, 42, 504003. 10.1088/1751-8113/42/50/504003. [DOI] [Google Scholar]
- Peschel I. Special Review: Entanglement in Solvable Many-Particle Models. Braz. J. Phys. 2012, 42, 267–291. 10.1007/s13538-012-0074-1. [DOI] [Google Scholar]
- Barnett S. M.; Phoenix S. J. Bell’s inequality and the Schmidt decomposition. Phys. Lett. A 1992, 167, 233–237. 10.1016/0375-9601(92)90196-S. [DOI] [Google Scholar]
- Acín A.; Andrianov A.; Costa L.; Jané E.; Latorre J. I.; Tarrach R. Generalized Schmidt Decomposition and Classification of Three-Quantum-Bit States. Phys. Rev. Lett. 2000, 85, 1560–1563. 10.1103/PhysRevLett.85.1560. [DOI] [PubMed] [Google Scholar]
- Ichikawa T.; Tsutsui I.; Cheon T. Quantum game theory based on the Schmidt decomposition. J. Phys. A: Math. Theor. 2008, 41, 135303. 10.1088/1751-8113/41/13/135303. [DOI] [Google Scholar]
- Knizia G.; Chan G. K.-L. Density Matrix Embedding: A Simple Alternative to Dynamical Mean-Field Theory. Phys. Rev. Lett. 2012, 109, 186404. 10.1103/PhysRevLett.109.186404. [DOI] [PubMed] [Google Scholar]
- Knizia G.; Chan G.K.-L. DensityMatrix Embedding: A Strong-Coupling Quantum Embedding Theory. J. Chem. Theory Comput. 2013, 9, 1428–1432. 10.1021/ct301044e. [DOI] [PubMed] [Google Scholar]
- Zheng B.-X.; Chan G. K.-L. Groundstate phase diagram of the square lattice Hubbard model from density matrix embedding theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 035126 10.1103/PhysRevB.93.035126. [DOI] [Google Scholar]
- Zheng B.-X.; Kretchmer J. S.; Shi H.; Zhang S.; Chan G. K.-L. Cluster size convergence of the density matrix embedding theory and its dynamical cluster formulation: A study with an auxiliary-field quantum Monte Carlo solver. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 045103 10.1103/PhysRevB.95.045103. [DOI] [Google Scholar]
- Bulik I. W.; Scuseria G. E.; Dukelsky J. Density matrix embedding from broken symmetry lattice mean fields. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 035140 10.1103/PhysRevB.89.035140. [DOI] [Google Scholar]
- Bulik I. W.; Chen W.; Scuseria G. E. Electron correlation in solids via density embedding theory. J. Chem. Phys. 2014, 141, 054113 10.1063/1.4891861. [DOI] [PubMed] [Google Scholar]
- Fertitta E.; Booth G. H. Rigorous wave function embedding with dynamical fluctuations. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98, 235132. 10.1103/PhysRevB.98.235132. [DOI] [Google Scholar]
- Fertitta E.; Booth G. H. Energyweighted density matrix embedding of open correlated chemical fragments. J. Chem. Phys. 2019, 151, 014115 10.1063/1.5100290. [DOI] [PubMed] [Google Scholar]
- Wu X.; Cui Z.-H.; Tong Y.; Lindsey M.; Chan G. K.-L.; Lin L.. Projected Density Matrix Embedding Theory with Applications to the Two-Dimensional Hubbard Model, arXiv:1905.00886v2; 2019. [Google Scholar]
- Tsuchimochi T.; Welborn M.; Van Voorhis T. Density matrix embedding in an antisymmetrized geminal power bath. J. Chem. Phys. 2015, 143, 024107 10.1063/1.4926650. [DOI] [PubMed] [Google Scholar]
- Hermes M. R.; Gagliardi L. Multiconfigurational Self-Consistent Field Theory with Density Matrix Embedding: The Localized Active Space Self-Consistent Field Method. J. Chem. Theory Comput. 2019, 15, 972–986. 10.1021/acs.jctc.8b01009. [DOI] [PubMed] [Google Scholar]
- Pham H. Q.; Bernales V.; Gagliardi L. Can Density Matrix Embedding Theory with the Complete Activate Space SelfConsistent Field Solver Describe Single and Double Bond Breaking in Molecular Systems?. J. Chem. Theory Comput. 2018, 14, 1960–1968. 10.1021/acs.jctc.7b01248. [DOI] [PubMed] [Google Scholar]
- Booth G. H.; Chan G. K.-L. Spectral functions of strongly correlated extended systemsviaanexactquantumembedding. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 155107. 10.1103/PhysRevB.91.155107. [DOI] [Google Scholar]
- Kretchmer J. S.; Chan G. K.-L. A realtime extension of density matrix embedding theory for non-equilibrium electron dynamics. J. Chem. Phys. 2018, 148, 054108 10.1063/1.5012766. [DOI] [PubMed] [Google Scholar]
- Tran H. K.; Van Voorhis T.; Thom A. J. W. Using SCF meta-dynamics to extend density matrix embedding theory to excited states. J. Chem. Phys. 2019, 151, 034112. 10.1063/1.5096177. [DOI] [PubMed] [Google Scholar]
- Wouters S.; Jiménez-Hoyos C. A.; Sun Q.; Chan G. K.-L. A Practical Guide to Density Matrix Embedding Theory in Quantum Chemistry. J. Chem. Theory Comput. 2016, 12, 2706–2719. 10.1021/acs.jctc.6b00316. [DOI] [PubMed] [Google Scholar]
- Welborn M.; Tsuchimochi T.; Van Voorhis T. Bootstrap embedding: An internally consistent fragment-based method. J. Chem. Phys. 2016, 145, 074102 10.1063/1.4960986. [DOI] [PubMed] [Google Scholar]
- Hubbard J.; Flowers B. H. Electron correlations in narrow energy bands. Proc. R. Soc. London, Ser. A 1963, 276, 238–257. 10.1098/rspa.1963.0204. [DOI] [Google Scholar]
- Ricke N.; Welborn M.; Ye H.-Z.; Van Voorhis T. PerformanceofBootstrapEmbedding for long-range interactions and 2D systems. Mol. Phys. 2017, 115, 2242–2253. 10.1080/00268976.2017.1290839. [DOI] [Google Scholar]
- Ye H.-Z.; Welborn M.; Ricke N. D.; Van Voorhis T. Incremental embedding: A density matrix embedding scheme for molecules. J. Chem. Phys. 2018, 149, 194108. 10.1063/1.5053992. [DOI] [PubMed] [Google Scholar]
- Yang W.; Wu Q. Direct Method for Optimized Effective Potentials in DensityFunctional Theory. Phys. Rev. Lett. 2002, 89, 143002. 10.1103/PhysRevLett.89.143002. [DOI] [PubMed] [Google Scholar]
- Wu Q.; Yang W. A direct optimization method for calculating density functionals and exchange-correlation potentials from electron densities. J. Chem. Phys. 2003, 118, 2498–2509. 10.1063/1.1535422. [DOI] [Google Scholar]
- Wu Q.; Van Voorhis T. Direct optimization method to study constrained systems within density-functional theory. Phys. Rev. A: At., Mol., Opt. Phys. 2005, 72, 024502 10.1103/PhysRevA.72.024502. [DOI] [Google Scholar]
- Schlegel H. B.; McDouall J. J. W. In Computational Advances in Organic Chemistry: Molecular Structure and Reactivity; Ögretir C., Csizmadia I. G., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1991; pp 167–185. [Google Scholar]
- Boys S. F. Construction of Some Molecular Orbitals to Be Approximately Invariant for Changes from One Moleculeto Another. Rev. Mod. Phys. 1960, 32, 296–299. 10.1103/RevModPhys.32.296. [DOI] [Google Scholar]
- Yang J.; Kurashige Y.; Manby F. R.; Chan G. K. L. Tensor factorizations of local second-order Møller-Plesset theory. J. Chem. Phys. 2011, 134, 044123 10.1063/1.3528935. [DOI] [PubMed] [Google Scholar]
- Yang J.; Chan G. K.-L.; Manby F. R.; Schütz M.; Werner H.-J. The orbitalspecific-virtual local coupled cluster singles and doubles method. J. Chem. Phys. 2012, 136, 144105. 10.1063/1.3696963. [DOI] [PubMed] [Google Scholar]
- Häser M.; Ahlrichs R. Improvements on the direct SCF method. J. Comput. Chem. 1989, 10, 104–111. 10.1002/jcc.540100111. [DOI] [Google Scholar]
- Strout D. L.; Scuseria G. E. A quantitative study of the scaling properties of the Hartree-Fock method. J. Chem. Phys. 1995, 102, 8448–8452. 10.1063/1.468836. [DOI] [Google Scholar]
- Eichkorn K.; Treutler O.; Öhm H.; Häser M.; Ahlrichs R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995, 240, 283–290. 10.1016/0009-2614(95)00621-A. [DOI] [Google Scholar]
- Eichkorn K.; Weigend F.; Treutler O.; Ahlrichs R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Acc. 1997, 97, 119–124. 10.1007/s002140050244. [DOI] [Google Scholar]
- Weigend F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
- Weigend F. A fully direct RI-HF algorithm: Implementation, optimized auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. 10.1039/b204199p. [DOI] [Google Scholar]
- Becke A. D. A new mixing of HartreeFock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. 10.1063/1.464304. [DOI] [Google Scholar]
- Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Shao Y.; Gan Z.; Epifanovsky E.; Gilbert A. T.; Wormit M.; Kussmann J.; Lange A. W.; Behn A.; Deng J.; Feng X.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. 10.1080/00268976.2014.952696. [DOI] [Google Scholar]
- Ye H.-Z.Frankenstein: An Electronic Structure Method Development Platform. https://github.com/hongzhouye/frankenstein (2019).
- Press W.; Vetterling W.. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press, 1992. [Google Scholar]
- Ghosh D.; Hachmann J.; Yanai T.; Chan G. K.-L. Orbital optimization in the density matrix renormalization group, with applications to polyenes and βcarotene. J. Chem. Phys. 2008, 128, 144117. 10.1063/1.2883976. [DOI] [PubMed] [Google Scholar]
- Sharma S.; Chan G. K.-L. Spin-adapted density matrix renormalization group algorithms for quantum chemistry. J. Chem. Phys. 2012, 136, 124121. 10.1063/1.3695642. [DOI] [PubMed] [Google Scholar]
- Olivares-Amaya R.; Hu W.; Nakatani N.; Sharma S.; Yang J.; Chan G. K.-L. The ab-initio density matrix renormalization group in practice. J. Chem. Phys. 2015, 142, 034102 10.1063/1.4905329. [DOI] [PubMed] [Google Scholar]
- Roos B. O.; Taylor P. R.; Sigbahn P. E. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. 10.1016/0301-0104(80)80045-0. [DOI] [Google Scholar]
- Hehre W. J.; Stewart R. F.; Pople J. A. Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals. J. Chem. Phys. 1969, 51, 2657–2664. 10.1063/1.1672392. [DOI] [Google Scholar]
- Hachmann J.; Dorando J. J.; Avilés M.; Chan G. K.-L. The radical character of the acenes: A density matrix renormalization group study. J. Chem. Phys. 2007, 127, 134309. 10.1063/1.2768362. [DOI] [PubMed] [Google Scholar]
- Hajgató B.; Szieberth D.; Geerlings P.; De Proft F.; Deleuze M. S. A benchmark theoretical study of the electronic ground state and of the singlet-triplet split of benzene and linear acenes. J. Chem. Phys. 2009, 131, 224321. 10.1063/1.3270190. [DOI] [PubMed] [Google Scholar]
- Sharma P.; Bernales V.; Knecht S.; Truhlar D. G.; Gagliardi L. Density matrix renormalization group pair-density functional theory (DMRG-PDFT): singlet-triplet gaps in polyacenes and polyacetylenes. Chem. Sci. 2019, 10, 1716–1723. 10.1039/C8SC03569E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C. Embedded Cluster Density ApproximationforExchange-CorrelationEnergy: A Natural Extension of the Local Density Approximation. J. Chem. Theory Comput. 2018, 14, 6211–6225. 10.1021/acs.jctc.8b00471. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.