Abstract
Conservation practitioners have long recognized ecological connectivity as a global priority for preserving biodiversity and ecosystem function. In the early years of conservation biology, ecologists extended principles of island biogeography to assess connectivity using measures of source patch proximity and other metrics derivable from binary maps of habitat. From 2006–2008, the late Brad McRae introduced circuit theory to many ecologists and conservation biologists as an alternative approach to model gene flow and the dispersal or movement routes of organisms. He posited concepts and metrics from electrical circuit theory as a robust way to quantify movement across multiple possible paths in a landscape, not just a single least-cost path or corridor. Here we discuss applications of circuit theory and related tools to the science and practice of connectivity conservation. We begin with a brief introduction to the foundations of circuit theory and a synthesis of recent publications from multiple geographies. We then sample and explore the diverse array of applications of circuit theory and the open-source software Circuitscape, focusing on how these tools have been used to understand genetic structuring, the movement and dispersal paths of organisms, habitat corridors and barriers, and the impacts of humans and climate change on connectivity. Finally, we consider the impact that circuit theory is likely to have on conservation science and practitioners, as well as the maintenance and restoration of connectivity for species and fundamental ecological processes around the globe.
INTRODUCTION
Ecological connectivity is a global priority for preserving biodiversity and ecosystem function (UNEP 2015; IUCN 2017) and has long been of interest to conservation biologists (Harris 1984). In the early years of conservation biology, ecologists extended principles of island biogeography to assess connectivity based upon proximity to source patches (MacArthur & Wilson 1967) and other metrics derivable from binary maps containing habitat patches embedded in a non-habitat matrix (e.g., With et al. 1997). The introduction of least-cost modeling in the early 1990s (Knaapen et al. 1992) was a major advancement in connectivity and movement corridor research and quickly became the dominant paradigm for evaluating connectivity for animals. However, least-cost paths often have clear limitations, including an assumption that individuals have perfect knowledge of the landscape and therefore select a single optimal route. In three papers published during 2006–2008, Brad McRae introduced circuit theory to many ecologists and conservation biologists as an alternative, process-driven approach to modeling gene flow and the dispersal or movement routes of organisms (see below). Drawing from his background in electrical engineering, as well as the seminal work of Doyle & Snell (1984) and others, McRae’s key innovation was recognizing that circuit theory permitted a robust way to quantify gene flow. The approach provided a much-needed theoretical basis for understanding and mapping patterns of connectivity and has been rapidly adopted in conservation biology, other ecological disciplines, and beyond. The development of accompanying software, such as the open-source program Circuitscape (McRae et al. 2008, 2013; www.circuitscape.org), has provided accessible means of implementing circuit theory concepts across a range of projects and disciplines. Additional software and development topics are described in Supporting Information.
In the wake of Brad McRae’s untimely death in July 2017 (Lawler et al. in review), this review explores the importance and key contributions of circuit theory to connectivity conservation and related issues. We begin by briefly describing the foundations of circuit theory, including key concepts, outputs, and comparisons with other approaches to evaluating connectivity. We then describe the theory’s diversity of applications in conservation and ecology, including a synthesis of relevant publications across a variety of topics and from multiple geographies. Finally, we look toward the future and consider how new applications of circuit theory might continue to benefit conservation theory and practice, particularly in an era of global change.
Foundations of Circuit Theory in Conservation
Brad McRae posited circuit theory as an elegant alternative approach to model gene flow and organismal movement in a series of three papers published during 2006–2008. McRae (2006) linked the findings of Doyle & Snell (1984) and Chandra et al. (1996) to population genetics and landscape ecology. Specifically, Doyle & Snell (1984) demonstrated that resistance distances from circuit theory are directly proportional to the movements of Markovian random walkers on graphs, and Chandra et al. (1996) related resistance distances to “commute times,” or the time it takes a random walker to travel from one point to another and back again. McRae (2006) described the concept that the genetic distance among subpopulations of interest can be estimated by representing the landscape as a circuit board, where each pixel in a raster depiction of the landscape is a resistor, and gene flow between any two subpopulations occurs via all possible chains of resistors linking them, not just along the single chain with the lowest sum of resistances (i.e., the least-cost path). He coined this notion “isolation by resistance” (IBR), which has practical consequences in the context of conservation. For example, in IBR (but not least-cost models) increasing the number of paths always decreases the total resistance and genetic distance among subpopulations, and habitat degradation increases genetic distance, even outside the least-cost path. Its theoretical foundation and computational efficiency has made circuit theory a powerful and defensible tool for understanding potential gene flow, animal movement routes, and landscape connectivity.
The second foundational paper (McRae & Beier 2007) demonstrated that IBR explained genetic patterns of mammal (wolverine, Gulo gulo) and plant (bigleaf mahogany, Swetenia macrophylla) populations about 50–200% better than two conventional approaches, namely isolation by distance and least-cost paths. The findings were striking because the species were undergoing rapid human-caused demographic changes, violating the IBR model assumption that all populations are in genetic equilibrium (i.e., based on the response variable, FST). This robustness suggested that circuit theory could be applied to the variety of other landscapes experiencing human-caused changes.
Finally, McRae et al. (2008) introduced many readers to the key concepts and metrics used in electrical circuit theory, and how they could be applied to model and map the process of connectivity over extensive landscape, habitat, or population networks (using georeferenced raster grids). Two of the most commonly used metrics include current density and effective resistance. Current density provides an estimate of the net movement probabilities (or flow) of random walkers through a given grid cell. Effective resistance permits a pairwise distance-based measure of isolation among populations or sites (see also McRae & Beier 2007). McRae et al. (2008) illustrated how circuit theory could be used to identify multiple (i.e., redundant) movement pathways or habitat corridors and reveal, for example, critical ‘pinch points’ constraining potential flow between focal areas. Redundancy is a measure of the number of possible pathways between focal points and reflects a fundamental relationship that is the ratio of least-cost distance to effective resistance (see also Koen et al. 2012 and Marrotte & Bowman 2017 for in depth treatments of this topic). Because circuit theory uses the same underlying landscape resistance data used by least-cost and other connectivity models, it could readily be added to the toolkits of conservation planners. In addition, McRae et al. (2008) introduced many readers to Circuitscape software, opening the door to diverse applications.
Applications of Circuit Theory to Conservation
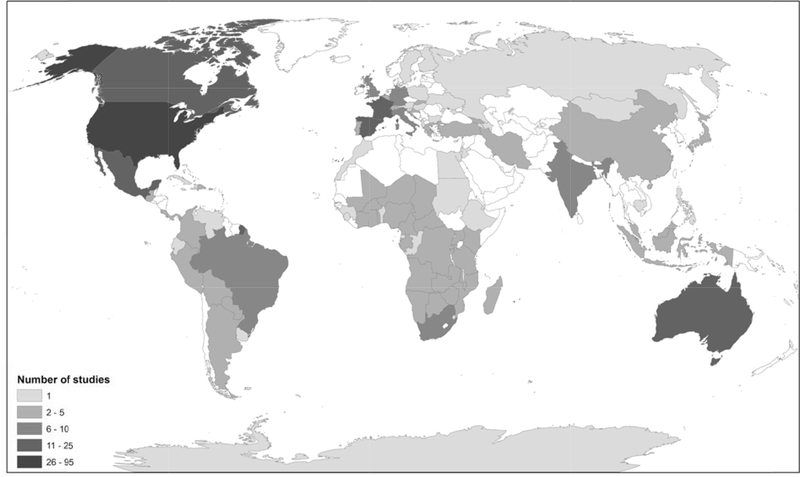
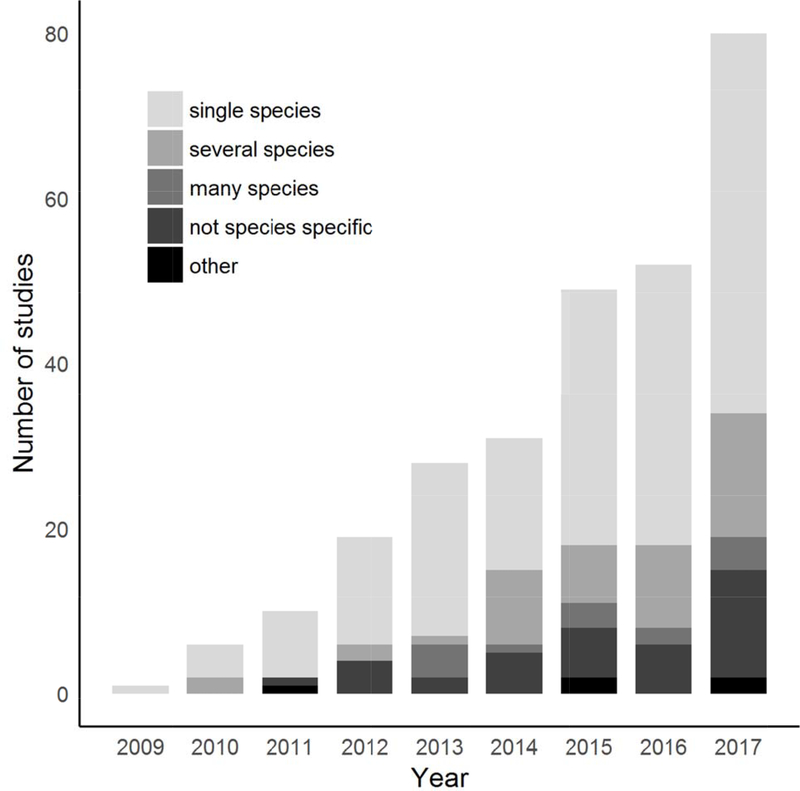
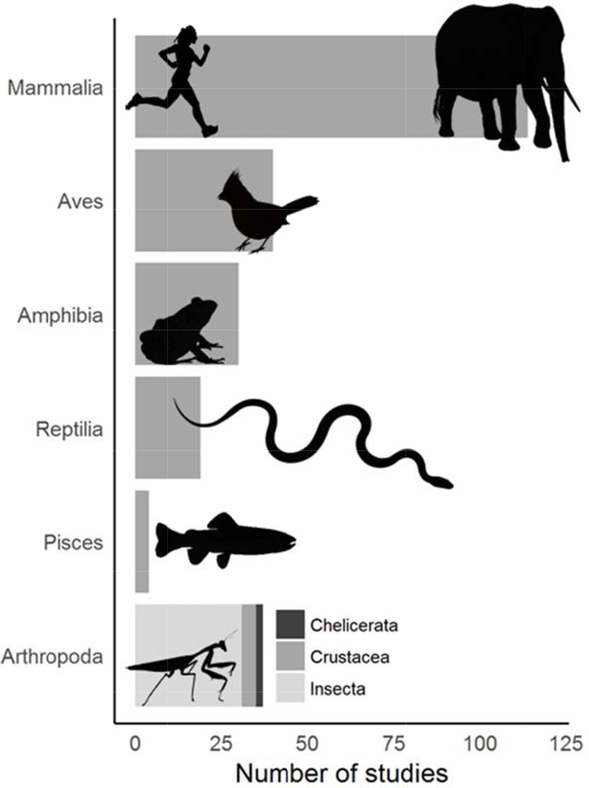
Circuit theory has been applied to a wide range of conservation questions and challenges. Because Circuitscape is the principal tool that researchers and practitioners use to apply the method, we reviewed 459 papers identified by either Web of Science or Google Scholar that cited McRae et al. (2008) or the Circuitscape user guide (McRae & Shah 2009; McRae et al. 2013). Of these studies, 277 directly used the software. Applications ranged across disciplines from conservation to evolutionary biology, from anthropology to epidemiology, and more. Circuitscape has been applied on every continent (including off the coast of Antarctica; Dambach et al. 2016), and several applications spanned multiple continents (e.g., Lawler et al. 2013, Tassi et al. 2015; Fig. 1). Whatever the geographic or conservation context, Circuitscape has been most frequently applied to single, focal species, though studies of two or more species are becoming more common (Fig. 2). The vast majority of studies addressed animals (n = 228), but ten focused on plants, and one on protists (Dong et al. 2016). Mammals were by far the most common vertebrates studied, followed by birds, amphibians, reptiles, and fish, though arthropods have been studied almost as frequently as birds (Fig. 3). At least five mammal-focused studies addressed human genomics or movement patterns.
Figure 1.
Number of peer-reviewed studies that used Circuitscape, by nation for the period January 2009 – February 2018. Three studies that were continental in their spatial extent are not represented in this map.
Figure 2.
Number of peer-reviewed studies that used Circuitscape, by year (through 2017) and number of species (several species, 2–10; many species, > 10). Studies that modeled structural connectivity or addressed communities without targeting particular species are termed ‘not species specific;’ studies that compared models, or modeled physical processes (e.g., hydraulic resistance in roots; Zeppenfeld et al. 2017) are termed ‘other.’
Figure 3.
Number of peer-reviewed studies that applied Circuitscape to research questions in the animal kingdom (vertebrate classes Mammalia, Aves, Amphibia, Reptilia, and Pisces; invertebrate arthropod subphyla Chlicerata, Crustacea, and Insecta) for the period January 2009 – February 2018.
Below, we examine the impressive range and diversity of circuit-theoretic and Circuitscape applications. Specifically, we highlight how circuit theory has been used to understand genetic structuring, the movement and dispersal paths of organisms, habitat corridors and barriers, and the impacts of humans and climate change on connectivity. Additional topic areas and examples may be found in the Supporting Information.
Landscape and Population Genetics
The foundational papers on circuit theory energized the emerging field of landscape genetics (Guillot et al. 2009; Manel & Holderegger 2013). Using genetic data to inform models of landscape resistance to movement using circuit theory has since become a standard practice (Zeller et al. 2012; Simpkins et al. 2018). This information has been useful in formalizing the incorporation of landscape structure and complexity into conservation plans for many species and ecosystems. For example, the multi-species Washington Connected project (WWHCWG 2010) incorporated mountain goat connectivity based on genetic circuit theory models (Shirk et al. 2010), and the Washington-British Columbia Climate-Connectivity project (Krosby et al. 2016) spurred additional research using genetic and circuit theoretic approaches for assessing potential impacts and adaptation actions under climate change (Parks et al. 2015). Indeed, circuit theory has been used in multiple ways to explore the potential impacts of climate change on landscape genetics. A few studies have explored how historical changes to Earth’s climate have affected connectivity, resulting in modern genetic patterns (Bell et al. 2010; Ortego et al. 2015) or have examined the impact climate change will have on future genetic patterns (Velo-Anton et al. 2013).
Despite its widespread use and contributions, the application of circuit theory in genetics is not yet fully realized. Initial statistical approaches based on comparing inter-individual genetic distances with resistance distances (e.g., using Mantel tests) often led to faulty inferences by incorrectly assuming linearity, ignoring spatial structure in the data, and failing to recognize that genetic distances can be affected by variable local population density (Legendre & Fortin 2010; Jaquiéry et al. 2011; Graves et al. 2013). Other recent approaches use appropriate probability distributions for distance data (Hanks & Hooten 2013) and newer IBR models accommodate variation in population sizes to some extent (Petkova et al. 2016). Even if the basic IBR model assumptions are met, challenges remain in automating procedures for how to weigh various environmental factors and how to account for uncertainty in noisy estimates of landscape variables (Dudaniec et al. 2016). In their comparison of microsatellite genetic datasets to maps of current density derived using circuit theory, Marrotte et al. (2017) found that current density was not usually a good predictor of gene flow for four terrestrial mammal species in Ontario, especially where habitat amount was high or pinch points were observed. Overall, these and numerous other efforts to extend circuit theory underscore its foundational and future importance to landscape genetics.
Identifying and Conserving Pathways and Corridors for Animal Movement
Circuit theory was quickly taken up and applied by conservation biologists and ecologists not only to predict population-level patterns of gene flow, but also to understand how landscape features influence individual movement paths, with implications for the conservation and restoration of habitat corridors, as well as targeted studies of movement (Dickson et al. 2013). The breadth of applications, along with comparative method studies, have increased our understanding of the strengths of circuit theory in conservation, and highlighted its complementarity with other methods for predicting movement, including least-cost paths (e.g., Howey et al. 2011; Mateo-Sanchez et al. 2015; Marrotte & Bowman 2017). Circuit theory is particularly appropriate when the assumption of moving individuals having limited knowledge of the surrounding landscape is met (McClure et al. 2016; Keeley et al. 2017; Maiorano et al. 2017).
Circuit theory’s basis in random walk theory results in an implicit assumption that individuals moving across a landscape have no knowledge of relative resistance beyond their immediate surroundings, making it particularly appropriate for modeling natal dispersal paths (McRae et al. 2008). Applications to predicting dispersal corridors for large, wide-ranging carnivores have been common (e.g., Proctor et al. 2015; Ahmadi et al. 2017; Gantchoff & Belant 2017; McClure et al. 2017), but circuit theory has also seen utility in modeling amphibian dispersal via surface water networks of Australia (Bishop-Taylor et al. 2015), dispersal paths of subterranean beetles via substratum karst systems (Rizzo et al. 2017), marine shrimp larvae dispersal via ocean currents (Dambach et al. 2016), the dispersal of early human populations in Africa and the Caucasus (Tassi et al. 2015; Tarkhnishvili et al. 2016), and even the pathways of early explorers (e.g., Hernando de Soto’s route through the Appalachian Mountains in 1540; Thayn et al. 2016). Advantages of circuit theory may be less pronounced when applied to the movements of individuals through known landscapes. For example, circuit theory and least-cost path models have been shown to perform comparably in predicting seasonal ungulate migration routes (Poor et al. 2012; McClure et al. 2016). Still, circuit theory has been found suitable for characterizing relative frequency of routine movements along multiple potential paths through urban and other fragmented landscapes (e.g., Braaker et al. 2014; Rödder et al. 2016; Grafius et al. 2017).
Given its utility for predicting high-use animal movement routes, researchers have applied circuit theory to evaluate alternatives for establishment of protected areas to enhance connectivity among populations, e.g., for pumas in the Atlantic Forest of southeast Brazil (Castilho et al. 2015), for forest understory birds in Costa Rica (Fagan et al. 2016), and for giant pandas (Ailuropoda melanoleuca) in China’s Qinling Mountains (Wang et al. 2014). Circuit theory models have also been used to identify corridors between occupied and unoccupied habitat areas to promote recolonization of a species’ historic range, or to identify areas suitable for habitat restoration (e.g., Jarchow et al. 2016; Ziółkowska et al. 2016; Gantchoff & Belant 2017). Similarly, other applications have identified potential pathways for spread of invasive species, diseases, and pathogens (see Supporting Information for further details).
Conservation biologists often wish to protect corridors that promote movement of more than one species, and have used circuit theory to assess the functionality and efficiency of potential multi-species corridors (e.g., Koen et al. 2014; Bleyhl et al. 2017; Lechner et al. 2017). Several studies (e.g., Epps et al. 2011; Breckheimer et al. 2014) have shown that corridors designed for wide-ranging umbrella species enhance connectivity for less vagile organisms with similar habitat requirements, and Brodie et al. (2015) showed that multi-species corridors tailored to ecologically similar species (e.g., carnivores and herbivores) can be highly effective for all species. Dilkina et al. (2017) explored the cost effectiveness of grizzly bear (Ursus arctos) and wolverine (Gulo gulo) corridors by optimizing corridor selection under a constrained budget. Even greater generality can result from ‘species-agnostic’ approaches to estimating ecological flows that base landscape resistance on the degree to which habitats are unaltered or otherwise modified by humans (e.g., Bennie et al. 2014; Dickson et al. 2017).
Anthropogenic Barriers to Connectivity
Circuit theory has been used to understand how humans impact movement corridors and where mitigating these impacts might be most crucial to maintaining or restoring connectivity. Indeed, understanding the effects of linear infrastructure such as transportation corridors and other barriers (e.g., international boundary structures, fence lines) on connectivity and gene flow was a primary impetus for McRae’s interest in the theory and development of Circuitscape (McRae 2006). Examples include work by Litvaitis et al. (2015) exploring the potential effects of roads on the movement of wide-ranging carnivores in New Hampshire, and work by Naidoo et al. (2018) examining barrier effects on movement corridors for African elephants (Loxodonta africana). Guidance for direct application of these approaches with transportation agencies has been provided by Beier et al. (2011), and initial explorations are underway that explicitly incorporate volume of traffic on highways into estimates of landscape permeability (e.g., Theobald et al. 2012). Yet, work integrating connectivity across transportation infrastructure, particularly within the context of regional transportation planning, remains understudied (e.g., Mateo-Sanchez et al. 2014), and this gap is especially important given the ubiquity of transportation and its strong population and genetic effects on various animals globally (Trombulak & Frissell 2000). Beyond the impacts of transportation corridors, circuit theory applications have addressed a wide range of anthropogenic impacts on connectivity, including urbanization, agriculture, and energy infrastructure (see Supporting Information).
More recent studies have assessed the vulnerability of populations to climate change due to fragmentation that could potentially impede adaptive shifts in distributions (e.g., Leonard et al. 2017a). A number of studies used Circuitscape to explicitly plan for climate-driven movements. For example, Lawler et al. (2013) used species distribution models to map the routes that organisms might follow to track shifting climates, and Littlefield et al. (2017) mapped connections between climatic conditions today and where those conditions will be in the future (i.e., climate analogs). These and other studies have used Circuitscape to model climate, sea-level rise, range shifts, and climate-driven landscape change projections to understand or anticipate the impact of climate change on species and their movements.
Non-traditional and Emergent Applications of Circuit Theory
Fire Spread
Circuit theory has provided an intuitive analogue to the process of wildfire movement (i.e., spread) across heterogeneous landscapes. The approach accommodates important stochastic properties of wildfire by modeling probabilistic spread between adjacent neighbors in a landscape network (Gray & Dickson 2015). Circuit theory also accommodates the critical role of spatial context in estimating fire likelihood, as areas on the landscape can burn far away from an ignition source. In this case, circuit conductance (the inverse of resistance) is a surrogate for the ease of fire spread across the landscape. Fuels, topography, and other biophysical variables that influence the spread of fire may be flexibly integrated into a conductance surface in a circuit-theoretic model (Gray & Dickson 2015, 2016). Resulting metrics (e.g., current density and centrality) and maps of potential fire connectivity may be used to target areas on the landscape where fuel breaks could most effectively hinder fire movement through wildlife habitat (Welch et al. 2015), and disrupt the invasive grass-fire cycle (Gray & Dickson 2016). In addition, wall-to-wall estimates of fire connectivity can be useful to identify areas of highest fire likelihood across a landscape and, consequently, the natural and human infrastructure at greatest relative risk from wildfire (Gray & Dickson 2015).
Water Flow
The electronic circuit analogy has been used in a variety of subdisciplines within the field of hydrology. As early as 1962, electronic circuit models were seen as an innovative approach to analyzing groundwater flows (Robinove 1962). In these early studies, physical circuit models, often involving the careful placement and soldering of thousands of resistors for each individual run, were constructed in the lab to simulate the groundwater system (Miley & Kuelske 1990). With increased computer processing power this approach was supplanted by more contemporary node-based numerical models that are in wide use today (Fetter 2001). The use of such models has significantly advanced scientists’ understanding of flow connectivity within aquifers as well as between ground- and surface-waters (Singh 2014). Application of resistance-based groundwater models has provided insights into questions that are highly relevant to the field of conservation biology, including understanding water budgets in the midst of rapid human development (Tillman et al. 2016), the effects of flow management (Shafroth et al. 2010) groundwater pumping (Falke et al. 2011) on dryland stream habitats and riparian ecosystems, and the impacts of climate change on stream summer baseflows (Huntington & Niswonger 2012).
Ecosystem Services
In the context of ecosystem services, circuit theory has been used to examine the landscape genetic structure and movements of pollinators, especially bees, in response to habitat and land-use changes (e.g., Goulson et al. 2011; Lander et al. 2013; Lozier et al. 2013; Jaffe et al. 2016a, 2016b). In southeastern Australia, Luck et al. (2014) used Circuitscape to investigate the potential movements of Regent Parrots (Polytelis anthopeplus) through almond orchards, which may benefit from parrots foraging on nuts remaining after harvest, reducing the need for manual or mechanical removal. Koh et al. (2013) used circuit theory to estimate the potential flow of agricultural insect predators across habitat networks in the Midwest U.S., quantifying the pest control benefit of grassland restoration and native prairie remnants. They concluded that the flow of multiple predators on soybean aphids (Aphis glycines) was improved by the presence of adjacent, native ‘conservation plantings’ that maximize such biocontrol services.
Impacts of Circuit Theory and Future Opportunities
Circuit theory’s widespread application across multiple disciplines (beyond genetics and wildlife ecology) is a testament to its power and flexibility as a tool for exploring movement and flow across a range of scales and settings. For example, novel applications of the theory to understanding the spread of fire, water, diseases, and invasive species, as well as the future impacts of climate change on natural and human systems are transforming the way scientists, planners, managers, and decision makers think about or incorporate connectivity processes into their work. From these diverse applications, we anticipate that new areas of inquiry and tools will emerge that also can benefit the field of conservation.
Looking forward, we see a variety of opportunities for circuit theory’s continued development and use in conservation. First, a new wave of applications are emerging from advances in how we conceptualize connectivity, such as by recognizing that a range of habitat conditions can serve as a source for individuals (and genes) moving between populations. ‘Omnidirectional’ or ‘wall-to-wall’ approaches (e.g., Walpole et al. 2012; Koen et al. 2014; Pelletier et al. 2014; Anderson et al. 2016; McRae et al. 2016; Supporting Information) avoid the need to arbitrarily define and delineate discrete areas to connect (e.g., habitat cores or patches), revealing important areas for connectivity over continuous landscape gradients. Because circuit theory extends easily to other, nontraditional ‘landscapes,’ we also see a rapid expansion in efforts to quantify connectivity in other dynamic systems, such as seascapes, riverscapes, and below-ground environments (e.g., cave or karst habitats). In addition, circuit theory can be used to identify key places for mitigating or restoring connectivity (e.g., McRae et al. 2012; Torrubia et al. 2014) in areas where new investments in transportation infrastructure might prioritize crossing structures for wildlife. Second, tighter coupling between near real-time data on landscape dynamics (e.g., derived using remotely sensed images within Google’s Earth Engine environment) and estimates of landscape resistance and current flow, as well as increasingly available information (e.g., Global Positioning System or other telemetry data) specific to the movement behaviors or seasonal life-history traits of a target organism, will greatly improve insights into or tests of potential connectivity. Third, we expect that in the future, outputs from Circuitscape will see more frequent use as hypotheses to strategically inform the design and monitoring of habitat use studies and to strengthen statistical inferences drawn from hard-won field data.
Although circuit theory provides a robust and intuitive framework for analyses of gene flow, animal movement, and corridor use, it has been shown that IBR may not perform as well as some other frameworks (e.g., isolation by distance) in less fragmented landscapes (Ruiz-Gonzalez et al. 2015) or when connectivity is being assessed for migration pathways as opposed to dispersal pathways (e.g., Poor et al. 2012; McClure et al. 2016). As with any modeling framework, the assumptions and utility of a circuit-theoretic approach should always be assessed on a project-by-project basis. Additionally, several assumptions and caveats still need to be addressed, such as modeling long-distance dispersal events (McRae 2006) and asymmetric migration (McRae et al. 2008; but see Hanks 2017). Future applications of circuit theory could account for temporal variation in dispersal rates (Anderson et al. 2010; Cushman & Lewis 2010) and predicting patterns of variation at adaptive loci (e.g., Creech et al. 2017).
Since the initial applications of circuit theory in conservation, Circuitscape and other related applications have undergone rapid and near constant refinement and improvement. Increasingly, circuit theory-based analyses are being conducted on larger and more complex datasets through recent advances in open-source software (e.g., gflow; Leonard et al. 2017b), programming (e.g., the Julia numerical computing language; Bezanson et al. 2017), and cluster- or cloud-based computing resources. The Julia implementation of Circuitscape (v. 5.0) has greatly improved performance and scalability. Users are now able to solve for landscape grids that are larger or derived at finer resolutions than those used in earlier versions, as well as pairwise resistance calculations between a higher number of focal points (see also Supporting Information).
Similarly, advances in data visualization tools have assisted the communication of circuit theory results to a broader set of conservation practitioners, stakeholders, and planning efforts. A leading example is “migrations in motion” (http://maps.tnc.org/migrations-in-motion), which uses a dynamic illustration of projected species migrations under climate change (Lawler et al. 2013) and has been a powerful and accessible way for The Nature Conservancy (TNC) to communicate the potential risks of climate change to a variety of audiences, including the general public. Importantly, these advances are often occurring as scientists around the world apply circuit theory to inform applications and decision makers. In his work at TNC, McRae played a major role in the development of generalized connectivity maps produced with wall-to-wall (Anderson et al. 2016) and ‘Omniscape’ (McRae et al. 2016; Supporting Information) versions of Circuitscape models. These regional-scale flow maps remain a key component in TNC’s Conserving Nature’s Stage approach for identifying land protection priorities, which to date has helped guide decisions on US$38 million in land protection funding. In India, national policy associated with the Wildlife Protection Act, which delineates key habitat areas as tiger reserves, has been informed by Circuitscape-derived models and maps (Qureshi et al. 2014; Dutta et al. 2016).
We believe that the impact of circuit theory and Circuitscape on conservation has come from not only the theoretical basis and elegance of the approach, but also the powerful collaborations and active user community that have emerged. Because circuit theory took root so quickly and broadly, it can be expected to continue to provide a springboard for ecological understanding and remain an important tool for future researchers and conservation practitioners around the globe.
Supplementary Material
Footnotes
Supporting Information
Additional topic areas and examples using circuit theory or Circuitscape software and numerical computing methods (Appendix S1) as well as a sample gallery of map-based outputs (Appendix S2–S3), are available online. The authors are solely responsible for the content and functionality of these materials. Queries (other than absence of the material) should be directed to the corresponding author.
Literature Cited
- Ahmadi M, Nezami Balouchi B, Jowkar H, Hemami MR, Fadakar D, Malakouti-Khah S, Ostrowski S. 2017. Combining landscape suitability and habitat connectivity to conserve the last surviving population of cheetah in Asia. Diversity & Distributions 23:592–603. [Google Scholar]
- Anderson CD, Epperson BK, Fortin MJ, Holderegger R, James P, Rosenberg MS, Scribner KT, Spear SF. 2010. Considering spatial and temporal scale in landscape-genetic studies of gene flow. Molecular Ecology 19:3565–3575. [DOI] [PubMed] [Google Scholar]
- Anderson MG, Barnett A, Clark M, Prince J, Olivero Sheldon A, Vickery B. 2016. Resilient and Connected Landscapes for Terrestrial Conservation. The Nature Conservancy; Boston, MA, USA. [Google Scholar]
- Bell RC, Parra JL, Tonione M, Hoskin CJ, Mackenzie JB, Williams SE, Moritz C. 2010. Patterns of persistence and isolation indicate resilience to climate change in montane rainforest lizards. Molecular Ecology 19:2531–2544. [DOI] [PubMed] [Google Scholar]
- Beier P, Spencer W, Baldwin RF, McRae B. 2011. Toward best practices for developing regional connectivity maps. Conservation Biology 25:879–892. [DOI] [PubMed] [Google Scholar]
- Bennie J, Davies TW, Inger R, Gaston KJ. 2014. Mapping artificial lightscapes for ecological studies. Methods in Ecology and Evolution 5:534–540. [Google Scholar]
- Bezanson J, Edelman A, Karpinski S, Shah VB. 2017. Julia: A fresh approach to numerical computing. SIAM Review 59:65–98. [Google Scholar]
- Bishop–Taylor R, Tulbure MG, Broich M. 2015. Surface water network structure, landscape resistance to movement and flooding vital for maintaining ecological connectivity across Australia’s largest river basin. Landscape Ecology 30:2045–2065. [Google Scholar]
- Bleyhl B, Baumann M, Griffiths P, Heidelberg A, Manvelyan K, Radeloff VC, Zazanashvili N, Kuemmerle T. 2017. Assessing landscape connectivity for large mammals in the Caucasus using Landsat 8 seasonal image composites. Remote Sensing of Environment 193:193–203. [Google Scholar]
- Braaker S, Moretti M, Boesch R, Ghazoul J, Obrist MK, Bontadina F. 2014. Assessing habitat connectivity for ground-dwelling animals in an urban environment. Ecological Applications 24:1583–1595. [DOI] [PubMed] [Google Scholar]
- Breckheimer I, Haddad NM, Morris WF, Trainor AM, Fields WR, Jobe RT, Hudgens BR, Moody A, Walters JR. 2014. Defining and evaluating the umbrella species concept for conserving and restoring landscape connectivity. Conservation Biology 28:1584–1593. [DOI] [PubMed] [Google Scholar]
- Brodie JF, Giordano AJ, Dickson B, Hebblewhite M, Bernard H, Mohd-Azlan J, Anderson J, Ambu L. 2015. Evaluating multispecies landscape connectivity in a threatened tropical mammal community. Conservation Biology 29:122–132. [DOI] [PubMed] [Google Scholar]
- Castilho CS, Hackbart VCS, Pivello VR, dos Santos RF. 2015. Evaluating landscape connectivity for Puma concolor and Panthera onca among Atlantic Forest Protected Areas. Environmental Management 55:1377–1389. [DOI] [PubMed] [Google Scholar]
- Chandra A, Raghavan P, Ruzzo W, Smolensky R, Tiwari P. 1996. The electrical resistance of a graph captures its commute and cover times. Computational Complexity 6:312–340. [Google Scholar]
- Creech TG, Epps CW, Landguth EL, Wehausen JD, Crowhurst RS, Holton B, Monello RJ. 2017. Simulating the spread of selection-driven genotypes using landscape resistance models for desert bighorn sheep. PloS ONE 12:e0176960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cushman SA, Lewis JS. 2010. Movement behavior explains genetic differentiation in American black bears. Landscape Ecology 25:1613–1625. [Google Scholar]
- Dambach J, Raupach MJ, Leese F, Schwarzer J, Engler JO. 2016. Ocean currents determine functional connectivity in an Antarctic deep-sea shrimp. Marine Ecology 37:1336–1344. [Google Scholar]
- Dickson BG, Roemer GW, McRae BH, Rundall JM. 2013. Models of regional habitat quality and connectivity for pumas (Puma concolor) in the southwestern United States. PLoS ONE 8:e81898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson BG, Albano CM, McRae BH, Anderson JJ, Theobald DM, Zachmann LJ, Sisk TD, Dombeck MP. 2017. Informing strategic efforts to expand and connect protected areas using a model of ecological flow, with application to the western United States. Conservation Letters 10:564–571. [Google Scholar]
- Dilkina B, Houtman R, Gomes CP, Montgomery CA, McKelvey KS, Kendall K, Graves TA, Bernstein R, Schwartz MK. 2017. Trade-offs and efficiencies in optimal budget-constrained multispecies corridor networks. Conservation Biology 31:192–202. [DOI] [PubMed] [Google Scholar]
- Dong X, Li B, He F, Gu Y, Sun M, Zhang H, Tan L, Xiao W, Liu S, Cai Q. 2016. Flow directionality, mountain barriers and functional traits determine diatom metacommunity structuring of high mountain streams. Scientific Reports 6:24711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle PG, Snell JL. 1984. Random walks and electrical networks. Mathematical Association of America, Washington, DC. [Google Scholar]
- Dudaniec RY, Worthington Wilmer J, Hanson JO, Warren M, Bell S, Rhodes JR. 2016. Dealing with uncertainty in landscape genetic resistance models: a case of three co-occurring marsupials. Molecular Ecology 25:470–486. [DOI] [PubMed] [Google Scholar]
- Dutta T, Sharma S, McRae BH, Roy PS, DeFries R. 2016. Connecting the dots: mapping habitat connectivity for tigers in central India. Regional Environmental Change 16:53–67. [Google Scholar]
- Epps CW, Mutayoba BM, Gwin L, Brashares JS. 2011. An empirical evaluation of the African elephant as a focal species for connectivity planning in East Africa. Diversity & Distributions 17:603–612. [Google Scholar]
- Fagan ME, DeFries RS, Sesnie SE, Arroyo-Mora JP, Chazdon RL. 2016. Targeted reforestation could reverse declines in connectivity for understory birds in a tropical habitat corridor. Ecological Applications 26:1456–1474. [DOI] [PubMed] [Google Scholar]
- Falke J, Fausch K, Magelky R, Aldred A, Durnford D, Riley L, Oad R. 2011. The role of groundwater pumping and drought in shaping ecological futures for stream fishes in a dryland river basin of the western Great Plains, USA. Ecohydrology 4:682–697. [Google Scholar]
- Fetter C 2001. Applied Hydrogeology (Fourth Edition). Prentice Hall, Upper Saddle River, New Jersey. [Google Scholar]
- Gantchoff MG, Belant JL. 2017. Regional connectivity for recolonizing American black bears (Ursus americanus) in southcentral USA. Biological Conservation 214:66–75. [Google Scholar]
- Goulson D, Kaden JC, Lepais O, Lye GC, Darvill B. 2011. Population structure, dispersal and colonization history of the garden bumblebee Bombus hortorum in the Western Isles of Scotland. Conservation Genetics 12:867–879. [Google Scholar]
- Grafius DR, Corstanje R, Siriwardena GM, Plummer KE, Harris JA. 2017. A bird’s eye view: using circuit theory to study urban landscape connectivity for birds. Landscape Ecology 32:1771–1787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graves TA, Beier P, Royle JA. 2013. Current approaches using genetic distances produce poor estimates of landscape resistance to interindividual dispersal. Molecular Ecology 22:3888–3903. [DOI] [PubMed] [Google Scholar]
- Gray ME, Dickson BG. 2015. A new model of landscape-scale fire connectivity applied to resource and fire management in the Sonoran Desert, USA. Ecological Applications 25:1099–1113. [DOI] [PubMed] [Google Scholar]
- Gray ME, Dickson BG. 2016. Applying fire connectivity and centrality measures to mitigate the cheatgrass-fire cycle in the arid West, USA. Landscape Ecology 31:1681–1696. [Google Scholar]
- Guillot G, Leblois R, Coulon A, Frantz AC. 2009. Statistical methods in spatial genetics. Molecular Ecology 18:4734–4756. [DOI] [PubMed] [Google Scholar]
- Hanks EM, Hooten MB. 2013. Circuit theory and model-based inference for landscape connectivity. Journal of the American Statistical Association 108:22–33. [Google Scholar]
- Hanks EM. 2017. Modeling spatial covariance using the limiting distribution of spatio-temporal random walks. Journal of the American Statistical Association 112:497–507. [Google Scholar]
- Harris LD. 1984. The fragmented forest: island biogeography theory and the preservation of biotic diversity. University of Chicago Press. [Google Scholar]
- Howey M 2011. Multiple pathways across past landscapes: circuit theory as a complementary geospatial method to least cost path for modeling past movement. Journal of Archaeological Science 38:2523–2535. [Google Scholar]
- Huntington JL, Niswonger RG. 2012. Role of surface-water and groundwater interactions on projected summertime streamflow in snow dominated regions: An integrated modeling approach. Water Resources Research 48. [Google Scholar]
- International Union for Conservation of Nature (IUCN). 2017. Connectivity Conservation. Available at: https://www.iucn.org/theme/protected-areas/wcpa/what-wedo/connectivity-conservation [DOI] [PubMed]
- Jaquiéry J, Broquet T, Hirzel AH, Yearsley J, Perrin N. 2011. Inferring landscape effects on dispersal from genetic distances: how far can we go? Molecular Ecology 20:692–705. [DOI] [PubMed] [Google Scholar]
- Jarchow CJ, Hossack BR, Sigafus BH, Schwalbe CR, Muths E. 2016. Modeling habitat connectivity to inform reintroductions: a case study with the Chiricahua leopard frog. Journal of Herpetology 50:63–69. [Google Scholar]
- Jaffé R, Castilla A, Pope N, Imperatriz-Fonseca VL, Metzger JP, Arias MC, Jha S. 2016a. Landscape genetics of a tropical rescue pollinator. Conservation genetics 17:267–278. [Google Scholar]
- Jaffé R, Pope N, Acosta AL, Alves DA, Arias MC, De la Rúa P, Francisco FO, Giannini TC, González-Chaves A, Imperatriz-Fonseca VL, Tavares MG, Jha S, Carvalheiro LG. 2016b. Beekeeping practices and geographic distance, not land use, drive gene flow across tropical bees. Molecular Ecology 25:5345–5358. [DOI] [PubMed] [Google Scholar]
- Keeley AT, Beier P, Keeley BW, & Fagan ME. 2017. Habitat suitability is a poor proxy for landscape connectivity during dispersal and mating movements. Landscape & Urban Planning 161:90–102. [Google Scholar]
- Knaapen JP, Scheffer M, Harms B. 1992. Estimating habitat isolation in landscape planning. Landscape & Urban Planning 23:1–16. [Google Scholar]
- Koen EL, Bowman J, Walpole AA. 2012. The effect of cost surface parameterization on landscape resistance estimates. Molecular Ecology Resources 12:686–696. [DOI] [PubMed] [Google Scholar]
- Koen EL, Bowman J, Sadowski C, Walpole AA. 2014. Landscape connectivity for wildlife: development and validation of multispecies linkage maps. Methods in Ecology & Evolution 5:626–633. [Google Scholar]
- Koh I, Rowe HI, Holland JD. 2013. Graph and circuit theory connectivity models of conservation biological control agents. Ecological Applications 23:1554–1573. [DOI] [PubMed] [Google Scholar]
- Krosby M, Michalak J, Robbins TO, Morgan H, Norheim R, Mauger G, Murdock T. 2016. The Washington-British Columbia Transboundary Climate-Connectivity Project: Identifying climate impacts and adaptation actions for wildlife habitat connectivity in the transboundary region of Washington and British Columbia. Climate Impacts Group, University of Washington, Seattle, WA, USA. [Google Scholar]
- Lander TA, Klein EK, Stoeckel S, Mariette S, Musch B, Oddou-Muratorio S. 2013. Interpreting realized pollen flow in terms of pollinator travel paths and land-use resistance in heterogeneous landscapes. Landscape ecology 28:1769–1783. [Google Scholar]
- Lawler JJ, Ruesch AS, Olden JD, McRae BH. 2013. Projected climate-driven faunal movement routes. Ecology Letters 16:1014–1022. [DOI] [PubMed] [Google Scholar]
- Lechner AM, Sprod D, Carter O, Lefroy EC. 2017. Characterising landscape connectivity for conservation planning using a dispersal guild approach. Landscape Ecology 32:99–113. [Google Scholar]
- Legendre P, Fortin MJ. 2010. Comparison of the Mantel test and alternative approaches for detecting complex multivariate relationships in the spatial analysis of genetic data. Molecular Ecology Resources 10:831–844. [DOI] [PubMed] [Google Scholar]
- Leonard PB, Duffy EB, Baldwin RF, McRae BH, Shah VB, Mohapatra TK. 2017a. gflow: software for modelling circuit theory-based connectivity at any scale. Methods in Ecology & Evolution 8:519–526. [Google Scholar]
- Leonard PB, Sutherland RW, Baldwin RF, Fedak DA, Carnes RG, Montgomery AP. 2017b. Landscape connectivity losses due to sea level rise and land use change. Animal Conservation 20:80–90. [Google Scholar]
- Littlefield CE, McRae BH, Michalak JL, Lawler JJ, Carroll C. 2017. Connecting today’s climates to future climate analogs to facilitate movement of species under climate change. Conservation Biology 31:1397–1408. [DOI] [PubMed] [Google Scholar]
- Litvaitis JA, Reed GC, Carroll RP, Litvaitis MK, Tash J, Mahard T, Broman DJA, Callahan C, Ellingwood M. 2015. Bobcats (Lynx rufus) as a model organism to investigate the effects of roads on wide-ranging carnivores. Environmental Management 55:1366–1376. [DOI] [PubMed] [Google Scholar]
- Lozier JD, Strange JP, Koch JB. 2013. Landscape heterogeneity predicts gene flow in a widespread polymorphic bumble bee, Bombus bifarius (Hymenoptera: Apidae). Conservation Genetics 14:1099–1110. [Google Scholar]
- Luck GW, Spooner PG, Watson DM, Watson SJ, Saunders ME. 2014. Interactions between almond plantations and native ecosystems: Lessons learned from north-western Victoria. Ecological Management & Restoration 15:4–15. [Google Scholar]
- MacArthur RH, Wilson EO. 1967. The Theory of Island Biogeography. Acta Biotheoretica 50:133–136. [Google Scholar]
- Maiorano L, Boitani L, Chiaverini L, Ciucci P. 2017. Uncertainties in the identification of potential dispersal corridors: The importance of behaviour, sex, and algorithm. Basic & Applied Ecology 21:66–75. [Google Scholar]
- Manel S, Holderegger R. 2013. Ten years of landscape genetics. Trends in Ecology & Evolution 28:614–621. [DOI] [PubMed] [Google Scholar]
- Marrotte RR, Bowman J. 2017. The relationship between least-cost and resistance distance. PLoS ONE 12:e0174212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrotte RR, Bowman J, Brown MGC, Cordes C, Morris KY, Prentice MB, Wilson PJ. 2017. Multispecies genetic connectivity in a terrestrial habitat network. Movement Ecology 5:21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mateo-Sánchez MC, Cushman SA, Saura S. 2014. Connecting endangered brown bear subpopulations in the Cantabrian Range (north-western Spain). Animal conservation 17:430–440. [Google Scholar]
- Mateo-Sánchez MC, Balkenhol N, Cushman S, Pérez T, Domínguez A, Saura S. 2015. Estimating effective landscape distances and movement corridors: comparison of habitat and genetic data. Ecosphere 6:1–16. [Google Scholar]
- McClure ML, Hansen AJ, Inman RM. 2016. Connecting models to movements: testing connectivity model predictions against empirical migration and dispersal data. Landscape Ecology 31:1–14. [Google Scholar]
- McClure ML, Dickson BG, Nicholson KL. 2017. Modeling connectivity to identify current and future anthropogenic barriers to movement of large carnivores: a case study in the American Southwest. Ecology & Evolution 7:3762–3772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McRae BH. 2006. Isolation by resistance. Evolution 60:1551–1561. [PubMed] [Google Scholar]
- McRae BH, Beier P. 2007. Circuit theory predicts gene flow in plant and animal populations. Proceedings of the National Academy of Sciences 104:19885–19890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McRae BH, Dickson BG, Keitt TH, Shah VB. 2008. Using circuit theory to model connectivity in ecology, evolution, and conservation. Ecology 89:2712–2724. [DOI] [PubMed] [Google Scholar]
- McRae BH, Shah VB. 2009. Circuitscape user’s guide. The University of California; Santa Barbara. [Google Scholar]
- McRae BH, Hall SA, Beier P, Theobald DM. 2012. Where to restore ecological connectivity? Detecting barriers and quantifying restoration benefits. PLoS ONE 7:e52604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McRae BH, Shah V, Mohapatra T. 2013. Circuitscape 4 user guide. The Nature Conservancy; Available at http://www.circuitscape.org [Google Scholar]
- McRae BH, Popper K, Jones A, Schindel M, Buttrick S, Hall KR, Unnasch RS, Platt J. 2016. Conserving Nature’s Stage: Mapping Omnidirectional Connectivity for Resilient Terrestrial Landscapes in the Pacific Northwest. The Nature Conservancy, Portland OR, USA: Available at: http://nature.org/resilienceNW [Google Scholar]
- Miley GH, Kuelske KJ. 1990. Groundwater flow analysis of potential low level radioactive waste disposal sites using electrical circuit analogies Pages 229–240 in Heller M, editor. Nuclear Simulation. Springer, Berlin, Germany. [Google Scholar]
- Naidoo R, Kilian JW, Du Preez P, Beytell P, Aschenborn O, Taylor RD, Stuart-Hill G. 2018. Evaluating the effectiveness of local-and regional-scale wildlife corridors using quantitative metrics of functional connectivity. Biological Conservation 217:96–103. [Google Scholar]
- Ortego J, Gugger PF, Sork VL. 2015. Climatically stable landscapes predict patterns of genetic structure and admixture in the Californian canyon live oak. Journal of Biogeography 42:328–338. [Google Scholar]
- Parks LC, Wallin DO, Cushman SA, McRae BH. 2015. Landscape-level analysis of mountain goat population connectivity in Washington and southern British Columbia. Conservation Genetics 16:1195–1207. [Google Scholar]
- Pelletier D, Clark M, Anderson MG, Rayfield B, Wulder MA, Cardille JA. 2014. Applying circuit theory for corridor expansion and management at regional scales: tiling, pinch points, and omnidirectional connectivity. PLoS ONE 9:e84135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkova D, Novembre J, Stephens M. 2016. Visualizing spatial population structure with estimated effective migration surfaces. Nature Genetics 48:94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poor EE, Loucks C, Jakes A, Urban DL. 2012. Comparing habitat suitability and connectivity modeling methods for conserving pronghorn migrations. PLoS ONE 7:e49390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proctor MF, Nielsen SE, Kasworm WF, Servheen C, Radandt TG, Machutchon AG, Boyce MS. 2015. Grizzly bear connectivity mapping in the Canada–United States trans-border region. The Journal of Wildlife Management 79:544–558. [Google Scholar]
- Qureshi Q, Saini S, Basu P, Gopal R, Raza E, Jhalam Y. 2014. Connecting tiger populations for long-term conservation. National Tiger Conservation Authority & Wildlife Institute of India Dehradun; TR2014–02. Available at: http://www.wii.gov.in/images//images/documents/connecting_tiger.pdf [Google Scholar]
- Rizzo V, Sánchez-Fernández D, Alonso R, Pastor J, Ribera I. 2017. Substratum karstificability, dispersal and genetic structure in a strictly subterranean beetle. Journal of Biogeography 45:2527–2538. [Google Scholar]
- Robinove CJ. 1962. Ground-water studies and analog models Geological Survey Circular 468. US Department of the Interior, Geological Survey, Washington DC, USA. [Google Scholar]
- Rödder D, Nekum S, Cord AF, Engler JO. 2016. Coupling satellite data with species distribution and connectivity models as a tool for environmental management and planning in matrix-sensitive species. Environmental Management 58:130–143. [DOI] [PubMed] [Google Scholar]
- Ruiz-Gonzalez A, Cushman SA, Madeira MJ, Randi E, Gómez-Moliner BJ. 2015. Isolation by distance, resistance and/or clusters? Lessons learned from a forest-dwelling carnivore inhabiting a heterogeneous landscape. Molecular Ecology 24:5110–29. [DOI] [PubMed] [Google Scholar]
- Shafroth PB, Wilcox AC, Lytle DA, Hickey JT, Andersen DC, Beauchamp VB, Hautzinger A, McMullen LE, Warner A. 2010. Ecosystem effects of environmental flows: modelling and experimental floods in a dryland river. Freshwater Biology 55:68–85. [Google Scholar]
- Shirk AJ, Wallin DO, Cushman SA, Rice CG, Warheit KI. 2010. Inferring landscape effects on gene flow: a new model selection framework. Molecular Ecology 19:3603–3619. [DOI] [PubMed] [Google Scholar]
- Simpkins CE, Dennis TE, Etherington TR, Perry LW. 2018. Assessing the performance of common landscape connectivity metrics using a virtual ecologist approach. Ecological Modelling 367: 13–23. [Google Scholar]
- Singh A 2014. Groundwater resources management through the applications of simulation modeling: A review. Science of The Total Environment 499:414–423. [DOI] [PubMed] [Google Scholar]
- Tassi F, Ghirotto S, Mezzavilla M, Vilaca ST, De Santi L, Barbujani G. 2015. Early modern human dispersal from Africa: genomic evidence for multiple waves of migration. Investigative Genetics 6:13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarkhnishvili D, Gavashelishvili A, Murtskhvaladze M, Latsuzbaia1 A. 2016. Landscape complexity in the Caucasus impedes genetic assimilation of human populations more effectively than language or ethnicity. Human Biology 88:287–300. [DOI] [PubMed] [Google Scholar]
- Thayn JB, Sampeck K, Spaccapaniccia M. 2016. Refining Hernando de Soto’s route using electric circuit theory and Circuitscape. The Professional Geographer 68:595–602. [Google Scholar]
- Theobald DM, Reed SE, Fields K, Soule M. 2012. Connecting natural landscapes using a landscape permeability model to prioritize conservation activities in the United States. Conservation Letters 5:123–133. [Google Scholar]
- Tillman FD, Wiele SM, Pool DR. 2016. A comparison of estimates of basin-scale soil-moisture evapotranspiration and estimates of riparian groundwater evapotranspiration with implications for water budgets in the Verde Valley, Central Arizona, USA. Journal of Arid Environments 124:278–291. [Google Scholar]
- Torrubia S, McRae BH, Lawler JJ, Hall SA, Halabisky M, Langdon J, Case M. 2014. Getting the most connectivity per conservation dollar. Frontiers in Ecology & Environment 12:491–497. [Google Scholar]
- Trombulak SC, Frissell CA. 2000. Review of ecological effects of roads on terrestrial and aquatic communities. Conservation Biology 14:18–30. [Google Scholar]
- United Nations Environment Programme (UNEP). 2015. UNEP launches global connectivity conservation project. Available at: http://www.unep-wcmc.org/news/unep-launchesglobal-connectivity-conservation-project.
- Velo-Anton G, Parra JL, Parra-Olea G, Zamudio KR. 2013. Tracking climate change in a dispersal-limited species: reduced spatial and genetic connectivity in a montane salamander. Molecular Ecology 22:3261–3278. [DOI] [PubMed] [Google Scholar]
- Walpole AA, Bowman J, Murray DL, Wilson PJ. 2012. Functional connectivity of Canada lynx at their southern range boundary. Landscape Ecology 27:761–773. [Google Scholar]
- Wang F, McShea WJ, Wang D, Li S, Zhao Q, Wang H, Lu Z. 2014. Evaluating landscape options for corridor restoration between giant panda reserves. PLoS ONE 9:e105086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch N, Provencher L, Unnasch RS, Anderson T, McRae BH. 2015. Designing regional fuel breaks to protect large remnant tracts of Greater Sage-Grouse habitat in parts of Idaho, Nevada, Oregon, and Utah. Final Report to the Western Association of Fish & Wildlife Agencies, Contract Number SG-C-13-02. The Nature Conservancy, Reno, NV. [Google Scholar]
- Washington Wildlife Habitat Connectivity Working Group (WWHCWG). 2010. Washington Connected Landscapes Project: Statewide Analysis. Washington Departments of Fish & Wildlife and Transportation, Olympia, WA: Available at: www.waconnected.org. [Google Scholar]
- With KA, Gardner RH, Turner MG. 1997. Landscape connectivity and population distributions in heterogeneous landscapes. Oikos 78:151–169. [Google Scholar]
- Zeller KA, McGarigal K, Whiteley AR. 2012. Estimating landscape resistance to movement: a review. Landscape Ecology 27: 777–797. [Google Scholar]
- Zeppenfeld T, Balkenhol N, Kóvacs K, Carminati A. 2017. Rhizosphere hydrophobicity: A positive trait in the competition for water. PloS ONE 12:e0182188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziółkowska E, Perzanowski K, Bleyhl B, Ostapowicz K, Kuemmerle T. 2016. Understanding unexpected reintroduction outcomes: Why aren’t European bison colonizing suitable habitat in the Carpathians? Biological Conservation 195:106–117. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.