Investigating Ions at Amphiphilic Monolayers with X-ray Fluorescence

Abstract

Amphiphilic monolayers formed at the soft air/liquid interface are easy-to-handle and versatile model systems for material and life sciences. Helmuth Möhwald was one of the pioneers in this field. Over the last few decades, total-reflection X-ray fluorescence (TRXF) has become an important analytical tool for the investigation of monolayer interactions with ions. Here, the theoretical background of TRXF is described, and practical aspects are discussed. The experimentally determined fluorescence intensity from the adsorbed ions can be interpreted quantitatively either by a calibration procedure utilizing monolayers with known charge density or by calibration with respect to the bare aqueous surface. Both calibration approaches yield quantitatively consistent results within <10% accuracy. Some examples demonstrating the power of TRXF for the study of ion adsorption to charged and noncharged monolayers as well as for the characterization of the physicochemical properties of novel cationic lipids used for improved gene delivery are given.

Introduction

For a long time, phospholipid monolayers have been recognized as meaningful models of half of the biomembranes. They are very useful for understanding structure formation in 2D; the interactions of biologically important molecules, such as peptides, proteins, and even nanoparticles dissolved in the subphase, with the membrane surface; and also lipid mixing behavior in membranes. The main limitation of early work on amphiphilic monolayers was the absence of truly surface-sensitive tools for investigating liquid interfaces with molecular and microscopic resolution. This has changed over the last 40 years because of the development of numerous surface-sensitive techniques such as Brewster angle microscopy, X-ray and neutron scattering, infrared reflection–absorption spectroscopy (IRRAS), and nonlinear optical spectroscopy, leading to a drastic increase in the number of publications.¹⁻¹⁰ The success of the use of monolayers in many areas of material and life sciences is indelibly connected to Helmuth Möhwald^2,6,11−13 Meanwhile, Langmuir monolayers were demonstrated to have great application potential. Monolayers not only form the interfaces in technically important emulsions and therefore play a key role in colloid science but also are precursors to Langmuir–Blodgett films.^14,15 In this article, we focus on the use of total-reflection X-ray fluorescence (TRXF) as an important analytical tool to describe and quantify the interaction of monolayers with ions or (macro)molecules dissolved in the aqueous subphase. While X-ray reflectivity (XR) measures the spatial distribution of the total electron density and therefore cannot discern different atoms, TRXF is a highly surface-sensitive technique capable of distinguishing between chemical elements. Here, we will describe the method and give some examples of its applications in the fields of ion specific effects at highly charged and noncharged monolayers as well as in the search for new nonviral vectors used in improved gene delivery.

In the case of charged monolayers, the part of the subphase close to the surface is enriched with counterions and depleted of co-ions. In this way, the so-called electrical double layer (EDL) is formed. The EDL is heterogeneous, having a dense inner part and a more diffuse outer part.^16,17 The description of the outer part, given by Gouy and Chapman (in the GC model),^16,18,19 practically did not change during the last few decades. However, the inner part, which is largely independent of the bulk ion concentration, still eludes a comprehensive understanding. There are many extensions of the GC model, but none of them was ever generally accepted.²⁰ Obtaining precise experimental data as a basis for better theoretical models is therefore highly desirable but still poses great challenges. TRXF yields quantitative information on ion adsorption to monolayers and, within limitations, also resolves their depth distribution when the angle of incidence is systematically varied. For layers in which ion interactions occur in a narrow depth region, such as lipid monolayers with compact, charged headgroups, the inner part of the EDL is only a few angstroms thick and densely filled with counterions. The diffuse part then deviates only slightly from the surrounding electrolyte solution. Under such conditions, the fine structure of the layer of adsorbed ions is of little interest and cannot be practically resolved by TRXF. A simple and quantitative TRXF method for the study of thin monolayers, based on measurements at a single angle of incidence, was established in Helmuth Möhwald’s group.^12,21 Meanwhile, this approach has been successfully used by many groups. Absolute values of the ion excess near monolayers can be determined in two alternative ways, which are shown here to be equivalent, namely, (i) the use of a calibration monolayer and (ii) a calibration with respect to the fluorescence from the bare aqueous solution. In the last few years, TRXF has been extended to investigate ion adsorption to noncharged monolayers and to quantify the degree of protonation of novel lipids designed for use as nonviral vectors in gene delivery.

TRXF: Theoretical Background and Practical Aspects

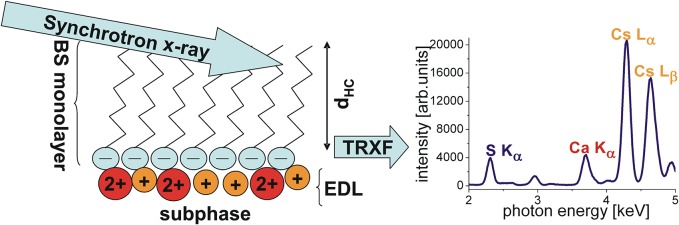
In the 1980s, Helmuth Möhwald and Jens Als-Nielsen were among the pioneers who introduced grazing incidence X-ray diffraction (GIXD) for the structural characterization of condensed Langmuir monolayers at the liquid–air interface. The use of this technique gave a significant boost to monolayer research in biophysics and materials science.^{2,3,11,13,22−36} TRXF was established as an element-specific complementary scattering technique.³⁷⁻³⁹ Let us briefly recollect the basics of the method. In a TRXF experiment, the water surface accommodating an amphiphilic monolayer in a Langmuir trough is illuminated with a monochromatic synchrotron X-ray beam at an angle of incidence θ below the critical angle of total reflection, θ_c. As in GIXD, the illuminated area is typically of the order of 100 mm². To avoid beam-induced monolayer oxidation, the trough is placed in a helium-flushed container with Capton windows that are transparent to X-rays. The exposure of the interface to X-rays induces the ionization of its constituent atoms when the X-rays are energetic enough to expel electrons from the inner orbitals of the atom. As a consequence, electrons from higher orbitals fill the holes virtually instantaneously, thereby emitting X-ray fluorescence with element-characteristic energy. The main transitions observed are Kα (L → K), Kβ (M → K), Lα (M → L), and so on. To induce fluorescence in an element of interest, the X-ray energy has to exceed the electron binding energy, but the fluorescence yield substantially decreases when the X-ray energy is too high. The fluorescence signal can be measured with an energy-sensitive detector (e.g., a Peltier-cooled silicon drift detector) with an entrance window directed toward the center of the footprint of the incident beam. Over the last 10 years, TRXF has been developed as a very simple quantitative analytical method.^{12,21,38,40,41}

For hard X-rays in the commonly used wavelength range (0.5 Å < λ < 2 Å), the refractive index of matter is slightly less than unity (n = 1 – δ – iβ). Here, β is related to the linear absorption coefficient and is much smaller than δ (β ≪ δ). Therefore, it can be safely ignored for the following considerations. The magnitude of δ is proportional to the electron density ρ_e of the matter, δ = r_eλ²ρ/(2π) (with the classical electron radius of r_e = 2.82 fm) and amounts to 10^–6 to 10^–5 for condensed matter and only 10^–9 for air. The critical angle can be easily calculated as 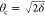(ref (42)). For example, θ_c = 0.13° for an air/water interface and a wavelength of λ = 1.3 Å, where ρ = 0.334 e^–/ų for water.

A total-reflection configuration (θ < θ_c) gives rise to a long-period X-ray standing wave (SW) on the air side as a result of the interference of the incident and reflected waves. The exponentially decaying evanescent tail of the SW reaches a few nanometers into the aqueous hemispace.^43,44 Element-characteristic X-ray fluorescence is therefore generated only within a shallow interfacial region accommodating the monolayer. As θ is increased from 0 to θ_c, the nodes and antinodes of the SW on the air side move toward the interface while the SW period becomes gradually smaller. At the same time, the decay length Λ of the evanescent wave in the aqueous hemispace increases, starting from several nanometers until it practically diverges at θ_c in the limit of β → 0 according to the relation⁴²

1

The intensities Φ(z) of standing waves for incident angles far below, close to, and slightly above θ_c are schematically depicted in Figure 1, where z denotes the spatial coordinate perpendicular to the interface and z = 0 coincides with the film/air interface. It is seen that different regions in the vicinity of the interface are illuminated by the SW for the different incident angles. In a typical experiment with θ ≈ 0.85θ_c, the decay length of the evanescent wave is Λ ≈ 8 nm, making this method truly surface-sensitive. On a quantitative level, the angle-dependent intensity of the characteristic fluorescence from element species j, I_j(θ), is determined by the interfacial depth profile c_j(z) of that species.^43,44 More formally, I_j(θ) is proportional to the spatial integral over the product of c_j(z) and the angle-dependent SW intensity Φ(θ, z):

2

With that, the depth profile of an element species of interest in principle can be reconstructed from the angle dependence of its characteristic fluorescence. For a given angle of incidence θ, Φ(θ, z) follows from the interfacial electron density profile ρ(z) and can be computed via the phase-correct summation of all reflected and transmitted partial waves,⁴⁵ as has been described previously.^44,46A_j(z) in eq 2 denotes the depth-dependent transmission of the emitted fluorescence intensity of element j. It accounts for the fact that the fluorescence from regions deeper in the aqueous region is attenuated more strongly on its way to the detector.⁴⁷ For heavy-enough elements whose fluorescence exhibits transmission lengths in the micrometer range, the attenuation is negligible (A_j(z) ≈ 1). B_j is a prefactor determined by the fluorescence yield of species j and the detection efficiency, which in general also depends on the incident angle.^43,48

Figure 1.

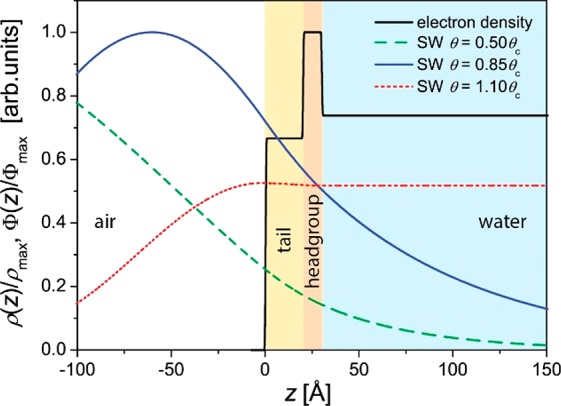
Schematic illustration of an amphiphilic monolayer at an air/water interface with a slab description of the electron density profile and calculated SW X-ray intensity distributions for three angles of incidence, θ = 0.50θ_c, 0.85θ_c, and 1.10θ_c. Φ_max and ρ_max denote the maximal values of Φ(z) and ρ(z), respectively.

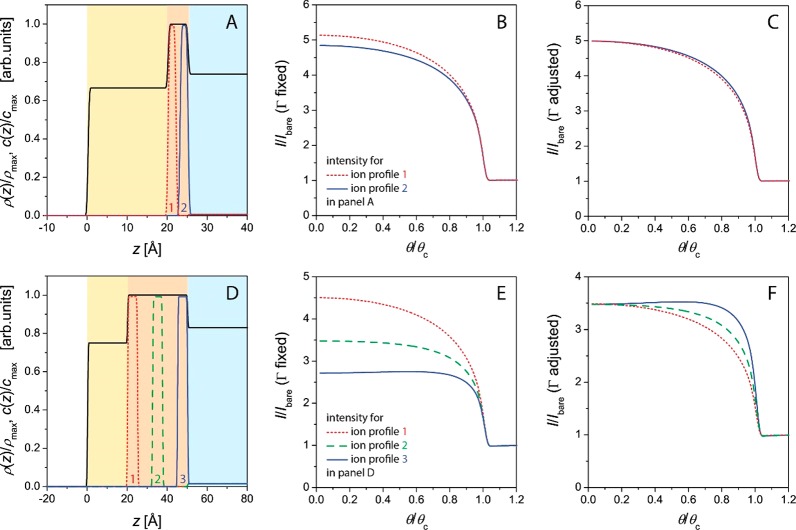
The average electron density of an organic monolayer is usually similar to that of water. At the low incident angles relevant for TRXF, the presence of the monolayer therefore only weakly modulates the shape of the SW. In practice, the electron density profile ρ(z) can be described with a slab model, typically comprising tail and headgroup layers (Figures 1 and 2). The interfacial roughness between these slabs does not have to be considered because at low angles of incidence corresponding to low values of q_z = (4π/λ)sin θ, typical roughnesses have little impact on the illumination profile. The layer thicknesses can be either determined by X-ray reflectometry²⁵ or GIXD^22,30 or estimated from the molecular structure and the area per molecule.⁴⁹ Panels A and D in Figure 2 schematically illustrate the electron density profiles ρ(z) of monolayers with thin (panel A) and thick (panel D) headgroups within a slab model description, together with various hypothetical depth profiles c(z) of the adsorbed ions. The associated angle-dependent fluorescence intensities according to eq 2 are shown in panels B and E, respectively. For clarity, the intensities are normalized by the intensities of the respective bare aqueous surfaces (I_bare) (i.e., in the absence of the monolayers^46,50,51), assuming a homogeneous ion concentration in the aqueous phase without a monolayer. (See the text further below.) For illumination θ > θ_c, the signal is dominated by the bulk (Figure 1) so that I/I_bare → 1.

Figure 2.

Various modeled ion depth profiles c(z) in lipid monolayers with thin (A) and thick (D) hydrated headgroup regions. The solid black line indicates the electron density profiles within a slab model description, and c_max and ρ_max denote the maximal values of c(z) and ρ(z), respectively. Panels B and E show the associated normalized angle-dependent fluorescence intensities as calculated with eq 2. Panels C and F show the curves that result when Γ is adjusted such that the intensities converge in the limit of small θ.

Ion Excess per Unit Area

In many cases, the z position (depth) at which ions adsorb to a monolayer is known a priori within a precision of a few angstroms, and one is primarily interested in the ion excess per unit area at an interface, Γ. This quantity is given as the spatial integral of the ion density excess [c(z) – c(∞)], where c(∞) denotes the bulk ion density in the aqueous solution and z_min is the boundary of the aqueous hemispace:

3

For lipid monolayers with compact, charged headgroups, the inner part of the EDL containing 95% of the counterions (simple inorganic ions) is less than 5 Å thick, as suggested by various theoretical models.^21,52 As shown in Figure 2A,B, the precise ion depth distribution on the angstrom scale for a given value of Γ affects the fluorescence intensity by only a few percent for typical angles of incidence (e.g., θ ≈ 0.85θ_c). In other words, Γ follows directly from the measured intensity as long as the distribution is narrow and the z position of its center of mass is known within, say, ±5 Å or better. Under such conditions, measurements at a single angle of incidence are sufficient to determine Γ, as was established by the Möhwald group,^12,21 and θ scans are not rewarding. Nonetheless, in view of the structure of eq 2, a calibration is needed to determine Γ on an absolute scale (i.e., the absolute number of excess ions per nm²). In the following text, we briefly introduce two different approaches to this problem, discuss their advantages and limitations, and demonstrate that they are equivalent and yield consistent results.

Calibration with Respect to a Charged Reference Monolayer

An established way of determining absolute ion excesses is a calibration procedure utilizing monolayers with known charge density on subphases that contain only one type of counterion. Plausibly assuming that counterion adsorption to the reference monolayer is dominated by unspecific electrostatic attraction and fully charge-neutralizing, the ion excess follows directly from the area per charged molecule A_m as

4

where z_m is the charge number of the amphiphilic molecules and z_j is the ion valence. With that, Γ of the reference monolayer is known a priori, and the associated measured ion fluorescence intensity can be used for calibration. In this procedure, the bulk ion concentration has to be kept preferentially around 1 mM for highly charged monolayers to ensure that the measured intensity has a negligible contribution from the bulk ions present in the nanometric illuminated interfacial region and therefore can be attributed to the excess ions alone. Moreover, the (de)protonation state of the reference monolayer has to be known, which can be achieved by the use of highly pH-tolerant ionizable groups such as quaternary amines or sulfates. Typical reference monolayers are dioctadecyldimethylammonium bromide (DODAB) for the study of anions and behenylsulfate (BS) for the study of cations.^21,49 The relation between fluorescence intensities from the sample and the reference has to be corrected for differences in the thickness of the hydrophobic region with an exponential factor accounting for the different illumination situations, as described further below for a practical example.

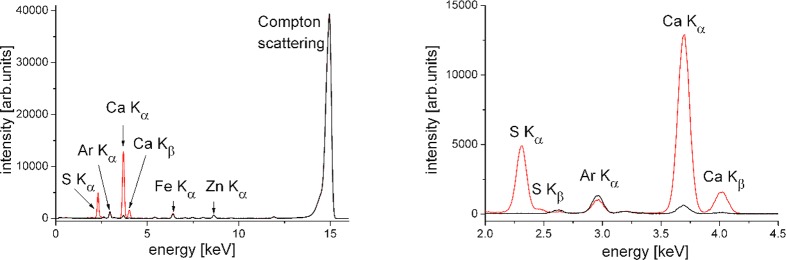
The fluorescence spectrum of a BS monolayer on a subphase containing 1 mM CaBr₂ is shown in Figure 3 (red line). In addition to the Ca lines, originating from the surface excess of Ca²⁺ ions, the spectrum also exhibits the lines of S from the sulfate group of BS, Ar from the air, and Zn and Fe, which are parts of the measurement setup. The latter appear with the same intensity also in background measurements from the surface of bare aqueous salt solution (black line) or from the surface of pure water. It is therefore recommended to subtract such background measurements prior to further analysis. The Compton scattering appears at a slightly lower energy compared to that of the incoming X-ray beam.⁵³

Figure 3.

X-ray fluorescence spectra of BS at a surface pressure of π = 20 mN·m^–1 on a subphase containing 1 mM CaBr₂ (red) and for the same subphase with no BS monolayer on top (black). The total spectrum is shown on the left, and the selected part with the most interesting fluorescence lines is shown on the right. The measurements were performed at the P08 synchrotron beamline at PETRA III of DESY (Hamburg, Germany) using a photon energy of 15 keV (wavelength λ = 0.826 Å) and an angle of incidence of 0.07°.

Calibration with Respect to the Bare Aqueous Surface

For high-enough bulk ion concentrations (say c(∞) ≳ 1 mM), the presence of ions in the nanometric illuminated interfacial region gives rise to a significant level of fluorescence even for zero ion excess. Because c(∞) is precisely known, this “bulk” fluorescence signal, once measured, is suited for an absolute calibration of the fluorescence intensity.^46,50,54 Recalling that most ions have negligible preferential interactions with the water surface,^55,56 the bare interface between air and the aqueous phase qualifies as a good reference system for this purpose. The effect of ion adsorption to a monolayer can then be conveniently described by dividing the fluorescence intensity measured in the presence of the monolayer, I, by the intensity I_bare measured in the absence of the monolayer at the same ion concentration, as was done for the theoretical curves in Figure 2B,C,E,F. Consequently, background measurements for subtraction in this case have to be performed with pure water rather than with aqueous salt solution. The absolute ion excess Γ is then determined by modeling the experimental I/I_bare with suitable descriptions of the electron density profile and the ion distribution according to eqs 2 and 3. Limitations of this calibration approach are reached when ions exhibit preferential interactions with the bare air/water interface, which is the case, for example, for “hydrophobic” ions.⁵⁷

Equivalence of the Two Calibration Approaches

In the following text, we show for a standard monolayer system that both calibration approaches yield quantitatively consistent results within <10% accuracy. A BS monolayer was studied on a subphase containing 1 mM CaBr₂. The measurements were carried out at the P08 beamline of Synchrotron DESY (Hamburg, Germany) at a beam energy of 15 keV (corresponding to λ = 0.826 Å) and an angle of incidence of θ = 0.07° ≈ 0.85 θ_c. Further details of the measurement setup are described elsewhere.⁵⁴ The measured ratio between the calcium fluorescence intensities in the presence and absence of the BS monolayer after background subtraction was I/I_bare = 305. The strongly acidic BS headgroup is completely deprotonated, and the surface carries a charge density of σ ≈ 0.64 C/m² at high lateral compression corresponding to a packing density of A_m ≈ 25 Ų per molecule. For the BS monolayer in contact with a CaBr₂ solution, the ion excess corresponding to charge compensation according to eq 4 therefore is Γ ≈ 0.021 Å^–2. Further assuming an alkyl chain layer thickness of 22 Å and a headgroup (sulfate) layer thickness of 4 Å in the electron density slab model, the relative calibration based on eqs 2 and 3 yields I/I_bare = 283. The agreement with the experimental value (I/I_bare = 305) is within 10%, so the two methods can be considered to be consistent. As a rough guideline, calibration with a reference monolayer appears to be preferable when the bulk ion concentration is low and the ions have a strong adsorption affinity. Calibration with respect to the bare aqueous interface, on the other hand, appears to be preferable for weaker ion adsorption at higher bulk concentration.

Depth Distributions

As already stated above, fluorescence measurements as a function of the angle of incidence yield insight into the depth distribution of the adsorbed ions, according to eq 2. The possibility to localize chemical elements and ions on the z axis (i.e., in the direction perpendicular to the interface) by TRXF was demonstrated earlier.^{44,46,50,51,58−61} The prerequisite is good a priori knowledge of the electron density profile ρ(z), from which the angle-dependent SW intensity profile Φ(θ, z) directly follows.⁴⁶ With Φ(θ, z) at hand, the depth distribution is then commonly reconstructed in a fitting procedure by generating a parameter-based mathematical model of c(z) and subsequent variation of the parameters until eq 2 yields the best possible agreement with the experimental intensity data I(θ). It should be noted, however, that the z resolution to which c(z) can be obtained is limited. Consequently, as pointed out earlier,²¹ the amount of depth information is negligible for highly localized ion distributions such as those at charged lipid monolayers. This can be seen in Figure 2 B, which shows the modeled angle-dependent fluorescence intensities for two narrow ion distributions offset by Δz = 3 Å within a compact headgroup layer (Figure 2A) but with identical Γ values. Although the absolute fluorescence intensities from the two distributions differ by a few percent, the overall shapes of the curves are very similar. This similarity is highlighted in Figure 2 C, where Γ was adjusted such that the intensities converge in the limit of small θ. The adjustment of Γ is achieved by the variation of c_max from c_max ≈ 394c(∞) (dotted line) to c_max ≈ 424c(∞) (solid line). The two curves are then virtually indistinguishable. For a monolayer with an unknown ion excess, it is therefore practically impossible to localize the adsorbed ions to a resolution of a few angstroms. Useful depth information can be accessed only when the depth at which ions or chemical elements are localized is unknown on the scale of nanometers or extended over such length scales.^{46,50,51,59−61} This is illustrated in Figure 2D–F, where various ion distributions in a monolayer with extended headgroups are considered. For ion distributions offset by Δz > 10 Å (Figure 2D), the fluorescence intensities differ substantially (Figure 2E). Importantly, not only the absolute intensities but also the shapes of the curves are clearly different (Figure 2F) so that meaningful depth information can be extracted even when Γ is unknown. The shape of I(θ) is primarily sensitive to the center-of-mass position of the distribution, moderately sensitive to its width, and less sensitive to higher moments. For thin layers with highly localized ion or elemental distributions, a related X-ray fluorescence technique known as standing-wave X-ray fluorescence (SWXF)^43,62 is better suited because it offers much higher depth resolution than does TRXF. In SWXF, the periodic region of an SW above a solid surface rather than the exponentially decaying tail of the SW is exploited to induce element-characteristic X-ray fluorescence,^48,63,64 but the lipid monolayers for this purpose have to be immobilized at a solid surface.

Applications in Modern Monolayer Research

The interactions of ions with surfaces are important in many physical–chemical and biological processes. For example, metal ions are required for the activity of a large number of enzymes and proteins. Alkali metal ions Na⁺ and K⁺ are found in all biological fluids, where they play important roles in the stabilization of catalytic intermediates or in optimal positioning of substrates with respect to enzymes. Ions differ in their ability to salt out proteins from solution (Hofmeister series of cations and anions). A big challenge in modern biophysical research is still the understanding of such effects on a molecular level as well as of specific roles of ions in various biological functionalities.⁶⁵ Ions may trigger and influence the onset of β-sheet formation⁶⁶ as an early stage in a variety of diseases (e.g., Alzheimer’s disease). Specific sequence motifs in histidine-rich domains can strongly influence the conformational structure and metal-binding geometry relevant to the assembly and biological function of the mussel byssus.⁶⁷ A significant increase in the thermodynamic and mechanical stability of the folded state of the protein has been observed in the presence of metal ions. For such problems, monolayers are an ideal model system. Other important examples will be discussed in more detail in the following section. They concern the interactions of ions with charged and noncharged monolayers, the determination of the degree of protonation of new lipids for gene delivery, and the determination of elemental depth profiles in structurally more extended monolayers of amphiphiles.

Charged Monolayers

From the end of the 1990s onward, charged surfaces in general and their interactions with ions in particular¹² were two of the central themes within the French–German network concerning complex fluids, as initiated by Helmuth Möhwald and Thomas Zemb. To describe an electric field and concentration profiles near a charged interface, the classical Gouy–Chapman (GC) model of the electrical double layer (EDL) is commonly used. However, some basic assumptions of this model are not always justified. For example, the membrane surface is not homogeneously charged and ions, which are not point charges, may penetrate it. In particular, the properties of charged monolayers,⁶⁸⁻⁷² micelles,^73,74 vesicles,⁷⁵ and dispersions^76,77 depend on the type of counterions. These effects are usually discussed in terms of the Hofmeister series for cations or anions.⁷⁸⁻⁸¹ When specific chemical interactions can be excluded, the effect of the counterion species can result only from its effect on the EDL, in which case the GC model breaks down. The limits of the GC model can be illustrated for a 1:1 electrolyte at high surface charge densities σ. For the electric potential ψ, given by GC theory, the Boltzmann equation yields nonphysically high counterion concentrations.^82,83 For example, σ = 0.6 C·m^–2 (fully ionized condensed monolayers of single-chain amphiphiles used as standard samples in our approach) leads to a counterion concentration near the headgroup plane exceeding 100 M. This value clearly conflicts with packing density restrictions of the counterions. The concentration of densely packed spherical particles with a radius of 3 Å is only about 10 M.⁸⁴ Since the early 2000s, TRXF has been shown to be a very appropriate method for elucidating the formation of the EDL. The most important constraint to solving the above-described problems was to use charged amphiphiles and ions with no noticeable mutual complexing ability. This is achieved in highly charged Langmuir monolayers of long-chain alkylsulfates on subphases containing different alkali metal counterions. The headgroups of these monolayers are strongly acidic. At pH 5 to 6 (ultrapure water) and salt concentrations above 1 mM, they are completely deprotonated (negatively charged). The maximum packing density, observed in pressure–area isotherms of Langmuir monolayers, is close to 25 Ų·molecule^–1, corresponding to a surface charge density of 0.64 C·m^–2.

The isotherms of behenylsulfate (BS) monolayers on subphases containing different alkali metal chlorides at 1 mM differ significantly.⁸⁵ In the presence of Li⁺, the isotherm exhibits a plateau region at a surface pressure of π ≈ 5 mN·m^–1. This plateau has been interpreted to be a 2D gas-condensed coexistence (resublimation). For the other alkali cations, this plateau is hardly observable because the transition pressure is much smaller. At π = 40 mN·m^–1, the maximum slope (elasticity modulus) increases monotonically from Li⁺ to Cs⁺, and the area per molecule decreases monotonically from Cs⁺ to Na⁺ (Li⁺ is the only exception). The surface potential of condensed BS monolayers (30 Ų·molecule^–1) on subphases containing 10 mM alkali metal chlorides increases monotonically from Li⁺ (−110 mV) to Cs⁺ (+130 mV). This shows that the surface potential depends on the type of monovalent counterion. Because the magnitude of the potential increases with increasing size of the hydrated counterion, packing density limitations seem to play an important role in EDL formation. Therefore, in the presence of two counterions, preferential participation of the smaller one in EDL formation is expected to be favorable in terms of free energy. Indeed, X-ray reflectivity experiments using BS monolayers on 9:1 LiCl/CsCl subphases proved that the Li⁺/Cs⁺ ratio in the EDL is close to 1:1 (50–60% of Cs in the EDL in contrast to only 10% in the subphase).^12,21,38,85 This discrepancy with the classical model diminishes with decreasing monolayer charge density. For negatively charged double-chain phospholipids such as DOPG and DPPG with a charge density of only 0.1–0.3 C·m^–2, this effect is hardly observable for alkali cations in surface potential experiments.^86,87 Pressure–area isotherms, surface potential, and the X-ray diffraction and reflectivity of such monolayers in the presence of different alkali cations exhibit practically no influence of the counterion type. The variation of the surface potential is below 20 mV. This is rather close to the accuracy limit of the experimental setup and procedures. The DOPG monolayer with low surface charge density behaves in good agreement with the GC model.

In the case of highly charged monolayers such as BS, small monovalent Cs⁺ cations can even compete with large divalent Mg²⁺ ions. X-ray reflectivity data taken for BS monolayers in the presence of equal concentrations of Cs⁺ and Mg²⁺ in the subphase yield a Cs⁺/Mg²⁺ ratio in the range of 1.3 to 2 (as estimated from the excess electron density), whereas the GC model predicts only 0.04. In contrast, large hydrated Li⁺ cations are unable to compete with divalent Mg²⁺ (ref (85)). The competition of counterions for participation in the EDL²¹ was later directly quantified by TRXF. Because Li is invisible with TRXF (K-edge energy near 0.05 keV), its amount can be estimated by assuming electrical neutrality (charge compensation) in competition experiments. The relative intensity of the Cs⁺ fluorescence is approximately 50% compared to experiments on a subphase containing only CsCl. This result is in good agreement with the above-described value of 50–60% obtained by X-ray reflectometry. For a 1:1 KCl:CsCl subphase, TRXF revealed that the K⁺/Cs⁺ ratio in the EDL of BS monolayers is approximately the same as in bulk, in good agreement with the similar radii of hydrated K⁺ and Cs⁺ cations.^12,21 Experiments with mixed subphases containing mono- and divalent cations provide another proof that smaller monovalent cations are even able to compete with larger divalent ones in the formation of the EDL. The relative intensity of the Cs⁺ fluorescence for BS on a 9:1 Cs⁺/Ca²⁺ mixture in the bulk is 0.42 compared to that of BS on a subphase with only Cs⁺. The corresponding value for Ca²⁺ is 0.57. Neglecting small differences in the monolayer packing density on the different subphases, XR and TRXF experiments demonstrated clearly that the smaller monovalent Cs⁺ is able to compete with larger divalent cations Mg²⁺, Ca²⁺, and Ba²⁺. The ratio of Cs⁺ to the corresponding divalent cation in the EDL is always higher than predicted by the classical GC model, for example, 1.5 experimentally observed for BS on the 9:1 Cs⁺/Ca²⁺ subphase and 0.5 experimentally observed for BS on the 9:1 Cs⁺/Ba²⁺ subphase compared to 0.14 predicted by the classical GC model.^12,21

Figure 4 shows the first experiments which might be important for many groups using ultrapure water for experiments with charged monolayers. From these TRXF experiments, several important conclusions can be drawn: (i) the small monovalent Cs⁺ is able to compete with the larger divalent Ca²⁺, (ii) ultrapure water contains traces of divalent Ca²⁺ which has to be eliminated by EDTA in quantitative TRXF experiments, and (iii) for the calibration with a monolayer of known charge density, molecules with complexing ability that is as low as that for BS are needed. The competition between Ca²⁺ and Cs⁺ leads to different results when DPPG is used, clearly indicating that the phosphate group of DPPG is prone to specific interactions with calcium in contrast to BS.

Figure 4.

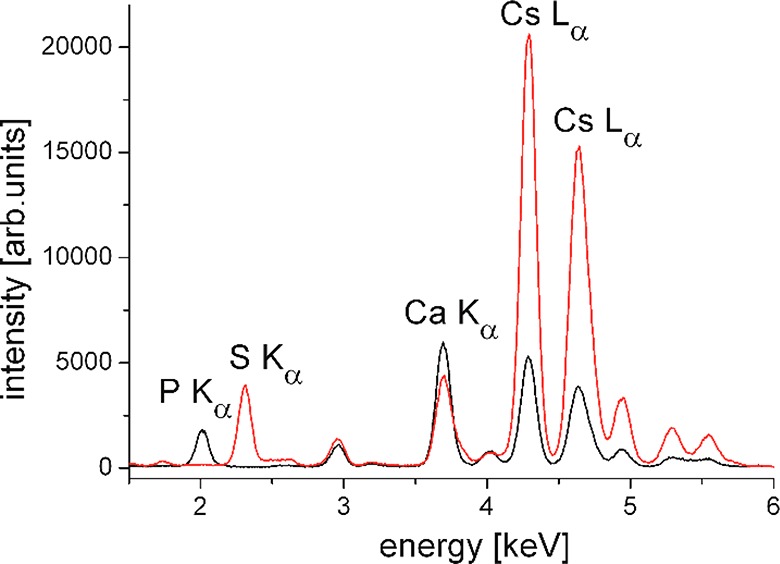
Selected part of the X-ray fluorescence spectra of BS at π = 20 mN·m^–1 (red) and DPPG at π = 30 mN·m^–1 (black) on a subphase containing 1 mM CsBr and traces of calcium. The most interesting fluorescence lines are assigned. The measurements were performed at synchrotron beamline P08 at PETRA III of DESY (Hamburg, Germany) using a photon energy of 15 keV (wavelength λ = 0.826 Å) and an angle of incidence of 0.07°.

Formation of Lipoplexes

One of the current hot topics in medicine is gene therapy.^88,89 The concept of modulating targeted gene expression by exogenous genetic material in order to cure a disease is no longer only a vision.^90,91 However, viral vectors carry immunogenic and oncogenic residual risks, and the production costs are very high. Nonviral vectors have therefore gained enormous scientific interest. Lipoplexes (complexes formed by cationic lipids and DNA) are characterized by high loading capacity, biodegradability, and higher safety. Another advantage is their large-scale, low-cost production compared to that of viral systems.⁹²⁻⁹⁴ The main problem is the low transfection efficiency.⁹⁵ Therefore, the determination of the most important parameters for efficient transfection has become a subject of intensive research in recent years. By modifying the chemical structure of the cationic lipids, the physical–chemical properties of lipoplexes can be systematically investigated.⁹⁶ One crucial parameter for the coupling of DNA to liposomes is the protonation state of the novel cationic lipids that are used. This can be readily investigated using Langmuir monolayers on aqueous subphases over a wide range of pH. TRXF is the method of choice for obtaining quantitative information about the concentration of counterions adsorbed to the monolayer surfaces and therefore of the charge density, which in turn is determined by the degree of protonation. The selection of relevant buffer subphases containing only one type of anion is very important in avoiding any competition in the EDL.^49,97−99 The first experiments have been performed on subphases with a constant concentration (2 mM) of Br^– anions. The TRXF intensity of Br (proportional to the number of Br^– anions in the EDL) has been measured as a function of the bulk-phase pH. The intensity of the Br fluorescence bands decreases with increasing pH and is close to 0 above pH 10. This indicates that around pH 10 the headgroups of the used cationic lipids are fully deprotonated. The measured fluorescence intensity I from the counterions in the EDL is directly proportional to the degree of protonation p of the monolayer molecules, their surface concentration C, and the intensity of the evanescent X-ray standing wave Φ at the location of the counterions

5

where d_HC is the thickness of the hydrophobic part of the monolayer. As described above, the intensity of the evanescent tail of the standing wave decays approximately exponentially with the depth

6

where Λ ≈ 8 nm is the decay length. The degree of protonation is therefore proportional to

7

with I_ref being the fluorescence intensity of the reference monolayer (DODAB) on a subphase with the same counterion concentration (2 mM Br^–), d_HC^ref being the thickness of the hydrophobic part of the reference monolayer (i.e., the distance of Br^– ions from z = 0), and C_ref being the surface concentration of DODAB determined from isotherm experiments. Different approaches can be used to estimate d_HC. X-ray reflectometry is one of the methods that can be used for any kind (disordered or ordered) of layer.²⁵ In condensed monolayers, the tilt angle of the alkyl chains, which are in an all-trans conformation, can be determined by GIXD.^22,30 Therefore, d_HC can be directly estimated using the theoretical length of a stretched chain and the determined tilt angle t with respect to the surface normal. The maximum length of a stretched alkyl chain¹⁶ with n CH₂ groups is l_max = (n1.26 + 1.5) Å so that

8

Instead of using sophisticated X-ray scattering methods, the thickness of fluid monolayers can also be estimated by the simple consideration that d_HC depends on the molecular weight of the hydrophobic chains (MW_HC), the monolayer area per molecule (A), which can be determined by pressure–area isotherms, and the mass density ρ_m of the hydrophobic layer, which can be taken to be 0.9 g·cm^–3 as a good estimate

9

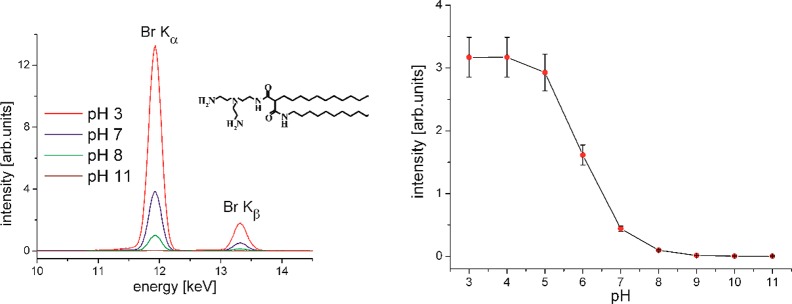
with N_a being Avogadro’s constant. With this simple approach, the degree of protonation of several new cationic lipids has been quantified.^49,99 One example is shown in Figure 5. The degree of protonation of the headgroups changes depending on the subphase pH. The molecules, designed for transfection experiments, are protonated (positively charged) at low pH and deprotonated (uncharged) at high pH. The intensity of the Kα and Kβ lines of Br, which in all experiments is present in the subphase at a concentration of 2 mM, changes clearly. The integral intensity can be plotted against the pH to yield a protonation curve. The comparison with a standard sample (in this case DODAB) allows the calculation of the charge density (how many of the protonable groups are really protonated). One conclusion was that densely packed molecules in highly ordered condensed monolayers are less protonated in comparison to fluid layers of molecules with the same headgroup. The higher surface density of positive charges leads to the decrease in the surface proton concentration according to the Boltzmann equation, resulting in the decrease in the monolayer degree of protonation.

Figure 5.

Selected part of the X-ray fluorescence spectra of N-2{[bis(2-aminoethyl)amino]ethyl}-2,N′-dihexadecyl-propandiamid at π = 30 mN·m^–1 on subphases with different pH values containing 2 mM Br^– ions (left). Integral Br X-ray fluorescence intensity versus the subphase pH (right). (This figure was adapted from ref (49).)

Surprisingly, DNA that was dissolved in the subphase coupled to the cationic monolayers at pH 4 as well as at pH 8 even if only approximately 1% of the lipid molecules in the monolayer can be protonated at pH 8. Obviously, even such a low charge density can attract some DNA. On the other hand, the coupled DNA affects the potential of the EDL and therefore changes the surface pH in accordance with the Boltzmann equation. This leads to an increasing degree of protonation of the monolayer followed by further binding of DNA molecules. Therefore, the pH cannot be so easily taken as a switch in gene therapy using lipids with protonatable groups.

Another important parameter, which is connected to the charge density in the lipid monolayer, is the amount of DNA coupled to the lipids to form lipoplexes. One efficient method of quantifying the amount of DNA is IRRAS (infrared reflection–absorption spectroscopy), which has been used very successfully in the case of cationic lipids with no phosphate groups to avoid the overlapping of fluorescence signals from the DNA backbone with those of the phosphate groups of the lipid molecules.¹⁰⁰ However, there is great interest in using zwitterionic phospholipids (mainly for toxicity reasons) and mediating the complex formation with DNA by divalent cations.^101−104 The possibilities to quantify the amount of DNA bound to such a lipid monolayer are restricted. The application of TRXF to DNA systems turned out to be difficult. DNA molecules contain only elements which are also present in the lipid monolayer, notably P. Therefore, labeling with an element which possesses a high absorption cross-section and strong K emission lines was a way to circumvent this problem.⁹⁷ Bromine is a marker which can be inserted by electrophilic addition to the 5,6 double bond of pyrimidine bases and pyrimidine nucleotides.¹⁰⁵ Purine bases (adenine and adenosine) are not as readily brominated.¹⁰⁶ The integrity of DNA remains largely intact even at high bromination degrees of up to 1 bromine atom per 4 DNA bases.¹⁰⁷ Different approaches to the bromination of DNA have been used, and the applicability of TRXF to binding studies using modified Br-DNA has been shown.⁹⁷ The analytical procedure developed and used for the quantification of bromine in labeled DNA has a detection limit of 10–20 μg. This amount is high enough to successfully apply TRXF. One interesting result of the TXRF experiments was the experimental proof that the binding affinity of DNA to a cationic monolayer is substantially stronger than that of bromide anions. Because of the high negative charge of the Br-DNA macromolecules, the single charged anions are almost completely replaced from the EDL. Another striking result, which is important for further applications of lipids as transfection tools, is that the amount of adsorbed Br-DNA increases with increasing electrolyte concentration up to physiological quantity (Figure 6). This can be understood because the ionic atmosphere around a macromolecule becomes more compact and stable with increasing ionic strength. The reduction of the effective charge requires larger amounts of Br-DNA to be coupled for the compensation of the overall monolayer charge.⁹⁷

Figure 6.

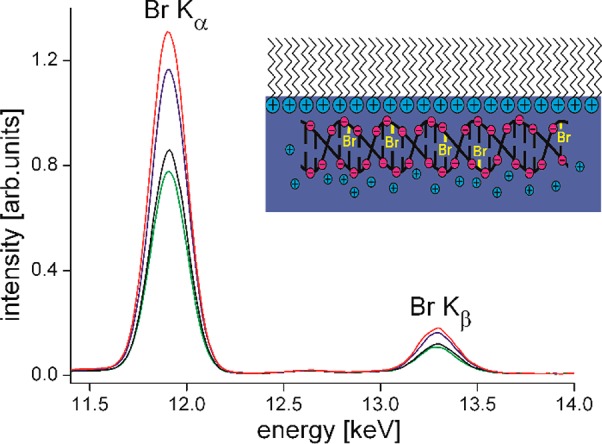
Selected part of X-ray fluorescence spectra of DODAB at 30 mN·m^–1 on a subphase containing 0.1 mM Br-DNA and different concentrations of KCl (1 mM (black), 3 mM (green), 10 mM (blue), and 100 mM (red)). The inset is a schematic representation of Br-DNA coupled to the positively charged DODAB monolayer. (This figure was adapted from ref (97).)

Noncharged Monolayers

Selective interactions of ions with charge-neutral saccharides can have important consequences in technological and biological contexts. Indirect evidence of selective ion interactions with saccharide surfaces is the known ion specificity in the swelling of wood materials in salt solutions,¹⁰⁸ but ions are also believed to promote the specific interaction of saccharide headgroups even if the latter are neither charged nor zwitterionic. To this end, the homotypic interaction between lipid-anchored LewisX trisaccharides, involved in membrane–membrane adhesion processes, was reported to be strengthened by calcium ions.^109,110 In a recent study,⁵⁴ preferential interactions of ions with uncharged saccharide surfaces in the form of glycolipid Langmuir monolayers at air/water interfaces were probed with TRXF. The monolayers exhibited different levels of structural ordering, as revealed by GIXD. The aqueous subphases contained 1 mM KI, CsBr, or CaBr₂ salts with pronounced effects on wood swelling and good detectability by TRXF. Significant selective interactions with ions from the aqueous subphase (Γ > 0) were observed only for monolayers featuring crystalline ordering of the saccharide headgroups. The magnitude of the excess ions was on the order of Γ ≈ 0.01–0.02 nm^–2, corresponding to an area of A = 1/Γ ≈ 50–100 nm² per adsorbed ion or 1 ion per approximately 100–200 glycolipids, which is much lower than the corresponding values obtained with charged monolayers. (See the previous sections.) The attracted ion species was found to depend on the structural motifs displayed by the ordered saccharide layer, suggesting a selection mechanism similar to that of crown ethers.¹¹¹

Elemental Depth Profiles in Amphiphilic Layers at Air/Water Interfaces

Amphiphilic layers at air/water interfaces constitute meaningful and well-defined models of biological or technologically relevant interfaces. While their structures in terms of the profiles of the overall electron density are by now routinely determined with X-ray reflectometry, more selective structural insight can be gained from the depth distribution of chemical elements of interest. As explained further above, TRXF is generally capable of resolving the average depth and width of elemental distributions. For monolayers at air/water interfaces this was initially demonstrated with phthalocyanines comprising Sn, Cu, or Fe atoms.^58,61 The bulk concentration of these elements in the aqueous subphase was negligible. Their characteristic fluorescence intensities obtained in scans of the incident angle were reproduced with calculations assuming these elements to be a shorter distance (<1 nm) from the outermost surface, in agreement with the chemical structure. Later on, the distributions of Ni, Zn, and P in a relatively thick (≈100 nm) composite film at an air/water interface were determined.⁶⁰ The film was composed of a lipid monolayer (containing P), a layer of adsorbed lipid micelles (containing P), and a layer of adsorbed proteins (containing Zn). Ni was found to be a trace contamination in the layers. More recently, TRXF was employed to localize monovalent and divalent cations adsorbing to negatively charged lipopolysaccharide (LPS) monolayers mimicking the outer surfaces of Gram-negative bacteria.^46,50 LPSs are bacterial glycolipids with four to seven alkyl chains and a negatively charged oligo- or polysaccharide headgroup.¹¹² For rough mutant LPS Re having a headgroup of four sugar rings and carrying up to four negative charges, the counterion fluorescence intensities (K⁺ and Ca²⁺) were best reproduced for a distribution maximum within the first 10 Å from the interface between the hydrophobic tails and the hydrophilic saccharide headgroups.⁴⁶ Interestingly, essentially the same counterion distribution was also reported for rough mutant LPS Ra, which has a much larger headgroup comprising up to 12 sugar rings.⁵⁰ This result can be rationalized by the fact that only the inner saccharides of LPS Ra carry negative charges, while the outer saccharides are uncharged. In a study by Körner et al., recombinant proteins were anchored to phospholipid monolayers at the air/water interface via Ni²⁺ chelation using DOGS-NTA.⁵¹ The Ni²⁺ distribution maximum was reported to be ≈15 Å from the interface between the hydrophobic lipid tails and the hydrophilic lipid headgroups, reflecting a rather extended conformation of the ≈1.5–2-nm-long headgroup of DOGS-NTA. Angle-dependent fluorescence of the S atoms present in the proteins was at least consistent with the formation of an extended protein layer. Seregrin et al. used TRXF to investigate monolayers of porphyrin–fullerene dyad molecules containing Zn atoms at air/water interfaces and on Si substrates.⁵⁹ By localizing the depth of the Zn distribution, they observed that the molecules exhibit a preferential orientation at the air/water interface, which is retained when the monolayer is transferred to the solid surface. In the future, angle-dependent TRXF holds much promise for the investigation of ion distributions around lipid-anchored charged macromolecules, dendrimers, and brushes but also for the distributions of chemical elements such as phosphorus and sulfur covalently bound to highly hydrated parts of amphiphilic biomacromolecules.

Concluding Remarks

The growing importance of TRXF in modern monolayer research for studying the interactions of ions with monolayer surfaces was pointed out. Although Langmuir monolayers are not directly relevant to current applications, they have gained increasing importance as very useful and easy-to-handle model systems for understanding basic problems on a molecular level. In this context, the X-ray fluorescence techniques used to study monolayers with molecular and supramolecular resolution are of utmost relevance. There has been much progress in making those techniques available to a large community of researchers, and this process will continue. New systems such as peptides and glycolipids will become more important to studying membrane processes such as molecular recognition, multivalent interactions, and cooperative binding.

The authors declare no competing financial interest.