Abstract
We formulated a spatially resolved model to estimate forces exerted by a polymerizing actin meshwork on an invagination of the plasma membrane during endocytosis in yeast cells. The model, which approximates the actin meshwork as a visco-active gel exerting forces on a rigid spherocylinder representing the endocytic invagination, is tightly constrained by experimental data. Simulations of the model produce forces that can overcome resistance of turgor pressure in yeast cells. Strong forces emerge due to the high density of polymerized actin in the vicinity of the invagination and because of entanglement of the meshwork due to its dendritic structure and cross-linking. The model predicts forces orthogonal to the invagination that are consistent with formation of a flask shape, which would diminish the net force due to turgor pressure. Simulations of the model with either two rings of nucleation-promoting factors (NPFs) as in fission yeast or a single ring of NPFs as in budding yeast produce enough force to elongate the invagination against the turgor pressure.
INTRODUCTION
Assembly of actin filaments at sites of endocytosis is necessary for invagination of the plasma membrane in both budding and fission yeast (Aghamohammadzadeh and Ayscough, 2009; Basu et al., 2014). The transient accumulation of actin filaments around the invaginating plasma membrane is called an “actin patch.” Patches form in ∼10 s, peak, and disappear over ∼10 s. Polymerizing actin is believed to produce the forces required to form a tubular invagination of the plasma membrane with a clathrin-coated hemisphere at the tip (Kaksonen and Roux, 2018). Force is required to overcome the very high turgor pressure in yeast cells, which is estimated to be on the order of 10 atm in fission yeast (Basu et al., 2014). This amounts to a force on the order of 3000 pN on a typical endocytic tubule (Carlsson, 2018). Previous modeling studies concluded that actin polymerization alone is unlikely to generate such a force, and various additional mechanisms were proposed (Scher-Zagier and Carlsson, 2016; Lacy et al., 2018).
We used simulations of mathematical models to estimate the forces exerted on an endocytic, plasma membrane tubule by a surrounding network of actin filaments. In our model, mechanics of the filamentous meshwork is coupled to a detailed description of actin nucleation and polymerization (Berro et al., 2010). We assumed that proteins called nucleation-promoting factors (NPFs) reside on the membrane tubule and stimulate the Arp2/3 complex to nucleate branched actin filaments. Simulations of the model constrained by experimental parameters yielded dense networks of actin filaments around the tubule in the vicinity of the NPFs. Entanglement of the branched filaments makes the network highly viscous, so that the energy released during the polymerization generates forces sufficient to work against the turgor pressure and elongate the nascent invagination.
The elongating invaginations were simulated with either one or two narrow bands of NPFs around the membrane tubule. Fission yeast has two rings of NPFs, one that remains in the initial position at the base of the invagination, while the other moves with the tip of the tubule (Arasada and Pollard, 2011; Arasada et al., 2018). Budding yeast has one ring of NPFs that remains near the base of the invagination (Mund et al., 2018). Consistent with experimental observations, both versions of the model yielded similar forces, elongation rates, and lengths of the invaginations.
MODEL
Generalized description of the biochemistry and physics of the expanding actin filament network
The model of the actin filament network is formulated in a continuous approximation, such that the distribution of filaments in the patch is characterized by a continuous density of actin subunits ρ (x, t), which is a function of location x and time t. The peak number of ∼6500 actin subunits per patch in fission yeast (Sirotkin et al., 2010) suffices for a continuous formulation to provide reasonably accurate results. This large number makes a discrete stochastic approach logistically burdensome, though such an approach would otherwise be appropriate, given the submicron sizes of endocytic patches (Mund et al., 2018).
We describe filamentous actin as a visco-active fluid (Kruse et al., 2005; Prost et al., 2015). In a viscosity-dominated environment, a balance between active and dissipative forces governs the mechanics of actin filament networks. The active repulsive stress, originating from the impingement of polymerizing subunits on existing filaments, is elastically stored in the meshwork, causing it to expand with velocities limited by dissipation due to viscosity of the meshwork.
The force balance requires that the divergence of the total stress tensor be zero everywhere in the fluid (Kruse et al., 2005): 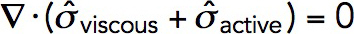 . Here, the viscous stress tensor is
. Here, the viscous stress tensor is 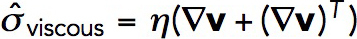 , where v = v (x, t) is the the local actin velocity, (∇v)T is the transpose of the velocty gradient tensor ∇v, and the viscosity coefficient η is a function of the local densities ρ and local average length of actin filaments, L: η = η(ρ,L) (Doi and Edwards, 1998). Because ρ is allowed to vary in space, actin velocities v = v(x,t) are not subjected in our model to the incompressibility condition. The density of actin subunits, however, has an upper limit due to excluded volume, as explained further in this section.
, where v = v (x, t) is the the local actin velocity, (∇v)T is the transpose of the velocty gradient tensor ∇v, and the viscosity coefficient η is a function of the local densities ρ and local average length of actin filaments, L: η = η(ρ,L) (Doi and Edwards, 1998). Because ρ is allowed to vary in space, actin velocities v = v(x,t) are not subjected in our model to the incompressibility condition. The density of actin subunits, however, has an upper limit due to excluded volume, as explained further in this section.
The active stress tensor is approximated as isotropic: 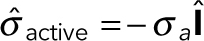 , where
, where 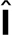 is the unit tensor and σa can be interpreted as the energy per unit volume stored in the meshwork during polymerization. Active stress is generated when a polymerizing subunit impinges on an existing filament. This requires high filament densities characteristic of the endocytic actin patches, where large numbers of polymerized subunits are concentrated in submicron volumes, resulting in high ρ. The requirement of a direct interaction between two filaments is consistent with the quadratic ρ dependence of the “storage” modulus of overlapping actin filaments (MacKintosh et al., 1995; Satcher and Dewey, 1996; Gardel et al., 2003); see subsection Parameterization of the force-balance equation (Eq. 1). Hydrostatic pressure is not included in the force-balance equation in our model, because the mechanics of the actin filament network decouples from mechanics of the cytoplasm. Indeed, the viscous drag exerted on actin filaments by the cytoplasm is much weaker than the intrinsic viscous forces due to direct contacts of the filaments and can thus be ignored (Nickaeen et al., 2017). Technically, the repulsive active stress can be viewed as playing a role of pressure in our model. Overall, the equation governing v (x,t) is written as
is the unit tensor and σa can be interpreted as the energy per unit volume stored in the meshwork during polymerization. Active stress is generated when a polymerizing subunit impinges on an existing filament. This requires high filament densities characteristic of the endocytic actin patches, where large numbers of polymerized subunits are concentrated in submicron volumes, resulting in high ρ. The requirement of a direct interaction between two filaments is consistent with the quadratic ρ dependence of the “storage” modulus of overlapping actin filaments (MacKintosh et al., 1995; Satcher and Dewey, 1996; Gardel et al., 2003); see subsection Parameterization of the force-balance equation (Eq. 1). Hydrostatic pressure is not included in the force-balance equation in our model, because the mechanics of the actin filament network decouples from mechanics of the cytoplasm. Indeed, the viscous drag exerted on actin filaments by the cytoplasm is much weaker than the intrinsic viscous forces due to direct contacts of the filaments and can thus be ignored (Nickaeen et al., 2017). Technically, the repulsive active stress can be viewed as playing a role of pressure in our model. Overall, the equation governing v (x,t) is written as
| (1) |
Equation 1 is coupled with the spatiotemporal dynamics of the molecules regulating actin filament assembly. In both types of yeast cells, NPFs initiate the assembly of the actin filament networks by stimulating the Arp2/3 complex to nucleate new actin filaments on the sides of existing filaments, forming a dendritic network.
The model includes a spatial description of actin nucleation and polymerization that follows a kinetic model used by Berro et al. (2010), which consists of rate equations detailing actin filament nucleation, polymerization, and aging, as well as the capping of the barbed ends of polymerizing filaments and severing of aged filaments by cofilin. Simulations of the model using protein concentrations measured in cells (Berro et al., 2010) adequately describe experimentally measured time courses of the appearance and disappearance of patch proteins (Sirotkin et al., 2010). The rate constants giving good fits of the simulations to the experimental data were larger than expected from biochemical measurements, owing in part to molecular crowding in cells (Schmit et al., 2009). We use the rate constants and equations of Berro et al. (2010) to integrate measurements of actin kinetics into our model.
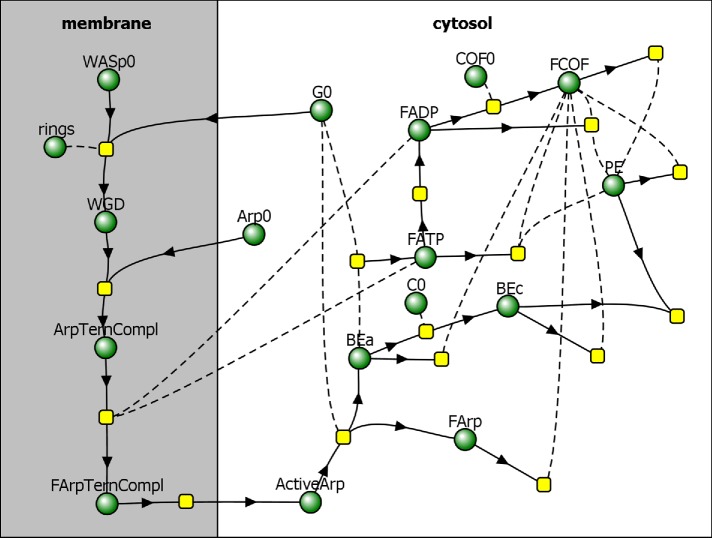
The actin density ρ is determined by concentrations of all of the species of actin in an actin patch. These species include newly polymerized ATP-bound subunits (FATP), subunits aged by ATP hydrolysis and phosphate dissociation (FADP), and subunits bound by cofilin (FCOF), as shown in the reaction diagram in Figure 1. In our model, ρ also includes concentrations of the filaments’ barbed ends, both active and capped (BEa and BEc, respectively), and slowly depolymerizing pointed ends (PE). Overall,
FIGURE 1:
Reaction diagram corresponding to the kinetic model by Berro et al. (2010), with added partitioning of species between membrane and cytosol. Directions of arrows toward or away from reaction nodes (yellow squares) determine roles of species (green circles) in a particular reaction as reactants or products, and reactions without products describe disappearance of reactants from the patch. Species connected to reactions by dashed curves act as “catalysts,” that is, they are not consumed in those reactions.
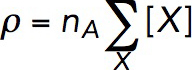 |
where X stands for FATP, FADP, FCOF, BEa, BEc, and PE, and [X] is the concentration of molecule X (in μM); the prefactor nA converts the concentration (in μM) into the density expressed in molecules per cubic micrometer (nA = 602 μm–3/μM).
All concentrations [X], with the exception of [ActiveArp], are governed by reaction-transport equations of the following type,
| (2) |
where the first term in the right-hand side describes the flow of X with velocity v, and RX is the sum of the rates of all reactions affecting X. The next subsection describes the equations for [ActiveArp].
Functional forms of RX and parameters are from Berro et al. (2010), with modifications reflecting the effects of mechanical forces and high local filament densities on polymerization kinetics. In locations where the filament network is dense, molecular diffusion slows down (Novak et al., 2009), which affects reaction rates (Schmit et al., 2009). Because the effective diffusion coefficient of molecules in spaces filled with the filaments reduces by the factor (1 – ρ /ρmax)1/2 (Novak et al., 2011), we modify by this factor the on- and off-rate constants of polymerization, capping, cofilin binding, and cofilin-dependent severing. This ensures that the above-mentioned processes slow down as ρ approaches ρmax = (4πδ 3/3)–1, where δ = 2.7 nm is the subunit radius, and, therefore, ρ never exceeds ρmax = 20.15 mM. Note that the factor (1–ρ/ρmax)1/2 is significantly different from unity only where ρ approaches ρmax, so in most locations, the rate constants are essentially unchanged. We also take into account that the filaments that generate active stress polymerize under load. The fraction of such filaments is estimated as follows. Assuming that one of the two filament ends is immobilized at the membrane or a branching point, the probability of the filament growing under load is equivalent to that of its other end pushing against the network, which is p (x, t) = ρ (x, t)/ρmax. Thus, the affected rates need to be multiplied by (1 – p(x, t)) + p(x, t) exp (–σαδ3/(kBT)). For simplicity, we ignore the contributions of such filaments to actin density altogether, dropping the second term and modifying the rates of polymerization and capping by an additional factor 1 – ρ (x, t)/ρmax.
Reaction steps that lead to formation of ActiveArp occur on the surface of the membrane (Figure 1) and involve dimers of WASp bound to G-actin monomers (WGD), Arp2/3 ternary complexes consisting of Arp2/3 complex bound to WGD (ArpTernCompl), and activated Arp2/3 ternary complexes (FArpTernCompl). These reactions are described by rate equations,
| (3) |
where [Y] is the surface density of a membrane-bound protein Y. Note that while these variables are governed by ordinary differential equations, they also depend on spatial coordinates, given that RY is nonzero only at the locations of NPFs (see below) and RArpTemCompl depends on [FATP] and [FADP] near the plasma membrane.
Table 1 and Table S2 in the Supplemental Text summarize, respectively, the parameters used in the model and all the variables and their governing equations.
TABLE 1:
Model parameters.
| Parameter | Value/units | Definition | Source |
|---|---|---|---|
| L | 36–138 nm | Local average lengths of actin filaments | Estimated in Results |
| N | 12–46 | Local numbers of subunits in a filament | |
| t0 | 13 s | Parameter used in modeling fc(t) | |
| τ | 0.66 s | Parameter used in modeling fc(t) | |
| ηA | 602 μm–3/μM | Conversion factor | |
| μ | 0.4 nm/(s · pN) | Mobility coefficient | Defined in Model |
| kactive |
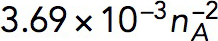 Pa/(μM)2 Pa/(μM)2
|
Active stress coefficient | Computed in Model |
| kvisc |
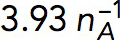 Pa⋅s/μM Pa⋅s/μM |
Shear viscosity coefficient | Estimated in Model |
| ρmax | 20.15 × 103nA μM | Maximum actin density | Defined in Model |
| nmax | 6500 | Maximum number of actin subunits in a patch | Berro et al., 2010 |
| RArp2/3 | 0.035–0.06 | Molar Arp2/3 complex-to-actin ratio | |
| G0 | 21.6 μM | Concentration of actin monomers | |
| fstall | 10.5 pN | Actin polymerization stalling force | Estimated in Results |
| εmax | 6.9 kBT | Maximum energy stored in the patch per subunit | Estimated in Results |
| E | 1 GPa | Young’s modulus of the actin filament | Broedersz and MacKintosh, 2014 |
| I | πa4/4 nm4 | Rotational inertia of the filament | |
| a | 3.5 nm | Radius of the filament cross-section | |
| δ | 2.7 nm | Radius of actin subunit | |
| WASp0 | 259.6 μm–2 | Surface density of NPFs | Based on Berro et al., 2010 |
| Arp0 | 1.3 μM | Concentration of Arp2/3 complex | Berro et al., 2010 |
| C0 | 0.8 μM | Concentration of capping protein | |
| COF0 | 40 μM | Concentration of cofilin |
Coupling the expansion of the actin filament network to the membrane invagination
Equations 1 and 2 are solved in a sufficiently large neighborhood of the invagination, denoted Ω in Figure 2. The plasma membrane Γ includes the invagination. Equation 3 is solved on the parts of the invagination occupied by NPFs. Fission yeast assembles two rings containing different NPFs around the invagination of the plasma membrane (dark red bands in Figure 2) (Arasada and Pollard, 2011; Arasada et al., 2018). Both zones start near the cell surface at the neck of the invagination. One ring is stationary, while the other moves with the tip of the invagination, where it is assumed to be attached to a hemisphere of the protein clathrin. Budding yeast has a single zone containing both types of NPFs, which remains at the base of the invagination (Mund et al., 2018).
FIGURE 2:
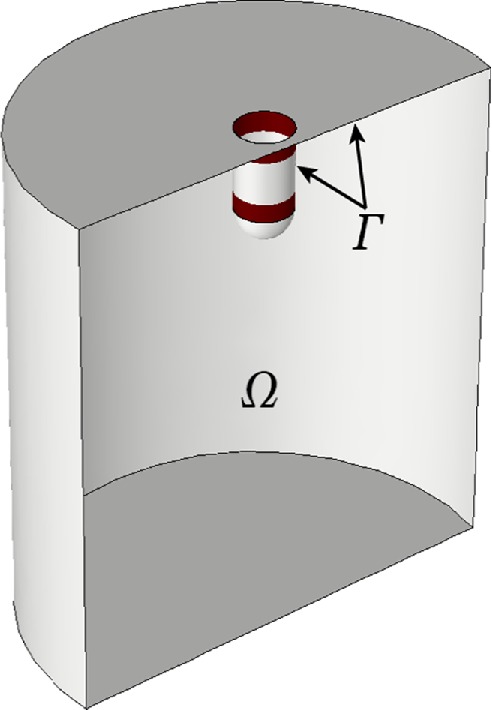
Computational domain, Ω, and plasma membrane, Γ, including invagination. Two rings of NPFs are shown in dark red. When the invagination elongates, both Γ and Ω change with time.
We assume that an initial invagination forms by an unknown mechanism before the assembly of the actin patch. This coated pit of plasma membrane is associated with clathrin molecules and adapter proteins (Arasada and Pollard, 2011; Chen and Pollard, 2013). Our modeling starts after the initial invagination has a depth sufficient to accommodate two adjacent rings of NPFs. The next section describes the shape and size of the initial invagination used in simulations.
Actin filaments polymerizing around the initial invagination are constrained by the plasma membrane, which is pressed against the stiff cell wall. This resistance causes the actin filament network to expand inward from, and laterally along, the cell surface. The flow of actin filaments exerts a drag on an initial invagination, counterbalancing the forces of turgor pressure and elongating the invagination further inward. It is believed that the drag occurs because the actin filaments bind to proteins associated with the membrane (Lacy et al., 2018), though little is known about the biochemical mechanism. The connection between the actin meshwork and the plasma membrane is included in the model as a condition that the membrane and the adjacent actin filaments move with the same velocities: (v – u) | Γ = 0, where u | Γ are the velocities of the points of the membrane. This condition is consistent with the treatment of viscous fluids at interfaces with adjacent media in continuum mechanics (Landau and Lifshitz, 1987). Mathematically, it serves as a boundary condition for Eq. 1 at Γ. The conditions at other boundaries of the computational domain were zero-stress, though they did not affect the solution significantly, because Ω was substantially larger than the size of the invagination (see “Methods” in the Supplemental Text).
The net force exerted on the endocytic invagination is obtained by evaluating an integral of the tangential force density, 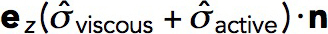 , over the surface of the invagination S:
, over the surface of the invagination S:
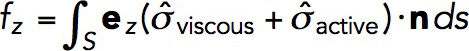 |
(4) |
where n is the outward normal vector to Γ (directed from Γ toward the interior of Ω ), ez is the unit vector orthogonal to the cell wall, and ds is the infinitesimal surface element (Landau and Lifshitz, 1987). The Results section considers in detail the rheological data for actin networks that are critically important for the constitutive dependences σa = σa (ρ) and η = η (ρ, L) used in Eq. 1.
Equation 2 is subject to zero-flux boundary conditions at Γ for all X, except for ActiveArp, for which there is an incoming flux from the rings that describes the detachment of FArpTernCompl from the membrane; see Figure 1. The magnitude of the corresponding flux density is equal to the detachment rate, RFArpTernCompl->ActiveArp | γrings, where γrings denotes the zones of Γ occupied by the rings (see Figure 2 and “Methods” in the Supplemental Text). The existence of a nonzero influx of ActiveArp requires modification of the transport term in Eq. 2 for this variable. Indeed, given the boundary condition for v, pure advection is generally incompatible with a nonzero influx, resulting in unphysical Dirac-delta singularities. The inconsistency is resolved by taking into account that the detachment of the ternary complex from the membrane inherently involves diffusion. Adding the diffusive term restricted to the vicinity of the rings, we arrive at
and a corresponding boundary condition, (D(x)∇([ActiveArp]) + RFArpTernCompl->ActiveArp ) | γrings = 0, where D (x) is nonzero only in the vicinity of the rings (see “Methods” in the Supplemental Text).
At all other boundaries of the computational domain, Eq. 2 was subject to the outflow boundary conditions. As we have noted in the context of Eq. 1, the type of these boundary conditions does not really matter, because, so long as the size of Ω is sufficiently large, they do not affect the solution in any significant way (see “Methods” in the Supplemental Text).
Simulations of the models
Equations 1–3 coupled with respective boundary conditions were solved numerically. Importantly, when the membrane elongates, Γ and Ω in Figure 2 are changing: Γ increases and Ω decreases, so the model must be solved in a domain with a moving boundary (see “Methods” in the Supplemental Text). Note that the concentrations of molecules with names followed by zero in Figure 1 are constants, and the surface density of the NPFs, WASp0, is uniform within the rings and varies over time as a bell-shaped curve (Berro et al., 2010; Sirotkin et al., 2010). The initial values of all other concentrations and v(x, 0) were set to zero, except for [FADP], [BEa], and [PE], which were assigned small initial values, corresponding to a small number of seed filaments (Chen and Pollard, 2013).
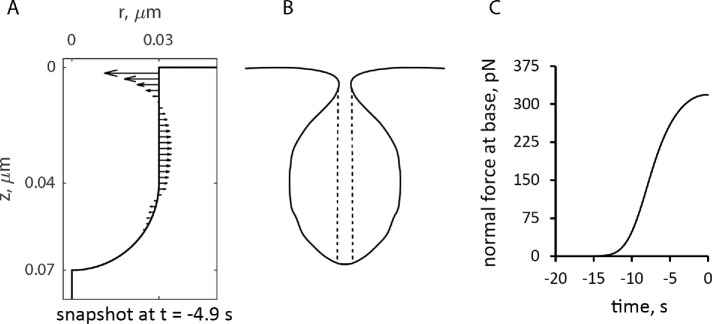
The geometry of the initial invagination was a cylinder with radius 30 nm capped with a hemisphere of the same radius. The initial length of the cylindrical part was 40 nm, accommodating two 20-nm-wide rings positioned next to each other. It was assumed, for simplicity, that during elongation, the invagination preserves its (sphero)cylindrical shape and is infinitely rigid, that is, all points of the tubular membrane have the same instantaneous velocities collinear with the axis of the cylinder. Realistically, the invaginations are not infinitely rigid. Indeed, electron micrographs showed the endocytic invaginations of budding yeast are flask shaped (Kukulski et al., 2012). Our model yields forces orthogonal to the tubule distributed in a way that is consistent with such a shape (see Figure 6, discussed in detail later).
FIGURE 6:
Simulated forces exerted by actin assembly normal to the endocytic tubule. (A) Distribution of forces at ≈5 s before peak on a static tubule. (B) Rough sketch of a plausible shape if the membrane lining the invagination is flexible. The vertical dashed lines show the area of the pore that determines the force produced by the turgor pressure. (C) Time course of the force normal to the tubule at its base. Time zero is the peak of actin assembly.
We computed the time-dependent magnitude of these velocities, assuming a linear force-velocity relationship (Peskin et al., 1993),
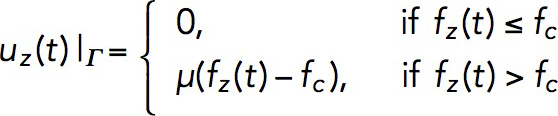 |
(5) |
where fz (t) is the force exerted on the invagination at time t, defined by Eq. 4, fc is the critical force due to turgor pressure, and μ is a given mobility coefficient (see Results and “Methods” in the Supplemental Text).
Parameterization of the force-balance equation ( Eq. 1)
We begin with a description of constitutive relations for active stress and viscosity of actin meshwork in the absence of branching and cross-linking. Measurements of the viscoelasticity of filaments of purified actin can explain how the active stress and viscosity of the meshwork depend on its density and the properties of the filaments. Rheological data usually include information about dynamic (i.e., frequency-dependent) “storage” and “loss” moduli, denoted as G′(ω) and G″(ω), respectively (Wirtz, 2009). The active stress, σa, which is determined by the energy released during polymerization and elastically stored in the meshwork, should be proportional to G′. For overlapping actin filaments, G′(ω) scales with actin density ρ as ∝ρ2 for any ω (Gardel et al., 2003). We therefore assume σa = kactive ρ2, where the proportionality coefficient kactive depends on the extent of branching and cross-linking.
Obtaining a constitutive relation for viscosity η is not as straightforward. Based on polymer physics, it is expected to be of the form, η ∝ ραLβ, where L is the polymer length and exponents α and β depend on whether the polymer is flexible or rigid and whether the solution is dilute or concentrated (Doi and Edwards, 1998). For concentrated solutions of certain flexible chemical polymers, measurements yielded α = 4–5 and β ≈ 3.5, in agreement with theoretical results. Note that the same theory predicts that the viscosity of a polymer solution is always proportional to the viscosity of a solvent; this is based on the assumption that the cross-sectional area of a polymer is vanishingly small. While this assumption is adequate for chemical polymers, it does not apply to a biopolymer meshwork, where the viscosity originates from direct interactions between filaments and is essentially independent of viscosity of the medium. It is intuitive to assume that viscosity of overlapping actin filaments increases as a function of the number of contacts made by the filaments and how long these contacts “slide” along the filaments. The average number of contacts a given filament makes with its neighbors can be estimated as the average number of subunits per volume occupied by a filament, that is, ∼ρNδ 3, where N is the average number of subunits per filament and δ is the radius of the actin subunit, as defined earlier. The contact density is then obtained as a product of the number of contacts per filament and the number of filaments per unit volume. The latter is ρ /N, so that the density of contacts is ∼ρ2δ 3. Assuming further that, for the rod-like filaments, the “lifetime” of a contact is proportional to the number of subunits in a filament N, we arrive at η ∼ ρ2δ 3N = ρ2δ 2L, or
| (6) |
where the proportionality coefficient kvisc can depend on the structural properties of an actin meshwork, such as branching or cross-linking.
We corroborated the constitutive relation of Eq. 6 by estimating η from rheological data for filaments of purified actin. The estimation of η is complicated by the fact that solutions of actin filaments are non-Newtonian fluids with viscosities depending on the shear rates (Buxbaum et al., 1987). This was approximated by deriving kvisc, treated as a constant, from G′ (ω) and G″ (ω), with ω close to the shear rates in actin patches, which are ∼1 s−1 (see Salient properties of the model in Results). It is also important to note that the shear viscosity of the meshwork differs from η′(ω) = G″(ω)/ω (Cox and Merz, 1958; Wirtz, 2009). The effective shear viscosity is often well approximated by an empirical Cox-Merz rule η = ω–1 (G′2 (ω) + G″(ω))1/2, with ω being identified with the shear rate (Cox and Merz, 1958). In what follows, values of η were computed by applying the Cox-Merz formula to the moduli measured at ω = 1 s−1. The length dependence in Eq. 6 is close to η ∝ L0.7, as proposed by Zaner and Stossel (1983), who measured dynamic moduli of solutions of overlapping actin filaments with controlled lengths and applied the Cox-Merz rule to compute η. More recent data by Kasza et al. (2010) point to a linear dependence, η ∝ L. These authors measured G′(ω) and G″(ω) of overlapping actin filament networks prepared with a fixed actin concentration and varying filament lengths and concentrations of linkers. Extrapolation of the data of Kasza et al. (2010) to a zero cross-linker concentration gives the filament length dependence of η without cross-linking. Specifically, the data points of Figure 4c in Kasza et al. (2010), corresponding to ω = 1 s−1, were extrapolated to the linker-to-actin concentration ratio R = 0 by approximating the increase in viscosity due to cross-linking as ∝ (RL)2 (McFadden et al., 2017). Figure 3, which also includes data for R = 0 of Figure 4a in Kasza et al. (2010), shows the dependence of η on filament length in the absence of cross-linking or branching.
FIGURE 3:
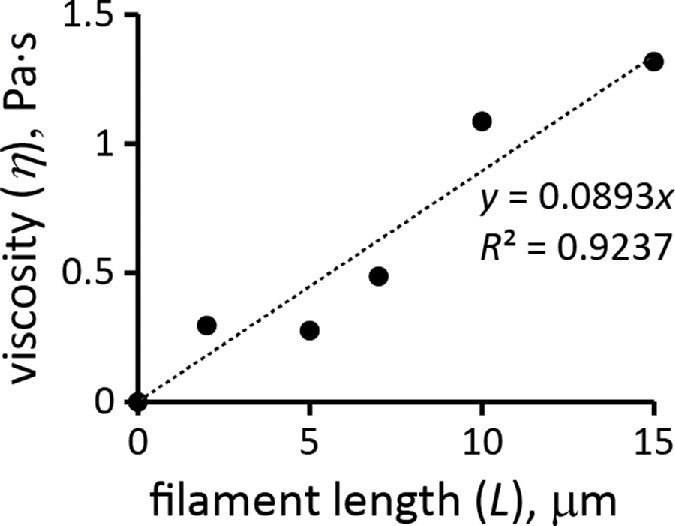
Viscosity of actin filament meshwork as a function of mean filament length at ρ/nA = 12 µM. Extrapolated from data of Kasza et al. (2010).
To confirm the quadratic ρ dependence of Eq. 6, one would need rheological data for actin filament samples with a fixed filament length and a range of actin concentrations. The data closest to these requirements are for G′(ω) and G″(ω) of pure actin filaments without branching or cross-linking at concentrations of 1 mg/ml and 0.3 mg/ml (Gardel et al., 2003). Measurements at ω = 1 s−1 yielded η ∝ ρα with α = 1.98. Equation 6 also yields plausible average filament lengths, 15 and 12 μm, based on the data for pure actin filaments reported in Sato et al. (1987) and Mullins et al. (1998), respectively. These values were obtained using kvisc for pure actin filaments that was estimated by applying Eq. 6 to data points in Figure 4a of Kasza et al. (2010) corresponding to R = 0 (open and filled triangles) and ω = 1 s−1. In this experiment, L = 15 μm, ρ/nA = 0.5 mg/ml = 12 μM, and the respective viscosity η, computed by the Cox-Merz rule, is 1.32 Pa ∙ s, yielding kviscnA ≈ 0.14 Pa s/μM.
Note that Eq. 6 holds only for overlapping filaments, that is, for dense actin networks of sufficiently long filaments, such that (ρN2)1/3 × δ > 1 (Doi and Edwards, 1998). This condition is most certainly violated at early stages of patch assembly, when only few short filaments are present. In this limit, η is expected to be a multiple of solvent viscosity and ∝ρ. Because noticeable stresses and shear rates are generated only after filaments begin to overlap, the two regimes were bridged in our computations by using a simple “interpolation” formula that crosses over to Eq. 6 when the condition for the filament overlapping is met,
In this formula, the number of subunits per filament N was computed as [Ftot]/([BEa] + [BEc]]), where [Ftot] = ρ /nA and [BEa] + [BEc] is equivalent to local filament number density, and the filament length is L = Nδ, as above.
RESULTS
Salient properties of the model
Substituting the constitutive relations σα(ρ) = kactiveρ2 and η (ρ, L) = kvisc ρ2δ2L in Eq. 1 yields
from which it follows that both actin densities ρ (x, t) and velocities v(x, t) are controlled by the ratio kactive/kvisc, rather than separately by kactive and kvisc (as defined earlier, here and below, vector x denotes spatial coordinates of a location in the cell). We confirmed, by solving the model numerically with varying kactive and kvisc, that v(x,t) did not change beyond numerical error when both coefficients were varied proportionally. Also in agreement with the prediction, we found that kactive/kvisc controls a maximum number of polymerized subunits in a patch 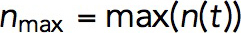 , where
, where  is the number of subunits at time t in the volume Ωpatch occupied by the invagination and surrounding network of actin filaments. Modeling an elongating cylindrical invagination with varying kactive/kvisc (see Dynamics of the invagination during elongation), we found that the ratios
is the number of subunits at time t in the volume Ωpatch occupied by the invagination and surrounding network of actin filaments. Modeling an elongating cylindrical invagination with varying kactive/kvisc (see Dynamics of the invagination during elongation), we found that the ratios 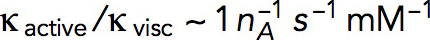 result in nmax close to the experimental numbers. For example, the maximum number of 6500 subunits inside a cylinder Ωpatch of radius 0.15 μm and length 0.3 μm, enveloping the endocytic tubule, is obtained with
result in nmax close to the experimental numbers. For example, the maximum number of 6500 subunits inside a cylinder Ωpatch of radius 0.15 μm and length 0.3 μm, enveloping the endocytic tubule, is obtained with 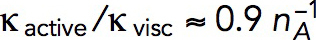 s−1 mM−1. The ratio kactive/kvisc, constrained by the experimental nmax, in turn determines actin velocities v(x,t) and the corresponding shear rates, which are found to be ∼1 s−1 (see below).
s−1 mM−1. The ratio kactive/kvisc, constrained by the experimental nmax, in turn determines actin velocities v(x,t) and the corresponding shear rates, which are found to be ∼1 s−1 (see below).
Figure 4 depicts a snapshot of a solution of the two-ring model with 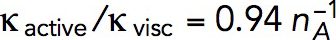 s−1 mM−1, showing distributions of actin density (colors) and actin velocities (white arrows) for an r–z section (r and z are cylindrical coordinates) at a time when the rings on an elongating invagination have separated. The solution yields two zones of actin filaments that are particularly dense in the vicinity of the rings. Note that, even though the two rings are identical in size and NPF density, the actin filament density is higher near the plasma membrane, owing to the inhomogeneity of active barbed ends whose transport is restricted by the rigid cell wall surrounding the plasma membrane. The gradient of actin density then results, as expected, in a net tangential force directed toward the tip of the invagination. Figure 4 indicates low filament densities at the tip of the invagination. Thus, the tip lacks the support of actin and must be sufficiently stiff to withstand turgor pressure. We show in “Actin density and forces at a tip of a tubule” in the Supplemental Text that measurements of rigidity of clathrin-coated vesicles by Nossal and coworkers (Jin et al., 2006) lend support for this assumption. Note that radial and tangential components of actin velocities in the vicinity of the invagination are ∼0.02 μm/s, yielding patch diameters of ∼100–200 nm, consistent with experimental data (Berro et al., 2010; Arasada et al., 2018). The solution also indicates (unpublished data) that tangential components of actin velocity vary significantly in the normal direction over distances ∼0.02 μm from the membrane, yielding shear rates of ∼1 s−1, as mentioned earlier.
s−1 mM−1, showing distributions of actin density (colors) and actin velocities (white arrows) for an r–z section (r and z are cylindrical coordinates) at a time when the rings on an elongating invagination have separated. The solution yields two zones of actin filaments that are particularly dense in the vicinity of the rings. Note that, even though the two rings are identical in size and NPF density, the actin filament density is higher near the plasma membrane, owing to the inhomogeneity of active barbed ends whose transport is restricted by the rigid cell wall surrounding the plasma membrane. The gradient of actin density then results, as expected, in a net tangential force directed toward the tip of the invagination. Figure 4 indicates low filament densities at the tip of the invagination. Thus, the tip lacks the support of actin and must be sufficiently stiff to withstand turgor pressure. We show in “Actin density and forces at a tip of a tubule” in the Supplemental Text that measurements of rigidity of clathrin-coated vesicles by Nossal and coworkers (Jin et al., 2006) lend support for this assumption. Note that radial and tangential components of actin velocities in the vicinity of the invagination are ∼0.02 μm/s, yielding patch diameters of ∼100–200 nm, consistent with experimental data (Berro et al., 2010; Arasada et al., 2018). The solution also indicates (unpublished data) that tangential components of actin velocity vary significantly in the normal direction over distances ∼0.02 μm from the membrane, yielding shear rates of ∼1 s−1, as mentioned earlier.
FIGURE 4:
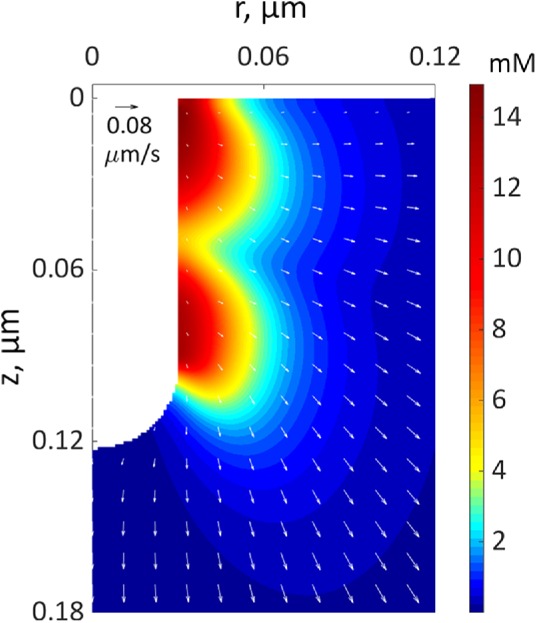
A snapshot from a simulation of an elongating endocytic invagination shown for r–z cross-section of three-dimensional geometry. The extracellular space is white. The color shows the density distribution of actin filaments, and the arrows show the local velocities of their movements at the peak of actin assembly (see Figure 7C for snapshots at other time points). The velocity scale bar in the upper left corner corresponds to 0.08 μm/s.
Control of the shear rates and actin densities by kactive/kvisc has another consequence: for a given nmax, the force exerted on the invagination depends on kvisc (or alternatively on kactive, given that kactive/kvisc is fixed). Mathematically, this is seen upon substitution of the constitutive relations in Eq. 4. Qualitatively, the tangential force exerted on the invagination, which largely originates from the viscous stress, is locally defined by a product of viscosity and shear rates. Because the latter are fixed by the known nmax, this leaves the tangential force to be directly proportional to kvisc. We confirmed this assertion computationally by solving the model with constant kactive/kvisc over a range of kvisc (see “Model Solutions with Varying kactive and kvisc” in the Supplemental Text).
Patch assembly can generate pushing forces comparable to turgor pressure in fission yeast
We use the model with 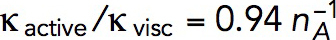 s−1 mM−1 to determine the kvisc required to obtain forces sufficient to exceed the turgor pressure. For this, we solved the model in a static geometry with the shape and size of the initial invagination described in Simulations of the models. We found that the required kvisc is
s−1 mM−1 to determine the kvisc required to obtain forces sufficient to exceed the turgor pressure. For this, we solved the model in a static geometry with the shape and size of the initial invagination described in Simulations of the models. We found that the required kvisc is 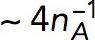 Pa · s/μM. For example, a tangential force of ∼2538 pN, sufficient to withstand turgor pressure of ∼9 atm, requires
Pa · s/μM. For example, a tangential force of ∼2538 pN, sufficient to withstand turgor pressure of ∼9 atm, requires 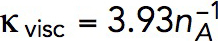 Pa · s/μM and, correspondingly,
Pa · s/μM and, correspondingly, 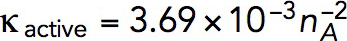 Pa/(μM)2. The obtained value of kvisc is ∼28-fold larger than
Pa/(μM)2. The obtained value of kvisc is ∼28-fold larger than 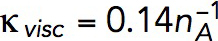 Pa · s/μM of actin filaments alone.
Pa · s/μM of actin filaments alone.
Two factors in patches contribute to a higher viscosity than actin filaments alone. First, the meshwork is highly entangled due to the high density of branching. For example, the viscosity of 24 μM of actin filaments at a shear rate of ω = 1 s−1 was more than sevenfold higher when polymerized with 0.12 μM of Arp2/3 complex according to Figure 3 in Tseng and Wirtz (2004). The molar ratio of Arp2/3 complex-to-actin in these experiments, RArp2/3 = 0.005, was significantly lower than the range of 0.035 and 0.06 observed in actin patches (Berro et al., 2010). Such high values of RArp2/3 increase the viscosity by at least a factor of 2.5, according to rheological measurements of actin filaments with a range of concentrations of Arp2/3 complex (Mullins et al., 1998). Overall, the entanglement of the filaments due to branching alone yields an 18-fold increase of the patch viscosity compared with filament networks obtained in the absence of Arp2/3 complex. Second, actin patches accumulate a very high concentration of the cross-linking protein fimbrin (Berro and Pollard, 2014), which also increases the viscosity. Rheological data indicate that the viscosity of actin networks cross-linked by soft (muscle alpha-actinin, filamin) and rigid (avidin-biotin) linkers ranges from few fold to an order of magnitude higher than actin filaments that are not cross-linked (Wachsstock et al., 1994; Kasza et al., 2010). The properties of actin filaments cross-linked by fimbrin are likely to be in the same range. Thus, cross-linking by fimbrin accounts for the remaining increase of kvisc by a factor of 1.6.
Our simulations of patch formation and force generation must satisfy several constraints. For a fixed kactive/kvisc, the increase of kvisc implies a similar increase of kactive and hence the corresponding increase of σa. The latter is limited by free energy released during a polymerization step: εmax = kBT In (G0/Gcrit), where G0 is the concentration of actin monomers and the critical concentration Gcrit = k–Depolymerization/k+Polymerization (Footer et al., 2007). For the parameter values used in our model, the upper bound for the stored energy is εmax = 6.9 kBT, corresponding to the stalling force εmax/δ ≈ 10.5 pN per filament, which is consistent with published estimates (Lacy et al., 2018). In simulations, the mechanical work per filament polymerizing under load depends on the local actin density: 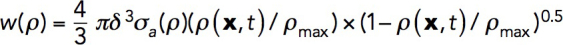 , where σa = kactive
ρ2; see Parameterization of the force-balance equation (Eq. 1). The maximum of w (x, t) evaluated for the above-mentioned solution in static geometry yields
, where σa = kactive
ρ2; see Parameterization of the force-balance equation (Eq. 1). The maximum of w (x, t) evaluated for the above-mentioned solution in static geometry yields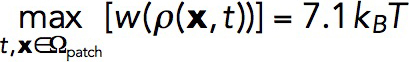 , which is comparable to εmax.
, which is comparable to εmax.
The ability of a filament to sustain generated forces is another constraint on the system; the force per filament should not exceed the buckling threshold, fcrit = π2 EI/(2L)2 (Broedersz and MacKintosh, 2014). In this formula, E = 1 GPa is Young’s modulus of the actin filament; I = πa4/4 is the rotational inertia of the filament, where a = 3.5 nm is the radius of the filament cross-section; and L is the filament length. To satisfy the constraint, the force per filament in the vicinity of the invagination must be less than the critical load fcrit. For the solution with the static geometry described earlier, at the time of peak actin assembly, the filament lengths in the vicinity of the endocytic tubule varied from 36 to 138 nm (recall that filament lengths are calculated as L = Nδ , where N = ρ(x, t)/ρBE (x, t)). These lengths are consistent with previous estimates (Berro et al., 2010). Then, the number of filaments in the vicinity of the invagination, obtained by integrating the density of barbed ends ρBE(x, t) = nA([BEa] + [BEc]) in a shell with thickness equal to the shortest filament length, is 96. So for this solution, the average force per filament is 2538 pN/96 ≈ 26 pN. Of the total 146 filaments inside the shell with thickness of 138 nm, the lengths of 67 filaments are under 103 nm, and their critical loads are above 27 pN. Thus, these shorter filaments endure the generated force on their own. The longer filaments sustain their share of the load through cross-linking by fimbrin: because the critical load for a bundle of filaments grows roughly as the square of the number of filaments in a bundle, the buckling threshold for a bundle of just two filaments will be at least 100 pN.
We thus conclude that the forces generated during patch assembly can withstand the opposing forces from turgor pressure in fission yeast.
Dynamics of the invagination during elongation
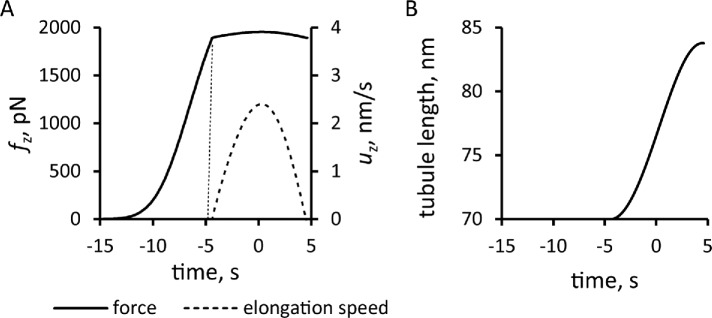
In this section, we elucidate factors determining the dynamics of elongating invaginations and their maximum length. For this, we solve our model in a moving geometry, allowing the invagination to grow freely. We also show that the invagination dynamics are similar in fission and budding yeast, despite different localizations of the NPFs.
Once the force exerted on the invagination exceeds the turgor pressure threshold, the invagination will grow inward. The rate of the growth in our model is given by Eq. 5: uz(t) = μ(fz(t)–fc). It may seem that the length, which the invagination can attain during patch assembly, is controlled by the mobility coefficient μ. However, solving the model in a dynamic geometry with varying μ indicates that the final length of the endocytic tubule is virtually insensitive to μ. This is because the increase of μ is mitigated by the drop in fz that depends on the shear rates ∂rvz , so the elongation rate uz does not change appreciably (in computations, we used μ = 0.4 nm s–1/pN).
The kinetic parameters of actin nucleation and polymerization govern the duration of patch assembly, so the time during which the patch elongates depends on how quickly fz overcomes the critical threshold fc from turgor pressure. The time before fz exceeds fc is shorter for larger kvisc, but kvisc has an upper bound. The reason for this is that kactive must increase in proportion to kvisc, because the ratio kactive/kvisc is limited by a maximum number of subunits in a patch, and kactive is limited by the energy constraints considered in the previous subsection.
Solving the model in a geometry allowing the invagination to lengthen freely yields a growing endocytic tubule (Supplemental Movie S1). Figure 5 illustrates the time courses of fz, uz, and invagination length obtained with 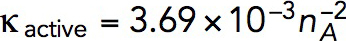 Pa/(μM)2,
Pa/(μM)2, 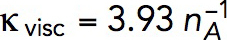 Pa · s/μM, and the threshold fc = 1894 pN corresponding to a turgor pressure of ≈7 atm. Note that the rate of increase of fz drops sharply when the exerted force crosses the turgor-pressure threshold (Figure 5A). Above this threshold, the surface area increases, but fz plateaus below the values reached in static geometry with the same kactive and kvisc, due to the drop of shear rates when the invagination starts to move. This results in a relatively short elongation (Figure 5B).
Pa · s/μM, and the threshold fc = 1894 pN corresponding to a turgor pressure of ≈7 atm. Note that the rate of increase of fz drops sharply when the exerted force crosses the turgor-pressure threshold (Figure 5A). Above this threshold, the surface area increases, but fz plateaus below the values reached in static geometry with the same kactive and kvisc, due to the drop of shear rates when the invagination starts to move. This results in a relatively short elongation (Figure 5B).
FIGURE 5:
Simulation of the elongation of an endocytic tubule with a fixed threshold corresponding to turgor pressure of ≈7 atm. Time zero is the peak of actin assembly. (A) Time course of net tangential force (solid line) and the speed of elongation (dashed line). (B) Tubule length over time.
Movie S1.
Simulation of an elongating invagination with fixed resisting force. Results are shown for turgor pressure ≈7 atm. Left panel: 3D distribution of actin density (color) in the vicinity of the tubule. Middle panel: actin density and its velocities (arrows, scale bar in upper-left corner of the middle panel corresponds to 0.08 μm/s) are shown for r-z sections of 3D geometry. Right panel: deformable computational mesh used in the simulations; deformations of mesh conform to moving invagination. The movie was made with a color code built into COMSOL, which is slightly different from that used in the Figures.
The model produces longer invaginations if we take into account the effects of the forces produced by actin polymerization on the shape of the plasma membrane invagination. The distribution of force density er · 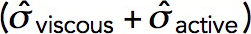 · n orthogonal to an invagination, shown in Figure 6A for the static geometry solution of the previous subsection, suggests that normal forces tend to squeeze the invagination near the plasma membrane and stretch the middle of the invagination. If the tubule were not modeled as infinitely rigid, these forces would likely distort the invagination into a flask or “head-and-neck” shape (Figure 6B), as observed in electron micrographs of budding yeast actin patches (Kukulski et al., 2012).
· n orthogonal to an invagination, shown in Figure 6A for the static geometry solution of the previous subsection, suggests that normal forces tend to squeeze the invagination near the plasma membrane and stretch the middle of the invagination. If the tubule were not modeled as infinitely rigid, these forces would likely distort the invagination into a flask or “head-and-neck” shape (Figure 6B), as observed in electron micrographs of budding yeast actin patches (Kukulski et al., 2012).
Because turgor pressure is isotropic, the net resistance force fc it would produce for the flask shape is proportional to the cross-sectional area of the opening of the invagination delineated in Figure 6B by dashed lines. Indeed, the net force exerted by turgor pressure in the upward direction along the tubule’s axis is 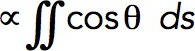 , where θ (θ∈[0, π]) is the angle that the outward, with respect to the cytoplasm, normal vector makes with the axis of symmetry; ds is the area of a surface element; and the integral is taken over the surface of the invagination. Because cosθ ds is the signed area of the surface element projection on the plane perpendicular to the axis, the integral yields the difference of the projection area obtained for the surface points with θ ≤ π/2 and that for the points with θ > π/2. This difference is exactly the cross-sectional area of the opening delineated by the dashed lines in Figure 6B, which is πr2, where r is the radius of the opening. Thus, as the opening tightens and r diminishes, fc decreases in proportion to r2, while the turgor pressure remains unchanged. We further assume that the radius of the opening, initially equal to the radius of the tubule R, decreases linearly with the normal force fn(t) (Figure 6C), starting with some threshold value fn,0 . Then, fc (t,fn,0) = fc,maxr2(t)/R2, where fc,max = πR2Pturgor, with the turgor pressure Pturgor fixed at ≈9 atm, and r(t) = R–k (fn(t)–fn,0) for fn(t) ≥ fn,0. We define the proportionality coefficient k to find the maximum invagination length that our model could yield. The corresponding condition is that r approaches zero as fn(t)→fn,max. For a full derivation, see “Modeling the time-dependent force due to turgor pressure” in the Supplemental Text.
, where θ (θ∈[0, π]) is the angle that the outward, with respect to the cytoplasm, normal vector makes with the axis of symmetry; ds is the area of a surface element; and the integral is taken over the surface of the invagination. Because cosθ ds is the signed area of the surface element projection on the plane perpendicular to the axis, the integral yields the difference of the projection area obtained for the surface points with θ ≤ π/2 and that for the points with θ > π/2. This difference is exactly the cross-sectional area of the opening delineated by the dashed lines in Figure 6B, which is πr2, where r is the radius of the opening. Thus, as the opening tightens and r diminishes, fc decreases in proportion to r2, while the turgor pressure remains unchanged. We further assume that the radius of the opening, initially equal to the radius of the tubule R, decreases linearly with the normal force fn(t) (Figure 6C), starting with some threshold value fn,0 . Then, fc (t,fn,0) = fc,maxr2(t)/R2, where fc,max = πR2Pturgor, with the turgor pressure Pturgor fixed at ≈9 atm, and r(t) = R–k (fn(t)–fn,0) for fn(t) ≥ fn,0. We define the proportionality coefficient k to find the maximum invagination length that our model could yield. The corresponding condition is that r approaches zero as fn(t)→fn,max. For a full derivation, see “Modeling the time-dependent force due to turgor pressure” in the Supplemental Text.
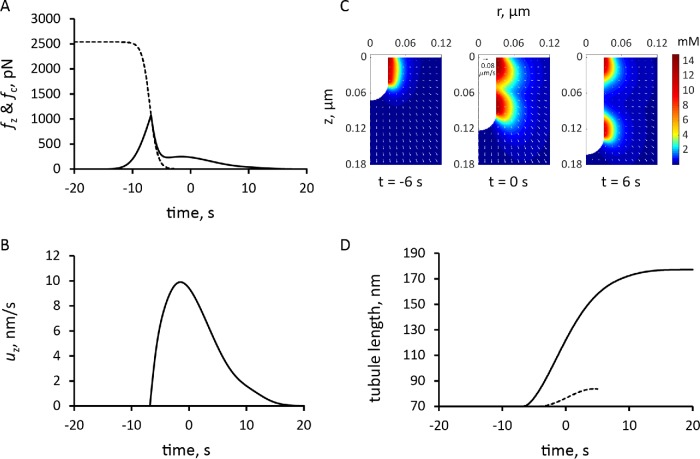
To facilitate the incorporation of the numerically defined fn(t) in the model, we observe that the time-dependent threshold fc(t, fn,0) is accurately approximated by an analytical function fc,max (1 + exp((t − t0)/τ))−1 . The fitting of the analytical function to fc(t, fn,0) was done by varying t0 and τ. Parameter τ is largely constrained by the time window within which fn(t) takes off, and t0, which is the timing of the fc(t) decrease, depends in part on fn,0. Varying fn,0 resulted only in marginal changes of the simulation outputs. The dashed curve in Figure 7A, obtained with t0 = 13 s and τ = 0.66 s, is an approximation of fc(t) with fc,max = 2538 pN, corresponding to Pturgor ≈ 9 atm, and fn,0 = 120 pN. Using the same values of κactive, κvisc and other model parameters as before, solutions of the model with the time-dependent threshold yielded a longer invagination than the model with a fixed threshold (Figure 7D and Supplemental Movie S2).
FIGURE 7:
Simulation of endocytic tubule elongation with the force threshold from turgor pressure decreasing with time. Time zero is the peak of actin assembly. (A) Time course of the assumed decrease in force threshold due to turgor pressure, fc (dashed curve), and the simulated pushing force, fz (solid line). (B) Time course of the variation in the speed of invagination, which begins when fz is greater than fc. (C) Snapshots of r–z sections of the actin filament density around the endocytic tubule and its velocities (arrows; scale bar in upper left corner of snapshot in the middle corresponds to 0.08 μm/s); see also Supplemental Movie S2. (D) Comparison of the time courses of tubule elongation with decreasing force from turgor pressure (solid line) against that with a fixed threshold due to turgor pressure in Figure 5B (dashed curve).
Movie S2.
Simulation of elongating invagination with force threshold decreasing with time. Left panel: 3D distribution of actin density (color) in the vicinity of the tubule. Middle panel: actin density and its velocities (arrows, scale bar in upper-left corner of the middle panel corresponds to 0.08 μm/s) are shown for r-z sections of 3D geometry. Right panel: deformable computational mesh used in simulation; deformations of mesh conform to moving invagination. The movie was made with a color code built into COMSOL, which is slightly different from that used in the Figures.
The lengths of modeled invaginations are similar to the distances that actin patch proteins moved from the cell surface in superresolution movies, taking into account the size of the protein coat around the membrane (Arasada et al., 2018). To illustrate the qualitative agreement between the model and experiment, we processed the simulation data using the protocol of Arasada and Pollard (see “Methods” in the Supplemental Text for details), so that the results shown in Figure 8 can be directly compared with the experimental data (see Figure 3, A–F, in Arasada et al., 2018).
FIGURE 8:
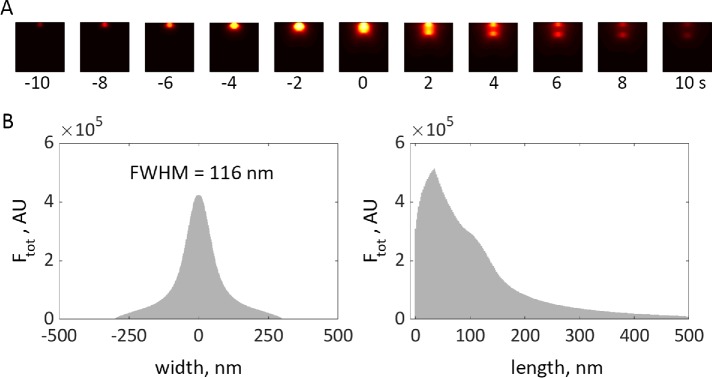
Simulation of elongating tubule with time-dependent force threshold is consistent with experimental data. (A) Heat maps of simulated actin density (see Figure 7), projected on plane of image and subjected to median filtering to mimic 35-nm resolution limit due to convolution with point-spread function, are shown for selected time points. See “Methods” in the Supplemental Text for details of how simulation results were processed for this figure; see Supplemental Figure 2 for results before filtering. (B) Width and length distributions of actin density, obtained by integrating results of A over time, are consistent with experimental data in Arasada et al. (2018). FWHM is the full width of a distribution at half-maximum.
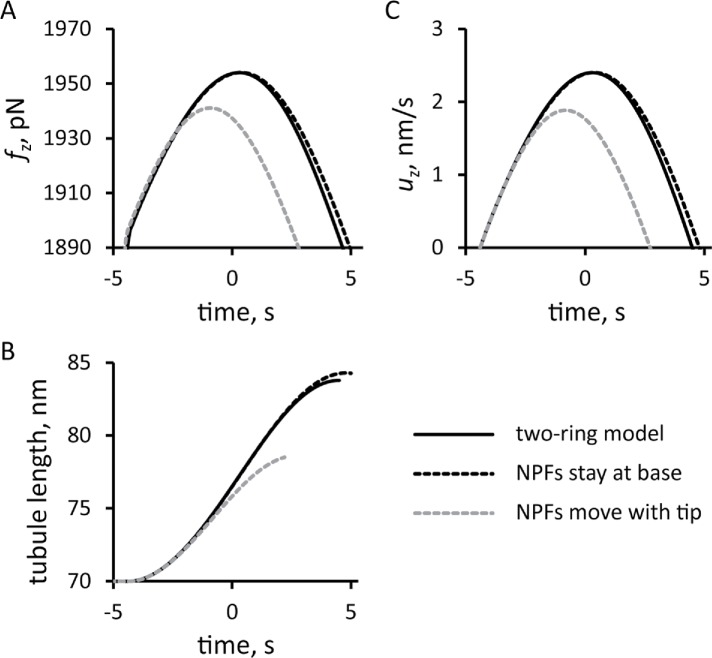
We compared the solution of the two-ring model with a fixed threshold fc against the corresponding solutions of the models, in which all of the NPFs remained at the base or moved together with the tip of the tubule (Figure 9). For all three versions of the model, we used invaginations with the same widths and total numbers of NPFs and ran the simulations with the same initial conditions. The model with the NPFs remaining at the base slightly overperforms the two-ring model. In contrast, the model with the NPFs moving together with the tip generates significantly weaker forces, resulting in a slower movement and much shorter invagination than the two-ring model. These results highlight the importance of the cell wall in supporting the actin meshwork to generate traction forces. The partial absence of such support in the two-ring model is mitigated almost entirely by the repulsion of the two zones of polymerizing actin.
FIGURE 9:
Comparison of the simulation results from models with three different locations of NPFs: solid lines, two-ring model with NPFs at the base and tip of the invagination; dashed line, one-ring model in which all NPFs stay at the base of the invagination; and gray dashed line, one-ring model with all NFPs at the tip. Time zero is the peak of actin assembly in the two-ring model. Time dependencies for pushing force (A), elongation speed (C), and tubule length (B) are shown for elongating invaginations with fixed threshold corresponding to turgor pressure ≈7 atm.
DISCUSSION
Endocytosis in fission and budding yeast depends on forces produced by the assembly of expanding networks of actin filaments that drive invagination of the plasma membrane against the high internal turgor pressure. However, it was unclear whether actin assembly generates forces sufficient to overcome the turgor pressure.
We formulated a mathematical model of the forces based on principles of polymer physics that integrates the kinetics of the biochemical reactions (actin filament nucleation, elongation, capping, and severing), the rheological properties of actin filament networks, and the time course of numbers of participating proteins. Certain modeling assumptions and approximations used in this study are similar to those adopted in other models of endocytosis in yeast (Carlsson and Bayly, 2014; Carlsson, 2018; Lacy et al., 2018; Mund et al., 2018). In particular, as in previous studies, we assume that movement is transmitted from a growing actin patch to the endocytic invagination via connections of actin filaments to the plasma membrane. As assumed previously (Carlsson and Bayly, 2014), our model approximates a network of actin filaments as a continuous medium, though Carlsson and coworkers (as well as the authors of a discrete model in Mund et al., 2018) approximate the actin patch as a growing elastic solid. Taking into account the turnover of actin in the patch, largely due to severing of the filaments by cofilin, we interpret the mechanics of the endocytic actin meshwork as that of a viscoelastic fluid, with parameters constrained by measured rheological properties of overlapping filaments. This has yielded forces sufficient to withstand turgor pressure in fission yeast. Simulations of the model also reproduce the temporal and spatial distributions of actin filaments at sites of endocytosis and point to the flask-type shapes of invaginations of the plasma membrane observed by electron microscopy (Kukulski et al., 2012).
Our model allows for different assumptions about the location of the NPFs that activate the Arp2/3 complex to drive the assembly of the actin filament networks. We compared a two-ring hypothesis proposed for fission yeast (Arasada and Pollard, 2011; Arasada et al., 2018), a model proposed for budding yeast (Picco et al., 2015; Sun et al., 2017; Mund et al., 2018) in which all NPFs remain at the base of the invagination, and a hypothetical model in which the NPFs move with the tip of the invagination.
Simulations of the two-ring model produced two interacting zones of actin filaments with high densities near the rings. The internal repulsive stress generated by actin polymerization causes the entire patch to expand. Constraints imposed by the plasma membrane and cell wall result in expansion of the network inward and laterally, exerting drag on an initial invagination and thus pulling it inward. Given the known number of polymerized actin subunits and viscosity of the actin meshwork, we estimate the magnitude of this drag. The dendritic structure of the meshwork produces entanglement that enhances viscosity to levels sufficient to produce forces in the range of 2200–3000 pN, which, for invaginations with typical diameters, would overcome turgor pressure ∼8–10 atm. The estimates are within the energy and critical load constraints, with the buckling threshold being met, in part, with the aid of cross-linking by fimbrin.
Simulations of the one-zone models with the numbers of NPFs and initial conditions used for the two-zone model also produced drag on the invagination. The budding yeast model with the NPFs remaining at the base of the invagination generated forces close to those in the two-ring model. This result underscores the importance of the cell wall, which provides support necessary for the actin filament network to generate a traction force. In the two-ring model, mutual repulsion of the two zones of actin filaments compensates for the partial loss of support from the cell wall. The model with the NPFs moving at the tip generated significantly weaker forces, resulting in a much shorter invagination than the two other models.
The general model allowed us to simulate the forces required to elongate an endocytic tubule, although we used the simplifying assumption that the invagination is a spherocylinder with a fixed radius. We also assumed that, once the generated force overcomes the turgor threshold, all the points on the invagination move with the same (but time-dependent) speed 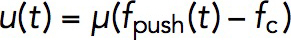 . Somewhat counterintuitively, the speed and the length attained by the invagination is virtually insensitive to the mobility coefficient μ, but rather depends on how early during patch assembly the force produced by actin assembly fpush(t) overcomes the opposing force from turgor pressure fc. For fc corresponding to ∼7-atm turgor pressure, the simulations yielded a maximum tubule length somewhat shorter than experimental patch sizes.
. Somewhat counterintuitively, the speed and the length attained by the invagination is virtually insensitive to the mobility coefficient μ, but rather depends on how early during patch assembly the force produced by actin assembly fpush(t) overcomes the opposing force from turgor pressure fc. For fc corresponding to ∼7-atm turgor pressure, the simulations yielded a maximum tubule length somewhat shorter than experimental patch sizes.
We discovered that expansion of the actin filament network produces radial forces normal to the tubule. The distribution of these radial forces along the tubule would tend to squeeze the invagination near its opening and stretch the middle, producing a shape like a flask, as observed by electron microscopy in budding yeast (Kukulski et al., 2012). Without reliable information about elastic properties of endocytic invaginations, we could not solve for shape of the invagination. However, a small pore between the exterior and the lumen of the invagination reduces fc as actin assembles. We approximated the effect of this shape change by using a threshold fc(t) decreasing over time to show that reducing the size of the pore favors the formation of longer tubules.
Supplementary Material
Acknowledgments
Research reported in this publication was supported by National Institute of General Medical Sciences of the National Institutes of Health (NIH) under award numbers R01GM026338, P41GM103313, and R01GM115636 and by the National Science Foundation (NSF) under award number MCB171605. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or the NSF. We thank Rajesh Arasada for advice and superresolution measurements of actin patch dynamics. M.N. and B.M.S. thank Leslie Loew for continuing support and helpful discussions. The research presented in this paper was supported by the systems, services, and capabilities provided by the University of Connecticut High Performance Computing facility.
Abbreviations used:
- ArpTernCompl
Arp2/3 complex bound to WGD
- BEa
active barbed ends
- BEc
capped barbed ends
- FADP
subunits aged by ATP hydrolysis and phosphate dissociation
- FArpTernCompl
Arp2/3 ternary complexes
- FATP
ATP-bound subunits
- FCOF
subunits bound by cofilin
- NPF
nucleation-promoting factor
- PE
pointed ends
- WGD
WASp bound to G-actin monomers.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E19-01-0059) on June 26, 2019.
REFERENCES
- Aghamohammadzadeh S, Ayscough KR. (2009). Differential requirements for actin during yeast and mammalian endocytosis. Nat Cell Biol , 1039–1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arasada R, Pollard TD. (2011). Distinct roles for F-BAR proteins Cdc15p and Bzz1p in actin polymerization at sites of endocytosis in fission yeast. Curr Biol , 1450–1459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arasada R, Sayyad WA, Berro J, Pollard TD. (2018). High-speed superresolution imaging of the proteins in fission yeast clathrin-mediated endocytic actin patches. Mol Biol Cell , 295–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basu R, Munteanu EL, Chang F. (2014). Role of turgor pressure in endocytosis in fission yeast. Mol Biol Cell , 679–687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berro J, Pollard TD. (2014). Synergies between Aip1p and capping protein subunits (Acp1p and Acp2p) in clathrin-mediated endocytosis and cell polarization in fission yeast. Mol Biol Cell , 3515–3527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berro J, Sirotkin V, Pollard TD. (2010). Mathematical modeling of endocytic actin patch kinetics in fission yeast: disassembly requires release of actin filament fragments. Mol Biol Cell , 2905–2915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broedersz CP, MacKintosh FC. (2014). Modeling semiflexible polymer networks. Rev Mod Phys , 995–1036. [Google Scholar]
- Buxbaum RE, Dennerll T, Weiss S, Heidemann SR. (1987). F-actin and microtubule suspensions as indeterminate fluids. Science , 1511–1514. [DOI] [PubMed] [Google Scholar]
- Carlsson AE. (2018). Membrane bending by actin polymerization. Curr Opin Cell Biol , 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlsson AE, Bayly PV. (2014). Force generation by endocytic actin patches in budding yeast. Biophys J , 1596–1606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Q, Pollard TD. (2013). Actin filament severing by cofilin dismantles actin patches and produces mother filaments for new patches. Curr Biol , 1154–1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox WP, Merz EH. (1958). Correlation of dynamic and steady-flow viscosities. J Polym Sci , 619–622. [Google Scholar]
- Doi M, Edwards S. (1998). The Theory of Polymer Dynamics, New York: Oxford University Press. [Google Scholar]
- Footer MJ, Kerssemakers JWJ, Theriot JA, Dogterom M. (2007). Direct measurement of force generation by actin filament polymerization using an optical trap. Proc Natl Acad Sci USA , 2181–2186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardel ML, Valentine MT, Crocker JC, Bausch AR, Weitz DA. (2003). Microrheology of entangled F-actin solutions. Phys Rev Lett , 158302. [DOI] [PubMed] [Google Scholar]
- Jin AJ, Prasad K, Smith PD, Lafer EM, Nossal R. (2006). Measuring the elasticity of clathrin-coated vesicles via atomic force microscopy. Biophys J , 3333–3344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaksonen M, Roux A. (2018). Mechanisms of clathrin-mediated endocytosis. Nat Rev Mol Cell Biol , 313–326. [DOI] [PubMed] [Google Scholar]
- Kasza KE, Broedersz CP, Koenderink GH, Lin YC, Messner W, Millman EA, Nakamura F, Stossel TP, MacKintosh FC, Weitz DA. (2010). Actin filament length tunes elasticity of flexibly cross-linked actin networks. Biophys J , 1091–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruse K, Joanny J-F, Jülicher F, Prost J, Sekimoto K. (2005). Generic theory of active polar gels: a paradigm for cytoskeletal dynamics. Eur Phys J E: Soft Matter , 5–16. [DOI] [PubMed] [Google Scholar]
- Kukulski W, Schorb M, Kaksonen M, Briggs JA. (2012). Plasma membrane reshaping during endocytosis is revealed by time-resolved electron tomography. Cell , 508–520. [DOI] [PubMed] [Google Scholar]
- Lacy MM, Ma R, Ravindra NG, Berro J. (2018). Molecular mechanisms of force production in clathrin- mediated endocytosis. FEBS Lett , 3586–3605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau LD, Lifshitz EM. (1987). Fluid Mechanics, Vol. 6, Course of Theoretical Physics, New York: Pergamon Press. [Google Scholar]
- MacKintosh FC, Käs J, Janmey PA. (1995). Elasticity of semiflexible biopolymer networks. Phys Rev Lett , 4425. [DOI] [PubMed] [Google Scholar]
- McFadden WM, McCall PM, Gardel ML, Munro EM. (2017). Filament turnover tunes both force generation and dissipation to control long-range flows in a model actomyosin cortex. PLoS Comp Biol , e1005811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mullins RD, Kelleher JF, Xu J, Pollard TD. (1998). Arp2/3 complex from Acanthamoeba binds profilin and cross-links actin filaments. Mol Biol Cell , 841–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mund M, van der Beek JA, Deschamps J, Dmitrieff S, Hoess P, Monster J-L, Picco A, Nédélec F, Kaksonen M, Ries J. (2018). Systematic nanoscale analysis of endocytosis links efficient vesicle formation to patterned actin nucleation. Cell , 884–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nickaeen M, Novak IL, Pulford S, Rumack A, Brandon J, Slepchenko BM, Mogilner A. (2017). A free-boundary model of a motile cell explains turning behavior. PLoS Comp Biol , e1005862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novak IL, Gao F, Kraikivski P, Slepchenko BM. (2011). Diffusion amid random overlapping obstacles: similarities, invariants, approximations. J Chem Phys , 154104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novak IL, Kraikivski P, Slepchenko BM. (2009). Diffusion in cytoplasm: effects of excluded volume due to internal membranes and cytoskeletal structures. Biophys J , 758–767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peskin CS, Odell GM, Oster GF. (1993). Cellular motions and thermal fluctuations: the Brownian ratchet. Biophys J , 316–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picco A, Mund M, Ries J, Nédélec F, Kaksonen M. (2015). Visualizing the functional architecture of the endocytic machinery. eLife , e04535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prost J, Jülicher F, Joanny J-F. (2015). Active gel physics. Nat Phys , 111–117. [Google Scholar]
- Satcher RL, Jr, Dewey CF., Jr (1996). Theoretical estimates of mechanical properties of the endothelial cell cytoskeleton. Biophys J , 109–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato M, Schwarz WH, Pollard TD. (1987). Dependence of the mechanical properties of actin/α-actinin gels on deformation rate . Nature , 828–830. [DOI] [PubMed] [Google Scholar]
- Scher-Zagier JK, Carlsson AE. (2016). Local turgor pressure reduction via channel clustering. Biophys J , 2747–2756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmit JD, Kamber E, Kondev J. (2009). Lattice model of diffusion-limited bimolecular chemical reactions in confined environments. Phys Rev Lett , 218308. [DOI] [PubMed] [Google Scholar]
- Sirotkin V, Berro J, Macmillan K, Zhao L, Pollard TD. (2010). Quantitative analysis of the mechanism of endocytic actin patch assembly and disassembly in fission yeast. Mol Biol Cell , 2894–2904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y, Leong NT, Jiang T, Tangara A, Darzacq X, Drubin DG. (2017). Switch-like Arp2/3 activation upon WASP and WIP recruitment to an apparent threshold level by multivalent linker proteins in vivo. eLife , e29140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tseng Y, Wirtz D. (2004). Dendritic branching and homogenization of actin networks mediated by Arp2/3 complex. Phys Rev Lett , 258104. [DOI] [PubMed] [Google Scholar]
- Wachsstock DH, Schwarz WH, Pollard TD. (1994). Cross-linker dynamics determine the mechanical properties of actin gels. Biophys J , 801–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wirtz D. (2009). Particle-tracking microrheology of living cells: principles and applications. Annu Rev Biophys , 301–326. [DOI] [PubMed] [Google Scholar]
- Zaner KS, Stossel TP. (1983). Physical basis of the rheologic properties of F-actin. J Biol Chem , 11004–11009. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.