Abstract
This review describes off-resonance R1ρ relaxation dispersion NMR methods for characterizing microsecond-to-millisecond chemical exchange in uniformly 13C/15N labeled nucleic acids in solution. The review opens with a historical account of key developments that formed the basis for modern R1ρ techniques used to study chemical exchange in biomolecules. A vector model is then used to describe the R1ρ relaxation dispersion experiment, and how the exchange contribution to relaxation varies with the amplitude and frequency offset of an applied spin locking field, as well as the population, exchange rate, and differences in chemical shifts of two exchanging species. Mathematical treatment of chemical exchange based on the Bloch-McConnell equations is then presented and used to examine relaxation dispersion profiles for more complex exchange scenarios including three-state exchange. Pulse sequences that employ selective Hartmann-Hahn cross-polarization transfers to excite individual 13C or 15N spins are then described for measuring off-resonance R1ρ(13C) and R1ρ(15N) in uniformly 13C/15N labeled DNA and RNA samples prepared using commercially available 13C/15N labeled nucleotide triphosphates. Approaches for analyzing R1ρ data measured at a single static magnetic field to extract a full set of exchange parameters are then presented that rely on numerical integration of the Bloch-McConnell equations or the use of algebraic expressions. Methods for determining structures of nucleic acid excited states are then reviewed that rely on mutations and chemical modifications to bias conformational equilibria, as well as structurebased approaches to calculate chemical shifts. Applications of the methodology to the study of DNA and RNA conformational dynamics are reviewed and the biological significance of the exchange processes is briefly discussed.
Keywords: R1ρ relaxation dispersion, chemical exchange, nucleic acid dynamics, Hoogsteen, tautomers
Graphical abstract
1. Introduction
The fundamental importance of conformational flexibility to the biological function of nucleic acids was evident at the birth of structural biology when it was immediately apparent that the two strands in DNA had to come apart to allow access to genetic information[1]. However only over the past decade, thanks in part to developments in solution-state NMR[2–6], has the true nature of nucleic acid flexibility and its roles in replication, gene expression, and regulation come to light[3, 4, 7–9]. Like proteins, the structures of nucleic acids undergo complex fluctuations over timescales spanning more than twelve orders of magnitude from picoseconds to seconds[10–12].
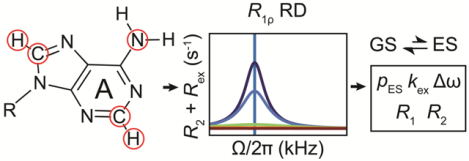
Here, we review methods based on the measurement of R1ρ(13C) and R1ρ(15N) relaxation dispersion (RD)[13, 14] for characterizing microsecond-to-millisecond chemical exchange in uniformly 13C/15N labeled nucleic acids in solution. Motions on this timescale are of particular interest because they coincide with the timescales for breaking base pairs (BPs, see glossary for abbreviations), the basic building block of nucleic acid structure. These motions can lead to formation of high-energy non-native conformations referred to as “excited states” (ESs)[15] that correspond to local minima in the free energy landscape. ESs have structural and therefore functional properties that can differ substantially from the native “ground state” (GS) conformation, enabling them to serve as molecular switches or targets for drug discovery. R1ρ RD experiments have revealed a wide variety of such motions in DNA and RNA, which were previously unknown, and are now believed to play important roles in gene expression and regulation[9, 11, 16–18].
R1ρ is one of several RD experiments that can be used to characterize microsecond-tomillisecond chemical exchange. R1ρ experiments offer some advantages relative to Carr Purcell-Meiboom-Gill (CPMG) experiments[19, 20], particularly for nucleic acid applications given the scarcity of ideal 15N spin probes[9, 21]. These advantages include enhanced sensitivity to faster microsecond timescale motions[22], ability to robustly determine a complete set of exchange parameters using experiments performed at a single static magnetic field[23], and perhaps most importantly, applicability to uniformly 13C/15N labeled samples[13, 21], which can be readily prepared using standard biochemical protocols. However, relative to CPMG, offresonance R1ρ experiments can be more difficult to implement, and perhaps for this reason, have not been as widely applied to the study of chemical exchange in biomolecules. The goal of this review is to provide readers with the conceptual foundations needed to use R1ρ RD experiments for characterizing chemical exchange. While the focus is on nucleic acids, many topics covered should be of utility to those interested in studying proteins, and to those who are using other RD methods to characterize chemical exchange in nucleic acids. The reader is also referred to other excellent reviews on R1ρ RD methods, with specific application to proteins[5, 13]. It should be noted that in recent years, there have also been significant developments in the application of Chemical Exchange Saturation Transfer (CEST) experiments for characterizing slow millisecond timescale chemical exchange in proteins[24–27], that have been extended to nucleic acids[28–32] and that afford advantages similar to those of R1ρ.
The review is organized in the following manner: Section 2 provides a historical account of key developments that led to R1ρ RD methods described here. Section 3 uses a vector model to describe dephasing of the magnetization during the R1ρ experiment as a conceptual framework for understanding basic aspects of the experiment, with a focus on two-state exchange. This is followed by mathematical treatment of chemical exchange using the Bloch-McConnell equations in Section 4. Section 5 reviews pulse sequences for measuring offresonance R1ρ(13C) and R1ρ(15N) RD in uniformly labeled nucleic acids while Section 6 is devoted to data analysis methods to obtain the exchange parameters. Section 7 reviews methods for determining structures of nucleic acid ESs, and finally Section 8 reviews some example applications to DNA and RNA. Since we have carried out many off-resonance R1ρ studies of chemical exchange in nucleic acids, most of the applications reviewed in Sections 7 and 8 come from our group. However, to provide a more balanced perspective of what is now a rapidly evolving field applying a range of NMR RD methods to the study of chemical exchange in nucleic acids, we also refer to earlier on-resonance R1ρ studies which set the stage for the off resonance R1ρ applications, and also make references to CPMG and CEST studies of nucleic acids when appropriate.
2. Brief historical account of relaxation dispersion in NMR with a focus on R1ρ and nucleic acids
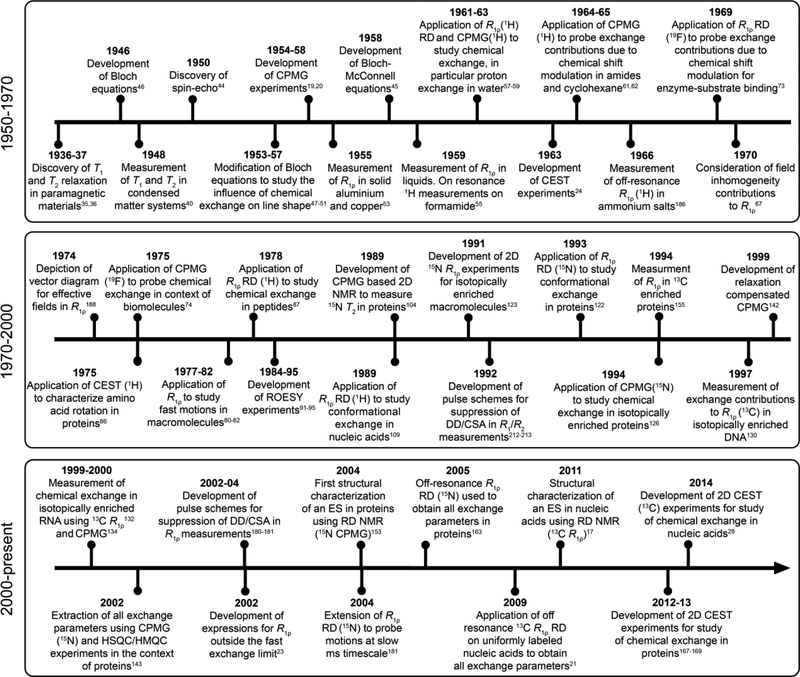
The theoretical and experimental underpinnings of NMR RD techniques were conceived soon after the observation of NMR in condensed matter systems independently by Bloch, Hansen, and Packard at Stanford University[33], and by Purcell, Torrey, and Pound at Harvard University[34]. Examining the historical progression from these initial studies helps one to highlight the motivation behind these developments, which frequently was unrelated to measuring dynamics, as well as key challenges that had to be overcome to make modern biological applications possible. We will find that, while the basics of RD experiments were conceived for applications to small organic molecules, the desire to characterize chemical exchange in biomolecules drove key developments in both theory and experiment that made it possible to robustly and quantitatively extract exchange parameters of interest. While the focus will be on R1ρ, we shall also make references to CPMG and CEST RD experiments to help place these developments into a broader context. A timeline showing some of the milestones to the development of RD NMR is provided in Fig. 1. While we have tried our best to provide an accurate portrayal of this history, this is not intended to be an exhaustive compilation of the many important contributions to the development of RD NMR, and we apologize for any omissions.
Figure 1.
Time diagram showing key developments in RD NMR techniques for characterizing chemical exchange in biomolecules with emphasis placed on R1ρ studies and their application to nucleic acids.
2.1. 1930–1960: Genesis of NMR relaxation dispersion methods
The R1ρ experiment involves measuring exchange contributions (Rex) to nuclear spin relaxation in the rotating frame. The phenomenon of spin relaxation and its experimental measurement was well established for electrons even before the observation of NMR by Bloch and Purcell. The Dutch physicist Cornelis Gorter first reported electron spin-lattice and spinspin relaxation in the mid 1930s[35, 36]. Gorter found that the electron magnetic moments of paramagnetic substances such as the sulfate salts of iron and chromium needed some time to return back to equilibrium after changing the external magnetic field[36]. Gorter, who is credited with coining the term “NMR”[37], is also well-known for his unsuccessful attempt to observe NMR, a failure which ironically could be attributed to his poor choice of lithium fluoride as a sample given its long spin-lattice relaxation time[38].
Theoretical estimates for nuclear spin-lattice relaxation times were available as early as the 1930s[39]. Some of the first quantitative experimental measurements were performed in 1948, when Pound et al. measured spin-lattice (T1) and spin-spin (T2) relaxation times in condensed matter[40]. Pound also derived expressions relating T1 and T2 to the rotational correlation time, thus establishing a link between relaxation and dynamics[40]. Later efforts were focused on improving the methods used to measure T1 and T2[41–43]. While attempting to develop methods for measuring T1, Erwin Hahn “accidently” discovered the spin-echo which would prove invaluable to measure T2 and form the basis for the very first RD experiments[44]. A few years later, Carr, Purcell, Meiboom, and Gill[19, 20] extended the spin-echo into a series of 180° pulses to suppress contributions of the static field inhomogeneity and of translational diffusion, resulting in the development of the CPMG experiment. As an unintended consequence, the train of 180° pulses also provided a means to suppress Rex to a variable extent, thus forming the basis for the CPMG RD experiment (see below).
The phenomena of chemical exchange and many aspects of RD experiments can be described without recourse to a quantum description. The origins of the Bloch-McConnell (B-M) equations[45], which constitute the theoretical foundation for NMR RD experiments, can be traced back to the phenomenological Bloch equations, which were introduced in 1946, that use classical physics to describe the motion of macroscopic nuclear magnetization. Bloch realized that bulk magnetization resulting from the application of a longitudinal magnetic field (B0) could be forced to undergo precession by application of a transverse magnetic field. He developed equations to describe this dynamic behavior that also treat the influence of T1 and T2 relaxation on the magnetization[46]. Bloch theorized that forced precession would induce an electric signal (“nuclear induction”) in an appropriately placed coil, and subsequently verified this prediction using a water sample[33]. Gutowsky, Slichter, Meiboom and others[47–51] later extended the Bloch equations and developed expressions that took into account the influence of chemical exchange on the behavior of magnetization in the absence of transverse magnetic fields. These expressions helped explain why line shapes changed when altering temperature or pH. In the late 1950s, McConnell recognized that chemical exchange provides mechanisms for directly transferring components of magnetization between exchanging states (i.e., Mji→ Mki; i = x, y or z; for states j and k), and explicitly introduced exchange terms into the Bloch equations to take this transfer into account, resulting in the development of the B-M equations[45]. Hahn independently came to a similar realization even earlier in 1952 while accounting for the influence of scalar couplings and chemical shifts during spin-echoes[52].
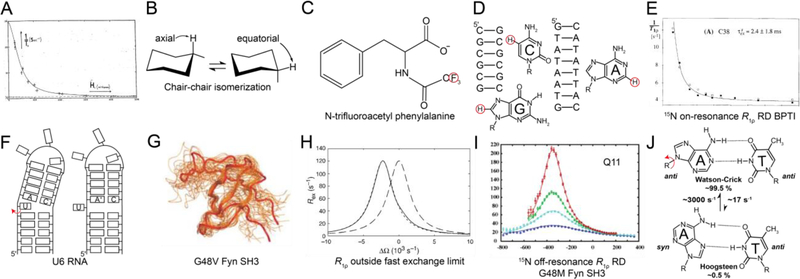
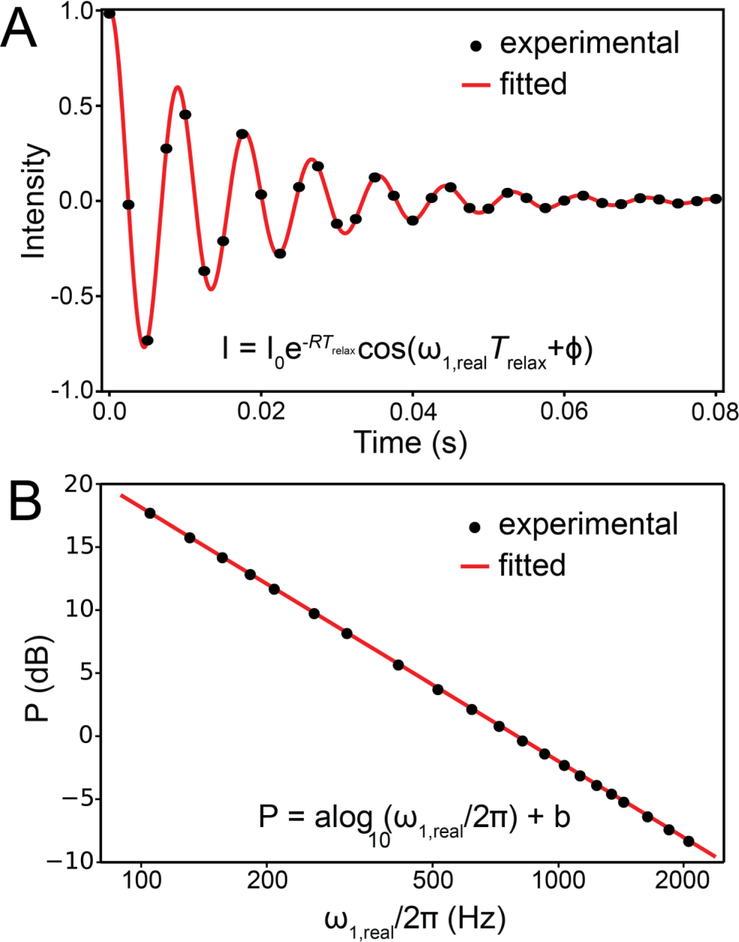
As is the case for CPMG, the R1ρ experiment was not conceived for the purpose of measuring chemical exchange. In the mid 1950s, while developing a theory to account for the magnetic behavior of solids under the influence of strong transverse radio frequency (RF) fields, Redfield discovered a phenomenon that he referred to as “rotary saturation” or “saturation in the rotating frame”[53]. Redfield realized that one could spin-lock magnetization along an effective field direction through application of an RF field. Inspired by Rabi’s picture of the rotating frame[54], Redfield recognized that spin-locked magnetization could be tilted through application of a second RF field perpendicular to the effective field, in a manner analogous to how Bloch tilted magnetization away from the B0 field[33]. The subsequent recovery of the magnetization along the effective field following removal of the second RF field was described by a relaxation time T1ρ, which Redfield recognized to be sensitive to spin-spin interactions in the solid. Redfield measured T1ρ for metals such as aluminium and copper as a function of the strength of the applied transverse RF field, thus performing the very first R1ρ RD measurements. R1ρ RD measurements in liquids were reported some four years later by Solomon in 1959[55] who tested theoretical expressions relating R1ρ to the rotational correlation time that were developed earlier by Winter et al.[56]. Solomon performed these R1ρ measurements in a manner similar to the pulsed methods used routinely nowadays. An adiabatic half passage was used to tilt the magnetization to the transverse plane, following which the spin-locking field was applied for a given time and switched off to measure the signal in the transverse plane. The variation of the signal amplitude with the time for which the spin-locking field was applied was used to obtain R1ρ. An on-resonance RD profile was reported showing the dependence of R1ρ(1H) on the applied spin-lock amplitude for the protons of formamide (Fig. 2A).
Figure 2.
Historical progression of the development of R1ρ RD techniques for applications to nucleic acids. A) The on-resonance R1ρ(1H) RD profile measured for formamide by Solomon et al.[55] was the first reported measurement of R1ρ in liquids. Reproduced with permission from Bibliotheque nationale de France (BNF).B) The chair-chair inter-conversion in cyclohexane was one of the earliest conformational transitions characterized by RD methods[62, 63].C) R1ρ(19F)measurements on N-trifluoroacetyl phenylalanine in exchange between free and enzyme-bound states by Sykes et al.[73] constituted the first application of R1ρ RD in the context of biological macromolecules. D) Some of the earliest applications of R1ρ in studies of conformational exchange in biomolecules targeted 1H nuclei (red circles) in nucleic acid duplexes in the early 1990s[109–111]. E) On-resonance R1ρ(15N) RD profile for backbone amide 15N of C38 in bovine pancreatic trypsin inhibitor was one of the first reported characterizations of conformational exchange in isotopically labeled proteins using R1ρ[122]. Reprinted by permission from [122]. F) Secondary structure transition in U6RNA involving flipping out of a bulge nucleotide; this was one of the first validated models for ESs in nucleic acids[135]. G) First structure of an ES by Kay et al.[153] for a folding intermediate of the G48V mutant of the Fyn SH3 domain obtained using chemical shifts measured using CPMG RD and structurebased chemical shift calculations. Reprinted by permission from [153]. H) Expressions for R1ρ outside the fast exchange limit by Palmer et al.[23] allowed extensions of the R1ρ method by demonstrating the feasibility of extracting all exchange parameters at a single magnetic field. RD profiles were shown to be centered at the ES chemical shift. Simulated off-resonance profiles (for pES = 0.048, kex = 1500 s−1, Δω = 2400 rad s−1, R1,GS = R1,ES = 1.5 s−1, R2,GS = R2,ES = 11 s−1 and ω1/2π = 1000 Hz) are shown using the asymmetric population expression in Palmer et al.[23] (dotted line) and fast exchange expression (dashed line). The exact numerical solution is shown as a solid black line. Reproduced with permission from [23]. I) Off-resonance R1ρ(15N) RD profile for the amide 15N of Q11 in a G48M mutant of the Fyn-SH3 domain; this was the first experimental measurement of off-resonance R1ρ using low spin-lock amplitudes and selective excitation experiments[163]. This study also represented the first instance wherein a complete set of exchange parameters was extracted using R1ρ measurements. Reprinted with permission from [163]. J) Excited state Hoogsteen BPs in duplex DNA were the first ESs to be structurally characterized in nucleic acids using R1ρ RD.Rates and populations were obtained using off-resonance R1ρ experiments as described by Al-Hashimi et al.[115].
2.2. 1960–1970s: Applications to small molecules
In the early 1960s, Meiboom and colleagues realized that RD experiments could be used to characterize chemical exchange. Using on-resonance R1ρ(1H)[57] and CPMG(1H)[58, 59] experiments, they estimated the rates of proton transfer in water. These experiments did not rely on the modulation of the chemical shift by the exchange process, but rather, on the modulation of the proton resonance frequency due to changes in scalar couplings and quadrupolar interactions as the protons exchanged between water molecules containing 16O and 17O. During the same period, approaches based on saturation transfer, which later were to form the basis for the CEST experiment, were used to investigate the kinetics of proton exchange between 2-hydroxy acetophenone and salicylaldehyde in 1963[24] and internal proton-transfer in acetylacetone in 1964[60].
RD measurements probing exchange contributions due to the modulation of chemical shifts soon followed with applications to small organic compounds. These landmark studies of conformational exchange in small molecules formed the basis for the modern RD applications to biomolecules. In an early application, Allerhand and Gutowsky used CPMG(1H) experiments to characterize the hindered rotation of amide groups in dimethylcarbamyl chloride and N,N dimethyltrichloroacetamide[61] as well as chair-to-chair inter-conversion in cyclohexane[62] (Fig. 2B). Analogous R1ρ RD studies were conducted in the early 1970s by Morgan, Strange and colleagues[63]. The exchange rate (250–2000 s−1) and difference in chemical shift between the exchanging axial and equatorial protons (20–25 Hz) deduced for the chair-to-chair interconversion of cyclohexane (Fig. 2B), assuming two-state exchange between equally populated states, were in good agreement with the values measured previously using CPMG[62]. Morgan, Strange and colleagues also demonstrated the feasibility of using on-resonance R1ρ(31P) and R1ρ(1H) to measure J-couplings and T2 for halides of phosphorus[64] and hydrogen[65, 66], and also examined the impact of RF and B0 field inhomogeneity on the accuracy of R1ρ measurements[67]. Other early applications included the determination of the activation energies for the rotation of amide groups in urea derivatives, based on the temperature dependence of R1ρ[68]. This period also saw applications of saturation transfer to characterize conformational exchange in small molecules[69, 70], kinetics of proton exchange[71], and reaction rates[72].
2.3. 1970s–2000s: Applications to biomolecules
Applications of RD methods to biomolecules began to emerge in the early 1970s with initial studies focusing on measuring RD data on small substrates to characterize enzymesubstrate binding kinetics. In one of the earliest applications of R1ρ RD to the study of chemical exchange in biomolecules, Sykes[73] in 1969 measured on-resonance R1ρ(19F) RD on the trifluoroacetyl-phenylalanine substrate and thereby characterized its binding kinetics to the enzyme chymotrypsin (Fig. 2C). Not only was this the first measurement of R1ρ RD involving biological macromolecules, it was also the first measurement of exchange contributions to R1ρ arising from chemical shift modulation. It was shown that the rate constants for binding as well as the chemical shifts of the bound trifluoroacetyl-phenylalanine could be deduced from R1ρ RD measurements. In analogy to R1ρ, the first biological application of CPMG RD involved characterizing the kinetics of N-fluoroacetyl-D-tryptophan binding to α-chymotrypsin using 19F as a probe[74]. During the same period, 1H CEST experiments were also applied to study the kinetics of trimethoprim binding to dihydrofolate reductase[75]. Many modern applications have continued to use RD NMR with great success to probe the kinetics of intermolecular association[76–79]. This period also saw the application of R1ρ[80–82] and CPMG[83–85] experiments to measure T2 for the purpose of characterizing fast picosecond-to-nanosecond timescale motions in proteins and nucleic acids.
During the 1970s and 80s, 1H RD was used to study chemical exchange due to conformational changes in the biomolecules themselves, with initial applications to protein side chains and oligonucleotides. In one of the earliest applications, Williams et al. used 1H CEST to measure the temperature-dependent kinetics of rotation of a tyrosine residue about the Cβ-Cγ bond in ferrocytochrome C, and obtain the activation energy for the process[86]. R1ρ(1H) RD experiments were also used to characterize backbone and side-chain conformational exchange in peptides[87–90]. This period also witnessed the introduction of ROESY experiments that relied on transverse cross relaxation in the presence of a spin-locking field for transferring magnetization between spins[91, 92]. The experiment was later extended to include spin-locking fields far off-resonance[93–95] and has been used to study conformational changes[96], reaction rates[97] and base opening[98] in the context of nucleic acids, in addition to investigating their hydration dynamics[99, 100]. The 1980s also saw the application of imino proton exchange methods by Gueron, Leroy, and co-workers, to study base pair opening in DNA duplexes[101, 102] and tetrads[103].
By the early 1990s, RD NMR had emerged as a technique for probing micro-to-millisecond timescale motions, bridging the gap between picosecond-to-nanosecond timescale motions accessible by T1, T2, and NOE measurements[104–106] and millisecond timescale motions detectable by T2 measurements and line-shape analysis. Given the advances in hardware[107, 108], the stage was set for applications to measure chemical exchange in biomolecules, initially using 1H probes and later 13C and 15N probes as well.
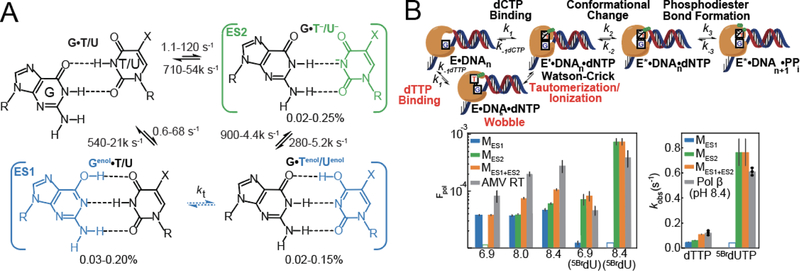
It may come as a surprise that early applications of RD to study conformational exchange in large biomolecules used R1ρ rather than CPMG, and that the first target molecules were DNA duplexes rather than proteins. Ikuta[109], James[110] and Frenkiel[111] measured onresonance R1ρ(1H) RD for cytosine-H5, guanine-H8 and adenine-H2 and reported micro-tomillisecond timescale exchange in the DNA double helix (Fig. 2D). These early experiments did not provide the chemical shifts of the exchanging species, and as a consequence, it was not possible to deduce the identity of the ES. We now know that these very first observations of chemical exchange in DNA most likely represented transitions between Watson-Crick and Hoogsteen BPs, based on off-resonance R1ρ measurements performed a quarter century later[17, 112–117] (see Fig 2J). Analogous Hoogsteen transitions were characterized in G-G mismatches during the mid 1990s by Peck and colleagues[118] using R1ρ(1H) RD measurements targeting base guanine-H8.
Following the introduction of methods for preparing 13C/15N labeled proteins in the late 1980s and 1990s (reviewed in Bolton et al.[119]) and the development of 2D methods for measuring heteronuclear spin-lattice R1 (= 1/T1) and spin-spin R2 (= 1/T2) relaxation rate constants[104, 120, 121], it became feasible to carry out detailed residue specific studies of conformational exchange in biomolecules. In an early application, Wuthrich et al.[122] used a 2D R1ρ(15N) RD experiment developed by Wagner et al.[123] to probe the kinetics of backbone conformational changes in bovine pancreatic trypsin inhibitor (BPTI) (Fig. 2E). During the same period, Kay, Torchia, and Bax pioneered the 2D CPMG(15N) experiment[104] to suppress chemical exchange contributions and allow the accurate measurement of residue specific T2 values in proteins for studies of picosecond-to-nanosecond dynamics. Early applications of CPMG to measure T2 frequently revealed micro-to-millisecond exchange contributions, but these were often not investigated further to obtain details regarding the underlying exchange process[124, 125]. This changed in 1994, when Arseniev et al. performed the first 2D 15N CPMG RD measurement on a protein[126] by varying the delay between the hard 180° pulses. Millisecond timescale backbone motions in a fragment of bacteriorhodopsin were characterized and tentatively assigned to the bending of the transmembrane alpha helices. Many studies appeared thereafter during the 1990s applying R1ρ and CPMG to study conformational exchange in a variety of proteins (reviewed by Loria et al.[22]). Other early applications included the use of CPMG(1H) RD to investigate the dynamics of water molecules as they exchanged between the bulk and the hydration layer of proteins[127].
The development of methods for preparing 13C/15N labeled RNA[128] and DNA[129] during the late 1980s and early 1990s also opened the door for the application of heteronuclear 2D R1ρ experiments to nucleic acids, initially with a focus on measuring on-resonance R1ρ(13C). Using on-resonance adenine sugar R1ρ(C1’) RD measurements, Lancelot et al. in 1997[130] and Chattopadhyaya et al. in 2000[131] reported microsecond timescale exchange in a DNA duplex. While the nature of the exchange process was unknown, it again likely represented Watson Crick to Hoogsteen transitions[17, 112–117]. During the same period, Pardi and Hoogstraten performed some of the first R1ρ RD measurements on RNA, reporting microsecond timescale exchange in the lead-dependent ribozyme[132] and hammerhead ribozyme[133] based on aromatic base R1ρ(13C) measurements. From these measurements, kex as well as the product pGSpESΔω2 could be determined, where kex is the exchange rate (units s−1), Δω is the difference in chemical shift between the exchanging species (units rad s−1), and pGS and pES are the populations of the GS and ES, respectively. This period also saw application of CPMG(13C) RD to RNA by Marion et al., who estimated exchange contributions to transverse relaxation using random fractionally 13C labeled samples to suppress homonuclear C-C scalar couplings[134].
This was followed by many studies employing R1ρ(13C) experiments to examine chemical exchange in RNA and DNA during the 2000s. For example, Butcher et al. characterized widespread chemical exchange in the U6-RNA stem loop containing a single nucleotide bulge[135]. The exchange was hypothesized to arise from the flipping out of a bulge nucleotide in a manner dependent on protonation of a flanking A-C mismatch (Fig. 2F). This was validated based on pH-dependent chemical shift measurements, providing a rare example in which structural features of nucleic acid ESs could be deduced and tested. Other studies exposed exchange on a microsecond timescale involving changes in sugar pucker in the GAAA tetraloop[136] as well as changes in exchange dynamics in RNA upon binding to proteins[137]. Subsequent studies by Varani et al. also revealed micro-to-millisecond timescale exchange related to motions of loop residues in RNA and G-C BPs in duplex DNA[138–140].
2.4. 2000s-present: Detailed characterization of chemical exchange in biomolecules
The 2000s witnessed key advances in methodology that improved the ability to characterize chemical exchange using NMR RD methods. CPMG(13C and 15N) experiments could not be used to study processes slower than ~2 ms due to difficulties associated with deconvoluting in-phase and anti-phase relaxation contributions during the relaxation period when using long interval periods between 180° pulses[141]. This drawback was addressed by the development of relaxation-compensated CPMG experiments by Palmer and Loria in 1999[142] that permitted the usage of 180° pulse trains with larger intervals by averaging the contributions of in-phase and anti-phase relaxation during the relaxation period. Another limitation was that CPMG data could only be used to determine the magnitude of Δω, but not its sign. This prevented determination of the ES chemical shifts that later proved critical for their structural elucidation. This problem was addressed in 2002 when Kay et al.[143] introduced HSQC/HMQC methods for determining the sign of Δω, permitting for the first time complete characterization of an exchange process using CPMG based methods, for a mutant of T4 lysozyme. Other developments in CPMG experiments (reviewed in Palmer et al.[5]) soon followed, including the use of constant time relaxation periods[144, 145], double/multiple quantum based methods[146–148], extension to different types of spins in proteins[149, 150], and TROSY[151] based methods to extend applications to larger proteins[142, 152]. The first structural characterization of an ES was reported in 2004, when in a landmark study, Kay et al. reported the structure of a protein folding intermediate of a mutant Fyn SH3 domain, using chemical shifts obtained from CPMG(15N) RD measurements[153] (Fig. 2G).
During the same time period, advances were also being made in the R1ρ experiment with specific application to proteins. Early R1ρ RD experiments[123, 154, 155] employed hard pulses to align the magnetization of all spins along their effective fields. This limited the experiment to relatively high spin-lock amplitudes (>1000 Hz), consequently leaving millisecond motions largely undetected. In addition, algebraic expressions relating R1ρ RD to the exchange parameters (pES, kex, Δω, R1 and R2) were only available for the fast exchange limit[63, 87, 156]. While this allowed estimation of kex, resolving pES and Δω was not possible; rather only the product pESpGSΔω2 could be determined. Finally, methods for suppressing dipole-dipole CSA cross correlated relaxation (DD/CSA)[157] had yet to be developed, and discrepancies were being reported for relaxation rates measured using R1ρ and CPMG[158, 159].
In the early 2000s, advances were made that addressed these limitations. In a milestone study, Palmer et al. in 2002[23] provided expressions for the exchange contribution to R1ρ outside of the fast exchange limit (Fig. 2H). These expressions showed that a complete thermodynamic and kinetic characterization of an exchange process including the sign of Δω was feasible based on off-resonance R1ρ RD data measured at a single static magnetic field. In 2005, Kay et al. introduced an R1ρ RD experiment that employed a selective excitation scheme developed by Bodenhausen and co-workers[160–162] to investigate exchange contributions at individual 15N spins in a 1D manner[163]. In addition to permitting facile alignment of the magnetization along the effective field for a wide variety of offsets and spin-lock amplitudes, contributions from cross-correlated dipole-dipole/CSA relaxation[157] and evolution under JNH scalar couplings could be optimally suppressed with the use of continuous-wave 1H irradiation during the spin-lock period. This culminated in the first extraction of all exchange parameters using R1ρ measurements at a single magnetic field by Kay et al. in 2005[163] for a mutant of the Fyn SH3 domain, thus demonstrating the utility of the expressions developed earlier by Palmer et al.[23] (Fig. 2I).
These advances initially made for proteins were later integrated in 2009[21] into a pulse sequence employing low spin-lock amplitudes optimized for measuring R1ρ(13C) for base (C6/C8) and sugar (C1′) spins in nucleic acids. This study demonstrated the feasibility of performing off-resonance R1ρ RD experiments on uniformly 13C/15N nucleic acids, which could be prepared using commercially available 13C/15N labeled nucleotide triphosphates. This made it possible for the first time to extract all exchange parameters in nucleic acids, including the sign of Δω. By permitting the use of low spin-lock amplitudes, the experiment also made it possible to access slow millisecond timescale exchange in nucleic acids, given the challenges of applying CPMG(13C) to uniformly 13C/15N labeled samples. This R1ρ experiment permitted more detailed studies of chemical exchange in nucleic acids, and when combined with methods for modulating conformational exchange using mutagenesis and chemical modifications (Section 7), it became possible to visualize the structural identity of the nucleic acid ESs, first in DNA[17] (Fig. 2J) and soon after in RNA[16]. The experiment was later extended to target base imino[112, 164] and amino[165] 15N spins as well as sugar 13C spins[117, 166], culminating in 3D structure determination of an ES in the DNA double helix, specifically the Hoogsteen BPs mentioned earlier[116, 117].
Five years following the application of low spin-lock off-resonance R1ρ to nucleic acids, and building on efforts that resurrected the CEST experiment to characterize chemical exchange in proteins[167–169], Zhang et al.[28, 170] demonstrated the utility of 13C CEST for characterizing slow millisecond timescale chemical exchange in uniformly 13C/15N labeled RNA samples, as well as allowing direct access to structural and dynamic properties of ESs such as residual dipolar couplings (RDCs)[171, 172]. Like R1ρ, the CEST experiment also allows the determination of all exchange parameters and has been widely applied in studies of nucleic acid dynamics[29–32]. Concurrently, significant advances were made in preparing RNA samples with selective labeling schemes, which further extended the domain of applicability of CPMG to nucleic acids[18, 136, 173–177]. With the R1ρ, CEST, and CPMG methodologies in place, one is now in a much better position to characterize motions in DNA and RNA occurring on the microto-millisecond timescale and to examine their roles in gene expression and regulation.
Perhaps the most important lesson that can be drawn from this brief historical account is that RD methods have their roots in magnetic resonance studies that were not intended to characterize chemical exchange, but rather, flow from human curiosity. This underscores the importance of fostering basic science research in magnetic resonance even if clear applications are not obvious in the short run. Indeed, it is very likely the case that there are other NMR phenomena such as Hahn’s echo discovered many decades ago, that can be adapted to modern applications to biological problems. Our account also illustrates how important it was following the initial discovery of the RD methods to tightly integrate developments in hardware, sample labeling, theory, and pulse sequence design to make possible the modern quantitative applications to biomolecules.
3. Description of R1ρ relaxation dispersion using a vector model
RD experiments for studying equilibrium chemical exchange can be understood without recourse to a rigorous quantum mechanical description. To understand the R1ρ RD experiment, one needs to understand how exchange between a GS and an ES leads to dephasing of the observable bulk magnetization, and to what extent dephasing varies with the amplitude (ω1, units rad s−1) and offset frequency (Ω, units rad s−1) of an applied spin-locking field, as well as the exchange parameters of interest, namely the fractional population of the GS (pGS) and ES (pES), the exchange rate (kex, units s−1), and the difference between the chemical shifts of the GS and ES (Δω = ω0,ES - ω0,GS and , where ω0,ES and , and ω0,GS and are the Larmor frequencies, of the spin in the ES and GS, in units of rad s−1 and ppm respectively). In this section, we use a vector model to describe how two-state exchange leads to dephasing of the magnetization during an R1ρ RD experiment. The goal is to help the reader visualize and thereby better understand the R1ρ experiment. A mathematical treatment applicable to n-state exchange will be presented in Section 4.1. This section will ignore the influence of scalar couplings, the treatment of which requires a quantum-mechanical description based on the Liouville-von Neumann equation[178–180] or average Hamiltonian theory[181].
3.1. Free precession chemical exchange
We first consider the simplest case and examine how chemical exchange leads to dephasing of the magnetization under free precession, i.e., in the absence of a spin-locking field. We will find that similar mechanisms lead to dephasing of the magnetization in the presence of a spin-locking field during an R1ρ experiment. We consider conformational exchange between a major GS and a sparsely populated ES (Fig. 3A). We will ignore the effects of longitudinal and transverse relaxation, and consider a spin that has different chemical shifts in the GS and ES (ω0,GS ≠ ω0,ES).
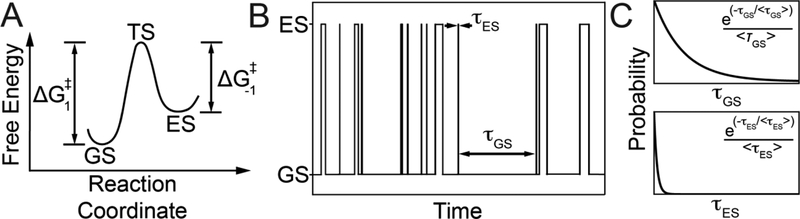
Figure 3.
Thermodynamic and kinetic characteristics of a system undergoing two-state chemical exchange. A) Free energy diagram for two-state exchange. B) Time evolution of a molecule exchanging between a dominant GS and sparsely populated and short-lived ES. C) Distribution of τGS and τES, the dwell times for the GS and ES.
To understand how chemical exchange impacts the NMR spectrum, we first need to understand the stochastic nature of the exchange process as this ultimately dictates how it will dephase bulk magnetization. Two-state exchange can be described by forward (k1) and backward (k−1) rate constants (units s−1):
| (1) |
with the exchange rate kex = k1 + k−1 (units s−1), which can be understood to be the rate constant at which the equilibrium state is restored following a perturbation that pushes the system away from equilibrium. Assuming transition-state theory, the rate constants are related to the free energies of activation according to the Eyring equation:
| (2) |
| (3) |
where κ is the transmission coefficient describing the fraction of barrier crossing events that lead to the formation of the products from the reactants, R is the universal gas constant (units J K−1 mol−1), kB is the Boltzmann constant (units J K−1), T is the temperature (units K), h is Planck’s constant (units J s), and and are free energies of activation (units J mol−1) for the forward and backward reactions, respectively.
Importantly, molecules do not spend a fixed amount of time in either the GS or ES before interconverting (Fig. 3B). Rather, they spend variable amounts of time. A molecule may spend a short time visiting the ES on one occasion but spend a longer time on a second visit. Why is that the case? At the microscopic level, not all molecules are equal; rather they have free energies that follow a Boltzmann distribution where ΔG is the free energy of a molecule relative to a reference state. The probability that a molecule has the energy required to cross a barrier ΔG‡ will be proportional to . As a consequence, the dwell time (τ) molecules spend in conformation i follows an exponential distribution where <τi>is the average dwell time or lifetime of the ith state (Fig. 3C). Therefore, while we will often simply refer to the lifetime of the GS or ES, this actually represents an average over what in reality is an exponential distribution of dwell times. The lifetimes of the GS <τGS>and ES <τES> are given by reciprocals of k1 and k−1, respectively:
| (4) |
| (5) |
We first consider a hypothetical scenario where a molecule exists in two distinct conformations GS and ES that do not interconvert. The transverse magnetizations MGS and MES are initially aligned along the x-axis after application of a 90°y pulse and will experience an effective field (Beff, bold refers to a vector) equal to B0 aligned along the z-axis of the laboratory frame. Consequently, MGS and MES will precess around B0 with frequencies ω0,GS and ω0,ES, respectively, and the NMR spectrum consists of two lines centered at frequencies ω0,GS and ω0,ES.
It is instructive to examine the behavior of the magnetization in a rotating frame, as this will also prove important when describing the dephasing of the magnetization during an R1ρ experiment (Section 3.2). In a rotating frame precessing at a frequency ωrf (units rad s−1), MGS and MES precess with offset frequencies ΩGS and ΩES (units rad s−1) respectively, around the z axis:
| (6) |
| (7) |
The magnitude of the effective fields experienced by the GS (Beff,GS) and the ES (Beff,ES) is reduced from B0 to ΔBGS and ΔBES (units Tesla), respectively:
| (8) |
| (9) |
where γ is the gyromagnetic ratio (units rad s−1 Tesla−1).
We now examine how chemical exchange affects MGS and MES, and the NMR spectrum. The exchange contribution will vary depending on the NMR chemical shift timescale, defined as the ratio between kex and Δω (kex/Δω). Under the slow exchange limit (kex << Δω), the GS and ES are long-lived and two discrete resonances are observed in the NMR spectrum centered at ω0,GS and ω0,ES (Fig. 4A). However, compared to the case in which the GS and ES do not interconvert, the resonances are broadened by the exchange process. This is because exchange leads to the dephasing of the magnetization.
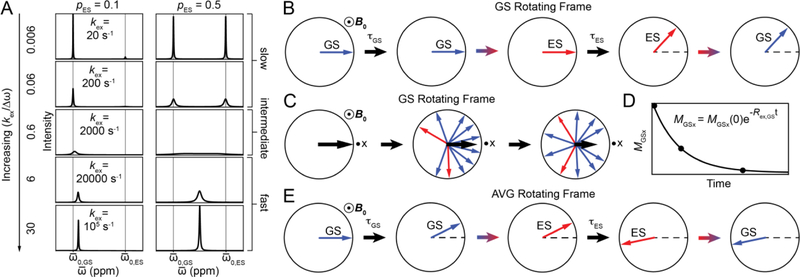
Figure 4.
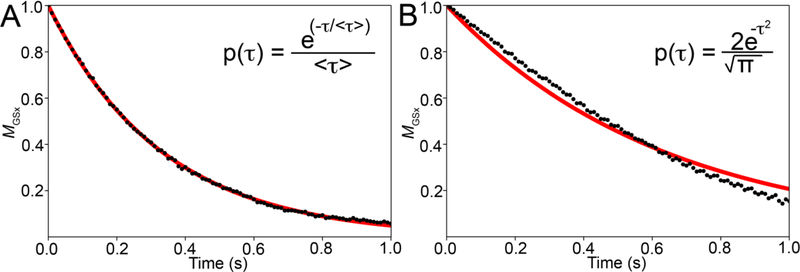
Chemical exchange under free precession. A) NMR spectra for a system undergoing two-state GS-ES chemical exchange simulated using the B-M equations. Columns correspond to different values of pGS while rows correspond to different values of kex. Simulations were performed assuming , γ(1H)B0/2π = 700 MHz and R2,GS = R2,ES = 10 s−1. B) Magnetization of GS (blue) and ES (red) spins in the rotating frame of the GS at the slow exchange limit. Black arrows represent the passage of time while colored arrows represent exchange events. Dots surrounded by circles denote vectors perpendicular to the plane of the figure. C) GS-ES chemical exchange leads to dephasing with time of the bulk magnetization corresponding to the GS (black arrow). The black dot near the x-axis corresponds to the receiver phase. D) Exponential decay due to chemical exchange of the bulk GS magnetization along the x axis (MGSx) as a function of time. E) The magnetization of the GS (blue) and ES (red) spins in the rotating frame of the population-weighted average (AVG) resonance in the fast exchange limit.
To visualize dephasing of MGS, initially aligned along the x-axis, we move into a rotating frame precessing at a frequency of ω0,GS. In this frame, the magnetization of the GS spins is stationary (ΩGS = 0) while that of the ES spins precesses with frequency Δω (Fig. 4B). The magnetization belonging to a GS spin will be stationary for the duration of the dwell time τGS. When the molecule transforms into the ES, the magnetization associated with the spin will start to precess with frequency ΩES = Δω for duration τES, leading to a change in phase angle given by τESΔω (Fig. 4B). The precession then stops again for some duration τGS when the molecule switches back to the GS, and so on. Depending on the exchange rate, many such transitions may occur during acquisition. As spins within the same molecule or across molecules will spend varying amounts of time in the GS or ES, the GS spins will be associated with different phase angles leading to dephasing of the bulk GS magnetization along the x-axis (MGSx) (Fig. 4C). This causes MGSx to decrease exponentially over time with the rate constant given by Rex,GS (Fig. 4D). Why is the decay exponential? This again goes back to the exponential distribution of the dwell times τGS and τES (Fig. 5), which causes the probability that the magnetization of the different spins are aligned to decrease exponentially with time. Chemical exchange leads to a line-broadening contribution given by Rex,GS/⫪ to the GS resonance in addition to the linebroadening due to intrinsic transverse relaxation (R2,GS/⫪). Put alternatively, Rex,GS denotes the contribution to transverse relaxation of the GS resonance due to chemical exchange, and is dependent on the exchange parameters pES, kex and Δω.
Figure 5.
The mono-exponential decay of magnetization due to chemical exchange under free precession conditions is a consequence of the exponential dwell time distributions of the GS and ES. (A and B) Normalized bulk x-magnetization MGSx (black dots) of the GS as a function of time for a system undergoing GS-ES exchange, simulated using the vector model. An exponential fit to the magnetization is shown in red. Panel A is simulated assuming exponential probability distributions for the GS and ES dwell times (< τGS > = 0.33 s and < τES > = 0.14 s), while panel B is simulated assuming that the ES and GS dwell times follow a standard normal distribution. Expressions for the probability distributions of τGS and τES are given in the inset. Simulations assumed the following exchange parameters: , γ(1H)B0/2π = 700 MHz, and R1,GS= R1,ES = R2,GS = R2,ES = 0 s−1 for panels A and B.
In an analogous manner, the dephasing of MES can be visualized by moving into a rotating frame precessing at ω0,ES. In this frame, the ES magnetization is stationary (ΩES = 0) but will much more quickly transform into the GS and start to precess with frequency ΩGS = − Δω, typically for a longer time relative to the GS when it transforms to the ES. As a result, the ES bulk magnetization experiences a greater degree of dephasing and the ES resonance experiences a greater degree of line-broadening as compared to the GS resonance, i.e., Rex,ES > Rex,GS.
Algebraic expressions for Rex,GS and Rex,ES at the slow exchange limit (kex << Δω) can be obtained by solving the B-M equations under free precession conditions (Section 4.1)[13, 14, 22]:
| (10) |
| (11) |
| (12) |
In the slow exchange limit, Rex,ES > Rex,GS and are equal to the backward and forward rate constants, respectively. In addition, increasing kex increases Rex because this increases the frequency of transitions between the GS and ES. Furthermore, Rex is independent of Δω (valid for kex/Δω ~< 0.2, Fig. 6) but does depend on pES. For kex/Δω ~< 0.2, changing Δω for a fixed kex does not significantly change the NMR chemical shift timescale and therefore the Rex contribution. However, it should be noted that the NMR timescale can vary in the presence of a spin-locking field during the R1ρ experiment[13, 182]. Consequently, although Rex is independent of Δω in general under slow exchange (Fig. 6), this will not necessarily be the case during the R1ρ experiment (see Section 6.2). The observed transverse relaxation rate (R2,obs) is given by the sum of contributions due to intrinsic relaxation (R2,GS and R2,ES) and due to chemical exchange (Rex,GS and Rex,ES):
| (13) |
| (14) |
Figure 6.
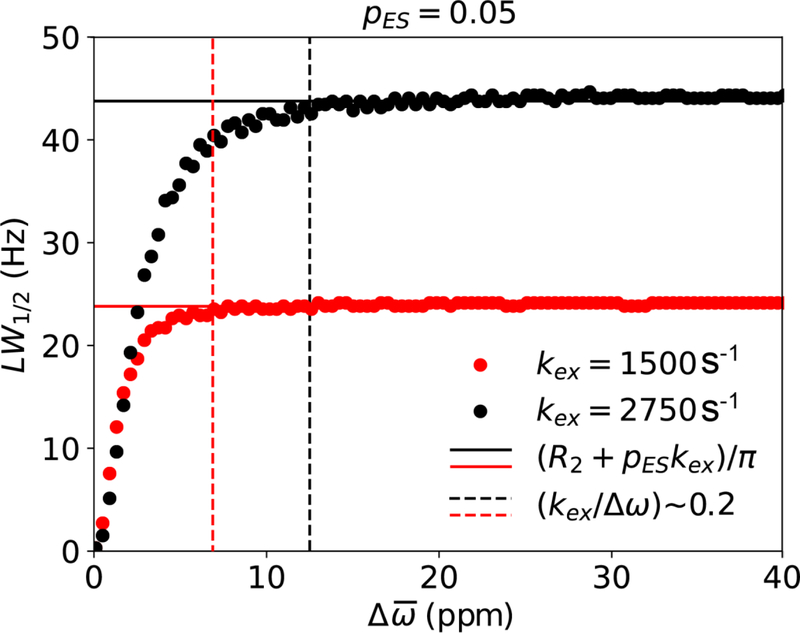
Line-width at half maximum (LW1/2, units Hz) for the dominant GS resonance as a function of for a system undergoing GS-ES exchange under free precession, simulated using the B-M equations (kex = 1500 in red and kex = 2750 in black). Simulations assumed the following exchange parameters: pES = 0.05, γ(1H)B0/2π = 700 MHz, R1,GS= R1,ES = R2,GS = R2,ES = 0.0 s−1, while was varied linearly between 0.1 and 40 ppm in 100 equally spaced increments. Solid lines denote (R2+pESkex)/π while dotted lines denote a Δω value where (kex/Δω) ~ 0.2.
As kex increases, Rex continues to increase in the slow exchange regime, which can be defined as kex/Δω < 0.2. Under slow exchange, the observed resonance frequencies for the GS and ES are to a good approximation given by ω0,GS and ω0,ES, respectively. Increasing kex further moves the system into the intermediate exchange regime, which can be defined as 0.2 < kex/Δω < 2 (Fig. 4A). The broadened GS and ES resonances now begin to shift toward one another until they coalesce when kex ~ Δω, at a frequency (ω0,OBS) distinct from the populationweighted average of ω0,GS and ω0,ES (ω0,AVG = pGSω0,GS + pESω0,ES). At coalescence, the line broadening is maximum. This is because the GS-ES transition frequency is high, while <τGS> and <τES> are sufficiently long to cause substantial dephasing of the magnetization. The exchange contribution can again be visualized by moving into a rotating frame precessing at the frequency ω0,OBS. In this frame, both the GS and ES magnetizations undergo precession, resulting in dephasing of the bulk magnetization corresponding to the observed resonance. In contrast to the slow exchange limit, B-M simulations indicate that Rex depends on Δω in the intermediate exchange regime[14, 22].
As kex increases further, the broadened resonance begins to shift and sharpen, and the system moves into the fast exchange regime (kex/Δω > 2) (Fig. 4A). Under these conditions, the observed resonance frequency ω0,OBS is to a good approximation given by the populationweighted average ω0,AVG. The exchange contribution can again be visualized by moving into a rotating frame precessing at frequency ω0,AVG (Fig. 4E), in which exchange results in dephasing of the bulk magnetization corresponding to the AVG resonance. Expressions for the exchange contribution (Rex,AVG) to the observed relaxation rate (R2,obs,AVE) at the fast exchange limit (kex >> Δω) can be obtained by solving the B-M equations (Section 4.1) and are given by[13]:
| (15) |
As in slow exchange, Rex depends on pES under fast exchange. However, in contrast to slow exchange, decreasing kex increases Rex under fast exchange, as spins spend longer periods of time in the GS and/or ES and conversely, increasing kex decreases Rex as <τGS> and/or <τES> decrease. Moreover, Rex is now proportional to Δω2. Note that the appearance of a single resonance in the NMR spectrum does not imply that the system is in fast exchange; the system could be in intermediate exchange or even under slow exchange since the larger Rex contribution to a minor ES resonance could render it undetectable[22, 183].
3.2. R1ρ in the absence of chemical exchange
While NMR line shapes carry rich information about chemical exchange[184], they cannot be used to reliably determine all exchange parameters of interest. The R1ρ experiment, and RD experiments in general, provide an alternative means to extract this information. These experiments modulate the effective field experienced by a given spin, thereby enhancing the sensitivity to the exchange parameters.
The R1ρ experiment entails the application of a continuous RF spin-locking B1 field along the x or y-axis, transverse to the static B0 field. The purpose of the spin-locking field is to control Beff,GS and Beff,ES, and therefore, the extent to which the bulk magnetization is dephased due to chemical exchange. In this section, we will ignore chemical exchange and first examine how the magnetization is spin-locked, how changing the spin-lock parameters alters the effective field, and lay out the theoretical basis for describing the R1ρ experiment using a vector model.
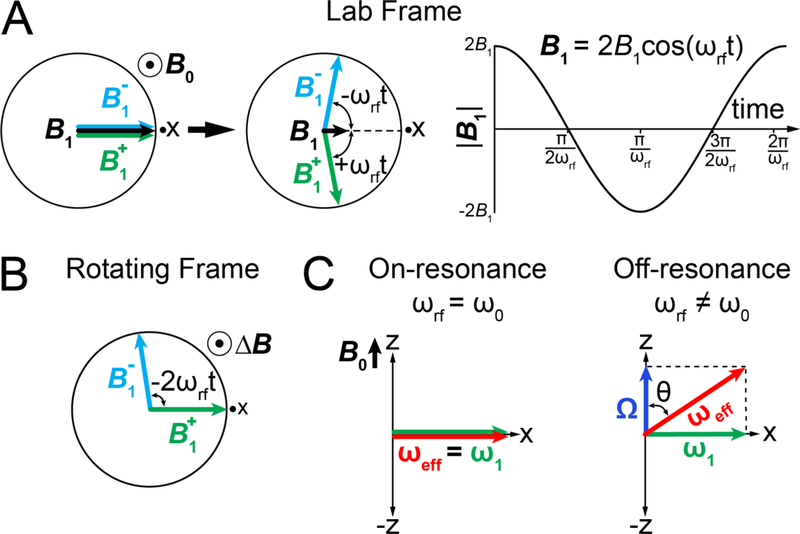
Let us first examine how B1 applied along the x-axis affects Beff experienced by a given spin. B1 is a linearly oscillating field with amplitude 2B1 (units Tesla) and frequency ωrf (units rad s−1; positive/negative values refer to clockwise/anti-clockwise rotations, respectively), both of which are specified by the user (Fig. 7A):
| (16) |
The linearly oscillating B1 field can be decomposed into two rotating fields B1+ and B1− each with an amplitude B1 rotating in opposite directions in the transverse plane with frequencies ωrf (clockwise) and −ωrf (counterclockwise) (Fig. 7A):
| (17) |
| (18) |
| (19) |
The treatment of B1 is simplified by working in a frame rotating with frequency +ωrf (Fig. 7B). In this frame, the vector B1+ is aligned along the x-axis and has a length B1, while B1− rotates at 2ωrf and can be ignored. The magnetization precesses with an offset frequency Ω around the zaxis and the spin experiences a reduced field ΔB along the z-axis as described in Section 3.1. Beff experienced by an ensemble of spins with an offset Ω is given by the vector sum:
| (20) |
It is common practice to express Beff, B1, and ΔB in terms of the precession frequency ω (units rad s−1) of the magnetization around the effective field:
| (21) |
| (22) |
Using ω is useful because dephasing of the magnetization due to chemical exchange during the R1ρ experiment is governed by the frequencies of precession. For the remainder of the review, we will replace the vector B and its magnitude B with ω and ω, respectively:
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
Figure 7.
Influence of the spin-locking field during an R1ρ experiment in the absence of chemical exchange. A) In the lab frame (left), the spin-locking field B1 (black arrow) can be decomposed into two fields and rotating in opposite directions (green and cyan arrows). The short black arrow represents the passage of time. A black dot surrounded by a circle represents a vector perpendicular to the plane of the figure. Black dots near the x-axes correspond to the receiver phase. ωrf is the angular frequency of the spin-lock. Variation of the spin-locking field amplitude as a function of time is shown on the right. B) Evolution of and in the rotating frame of . The static magnetic field is reduced to ΔB. C) Effective fields under on- and off-resonance conditions in the rotating frame of the spin-lock.
The applied ω1 field will change both the orientation and the magnitude of the effective field ωeff experienced by a spin in a manner dependent on both Ω and ω1 as shown in Fig. 7C. For example, when ω1 is applied on resonance (ωrf = ω0), Ω = 0, ωeff = ω1 and ωeff is aligned along the x-axis (Fig. 7C). If on the other hand ω1 is applied off-resonance (ωrf ≠ ω0), Ω ≠ 0, ωeff = ω1 + Ω, and ωeff is no longer in the transverse plane but is tilted away from the z-axis by an angle θ (units rad) that depends on both ω1 and Ω (Fig. 7C):
| (29) |
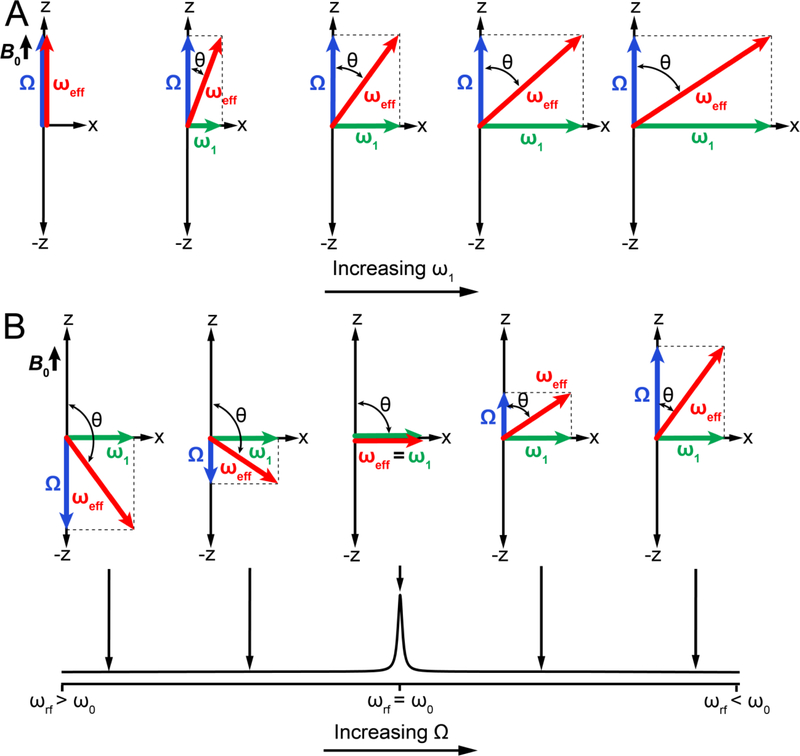
Figure 8 shows additional examples of how changing ω1 or Ω (through changes in ωrf) changes both the amplitude and orientation of ωeff. In principle, all possible orientations and amplitudes of ωeff can be realized experimentally by a suitable choice of ω1 and Ω. As R1ρ experiments are most sensitive to an exchange process when kex ~ ωeff, the experimentally accessible effective fields define the detection limit of the experiment, as elaborated in Section 4.2.1.
Figure 8.
Modulation of the effective field by variation of the spin-lock amplitude (ω1) and offset frequency (Ω) in an R1ρ experiment in the absence of chemical exchange. Influence of changing ω1 (A) and Ω (B) on the effective field ωeff in the rotating frame.
During the R1ρ experiment, ω1 is applied immediately after the magnetization of interest has been aligned along z′, the direction of ωeff, using an appropriate preparatory pulse as described in Section 5.2 (Fig. 9). In the absence of ω1, the magnetization precesses around B0 with frequency ω0. However, in the presence of ω1, precession is eliminated, and the magnetization is ‘spin-locked’ along ωeff, although its magnitude is subject to decay due to relaxation (Fig. 9). It is important to note that the magnetization remains spin-locked along ωeff as long as R2 and R1 are both smaller than ω1 and Ω. If those conditions are not met, the magnetization can veer off and deviate from ωeff (Fig. 10).
Figure 9.
Schematic representation of the R1ρ experiment in the absence of chemical exchange. The equilibrium magnetization tilted along z′, the direction of ωeff,OBS, is immediately spin-locked by the application of an RF field (green arrow), after which it decays exponentially due to relaxation with a rate constant R1ρ. A cross within a circle denotes a vector perpendicular to the plane of the figure. All vector diagrams are in the rotating frame where the spin-locking field appears stationary.
Figure 10.
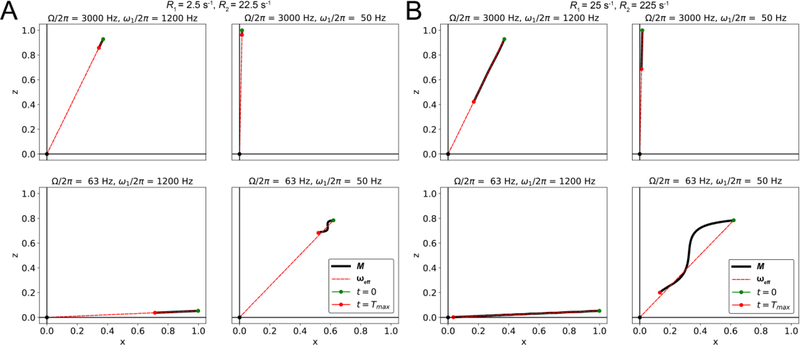
Time course of the evolution of normalized magnetization during an R1ρ experiment in the absence of chemical exchange, as a function of the spin-lock amplitude ω1, the offset Ω and the relaxation rates, simulated using the B-M equations. A) R1 = 2.5 s−1 and R2 = 22.5 s−1; B) R1 = 25 s−1 and R2 = 225 s−1. The time course for the position of the tip of the net magnetization vector M (with its base at the origin) is denoted as a solid black line, with green and red dots denoting the positions of the vector tip at the start and end (Tmax = 0.015s) of the relaxation period, respectively. The effective field direction is denoted using a dashed red line.
The R1ρ experiment measures the rate of relaxation of the magnetization that is spinlocked along ωeff (Fig. 9). In the absence of chemical exchange, the relaxation will be governed by R1 and R2[13]. To obtain expressions relating R1ρ to R1 and R2, we use the Bloch equations[46], which model the behavior of the magnetization in the rotating frame of the spin locking field:
| (30) |
where Mx, My and Mz are the x, y and z components of the bulk magnetization respectively and Mz,eq refers to the equilibrium z magnetization. The diagonal and Mz,eq terms describe the influence of relaxation while off-diagonal terms describe interchange between Mx and My, and My and Mz, due to precession around Ω/z-axis and ω1/x-axis, respectively, in the absence of chemical exchange and spin-locking field. The Bloch equations assume that the interactions between spins are independent of, and significantly weaker than, the interactions between the spins and the external field, i.e., τc << T2, where τc is the rotational correlation time[53]. This condition is readily satisfied for biomacromolecules in solution where τc ~ 5–30 ns and T2 ~ 5 – 200 ms.
Moving into a doubly rotating frame in which the z-axis is aligned along z′ (Fig. 9) simplifies the description of the magnetization and allows derivation of a key expression for R1ρ[123, 185–188]. This is achieved through rotation of the coordinate frame (in the rotating frame of the spin-locking field) around the y-axis by the angle θ. This second rotation has the effect of nullifying rotations about ωeff at a frequency of ωeff. The Bloch equations in the doubly rotating frame are given by:
| (31) |
where Mx′, My′ and Mz′ are the components of the magnetization in the doubly rotated frame. Mx′ and My′ are perpendicular to ωeff, while Mz′ is oriented along ωeff. Although algebraic expressions for Mz′ are complicated in the general case, one can make the simplifying assumption[187] ω1 ≫ (R1 − R2)sin(θ)cos(θ) which is valid under most experimental conditions. In general, rapid interconversion between the Mx′ and My′ components of the magnetization due to the term averages the cross-relaxation term (R1 − R2)sin(θ)cos(θ) between Mx′ and Mz′ to zero[187]. The evolution of Mx′ and My′, and Mz′ are uncoupled and Mz′ decays mono-exponentially with a rate constant R1ρ given by a weighted sum of R1 and R2:
| (32) |
| (33) |
Thus, rotating the coordinate frame introduces contributions to decay along ωeff due to longitudinal and transverse relaxation to variable extents[13], depending on the orientation (tilt angle) of ωeff. The relative weights of R1 (cos2 θ) and R2 (sin2 θ) can be understood as corresponding to their fractional contributions to the length of a unit vector oriented along ωeff. The above expression shows that in the absence of chemical exchange, R1ρ does not provide any information beyond that which can be obtained from measuring R1 and R2.
The above expressions also lay the basis for the vector model that will be used to describe the R1ρ experiment in subsequent sections. Setting R1 and R2 to 0, the B-M equations in the doubly rotating frame reduce to:
| (34) |
| (35) |
| (36) |
From above equations, in the absence of relaxation Mx′ and My′ vary sinusoidally with time, while Mz′ stays constant. Therefore, if the magnetization is initially aligned along ωeff, Mx′(0) = 0 and My′(0) = 0, Mz′ does not change with time while Mx′ and My′ remain zero; the magnetization is always aligned along ωeff and is spin-locked. In contrast, the magnetization tilted away from ωeff (Mx′(0) ≠ 0 or My′(0) ≠ 0) will precess around ωeff on the surface of a cone with a constant amplitude of Mz′(0) and with precession frequency . Precession of the GS and ES magnetizations around their respective effective fields forms the basis for the vector model, which will be used to describe the Rex contribution to R1ρ.
3.3. Dephasing of magnetization during R1ρ
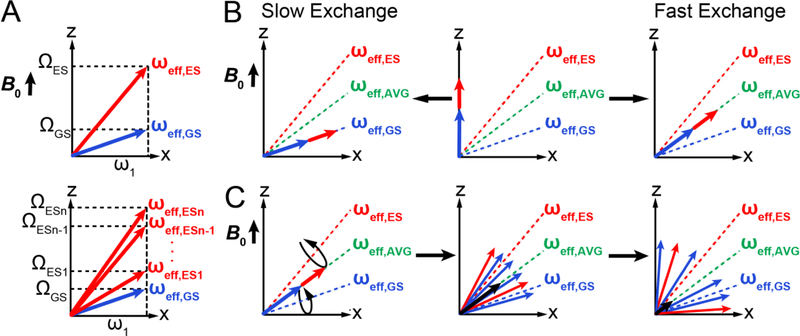
We now examine how chemical exchange leads to dephasing of the magnetization in the rotating frame during an R1ρ experiment. For Δω ≠ 0, the GS and ES will be associated with effective fields ωeff,GS and ωeff,ES respectively, in the rotating frame of ω1 (Fig. 11A):
| (37) |
| (38) |
| (39) |
| (40) |
where the offsets ΩGS and ΩES are defined in Section 3.1. We see that in the presence of 2-state chemical exchange between GS and ES, one must consider two non-parallel effective fields ωeff,GS and ωeff,ES that have different amplitudes, and around which the GS and ES magnetization vectors precess (Fig 11A). For n-state chemical exchange with n unique chemical shifts, there would be one effective field for each of the n states (Fig. 11A). As described below, the dephasing of the magnetization during R1ρ is analogous to that in free precession, the major difference being that the axes of rotation for the GS and ES magnetization are different.
Figure 11.
R1ρ in the presence of chemical exchange. A) ωeff,GS (blue) and ωeff,ES (red) in the rotating frame where the spin-locking field ω1 appears stationary, for two-state and n-state exchange. B) Alignment of the net magnetization at the start of an R1ρ experiment for a system undergoing GS-ES exchange under fast and slow exchange regimes. C) Rotation of the magnetization of GS/ES spins around their respective effective fields leads to dephasing of the bulk magnetization along ωeff,OBS during the R1ρ experiment. Shown is a representative example under conditions of fast exchange.
For intermediate and fast exchange, it is useful to define an average effective field ωeff,AVG corresponding to ω0,AVG:
| (41) |
| (42) |
| (43) |
In the selective 1D R1ρ experiments reviewed here in Section 5.2, both MGS and MES are initially aligned along an effective field ωeff,OBS before the application of the spin-locking field, which depends on ω1 and Ω = ω0,OBS – ωrf, where ωOBS corresponds to the GS resonance frequency (ω0,OBS = ω0,GS) in the case of slow exchange or to the average resonance frequency (ω0,OBS = ω0,AVG) in the case of fast exchange (Fig. 11B). In general, simulations indicate that for intermediate to fast exchange (0.1 < kex/Δω < 5) and low pES (< 10%), alignment along ωeff,AVG is a valid approximation and does not appreciably influence the RD profiles. However, deviations can arise particularly for high pES (> 10%)(Section 6.1).
Now let us examine how the magnetization is dephased due to exchange in the rotating frame in the presence of the spin-locking field. MGS and MES are initially aligned along ωeff,OBS and precess around ωeff,GS and ωeff,ES with frequencies ωeff,GS and ωeff,ES, respectively (Fig. 11C). When a GS spin switches to the ES, its associated magnetization starts to precess around ωeff,ES with frequency ωeff,ES. When the molecule switches back to the GS, the magnetization associated with the spin starts again to precess around ωeff,GS with frequency ωeff,GS and so on. Once again, because molecules spend varying amounts of time in the GS precessing around ωeff,GS or in the ES precessing around ωeff,ES, exchange causes dephasing of the bulk magnetization (Fig. 11C) in a manner analogous to free precession in the absence of a spinlocking field (Fig. 4C). Here, ωeff,GS and ωeff,ES acts as ‘dephasers’ that scramble or randomize the orientation of MGS and MES. Unlike free precession, in which the magnetization remains transverse, the exchange in this case results in magnetization that is arranged in a 3D “bouquet”, which fans out exponentially with time (Fig. 11C). As in free precession, the exchange causes the projection of the bulk magnetization onto the vector ωeff,OBS to decay exponentially with time resulting in an Rex contribution to R1ρ. The R1ρ experiment entails measuring the exponential decay of the magnetization along ωeff,OBS as a function of time, from which Rex can be deduced. The R2ρ experiment measures the decay of Mx′/My′ orthogonal to ωeff,OBS[13, 182].
The exponential decay of the magnetization associated with a single 3D bouquet provides a single R1ρ value that is not sufficient to extract all exchange parameters of interest. Thus, additional data is needed. This is accomplished by changing the scramblers ωeff,GS and ωeff,ES by changing the spin-lock parameters ω1 and Ω (via changes in ωrf). This changes the extent of dephasing of the magnetization, the resulting magnetization bouquets and the associated Rex contributions, in a manner that depends on the exchange parameters, providing a means for their determination. Experiments in which the carrier is on-resonance and ω1 is varied are referred to as “on-resonance” R1ρ experiments, while those that vary both ω1 and Ω are referred to as “off-resonance” R1ρ experiments. The validity of the vector description of the R1ρ experiment can be verified through comparison with numerical solutions to the B-M equations (Fig. 12).
Figure 12.
Comparison of off-resonance R1ρ RD profiles as obtained from B-M simulations and the vector model, in the absence of relaxation, for a wide variety of exchange parameters. Rows correspond to variations in kex while columns correspond to variations in pES. Spin-lock amplitudes are color coded while solid vertical green lines correspond to an offset Ω = –Δω; , γ(1H)B0/2π = 700 MHz. 10,000 spins were used for the vector model simulations. The initial alignment of the magnetization for the B-M and vector simulations was performed as described in Section 6.1. In the vector model simulations, the magnetization of the GS and ES spins initially aligned along ωeff,OBS was allowed to precess about ωeff,GS and ωeff,ES with angular velocities ωeff,GS and ωeff,ES, respectively. The dwell times of the spins in the GS and ES were sampled from exponential probability distributions as described in Section 3.1, following which they were allowed to exchange with each other, while retaining the same orientation of the magnetization in 3D space prior to exchange. The sum of the magnetization of all the spins is projected along ωeff,OBS as a function of time to obtain R1ρ, which is used to obtain Rex, as described in Section 3.2 – 3.4.
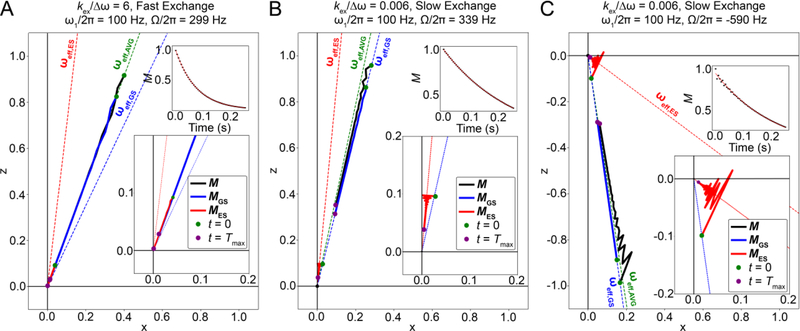
It is interesting to ask whether the net magnetization resulting from the vector sum over the bouquet remains perfectly aligned along ωeff,OBS. The answer depends on the timescale for chemical exchange as defined under free precession conditions. For fast exchange, the net magnetization as well as MGS and MES are aligned along ωeff,AVG (Fig. 13A). In contrast, under slow exchange conditions, MES can deviate from its initial alignment along ωeff,GS towards ωeff,ES while MGS remains along ωeff,GS, causing the net magnetization to deviate towards ωeff,AVG (Fig. 13B). This deviation of the net magnetization is proportional to pES and Δω. Even when the net magnetization is not along ωeff,GS under slow exchange, the decay of the component along ωeff,GS can still be mono-exponential (Fig. 13B). Note that the above statements are only valid under conditions when the relaxation rates R1 and R2 are smaller than ω1 and Ω, as discussed in Section 3.2.
Figure 13.
Time course of the evolution of the normalized GS, ES and net magnetization during an off-resonance R1ρ experiment, simulated using the B-M equations. Time course for the positions of the tips of the GS, ES and net magnetization vectors (each with their base at the origin), denoted as solid blue, red and black lines respectively, with green dots in each case denoting the positions of the vector tips at the start of the relaxation period, and violet dots denoting their positions at the end of the relaxation period, respectively. Directions for the GS,ES and AVG effective fields are denoted using blue, red and green dashed lines, respectively. Also shown as insets are the variations of the normalized projections of the net magnetization along ωeff,OBS (M) as a function of time (black dots), along an exponential fit of the same (red line). Simulations were performed using kex = 20000 s−1 for panel A, kex = 20 s−1 for panels B and C. The other parameters used for all simulations were pES = 0.1, , γ(1H)B0/2π = 700 MHz, R1,GS = R1,ES = 2.5 s−1, R2,GS = R2,ES = 22.5 s−1 and Tmax = 0.25 s. The initial alignment of the magnetization for the B-M and vector simulations was achieved as described in Section 6.1.
3.4. On-resonance R1ρ
While off-resonance R1ρ experiments provide the best means for characterizing exchange as they afford the maximal amount of data, on-resonance experiments are often performed initially, typically to screen spins for the presence of chemical exchange. We review this simpler on-resonance R1ρ experiment and then later move to the more general offresonance R1ρ experiments.
In the on-resonance experiment, Ω = 0, ωeff = ω1, and Rex simply adds to R2 in a manner analogous to free precession (Section 3.1)[23, 63, 87, 156, 189]:
| (44) |
where R2 is assumed to be the population-weighted average of R2,GS and R2,ES, i.e., R2 = pGSR2,GS + pESR2,ES, which is valid for |R2,GS − R2,ES| << kex[13, 190]. It is also assumed that Rex and R2 are not correlated, which is a reasonable approximation given that they report on dynamics occurring on different timescales (i.e., τc << 1/kex)[13, 45]. It is also assumed that τc << T2 as described in Section 3.2, kex < ωGS,0 and kex < ωES,0[191], and that the decay of the magnetization is mono-exponential; deviations from mono-exponential behavior can arise under slow exchange conditions with high pES[23](Section 4.2).
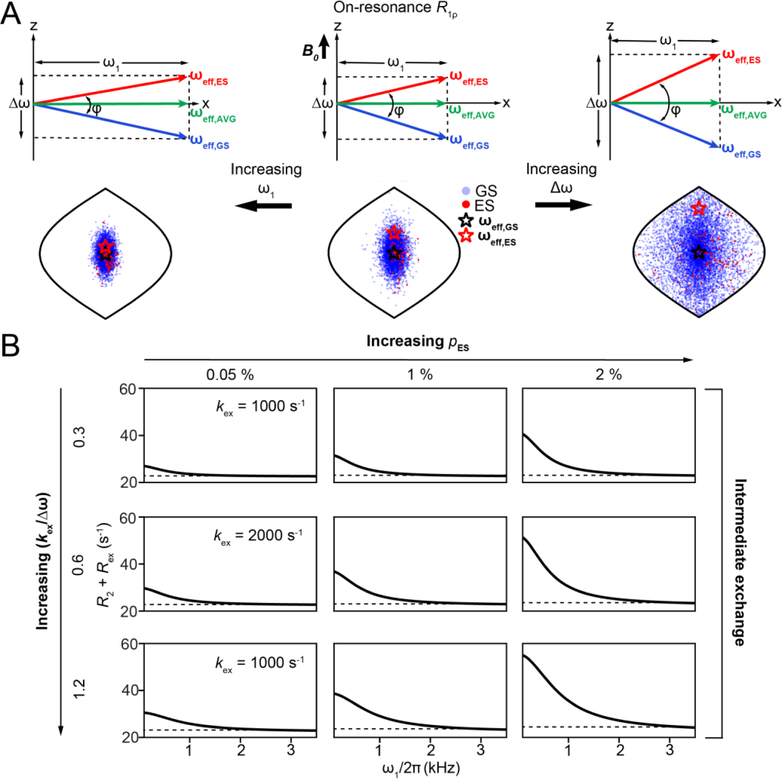
Setting R1 = R2 = 0, R1ρ = Rex, a vector description can be used to model how Rex varies with ω1. Increasing ω1 decreases the angle φ between ωeff,GS and ωeff,ES (Fig. 14A). Intuitively, this should reduce dephasing of the magnetization and Rex since rotations around axes that have similar orientations should be less effective in scrambling magnetization compared to the case when the axes have very different orientations. Indeed, vector simulations show that for hypothetically fixed ωeff,GS and ωeff,ES, Rex is maximum for φ = π/2 while it is zero for φ = 0 (Fig. 15A). It is important to note that in an actual on-resonance R1ρ experiment, changing ω1 also changes ωeff,GS and ωeff,ES (Fig. 14A). Simulations show that when fixing φ, Rex increases with ωeff,ES until it approaches kex after which it plateaus, while showing little variation with ωeff,GS (Fig. 15B). Simulations also suggest that overall, the decrease in φ outweighs the increase in ωeff,ES to cause a net decrease in Rex with increasing ω1 under on-resonance conditions. This can be appreciated from the diminished spread of the magnetization bouquet depicted using a Sanson Flamsteed projection[192] in Fig. 14A and Supplementary Movie 1. At very high ω1, the measured value of R1ρ approaches R2 and this illustrates how by changing ω1 it is feasible to resolve the R2 contribution to R1ρ (Fig. 14B).
Figure 14.
Dependence of on-resonance R1ρ on exchange and spin-lock parameters.A) Δω and ω1 modulate Rex via changes in φ, the angle between ωeff,GS and ωeff,ES. Also shown are positions of the magnetization vectors corresponding to GS (blue circles) and ES (red circles) obtained using vector model simulations in the form of Sanson-Flamsteed projections[192]. ωeff,GS and ωeff,ES are indicated by black and red stars respectively. Simulations were performed with the following parameters - pES = 0.01, kex = 20,000 s−1, , γ(1H)B0/2π = 700 MHz, ω1/2π = 1000 Hz when on-resonance with the AVG state. Positions of the spins for a larger (right) and ω1/2π = 3000 Hz (left) are also shown. Simulations employed 10,000 spins with a relaxation delay of 0.012s.B) Variation of R2 + Rex with ω1 under on-resonance conditions as a function of exchange parameters, as obtained using B-M simulations. Rows and columns correspond to the indicated values of kex and pES, respectively. Dashed line denotes the value of R2. The other exchange parameters used were , γ(1H)B0/2π = 700 MHz, R1,GS= R1,ES = 2.5 s−1 and R2,GS = R2,ES = 22.5 s−1. The initial alignment of the magnetization during the B-M simulations was performed as described in Section 6.1.
Figure 15.
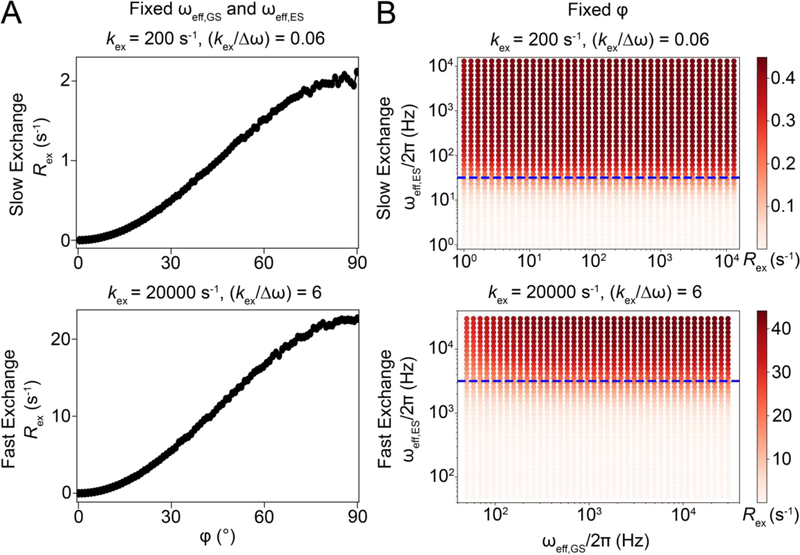
Vector model simulations to illustrate the dependence of Rex on φ, ωeff,GS and ωeff,ES during an on-resonance R1ρ experiment for a system undergoing two-state GS-ES exchange. A) Variation of Rex with φ for a fixed ωeff,GS and ωeff,ES, under fast and slow exchange conditions. Simulations were performed using ωeff,GS = 1000*2π rad s−1 and ωeff,ES = 1131*2π rad s−1 when on-resonance with the GS under slow exchange conditions. ωeff,GS = 1000*2π rad s−1 and ωeff,ES = 1128*2π rad s−1 under fast exchange conditions while maintaining the AVG state onresonance by suitably adjusting the offset of the GS and ES. Similar trends are observed for alternative values of the precession frequencies (data not shown). B) Heat maps of Rex as a function of ωeff,GS and ωeff,ES for a fixed φ under fast and slow exchange conditions. Horizontal dotted lines (blue) correspond to the condition ωeff,ES = kex. Orientations of the effective fields were kept fixed at those corresponding to application of ω1/2π = 1000 Hz on resonance. Similar trends are also observed for R1ρ, and for both Rex and R1ρ under off-resonance conditions, as long as the magnetization decay is mono-exponential (data not shown). For panels A and B, simulations were performed using 10,000 spins with pES = 0.01, , γ(1H)B0/2π = 700 MHz, R1,GS= R1,ES = 0.0 s−1, R2,GS = R2,ES = 0.0 s−1. The relaxation delays used were 3 s and 0.6 s for kex = 200 and 20000 s−1, respectively. For both panels, the initial alignment of magnetization and its projection to calculate Rex, was performed as described in Section 6.1.
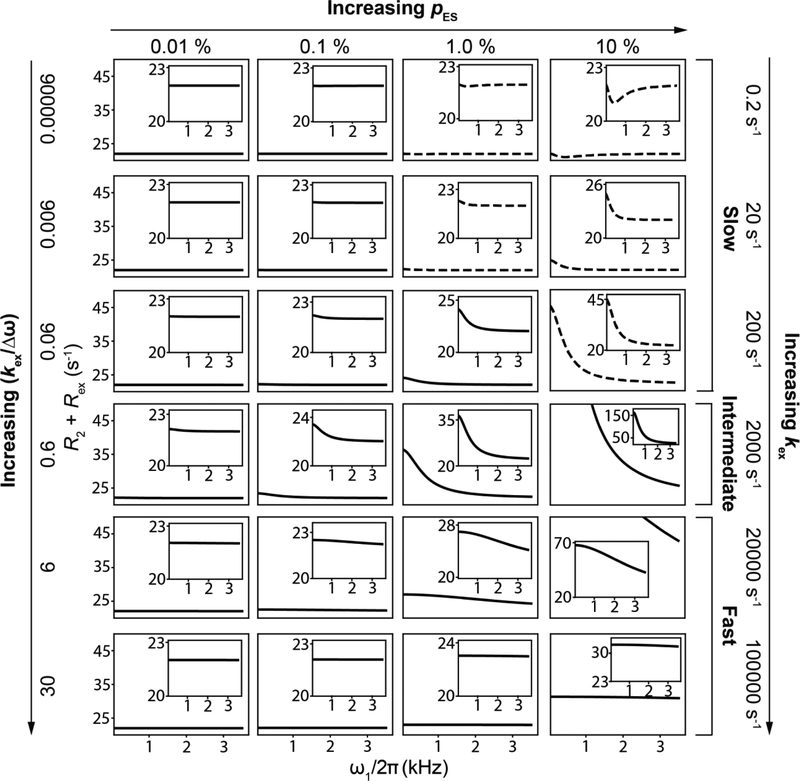
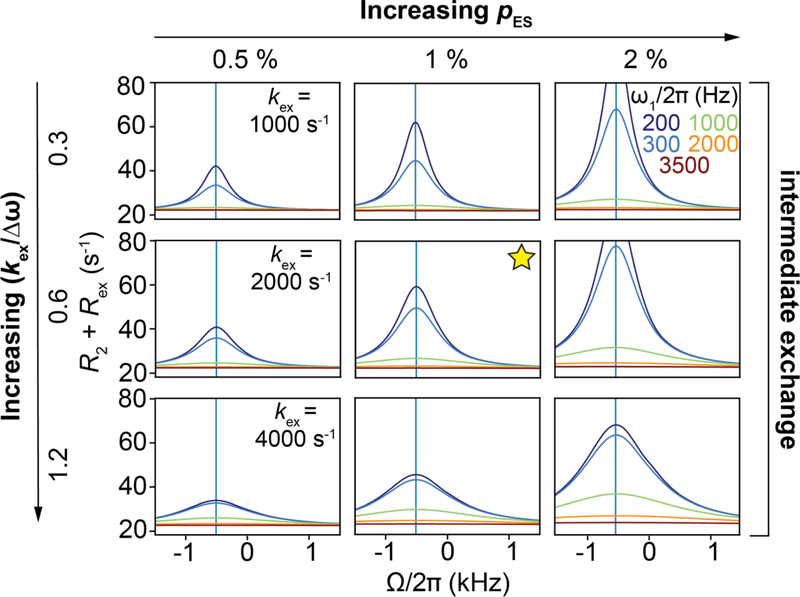
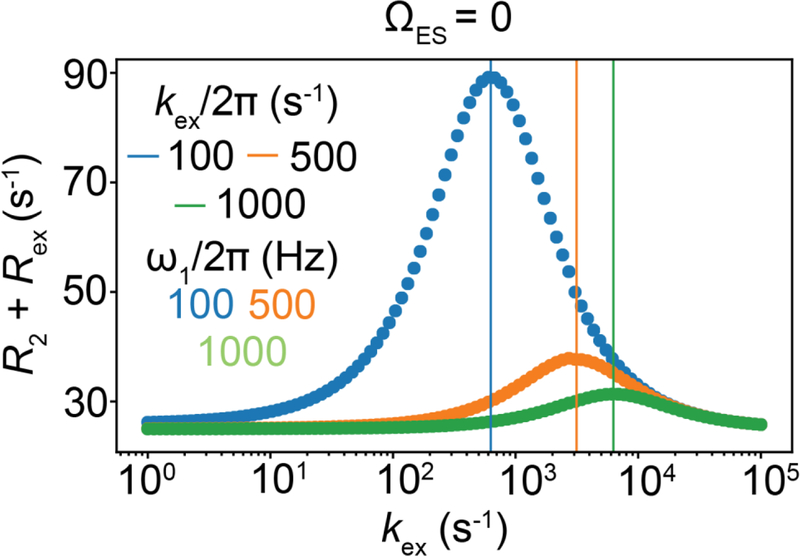
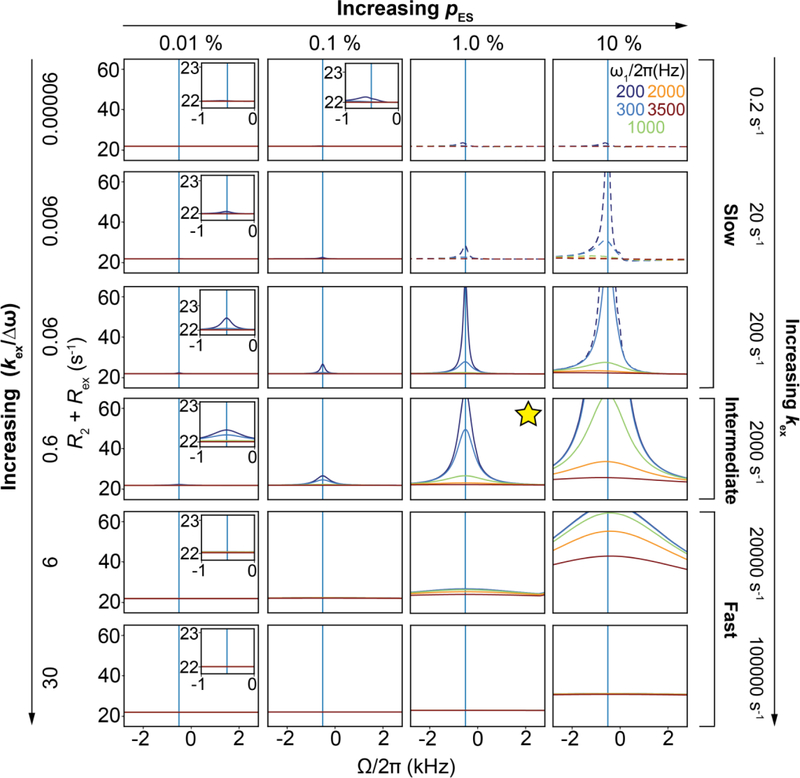
The above framework also helps us rationalize why Rex increases with Δω; as Δω increases so does φ, thus increasing Rex (Fig. 14A, Supplementary Movie 2). Algebraic expressions (Section 6.2) show that Rex is proportional to Δω2 in the presence of a spin-locking field. How Rex varies with ω1 will also depend on other exchange parameters. Fig. 14B shows on-resonance RD profiles for various values of pES and kex. Corresponding profiles for a wider range of kex and pES are shown in Fig. 16. From these RD profiles, we see that Rex increases with pES. For pES << pGS, Rex will be maximum at a given ω1 when and will decrease for other kex values, as can be appreciated from algebraic expressions in Section 6.2.
Figure 16.
Variation of R2 + Rex as a function of ω1 under on-resonance conditions as a function of exchange parameters, obtained using B-M simulations. Rows and columns correspond to the indicated values of kex and pES respectively. Panels with dotted lines correspond to exchange scenarios where the decay of the magnetization is not mono-exponential. Other parameters were: , γ(1H)B0/2π = 700 MHz, R1,GS = R1,ES = 2.5 s −1 and R2,GS = R2,ES = 22.5 s−1. The initial alignment of the magnetization was performed as described in Section 6.1.
3.5. Off-resonance R1ρ
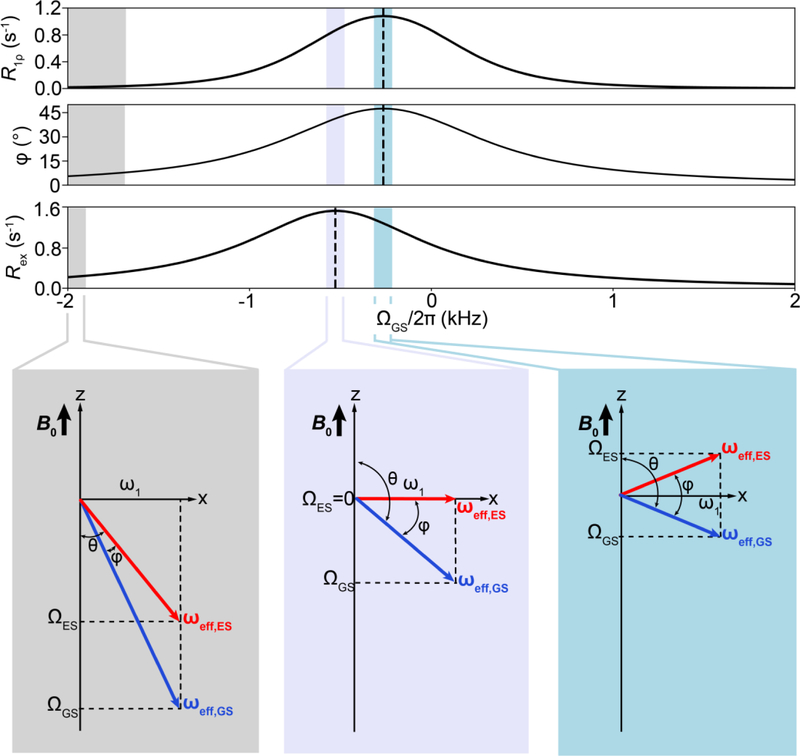
Although the variation of Rex with ω1 depends on all exchange parameters, it is not possible to determine each of them individually from on-resonance R1ρ RD profiles measured at a single magnetic field[13]. Rather, inspection of algebraic equations (see Section 6.2) reveals that in general only kex and pGSpESΔω2 can be obtained under fast exchange (Eqn. 66) while pGSpESΔω2kex and (Δω2 + kex2) can be determined under slow exchange when pES << pGS (Eqn. 65). Changing ωrf, the carrier frequency of the spin-locking field, provides a means of obtaining additional data that can address this gap. As will be elaborated upon in Section 4.2, the variation of Rex with ωrf during an off-resonance R1ρ experiment features a symmetric peak centered at a position that corresponds to ω0,ES[23]. This makes it possible to determine Δω including its sign, thereby enabling one to resolve the pGSpESΔω2 term obtained in the onresonance experiment, while generally also improving the ability to characterize all other exchange parameters.
Under fast exchange conditions, changing ΩAVG in an off-resonance R1ρ experiment makes it possible to sample additional configurations of ωeff,GS and ωeff,ES relative to the onresonance R1ρ experiment. In principle, ωeff,GS and ωeff,ES are each specified by two parameters (length and angle with respect to the z-axis) that can vary independently to assume all allowed configurations. However, experimentally, since both the GS and ES always sense the same ω1, not all parameters can be varied independently. Rather, once ω1 and ΩAVG are specified, all four remaining parameters (two lengths and two angles) are fixed, due to the relations:
| (45) |
| (46) |
Consequently, specifying ω1 and ΩAVG determines ωeff,GS and ωeff,ES, and the angle φ between them:
| (47) |
In an analogous manner, specifying ΩGS in addition to ω1 during an off-resonance R1ρ experiment under slow exchange conditions also fixes ωeff,GS and ωeff,ES.
A general expression for R1ρ applicable for off-resonance conditions is given by[23]:
| (48) |
where θ is the angle between ωeff,OBS and the z-axis, which corresponds to ωeff,AVG for intermediate and fast exchange, and ωeff,GS for slow exchange (Fig. 11B). Similar assumptions apply as for on-resonance R1ρ (Section 3.4). The expression is analogous to that for R1ρ in the absence of exchange, except for the addition of the Rex term. Note that because Rex adds to transverse relaxation, it is also weighted by sin2θ. Thus, Rex will depend on the extent of dephasing of the total magnetization along the effective field as measured by R1ρ, which in turn depends on both the angle φ and ωeff,ES as described in Section 3.4, and also on sin2θ, which measures the fractional contribution to R1ρ from dephasing in the transverse plane.
As mentioned earlier, a key feature of the off-resonance experiment is that Rex is maximum when on-resonance with the ES, providing a means of determining Δω and ω0,ES. We can use the vector model to understand this important point. We focus on the case in which ωeff,ES > kex, typically valid for kex < ~300 s−1 usually corresponding to the slow exchange regime. Under these conditions, the variation of R1ρ with ΩGS is dominated by changes in φ, while the dependency on ωeff,ES is weak, as R1ρ has already reached saturation relative to ωeff,ES (Fig. 15B).
Let us first consider the case in which ω1 is fixed and the carrier is gradually moved far off-resonance, i.e., |ΩGS| >> 0. This causes ωeff,GS and ωeff,ES to gradually tilt away from the transverse plane, decreasing φ while θ→π for ΩGS << 0 and θ→0 for ΩGS >> 0. As the angle φ decreases, the decrease in R1ρ due to reduced scrambling of the magnetization outweighs the decrease in sin2θ, leading to a net decrease in Rex (Fig. 17). There comes a point at which ωeff,GS and ωeff,ES are aligned nearly parallel to ω0 (θ→0) and R1ρ is dominated by R1 rather than by R2 + Rex. This provides a means for resolving the R1 contribution to R1ρ. Furthermore, this also increases the uncertainty in Rex as one moves off-resonance. In practice, Ω is chosen such that |Ω| < 3.5ω1 and θ < 15°[21].
Figure 17.
Variation of R1ρ, φ and Rex with ΩGS during an off-resonance R1ρ experiment under slow-exchange conditions with ωeff,ES < kex. Representative diagrams showing ωeff,GS (blue vector) and ωeff,ES (red vector) at selected offsets are also shown. The exchange parameters used were: pES = 0.01, kex = 200 s−1, , γ(1H)B0/2π = 700 MHz, R1,GS= R1,ES = 0.0 s−1, R2,GS = R2,ES = 0.0 s−1, ω1/2π = 600 Hz along with a relaxation delay of 3.0 s. The initial alignment of the magnetization during the B-M simulation was performed as described in Section 6.1.
As we move closer to being on-resonance with the GS or ES, both ωeff,GS and ωeff,ES decrease in amplitude and are increasingly tilted toward the transverse plane, tending towards θ→π/2 and consequently increasing sin2θ. This increase in sin2θ is outweighed by the increase in R1ρ due to the concurrent increase in φ, resulting in a net increase in Rex (which, in the absence of relaxation, is equal to R1ρ/sin2θ) (Fig. 17). Again, intuitively, the maximum dephasing and therefore R1ρ should be achieved when the angle φ is maximum. This is indeed the case; R1ρ is maximum when placing the carrier right in the middle between ω0,GS and ω0,ES (ωrf = ½ (ω0,GS + ω0,ES), ΩGS = ½(ω0,GS − ω0,ES)) (Fig. 17). However, this is not the offset that maximizes Rex. Rather, as noted by Palmer[23], the maximum Rex is always achieved when placing the offset on-resonance with ω0,ES as this maintains a large φ angle while also minimizing θ and therefore sin2θ. This results in a smaller sin2θ term and a larger R1ρ value, consequently maximizing Rex (Fig. 17). Put in different words, the trade-off between maximizing φ and consequently R1ρ, in combination with minimizing θ to reduce sin2θ is best satisfied when onresonance with the ES. The underlying basis for this rule lies in the fact that the orientations of the effective fields are coupled to the angle φ in R1ρ experiments. Thus, under slow exchange, off-resonance RD profiles are centered at −Δω, while under fast exchange conditions they are centered at -pGSΔω ~ -Δω when pES << pGS, as described by Palmer et al.[23, 179, 182]. Under intermediate exchange, they are centered at −(Δω-ψ), where ψ is the observed resonance frequency in the presence of exchange, assuming ω0,GS = 0 and ω0,ES = Δω.
It should be apparent that off-resonance R1ρ not only provides a means of characterizing the exchange parameters associated with Rex and micro-to-millisecond exchange, but, as an added bonus, it simultaneously allows one to determine R1 and R2, which can be used to characterize fast picosecond-to-nanosecond dynamics.
4. Illustrative examples of R1ρ relaxation dispersion profiles
In this section, we review the B-M equations, which are first-order differential equations describing the evolution of the magnetization in the presence of chemical exchange, relaxation, and B0 and B1 magnetic fields. We then use the B-M equations to simulate off-resonance R1ρ RD profiles for a wide range of exchange scenarios, including three-state exchange with various topologies, and for cases in which R2,GS and R2,ES are unequal. Theoretical simulations will be accompanied in some cases with experimental examples. The goal is to develop a deeper understanding regarding how off-resonance R1ρ RD profiles vary as a function of the exchange parameters and to extend description of the R1ρ experiment to three-state exchange.
4.1. Description of chemical exchange using Bloch-McConnell equations
We first review the B-M equations for a two-state system in the absence of chemical exchange, and later move to systems with two-state chemical exchange. In the absence of chemical exchange, MGS and MES can be treated independently, evolving according to their respective relaxation matrices. For a two-state system without chemical exchange, the Bloch equations take the following form in the rotating frame of ω1:
| (49) |
As in the case for the Bloch equations for a single state (Section 3.2), the diagonal elements of the relaxation matrix and Mz,eq terms describe the influence of R1 and R2 on MGS and MES. The off-diagonal elements in the relaxation matrix describe the interchange between the x and y components (MGSx→MGSy and MESx→MESy) and between the y and z components (MGSy→MGSz and MESy→MESz) components due to precession about the z and x-axes under Ω and ω1, respectively. The equations are valid for τc << T2 (see Section 3.2).
The Bloch equations can be modified to accommodate chemical exchange, by adding exchange terms describing the magnetization transfer between the states at rates equal to the rate constants for chemical exchange[45]. They can be written in matrix form as follows:
| (50) |
where
| (51) |
| (52) |
and
| (53) |
The diagonal terms in the matrix of rate constants correspond to the decrease of MGS and MES due to exchange events in which spins leave the GS (MGS→MES) or the ES (MES→MGS). In contrast, the off-diagonal terms correspond to the increase of MGS and MES due to exchange events in which spins arrive at the GS (MES→MGS) or the ES (MGS→MES). As molecules in the GS transform into the ES with a rate of k1[GS], where [GS] is the concentration of the GS species, the associated components of the magnetization of the GS (MGSi, i = x, y or z) decrease with rates of k1MGSi, as MGSi is proportional to [GS]. Analogous considerations are also applicable for the case of n-state exchange. The assumptions under which the above equations are valid are given in Section 3.4. It should be noted that the B-M equations can be used to treat the behavior of the magnetization under free precession conditions by setting ω1 = 0.
The solution to a first-order linear differential equation such as has the form:
| (54) |
where λi and are the ith eigenvalue and eigenvector of matrix K respectively, and is the stationary solution[23, 193]. For realistic values of exchange parameters, considering the presence of an inhomogeneous spin-locking field, the decay of the magnetization in most cases is mono-exponential and dominated by the least negative eigenvalue, denoted as R1ρ[23, 163]. Indeed, even if the spin-locking field is homogeneous, with the exception of exchange scenarios with low kex and high pES, the decay of the magnetization is mono-exponential, as described in Section 4.2. A non-monoexponential decay of the magnetization is typically a consequence of oscillatory motions of a component of the magnetization that is not parallel to the effective field. The effects of such oscillatory motions are diminished by inhomogeneous spin-locking fields because of differences in the frequencies of oscillation of the magnetization in different parts of the sample. An analogous solution is also valid for the case of n-state exchange with arbitrary topological complexity as described by Palmer[193, 194]. Thus, the variation of R1ρ with ω1 and Ω can be used to characterize chemical exchange, including n > 2 state exchange with arbitrary topologies, so long as the decay of magnetization is mono-exponential.
4.2. Off-resonance R1ρ relaxation dispersion profiles for two and three-state exchange
Understanding how off-resonance R1ρ RD profiles vary with exchange parameters is essential when analyzing R1ρ data. Here, we explore these variations by numerically integrating the B-M equations. The initial alignment of magnetization assumed in these simulations was performed as described in Section 6.1.
4.2.1. Two-state exchange
Fig. 18 shows representative off-resonance RD profiles for two-state GS⇌ES exchange as a function of pES and kex. These profiles show the dependence of R2,eff = R2 + Rex on Ω and ω1. Over this range of pES and kex, the RD profiles feature a symmetric peak centered near −Δω. The height of the peak relative to the baseline (which is at R2) is equal to Rex.
Figure 18.
Changes in R2 + Rex as a function of kex and pES for two-state exchange during an off-resonance R1ρ experiment, simulated using the B-M equations. Horizontal comparisons show changes in kex while vertical comparisons show changes in pES. Spin-lock amplitudes are denoted using different colors. Solid gray vertical lines correspond to an offset of –Δω, while the yellow star denotes exchange parameters typical of Watson-Crick to Hoogsteen exchange in B-DNA[115]. Other exchange parameters used are: , γ(1H)B0/2π = 700 MHz, R1,GS = R1,ES = 2.5 s −1 and R2,GS = R2,ES =22.5 s−1. The initial alignment of the magnetization was performed as described in Section 6.1.
Increasing pES increases the peak height (Rex) in addition to its width, and higher spin-lock amplitudes are needed to suppress larger Rex contributions (Fig. 18). For a given ω1 and Ω, algebraic expressions in Section 6.2 (Eqn. 65) show that Rex increases until kex approaches (for pES << pGS) where it reaches a maximum (Fig. 19), and is maximally dependent on ω1. Representative experimental RD profiles for two-state exchange are shown in Fig. 20 for nucleic acid systems with different exchange regimes.
Figure 19.
Variation of R2 + Rex with kex during an R1ρ experiment when on-resonance with the ES (pES = 0.01, , γ(1H)B0/2π = 700 MHz, R1,GS = R1,ES = 2.5 s −1 and R2,GS = R2,ES =22.5 s−1). Spin-lock amplitudes are color-coded. Vertical lines denote the indicated values of kex. The initial alignment of the magnetization during the B-M simulations was performed as described in Section 6.1.
Figure 20.
Representative experimental off-resonance R1ρ RD profiles for two-state exchange under fast and intermediate exchange. The profiles were measured for U31-C1′ and C24-C1′ in HIV-1 TAR at 25 °C and 35 °C, respectively[166]. Spin-lock amplitudes are color-coded. Error bars represent experimental uncertainties determined by a Monte-Carlo scheme (Section 6.3). Solid lines denote global fits to the RD data using the B-M equations[166]. The initial alignment of the magnetization during the B-M fitting was performed as described in Section 6.1. Gray vertical lines correspond to the offset value when on resonance with the ES. Reproduced with permission from [166].
Simulated RD profiles for a wider range of pES and kex are shown in Fig. 21. The RD profiles are flat for extremes of very slow (≤ 0.2 s−1) or fast (≥ 100,000 s−1) kex and for low pES (≤ 0.01 %) (Fig. 21). In line with this, exchange processes in nucleic acids that have been experimentally characterized using off-resonance R1ρ RD have pES between 0.02 % and 14 %, and kex between ~400 s−1 to 50,000 s−1[16, 164, 195]. In general, for fast exchange with kex on the order of 20,000 s−1, the RD profiles are broad with small Rex, making it more difficult to define the peak center and therefore Δω, and higher spin-lock amplitudes are needed to suppress the smaller Rex contributions. However, the profiles continue to remain centered at −Δω. This is in contrast to the fast exchange equations, which predict that the profiles should be centered at 0[196] (Eqn. 66, Section 6.2).
Figure 21.
Variation of R2 + Rex during off-resonance R1ρ experiments, for a wide range of kex and pES values for two-state exchange, simulated using the B-M equations. Horizontal comparisons show changes in kex while vertical comparisons show changes in pES. Different spin-lock amplitudes are denoted by colors. Dotted lines correspond to cases where the decay of the magnetization is not mono-exponential. Solid gray vertical lines correspond to an offset of –Δω, while the yellow star denotes a typical Watson-Crick to Hoogsteen exchange scenario in DNA[115]. Simulations assumed the following parameters: , γ(1H)B0/2π = 700 MHz, R1,GS = R1,ES = 2.5 s −1 and R2,GS = R2,ES = = 22.5 s−1. The initial alignment of the magnetization was performed as described in Section 6.1.
Additional simulations were performed to assess more rigorously the detection limits of the off-resonance R1ρ RD experiment for two-state exchange. While the results vary depending on the exchange parameters and measurement uncertainty, some general remarks can be made. For typical values of , the slowest exchange process that can be reliably detected has kex ~ 10 s−1 although even kex ~ 1 s−1 can be reliably characterized for high pES (Fig. 22). The upper limit for kex is ~50,000 s−1 although this can vary depending on the exchange parameters and measurement uncertainty. The lower limit for pES is ~0.02 % for a 15N spin with very large associated with deprotonation[197], but is more typically ~0.1 % for a 13C spin with (Fig. 22). As expected, doubling Δω allows ~4-fold smaller pES values to be characterized given that Rex is proportional to pESΔω2 (Section 6.2).
Figure 22.
Exploring the limits of the sensitivity for off-resonance R1ρ experiments using B-M simulations for R1ρ(15N)(left) and R1ρ(13C) (right), at γ(1H)B0/2π = 700 MHz. For each value, detectability of R1ρ was assessed for 10,000 (pES, kex) combinations. 100 pES values ranging between 0.005 % to 20 % were chosen such that they were equally spaced on a logarithmic scale. For each of these pES values, 100 kex values ranging from 1 to 400000 s−1 were chosen such that they were equally spaced on a logarithmic scale. For each (pES, kex) combination, offresonance R1ρ RD Profiles were simulated using the B-M equations, assuming spin-locking amplitudes ω1/2π = 100, 250, 500, 1000 and 2000 Hz, each with 24 offset points Ω evenly spaced such that −3.5*ω1 < Ω < +3.5*ω1, without experimental error. A rate Rex of at least 5 Hz above the baseline R2 was assumed to be the threshold of detectability. The above curves were obtained by drawing a line through the lowest detectable pES for every kex value; thus all combinations of kex and pES to the right of the curves are detectable. Similar limits are observed when profiles are simulated with 5% error and re-fit to the Bloch-McConnell equations, and considered to be detectable when the fitted exchange parameters deviate from the simulated exchange parameters by less than 2-fold. For each panel, the values are color-coded. For all simulations, R1,GS = R1,ES = 2.5 s−1 and R2,GS = R2,ES = 22.5 s−1. The initial alignment of the magnetization during the B-M simulations was performed as described in Section 6.1.
Interestingly, under slow exchange (kex/Δω < 0.1) with high pES (> 1 %), the simulated RD profiles are asymmetric, particularly for low ω1 (Fig. 21). These asymmetries arise due to gradual changes in the alignment of MES from its initial state along ωeff,GS toward ωeff,ES during the relaxation period. For high pES, this veering off of MES also leads to oscillations in the magnetization decay[23, 163](pES ≥ 1%, kex ≤ 20 s−1) (Fig. 13C). These contributions can be suppressed by avoiding an equilibration delay following selective excitation of the GS so as to minimize MES during the relaxation period (Section 5.2)[28].
The RD profiles in Fig. 21 also show that 10-fold changes in pES or kex can result in very large changes in the RD profiles. For example, large and significant RD (pES = 10 %, kex = 20000 s−1) can become undetectable (pES = 10 %, kex = 100000 s−1). One cannot therefore simply relate a change in magnitude in the RD profile to a corresponding change in exchange parameters. A related point is that there is a danger of over-interpreting the absence of RD as evidence for the absence of an ES. Thus, it is advisable to vary experimental conditions in order to bring exchange processes within the detection limits of the experiment.
4.2.2. Three-state exchange: Star-like topology without minor exchange
So far we have considered two-state exchange involving a single ES. However, several R1ρ studies report two detectable ESs in nucleic acids[117, 195, 197]. As detailed by Palmer[193], the way in which a second ES impacts the RD profile will depend on the kinetic topology. We first consider the topology ES2⇌GS⇌ES1 in which direct exchange between ES1 and ES2 (ES1⇌ES2) is assumed to be sufficiently slow as to have a negligible effect on R1ρ (Fig. 23). The shape of such topologies in which multiple ESs exchange with the GS, but not amongst each other, resembles a star, and therefore these topologies are called “star-like”. We examine how inclusion of ES2⇌GS exchange impacts the two-state RD profiles observed for GS⇌ES1 exchange. To aid in visualizing the two ES contributions, the simulations assume that the ESs have Δω values with opposite signs, i.e., Δω1Δω2 < 0, where Δω1 = ω0,ES1 - ω0,GS and Δω2 = ω0,ES2 - ω0,GS, ω0,ES1 and ω0,ES2 being the Larmor frequencies of ES1 and ES2, respectively.
Figure 23.
Off-resonance R1ρ RD profiles for three-state exchange simulated using B-M equations. A) Off-resonance R1ρ RD profiles for three-state exchange in a star-like topology with pES1 = 1 %, pES2 = 2 %, kex,1 = 2,000 s−1, (13C) = 5 ppm 13C, (13C) = −7 ppm, γ(1H)B0/2π = 700 MHz, R1,GS = R1,ES = 2.5 s-1 and R2,GS = R2,ES = 22.5 s-1, with kex,2 = 1,000 s-1 (left) and kex,2 = 10,000 s−1 (right). Dotted lines correspond to RD profiles for individual GS-ES1 and GS-ES2 exchange, while the solid lines correspond to the RD profiles for the three-state exchange process. Solid blue and green lines correspond to offsets of -Δω1 and -Δω2 respectively. B) ESs exchanging in a three-state star-like topology with similar chemical shifts ((13C) = (13C)= 3 ppm, γ(1H)B0/2π = 700 MHz) but different exchange rates and populations (pES1 = 3 %, pES2 = 5 %, kex,1 = 15000 s-1, kex,2 = 1000 s-1, R1,GS = R1,ES = 2.5 s-1 and R2,GS = R2,ES = 22.5 s-1) can be resolved using off-resonance R1ρ RD (fitted parameters: pES1 = 2.5 ± 0.4 %, pES2 = 5.0 ± 0.7 %, kex,1= 14092 ± 1605 s−1, kex,2= 926 ± 220 s−1, and . The B-M profiles were corrupted by noise with 5 % errors in R1ρ prior to fitting. A vertical green line denotes an offset of -Δω1. In both panels, spin-lock amplitudes are color coded. The direction of the initial alignment of the magnetization during B-M simulations was determined as described in Section 6.1, while taking into consideration the ES with the highest population.
As shown in Fig. 23A, the RD profiles for star-like three-state exchange are approximately given by the sum of two RD profiles for each of the two two-state exchange processes, with the three-state exchange resulting in a larger Rex compared to either of the two separate two-state processes[193]. Two separate RD peaks are observed centered at −Δω1 and −Δω2. Similar behavior would be applicable for the case of having three or more ESs in a startopology, in which each ES would be associated with its own RD profile. It should be noted that two ESs in a star-like topology can be resolved even if they have identical Δω values, as long as they have sufficiently different kex and/or pES values (Fig. 23B).
An example of a star-like topology has been reported for DNA duplexes in the context of Watson-Crick to Hoogsteen (A(anti)-T(anti) to A(syn)-T(anti) and G(anti)-C(anti) to G(syn)-C+(anti)) transitions in B-DNA. The RD profiles measured for the sugar C3′ show two discrete peaks[117] (Fig. 24). Here, the C3′ spins sense Watson-Crick to Hoogsteen transitions of the constituent BP and its neighbor. The RD profiles could be satisfactorily fitted to three-state exchange with a star-like exchange topology as expected, given that the Watson-Crick to Hoogsteen transitions at neighboring BPs are independent of one another and can occur with different rates[117].
Figure 24.
Representative experimental off-resonance R1ρ RD profiles for a system with threestate exchange in a star-like topology. Measurements were performed on C15-C3′ in A6-DNA at pH 6.8, 25 °C, as described by Al-Hashimi et al.[117]. Spin-lock amplitudes are color-coded. Error bars represent experimental uncertainties determined by a Monte-Carlo scheme (Section 6.3). Solid lines denote a global fit to the RD data[117]. The initial alignment of the magnetization during the B-M fitting was performed as described in Section 6.1, while taking into consideration the ES with the highest population. Vertical black lines correspond to offsets of -Δω1 and -Δω2. Reprinted by permission from [117].
4.2.3. Three-state exchange: Triangular and linear topologies with minor exchange
We now consider how the off-resonance R1ρ RD profiles vary for three-state exchange in the presence of direct exchange between the two ESs in a triangular topology. By definition exchange processes not involving the dominant GS are referred to as ‘minor’[193], thus the exchange rate between the two ESs is denoted by kex,minor. As expected, when kex,minor is slow relative to kex,1 describing GS⇌ES1 and kex,2 describing ES2⇌GS exchange, the RD profiles are identical to those obtained for the star topology (Fig. 25). The contribution from exchange between the two ESs increases as kex,minor approaches kex,1 or kex,2. This has the effect of ‘averaging’ the ES1 and ES2 chemical shifts[195], resulting in an asymmetric RD profile in which the positions of RD peaks of the two ESs shift toward one another. Further increasing kex,minor results in coalescence of the two ES RD peaks at a position determined by a populationweighted average over the Δω values of ES1 and ES2 (Fig. 25). This is analogous to what happens in free precession chemical exchange when two resonances coalesce in going from slow to fast exchange (Fig. 4A)[22].
Figure 25.
Off-resonance R1ρ RD profiles for three-state exchange in the presence of direct “minor” exchange between the ES1 and ES2, simulated using B-M equations. Variation of offresonance R1ρ RD profiles for three-state exchange with triangular and linear exchange topologies as a function of kex,minor and kex,1. Vertical blue and green lines correspond to offsets Δω1 and -Δω2, respectively. The RD profile in gray corresponds to three-state exchange in a star-like topology (pES1 = 1 %, pES2 = 2 %, kex,1= 2000 s−1, kex,2 = 1000 s−1, ,, γ(1H)B0/2π = 700 MHz, R1,GS = R1,ES = 2.5 s−1 and R2,GS = R2,ES = 22.5 s−1). Exchange parameters (other than kex values) for the linear exchange topologies were the same as for the star-like topology. Different spin-lock amplitudes are indicated by colors. The direction of initial alignment of the magnetization during B-M simulations was determined as described in Section 6.1, while taking into consideration the ES with the highest population.
Direct exchange between ESs has been reported experimentally for G-T/U mismatches exchanging between the wobble GS and two Watson-Crick-like ESs formed by tautomerization (ES1) or ionization (ES2) of the bases[165, 195, 197]. Under neutral pH, the RD profiles show a single ES (ES1), which was shown to be comprised of two distinct tautomeric species that exist in rapid equilibrium Genol-T/U⇌G-Tenol/Uenol leading to a single coalesced RD peak[195]. Interestingly, a second ES (ES2) comprising anionic Watson-Crick G-T−/U− was observed at higher pH, leading to deviations in the RD profiles from the perfect symmetry expected for two-state exchange. Some RD profiles showed a statistically significant improvement when fitted to a three-state model with minor exchange in a triangular rather than a star-like topology[195] (Fig. 26). It should be noted that fitting RD profiles for a three-state system undergoing minor exchange without taking it into account can result in errors in the estimates of Δω1 and Δω2.
Figure 26.
Representative experimental off-resonance R1ρ RD profiles showing three-state exchange with “minor” exchange i.e., direct exchange between the two excited states[195]. Shown in solid lines are three-state fits to the experimental off-resonance R1ρ RD profiles (hpGT-GGC, pH 8.0, 10 °C) with and without direct “minor” exchange between the two excited states[195], with the inclusion of “minor” exchange fitting the data better. Spin-lock amplitudes are color-coded. Error bars represent experimental uncertainty determined based on a Monte-Carlo error propagation scheme (Section 6.3). The direction of initial alignment of the magnetization during B-M fitting was determined as described in Section 6.1, while taking into consideration the ES with the highest population. Reprinted by permission from [195].
When the exchange is slow between the GS and one of the two ESs, the system can be described by a ‘linear’ topology GS⇌ES1⇌ES2[193]. Here, the detectability of ES2 can be determined by the kinetics of the GS⇌ES1 exchange. Once again, two discrete ESs peaks are observed or a single coalesced peak, depending on the exchange parameters including the relative values of kex,1 and kex,minor (Fig. 25).
As the appearance of three-state RD profiles can vary greatly with exchange parameters, the authors’ group provides an interactive tool (https://github.com/alhashimilab/InteractiveProfiles), which allows a user to vary the exchange parameters for a three-state system and simulate the effect on the RD profile.
4.2.4. Impact of unequal R2 for ground and excited states
The above simulations assume equal R1 and R2 values for the GS and ES, i.e., ΔR1 = R1,ES – R1,GS = 0 and ΔR2 = R2,ES – R2,GS = 0. Deviations from this assumption can arise, particularly for R2. For example, transitions toward ESs can entail the flipping in or out of nucleotide bases[16] that can be accompanied by large changes in ps-ns dynamics and therefore R2[7, 198–200]. Especially for large RNAs, this can amount to ΔR2 for C6/C8 and C1′ as large as ~100 s−1[201]. Secondly, nucleic acid ESs can feature ionized or tautomeric bases[195, 197], which can have different dipolar contributions to relaxation, profoundly affecting R2. Finally, melting/annealing of duplexes as well as dimerization of hairpins can involve large changes in overall molecular tumbling that can also lead to large ΔR2[190]. It is therefore instructive to understand how differences in ΔR2 impact the RD profiles.
As noted by Kay et al., a non-zero ΔR2 has characteristic effects on the RD profile[187, 202]. For large ΔR2 ~ 100 s−1, the RD peak is no longer symmetric, and R2,eff values are larger for offsets that correspond to having the ES near resonance[187] (Fig. 27A). The magnitude of the asymmetry depends primarily on ΔR2/kex; in the limit of ΔR2/kex = 0, the RD profiles are symmetric but they become increasingly more asymmetric with increasing ΔR2/kex[202]. The asymmetry due to unequal R2 is in general larger for smaller values (Fig. 27B). Even in the limit of , an ES can be detected provided it has a sufficiently large ΔR2; for pES > 10 %, ΔR2 as small as 20 – 30 s−1 can be detected even when [187]. The off-resonance RD profiles in such cases are symmetrically centered at the carrier frequency but are ‘inverted’ (Fig. 27C) relative to the canonical two-state RD profiles (Section 4.2.1).
Figure 27.
Impact of unequal R2,GS and R2,ES on off-resonance R1ρ RD profiles for two-state exchange simulated using B-M equations. Variation of off-resonance R1ρ RD profiles with ΔR2 as function of kex for A) , B) and C) . Different ΔR2 values are color coded. Exchange parameters are specified in inset. For all simulations γ(1H)B0/2π = 700 MHz and R1,GS = R1,ES = 2.5 s−1. Direction of initial alignment of the magnetization during B-M simulations was determined as described in Section 6.1. While fitting the mono-exponential decay, the magnetization for the first 0.05 s was not considered, in order to exclude the fast initial decay, as proposed by Kay et al.[187].
5. Experiments for measuring off-resonance R1ρ relaxation dispersion in uniformly 13C/15N labeled nucleic acids
5.1. Challenges and solutions for measuring off-resonance R1ρ
1D R1ρ experiments employing selective excitation schemes reviewed here for measuring R1ρ(15N) and R1ρ(13C) in nucleic acids are straightforward adaptations of experiments originally developed to measure R1ρ(15N) and R1ρ(13C) in proteins[154, 203, 204]. Before we describe the 1D R1ρ experiments, we review three key challenges that were addressed to allow optimal measurements of R1ρ in biomolecules.
5.1.1. Spin-lock amplitude limitations associated with alignment of magnetization along the effective field
So far we have considered the behavior of a single spin during the R1ρ experiment. In practice, one is interested in measuring R1ρ simultaneously for a large number of spins in a biomolecule. This presents a challenge, as the different spins in a molecule generally have different Larmor frequencies and will therefore be associated with different effective fields. Aligning all spins along their respective effective fields is not straightforward, particularly when using low spin-lock amplitudes, for which differences in the effective field orientations are most significant. Early heteronuclear 2D R1ρ experiments employed high spin-lock amplitudes (>1000 Hz) and/or high offsets and used hard pulses to align the magnetization of all spins along a common effective field[154, 203, 204]. As R1ρ experiments are sensitive to exchange processes with kex ~ ωeff, this limited sensitivity to motions on the fast microsecond timescale. The misalignment of spins that are far off-resonance, and gradual decay of the magnetization component perpendicular to ωeff,OBS due to the inhomogeneity of the spin-locking field results in oscillations during the relaxation period and in losses in sensitivity[205, 206]. Alternative magnetization alignment schemes were subsequently developed that used adiabatic ramps with amplitude, phase or frequency modulation to optimally align as many spins as possible along their respective effective fields[181, 205, 207–209]. While these schemes improved magnetization alignment, they were still limited to high spin-lock amplitudes, since low amplitudes require long adiabatic sweeps to optimally align the magnetization of individual spins along a broad range of effective field orientations, resulting in large sensitivity losses due to relaxation[181, 208].
5.1.2. Suppressing cross-correlated relaxation and heteronuclear scalar couplings
It has long been recognized that cross correlation between dipolar and chemical shift anisotropy (DDNH/CSAN) contributions to relaxation can affect 15N T1 and T2 measurements in macromolecules[157, 210, 211]. Cross-correlated relaxation converts transverse or longitudinal spin operators of order one to order two (Sx -> 2SxIz and Sz -> 2SzIz where S = 15N and I = 1H), thus introducing an alternative mode of relaxation in addition to auto-relaxation. For nucleic acids, in addition to sizeable DDNH/CSAN contributions to imino 15N relaxation, suppressing DDCH/CSAC is also important for 13C relaxation measurements in which the DDCH/CSAC contributions can be significant[201].
During the 1990s, it became apparent that various schemes used to suppress DDNH/CSAN interactions in 15N RD experiments, such as appropriately spaced 180° 1H pulses and 1H decoupling elements[122, 205, 207, 209, 212, 213] were leading to systematic discrepancies in T2 values measured using R1ρ and CPMG[158, 159]. This was later attributed to the evolution of heteronuclear 1JNH couplings[180, 181] during the R1ρ experiment, as a result of simultaneously pulsing on15N and 1H for spin-locking and decoupling respectively. This led to the development of new approaches for more effectively suppressing both CSAN/DDNH and 1JNH scalar coupling evolution in R1ρ experiments that employ appropriately spaced 1H pulses[181] or continuous wave 1H irradiation with periodic phase inversion[180]. Although the 2D experiment developed by Palmer et al.[181] could be used to measured R1ρ(15N) RD using low spin-lock amplitudes (150–1000 Hz), in practice, the use of adiabatic pulses for magnetization alignment resulted in significant losses in sensitivity, precluding collection of a large set of off-resonance R1ρ RD data for obtaining a complete set of exchange parameters.
5.1.3. Homonuclear scalar couplings complicate application of CPMG(13C) in uniformly labeled nucleic acids
For proteins, CPMG(15N) RD experiments provide a wealth of information regarding chemical exchange[22]. For nucleic acids, suitable imino 15N probes are only available for half the residues (guanine and uridine/thymine) and rarely for flexible sites of interest due to rapid exchange of imino protons with the solvent. For this reason, there has always been interest in using 13C spins as probes of nucleic acid dynamics[134]. However, extensive homonuclear C-C scalar (JCC) coupling networks in base and sugar moieties in uniformly 13C labeled nucleic acid samples complicate the application of CPMG RD experiments as hard 180° pulses can excite many coupled 13C spins simultaneously[134, 136]. To address this problem, much effort has been directed toward the production of site-labeled[136, 177] or fractionally labeled[134] nucleotide-triphosphates (NTPs) through biomass production for use in enzymatic synthesis. Unfortunately, the site-labeled precursors are not commercially available. Interestingly, even though methods for site-specific incorporation of 13C labels using phosphoramidite chemistry were available as early as the 1990s[214], it is only recently[18, 173, 174, 176, 215] that these methods have been used to enable CPMG studies of chemical exchange in nucleic acids. However, as is the case with site-labeled NTPs, these amidites are not commercially available. Furthermore, obtaining a large number of chemical shifts for ES characterization can become prohibitive with site-labeled samples, owing to the necessity for synthesizing separate samples with different labeling schemes.
5.1.4. Selective excitation addresses challenges in R1ρ relaxation dispersion studies of nucleic acids
The 1D R1ρ(15N) experiment introduced by Kay et al. in 2005[163] addresses many of the above-mentioned limitations. The experiment employs selective excitation schemes pioneered by Bodenhausen and colleagues[160–162] to excite signals corresponding to individual spins of interest. Rather than measuring R1ρ simultaneously for multiple spins at once, off-resonance R1ρ RD profiles are measured one at a time for specific spins in a molecule. This bypassed the need to simultaneously align multiple spins along their effective fields altogether since each spin is aligned one at a time. By obviating the need for adiabatic ramps, much lower spin-lock amplitudes (~25 Hz for 15N) could be employed, broadening the sensitivity of R1ρ to millisecond timescale motions[163]. In addition, DDNH/CSAN (or DDCH/CSAC) and heteronuclear JNH (or JCH) scalar coupling evolution could be effectively suppressed by the application of an on-resonance 1H continuous wave field[163, 211] during the spin-lock period. In addition, JCN and JCC scalar couplings could be more readily suppressed in R1ρ experiments by application of selective spin locking fields during the relaxation period. One downside is as the extra time needed to collect separate RD profiles for individual spins in a given molecule, relative to 2D R1ρ experiments.
A straightforward modification of the original 1D R1ρ(15N) experiment allows R1ρ(15N) and R1ρ(13C) data to be measured in uniformly 13C/15N labeled nucleic acids[21, 112], and will be described in Section 5.2. These R1ρ experiments have been used to measure RD for a variety of sugar and base 13C/15N probes to obtain insights into chemical exchange over a broad range of timescales from micro to milliseconds in uniformly 13C/15N labeled nucleic acids ranging in size from 24–56 nucleotides[16, 21, 112, 117, 164–166].
5.2. Selective 1D pulse sequences for measuring R1ρ in uniformly 13C/15N labeled nucleic acids
Pulse sequences for measuring R1ρ(15N) and R1ρ(13C) in uniformly labeled nucleic acids in a 1D manner are shown in Fig. 28A. The experiments employ selective cross polarization (CP)[160–162] to excite individual 15N or 13C spins of interest through the selective transfer of magnetization from directly bonded 1H spins. This is accomplished by applying a 90°x pulse to create transverse Iy (I = 1H) magnetization followed by spin-locking in the rotating frame by application of a long and selective 90° RF pulse (BI) along the y-axis. Simultaneously, a long RF pulse (BS) is applied along x on the S spin (S = 13C or 15N) to satisfy the Hartmann-Hahn matching condition γIBI = γSBS. The spins are then allowed to exchange magnetization in a manner dependent on the magnitude and duration of the RF fields, leading to generation of transverse Sx magnetization. In theory, complete transfer of magnetization from spin I to spin S takes place when the duration of the CP transfer (τCP) is set to (2k-1)/JIS and the amplitude of the RF pulses (ωCP = γIBI = γSBS) is set to (valid for 2(ωCP/2π) ~ JIS), where n and k are positive integers such that n ≥ k and JIS is the scalar coupling between spins I and S. In practice, smaller values of τcp (= 1/JIS) are preferred so as to minimize sensitivity losses due to relaxation. Furthermore, as demonstrated by Bodenhausen et al.[216] lower values of are also preferred because the transfer is more selective and less sensitive to RF field inhomogeneities and mismatches in the Hartmann-Hahn matching condition. The values of ωCP and τCP are adjusted from their initial settings (Table 1) to maximize the signal intensity at the end of the R1ρ experiment, when setting the relaxation delay Trelax = 0. For AX and non-equivalent AX2 spin systems (A = 13C/15N, X = 1H), the CP transfer generates Ax magnetization from longitudinal Xz. For equivalent AX2 spin systems, the transfer generates Ax + 4X1ZX2ZAX coherences. In the latter case, some magnetization will be lost due to competing pathways arising from evolution of the three-spin coherences[217].
Figure 28.
A) Pulse sequences for measuring off-resonance R1ρ(13C) and R1ρ(15N) in nucleic acids with selective excitation and low spin-lock amplitudes. Hard90° pulses are denoted using filled narrow rectangles, while open narrow rectangles (excluding the purge elements in the 13C sequence) denote hard pulses with flip angles φ. The flip angle φ of the hard pulses φ3 and φ4 is equal to arctan(ω1/Ω), where ω1 and Ω are the spin-locking amplitude and offset for 13C or 15N. The flip angle of the hard pulse on the proton channel in the 15N R1ρ sequence is equal to tan−1(ω1H/ΩH) where ω1H is the amplitude of the proton spin-locking field and ΩH is the frequency offset of the signal of interest from water. Wide open rectangles denote periods of continuous RF irradiation. Reprinted with permission from [9].(B) The different spins that can be targeted for R1ρ RD measurements in uniformly 13C/15N enriched nucleic acids using the pulse sequences in part (A) are highlighted by red circles. The 1H spins that can be targeted using the 1D R1ρ pulse sequence developed by Petzold et al.[222] are also shown using red circles. Spectral crowding in RNA between the C3′ and C2′ sugar carbons prevents measurement of R1ρ(C3′ and C2′) in RNA[166] unless one uses selectively labeled samples, while relaxation contributions from germinal protons complicates R1ρ(C5′) measurements in both DNA and RNA[166] and R1ρ(C2′) measurements in DNA unless selective deuteration is used[131].
Table 1. Optimal settings for 1D off-resonance R1ρ experiments using the pulse sequences shown in Fig. 21A.
| Parameter | Optimal Value | |
|---|---|---|
| ωCP/2πa | 85 Hzb, c | |
| τCP | ~1/4 |1JAH|d, ~3/4 |1JAH|e | |
| Τeq | ~3/kex | |
| ω1/2πf | ||
| A-NH2/G-NH2/C-NH2 | > ~70 Hz | |
| ω1H/2π | ~10 kHz for 13C and ~5 – 8 kHz for 15Ng | |
| ζ | π/2δh | |
(ωCP/2π) >3½/4 |1JAH|, A = 13C/15N
R1ρ(15N) measurements on imino 15N (N1/N3). In theory, ωCP/2π should be chosen to be equal to 3½JIS/4, the smallest value that can lead to complete magnetization transfer between spins, while also being selective and less sensitive to RF field inhomogeneities and mismatches in the Hartmann-Hahn matching condition[216]. However, in practice, a value of ωCP/2π (= 85 Hz) larger than 3½JIS/4 ~ 39 Hz is typically employed so as to minimize losses of the magnetization due to conformational exchange[163].
R1ρ(13C) measurements on aromatic and sugar 13C nuclei (C2/C5/C6/C8/C1′/C3′/C4′)
For AX (e.g. N1–H1 and C8–H8) and non-equivalent AX2 (e.g. amino NH2 group in WatsonCrick G-C BPs) spin systems[161, 217]
For equivalent AX2 spin systems (e.g. amino NH2 group in G-T/U wobbles)[161].
Should be greater than 3 times 2JNN or 1JCC[21, 28]. The largest value that can be used depends on probe hardware limitations.
Should be > ωeff(max)
δ is the offset in Hz of the undesired resonance in the 13C/15N dimension from the resonance of interest
The transverse Sx magnetization is then rotated to Sz through application of a hard 90° pulse. This is a followed by a delay τeq ~ 3/kex to allow equilibration of pGS and pES (Fig. 28A). This is necessary as the ES, since it has a chemical shift different from the GS, may not have been excited by the selective Hartmann-Hahn transfer. A second hard pulse with a tip angle θ, i.e., the tilt angle of ωeff,OBS, is then used to align the Sz magnetization of both the GS and ES along ωeff,OBS (Fig. 11B). A purge element is used to suppress magnetization from spins that have similar 1H but different 13C or 15N Larmor frequencies via the application of a delay (ζ), that allows for dephasing of spins precessing with a frequency different from that of the target[163]. The ζ delay and purge element can be placed either before[21] or right after the spin-lock period[112, 163] (Fig. 28A).
The 13C/15N magnetization is then spin-locked during the relaxation period (Trelax) along ωeff,OBS by the application of a spin-locking field to the spin of interest. Here, care is taken to minimize Hartmann-Hahn transfers between pairs of scalar coupled spins such as C5–C6 (in pyrimidines), C1′-C2′, and C4/6-C8 (in purines) to typically < 1% of the maximum transfer efficiency[21]. This is accomplished by ensuring that the difference in the effective field strengths experienced by two coupled spins (S1 and S2) is much greater than the coupling constant between them. The Hartmann-Hahn transfer efficiencies (AHAHA) between spins S1 and S2 can be computed using[92]:
| (55) |
where ωeff and θ are the effective fields and tip angles of the two spins, and Jn is the scalar coupling between them. The offsets that minimize unwanted Hartmann-Hahn transfers (AHAHA < 1%) in R1ρ(13C) RD experiments are listed for a variety of 13C spins in Table 2. In general, extraneous Hartmann-Hahn magnetization transfers are less relevant for 15N spins compared to 13C, owing to the smaller size of the Jn couplings (< 10 Hz)[218].
Table 2. Offsets for R1ρ(13C) measurements in nucleic acids that are susceptible to Hartmann-Hahn transfers during application of a spin-lock.
Magnetization transfer between nuclei that are coupled to each other can serve as an extraneous mode of relaxation during the application of spin-locking pulses in an R1ρ experiment. Offset values that are susceptible to such magnetization transfer via attainment of a Hartmann-Hahn matching condition (efficiency AHAHA > 1%, Eqn. 55) for a pair of spins S1 and S2 were computed assuming γ(1H)B0/2π = 700 MHz and spin-lock amplitudes between 50–3600 Hz. Jn is the multiple-bond scalar coupling constant between the spins under consideration while is the average difference in chemical shift between them. Jn couplings were obtained by van Buuren et al.[218].
| S1 | S2 | Nucleic Acid | Jn(Hz) | Offsets (Hz) | |
|---|---|---|---|---|---|
| C4′ | C5′ | RNA | −40 | −17 | (−1700, −1300) |
| C4′ | C3′ | RNA | −40 | −9 | (−900, −700) |
| C4′ | C5′ | DNA | −40 | −20 | (−1900, −1600) |
| C4′ | C3′ | DNA | −40 | −9 | (−900, −700) |
| C3′ | C4′ | DNA | −40 | 9 | (700, 900) |
| C3′ | C2′ | DNA | −40 | −38 | (−3500, −3100) |
| C1′ | C2′ | RNA | −42 | −15 | (−1450, −1150) |
| C1′ | C2′ | DNA | −42 | −46 | (−4200, −3900) |
| C/U-C6 | C/U-C5 | RNA/DNA | −68 | −44 | (−4100, −3600) |
| C/U-C5 | C/U-C6 | RNA/DNA | −68 | 44 | (3600, 4100) |
| C/U-C5 | C/U-C4 | RNA/DNA | −60 | 70 | (5800, 6400) |
Selective irradiation of the 13C or 15N spins with a spin-locking field (Fig. 28A) during the relaxation period also serves to suppress evolution under JCC, JNC, and JNN. These scalar coupling constants also set a lower limit on the spin-lock amplitude that can be used and, consequently, the slowest process that can be probed using R1ρ when working with isotopically labeled samples. Typically, ω1 is set to be approximately three times larger than the largest relevant scalar coupling (Table 1). In contrast, the highest spin-lock amplitude that can be used is determined by the probe hardware, and this in turn determines the fastest process that can be probed using off-resonance R1ρ (Table 1). Spin-lock amplitudes as high as ~6.4 kHz for 15N can be used with a cryo-probe (QCI Bruker) as compared to 4 kHz for a room-temperature probe, allowing measurement of exchange processes with exchange rates as high as 40000 s−1[219].
During the relaxation period, evolution under 1JNH (or 1JCH) and DDNH/CSAN (or DDCH/CSAC) are efficiently suppressed using a strong 1H continuous-wave field (ω1H) applied on the resonance of interest[211, 220] (Fig. 28A). ω1H is chosen to be larger than the maximum effective (13C/15N) spin-locking field (ω1H > ωeff(max)) to avoid unwanted C-H or N-H polarization transfers during the spin-lock period through accidentally fulfilling a Hartmann-Hahn matching condition[163] (Table 1). The amino NH2 spin system is also subject to dipole-dipole (DDNHA/DDNHB) cross-correlated relaxation, which can result in the generation of doubly antiphase magnetization (4I1zI2zSx) from in-phase magnetization during the relaxation period. The DDNHA/DDNHB cross-correlated relaxation contribution scales as (τc/2)(3cos2θ − 1)[221], where θ is the angle between the two N-H bonds. The angular term is small (~ −0.125) for amino –NH2 groups in which the angle between the bonds is ~120°. Thus, the DDNHA/DDNHB contribution for a 10 BP duplex is estimated to be ~0.5 s−1 and can be safely ignored[165]. In an analogous manner, extraneous contributions from J couplings and cross relaxation must also be taken into account when performing 1H RD experiments, for which pulse sequences based on selective 1D excitation have also been reported[222, 223]. As the higher γ value for 1H allows one to achieve higher spin-lock amplitudes, R1ρ(1H) holds great promise for characterizing faster exchange processes in nucleic acids in the future, potentially without the need for isotopic enrichment.
At the end of the relaxation period, the component of the net magnetization along ωeff,OBS is tilted back along z by the application of a hard pulse, and is transferred back from 13C or 15N to 1H using CP for subsequent detection (Fig. 28A). Consistent temperature throughout the experiment is maintained by a heat-compensation element[21, 163] that is applied far offresonance; this consists of 1H and 13C or 15N spin-locking fields applied for a given amount of time (Tmax – Trelax), where Tmax is the longest relaxation time and Trelax is the relaxation time in a given scan. Tmax is typically set to a value that results in ~30% intensity loss relative to the value measured at Trelax = 0 for the resonance of interest, while also taking into account probe hardware limitations that may arise for longer Tmax. The water signal is suppressed using either low amplitude presaturation during inter-scan delays with additional purge elements for 13C experiments or with a WATERGATE element[224] before acquisition for 15N experiments (Fig. 28A). Decoupling pulses are applied to 13C or 15N during acquisition. The spins in nucleic acids that can be targeted using these 1D R1ρ experiments are shown in Fig. 28B.
The experiment yields a 1D 1H NMR spectrum for the resonance of interest and in some cases additional nearby resonances, especially if their chemical shifts overlap in both 1H and 13C/15N dimensions (Fig. 29). A total of ~10 Trelax delays are typically measured and the intensity of the peak of interest is fitted to a mono-exponential decay I = I0 exp(−R1ρTrelax) using a nonlinear fitting algorithm to obtain the value of R1ρ (Fig. 29). On-resonance R1ρ data is typically collected initially by setting Ω = 0 and decay curves are measured at ~ 20 ω1/2π values ranging between 50 – 2000 Hz and 50 – 3600 for 15N and 13C, respectively. Off-resonance R1ρ data are then measured by varying both Ω/2π and ω1/2π (typically three or more values spanning the ranges described above). The maximum value Ωmax/2π is generally set to ~3 – 4 × ω1/2π (Section 3.5). Typically, a total of ~ 24 values of Ω/2π are chosen with equal spacing to span ± Ωmax/2π symmetrically about Ω/2π = 0. In cases where there is an a priori estimate of ω0,ES, offsets can be chosen accordingly to sample points where Rex would be non-zero. Note that it may be important to collect R1ρ data for multiple experimental sample conditions, as the appearance of the profiles is sensitive to the conditions used (Section 4.2, Section 7.2.3).
Figure 29.
Flowchart describing the various steps for measuring and analyzing R1ρ RD data using the pulse sequences shown in Fig. 28A.
5.3. Calibrating the spin-lock amplitude
When setting up the R1ρ experiment it is important to calibrate the 13C and 15N spin-lock amplitudes[22, 180]. This involves finding the optimal power in dB (decibels) or W (watts) for the spin-lock pulse of a given frequency. In general, spin-lock amplitude calibration is done when setting up experiments on a new probe and need not be repeated when switching samples or changing temperature. The calibration is performed using a modified version of the R1ρ pulse sequence in which the pulses with phases ϕ 3 and ϕ 4 flanking the spin-lock element that tilt magnetization along ωeff,OBS have been removed (Fig. 28A). This can be done by omitting the pulses from the pulse program or by simply setting the pulse duration to zero. The rationale is to detect the precession of net magnetization around the x or y axis due to the spin-locking field, and use this information to infer its amplitude. The following protocol can be used for calibration:
Select a sharp and well-resolved resonance for calibration that exhibits minimal or no chemical exchange to avoid complications from exchange processes. For experiments with nucleic acids, it is preferable to perform 13C calibration using A-C8 or G-C8 spins as they permit the use of spin-lock amplitudes as low as ~50 Hz (Table 1).
Compile a table containing ω1/2π values (in Hz) to be calibrated and associated power levels P (in dB). For 13C/15N calibration, we choose 24 ω1/2π values between 50 and 3600 Hz and 50 and 2000 Hz respectively. The power levels P for each spin-locking field can initially be estimated based on the calibration of rectangular 90° pulse lengths for 15N or 13C.
Record 1D experiments for an array of spin-lock durations Trelax under on-resonance conditions for each ω1 value. Usually, 33 durations are used in increments of π/(2ω1) from 0 to 8*2π/ω1 s[21]. For example, a spin-lock amplitude ω1/2π of 100 Hz would be incremented 33 times from 0–80 ms in increments of 2.5 ms. This ensures that there are 4 points for one rotation of the net magnetization about the spin-locking field, enabling extraction of the frequency of rotation, in accordance with the Nyquist sampling theorem.
The resultant peak intensity should be a sinusoidal function of ω1,realTrelax where ω1,real is the real spin-lock frequency corresponding to the power P (Fig. 30A). Calculate ω1,real by fitting the peak intensities to the equation I(Trelax) = I0exp(−R · Trelax)cos(ω1,realTrelax + ϕ), where I is the peak intensity, I0 is the intensity when Trelax = 0, R is the relaxation rate and ϕ is a phase correction factor.
Repeat Step 2 and 3 for all ω1 in the table, and obtain ω1,real for all P values.
Fit P and ω1,real to a logarithmic equation P = alog10(ω1,real) + b. Ideally this fit should give R2 > 0.99. If the data points deviate from linearity, polynomial fitting can be adopted instead. An example of an ideal calibration curve is shown in Fig. 30B.
Use the equation given by the fit in step 6 to back-calculate P for a desired ω1 within the range of amplitudes used for calibration.
Figure 30.
Calibration of the spin-lock amplitude in R1ρ experiments. A) Nutation curve showing variation of signal intensity (black dots) as a function of time during an R1ρ calibration experiment. The red line is a fit of the intensity to the equation in the inset. B) Variation of the actual spin-lock frequency ω1,real, with the power P of the spin-lock field, obtained by fitting nutation curves in part (A) (black dots). The red line denotes a fit to the equation in the inset.
6. Data Analysis
Two general approaches can be used to analyze off-resonance R1ρ data to extract the exchange parameters (Fig. 29). The most general approach involves numerically integrating the B-M equations[45] to find exchange parameters that best satisfy the measured R1ρ data. A second approach to fit R1ρ data involves using algebraic expressions that make various assumptions and which are valid for different ranges of exchange conditions. The two approaches are often used hand in hand, with the algebraic expressions often being used to obtain initial guesses for the B-M fitting as well as for developing an intuitive understanding for how the RD profiles vary with spin-lock and exchange parameters.
6.1. Numerical integration of Bloch-McConnell equations
In the authors’ group, we use an in-house python program called “Bloch-McConnell Numerical Simulator” or BMNS (available from https://github.com/alhashimilab/BMNS) to numerically integrate the B-M equations and thereby simulate or fit R1ρ data. The analysis described below is valid when the magnetization decay is dominated by a single exponential decay[13, 23]. In uncommon cases where the decay is not mono-exponential, one needs to directly fit it by integrating the B-M equations, without extracting R1ρ. BMNS takes the following parameters as input:
List of Ω, ω1, R1ρ and the uncertainty of R1ρ (see Section 6.3).
Initial guesses for the exchange parameters (pES1, pES2, kex1, kex2, Δω1, Δω2, R2,GS, R2,ES1, R2,ES2, R1,GS, R1,ES1, R1,ES2) for a given exchange topology as well as their ranges. For example, for three-state exchange, one has to specify whether the topology is star-like, linear, or triangular by appropriately setting individual rate constants to zero (Section 4.2). The initial guesses are typically either assigned arbitrarily and/or obtained from fitting the R1ρ data to an appropriate algebraic expression (Section 6.2). The ranges for the exchange parameters are typically chosen to be large to avoid biases. In general, fitting the RD data is carried out assuming R1,GS = R1,ES and R2,GS = R2,ES unless there is reason to suspect otherwise. Note that deviations from the latter assumption can result in significant errors in the fitted pES and kex values even when |R2,GS- R2,ES| << kex[190].
The initial alignment of the magnetization. For slow exchange, the magnetization is initially aligned along ωeff,GS (GS alignment), while more typically, for fast and intermediate exchange, the magnetization is aligned along ωeff,AVG (AVG alignment). If not known a priori, the mode of alignment can be determined during the fitting procedure based on the value of kex/|Δω|; with kex/|Δω| ≤ 1 and kex /|Δω| > 1 corresponding to GS and AVG alignments, respectively. We recommend fitting RD profiles assuming both possible alignments for completeness. For low pES, the choice of alignment has little effect on fitting R1ρ data. However, for intermediate to fast exchange (0.1 < kex /Δω < 5), with high pES (> 10%), a line shape analysis shows that the observed peak is actually neither at ω0,GS nor at ω0,AVG (Fig. 31A). Thus, calculation of effective fields assuming GS or AVG alignments leads to asymmetries in the RD profile around Ω = 0, that are especially pronounced at low ω1, when deviations in Ω can have a large influence on the effective field orientations (Fig. 31B, 31C). This artifact can be corrected by selecting an initial magnetization alignment based on line shape simulations, and then adjusting the effective fields to take this into account (Eqn. 37, 39). This also enables determination of the effective fields and alignment directions for any arbitrary set of exchange parameters. Temperaturedependent R1ρ measurements can also be used to deduce the alignment scheme when both schemes equally fit the data well, as described in Section 6.4.3. Each of the above inputs can be specified for individual R1ρ data sets measured on multiple spins, which can also be fit globally using shared parameters.
Figure 31.
Asymmetries near 0 offset observed in off-resonance R1ρ RD profiles due to improper alignment of the initial magnetization under intermediate exchange conditions for two-state exchange, obtained using B-M simulations. A) Line shape (LS) simulation using the B-M equations in free precession conditions in the absence of a spin-locking field, for a system in intermediate exchange (pES = 10 %, kex = 3000 s−1, , γ(1H)B0/2π = 700 MHz,R1,GS = R1,ES = 0 s−1, R2,GS = R2,ES = 16 s−1). B) Directions of the effective fields (ωeff,GS: blue, ωeff,ES: red, ωeff,AVG: green, ωeff,OBS: black dotted lines) and initial alignment of the bulk magnetization (GS: blue, ES: red arrows) at the start of the R1ρ experiment (ω1/2π = 100 Hz, Ω = −300 Hz) for the system in (A) where the magnetization is initially aligned along the effective field of the ground state (GS Align, left), population weighted average (AVG Align, middle) and the observed (OBS) resonance obtained from a lineshape simulation (LS Align, right) . (C) Offresonance R1ρ RD profiles for the system in (A) with R1,GS = R1,ES = 2.5 s−1, when the magnetization is initially aligned along ωeff,GS (GS Align, left), ωeff,AVG (AVG align, middle) and ωeff,OBS (LS Align, right). Note that in all cases, the magnetization at the end of the relaxation delay (0.05 s) is projected parallel to the initial alignment direction to calculate R1ρ. The different spin-lock amplitudes are color coded. Also shown in insets are representative decays of the normalized magnetization (black dots) along the initial alignment direction during the relaxation decay, along with exponential fits (red line).
Fitting of the R1ρ data is then carried out through least-squares minimization of the function F that quantifies the agreement between the experimentally measured R1ρ data and values calculated using the B-M equations for a given set of exchange parameters and a user-specific exchange topology:
| (56) |
| (57) |
σexp(i) is the experimental uncertainty in R1ρ (estimated using Monte-Carlo or bootstrap approaches outlined in Section 6.3) and the summation i is over the total number of R1ρ data points N (total number of combinations of spin-lock amplitudes and offsets).
The initial guesses for the exchange parameters are used as input to predict the R1ρ data by using the B-M equations (Section 4.1). This involves numerically integrating the B-M equations to determine MGS and MES as a function of time, and then fitting the projection of the net magnetization along ωeff,OBS (depending on the initial alignment of the magnetization) to determine R1ρ. The χ2 value is then computed and a second iteration is attempted choosing different values for the exchange parameters from the user defined range, in a manner that minimizes the χ2, using least-squares minimization[225]. BMNS uses a Trust Region Reflective algorithm for this purpose. This process is repeated iteratively until a local minimum is found. To minimize computational cost and also avoid being trapped in local minima in the multidimensional parameter space during least-squares minimization, an adaptive memory programming framework[226] for global space optimization can be used. Here, once a local minimum is found, the search function tunnels out of this local minimum and resumes optimization from a new starting point. Alternatively, a brute force grid search over the multidimensional parameter space can also be performed, although it is computationally expensive.
The goodness of the fit is evaluated by normalizing the computed χ2 values to take into account the degrees of freedom to obtain a reduced χ2 (χ2red), so as to enable comparisons between different exchange models:
| (58) |
where N is the total number of R1ρ data points and K the number of fitted parameters for a given exchange model. In general, a value χ2red < 1.5 is considered to be reasonable though care should be taken if a fit gives χ2red < 1 as this may indicate over-fitting of the data. Convergence of the fitted exchange parameters when starting with different initial guesses can also be used to assess the robustness of the fit. The different exchange models (two-state versus three-state star-like/triangular/linear) and fitting modes (individual versus global) used in the B-M fitting are evaluated for statistical significance using Akaike information (AIC) and Bayesian information (BIC) criteria[227, 228] (Fig. 29). They quantify the likelihood or probability of one model relative to another for fitting a given data set, by taking into account the goodness of fit and the complexity or degrees of freedom of the models:
| (59) |
| (60) |
where ΔAIC and ΔBIC denote the differences in AIC and BIC values between the models. The AIC and BIC values themselves are defined as follows:
| (61) |
| (62) |
where is the residual sum of squares for a given exchange model. Degeneracies can arise near under particular exchange scenarios that can make it difficult to reliably determine all exchange parameters. Near the fast exchange limit (kex/Δω > 10), it becomes difficult to reliably separate Δω from pES as Rex becomes proportional to pESΔω2[13, 196]. Under slow exchange conditions, there are also degeneracies in resolving pES and kex as Rex becomes proportional to pESkex[229, 230].
6.2. Algebraic equations
Algebraic expressions that make various approximations can also be used to fit the variations of off-resonance R1ρ with ω1 and Ω to extract the desired exchange parameters (reviewed in Massi et al.[13]). They give a better understanding of the dependence of R1ρ on the exchange parameters relative to the B-M equations. These expressions assume that the decay of the magnetization is mono-exponential. The most versatile expression for two-site chemical exchange is given by the following equation derived from a Laguerre approximation[231] and more recently via perturbation theory applied to an n-site BM evolution matrix[194]:
| (63) |
| (64) |
The Laguerre equation is valid under conditions of fast exchange, and deviations can arise for slow to intermediate exchange when pES > 30% especially for low spin-lock amplitudes (< 400 Hz)[9, 231]. This results from the fact that the Laguerre equation assumes AVG alignment.
Simpler expressions have also been derived that entail the use of alternative approximations[13]. An expression for R1ρ valid for very asymmetric populations (pES << pGS) for arbitrary chemical shifts is given below:
| (65) |
while an alternative expression that is valid only in the fast exchange limit (kex >> Δω) for arbitrary populations is given by[63, 189]:
| (66) |
The two equations above can be used to fit off-resonance data; however, deviations can arise under conditions when the assumptions inherent to the equations are not satisfied.
For three-state exchange without direct “minor” exchange between ES1 and ES2 (ES2⇌GS⇌ES1), one can use the following equation[193]:
| (67) |
where k1 and k-1 are the GS⇌ES1 forward and reverse rate constants, and k2 and k-2 are the GS⇌ES2 forward and reverse rate constants, respectively. From the equation, it can be appreciated that the exchange contribution for a star-like three-state topology is essentially the sum of exchange contributions due to the individual two-state processes as described in Section 4.2.2. Expressions for three-state exchange with significant minor exchange have also been reported[193]. These equations have been generalized to n-site exchange for star-like, complex linear, and non-linear topologies by Palmer et al.[194]. All the above equations assume that R2 results from a population-average over all ES and GS species. Algebraic expressions for R1ρ for cases where R2 for the GS and ES are not equal have also been reported in the literature[187, 202].
When fitting R1ρ data using the above equations, one starts with broad initial estimates for the exchange parameters and optimizes initial guesses to achieve agreement with the experimental data. However, biased starting estimates coupled with conventional local optimization methods can lead to being trapped in local minima. In such cases, the use of simulated annealing and basin-hopping schemes[226] can prove beneficial for finding global minima and for exploring the search space more broadly.
χ2red values can be used to assess the quality of fit as described in Section 6.1. A poor fit may suggest deviations from the assumed exchange model or from the range of validityof the algebraic equations used. Once again, statistical tests (e.g. AIC and BIC weights)[227, 228] can be used to assess the likelihood of one model or exchange topology over the other.
6.3. Estimating uncertainties in exchange parameters
Uncertainty in the fitted exchange parameters can be estimated using the standard error of the fit, as well as bootstrap and Monte Carlo based approaches[196]. A parent set of R1ρ rates (Ω, ω1, R1ρ and σ) is used for all methods. The standard error of a fit can be obtained as the square root of the diagonal elements of the covariance matrix of the fitted parameters.
In the bootstrap approach:
A large number (typically 500–1000) child data sets of the same size as the parent data set are generated by randomly sampling R1ρ data points with replacement from the parent data set. Here, an individual data point can be either excluded or chosen multiple times in a given child data set.
Each child data set and the parent data set are fit to the Laguerre[231] or B-M equations to obtain the five exchange parameters: pES, kex, Δω, R1 and R2.
The uncertainty in the exchange parameters is then determined by calculating the standard deviation between the fitted parameters of the child data sets and those of the parent data set.
In the Monte Carlo approach:
The parent data set is fit to the Laguerre equation[231] or B-M equations[45] to obtain the exchange parameters.
1000 child data sets are generated using the exchange parameters and the Laguerre or B-M equations, and the associated Ω and ω1 values of the parent data set. Each child data set is then corrupted by noise according to the R1ρ error from the parent data set and re-fitted using the Laguerre equation or B-M integration.
The uncertainty in the exchange parameters is then determined by calculating the standard deviation between the fitted parameters of the child data sets and those of the parent data set.
Similar methods can also be used for determination of errors in R1ρ for each ω1 and Ω combination while fitting the mono-exponential decays.
6.4. Extracting exchange parameters
6.4.1. Deducing the total number of excited states
Early on, it is important to deduce the total number of ESs sensed by the R1ρ measurements as this influences the models used in fitting the data. Deviations from symmetric RD profiles expected for two-state exchange, and the appearance of more than one RD peak is an indication of additional ESs as described for three-state exchange in Figure 24. In addition, different spins in a molecule may sense different ESs. To gauge such cases, the R1ρ data measured for the spins are initially subjected to B-M fitting individually. A plot of kex versus pES for the different spins is then examined to identify the total number of distinct ESs. A representative kex vs. pES plot for HIV-1 TAR shows clusters at two distinct locations consistent with two ESs (Fig. 32). Whether or not global fitting of the data with a common pES and kex is statistically justified also provides a means of gauging the total number of ESs.
Figure 32.
Deducing the number of ESs sensed by R1ρ RD measurements. A plot of pES vs. kex as obtained from R1ρ measurements on individual spins in a given molecule displays clusters corresponding to kinetic and/or thermodynamically distinct ESs. Shown is a representative pES vs. kex plot obtained from 13C R1ρ RD (C6/C8/C4′/C1′ spins) measurements on HIV-1 TAR (secondary structure shown on the left) at pH 6.4, 25 °C[166], indicating the presence of two distinct ESs (ES1 and ES2). The zoomed in view of the ES2 region is provided in the inset. Errors were estimated using a Monte-Carlo approach while fitting the individual RD profiles, as explained in Section 6.3.
6.4.2. Deducing the chemical shifts of the excited states
The chemical shift of the ES (ω0,ES) can be calculated from the Δω value obtained from fitting the RD data and peak position (ω0,OBS) measured from a 2D HSQC spectrum. For intermediate-slow exchange with kex /Δω < 1, the initial alignment of the magnetization is along ωeff,GS (Section 6.1) and ω0,ES is given by:
| (68) |
For intermediate-fast exchange kex /Δω > 1 for which the initial alignment of the magnetization is along ωeff,AVG (Section 6.1), ω0,ES can be calculated using:
| (69) |
Note that for special exchange scenarios such as intermediate to fast exchange (0.1 < kex /Δω < 5) with high pES > 10% (Section 6.1), ω0,OBS does not correspond to either ω0,AVG nor ω0,GS. Here, line shape simulations under free precession assuming the fitted exchange parameters with ω0,GS = 0 and ω0,ES = Δω are used to estimate the shift (ψ) in resonance frequency due to the exchange and obtain ω0,ES:
| (70) |
6.4.3. Obtaining kinetic and thermodynamic parameters
Kinetic and thermodynamic parameters that provide important insights into the energetics of the ES and transition state (TS) can be derived from the exchange parameters[15, 17]. The free energy difference between the ES and GS (ΔGES-GS) at a given temperature can be obtained from the measured pES and pGS using the following equation:
| (71) |
The activation barrier for the forward or reverse reaction and the corresponding enthalpies ( and ) can be obtained from temperature-dependent R1ρ measurements using the following equation derived by Russu et al.[232] that is free of statistical compensation effects and is valid if the specific heat capacity can be assumed to be constant:
| (72) |
| (73) |
where i = 1 or −1 and Thm is the harmonic mean of the experimental temperatures used. The transmission coefficient κ is often assumed to be equal to 1. This assumes that the frequency of crossing the activation barrier can be approximated by , which is valid for the case of a bond vibration. However, as noted by Kay et al., this frequency may be different in the context of conformational changes in biomolecules[233]. Indeed, taking this into account by adjusting the value of κ to be different from 1 can have a large impact on the obtained free energies of activation. For example, assuming κ = 3.3 * 10−6 as determined by Kay et al. for transitions involving formation of ESs in proteins[233] can change the free energies of activation for Watson-Crick to Hoogsteen transitions by as much as 7 kcal/mol (or 29 kJ/mol) (Fig. 33). In contrast, the enthalpies for the forward and backward reactions do not depend on κ and therefore can be reliably extracted from temperature-dependent rate constants obtained from RD measurements. The free energies and enthalpies obtained as described above can be used to obtain the entropy ( and ) of activation for the forward and reverse reactions:
| (74) |
While performing R1ρ RD measurements as a function of temperature, accurate estimates for the sample temperature can be obtained by recording spectra of 99.8% methanol-d4 (Cambridge Isotope Laboratories, Inc.) as described by Berger et al.[234]. The enthalpy (ΔHES–GS) and entropy (ΔSES–GS) change for the GS-ES transition can also be calculated as follows:
| (75) |
| (76) |
Figure 33.
Thermodynamics and kinetics of GS-ES exchange characterized using temperature dependent R1ρ RD measurements. Free energy diagram (1 kcal/mol = 4.184 kJ/mol) for the Watson-Crick to Hoogsteen transition (κ = 1, left and κ = 3.3 * 10−6, right) for A16-T9 in A6-DNA at pH 5.4, 25 °C obtained using off-resonance R1ρ RD, as reported by Al-Hashimi et al.[17]. The secondary structure of A6-DNA is shown in inset.
The temperature dependence from a van’t Hoff analysis can also be used to discriminate between GS versus AVG alignment during B-M fitting[235], in cases where the initial magnetization alignment is ambiguous, and both schemes fit the data equally well. A van’t Hoff plot of ln(k1/T) (or k-1) versus (1/T – 1/Thm)(K−1) (Eqn. 72 and 73) is expected to exhibit linearity if the correct magnetization alignment scheme is assumed, provided that it does not change as a function of temperature. Such an analysis was used to select AVG over GS alignment while fitting RD profiles by Al-Hashimi et al.[235].
In addition to obtaining insights into the thermodynamics of transition states and their kinetics, RD methods can also be used for structural characterization of the TS via ϕ value analysis[115, 236] or measurement of kinetic isotope effects for exchange processes[237].
7. Determining structures of excited states in nucleic acids
The biological significance of an exchange process cannot be fully appreciated without determining the structure of the ES. RD experiments provide structural information regarding the ES in the form of chemical shifts. Here, we review how chemical shifts, combined with methods for stabilizing or destabilizing ESs using mutagenesis and chemical modifications, as well as computational approaches for predicting chemical shifts and nucleic acid structures, can be used to determine structures for nucleic acid ESs at various degrees of resolution. These approaches are generally applicable, and can be used in conjunction with CPMG and CEST experiments as well.
7.1. Inferring base pairing and secondary structure from chemical shift fingerprints
Most if not all ESs in nucleic acids characterized to date involve changes in base pairing or secondary structure. The need to break one or two BPs during the transition explains why they occur on the slow micro-to-millisecond timescale. The set of chemical shifts measured for a given ES constitutes a ‘fingerprint’, which can be used to infer various aspects of its base pairing and secondary structure. Key to this approach are recent improvements in our understanding of chemical shift-structure relationships in nucleic acids (reviewed in Chi et al.[238]). The 13C chemical shifts primarily depend on the base and sugar conformation[239–248], whereas the 15N chemical shifts primarily report on base pairing and hydrogen bonding[240, 249–255], respectively. Below, we review how these dependencies of chemical shifts on structure give rise to chemical shift fingerprints that can aid structural elucidation of nucleic acid ESs.
Nucleic acids are primarily composed of canonical Watson-Crick A-T/U and G-C BPs in A-form RNA and B-form DNA helices, respectively. G-C and A-T/U Watson-Crick BPs that are sandwiched between other Watson-Crick BPs have characteristic 13C and 15N chemical shifts that fall within a narrow spectral region[9], owing to their well defined and regular geometry characterized by canonical values for the backbone torsion angles (anti χ, α~300°, β~180°, γ~60°, ε~210°, ζ~270°) and sugar pucker (C3′-endo in RNA & primarily C2′-endo in DNA) (Fig. 34A). These chemical shift fingerprints can readily be used to infer whether transitions toward an ES entail creation or loss of Watson-Crick BPs.
Figure 34.
Chemical shift/structure relationships in nucleic acids can aid structural elucidation of ESs. A) Scatter plot of 13C chemical shifts obtained from the BMRB for different secondary structure contexts in RNA (Watson-Crick BPs in A-form helices: black; nucleotides in bulges, internal or apical loops: gold; syn bases: blue). B) Distribution of 1H and 15N chemical shifts for U-N3 and G-N1 as a function of the BP type (G-C Watson-Crick BPs: red; U-A Watson-Crick BPs: blue; G-U wobbles: purple; U-G and U-U wobbles: green; sheared G-A mispairs: orange, with the base whose shifts are shown being colored), as obtained from the BMRB. C) Correlation between the C1′ and C4′ chemical shifts in RNA as obtained from a survey of the BMRB for nucleotides in different structural contexts (helical: blue; non-helical: orange; flanking,i.e., helical BP neighboring loops or bulges: green). Black lines correspond to the upper boundaries for C3′-endo sugar chemical shifts as obtained based on the average and standard deviation of the chemical shifts for helical nucleotides.(A) and (B) were reprinted with permission from [9] while (C) was reproduced with permission from [166].
On the other hand, nucleotides not involved in Watson-Crick pairing have chemical shifts that differ from canonical Watson-Crick BPs for at least a subset of 13C and 15N spins. For example, Hoogsteen BPs such as G(syn)-C+(anti), A(syn)-T/U(anti), and G(syn)-G(anti), G(syn)A+(anti) and G(anti)-A(syn) have and values for the syn nucleotide, that are shifted downfield by 1 – 4 ppm relative to Watson-Crick BPs[17, 235]. Furthermore, many mismatches such as A(anti)+-C(anti), A(anti)+-G(syn), G(syn)-C+(anti), and C(anti)-C(anti)+ have protonated bases with , , , and relative to their non-protonated counterparts[17, 235, 253, 256]. Rare tautomeric and anionic forms of the bases which occur for example in Watson-Crick-like mismatches such as Genol-T/U, GTenol/Uenol and G-T−/U−[257], feature and , and and relative to bases in their canonical tautomeric and ionic forms[165, 195, 197]. The imino 15N chemical shifts are also sensitive to changes in base pairing, with upfield shifts in T/UN3 and G-N1 occurring upon transitions of Watson-Crick A-T/U or G-C BPs to mismatches such as T/U-G, T/U-T/U and G-T/U[9] (Fig. 34B). Unpaired nucleotides in DNA and RNA also have characteristic chemical shifts relative to their duplex counterparts, particularly for the sugar 13C (C1′, C3′, and C4′) due to changes in sugar pucker[166, 239, 244–247] away from canonical C2′endo and C3′-endo geometries respectively (see below) as well as 1D6D8 angles. This may also be accompanied by changes in the base 13C chemical shifts (C6/C8) due to changes in stacking and χ angle[239–243].
In general, C3′-endo sugars in RNA helices have downfield shifted ωC1′ and upfield shifted ωC4′ relative to C2′-endo sugars, which typically occur in non-helical residues such as in bulges, and which tend to have upfield shifted ωC1′ and downfield shifted ωC4′[166, 240, 242, 244, 247] (Fig. 34C). In RNA, changes in sugar pucker are frequently accompanied by coupled changes in χ angle[258] that also influence ωC1′. In some cases, these changes can be compensatory leading to small changes in ωC1′, and consequently, to a lack of observable RD[166]. This shows how the absence of detectable RD for a particular spin cannot be taken as evidence for the absence of chemical exchange. This also underscores the importance of characterizing the conformation of the ES using as many chemical shift probes as possible, in addition to highlighting potential pitfalls of inferring structural changes based on a limited set of RD measurements. In DNA, C3′-endo sugars have and relative to C2′-endo sugars[239, 240, 245, 246].
R1ρ(1H) experiments[222] make it possible to measure 1H chemical shifts that provide information regarding the ES structure that is complementary to 13C and 15N chemical shifts. Proton chemical shifts are sensitive to ring-currents and magnetic anisotropy effects and therefore stacking and χ angles[238]. When combined with empirical tools to predict 1H chemical shifts based on structure[259–261] and sequence[262, 263], it is likely that proton chemical shifts will be extensively used in the future to help determine the structures of nucleic acid ESs.
Based on the above chemical shift-structure relationships, chemical shift fingerprints (Fig. 35A) can be used to obtain insights into structural features of ESs, and guide the development of structural models for the ES, which can range from localized changes in pairing at an individual BP, to more concerted changes in base pairing that lead to changes in secondary structure as is often observed in RNA[16, 264]. Inferring possible structures for such RNA ESs is greatly aided by secondary structure prediction programs such as Mfold[265] and MC-Fold[266], which can be used to generate a list of putative ES secondary structures ranked according to their predicted free energies[16, 264]. While the lowest energy structures typically correspond to the GS, RNA ESs frequently appear as higher energy structures that form through reshuffling of at least one BP. These putative ES structures are examined for their ability to explain the observed chemical shift fingerprints at sites where conformational changes occur, as well as the absence of RD at sites where little or no conformational change is expected.
Figure 35.
Probing base pairing in nucleic acid ESs using mutations or chemical modifications designed to stabilize the ES relative to the GS. A) Secondary structure of HIV-1 TAR RNA with the values obtained from off-resonance R1ρ RD experiments[16, 166, 264], color-coded for ES1 and ES2. White circles correspond to sites where no RD was observed. B) Kinetic network of chemical exchange for HIV-1 TAR with ES1 and ES2[16, 264]. Regions undergoing structural changes when transforming into the ES are indicated in red. The exchange rates and populations shown were obtained using NMR RD measurements[16, 264]. Mutations used for stabilizing the ESs are indicated in green. C) Secondary structure of the G28U mutant of HIV-1 TAR in the GS and ES2 conformations. The mutation site is highlighted in red. D)Correlation between , the chemical shift difference between the indicated mutant and unmodified HIV-1 TAR and , the change in chemical shift obtained using RD measurements on unmodified HIV-1 TAR, monitoring the GS to ES2 exchange[16, 264]. Vertical line of points at correspond to resonances where RD was flat and was assumed to be equal to zero. E) m1A and m1G disrupt Watson-Crick base pairing and create an energetic bias towards the formation of Hoogsteen BPs in DNA. In panels (B) and (C) Watson-Crick BPs and G-U mismatches are indicated using thick lines while thin lines correspond to all other mismatches.
7.2. Using chemical and environmental perturbations to determine the structure and function of excited states in nucleic acids
Once generated, a putative ES model is subjected to experimental tests. This involves testing predictions about the impact of mutations, modifications or changes in experimental conditions that bias the system toward or away from the ES. These predictions are then tested experimentally using chemical shift or RD measurements. As ESs are typically destabilized relative to the GS by < 4 kcal/mol or 17 kJ/mol, it often proves feasible to invert the GS-ES equilibrium and achieve pES > 50 % through single nucleotide or atom substitutions[16, 31, 116, 264, 267, 268]. This can be achieved by stabilizing the ES, destabilizing the GS, or both.
7.2.1. Stabilizing the excited state relative to the ground state by mutations or chemical modifications
If a putative ES model is accurate, one would predict that a mutation or modification stabilizing an ES would cause changes in chemical shifts throughout the RNA at sites with significant RD, resulting in chemical shifts for the mutant that are similar to those measured for the ES using RD measurements in the parent wild-type RNA. Equally important, the mutation/modification should minimally induce changes in chemical shifts for sites that do not show any RD. In addition to verifying the putative ES model, mutations/modifications provide a means by which to verify whether or not an exchange process involving multiple spins is indeed concerted. This is important because similar pES and kex amongst various spins cannot be taken as definitive evidence for a concerted exchange process as various segments in a molecule may undergo transitions independently, yet have similar exchange parameters by chance. In the latter case, one would expect that mutations/modifications would lead to local stabilization of a given segment without affecting other segments. On the other hand, for a cooperative process, the mutation/modification would affect spins in multiple segments. In this manner, mutations and modifications can provide insights into the cooperativity of conformational transitions.
A general strategy for stabilizing the ES relative to the GS is to convert non-canonical mismatches unique to the ES into more stable canonical Watson-Crick BPs while simultaneously converting canonical Watson-Crick BPs in the GS into non-canonical mismatches[9, 16, 264]. For example, in HIV-1 TAR, an ES could be stabilized by a G28U point substitution mutation, which replaces the G28-A35 BP in the ES with a more stable U28-A35 BP while at the same time replacing the G28-C37 BP in the GS with a less stable U28-C37 BP[264] (Fig. 35B, 35C). 2D NOESY-based distances confirm that the G28U mutant folds into the predicted ES2-like secondary structure[264]. The chemical shifts measured for the G28U mutant were found to be in good agreement with those measured for ES2 in HIV-1 TAR using R1ρ (Fig. 35D). In addition, only small differences in chemical shifts were observed for several sites that do not show any RD (e.g. U42-N3 and A22-C8)[264]. The fact that a single point substitution mutation in the upper helix changed the conformation of remotely positioned nucleotides in the bulge such as U23, provides independent support for a concerted transition, in which all BPs are reshuffled in going from the GS to ES2.
ES structures can also be stabilized using commercially available chemical modifications. For example, the definitive confirmation that a Hoogsteen BPs in duplex DNA was the ES detected by R1ρ came with the use of N1-methyl adenosine (m1A) and N1-methyl guanosine (m1G) modifications, to induce Hoogsteen BPs at specific sites within DNA duplexes[17, 116]. m1A and m1G sterically block Watson-Crick type hydrogen-bonding and knock out one hydrogen bond in the Watson-Crick BP without significantly affecting the stability of the Hoogsteen BP (Fig. 35E). The modified nucleotides formed the expected Hoogsteen BPs as verified by 2D NOESY without affecting Watson-Crick base pairing at neighboring sites, which is expected if the Watson-Crick to Hoogsteen transitions occur independently of one another[17, 116]. The chemical shifts of the m1A and m1G modified duplexes were in excellent agreement with those measured by RD on the C1′ and C6/C8 atoms, and Density Functional Theory (DFT) calculations[17]. Moreover, the m1A and m1G mutants revealed that other resonances should experience large chemical shift perturbations due to formation of Hoogsteen BPs, including upfield shifted 15N signals in imino guanine-N1 and thymine-N3, due to changes in hydrogen bonding[112], and changes in sugar 13C signals (adenine and guanine C3′ and C4′, and thymine and cytosine C3′) indicative of changes in sugar pucker[117]. These predictions were confirmed in subsequent studies in which R1ρ RD were used to measure the ES chemical shifts at these new sites[112, 117]. Once again, no RD was observed for 13C signals (e.g. thymine and cytosine C4′) showing small chemical shift perturbations in the m1A and m1G mutants[117].
An ES stabilizing mutant is not expected to reproduce all ES chemical shifts, especially for residues near the mutation site, and in many cases more than one mutant will be required to verify different aspects of the ES structure[16, 264]. Returning to the G28U mutant mimic of ES2 in TAR, differences as large as 1.5 ppm for C1′ and N1 were observed near the site of the mutation[264] (Fig. 35D). As this mutant replaces tandem G-A mismatches in ES2 with a single G-A mismatch and a Watson-Crick BP, it is likely to alter the structure around these sites. Much better agreement for the G-A mismatch chemical shifts was obtained with a second mutant (ES2uucg) that retains the tandem G-A mismatches[269] (Fig. 35B, D). Likewise, in the case of ES Hoogsteen BPs, the m1A modification introduces a positive charge to the base, and consequently, the m1A-C8 chemical shift was downfield-shifted more significantly than in the ES Hoogsteen BP[17, 116]. The A-C8 chemical shifts measured for an A-T Hoogsteen BPs stabilized using a drug were found to be in better agreement with those measured by RD[17, 270].
7.2.2. Destabilizing the excited state relative to the ground state by mutations or chemical modifications
Putative ES models can also be tested by introducing mutations or modifications that are predicted to destabilize the ES relative to the GS, reducing pES, or even making the ES invisible to RD detection. Returning to the TAR example, ES2 could be destabilized by replacing the wild-type apical loop with a UUCG apical loop (Fig. 36A). This mutation quenched RD at all sites sensitive to ES2 including sites within the bulge that are distant from the mutation site[264].
Figure 36.
Probing the structure of nucleic acid ESs using mutations or chemical modifications designed to stabilize the GS relative to the ES. A) Replacement of the HIV-1 TAR apical loop with a UUCG tetraloop destabilizes ES2[264]. B) N6,6-dimethyl adenine (m6,6A) disrupts base pairing of adenine via the Watson-Crick face in RNA, thereby shifting the GS-ES1 equilibrium in HIV-1 TAR towards the GS[16], in which A35 is unpaired. C) N7-deaza guanine and adenine disrupt Hoogsteen hydrogen bonding and bias A-T and G-C BPs towards the native Watson-Crick conformation[112]. D) Inosine disrupts hydrogen bonding involving the Guanine amino group thereby destabilizing Watson-Crick-like mismatched BPs[165]. In all cases, modifications are highlighted in red. In panels (A) and (B) Watson-Crick BPs and G-U mismatches in the secondary structures are indicated using thick lines while thin lines correspond to all other mismatches.
The chemical modification N6,N6-dimethyl substituted adenine (m6,6A), which blocks interactions of adenine at the Watson-Crick face was used to disrupt an A-C mismatch that forms in TAR ES1 (Fig. 35B), favoring instead the conformation where adenine bulges out as observed in the GS[16] (Fig. 36B). As ES1 is in fast exchange and is highly populated (pES = 13 %), the m6,6A mutant showed perturbations in the chemical shifts towards the GS at sites showing RD for ES1[16].
Destabilizing a putative ES structure also provides a powerful strategy to test hydrogen bonding that is unique to the ES. For example, if Hoogsteen BPs in DNA were indeed stabilized by hydrogen bonds involving purine-N7, replacement of N7 with C7 (N7-deaza-purines, c7A and c7G) should significantly destabilize the BP[112] (Fig. 36C). Indeed, N7-deaza-purines quenched Watson-Crick to Hoogsteen RD in DNA selectively at the modified BP without affecting Watson-Crick to Hoogsteen exchange at neighboring sites[112]. As a second example, inosine was used to show that ES Watson-Crick-like G-T mismatches were hydrogen bonded in a Watson-Crick-like fashion[165] (Fig. 36D). Removal of the exocyclic amino group was predicted to destabilize ES Watson-Crick-like mismatches by 1–2 kcal/mol or 4–8 kJ/mol, pushing them beyond the limit of detection of R1ρ RD experiments, as was verified experimentally[165].
7.2.3. Stabilizing the ground or excited states by changing experimental conditions
Changing pH or temperature provides an alternative means for testing putative ES models. Many ESs feature the formation of BPs that are stabilized by base protonation or deprotonation such as A+(anti)-C(anti), A+(anti)-G(syn), and G(syn)-C+(anti), while examples of deprotonated BPs include Watson-Crick-like G-T−/U− mismatches. Insights into the appearance or loss of such BPs upon formation of an ES can be obtained from pH-dependent RD measurements. For example, in the case of TAR ES1, decreasing the pH increased the population of ES1, supporting the interpretation that ES1 contained a protonated A+-C BP[16]. The pH dependence of RD measurements was also used to resolve anionic Watson-Crick-like G-T− (in DNA) and G-U− (in RNA) mismatches from their tautomeric counterparts (Genol-T/U and G-Tenol/Uenol) based on the observed increase in pES with increasing pH (Section 8.2). In contrast, the population of the tautomeric ES (Genol-T/U and G-Tenol/Uenol) was found to be independent of pH, consistent with a tautomeric species. Changes in pH were also used to stabilize the structure of an ES of U6RNA[135] and the Murine Leukemia Virus pseudoknot[267], both of which involved the formation of A-C+ BPs.
Changing the temperature can also help to resolve RD contributions from two distinct exchange processes. For example, in the case of HIV-1 TAR, the Rex contribution from a fast exchange process involving ES1 could be diminished by increasing the temperature, allowing better resolution of a second and slower exchange process involving ES2[264].
Lastly, for the case of exchange scenarios where one is monitoring binding equilibria, it is feasible to bias the equilibrium towards the bound or free conformation by altering the concentrations of the binding partners, so as to obtain their chemical shifts[32, 78, 79].
7.3. Solving high-resolution structures and dynamic ensembles for excited states in nucleic acids
Once validated, high resolution structures or dynamic ensembles can be obtained for a given ES-mutant and be used as high-resolution models for the ES conformation[117]. While this is a potentially general strategy for determining structures of ESs in nucleic acids, a number of precautions have to be taken. First, care must be taken to validate the mutant that stabilizes the ES using a large number of R1ρ measurements on a variety of spins. Second, the structure or dynamic ensemble of the ES mutant determined using NOEs and/or RDCs should be further validated for its ability to independently predict additional experimental data such as the ES chemical shifts.
The above approach has been applied to determine the first atomic resolution structure of a nucleic acid ES, in particular Hoogsteen BPs in two different DNA duplexes, using m1A to stabilize the Hoogsteen conformation[117] (Fig. 35E). The m1A mutant was validated based on the excellent agreement observed between its chemical shifts and those measured for the ES using RD for a variety of base and sugar spins (Fig. 37A). Dynamic structural ensembles (Fig. 37C) were determined for the m1A-T mutants and the corresponding unmodified duplexes[116] using RDCs and computational molecular dynamics simulations[271–274]. An Automated Fragmentation Quantum Mechanics/Molecular mechanics approach[275] was then used to predict chemical shifts for every conformer in the ensembles of the m1A-T mutant as well as the unmodified DNA[117]. The computed chemical shifts were averaged over the ensembles and the differences between the GS and ES chemical shifts thus computed (ΔωEns) were compared to values obtained using RD (ΔωRD). Excellent agreement was observed between the ΔωEns and ΔωRD values (Fig. 37B), thus validating the generated ensembles. This also made it possible to rationalize the unique chemical shift signatures associated with the ES in terms of structural features[117].
Figure 37.
High-resolution structural characterization of ES Hoogsteen BPs in B-DNA.A) Validation of the ES mutant (m1A) using an extensive set of chemical shifts. Shown is a representative example of A6-DNA (secondary structure on the left), with the site of m1A16 modification to trap Hoogsteen BPs indicated in red. Correlation between (the chemical shift difference between the Hoogsteen-stabilizing A6-DNAm1A16 and unmodified A6-DNA duplex), and values obtained from R1ρ RD measurements on unmodified A6-DNA, monitoring the Watson-Crick to Hoogsteen exchange at A16. B) Correlation between , the calculated chemical shift difference between the ensembles of the A6-DNAm1A16 and A6-DNA duplexes, and (C) Dynamic ensembles for A6-DNA (green, left) and A6-DNAm1A16 (red, right) obtained as described by Al-Hashimi et al.[116]. The average inter-helical kink angle β, obtained from an Euler angle analysis[296, 297] is also indicated. In panels A and B, two RMSD and R values are shown. The first value is calculated with the inclusion of all the resonances for which RD was measured, while the second value is calculated excluding data with flat RD where was assumed to be zero. Reprinted by permission from [117].
The above strategy can in principle be extended to RNA, for which there is a growing number of tools for predicting 13C/15N chemical shifts based on 3D structures[259, 276]. In addition, even prior to the above study, methods had been developed to solve ES structures of proteins that involve measuring direct structural restraints, such as residual dipolar coupings (RDCs)[277–279], residual chemical shift anisotropies (RCSAs)[280], as well as paramagnetic relaxation enhancements (PREs)[281]. Building on these applications, CEST approaches have recently been developed to measure RDCs for nucleic acid ESs[170]. These approaches can readily be extended in the future to measure ES RCSAs in nucleic acids[282, 283]. These new types of data could be used in the future in conjunction with the mutation strategy described above to robustly determine structures and dynamic ensembles for nucleic acid ESs.
7.4. Using mutations to assess the biological functions of excited states in nucleic acids
Importantly, GS or ES stabilizing mutants can also be used in functional assays to assess the biological importance of the ES[16, 284]. For example, a mutation that destabilizes an ES in the HIV-1 Stem Loop 1 (SL1) was shown to impede duplex dimerization, implying that the ES plays a role for nucleating the transition[16]. More recently, ES-mutants of HIV-1 TAR were used in cell-based experiments to show that the non-native conformation disrupts transactivation[284]. Key to this assessment was the use of subsequent “rescue mutations” that push the ES-GS equilibrium to favor the GS; such mutations reinforce the fact that changes in conformation, rather than changes in sequence due to the mutations themelves, are responsible for the observed biological response.
8. Examples of applications of 1D selective R1ρ relaxation dispersion for the analysis of chemical exchange in nucleic acids
In this section, we review examples of applications of R1ρ RD to the study of chemical exchange in nucleic acids that illustrate the different types of motions characterized to date and their biological implications.
8.1. Watson-Crick to Hoogsteen exchange in DNA and RNA duplexes
As stated throughout this review, application of off-resonance R1ρ RD methodology resulted in the discovery that in the DNA double-helix, A-T and G-C Watson-Crick BPs continually undergo exchange with their Hoogsteen counterparts. Based on these studies, at any given point in time, ~1% and ~0.1% of A-T and G-C BPs in the DNA double helix are Hoogsteen rather than Watson-Crick BPs. This implies that at any given point in time, there could potentially be tens of millions of Hoogsteen BPs in the human genome. In vivo, DNA experiences supercoiling, torsional stress, under-winding, and stretching as it wraps around histones to form nucleosomes. Hoogsteen BPs could provide mechanisms for stabilizing such stressed structures of highly compacted DNA. Furthermore, in addition to the currently known proteins such as p53 that bind to Hoogsteen BPs, other proteins may also promote or recognize Hoogsteen BPs when binding to DNA[114]. Indeed, drugs have been shown to bind duplex DNA and to induce dramatic changes in the Hoogsteen breathing dynamics[270]. We are today still in the early stages of examining the occurrence and biological significance of Hoogsteen BPs in DNA.
In sharp contrast to B-DNA, transient Hoogsteen BPs were not detected in A-RNA duplexes using R1ρ RD[235]. It was later shown that Hoogsteen BPs are less stable in A-RNA because syn purine bases are sterically disfavored in the A-form conformation, and because there is a greater energetic cost associated with constricting the backbone to form Hoogsteen type hydrogen bonds in A-RNA relative to that in B-DNA[285]. The markedly different propensities to accommodate Hoogsteen BPs in RNA and DNA duplexes is another important difference between the two nucleic acid polymers, in addition to the presence or absence of the 2′-hydroxyl group. The ability to absorb chemical damage at the Watson-Crick face by forming Hoogsteen BPs makes DNA a better custodian of genetic information and may represent one of the evolutionary pressures that resulted in B-DNA becoming the main carrier of genetic information in higher-order organisms[235]. On the other hand, the inability of A-RNA to accommodate Hoogsteen BPs explains how post-transcriptional modifications such as m1A and m1G can markedly influence RNA folding and function[235].
8.2. Exchange between wobble and Watson-Crick-like tautomeric and anionic G-T/U base pairs in DNA and RNA duplexes
Watson-Crick to Hoogsteen exchange converts canonical Watson-Crick G-C and A-T BPs into non-canonical Hoogsteen conformations. R1ρ studies have also uncovered an inverse process in which non-canonical G-T/U wobble mismatches are converted into canonical Watson-Crick-like BPs stabilized by rare tautomeric and anionic forms of the bases[165, 195, 197] (Fig. 38A). In contrast to Hoogsteen transitions, this exchange process occurs in both BDNA and A-RNA duplexes. By adopting conformations similar to Watson-Crick BPs, these ESs can evade fidelity checkpoints and contribute to errors during replication, transcription, and translation[286, 287]. These rare tautomeric bases were originally proposed as a potential source of replication errors by Watson and Crick in 1954, who outlined analogous tautomeric BPs in the case of the A-C mismatch[288].
Figure 38.
Watson-Crick-like G-T mismatches and their roles in generating spontaneous mutations during DNA replication. A) Kinetic topology for transforming between G-T/U wobble mismatches and their Watson-Crick-like counterparts formed via tautomerization or ionization. The exchange rates shown were obtained using NMR RD measurements[195, 197]. B) Minimal kinetic model for Watson-Crick BP incorporation by DNA polymerases. The incorporation of a G-T mismatch requires in addition, as shown in the lower pathway, a tautomerization or ionization step allowing for the formation of a Watson-Crick-like species.(Bottom left) Histograms showing Fpol, the fidelity of dTTP/5BrdUTP mis-incorporation errors catalyzed by Alfalfa Mosaic Virus Reverse Transcriptase (AMV RT) as computed using kinetic simulations allowing incorporation of tautomeric (blue, MES1), ionic (green, MES2) or both (orange, MES1 + MES2) Watson-Crick-like excited states, and experimentally measured values (gray).(Bottom right) Measured and simulated rates (kobs) of mis-incorporation for dTTP/5BrdUTP catalyzed by human DNA polymerase β. Reprinted by permission from [195].
A kinetic model for the generation of errors during DNA replication constructed using the rate constants of the formation of Watson-Crick-like BPs measured by NMR could predict the frequency of G-T mis-incorporation across a wide range of pH, polymerases, and modified mutagenic bases[195] (Fig. 38B). Likewise, the uridine 5-oxyacetic acid (cmo5U) modification found in tRNA was recently shown to bias the G-cmo5U ensemble toward anionic Watson-Cricklike conformations, potentially explaining how the modification “reprograms” translation[289]. Taken together, these studies suggest that Watson-Crick-like ESs provide a general mechanism to explain the generation of errors and re-writing of information transfer in every step of the central dogma of molecular biology.
8.3. Exchange between alternative secondary structures in RNA
RNA molecules can form ESs that dramatically alter their secondary structure. Fig. 39 shows different types of ESs in RNA that have been characterized to date using off-resonance R1ρ RD methods[16, 164]. Functions are beginning to emerge for many of these ESs in RNA. For example, as mentioned previously in the context of HIV-1 SL1[16], RNA ESs appear to provide means by which to break down large conformational transitions into multiple kinetically labile microscopic steps[290]. A similar mechanism has been proposed for an ES in P5abc, which is proposed to form an intermediate during tertiary folding[164]. RNA ESs characterized by other RD methods have also been shown to play important roles in gene regulation[31] and in ligand binding[32, 78, 79].
Figure 39.
RNA ESs feature localized changes in secondary structure. Shown are the secondary structures of ES determined for A) bacterial A-site, B) p5abc and C) HIV-SL1 using selective 1D R1ρ RD measurements. The part of the ES undergoing structural changes on transforming from the GS is indicated in red. Thick lines correspond to Watson-Crick BPs and G-U mismatches, whereas thin lines denote other non-canonical mispairing. The populations of the states and the rate constants for GS-ES exchange, as obtained using R1ρ RD measurements[9, 16] are also shown.
As they remodel structure and disrupt biological activity, RNA ESs are proposed as opportune targets for the development of RNA-targeted therapeutics[16]. In addition, there is mounting evidence that the mechanism underlying the disease phenotype of many single nucleotide polymorphisms (SNPs) involves changes in RNA ensembles by stabilizing alternative ES conformations[291 – 293]. Future studies of ESs in RNA will undoubtedly clarify their potential roles in biology and disease.
9. Conclusions
Since the earliest studies of chemical exchange in DNA in the late 1980s, the R1ρ RD methodology has matured significantly during the past four decades to the point that it can now be routinely applied to characterize ESs in DNA and RNA. These advances coupled to development of CEST[28, 31] as well as CPMG[18, 136, 174, 294] methodology have opened the door to a world of previously unknown dynamics in DNA and RNA that play essential roles in gene expression and regulation. Central to these developments are experiments for accurately measuring RD data for a variety of spins in uniformly 13C/15N labeled samples over a range of spin-lock amplitudes, using mutations and chemical modifications to stabilize or destabilize ESs relative to the GS, an improved understanding of chemical-shift/structure relationships in nucleic acids, as well as advances in predicting nucleic acid chemical shifts based on 3D structure. Existing methods can immediately be applied to study the dynamics in higher-order DNA structures (e.g. quadruplexes, triplexes etc.)[295] and in RNAs ranging from simple singlestrands[199] to RNAs with complex tertiary folds[31, 164]. We can also anticipate advances that extend the methodology in the future to allow studies of dynamics in larger RNAs and DNAs and their complexes with proteins, and provide additional structural and dynamic information regarding ESs. We hope that this review will provide a useful resource for these future studies.
Supplementary Material
Highlights.
Historical account of NMR RD with a focus on nucleic acid R1ρ is presented
A vector model is used to conceptually understand R1ρ RD
Approaches for fitting, simulating and visualizing R1ρ data are described
Application of R1ρ RD to study complex three-state exchange scenarios are examined
Strategies for determining structures of nucleic acid ESs are reviewed
Acknowledgements
We thank Zachary Stein for fruitful discussions as well as other members of the Al-Hashimi laboratory for critically reading the manuscript. This work was supported by the US National Institutes of Health (R01AI066975, R01GM089846) and US National Institute for General Medical Sciences (4P50GM103297, P01GM0066275) grants to H. M. A.
Glossary
- A
Adenine
- AIC
Akaike Information Criterion
- AVG
population-weighted average
- BIC
Bayesian Information Criterion
- B-M
Bloch-McConnell
- BMNS
Bloch-McConnell Numerical Simulator
- BPs
base pairs
- BPTI
Bovine Pancreatic Trypsin Inhibitor
- C
Cytosine
- CEST
Chemical Exchange Saturation Transfer
- cmo5U
Uridine 5-oxyacetic acid
- CP
cross polarization
- CPMG
Carr-Purcell-Meiboom-Gill
- CSA
Chemical Shift Anisotropy
- c7A
N7-deaza adenosine
- c7G
N7-deaza guanosine
- DD/CSA
Dipole-Dipole CSA cross-correlated relaxation
- DD/DD
Dipole-dipole cross-correlated relaxation
- DNA
Deoxyribonucleic acid
- ES
Excited State
- ES1/ES2
Excited State 1/Excited State 2
- G
Guanine
- GS
Ground State
- HMQC
Heteronuclear Multiple Quantum Coherence
- HSQC
Heteronuclear Single Quantum Coherence
- I
Inosine
- ms
millisecond
- m1A
N1-methyl adenosine
- m1G
N1-methyl guanosine
- m6,6A
N6,N6-dimethyl adenine
- NMR
Nuclear Magnetic Resonance
- NOE
Nuclear Overhauser Effect
- ns
nanosecond
- NTP
nucleotide tri-phosphate
- OBS
observed
- ps
picosecond
- RCSA
Residual Chemical Shift Anisotropy
- RD
Relaxation Dispersion
- RDC
Residual Dipolar Coupling
- RF
Radio Frequency
- RNA
Ribonucleic acid
- RSS
residual sum of squares
- SH3
SRC Homology Domain 3
- SL1
Stem Loop 1
- T
Thymine
- TROSY
Transverse Relaxation Optimized Spectroscopy
- TS
Transition State
- U
Uracil
- ROESY
Rotating frame Overhauser Spectroscopy
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
Hashim M. Al-Hashimi (H.M.A.) is an advisor to and holds an ownership interest in Nymirum Inc., which is an RNA-based drug discovery company. The research reported in this article was performed by Duke University faculty and students and was funded by NIH and NIGMS contracts to H.M.A.
Dedication: This review is dedicated to Prof. James H. Prestegard on the occasion of his 75th birthday
References
- [1].Watson JD, Crick FHC, A Structure for Deoxyribose Nucleic Acid, Nature, 171 (1953) 737–738. [DOI] [PubMed] [Google Scholar]
- [2].Bardaro MF Jr., Varani G, Examining the relationship between RNA function and motion using nuclear magnetic resonance, Wiley interdisciplinary reviews. RNA, 3 (2012) 122–132. [DOI] [PubMed] [Google Scholar]
- [3].Rinnenthal J, Buck J, Ferner J, Wacker A, Furtig B, Schwalbe H, Mapping the landscape of RNA dynamics with NMR spectroscopy, Accounts of chemical research, 44 (2011) 1292–1301. [DOI] [PubMed] [Google Scholar]
- [4].Bothe JR, Nikolova EN, Eichhorn CD, Chugh J, Hansen AL, Al-Hashimi HM, Characterizing RNA dynamics at atomic resolution using solution-state NMR spectroscopy, Nature methods, 8 (2011) 919–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Palmer AG 3rd, Chemical exchange in biomacromolecules: Past, present, and future, Journal of magnetic resonance (San Diego, Calif. : 1997), 241 (2014) 3–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Mittermaier A, Kay LE, New tools provide new insights in NMR studies of protein dynamics, Science (New York, N.Y.), 312 (2006) 224–228. [DOI] [PubMed] [Google Scholar]
- [7].Getz MM, Andrews AJ, Fierke CA, Al-Hashimi HM, Structural plasticity and Mg2+ binding properties of RNase P P4 from combined analysis of NMR residual dipolar couplings and motionally decoupled spin relaxation, RNA (New York, N.Y.), (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Shajani Z, Varani G, NMR studies of dynamics in RNA and DNA by (13)C relaxation, Biopolymers, 86 (2007) 348–359. [DOI] [PubMed] [Google Scholar]
- [9].Xue Y, Kellogg D, Kimsey IJ, Sathyamoorthy B, Stein ZW, McBrairty M, Al-Hashimi HM, Characterizing RNA Excited States Using NMR Relaxation Dispersion, Methods in enzymology, 558 (2015) 39–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Salmon L, Yang S, Al-Hashimi HM, Advances in the Determination of Nucleic Acid Conformational Ensembles, Annual review of physical chemistry, 65(1) (2013) 293–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Dethoff EA, Chugh J, Mustoe AM, Al-Hashimi HM, Functional complexity and regulation through RNA dynamics, Nature, 482 (2012) 322–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Mustoe AM, Brooks CL, Al-Hashimi HM, Hierarchy of RNA functional dynamics, Annual review of biochemistry, 83 (2014) 441–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Palmer AG 3rd, Massi F, Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy, Chemical reviews, 106 (2006) 1700–1719. [DOI] [PubMed] [Google Scholar]
- [14].Palmer AG, Chemical Exchange Effects in Biological Macromolecules, eMagRes, (2007). [Google Scholar]
- [15].Mulder FA, Mittermaier A, Hon B, Dahlquist FW, Kay LE, Studying excited states of proteins by NMR spectroscopy, Nature structural biology, 8 (2001) 932–935. [DOI] [PubMed] [Google Scholar]
- [16].Dethoff EA, Petzold K, Chugh J, Casiano-Negroni A, Al-Hashimi HM, Visualizing transient low-populated structures of RNA, Nature, 491 (2012) 724–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Nikolova EN, Kim E, Wise AA, O’Brien PJ, Andricioaei I, Al-Hashimi HM, Transient Hoogsteen base pairs in canonical duplex DNA, Nature, 470 (2011) 498–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Strebitzer E, Nussbaumer F, Kremser J, Tollinger M, Kreutz C, Studying sparsely populated conformational states in RNA combining chemical synthesis and solution NMR spectroscopy, Methods (San Diego, Calif.), 148 (2018) 39–47. [DOI] [PubMed] [Google Scholar]
- [19].Carr HY, Purcell EM, Effects of Diffusion on Free Precession in Nuclear Magnetic Resonance Experiments, Phys. Rev, 94 (1954) 630–638. [Google Scholar]
- [20].Meiboom S, Gill D, Modified Spin-Echo Method for Measuring Nuclear Relaxation Times, Rev. Sci. Instrum, 29 (1958) 688–691. [Google Scholar]
- [21].Hansen AL, Nikolova EN, Casiano-Negroni A, Al-Hashimi HM, Extending the range of microsecond-to-millisecond chemical exchange detected in labeled and unlabeled nucleic acids by selective carbon R(1rho) NMR spectroscopy, Journal of the American Chemical Society, 131 (2009) 3818–3819. [DOI] [PubMed] [Google Scholar]
- [22].Palmer AG 3rd, Kroenke CD, Loria JP, Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules, Methods in enzymology, 339 (2001) 204–238. [DOI] [PubMed] [Google Scholar]
- [23].Trott O, Palmer AG 3rd, R1rho relaxation outside of the fast-exchange limit, Journal of magnetic resonance (San Diego, Calif. : 1997), 154 (2002) 157–160. [DOI] [PubMed] [Google Scholar]
- [24].Forsen S, Hoffman R, Study of Moderately Rapid Chemical Exchange Reactions by Means of Nuclear Magnetic Double Resonance, J. Chem. Phys, 39 (1963) 2892–2901. [Google Scholar]
- [25].Fawzi NL, Ying J, Ghirlando R, Torchia DA, Clore GM, Atomic-resolution dynamics on the surface of amyloid-beta protofibrils probed by solution NMR, Nature, 480 (2011) 268–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Vallurupalli P, Bouvignies G, Kay LE, Studying “invisible” excited protein states in slow exchange with a major state conformation, Journal of the American Chemical Society, 134 (2012) 8148–8161. [DOI] [PubMed] [Google Scholar]
- [27].Long D, Bouvignies G, Kay LE, Measuring hydrogen exchange rates in invisible protein excited states, Proceedings of the National Academy of Sciences of the United States of America, 111 (2014) 8820–8825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Zhao B, Hansen AL, Zhang Q, Characterizing slow chemical exchange in nucleic acids by carbon CEST and low spin-lock field R(1rho) NMR spectroscopy, Journal of the American Chemical Society, 136 (2014) 20–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Longhini AP, LeBlanc RM, Becette O, Salguero C, Wunderlich CH, Johnson BA, D’Souza VM, Kreutz C, Dayie TK, Chemo-enzymatic synthesis of site-specific isotopically labeled nucleotides for use in NMR resonance assignment, dynamics and structural characterizations, Nucleic acids research, 44 (2016) e52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Roy S, Lammert H, Hayes RL, Chen B, LeBlanc R, Dayie TK, Onuchic JN, Sanbonmatsu KY, A magnesium-induced triplex pre-organizes the SAM-II riboswitch, PLoS computational biology, 13 (2017) e1005406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Zhao B, Guffy SL, Williams B, Zhang Q, An excited state underlies gene regulation of a transcriptional riboswitch, Nature chemical biology, 13 (2017) 968–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Chen B, LeBlanc R, Dayie TK, SAM-II Riboswitch Samples at least Two Conformations in Solution in the Absence of Ligand: Implications for Recognition, Angewandte Chemie (International ed. in English), 55 (2016) 2724–2727. [DOI] [PubMed] [Google Scholar]
- [33].Bloch F, Hansen WW, Packard M, Nuclear Induction, Phys. Rev, 69 (1946) 127. [Google Scholar]
- [34].Purcell EM, Torrey HC, Pound RV, Resonance Absorption by Nuclear Magnetic Resonance in a Solid, Phys. Rev, 69 (1945) 37–38. [Google Scholar]
- [35].Gorter CJ, Brons F, Magnetic Inhibition of Susceptibilities at Radio Frequencies, Physica, 7 (1937) 579–584. [Google Scholar]
- [36].Gorter CJ, Paramagnetic Relaxation, Physica, 3 (1936) 503–514. [Google Scholar]
- [37].Gorter CJ, Broer LJF, Negative Result of an Attempt to Observe Nuclear Magnetic Resonance in Solids, Physica, 6 (1942) 591–596. [Google Scholar]
- [38].Gorter CJ, Negative Result of an Attempt to Detect Nuclear Magnetic Spins, Physica, 9 (1936) 995–998. [Google Scholar]
- [39].Heitler W, Wills HH, Teller E, Time Effects in the Magnetic Cooling Method-I, Proc. Roy. Soc. A, 155 (1936) 629–639. [Google Scholar]
- [40].Bloembergen N, Purcell EM, Pound RV, Relaxation Effects in Nuclear Magnetic Resonance Absorption, Phys. Rev, 73 (1948) 679–712. [Google Scholar]
- [41].Torrey HC, Transient Nutations in Nuclear Magnetic Resonance, Phys. Rev, 76 (1949) 1059–1068. [Google Scholar]
- [42].Hahn EN, An Accurate Nuclear Magnetic Resonance Method for Measuring Spin-Lattice Relaxation Times, Phys. Rev, 76 (1949) 145–146. [Google Scholar]
- [43].Drain LE, A Direct Method of Measuring Nuclear Spin-Lattice Relaxation Times, Proc Phys Soc A, 62 (1949) 301–306. [Google Scholar]
- [44].Hahn EN, Spin Echoes, Phys. Rev, 80 (1950) 580–594. [Google Scholar]
- [45].McConnell HM, REACTION RATES BY NUCLEAR MAGNETIC RESONANCE, J. Chem. Phys, 28 (1958) 430–431. [Google Scholar]
- [46].Bloch F, Phys. Rev, 70 (1946) 460–474. [Google Scholar]
- [47].Meiboom S, Luz Z, Gill D, Proton Relaxation in Water, J. Chem. Phys, 27 (1957) 1411–1412. [Google Scholar]
- [48].Grunwald E, Lowenstein A, Meiboom S, Rates and Mechanisms of Protolysis of Methylammonium Ion in Aqueous Solution Studied by Proton Magnetic Resonance, J. Chem. Phys, 27 (1957) 630–640. [Google Scholar]
- [49].Gutowsky HS, McCall DW, Slichter CP, Nuclear Magnetic Resonance Multiplets in Liquids, J. Chem. Phys, 21 (1953) 279–292. [Google Scholar]
- [50].Gutowsky HS, Saika A, Dissociation, Chemical Exchange, and the Proton Magnetic Resonance in Some Aqueous Electrolytes, J. Chem. Phys, 21 (1953) 1688–1694. [Google Scholar]
- [51].Gutowsky HS, Holm CH, Rate Processes and Nuclear Magnetic Resonance Spectra. II. Hindered Internal Rotation of Amides, J. Chem. Phys, 25 (1956) 1228–1234. [Google Scholar]
- [52].Hahn EL, Maxwell DE, Spin Echo Measurements of Nuclear Spin Coupling in Molecules, Phys. Rev, 88 (1952) 1070–1083. [Google Scholar]
- [53].Redfield AG, Nuclear Magnetic Resonance Saturation and Rotary Saturation in Solids, Phys. Rev, 98 (1955) 1787–1809. [Google Scholar]
- [54].Rabi II, Ramsey NF, Schwinger J, Use of Rotating Coordinates in Magnetic Resonance Problems, Rev. Mod. Phys, 26 (1954) 167–171. [Google Scholar]
- [55].Solomon I, Relaxation magnetique dans les liquides en Presence d’un champ de haute frequence, Compt. Rend, 249 (1959) 1631–1632. [Google Scholar]
- [56].Winter JM, Resonance Magnetique, Compt. Rend, 249 (1959) 1346–1347. [Google Scholar]
- [57].Meiboom S, Nuclear Magnetic Resonance Study of the Proton Transfer in Water, J. Chem. Phys, 34 (1961) 375–388. [Google Scholar]
- [58].Luz Z, Meiboom S, Nuclear Magnetic Resonance Study of the Protolysis of Trimethylammonium Ion in Aqueous Solution—Order of the Reaction with Respect to Solvent, J. Chem. Phys, 39 (1963) 366–370. [Google Scholar]
- [59].Luz Z, Meiboom S, The Activation Energies of Proton Transfer Reactions in Water, J. Am. Chem. Soc, 86 (1964) 4768–4769. [Google Scholar]
- [60].Forsen S, Hoffman RA, Exchange Rates by Nuclear Magnetic Multiple Resonance. III. Exchange Reactions in Systems with Several Nonequivalent Sites, J. Chem. Phys, 40 (1964) 1189–1196. [Google Scholar]
- [61].Allerhand A, Gutowsky HS, Spin—Echo NMR Studies of Chemical Exchange. I. Some General Aspects, J. Chem. Phys, 41 (1964) 2115–2126. [DOI] [PubMed] [Google Scholar]
- [62].Allerhand A, Chen F, Gutowsky HS, Spin-Echo NMR Studies of Chemical Exchange. III. Conformational Isomerization of Cyclohexane and d11-Cyclohexane, J. Chem. Phys, 3040 (1965) 3040–3047. [Google Scholar]
- [63].Deverell C, Morgan RE, Strange JH, Studies of chemical exchange by nuclear magnetic relaxation in the rotating frame, Mol. Phys, 18 (1970) 553–559. [Google Scholar]
- [64].Rhodes M, Aksness DW, Strange JH, Spin-lattice relaxation in liquid phosphorus tribromide, Mol. Phys, 15 (1968) 541–547. [Google Scholar]
- [65].Norris MO, Strange JH, Powles JG, Rhodes M, Marsden K, Krynicki K, Nuclear magnetic spin relaxation in solid solutions of hydrogen bromide in deuterium bromide, J. Phys. C: Solid State Phys, 1 (1968) 422–444. [Google Scholar]
- [66].Morgan RE, Strange JH, Measurements of scalar spin-spin coupling in liquid HCl and HBr by N.M.R. relaxation in the rotating frame, Mol. Phys, 17 (1969) 397–400. [Google Scholar]
- [67].Strange JH, Morgan RE, Nuclear magnetic interactions and molecular motion in liquids by n.m.r. relaxation in the rotating frame, J. Phys. C: Solid State Phys, 3 (1970) 1999–2011. [Google Scholar]
- [68].Stilbs P, Moseley ME, Chemical Exchange Rates from Fourier Transform Measurements of Nuclear Spin-Lattice Relaxation in the Rotating Frame. Application to Hindered Internal Rotation in Ureas, J. Magn. Reson, 31 (1978) 55–61. [Google Scholar]
- [69].Campbell ID, Dobson CM, Ratcliffe RG, Williams RJP, Fourier Transform NMR Pulse Methods for the Measurement Slow-Exchange Rates J. Magn. Reson, 29 (1978) 397–417. [Google Scholar]
- [70].Dahlquist FW, Longmuir KJ, DuVernet RB, Direct Observation of Chemical Exchange by a Selective Pulse NMR Technique, J. Magn. Reson, 17 (1975) 406–410. [Google Scholar]
- [71].Campbell ID, Dobson CM, Ratcliffe RG, Fourier Transform Proton NMR in H2O. A Method for Measuring Exchange and Relaxation Rates J. Magn. Reson, 27 (1977) 455–463. [Google Scholar]
- [72].Brown TA, Saturation transfer in living systems, Phil. Trans. R. Soc. Lond. B, 289 (1980) 441–444. [DOI] [PubMed] [Google Scholar]
- [73].Sykes BD, An Application of Transient Nuclear Magnetic Resonance Methods to the Measurement of Biological Exchange Rates. The Interaction of Trifluoroacetyl-D-phenylalanine with the Chymotrypsins, J. Am. Chem. Soc, 91 (1969) 949–955. [DOI] [PubMed] [Google Scholar]
- [74].Gerig JT, Stock AD, Studies of the Kinetics of the Interaction between N-Trifluoroacetyl-D-tryptophan and a-Chymotrypsin by Pulsed Nuclear Magnetic Resonance, Org. Magn. Reson, 7 (1975) 249–255. [Google Scholar]
- [75].Cayley PJ, Albrand JP, Feeney J, Roberts GCK, Piper EA, Burgen ASV, Nuclear Magnetic Resonance Studies of the Binding of Trimethoprim to Dihydrofolate Reductase, J. Am. Chem. Soc, 18 (1979) 3886–3895. [DOI] [PubMed] [Google Scholar]
- [76].Lee AR, Hwang J, Hur JH, Ryu KS, Kim KK, Choi BS, Kim NK, Lee JH, NMR Dynamics Study Reveals the Zalpha Domain of Human ADAR1 Associates with and Dissociates from Z-RNA more slowly than Z-DNA, ACS chemical biology, (2018). [DOI] [PubMed] [Google Scholar]
- [77].Moschen T, Grutsch S, Juen MA, Wunderlich CH, Kreutz C, Tollinger M, Measurement of Ligand-Target Residence Times by (1)H Relaxation Dispersion NMR Spectroscopy, J Med Chem, 59 (2016) 10788–10793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Wunderlich CH, Spitzer R, Santner T, Fauster K, Tollinger M, Kreutz C, Synthesis of (6-(13)C)pyrimidine nucleotides as spin-labels for RNA dynamics, Journal of the American Chemical Society, 134 (2012) 7558–7569. [DOI] [PubMed] [Google Scholar]
- [79].Moschen T, Wunderlich CH, Spitzer R, Levic J, Micura R, Tollinger M, Kreutz C, Ligand-detected relaxation dispersion NMR spectroscopy: dynamics of preQ1-RNA binding, Angewandte Chemie (International ed. in English), 54 (2015) 560–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].James TL, Matson GB, Kuntz ID, Protein Rotational Correlation Times Determined in Aqueous Solution by Carbon-13 Rotating Frame Spin-Lattice Relaxation in the Presence of an Off-Resonance Radiofrequency Field, J. Am. Chem. Soc, 100 (1978) 3590–3594. [Google Scholar]
- [81].James TL, Sawan SP, Unfolding of Ribonuclease A by Guanidinium Chloride. Protein Internal Motions Studied by Nuclear Magnetic Resonance Spin-Lattice Relaxation in an Off-Resonance Rotating Frame, J. Am. Chem. Soc, 101 (1979) 7050–7055. [Google Scholar]
- [82].Bolton PH, James TL, Molecular Motions in RNA and DNA Investigated by Phosphorus-31 and Carbon-13 NMR Relaxation, J. Phys. Chem, 83 (1979) 3359–3366. [Google Scholar]
- [83].Smith GM, Yu LP, Domingues DJ, Directly Observed 15N NMR Spectra of Uniformly Enriched Proteins, Biochemistry, 26 (1987) 2202–2207. [DOI] [PubMed] [Google Scholar]
- [84].McCain DC, Ulrich EL, Markley JL, NMR Relaxation Study of Internal Motions in Staphylococcal Nuclease, J. Magn. Resonan, 80 (1988) 296–305. [Google Scholar]
- [85].Schmidt PG, Playl T, Agris PF, Internal Dynamics of Transfer Ribonucleic Acid Determined by Nuclear Magnetic Resonance of Carbon-13-Enriched Ribose Carbon V, Biochemistry, 22 (1983) 1408–1415. [DOI] [PubMed] [Google Scholar]
- [86].Campbell ID, Dobson CM, Moore GR, Perkins SJ, Williams RJP, Temperature Dependent Molecular Motion of a Tyrosine Residue of Ferrocytochrome C, Febs Lett, 70 (1976) 96–100. [DOI] [PubMed] [Google Scholar]
- [87].Bleich HE, Glasel JA, Rotating Frame Spin-Lattice Relaxation Experiments and the Problem of Intramolecular Motions of Peptides in Solution, Biopolymers, 17 (1978) 2445–2457. [Google Scholar]
- [88].Kopple KD, Wang Y, N.m.r. studies of internal mobility in a cyclic tetrapeptide, Int. J. Peptide Protein Res, 33 (1989) 82–85. [DOI] [PubMed] [Google Scholar]
- [89].Kopple KD, Wang Y, Cheng AG, Bhandary KK, Conformations of Cyclic Octapeptides. 5. Crystal Structure of Cyclo(Cys-Gly-Pro-Phe)2 and Rotating Frame Relaxation (T1p) NMR Studies of Internal Mobility in Cyclic Octapeptides, J. Am. Chem. Soc, 110 (1988) 4168–4176. [Google Scholar]
- [90].Blackledge MJ, Bruschweiler R, Griesinger C, Schmidt JM, Xu P, Ernst RR, Conformational Backbone Dynamics of the Cyclic Decapeptide Antamanide. Application of a New Multiconformational Search Algorithm Based on NMR data, Biochemistry, 32 (1993) 10960–10974. [DOI] [PubMed] [Google Scholar]
- [91].Bothner-By AA, Stephens RL, Lee J, Warren CD, Jeanloz RW, Structure determination of a tetrasaccharide: transient nuclear Overhauser effects in the rotating frame, Journal of the American Chemical Society, 106 (1984) 811–813. [Google Scholar]
- [92].Bax A, Davis DG, Practical Aspects of Two-Dimensional Transverse NOE Spectroscopy, J. Magn. Reson, 63 (1985) 207–213. [Google Scholar]
- [93].Cavanagh J, Keeler J, Suppression of HOHAHA and “False” NOE Cross Peaks in CAMELSPIN Spectra, Journal of magnetic resonance (San Diego, Calif. : 1997), 80 (1988) 186–194. [Google Scholar]
- [94].Desvaux H, Berthault P, Birlirakis N, Goldman M, Piotto M, Improved Versions of Off-Resonance ROESY, Journal of Magnetic Resonance, Series A, 113 (1995) 47–52. [Google Scholar]
- [95].Desvaux H, Berthault P, Birlirakis N, Goldman M, Off-Resonance ROESY for the Study of Dynamic Processes, Journal of magnetic resonance (San Diego, Calif. : 1997), 108 (1994) 219–229. [Google Scholar]
- [96].Isaksson J, Zamaratski E, Maltseva TV, Agback P, Kumar A, Chattopadhyaya J, The first example of a Hoogsteen base-paired DNA duplex in dynamic equilibrium with a Watson-Crick base-paired duplex--a structural (NMR), kinetic and thermodynamic study, Journal of Biomolecular Structure & Dynamics, 18 (2001) 783–806. [DOI] [PubMed] [Google Scholar]
- [97].Boulton S, Akimoto M, Akbarizadeh S, Melacini G, Free energy landscape remodeling of the cardiac pacemaker channel explains the molecular basis of familial sinus bradycardia, J Biol Chem, 292 (2017) 6414–6428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98].Maltseva TV, Yamakage SI, Agback P, Chattopadhyaya J, Direct estimation of basepair exchange kinetics in oligo-DNA by a combination of NOESY and ROESY experiments, Nucleic acids research, 21 (1993) 4288–4295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99].Halle B, Denisov VP, Water and Monovalent Ions in the Minor Groove of B-DNA Oligonucleotides as Seen by NMR, Biopolymers, 48 (2000) 210–233. [DOI] [PubMed] [Google Scholar]
- [100].Conte MR, Conn GL, Brown T, Lane AN, Hydration of the RNA duplex r(CGCAAAUUUGCG)2 determined by NMR, Nucleic acids research, 24 (1996) 3693–3699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Leroy JL, Broseta D, Gueron M, Proton exchange and base-pair kinetics of poly(rA).poly(rU) and poly(rI).poly(rC), Journal of molecular biology, 184 (1985) 165–178. [DOI] [PubMed] [Google Scholar]
- [102].Gueron M, Kochoyan M, Leroy JL, A single mode of DNA base-pair opening drives imino proton exchange, Nature, 328 (1987) 89–92. [DOI] [PubMed] [Google Scholar]
- [103].Leroy JL, Gehring K, Kettani A, Gueron M, Acid multimers of oligodeoxycytidine strands: stoichiometry, base-pair characterization, and proton exchange properties, Biochemistry, 32 (1993) 6019–6031. [DOI] [PubMed] [Google Scholar]
- [104].Kay LE, Torchia DA, Bax A, Backbone Dynamics of Proteins As Studied by 15N Inverse Detected Heteronuclear NMR Spectroscopy: Application to Staphlococcal Nuclease, Biochemistry, 28 (1989) 8972–8979. [DOI] [PubMed] [Google Scholar]
- [105].Lipari G, Szabo A, Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation in Macromolecules. 1. Theory and Range of Validity, Journal of the American Chemical Society, 104 (1982) 4546–4559. [Google Scholar]
- [106].Lipari G, Szabo A, Nuclear magnetic resonance relaxation in nucleic acid fragments: models for internal motion, Biochemistry, 20 (1981) 6250–6256. [DOI] [PubMed] [Google Scholar]
- [107].Liepert TK, Noggle JH, Freeman WJ, Dalrymple DL, Rotating Frame Nuclear Relaxation of PBr, : Off-ResonanceStudiesby Fourier Transform NMR, Journal of magnetic resonance (San Diego, Calif. : 1997), 19 (1975) 208–221. [Google Scholar]
- [108].Freeman R, Hill HDW, Fourier Transform Study of NMR Spin–Spin Relaxation, The Journal of chemical physics, 55 (1971) 1985–1986. [Google Scholar]
- [109].Wang Y, Ikuta S, Proton On-Resonance Rotating Frame Spin-Lattice Relaxation Measurements of B and Z Double-Helical Oligodeoxyribonucleotides in Solution, J. Am. Chem. Soc, 111 (1989) 1243–1248. [Google Scholar]
- [110].Schmitz U, Sethson I, Egan WM, James TL, Solution Structure of a DNA Octamer Containing the Pribnow Box via Restrained Molecular Dynamics Simulation with Distance and Torsion Angle Constraints Derived from Nuclear Magnetic Resonance Spectral Fitting, J. Mol. Biol, 227 (1992) 510–531. [DOI] [PubMed] [Google Scholar]
- [111].Lane AN, Bauer CJ, Frenkiel TA, Determination of conformational transition rates in the trp promoter by NMR rotating-frame and cross-relaxation rate measurements, Eur. J. Biochem, 21 (1993) 425–431. [DOI] [PubMed] [Google Scholar]
- [112].Nikolova EN, Gottardo FL, Al-Hashimi HM, Probing transient Hoogsteen hydrogen bonds in canonical duplex DNA using NMR relaxation dispersion and single-atom substitution, Journal of the American Chemical Society, 134 (2012) 3667–3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Nikolova EN, Goh GB, Brooks CL 3rd, Al-Hashimi HM, Characterizing the Protonation State of Cytosine in Transient G.C Hoogsteen Base Pairs in Duplex DNA, Journal of the American Chemical Society, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114].Nikolova EN, Zhou H, Gottardo FL, Alvey HS, Kimsey IJ, Al-Hashimi HM, A historical account of hoogsteen base-pairs in duplex DNA, Biopolymers, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115].Alvey HS, Gottardo FL, Nikolova EN, Al-Hashimi HM, Widespread transient Hoogsteen base pairs in canonical duplex DNA with variable energetics, Nature communications, 5 (2014) 4786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].Sathyamoorthy B, Shi H, Zhou H, Xue Y, Rangadurai A, Merriman DK, Al-Hashimi HM, Insights into Watson-Crick/Hoogsteen breathing dynamics and damage repair from the solution structure and dynamic ensemble of DNA duplexes containing m1A, Nucleic acids research, 45 (2017) 5586–5601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [117].Shi H, Clay MC, Rangadurai A, Sathyamoorthy B, Case DA, Al-Hashimi HM, Atomic structures of excited state A-T Hoogsteen base pairs in duplex DNA by combining NMR relaxation dispersion, mutagenesis, and chemical shift calculations, Journal of biomolecular NMR, 70 (2018) 229–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Lane AN, Peck B, Conformational flexibility in DNA duplexes containing single G G mismatches, Eur. J. Biochem, 230 (1995) 1073–1087. [DOI] [PubMed] [Google Scholar]
- [119].Bolton PH, A Primer on Isotopic Labeling in NMR Investigations of Biopolymers, Prog. Nucl. Magn. Resonan. Spectrosc, 22 (1991) 423–452. [Google Scholar]
- [120].Nirmala NR, Wagner G, Measurement of 13C Relaxation Times in Proteins by Two-Dimensional Heteronuclear 1H-13C Correlation Spectroscopy, Journal of the American Chemical Society, 110 (1988) 7557–7558. [Google Scholar]
- [121].Nirmala NR, Wagner G, Measurement of 13C Spin-Spin Relaxation Times by Two- Dimensional Heteronuclear’H- “C Correlation Spectroscopy, J. Magn. Reson, 82 (1989) 659–661. [Google Scholar]
- [122].Szyperski T, Luginbuhl P, Otting G, Guntert P, Wuthrich K, Protein dynamics studied by rotating frame 15Nspin relaxation times, J. Biomol. NMR, 3 (1993) 151–164. [DOI] [PubMed] [Google Scholar]
- [123].Peng JW, Thanabal V, Wagner G, 2D Heteronuclear NMR Measurements of Spin-Lattice Relaxation Times in the Rotating Frame of X Nuclei in Heteronuclear HX Spin Systems, J. Magn. Reson, 94 (1991) 82–100. [Google Scholar]
- [124].Stone MJ, Fairbrother WJ, Palmer AG, Reizer J, Saier MH, Wright PE, Backbone Dynamics of the Bacillus subtilis Glucose Permease IIA Domain Determined from 15N NMR Relaxation Measurements, Biochemistry, 31 (1992) 4394–4406. [DOI] [PubMed] [Google Scholar]
- [125].Stone MJ, Chandrasekhar K, Holmgren A, Wright PE, Dyson HJ, Comparison of Backbone and Tryptophan Side-Chain Dynamics of Reduced and Oxidized Escherichia coli Thioredoxin Using 15N NMR Relaxation Measurements, Biochemistry, 32 (1993) 426–435. [DOI] [PubMed] [Google Scholar]
- [126].Orekhov VY, Pervushin KV, Arseniev AS, Backbone dynamics of (1–7l)bacterioopsin studied by two-dimensional ‘H-l5N NMR spectroscopy, Eur. J. Biochem, 219 (1994) 887–896. [DOI] [PubMed] [Google Scholar]
- [127].Zhong J, Gore JC, Armitage IM, Relative Contributions of Chemical Exchange and Other Relaxation Mechanisms in Protein Solutions and Tissues, Magn Reson Med, 11 (1989) 295–308. [DOI] [PubMed] [Google Scholar]
- [128].Milligan JF, Groebe DR, Witherell GW, Uhlenbeck OC, Oligoribonucleotide synthesis using T7RNA polymerase and synthetic DNA templates, Nucleic acids research, 15 (1987) 8783–8798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129].Zimmer DP, Crothers DM, NMR of enzymatically synthesized uniformly 13C15N-labeled DNA oligonucleotides, Proc. Natl. Acad. Sci. U. S. A, 92 (1995) 3091–3095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130].Gaudin F, Chanteloup L, Thuong NT, Lancelot G, Selectively 13C-Enriched DNA: Dynamics of the C1’H1’ and C5’H5’ or C5’H5” Vectors in d(CGCAAATTTGCG)2, Magn. Reson. Chem, 35 (1997) 561–565. [Google Scholar]
- [131].Maltseva TV, Foldesi A, Ossipov D, Chattopadhyaya J, Comparative 13C and 2H relaxation study of microsecond dynamics of the AT tract of selectively 13C/2H double-labelled DNA duplexes, Magn. Reson. Chem, 38 (2000) 403–414. [Google Scholar]
- [132].Hoogstraten CG, Wank JR, Pardi A, Active site dynamics in the lead-dependent ribozyme, Biochemistry, 39 (2000) 9951–9958. [DOI] [PubMed] [Google Scholar]
- [133].Latham MP, Brown DJ, McCallum SA, Pardi A, NMR methods for studying the structure and dynamics of RNA, Chembiochem : a European journal of chemical biology, 6 (2005) 1492–1505. [DOI] [PubMed] [Google Scholar]
- [134].Boisbouvier J, Brutscher B, Simorre J, Marion D, 13C spin relaxation measurements in RNA: Sensitivity and resolution improvement using spin-state selective correlation experiments, J. Biomol. NMR, 14 (1999) 241–252. [Google Scholar]
- [135].Blad H, Reiter NJ, Abildgaard F, Markley JL, Butcher SE, Dynamics and metal ion binding in the U6 RNA intramolecular stem-loop as analyzed by NMR, Journal of molecular biology, 353 (2005) 540–555. [DOI] [PubMed] [Google Scholar]
- [136].Johnson JE Jr., Hoogstraten CG, Extensive backbone dynamics in the GCAA RNA tetraloop analyzed using 13C NMR spin relaxation and specific isotope labeling, Journal of the American Chemical Society, 130 (2008) 16757–16769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137].Oberstrass FC, Allain FHT, Ravindranathan S, Changes in Dynamics of SRE-RNA on Binding to the VTS1p-SAM Domain Studied by 13C NMR Relaxation, Journal of the American Chemical Society, 130 (2008) 12007–12020. [DOI] [PubMed] [Google Scholar]
- [138].Shajani Z, Varani G, 13C NMR relaxation studies of RNA base and ribose nuclei reveal a complex pattern of motions in the RNA binding site for human U1A protein, Journal of molecular biology, 349 (2005) 699–715. [DOI] [PubMed] [Google Scholar]
- [139].Shajani Z, Drobny G, Varani G, Binding of U1A Protein Changes RNA Dynamics As Observed by (13)C NMR Relaxation Studies(,), Biochemistry, 46 (2007) 5875–5883. [DOI] [PubMed] [Google Scholar]
- [140].Shajani Z, Varani G, 13C relaxation studies of the DNA target sequence for hhai methyltransferase reveal unique motional properties, Biochemistry, 47 (2008) 7617–7625. [DOI] [PubMed] [Google Scholar]
- [141].Cavanagh J, Venters RA, Protein dynamic studies move to a new time slot, Nature Struct Biol, 8 (2001) 912–914. [DOI] [PubMed] [Google Scholar]
- [142].Loria JP, Rance M, Palmer AG, A relaxation-compensated Carr-Purcell-Meiboom-Gill sequence for characterizing chemical exchange by NMR spectroscopy, Journal of the American Chemical Society, 121 (1999) 2331–2332. [Google Scholar]
- [143].Skrynnikov NR, Dahlquist FW, Kay LE, Reconstructing NMR Spectra of “Invisible” Excited Protein States Using HSQC and HMQC Experiments, J. Am. Chem. Soc, 124 (2002) 12352–12360. [DOI] [PubMed] [Google Scholar]
- [144].Mulder FA, Skrynnikov NR, Hon B, Dahlquist FW, Kay LE, Measurement of slow (micros-ms) time scale dynamics in protein side chains by (15)N relaxation dispersion NMR spectroscopy: application to Asn and Gln residues in a cavity mutant of T4 lysozyme, Journal of the American Chemical Society, 123 (2001) 967–975. [DOI] [PubMed] [Google Scholar]
- [145].Skrynnikov NR, Mulder FAA, Hon B, Dahlquist FW, Kay LE, Probing Slow Time Scale Dynamics at Methyl-Containing Side Chains in Proteins by Relaxation Dispersion NMR Measurements: Application to Methionine Residues in a Cavity Mutant of T4 Lysozyme, Journal of the American Chemical Society, 123 (2001) 4556–4566. [DOI] [PubMed] [Google Scholar]
- [146].Orekhov VY, Korzhnev DM, Kay LE, Double- and zero-quantum NMR relaxation dispersion experiments sampling millisecond time scale dynamics in proteins, Journal of the American Chemical Society, 126 (2004) 1886–1891. [DOI] [PubMed] [Google Scholar]
- [147].Korzhnev DM, Kloiber K, Kay LE, Multiple-quantum relaxation dispersion NMR spectroscopy probing millisecond time-scale dynamics in proteins: theory and application, Journal of the American Chemical Society, 126 (2004) 7320–7329. [DOI] [PubMed] [Google Scholar]
- [148].Dittmer J, Bodenhausen G, Evidence for Slow Motion in Proteins by Multiple Refocusing of Heteronuclear Nitrogen/Proton Multiple Quantum Coherences in NMR, Journal of the American Chemical Society, 126 (2003) 1314–1315. [DOI] [PubMed] [Google Scholar]
- [149].Lundstrom P, Hansen DF, Vallurupalli P, Kay LE, Accurate measurement of alpha proton chemical shifts of excited protein states by relaxation dispersion NMR spectroscopy, Journal of the American Chemical Society, 131 (2009) 1915–1926. [DOI] [PubMed] [Google Scholar]
- [150].Ishima R, Baber J, Louis JM, Torchia DA, Carbonyl carbon transverse relaxation dispersion measurements and ms-micros timescale motion in a protein hydrogen bond network, Journal of biomolecular NMR, 29 (2004) 187–198. [DOI] [PubMed] [Google Scholar]
- [151].Pervushin K, Riek R, Wider G, Wuthrich K, Transverse relaxation-optimized spectroscopy (TROSY) for NMR studies of aromatic spin systems in C-13-labeled proteins, Journal of the American Chemical Society, 120 (1998) 6394–6400. [Google Scholar]
- [152].Korzhnev DM, Kloiber K, Kanelis V, Tugarinov V, Kay LE, Probing Slow Dynamics in High Molecular Weight Proteins by Methyl-TROSY NMR Spectroscopy: Application to a 723-Residue Enzyme, J. Am. Chem. Soc, 126 (2004) 3964–3973. [DOI] [PubMed] [Google Scholar]
- [153].Korzhnev DM, Salvatella X, Vendruscolo M, Di Nardo AA, Davidson AR, Dobson CM, Kay LE, Low-populated folding intermediates of Fyn SH3 characterized by relaxation dispersion NMR, Nature, 430 (2004) 586–590. [DOI] [PubMed] [Google Scholar]
- [154].Akke M, Palmer AG, Monitoring macromolecular motions on microsecond to millisecond time scales by R(1)rho-R(1) constant relaxation time NMR spectroscopy, Journal of the American Chemical Society, 118 (1996) 911–912. [Google Scholar]
- [155].Yamazaki T, Muhandiram R, Kay LE, NMR Experiments for the Measurement of Carbon Relaxation Properties in Highly Enriched, Uniformly 13C,15N-Labeled Proteins: Application to 13Ca Carbons, J. Am. Chem. Soc, 116 (1994) 8266–8278. [Google Scholar]
- [156].Wang Y-S, NMR rotating frame relaxation measurement of conformational exchanges on the microsecond time scale (part 1), Conc. Magn. Reson, 4 (1992) 327–337. [Google Scholar]
- [157].Goldman M, Interference effects in the relaxation of a pair of unlike spin-½ nuclei, Journal of magnetic resonance (San Diego, Calif. : 1997), 60 (1984) 437–452. [Google Scholar]
- [158].Lee AL, Wand AJ, Assessing potential bias in the determination of rotational correlation times of proteins by NMR relaxation, Journal of biomolecular NMR, 13 (1999) 101–112. [DOI] [PubMed] [Google Scholar]
- [159].Korzhnev DM, Tischenko EV, Arseniev AS, Off-resonance effects in 15N T2 CPMG measurements, Journal of biomolecular NMR, 17 (2000) 231–237. [DOI] [PubMed] [Google Scholar]
- [160].Pelupessy P, Chiarparin E, Bodenhausen G, Excitation of selected proton signals in NMR of isotopically labeled macromolecules, Journal of magnetic resonance (San Diego, Calif. : 1997), 138 (1999) 178–181. [DOI] [PubMed] [Google Scholar]
- [161].Pelupessy P, Chiarparin E, Hartmann – Hahn Polarization Transfer in Liquids: An Ideal Tool for Selective Experiments, Concepts Magn Reson, 12 (2000) 103–124. [Google Scholar]
- [162].Ferrage F, Eykyn TR, Bodenhausen G, Frequency-switched single-transition cross-polarization: a tool for selective experiments in biomolecular NMR, Chemphyschem, 5 (2004) 76–84. [DOI] [PubMed] [Google Scholar]
- [163].Korzhnev DM, Orekhov VY, Kay LE, Off-resonance R1(p) NMR studies of exchange dynamics in proteins with low spin-lock fields: An application to a fyn SH3 domain, Journal of the American Chemical Society, 127 (2005) 713–721. [DOI] [PubMed] [Google Scholar]
- [164].Xue Y, Gracia B, Herschlag D, Russell R, Al-Hashimi HM, Visualizing the formation of an RNA folding intermediate through a fast highly modular secondary structure switch, Nature communications, 7 (2016) ncomms11768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [165].Szymanski ES, Kimsey IJ, Al-Hashimi HM, Direct NMR Evidence that Transient Tautomeric and Anionic States in dG.dT Form Watson-Crick-like Base Pairs, Journal of the American Chemical Society, 139 (2017) 4326–4329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [166].Clay MC, Ganser LR, Merriman DK, Al-Hashimi HM, Resolving sugar puckers in RNA excited states exposes slow modes of repuckering dynamics, Nucleic acids research, (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [167].Bouvignies G, Kay LE, Measurement of proton chemical shifts in invisible states of slowly exchanging protein systems by chemical exchange saturation transfer, The journal of physical chemistry. B, 116 (2012) 14311–14317. [DOI] [PubMed] [Google Scholar]
- [168].Bouvignies G, Kay LE, A 2D (1)(3)C-CEST experiment for studying slowly exchanging protein systems using methyl probes: an application to protein folding, Journal of biomolecular NMR, 53 (2012) 303–310. [DOI] [PubMed] [Google Scholar]
- [169].Vallurupalli P, Bouvignies G, Kay LE, Studying “invisible” excited protein states in slow exchange with a major state conformation, Journal of the American Chemical Society, 134 (2012) 8148–8161. [DOI] [PubMed] [Google Scholar]
- [170].Zhao B, Zhang Q, Measuring Residual Dipolar Couplings in Excited Conformational States of Nucleic Acids by CEST NMR Spectroscopy, Journal of the American Chemical Society, 137 (2015) 13480–13483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [171].Tolman JR, Flanagan JM, Kennedy MA, Prestegard JH, Nuclear Magnetic Dipole Interactions in Field-Oriented Proteins - Information For Structure Determination in Solution, Proceedings of the National Academy of Sciences of the United States of America, 92 (1995) 9279–9283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [172].Tjandra N, Bax A, Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium, Science (New York, N.Y.), 278 (1997) 1111–1114. [DOI] [PubMed] [Google Scholar]
- [173].Nussbaumer F, Juen MA, Gasser C, Kremser J, Muller T, Tollinger M, Kreutz C, Synthesis and incorporation of 13C-labeled DNA building blocks to probe structural dynamics of DNA by NMR, Nucleic acids research, 45 (2017) 9178–9192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [174].LeBlanc RM, Longhini AP, Tugarinov V, Dayie TK, NMR probing of invisible excited states using selectively labeled RNAs, Journal of biomolecular NMR, 71 (2018) 165–172. [DOI] [PubMed] [Google Scholar]
- [175].Neuner S, Santner T, Kreutz C, Micura R, The “Speedy” Synthesis of Atom-Specific 15N Imino/Amido labeled RNA, Chem. Eur. J, 21 (2015) 11634–11643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [176].Kloiber K, Spitzer R, Tollinger M, Konrat R, Kreutz C, Probing RNA dynamics via longitudinal exchange and CPMG relaxation dispersion NMR spectroscopy using a sensitive 13C-methyl label, Nucleic acids research, 39 (2011) 4340–4351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [177].Thakur CS, Luo Y, Chen B, Eldho NV, Dayie TK, Biomass production of site selective 13C/15N nucleotides using wild type and a transketolase E. coli mutant for labeling RNA for high resolution NMR, Journal of biomolecular NMR, 52 (2012) 103–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [178].Palmer AG 3rd, Koss H, Chemical Exchange, Methods in enzymology, 615 (2019) 177–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [179].Trott O, Abergel D, Palmer AG, An average-magnetization analysis of R 1ρ relaxation outside of the fast exchange limit, Mol. Phys, 101 (2003) 753–763. [Google Scholar]
- [180].Korzhnev DM, Skrynnikov NR, Millet O, Torchia DA, Kay LE, An NMR experiment for the accurate measurement of heteronuclear spin-lock relaxation rates, Journal of the American Chemical Society, 124 (2002) 10743–10753. [DOI] [PubMed] [Google Scholar]
- [181].Massi F, Johnson E, Wang C, Rance M, Palmer AG 3rd, NMR R1 rho rotating-frame relaxation with weak radio frequency fields, Journal of the American Chemical Society, 126 (2004) 2247–2256. [DOI] [PubMed] [Google Scholar]
- [182].Abergel D, Palmer AG, On the use of the Stochastic Liouville Equation in Nuclear Magnetic Resonance: Application to R1p Relaxation in the Presence of Exchange, Concepts Magn. Reson, 19A (2003) 134–148. [Google Scholar]
- [183].Ishima R, Torchia DA, Estimating the time scale of chemical exchange of proteins from measurements of transverse relaxation rates in solution, J. Biomol. NMR, 14 (1999) 369–372. [DOI] [PubMed] [Google Scholar]
- [184].Rao BDN, Nuclear Magnetic Resonance Line-Shape Analysis and Determination of Exchange Rates Meth Enzymol, 176 (1989) 279–311. [DOI] [PubMed] [Google Scholar]
- [185].Peng JW, Thanabal V, Wagner G, 2D Heteronuclear NMR Measurements of Spin-Lattice Relaxation Times in the Rotating Frame of X Nuclei in Heteronuclear HX Spin Systems, Journal of Magnetic Resonance, 94 (1991) 82–100. [Google Scholar]
- [186].Jones GP, Spin-Lattice Relaxation in the Rotating Frame: Weak-Collision Case, Phys. Rev, 148 (1966) 332–335. [Google Scholar]
- [187].Yuwen T, Brady JP, Kay LE, Probing Conformational Exchange in Weakly Interacting, Slowly Exchanging Protein Systems via Off-Resonance R1rho Experiments: Application to Studies of Protein Phase Separation, Journal of the American Chemical Society, 140 (2018) 2115–2126. [DOI] [PubMed] [Google Scholar]
- [188].Cornell BA, Pope JM, A Pulsed NMR Study of Nuclear Spin-Lattice Relaxation in the Off-Resonance Rotating Frame, J. Magn. Reson, 16 (1974) 172–181. [Google Scholar]
- [189].Davis DG, Perlman ME, London RE, J. Magn. Reson. B, 104 (1994) 266–275. [DOI] [PubMed] [Google Scholar]
- [190].Ishima R, Torchia DA, Accuracy of optimized chemical-exchange parameters derived by fitting CPMG R2 dispersion profiles when R2(0a) not = R2(0b), Journal of biomolecular NMR, 34 (2006) 209–219. [DOI] [PubMed] [Google Scholar]
- [191].Kaplan J, Exchange Broadening in Nuclear Magnetic Resonance, J. Chem. Phys, 28 (1958) 278–282. [Google Scholar]
- [192].Snyder JP, Map projections: A working manual, in: Professional Paper, Washington, D.C., 1987. [Google Scholar]
- [193].Trott O, Palmer AG 3rd, Theoretical study of R(1rho) rotating-frame and R2 free-precession relaxation in the presence of n-site chemical exchange, Journal of magnetic resonance (San Diego, Calif. : 1997), 170 (2004) 104–112. [DOI] [PubMed] [Google Scholar]
- [194].Koss H, Rance M, Palmer AG 3rd, General expressions for R1rho relaxation for N-site chemical exchange and the special case of linear chains, Journal of magnetic resonance (San Diego, Calif. : 1997), 274 (2017) 36–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [195].Kimsey IJ, Szymanski ES, Zahurancik WJ, Shakya A, Xue Y, Chu CC, Sathyamoorthy B, Suo Z, Al-Hashimi HM, Dynamic basis for dG*dT misincorporation via tautomerization and ionization, Nature, 554 (2018) 195–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [196].Bothe JR, Stein ZW, Al-Hashimi HM, Evaluating the uncertainty in exchange parameters determined from off-resonance R1rho relaxation dispersion for systems in fast exchange, Journal of magnetic resonance (San Diego, Calif. : 1997), 244 (2014) 18–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [197].Kimsey IJ, Petzold K, Sathyamoorthy B, Stein ZW, Al-Hashimi HM, Visualizing transient Watson-Crick-like mispairs in DNA and RNA duplexes, Nature, 519 (2015) 315–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [198].Dethoff EA, Hansen AL, Musselman C, Watt ED, Andricioaei I, Al-Hashimi HM, Characterizing complex dynamics in the transactivation response element apical loop and motional correlations with the bulge by NMR, molecular dynamics, and mutagenesis, Biophysical journal, 95 (2008) 3906–3915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [199].Eichhorn CD, Feng J, Suddala KC, Walter NG, Brooks CL 3rd, Al-Hashimi HM, Unraveling the structural complexity in a single-stranded RNA tail: implications for efficient ligand binding in the prequeuosine riboswitch, Nucleic acids research, 40 (2012) 1345–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [200].Sun X, Zhang Q, Al-Hashimi HM, Resolving fast and slow motions in the internal loop containing stem-loop 1 of HIV-1 that are modulated by Mg2+ binding: role in the kissing-duplex structural transition, Nucleic acids research, 35 (2007) 1698–1713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [201].Hansen AL, Al-Hashimi HM, Dynamics of large elongated RNA by NMR carbon relaxation, Journal of the American Chemical Society, 129 (2007) 16072–16082. [DOI] [PubMed] [Google Scholar]
- [202].Baldwin AJ, Kay LE, An R(1rho) expression for a spin in chemical exchange between two sites with unequal transverse relaxation rates, Journal of biomolecular NMR, 55 (2013) 211–218. [DOI] [PubMed] [Google Scholar]
- [203].Peng JW, Thanabal V, Wagner G, Improved Accuracy of Heteronuclear Transverse Relaxation Time Measurements in Macromolecules. Elimination of Antiphase Contributions, Journal of Magnetic Resonance, 95 (1991) 421–427. [Google Scholar]
- [204].Yamazaki T, Muhandiram R, Kay LE, NMR Experiments for the Measurement of Carbon Relaxation Properties in Highly Enriched, Uniformly 13C, 15N-Labeled Proteins: Application to 13Ca Carbons, J . Am. Chem. Soc, 116 (1994) 8266–8278. [Google Scholar]
- [205].Mulder FAA, de Graaf RA, Kaptein R, Boelens R, An off-resonance rotating frame relaxation experiment for the investigation of macromolecular dynamics using adiabatic rotations, Journal Of Magnetic Resonance, 131 (1998) 351–357. [DOI] [PubMed] [Google Scholar]
- [206].Mulder FAA, Van Tilborg PJA, Kaptein R, Boelens R, Microsecond time scale dynamics in the RXR DNA-binding domain from a combination of spin-echo and off-resonance rotating frame relaxation measurements, J. Biomol. NMR, 13 (1999) 275–288. [DOI] [PubMed] [Google Scholar]
- [207].Konrat R, Tollinger M, Heteronuclear relaxation in time-dependent spin systems: (15)NT1 (rho) dispersion during adiabatic fast passage, Journal of biomolecular NMR, 13 (1999) 213–221. [DOI] [PubMed] [Google Scholar]
- [208].Kim S, Baum J, An on/off resonance rotating frame relaxation experiment to monitor millisecond to microsecond timescale dynamics, Journal of biomolecular NMR, 30 (2004) 195–204. [DOI] [PubMed] [Google Scholar]
- [209].Zinn-Justin S, Berthault P, Guenneugues M, Desvaux H, Off-resonance rf fields in heteronuclear NMR: Application to the study of slow motions, Journal of biomolecular NMR, 10 (1997) 363–372. [DOI] [PubMed] [Google Scholar]
- [210].Gueron M, Leroy JL, Griffey RH, Proton Nuclear Magnetic Relaxation of 15N-Labeled Nucleic Acids via Dipolar Coupling and Chemical Shift Anisotropy, Journal of the American Chemical Society, 105 (1983) 7262–7266. [Google Scholar]
- [211].Boyd J, Hommel U, Campbell ID, Influence of cross - correlation between dipolar and anisotropic chemical shift relaxation mechanisms upon longitudinal relaxation rates of nitrogen-15 in macromolecules, Chem. Phys. Lett, 175 (1990) 477–482. [Google Scholar]
- [212].Palmer AG III, Skelton NJ, Chazin WJ, Wright PE, Rance M, Suppression of the effects of cross correlation between dipolar and anisotropic chemical-shift relaxation mechanisms in the measurement of spin-spin relaxation rates, Mol. Phys, 75 (1992) 699–711. [Google Scholar]
- [213].Kay LE, Nicholson LK, Delaglio F, Bax A, Torchia DA, J. Mag. Reson, 97 (1992) 359–375. [Google Scholar]
- [214].Williamson JR, Boxer SG, Multinuclear NMR studies of DNA hairpins. 1. Structure and dynamics of d(CGCGTTGTTCGCG), Biochemistry, 28 (1989) 2819–2831. [DOI] [PubMed] [Google Scholar]
- [215].Spitzer R, Kloiber K, Tollinger M, Kreutz C, Kinetics of DNA refolding from longitudinal exchange NMR spectroscopy, Chembiochem : a European journal of chemical biology, 12 (2011) 2007–2010. [DOI] [PubMed] [Google Scholar]
- [216].Chiarparin E, Pelupessy P, Bodenhausen G, Selective cross-polarization in solution state NMR, Mol Phys, 95 (1998) 759–767. [Google Scholar]
- [217].Chiarparin E, Pelupessy P, Ghose R, Bodenhausen G, Relative orientation of (CH alpha)-H-alpha-bond vectors of successive residues in proteins through cross-correlated relaxation in NMR, Journal of the American Chemical Society, 122 (2000) 1758–1761. [Google Scholar]
- [218].Wijmenga SS, van Buuren BNM, The use of NMR methods for conformational studies of nucleic acids, Progress in nuclear magnetic resonance spectroscopy, 32 (1998) 287–387. [Google Scholar]
- [219].Ban D, Gossert AD, Giller K, Becker S, Griesinger C, Lee D, Exceeding the limit of dynamics studies on biomolecules using high spin-lock field strengths with a cryogenically cooled probehead, Journal of magnetic resonance (San Diego, Calif. : 1997), 221 (2012) 1–4. [DOI] [PubMed] [Google Scholar]
- [220].Boyd J, Hommel U, Krishnan VV, Influence of Cross-Correlation Between Dipolar and Chemical Shift Anisotropy Relaxation Mechanisms Upon the Transverse Relaxation Rates of 15N in Macromolecules, Chemical Physics Letters, 187 (1991) 317–324. [Google Scholar]
- [221].Kumar A, Grace RCR, Madhu PK, Cross-correlations in NMR, Prog. NMR Spectroscopy, 37 (2000) 191–319. [Google Scholar]
- [222].Steiner E, Schlagnitweit J, Lundstrom P, Petzold K, Capturing Excited States in the Fast-Intermediate Exchange Limit in Biological Systems Using (1) H NMR Spectroscopy, Angewandte Chemie (International ed. in English), 55 (2016) 15869–15872. [DOI] [PubMed] [Google Scholar]
- [223].Schlagnitweit J, Steiner E, Karlsson H, Petzold K, Efficient Detection of Structure and Dynamics in Unlabeled RNAs: The SELOPE Approach, Chem. Eur. J, 24 (2018) 6067–6070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [224].Piotto M, Saudek V, Sklenar V, Gradient -tailored excitation for single-quantum NMR spectroscopy of aqueous solutions, J. Biomol. NMR, 2 (1992) 661–665. [DOI] [PubMed] [Google Scholar]
- [225].More J, The Levenberg-Marquardt Algorithm: Implementation and Theory, in, Springer Verlag, 1977, pp. 105–116. [Google Scholar]
- [226].Lasdon L, Duarte A, GLover F, Laguna M, Marti R, Adaptive memory programming for constrained global optimization, Computers and Operations Research, 37 (2010) 1500–1509. [Google Scholar]
- [227].Wagenmarkes E, Farrel S, AIC model selection using Akaike weight, Bull. Rev, 11 (2004) 192–196. [DOI] [PubMed] [Google Scholar]
- [228].Burnham KP, Anderson DR, Multimodel Inference: Understanding AIC and BIC in Model Selection, Sociol. Methods Res, 33 (2004) 261–304. [Google Scholar]
- [229].Shi H, Liu B, Nussbaumer F, Kreutz C, Al-Hashimi HM, m6A slows down the kinetics of RNA duplex hybridization, Submitted, (2019). [Google Scholar]
- [230].Bouvignies G, Hansen DF, Vallurupalli P, Kay LE, Divided-evolution-based pulse scheme for quantifying exchange processes in proteins: powerful complement to relaxation dispersion experiments, Journal of the American Chemical Society, 133 (2011) 1935–1945. [DOI] [PubMed] [Google Scholar]
- [231].Miloushev VZ, Palmer AG 3rd, R(1rho) relaxation for two-site chemical exchange: general approximations and some exact solutions, Journal of magnetic resonance (San Diego, Calif. : 1997), 177 (2005) 221–227. [DOI] [PubMed] [Google Scholar]
- [232].Coman D, Russu IM, A nuclear magnetic resonance investigation of the energetics of basepair opening pathways in DNA, Biophysical journal, 89 (2005) 3285–3292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [233].Vallurupalli P, Chakrabarti N, Pomes R, Kay LE, Atomistic picture of conformational exchange in a T4 lysozyme cavity mutant: an experiment-guided molecular dynamics study, Chem Sci, 7 (2016) 3602–3613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [234].Findeisen M, Brand T, Berger S, A 1H-NMR thermometer suitable for cryoprobes, Magnetic resonance in chemistry : MRC, 45 (2007) 175–178. [DOI] [PubMed] [Google Scholar]
- [235].Zhou H, Kimsey IJ, Nikolova EN, Sathyamoorthy B, Grazioli G, McSally J, Bai T, Wunderlich CH, Kreutz C, Andricioaei I, Al-Hashimi HM, m(1)A and m(1)G disrupt ARNA structure through the intrinsic instability of Hoogsteen base pairs, Nature structural & molecular biology, 23 (2016) 803–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [236].Neudecker P, Zarrine-Afsar A, Davidson AR, Kay LE, Phi-value analysis of a three-state protein folding pathway by NMR relaxation dispersion spectroscopy, Proceedings of the National Academy of Sciences of the United States of America, 104 (2007) 15717–15722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [237].Kovrigin EI, Loria JP, Characterization of the Transition State of Functional Enzyme Dynamics, J. Am. Chem. Soc, 128 (2006) 7724–7725. [DOI] [PubMed] [Google Scholar]
- [238].Lam SL, Chi LM, Use of chemical shifts for structural studies of nucleic acids, Progress in nuclear magnetic resonance spectroscopy, 56 (2010) 289–310. [DOI] [PubMed] [Google Scholar]
- [239].Fonville JM, Swart M, Vokacova Z, Sychrovsky V, Sponer JE, Sponer J, Hilbers CW, Bickelhaupt FM, Wijmenga SS, Chemical shifts in nucleic acids studied by density functional theory calculations and comparison with experiment, Chemistry (Weinheim an der Bergstrasse, Germany), 18 (2012) 12372–12387. [DOI] [PubMed] [Google Scholar]
- [240].Xu XP, Au-Yeung SCF, Investigation of chemical shift and structure relationships in nucleic acids using NMR and density functional theory methods, Journal of Physical Chemistry B, 104 (2000) 5641–5650. [Google Scholar]
- [241].Greene KL, Wang Y, Live D, Influence of the glycosidic torsion angle on 13C and 15Nshifts in guanosine nucleotides: Investigations of G-tetrad models with alternating syn and anti bases, J. Biomol. NMR, 5 (1995) 333–338. [DOI] [PubMed] [Google Scholar]
- [242].Rossi P, Harbison GS, Calculation of 13C chemical shifts in rna nucleosides: structure-13C chemical shift relationships, Journal of magnetic resonance (San Diego, Calif. : 1997), 151 (2001) 1–8. [DOI] [PubMed] [Google Scholar]
- [243].Ghose R, Marino JP, Wiberg KB, Prestegard JH, Dependence of C-13 Chemical-Shifts On Glycosidic Torsional Angles in Ribonucleic-Acids, Journal of the American Chemical Society, 116 (1994) 8827–8828. [Google Scholar]
- [244].Ebrahimi M, Rossi P, Rogers C, Harbison GS, Dependence of 13C NMR chemical shifts on conformations of rna nucleosides and nucleotides, Journal of magnetic resonance (San Diego, Calif. : 1997), 150 (2001) 1–9. [DOI] [PubMed] [Google Scholar]
- [245].Santos RA, Tang P, Harbison GS, Determination of DNA sugar pucker using 13C NMR Spectroscopy, Biochemistry, 28 (1989) 9372–9378. [DOI] [PubMed] [Google Scholar]
- [246].Dejaegere AP, Case DA, Density functional study of ribose and deoxyribose chemical shifts, Journal of Physical Chemistry A, 102 (1998) 5280–5289. [Google Scholar]
- [247].Ohlenschlager O, Haumann S, Ramachandran R, Gorlach M, Conformational signatures of 13C chemical shifts in RNA ribose, Journal of biomolecular NMR, 42 (2008) 139–142. [DOI] [PubMed] [Google Scholar]
- [248].Fares C, Amata I, Carlomagno T, 13C-detection in RNA bases: revealing structure-chemical shift relationships, Journal of the American Chemical Society, 129 (2007) 15814–15823. [DOI] [PubMed] [Google Scholar]
- [249].Goswami B, Gaffney BL, Jones RA, Nitrogen-15-labeled oligodeoxynucleotides. 5. Use of 15N NMR to probe H-bonding in an O6MeG.cntdot.T base pair, Journal of the American Chemical Society, 115 (1993) 3832–3833. [Google Scholar]
- [250].Gaffney BL, Kung P, Wang C, Jones RA, Nitrogen-15-Labeled Oligodeoxynucleotides. 8. Use of 15N NMR To Probe Hoogsteen Hydrogen Bonding at Guanine and Adenine N7 Atoms of a DNA Triplex, Journal of the American Chemical Society, 117 (1995) 12281–12283. [Google Scholar]
- [251].Wang C, Gao H, Gaffney BL, Jones RA, Nitrogen-15-Labeled Oligodeoxynucleotides. 3. Protonation of the Adenine N1 in the A.G and A-C mispairs of the Duplexes d[CG(15N1)AGAATTCCCG]2 and (d[CGCGAAITC(‘5N’)ACC]J, Journal of the American Chemical Society, 113 (1991) 5486–5488. [Google Scholar]
- [252].Tanaka Y, Kojima C, Yamazaki T, Kodama TS, Yasuno K, Miyashita S, Ono AM, Ono AS, Kainosho M, Kyogoku Y, Solution Structure of an RNA Duplex Including a C-U Base Pair, Biochemistry, 39 (2000). [DOI] [PubMed] [Google Scholar]
- [253].Nixon PL, Rangan A, Kim YG, Rich A, Hoffman DW, Hennig M, Giedroc DP, Solution Structure of a Luteoviral P1–P2 Frameshifting mRNA Pseudoknot, J. Mol. Biol, 322 (2002) 621–633. [DOI] [PubMed] [Google Scholar]
- [254].Sowers LC, Eritja R, Chen FM, Khwaja T, Kaplan BE, Goodman MF, Fazakerley GV, Characterization of the high pH wobble structure of the 2-aminopurine cytosine mismatch by N-15 NMR spectroscopy, Biochem. Biophys. Res. Commun, 165 (1989) 89–92. [DOI] [PubMed] [Google Scholar]
- [255].Cho BP, Kadlubar FF, Culp SJ, Evans FE, 15N Nuclear Magnetic Resonance Studies on the Tautomerism of 8-Hydroxy-2’-deoxyguanosine, 8-Hydroxyguanosine, and Other OS-Substituted Guanine Nucleosides, Chem. Res. Toxicol, 3 (1990) 445–452. [DOI] [PubMed] [Google Scholar]
- [256].Legault P, Pardi A, Journal of the American Chemical Society, 116 (1994) 8390–8391. [Google Scholar]
- [257].Westhof E, Isostericity and tautomerism of base pairs in nucleic acids, FEBS letters, 588 (2014) 2464–2469. [DOI] [PubMed] [Google Scholar]
- [258].Leeuw HPM, Haasnoot CAG, Altona C, Empirical Correlations Between Conformational Parameters in b-D-Furanoside Fragments Derived from a Statistical Survey of Crystal Structures of Nucleic Acid Constituents, Isr J Chem, 20 (1980) 108–126. [Google Scholar]
- [259].Frank AT, Law SM, Brooks CL, A Simple and Fast Approach for Predicting H and C Chemical Shifts: Toward Chemical Shift-Guided Simulations of RNA, The journal of physical chemistry. B, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [260].Sitkoff D, Case DA, Theories of chemical shift anisotropies in proteins and nucleic acids, Progress in NMR Spec, 32 (1998) 165–190. [Google Scholar]
- [261].Cromsight JAMTC, Hilbers CW, Wijmenga SS, Prediction of proton chemical shifts in RNA, J. Biomol. NMR, 21 (2001) 11–29. [DOI] [PubMed] [Google Scholar]
- [262].Barton S, Heng X, Johnson BA, Summers MF, Database proton NMR chemical shifts for RNA signal assignment and validation, Journal of biomolecular NMR, 55 (2013) 33–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [263].Altona C, Faber DH, Hoekzema AJAW, Double-helical DNA 1H chemical shifts: an accurate and balanced predictive empirical scheme, Magn. Reson. Chem, 38 (2000) 95–107. [Google Scholar]
- [264].Lee J, Dethoff EA, Al-Hashimi HM, Invisible RNA state dynamically couples distant motifs, Proceedings of the National Academy of Sciences of the United States of America, 111 (2014) 9485–9490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [265].Zuker M, Mfold web server for nucleic acid folding and hybridization prediction, Nucleic acids research, 31 (2003) 3406–3415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [266].Parisien M, Major F, The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data, Nature, 452 (2008) 51–55. [DOI] [PubMed] [Google Scholar]
- [267].Houck-Loomis B, Durney MA, Salguero C, Shankar N, Nagle JM, Goff SP, D’Souza VM, An equilibrium-dependent retroviral mRNA switch regulates translational recoding, Nature, 480 (2011) 561–564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [268].Reining A, Nozinovic S, Schlepckow K, Buhr F, Furtig B, Schwalbe H, Three-state mechanism couples ligand and temperature sensing in riboswitches, Nature, 499 (2013) 355–359. [DOI] [PubMed] [Google Scholar]
- [269].Merriman DK, Xue Y, Yang S, Kimsey IJ, Shakya A, Clay M, Al-Hashimi HM, Shortening the HIV-1 TAR RNA Bulge by a Single Nucleotide Preserves Motional Modes overa Broad Range of Time Scales, Biochemistry, 55 (2016) 4445–4456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [270].Xu Y, McSally J, Andricioaei I, Al-Hashimi HM, Modulation of Hoogsteen dynamics on DNA recognition, Nature communications, 9 (2018) 1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [271].Zhang Q, Stelzer AC, Fisher CK, Al-Hashimi HM, Visualizing spatially correlated dynamics that directs RNA conformational transitions, Nature, 450 (2007) 1263–1267. [DOI] [PubMed] [Google Scholar]
- [272].Frank AT, Stelzer AC, Al-Hashimi HM, Andricioaei I, Constructing RNA Dynamical Ensembles by Combining MD and Motionally Decoupled NMR RDCs: New insights into RNA Dynamics and Adaptive Ligand Recognition, Nucleic acids research, 37 (2009) 3670–3679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [273].Salmon L, Bascom G, Andricioaei I, Al-Hashimi HM, A General Method for Constructing Atomic-Resolution RNA Ensembles using NMR Residual Dipolar Couplings: The Basis for Interhelical Motions Revealed, Journal of the American Chemical Society, 135 (2013) 5457–5466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [274].Salmon L, Giambasu GM, Nikolova EN, Petzold K, Bhattacharya A, Case DA, Al-Hashimi HM, Modulating RNA Alignment Using Directional Dynamic Kinks: Application in Determining an Atomic-Resolution Ensemble for a Hairpin using NMR Residual Dipolar Couplings, Journal of the American Chemical Society, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [275].Swails J, Zhu T, He X, Case DA, AFNMR: automated fragmentation quantum mechanical calculation of NMR chemical shifts for biomolecules, Journal of biomolecular NMR, 63 (2015) 125–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [276].Frank AT, Bae SH, Stelzer AC, Prediction of RNA 1H and 13C chemical shifts: a structure based approach, The journal of physical chemistry. B, 117 (2013) 13497–13506. [DOI] [PubMed] [Google Scholar]
- [277].Vallurupalli P, Hansen DF, Stollar E, Meirovitch E, Kay LE, Measurement of bond vector orientations in invisible excited states of proteins, Proceedings of the National Academy of Sciences of the United States of America, 104 (2007) 18473–18477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [278].Igumenova TI, Brath U, Akke M, Palmer AG, Characterization of Chemical Exchange Using Residual Dipolar Coupling, Journal of the American Chemical Society, 129 (2007) 13396–13397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [279].Hansen DF, Vallurupalli P, Kay LE, Quantifying Two-Bond 1HN-13CO and One-Bond 1Hr-13Cr Dipolar Couplings of Invisible Protein States by Spin-State Selective Relaxation Dispersion NMR Spectroscopy, Journal of the American Chemical Society, 130 (2008) 8397–8405. [DOI] [PubMed] [Google Scholar]
- [280].Vallurupalli P, Hansen DF, Kay LE, Probing structure in invisible protein states with anisotropic NMR chemical shifts, Journal of the American Chemical Society, 130 (2008) 2734–2735. [DOI] [PubMed] [Google Scholar]
- [281].Sekhar A, Rosenzweig R, Bouvignies G, Kay LE, Hsp70 biases the folding pathways of client proteins, Proceedings of the National Academy of Sciences of the United States of America, 113 (2016) E2794–2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [282].Hansen AL, Al-Hashimi HM, Insight into the CSA tensors of nucleobase carbons in RNA polynucleotides from solution measurements of residual CSA: towards new long-range orientational constraints, Journal of magnetic resonance (San Diego, Calif. : 1997), 179 (2006) 299–307. [DOI] [PubMed] [Google Scholar]
- [283].Ying J, Grishaev A, Bryce DL, Bax A, Chemical shift tensors of protonated base carbons in helical RNA and DNA from NMR relaxation and liquid crystal measurements, Journal of the American Chemical Society, 128 (2006) 11443–11454. [DOI] [PubMed] [Google Scholar]
- [284].Ganser L, Chu CC, Bogerd HP, Kelly ML, Cullen BR, Al-Hashimi HM, Stabilizing non-native excited states as a therapeutic strategy for targeting RNA, Submitted, (2019). [Google Scholar]
- [285].Rangadurai A, Zhou H, Merriman DK, Meiser N, Liu B, Shi H, Szymanski ES, Al-Hashimi HM, Why are Hoogsteen base pairs energetically disfavored in A-RNA compared to BDNA?, Nucleic acids research, 46 (2018) 11099–11114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [286].Kool ET, Active site tightness and substrate fit in DNA replication, Annual review of biochemistry, 71 (2002) 191–219. [DOI] [PubMed] [Google Scholar]
- [287].Rozov A, Demeshkina N, Westhof E, Yusupov M, Yusupova G, New Structural Insights into Translational Miscoding, Trends in biochemical sciences, 41 (2016) 798–814. [DOI] [PubMed] [Google Scholar]
- [288].Watson JD, Crick FH, The structure of DNA, Cold Spring Harbor symposia on quantitative biology, 18 (1953) 123–131. [DOI] [PubMed] [Google Scholar]
- [289].Strebitzer E, Rangadurai A, Plangger R, Kremser J, Juen MA, Tollinger M, Al-Hashimi HM, Kreutz C, 5-Oxyacetic Acid Modification Destabilizes Double Helical Stem Structures and Favors Anionic Watson-Crick like cmo(5) U-G Base Pairs, Chemistry (Weinheim an der Bergstrasse, Germany), (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [290].Gracia B, Al-Hashimi HM, Bisaria N, Das R, Herschlag D, Russell R, Hidden Structural Modules in a Cooperative RNA Folding Transition, Cell reports, 22 (2018) 3240–3250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [291].Halvorsen M, Martin JS, Broadaway S, Laederach A, Disease-associated mutations that alter the RNA structural ensemble, PLoS genetics, 6 (2010) e1001074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [292].Kutchko KM, Sanders W, Ziehr B, Phillips G, Solem A, Halvorsen M, Weeks KM, Moorman N, Laederach A, Multiple conformations are a conserved and regulatory feature of the RB1 5’ UTR, RNA (New York, N.Y.), 21 (2015) 1274–1285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [293].Dallaire P, Tan H, Szulwach K, Ma C, Jin P, Major F, Structural dynamics control the MicroRNA maturation pathway, Nucleic acids research, 44 (2016) 9956–9964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [294].Alvarado LJ, LeBlanc RM, Longhini AP, Keane SC, Jain N, Yildiz ZF, Tolbert BS, D’Souza VM, Summers MF, Kreutz C, Dayie TK, Regio-selective chemical-enzymatic synthesis of pyrimidine nucleotides facilitates RNA structure and dynamics studies, Chembiochem : a European journal of chemical biology, 15 (2014) 1573–1577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [295].Al-Hashimi HM, Majumdar A, Gorin A, Kettani A, Skripkin E, Patel DJ, Field- and phage-induced dipolar couplings in a homodimeric DNA quadruplex, relative orientation of G center dot(C-A) triad and G-tetrad motifs and direct determination of C2 symmetry axis orientation, Journal of the American Chemical Society, 123 (2001) 633–640. [DOI] [PubMed] [Google Scholar]
- [296].Bailor MH, Sun X, Al-Hashimi HM, Topology links RNA secondary structure with global conformation, dynamics, and adaptation, Science (New York, N.Y.), 327 (2010) 202–206. [DOI] [PubMed] [Google Scholar]
- [297].Bailor MH, Mustoe AM, Brooks CL 3rd, Al-Hashimi HM, 3D maps of RNA interhelical junctions, Nature protocols, 6 (2011) 1536–1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.