Role of Valence and Semicore Electron Correlation on Spin Gaps in Fe(II)-Porphyrins

Abstract

The role of valence and semicore correlation in differentially stabilizing the intermediate spin state of Fe(II)-porphyrins is analyzed. For CASSCF treatments of valence correlation, a (32,34) active space containing metal 3d, d′ orbitals and the entire π system of the porphyrin is necessary to stabilize the intermediate spin state. Semicore correlation provides a minor (−1.6 kcal/mol) but quantitatively significant correction. Accounting for valence, semicore, and correlation beyond the active space enlarges the (³E_g–⁵A_1g) spin gap to −5.7 kcal/mol.

Many questions remain unanswered regarding the electronic structure and reactivity of metal-porphyrins. In spite of the plethora of experimental and theoretical data, a definitive understanding of the ground state electronic structure of the four-coordinated Fe(II)-porphyrins remains elusive, and the electronic mechanisms ruling the relative stability of the spin states along reaction pathways remain unknown.

In recent work, Li Manni and Alavi¹ explained the stabilization of the triplet state over the quintet state in a Fe(II)-porphyrin model system on the basis of calculations using the novel Stochastic-CASSCF approach² with a large active space of 32 electrons in 34 orbitals, which revealed a complex interplay between ring correlation in the π-system, correlated breathing of the 3d electrons in the metal center, and charge redistribution between the metal center and macrocycle. For the same model system, CASSCF calculations with smaller active spaces, up to CAS(14,16), and with a second order perturbative correction, CASPT2, understabilize the triplet state (see Figure 2 in ref (1)). This is because CASPT2 is not able to capture the higher order correlation effects and orbital relaxation outside the smaller active space. Li Manni and Alavi’s CAS(32,34) is a valence only active space, and the role of the semicore correlation was not explicitly accounted for.

Another recent work by Phung, Pierloot, and co-workers³ addresses the bias of the CASPT2 approach toward high spin states due to a poor perturbational treatment of the transition metal semicore (3s3p) shell.⁴ This well documented weakness of CASPT2 is not solved by using other zeroth-order partitionings, such as Dyall’s Hamiltonian used in NEVPT2.⁵ Pierloot and co-workers proposed a combined CASPT2/CC approach, with frozen semicore CASPT2 in a large orbital basis, for valence correlation, and coupled cluster with singles and doubles, and a perturbative triples correction, CCSD(T),^6,7 in a smaller one-electron basis, to account for the (3s3p) semicore correlation energy, Δ_sp. They report that semicore (3s3p) correlation contributes some 2.6 kcal/mol to the spin gap estimate in favor of the intermediate spin state. However, they also state “the original CASPT2 bias toward HS [high spin] states is not completely lifted in the CASPT2/CC”. CASPT2 fails here not only for semicore correlation but also for valence correlation, as already pointed out in ref (1).

In this Letter we report a unified analysis of the roles of valence and semicore correlation in the spin gaps of metal-porphyrins. In Section 2 we discuss the results of CASSCF calculations and the correlation mechanisms they reveal, and in Section 3 we analyze the performance of coupled cluster theory for treating the valence and semicore correlation.

1. Computational Details

All calculations were performed on the same model system as our earlier work,¹ where the carbon atoms in β-positions of the porphyrin ring have been replaced with H atoms. This model preserves the chemical properties of the larger metal-porphyrin complexes and, crucially, includes a π-conjugated macrocycle with the four Gouterman orbitals involved in determining the spin energetics. The calculations were all performed at a single geometry, chosen to match the ground state (triplet) geometry of the Fe(II)-porphyrin, which has a small Fe–N bond length. At this geometry ROHF, CASSCF, and CASPT2 (with small active space wave functions) all predict the ordering of the spin states incorrectly.

We report results of Stochastic-CASSCF calculations using two sets of active spaces. The (32,34) valence active space is the same as our earlier work¹ and consists of the four doubly occupied σ-orbitals on the macrocycle, pointing at the metal center, the entire π system (18 electrons in 16 orbitals), five 3d orbitals and their six electrons, five empty correlating d′ orbitals, and the empty (4s4p) shell. The larger (40,38) active space adds the four semicore orbitals (3s3p) and their eight electrons to the (32,34) active space. We employ the same ANO-RCC-VTZP basis set, integral evaluation, MCSCF procedure, and FCIQMC setup as our earlier work.¹ We used 1 billion (1B) walkers for the CASSCF(32,34) calculations and 4B walkers for the CASSCF(40,38) calculations. Increasing the walker number further to fully converge the energies with respect to the initiator error is possible using our code but was not necessary for the present work.

We also report results of calculations using coupled cluster theory. To enable direct comparison to the CASSCF calculations, we performed active space only coupled-cluster calculations up to CCSDTQ, where the correlated occupied orbitals and virtual orbitals span only the 34 or 38 active orbitals from the CASSCF(32,34) or CASSCF(40,38) calculations. The reference determinant was obtained by first performing a ROHF calculation with 32 or 40 electrons in the 34 or 38 active orbitals, respectively. In addition, we performed DCSD^8,9 and CCSD(T) calculations using the full ANO-RCC-VTZP orbital basis but with frozen orbitals obtained either from a ROHF or a CASSCF(32,34) calculation. In all cases the remaining orbitals and reference determinant are defined by performing a frozen-core ROHF calculation. We freeze the orbitals that correspond to the 1s atomic orbitals for the C and N atoms and either the 1s2s2p3s3p or 1s2s2p atomic orbitals of the metal atom, for valence and semicore calculations, respectively.

All CASSCF, Stochastic-CASSCF, and CASPT2 calculations were performed using the OpenMolcas chemistry software package,¹⁰ while the coupled cluster calculations were performed using the MOLPRO¹¹ and the MRCC¹² software packages. An ad hoc interface was created to translate orbital coefficients from the Molcas to the MOLPRO format.¹³

2. Stochastic-CASSCF Calculations

2.1. Valence Correlation via Stochastic-CASSCF(32,34)

In our earlier investigation,¹ Stochastic-CASSCF(32,34) calculations revealed that the ground state is the intermediate spin state ³E_g, characterized by a (d_x²–y²)²(d_xz)²(d_yz)¹(d_z²)¹(d_xy)⁰ electronic configuration, and that the ³A_2g state is less than 1 kcal/mol above this. The lowest energy high spin state is ⁵A_1g, characterized by a (d_z²)²(d_x²–y²)¹(d_xz)¹(d_yz)¹(d_xy)¹ electronic configuration, and was computed to be 3.1 kcal/mol above the ³E_g ground state. ROHF theory incorrectly predicts the ⁵A_1g high spin state to be the lowest in energy. The relative energies of the spin states are determined by a competition between on-site repulsion at the metal center, which favors the high-spin states, and the strength of the σ :→ d_xy dative bond interaction, which favors the intermediate spin states. At the mean-field level, the on-site repulsion among the d electrons is larger than the enhancement in the σ-donation bonding interaction that results from the vacant d_xy of the intermediate spin state. Our earlier investigation¹ revealed two correlation mechanisms that generate an enhanced σ-donation/π-back-donation interaction and stabilize the intermediate spin states.

Ring Correlation

The π natural orbitals of the Stochastic-CASSCF(32,34) wave function, the four Gouterman orbitals in particular, have occupation numbers that deviate substantially from two and zero (Figure 5 of ref (1)). This striking finding represents an important validation of Gouterman’s four-orbital model, suggested more than 60 years ago on the basis of symmetry arguments.^14,15 Ring correlation reduces the electron repulsion among the π electrons, making the macrocycle a better electron acceptor and enhancing the σ-donation/π-backdonation bonding stabilization, which favors the triplet.

Orbital Relaxation at the Metal Center

The double-shell d′ orbitals in the active space provide the necessary flexibility for the orbital relaxation induced by charge transfer excitations from the nitrogen lone pairs to the iron. This correlated breathing in turn increases the overlap with the π system and enhances π-backdonation to the macrocycle. The double-shell d′ orbitals also introduce radial correlation for the 3d electrons, further reducing on-site repulsion.

These correlation mechanisms act in synergy to stabilize the triplet state. CASSCF and CASPT2 calculations using smaller active spaces fail to stabilize the triplet since they miss one or more aspects of these coupled correlation effects, which cannot be recovered through first order perturbative corrections to the wave function.

The correlation mechanisms are also responsible for a differential redistribution of charges between metal and macrocycle. In Figure 1 we illustrate this by plotting the difference between the electron densities obtained from the CAS(32,34) and the ROHF wave functions for each of the ³E_g and ⁵A_1g states. The green areas represent regions with reduced electron density, and red areas represent regions with increased electron density, due to correlation. For both states there is a similar redistribution of electron density upon correlation. Electron density is reduced in the regions of the nitrogen lone-pairs and the inner 3d orbital region of the metal center. Electron density is increased in the π-system of the macrocycle and at the outer region of the metal center, mostly with spherical distribution (4s orbital). In the ³E_g state the formally vacant d_xy becomes populated, and the formally doubly occupied d_x²–y² orbital is depopulated due to charge transfer and on-site correlation. In the quintet state, there is almost no additional population of the singly occupied d_xy, and depletion has the symmetry of the doubly occupied d_z² orbital.

Figure 1.

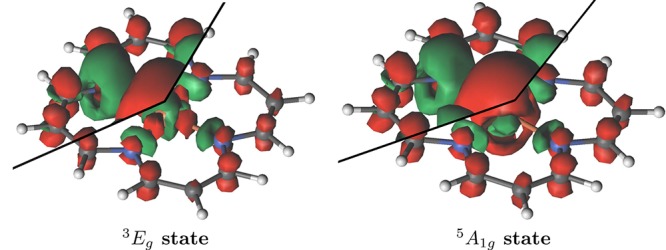
Real space total electron density difference between correlated Stochastic-CASSCF(32,34) and ROHF wave functions for the ³E_g (left) and the ⁵A_1g (right) states. For the upper-left and the lower-right corners values of 0.01 and 0.03 were used for the iso-surface contour level, respectively.

In Figure 2 we plot the difference between the density differences, namely

1

Figure 2.

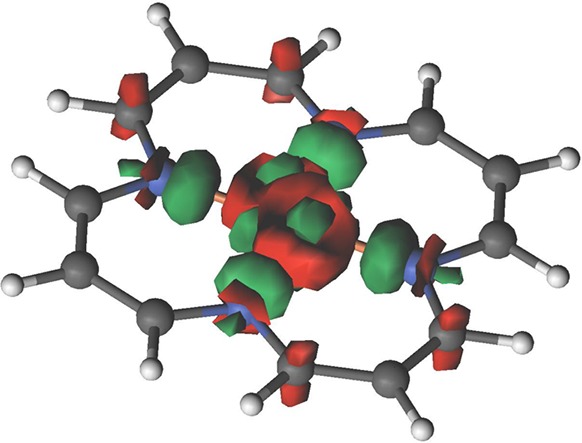
Density difference as given by eq 1. Positive and negative differences are in red and green, respectively.

There is a larger correlation induced electron redistribution in the triplet state than in the quintet, comprising of ligand-to-metal σ-donation and metal-to-ligand π-backdonation. The charge redistributions shown in Figures 1 and 2 are a consequence of correlation enhanced σ-donation/π-backdonation, where radial correlation and breathing mechanisms accommodate enhanced σ donation, reducing on-site repulsion, which in turn, together with ring correlation, enhances the π-backdonation. As discussed earlier,¹ these mechanisms are stronger for the triplet state and preferentially stabilize it, which also explains the shorter metal–ligand bond length of this state.

In Figure 3 we display the difference between the CASSCF(8,11) and the ROHF electron densities, to illustrate the failings associated with too small active spaces. The CAS(8,11) includes only the five 3d, the five d′, and the bonding σ-orbital. Although some electron redistribution associated with σ-donation and radial correlation is observed, there is no transfer of charge to the macrocycle. Since the π system is absent from this active space, the only way this could occur is via orbital mixing, but this is not observed. Also, the subsequent CASPT2(8,11) incorrectly predicts the quintet state to be 1.6 kcal/mol lower in energy than the triplet. The correlation missing from the small active space is not fully recovered through the CASPT2 correction.

Figure 3.

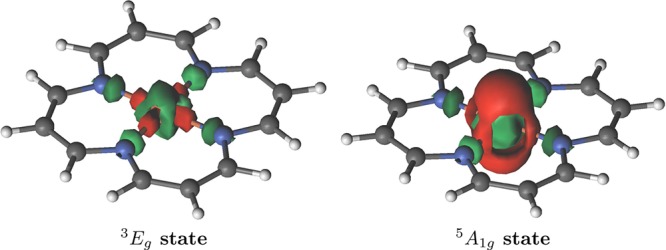
Real space total electron density difference between correlated CASSCF(8,11) and ROHF wave functions for the ³E_g (left) and the ⁵A_1g (right) states.

2.2. Semicore Relaxation via Stochastic-CASSCF(32,34)

We are interested in the effect of the semicore correlation on the relative stability of the high and intermediate spin states. First we examine how the semicore orbitals change upon correlating the valence electrons in the CASSCF optimization. Two aspects of orbital optimization in CASSCF should be borne in mind. First, the inactive orbitals relax because the mean repulsion from the active electrons changes due to the correlation in the active space. Second, core–valence orbital mixing can occur if it is energetically favorable to bring some core-orbital character into the active space.

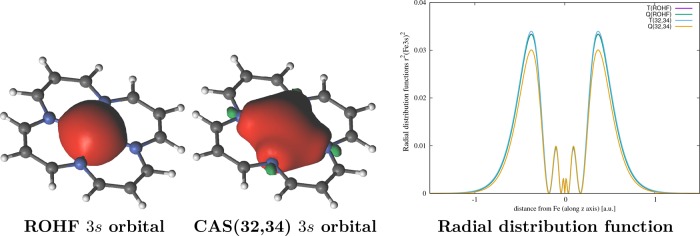
In Figure 4 we display isosurface plots and radial distribution functions for the 3s orbital at ROHF and CASSCF(32,34) levels of theory. The ROHF 3s orbitals of the triplet and quintet states are very similar and fairly localized. The CASSCF(32,34) 3s orbitals of both states exhibit significant contributions from the σ-orbitals of the ligand. However, the quintet 3s orbital is more oblate than the triplet, indicating a greater degree of hybridization. These findings suggest that there is a certain amount of semicore correlation that contributes to the metal–ligand σ interactions, in addition to the correlation-induced semicore orbital relaxation. This semicore correlation is partially accounted for via orbital optimization at the CASSCF(32,34) level.

Figure 4.

ROHF and CAS(32,34) isosurface plots of the 3s orbital for the ³E_g state and radial distribution functions along the out-of-plane z axis for the ³E_g and ⁵A_1g states.

2.3. Semicore Correlation via Stochastic-CASSCF(40,38)

To assess the influence of semicore correlation on the spin gap, we performed Stochastic-CASSCF(40,38) calculations where the 3s3p and their 8 electrons are added to the (32,34) active space. This enlarged active space contains both 3s3p and 4s4p orbitals and can therefore additionally account for radial correlation of the core orbitals and their correlated breathing relaxation. These Stochastic-CASSCF(40,38) calculations represent the most complete multireference treatment of the model Fe(II)-porphyrin system to date. At this level of theory the (³E_g–⁵A_1g) spin gap is −4.4 kcal/mol. Semicore correlation stabilizes the triplet state by a further 1.3 kcal/mol relative to the CASSCF(32,34) result of −3.1 kcal/mol. This semicore stabilization is smaller than the 2.6 kcal/mol reported by Pierloot and co-workers on the basis of coupled-cluster calculations.³

3. Coupled Cluster Calculations

3.1. Valence Correlation via the Coupled Cluster Approach

We are interested in the extent to which single reference coupled cluster theory can recover the correlation mechanisms and triplet-quintet spin gaps and the extent to which it can be used to treat semicore correlation in the manner proposed by Pierloot and co-workers.³

We performed active space only coupled cluster calculations using the optimized CASSCF(32,34) orbitals from our previous work¹ to assess the CC correlation treament within the active space against the Stochastic-CASSCF(32,34)/1B benchmark. The results are summarized in Table 1. CCSD undercorrelates both states, resulting in an underestimated spin gap. Inclusion of the (T) three-body correlation correction greatly reduces the error in the spin gap, to ∼1 kcal/mol. The DCSD prediction is remarkably close to CCSD(T). Although CCSDT provides energetics that closely agree with the Stochastic-CASSCF(32,34) values, the CCSDTQ spin gap is 0.5 kcal/mol larger. It is likely that the Stochastic-CASSCF(32,34) result with 1B walkers from ref (1) is not fully converged with respect to walker population in the FCIQMC dynamic and that this difference is primarily due to the residual initiator error.¹⁶ The convergence of the coupled cluster series is similar to that expected for a quasi single reference system. Higher-order correlation contributions beyond CCSD(T) are significant and must be included to obtain quantitative prediction of the spin gap energetics to subkcal/mol accuracy.

Table 1. ³E_g and ⁵A_1g Absolute Energies (au) and Spin Gap (kcal/mol) within the (32,34) Active Space for Various Truncation of the Many-Body Expansion in the CC Ansatz.

state	CAS(32,34)/1B	CCSD	DCSD	CCSD(T)	CCSDT	CCSDTQ
3Eg	–1951.3580	–1951.3366	–1951.3508	–1951.3538	–1951.3580	–1951.3596
5A1g	–1951.3530	–1951.3353	–1951.3466	–1951.3495	–1951.3530	–1951.3539
ΔE	–3.1	–0.8	–2.6	–2.7	–3.1	–3.6

3.2. Semicore Correlation via the Coupled Cluster Approach

In Table 2 we report the results of a series of active space only coupled-cluster calculations using the optimized CASSCF(40,38) orbitals from Section 2.3 and compare them to the Stochastic-CASSCF(40,38)/4B benchmark. The observed behavior is similar to that of Table 1. Higher-order excitations are significant, and, as before, the difference between CCSDTQ and Stochastic-CASSCF(40,38) is most likely due to the initiator error in the FCIQMC dynamic. Table 2 also reports Δ_sp, the difference between the spin gaps computed in the (40,38) and (32,34) active spaces. We find that, while CCSD and DCSD underestimate the Δ_sp semicore correlation stabilization, the CCSD(T) value is very close to CASSCF(40,38) and CCSDTQ. However, these observations apply to calculations using semicore CASSCF orbitals, which are already relaxed due to the correlation of the valence electrons.

Table 2. ³E_g and ⁵A_1g Absolute Energies (au) and Spin Gap (kcal/mol) within the (40,38) Active Space for Various Truncation of the Many-Body Expansion in the CC Ansatz.

state	CAS(40,38)/4B	CCSD	DCSD	CCSD(T)	CCSDT	CCSDTQ
3Eg	–1951.4360	–1951.4142	–1951.4281	–1951.4315	–1951.4357	–1951.4372
5A1g	–1951.4290	–1951.4124	–1951.4232	–1951.4253	–1951.4286	–1951.4295
ΔE	–4.4	–1.2	–3.1	–3.9	–4.4	–4.8
Δsp	–1.3	–0.4	–0.5	–1.2	–1.3	–1.3

To probe the respective impacts of semicore relaxation and dynamic correlation among the core and valence electrons in the context of coupled-cluster theory, we performed a series of calculations using both relaxed and unrelaxed frozen orbitals. Here we use the full ANO-RCC-VTZP orbital basis, as described in Section 1, which enables us to assess the Δ_sp correction approach used by Pierloot.³ The results are listed in Table 3.

Table 3. (³E_g–⁵A_1g) Spin Gaps (kcal/mol) with and without the 3s3p Correlation and Using Core Orbitals from Different Sources.

	CAS(32,34)			ROHF
	CCSD	CCSD(T)	DCSD	CCSD	CCSD(T)	DCSD	DCSD(T1sp)	CAS(8,11) CASPT2
ΔEnosp	3.5	–1.0	1.2	4.0	–0.4	1.8	0.2	1.6
ΔE+sp	2.3	–2.7	–0.5	2.3	–2.7	–0.5	–0.5	2.9
Δsp	–1.2	–1.6	–1.7	–1.7	–2.2	–2.3	–0.7	1.3

Comparison with the active space only coupled-cluster values in Tables 1 and 2 reveals a systematic stabilization of the quintet state upon including the full virtual set. The ANO-RCC-VTZP basis set is too small to capture the short-range features of dynamic correlation, particularly for opposite spin pairs of electrons,¹⁷ which results in an artificial basis set bias toward the high spin state. We therefore computed a ΔF12 basis set incompleteness correction as the difference between semicore–valence CCSD-F12b¹⁸ and CCSD calculations, using the ANO-RCC-VTZP basis, ROHF orbitals, and a nonrelativistic Hamiltonian. The ΔF12 correction is −2.1 kcal/mol, and the ROHF-CCSD(T)-F12 spin gap is −4.8 kcal/mol.

Turning to the coupled-cluster treatment of semicore correlation, we first computed Δ_sp as the difference between valence and semicore calculations using relaxed core orbitals, taken from our CASSCF(32,34) calculations. The CCSD(T) value is −1.6 kcal/mol, in broad agreement with the active space only value of −1.2 kcal/mol. This contribution is attributed to dynamic correlation among the core and valence electrons. We then computed Δ_sp using unrelaxed core orbitals, i.e. those from ROHF theory, which gives a combined relaxation and dynamic correlation value of −2.2 kcal/mol. Noting that the CCSD(T) value for ΔE_nosp reduces from −1.0 to −0.4 kcal/mol, we deduce that the correlation-induced relaxation of the core orbitals accounts for −0.6 kcal/mol of the spin gap, which is 28% of the overall CCSD(T) core–valence correlation contribution.

In a development version of MOLPRO, we introduced the possibility to restrict the coupled cluster excitation rank from the core orbitals to singles only. In this way we can perform valence correlation calculations where the core orbitals can relax through single excitations due to coupling with valence correlation, but without introducing pair correlations involving core orbitals into the wave function. Since CCSD theory is notably inaccurate, we performed ROHF-DCSD calculations using this approach, denoted (T₁^sp). The effect of the (T₁) semicore relaxation on valence DCSD energies is to differentially stabilize the triplet by 1.6 kcal/mol, which is 70% of the overall ROHF-DCSD Δ_sp.

Pierloot and co-workers correct their CASPT2(8,11) valence energies by adding Δ_sp computed as the difference between valence and semicore CCSD(T) calculations using ROHF orbitals.³ The valence CASPT2(8,11) spin gap for our system is 1.6 kcal/mol, and the spin ordering is incorrect. Computing the semicore correlation contribution using CASPT2 theory adds a further 1.3 kcal/mol overstabilization of the quintet, as pointed out in ref (3). Adding, our ROHF-CCSD(T) Δ_sp correction of −2.2 kcal/mol, which agrees well with the value of −2.61 kcal/mol in ref (3) (Table 3), does produce the correct ordering, but the gap is only −0.6 kcal/mol (a similarly small value is reported in ref (3)). However, the ROHF-CCSD(T) Δ_sp correction includes the effect of both dynamic correlation and relaxation and adding it to CASSCF or CASPT2 energies that already contain relaxation contributions introduces double counting, which in this case artificially stabilizes the triplet. The predicted spin gap would be even smaller if we removed the semicore relaxation contribution already accounted for in the valence CASPT2(8,11) energies.

Reference (3) concludes that the high spin state bias of the CASPT2 is not completely lifted by the CASPT2/CC approach. We certainly agree. CASPT2(8,11) fails at a fundamental level because the too small active space cannot describe the synergetic correlation involved in the σ-donation/π-backdonation and because the CASPT2 correction is too low order to properly capture these cooperative effects.

Combining a coupled cluster treatment of semicore correlation with a multireference treatment of valence correlation is reasonable, provided that the active space is capable of describing the σ-donation/π-backdonation correlation mechanisms and provided that the coupled-cluster Δ_sp correction does not contain the relaxation contribution already present in the CASSCF energies. We propose a more consistent approach. Rather than using a ROHF-CCSD(T) Δ_sp correction, we instead use a CCSD(T) Δ_sp correction computed using the CASSCF frozen orbitals, which avoids the double counting. Adding the CAS(32,34)-CCSD(T) Δ_sp value of −1.6 kcal/mol to the valence spin gap in the (32,34) active space of −3.6 kcal/mol yields a core–valence corrected gap of −5.3 kcal/mol. This value is not expected to coincide with the CAS(40,38) spin gap of −4.8 kcal/mol because the CCSD(T) Δ_sp correction contains correlation contributions beyond the active space.

4. Conclusions

We have performed a series of Stochastic-CASSCF and coupled cluster calculations to analyze the origins of the stabilization of the intermediate spin state in a model system for Fe(II)-porphyrin. ROHF, CASSCF, and CASPT2 theories, with small active spaces, all incorrectly predict a high spin quintet ground state. We analyzed the charge redistribution due to electron correlation via CASSCF(32,34) calculations, which reveal that the triplet state is stabilized by a correlation enhanced σ-donation/π-back-donation interaction with the macrocycle. This stabilization arises from the concerted effect of ring correlation, correlated breathing, and charge transfer mechanisms and is only properly described when the 3d orbitals, the σ lone pairs, and the entire π system of the macrocycle are included simultaneously in the correlation treatment. If any of these are absent from the active space, the mechanisms that stabilize the triplet are quenched and CASPT2 fails.

Although valence correlation is primarily responsible for the stabilization mechanism, we show that the 3s3p semicore orbitals relax significantly due to the valence correlation. Semicore–valence correlation increases the vertical spin gap by −1.6 kcal/mol. The CCSD(T)-based Δ_sp correction proposed by Pierloot and co-workers overestimates this stabilization due to a double counting of the semicore relaxation energy. We show that the CCSD(T)-based Δ_sp does provide an accurate semicore–valence correlation energy, provided that the orbitals are taken from an accurate CASSCF wave function. We find that CCSD(T) performs reasonably well for valence correlation but that higher-order correlation effects account for ∼1 kcal/mol of the spin gap for this system.

Our most complete multireference treatment of the vertical (³E_g–⁵A_1g) spin gap for our Fe(II)-porphyrin model is CCSDTQ calculations in the CASSCF(40,38) active space, which yield a spin gap of −4.8 kcal/mol. This active space only treatment includes both semicore and valence correlation effects but does not include the effect of dynamic correlation, which influences the relative strengths of the correlation mechanisms that determine the spin energetics. The difference between the semicore–valence CCSD(T)-F12 spin gap of −4.8 kcal/mol and the (40,38) active space only CCSD(T) spin gap of −3.9 kcal/mol provides a CCSD(T) estimate of −0.9 kcal/mol for the effect of the correlation beyond the active space. Adding this to the active space only value yields a vertical (³E_g–⁵A_1g) spin gap of −5.7 kcal/mol. Our treatment of correlation beyond the (40,38) active space is deficient in two regards: the (T) energy contribution is not converged with respect to basis set; the neglected higher-order contributions beyond (T) are significant. Both deficiencies add a bias toward the high spin state, and it is likely that an even more complete correlation treatment would further increase the vertical spin gap.

The authors declare no competing financial interest.