Deuterium Isotope Effect on the Dissociation of Weak Acids in Water and Deuterium Oxide

Abstract

The dissociation constants of o-nitroanilinium ion, m-nitroanilinium ion, and 4-chloro-2,6-dinitrophenol in deuterium oxide at 25 °C have been determined by a spectrophotometric method, and an emf method has been used to obtain (pK₁ + pK₂)/2 for citric acid in deuterium oxide. In addition, data for the dissociation constants of other weak acids in ordinary and heavy water have been critically examined with a view to clarifying the relationship between the deuterium isotope effect and the intrinsic strength of the acid. The difference ΔpK between the pK value in deuterium oxide and that in water varies linearly with pK above pK = 7. Two stronger inorganic acids (sulfuric and phosphoric) also appear to lie on an extension of this same line. On the contrary, a considerable group of organic acids with pK less than 7 have values of ΔpK that are more or less constant near ΔpK = 0.55. It appears, therefore, that the isotope effect is more complex than has heretofore been assumed.

1. Introduction

Shortly after the discovery of heavy water by Urey, Brickwedde, and Murphy [1]² in 1932, it was shown by Lewis and Schutz [2] that acids are weaker in deuterium oxide than they are in ordinary water as solvent. For example, the dissociation constant of chloroacetic acid was found to be 2.7 times greater in ordinary water than in heavy water. From this study and the work of LaMer and his colleagues [3, 4, 5] and of Martin and Butler [6], it appears that the difference in pK value, ΔpK = pK (in D₂O)−pK (in H₂O), increases approximately linearly with an increase in pK (in H₂O). This relation has been ascribed [7] to a difference in zero-point energy between the isotopes in the acid molecules or perhaps [8] to a difference in zero-point energy between the hydrogen-bonded molecules and the solvent. Thus, ΔpK = 0.43 for chloroacetic acid, 0.50 for benzoic acid [5], and 0.56 for p-nitrophenol [6]. Figure 1 is a plot of these pK differences for 11 acids from measurements made prior to 1940.

Figure 1.

Deuterium isotope effects (ΔpK) for weak acids obtained prior to 1940, plotted as a function of the pK of the acid in H₂O.

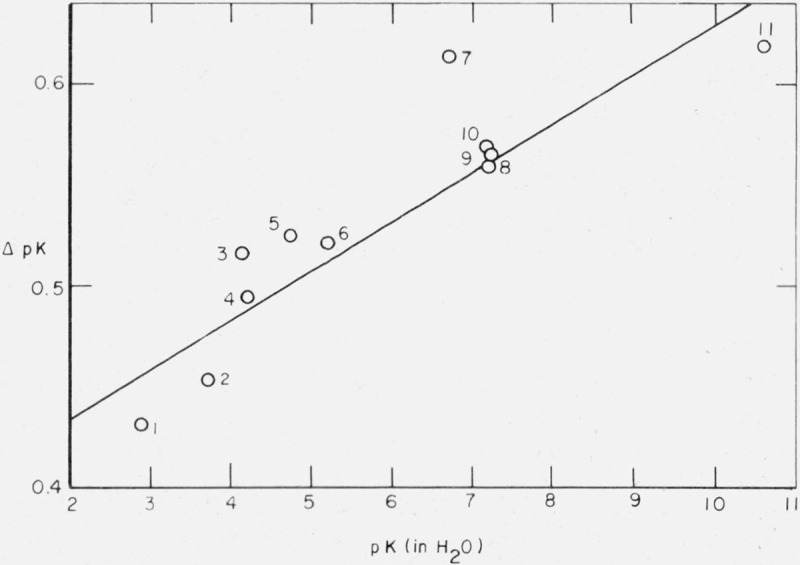
1. Chloroacetic acid
2. 2,6-Dinitrophenol
3. 2,4-Dinitrophenol
4. Benzoic acid
5. Acetic acid
6. 2,5-Dinitrophenol
7. 3,5-Dinitrophenol
8. Dihydrogen phosphate ion
9. p-Nitrophenol
10. o-Nitrophenol
11. Hydroquinone.

Curry and Hugus [9] have found ΔpK = 0.60 for the second stage of dissociation of carbonic acid, giving a point not far from the straight line drawn in figure 1. This is true also for the data for 2,2,2-trifluoroethanol and 2-chloroethanol [10]. McDougall and Long [11] have determined the pK differences for 13 acids – iodic, oxalic (both stages of dissociation), γ-resorcylic, phosphoric (first stage), chloroacetic, salicylic, m-nitrobenzoic, and glycolic acids and for 2,4- and 2,6-dinitrophenol and o- and p-nitrophenol. A plot of their data gives points not far from the straight line in figure 1.

Other results, however, do not always support this relationship. For phosphoric acid, pK₁ = 2.148 (in H₂O), McDougall and Long found ΔpK = 0.234, in contrast to the value of ΔpK = 0.438 predicted from figure 1. For salicylic acid, with pK = 2.996 (in H₂O), ΔpK = 0.75, whereas ΔpK = 0.46 would be consistent with the plot in figure 1; this discrepancy may well be due to the abnormal amount of hydrogen bonding in salicylic acid. Although, more recently, Glasoe [12] has found ΔpK = 0.56 for salicylic acid, this is still higher than one would expect from figure 1.

Furthermore, the isotope effect found by McDougall and Long [11] for o-nitrophenol (ΔpK = 0.75) seems high: Martin and Butler [6] gave ΔpK = 0.57 and Glasoe [12] gave ΔpK = 0.60. On the contrary, the value for p-nitrophenol ΔpK = 0.48, seems somewhat low: Martin and Butler found ΔpK = 0.56 and Glasoe ΔpK = 0.58. The value (ΔpK = 0.70) for 2,4-dinitrophenol is higher than that of Martin and Butler (ΔpK = 0.52) and of Glasoe (ΔpK = 0.56); Bell and Kuhn [13] found ΔpK = 0.52.

The apparent effect of an unusual amount of hydrogen bonding is also noted [14] in maleic acid. It was found that ΔpK = 0.625 for the first stage in the dissociation of maleic acid. As the pK value in ordinary water is 1.921, one might expect, from figure 1, that ΔpK would be about 0.43. On the contrary, for the second stage in the dissociation of maleic acid ΔpK was found to be 0.379; with pK₂ = 6.225 in ordinary water, one might expect ΔpK = 0.54.

This abnormal hydrogen bonding is often associated with an unusually high value of the ratio of K₁/K₂ in ordinary water. For maleic acid, this ratio is 2 × 10⁴. But a high value of this ratio does not always mean an abnormal value of ΔpK. Thus, Glasoe [15] found for diethylmalonic acid (pK₁ = 2.21, pK₂ = 7.33 in ordinary water, K₁/K₂ = 1.32 × 10⁵) that ΔpK = 0.49 for the first stage of dissociation and ΔpK = 0.41 for the second stage. Further anomalies are found in highly alkylated succinic acids [16]; thus, a difference of ΔpK = 0.90 is indicated for the first stage of dissociation of tetraethylsuccinic acid, the pK value in ordinary water being 3.39. This is almost the highest value of ΔpK yet found.

Bell and Kuhn [13] have studied the isotope effect on the dissociation of 13 acids. The pK values of these acids in ordinary water ranged from 2.50 to 5.20 and their values of ΔpK, with one exception, lie within 0.05 of the straight line in figure 1. The exception is bromoacetic acid. Their conclusion is that there is little to support a linear relation for the carboxylic acids, although a better case can be made for the phenols and alcohols.

In recent years, we have made a number of measurements of the pK values of acids in deuterium oxide solution, and it seems worthwhile to examine the relation of our results to other work. While we do not claim to have a complete solution to the problem, we have come to the very tentative conclusion that the linear relation may be valid for acids with pK greater than about 7, but that ΔpK is more or less constant at about 0.55 for stronger acids. Two notable exceptions, namely the first acid group of phosphoric acid and the second of sulfuric acid, will be discussed later in this paper.

2. Experimental Procedures

A commercial preparation of o-nitroaniline was recrystallized twice from methanol. m-Nitroaniline and 4-chloro-2,6-dinitrophenol were purified as described before [17]. A solution of deuterium chloride obtained commercially was standardized by gravimetric determination of chloride (weighing as silver chloride). The dissociation constants of the phenol and the two anilines were measured by a spectrophotometric method already described [18].

The potassium dihydrogen citrate was a portion of the same sample used in other work [19]. Emf measurements were made with cells containing potassium dideuteriocitrate and potassium chloride, using deuterium gas electrodes and silver-silver chloride electrodes; the cells were those used in the earlier work [19]. The dideuteriocitrate was formed in solution by exchange between potassium dihydrogen citrate and the deuterium oxide solvent.

3. Results

3.1. Results of Present Work

The spectrophotometric data for the two anilines and the phenol are given in tables 1, 2, and 3. The notation is the same as that used previously [18]. For the case of the anilines, the pK values quoted are those corresponding to the acidic dissociation of the anilinium ion,

$${\text{BH}}^{+}\leftrightharpoons {\text{H}}^{+}+\text{B.}$$

Table 1.

The dissociation constant of o-nitroanilinium ion in deuterium oxide solution at 25 °C

Conc. of o-Nitroaniline: 1.74 × 10⁻⁴ M, 1 cm cell, 418 nm, D₁ = 0, D₂ = 0.776.

Conc. of DCla	D	$\text{log}\frac{D_2-D}{D-D_1}$	− log mD+	pK’
0				b 0.305
0.1552	0.580	−0.471	0.809	.338
.2983	.455	−.151	.525	.374
.4010	.398	−.022	.397	.375
.4536	.366	+ .049	.343	.392
.5352	.321	−.151	.271	.422
.6447	.280	+ .248	.191	.439

^aIn moles per kilogram of solvent.

^bExtrapolated by means of the equation pK′ = 0.305 + 0.204 m_DCl.

Table 2.

The dissociation constant of m-nitroanilinium ion in deuterium oxide solution at 25 °C

Conc. of m-Nitroaniline: 3.98 × 10⁻⁴ M (3.61 × 10⁻⁴ mol/kg), 1 cm cell, 360 nm, D₁ = 0.038, D₂ = 0.568.

Conc. of DCla	D	$\text{log}\frac{D_2-D}{D-D_1}$	− log mD+	pK
0.000801	0.362	−0.197	3.180	2.983
.000984	.334	−.102	3.083	2.981
.001460	.272	+ .102	2.900	3.002
.001784	.244	+ .197	2.806	3.003
.002081	.225	+ .263	2.733	2.996
Average pK				2.993

^aIn moles per kilogram of solvent.

Table 3.

The dissociation constant of 4-chloro-2,6-dinitrophenol in deuterium oxide solution at 25 °C

Conc. of 4-Chloro-2,6-dinitrophenol: 8.06 × 10⁻⁵ M (7.30 × 10⁻⁵ mol/kg), 1 cm cell, 447 nm, D₁ = 0.002, D₂ = 0.583.

Conc. of DC1a	D	$\text{log}\frac{D_2-D}{D-D_1}$	−log mD+	−2 log γb	pK
0.0002153	0.341	−0.146	3.589	0.017	3.460
.0002587	.317	−.073	3.525	.018	3.470
.0002807	.311	−.055	3.495	.019	3.459
.0004352	.248	+ .134	3.331	.023	3.488
.0004617	.239	+ .162	3.308	.023	3.493
.0005448	.217	+ .231	3.243	.025	3.499
.0008741	.160	+ .428	3.049	.031	3.508
Average pK					3.482

^aIn moles per kilogram of solvent.

^bCalculated by means of the equation $-2\text{\hspace{0.17em}log\hspace{0.17em}}\gamma =\frac{1.0826I^{1/2}}{1+1.5I^{1/2}}.$

All values are expressed on the molality scale. The results are collected in table 4 and compared with the pK values found previously in ordinary water as solvent.

Table 4.

Dissociation constants in aqueous and deuterium oxide solutions at 25 °C determined by the spectrophotometric method

	pK (in H2O)	pK (in D2O)	ΔpK
o-Nitroanilinium ion	−0.263 [20]	0.305	0.568
m-Nitroanilinium ion	2.460 [17]	2.993	.533
4-Chloro-2,6-dinitrophenol	2.969 [17]	3.482	.513

The pK values of o-nitroaniline and m-nitroaniline given by Högfeldt and Bigeleisen [21] are not in good agreement with the present data. Nevertheless, the differences of pK (ΔpK = 0.61 for o-nitroaniline and 0.56 for m-nitroaniline) are in moderate agreement with those found in the present work. These pK differences give points lying considerably above the straight line in figure 1.

Bell and Kuhn [13] give pK (in H₂O) = 2.96, ΔpK = 0.49, for 4-chloro-2,6-dinitrophenol, so that pK (in D₂O) = 3.45. However, Bell and Kuhn based all their data for deuterium oxide solutions on pK = 5.28 for acetic acid. We now know [22] that pK = 5.313 for acetic acid in deuterium oxide (molal scale) or pK = 5.270 (molar scale), so it is evident that their values all relate to the molar scale. Their value for 4-chloro-2,6-dinitrophenol on the molal scale is, therefore, 3.49, in agreement with the value found in the present work.

Table 5 gives values of the emf of the cell

Table 5.

Emf measurements of cells containing potassium dideuteriocitrate at 25 °C

Pt;D₂, KD₂Cit (m), KCl(m = 0.01), AgCl; Ag

m	0.02	0.06	0.08	0.10
E(V)	0.59167	0.58975	0.58913	0.58863
p(aDγCl)	4.4067	4.3743	4.3638	4.3554
−log γCl	0.0744	0.1025	0.1120	0.1199
p(aDγCl)−log γCl	4.481	4.477	4.476	4.475
(PK1+pK2)/2	4.468	4.467	4.470	4.469

Pt;D₂(g, 1 atm), KD₂Cit (m), KCl(m = 0.01), AgCl; Ag

at 25 °C for four molalities of the citrate salt. The emf of this cell, E, is related to the p(a_Dγ_Cl) (≡ −log m_D+ · γ_D+ · γ_Cl−) value of the buffer solution by the equation

$$\frac{E-E^{°}}{k}+\text{log}{m}_{\text{KCl}}=p\left(a_{\text{D}}{\gamma }_{\text{Cl}}\right)$$ (1)

where m_KCl = 0.01 mol kg⁻¹, k = (RT ln 10)/F, and E°, the standard potential of the silver-silver chloride electrode, is taken to be 0.21266 V at 25 °C [23].

With the aid of the following convention [24],

$$-\text{log}{\gamma }_{{\text{Cl}}^{-}}=\frac{A\sqrt{I}}{1+1.5\sqrt{I}}$$ (2)

values of log γ_Cl− can be calculated and are given in the fourth row of table 5. As will be shown in the appendix at the end of this paper, p(a_Dγ_Cl) − log γ_Cl− (values of which are given in the fifth row) is a first approximation to (pK₁ + pK₂)/2. A good value of this quantity is obtained by extrapolation to I = 0, whereupon (pK₁ + pK₂)/2 is found to be 4.483. A more detailed analysis, taking into account the effect of overlapping stages of dissociation, is also given in the appendix and leads to values of (pK₁ + pK₂)/2 = 4.468, ΔpK = 0.523.

3.2. Results Derived From Earlier Work at NBS

Some additional values of ΔpK can be derived from emf measurements of cells without transference. These are summarized in table 6. All of the pK values are on the molal scale.

Table 6.

Dissociation constants from emf measurements in aqueous and deuterium oxide solutions at 25 °C

	pK (in H2O)	pK (in D2O)	ΔpK
Acetic acid	4.756 [25]	5.313 [22]	0.557
Deuterioacetic acid	4.771 [26]	5.325 [27]	.554
Phosphoric acid (second step).	7.201 [28]	7.780 [29]	.579
Self-dissociation of solvent.	13.997 [30]	14.955 [31]	.958

In addition, the pK values of a few acids in deuterium oxide can be derived from emf measurements which were made for a different purpose [32]. For example, the emf of the cell

Pt; D₂, NaDCO₃ (0.025 m), Na₂CO₃ (0.025 m), NaCl (0.025 m), AgCl; Ag

was found to be 0.94815 V at 25 °C and, therefore, −log (a_D+ γ_Cl−), designated p(a_Dγ_Cl), is 10.831. The dissociation constant is given by the expression

$$pK=p\left(a_{\text{D}}{\gamma }_{\text{Cl}}\right)-\text{log}\frac{m_{{\text{CO}}_{{}_3}^{--}}^{}}{m_{{\text{DCO}}_{{}_3}^{-}}^{}}-\text{log}\frac{{\gamma }_{{\text{CO}}_3^{--}}}{{\gamma }_{{\text{DCO}}_3^{-}}}$$ (3)

where this pK refers to the second stage of dissociation of carbonic acid in deuterium oxide. For this acid in ordinary water, Harned and Scholes [33] found that the equation

$$-\text{log}\frac{{\gamma }_{{\text{CO}}_3^{--}}}{{\gamma }_{{\text{HCO}}_3^{-}}{\gamma }_{{\text{Cl}}^{-}}}=\frac{2A{I}^{1/2}}{1+1.414I^{1/2}}$$ (4)

gave a good representation of the activity coefficient term in eq (3). Thus, for a cell in which all three solutes were present at a concentration of 0.02620 m, −log $\left(a_{\text{H}}^{+}\cdot {\gamma }_{{\text{Cl}}^{-}}\right)$ [designated p(a_Hγ_Cl)] = 10.096, 2 A I^1/2/(1 + 1.414 I^1/2) = 0.245, and the apparent pK value is 10.340; this requires only a small correction of −0.011, an allowance for the inadequacy of eq (4) and the necessity of a small, additional term linear in I, to give the true value, pK = 10.329. Assuming that eq (4), together with this small correction, is valid for solutions in deuterium oxide, and making the appropriate changes in the numerical value of the A parameter in eq (4) to allow for the different dielectric constant and density of heavy water, we calculate $-\text{log}{\gamma }_{{\text{CO}}_3^{--}}/\left({\gamma }_{{\text{DCO}}_3^{-}}{\gamma }_{{\text{Cl}}^{-}}\right)=0.250$ and pK = 11.070 in deuterium oxide; ΔpK = 0.741.

The pK for the second dissociation of deuteriocarbonic acid in heavy water has recently been determined carefully in this laboratory [34]. The value obtained (11.076 at 25 °C) lends confidence to the procedure described above, which provided a value of pK = 11.070 from a single measurement of p(a_Dγ_Cl).

Similarly, the emf of the cell

Pt; D₂, Na₂B₄O₇ (0.05 m), NaCl (0.05 m), AgCl; Ag is 0.87378 V at 25 °C and, hence, p(a_Dγ_Cl) = 9.875. The pK value of boric acid in deuterium oxide is given by the equation

$$pK=p\left(a_{\text{D}}{\gamma }_{\text{Cl}}\right)-\text{log}\frac{m_{{\text{BO}}_2^{-}}}{m_{{\text{DBO}}_2}}-\text{log}\frac{{\gamma }_{{\text{BO}}_2}-}{{\gamma }_{{\text{DBO}}_2}\cdot {\gamma }_{\text{Cl}}^{{-}^{\cdot }}}$$ (5)

In their investigation of this acid in ordinary water, Manov, DeLollis, and Acree [35] found that the corresponding equation for aqueous solutions could be written

$$pK=p\left(a_{\text{H}}{\gamma }_{\text{Cl}}\right)-\text{log}\frac{m_{{\text{BO}}_2^{-}}}{m_{{\text{HBO}}_2}}-\beta I$$ (6)

with β = 0.07 mol⁻¹ kg. Assuming that the same value of β can be used for deuterium oxide solutions, the pK value of boric acid in deuterium oxide is found to be 9.864, from which ΔpK = 0.630.

For phosphoric acid, a solution containing D₃PO₄ (m₁ = 0.06544), KD₂PO₄ (m₂ = 0.01579), KCl (m₃ = 0.06544), I = 0.1, it was found [32] that p(a_Dγ_Cl) = 2.107. The equation for the first dissociation constant is

$$p{K}_1=p{a}_{\text{D}}-\text{log}\frac{m_{{\text{D}}_2{\text{PO}}_4^{-}}^{}}{m_{{\text{D}}_3{\text{PO}}_4}}-\text{log}\frac{{\gamma }_{{\text{D}}_2{\text{PO}}_4^{-}}}{{\gamma }_{{\text{D}}_3{\text{PO}}_4}}=p{a}_{\text{D}}-\text{log}\frac{m_2+m_{{\text{D}}^{+}}}{m_1-m_{{\text{D}}^{+}}}-\text{log}\frac{{\gamma }_{{\text{D}}_2{\text{PO}}_4^{-}}}{{\gamma }_{{\text{D}}_3{\text{PO}}_4}}.$$ (7)

In calculating pa_D from p(a_Dγ_Cl), Covington, Paabo, Robinson, and Bates [32] calculated the activity coefficient of the chloride ion by means of the Bates-Guggenheim convention [24], eq (2). If we assume that −log γ_D+ = −log γ_Cl− = 0.114, then −log m_D+ = 1.879, m_D+ = 0.01321, and also assume that −log ${\gamma }_{{\text{D}}_2{\text{PO}}_4^{-}}/{\gamma }_{{\text{D}}_3{\text{PO}}_4}=0.114$, then, by eq (7), pK₁ = 2.362. The result is, however, very sensitive to the assumption made about the activity coefficient terms; if we assume the validity of the limiting Debye-Hückel equation,

$$-\text{log}\gamma =A{I}^{1/2}$$ (8)

then −log γ = 0.171, pa_D = 1.936, −log m_D+ = 1.765, m_D+ = 0.01718, and pK₁ = 2.273. On the contrary, if we assume the equation,

$$-\text{log}\gamma =\frac{A{I}^{1/2}}{1+7B{I}^{1/2}}$$ (9)

then −log γ = 0.100, pa_D= 2.007, −log m_{D +}= 1.907, m_D+ = 0.01239, and pK₁ = 2.382. As pK₁ = 2.148 in ordinary water [36], ΔpK = 0.214, 0.125, or 0.234, depending on which of these assumptions about the activity coefficient terms is chosen.

Alternatively, pK₁ can be expressed in terms of p(a_Dγ_Cl) as follows:

$$p{K}_1\approx p\left(a_{\text{D}}{\gamma }_{\text{Cl}}\right)-\text{log}\frac{m_2+m_{{\text{D}}^{+}}}{m_1-m_{{\text{D}}^{+}}}$$ (10)

with the plausible assumption that ${\gamma }_{{\text{D}}_2{\text{PO}}_4^{-}}/\left({\gamma }_{{\text{D}}_3{\text{PO}}_4}{\gamma }_{{\text{Cl}}^{-}}\right)$ is close to unity in these dilute buffer solutions. Unfortunately, this procedure does not remove the major source of uncertainty, namely the estimation of m_D+ needed to calculate the concentration term in eq (7). The same value of pK₁ is obtained from the two equations when log γ and m_D+ are estimated in the same way.

Data are available for succinate buffer solutions, but the evaluation of the dissociation constants is complicated by the correction which has to be made for the deuterium ion concentration and the overlapping of the dissociation constants. Detailed consideration is reserved for the appendix at the end of this paper where it is shown that ΔpK = 0.546 for the first stage of dissociation of succinic acid and ΔpK = 0.533 for the second stage.

4. Discussion

4.1. Isotope Effects Calculated From Data Obtained at NBS

Figure 2 is a plot of ΔpK against pK (in H₂O) for all the systems we have studied. The figure suggests an approximately linear variation of ΔpK with pK for values of pK greater than about 7. For stronger acids, with a single exception, ΔpK seems to be approximately constant at about 0.55, or even to pass through a flat minimum and then to increase slowly with decreasing pK value.

Figure 2.

Deuterium isotope effects (ΔpK) for weak acids at 25 °C, critically evaluated.

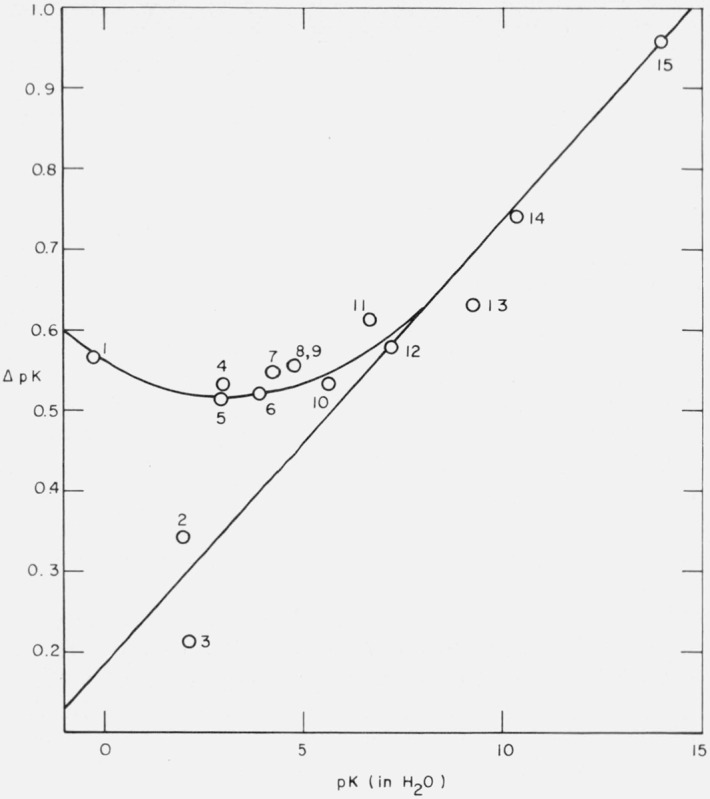
1. o-Nitroanilinium ion
2. Bisulfate ion
3. Phosphoric acid (first step)
4. m-Nitroanilinium ion
5. 4-Chloro-2,6-dinitrophenol
6. Citric acid [(pK₁ + pK₂)/2]
7. Succinic acid (first step)
8. Acetic acid
9. Deuterioacetic acid
10. Hydrogen succinate ion
11. 3,5-Dinitrophenol
12. Dihydrogen phosphate ion
13. Boric acid
14. Bicarbonate ion
15. Self-dissociation of solvent.

The single exception we have found relates to the first stage of dissociation of phosphoric acid. Another exception (the second stage of sulfuric acid) will be discussed in the next section. The point shown in figure 2 for phosphoric acid is at ΔpK = 0.214. It was derived on the assumption of the Bates-Guggenheim convention not only for the activity coefficient of the chloride ion but also for the other ions taking part in the dissociation equilibrium. We have seen that the value of ΔpK for acids as strong as phosphoric (K₁) and sulfuric (K₂) is very sensitive to the assumption made about the value of this activity coefficient, but no reasonable assumption can raise ΔpK to a value consistent with the upper curve of figure 2.

4.2. Isotope Effects Calculated From Data Obtained in Other Laboratories

The pK value for 3,5-dinitrophenol in ordinary water has been found [37] to be 6.692 at 25 °C. Martin and Butler [6] found that ΔpK for this phenol, when plotted on a graph such as that shown in figure 1, gives a point lying above the straight line shown in this figure. This value has been confirmed recently [38] when pK = 7.305 and ΔpK = 0.613 were derived from spectrophotometric measurements in deuterium oxide buffer solutions containing potassium dideuteriophosphate and disodium deuteriophosphate, the p(a_Dγ_Cl) values of which are known [29]. The point corresponding to this ΔpK value is plotted in figure 2. It can be seen that it lies about 0.03 above the curve drawn in the figure; it departs even further from the straight line drawn in this figure.

Lietzke and Stoughton [39] have studied the second stage of dissociation of deuteriosulfuric acid and derived a value of pK₂ = 2.326 at 25 °C from measurements of the solubility of silver sulfate in deuteriosulfuric acid. Spectrophotometric measurements [40] have given pK₂ = 1.983 for the second stage of dissociation of sulfuric acid in ordinary water, and hence ΔpK = 0.343. This value gives a point which is included in figure 2 and which undoubtedly belongs to the lower curve.

We now have measurements on 15 acids (only 14 points are shown in figure 2, because those for acetic acid and deuterioacetic acid are almost coincident). All of these determinations depend on sound thermodynamic theory. A well-established solubility method was utilized for one acid, and highly accurate emf measurements of cells without liquid junction gave results for 10 other acids; the data for four acids were obtained by spectrophotometric measurements. For three of these the acidity of the medium was determined by the addition of known amounts of deuterium chloride, while the fourth depended on p(a_Dγ_Cl) values calculated from the emf of cells without liquid junction. The results are collected in table 7.

Table 7.

Values of ΔpK at 25 °C

Acid	pK (in H2O)	ApK
o-Nitroanilinium ion	−0.263	0.568
Sulfuric acid (second step)	1.983	.343
Phosphoric acid (first step)	2.148	.214
m-Nitroanilinium ion	2.993	.533
4-Chloro-2,6-dinitrophenol	2.969	.513
Citric acid [(pK1 +pK2)/2]	3.945	.523
Succinic acid (first step)	4.207	.546
Acetic acid	4.756	.557
Deuterioacetic acid	4.771	.554
Succinic acid (second step)	5.638	.533
3,5-Dinitrophenol	6.692	.613
Phosphoric acid (second step)	7.201	.579
Boric acid	9.234	.630
Carbonic acid (second step)	10.329	.741
Self-dissociation of solvent	13.997	.958

From the results given in table 7 and illustrated in figure 2, it therefore seems evident that there are two distinct isotope effects. The only common factor which appears to separate the two effects seems to be that all “organic” acids give points on the upper curve, whereas the two acids which give points on the lower curve are “inorganic” or “mineral” acids. This unexpected conclusion must be regarded as a tentative one, since we have only two examples of the latter category, and we must await further work to confirm or deny its validity.

As both curves merge into one at pK values greater than about 7, it is the behavior of acids of lower pK which is of most interest. Nevertheless, some recent measurements of acids of high pK are of interest. Wehry and Rogers [41] have studied phenol and a number of substituted phenols in both ordinary water and in heavy water. For phenol itself (pK = 10.00 in H₂O), they find ΔpK = 0.62 on the molarity scale, and therefore ΔpK = 0.66 on the molality scale. This is consistent with the curve in figure 2. Similarly, they find ΔpK = 0.59, again on the molality scale, for the 4-phenolsulphonate ion with pK (in H₂O) = 8.97, which is also consistent with the curve in figure 2. Furthermore, Wehry and Rogers give data for p-nitrophenol, o-bromophenol, m-methoxyphenol, 2-naphthol, and 4-hydroxyphenyltrimethylammonium chloride, all of which are consistent with this curve. Of more interest for our present purpose are their findings for two acids of lower pK value. For 2,4-dinitrophenol [pK (in H₂O) = 4.06], ΔpK (molality scale) = 0.53; and for 2,5-dinitrophenol [pK (in H₂O) = 5.19], ΔpK (molality scale) = 0.55. Both these values of ΔpK clearly lie on the upper curve and not on the lower curve of figure 2.

Pentz and Thornton [42] find ΔpK = 0.57, 0.62, and 0.54 for 2,4-dinitrophenol, o-nitrophenol, and the imidazolinium ion, respectively, all based on the molality scale. Their value for o-nitrophenol certainly does not fall on the lower curve of figure 2 and seems somewhat higher than one would expect for the upper curve. However, Martin and Butler [6] found ΔpK = 0.61 and Glasoe [12] ΔpK = 0.64, both values converted to the molality scale; there are thus three values for o-nitrophenol which suggest that the ΔpK value for this phenol is about 0.05 higher than the point read for the upper curve of figure 2.

We have already mentioned that Bell and Kuhn [13] obtained a value of ΔpK = 0.49 on the molarity scale (0.53 on the molality scale) for 4-chloro-2,6-dinitrophenol, which compares well with our value of 0.513 (table 4). Neither value falls on the lower curve of figure 2. It is very useful to have this confirmation of the ΔpK value for an acid of this charge type with such a low pK value, because it disposes of the argument that the part of the upper curve for pK < 3 is peculiar to acids of the anilinium ion type. We now have a substituted phenol whose ΔpK value lies on the same curve. Bell and Kuhn obtained data for 12 other acids. Their ΔpK value for 2,4-dinitrophenol, pK (in H₂O) = 4.07, is 0.56 (molality scale). In agreement with the findings of Pentz and Thornton [42] (ΔpK = 0.57) and of Wehry and Rogers [41] (ΔpK = 0.53), this gives a point on the upper curve of figure 2.

For 2,5-dinitrophenol, pK (in H₂O) = 5.20, Bell and Kuhn give ΔpK = 0.57 (molality scale), in agreement with ΔpK = 0.55 given by Wehry and Rogers and consistent with the upper curve of figure 2. Bell and Kuhn give ΔpK = 0.53 (molality scale) for 2,6-dinitrophenol, pK (in H₂O) = 3.73; this gives a useful point in figure 2 because it relates to an acid of comparatively low pK, and the point lies exactly on the upper curve. They also found ΔpK values for 9 substituted acetic acids; the values of pK (in H₂O) ranged from 2.50 to 5.03 and ΔpK from 0.45 to 0.58.

Högfeldt and Bigeleisen [21] measured ΔpK for 8 acids of the anilinium ion charge type with pK (in H₂O) ranging from −1.05 (4-chloro-2-nitroanilinium ion) to 2.76 (the protonated form of aminoazobenzene), and ΔpK (presumably on the molarity scale) ranged from 0.61 for the o-nitroanilinium ion to 0.50 for the 2,6-dichloroanilinium ion. Again, these ΔpK values do not fall on the lower curve of figure 2.

Benzoic acid is important because it is the archetype of many organic acids. Rule and La Mer [5] found K (in H₂O)/K (in D₂O) = 3.13 for this acid. They found pK (in D₂O) = 7.749 for the second stage of dissociation of phosphoric acid; a value of pK = 7.780 on the molality scale has been measured recently [29], and it would seem therefore that Rule and La Mer were using either the “aquamolality” or the molarity scale. The correction to the molality scale is the same in either case, and hence Rule and La Mer’s result for benzoic acid corresponds to ΔpK = 0.54 on the molality scale, again consistent with the upper but not the lower curve of figure 2.

4.3. Influence of Temperature on the Isotope Effect

Most of the measurements referred to have been made at 25 °C. It is known [30, 43] however, that the dissociation constants of many acids increase with an increase in temperature, pass through a maximum, and then decrease in value at higher temperatures. The pK value of an acid can often [30] be represented by the equation

$$pK=\frac{A_1}{T}-A_2+A_{3}T$$ (11)

in which event the temperature corresponding to the maximum value of K (or minimum value of pK) is

$$T_{\text{max}}={\left(A_1/A_3\right)}^{1/2}$$ (12)

and the pK value at this temperature is given by the equation

$$p{K}_{\text{min}}=2{\left(A_1{A}_3\right)}^{1/2}-A_2$$ (13)

It might well be argued that a comparison between pK values in ordinary water and in deuterium oxide should be made, not at the same temperature, but at the temperature of minimum pK value in each solvent. There are, unfortunately, few measurements over a temperature range by means of which this suggestion can be verified. Nevertheless, from measurements of the dissociation constants of acetic acid [22, 25] and deuterioacetic acid [26, 27] and that of the second stage of phosphoric acid [28, 29] in ordinary water and in deuterium oxide, as well as the “self-dissociation” constants of these two solvents [30, 31], we can derive the data in table 8.

Table 8.

Values of pK in ordinary water and in heavy water at the temperature of the minimum pK value

	Water		Deuterium oxide
	tmin	pKmin	tmin	pKmin	ΔpKmin
Acetic acid	22.4	4.756	32.0	5.310	0.554
Deuterioacetic acid	22.9	4.771	32.4	5.323	0.552
Phosphoric acid (2nd step)	42.7	7.180	47.7	7.744	0.564
“Self-dissociation” constant	239	11.382	221	12.356	0.974

The temperature of maximum K value (or minimum pK value) is expressed in degrees Celsius. All pK values are on the molality scale.

The ΔpK_min value for the “self-dissociation” of the solvent obviously is not the same as those of the other three dissociation processes. It should be remembered, however, that the value for the “self-dissociation” of ordinary water at 239 °C (pK_min= 11.382) was obtained by means of an equation fitted to experimental data covering the temperature range 0 to 60 °C, the pK value at 60 °C being 13.017. Similarly, the value for deuterium oxide (pK_min= 12.356 at 221 °C) was obtained by an extrapolation of experimental data covering the temperature range 5 to 50 °C, the pK value at 50 °C being 14.182.

Extrapolation to temperatures so far from the experimental range cannot give more than a qualitative value of t_min and pK_min, and more has never been claimed. The value of ΔpK_min in table 8, therefore, contributes little to any quantitative theory that may be developed using the temperature of minimum pK value as a criterion of comparison.

Clarke and Glew [44] have suggested recently that eq (11), which expresses the variation of pK with temperature, be expanded by the addition of an A₄ ln T term and even A₅T², A₆T³ terms on the right side. We find that the addition of an A₄ln T term in eq (11) leads, in some cases, to almost the same values of t_min and pK_min as those recorded in table 8. Thus, for acetic acid in deuterium oxide, t_min = 32.6 °C, pK_min = 5.309; for deuterioacetic acid in deuterium oxide, t_min = 32.3, pK_min = 5.323; for the second step in the dissociation of phosphoric acid in deuterium oxide, t_min = 49.1 °C, pK_min= 7.743. In these three cases, t_min lies within the temperature range over which pK values were measured. But for the self-dissociation of water, where t_min is considerably above the highest temperature (60 °C) at which measurements were made, the addition of an A₄ ln T term to eq (11) leads to a value of t_min = 327 °C and pK_min= 10.982. Moreover, a similar procedure with the self-dissociation constant of deuterium oxide leads to the conclusion that there is no minimum in the pK versus T curve. Hence, a valid treatment along these lines can be made only when experimental measurements at high temperatures are available.

The values of ΔpK_min given in table 8 for acetic acid and deuterioacetic acid are almost identical. This not surprising; it would have been most unexpected to find any significant difference. However, the values of ΔpK_min for acetic acid and for the second stage of dissociation of phosphoric acid differ by only 0.010, despite the fact that for acetic acid pK_min (in H₂O) = 4.756 and for phosphoric acid pK_min (in H₂O) is higher by 2.424.

Although these results suggest that ΔpK at t_min may be independent of the strength of the acid, confirmation of this simple rule must await the availability of deuterium isotope effects for many more acids over a temperature range.

5. Appendix

5.1. Dissociation Constants of Citric Acid at 25°C

We have measured the emf at 25 °C of the cell

Pt;D₂, KD₂Cit (m), KC1 (m = 0.01), AgCl;Ag

where Cit = citrate, using cells with four different values of the citrate molality (m). These values of m, together with the emf of the cell, are given in table 5, along with the values of p(a_Dγ_Cl) calculated with the aid of the standard potential of the silver-silver chloride electrode in deuterium oxide at 25 °C, namely 0.21266V [23].

For the dissociation processes

$${\text{D}}_3\text{Cit}={\text{D}}^{+}+{\text{D}}_2{\text{Cit}}^{--}$$

and

$${\text{D}}_2{\text{Cit}}^{-}={\text{D}}^{+}+{\text{DCit}}^{--}$$

the following mass-law expressions can be written:

$$K_1=a_{{\text{D}}^{+}}\frac{m_{{\text{D}}_2\text{Cit}-}}{m_{{\text{D}}_3\text{Cit}}}\frac{{\gamma }_1}{{\gamma }_0}$$ (14)

and

$$K_2=a_{{\text{D}}^{+}}\frac{m_{{\text{DCit}}^{--}}}{m_{{\text{D}}_2{\text{Cit}}^{-}}}\frac{{\gamma }_2}{{\gamma }_1}$$ (15)

where the subscripts to γ denote the charge of the citrate species. The condition for mass balance is $m=m_{{\text{D}}_3\text{Cit}}+m_{{\text{D}}_2{\text{Cit}}^{-}}+m_{{\text{DCit}}^{--}}$, and the condition for electrical neutrality is

$$m+m_{{\text{D}}^{+}}=m_{{\text{D}}_2{\text{Cit}}^{-}}+2m_{{\text{DCit}}^{--}}+m_{{\text{OD}}^{-}}.$$

Hence, if m_D+ and m_OD− are negligible compared with m,

$$m_{{\text{D}}_3\text{Cit}}=m_{{\text{DCit}}^{--}}$$ (16)

Thus

$$K_1{K}_2={\left(a_{{\text{D}}^{+}}\right)}^2\frac{{\gamma }_2}{{\gamma }_0}$$ (17)

or

$$\left(p{K}_1+p{K}_2\right)/2=p{a}_{\text{D}}-1/2\text{\hspace{0.17em}log}\frac{{\gamma }_2}{{\gamma }_0}.$$ (18)

Making the reasonable assumption that γ_o ≈ 1 and that log γ₂ = 4 log γ_Cl−, where log γ_Cl− is given by eq (2), the convention proposed by Bates and Guggenheim [24], eq (18) can be written

$$\left(p{K}_1+p{K}_2\right)/2=p\left(a_{\text{D}}{\gamma }_{\text{Cl}}\right)-\text{log}{\gamma }_{{\text{Cl}}^{-}}$$ (19)

Values of log γ_Cl−, calculated with the aid of (eq 2), are given in table 5, together with values of p(a_Dγ_Cl)−log γ_Cl−. If eq (19) were exact, the quantities on each side of the equation would be constant, independent of the total ionic strength. Table 5 shows that this is not strictly true, the value of p(a_Dγ_Cl)−log γ_Cl^_ increasing slowly as the concentration of potassium dideuteriocitrate in the cell solution decreases. This is undoubtedly due to minor imperfections in the assumptions we have made. These can be allowed for by rewriting eq (19) as follows:

$$\left(p{K}_1+p{K}_2\right)/2=p\left(a_{\text{D}}{\gamma }_{\text{Cl}}\right)-\text{log}{\gamma }_{{\text{Cl}}^{-}}+\beta I=\alpha +\beta I.$$ (20)

Using the method of least squares, we find α = 4.483, β = −0.0747 kg mol−¹. Hence (pK₁ + pK₂) /2 = 4.483. As the corresponding quantity for ordinary water as solvent is 3.945 [45], it follows that ΔpK = 0.538.

Equation (18), however, is also not exact. A detailed examination of the problem requires a consideration of the effect of the third dissociation constant of citric acid [46, 47]. Let us consider the case of a tribasic acid at an initial concentration m, to which strong alkali is added in amount xm. Solution of the equations for electrical neutrality and mass balance yields the equation

$$S{K}_1{K}_2{K}_3+R{a}_{\text{D}+}{K}_1{K}_2+Q{a}_{{\text{D}}^{+}}^2{K}_1=P{a}_{{\text{D}}^{+}}^3$$ (21)

where, for solutions sufficiently acidic that m_OD− can be neglected,P = (xm + m_D+)/γ₀, Q = [(1 − x)m − m_D+]/γ₁, R = [(2 − x)m − m_D+]/γ₂, and S = [(3 − x)m − m_D+]/γ₃, where again the subscript to γ indicates the charge on the particular citrate species. The case with which we are now concerned is that in which sufficient alkali has been added to citric acid to complete the first stage of neutralization: x = 1. Then

$$K_1{K}_2=\frac{m+m_{{\text{D}}^{+}}}{m-m_{{\text{D}}^{+}}}\frac{{\gamma }_2}{{\gamma }_0}{a}_{\text{D}+}^2+\frac{m_{{\text{D}}^{+}}}{m-m_{{\text{D}}^{+}}}\frac{{\gamma }_2}{{\gamma }_1}{K}_1{a}_{{\text{D}}^{+}}-\frac{2m-m_{{\text{D}}^{+}}}{m-m_{{\text{D}}^{+}}}\frac{{\gamma }_2}{{\gamma }_3}\frac{K_1{K}_2{K}_3}{a_{{\text{D}}^{+}}}.$$ (22)

The second and third terms on the right of eq (22) are small compared with the first term; consequently, only approximate values of K₁, K₂, and K₃ are needed. These were obtained from the known values in water, together with ΔpK values read from figure 2. The values used were pK₁ = 3.67, pK₂ = 5.30, and pK₃ = 6.97. Hence, K₁K₂ could be calculated, and the quantity (pK₁ + pK₂)/2 is given in the last row of table 5. There is no systematic trend with change in concentration m, and we take the mean, 4.468, as the best value of (pK₁+ pK₂)/2. Thus ΔpK = 0.523.

5.2. First Dissociation Constant of Succinic Acid in Deuterium Oxide at 25 °C

We follow the method of Pinching and Bates [48]. Consider a solution of D₂S (3m) + NaDS (m) + NaCl (m′), where S represents succinate. The first dissociation constant is given by the expression

$$K_1=\frac{a_{{\text{D}}^{+}}{m}_{\text{DS}}-{\gamma }_{{\text{DS}}^{-}}}{m_{{\text{D}}_2\text{S}}{\gamma }_{{\text{D}}_2\text{S}}}$$ (23)

and the second dissociation constant by

$$K_2=\frac{a_{{\text{D}}^{+}}{m}_{{\text{S}}^{--}}{\gamma }_{{\text{S}}^{--}}}{m_{{\text{DS}}^{-}}{\gamma }_{{\text{DS}}^{-}}}$$ (24)

From eq (24),

$$m_{{\text{DS}}^{-}}=\frac{a_{{\text{D}}^{+}}}{K_2}\cdot m_{{\text{S}}^{--}}\cdot \frac{{\gamma }_{{\text{S}}^{--}}}{{\gamma }_{{\text{DS}}^{-}}}.$$ (25)

By the condition of electrical neutrality,

$$m+m_{{\text{D}}^{+}}=m_{{\text{DS}}^{-}}+2m_{{\text{S}}^{--}}$$ (26)

and by the condition of mass balance,

$$m_{{\text{D}}_2\text{S}}+m_{{\text{DS}}^{-}}+m_{{\text{S}}^{--}}=4m.$$ (27)

From (26) and (27) it follows that

$$m_{{\text{D}}_2\text{S}}=3m-m_{{\text{D}}^{+}}+m_{{\text{S}}^{--}}$$ (28)

and from (25) and (26),

$$m_{{\text{S}}^{--}}\left(2+\frac{a_{{\text{D}}^{+}}}{K_2}\cdot \frac{{\gamma }_{{\text{S}}^{--}}}{{\gamma }_{{\text{DS}}^{-}}}\right)=m+m_{{\text{D}}^{+}}.$$ (29)

For a solution of (0.03689 m D₂S + 0.01230 m NaDS + 0.08609 m NaCl) in deuterium oxide at 25 °C (ref. 32, table 1, solution No. 4a), it has been found that p(a_Dγ_Cl) = 4.253 and, by the Bates-Guggenheim convention [24], −log γ_Cl− = 0.114; hence, pa_D = 4.139. Assuming that log γ_D+ = log γ_Cl−, we have −log m_D+ = 4.025, m_D+ = 9.44 × 10⁻⁵. The value of pK₂ is taken to be 6.209 (see the next section of the appendix). It is further assumed that log (γ_S−−/γ_DS−) in eq (25) is equal to 3 log γ_Cl−; it thus has the value −0.342. Then by eq (29), m_S−− = 0.00023 and, by eq (28), $m_{{\text{D}}_2\text{S}}=0.03703$, and, finally, by eq (27), m_DS− = 0.1193. Substitution of these values in eq (23), along with the approximation $\text{log}\left({\gamma }_{{\text{DS}}^{-}}/{\gamma }_{{\text{D}}_2\text{S}}\right)=\text{log}{\gamma }_{{\text{Cl}}^{-}}=-0.114$, gives pK₁ = 4.745.

It is appropriate now to examine the assumptions we have made about the activity coefficient terms. Following the procedure of Pinching and Bates [48] for succinic acid in aqueous solution, we can write

$$-\text{log}{m}_{\text{D}+}=p\left(a_{\text{D}}{\gamma }_{\text{Cl}}\right)+2\text{\hspace{0.17em}log\hspace{0.17em}}\gamma$$ (30)

where

$$-\text{log}\gamma =\frac{A{I}^{1/2}}{1+7B{I}^{1/2}}$$ (31)

and A and B are the appropriate Debye-Hückel constants for deuterium oxide solutions (A = 0.5413 kg^1/2 mol^−1/2, B = 0.3467 × 10⁸ kg^1/2 mol^−1/2 cm⁻¹ at 25 °C). Substitution of these values in eq (31) for the solution considered above, with I = 0.09839, gives −log γ = 0.097, m_d+ = 8.73 × 10⁻⁵. If it is assumed with Pinching and Bates that the activity coefficients in eqs (23) and (25) can be calculated in the same way, we find m_S−− = 0.00021, $m_{{\text{D}}_2\text{S}}=0.03701$, m_DS− = 0.01197, and pK₁ = 4.743.

Applying the first approach to a solution containing 0.03689 m D₂S + 0.01230 m NaDS + 0.01500 m NaCl (see ref. 32, table 1, solution No. 4b) for which I = 0.02730, we find pK₁ = 4.751. Since we now have pK₁ = 4.751 at I = 0.02730 and pK₁ = 4.745 at I = 0.09839, the value of pK₁ at infinite dilution must be close to 4.753. In ordinary water, pK₁ = 4.207 and, therefore, pK₁= 0.546.

5.3. Second Dissociation Constant of Succinic Acid in Deuterium Oxide at 25 °C

The calculation follows the method of Pinching and Bates [49]. Consider a solution of NaDS (m) + Na₂S (m) + NaCl (m′). From eq (23)

$$m_{{\text{DS}}^{-}}=\frac{K_1}{a_{{\text{D}}^{+}}}\cdot m_{{\text{D}}_2\text{S}}\cdot \frac{{\gamma }_{{\text{D}}_2\text{S}}}{{\gamma }_{{\text{DS}}^{-}}}.$$ (32)

By the condition of electrical neutrality,

$$3m+m_{\text{D}+}=m_{\text{DS}-}+2m_{\text{S}--}$$ (33)

and by the condition of mass balance,

$$m_{{\text{D}}_2\text{S}}+m_{\text{DS}-}+m_{\text{S}--}=2m.$$ (34)

From eq (33) and (34), it follows that

$$m_{\text{DS}-}=m-m_{\text{D}+}-2m_{{\text{D}}_2\text{S}}.$$ (35)

Combining eq (35) with eq (32) gives

$$m_{{\text{D}}_2\text{S}}\left(2+\frac{K_1}{a_{\text{D}+}}\cdot \frac{{\gamma }_{{\text{D}}_2\text{S}}}{{\gamma }_{\text{DS-}}}\right)=m-m_{\text{D}+}.$$ (36)

For a solution of 0.02007 m NaDS + 0.02007 m Na₂S + 0.02007 m NaCl in deuterium oxide at 25 °C (ref. 32, table 1, solution No. 6), p(a_Dγ_Cl) has been found to be 6.043, and, again by the Bates-Guggenheim convention [24], −log γ_Cl− = 0.114, pa_D = 5.929. If log γ_D+ is again taken equal to log γ_Cl−, we have −log m_D+ = 5.815, m_D+ = 1.53 × 10⁻⁶, and the deuterium ion correction is negligible. Putting pK₁ = 4.753 (see appendix 5.2 above), eq (36) gives $m_{{\text{D}}_2\text{S}}\text{= 0.00093}$ and, by eq (35), m_DS− = 0.01821. Finally, by eq (34), m_S−− = 0.02100 and, hence, by eq (24), pK₂ = 6.205. Pinching and Bates used eq (31) to express all the activity coefficients and, if we follow this procedure, we find pK₂ = 6.171. This is probably the better value, especially if a comparison with the pK₂ value in ordinary water (5.638 at 25 °C) is to be made; hence, ΔpK = 0.533.