Abstract
The investigation of the effects of sorption in a gas thermometer used to realize the Thermodynamic Kelvin Temperature Scale has been continued. By eliminating sorbable material more completely from the gas thermometer, we attained higher gas purity. So little contaminant remained that further cleanup produced no significant effect on the values of thermodynamic temperatures measured between 0 °C and 142 °C. The results are presented by giving the differences between the values on the thermodynamic scale and the International Practical Temperature Scale of 1968. The value of the steam point was determined to be 99.970 °C(therm) with an uncertainty of ±3.5 mK at the 99 percent confidence level (based on 3 times the estimate of the standard deviation).
Keywords: Gas thermometry, International Practical Temperature Scale of 1968, sorption, steam point, temperature standards, Thermodynamic Kelvin Temperature Scale
1. Introduction
The value, 273.16 K, was assigned in 1954 [1]1 to the temperature of the triple point of water on the Thermodynamic Kelvin Temperature Scale (TKTS). In selecting a single value to fix the size of the degree, the Comité Consultatif de Thermométrie (CCT) [2] acted as Kelvin had suggested in 1854. It was the consensus of the CCT then that this choice would make the temperature interval between the ice and steam points very near to 100 degrees.
The value chosen was a rounded average of four single values, each derived from researches at the following institutions: the Physikalisch-Technisches Reichsanstalt (Germany), the Kamerlingh Onnes Laboratory (the Netherlands), the Tokyo Institute of Technology (Japan) and the Massachusetts Institute of Technology. It happened that the first three of these values had a spread of only 0.005 °C, but the MIT value exceeded their average by 0.02 °C. This exception led some members of the committee to suspect that the large MIT value had resulted from systematic errors, and thus would justify its rejection. However, its inclusion did not change the average enough to change the preferred figure to the nearest hundredth of a degree so it was retained, and the choice was considered felicitous.
The MIT value had been an average value itself [3], obtained from experiments with different gas thermometers. Each research was as self-consistent as any of the foreign researches, but these different researches at the MIT yielded different values. This indicated that there were indeed systematic errors, but their identities were not apparent at that time.
Subsequently a value for the steam point was obtained at the Physikalisch-Technische Bundesanstalt (Germany) (PTB) in 1956 and was reported to the session of the CCT in 1971 [4], as 99.984 °C(therm). However, when a new value for the steam point 99.999 °C (therm) [5] was determined at the National Research Council (Canada) during that portion of the session of the CCT held in Ottawa (1967), the 1954 choice of 273.16 K for the triple point of water tended to be confirmed.
Between 1900 and 1954, experimentally determined values of the ice point on the Kelvin Scale have differed by almost 0.2 K. We doubt that the variation of the results obtained from different good gas thermometers can be explained by unsuspected equipment difficulties, e.g., manometry. Sorption produces a systematic error which yields too high a ratio of the value for the steam point to that for the ice point. It now seems likely that much of the variation was caused by variation in the amount of sorption. Even though it has been recognized for a century that sorption may cause errors in gas thermometry, the subtleties of sorption are such that it is by no means certain that it has yet been eliminated. As a means of reducing sorption, Chappuis baked and pumped his gas thermometer bulb [6]. The MIT gas thermometers had been evacuated for periods of a month, during a part of which time the bulbs were at 500 °C. Moser, however, asserted that the PTB constant-bulb-temperature method of gas thermometry avoided sorption errors since the temperature of the bulb is not changed [7]. That assumption was probably incorrect, because with that method gas is expanded into a second bulb by withdrawing mercury, and additional cool surfaces are exposed. At the same time the reduction of pressure in the hot bulb will lead to re-equilibration of sorbable species. Despite the attention that had been given to cleanup in the foregoing researches, there is substantial variation in their results, which we interpret as due to significant but different amounts of sorption.
Varying amounts of sorption are usually involved when the fiducial state is not reproducible despite the attainment of a stable, gas-tight system. The measurements of the fiducial state were reported in detail in Chappuis’ publications [8–11], in those of Day and Sosman [12], and of Beattie et al. at the MIT [13]. They were also given by Oishi [14] and discussed by Moser et al. [15], among others, and there was, in general, considerable variation. In some other gas thermometry researches, important variation of the fiducial point has occurred, but the information was not published.
High precision of the fiducial and measuring states, however, is no guarantee that sorption was absent. If either the thermometric fluid was a sorbable species, or the thermometer contained sorbable contaminants, high precision may have been obtained because the sorption was quantitatively reversible within the time scale of the measurement.
Some gas thermometers were operated both as constant volume and as constant pressure thermometers. If the different values of temperature for the same state are found to vary significantly more than the equipment uncertainties justify, the variation is likely to have been caused by sorption effects. There are numerous examples in the literature of measurements made by both modes [16], and usually they show a distinct disparity in the results.
The possibility that sorption is the largest remaining systematic error of gas thermometry has been discussed in prior publications about the NBS gas thermometer. For the present state of knowledge, the evaluation of that error depends upon experimental measurements.
In our last paper, we reported a value of 99.973 °C (therm) as realized at the steam point by our gas thermometer [17]. This value had been significantly lowered by using techniques to reduce sorption, in particular by stringent cleanup and by the choice of a nonsorbable gas for the thermometric fluid. The cleanup was effected by vacuum bakeout of the thermometer bulb at 650 to 800 °C for 4 or more weeks, with prolonged evacuation of the rest of the system. The thermometric fluid was helium, which is not expected to be adsorbed or absorbed per se. Hence, to the extent that the helium had been sufficiently purified before being introduced into a scrupulously clean system, sorbable gases were eliminated, and the gas thermometer measurements were free of significant error from sorption.
We have shown that successively improved cleanup has reduced our experimentally measured values of the thermodynamic temperature of the steam point, but we have not yet demonstrated that a better cleanup procedure might not produce a further discernible effect. This paper presents the most recent efforts to reduce any contamination that might remain in the system or that might be introduced in the gas used as the thermometric fluid. The results of this gas thermometry are shown as the differences between the thermodynamic values, as realized, and the IPTS–68 values for the same temperatures in the range 0 < t68 < 142 °C.
2. Equipment
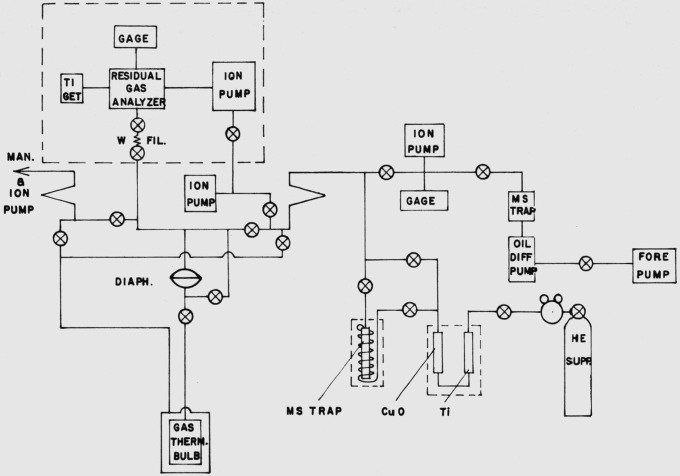
The NBS gas thermometer was operated as a “constant volume” type. It had a bulb in the shape of a right circular cylinder of platinum −12 percent rhodium, with internal dimensions of 7.620 cm in diameter and 9.972 cm in height. The sides and bottom were 0.094 cm thick, but the top was made 0.297 cm thick to give it more stiffness. The bulb was surrounded by a heavy Inconel 600 case with a uniform 0.025 cm clearance between them for a counter-pressure system. The bulb was connected by a 0.9 mm i.d. heavy-walled tube of platinum −10 percent rhodium to a valve and a pressure transducer (see fig. 1).
Figure 1.
Schematic of gas thermometer with gas handling, analysis and pumping system.
The pressure was determined by a mercury manometer with account being taken of the associated “pressure heads” and of the difference of pressure across a pressure transducer [18]. On the gas thermometer side the pressure transducer had a volume of about 100 mm3, separated from the manometer side by a brass diaphragm. The diaphragm position was determined by measuring the capacitance between it and a flat electrode on the manometer side. After the initial filling, the pressure in the gas thermometer was adjusted to balance the pressure for which the manometer was set by changing the gas thermometer temperature. Large changes of the temperature of the gas thermometer were made by lifting it from one thermostated stirred liquid bath and lowering it into another and small changes of the temperature were made by changing the regulating point of the thermostat. The pressure was deemed close enough to balance if the remainder of the pressure to be accounted for (by diaphragm deflection) was 1/3 μm Hg (0.44 Pa) or less.
The thermostated baths provided an environment, stable and uniform in temperature within 0.1 mK, over the range 0 to 142 °C. The temperature was measured on the IPTS–68 by three standard platinum resistance thermometers, newly calibrated at the steam point and at the triple point of water with an a.c. resistance thermometer bridge [19].
3. Measurement of Gas Thermometer Parameters
The volume of the connecting tube (the dead space) was calculated from the measured average inner diameter of each millimeter increment in length [20]. Values of temperature corresponding to each millimeter were derived from measurements of the e.m.f. produced by platinum-platinum 10 percent rhodium thermocouples, the junctions of which were spaced every 2.54 cm from the room temperature end for 30 cm along the tube into the bath. The values of Celsius temperature were converted to the reciprocal of the thermodynamic Kelvin values, which were then fitted by an appropriate polynomial equation as a function of position. These equations were chosen to fit the data well enough that the value of reciprocal Kelvin temperature for any position could be interpolated with sufficient accuracy for either the dead space or pressure head calculations. The anticipated uncertainty in a measured thermodynamic temperature as a consequence of the combined uncertainties of temperature and volume in the dead space is less than 1 ppm even at the gold point.
Because the gas thermometer bulb was in a counter-pressure system, the volume ratio for two states involved only the thermal expansion of the bulb. The volume ratio of the bulb varies with temperature as the cube of the corresponding length ratio, viz., , where , and Δt is the difference of the temperatures in °C (Int. 1698). The linear thermal expansion was determined for samples from the same sheet of material that was used to make the bulb. These were annealed at 1000 °C for 2 h in an argon atmosphere, and then the lengths of each sample at different temperatures were determined by an interferometer [21]. A quadratic equation was fitted to the data from repeated measurements of a single sample by least squares, yielding an estimated relative standard deviation of the mean of ± 5 × 10−7 in the range of 0 to 100 °C. The relative expansion of a sample taken from an earlier gas thermometer bulb after two years of operation differed from that of the average of other samples from the same sheet by 1 ppm at 100 °C. A final choice of values of thermal expansion will not be made until more measurements can be made on samples from the bulb itself. Any change of the final values is not expected to change the value of the steam point by more than 1 mK, but may change values above 100 °C by larger amounts where the values of thermal expansion are now extrapolations.
In the expression for calculating thermodynamic temperatures, the reference volume of the bulb, V0, occurs only in the dead space term. The effect of the dead space is equivalent to about 0.033 °C at the steam point, and remains relatively small up to the gold point. Thus, the reference volume of the gas thermometer bulb need not be known better than 0.1 percent, and can be obtained with sufficient accuracy from the dimensions measured during fabrication.
4. The Residual Gas Analyzer and the Gas Handling System
A year ago we had anticipated that we would use the residual gas analyzer (RGA) to detect very low levels of impurities in a direct analysis of the thermornetric fluid [17]. The RGA proved to be unsuitable because it was impossible to evaluate the concentration of sorbates evolved from its filament with sufficient accuracy. Nevertheless, the RGA was still valuable for identifying sources of sorbates from the gas thermometer system, from pump backstreaming, and from intermittent leaks. The knowledge made possible improvements in the system and in cleanup procedures. These, together with improved gas purification techniques, assured that sorption was reduced, certainly below the level needed to attain the first three criteria of cleanliness given in our previous paper [17], and possibly to an insignificant level.
Guided by the output from the RGA, we were able to reduce the concentration of sorbatesin the gas thermometer bulb. The residual impurity in the bulb at 650 °C was ultimately almost all H2. The vacuum bakeout was considered adequate when the hydrogen pressure in the bulb was 1 nm Hg or less,2 for, when the bulb had cooled down to 400 °C, no significant concentration of gas except helium was detectable above the system background.
Evidence derived from the RGA indicated that both CO and CH4 were backstreaming extensively from the oil diffusion pump. (This problem will be much reduced by changing to an improved oil diffusion pump [22]). The pumping equipment was therefore augmented, so that after an initial brief pumpdown by the oil diffusion pump to remove helium, the system could be isolated from it and then evacuated by ion pumps, in cascade if desired, as shown in figure 1. As part of a second modification, valves were installed so that the ion pumps could be isolated from any part of the system used for gas handling. Thus contamination by gases, released from the ion pumps when they had to be shut down, could be avoided.
The gas purification was also improved. In the final arrangement, helium (stated to be 99.9999 percent pure) was passed through a trap of titanium metal chips at 900 °C, where chemically reactive materials would combine with the Ti to form nonvolatile compounds, with, in some cases, the release of hydrogen. The titanium itself was further source of hydrogen, which is desorbed at temperatures above 400 °C. Therefore, the next trap in the purification train contained CuO, also at 900 °C, to convert all the hydrogen into water, which was then adsorbed in a third trap onto a zeolite material (Molecular Sieve # 13) held at liquid nitrogen temperature. As a result, it is expected that the emerging helium gas could contain sorbable impurities only in concentrations well below 1 ppm.
5. Measurements and Results
The measurement procedures and the development of equations have been given in detail in a previous publication [17]. The data at each temperature consist of values of gas thermometer measurements and corresponding platinum resistance thermometer readings. From these data, corresponding values of temperature on the gas thermometer scale and on the IPTS–68, respectively, are obtained. Measurements were made at a constant pressure ratio but over different pressure ranges, with the lower (fiducial) temperature close to the triple point of water. By extrapolating the difference between the corresponding values of temperature on the gas thermometer scale and on the IPTS–68 to zero measuring pressure, one obtains at the intercept the difference between the TKTS and the IPTS–68. This method of accounting for the imperfection of the thermometric fluid is applicable in this case where the manometer is capable of high accuracy even at low pressures.
It was our intent to study sources of contamination with the RGA and to improve the system until (1) the impurity level observed on the RGA was markedly reduced and (2) the measured difference between the TKTS and the IPTS–68 at given temperatures was not affected significantly by a reduction of impurity still measurable on the RGA. Rapid progress in improving the system could be made, and the process appears to have been sufficiently complete in only two steps. For the first step, the gas system was modified by installing ion pumping and a U-tube titanium trap, one leg at 900 °C and the other at 200 °C, to the gas purification train. For the second step, the vacuum system was rearranged so that the ion pumps could be isolated from the gas lines, and the improved purification train, described in the preceding section, was installed.
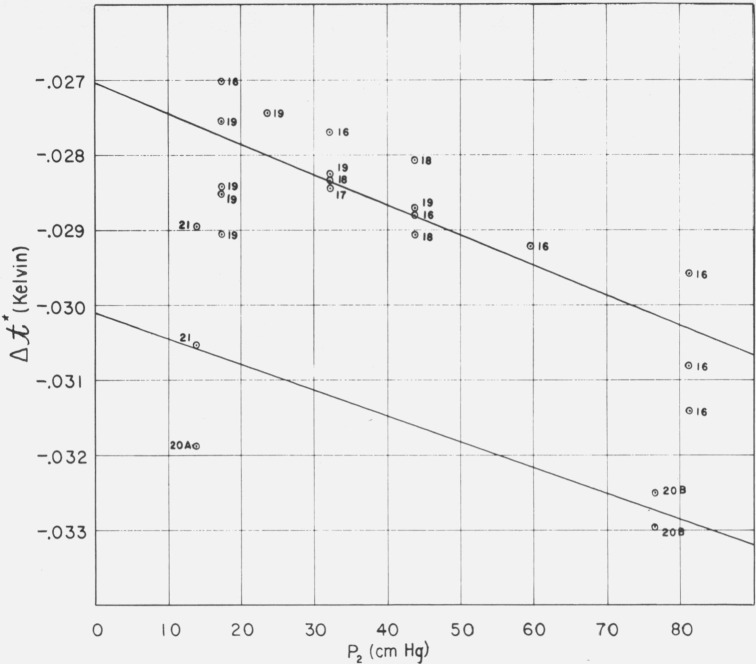
For the measurements of the first step, the gas thermometer was baked out until residual gas analysis indicated that the partial pressure of H2 remaining in the bulb was about 1 nm Hg (1 × 10−4 Pa). After cooling, helium was admitted to the system and the gas thermometer was filled. Measurements were made at 0, 100, 121, and 142 °C, based on fiducial conditions of 101.6 mm Hg (1.349 × 104 Pa) pressure at 0.01 °C (Run 20A). Further measurements in the first step were based on fiducial conditions of 560.5 mm Hg (7.441 × 104 Pa) pressure at 0.01 °C with measurements at 0 °C and 100 °C (Run 20B) made with the same pressure ratio as used in Run 20A for 100 °C. The results for the steam point are shown in figure 2; the previously presented [17] results of Runs 16–19, also at the steam point, are included for comparison.
Figure 2.
Extrapolation of gas thermometer–international scale differences to eliminate effects of gas imperfection.
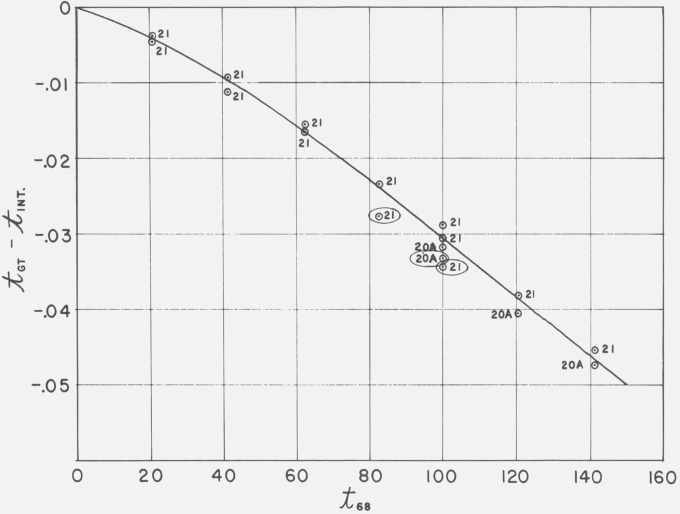
For the measurements of the second step, the gas thermometer was again baked out at 650 to 800 °C, and then it was filled with purified helium in an amount corresponding to fiducial conditions of 101.6 mm Hg (1.349 × 104 Pa) pressure at 0.01 °C. Gas thermometer measurements were made at 0 °C and at approximately 20 °C intervals up to 142 °C, and were repeated up to 100 °C (Run 21).
The difference at each measuring temperature between the values on the gas thermometer scale and the IPTS–68 is shown versus £68 in figure 3 for both Runs 20A and 21. Since the results of the two runs appeared to be indistinguishable, a polynomial was fitted to the values by least squares as
where
| (1) |
with an estimated standard deviation of the mean of
Figure 3.
Gas thermometer–international scale differences as a function of temperature.
Solid line represents eq (1). Measurements are based on a fiducial pressure of 101.6 mm Hg at 0.01 °C.
The scatter in Run 20A and Run 21 is larger than typical for the NBS gas thermometer. It occurred primarily because, at the low fiducial pressure used in these runs, a lower than usual sensitivity of the diaphragm made it impossible to detect a pressure balance with the same relative accuracy as is possible at a higher fiducial pressure. The three points enclosed by ellipses were excluded as “outlyers” on the basis that their deviation was inconsistently large for the number of points and the standard deviation. During Run 21, there were three measurements at the fiducial state which, reduced to a common basis, correspond to an average temperature of 0.00339 °C with an average deviation of ±0.00057 °C.
The effects of gas imperfection are small and approximately linear with t68 for the range 0 to 142 °C. Using the slope of the line in figure 2 to evaluate the difference at 100 °C, we can express the difference between the TKTS and the gas thermometer temperature scale as
| 2 |
for a fiducial pressure of 101.6 mm Hg (1.349 × 104 Pa) at 0.01 °C. Hence
| 3 |
where a’ = −0.157478 × 10−3 and b and c are as before. From these values of the constants, the calculated value of the steam point is 99.970 °C(therm), with an uncertainty of ±3.5 mK at the 99 percent confidence level.3
6. Discussion
Different purities are involved in the results presented in figure 2. The subsets formed by Runs 16–19 and Runs 20A–20B are each self-consistent, presumably as a result of uniform procedures within each subset. Furthermore, the subsets have an important element of consistency with respect to each other in that the slopes of the two lines are identical within experimental error. We think this feature has existed with other gas thermometry – that the data tend to be self-consistent
confidence level (3 standard deviations): 9.3 ppm or 3.5 mK because the experimenter maintained about the same level of gas purity by uniform experimental procedures, and that an approximately proportional displacement occurs for a different level of gas purity.
The measurements of Runs 16–19 were already made at a high level of system cleanliness, but means for further improvement were then developed with the help of the RGA. The displacement of the results of Runs 20A–20B from Runs 16–19 demonstrated that the improvement was significant. A further enhancement of gas purity was expected as a result of changes in the system and the procedures introduced between Runs 20 and 21, but it was expected to be small. In fact, as shown in figure 3, no effect on the results is evident. It is our opinion that the sorption in Runs 20 and 21 is sufficiently small that more cleanup is not likely to cause a significant shift of the values, and is most unlikely to be as large as 2 mK at 100 °C.
The effect of sorption, illustrated by this and our last paper [17], offers an explanation of the discrepancies which the CCT encountered in 1954 (and which must have existed for earlier gas thermometry as well). The first MIT work was carried out with vitreous silica bulbs and a thermometric fluid of nitrogen. The value of the ice point found as the average of two thermometers was T0 = 273.166 K, where the results of the other three laboratories gave an average of 273.147 K. For later work at the MIT, the gas thermometer bulb was made of Jena glass (1565III), and the thermometric fluid was helium. The values of the ice point found in three researches, one in 1943, and two in 1952, were still higher, with values of 273.174,273.188 and 273.191 °C. (The equivalent values from our results reported in our last paper and in this paper would be 273.222 and 273.232 K, respectively). The procedures used in the MIT work should have resulted in an enhanced system cleanliness over that of prior researches, and the use of helium should have reduced the effects of sorption relative to nitrogen. It appears to us that, of the values of the ice point realized up to 1954, none was high enough, but those of the MIT were the best.
The results of this research demonstrate that the TKTS differs much more from the IPTS–68 than was believed when the CCT assigned a value to the steam point of 100 °C, with a possible difference of 0.005 K from the thermodynamic value [24]. Any sorption that is uncorrected for must also affect the realization of the thermodynamic scale in other ranges of temperature. If systematic errors from sorption are the dominant uncertainty in the values adopted for the fixed points of IPTS–68 (a likely possibility in our view), the numbers below the triple point of water will prove to be too low, and above the triple point of water will prove to be too high on the thermodynamic scale. While we have no plans for measurement below 0 °C, the equipment was designed to measure the relationship between the TKTS and the IPTS–68 up to the gold point. The next set of measurements will cover the range from 160 to 450 °C. It seems almost certain that the departure of the TKTS from the IPTS will increase with increasing temperature, but the present evidence available fails to provide much quantitative guidance. If the effects of sorption are approximately linear with temperature, a difference of 0.3 K could be projected for the gold point from our work – a value in agreement with the total radiation measurements of Blevin and Brown at the National Standards Laboratory (Australia) [25]. On the other hand, spectral radiation measurements at the National Physical Laboratory (Great Britain) show a divergence of 0.5 K between the two scales over a range of only 720 to 1064 °C [26], consistent in sign with our own work. We can only conjecture that the value of the temperature of the freezing point of gold on the thermodynamic scale will prove to be lower than the value on the IPTS–68 by at least some tenths of a kelvin.
Even though the thermodynamic scale as a concept is exact, its realization in the laboratory is so difficult that the international scale in practice can be realized much more precisely. Consequently, improved knowledge of thermodynamic scale will remain a continuing goal, and it must be expressed in terms of a more certain laboratory scale. New realizations of the thermodynamic scale need not, and should not, be regarded as justifying modification of the international scale. Next to its exactness and universality, the invariance of the international scale is its most important quality. As improved realizations of the thermodynamic scale appear, they can then be recognized by adopting values of differences from the IPTS. Thus, even though conceptually the thermodynamic scale is fixed by the assignment of the value of 273.16 K to the triple point of water, and in principle the international scale may be changed, in practice the international scale can and should be held constant, while our understanding of the thermodynamic scale as realized experimentally will inevitably change.
Footnotes
Figures in brackets indicate the literature references at the end of this paper.
Deduced by multiplying the observed partial pressure of H2 observed in the RGA (1 × 10−10 mm Hg or less) by 104 in order to account for the resistance to flow through the connecting tube.
| ppm | |
|---|---|
| Estimate of the relative standard deviation of the mean of the fit to eq (1) | 2.63 |
| Estimate of the relative standard deviation of the mean of the thermal expansion | 1.5 |
| Estimate of the relative uncertainty of the dead space effect (1 standard deviation) | 0.3 |
| Estimate of the relative uncertainty of the gas imperfection correction (1 standard deviation) | 0.3 |
| Estimate of the relative uncertainty of the pressure ratio in addition to the first item (1 standard deviation) | 0.5 |
| Estimate of the total relative standard deviation of the steam point:. | 3.1 |
| Estimate of the total relative uncertainty of the steam point at the 99 percent confidence level (3 standard deviations): 9.3 ppm or 3.5 mK |
7. References
- [1].Comptes Rendus de la Dixième Conférence Générale des Poids et Mesures, p. 79 (1954). [Google Scholar]
- [2].Procès Verbaux des Séances du Comité International des Poids et Mesures, p. T 9 (1954). [Google Scholar]
- [3].Proces Verbaux des Seances du Comite International des Poids et Mesures, p. T 53 (1954). [Google Scholar]
- [4].Document 63/71, 9th Session of the Comite Consultatif de Thermométrie.
- [5].Preston-Thomas H., and Kirby C. G. M., Metrologia 4, 30 (1968). [Google Scholar]
- [6].Harker J. A., and Chappuis P., Phil. Trans. Roy. Soc. 194A, 37 (1900). [Google Scholar]
- [7].Moser H., Temperature, Its Measurement and Control in Science and Industry, Vol. 2, Chap. 7 (Reinhold Publishing Co., New York, New York: 1941). [Google Scholar]
- [8].Chappuis P., Trav. et Mem., Bureau International des Poids et Mesures 6 (1888). [Google Scholar]
- [9].Chappuis P., and Harker J. A., ibid 12 (1902). [Google Scholar]
- [10].Chappuis P., ibid. 13 (1907). [Google Scholar]
- [11].Chappuis P., ibid. 16 (1917). [Google Scholar]
- [12].Day A. L. and Sosman R. B., High Temperature Gas Thermometry (The Carnegie Institution of Washington, Washington, D.C. 1911). [Google Scholar]
- [13].Beattie J. A., Benedict M., Blaisdell B. E., and Kaye J., J. Chem. Phys. 42, 2274 (1965). [Google Scholar]
- [14].Oishi J., Awano M., and Mochijuki T.,J. Phys. Soc. Japan 11, 311(1956). [Google Scholar]
- [15].Moser H. Otto J., and Thomas W., Zeit f. Phys. 147, 76 (1957). [Google Scholar]
- [16].Beattie J. A., Temperature, Its Measurement and Control in Science and Industry, Vol. 2, p. 74–88 (Reinhold Publishing Company, New York, New York, 1941). [Google Scholar]
- [17].Guildner L. A., Anderson R. L., and Edsinger R. E., Effects of Sorption on the Realization of the Thermodynamic Scale, Temperature, Its Measurement and Control in Science and Industry, Vol. 4 (Instrument Society of America, Pittsburgh, Pennsylvania, 1973). [Google Scholar]
- [18].Guildner L. A., Stimson H. F., Edsinger R. E., and Anderson R.L., Metrologia 6, 1 (1970). [Google Scholar]
- [19].Cutkosky R. D., J. Res. Nat. Bur. Stand. (U.S.), 75C (Eng. and Instr.) Nos. 1 & 2, 15–18 (Jan-Jun 1970). [Google Scholar]
- [20].Edsinger R. E., Guildner L. A., and Anderson R. L., Rev. Sci. Instr. 42, 945 (1971). [Google Scholar]
- [21].Saunders J. B., J. Res. Nat. Bur. Stand. (U.S.), 35, 157–186 (September 1945) RP1668. [Google Scholar]
- [22].The ion pump operates by sputtering titanium. A considerable discussion of the affinity of titanium for various gases, and the contaminants which are present in a well-pumped system, is given in the paper of Shen, L. Y. L., Rev. Sci. Inst. 43, 1301 (1972). [Google Scholar]
- [23].Hablanian J. H., J. Vac. Sci. and Technol. 6, 265 (1968). [Google Scholar]
- [24].The International Practical Temperature Scale of 1968, Comptes Rendus des Seances de la Treizieme Conference Generale des Poids et Measures, Annexe 2 (1967–1968); Metrologia 5, 35 (1969). [Google Scholar]
- [25].Blevin W. R., and Brown W. J., Metrologia 7, 15 (1971). [Google Scholar]
- [26].Quinn T. J., Chandler T. R. D., and Crutch H. V., The departure of IPTS–68 from thermodynamic temperatures between 725 °C and 1064.43 °C, Metrologia (in press). [Google Scholar]