Abstract
The change in refractive index with temperature has been determined for some oxide glasses from about −200 to 700 °C. The change in refractive index with applied hydrostatic pressure has been determined at room temperature from a pressure of 105 to 108 Pa. All measurements were made using the yellow spectral line of helium. A calcium aluminate glass, an aluminum magnesium phosphate glass, a binary barium borate glass and a multicomponent germanate glass were studied, as were four commercial specimens of fused silica. From the data at room temperature, it has been possible to calculate the change in electronic polarizability with temperature at constant volume. This parameter has been found to be very high for the glasses as compared to crystals, and this agrees with the results of earlier research on silica-based optical glasses. Furthermore, over the entire temperature range, the change of refractive index with temperature is shown to be due predominantly to the temperature dependence at constant volume of the electronic polarizability. The relevance of the data to the molecular scattering of light in glasses is discussed.
Keywords: Intermerometry, light scattering, oxide glasses, polarizability, pressure, refractive index, temperature coefficient of refractive index, thermal expansion
1. Introduction
The dependence of refractive index, n, upon temperature, T, is important in optical design where systems must operate at inconstant temperature or at temperature extremes. The change of refractive index with hydrostatic pressure yields information on change with density which is interesting in itself and is important in elucidating thermo-optic theory because of the change in volume with temperature [1]1.
The thermal coefficient of refractive index has assumed greater practical importance with the advent of the laser because of the thermal lens effect which arises when an optical beam passes through a medium of finite absorption. The resulting temperature rise focuses the beam if the index increases with increasing temperature (dn/dT > 0). It has been shown that constraining stresses can cause thermal self-focusing even though the conventional value of (dn/dT < 0) [2]. Self-focusing, in general, has attracted much attention, as it is considered a precursor to filamentary damage in laser materials exposed to the high intensities obtained from oscillator-amplifier combinations in Q-switch operations [3].
The data are also of interest because of their relevance to the theory of molecular scattering of light in solids [4]. The theory predicts that the scattering is caused by small changes in the high frequency dielectric constant (or refractive index) that are induced by changes of density and temperature. At the same time, it has been observed that the central Rayleigh line in light scattered from glasses is much greater in intensity than the theory predicts. It was hoped that the basic data to be obtained in this study would help to resolve this problem. Also, to be able to reduce the optical attenuation caused by light scattering in glass would be of great practical interest for the development of optical transmission lines capable of carrying signals over large distances [5]. This might be accomplished by making a glass of the appropriate composition.
Investigations of the thermal change in refractive index and reports on the photoelastic constants for various commercial glasses have been reviewed by Baak [6]. The effect of hydrostatic pressure on refractive index may be calculated from a knowledge of the photoelastic constants. Measurements on the refractive index change resulting from the direct application of hydrostatic pressure have been reported for fused SiO2 by Vedam et al. [7], and for fused SiO2 and two commercial glasses by Waxler and Weir [8].
For solid dielectrics, including glasses, it is frequently assumed that dn/dT depends directly upon the temperature-induced change in density, ρ, but not on temperature itself. In fact,
| (1) |
| (2) |
where γ is the coefficient of volume expansion. For most substances, the first term in (2) is much smaller than the second, and dn/dT is essentially equivalent to the second term. It has been found in an earlier study that, for three optical glasses, (∂n/∂T)ρ was much larger than expected [8].
In the present study we have measured the effect of both temperature and pressure on the refractive index of some oxide glasses of different compositions and compared the values on glass with data on certain crystalline materials. We have also assessed some of of parameters of interest in optical and laser design. The materials studied were fused silica, a calcium aluminate glass, an aluminum magnesium phosphate glass, a binary barium borate glass, and a multicomponent germanate glass. The batch compositions in weight percent are listed in table 1. In addition, for the purpose of intercomparison, measurements were made on specimens of fused silica produced by Corning Glass Works, Dynasil Corporation of America and the General Electric Company. The brands are identified as Corning Code 7940 fused silica, Dynasil high-purity synthetic fused silica, General Electric Type 104 and General Electric Type 151.2
Table 1.
Glass batch compositions weight percent
| Oxide | Fused SiO2 | Glass | |||
|---|---|---|---|---|---|
| Calcium aluminate F75 | Phosphate F1329 | Barium borate E1583 | Germanate F998 | ||
| SiO2 | 100 | 5.0 | |||
| GeO2 | 35.9 | ||||
| B2O2 | 59.0 | ||||
| P2O5 | 77.7 | ||||
| AlO3 | 41.5 | 12.0 | |||
| MgO | 5.0 | 10.3 | |||
| CaO | 48.5 | ||||
| BaO | 41.0 | 21.0 | |||
| BaF2 | 5.3 | ||||
| La2O3 | 17.4 | ||||
| Ta2O5 | 3.4 | ||||
| TiO2 | 6.1 | ||||
| ZnO | 6.2 | ||||
| ZrO2 | 4.7 | ||||
2. Experimental Method
2.1. Change of Index Versus Temperature
The interference method employed by Austin and Pierce [9] offers the attractive features of high precision of measurement and the use of a small specimen, which reduces thermal gradients. The apparatus and experimental technique have been described earlier [10, 11], and will be mentioned only briefly here. Using this method the thermal expansion and thermal change in refractive index can be determined simultaneously.
The index specimen consisted of a small plate about 0.5 cm in thickness with flat, polished faces. The expansion specimen was a small tripod of the same material and thickness which separated two optical flats. For both the index and expansion specimen, a pattern of localized Fizeau-type interference fringes could be seen through a Pulfrich viewer when illuminated with collimated helium light of wavelength 587.6 nm. With change of temperature, a continuous photographic recording of the shift in fringes permitted a simultaneous measurement of the change of thickness, Δt, of the expansion specimen and the change in optical path length, Δ(nt), of the glass plate. From the photographic recording of the two fringe shifts, it was possible to calculate the change in refractive index, Δn. For the low temperature work, the specimens were enclosed in a cryostat [11] in which liquid nitrogen was used to reduce the temperature, and data were obtained from about +20 to −192 °C. For the high temperature range, the specimens were enclosed in a furnace [10] which permitted measurements from about +20 to +700 °C.
Because of the very low coefficient of thermal expansion of fused silica, no attempt was made to make this measurement (see sec. 3.2). However, for both high and low temperatures, the change in optical path length was measured on four specimens simultaneously, each specimen representing one of the brands mentioned in the introduction.
2.2. Change of Index Vs. Applied Hydrostatic Pressure
The apparatus and technique for finding the change in refractive index with applied hydrostatic pressures to 1 × 108 Pa have been described in previous publications [8, 10]. The same platelet, wavelength and technique of measuring the shift in Fizeau fringes described above was used to find the change in optical path length as a function of pressure. A pressure vessel equipped with glass windows and containing a highly transparent mineral oil was used. Pressure was generated by compressing the oil and was measured with a Heise gage to an accuracy of 1 percent or better. These measurements were made only at room temperature.
The change in thickness of the specimen was calculated from a knowledge of the elastic constants, which are shown in table 2. These constants were determined by an ultrasonic pulse echo technique for Glasses E1583 and F1329. A dynamic resonance technique was used for Glasses F75 and F998. All these measurements on the elastic constants are estimated to have an accuracy of ±2 percent. The change in refractive index with pressure for fused SiO2 has been previously reported [8] where the compression data of Bridgeman were used, and the elastic constants of fused SiO2 are not reproduced here.
Table 2.
Elastic constants
| Glass | ||||
|---|---|---|---|---|
| Calcium aluminate F75 | Phosphate Fl329 | Barium borate E1 583 | Germanate F998 | |
| Young's Modulus, E | 10.98 × l010Pa | 5.90 × l010Pa | 6.54 × 1010Pa | 9.08 × 1010Pa |
| Shear Modulus, G | 4.25 | 2.40 | 2.54 | 3.55 |
| Bulk Modulus, K | 8.79 | 3.63 | 5.08 | 6.78 |
| Poisson's ratio, y | 0.292 | 0.230 | 0.290 | 0.277 |
3. Results and Discussion
3.1. Stress-Optic Data
The quantity was calculated according to the relationship:
| (3) |
where B is the compressibility. The results are shown in table 3. The dependence of refractive index change upon density can be studied according to the theoretical Lorentz-Lorenz or Drude equations. Following Ramachandran [1], we have chosen the Drude equation:
| (4) |
where N is the number of oscillators per unit volume and α is the polarizability. If α were rigorously constant, eq (4) may be differentiated to obtain the change of index with density:
| (5) |
In eq (5), the subscript, Theor., has been added to the partial derivative to indicate that there may be a change in polarizability which has been neglected. Mueller [12, 1] has introduced the strain polarizability constant, Λ0, to measure the change in polarizability by means of the relationship:
| (6) |
where Values of Λ0 have been calculated according to the above equations and the results are given in table 3. It can be seen from the table that in every case Λ0 has a positive value. This decrease in polarizability with increase in density is typical behavior for condensed phases.
Table 3.
Analysis of change in refractive index and polarizability for glasses at wavelength, 587.6 nm
| n0 | (dn/dT) × 105 | γ×105 | (∂n/∂T)ρ × 105 | Λ0 | P ×105 | Q×105 | R × 105 | ||
|---|---|---|---|---|---|---|---|---|---|
| Fused SiO2 | 1.45846 | 0.87 | 0.13 | 0.32 | 0.91 | 0.17 | −0.05 | 0.01 | 0.91 |
| Calcium aluminate glass, F-75 | 1.67155 | 0.75 | 2.15 | 0.19 | 1.16 | 0.65 | −1.2 | 0.74 | 1.2 |
| Phosphate glass F-1329 | 1.48905 | 0.46 | 1.48 | 0.33 | 0.95 | 0.19 | −0.61 | 0.12 | 0.95 |
| Barium borate glass, E-1583 | 1.5822 | −0.11 | 1.85 | 0.40 | 0.63 | 0.16 | −0.88 | 0.14 | 0.63 |
| Germanate glass F-998 | 1.8550 | 0.86 | 2.18 | 0.39 | 1.71 | 0.41 | −1.4 | 0.58 | 1.7 |
The change in refractive index resulting from applied hydrostatic pressure on cubic crystals and glasses is attributed then to two opposing effects: (1) The increase in N, the number of scattering centers per unit volume which always produces an increase, and (2) a contraction of the electronic cloud which affords a decrease in atomic polarizability and the refractive index; this is shown by the positive values of Λ0. For MgO, diamond, and ZnS, this second effect outweighs the first and these crystals exhibit negative values of [13].
3.2. Thermo-Optic Data
For each glass, data on Δt/t versus temperature and Δn versus temperature were fitted by computer to a cubic equation of the form (y)T − (y)T = o = aT + bT2 + cT3, where T is the temperature in °C and t represents the thickness of the specimen at the beginning of the expansion. The parameters in the above equation are given in tables 4 and 5, and hold for a temperature range from −200 °C to an elevated temperature just short of the region of rapid thermal expansion. For convenience of presentation the data were made to have values of zero at 0 °C. The goodness of fit can be judged from the fact that, in every case, the standard deviation of the scatter of points about the fitted curve was no greater than 0.2 × 10−4. The fitted data were printed out by computer at 10 degree temperature intervals, and the results are presented in tables 6 and 7.
Table 4.
Parameters for determining the thermal expansion according to the equation, Δt/t = aT + bT2 + cT3
| Glass | a | b | c |
|---|---|---|---|
| Calcium aluminate F-75 | 6.82884E-2 | 6.87984E-5 | −5.13289E-8 |
| Phosphate F-1329 | 4.63538E-2 | 6.12428E-5 | −7.68437E-8 |
| Barium borate E-1583 | 5.92004E-4 | 5.20094E-5 | −4.05277E-8 |
| Germanate F-998 | .0699 | 5.88163E-5 | −3.21704E-8 |
Table 5.
Parameters for determining the change in the refractive index with temperature according to the equation, Δn = aT + bT2 + cT3
| Glass | a | b | c |
|---|---|---|---|
| Fused SiO2 | 8.16638E-2 | 1.04124E-4 | −5.59781E-8 |
| Calcium aluminate F-75 | 6.99293E-2 | 1.02150E-4 | −7.81014E-8 |
| Phosphate F-1329 | 4.31093E-2 | 6.17585E-5 | −2.17470E-10 |
| Barium borate E-1583 | −1.33162E-2 | 4.75242E-5 | 1.37501E-10 |
| Germanate F-998 | 7.94345E-2 | 1.28399E-4 | −8.96982E-8 |
Table 6.
Increase in length per unit length, Δt/t as a function of temperature
| Temperature °C | Calcium aluminate glass F75 | Phosphate glass F1329 | Barium borate glass E1583 | Germanate glass F998 | ||
|---|---|---|---|---|---|---|
| −200 | −10.5×10−4 | −6.2×10−4 | −9. 4×10−4 | −11.4×10−4 | ||
| −190 | −10.1 | −6.1 | −9.1 | −10.9 | ||
| −180 | −9.8 | −5.9 | −8.7 | −10.5 | ||
| −170 | −9.4 | −5.7 | −8.4 | −10.0 | ||
| −160 | −9.0 | −5.5 | −8.0 | −9.5 | ||
| −150 | −8.5 | −5.3 | −7.6 | −9.1 | ||
| −140 | −8.1 | −5.1 | −7.2 | −8.5 | ||
| −130 | −7.6 | −4.8 | −6.7 | −8.0 | ||
| −120 | −7.1 | −4.5 | −6.3 | −7.5 | ||
| −110 | −6.6 | −4.3 | −5.8 | −6.9 | ||
| −100 | −6.1 | −3.9 | −5.4 | −6.4 | ||
| −90 | −5.6 | −3.6 | −4.9 | −5.8 | ||
| −80 | −5.0 | −3.3 | −4.4 | −5.2 | ||
| −70 | −4.4 | −2.9 | −3.9 | −4.6 | ||
| −60 | −3.8 | −2.5 | −3.4 | −4.0 | ||
| −50 | −3.2 | −2.2 | −2.8 | −3.3 | ||
| −40 | −2.6 | −1.8 | −2.3 | −2.7 | ||
| −30 | −2.0 | −1.3 | −1.7 | −2.0 | ||
| −20 | −1.3 | −0.9 | −1.2 | −1.4 | ||
| −10 | −0.7 | −0.5 | −0.6 | −0.7 | ||
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| 10 | 0.7 | 0.5 | 0.6 | 0.7 | ||
| 20 | 1.4 | 1.0 | 1.2 | 1.4 | ||
| 30 | 2.1 | 1.4 | 1.8 | 2.2 | ||
| 40 | 2.8 | 1.9 | 2.4 | 2.9 | ||
| 50 | 3.6 | 2.5 | 3.1 | 3.6 | ||
| 60 | 4.3 | 3.0 | 3.7 | 4.4 | ||
| 70 | 5.1 | 3.5 | 4.4 | 5.2 | ||
| 80 | 5.9 | 4.1 | 5.0 | 6.0 | ||
| 90 | 6.7 | 4.6 | 5.7 | 6.8 | ||
| 100 | 7.5 | 5.2 | 6.4 | 7.6 | ||
| 110 | 8.3 | 5.7 | 7.1 | 8.4 | ||
| 120 | 9.1 | 6.3 | 7.8 | 9.2 | ||
| 130 | 9.9 | 6.9 | 8.5 | 10.0 | ||
| 140 | 10.8 | 7.5 | 9.2 | 10.9 | ||
| 150 | 11.6 | 8.1 | 9.9 | 11.7 | ||
| 160 | 12.5 | 8.7 | 10.6 | 12.6 | ||
| 170 | 13.3 | 9.3 | 11.4 | 13.4 | ||
| 180 | 14.2×10−4 | 9.9×10−4 | 12.1×10−4 | 14.3×10−4 | ||
| 190 | 15.1 | 10.5 | 12.8 | 15.2 | ||
| 200 | 16.0 | 11.1 | 13.6 | 16.1 | ||
| 210 | 16.9 | 11.7 | 14.3 | 17.0 | ||
| 220 | 17.8 | 12.3 | 15.1 | 17.9 | ||
| 230 | 18.7 | 13.0 | 15.9 | 18.8 | ||
| 240 | 19.6 | 13.6 | 16.6 | 19.7 | ||
| 250 | 20.6 | 14.2 | 17.4 | 20.7 | ||
| 260 | 21.5 | 14.8 | 18.2 | 21.6 | ||
| 270 | 22.4 | 15.5 | 19.0 | 22.5 | ||
| 280 | 23.4 | 16.1 | 19.8 | 23.5 | ||
| 290 | 24.3 | 16.7 | 20.6 | 24.4 | ||
| 300 | 25.3 | 17.3 | 21.3 | 25.4 | ||
| 310 | 26.3 | 18.0 | 22.1 | 26.4 | ||
| 320 | 27.2 | 18.6 | 22.9 | 27.3 | ||
| 330 | 28.2 | 19.2 | 23.7 | 28.3 | ||
| 340 | 29.2 | 19.8 | 24.5 | 29.3 | ||
| 350 | 30.1 | 20.4 | 25.4 | 30.3 | ||
| 360 | 31.1 | 21.0 | 26.2 | 31.3 | ||
| 370 | 32.1 | 21.6 | 27.0 | 32.3 | ||
| 380 | 33.1 | 22.2 | 27.8 | 33.3 | ||
| 390 | 34.1 | 22.8 | 28.6 | 34.3 | ||
| 400 | 35.0 | 23.4 | 29.4 | 35.3 | ||
| 410 | 36.0 | 24.0 | 30.2 | 36.3 | ||
| 420 | 37.0 | 24.6 | 31.0 | 37.4 | ||
| 430 | 38.0 | 25.1 | 31.8 | 38.4 | ||
| 440 | 39.0 | 25.7 | 32.7 | 39.4 | ||
| 450 | 40.0 | 26.3 | 33.5 | 40.4 | ||
| 460 | 41.0 | 26.8 | 34.3 | 41.5 | ||
| 470 | 42.0 | 27.3 | 35.1 | 42.5 | ||
| 480 | 43.0 | 27.9 | 35.9 | 43.6 | ||
| 490 | 43.9 | 28.4 | 36.7 | 44.6 | ||
| 500 | 44.9 | 28.9 | 37.5 | 45.6 | ||
| 510 | 45.9 | 29.4 | 46.7 | |||
| 520 | 46.9 | 29.9 | 47.7 | |||
| 530 | 47.9 | 30.3 | 48.8 | |||
| 540 | 48.9 | 49.8 | ||||
| 550 | 49.8 | 50.9 | ||||
| 560 | 50.8 | 51.9 | ||||
| 570 | 51.8 | 53.0 | ||||
| 580 | 52.7 | 54.1 | ||||
| 590 | 53.7 | 55.1 | ||||
| 600 | 54.7 | 56.2 | ||||
| 610 | 57.2 | |||||
| 620 | 58.3 | |||||
| 630 | 59.3 | |||||
| 640 | 60.4 | |||||
Table 7.
Change in refractive index, (Δn), as a function of temperature at 587.6 nm
| Temperature °C | Fused SiO2 | Calcium aluminate glass F75 | Phosphate glass F1329 | Barium borate glass E1583 | Germanate glass F998 |
|---|---|---|---|---|---|
| −200 | −11.8 × 10−4 | −9.3 × 10−4 | −6.1 × 10−4 | 4.6 × 10−4 | −10.0 × 10−4 |
| −190 | −11.6 | −9.1 | −6.0 | 4.2 | −9.8 |
| −180 | −11.3 | −8.8 | −5.8 | 3.9 | −9.6 |
| −170 | −11.0 | −8.6 | −5.5 | 3.6 | −9.4 |
| −160 | −10.7 | −8.3 | −5.3 | 3.3 | −9.1 |
| −150 | −10.3 | −7.9 | −5.1 | 3.1 | −8.7 |
| −140 | −9.8 | −7.6 | −4.8 | 2.8 | −8.4 |
| −130 | −9.3 | −7.2 | −4.6 | 2.5 | −8.0 |
| −120 | −8.8 | −6.8 | −4.3 | 2.3 | −7.5 |
| −110 | −8.2 | −6.4 | −4.0 | 2.0 | −7.1 |
| −100 | −7.6 | −5.9 | −3.7 | 1.8 | −6.6 |
| −90 | −6.9 | −5.4 | −3.4 | 1.6 | −6.0 |
| −80 | −6.2 | −4.9 | −3.1 | 1.4 | −5.5 |
| −70 | −5.5 | −4.4 | −2.7 | 1.2 | −4.9 |
| −60 | −4.8 | −3.8 | −2.4 | 1.0 | −4.3 |
| −50 | −4.0 | −3.2 | −2.0 | 0.8 | −3.6 |
| −40 | −3.2×10−4 | −2.6×10−4 | −1.6×10−4 | 0.6×10-4 | −3.0×10−4 |
| −30 | −2.4 | −2.0 | −1.2 | 0.4 | −2.3 |
| −20 | −1.6 | −1.4 | −0.8 | 0.3 | −1.5 |
| −10 | −0.8 | −0.7 | −0.4 | 0.1 | −0.8 |
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 |
| 10 | 0.9 | 0.7 | 0.4 | −0.1 | 0.8 |
| 20 | 1.7 | 1.4 | 0.9 | −0.3 | 1.6 |
| 30 | 2.5 | 2.2 | 1.3 | −0.4 | 2.5 |
| 40 | 3.4 | 3.0 | 1.8 | −0.5 | 3.4 |
| 50 | 4.3 | 3.7 | 2.3 | −0.5 | 4.3 |
| 60 | 5.3 | 4.5 | 2.8 | −0.6 | 5.2 |
| 70 | 6.2 | 5.4 | 3.3 | −0.7 | 6.2 |
| 80 | 7.2 | 6.2 | 3.8 | −0.8 | 7.1 |
| 90 | 8.2 | 7.1 | 4.4 | −0.8 | 8.1 |
| 100 | 9.2 | 7.9 | 4.9 | −0.9 | 9.1 |
| 110 | 10.2 | 8.8 | 5.5 | −0.9 | 10.2 |
| 120 | 11.2 | 9.7 | 6.1 | −0.9 | 11.2 |
| 130 | 12.3 | 10.6 | 6.6 | −0.9 | 12.3 |
| 140 | 13.3 | 11.6 | 7.2 | −0.9 | 13.4 |
| 150 | 14.4 | 12.5 | 7.9 | −0.9 | 14.5 |
| 160 | 15.5 | 13.5 | 8.5 | −0.9 | 15.6 |
| 170 | 16.6 | 14.5 | 9.1 | −0.9 | 16.8 |
| 180 | 17.8 | 15.4 | 9.8 | −0.9 | 17.9 |
| 190 | 18.9 | 16.4 | 10.4 | −0.8 | 19.1 |
| 200 | 20.1 | 17.4 | 11.1 | −0.8 | 20.3 |
| 210 | 21.2 | 18.5 | 11.8 | −0.7 | 21.5 |
| 220 | 22.4 | 19.5 | 12.5 | −0.6 | 22.7 |
| 230 | 23.6 | 20.5 | 13.2 | −0.5 | 24.0 |
| 240 | 24.8 | 21.6 | 13.9 | −0.5 | 25.2 |
| 250 | 26.1 | 22.6 | 14.6 | −0.4 | 26.5 |
| 260 | 27.3 | 23.7 | 15.4 | −0.2 | 27.8 |
| 270 | 28.5 | 24.8 | 16.1 | −0.1 | 29.0 |
| 280 | 29.8 | 25.9 | 16.9 | 0.0 | 30.3 |
| 290 | 31.1 | 27.0 | 17.7 | 0.1 | 31.7 |
| 300 | 32.4 | 28.1 | 18.5 | 0.3 | 33.0 |
| 310 | 33.7 | 29.2 | 19.3 | 0.4 | 34.3 |
| 320 | 35.0 | 30.3 | 20.1 | 0.6 | 35.6 |
| 330 | 36.3 | 31.4 | 20.9 | 0.8 | 37.0 |
| 340 | 37.6 | 32.5 | 21.8 | 1.0 | 38.3 |
| 350 | 38.9 | 33.6 | 22.6 | 1.2 | 40.0 |
| 360 | 40.3 | 34.8 | 23.5 | 1.4 | 41.1 |
| 370 | 41.6 | 35.9 | 24.4 | 1.6 | 42.4 |
| 380 | 43.0 | 37.0 | 25.3 | 1.8 | 43.8 |
| 390 | 44.4 | 38.2 | 26.2 | 2.0 | 45.2 |
| 400 | 45.7 | 39.3 | 27.1 | 2.3 | 46.6 |
| 410 | 47.1 | 40.5 | 28.0 | 2.5 | 48.0 |
| 420 | 48.5 | 41.6 | 29.0 | 2.8 | 49.4 |
| 430 | 49.9 | 42.7 | 29.9 | 3.1 | 50.8 |
| 440 | 51.3 | 43.9 | 30.9 | 3.3 | 52.2 |
| 450 | 52.7 | 45.0 | 31.9 | 3.6 | 53.6 |
| 460 | 54.2 | 46.2 | 32.9 | 3.9 | 55.0 |
| 470 | 55.6 | 47.3 | 33.9 | 4.3 | 56.4 |
| 480 | 57.0 | 48.5 | 34.9 | 4.6 | 57.8 |
| 490 | 58.4 | 49.6 | 35.9 | 4.9 | 59.2 |
| 500 | 59.9 | 50.7 | 37.0 | 5.2 | 60.6 |
| 510 | 61.3 | 51.9 | 38.0 | 62.0 | |
| 520 | 62.8 | 53.0 | 39.1 | 63.4 | |
| 530 | 64.2 | 54.1 | 40.2 | 64.8 | |
| 540 | 65.7 | 55.3 | 66.2 | ||
| 550 | 67.1 | 56.4 | 67.6 | ||
| 560 | 68.6 | 57.5 | 69.0 | ||
| 570 | 70.0 | 58.6 | 70.4 | ||
| 580 | 71.5 | 59.7 | 71.8 | ||
| 590 | 72.9 | 60.8 | 73.1 | ||
| 600 | 74.4 | 61.9 | 74.5 | ||
| 610 | 75.9 | 75.9 | |||
| 620 | 77.3 | 77.2 | |||
| 630 | 78.8 | 78.6 | |||
| 640 | 80.2 | 79.9 | |||
| 650 | 81.7 |
The values of thermal expansion for fused silica were taken from the data of Scheel and Heuse [14] which are recommended by Sosman [15], and are not reproduced in table 3. The data on Δn for fused silica given in table 7 agree with the values of Austin [9, 16] within the experimental error over the entire temperature range. Comparison showed that this same agreement pertained between the data for the four commercial brands of fused silica which have been mentioned in the introduction. An irregularity in the values of Δn in the range from 500 to 600 °C, which has been reported by several authors [17, 18, 19, 20] was not observed in this study nor in the research of Austin [16].
It can be seen in table 3 that for fused silica
at 25 °C. This agrees exactly with the value reported by Schott and Gen. [21], and there is very close agreement with the value of 0.85 × 10−5 calculated from the equation given by Austin and Pierce [9]. However, higher values have been found by other workers; both Tilton and Tool [22] and Rodney and Spindler [23] reported a value of 0.99 × 10−5, and Malitson [24] reported 1.0 × 10−5; a value of 1.08 × 10−5 was reported by Prod’homme [25].
Considering this quantity, (dn/dT), at room temperature, it has been found that some crystals exhibit negative values while others have an increase in refractive index with increase in temperature [1]. These latter crystals are the very ones which exhibit negative values of (ρ∂n/∂ρ), i.e., MgO, diamond, and ZnS, so that with change of temperature, the attendant change in density is still of paramount importance. The sign of dn/dT depends on whether the contribution from change in N or the change in polarizability caused by density change predominates. However, earlier data on a few glasses indicate that, for these solids, both (ρ∂n/∂ρ) and (dn/dT) are positive [8]. In table 3, room temperature values of n0, dn/dT, γ and ρ∂n/∂ρ are given, as are values of (∂n/∂T)ρ, which have been calculated from eq (2).
Starting with the Drude equation, Ramachandran [1] has shown that dn/dT consists of the sum of three independent contributions which he labels P, Q, and R. P is dependent only on change of density and arises from the change in the number of scattering centers, Q denotes the change in polarizability caused by change in density, and R represents the change in polarizability arising from temperature change alone. The equations are:
| (7) |
| (8) |
| (9) |
Values of P, Q, and R for the five glasses have been determined and are shown in table 3. It can be seen that P is always negative, reflecting the lessening in the number of scattering centers with rise in temperature. Values of P and Q for fused silica are very small because of the very small coefficient of thermal expansion. It can also be seen that R is positive and is significantly larger than Q in all cases, indicating that the change in polarizability is largely dependent solely on temperature change; this is not true for crystals where R may be of either sign and is always smaller than Q [1].
Polarizability is the fundamental optical property and in comparing the thermo-optic properties of different materials, it is necessary to compare values of Λ0, γ, and τ0, where is the temperature coefficient of polarizability. Ramachamdran has shown that the change in polarizability with temperature can be written as
| (10) |
and that
| (11) |
Calculations of Λ0 and τ0 for the glasses of the present study may be made Irom the entries of table 3 according to the equations
| (12) |
and
| (13) |
Values of Λ0, Λ0γ, τ0, and τ0/γ have been listed in table 8 where corresponding values for cubic crystals studied in this laboratory have also been listed for comparison. In the case of the cubic crystals, Ramachandran has noted that τ0 is much smaller than Λ0γ indicating that the change in polarizability, due to the pure temperature effect, is much smaller than that due to a change in the lattice parameter. It can be seen from the table that, for the five glasses, the relative importance of the two contributions is reversed. For the glass systems studied here, it is apparent that the polarizability is essentially dependent upon temperature change at constant density. The same conclusion can be drawn on considering the column of figures for Λ0 and τ0/γ. This distinctive property of glasses is brought out explicitly here from measurements on change of refractive index caused by changes of pressure and temperature, although it had been inferred by Ramachandran from a study restricted to thermo-optic data alone over an extended temperature range [26].
Table 8.
Strain and temperature coefficients of polarizability for glasses and crystals
| Λ0γ×105 | τ0 × 105 | Λ0 | τ0/ γ | |
|---|---|---|---|---|
| Fused SiO2 | 0.02 | 2.4 | 0.17 | 18.2 |
| Calcium aluminate glass, F—75 | 1.4 | 2.2 | 0.65 | 1.0 |
| Phosphate glass F-1329 | 0.28 | 2.4 | 0.19 | 1.6 |
| Barium borate glass, E-1583 | 0.30 | 1.3 | 0.16 | 0.72 |
| Germanate glass F-998 | 0.89 | 2.6 | 0.41 | 1.2 |
| LiF | 6.3 | 0.0 | 0.62 | 0.0 |
| NaCI | 4.6 | −0.89 | 0.38 | −0.07 |
| KCI | 2.6 | 0.24 | 0.23 | 0.02 |
| KBr | 2.9 | 1.3 | 0.24 | 0.11 |
| CaF2 | 2.5 | 0.0 | 0.43 | 0.0 |
| MgO | 6.0 | 0.68 | 1.53 | 0.17 |
Primak and Post have attributed this great dependence of polarizability to the strained bond configuration of the oxygen ions in the glasses [27]. Ramachandran has inferred that this effect is associated with a band edge shift of the ultraviolet frequencies toward lower energy with increase of temperature that is also essentially independent of change in lattice parameter [26]. This idea of Ramachandran has been extended by more recent studies [28, 29]: Apparently, the lack of long-range order and the random molecular structure in glass induces a broadening of the exitonic levels and a tail on the ultraviolet absorption edge, which varies exponentially with energy [28].
From the present study which includes an aluminate, phosphate, borate and germanate glass, it is inferred that this iso-volume effect is an important additional consideration in understanding the thermo-optic behavior of all glasses as distinguished from crystals. However, more glass systems should be studied, and it is recognized at the outset that for each particular glass (as for a crystal) there are important unique considerations of internal structure, i.e., whether the atoms are arranged in the form of chains or rings or sheets.
The data reported in tables 6 and 7 has been terminated just before the region of rapid expansion in the glass. However, it is interesting to consider the course of the refractive index curve and the thermal expansion curve over the whole range of temperatures up to the softening point. The barium borate glass, E1583, has been selected as being representative of the others, and curves for thermal expansion and change in refractive index for this glass are shown in the lower part of figure 1. There is a minimum in the refractive index curve around 150 °C, which behavior is typical of optical glass. Molby has reported on several optical glasses where dn/dT was initially negative and then became positive with rise in temperature [30]. The barium borate glass of this study is distinctive in that the minimum value is so high, most of the glasses reported by Molby had must lower minimum values, usually well below 0 °C. No minimum in refractive index was noted for the remaining glasses of this study, but the data indicate that all of them are approaching minimum values at the lowest temperatures.
Figure 1.
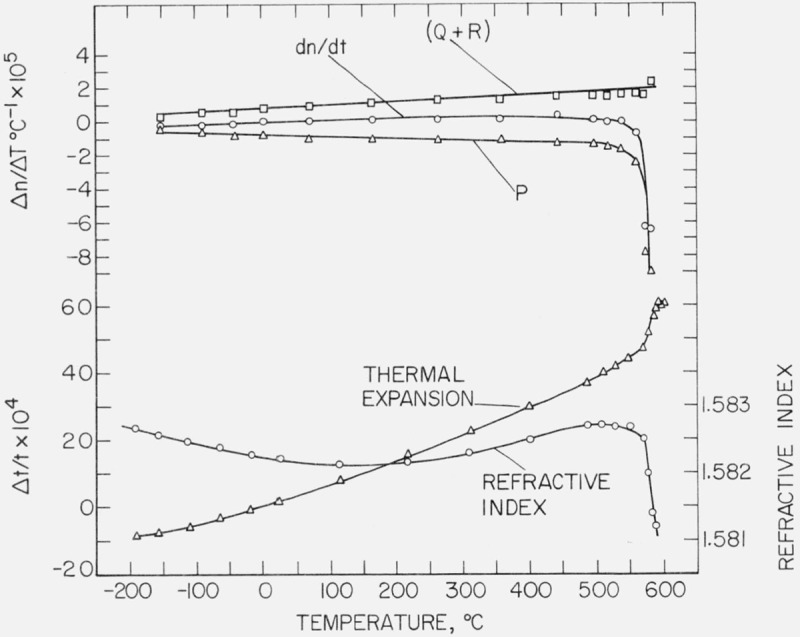
Analysis of the thermo-optical behavior of barium borate glass, E1583.
From the figure, it can be seen that dn/dT diminishes rapidly and then becomes negative as the temperature increases through the region of rapid thermal expansion. This dip in the refractive index curve is interpreted as resulting from the large decrease in the number of scattering centers per unit volume.
Because measurements were made at specific temperature intervals, it is possible to make some analysis of dn/dT over the entire temperature range following the earlier treatment of dividing dn/dT into contributions, P, Q, and R. However, the treatment must be limited to values of P and (Q + R) because measurements of the change in refractive index caused by applied hydrostatic pressure were restricted to room temperature. Calculations have been made and curves denoting dn/dT, P and (Q + R) are shown in the upper part of figure 1. It can be seen that P and (Q + R) are of opposite sign and that dn/dT is the sum of the two.
Because of the opposite sign, the sum is small until the region of rapid expansion is reached, whereupon dn/dT largely follows the course of P. An important point to be made is that (Q + R) is nearly a straight line over the entire temperature range. This would imply that R must be significantly greater than Q over the whole range, because Q itself depends on change in density. Another point to be made is that (Q + R) appears to approach zero at the lowest temperatures, which had been predicted by Ramachandran on the basis of thermo-optic behavior of glasses at higher temperatures [26].
3.3. Relevance of the Data to the Molecular Scattering of Light
As mentioned in the introduction, small changes in refractive index caused by changes of density and temperature account for the molecular scattering of light in transparent materials [4]. The theoretical formulations are usually expressed in terms of the optical dielectric constant, ϵ, where ϵ = n2. In both the well-known Einstein-Smoluchowski and Landau-Placzek formulations, the quantity (∂ϵ/∂T)ρ, has been treated as being negligibly small, but Fabelinskii [31] has developed an exact equation for the intensities of scattered light which includes the quantity (∂ϵ/∂T)ρ. O’Connor and Schlupf [32] have presented equations for the transformation of variables, so that the input parameters of the theoretical equations may be calculated from the refractive index data of this paper. Because (∂ϵ/∂T)ρ = 2n(∂n/∂T)ρ and we have found (∂n/∂T)ρ to be very high (see table 3), it was thought that this neglected factor could account for the fact that the intensity of light scattered from optical glasses greatly exceeds theoretical predictions [33]. However, calculations showed that it was not possible to account for the experimental data of fused SiO2 [34] by inserting parameters determined from this report.
It was concluded that, because glass is unstable thermodynamically, a theoretical formulation based on equilibrium conditions would be inadequate to account for the observed effects. Indeed, the current theory of light scattering in glass attributes the high intensity of the central Rayleigh line to nonpropagating density and composition fluctuations that are frozen into the melt as it is cooled through the transition range [35, 36, 37, 38]. The frozen-in density flucutations affect the intensity through the parameter, (ρ ∂ϵ/∂ρ), and (ρ ∂ϵ/∂ρ) = (2n ρ ∂n/∂ρ). It can be seen from table 3 that there are significant differences in values of (ρ ∂n/∂ρ). Although composition fluctuations would remain a problem, the point may be made here that (ρ ∂n/∂ρ) could be reduced to zero or some other low value by the proper adjustment of glass composition. This same point has been made before for the elimination of electro-striction in laser glasses [39], which phenomenon also manifests itself through the parameter (ρ ∂ϵ/∂ρ).
4. References
- [1].Ramachandran G. N., in Progress in Crystal Physics, Volume 1, edited by Krishnan R. S., (Interscience Publishers, New York, London, 1958), pp. 139–167. [Google Scholar]
- [2].Zverev G. M., and Pashkov V. A., Zh. Eksperim i. Teor. Fiz. Pis’ma Redaktsiyu 57, 1128 [Soviet Phys.–JETP, 30, 616 (1970)]. [Google Scholar]
- [3].Feldman A., Horowitz D., and Waxler R. M. (to be published).
- [4].Fabelinskii I. L., Molecular Scattering of Light, (Plenum Press, New York, 1968). [Google Scholar]
- [5].Schroeder J., Mohr R., Montrose C. J., and Macedo P. B. (to be published).
- [6].Bȧȧk T., Optics Athermalization, Report No. 8744, Systems Engineering Group, Research and Technology Division, Air Force Systems Command, USAF Wright-Patterson Air Force Base, Ohio: (1967). [Google Scholar]
- [7].Vedam K., Schmidt E. D. D., and Roy R., J. Am. Ceram. Soc. 49, 531 (1966). [Google Scholar]
- [8].Waxler R. M., and Weir C. E., J. Res. Nat. Bur. Stand. (U.S.), 69A (Phys. and Chem.), No. 4, 325 (July–Aug. 1965). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Austin J. B. and Pierce R. H. H. Jr., Physics 6, 43 (1935). [Google Scholar]
- [10].Waxler R. M., Cleek G. W., Malitson I. H., Dodge M. J. and Hahn T. A., J. Res. Nat. Bur. Stand. (U.S.), 75A (Phys. and Chem.), No. 3, 163 (May–June 1971). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Waxler R. M. and Cleek G. W., J. Res. Nat. Bur. Stand. (U.S.), 75A, (Phys. and Chem.), No. 4, 279 (July–Aug. 1971). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Mueller H., Physics 6, 179 (1935). [Google Scholar]
- [13].Vedam K. and Ramaseshan S., in Progress in Crystal Physics, Volume I, edited by Krishnan R. S. (Interscience Publishers, New York, London, 1958), pp. 102–138. [Google Scholar]
- [14].Scheel K. and Heuse W., Verh. Deutsch, Physik, Ges. 16, 1–3 (1914). [Google Scholar]
- [15].Sosman R. B., The Properties of Silica, (Chemical Catalog Co., New York, 1927), pp. 403–406. [Google Scholar]
- [16].Austin J. B., Physics 3, 240 (1932). [Google Scholar]
- [17].Rinne F., Nues Jahrb, Mineral, Beil. 39, 388 (1914). [Google Scholar]
- [18].Reference See 15, p. 687. [Google Scholar]
- [19].Chandrasekhar S., Proc. Indian Acad. Sci. A34, 275 (1951). [Google Scholar]
- [20].Narayanan P. S., Proc. Indian Acad. Sci. A35, 9 (1953). [Google Scholar]
- [21].See reference 6, p. 114.
- [22].Tilton L. W. and Tool A. Q., J. Res. Nat. Bur. Stand. (U.S.), 3, 619 (1929) RP112. [Google Scholar]
- [23].Rodney W. S. and Spindler R. J., J. Res. Nat. Bur. Stand. (U.S.), 53, No. 3, 185 (Sept. 1954). [Google Scholar]
- [24].Malitson I. H., J. Opt. Soc. Am. 55, No. 10, 1205 (1965). [Google Scholar]
- [25].Prod’homme L., Phys. and Chem. of Glasses 1, No. 4, 119 (1960). [Google Scholar]
- [26].Ramachandran G. N., Proc. Indian Acad. Sci. 25A, 498 (1947). [Google Scholar]
- [27].Primak W. and Post D., J. App. Phys. 30, No. 5, 779 (1959). [Google Scholar]
- [28].Dow J. D. and Redfield D., Phys. Rev. Letters 26, No. 13, 762 (1971). [Google Scholar]
- [29].Wood D. L. and Tauc J., Phys. Rev. B 5, No. 8, 3144 (1972). [Google Scholar]
- [30].Molby F. A., J. Opt. Soc. Am. 39, 600 (1949). [Google Scholar]
- [31].See reference [4], p. 96.
- [32].O’Connor C. L. and Schlupf J. P., J. Chem. Phys. 47, No. 1, 31 (1967). [Google Scholar]
- [33].See reference [4], Chapter VII.
- [34].Flubacher P., Leadbetter A. J., Morrison J. A. and Stoicheff B. P., Int. J. Phys. Chem. Solids 12, 53 (1960). [Google Scholar]
- [35].Mueller H., Proc. Roy. Soc. A, 166, 425 (1938). [Google Scholar]
- [36].Maurer R. D., J. Chem. Phys. 25, 1206 (1956). [Google Scholar]
- [37].Pinnow D. A., Candau S. J., La Macchia J. T. and Litovitz T. A., J. Acoust. Soc. Am. 43, 131 (1968). [Google Scholar]
- [38].Mohr R., Schroeder J., Macedo P. B. and Montrose C. J., J. Am. Ceram. Soc. (to be published).
- [39].Waxler R. M., IEEE J. Quantum Electron, QE–7, 166 (1971). [Google Scholar]


