Thermal Analysis of Calcium Sulfate Dihydrate and Supposed α and β Forms of Calcium Sulfate Hemihydrate from 25 to 500 ° C

Abstract

Thermal studies were carried out on CaSO₄ · 2H₂O and the supposed α and β forms of CaSO₄ · 1/2H₂O in the region of 25 to 500 ° C. using differential thermal analysis, thermogravimetry, and differential scanning calorimetry methods.

Two large endothermic effects and a smaller exothermic effect were found in the differential thermogram of CaSO₄ · 2H₂O while a single endothermic as well as an exothermic effect were found in the thermograms of the supposed α and β forms of CaSO₄ · 1/2H₂O. However, the exotherm of α-CaSO₄ · 1/2H₂O had lower peak and first-break temperatures than that of the β-form. The peak and first-break temperatures of the endothermie effects of CaSO₄ · 2H₂O) and α and B-CaSO₄ · 1/2H₂O and the exothermic effect of α-CaSO)₄ · 1/2H₂O were pressure dependent, shifting to lower temperatures as the gaseous pressure within the DTA cell was decreased. The noted differences in the thennogrms possibly are due to kinetic factors because of the differences in crystallinity of the supposed α- and β-CaSO₄ · 1/2H₂O.

No differences in the supposed a and β forms of CaSO₄ · 1/2H₂O were detected by thermogravimetry and differential scanning calorimetry studies. The formulation of a two-step dissociative process in the complete dehydration of CaSO₄ · 2H₂O was supported by the results of the thermogravimetry study.

1. Introduction

As a part of the continuing study of gypsum plaster [1]¹ the properties of calcium sulfate dihydrate (CaSO₄ · 2H₂O) and calcium sulfate hemihydrate (CaSO4 · 1/2H₂O) were studied by differential thermal analysis, thermogravimetry, and differential scanning calorimetric techniques. These investigations were undertaken in order to gain a more complete understanding of the dehydration processes of CaSO4 · 2H₂O and to attempt to verify the existence of two forms of CaSO₄ · 1/2H₂O.

In addition to the calcium sulfate hydrates, two types of anhydrous calcium sulfate exist, hexagonal (γ-CaSO₄) and orthorhombic (β-CaSO₄) forms [2]. The γ form results from the dehydration of the hydrates and is regarded as the low-temperature species, although it is apparently metastable and even at room temperature very slowly converts to the “high-temperature” species, β-CaSO₄ [2].

The main features in the differential thermal analysis previously reported for CaSO₄ · 2H₂O [3–7] are two large endothermic effects occurring below 250 °C. and a smaller exotherm found near 400 °C. Some other smaller effects have been reported [6], which were not observed in the present study. There is a lack of consistency in the values reported by different investigators for the temperatures of the main effects. This perhaps can be traced to uncertainties in the operating parameters of individually constructed instruments used in the past, and probably by using modern instruments of known operational characteristics more consistent results can be obtained. The present differential thermal analysis includes studies at normal atmospheric pressure and has been extended to determine the effects on the thermograms of reduced atmospheric pressures within the differential thermal cell, which has not been previously undertaken. Only brief studies of the thermogravigrams of CaSO₄ · 2H₂O have been reported [8]. Of particular interest in the thermogravimetric studies is the possibility of differentiating between two dehydration reactions when CaSO₄ · 2H₂O is completely dehydrated. Few, if any, differential scanning calorimetry studies on CaSO₄ · 2H₂O have been reported previously.

The existence of two forms of CaSO₄ · 1/2H₂O, a and β, has not been firmly established. Apparent slight differences in densities [9, 10], heats of solutions [9], and gauging water requirements [11] have been cited as evidence for two forms of CaSO₄ · 1/2H₂O. The results of x-ray structural analysis are not at the present conclusive. Morris [12] found a slight difference in the x-ray powder diffraction patterns between the a and β forms when the value of 2θ was in the range of 48 to 50°. The pattern associated with α-CaSO₄ · 1/2H₂O in this region has triplet character (two slightly resolved small peaks on each side of a larger peak) whereas that of β-CaSO4 · 1/2H₂O consists of a broad single peak. This difference has been attributed to stacking fault crystal imperfections by Morris [12] and to the intergrowth of a substructure of lower symmetry by Gay [13]. Based upon the results of optical and x-ray studies Flörke [14] suggested that both orthorhombic and triclinic varities of the hemihydrate can exist. Gay, however, recently reported [13] that only a monoclinic structure exists.

Recently, the two forms have been shown [1] to have the same infrared spectra. It has been reported [15] that the exothermic effect in the differential thermograms of α-CaSO₄ · 1/2H₂O occurs at a much lower temperature than in the β form, while other observers have claimed [16] that the thermogram of the α form does not exhibit any exothermic effect. Therefore, it was felt that a detailed thermal analysis study of the postulated α- and β-CaSO₄ · 1/2H₂O was desirable.

The results of differential thermal analysis, thermogravimetry, and differential scanning calorimetry studies of CaSOa · 2H₂O and the supposed α and β forms of CaSO₄ · 1/2H₂O, carried out in the region of 25 to 500 °C., are presented and interpreted in this paper.

The a and β terminology used in this paper is a qualified notation referring to the supposed forms of CaSO₄ · 1/2H₂O and does not imply that their existence has been verified.

2. Experimental Procedure

2.1. Differential Thermal Analysis (DTA)

The DTA curves were recorded using a DuPont Model 900 DTA instrument² equipped with a microsample standard cell. The reference material was anhydrous reagent grade Al₂O₃ heated to 400 °C. for an hour and stored in a vacuum desiccator over phosphorous (V) oxide until used. The reference material treated in this manner gave a flat DTA curve. Gaseous pressures within the DTA cell were measured with the gage accompanying the instrument and may be subject to errors of about ± 8 percent. Temperature measurements were made with chromel alumel thermocouples, using a reference junction temperature of 0 °C., and are accurate to within 2 °C. The thermocouples were calibrated using benzoic acid (National Bureau of Standards, Standard Reference Material No. 350). The vacuum system was able to reduce the residual pressure in the DTA cell to about 1 torr. Heating rates between 3 to 20 °C/min were used.

Evaluation of atmospheric conditions within the specimen compartment was complicated by the furnace and sample housing arrangement of the DTA cell. Samples were loaded into small borosilicate glass tubes, which were closed at one end; the thermocouple wires were inserted into the tubes above the sample, with the thermocouple junction being embedded in the sample. The thermocouple wires fitted tightly in the tube, thereby hindering the diffusion of water vapor from samples and increasing the partial pressure of water vapor in the specimen tube above that in the bulk atmosphere.³ Furthermore, allowing nitrogen gas to flow into the DTA cell probably did not produce dynamic conditions within the specimen tubes, as the nitrogen gas was prevented by the tight fit to be an effective purging agent. For the same reasons, in studies carried out under reduced pressures the water vapor pressures within the sample tubes were probably much greater than the bulk residual pressures.

2.2. Thermogravimetry (TG)

The curves of weight-loss as a function of temperature were recorded using a combination of the DuPont 900 Thermal Analyzer (see footnote 2) and the 950 TGA Module.⁴ The furnace atmosphere was either laboratory air or dry nitrogen gas. The weights of samples were 20 to 24 mg and weight suppressions between 16 to 20 mg were instrumentally set so that the full chart range on the ordinate scale would correspond to a weight loss of not more than 6 mg. Heating rates between 3 to 20 °C/min were used.

2.3. Differential Scanning Calorimetry (DSC)

A Perkin-Elmer DSC-1B Differential Scanning Calorimeter (see footnote 2) was used to measure the DSC curves. Both loosely and hermetically sealed sample capsules were used.

In order to determine the ΔHof dissociation for CaSO₄ · 2H₂O, the instrument was calibrated using the ΔH of fusion of pure indium and tin as standards. Weights of samples were 3 to 5 mg. Heating rates between 5 to 20 °C/min were used.

2.4. Materials

a. CaSO₄ · 2H₂O

Reagent grade CaSO₄ · 2H₂O was used in this study and was found by dehydration at 375 °C to contain the stoichiometric percentage of water (theoretical 20.9%, found 21.0%).

b. α-CaSO₄ · 1/2H₂O

α-CaSO₄ · 1/2H₂O was prepared by the method outlined by Weiser and Milligan [17]. In this method an aqueous solution of Ca(NO₃)₂ · 4H₂O was added to a mixture of dilute nitric and dilute sulfuric acid and the resulting precipitate was allowed to age for 14 days at 50 °C. The white product contained the stoichiometric amount of H₂O (theoretical 6.62%, found 6.68%) and gave the differential thermogram [15] and x-ray powder diffraction pattern [12] ascribed to α-CaSO₄ · 1/2H₂O.

c. β-CaSO₄ · 1/2H₂O

β-CaSO₄ · l/2H₂O was prepared from CaSO₄ · 2H₂O by two completely different dehydration methods. In one method samples of CaSO₄ · 2H₂O were dehydrated in an air oven at 150 to 175 °C. for three to twelve hours, to give γ-CaSO₄. This γ-CaSO₄ was allowed to equilibrate with laboratory air of 50 percent relative humidity at 22 °C. This resulted in the uptake of water with the final product having slightly more than the stoichiometric amount of H₂O, ranging from 0.54 to 0.57 moles of H₂O per mole of CaSO₄. The extra quantity of H₂O possibly has zeolitic character since Saito has reported [18] that NMR studies suggest the existence of two forms of water in CaSO₄ · 1/2H₂O, one of which is zeolitic.

An alternate method was the removal of 1 1/2 molecules of H₂O from CaSO₄ · 2H₂O by vacuum line techniques at 100 °C. It was necessary to anneal the product at 100 °C. for 60 hours as otherwise an impure material was obtained which consisted largely of β-CaSO₄ · 1/2H₂O and about 5 percent of CaSO₄ · 2H₂O and γ-CaSO₄.

The x-ray powder diffraction patterns and differential thermograms of products from both preparative methods were identical to those reported for authentic)3-CaSO₄ · 1/2H₂O [12, 15].

3. Results

3.1. Differential Thermal Analysis

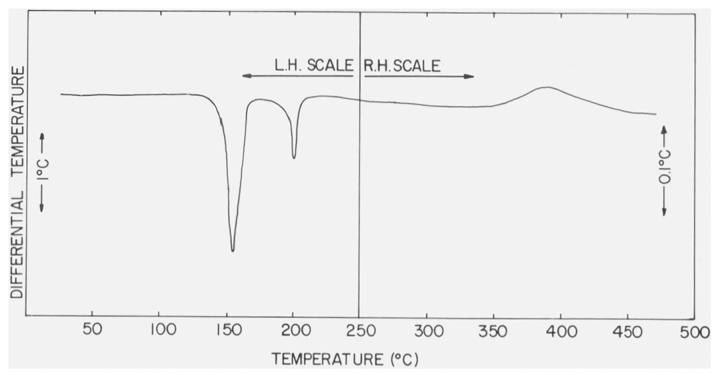
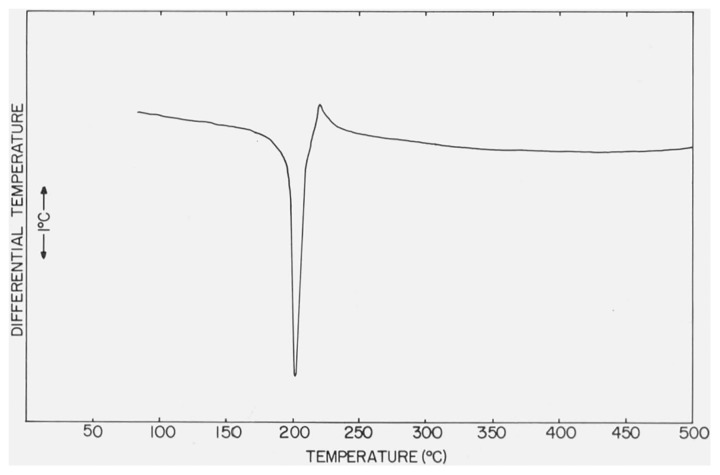
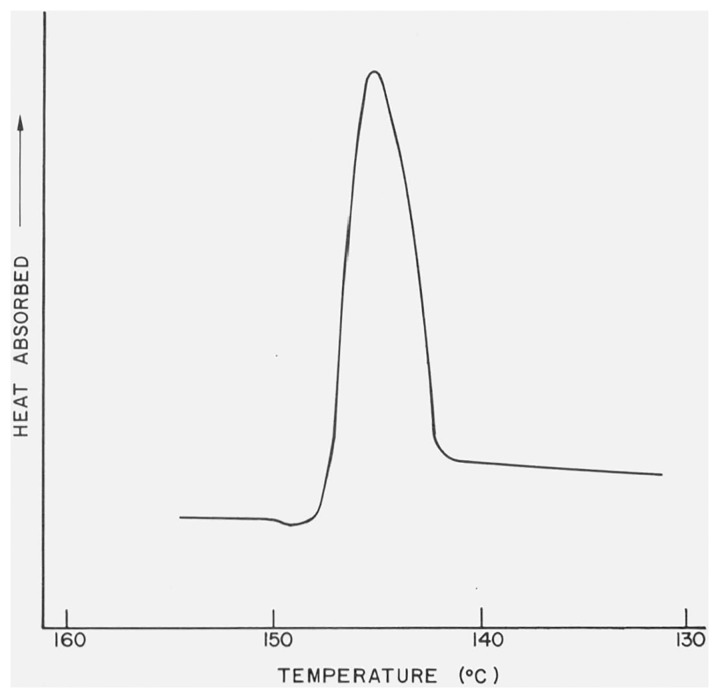
Several of the differential thermograms of CaSO₄ · 2H₂O, measured under different bulk atmospheric conditions in the DTA cell, are reproduced in figures 1 and 2. Decreases in the peak temperatures,⁵ T_peak, and the first-break temperatures (see footnote 5), T_fb, of the two endothermic effects were observed when the gaseous pressure in the cell was reduced and when the residual pressure approached 1 torr the second endothermic curve had either merged with the first curve or had vanished. The peak temperatures and, when measurable, the first break temperatures are listed in table 1. The T_peak and T_fb of the exothermic effect observed in the differential thermograms of CaSO₄ · 2H₂O were not sensitive to changes in the gaseous pressures.

Figure 1.

DTA curve of CaSO₄ · 2H₂O with atmosphere of N₂ at 760 torr in the DTA cell.

Figure 2. Differential thermograms of CaSO₄ · 2H₂O at reduced pressures in the DTA cell.

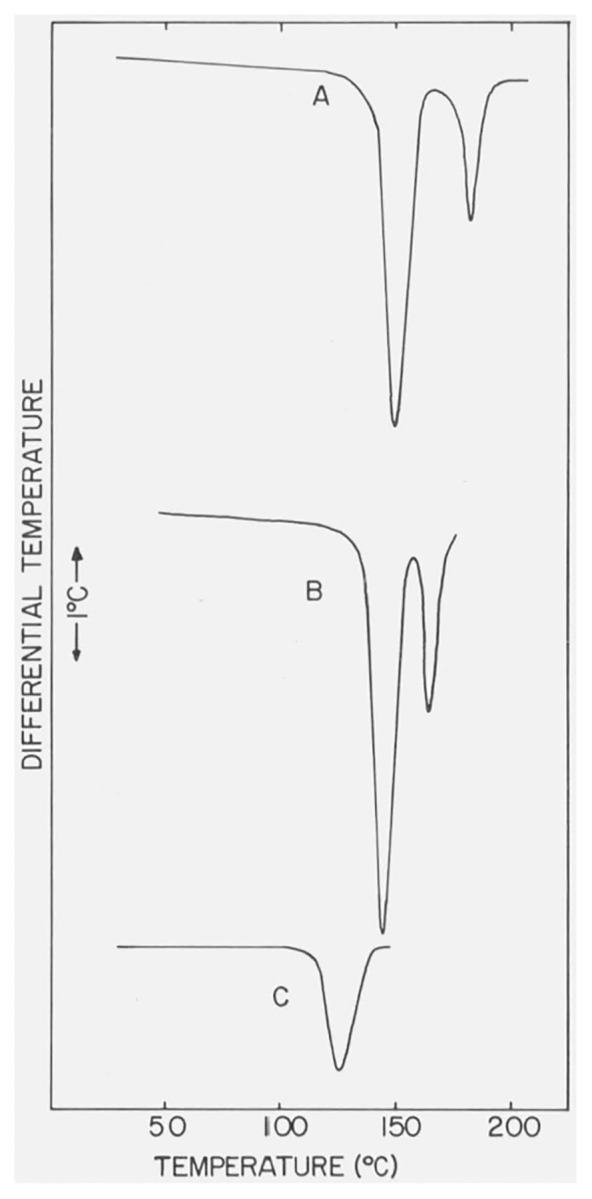
The pressures with thermograms A, B, and C were 590, 380, and ca. 1 torr, respectively.

Table 1.

Peak and first-break temperatures of endothermic DTA curves of CaSO₄ · 2H₂O

Bulk pressure (torr)	First curve		Second curve
	Tpeaka (°C)	Tfbb (°C)	Tpeakc (°C)
760	150	126	197
590	147	123	179
380	144	121	162
138	133	112	147
74	130	109	130
1	123	99	(d)

^aT_peak is the peak temperature.

^bT_fb is the first-break temperature.

^cBecause of overlapping curves not possible to determine T_fb for the second curve.

^dSecond curve had detected at 1 torr.

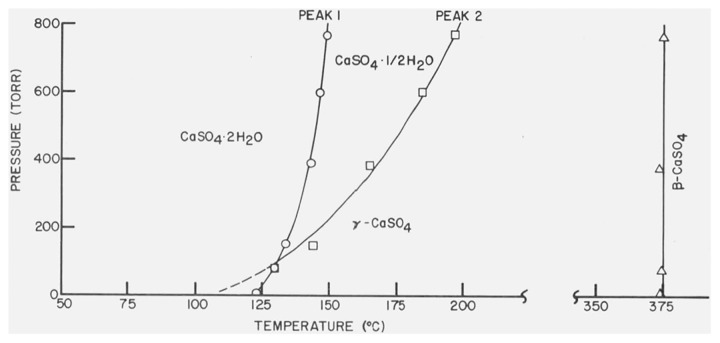
A phase diagram constructed by plotting peak temperatures of the endothermic and exothermic effects versus the atmospheric pressures within the DTA cell is shown in figure 3 for CaSO₄ · 2H₂O. DTA curves obtained under a static nitrogen atmosphere were similar to those observed with supposed dynamic nitrogen flow.

Figure 3. Phase diagram for CaSO₄ · 2H₂O.

Gaseous pressure in the DTA cell plotted versus the peak temperatures of the endothermic and exothermic effects.

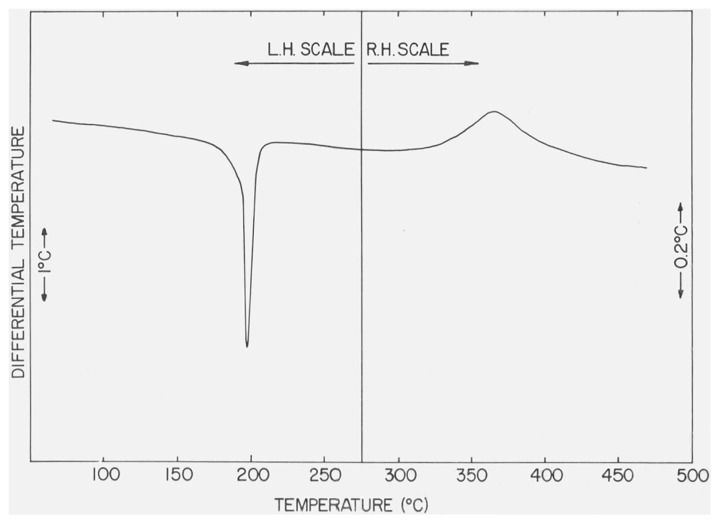
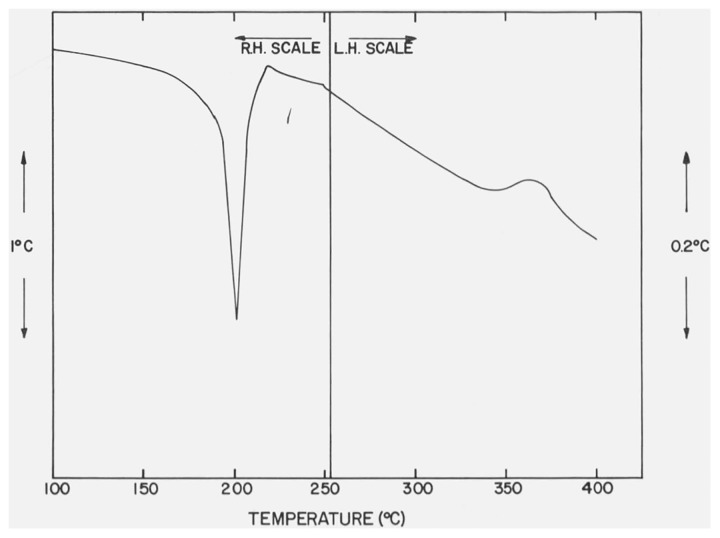
In figures 4 and 5 are shown the DTA curves of β-CaSO₄ · 1/2H₂O recorded, respectively, with a dynamic N₂ atmosphere of ca. 760 torr and with a small residual pressure (ca. 1 torr) in the DTA cell. The heating rate was 12 °C/min. The endothermic peak has the same temperature-pressure behavior (table 2) as previously noted for the second endothermic curve of CaSO₄ · 2H₂O. The position and shape of the small exothermic peak, T_peak = 375 °C and T_fb = 322 °C, were not significantly affected by changes in atmospheric pressures in the DTA cell.

Figure 4.

DTA curve of β-CaSO₄ · 1/2H₂O with N₂ at 760 torr in the DTA cell.

Figure 5.

DTA curve of β-CaSO₄ · 1/2H₂O with a residual pressure of ca. 1 torr in the DTA cell.

Table 2.

Peak and first-break temperatures of DTA curves of α and β-CaSO₄· 1/2H₂O

Bulk pressure (torr)	Endotherm		Exotherm
	TPeaka(°C)	Tfbb(°c)	Tpeaka(°C)	Tfbb(°c)
α-CaS04·1/2H20
760	198	158	217	(c)
380	182	146	200	(c)
1	132	97	163	(c)
β-CaS04·1/2H20
760	195	155	375	322
1	132	94	375	324

^aT_peak is the peak temperature.

^bT_fb is the first-break temperature.

^cBecause the endothermic and exothermic curves overlap not possible to determine T_fb for exothermic curve.

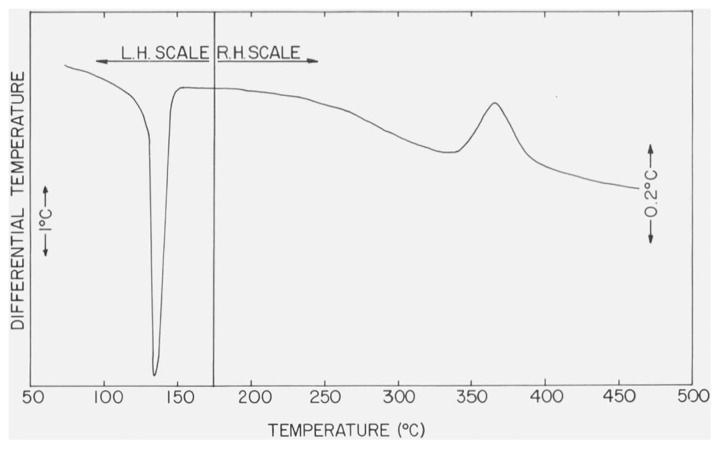
The DTA curve of α-CaSO₄ · 1/2H₂O, recorded with an N₂ atmosphere of ca. 760 torr in the DTA cell and a heating rate of 12 °C/min is shown in figure 6. Results of pressure dependence studies on the shape and position of the endothermic peaks are reproduced in figure 7 and the values of T_peak and T_fb are listed in table 2. The position of the endothermic effect of α-CaSO₄ · 1/2H₂O shifts to lower temperatures with reductions in the gaseous pressure in the DTA cell. The small exothermic effect also has a similar temperature-pressure behavior.

Figure 6.

DTA curve of α-CaSO₄ · 1/2H₂O with N₂ at 760 torr in the DTA cell.

Figure 7. Differential thermograms of α-CaSO₄ · 1/2H₂O with reduced pressures in the DTA cell.

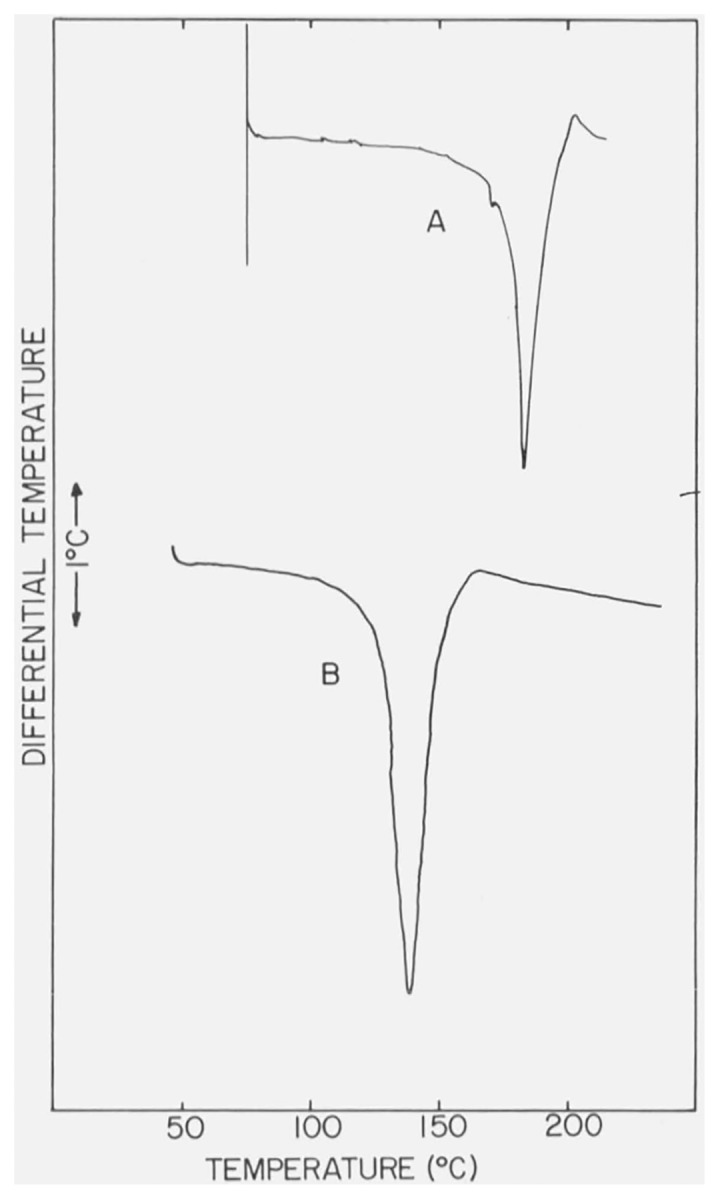
Pressures were 380 and ca. 1 torr, respectively, for thermograms A and B.

The differential thermogram of an equal molar mixture of a and β-CaSO₄ · 1/2H₂O includes the small exothermic effects of the respective components (fig. 8), which indicates that this method can be used to identify the two forms in the presence of each other.

Figure 8.

DTA curve of an equal molar mixture of α and β-CaSO4 · 1/2H₂O at 760 torr.

3.2. Thermogravimetry

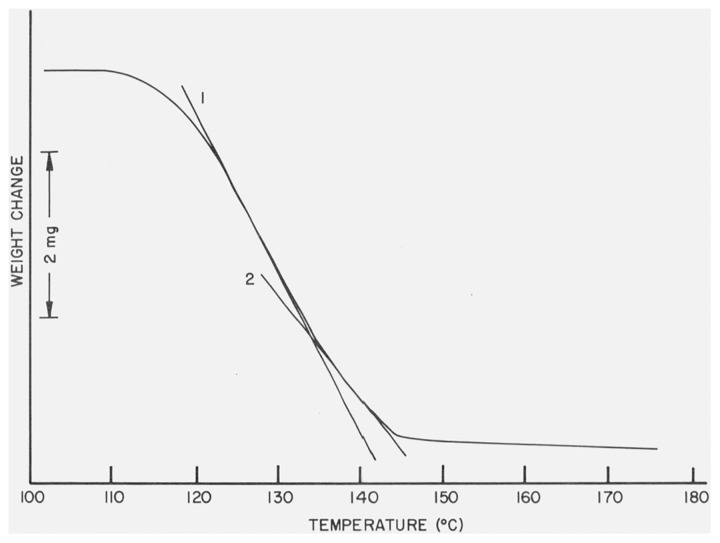
The thermogravigram of CaSO₄ · 2H₂O recorded using a heating rate of 3 °C/min and a temperature scale of 10 °C/inch is reproduced in figure 9. Although a two-step dehydration process was suggested by an apparent change in slope of the weight loss curve, indicated by the tangent lines in figure 9, a well defined inflection point attributed to the completion of the first dehydration process and the commencing of the second was not found (there was no indication of any plateau between the two reactions thus making it appear that they took place consecutively). The location of this point in the weight-loss curve was estimated by dropping a tangent line to the most straight portions of the segments associated with the two dehydration reactions and taking as the inflection point the intersection of the two lines, as shown in figure 9. The estimated inflection point corresponds to the removal of 65 percent of the water content of CaSO₄ · 2H₂O compared to the theoretical value of 75 percent (assuming that CaSO₄ ·1/2H₂O is formed).

Figure 9. TG curve of CaSO₄ · 2H₂O.

Line 1 is drawn tangent to the portion of the curve corresponding to the dehydration of CaSO₄ · 2H₂O to β-CaSO₄ · 1/2H₂O while tangent line 2 indicates the dehydration of β-CaSO., · 1/2H₂O to γ-CaSO₄.

One TG run was terminated at a weight-loss value equalling the removal of 1 1/2 molecules of H₂O from CaSO4 · 2H₂O, thus, theoretically producing either pure α- or β-CaSO₄ · 1/2H₂O. The DTA curves of the product, however, indicated that together with β-CaSO₄ · 1/2H₂O about 5 percent of unchanged CaSO₄ · 2H₂O and γ-CaSO₄ was present. These results were confirmed by x-ray powder diffraction analysis.

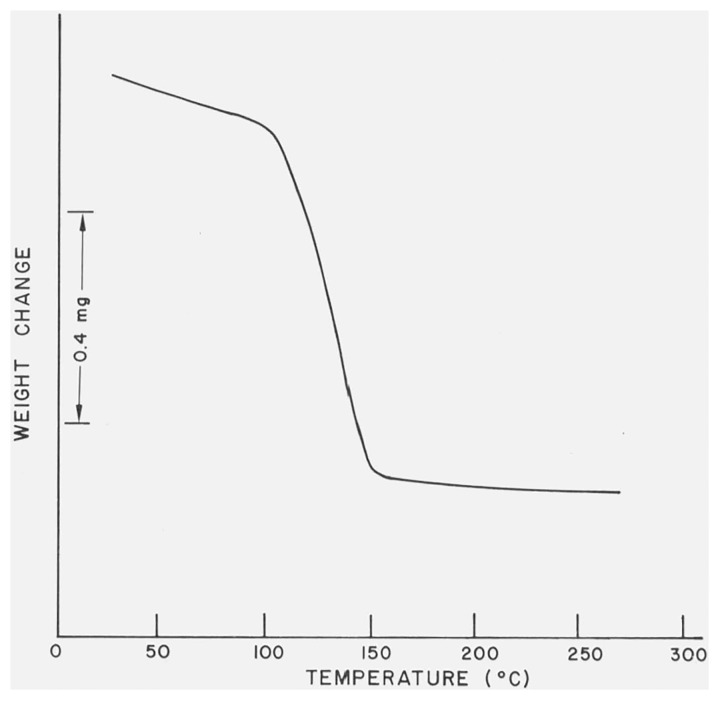
The TG curves of α- and β-CaSO₄ · 1/2H₂O were identical when using the same heating rates and the curve of the β-form, recorded using a heating rate of 12 °C/min and a temperature scale of 50 °C/in, is shown in figure 10. Well-defined incipient temperatures were not observed, i.e., the dehydration processes appeared to have commenced at the start of the runs, which was at 22 °C.

Figure 10.

The TG curve of β-CaSO₄ · 1/2H₂O.

The endothermic effects in the differential thermograms of CaSO₄ · 2H₂O and the CaSO₄ · 1/2H₂O set, at 760 torr, were found at higher temperatures than the weight-loss processes observed in their respective thermogravigrams (compare figs 1 and 9 and figs. 4 and 10), although these two phenomena are associated with the same dehydration reactions. These apparent discrepancies are probably due to both differences in the heating rates used in the respective studies and to physical differences in the TG and DTA cells in such components as sample holders, heating units and location of thermocouples. The size and shape of the sample holders can have a pronounced effect on the temperature location of weight-loss curves and the endothermic peaks because of their differences in heat capacities.

3.3. Differential Scanning Calorimetry

The DSC curve of CaSO₄ · 2H₂O is reproduced in figure 11. A heating rate of 5 °C/min was used. Only a single endothermic effect was measured because thermal equilibrium was not attained between the reference and sample cells after the first dehydration step was complete and before the second dehydration step had commenced. When normal sample crucibles, which had loosely fitting covers, were used, the resulting curves were very broad, virtually merging into the base line. Sharper curves (fig. 11) were obtained using hermetically sealed crucibles. The change in the base line before and after the observed dehydration reaction is attributed to a difference in the heat capacities between CaSO₄ · 2H₂O and the decomposition products.

Figure 11.

The DSC curve of CaSO₄ · 2H₂O.

The DSC curves of α- and β-CaSO₄ · 1/2H₂O were essentially identical as both were very broad even when hermetically sealed crucibles were used.

4. Discussion

4.1. Thermal Dissociation of CaSO₄ · 2H₂O

The thermal dissociation of CaSO₄ · 2H₂O in the region of 25 to 500 °C was monitored by both differential thermal analysis and thermal gravimetric analysis techniques and the pertinent features of the thermograms will be discussed in this section.

The differential thermogram of CaSO₄ · 2H₂O under a nitrogen atmosphere of 760 torr, fig. 1, is similar to thermograms observed by other investigators [3–7]. In the present study, however, the extent of overlapping of the first and second endothermic curves is smaller than previously reported, possibly because of our use of micro samples. Furthermore, a small endothermic dent reported by some investigators, [19], to be located just after the second endothermic effect was not observed in the present study. This small effect has been attributed to the expulsion of small amounts of residual water from the hemihydrate [19]; alternatively, this endothermic peak could denote the presence of a small impurity.

The differential thermogram of CaSO₄ • 2H₂O, reproduced in figure 1, can be understood on the basis of three transformations have peak temperatures of 150, 197, and 375 °C at 760 torr:

$$CaS{O}_4\cdot 2{\text{H}}_2{\text{O}}_{(\text{s})}\stackrel{{150}^{°}\text{C}}{\rightleftarrows }\beta -{\text{CaSO}}_4\cdot 1/2{\text{H}}_2{\text{O}}_{(\text{s})}+3/2{\text{H}}_2{\text{O}}_{(\text{v})}$$ (1)

$$\beta -{\text{CaSO}}_4\cdot 1/2{\text{H}}_2{\text{O}}_{(\text{s})}\stackrel{{197}^{°}\text{C}}{\rightleftarrows }\gamma -{\text{CaSO}}_{4(\text{s})}+1/2{\text{H}}_2{\text{O}}_{(\text{v})}$$ (2)

$$\gamma -{\text{CaSO}}_{4(\text{s})}\stackrel{{375}^{°}\text{C}}{\rightleftarrows }\beta -{\text{CaSO}}_{4(\text{s})}$$ (3)

T_fb of reactions (1) and (3) were 126 and 325 °C, respectively. However, T_fb of reaction (2) could not be determined because the two endothermic effects overlapped. This phenomenon will later be discussed in more detail.

According to this scheme, reactions (1) and (2) are dehydration processes and, consequently, give rise to endothermic curves, while reaction (3) is attributed to a lattice modification from a hexagonal to an orthorhombic unit cell [2] and gives rise to an exotherm. It is felt that the formulation of a two-step dehydration process, reactions (1) and (2), was supported by the apparent change in the slope of the weight-loss curve of CaSO₄ · 2H₂O (fig. 9). As previously mentioned, the endothermic effects in the differential thermograms takes place at higher temperatures than the corresponding weight-loss curves because of differences in the DTA and TG modules and the use of different heating rates in the respective studies.

The solid product formed in reaction (1) is presumed to be β-CaSO₄ 1/2H₂O since the DTA curves associated with reactions (2) and (3) are identical to those observed for authentic β-CaSO₄ · 1/2H₂O (fig. 4).

The proposed scheme for the dehydration of CaSO₄ · 2H₂O assumes reaction (1) is completed as reaction (2) commences. This assumption cannot be substantiated by the DTA study alone because the two endothermic effects overlap and it is not possible to ascertain when the reaction responsible for the first effect terminates and the next reaction commences. The temperature at the end of an endothermic of exothermic effect does not necessarily coincide with the completion of the chemical reaction due to such factors as heat transfer and differences in the heat capacities of the reactant and products. In this matter, the TG studies are of assistance. As reported in Section 3.2, a TG run was terminated at a weight-loss value equalling the removal of 1 1/2 molecules of H₂O from CaSO₄ · 2H₂O. The product was largely β-CaSO₄ · 1/2H₂O but did contain some 5 percent of unchanged CaSO₄ · 2H₂O and γ-CaSO₄. The phase types present were determined by DTA and x-ray powder diffraction techniques. A similar impure product was obtained when the stoichiometric amount of H₂O was removed, in vacuo, from CaSO₄ · 2H₂O to form β-CaSO₄ · 1/2H₂O. Therefore, it is likely that with the nonuniformity fo heating conditions of DTA, reactions (1) and (2) can proceed to a small extent concurrently within a sample, especially, when the supply of CaSO₄ · 2H₂O is nearly depleted, and that the proposed reaction scheme is somewhat over simplified.

Further evidence for the overlapping of the two endothermic reactions is provided by the thermogravigram of CaSO₄ · 2H₂O reproduced in figure 9. Neither a well-defined inflection point denoting the completion of one reaction and the start of the other dehydration process nor a plateau in the weight-loss curve signifying a separation of the two reactions was observed in the thermogravigram. Furthermore, the change in slope between the two segments of the weight-loss curve associated with the two dehydration reactions was small. In the following, an interpretation to account for the observations is proposed. Possibly very little lattice rearrangement takes place when passing from CaSO₄ · 2H₂O to β-CaSO₄ · 1/2H₂O as only lattice water is being removed and the layer structure [20] of the Ca²⁺ and ${\text{SO}}_4^{2-}$ grouping should retain its integrity. If this describes the actual situation, then it is reasonable to expect similar dehydration mechanisms for both CaSO₄ · 2H₂O and β-CaSO₄ · 1/2H₂O.

The following will focus upon the interesting perturbations noted in the differential thermograms of CaSO₄ · 2H₂O when they were measured with reduced pressures in the DTA cell.

The influence of bulk atmospheric pressures on the values of T_peak and T_fb is given in table 1 and figure 2. T_peak of the first endothermic curve was decreased from 150 to 123 °C while T_fb decreased from 126 to 99 °C when the pressure was reduced from 760 torr to ca. 1 torr. T_peak of the second endothermic curve was decreased even more, being 197 °C at 760 torr and either merged into the first curve or vanished when the residual pressure was reduced to ca. 1 torr. The position of the small exothermic curve was not pressure dependent. Of particular interest to the present study is the mechanism proposed by several investigators [21, 22], based on other types of dehydration experiments on CaSO₄ · 2H₂O. According to their mechanism, two dehydration reactions do take place if CaSO₄ · 2H₂O is in contact with appreciable amounts of water vapor. Dehydration in vacuo, however, leads directly to the formation of γ-CaSO₄ without β-CaSO₄ · 1/2H₂O being an intermediate specie. Removal of 1 1/2 molecules of H₂O from CaSO₄ · 2H₂O in vacuo, therefore, should result in a product which is a mixture of CaSO₄ · 2H₂O and γ-CaSO₄ and possibly containing a trace of β-CaSO₄ · 1/2H₂O. The above views are untenable, however, for in the present study it was found that β-CaSO₄ · 1/2H₂O was the main product formed by the removal of H₂O in vacuo and only about 5 percent of CaSO₄ · 2H₂O and γ-CaSO₄ was found.

A reasonable explanation of the formation of β-CaSO₄ · 1/2H₂O by dehydration in vacuo of CaSO₄ · 2H₂O is embodied in the phase diagram shown in figure 3. The gaseous pressures within the DTA cell were plotted versus the peak temperatures for the dehydration reactions of CaSO₄ · 2H₂O and the subsequent transformation of γ-CaSO₄ to β-CaSO₄. According to this scheme the second endothermic curve does vanish rather than merging with the first endothermic curve. The formation of β-CaSO₄ · 1/2H₂O by the dehydration in vacuo of CaSO₄ · 2H₂O is accounted for by the metastable prolongation (indicated by the dot-dash line) of the univariant curve.

The merging tendency of the two endothermic curves can be explained on the basis of. the van’t Hoff equation:

$$\frac{d\text{ln}{K}_p}{dT}=\frac{\Delta H}{R{T}^2}.$$

The gaseous pressures are low in the present case and ideal gas behavior is assumed.

In the above equation ΔH is the heat of reaction at temperature T, and therefore is not a constant. The standard heat of reaction, ΔH₀, at T₀ is introduced by using the Kirchoff equation:

$${\left(\frac{\partial (\Delta H)}{\partial T}\right)}_p=\Delta C_p$$

$$\Delta H=\Delta H_0+\underset{T_0}{\overset{T}{\int }}\Delta C_{p}dT\approx \Delta H_0+\Delta {\overline{C}}_p\left(T-T_0\right)$$

$$\frac{d\text{ln}{K}_p}{dT}=\frac{\Delta H_0+\Delta {\overline{C}}_p\left(T-T_0\right)}{R{T}^2}=\frac{\Delta H_0}{R{T}^2}+\frac{\Delta {\overline{C}}_p}{RT}-\frac{\Delta {\overline{C}}_p{T}_0}{R{T}^2}$$

The integrated form of the above equation, when considering the interval between T₁ and T₂, becomes

$$\text{ln}\frac{K_{p_2}}{K_{p_1}}=-\frac{\Delta H_0}{R}\left(\frac{1}{T_2}-\frac{1}{T_1}\right)+\frac{\Delta {\overline{C}}_p}{R}\text{ln}\frac{T_2}{T_1}+\frac{\Delta {\overline{C}}_p{T}_0}{R}\left(\frac{1}{T_2}-\frac{1}{T_1}\right).$$

The last term vanishes at T₀ = 0 K, resulting in the following equation:

$$\text{ln}\frac{K_{p_2}}{K_{p_1}}=-\frac{\Delta H_0}{R}\left(\frac{1}{T_2}-\frac{1}{T_1}\right)+\frac{\Delta {\overline{C}}_p}{R}\text{ln}\frac{T_2}{T_1}.$$

The pressure decrease necessary to shift T_peak of the second endothermic curve in the thermogram of CaSO₄ · 2H₂O from 197 to 123 °C can now be estimated by setting T=T_peak and K_p = p^1/2 and using the values of ΔH₀ and ΔC_P reported by Kelly, Southard, and Anderson [9] for the reaction β-CaSO₄ · l/2H₂O_(s) ⇆ γ-CaSO_4(s) + l/2H₂O_(v). The calculated value P₂/P₁ = 0.06 suggests that a 16 fold decrease in the partial pressure of water vapor within the specimen tube can account for the shift in T_peak observed when the bulk atmospheric pressure is decreased from 760 torr to ca. 1 torr. By a similar method, with K_P = P^3/2, a value of P₂/P₁ =0.36 was calculated for the case when T_peak of the first endothermic effect was decreased from 150 to 123 °C. These values can be only considered as approximations to the actual situations because of the nonrigorous treatment.

4.2. Thermal Analysis of α- and β-CaSO₄ · 1/2H₂0

In the following discussion, the differential thermograms and the thermogravigrams of α- and β-CaSO₄ · 1/2H₂O, measured from 25 to 500 °C, will be analyzed

The differential thermograms will be discussed in detail since it has been reported [15] that the two forms of CaSO₄ · 1/2H₂O can be identified by their thermograms. The thermograms of the a and β forms measured under an atmospheric pressure of 760 torr are shown in figures 6 and 4, respectively. Each thermogram consisted of a single endothermic and a smaller exothermic curve. Budnikov and Kosyreva have reported [16] that a difference of about 20 °C was found between the T_peak of the endothermic effects in α- and β-CaSO₄ · 1/2H₂O. A difference of only 3 °C (table 2) between the respective values of T_peak as well as T_fb, however, was measured in the present study. This small ΔT can possibly be attributed to porosity differences in the a and β forms. The only essential difference between the thermograms are in the exothermic effects. The exothermic effect of α-CaSO4 · 1/2H₂O closely follows the endothermic effect and has a T_peak of 217 °C, while the exothermic effect of β-CaSO₄ · 1/2H₂O is much broader and has a T_peak of 375 °C and T_fbof 322 °C. Both exothermic effects have been attributed to phase changes [15].

The values of T_peak and T_fb for the endothermic effects of a and β-CaSO₄ · 1/2H₂O have a similar pressure dependence (table 2 and fig. 5 and 7) as the second endothermic effect of CaSO₄ · 2H₂O and can be interpreted in the same manner.

The location of the exothermic effect observed in the thermogram of α-CaSO₄ · 1/2H₂O was pressure sensitive in the same manner as the preceding endothermic effect (table 2 and fig. 7). Possibly this exothermic effect can be attributed to the formation of a new phase, the conversion being triggered by the removal of the lattice water. Because this apparent phase conversion took place immediately after the dehydration reaction, it is reasonable to expect the location of the exothermic effect would shift in the same direction as the endothermic effect. In contrast, the location of the exothermic effect of β-CaSO₄ · 1/2H₂O was not significantly pressure dependent.

The difference observed in the exothermic effects of the thermograms of α and β-CaSO₄ · 1/2H₂O do not necessarily indicate a structural difference between the two forms, but possibly are associated with the dehydration kinetics. The kinetics can depend upon such factors as the surface area, porosity and crystallinity. The β form is produced by dry decomposition which should yield a poorly crystalline and porous material with a larger surface area than the α form, which was a precipitated material and, therefore, should consist of well-formed crystals.

The thermogravigrams of α- and β-CaSO₄ · 1/2H₂O were so similar that it was impossible to differentiate between the two forms on the basis of TG studies. The thermogravigram of β-CaSO₄ · 1/2H₂O is reproduced in figure 10. Note that the dehydration reaction appeared to be initiated at room temperature. Probably, the loosely held zeolitic water of β-CaSO₄ · 1/2H₂O [18] is first removed then followed by dissociation of the lattice water. The removal of lattice water is indicated by the more pronounced sloping segment of the weight-loss curve.

4.3. Calorimetry Studies

On the assumption that the endothermic effect measured in the DSC curve of CaSO₄ · 2H₂O (fig 11) could be entirely attributed to the first dehydration step of CaSO₄ · 2H₂O, the heat of reaction of

$${\text{CaSO}}_4\cdot 2{\text{H}}_2{\text{O}}_{(\text{s})}\rightleftarrows {\text{CaSO}}_4\cdot 1/2{\text{H}}_2{\text{O}}_{(\text{s})}+3/2{\text{H}}_2{\text{O}}_{(\text{v})}$$

was estimated to be 23.8 kcal (9.96 × 10⁴ J) per gram mol. wt. This value is substantially higher than the calculated value of 19.9 kcal (8.33 × 10⁴ J) per gram mol. wt., obtained using the equation given by Kelly, Southard, and Anderson [9]. A reasonable explanation for this discrepancy has previously been discussed in section 4.1 for the cases of the thermogravigram and the differential thermogram of CaSO₄ · 2H₂O, i.e., the two dehydration steps involved in the complete dehydration of CaSO₄ · 2H₂O are to some extent taking place concurrently during the DSC measurements.

The endothermic curves for α- and β-CaSO₄ · 1/2H₂O were too broad to permit the calculation of the heat of reactions.

5. Summary and Conclusions

The dehydration of CaSO₄ · 2H₂O to γ-CaSO₄ is a two-step dissociative process, with β-CaSO₄ · 1/2H₂O being the intermediate product, irrespective of the dehydration methods.

The differential thermogram of CaSO₄ · 2H₂O, measured under gaseous pressures of a 760 torr, has two large endothermic effects with peak temperatures of 150(T_fb of 126 °C) and 197 °C and a smaller exotherm with peak temperature of 375 °C (T_fb, of 325 °C) The endothermic effects were associated with dehydra tion processes whereas the exothermic effect indicated phase transformation of γ-CaSO₄ to β-CaSO₄. When the dissociative reactions were carried out under reduced pressure the endothermic effects shifted to lower temperatures and tended to merge. With residual pressures of about 1 torr, a single endothermic effect was observed. These phenomena can be explained from the application of the van’t Hoff equation and on the basis of a phase diagram constructed by plotting gaseous pressures in the DTA cell versus peak temperatures. Location of the exothermic effect was not significantly pressure dependent.

The small change in slope observed between the two segments of the weight-loss curve of CaSO₄ · 2H₂O indicates that there is little difference in the dissociative mechanisms of the two dehydration reactions.

While it was not possible to differentiate between the supposed α and β forms of CaSO₄ · 1/2H₂O on the basis of TG and DSC studies, the differential ihermograms of the two forms were somewhat dissimilar. An endothermic effect with a peak temperature of ca. 197 °C and T_fb of ca. 158 °C, was found in the differential thermograms of both forms of CaSO₄ · 1/2H₂O. The α form had a single exothermic effect with a peak temperature of 217 °C, while the exotherm of the β form had a peak temperature of 375 °C, T_fb of 322 °C, under bulk pressures of 760 torr. The peak temperature of the exothermic effect of α-CaSO₄ · 1/2H₂O was pressure dependent, whereas, the exothermic effect of β-CaSO₄ · 1/2H₂O was not influenced by changes in the atmospheric pressure within the DTA cell. The differences in the thermograins could possibly be associated with the dehydration kinetics, because the α form should have a more perfect crystalline structure than the β form. Therefore, while slight differences have been observed between the properties of α- and β-CaSO₄ · 1/2H₂O, at the present it cannot be conclusively determined if these differences are sufficiently significant to consider the supposed α and β forms as separate entities.