Emergence of Hierarchical Modularity in Evolving Networks Uncovered by Phylogenomic Analysis

Abstract

Networks describe how parts associate with each other to form integrated systems which often have modular and hierarchical structure. In biology, network growth involves two processes, one that unifies and the other that diversifies. Here, we propose a biphasic (bow-tie) theory of module emergence. In the first phase, parts are at first weakly linked and associate variously. As they diversify, they compete with each other and are often selected for performance. The emerging interactions constrain their structure and associations. This causes parts to self-organize into modules with tight linkage. In the second phase, variants of the modules diversify and become new parts for a new generative cycle of higher level organization. The paradigm predicts the rise of hierarchical modularity in evolving networks at different timescales and complexity levels. Remarkably, phylogenomic analyses uncover this emergence in the rewiring of metabolomic and transcriptome-informed metabolic networks, the nanosecond dynamics of proteins, and evolving networks of metabolism, elementary functionomes, and protein domain organization.

Introduction

Systems are made of parts, which often interact with each other in an organized manner to form integrated wholes.¹ They are confined by spatial, temporal, and functional boundaries and are influenced by the external environment. Graph theoretical approaches model systems with graphs, mathematical constructs that connect vertices to each other with lines.² Vertices describe parts of a system and lines describe pairwise interaction between parts. When connections are undirected, lines are called edges. When connections are directed (ie, each connection involves an initial vertex and a terminal vertex), lines are called arcs. Graphs become networks when functions or other properties are mapped onto the vertices and lines of the graphs, with vertices now being called nodes and lines being called links of the network. This mapping is not trivial.

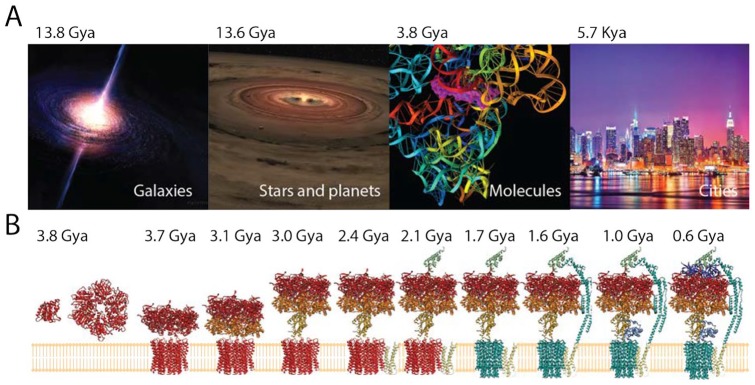
As systems evolve, they often grow from parts to form bigger wholes in an expanding process of “accretion” and “diversification.”³ We define accretion as growth and increase that typically results in the accumulation of entities and their interconnections. In turn, diversification can be defined as the gradual accumulation of change and the diffusional spread of variation through time. Both accretion and diversification are tightly interlinked and manifest at different degrees in different contexts and timeframes of evolving systems. Despite being controlled by a diverse set of mechanisms, they are also well-known phenomena that are likely universal (Figure 1A). Phylogenetic and polyphasic analyses reveal evolutionary growth and diversification of galaxies, stars, and planets^4-6; comparative and evolutionary genomic analyses support the rise of macromolecular structure making up increasingly complicated cellular machinery³; and archeology and historical records trace the rise and growth of cities^8-11 and other sociotechnical systems (eg, the Internet).¹² Accretion and diversification are particularly pervasive in biology at many levels of biological organization. Paleontology provides an empirical pattern of increase of species from one to many that is robust in land and sea and is independent from extinction.¹³ However, different diversification regimes exist through geological time, which constrain the size of clades and stem-to-tip branching events and often result in burst patterns followed by declining diversification. Currently, there are more than 1.8 × 10⁶ named species¹⁴ and an estimated 10¹² microbial species on Earth that have not been surveyed.¹⁵ All of these diversified entities must have gradually accumulated in evolution as their proteomes follow the Heaps law and the principle of historical continuity.¹⁶ The molecular components of an organism also accrete.³ They become parts of growing molecules and macromolecules, which also interact and merge with other growing molecules to form molecular complexes.¹⁷ For example, Figure 1B describes the accretion of the molecular components of the F₁/F₀ ATP (adenosine triphosphate) synthase, a 600-kDa multisubunit complex that is central to cellular bioenergetics. The complex is a motor with 2 rotors connected by an axle and regulated by a stator. The F₀ rotor is embedded in the membrane and its movement is driven by transmembrane proton gradients. The F₁ rotor is a rotating head that catalyzes ATP synthesis/hydrolysis. The complex originated in a ring structure of the F₁ rotor 3.8 Gya, then accreted the F₀ rotor, and finally added the axel and then the stator 0.6 Gya to form the fully developed bioenergetic machine.⁷ Molecular complexes make up cellular machinery and assemblies, which end forming higher levels of molecular and cellular structure. The resulting cells accrete into more complex cellular and organismal assemblies, including cellular consortia, multicellular organisms, and organismal populations. In one extreme example, eusocial communities such as those of Argentine ants were found to quickly accrete into super-colonies of billions of individuals encompassing the Mediterranean and Atlantic coasts of Southern Europe¹⁸ and to later unify with Japanese and Californian counterparts into a worldwide mega-colony.¹⁹ Accretion is always accompanied by diversification. At biological level, for example, the world of cellular organisms and viruses diversify into groups that have evolved distinct features. Their diversity and evolution can be described with taxonomies or by the reconstruction of a “tree of life.”²⁰ Despite significant horizontal exchange of genetic information, there are strong vertical (phylogenetic) signatures in biological evolution (eg, in viral evolution).²¹ These signatures are often responsible for the conservation of biological features, such as the structural design of molecules or the functional allosteric, regulatory, and active sites of proteins.²²

Figure 1.

Accretion and diversification appear universal. (A) Galaxies, stars, planets, macromolecules, and cities grow and evolve. For example, gravitational attraction causes gas, molecular clouds, dust grains, and particles to accumulate into massive objects in the cosmos. This usually occurs by the formation of spiraling accretion disks, which form out of diffused material in orbital motion around a central body.⁴ This is the case for protoplanetary and circumstellar disks and active galactic nuclei, some of which associate with astrophysical jets of ionized matter.⁵ Accretion is tightly coupled to diversification. For example, a number of transforming processes—including monolithic collapse, interaction between accretion and mergers, gravitational interaction, and sweeping and ejection events—cause galaxies to diversify.⁶ Time of origin is given in billions or thousands of years ago (Gya and Kya, respectively). (B) The molecular structure of the F₁/F₀ ATP synthase complex that is involved in bioenergetics of the cell evolves by adding protein structural domains.⁷ Domains are colored according to their evolutionary age, from red (early) to blue (late).

Accretion and diversification can be portrayed by a series of evolving networks that grow by gradually adding and subtracting nodes and links. As networks grow and nodes diversify, their complexity also increases. Many networks exhibit higher order organization in connectivity, ie, in the establishment of links, which can be modeled using small network subgraphs.²³ Here, we review how network growth and complexification tailor evolving biological systems with two processes, one that unifies and the other that diversifies. We explain unification and diversification with a “network” paradigm (tela vitae) of systems of interconnected things that grow. The paradigm is congruent with a biphasic model of generation of structure,²⁴ a “double tale” of accretion and evolutionary change in which accretion unifies disparate parts to form bigger wholes and change fosters growth and innovation. The theory is supported by considerable phylogenomic data. The hallmark of this model is the emergence of an important fractal-like pattern that exists in the structure of biological networks, hierarchical modularity.

A Biphasic Pattern Exists in “omic” Repertoires and Evolutionary History

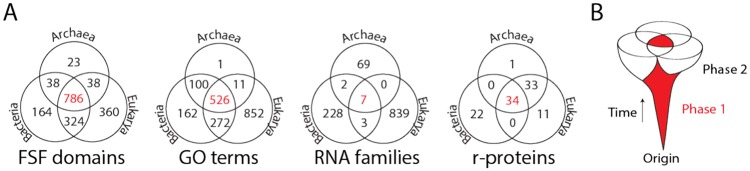
Comparative genomics dissects genomic features that are distinct or similar in different organisms, including those of chromosomal, genetic, regulatory, and functional organization. These signatures are often features that are evolutionarily highly conserved. They include the fold structure of protein structural domains categorized by the SCOP²⁵ or CATH²⁶ gold standards of protein taxonomy, Gene Ontology (GO) definitions of biological functions,²⁷ the global structure of functional RNA molecules (eg, cataloged by the Rfam database),²⁸ or proteins (r-proteins) associated with the ribosome, the central protein biosynthetic machinery of the cell.²⁹ The general comparative analysis approach does not reconstruct history and is therefore an evolutionary inference made from extant data. However, the fundamental evolutionary role of accretion and diversification can be made plainly evident (Figure 2). Venn diagrams describing the distribution of structural domains, functional RNA, GO molecular functions, and r-protein repertoires in the 3 cellular domains of life, Archaea, Bacteria and Eukarya, show significant “omic” sets that are universal (colored in red) and significant domain-specific repertoires (Figure 2A). As expected, the 7 RNA families that are universal include functional RNA that is known to be very ancient, including ribosomal RNA (rRNA) and transfer RNA (tRNA) molecules. The distributions in Venn diagrams can be explained by a biphasic evolutionary model in which an ancient core of conserved features is built piecemeal and is then diversified by the appearance of organismal lineages (Figure 2B).

Figure 2.

Ancient universal cores and derived peripheries support a biphasic process of accretion. (A) Venn diagrams describe censuses of protein structural domains defined at fold superfamily (FSF) level of structural classification of the SCOP taxonomy, Gene Ontology (GO) terms of molecular functions, RNA families defined by the Rfam database, and homologies of ribosomal proteins (r-proteins). The universal repertoires shared by Archaea, Bacteria, and Eukarya are colored in red. (B) Model of accretion explaining the Venn diagrams. In phase 1, biological repertoires of parts accrete into universal cores, which in phase 2 diversify together with the evolving organisms of the 3 cellular superkingdoms of life.

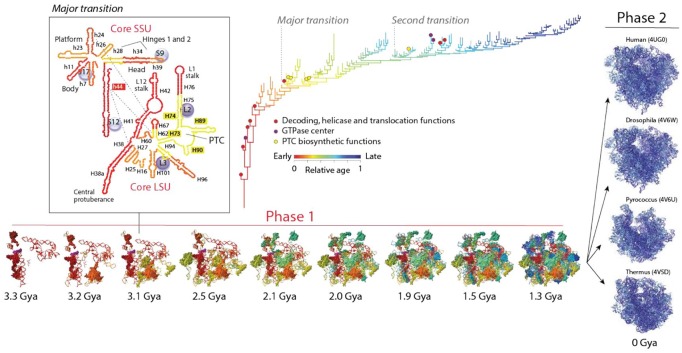
Evolutionary genomics supports the evolutionary biphasic pattern. Powerful methods of phylogenetic analysis can be used to reconstruct the history of molecules and organisms from highly conserved molecular features that carry deep phylogenetic history (Box 1). These features include the topology and thermodynamics of RNA molecules and the folds of the protein structural domains identified with hidden Markov models of structural recognition in thousands of genomes.³¹ For example, phylogenomic tree–like statements (phylogenies) portraying the histories of molecular parts, including the structural domains of proteins³⁵ or the helical stems of RNA molecules,³⁶ allow to map the progression of accretion in the most central macromolecular complex of the cell, the ribosome. The ribosome is an essential molecular machine that is universally present in cells. It contains a small subunit (SSU) and a large subunit. The SSU typically contains 30 to 40 r-proteins and 1 rRNA molecule with ~50 universal helical stems that fold independently into 3 major domains. The LSU typically contains 30 to 45 r-proteins and 2 to 3 rRNAs with ~100 universal helices that fold into 6 domains (5S rRNA is the seventh domain). The history of the entire ribosomal complex revealed piecemeal buildup of a universal structural core and later on ribosomal diversification.^31,34,36 Phylogenomic trees of rRNA helical stems and protein structural domains that are part of the small and large ribosomal subunits uncovered an evolutionary chronology of accretion (Figure 3). This timeline described the evolution of the universally conserved ribosomal core, which was visualized by coloring relative evolutionary ages (derived directly from the trees) in 3-dimensional (3D) atomic ribosomal models. A molecular clock of folds linked these chronologies to the geological record.³⁷ The study confirmed the coevolutionary history of rRNA and r-proteins, which was already intimated in an initial accretion study of the 5S rRNA molecule in interaction with its associated r-proteins.³⁸ A tight linear correlation between the age of rRNA stems and interacting domains of r-proteins (R² = 0.961; F = 221.3, P < 0.0001) was evident as structures coevolved. This observation challenged the popular ancient “RNA world” hypothesis, in which RNA preceded proteins in evolution. The oldest protein (S12, S17, S9, L3) appeared 3.3 to 3.4 Gya, concurrently with the oldest rRNA substructures responsible for decoding and ribosomal dynamics, which included the central ribosomal ratchet and 2 hinges of the SSU and the L1 and L7/L12 stalks of the LSU (Figure 3). All these structures are important for tRNA movement in the ribosomal complex. Accretion continued unabated until the formation of a 5-way and a 10-way junction in the SSU and LSU, respectively, at which point a “major transition” in ribosomal evolution occurred 2.8 to 3.1 Gya (Figure 3). This transition brought ribosomal subunits together through intersubunit bridge contacts, interactions with tRNA, and materialized a fully fledged peptidyl transferase center (PTC) with exit pore responsible for the enzymatic activity of protein biosynthesis. A “second transition” occurred later, during the Great Oxygenation Event of our planet ~2.4 Gya. At that time, the ribwosome accreted the L7/12 protein complex that stimulates the GTPase activity of elongation factor EF-G and enhances ribosomal efficiency. The chronology showed that the ribosomal core was fully formed 1.3 Gya, but continued to exhibit differential growth in different organismal lineages. During this second phase of accretion, eukaryotic ribosomes diversified by growing additional eukaryotic-specific structural appendages that expanded the network of molecular interactions and surrounded the universal core.³⁹ These structures also remodeled intersubunit interfaces, which affected rotational movements of the subunits.⁴⁰ The late impact of organismal diversification on the eukaryotic ribosomal core that started ~1.3 Gya, ~1.5 billion years after the rise of aerobic metabolism and the last universal common ancestor (LUCA) of cellular life,³⁷ can be explained by the rise of early multicellular organisms during that time. The appearance of ultrastructurally complex microfossils (acritarchs) of eukaryotes 1.5 Gya⁴¹ has been pushed back to the Paleoproterozoic ~1.65 Gya,⁴² and recently discovered eukaryotic microfossils suggest that multicellular organisms of unprecedented large size (decimeter-scale) were already present 1.56 Gya.⁴³ Their large size overcomes life at low Reynolds numbers,⁴⁴ which makes inertia irrelevant, perhaps relieving known reductive evolutionary pressures on molecules imposed by microbial (genome) size. Note that the length of macromolecules of prokaryotic microbes evolves reductively, whereas that of eukaryotes does not, as evidenced by the study of proteomes and structural domains.⁴⁵ Although reductive evolution can explain why prokaryotes remained bound to the ribosomal core design, recent studies in bacteria provide evidence suggesting the presence of functional selective ribosomal subpopulations that show variations in both rRNA or r-protein components.⁴⁶ This suggests regulatory variability may be linked to ribosomal specialization and may be a general evolutionary strategy adopted by prokaryotes.

Box 1.

A brief primer of structural phylogenomic methodology. A phylogenetic tree is a branching diagram that explicitly represents the history of a biological system.³⁰ Trees are graphs with branches (nodes) and leaves (taxa) (see example in Figure 3) that are built from data, observable features (characters) that are characteristic of the system that is being studied. Tree reconstruction involves optimizing the fit of data along the branches of all possible trees according to some optimality criterion and a model of character state change. Only “shared and derived” features of characters are phylogenetically informative. Finally, trees are rooted by establishing the direction of change, which tests the existence of historical memory (homology).³⁰ The structure of macromolecules is evolutionarily conserved and can be effectively used to generate intrinsically rooted phylogenetic trees that describe the deep evolution of RNA and protein molecules, individually or globally. In particular, trees describing the evolution of parts of a molecular system help uncover patterns of macromolecular accretion and diversification.^31-33 They are atypical (see Harish and Caetano-Anollés.³⁴ and Sun and Caetano-Anollés³³ for more extensive discussion): (1) Trees are global phylogenetic statements that are intrinsically rooted and are highly unbalanced: This allows to build a chronology of appearance of taxa describing a system, such as helical substructures of rRNA or tracings of r-proteins onto ribosomal structure (Figure 3); (2) the leaves of trees (taxa) are structural elements (eg, RNA substructures, protein structural domains) or complete structures (eg, single or multidomain proteins): this contrasts with the typical trees of systematic biology, which hold taxa that are diagnostic of organisms; (3) the branches (or internal nodes) of the trees define chronologies of structural diversification: branches (or nodes) represent diversification events that occur as innovations in features of RNA or popularity and spread of structures in proteomes develop in time; (4) characters describe features or abundance of molecular structure: characters are features (eg, topology, thermodynamic parameters of a molecular morphospace) or abundance (eg, domains encoded in genomes) of molecular structure that change along branches of the trees; they are often identified with, for example, machine learning approaches or other computational methods; (5) the criterion of primary homology rests on the feature of substructure or structure being studied or their genomic abundance levels: tree reconstruction demands a criterion of homology that establishes correspondences arising from common ancestry. Criteria for the study of accretion and diversification involve topographic correspondences of structures according to transformation sequences of ordered multistate characters. These serial homologies are tested by rooting trees with Weston’s generality criterion³⁰; and (6) trees provide by definition a model of structural evolution: the trees describe how molecules evolve from an originating substructure by addition of substructure components or how repertoires of molecules evolve from an originating molecule by addition of molecules. The frameworks are, for example, described for RNA in the work by Sun and Caetano-Anollés.³³

Figure 3.

The biphasic history of the ribosome. An evolutionary timeline of ribosomal RNA (rRNA) and proteins (r-proteins) inferred directly from phylogenomic data shows 2 evolutionary phases. During an initial phase (phase 1), helical structures of rRNA and r-proteins accreted to form a universal ribosomal core. The second phase of ribosomal evolution (phase 2) started 1.3 Gya (or earlier) when the universal core diversified alongside with evolving organismal lineages. The phylogenomic tree describes the accretion of rRNA helical stems and is colored according to relative age. Every new branch reflects the addition of a new part to the whole. Only selected functional taxa are labeled in the tree with colored circles. The first RNA structures to accrete include the head and ratchet, the central protuberance, and stalks, which are involved in ribosomal dynamics. Early structures are also involved in energetics, decoding, helicase activity, and translocation. The peptidyl transferase center (PTC) that is responsible for protein biosynthesis accretes later in time (in yellow), whereas RNA helices gradually gained interaction with r-proteins to form a processivity core 2.8 to 3.1 Gya at a time when a crucial “major transition” in ribosomal evolution brought small and large subunits (SSU and LSU) together through protein structural stabilization, interaction surfaces, and formation of intersubunit bridges. The inset shows secondary structure representations of the primordial ribosomal ensemble, with r-proteins visualized as bubbles and bridge interactions as dashed blue lines. This initial proto-ribosome served as center for coordinated ribonucleoprotein accretion to form a highly processive universal ribosome core during a “second transition” that took place 2.4 Gya. A molecular clock of folds linked structural and geological timescales.

Source: Data from previous studies.^31,34,36

A number of tRNA sequence similarities believed to arise from common ancestry were detected in both subunits of rRNA, including homologies to the PTC.^47-49 These “remote homologies” suggested that the ribosome was at first built piecemeal from a multiplicity of primordial tRNA-like molecules, and that both tRNA and the ribosome had a common remote evolutionary origin. The historical patchwork observed when the age of rRNA stems is traced onto crystallographic models of the ribosome (Figure 3), supports rRNA having numerous independent origins.⁵⁰ Thus, a number of separate molecules were likely recruited to build higher ribosomal structure during early ribosomal evolution. Remarkably, tRNA sequence homologies in rRNA also showed remote homologies to elongation factors, synthetases, RNA polymerases, and nucleotide biosynthetic enzymes.⁴⁹ It is therefore likely that primordial ribosomes could have originally consisted of a multiplicity of tRNA-like molecules that were loosely linked together and acted as primordial genomes. With time, these building blocks integrated into a cohesive molecular machine. This scenario suggests a strong force of unification during ribosomal accretion that must be placed within the context of molecular biodiversity.

A Biphasic (bow-tie) Model of Module Creation

The biphasic evolutionary behavior of the evolving ribosome depicts a general “hourglass” pattern of unification and diversification that is pervasive in biology: diversity decreases to a minimum as parts unify and then increases again when the whole diversifies. To account for this pattern, Mittenthal et al.²⁴ developed a theory of emergence of nested hierarchies of modules, in which diversifying parts of a system converge under optimization or selection into tightly linked groups, which subsequently diversify. Modules are sets of integrated component parts that cooperate to perform a task and interact more strongly with each other than with other parts and modules of the system.⁵¹ Modularity appears the result of a “nucleation” process that enhances cohesion, ie, adopted constraints that the system as a whole imposes on the dynamical stabilities of component parts.⁵² These stabilities ultimately determine if the system can be easily decomposed into building blocks that are relatively autonomous.¹ Examples of building blocks that are modularly connected in biology include amino acids, secondary and supersecondary structures, and structural domains in proteins. Similarly, nucleotides, helical stems, and junctions are modules of RNA molecules. These building blocks represent different levels of organization of a hierarchical system with convergences of diversifying parts into modules occurring at different timeframes and levels. The theory of module creation centers on linkage, the extent of interaction between parts of a system.²⁴ In the first phase, parts are weakly linked and associate variously. Through mutation, reassortment, and recruitment, parts become more numerous and diverse. Links that help perform a task will persist because they increase fitness or functional capabilities. These emerging interactions are costly and constrain the structure and organization of the system as parts compete with each other to meet the optimization or selection criterion, forcing the system to undergo competitive optimization. This decreases diversity and increases the chances of tighter linkages. The modules that emerge from the growing interactions are dynamically resistant to fluctuations and change. In the second phase, the modules become new building blocks for a new generative cycle of higher level organization. Because linkage is tighter within modules than between modules, modules are now free to diversify by mutation, reassortment, and/or be accreted into different contexts to form higher level modules. Thus, unification occurs through diversification: accretion brings together disparate parts to form bigger wholes, whereas change provides opportunities for growth and innovation.

The biphasic theoretical framework is supported by several lines of evidence, including the diversification of the sequence and structure of proteins, nucleic acids, and other polymers used by biological systems to function or store information; the establishment of intracellular networks such as metabolism; the generation of biological codes (eg, the genetic code and translation); and competitive optimization in embryo development and epigenetics.^24,50 For example, transcriptional patterns explain a developmental “hourglass” operating in embryogenesis,^53-55 which is compatible with conservation patterns in a bow-tie structure that relate inputs and outputs.⁵⁶ The developmental hourglass model helps explain the observation that the form of animal embryos converges before diversifying into a common embryonic design during the “phylotypic” stage and the discovery of evolutionarily conserved clusters of gene expression of Hox genes.^57,58 Recent genomic analyses have shown that the age of genes encoding phenotypes of the temporal waist of the hourglass is older and more conserved than those at the beginning or end of embryonic development.^53-55 Comparison of genome-wide expression patterns across embryonic development in 6 species of fruit flies showed that gene expression variations were minimal during the phylotypic stage, suggesting strong selective constraints operating at this stage.⁵³ Similarly, morphologies were connected to the evolutionary age of genes inferred using conservation-level classification (phylostratigraphy) in zebrafish, nematodes, and fruit flies.⁵⁴ In all cases, the differentially expressed genes were evolutionarily older during the phylotypic stage of animal development, which likely describe modules of gene expression networks necessary to establish the basic rules of the body plan that is common between the diversifying animal organisms (though other hypothesis are possible).⁵⁹

We note, however, similarities and distinctions between temporal biphasic patterns expressing at behavioral, developmental, and evolutionary levels.²⁴ All hourglasses describe restrictions to variation in behavior, development, or evolution of a system. However, the spatial distribution of diversification may be wide or localized during the early and late temporal phases. It can occur in several timeframes, with various degrees of repetition, generally to achieve some level of complexity before acquiring the potential to diversify. A behavioral hourglass may occur once or repeatedly in the life cycle of an organism (eg, metabolic rewiring in the presence of stress). Similarly, a developmental hourglass bundles the diverse developmental trajectories of a group of related embryos in animal development. In contrast, the biphasic change in the rate of diversification of an evolutionary hourglass, such as the hourglass of ribosomal accretion (Figure 3), occurs only once in the entire course of evolution, tallying the number of parts existing at a sequence of times, without presenting trajectories between the parts. Finally, some hourglasses resemble a “bow-tie,” a structure that was first described in a sociotechnical system that exchanges information between computers, the World Wide Web (WWW),⁶⁰ but is widely present in biology (eg, metabolism).⁶¹ The first phase of the hourglass contributes inputs to a system’s central core (the “knot”), which then processes these inputs into outputs, all of which contribute to the efficiency, robustness, and evolvability of the system as it responds to varying environments.⁵⁶ In the example of Figure 3, the rRNA and protein structural modules contribute biological functions as inputs to a growing ribosomal core. When the structural core achieves certain level of complexity, it then acquires functionalities (processivities or innovations) as outputs that endow the molecular system with the potential to diversify.

Emergence of Community Structure in Evolving Networks

We now use a network paradigm to discuss how the biphasic model of module generation explains the evolutionary emergence of both modularity and hierarchy in evolving networks (Figure 4). Modular networks harbor “communities,” groups of nodes that that are more densely connected with themselves than with the rest of the network.⁶² Modularity usually counterbalances power-law behavior of scale-free networks (which generally grow by preferential attachment of new nodes to highly connected nodes),⁶³ but both properties generally coexist in networks when modules coalesce hierarchically.⁶⁴ A hierarchy according to Herbert A. Simon¹ is a “system that is composed of interrelated subsystems, each of the latter being, in turn, hierarchic in nature until we reach some lowest level of elementary subsystem.” Hierarchy in the context of networks is the fractal-like reuse or embedding of simpler network modules into modules of higher complexity. Thus, lower level network modules are subordinated by an “authority relation” to higher network modules.¹ Modularity and hierarchy provide numerous benefits to a system when compared with monolithic integrated designs. For example, the design of a module occurs once but it can be reused many times, whereas every monolithic system must be built from scratch. Simon’s famous parable of the “Hora” and “Tempus” watchmakers illustrates the cost benefits of building, modifying, or updating modules.¹ In network biology, modules and hierarchy can increase evolvability (the ability to adapt and innovate)^65-67 and robustness (the maintenance of function in light of internal or external perturbation),⁶⁸ while decreasing the costs of establishing network connections.⁶⁹ Finally, modularity can improve the speed, stability, and quality of information transfer through networks.⁷⁰

Figure 4.

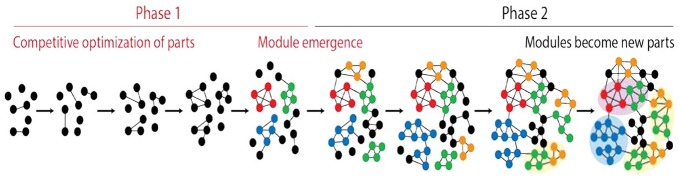
A generic biphasic model of module creation illustrates the emergence of network structure in evolution. Nodes and links of the network are parts of a growing system of entities and interactions. The larger number of links, the more cohesive and stable is the structure of a subnetwork. The rise of hierarchical modularity during phase 1 results in small highly connected subnetworks. These subnetworks become modules, which in phase 2 coalesce by combination into higher modules of network structure (highlighted with shades of yellow and blue). The model is inspired by the work of Mittenthal et al.²⁴

Network modularity can be detected with a variety of methods. A primary index of modularity is the average clustering coefficient—a metric that describes the average probability that 2 neighbors of a node are also connected.^64,71,72 The coefficient scales negatively with the number of links when modules are hierarchically organized in the networks.^2,64 Sets of nodes that are densely connected with each other are said to form a community. Communities can be detected with hierarchical clustering methods such as the Fast Greedy Community (FGC) detection algorithm,⁷³ the path-pruning Newman-Girvan algorithm,⁶² or the maximization of modularity functions (eg, the Louvain method).⁷⁴

In evolving networks, nodes become parts of a growing system and links become interactions that are established between them (Figure 4). The frustrated interplay of unification and diversification supporting the biphasic theory of module creation takes advantage of the stability that accretion of both nodes and links provide to the system. The larger the number of links, the more cohesive and stable is the structure of the evolving network. In the first phase of the biphasic model, the accretion of nodes and links is dynamic but with time it gives rise to highly connected subnetworks. These groups of nodes become modules when links are dynamically stabilized by competitive optimization. In the second phase, the emergent modules of the network diversify and coalesce by combination into higher level modules of network structure. The process is cyclic and gives rise to a fractal-like pattern of connectivity that is known as hierarchical modularity.⁷⁵ To support the theory and its consequence, the emergence of hierarchical modularity, we traced the history of a number of biological networks. We focused on networks unfolding at completely different timescales, from highly dynamic and stochastic (nanosecond-to-hours) to biologically entrenched (billions of years).

Rewiring of metabolomic networks and tripartite metabolic networks

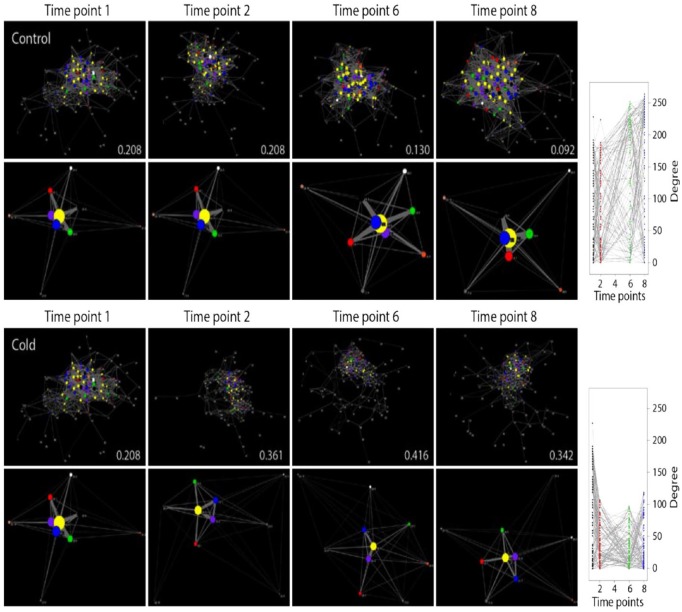
Organisms respond to environmental perturbation by changing physiology at molecular and cellular levels. Their responses can be viewed as models of how a system reacts to its environment and in doing so remembers constraints imposed by evolutionary history. We studied the metabolic responses of Escherichia coli to the environmental stimuli of cold, heat, diauxic shift, and oxidative stress.⁷⁶ Metabolomic data retrieved using gas chromatography-mass spectrometry⁷⁷ prior to perturbation (timepoint 1) and 0, 40, and 90 minutes following perturbation (time points 2, 6, and 8) were used to build metabolomic correlation networks (Figure 5). In these networks, nodes representing metabolites establish links when any 2 metabolites show strong correlation in their concentration levels. Our analysis revealed that the rewiring of metabolomic networks was highly dynamic and produced random networks of the Erdös-Rényi (ER) type, in which any 2 nodes are joined with some probability and connectivity is dictated by large network components rather than hubs. In all cases, we found wide departure from power-law behavior (γ ranging 0.061-0.496) and scale-free network structure (maximum likelihood scaling exponent α ranging 0.94-1.23). The fact that the dynamic metabolomic networks were largely random despite being hardwired to scale-free networks of metabolic reactions indicates that structure and function are loosely linked in metabolism. This does not mean that there is not a backbone structure behind dynamic interactions in these networks. Immediately upon perturbation by all nonlethal stressors, network connectivity initiated a biphasic pattern of metabolite rewiring in which connectivity abruptly decreased to enable the formation of modules and then increased but to lower levels (Figure 5). In the control, connectivity steadily increased with time. The rise of modularity is made evident using the FGC score of network community structure. Rewiring begins with energetics and carbon metabolism, both of which are needed for bacterial growth, and then focuses on lipids, hubs, and metabolic centrality needed for membrane restructuring. Rewiring patterns are better visualized in reduced graphs that were shrunk to combine all nodes of a same functional class and through an algorithm that places nodes that are more connected with shorter paths at the center of the graphs (Figure 5). Initially, nodes of metabolites pooled into “carbohydrate” (blue) and “energy” (green) functions were centrally located in the reduced graph. Perturbation pushed these nodes toward the periphery and away from the “hubs” (yellow) of the metabolomics networks. This suggests that bacterial cells quickly enter into an energy conservation mode, known to downregulate the tricarboxylic acid (TCA) cycle, glycolysis, and the pentose phosphate pathways and tightly control cell growth.⁷⁷ With the exception of cold and heat stressors, “amino acid” (purple) metabolites were also pushed toward the periphery. In contrast, metabolites of the “lipid” (red) group migrated to the periphery with slower rate and then gradually returned toward the core. This important delay relates to well-known perturbation-induced changes in membrane composition and fluidity that maintain an appropriate physical state of the membrane by incorporation of saturated fatty acids.^79,80

Figure 5.

Timeline of metabolomic networks (top) and reduced derivatives (bottom) showing biphasic-rewiring patterns in response to cold stress perturbation. The force-directed Fruchterman-Reingold algorithm⁷⁸ places nodes that are more connected with shorter paths in the center of the graphs and pushes sparsely connected nodes toward the periphery. Nodes are colored according to pathway maps in KEGG: yellow—hubs, blue—carbohydrate, green—energy, red—lipid, orange—nucleotide, purple—amino acid, brown—glycan, white—cofactors/vitamins, gray—secondary metabolites and xenobiotics, and black—miscellaneous. The group name “hubs” unifies metabolites associated with more than 1 pathway and are considered central to metabolism. Vertex size is proportional to connectivity. Values in panels indicate modularity scores inferred using the Fast Greedy Clauset-Newman-Moore (FGC) algorithm that measures the community structure of the networks.⁷³ Metabolite connectivity measured as node-degree of networks at each time point in time-resolved bacterial responses is provided on the right of the corresponding time series.

Source: Data from Aziz et al.⁷⁶

The metabolic effects of cold stress in plants can be explored with a metabolite-centric reporter analysis of the transcriptome of Arabidopsis thaliana.⁸¹ The most significantly changed reporter metabolites were algorithmically identified by mining the gene expression of neighboring genes and gene-metabolite associations. Data were visualized using an open tripartite graph representation in which nodes representing genes and metabolites are connected by links when metabolic genes and metabolites are associated at some P value, and nodes representing metabolites and pathways are connected by links through association with metabolic reactions. Remarkably, cold perturbation of plants quickly rewired the tripartite graphs in ways reminiscent of the rewiring of metabolomic networks. Network modularity increased upon perturbation (with high FGC scores of ~0.74) and then slightly decreased 24 hours postacclimation. Tripartite networks also gained decentralized structure with cold acclimation (eg, showing significant decreases in path length) but maintained a random-like structure; both power-law behavior and scale-free structure were rejected. Metabolically, plants initially mobilized energy from glycolysis and ethanol degradation to help the functioning of the TCA cycle. Concomitantly, many metabolic pathways were activated to produce cellular materials needed to offset stress, including diverting main carbon flux routes to amino acid and lipid metabolic pathways, which were later activated to change cell membrane lipid composition. This is expected because plants under cold acclimation are able to change membrane lipid fluidity by increasing the levels of unsaturated fatty acids.⁸²

These 2 examples show that environmental perturbations in both bacteria and plants cause biphasic modularization of the networks. The analysis reveals how external change is conducive to similar rewiring patterns of metabolic modularity, highlighting the need of the cell to stop growing and to prepare for uncertainty by modifying membranes and modularizing metabolic responses. Experiments also confirm simulations that show a rise of modularity when varying goals are defined by external perturbation.^65-67

Nanosecond-level molecular dynamics simulation of protein enzymes

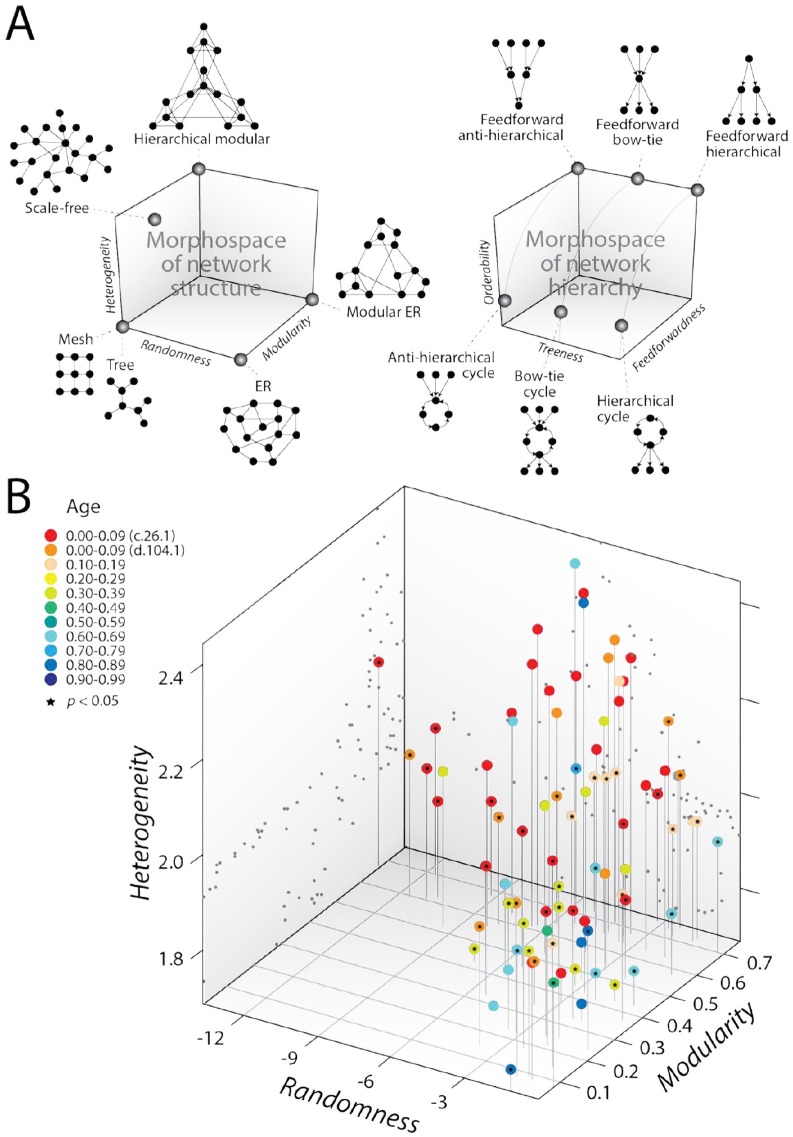
Network rewiring by external perturbation could be evolutionarily hardwired to ancient modular structure. To test whether such an ancient link exists, we bridged physics and biology with molecular dynamics simulations at nanosecond (ns) timescales.⁸³ Protein dynamics is intricately related to the structure and function of proteins. It has been hypothesized that dynamics “preexist” and shape evolution of proteins as they adapt to carry specific sets of motions.⁸⁴ Both folding speed and flexibility are beneficial traits that are evolutionarily conserved.^85,86 Similarly, protein complexes assemble through ordered pathways with strong tendency to being evolutionarily conserved.⁸⁷ As flexible loop regions have been shown to be enriched by the evolutionary rise of genetics,⁸⁸ one initial goal was to use networks to capture deep history in the physical movement of the atoms of aminoacyl-tRNA synthetase (aaRS) enzymes that are responsible for the specificity of the genetic code. The initial exploration involved molecular trajectories of the loop structures of 87 aaRSs on timescales of 10 ns, visualized with networks describing a dynamic cross-correlation matrix of the motions of protein residues.⁸³ The structure of these networks was dissected with a morphospace, a phenotypic space defined by a limited number of variables that often describe the form, shape, and structure of a system.^89-91 Our morphospace is one of several that explores the “limits of the possible” in the structure of networks⁷⁰ by measuring the modularity, heterogeneity, and randomness of the graphs (Figure 6A). Modularity embodies “flexibility” in structuring network communities with dense and sparse connections. Graph heterogeneity describes the scalefreeness of connectivity, which measures the “economy” of traversing paths along network structure.² Randomness entails uniform connectivity of nodes throughout the network, a property of “robustness” that confers a network fault tolerance to stochastic error.⁹² Figure 6B shows the 3D scatter plot of molecular trajectory networks in a parameter space of those 3 traits. Modularity, heterogeneity, and randomness were measured with the maximum modularity score, the maximum likelihood scaling exponent α, and the logarithm of Bartel’s test statistic, respectively. Networks occupy an area of the phenotypic space with significant heterogeneity and modularity but lack substantial levels of randomness. The result is surprising for networks that are expected to be highly dynamic and stochastic. However, coloring the age of the structural domains that harbored the loops (inferred from phylogenomic trees)^88,93 onto the data cloud showed a more remarkable historical layering trend (red to blue in the direction from hierarchical modular to ER graphs; Figure 6B). With few exceptions, the networks corresponding to older loop structures were in general more modular and less random. The most modular of them with lower randomness corresponded to the catalytic aminoacylation domain structures of the Class II (SCOP c.26.1) and Class I (SCOP d.104.1) aaRS enzymes, respectively, matching their evolutionary age. As older networks transition into younger networks, lower levels of heterogeneity decreased and then increased generating a noisy “bow-tie” pattern in the morphospace. Conclusively, the modularity of highly dynamic network systems unfolding at ns-timescales increase with deep evolutionary time as the network system decreases its randomness and heterogeneity. The emergence of modularity (community structure) with a concomitant decrease of heterogeneity (scalefreeness) along the coordinates of dynamic network structure strongly suggests the evolutionary entrenchment of hierarchical modularity.⁶⁴

Figure 6.

Evolution in network morphospaces. (A) Morphospaces of network structure and hierarchy showing toy examples of typical graphs describing archetypes of the phenotypic landscapes. In one morphospace (left), Erdös-Rényi (ER) random graphs transform into regular graphs by decreasing randomness or into modular ER graphs by increasing modularity. Hierarchical modular structure requires both increasing modularity and heterogeneity and decreasing randomness. In another morphospace (right), treeness defines the unification or diversification of hierarchical signal in the network, whereas orderability defines the centrality of cycles in network structure. (B) Morphospace of network structure describing the molecular dynamics (MD) of protein loops of aminoacyl-tRNA synthetases. Networks of the MD trajectories of protein loops unfold in a dynamic morphospace of trade-off solutions between flexibility (network modularity), economy (network heterogeneity illustrating scalefreeness), and robustness (network randomness). Modularity, heterogeneity, and randomness were measured with the maximum modularity score, the maximum likelihood scaling exponent α, and the logarithm of Bartel’s test statistic, respectively. Tracing the evolutionary age of structural domains harboring the loop structures onto the cloud of data points reveals a layering pattern, from red (early origin) to blue (late origin). The networks that are less random and more modular are the oldest, whereas the youngest networks are more random and less modular. Data points of the 3-dimensional scatter plot are mapped onto projection planes and connected with vertical leading drop lines along the heterogeneity axis. Black stars indicate significant departure from power-law behavior (P < 0.05), which measures scale-free structure (heterogeneity).

The data cloud is expected to fall within a “noisy” polytope-delimiting archetypes and Pareto fronts of optimality when assuming that the fitness of the networks is a function of the 3 network traits and that the morphospace represents trade-off relationships between them.⁹⁰ However, the likely polytope is tailed and appears to involve at least 4 goals. This suggests that other goals besides those associated with flexibility, economy, and robustness are at play. Although hierarchy results from the interaction of graph heterogeneity and modularity, its expression in a network can be complex. Recently, the coordinates of hierarchy in directed networks have been modeled with a morphospace of orderability, feedforwardness, and treeness.⁹⁴ This morphospace and its rationale is described with toy examples in Figure 6A. A perfectly hierarchical system will have the following 3 properties: order, reversibility, and pyramidal structure, which are all typical of directed acyclic graphs (DAGs). Order implies a tendency of nodes to be “ordered” unambiguously without being compromised by cycles, ie, subgraphs formed by nodes and edges defining a path that begins and ends in the same node. Orderability measures order in a directed graph (in which links are arcs). Reversibility implies that there is “only one commander for any commanded” in the relationship of nodes in the graph. Pyramidal structure implies that the commander commands more than one node, there is only a single node commanded by another node, and all lower level nodes are subjected to a chain of commands of the same length. Feedforwardness measures which regions (modules) of the graph cannot be ordered and treeness accounts for both reversibility and pyramidal structure of the network when condensed into a DAG by applying statistical entropic principles to paths. The relationship of orderability and feedforwardness defines the number and location of cyclic regions in the graph. Sliding this morphospace plane along the treeness axis gradually changes the pyramidal structure of the network from “hierarchical” to “antihierarchical” with the transition forming a family of symmetric structures, where the diversity of downstream paths is canceled by the uncertainty of reversing those paths. This results in a “bow-tie” network organization, generally with a strongly connected cycle component stabilized by a balanced feedforward structure of inputs and outputs⁵⁶ or of degeneracy (many-to-one) and pluripotentiality (one-to-many)⁹⁵ (Figure 6A). One remarkable finding is that most real networks display a balance between the integration of information and control over multiple goals under a bow-tie structural network pattern, which unfolds within the cloud of random graphs.⁹⁴ For example, the bow-tie pattern of metabolic networks has a large central cycle component that reflects the metabolic advantage of reusing and recycling metabolites. Note that biological networks are in themselves directed by either physiology or time.

The deep evolution of biological networks

As previously mentioned, chronologies describing the evolutionary appearance and time events of origin of protein structural domains can be directly obtained from phylogenomic trees reconstructed from a census of protein structures in genomes.³⁵ A molecular clock of folds links those chronologies to the geological record.³⁷ Chronologies can be used to trace the origin and evolution of metabolic networks,^96-99 including the history of metallomes and metal utilization in ancient seas,¹⁰⁰ the planetary emergence of aerobic metabolism,^37,101 and the natural history of biocatalytic mechanisms.¹⁰² We now illustrate how phylogenomic analyses uncover hierarchical modularity of evolving networks (Figure 7):

Figure 7.

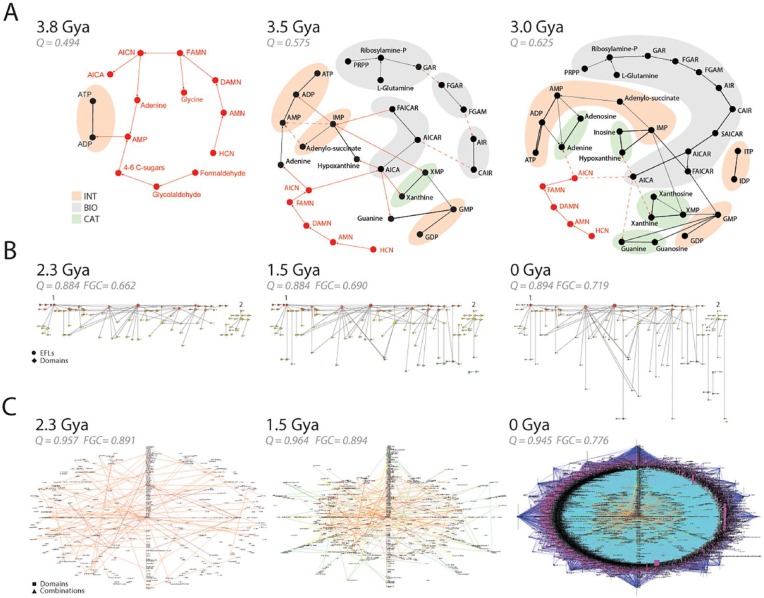
Emergence of modularity in biological networks. (A) Early evolution of the purine metabolic network. The reconstruction of metabolic subnetworks that were present 3.8, 3.5, and 3 Gya reveal the piecemeal recruitment of functional modules for the nucleotide interconversion (INT), catabolism and salvage (CAT), and biosynthetic (BIO) pathways. Plausible metabolites and prebiotic chemical reactions supporting the emergent enzymatic reactions are depicted with red nodes and connections, respectively. Unknown reaction candidates or withering prebiotic pathways are indicated with dashed lines. These ancient chemistries are gradually replaced by modern pathways and are unified from separate components into a cohesive network of INT, CAT, and BIO modules. The network was rendered using the energy spring embedders and the Fruchterman-Reingold algorithm⁷⁸ of Pajek.¹⁰³ Full metabolite names can be found in the work by Caetano-Anollés and Caetano-Anollés.⁹⁹ (B) The emergence of the elementary functionome (EF) network that connects protein structural domains to elementary functional loops (EFLs) when these substructures are embedded in protein structure. Bipartite networks are rendered as waterfall diagrams (see Figure 8), with time flowing from top to bottom. The first “p-loop” and second “winged helix” waves of recruitment are indicated with numbers. Data are from Aziz et al.³² (C) Evolution of networks of protein domain organization. The combination of structural domains in multidomain proteins induces connectivity between nodes representing domain and domain combinations in the network when a domain is present in a structure. As networks grow, older nodes are placed in the middle of radial graphs. Note how the “big bang” of domain combinations occurring 1.23 Gya during the rise of diversified organismal lineages results in a massive graph. Evolutionary data and networks from Wang and Caetano-Anollés¹¹³ and Aziz and Caetano-Anollés.¹⁰⁴ Protein ages were derived from phylogenomic trees describing the evolution of domains at fold family (FF) (panel A) and fold superfamily (FSF) (panels B and C) levels. Panels B and C describe networks present 2.3, 1.5, and 0 Gya during culmination of the architectural, superkingdom specification, and organismal diversification epoch of the protein world, respectively. Modularity (Q) measures connectivity density in node communities and Fast Greedy Community (FGC) measures community structure. In all cases, Q and FGC significantly increase in evolution much earlier than 2.3 Gya and then reach a plateau and decrease.

1. The early evolution of metabolic networks. The KEGG database divides metabolism into subnetworks,¹⁰⁵ which have been considered modules of metabolic pathways.¹⁰⁶ Figure 7A shows snapshots of the early evolution of the oldest metabolic subnetwork, purine metabolism.⁹⁹ The growing networks show that the early purine biosynthetic pathway assembled as a patchwork through processes of both enzymatic recruitments and enzymatic replacements of prebiotic chemistries that likely operated at planetary scale.⁹⁹ In the network, nodes represent metabolites and links represent metabolite transformations mediated by either enzymes (black lines) or well-known nonenzymatic prebiotic chemical reactions (red lines). At first, the graph is fragmented into small submodules. As prebiotic reactions are replaced by modern enzymatic counterparts, fragments unify into a functional core defining nucleotide interconversion (INT), metabolism/salvage (CAT), and biosynthetic (BIO) pathways of the purine metabolic pathways, which appear fully functional ~3 Gya. The statistical analysis of modularity with the Louvain maximization method shows that community structure that is typical of hierarchical modularity increases with time (Figure 7A). The same approach applied to the entire metabolic network also showed increases in clustering coefficients, modularity, and community structure, confirming the emergence of modularity and hierarchy in metabolic evolution.¹⁰⁷

2. The origin of the fold structures of protein domains by accretion of loops. Loops are flexible and irregular elements of protein structure that are largely responsible for biological functions. They are critical components of macromolecular dynamics.¹⁰⁸ The structural diversity of proteins can be described as a collection of loop regions arising from the rearrangement of supersecondary structural building blocks made of helix, strand, and turn segments (eg, αα-hairpins, ββ-hairpins, βαβ-elements).¹⁰⁹ Some recent studies identified noncombinable¹¹⁰ and combinable¹¹¹ loop motifs that were evolutionarily conserved and are likely responsible for very early molecular functions. The structures are generally ~25 to 30 amino acid residues long and collapse into loop structures stabilized by van der Waals locks.¹¹² Combinable prototypes are “elementary functional loops” (EFLs) that bind cofactors and exert molecular functions.¹¹¹ We generated bipartite networks of EFLs and structural domains and studied the evolution of these “elementary functionomes.”³² Figure 7B shows how early EFLs combine to form structural domains and perform new functions in a process that has been ongoing since the beginning of life. The evolving networks uncovered 2 clear waves of functional innovation that involved ancient EFLs and found “p-loop” and “winged helix” domain structures, confirming previous analyses of the origin of metabolic networks.⁹⁸ As with metabolism, both modularity and community structure were emergent properties of the evolving bipartite network when we used metrics of connectivity density, hierarchy, and modularity of network structure.

3. Emergence of multidomain proteins by combination of protein domains. A significant number of protein domains (26%-32%) combine to form a substantial number of multidomain proteins (58%-83%).^45,112 A phylogenomic data-driven study of the origin of these multidomain proteins showed that the early and gradual appearance of single-domain proteins harboring structures that were generally multifunctional was followed by an explosive increase of multidomain proteins.¹¹³ The onset of this massive “big bang” ~1.23 Gya coincided with the rise of eukaryotic and multicellular organisms . It is the product of fusions and fissions that combine, recruit, and split domains in proteins, thanks to known biological activities, including chromosomal recombination, retrotransposons, intronic rearrangement of domain-encoding exons, and faulty excision of introns. The combinatorial fusion of domains occurred earlier than the fission of proteins into smaller multidomain components, which were usually multifunctional. Figure 7C describes evolving networks of domain organization that portray the combination of domains in proteins.¹⁰⁴ Nodes of these bipartite “composition” networks (CX) represent either domains or domain combinations and links represent their common presence in proteins. Remarkably, we found a biphasic pattern of strong biases in the combinatorial connectivity of domains, with a preference to combine domains appearing during the early rise of translation (2.3-1.5 Gya) and during the “big bang” of domain combinations. Remarkably, it also uncovered the same “p-loop” and “winged helix” waves of domain innovation that we observed in evolution of elementary functionomes (Figure 7B) and in evolution of early metabolism.⁹⁸ Again, the modularity of evolving networks started to increase with time to significantly high levels (Figure 7C).

Summary

The biphasic (bow-tie) theory of module emergence explains temporal biphasic patterns of unification and diversification. When representing systems with networks, biphasic patterns are captured by the rise of both hierarchy and modularity in network structure (Figure 4). In the first phase, communities of nodes coalesce into highly connected subnetworks, which become modules. In the second phase, modules are co-opted into clusters of higher level organization. In the process, the network becomes increasingly modular and hierarchical. Our temporal study of biological networks confirmed our expectation and did so at different timescales.

The rewiring of metabolomic network minutes after bacterial perturbation with different stimuli was biphasic, first diminishing connectivity and pushing newly formed modules toward the periphery and then rewiring them back hierarchically into a different core in a process that increases modularity and fosters energy conservation and membrane lipid reformation. Similarly, cold stress caused a biphasic rewiring of tripartite networks that describes how transcripts control metabolic reactions in plants. The rewiring resembled that of metabolomic networks. Networks first gained decentralized structure and modularity upon perturbation and then rewired energy and carbon fluxes to enhance membrane lipid composition. These examples described similar temporal hourglasses of metabolic and transcriptomic-informed behavior.

To test whether behavioral hourglasses could be evolutionarily hardwired to ancient modular structure, and therefore linked to evolutionary hourglasses, we explored the nanosecond-dynamic behavior of proteins. Networks describing a dynamic cross-correlation matrix of the motions of residues in protein domains of different evolutionary age were hierarchically modular. However, older domains were more modular, more heterogeneous, and less random than modern counterparts, showing that the nanosecond dynamics is constrained by evolutionarily deep information.

Finally, we find temporal biphasic patterns describing evolutionary hourglasses of the diversification of early metabolites, elementary functionomes, and domain organization in proteins. In all cases, networks became increasingly hierarchically modular in evolution.

Evolutionary Mechanisms Behind Hierarchical Modularity

While the interplay of accretion and diversification can explain the emergence of hierarchical modularity, the underlying evolutionary agents of accretion and change remain controversial. Modules have been proposed to materialize through the action of biased mutational mechanisms and/or natural selection.¹¹⁴ One explanatory theme is that modularity is driven by a mutational process that approaches “neutrality” in terms of natural selection. An example of these nonadaptive models includes the generation of modules through patterns of duplication and differentiation.^115,116 For example, networks of protein-protein interactions can grow by randomly duplicating nodes (proteins), which maintain at first all links but can then loose or gain links through mutation. This is a biologically plausible scenario under a number of gene duplication and evolutionary models. It reproduces salient properties of real protein-protein interaction networks modeled from genomic data. An alternative theme is that modularity is driven by direct or indirect selection pressures that reinforce or take advantage of mutational biases.¹¹⁴ In direct models, modularity directly contributes to higher fitness. For example, modularity could be the direct target of individual-level selection if modules affect epistatic or pleiotropic “constraints” (eg, morphological or developmental).¹¹⁷ Alternatively, indirect models consider modularity as an adaptation to the effects of the environment. For example, changing the external environment of a system can lead to different goals, and this has been shown to enhance modularity.^65,66 Selection for evolvability under constantly changing environments, which leads to specialization, can also result in modularity.¹¹⁸ By being modular, a system can be more robust to external perturbations and more evolvable. For example, modularity in populations correlates with the rapidity and severity of environmental change.¹¹⁹

Recent simulations have convincingly shown that reducing connection costs in networks induce both modularity and hierarchy in network structure.^69,120 Moreover, making links costly to networks improves performance and adaptability. These costs relate to the manufacture of a link, its maintenance, or its ability to transmit information. For example, links that involve connecting molecules or molecular parts require developing interacting surfaces with costs constrained by surface area. Maintaining interacting surfaces in, for example, protein-protein interaction networks or networks of domain organization must also minimize costs incurred in the stability and robustness of interacting proteins or domains. Adding additional connections can hinder the delivery of information in signaling networks, the minimization of the wiring diagram of neural connection in the brain, and the flow of matter-energy in metabolic networks. Thus, modularity in these scenarios appears to be a by-product of cost-dependent selection.

In systems that simulate evolution, hierarchy rarely unfolds on its own and its emergence remains an open question.¹²¹ Nonadaptive theories posit that hierarchy may arise in some systems as a by-product of random processes.⁹⁴ Adaptive alternatives suggest hierarchy arises as a result of quick adaptation to novel environments (evolvability).^119,122 The bow-tie structure of directed networks that is popular in natural networks⁹⁴ embeds both hierarchy and modularity within a biphasic pattern (Figure 6A). The bow-tie can be explained by a preference to “reuse” modules of similar complexity instead of connecting to less complex modules.¹²³ It also decomposes nodes into 4 sets: input and output components, a central knot that may contain strongly connected components, and disconnected components known as tendrils.⁶⁰ The bottleneck of the central knot limits the flow of information and/or time duration in evolving networks as long as tendril connectivity remains constrained. The evolutionary significance of hierarchical modularity in terms of economy, flexibility, and robustness of the bow-tie network structure must now be explored.

Levels of Organization, Granularity, Flux, and the Arrow of Time

Philosophically, the rise of hierarchical modularity in networks requires explaining the instantiation of a hierarchy of modules. Simon’s definition of a hierarchical system as a nesting relationship of subordinated subsystems¹ has been elaborated further by Salthe,¹²² who divided hierarchies into 2 kinds: scalar and subsumption. Scalar hierarchies nest differently sized dynamical entities into each other by mereologically defining parts and wholes and invoking “is-a-part-of” relationships between them. A relevant example is the successive nesting of amino acid residues, secondary structures, loop structures, and domains in protein molecules. Nesting relationships are “compositional”: parts of the systems are treated as modules and are successively nested in expanding manner both outward (toward higher levels of the hierarchy) and inward (toward lower levels) from a focus level of organization. This is done without an integrative or historical rationale. In the example above, the focus level was the amino acid residue and the hierarchy expanded outwardly. In contrast, subsumption hierarchies nest entities by defining taxonomies that describe “general-to-specific” properties of a system and invoke a “is-a-kind-of” ordering principle of classification. Relevant examples are the National Center for Biotechnology Information (NCBI) taxonomy database¹²⁴ for the classification of species or the SCOP database²⁵ for the taxonomic classification of structural domains. For example, the SCOP classification of the family of aminoacylation domains of aaRS enzymes follows the taxonomical nesting of “Class I aminoacyl-tRNA synthetases (RS), catalytic domain” fold family; “Nucleotidylyl transferase” fold superfamily; “Adenine nucleotide alpha hydrolase-like” fold; “Alpha and beta (a/b)” class; and SCOP root, from specific to more general levels of classification. Such hierarchies integrate all aspects of the world being considered and their definition demands establishing history, ie, establishing “intermediate forms” or “prior forms” of a refining, developing, or evolving system. For example, the NCBI and SCOP database examples require models of species and structural domain evolution, respectively.

The scalar and subsumption hierarchical logical forms capture more broadly Simon’s view of hierarchies being described by “states,” the world as sensed through observables and goals, and “processes,” the world of actions capable of tailoring the system “purposefully upon its environment.”¹ Both views have been recently integrated into a model hierarchy, an information-based metascale description of 2 partial hyperscalar hierarchies, one focusing on the nested entities, the other focusing on the context of that nesting.¹²⁵ We contend that the scalar (states) view stresses the hierarchical modular makeup, whereas the subsumption (process) view stresses the instantiation of the system, which is likely driven by the evolutionary processes of unification and diversification that give rise to hierarchical modularity.

Implicit in the scalar (states) interpretation of a hierarchy is the existence of different levels of organization. While levels of organization imply “layered” structuring of some kind, its interpretation remains contentious.¹²⁶ Initial “layer-cake,” “mechanistic,” and “local maxima” accounts have been criticized as reductionist attempts that use comprehensive, rigid, and blanket statements of significance to describe Nature’s truly messy and pluralistic systems. Implicit in the subsumption (process) view is the unfolding of levels of organization with time and the imposition of constraints (or controls) that higher levels exert on lower levels of the network hierarchy. However, downward causation explanations can be conflicting and should be considered “local” explanations, suggesting that a pluralistic view should be more appropriate.¹²⁷ A graph theoretical account of hierarchy could resolve some of these problems. It is novel and somehow independent of some of the epistemic, ontological, or methodological limitations. It can also test layering in organization and downward causation. Two approaches are promising in this regard, flow hierarchies and bipartite networks.

Flow hierarchies unfold flux along the wiring diagrams of the network hierarchy, with flux describing flows of matter/energy, information, signs, and/or time.¹²⁸ These flow networks are directed or semidirected; arcs establish the directionality of the flux. Flow hierarchies are generally evaluated with global and local “reaching centralities” (measures of flow heterogeneities),¹²⁹ the percentage of links not included in cycles,¹²⁸ the use of random walks on the network,¹³⁰ or the decomposition into treeness, feedforwardness, and orderability mentioned above.⁹⁴ They stress the temporal subsumption (process) view, including their potential to unfold system’s history.

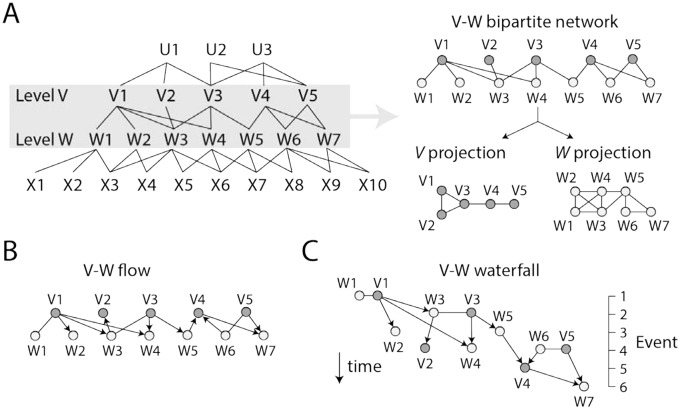
Bipartite networks are uniquely fit to study the evolutionary structuring of a system from both scalar and subsumption points of view. Once levels of organization are recognized with, for example, machine deep learning or task-specific algorithmic approaches, bipartite networks and their one-mode projections provide remarkable insights into patterns of network connectivity between levels of organization.³² Figure 8A shows a general diagram describing how links between nodes corresponding to 2 different levels of a hierarchical system contribute to the structuring of both the lower and higher levels in a bipartite network. Such structuring tests the scalar hierarchical view. For example, the bipartite network of EFLs and structural domains (Figure 7B) outlines how loop structures of proteins combine in evolution to form structural domains with new molecular functions.³² The one-mode EFL projection of the evolving bipartite network describes how domains are capable of structuring the emerging world of functional loop structures. Conversely, the domain projection describes how the world of domains is structured by the sharing of EFL structures.

Figure 8.

A bipartite network view of levels of organization. (A) Any system of interacting entities describable with networks can be dissected into a hierarchical system with nested entities defining different levels of organization (eg, U, V, W, and X). Network interactions that are tightly knit generate modules, which enable the functional activities of the system. A bipartite network makes explicit the relationship between any 2 levels of organization when it is dissected into its 2 one-mode projections. One projection describes how higher level entities link lower level entities to each other. The other describes how lower level entities link higher level entities to each other. As an example, a bipartite network describing interactions between entities of the V and W levels is shown in the right together with its corresponding V and W projections. For simplicity, links are left unweighted. (B) The V-W bipartite network is transformed into a flow hierarchy when some or all connections are described as arcs pointing in the direction of time. (C) The flow hierarchy becomes a waterfall diagram when the ages of nodes are treated as “time events” and are used to reorganize the network in the direction of time.

When the growth of the bipartite wiring diagrams and their projections is studied along an evolutionary timeline, the network provides a subsumption hierarchical view through flow and waterfall network visualizations. In a flow hierarchy, arcs point in the direction of time, but the age of nodes is not made explicit (Figure 8B). In contrast, a “waterfall” network harbors both arcs that point in the direction of time and time events of an evolutionary timeline specified by the age of nodes (Figure 8C). These visualizations can dissect the emergence and evolution of hierarchical modular structure, uncovering remarkable patterns between levels of organization. For example, the analysis of the evolution of the elementary functionome revealed how the lower level of structural organization transfers preferential attachment (heterogeneity) to the higher level, with a trend that is anticorrelated with modularity but generates hierarchical modular structure.³² The age of domains was traced onto the directed bipartite network structure, and the resulting “waterfall” networks established the direction of structural recruitments of loops and domains of the elementary functionome (Figure 7B). In another example, bipartite networks outlining how domains are recruited in the enzymes of metabolism showed that while modularity increases with time, higher levels of metabolic organization are weakly wired compared with lower levels.¹⁰⁷ The enzyme projection of the bipartite network of enzymes and subnetworks (defined by KEGG),¹⁰⁵ for example, shows how subnetworks are capable of structuring the emerging world of metabolic enzymes. In turn, the subnetwork projection reveals how the world of subnetworks is structured by the sharing of enzymes. The study did not impose an “arrow of time” on the links of the network (they were kept undirected), because nodes were indexed with evolutionary history. However, there was a clear trend of the system’s lower levels to become increasingly more granularly entrenched with time. This trend of “maximum granularity” generates an architecture of parts at lower levels acting almost independently from each other, supporting Simon’s prediction of near-decomposability of systems: “Each of the parts of a nearly-decomposable system has strong internal links among its sub-parts, but the several top-level parts are bound together with each other only by comparatively weak linkages.”¹³¹

Conclusions

Retrodictive methods can trace the evolution of complex biological systems along their ~3.8 billion-year history.^17,31 This allows exploration of the accumulation of evolutionary innovations and the emergence of hierarchy and modularity in networks. Two approaches are available for this task. Given a “tree of life,” hypothetical ancestral networks can be extrapolated back in time with “character state reconstruction” methods. The reconstructed networks are then analyzed with the tools of graph theory. The approach has been used to reconstruct ancestral metabolic networks and study their modularity.¹³² However, one drawback is that retrodiction cannot go deeper than the most ancestral node of the tree of life, ie, LUCA. The limitation can be severe in the case of metabolic networks, since metabolism originated in a “big bang” hundreds of millions of years before the onset of organismal diversification.⁹⁸ An alternative approach that is free of this limitation is to build phylogenomic trees portraying the histories of entire repertoires of molecular functions or molecular parts (eg, protein structural domains, helical RNA structures).^17,31-38,98 These trees allow to calculate the evolutionary ages of molecular functions or parts, from their origin in the very distant past to the present. Tracing of these ages onto wiring diagrams reveals patterns of emergence, growth, and evolution of biological networks at different timeframes (from nanosecond dynamics to billion-year history). These studies showed that even highly dynamic systems are evolutionarily entrenched and steadily evolve by increasing network hierarchy and modularity.

Network evolution can also be inferred in the absence of historical information. One approach is to use artificial data and in silico modeling. For example, computer simulations have been used to study the emergence of hub metabolites by functional specialization of group transfer reactions.¹³³ More ambitiously, modeling of metabolic reactions based on an artificial chemistry emerging from protein-protein interactions and genetics revealed the emergence of modularity in response to a multitude of functional goals that depend on the environment.¹³⁴ An alternative approach is to simulate the evolution of networks and determine whether properties of extant biological networks emerge in the simulations.⁹⁴ Mapping these simulations onto morphospaces describing network structure and hierarchy can uncover how extensive real (extant) networks cover the space of possible network designs.¹³⁵

Finally, we have reviewed the existence of biphasic patterns in the growth of complex biological systems. Examples include molecular machinery such as the ribosome or the collective of fold structures that make up the proteome of an organism. We explain the evolution of network structure with a paradigm of accretion and diversification and a biphasic (bow-tie) model of module generation, which embeds communities of nodes and links into each other as networks unfold in time. This fosters fractal-like patterns of complexification that are both entrenched and highly dynamic at all levels of organization. Remarkably, the 2000-year-old Strasbourg papyrus attributed to Empedocles of Akragas (ca. 495-435 BC) appears to summarize the double tale of module generation and its dynamic nature:

A double tale I’ll tell. At one time one thing grew to be just one

from many, at another many grew from one to be apart.

Double the birth of mortal things, and double their demise.

Union of all begets as well as kills the first;

The second nurtures them but shatters as they grow apart.

And never do they cease from change continual,

At one time all uniting into one from Love,

While at another each is torn apart by hate-filled Strife.

In the way that many arise as the one again dissolves,

in that respect they come to be and have no life eternal;

but in the way that never do they cease from change continual,

in this respect they live forever in a stable cycle.

—Papyrus of Empedocles, On Nature, P. Strasb. Gr. Inv. 1665-6, lines 233-244.¹³⁶