Abstract
Objective
The supply territories of main cerebral arteries are predominantly identified based on distribution of infarct lesions in patients with large arterial occlusion; whereas, there is no consensus atlas regarding the supply territories of smaller end-arteries. In this study, we applied a data-driven approach to construct a stroke atlas of the brain using hierarchical density clustering in large number of infarct lesions, assuming that voxels/regions supplied by a common end-artery tend to infarct together.
Methods
A total of 793 infarct lesions on MRI scans of 458 patients were segmented and coregistered to MNI-152 standard brain space. Applying a voxel-wise data-driven hierarchical density clustering algorithm, we identified those voxels that were most likely to be part of same infarct lesions in our dataset. A step-wise clustering scheme was applied, where the clustering threshold was gradually decreased to form the first 20 mother (>50 cm3) or main (1–50 cm3) clusters in addition to any possible number of tiny clusters (<1 cm3); and then, any resultant mother clusters were iteratively subdivided using the same scheme. Also, in a randomly selected 2/3 subset of our cohort, a bootstrapping cluster analysis with 100 permutations was performed to assess the statistical robustness of proposed clusters.
Results
Approximately 91% of the MNI-152 brain mask was covered by 793 infarct lesions across patients. The covered area of brain was parcellated into 4 mother, 16 main, and 123 tiny clusters at the first hierarchy level. Upon iterative clustering subdivision of mother clusters, the brain tissue was eventually parcellated into 1 mother cluster (62.6 cm3), 181 main clusters (total volume 1107.3 cm3), and 917 tiny clusters (total volume of 264.8 cm3). In bootstrap analysis, only 0.12% of voxels, were labelled as “unstable” – with a greater reachability distance in cluster scheme compared to their corresponding mean bootstrapped reachability distance. On visual assessment, the mother/main clusters were formed along supply territories of main cerebral arteries at initial hierarchical levels, and then tiny clusters emerged in deep white matter and gray matter nuclei prone to small vessel ischemic infarcts.
Conclusions
Applying voxel-wise data-driven hierarchical density clustering on a large number of infarct lesions, we have parcellated the brain tissue into clusters of voxels that tend to be part of same infarct lesion, and presumably representing end-arterial supply territories. This hierarchical stroke atlas of the brain is shared publicly, and can potentially be applied for future infarct location-outcome analysis.
Highlights
-
•
Using data-driven density clustering, a hierarchical brain atlas is constructed to identify voxels likely to infarct together.
-
•
Different clusters can potentially be extracted from dendrogram through thresholding at different reachability thresholds.
-
•
The hierarchical stroke atlas hypothetically represents the detailed anatomical distribution of distal arties in the brain.
-
•
The stroke atlas is made publicly available for potential future location-outcome correlation studies in stroke patients.
1. Introduction
Infarct location, in addition to lesion volume and severity of symptoms, is one of the most important predictors of functional outcome in stroke patients (Ernst et al., 2017; Payabvash et al., 2018; Payabvash et al., 2017b); however, integration of infarct lesion topography into location-outcome analysis could be challenging. Many authors have applied visual inspection of infarct lesion and the 10-region Alberta Stroke Program Early CT Score (ASPECTS) to assess the infarct location (Barber et al., 2000). Nevertheless, such brain atlases are devised based on consensus and anatomical observations (Nowinski et al., 2006), rather than a data-driven approach from distribution of infarct lesions among stroke patients. A potential solution for evaluation of infarct lesion topology would be automated parcellation of lesion mask based on a reference atlas of arterial perfusion territories.
Traditionally, perfusion territories of main cerebral arteries have been delineated based on correlation of angiographic findings with follow up anatomical evaluation of infarct distribution in patients with large vessel occlusion (Berman et al., 1980, Berman et al., 1984; Hayman et al., 1981; Nowinski et al., 2006). However, delineation of perfusion territories for the smaller distal end-arteries has been challenging given the anatomical variation in arterial branching pattern and their final supply territories. A hypothetical solution for delineation of brain end-arterial supply territories is to identify regions (voxels) which tend to infarct simultaneously among large cohort of stroke patients. One can assume that adjacent voxels that frequently belonged to same infarct lesion among consecutive stroke patients are supplied by a common end artery. A hierarchical clustering approach can identify and represent such clusters at different levels of contingency.
The density clustering, or DBSCAN (density-based spatial clustering of applications with noise) is one of the most common clustering algorithms used in data mining (Ester et al., 1996). Much like other data-driven clustering algorithms, the DBSCAN: (1) does not require specification of the number of output clusters a priori, (2) can find arbitrarily shaped clusters, depending on the distance metric definition, and (3) perhaps most notably, the algorithm has an inherent notion of noise, and hence is robust to outliers. Similar to DBSCAN, the ordering points to identify the clustering structure (OPTICS) is a density-based clustering algorithm which also assigns a reachability distance for all points (Ankerst et al., 1999). This reachability distance represents the minimum density that must be accepted for a cluster so that both points belong to same cluster. Subsequently, a reachability plot can be constructed from reachability distance, and presented like a dendrogram (tree diagram) in hierarchical clustering (Wang and Li, 2013; Wang et al., 2016). Once the full dendrogram is constructed, one may extract different sets of clusters from the dendrogram through thresholding at different reachability values – similar to hierarchical clustering. This method allows data exploration in an efficient manner through minimizing the number of computationally intensive operations.
In this study, we applied the OPTICS data-driven density clustering analysis to a large dataset of stroke lesions to generate a probability-varying atlas of the brain, delineating those voxels that tend to be part of same infarct lesion among our patients' cohort. The resultant atlas topology can change depending on reachability thresholds, allowing visualization of both small regions with extremely high probability of simultaneous infarct, to very large, but less probabilistically stringent, regions of simultaneous infarct probability. In theory, larger clusters formed at initial hierarchical levels represent arterial supply territory of main cerebral arteries; whereas, smaller clusters identified at subsequent hierarchical levels represent supply territories of smaller distal end-artery branches. The resultant brain-atlas, which is constructed in MNI-152 standard brain space, is made publicly available.
2. Methods
2.1. Data acquisition
The dataset for this study were collected from patients with acute and non-acute ischemic infarcts (Liew et al., 2018; Payabvash et al., 2017b). In 238 patients with acute stroke, infarct lesions were segmented on 2-mm thickness axial diffusion weighted images (DWI) scans, which were obtained on two MRI scanners from two university-affiliated hospitals (Payabvash et al., 2016, Payabvash et al., 2017b). In 220 patients with primarily chronic stroke, infarct lesions were segmented on 1 mm3 (isotropic) resolution T1-weighted images, which were obtained on 17 different scanners from 11 centers worldwide (Liew et al., 2018). The details of image acquisition and data collection have been previously described (Liew et al., 2018; Payabvash et al., 2017b). The MRI datasets were fully anonymized before data transfer. Image acquisitions were based on studies approved by local ethics committees and institutional review boards of corresponding centers.
2.2. Infarct lesion segmentation and coregistration
The infarct lesions were manually segmented on DWI or T1-weighted images depending on the chronicity of stroke. All manual segmentations were performed (or supervised) by neuroradiologists using MRIcro software (http://people.cas.sc.edu/rorden/mricro/mricro.html) (Rorden and Brett, 2000). A total of 405 acute and 393 chronic infarct lesions were segmented and saved as binary masks. All binary masks were smoothed using MRIcro smooth VOI (volume of interest) tool with full width half maximum parameter set to 2 mm and threshold set to 0.5 (Liew et al., 2018). Then, original DWI and T1 lesions along with binarized infarct lesion masks were coregistered to the 2-mm thickness isotropic standard MNI-152 template using a 12-parameters affine transformation from FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki) (Woolrich et al., 2009). In order to maximize the efficiency in computation of distance metric for clustering, all coregistered infarct masks were sub-sampled to 3 × 3 mm isotropic resolution; and voxels with no infarct in our cohort were excluded from computation.
2.3. Distance measure
In order to calculate the likelihood of a voxel belonging to an infarct lesion given another voxel belongs to same infarct lesion among provided binary masks, we have devised a distance metric for clustering based on probability theory. For n subjects, the probability of a voxel i being in an infarct lesion (Pi) is defined as the number of subjects with an infarct lesion at voxel i divided by the total number of subjects:
Hence a voxel, where all subjects have an infarct lesion will have a value of 1, whereas a voxel where none of the subjects have an infarct lesion will have a value of 0.
Conditional probability is a measure of probability, or likelihood, that an event occurs provided that another event has occurred. The probability of event B occurring – given the probability that an event A has occurred P(A) – is denoted as P(A| B). While conditional probability can explain the framework for our analysis, it is not a distance metric, suitable for our clustering algorithm. In order to satisfy the conditions of a distance metric, we instead opted to use the joint probability as defined as P(A ∩ B) = P(A| B)P(B). The joint probability satisfies non-negativity and symmetry conditions, but not subadditivity. In order to enforce subadditivity, we opted to use the Euclidean distance of joint probabilities for a voxel against all other voxels as the distance metric. For all pairs of voxels i and j, the distance between the two voxels is defined as the l2-norm of the joint probabilities of the voxels with all other voxels, i.e.:
The joint probabilities of all voxels against all other voxels where calculated, resulting in a N × N symmetrical matrix. The Euclidean distance between all rows (or columns) of the matrix against all other rows, resulting in another N × N symmetric matrix with zero diagonal (distance matrix), which is used as distance measure for clustering. The distance matrix was computed using our own implemented C code, using OpenMP (https://www.openmp.org/) CPU parallelization over 32 threads. Solely, the distance matrix computation took slightly longer than 3 weeks to complete at 2.6 Ghz per thread.
2.4. Density clustering
For exploratory analysis, a data driven analysis scheme is optimal to minimize subjective adjustment of input parameters. Density clustering (Duan et al., 2007), using the OPTICS algorithm is preferred since it is mostly data driven, and robust to outliers due to its inherent ability for filtering out noise, and relative computational efficiency. Furthermore, the OPTICS algorithm preserves the full reachability plot. This allows immediate extraction of voxel clusters at different reachability thresholds, without performing the full clustering algorithm each time, which can be computationally and memory intensive. This also enabled us to feasibly stratify the clustering results in a hierarchical fashion.
For computation of distance matrix, a C++ implementation of OPTICS with R (https://www.r-project.org/) wrappers was used to perform OPTICS (Hahsler et al., 2017). The OPTICS reachability plot was saved as an R-object for further analysis and extraction of cluster sets. The clustering computation took slightly <10 h, of which half the time was allocated for parsing the distance matrix. However, this operation requires over 650 GB of memory in total as the entire distance matrix needs to be loaded into memory at once.
2.5. Data analysis and cluster construction
The resulting stroke map can be viewed at different reachability, or “probability” thresholds. The reachability of a point p from a point o is defined as (Achtert et al., 2006):
The reachability is the minimum distance threshold of ε to make p density reachable from o, and thus part of the same cluster.
In order to extract meaningful information from the full reachability plot that are visually comprehensible, we have devised a visualization approach based on hierarchical cluster subdivision. This method allows us to view sections of the reachability plot and its corresponding clusters in a hierarchical fashion that is consistent throughout the exploration of the clustering structure. Given that exploration of infarct lesion clusters smaller than 1 cm3 is unlikely to be clinically relevant, we applied a hierarchical cluster sub-division scheme (implemented in R version 3.5.2), where beginning from the very top of the reachability plot, the reachability threshold is decreased until the first 20 mother/main clusters emerge. Any cluster between the size of 37 voxels (~1 cm3) and 1850 voxels (~50 cm3) are referred to as “main” clusters. Those clusters equal or smaller than the 37-voxel threshold are referred to as “tiny” clusters; whereas, clusters larger than 1850 voxels are referred to as “mother” cluster, and were iteratively subdivided applying the same scheme (Table 1). The analysis routine iterates through the entire density plot until no mother clusters remain or until the subdivision reaches zero. During iterative subdivision of mother clusters, a series of “orphan” voxels had stochastic behavior in sub-cluster assignment and were not included in any resultant main or tiny cluster. In other words, from a density clustering perspective, the algorithm considers these (“orphan”) voxels as outliers in relation to their tendency to infarct (or not infarct) together with other voxels within the mother cluster. One possible explanation would be that these “orphan” voxels represent tiny end-arterial supply regions or technically single-voxel tiny clusters.
Table 1.
Iterative subdividing scheme for density-based clusters.
| Relative hierarchy | Mother cluster size (cluster annotation) | No. of Mother Clusters (cluster annotation) | No. of main clusters | No. of tiny clusters | Tiny clusters – Average size | Tiny clusters – Cumulative size | Orphan voxelsa | Reachability threshold |
|---|---|---|---|---|---|---|---|---|
| 0 | 4 (#1, #6, #80, #71) | 16 | 123 | 8.59 | 1056 | 0 | 1.25 × e−3 | |
| 1 | 25961 (#1) | 2 (#1.1, #1.5) | 18 | 62 | 10.6 | 656 | 547 | 9.47 × e−4 |
| 2 | 14,183 (#1.1) | 1 (#1.1.1) | 18 | 35 | 13.2 | 463 | 134 | 8.05 × e−4 |
| 2 | 4121 (#1.5) | 0 | 20 | 62 | 13.4 | 834 | 255 | 3.41 × e−4 |
| 3 | 8818 (#1.1.1) | 1 (#1.1.1.1) | 20 | 26 | 11.0 | 287 | 103 | 6.20 × e−4 |
| 4 | 2703 (#1.1.1.1) | 0 | 13 | 83 | 12.5 | 1040 | 508 | 0 |
| 1 | 17,529 (#6) | 2 (#6.61, #6.84) | 21 | 52 | 9.65 | 502 | 622 | 1.06 × e−3 |
| 2 | 4829 (#6.61) | 0 | 12 | 106 | 11.5 | 1215 | 1185 | 0 |
| 2 | 2766 (#6.84) | 0 | 8 | 81 | 9.6 | 776 | 1562 | 0 |
| 1 | 4442 (#71) | 0 | 7 | 121 | 9.82 | 1188 | 1542 | 0 |
| 1 | 9130 (#80) | 1 (#80.588) | 18 | 108 | 11.0 | 1186 | 1879 | 8.72 × e−4 |
| 2 | 4520 (#80.588) | 1 (#80.588.1545) | 10 | 58 | 10.4 | 606 | 722 | 1.08 × e−19 |
| 3 | 2319 (#80.588.1545) | 1 (#80.588.1545)b | 0 | 0 | 0 | 0 |
An iterative scheme was applied for hierarchical clustering: the reachability threshold was initially set to form 20 mother/main clusters along with any number of tiny clusters. The same scheme was repeated for any mother cluster formed among subdivisions. Eventually, the brain was parcellated into 1 mother, 181 main, and 917 tiny clusters.
Mother clusters referred to those >1850 voxels (~50 cm3); main clusters were > 37 voxels (~1 cm3); and tiny clusters were ≤ 37 voxels.
Cluster size are presented in voxel, where each voxel is 0.027 cm3.
During subdivision clustering process, some voxels could not be assigned to any of sub-clusters generated at corresponding hierarchical level, and are referred to as “orphan” voxels. The column depicts the total number of orphan voxels generated at corresponding sub-clustering level.
One of the mother clusters at the 3rd hierarchical level (#80.588.1545) could not be resolved to smaller main or tiny clusters.
2.6. Bootstrapping analysis for assessment of cluster reliability
As a form of cross-validation, and in order to assess the statistical robustness of proposed clusters through permutation testing, we applied a bootstrapping cluster analysis similar to the framework proposed by Kerr and Churchill (Kerr and Churchill, 2001). Briefly, 2/3rd of the dataset was randomly selected and subsampled to 4-mm isotropic voxel resolution in order to achieve feasible processing times. The reachability distances were calculated for 100 iterations, and then super-sampled back to the 3-mm space for inference. Then, reachability distances in the 3-mm isotropic dataset were tested against the bootstrapped distribution of reachability distances. Thus, each voxel will possess a distribution of reachability distances from the permutations, which can be tested against the (original) clustering reachability distances achieved in Section 2.5. Those voxels with distances significantly (p < .05) greater than its corresponding mean bootstrapped reachability distance distribution were labelled as “unstable”, since they may not truly belong to the cluster assigned in the proposed atlas. Given the computationally intensive nature of bootstrapping, the number of iterations was limited to 100, where, even at the 4-mm isotropic resolution, each permutation required at least 6.4 GB memory space to store the distance matrix, and 30 h to compute using 15 CPU threads simultaneously.
3. Results
Overall, 1660.5 cm3 (90.9%) of the MNI-152 brain mask (1827.1 cm3) was covered by 793 infarct lesions from 458 patients. The median number of infarcts per each voxel was 4, with interquartile of 2 to 8.
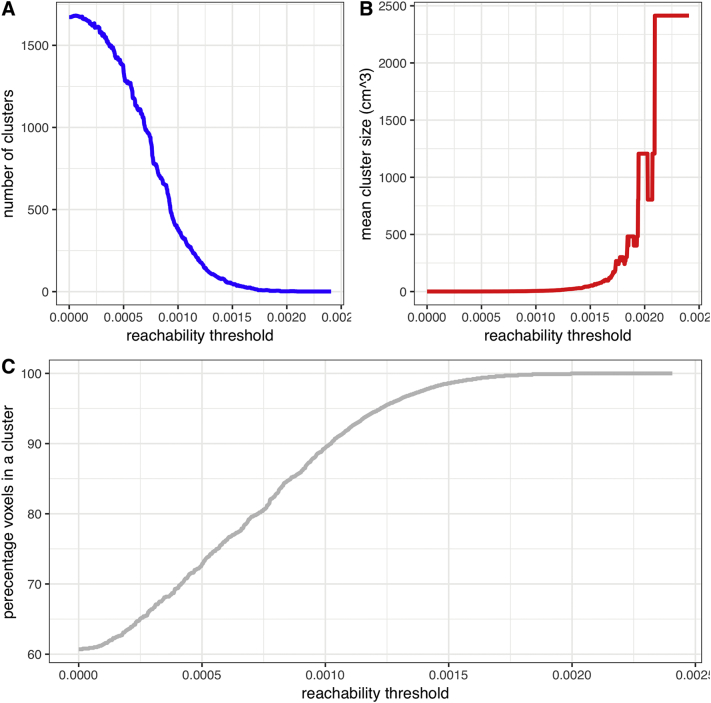
Fig. 1 demonstrates the relationship between reachability threshold with number and size of clusters, as well as percentage coverage of brain tissue. Clusters formed at a given threshold depict voxels/regions that are equally likely to be in the same infarct lesion among our cohort. In other words, if a voxel within a cluster is infarcted, other voxels within the same cluster have a high likelihood to be infarcted as well – depending on the reachability threshold.
Fig. 1.
In density-based hierarchical cluster analysis of infarct lesions, higher reachability thresholds were associated with smaller number of clusters (A), larger average size of clusters (B), and higher percentage of MNI-152 brain space coverage by clusters (C).
At relatively high reachability thresholds (allowing loose connection between voxels), the clustering yields large regions covering most of the brain (Fig. 1c). On the other hand, at the absolute zero threshold, numerous clusters, will be formed making many clusters intangible for further investigation. Alternatively, the intra-cluster homogeneity moves in the opposite direction of reachability threshold: when the intra-cluster homogeneity constraint is completely enforced without allowing any heterogeneity, we obtained 1672 clusters, most of which very tiny in size (mean cluster size of 24 voxels).
Table 1 summarizes the results of iterative clustering scheme. The hierarchical clustering scheme resulted in 1 mother cluster measuring 2319 voxels (62.6 cm3), 181 main clusters, and 917 tiny clusters. One of the mother clusters formed at the hierarchical level 2 – annotated as #80.588.1545 – could not be further subdivided. In this case, the reachability threshold has already reached zero and no further subdivision is possible. Also, it should be noted that intra-cluster homogeneity constraint is more tightened in subdivisions of mother clusters compared to those formed at upper hierarchical level; thus, the probability of simultaneous infarct in two voxels belonging to smaller sub-subdivision is much higher compared to two voxels from clusters formed at upper levels of hierarchy.
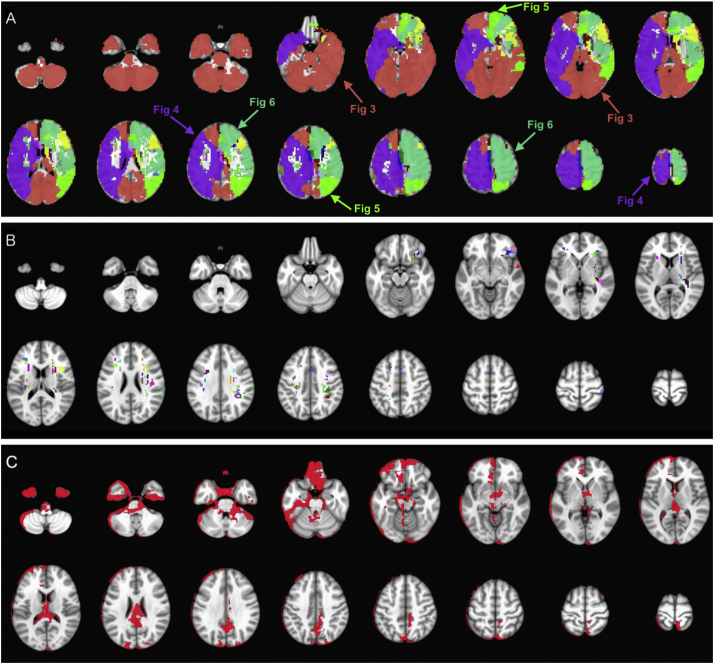
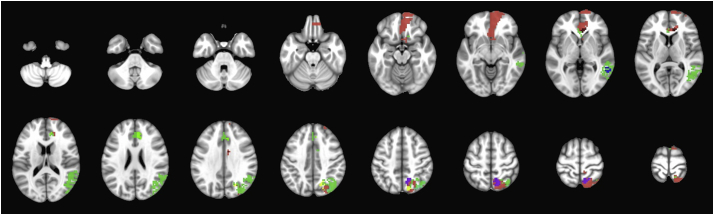
Fig. 2A depicts the first set of 20 mother/main clusters which were formed as we gradually increased the intra-cluster homogeneity in our hierarchical clustering scheme. In addition to these 20 clusters, 123 tiny clusters, averaging 8.59 voxels (~0.23 cm3) in size were formed (Fig. 2B). All infarcted voxels were included among 20 mother/main and 123 tiny clusters at hierarchical level 0 – covering 90.9% of MNI-152 brain mask. Fig. 2C depicts the 166.6 cm3 (9.1%) non-coverage area of MNI-152 brain mask, which was not covered by any infarct lesion among our cohort, predominantly localized to edges of the brain mask.
Fig. 2.
(A) The first 20 mother/main clusters formed at hierarchical level 0 after gradual increase of intra-cluster homogeneity. Among these clusters, there were 4 mother clusters (>50 cm3), which are marked with arrows, and further subdivided as depicted in Fig. 3, Fig. 4, Fig. 5, Fig. 6. In addition to 20 mother/main clusters, (B) a total of 123 tiny clusters (<1 cm3) were formed at this hierarchical level. (C) Red-colored mask depicts the 166.6 cm3 (9.2%) of MNI-152 brain mask which was not covered by infarct lesions in our cohort (793 infarct lesions in 458 patients). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The average size of the 181 main clusters was 227 voxels (6.1 cm3), with median size of 84 voxels (2.3 cm3). The 182 mother/main clusters measuring between ~1 to 62 cm3 covered 43,329 voxels (~1169.9 cm3 or 64.0% of MNI-152 brain mask), and the cumulative size of tiny clusters throughout the brain was 9809 voxels (264.8 cm3 or 14.5% of MNI-152 brain mask). In addition, during iterative subdivision of mother clusters, a total of 9057 orphan voxels (244.5 cm3 or 13.3% of MNI-152) could not be assigned to any sub-cluster. It should be noted that these orphan voxels were part of the larger mother cluster at the immediate upper hierarchical level, but could not be assigned to any sub-cluster in subdivision process. The hierarchical subdivisions and clusters are available at https://github.com/doggydaddy/stroke_atlas.
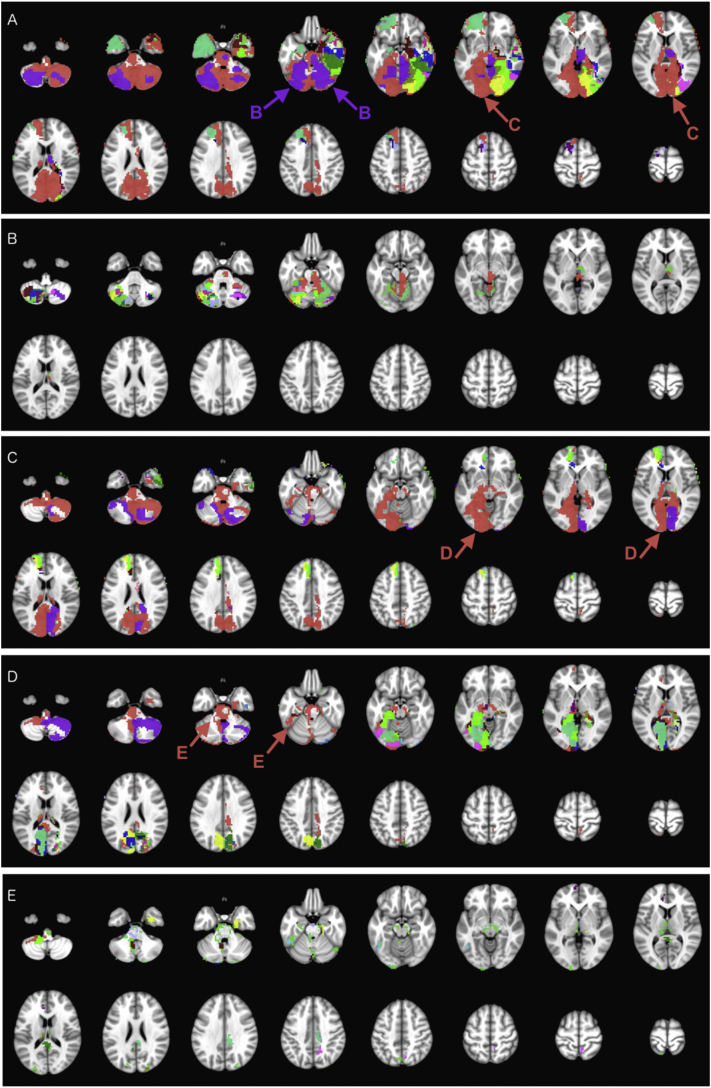
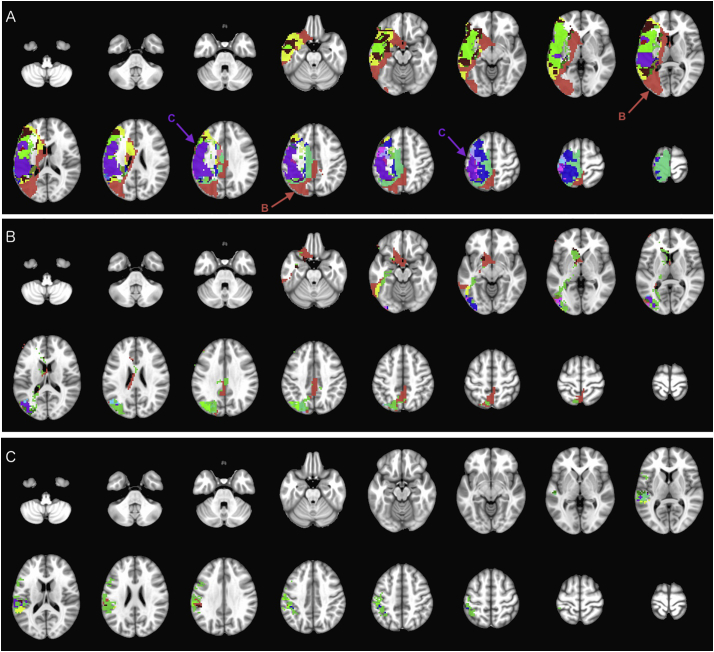
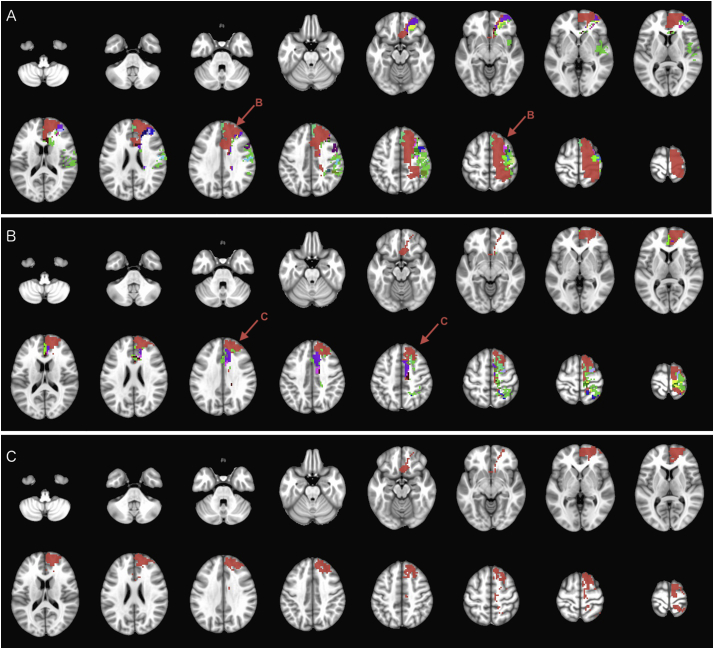
Fig. 3, Fig. 4, Fig. 5, Fig. 6 illustrate the iterative hierarchical cluster subdivisions of the four mother clusters formed at hierarchical level 0 (Fig. 2A). On visual inspection of clusters, the mother cluster #1 overlaps with right anterior cerebral artery (ACA), and bilateral posterior cerebral artery (PCA) territories, which are further parcellated in hierarchical subdivisions depicted in Fig. 3. The mother cluster #6 (Fig. 4) covers most of the right middle cerebral artery (MCA) territory as well as MCA-PCA border zone; whereas, mother cluster #71 (Fig. 5) covers left ACA and MCA-PCA border zone. The left MCA territory is parcellated into main or tiny clusters at hierarchical level 0 (Fig. 2), and subdivision of mother cluster #80 (Fig. 6). The #80.588.1545 mother cluster, which could not be further subdivided, overlaps with left MCA-ACA border zone (Fig. 6c). Table 2 lists the major arterial supply territories and their corresponding cluster subdivisions in Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6.
Fig. 3.
Iterative hierarchical subdivision of mother cluster #1 (red color on Fig. 2) from hierarchical level 0 into smaller clusters (Table 1). At hierarchical level 1 (A), two mother clusters (#1.1 in red – subdivided in C, − and #1.5 in purple – subdivided in B) are formed in addition to 19 main and 62 tiny clusters. At hierarchical level 2, the mother cluster #1.5 (B) is subdivided into 20 main and 62 tiny clusters; and the mother cluster #1.1 (C) is subdivided to one mother cluster (#1.1.1 in red – subdivided in D) in addition to 18 main and 35 tiny clusters. At hierarchical level 3 (D), the mother cluster #1.1.1 is subdivided into one mother cluster (#1.1.1.1 in red – subdivided in E), 20 main, and 26 tiny clusters. At hierarchical level 4 (E), the mother cluster #1.1.1.1 is subdivided into 13 main and 83 tiny clusters. Tiny clusters are all mutually color coded with emerald (#43D344) for visualization purposes. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 4.
Iterative hierarchical subdivision of mother cluster #6 (purple color on Fig. 2) from hierarchical level 0 (Table 1). At hierarchical level 1 (A), two mother clusters (#6.61 in red – subdivided in B, − and #6.84 in purple – subdivided in C) are formed in addition to 21 main and 52 tiny clusters. At hierarchical level 2, the mother cluster #6.61 (B) is subdivided into 12 main and 106 tiny clusters; and the mother cluster #6.84 (C) is subdivided into 8 main and 81 tiny clusters (Table 1). Tiny clusters are all mutually color coded with emerald (#43D344) for visualization purposes. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 5.
Iterative hierarchical subdivision of mother cluster #71 (light green color on Fig. 2) at hierarchical level 1, resulted in 7 main and 121 tiny clusters. Tiny clusters are all mutually color coded with emerald (#43D344) for visualization purposes. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 6.
Iterative hierarchical subdivision of mother cluster #80 (dark green color on Fig. 2) from hierarchical level 0 (Table 1). At hierarchical level 1 (A), one mother cluster (#80.588 in red – subdivided in B) in addition to 18 main and 108 tiny clusters are formed. At hierarchical level 2, the mother cluster #80.588 (B) was subdivided into one mother cluster (#80.588.1545 in red and marked with an arrow) in addition to 10 main and 58 tiny clusters. However, at hierarchical level 3, the mother cluster #80.588.1545 (C) could not be further subdivided (Table 1). Tiny clusters are all mutually color coded with emerald (#43D344) for visualization purposes. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Table 2.
Major arterial supply territories and corresponding cluster subdivision depictions.
| Left ACA | Fig. 5, Fig. 6 |
| Right ACA | Fig. 3a |
| Left ACA-MCA border zone | Fig. 6b |
| Right ACA-MCA border zone | Figs. 3a, and 4a |
| Left MCA | Figs. 2a, and 3a |
| Right MCA | Fig. 4a |
| Left MCA-PCA border zone | Figs. 3e, and 5 |
| Right MCA-PCA border zone | Fig. 4b and c |
| Left PCA | Fig. 3c and d |
| Right PCA | Fig. 3c and d |
| Cerebellum | Fig. 3b |
ACA = anterior cerebral artery; MCA = middle cerebral artery; PCA = posterior cerebral artery.
In bootstrap cluster analysis, only 0.12% (75 of 65181) of voxels were labelled as “unstable” – with a reachability distance in final cluster scheme greater than their corresponding mean bootstrapped reachability distance. Among 182 mother/main clusters, only 21 contained any of these “unstable” voxels (Supplemental Table 1, and Supplemental Fig. 1). Overall, these “unstable” voxels formed at most 5.19% of a single cluster, and <1% volume of 13 clusters as detailed in Supplemental Table 1. In total, 39 “unstable” voxels belonged to main/mother clusters; and the other 36 “unstable” voxels belonged to tiny clusters. Supplemental Fig. 1 depicts the topographic location of “unstable” voxels, and their corresponding mother/main clusters. Of note, the majority of “unstable” voxels localized to borders of the stroke-atlas clusters (Supplemental Fig. 1).
4. Discussion
Using a dataset of 793 infarct lesions, we have devised a stroke-atlas for the brain applying a hierarchical cluster subdivision scheme based on cluster size for exploratory analysis. The scheme explores the whole reachability plot in a consistent manner, producing sets of clusters at different reachability thresholds for parcellation of brain tissue in standard MNI-152 space. The clusters identified at different hierarchical levels depict the brain territories, where voxels are likely to be part of same infarct lesion in our study cohort. The hierarchical atlas allows parcellation of brain into small number of larger regions with moderate likelihood of simultaneous infarct among voxels; or large number of smaller regions with higher likelihood of simultaneous infarct among voxels. The final stroke atlas parcellates the brain into 182 regions measuring 1-to-62.6 cm3; and 917 tiny clusters measuring <1 cm3.
In addition, the bootstrap analysis of a randomly selected subset of subjects was applied to validate the proposed clustering scheme, and evaluate robustness of stroke-atlas clusters to inconsistency/mislabeling of any given voxel. As detailed in the methods Section 2.6, those voxels with reachability distance greater than the bootstrapped distribution of reachability distances were labelled as “unstable” since they may not truly belong to the assigned stroke-atlas cluster. Generally, smaller clusters tend to be less robust statistically compared to larger clusters, and more susceptible to noise. This may be especially detrimental in analyzing high dimensional data (such as functional or diffusion MRI), where random noise in the data due to artifacts in scan acquisition might result in false positives due to random chance. However, in our analysis, two factors partially counteracted the “curse of dimensionality”: First, clustering analysis was performed on binary masks, and hence each lesion has quite compact data points at its center. Even considering expected scanner noise and artifact as well as manual segmentation inconsistencies, the majority of data error are expected to localize along the boundaries of each infarct lesion, and likely not affecting the bulk of cluster voxels in our analysis. Indeed, Supplemental Fig. 1 shows that “unstable” voxels were typically found along the boundaries of proposed stroke-atlas clusters. Second, as the average cluster size decreases with subsequent sub-divisions, clusters obtained during sub-divisions are inherently more homogenous as the reachability threshold required to generate these clusters are more stringent. While this inherent property of density clustering neither can completely offset the multiple comparison problem, nor eases the impact of type I errors in small clusters, it is nevertheless noteworthy that voxels belonging to same cluster are identical in terms of the probability of being infarcted (or not) in the dataset. Finally, while application of dimensionality reduction techniques such as principle component analysis might have strengthened the statistical reliability of high-dimensional analyses, it could have – at least theoretically – limited the strength of a detailed analysis benefiting from all available data points, and biased the results towards the more commonly infarcted regions of the brain.
We hypothesize that infarct clusters identified at different hierarchical levels correspond to end-arterial perfusion territories. In patients with an atherosclerotic or embolic arterial occlusion, brain regions/voxels supplied by same arterial branches tend to infarct together, and such voxels are presumably more likely to aggregate in the same cluster. Indeed, mother clusters formed and further subdivided in hierarchical subdivision, follow the expected territories of cerebral arterial supply branches (Table 2, and Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6). The mother/main clusters generated on the top hierarchical level with high reachability threshold (loosely intra-connected clusters) correspond to major artery branch supply territories; whereas, cluster subdivisions at lower hierarchies with much more strict thresholds may represent supply territories of smaller end-arterial branches. While smaller (main) clusters along arterial border zones may represent watershed infarcts due to occlusion of proximal larger arteries, gradual delineation of these sub-clusters from arterial border zone mother clusters – upon application of stricter thresholds – suggests that watershed perfusion territories mostly presented as larger (mother)clusters, which were then further subdivided into smaller (main) sub-clusters representative of distal end-arterial supply territories; for example subdivisions of the right MCA-PCA border zone (mother cluster #6.61 on Fig. 4B). Having said that, the extent of sub-division and identification of smaller end-arterial supply territories are nevertheless limited by the presence of adequate subjects in our dataset.
Notably, the majority of tiny (and smaller main) clusters tend to localize to lenticulostriate regions, which are supplied by (small) deep perforator vessels and are common regions for lacunar infarcts (Fig. 2A). Lacunar infarcts of basal ganglia as well as white matter T2 hyperintensities presumably have vascular origin, and represent cerebral small vessel ischemic disease (Kloppenborg et al., 2017). It has been suggested that lacunar infarcts in the deep white matter are due to arteriolosclerosis or endothelial damage; whereas, lacunar infarcts in the basal ganglia represent thrombo-embolic occlusion of perforating arteries (Wardlaw et al., 2013a; Wardlaw et al., 2013b). Regardless of arteriolosclerosis or thrombo-embolic mechanism of (smaller) lacunar infarcts, the resultant ischemic lesions tend to represent end-arterial supply territory of small perforator arteries, and likely represented by tiny clusters in Figs. 2b, 3a, and 4a.
The supply territories of the main cerebral arteries are generally demarcated based on consensus from the infarct distribution in patients suffering from large vessel occlusion. Nowinski et al. have combined the anatomical information from Talairach atlas with consensus driven arterial perfusion maps to devise a three-dimensional atlas of 7 brain blood supply territories (Berman et al., 1980, Berman et al., 1984; Hayman et al., 1981; Nowinski et al., 2006). Delineation of supply territories for the smaller distal arterial branches is particularly challenging given the anatomical variation in branching pattern of cerebral arteries between individual subjects. In this study, we have used a data-driven approach to parcellate the MNI-152 brain space into (sub)clusters, where voxels are prone to infarct simultaneously, based on topographic distribution of 793 infarct lesions. The hierarchical clustering organization of our atlas allows visualization of presumable supply territories at different levels. The current atlas can potentially help with location-outcome correlation, or devising regional thresholds for identification of infarct core on CT perfusion scans. Nevertheless, the regional boundaries and topographic distribution should be interpreted with caution given the amount of anatomical variation in arterial supply pattern of the brain between individual subjects, as pointed out previously.
One of the potential applications of the proposed atlas is location-outcome correlation in stroke patients. The voxel-based lesion–symptom mapping (VLSM) offers a voxel-wise correlation analysis with no priori (Payabvash et al., 2017b); however, VLSM analysis requires a large sample size with a broad infarct lesion spread since only voxels infarcted in at least 10 subjects can reliably be included in the analysis (Payabvash et al., 2017b). In addition, integration of clinical variables in voxel-wise analysis is challenging and generally require more sophisticated regression models (Phan et al., 2010). An atlas-based assessment of lesion topography, on the other hand, generally requires smaller number of lesions for analysis, and location-based variables can be integrated in multivariate models along with clinical variables (Payabvash et al., 2010; Payabvash et al., 2012). The most commonly used brain atlas for evaluation of infarct location in stroke patients is ASPECTS, which was originally devised as a crude way for identification of infarcts involving greater than one third of MCA territory on non-contrast head CT scan (Barber et al., 2000). The anatomical boundaries of 10 cortical and deep gray matter regions in ASPECTS are vaguely defined; however, the atlas has widely been used for assessment of infarct lesion location in both CT and MRI scans (Payabvash et al., 2017a; Rosso et al., 2019), mainly due to familiarity of stroke neurologists, and its easy application based on visual assessment of brain scans. Other structural atlases of the brain are predominantly based on Talairach anatomical atlas (Talairach and Tournoux, 1988). Such consensus-driven atlases are, nevertheless, based on anatomical observations rather than a data-driven analysis, and may not best represent the distribution of infarct lesions among stroke patients. The next step in application of the proposed stroke-atlas is to determine the functional correlates of each cluster, which can potentially help with treatment triage and accurate prognostication in patients presenting with acute stroke.
Another potential application for the proposed stroke atlas is calculation of location-specific CT perfusion thresholds. Prior studies have shown regional variation in the cerebral blood flow/volume thresholds for prediction of infarct core in CT perfusion scans (Payabvash et al., 2011). Overall, brain regions which are more vulnerable to hypoperfusion, have higher relative cerebral blood flow (rCBF) thresholds for prediction of infarct core, since they tend to infract with lower degrees of rCBF drop compared to less vulnerable brain regions (Payabvash et al., 2011). By reverse co-registration of MNI-152 space to CT perfusion maps, one can potentially calculate and apply region-specific rCBF thresholds for prediction of infarct core in each of stroke atlas clusters.
Topographic delineation of brain regions that are likely to infarct together may also help with differentiation of ischemic infarct from other pathologies presenting with restricted diffusion (e.g. hypercellular metastasis) based on topographic distribution of suspicious lesions (Zacharzewska-Gondek et al., 2017). Thus, those lesions with reduced diffusion, which are not conforming to boundaries of stroke atlas, are more likely representing non-infarct lesions such as hypercellular metastases.
The proposed infarct clusters in this study are inherently limited by our lesion dataset. Approximately 91% of the MNI-152 brain mask was covered by large number of infarct lesions in our series. However, the slim non-coverage area along edges of the brain mask is – at least in part – due to susceptibility artifact distortion of DWI images along the periphery of the brain, especially rectus gyri and inferior temporal gyri (Fig. 2C). Also, an inherent limitation of hierarchical analysis – as an unsupervised learning algorithm – is that, those sub-clusters formed at higher hierarchical levels, and deeper subdivisions tend to be less statistically robust, which is an issue more related to the nature of analysis rather than anatomical correlates of our findings. The manual segmentation and co-registration process might also have contributed to non-coverage rim. Another limitation of our study is the uneven topographic distribution of infarct lesions: overall, stroke patients with MCA territory infarct and involvement of eloquent areas of the brain are more likely to present to hospital and get scanned (Payabvash et al., 2016). Presence of greater data points and concentration of infarct lesions may also explain why infarct clusters in MCA territories could be identified at initial hierarchical steps (Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6). Inclusion of infarcts in acute and chronic phase also contributes to data heterogeneity in our cohort. While acute phase infarcts lesions are inherently slightly edematous and may overestimate regions of parenchymal damage, the chronic phase infarcts – on the other hand – tend to have variable degrees of encephalomalacia and may underestimate the boundaries of parenchymal damage. Finally, as detailed in the methods section, during the process of subdividing mother clusters, a series of voxels could not be assigned to any (sub-)cluster, which were referred to as “orphan” voxels. While these voxels were assigned to specific mother clusters, they had stochastic behavior during iterative sub-cluster assignment, and could not be included in any main or tiny sub-cluster. While these may simply represent the lack of adequate sample size for robust statistical assignment of these voxels, one may hypothesize that these “orphan” voxels represent tiny end-arterial supply regions (e.g. single-voxel tiny clusters).
5. Conclusion
Applying a data-driven hierarchical voxel-wise density clustering on 793 infarct lesions from 458 stroke patients, we have parcellated the MNI-152 brain space into 182 regions (measuring 1 to 62.6 cm3), and devised a stroke atlas delineating brain regions (voxels) likely to infarct simultaneously. The statistical stability of the proposed regions was confirmed by bootstrapping cluster analysis. Adjustment of the reachability threshold allows us to tune the output from small, but probabilistically homogenous regions, to large brain regions, with less homogenous likelihood of simultaneous infarct. The proposed brain parcellation map theoretically represent end-arterial perfusion territories that tend to infarct simultaneously. The atlas is made publicly available, and can potentially be applied for infarct location-outcome analysis, devising multivariate prognostic models in stroke patients, or calculating region-specific CT perfusion thresholds for infarct core prediction.
Disclosures
All authors report no conflict of interests.
Source of funding
None.
Declaration of Competing interest
None.
Acknowledgements
We would like to thank Dr. J. Benson for assistance and support during data collection.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.nicl.2019.101981.
Contributor Information
Yanlu Wang, Email: yanlu.wang@ki.se.
Seyedmehdi Payabvash, Email: sam.payabvash@yale.edu.
Appendix A. Supplementary data
Supplementary material
References
- Achtert E., Böhm C., Kriegel H.-P., Kröger P., Müller-Gorman I., Zimek A. Springer Berlin Heidelberg; Berlin, Heidelberg: 2006. Finding Hierarchies of Subspace Clusters; pp. 446–453. [Google Scholar]
- Ankerst M., Breunig M.M., Kriegel H.-P., Sander J. ACM Sigmod record. ACM; 1999. OPTICS: ordering points to identify the clustering structure; pp. 49–60. [Google Scholar]
- Barber P.A., Demchuk A.M., Zhang J., Buchan A.M. Validity and reliability of a quantitative computed tomography score in predicting outcome of hyperacute stroke before thrombolytic therapy. ASPECTS Study Group. Alberta Stroke Programme Early CT Score. Lancet. 2000;355:1670–1674. doi: 10.1016/s0140-6736(00)02237-6. [DOI] [PubMed] [Google Scholar]
- Berman S.A., Hayman L.A., Hinck V.C. Correlation of CT cerebral vascular territories with function: I. Anterior cerebral artery. AJR Am. J. Roentgenol. 1980;135:253–257. doi: 10.2214/ajr.135.2.253. [DOI] [PubMed] [Google Scholar]
- Berman S.A., Hayman L.A., Hinck V.C. Correlation of CT cerebral vascular territories with function: 3. Middle cerebral artery. AJR Am. J. Roentgenol. 1984;142:1035–1040. doi: 10.2214/ajr.142.5.1035. [DOI] [PubMed] [Google Scholar]
- Duan L., Xu L., Guo F., Lee J., Yan B.P. A local-density based spatial clustering algorithm with noise. Inf. Syst. 2007;32:978–986. [Google Scholar]
- Ernst M., Boers A.M.M., Aigner A., Berkhemer O.A., Yoo A.J., Roos Y.B., Dippel D.W.J., van der Lugt A., van Oostenbrugge R.J., van Zwam W.H., Fiehler J., Marquering H.A., Majoie C. Association of computed tomography ischemic lesion location with functional outcome in acute large vessel occlusion ischemic stroke. Stroke. 2017;48:2426–2433. doi: 10.1161/STROKEAHA.117.017513. [DOI] [PubMed] [Google Scholar]
- Ester M., Kriegel H.-P., Sander J., Xu X. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd. 1996:226–231. [Google Scholar]
- Hahsler M., Piekenbrock M., Doran D. Dbscan: fast density-based clustering with R. J. Stat. Softw. 2017;25:409–416. [Google Scholar]
- Hayman L.A., Berman S.A., Hinck V.C. Correlation of CT cerebral vascular territories with function: II. Posterior cerebral artery. AJR Am. J. Roentgenol. 1981;137:13–19. doi: 10.2214/ajr.137.1.13. [DOI] [PubMed] [Google Scholar]
- Kerr M.K., Churchill G.A. Bootstrapping cluster analysis: assessing the reliability of conclusions from microarray experiments. Proc. Natl. Acad. Sci. U. S. A. 2001;98:8961–8965. doi: 10.1073/pnas.161273698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kloppenborg R.P., Nederkoorn P.J., Grool A.M., De Cocker L.J., Mali W.P., van der Graaf Y., Geerlings M.I. Do lacunar infarcts have different aetiologies? Risk factor profiles of lacunar infarcts in deep white matter and basal ganglia: the second manifestations of arterial disease-magnetic resonance study. Cerebrovasc. Dis. 2017;43:161–168. doi: 10.1159/000454782. [DOI] [PubMed] [Google Scholar]
- Liew S.-L., Anglin J.M., Banks N.W., Sondag M., Ito K.L., Kim H., Chan J., Ito J., Jung C., Khoshab N., Lefebvre S., Nakamura W., Saldana D., Schmiesing A., Tran C., Vo D., Ard T., Heydari P., Kim B., Aziz-Zadeh L., Cramer S.C., Liu J., Soekadar S., Nordvik J.-E., Westlye L.T., Wang J., Winstein C., Yu C., Ai L., Koo B., Craddock R.C., Milham M., Lakich M., Pienta A., Stroud A. A large, open source dataset of stroke anatomical brain images and manual lesion segmentations. Sci. Data. 2018;5 doi: 10.1038/sdata.2018.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowinski W.L., Qian G., Kirgaval Nagaraja B.P., Thirunavuukarasuu A., Hu Q., Ivanov N., Parimal A.S., Runge V.M., Beauchamp N.J. Analysis of ischemic stroke MR images by means of brain atlases of anatomy and blood supply territories. Acad. Radiol. 2006;13:1025–1034. doi: 10.1016/j.acra.2006.05.009. [DOI] [PubMed] [Google Scholar]
- Payabvash S., Kamalian S., Fung S., Wang Y., Passanese J., Kamalian S., Souza L.C., Kemmling A., Harris G.J., Halpern E.F., Gonzalez R.G., Furie K.L., Lev M.H. Predicting language improvement in acute stroke patients presenting with aphasia: a multivariate logistic model using location-weighted atlas-based analysis of admission CT perfusion scans. AJNR Am. J. Neuroradiol. 2010;31:1661–1668. doi: 10.3174/ajnr.A2125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payabvash S., Souza L.C., Wang Y., Schaefer P.W., Furie K.L., Halpern E.F., Gonzalez R.G., Lev M.H. Regional ischemic vulnerability of the brain to hypoperfusion: the need for location specific computed tomography perfusion thresholds in acute stroke patients. Stroke. 2011;42:1255–1260. doi: 10.1161/STROKEAHA.110.600940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payabvash S., Souza L.C.S., Kamalian S., Wang Y., Passanese J., Kamalian S., Fung S.H., Halpern E.F., Schaefer P.W., Gonzalez R.G., Furie K.L., Lev M.H. Location-weighted CTP analysis predicts early motor improvement in stroke. A preliminary study. 2012;78:1853–1859. doi: 10.1212/WNL.0b013e318258f799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payabvash S., Taleb S., Benson J.C., McKinney A.M. Interhemispheric asymmetry in distribution of infarct lesions among acute ischemic stroke patients presenting to hospital. J. Stroke Cerebrovasc. Dis. 2016;25:2464–2469. doi: 10.1016/j.jstrokecerebrovasdis.2016.06.019. [DOI] [PubMed] [Google Scholar]
- Payabvash S., Noorbaloochi S., Qureshi A.I. Topographic assessment of acute ischemic changes for prognostication of anterior circulation stroke. J. Neuroimaging. 2017;27:227–231. doi: 10.1111/jon.12383. [DOI] [PubMed] [Google Scholar]
- Payabvash S., Taleb S., Benson J.C., McKinney A.M. Acute ischemic stroke infarct topology: association with lesion volume and severity of symptoms at admission and discharge. AJNR Am. J. Neuroradiol. 2017;38:58–63. doi: 10.3174/ajnr.A4970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payabvash S., Benson J.C., Tyan A.E., Taleb S., McKinney A.M. Multivariate prognostic model of acute stroke combining admission infarct location and symptom severity: a proof-of-concept study. J. Stroke Cerebrovasc. Dis. 2018;27:936–944. doi: 10.1016/j.jstrokecerebrovasdis.2017.10.034. [DOI] [PubMed] [Google Scholar]
- Phan T.G., Chen J., Donnan G., Srikanth V., Wood A., Reutens D.C. Development of a new tool to correlate stroke outcome with infarct topography: a proof-of-concept study. Neuroimage. 2010;49:127–133. doi: 10.1016/j.neuroimage.2009.07.067. [DOI] [PubMed] [Google Scholar]
- Rorden C., Brett M. Stereotaxic display of brain lesions. Behav. Neurol. 2000;12:191–200. doi: 10.1155/2000/421719. [DOI] [PubMed] [Google Scholar]
- Rosso C., Blanc R., Ly J., Samson Y., Lehéricy S., Gory B., Marnat G., Mazighi M., Consoli A., Labreuche J., Saleme S., Costalat V., Bracard S., Desal H., Piotin M., Lapergue B. Impact of infarct location on functional outcome following endovascular therapy for stroke. J. Neurol. Neurosurg. Psychiatry. 2019;90:313–319. doi: 10.1136/jnnp-2018-318869. [DOI] [PubMed] [Google Scholar]
- Talairach J., Tournoux P. Thieme; 1988. Co-Planar Stereotaxic Atlas of the Human Brain. 3-Dimensional Proportional System: An Approach to Cerebral Imaging. [Google Scholar]
- Wang Y., Li T.Q. Analysis of whole-brain resting-state FMRI data using hierarchical clustering approach. PLoS One. 2013;8 doi: 10.1371/journal.pone.0076315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Msghina M., Li T.Q. Studying sub-dendrograms of resting-state functional networks with voxel-wise hierarchical clustering. Front. Hum. Neurosci. 2016;10:75. doi: 10.3389/fnhum.2016.00075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wardlaw J.M., Smith C., Dichgans M. Mechanisms of sporadic cerebral small vessel disease: insights from neuroimaging. Lancet Neurol. 2013;12:483–497. doi: 10.1016/S1474-4422(13)70060-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wardlaw J.M., Smith E.E., Biessels G.J., Cordonnier C., Fazekas F., Frayne R., Lindley R.I., O’Brien J.T., Barkhof F., Benavente O.R., Black S.E., Brayne C., Breteler M., Chabriat H., Decarli C., de Leeuw F.E., Doubal F., Duering M., Fox N.C., Greenberg S., Hachinski V., Kilimann I., Mok V., Oostenbrugge R., Pantoni L., Speck O., Stephan B.C., Teipel S., Viswanathan A., Werring D., Chen C., Smith C., van Buchem M., Norrving B., Gorelick P.B., Dichgans M. Neuroimaging standards for research into small vessel disease and its contribution to ageing and neurodegeneration. Lancet Neurol. 2013;12:822–838. doi: 10.1016/S1474-4422(13)70124-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolrich M.W., Jbabdi S., Patenaude B., Chappell M., Makni S., Behrens T., Beckmann C., Jenkinson M., Smith S.M. Bayesian analysis of neuroimaging data in FSL. Neuroimage. 2009;45:S173–S186. doi: 10.1016/j.neuroimage.2008.10.055. [DOI] [PubMed] [Google Scholar]
- Zacharzewska-Gondek A., Maksymowicz H., Szymczyk M., Sąsiadek M., Bladowska J. Cerebral metastases of lung cancer mimicking multiple ischaemic lesions - a case report and review of literature. Pol. J. Radiol. 2017;82:530–535. doi: 10.12659/PJR.902213. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material