Effects of Noncanonical Base Pairing on RNA Folding: Structural Context and Spatial Arrangements of G·A Pairs

Abstract

Noncanonical base pairs play important roles in assembling the three-dimensional structures critical to the diverse functions of RNA. These associations contribute to the looped segments that intersperse the canonical double-helical elements within folded, globular RNA molecules. They stitch together various structural elements, serve as recognition elements for other molecules, and act as sites of intrinsic stiffness or deformability. This work takes advantage of new software (DSSR) designed to streamline the analysis and annotation of RNA three-dimensional structures. The multi-scale structural information gathered for individual molecules, combined with the growing number of unique, well-resolved RNA structures, makes it possible to examine the collective features deeply and to uncover previously unrecognized patterns of chain organization. Here we focus on a subset of noncanonical base pairs involving guanine and adenine and the links between their modes of association, secondary structural context, and contributions to tertiary folding. The rigorous descriptions of base-pair geometry that we employ facilitate characterization of recurrent geometric motifs and the structural settings in which these arrangements occur. Moreover, the numerical parameters hint of the natural motions of the interacting bases and the pathways likely to connect different spatial forms. We draw attention to higher-order multiplexes involving two or more G·A pairs and the roles these associations appear to play in bridging different secondary structural units. The collective data reveal pairing propensities in base organization, secondary structural context, and deformability and serve as a starting point for further multi-scale investigations and/or simulations of RNA folding.

INTRODUCTION

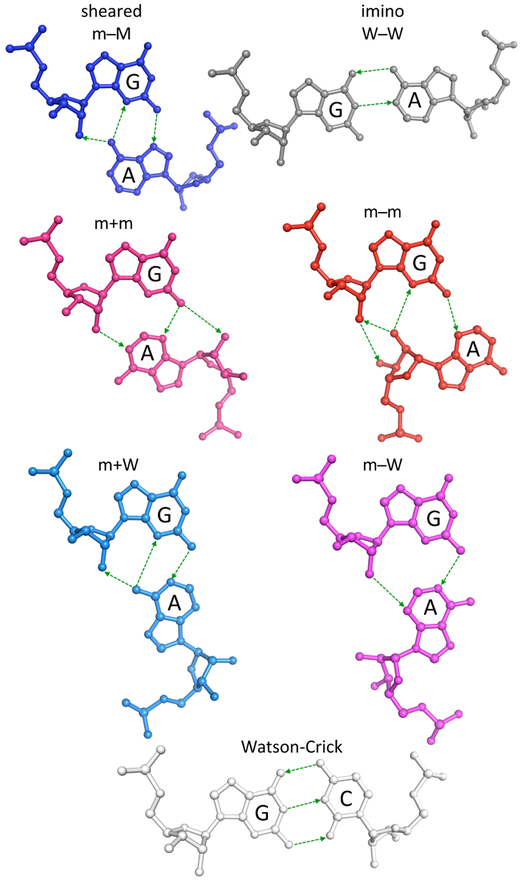
The structural and functional versatility of RNA arises in large part from the numerous modes of interaction of the constituent nucleotides. Notable in this regard are the various edge-to-edge associations of the planar, nitrogenous bases, such as the canonical Watson-Crick and wobble pairings found in short double-helical stretches of folded RNA molecules and the noncanonical arrangements of bases that may mediate long-range RNA interactions,^1-3 serve as recognition elements for proteins and other molecules,^4-6 and act as sites of intrinsic stiffness or deformability.^7,8 Among the most common noncanonical base pairs are those involving guanine (G) and adenine (A). The hydrogen-bonding capabilities of the two purine moieties make it possible to arrange a G and an A in multiple ways (Figure 1) and to incorporate the bases in different secondary structural contexts (Figure 2). For example, there are many anecdotal examples of Watson-Crick-like imino configurations of G and A interrupting stretches of canonical base pairs and forming so-called internal loops⁹ and numerous reported instances of sheared G·A pairs lying within an internal loop or at the end of a short hairpin loop, most notably in the GNRA tetraloop (where the N refers to any base and the R to G or A).^9-12 The adenines of sheared G·A pairs may also form stabilizing A-minor interactions with canonical Watson-Crick pairs in various structural contexts, such as at kink-turns,^13-15 and may contribute to larger, conserved multi-base-pair juxtapositions, such as the loop E/bulged-G,^16-18 sarcin-ricin,¹⁹ and 3RRs²⁰ motifs. While there are fewer documented examples of G·A pairing within the loops at the junctions of three or more covalently linked stretches of canonical base pairs,^21,22 recent studies point to the potential contribution of these noncanonical associations to the global flexing of ribosomal and transfer RNA molecules.⁸ Knowledge of the intrinsic deformabilities, the preferred structural contexts, and the likely transition pathways among the many modes of G·A association is accordingly important to understanding the global folds and motions of RNA and is potentially useful in the prediction of RNA three-dimensional (3D) structure from nucleotide sequence.

Figure 1.

Comparison of the hydrogen-bonding interactions, chemical structures, and relative spatial arrangements of nucleotides in the six dominant modes of G·A pairing and in a canonical Watson-Crick G−C pair. Hydrogen bonds shown by thin dashed lines, with arrows directed toward base/backbone atoms capable of accepting protons. Structures generated with 3DNA²⁴ and rendered in PyMOL (www.pymol.org) using the average rigid-body parameters in Table 1 and a canonical A-RNA backbone.³⁴ Structures depicted in the standard reference frame of G.³⁰ Color-coding denotes the mode of base association: sheared m−M (dark blue); imino W−W (gray); m+m (pink); m−m (red); m+W (light blue); m−W (magenta); canonical (white), where the combinations of signs and letters denote the orientation (parallel +/antiparallel −) and the approximate sites (minor m/major M/Watson-Crick W edges) of base association.²⁷ Interestingly, less than 10% of the + states reflect an anti-to-syn sugar-base rearrangement, and these examples all involve adenine.

Figure 2.

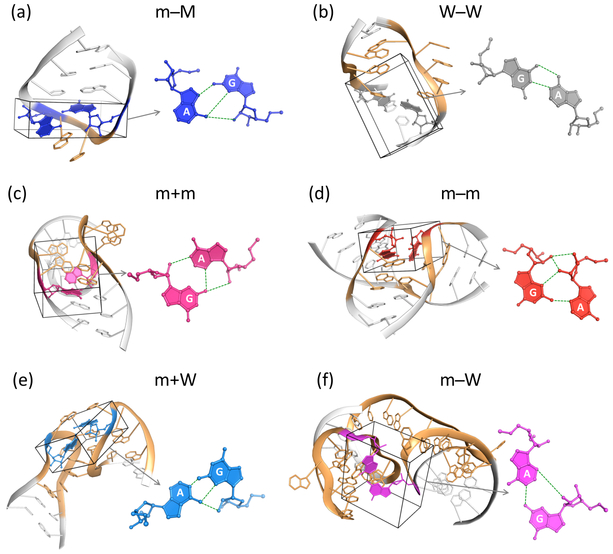
Molecular images of RNA secondary structural motifs incorporating each of the dominant modes of G·A base pairing. Motifs correspond to one of the common settings of the designated pairs: (a) sheared m−M pair closing the GNRA tetraloop at the end of the P4 helix of the glmS ribozyme bound to glucosamine 6-phosphate;³⁵ (b) imino W−W pair at the end of an asymmetric internal loop in the Thermus thermophilus 70S ribosome in complex with the hibernation factor pY;³⁶ (c) m+m pair linking the G in a double-helical stem and the A in an internal loop of the complex of Thermus thermophilus ribosomal protein L1 with a fragment of the L1 RNA from Methanoccocus vannielii;³⁷ (d) m−m pair joining a stem and single-stranded fragment within a three-way junction of the Thermoanaerobacter tengcongenesis ydaO riboswitch bound to cyclic di-AMP;³⁸ (e) m+W pair connecting the D and T hairpin loops of yeast initiator transfer RNA;³⁹ (f) m−W pair linking two hairpin loops of the 5S rRNA within the structure of the hibernating 100S ribosome dimer from pathogenic Staphylococcus aureus.⁴⁰ G·A pairs color-coded as in Figure 1 and shown at the nucleotide level within each structural element and in a separate local depiction to the right of each example. Loops depicted in gold and canonical base pairs at the ends of loops or within double-helical stems in white. Ribbons connect phosphorus atoms in successive nucleotides. See Table S3 for respective Protein Data Bank identifiers, chain names, and residue numbers of the depicted pairs and Figure S2 for simple secondary structural diagrams of the associated motifs.

One of the simplest ways to assess the deformations and structural context of RNA base pairing is through the spatial arrangements of the interacting bases with respect to one another and with respect to other bases and base pairs in the surrounding chemical environment. The relative orientation and displacement of the paired bases are easily understood in terms of six rigid-body parameters. The parameters — three translations (Shear, Stretch, Stagger) and three rotations (Buckle, Propeller, Opening), originally devised to characterize the arrangements of bases in double-helical DNA²³ — can be conceived without resort to detailed molecular models (Figure S1). Whereas the values of Shear, Stretch, and Opening distinguish different modes of base pairing, the values of Stagger, Buckle, and Propeller characterize the non-planarity of base association.^24-27 The precise numbers reflect the relative location and orientation of a pair of coordinate frames, one embedded in each of the interacting bases.^28,29 The frames are conventionally defined such that all six parameters are null in an ideal, planar, antiparallel Watson-Crick base pair,³⁰ where the faces of the two bases ^31,32 and the axes normal to the base planes point in opposing directions. One of the bases, however, may flip in other pairing schemes (through reversal of chain direction or syn/anti rotation about the glycosidic linkage between the sugar and base) so that the normal vectors point in the same direction.³³ The two directions of association (antiparallel and parallel) are respectively differentiated here by minus and plus signs.²⁴

The coordinate axes in the planes of the paired bases capture the hydrogen-bonding and groove characteristics of a Watson-Crick pair and thus provide an automatic description of the interacting edges of the bases (see Materials and Methods for details). The minor-and major-groove edges of a base, here respectively abbreviated as m and M, correspond approximately to the so-called sugar and Hoogsteen/C–H edges used in earlier classifications of RNA base pairing.^9,41 The minor-groove edge includes the atoms closest to the site of base attachment to the sugar-phosphate backbone; the major-groove edge, on the opposite side of the base, lies far from the attachment point (see Figure S1). The Watson-Crick or W edge includes the purine atoms involved in canonical associations of G and A with their pyrimidine complements, i.e., guanine N1, N2, O6 and adenine N1, N6 respectively paired in such arrangements to cytosine N3, O2, N4 and uracil/thymine N3, O4 (Figure 1).

The orientation and displacement of a base pair with respect to the coordinate frames on nearby bases determine whether that pair occurs in the context of a multiplet, i.e., a higher-order, hydrogen-bonded coplanar association of three of more bases, or an array of stacked residues.²⁷ The paired bases typically lie near one another in roughly the same plane and form one or more hydrogen bonds, while the bases in stacked arrays lie one above the other in closely spaced, overlapping arrangements. The locations of the two nearest neighbors in a stacked array determine whether a base pair lies at the end or in the middle of the array. That is, the two nearest neighbors lie on one side of a terminal pair but on opposing sides of an internal pair. The ends of a stacked array of covalently connected canonical base pairs, in turn, determine the locations and types of adjoining loops. For example, a hairpin loop abuts a single stacked array, a bulge or internal loop two arrays, and a junction (multi-branched loop) three or more arrays (Figures 2 and S2). Thus, knowledge of the spatial arrangements of the RNA bases leads to direct characterization of secondary structure and makes it possible to examine the effects of base pairing in a higher-order structural context.

Interest in deciphering the complexities of RNA folding and dynamics has prompted the development of assorted methods to detect,^25,27,42-46 characterize,^26,47,48 and simulate^48-51 the spatial properties of the base-pair components. The composite data reveal six major categories of G·A association in high-resolution structures (Figures 1, 2). The interactions are stabilized by two or more hydrogen bonds, albeit in some cases through atoms on the sugar-phosphate backbone. In addition to the sheared and imino patterns noted above, the guanine frequently associates through its minor-groove edge with the minor-groove or Watson-Crick edge of adenine in either a parallel or antiparallel orientation. These four combinations, which have no common names, are denoted in the illustrated examples in terms of the interacting base edges and the signs of association (Figures 1, 2), i.e., m±m, m±W, where the first letter refers to the hydrogen-bonded edge of guanine, the second to that of adenine, and the + or − to the parallel or antiparallel direction of the two base normals. The antiparallel, Watson-Crick-like associations of G and A in imino pairs are thus labeled W−W and the sheared interactions between the minor-groove edge of guanine and the major-groove edge of adenine m−M.

Current knowledge of the motions of noncanonical base pairs derives in large part from molecular simulations and/or computationally guided interpretations of solution measurements, e.g., models derived from atomic-level characterization of RNA energy landscapes^48-54 or consistent with observed experimental data.⁵⁵ Formation of a sheared G·A pair is predicted to stiffen an internal loop compared to an imino pair in terms of the simulated degree of bending of short double-helical molecules⁴⁹ and to lower the range of normal-mode deformations of rigid-body parameters.⁴⁸ On the other hand, the spread of rigid-body parameters of sheared base pairs is slightly wider compared to those of imino G·A pairs in some analyses of high-resolution RNA structures⁴⁷ and thus suggestive of greater deformability. The narrower range of parameters for sheared G·A base pairs reported here and in earlier studies from this lab²⁶ mirrors the lesser deformability detected in solution. Deciphering the effects of the two types of noncanonical pairs on the solution properties of RNA internal loops, however, is complicated by the very different sequence contexts in which the interactions have been examined, e.g., tandem imino G·A pairs closed by relatively stiff G·C pairs vs. tandem sheared G·A pairs closed by more deformable G·U pairs.^56,57 The spread of angular variables used to guide simulated transitions between sheared and imino states hints of a potentially wider range of accessible configurations for the imino pair but a deeper free-energy minimum for the sheared pair.⁵⁰

Recent analyses of RNA base interactions in terms of the observed spatial density distribution of a representative point on one base with respect to a point on another base provide an interesting basis for the prediction of RNA secondary structure and a novel way to visualize the deformations of paired bases.⁵¹ The distributions reveal characteristic zones of interaction on the edges and above a given base, disclosing the dominant sites of in-plane pairing and out-of-plane stacking. Treatment of G·A pairing in terms of the relative positions of the centers of the six-membered rings of the two bases, however, does not capture the diverse modes of their association. Guanine pairs through its minor-groove edge with adenine in at least five distinct ways (Figure 1), which are lost in representations of single points. Moreover, as reported below, the modes of base-pair association depend upon higher-order structural context. Predictions of RNA folding may benefit from this information.

Here we take advantage of new capabilities in the analysis of nucleic acid structures from the DSSR software program²⁷ to characterize the geometries, classes, and structural context of the base-pair interactions found in a set of representative, well-resolved RNA crystal structures. We focus on the abundant noncanonical pairings of guanine and adenine and find connections between the modes of association, the local deformations of the pair, and the secondary structural contexts in which the bases occur. The precise numerical descriptions of base-pair geometry that we employ facilitate classification of recurrent geometric motifs and the settings in which these arrangements occur, as well as hint of the natural motions of the interacting bases and the pathways likely to connect different spatial forms. The same approach can be applied to other base pairs, e.g., the diverse arrangements of guanine and uracil detected in recent solution studies,⁵⁸ and the 3D settings in which these interactions occur. We also draw attention to higher-order multiplexes involving two or more G·A pairs and the roles these associations appear to play in bridging different secondary structural units. The collective data illustrate what can potentially be learned about RNA spatial organization from the wide variety of information that can be extracted with DSSR and serve as a starting point for further multi-scale investigations of RNA folding.

MATERIALS AND METHODS

RNA Databases.

The modes of G·A association reported herein are taken from the RNA-containing structures found in the November 9, 2018 release (3.47) of the dataset of non-redundant high-resolution crystal structures curated by Leontis and Zirbel.⁵⁹ The sample includes 3256 G·A pairs in representative integrated function elements (IFEs) from 282 Protein Data Bank entries of 3.0 A or better resolution. The RNA molecules comprise assorted ribosomes, riboswitches, ribozymes, transfer RNAs, messenger RNAs, guide RNAs, RNA aptamers, isolated double- and multi-stranded helices, and protein/DNA/drug-RNA assemblies (see complete listing in Table S1).

Base-pair Identification/Characterization.

The modes of G·A association are based on the rigid-body parameters and hydrogen-bonding patterns derived from DSSR version 1.8.5 with a hydrogen-bond distance cutoff of 3.4 Å.²⁷ The pairs identified in the analysis (see complete listing in Table S2) do not include any of the close associations of G and A detected by the software with proton-donor interactions suggestive of base isomerization or protonation, e.g., the 53 examples of G·A pairs potentially held in place through G(N2)⋯A(N6) amino-imino hydrogen bonding.

The pairing between G and A can be in the form of A·G or G·A associations, depending upon the context or sequential order. At the base-pair level, however, the two forms are geometrically equivalent. Here, all the rigid-body parameters and hydrogen-bonding patterns are expressed in terms of G·A pairs. Thus, the values of parameters characterizing the 1360 occurrences of A·G pairing in the dataset are converted so that the buckle and shear of the A−G pairs are negated to describe an antiparallel interaction with respect to guanine as the leading residue, and all six parameters of A+G pairs are negated to describe a parallel interaction. The 3256 consolidated G·A associations include a total of 6873 hydrogen bonds, with a very small number of pairs (~1%) held in place by four or more donor-acceptor couples. Roughly a third of the hydrogen bonds involve the interaction of a base atom with a donor-acceptor atom on the sugar-phosphate backbone, most frequently with the guanine 2′-hydroxyl (~21%) and the adenine 5′-phosphate (~7%) groups but rarely with the adenine 2′-hydroxyl and the guanine 5′-phosphate. Interactions of the bases with the 3′-phosphate groups of G and A, i.e., the 5’-phosphate groups on succeeding residues, are also rare.

The rigid-body components that contribute to base-pair non-planarity — Stagger, Buckle, and Propeller — are distributed fairly uniformly about null values, with respective averages and standard deviations of 0.15±1.00 Å, −0.3±23.2°, and −0.5±20.2° (Figure S3). The three remaining parameters — Shear, Stretch, and Opening — cluster in several discrete ranges (Figure 3), which are useful in grouping the G·A pairs into distinct categories.^24,27 The qualitative categories of G·A pairing are named on the basis of the locations of the atoms on one base with respect to the coordinate frame of the partner (reference) base. For example, given the design of the standard base frame with the positive x-axis pointing in the direction of the major groove and the positive y-axis away from the Watson-Crick edge³⁰ (Figure S1), base atoms with positive x and y coordinates interact with the reference base through the major groove M, those with negative x and positive y coordinates through the minor groove m, and those with small x and negative y values through the Watson-Crick edge W. In cases where the base position is ambiguous, the atoms of the sugar and 5′-phosphate are added to the categorization, and if the interaction is still unclear, the category is denoted by a dot. Outlying states where the arrangements of G and A differ significantly from the values of Shear, Stretch, Opening characteristic of the initially assigned grouping are reclassified through stepwise comparison with the parameters from other groupings until no parameter deviates from the averages of the new grouping by more than two standard deviations, a process that accounts for all but three of the G·A pairs in the current dataset and assures that each grouping of base pairs falls in a well-behaved region of configuration space. The scalar product between the base normals, i.e., the z-axes of the base reference frames, determines the sign of the interaction (either ‘+’ for parallel or ‘−’ for antiparallel). See the DSSR Manual at http://docs.x3dna.org/dssr-manual.pdf for further details.

Figure 3.

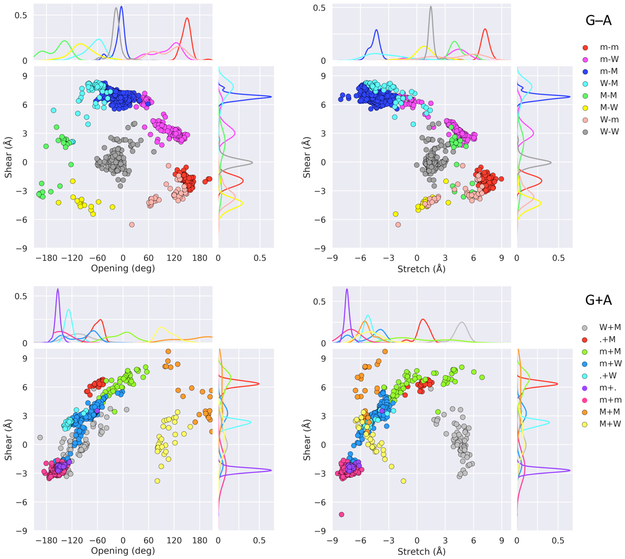
Scatter plots of the rigid-body components — Shear, Stretch, Opening — that distinguish the modes of G·A association in RNA-containing structures. Smooth curves on the edges of the scatter plots are the normalized densities of individual parameters. Points with the magnitude of Opening in excess of 180° include requisite changes in the signs of Shear, Stretch, Buckle, and Propeller. Color-coding of dominant pairs matches that in Figures 1, 2. Secondary states with 16 or more structural examples are noted by related hues. Images depict the spread of values in the Shear-Opening (left) and Shear-Stretch (right) planes for antiparallel G−A (top) and parallel G+A (bottom) arrangements.

Notably, the DSSR software returns the secondary structural context in which each of the bases occurs, including information on whether the bases lie within the same or a different structural unit and an expanded dot-bracket description of canonical pairing that serves as input for the simple secondary structural diagrams⁶⁰ that we report. Here we focus attention on whether the guanine and adenine bases occur within the four common RNA loop types — hairpin loops, internal loops (or bulges), and junctions — or within a canonical double-helical stem, where one of the bases participates in a Watson-Crick or wobble (G−U) pairing with a third base and the G·A pair forms part of a triplet. The loops identified by the software form ‘closed’ circles with sequential nucleotides connected by either a phosphodiester linkage or a canonical base pair. The number of stems determines the classification, with a hairpin loop closed by one stem, an internal loop or bulge by two stems, and a junction (multi-branched) loop by three or more stems. For simplicity, pseudoknots, which are also identified with the software, are not considered. Account is taken, however, of both higher-order multiplets, in which a G·A pair associates with additional bases, and single-stranded nucleotides outside of loops and double-helical stems. This knowledge of secondary and higher-order structure in combination with a quantitative depiction of the local geometry (rigid-body parameters) and hydrogen-bonding patterns of the G·A pairs makes it possible to see how the modes of base interaction and the range of local deformations depend upon structural context.

The range of conformational states associated with a specific pairing mode and/or structural context is described in terms of the volume of conformation space V_bp within one standard deviation of the average rigid-body parameters of the collected examples. Values of V_bp are obtained from the dispersion of parameters, given by the product of the eigenvalues of a matrix with elements $\langle \mathrm{\Delta }{\theta }_{ij}^2\rangle$ that incorporates the covariance of all pairwise combinations of parameters, $\langle \mathrm{\Delta }{\theta }_{ij}^2\rangle =\langle {\theta }_i{\theta }_j\rangle -\langle {\theta }_i\rangle \langle {\theta }_j\rangle$.⁶¹ The θ_i, (i=1–6) correspond respectively to the values of Shear, Stretch, Stagger, Buckle, Propeller, and Opening for each sample entry. The influence of specific variables and/or structural context on deformability is estimated from subsets of the data, e.g., out-of-plane parameters θ_i (i=3–5). Values are based on the full range of examples within a given structural category.

RESULTS

G·A Pairing Motifs and Transitions.

The rigid-body parameters used to describe the spatial arrangements of guanine and adenine in the chosen set of RNA structures reveal potential pathways connecting the many documented examples of G·A base pairing, including the six dominant edge-to-edge motifs^9,62 highlighted in Figures 1 and 2. Although the numerical values of the parameters corresponding to the various pairing schemes tend to cluster tightly in distinct domains, close examination of the data suggests possible links between the different 3D forms (Table 1, Figure 3). For example, a subset of the m−W associations of G and A that bring atoms along the minor-groove edge of guanine in hydrogen-bonding contact with atoms along the Watson-Crick edge of adenine (configurations labeled m−W_II in Table 1) differ only slightly from many of the sheared m−M arrangements of the two bases in terms of the six rigid-body parameters. Other configurations of the m−W pairs (m−W_I states in Table 1) adopt configurations more closely related to the hydrogen-bonded m−m arrangements of G and A, where the two bases interact via their minor-groove edges. The bimodality of the m−W associations stands out in the scatter and distributions of the Shear, Stretch, and Opening values of these pairs (Figure 3). The plotted points and histograms, color-coded to match the shades used in the preceding illustrations of G·A pairing modes and secondary structural occurrences, include two clusters of m−W configurations, one abutting the corresponding features of the sheared m−M states and the other in the vicinity of the m−M values. The images also disclose a subset of sheared G·A pairs in a secondary m−M_II geometric arrangement, with slightly more positive Shear and more negative Opening than the dominant m−M_I state (note the small secondary peaks in the distributions of individual parameters along the sides of the scatter plots).

Table 1.

Rigid-body parameters of G·A pairings in RNA structures^*

G·A pair		# †	Shear (Å)	Stretch (Å)	Stagger (Å)	Buckle (deg)	Propeller (deg)	Opening (deg)	Vbp (Å3deg3)
m−m		141	−1.84±0.86	7.19±0.62	0.01±1.54	−2.0±25.3	−8.9±22.1	150.0±15.3	1116
m−W		153	3.74±1.37	3.44±2.17	0.33±1.28	−8.0±30.2	−16.0±26.6	101.5±31.1	5851
m−WI		125	3.14±0.57	4.39±0.79	0.17±1.31	−3.4±29.9	−16.6±27.5	113.1±20.6	1700
m−WII		28	6.40±0.34	−0.83±0.74	1.04±0.84	−28.2±23.1	−13.2±22.0	49.6±8.8	274
m−M	sheared	1338	6.83±0.38	−4.48±0.58	0.37±0.57	5.8±16.0	−3.0±14.9	−8.5±14.1	153
m−MI		1216	6.75±0.28	−4.39±0.50	0.35±0.54	5.4±15.8	−2.2±14.9	−5.0±8.7	73
m−MII		122	7.63±0.35	−5.33±0.59	0.62±0.77	10.1±17.5	−10.4±12.0	−43.9±6.3	132
W−M		59	7.10±1.52	−2.84±2.36	−0.08±1.13	−1.5±25.4	−4.0±23.7	−69.6±24.5	14440
M−M		25	0.37±2.52	4.49±0.86	0.11±1.66	7.0±25.0	5.5±19.5	−154.1±25.5	1870
M−W		16	−4.24±0.74	0.89±1.23	−02±0.98	6.5±20.7	0.3±15.3	−93.4±28.6	386
W−m		38	−3.39±1.05	4.27±2.43	0.35±1.69	7.0±31.3	−0.2±36.9	106.2±33.7	6687
W−W	imino	344	0.07±0.72	1.55±0.42	−0.33±0.55	6.7±15.2	−9.6±16.8	−16.4±14.0	465
m+M		53	6.42±1.09	0.29±2.79	0.38±1.39	−15.5±24.3	11.4±23.9	−3.3±29.2	15556
.+W		27	2.35±0.48	−4.94±0.73	−0.34±1.47	5.1±34.3	8.2±18.8	−125.2±12.0	206
m+W		388	1.59±2.54	−5.11±1.58	−0.04±0.90	−4.4±22.7	11.8±21.5	−97.6±35.0	1762
m+WI		267	3.23±0.72	−4.12±0.64	−0.12±0.82	0.1±22.1	14.0±24.5	−77.2±19.9	553
m+WII		121	−2.02±0.64	−7.30±0.35	0.15±1.04	−13.8±21.2	6.7±11.5	−142.6±10.0	54
m+.		55	−2.31±0.82	−6.95±0.51	1.21±1.36	−35.7±31.7	1.6±9.9	−146.6±13.1	20
m+m		395	−2.70±0.35	−7.38±0.33	−0.08±1.42	−11.1±29.5	8.7±18.3	−153.8±9.8	111
W+M		69	0.29±1.68	4.47±0.90	0.22±1.05	−7.2±19.7	8.3±25.7	−104.8±39.2	14442
.+M		24	6.25±0.38	0.61±0.67	−0.01±1.10	−8.2±15.5	1.7±21.7	−61.2±11.8	58
M+M		26	0.19±6.06	1.08±5.39	0.17±0.94	−12.2±26.4	5.4±18.0	−30.2±142.0	56463
M+W		29	0.58±1.70	−4.8±1.20	−0.29±0.92	5.5±22.1	4.3±16.4	102.2±20.2	1960

^*Structures taken from the dataset of non-redundant, high-resolution RNA crystal structures curated by Leontis and Zirbel.59 Similar results are found with other datasets, e.g., the RNA09 coordinate files curated by the Richardson group at URL:http://kinemage.biochem.duke.edu/databases/rnadb.php.

^†Counts do not distinguish cis (c) and trans (t) arrangements of C1′–N9⋯N9–C1′angles reported by the software (Table S2) and used by others9,41 to distinguish pairing modes. This ‘chemical’ descriptor does not always match the ± directional criteria used here, e.g., the m−W states include a small number of t arrangements and the m+W states some c arrangements.

Thus one can deduce a continuum of movements, i.e., the in-plane displacements and the relative rotation of A with respect to G, that convert one pairing mode to another. Specifically, the composite data show how decreases in Stretch and Opening in combination with the increase in Shear successively transform the pairing of G and A from an m−m arrangement of antiparallel bases to m−W and m−M forms (Figure 4a and Table 1). The bimodal distribution of m−W configurations also points to a ‘smooth’ pathway linking the arrangements of imino and sheared G−A pairs. The rigid-body parameters of some of the W−W imino associations lie close to those of a few of the m−W pairs and, as noted above, the parameters of certain m−W forms abut those of the sheared base pairs. The interconversion between imino and sheared states seemingly occurs in two stages, first via the coupled increase of Stretch and Opening from the W−W state to a subset of m−W arrangements with unique hydrogen bonding (see below) followed by the correlated changes in Shear, Stretch, and Opening (noted above) that lead to the sheared m−M state. Reductions in the values of Stretch and Opening similarly transform the pairing of G and A in parallel orientations from m+W to m+m arrangements, albeit in combination with a decrease in Shear (Figure 4b). Changes in Shear, Stretch, and Opening of the opposite sense convert the m+W state to a low-populated m+M form (Figure 4b and Table 1).

Figure 4.

Succession of configurations illustrating the rigid-body motions that transform the associations of G and A between different pairing modes. Images of adenine oriented with respect to a common coordinate frame on guanine. Structures generated with 3DNA²⁴ using the average rigid-body parameters reported in Table 1. Base pairs color-coded by interaction mode (Figures 1-3), with the minor (II) substates of m±W and m−M pairs noted by lighter hues. Pathways connecting (a) antiparallel m−m, m−W_I, m−W_II, W−W, m−M_I, m−M_II states; (b) parallel m+m, m+W_II, m+W_I, m+M states. Note the counterclockwise rotation of ribose C1′ atoms (darkened spheres) along the top-to-bottom transformation of antiparallel pairs and the clockwise rotation along the corresponding progression of parallel pairs. Hydrogen bonds between base atoms depicted by thin dashed lines.

Hydrogen-bond Rearrangements.

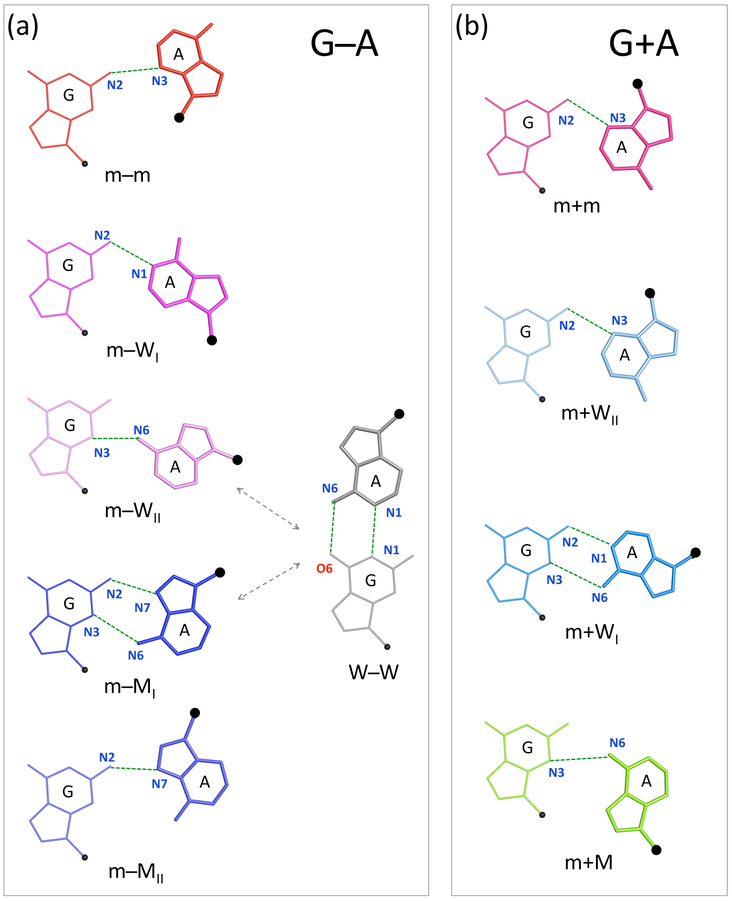
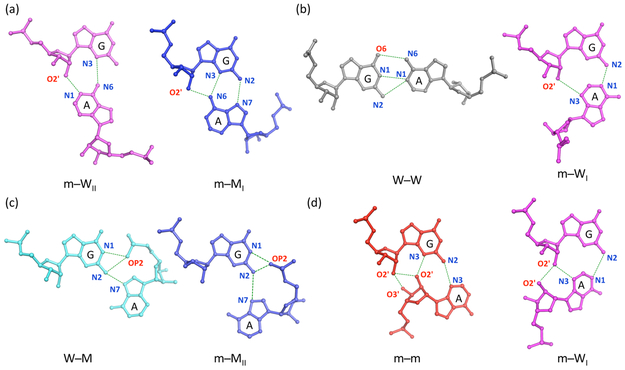
The relative movements of G and A naturally change the hydrogen-bonding patterns that stabilize the various associations of the two bases. The interactions found in one pairing motif, i.e., the polar atoms that share a hydrogen atom, however, may persist in a closely related form. For example, the N3 atom of guanine accepts a hydrogen atom from the exocyclic N6 amino group of adenine in both m−W_II and m−M_I base-paired arrangements, although with differently oriented hydrogens from the N6 amino group and with the change in base orientation attended by different hydrogen bonds (Figure 5a). The W−W and m−W_I states similarly include a common G(N2)⋯A(N1) hydrogen bond that occurs in concert with G(N1)⋯A(N1) and G(O6)⋯A(N6) interactions in the former arrangement and a G(O2′)⋯A(N3) interaction in the latter (Figure 5b). By contrast, the hydrogen bonding schemes in W−M pairs are identical to those of the small subset of sheared m−M_II pairs. The N2 amino group of guanine associates exclusively with the adenine 5′-phosphate and N7 atom in the two forms, but in slightly different rotational settings of the sugar-phosphate backbone (Figure 5c). The 59 examples of W−M pairing occur in 29 different RNA structures, including some riboswitches and ribozymes, the ribonuclease P specificity domain, and assorted ribosomal fragments and intact ribosomes (see Tables S1 and S2 for details).

Figure 5.

Molecular images illustrating hydrogen bonds (dashed lines) shared between different forms of G·A pairing: (a) the N3⋯N6 interaction common to m−W_II and m−M_I base-paired arrangements found respectively in a variant of the SAM-I riboswitch⁶⁴ and the complex of Escherichia coli ribosomal protein L25 with a 5S rRNA fragment;⁶⁵ (b) the respective N2⋯N1 associations in m−W_I and W−W pairs in the Leishmania donovani large ribosomal subunit⁶⁶ and the Saccharomyces cerevisiae 80S ribosome;⁶⁷ (c) the N2⋯N7, N1⋯OP2, and N2⋯OP2 hydrogen bonds respectively stabilizing W−M and m−M_II pairs in the central domain of the Thermus thermophilus 30S ribosomal subunit⁶⁸ and in the complex of the Thermus thermophilus 70S ribosome with hibernation factor pY;³⁶ (d) the respective paired association of 2′-hydroxyl groups, one from G and the other from A, adopted in m−m and m−W_I pairs within the complex of tetracycline with the U1052G-mutated 70S Escherichia coli ribosome.⁶⁹

Hydrogen bonding contributions from the ribose similarly persist in closely related modes of G·A pairing. For example, the paired association of 2′-hydroxyl groups, one from G and the other from A, sometimes components of a ribose zipper,⁶³ occurs in both m−m and m−W_I pairs (Figure 5d). Indeed, the guanine 2′-hydroxyl appears to serve as a pivot point for the rearrangement of G·A pairs, forming hydrogen bonds with different atoms on adenine as G and A convert from m−m to m−M_I arrangements. The m−m states are anchored by interactions of guanine O2′ with adenine O3′ and O2′, the m−W states by interactions with adenine O2′, N3, and N1, and the m−M_I states by interactions with adenine N6 (Figure S4). These and other patterns of hydrogen-bond association — e.g., the persistence of G(O6)⋯A(N6) associations in W−W, m−W, m−M, and various intermediate forms — are at once evident from comparison of scatter plots of the rigid-body parameters color-coded by G·A pairing mode (Figure 3) and by specific hydrogen-bond components (Figure S5).

Like their antiparallel m−W counterparts, the parallel m+W arrangements of guanine and adenine fall into two distinct classes with different hydrogen-bonding motifs (Figures 3, 4). The majority of m+W_I examples — held in place by G(O2′)⋯A(N6), G(N2)⋯A(N1) and G(N3)⋯A(N6) hydrogen bonds — adopt more positive values of Shear, Stretch, and Opening than their minor m+W_II counterparts (Table 1). The m+W_II population, stabilized by G(N2)⋯A(N3) and G(O2′)⋯A(N1) associations, differs only slightly from the m+m arrangements of the two bases. Some of the hydrogen bonds persist in lesser-populated parallel forms, revealing a potential route between the 20 W+W, 69 W+M, 26 M+M, 29 M+W, and 53 m+M collected pairings of guanine and adenine via the minor m+W_II state (see Table 1 and Figure S4).

Secondary Structural Context and Long-range Interactions.

The capability to detect the secondary structural context of the G·A pairs provides insights into how the modes of base association influence the higher-order spatial organization of RNA. For example, in nearly half the observed cases (627/1338) the sheared m−M pairs occur within internal loops (Table 2). Moreover, all but five of the bases in these examples lie within the same loop (Figure S6). The sheared G·A pairs occur in lesser numbers in hairpin and junction loops, with 351 and 261 examples, respectively, in the current dataset. The vast majority of the base associations in the latter loops also occur in the same secondary structural element (Figure S6) although there are eight examples, all in the structures of riboswitches, where a sheared G·A pair entails bases in different hairpin loops, e.g., G19 in loop L2 and A90 in loop L6 of the flavin mononucleotide riboswitch (Figure S7).⁷⁰ Interestingly, the subset of G·A pairs with more positive Shear and more negative Opening values, the minor m−M_II states noted above, occur exclusively in hairpin loops, all of length four and all involving a G(N1)⋯A(OP2) hydrogen bond unique to these arrangements (e.g., Figures 2a and S5). These base pairs constitute about a third of the GNRA tetraloops within the dataset and as noted above are further stabilized by hydrogen bonding of G(N2) with A(N7) and A(OP2).

Table 2.

Secondary structural composition of the six dominant forms of G·A pairing^*†

1292∣1338‡ m−M	blg_A	hpn_A	int_A	jct_A	stm_A	323∣344‡ W−W	blg_A	hpn_A	int_A	jct_A	stm_A
blg_G	123≠		3	1		blg_G	2				1
hpn_G	5	3516≠		8		hpn_G		202≠		3
int_G		2	6275≠	1		int_G			169
jct_G				261		jct_G	1	1		118	2
stm_G	12	3	4	2		stm_G	1	1		1	31≠
496∣395‡ m+m	blg_A	hpn_A	int_A	jct_A	stm_A	197∣141‡ m−m	blg_A	hpn_A	int_A	jct_A	stm_A
blg_G	2	2	3	12		blg_G		5	4	5
hpn_G		1614≠	1	12		hpn_G	3	95≠			2
int_G		16	4417≠	8		int_G	2	15	10	9	1
jct_G		17	7	6819≠	1	jct_G		11		225≠
stm_G	15	77	97	98		stm_G	5	31	28	35
500∣388‡ m+W	blg_A	hpn_A	int_A	jct_A	stm_A	187∣153‡ m−W	blg_A	hpn_A	int_A	jct_A	stm_A
blg_G	6	3	12	8		blg_G	52≠	6	1	1
hpn_G	1	8158≠	4	17		hpn_G		137≠	1	7
int_G	3	9	5513≠	26		int_G	1	7	176≠
jct_G	1	13	7	711≠		jct_G		7	2	30	1
stm_G	10	78	36	59		stm_G	12	35	18	23

^*Number of observations of the guanine and adenine in identified pairs in five common secondary structural forms: blg – bulge loop; hpn – hairpin loop; int – internal loop; jct – junction loop; stm – canonical double-helical stem. The subscript following each acronym refers to the base in the designated secondary structure, e.g., stm_G refers to a guanine in a canonical double-helical stem. The dataset includes a total of 149 G−A and 112 G+A pairs outside the 25 listed categories, i.e., 90% of the 1108 G+A and 93% of the G−A pairs occur within the listed structural categories.

^†The numerical entries in the set of grids correspond to the number of examples with a given combination of secondary structural states, e.g., 351 examples of sheared m−M pairs with both bases (hpn_{_G}·hpn_{_A}) found in a hairpin loop. The subscripted value for this and other diagonal entries denotes the number of examples where the paired bases occur in different (≠) hairpins, here the “_6≠” referring to six cases of m−M pairs with G in one hairpin and A in another. Blanks and missing subscripts refer to null values.

^‡Number of G·A pairs of the specified type in the survey of high-resolution structures followed by the total number of pairs of the same type in one of the 25 categories. See text for discussion of numerical differences.

As evident from Table 2, none of the adenines and only a small number of guanines in the set of sheared G·A pairs fall within a double-helical stem and thereby also participate in a canonical Watson-Crick or wobble base pair. The simultaneous involvement of guanine in both a canonical and a sheared base pair leads to the formation of a triplet, e.g., a C−G−A hydrogen-bonded association with the G contacting the A via the sheared G−A arrangement and the C through a G−C Watson-Crick pair. Surprisingly, despite the few examples of either G or A in a double-helical stem, nearly a quarter of the m−M arrangements of the two bases (296/1338) occur in multiplets. Moreover, over half of these multiplets (160/296) involve a different type of G·A pairing, including 78 m+m, 32 m+W, and 21 m−m associations. These multiplets bring different pieces of RNA secondary structure in contact with one another and also contribute to the spatial organization of RNA junctions (Figures 6 and S8). The connections more frequently involve an adenine shared by two guanines, one from the m−M interaction and the other from a different mode of G·A pairing, rather than a guanine shared by two adenines (145 examples of noncanonical G−A−G or G−A+G multiplets vs. 15 examples of A−G−A or A+G−A interactions).

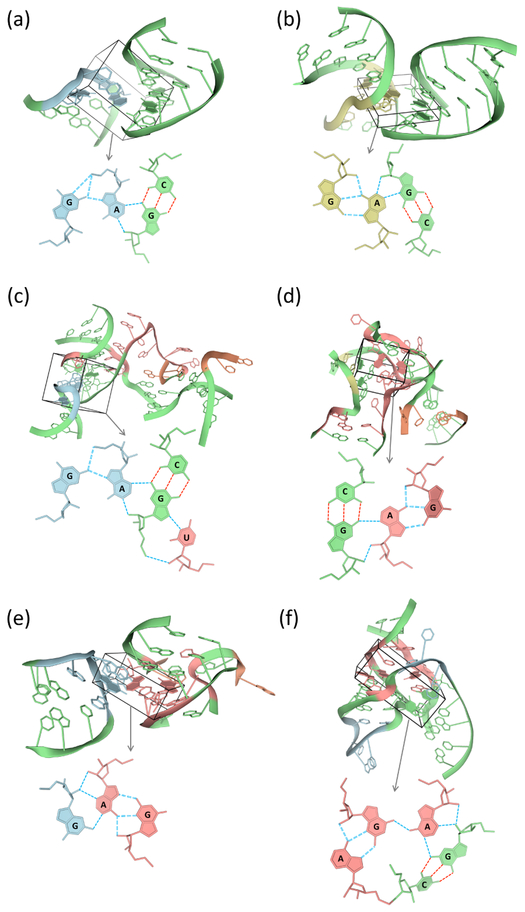
Figure 6.

Molecular images of multiplets with two or more modes of G·A pairing in the complex of tetracycline with the U1052G-mutated 70S Escherichia coli ribosome.⁶⁹ Loops incorporating m−M sheared pairs are linked by different associations of G and A (highlighted within boxes) to other secondary structural units. A local representation of the linked bases is shown below each global depiction of associated secondary structures. Examples include: (a) a tetraplex with m+m pairing between a hairpin loop and a double-helical stem; (b) a tetraplex with m+m pairing between an internal loop and a double-helical stem; (c) a pentaplex with m+W pairing between a hairpin loop and a double-helical stem that is linked in turn to a junction; (d) a tetraplex with m−m link pairing between an internal loop and a 5-way junction; (e) a triplex with m−W pairing between a hairpin loop and a 3-way junction; (f) a pentaplex with .–M and m−W pairing within a 7-way junction. G·A pairs and secondary structural motifs color-coded as in Figure 2. See Table S3 for respective Protein Data Bank identifiers, chain names, and residue numbers of depicted G·A-linked multiplets. Color-coding of bases and hydrogen bonds matches that in the corresponding secondary structural diagrams in Figure S8.

Despite the different mode of interaction, the imino W−W associations of guanine and adenine resemble the sheared G·A pairs in several respects. All but one of the imino interactions occur within the same secondary structural unit, and nearly a fifth (62/344) occur within a multiplet. Like the multiplets containing sheared G·A pairs, a large proportion of the multiplets containing imino pairs (40/62) entail a different mode of G·A pairing (including 12 m+W, 2 m−m, 6 m+m associations) and only a few incorporate a base in a canonical pair (five with G, two with A). The imino pairs also occur in roughly half the cases (169/344) within internal loops (e.g., Figure 2b) but rarely in hairpin loops (Table 2 and Figure S6a). The proportion of W−W pairs involving unstructured regions, such as the single-stranded fragments found at the ends of RNA chains, exceeds that of sheared m−m G·A base pairs by nearly a factor of two (30/344 vs. 66/1338). The W−W pairs frequently ‘extend’ a canonical double-helical stem, such as the G88·A10 association that abuts helix P2 in the tetrahydrofolate riboswitch⁷¹ and respectively links the single-stranded 3′- and 5′-tails of the molecule.

In contrast to the sheared and imino arrangements of G·A pairs, there are relatively few cases where m±m associations of the base minor-groove edges occur within the same secondary structural element (Table 2). Moreover, most of these interactions form within multiplets (372/395 m+m, 136/141 m−m) and a large proportion of the collected pairs include a guanine canonically hydrogen-bonded to C or U (312/395 m+m, 102/141 m−m; see Figures 2c,d). The adenine, almost always free of canonical A·U pairing (394/395 m+m, 138/141 m−m), typically lies outside of a double-helical stem and in over a third of the examples within a junction loop regardless of base orientation (164/395 m+m, 52/141 m−m). The sign of base association influences the relative numbers of adenines in hairpin vs. internal loops (107:143 m+m vs. 54:57 m−m) and the likelihood, albeit small, that minor-groove edge associations of G and A occur within the same secondary structural unit (27 of 44 m+m vs. 0 of 10 m−m internal loops). The m±m G·A pairs thus tend to ‘glue’ the guanine in a double-helical stem to different looped segments of an RNA structure (see examples in Figure 6).

Given that the loops include the base pairs found at the ends of double-helical stems and in isolated Watson-Crick pairs (see Materials and Methods), the counts of secondary structural motifs exceed the number of pairs of a given type, e.g., the 395 examples of m+m pairing occur in 496 secondary structural settings. Notable in this regard are (i) arrangements of G and A counted among both the m+m G·A pairs in internal loops and the m+m examples with G in a stem and A in an internal loop and (ii) arrangements counted among both the m+m G·A pairs in junctions and the m+m examples with G in a stem and A in a junction. The double counting of guanines within looped secondary structural units similarly accounts for differences between the number of observed m−m G·A pairs and the number of secondary structural settings in which they occur (141 m−m pairs vs. 197 settings).

The m±W associations of G and A resemble the m±m pairs in that they too occur in multiplets and serve as links between different RNA secondary structural units (Table 2). Although comparable in number to their m±m counterparts, the m±W pairs within multiplets (309/388 m+W and 118/153 m−W) occur with slightly lower frequency, i.e., roughly 80% of the m±W pairs vs. over 90% of the m±m pairs. These differences arise in part from the greater likelihood of the G in the m±W pairs to occur within a hairpin loop as opposed to a double-helical stem (e.g., Figures 2e,f). As a consequence, the m±W pairs are more apt to mediate interactions between different loops (Figure 6).

Deformability/Context.

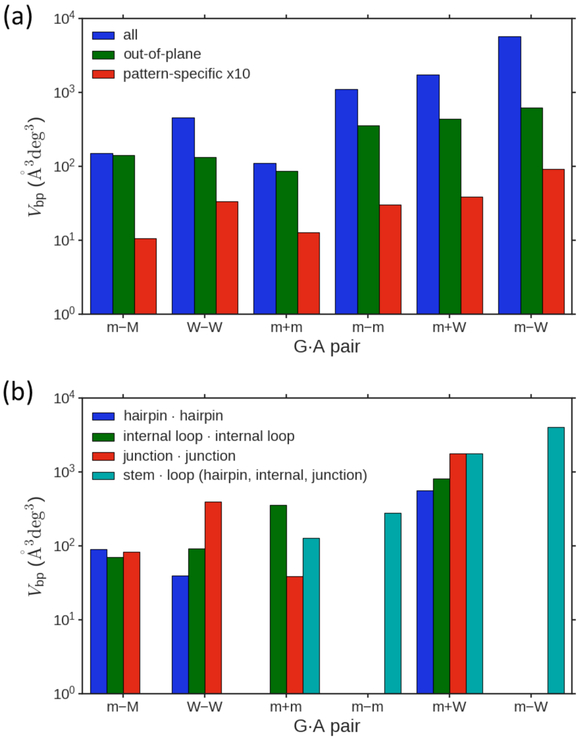
The distributions of rigid-body parameters describing the various modes of G·A association provide insight into the relative flexibility of the different arrangements. The volumes of rigid-body space V_bp, obtained by diagonalizing the matrix of parameter covariances (see Materials and Methods),⁶¹ offer a measure of the deformability seen in superimposed images of the bases comprised in the different pairing schemes (Figure S9). When combined with the average base-pair parameters, the set of volumes complete the ‘fingerprint’ of each G·A pair, making it possible to identify potentially tighter and looser pairing modes. At once apparent from the volumes of the major pairing arrangements (Figure 7) is the marked stiffness of the m+m associations compared to all other G·A pairs. The small conformational volume reflects the much narrower ranges of the pattern-specific variables — Shear, Stretch, Opening, i.e., θ₁,θ₂,θ₆ — in the documented examples. That is, the very small conformational volume of m+m states determined from Shear, Stretch, Opening has a greater influence on overall base-pair deformability than the out-of-plane parameters — Stagger, Buckle, and Propeller, i.e., θ₃,θ₄,θ₅ (Figure 7a). If the analysis were confined to the out-of-plane parameters, the imino W−W arrangements of G and A would appear to be stiffer than most pairing modes. If all six rigid-body parameters are considered, the imino pairs are more flexible than both the m+m and sheared m−M pairs (also see Figure S9). The m−m and m±W associations of G and A are even more deformable in terms of occupied conformational space. The larger conformational volumes of the m±W arrangements over the m−m forms reflect the wider ranges of Stagger, Buckle, and Propeller in the former pairs (Figure 7a).

Figure 7.

Histograms of G·A deformability expressed in terms of the volume of conformation space occupied by the two bases in the major pairing schemes: (a) comparative contributions of pattern-specific (Shear, Stretch, Opening – red bars), out-of-plane (Stagger, Buckle, Propeller – green bars), and all six rigid-body parameters (blue bars – values listed in Table 1) to base-pair mobility; (b) relative deformability of G·A pairs in different tertiary structural settings, each with 44 or more structural examples. Base pairs grouped in terms of the observed setting of G followed by that of A. Note the logarithmic scale of volume and the tenfold (×10) enhancement of pattern-specific values.

The deformability of the various G·A pairing schemes further depends upon structural context. For example, the sheared m−M pairs span a 1.3-fold wider range of rigid-body conformation space when located in hairpin loops as opposed to internal loops but a comparable proportion of the space adopted within junctions (Figure 7b). The imino W−W pairs show an even more pronounced (4.3-10.1-fold) enhancement in deformability when formed within junctions as opposed to internal loops and hairpins. The many m+m pairs that link a G within a double-helical stem to an A in a loop also span a wider range of conformation space than the smaller number of examples of the same pairing mode within a junction but a narrower range of space than the even fewer examples of the pair within an internal loop. The bridging m+m pairs, however, are more than an order of magnitude (over 14-fold) stiffer than their m+W counterparts in terms of rigid-body parameters. The bridging m+W linkers occupy larger conformational volumes than G·A pairs of the same type within hairpin and internal loops but roughly the same volume as those in junctions. The limited number of examples of m−m and m−W pairs in secondary structural settings other than stem-loop connectors rules out comparisons of deformability of such arrangements in different secondary structural contexts.

DISCUSSION

Conventional understanding of RNA folding derives in large part from the qualitative descriptions of macromolecular organization collected over time through the determination of individual, high-resolution structures, e.g., the noncanonical base pairs and the organized hairpin folds first observed in the yeast tRNA^Phe crystal,¹ the A-minor motifs that accompany the associations of secondary structural units in large ribosomes and ribozymes,^13,72 the novel base triples found in the Tetrahymena telomerase RNA pseudoknot,⁷³ etc. Despite the vast accumulated knowledge, understanding how the molecular components fit together remains an open question. While computations now capture the 3D folds of assorted small RNA molecules from combinations of local structural, chemical, and genetic information,^74,75 viable predictions of large ribozyme and ribosomal structures are still beyond reach. Success in this regard requires a higher-level perspective, incorporating information beyond the spatial arrangements and composition of isolated base pairs and secondary structural units and the sites of chemical modification or mutation. This article illustrates how one can begin to attack the problem by taking advantage of the multi-scale structural information collected with DSSR, including the identities, spatial arrangements, and secondary structure context of associated bases, as well as the nucleotide configurations and global arrangements of secondary structural units.²⁷

Here we focus on a subset of noncanonical base pairs involving guanine and adenine and the links between their modes of association, secondary structural context, and contributions to tertiary folding. The precise numerical descriptions of base-pair geometry that we employ not only facilitate classification of recurrent geometric motifs and the settings in which these arrangements occur but also hint of the natural motions of the interacting bases and the pathways likely to connect different spatial forms. The scatter of rigid-body parameters relating coordinate frame on the two bases point to ways by which the sheared and imino G·A pairs typically found within RNA hairpins, junctions, and internal loops might convert into spatially related forms that bridge different pieces of RNA secondary structure. The data also hint of a two-step mechanism linking sheared and imino G·A pairs, a result of potential utility in guiding computer-simulations of transitions between the two forms.⁵⁰ The reorientation of adenine with respect to guanine during these processes has a clear effect on RNA secondary structure. For example, the bulges incorporating sheared G·A pairs in the dataset of representative structures differ in length and assume quite different folds from those found in bulges with closely related (m−W_II) pairing. The former bulges tend to be shorter with simple base flip-outs compared to the latter, which adopt more circuitous pathways (Figure S10).

The current study also draws attention to higher-order multiplexes of two or more G·A pairs bridging different secondary structural units. Although included in earlier collections of higher-order base pairings,⁷⁶ most structural work has focused on the three-base, i.e., triplet, interactions formed by an adenine within a loop and a guanine hydrogen-bonded to C or U in a double-helical fragment. The states termed m+m here correspond to the type 1 A-minor motif first identified by Nissen et al. in the Haloarcula marismortui large ribosomal subunit¹³ and the m−W states to the type II triples found by Doherty et al. to contribute to helix packing in the Tetrahymena thermophila group I ribozyme.⁷² The present survey uncovers even more extensive base associations involving different modes and numbers of G·A pairs, e.g., tetraplexes and pentaplexes linking hairpins and internal loops to double-helical stems and junctions. The collective data further reveal pairing propensities in base organization and secondary structural context. For example, the vast majority of sheared and imino G·A base pairs (m−M and W−W) occur within a looped region, and almost always in the same loop. The guanine and adenine pairs that bridge different secondary structural units preferentially adopt parallel over antiparallel forms (m+m, m+W vs. m−m, m−W). Not surprisingly, the bridging G·A pairs tend to be more deformable than their sheared and imino counterparts within loops in terms of the observed distributions of spatial states.

The rigid-body parameters used to characterize the G·A pairs differ in some studies from those reported here owing to a different choice of base reference frame. Rather than expressing the geometric arrangement of two bases in terms of the standard reference frame,³⁰ other groups prefer to describe the interactions in terms of base-edge specific reference frames. That is, the location and orientation of the base frames depend upon the type of association.⁴⁷ The latter approach masks the pattern-specific parameters used here to distinguish modes of pairing and instead draws attention to the differences in base-pair non-planarity that accompany the various modes of interaction. This different point of view may underlie the greater deformability of sheared compared to imino G·A pairs deduced from studies based on this vantage point.⁴⁷ The treatment of deformability based solely on the out-of-plane rigid-body parameters collected in this survey would lead to a similar conclusion, given that the conformational volume occupied by Stagger, Buckle, and Propeller is slightly (1.05 ×) greater for sheared m−M compared to imino W−W pairs in the current dataset (Figure 7a). As demonstrated here, the complete set of pattern-specific parameters obtained with the standard reference frame is needed to understand and characterize the relative deformations and transitions between different modes of G·A pairing.

Qualitative descriptions of non-canonical RNA base pairing, pioneered by Leontis and Westhof^9,41 and linked in this work to the rigid-body parameters of interacting bases, have proven valuable in deciphering the connections between RNA primary, secondary, and tertiary structures. The present categorization is based on the positions of the hydrogen-bonded atoms with respect to a standard, embedded base reference frame³⁰ defined in terms of an idealized Watson-Crick base pair. The major- and minor-groove base edges used here correspond in most cases to what are termed the Hoogsteen and sugar edges in the Leontis-Westhof scheme (one can compare the two classification schemes in Table S2). The + and − symbols introduced in 3DNA²⁴ and DSSR²⁷ unambiguously distinguish the relative orientations of the two bases. The trans and cis designations used in the earlier literature, however, are qualitative in nature and often uncertain. There are many ‘nc’ (near cis, as in ncWW) and ‘nt’ (near trans, as in ntSH) annotations listed in the RNA Structure Atlas; see, for example, the base pair interactions in the sarcin-ricin domain of E. coli 23S rRNA found by entering PDB entry 1msy at URL:http://rna.bgsu.edu/rna3dhub/pdb. The assignment of qualitative descriptors of RNA associations on the basis of atomic identity alone is generally not clear-cut. Numerical differences in the rigid-body parameters are critical to differentiating pairing schemes that share a common hydrogen bond, e.g., the G(N3)⋯A(N6) interaction found in m−W_II and m−M_I arrangements of G and A (Table 1, Figures 4 and S3). The numerical data also provide a basis for following conformational transitions and may potentially be of value in making functional and other meaningful distinctions among RNA base pairs.

Finally, our findings illustrate what can potentially be learned about RNA spatial organization by taking advantage of the variety of information that can now be collected with software, i.e., DSSR, designed to streamline the analysis and annotation of RNA 3D structures.²⁷ The results serve as a starting point for further multi-scale investigations of RNA folding. In addition to examining the linkages between noncanonical base pairing and secondary structures reported here, one can immediately address classic biochemical questions with the accumulated data, such as the locations of noncanonical pairs relative to the ends of double-helical stems in RNA molecules²¹ or the sites of noncanonical pairing within and between different types of loops.^12,77 It is also possible to explore connections between the modes of base pairing and a number of 3D structural motifs linked to RNA tertiary interactions and automatically identified by the DSSR software, e.g., kissing-loop, A-minor, ribose-zipper, kink-turn, U-turn, pseudoknot, G-quadruplex, i motif. Finally, one can investigate the noncanonical pairs in the context of the global axes of the double-helical stems and/or coaxially stacked helices comprised within a structure and introduce these components in simplified depictions of overall chain folding.⁷⁸