Modular Premotor Drives and Unit Bursts as Primitives for Frog Motor Behaviors

Abstract

Spinal cord modularity impacts on our understanding of reflexes, development, descending systems in normal motor control, and recovery from injury. We used independent component analysis and best-basis or matching pursuit wavepacket analysis to extract the composition and temporal structure of bursts in hindlimb muscles of frogs. These techniques make minimal a priori assumptions about drive and motor pattern structure. We compared premotor drive and burst structures in spinal frogs with less reduced frogs with a fuller repertoire of locomotory, kicking, and scratching behaviors. Six multimuscle drives explain most of the variance of motor patterns (∼80%). Each extracted drive was activated with pulses at a single time scale or common duration (∼275 msec) burst structure. The data show that complex behaviors in brainstem frogs arise as a result of focusing drives to smaller core groups of muscles. Brainstem drives were subsets of the muscle groups from spinal frogs. The 275 msec burst duration was preserved across all behaviors and was most precise in brainstem frogs. These data support a modular decomposition of frog behaviors into a small collection of unit burst generators and associated muscle drives in spinal cord. Our data also show that the modular organization of drives seen in isolated spinal cord is fine-tuned by descending controls to enable a fuller movement repertoire. The unit burst generators and their associated muscle synergies extracted here link the biomechanical “primitives,” described earlier in the frog, rat, and cat, and to the elements of pattern generation examined in fictive preparations.

Introduction

The idea of a small set of burst generators and unitary premotor drives organized in spinal circuits may be important to link several areas of research. For example, these impact our understanding of reflex organization, locomotion, response to spinal cord injury and stroke, motor development, and motor learning.

Several kinds of modular multijoint and multisegmental spinal motor control systems have been proposed. These range from central pattern generators (CPGs; comprising half-centers, unit burst generators, and shared cores) (Grillner and Wallen, 1985; Stein et al., 1995, 1998a,b; Earhart and Stein, 2002; Stein and Daniels-McQueen, 2002) through individual joint controls, muscle group or synergy controls (Berkinblitt et al., 1986; Gottlieb, 1998; Kearney and Galiana, 2000), unitary premotor drives, and task groups (Loeb, 1985) to primitives generating specific limb force and dynamics (Bizzi et al., 1991; Giszter et al., 1993; Mussa-Ivaldi et al., 1994). Here, we examine the basis of spinal modularity in frogs by examining the groupings and burst patterns of premotor drives by using tools from signal and information theory to analyze electromyographic (EMG) data. We test the hypothesis that a small set of premotor drives activated as fixed duration bursts or pulses could compose the major basis for the frog's motor repertoire. This hypothesis is consistent with a combined CPG and motor primitive perspective.

It is currently not established whether the motor repertoire of both a spinal and a more complex frog preparation (medullopontine) could both be expressed as the combinations of the same small collection of independent premotor drives and bursts.

Several methods can provide minimalist descriptions of EMG, such as factor analysis and principal component analysis (PCA) (Flanders and Hermann, 1992; Davis and Vaughan, 1993; Olree and Vaughan, 1995; Poppele et al., 2002a,b; Ivanenko et al., 2003). To extract lower-dimensional elements from EMG recordings in a manner free from all but the structural hypothesis of motor drives distributed simultaneously to several motor pools, we used independent component analysis (ICA). This technique accomplishes blind separation of sources by relying on information separation techniques rather than simple signal variance (Bell and Sejnowski, 1995; Brown et al., 2001). This makes the method immune to changes in muscle pickup and to changes in relative contributions of premotor drives across behavioral conditions. Preliminary tests suggested this was an effective way to examine premotor drive (Giszter, 2001). Here, we also wanted to discover whether there was a dominant time scale (i.e., a characteristic burst type and duration) for premotor drives. To analyze the time structure of extracted drives, we applied a set of cosine packet temporal decompositions (matching pursuit and bestbasis cosine packet decompositions) (Coifman and Wickerhauser, 1992; Mallat and Zhang, 1993). Our results support a common set of premotor drives across animals and across behaviors that are mostly similar between spinal and medullary conditions and display a characteristic burst duration or time scale. The elements found match those seen in prior experiments (Kargo and Giszter, 2000a). These bursts or pulsed muscle drives are likely to account for the organization of biomechanical “force-field primitives” described in previous work.

Materials and Methods

Surgical methods

Twenty-four bullfrogs (Rana catesbaiana) were used. Frogs were anesthetized with 50 mg/kg of 5% 3-aminobenzoic acid ethyl esther (tricaine MS222) in ringer injected into the dorsal lymph sacs and placed on ice to facilitate anesthesia. Maintenance dosages were 25 mg/kg. The medulla base was exposed by cervical midline incision posterior to the frogs' tympanic membranes. Frogs were either spinalized at the base of the medulla or decerebrated at the caudal pons (removing the deep cerebellar nuclei from the preparation). In decerebration (“brainstem frogs”), bone was removed overlying the medulla, pons, and cerebellum. Brainstem frogs were transected at the border between the medulla and the pons by aspiration. The tectum and forebrain were ablated in all frogs by heat cautery. The lesion cavity was packed with gel foam. The reflected skin was closed with wound clips and sealed with Vet-Bond cyanoacrylate adhesive. To prepare spinalized frogs from brainstem frogs, an additional transection was made below the base of the medulla by aspiration after reopening the incisions. The data presented derive from eight brainstem frogs and eight spinal frogs (with four of the spinal frogs being preparations reduced from brainstem to spinalized status).

Intramuscular electrodes were implanted under light anesthesia on ice the next day. Pairs of electrodes (seven-strand Teflon-coated stainless steel wire, with recording surfaces 1 mm below a wax anchor ball) (Loeb and Gans, 1986) were implanted in the rectus anterior, rectus internus, adductor magnus, semimembranosous, gluteus, vastus internus, vastus externus, and semitendinosous. Patch electrodes, consisting of two Teflon-coated wires with exposed areas perforating a Silicone/Dacron patch (for review, see Kargo and Giszter, 2000), were inserted under the fragile sheet-like biceps and Sartorius muscles.

Spinal frogs and brainstem frogs had markedly different behaviors. Brainstem frogs showed a much larger repertoire of behaviors than spinal frogs. We attempted to elicit the whole motor repertoire possible in both preparations. Brainstem behaviors included kicks, jumps, some spontaneous locomotion, and complex escape sequences in response to pinch or grasp, and corrections, besides less stereotypic wipes than those seen in spinal animals. We recorded all movement types in the data collected here.

EMG collection and kinematic monitoring

EMGs were high-pass filtered using amplifiers (A-M Systems, Everett, WA), with a low-frequency cutoff at 100 Hz, amplified with gain of 10,000 and digitized at 2 kHz using a 16-channel Digidata (Axon Instruments, Foster City, CA). Data were displayed using Axoscope digital oscilloscope software (Axon Instruments), and gains were adjusted to avoid saturation.

Brainstem frogs had spontaneous movement. In spinal frogs, a pinch stimulus was delivered to the frog's left rear ankle to evoke reflexive responses. All frogs' movements were videotaped from a point ∼1 m directly overhead with the camera orthogonal to the horizontal plane, using a 1 msec/field shutter operating at 60 fields per second. Out-of-plane excursions in the frog are typically not large (Giszter et al., 1989; Schotland and Rymer, 1993; Sergio and Ostry, 1993). We confirmed that each frog's motions were kinematically similar to our previous work and that there were no individual motor aberrations in this study. Animals in which there were asymmetries or unusual motion patterns after surgery were removed from the study.

EMG analysis

Analysis of temporal and muscular composition of muscle synergies. We examined EMGs for high-frequency correlations to rule out cross talk. To find a small set of synchronous premotor drives that were common to all behaviors, we used ICA. This constrains the premotor drives extracted to a few synchronous muscle activations. This naturally links these drives both to the idea of force-field primitives and to premotor burst generators. Synchronous EMG drives are necessary to organize a collection of joint torques and end-point forces with the properties previously identified in force-field primitives (see Appendix 1, available at www.jneurosci.org).

Identification of muscle synergies using ICA. The use of ICA can be understood as follows. Imagine one is at a cocktail party with many attendees participating in several simultaneous conversations. Clearly, it is possible for a person to focus on one of these conversations or speakers and exclude cross talk from other conversations. However, creating computational algorithms to do the same task has been difficult. One possible solution to this problem is ICA (Bell and Sejnowski, 1995). This extracts statistically independent basis vectors from multichannel time series input, blindly separating sources. For the “cocktail party problem” above, we would plant microphones throughout the hall and collect each audio signal as a time series. By identifying the statistically independent waveforms underlying the collection of recorded signals, it should be possible to identify individual speakers and thus to examine separate conversations using these waveforms (assuming the conversations themselves are statistically independent). In our experiments, we consider the EMG electrodes as recording microphones, and premotor drives then represent the individual speakers. The net EMG motor patterns during behavior would then correspond to the recorded hubbub of the party (a sum of the independent conversations or summed premotor drives determining motor pool activity).

We speculate that a smaller number of drives than individual muscle EMGs account for most behavior. However, ICA always delivers as many components as inputs. To test our hypothesis of modularity, we predicted that only a few ICA components would be able to account for 80–90% of total EMG variance. Several noise sources (and not premotor drives) could also contribute to the EMG signals of individual muscles and form other components. Alternatively, if EMGs represented the best components, then the analysis would derive the identity matrix as the weights. Finally, if more components were present, each distributing activity to several muscles, then ICA would find the 10 best such components, perhaps of approximately similar variance contributions.

In practice, we found that high-frequency motor noise and motor unit desynchronization can cause each raw EMG to act mostly independently in terms of its local time series behavior. The ICA algorithm then identified each raw EMG channel as an independent component. This further confirmed that records were free of cross talk among EMG channels.

After EMG signals from the experiment were rectified and filtered, smoothing the independent high-frequency behavior of single motor units, we were able to identify a small set of synchronous drives, accounting for substantial variance. However, excessive smoothing of data prevented effective separation. For our analysis, we filtered the 2 kHz data off-line using a 40-point tapered boxcar moving average root mean square (RMS) filter. Filtered data were then down-sampled to 250 Hz and saved to a CD-ROM for subsequent analysis. Our subsequent ICA results were stable with filters ranging from 30 to 50 point moving averages. The 40-point filter and RMS operation passed ∼80% of signal power at 100 Hz, which dropped fairly uniformly to <5% power by 200 Hz. With filter windows <30 points, we began to obtain the identity matrix (i.e., EMG channels were “components”). With filter window sizes >50 points, the first six components began to collapse into a smaller number and develop negative values in the weight matrix. Ideally, premotor drive reflected in EMG should be positive. Filtered data from multiple recording sessions in the same frog were processed to remove periods of inactivity and concatenated into a single large file. Each EMG channel was also normalized to unit variance. As a result, estimates of variance reconstruction were unbiased by pickup variations between muscles. Typical matrices for analysis comprised 10 rows (corresponding to EMG channels) and 262,144 columns (corresponding to time). In each frog, such matrices corresponded to >17 min of contiguous motor activity (the equivalent of ∼2000 wiping movements). This EMG data structure was used in ICA [MATLAB implementation of the Bell–Sejnowski algorithm developed by Scott Makeig (Makeig et al., 1997)]. ICA yielded (1) a matrix of weights describing groupings of muscles comprising each synergy and (2) a matrix containing the set of time series describing independent component (IC) activations. Each IC activation corresponded to a single common drive to several muscles. EMGs were formed from a weighted sum of these drives, determined by the weight matrix.

ICA unmixes sources that were mixed in an entirely feedforward manner. However, we believed that feedback (homonymous and heteronymous) operating in the frog limb and the interactions and nonlinearities introduced by the motion of the physical limbs would not significantly degrade the performance of the ICA algorithm. To confirm this, we tested the ability of ICA to separate sources in a simulated two-link manipulator controlled by several proportional derivative controllers with variable gain, signal-dependent noise, and noisy feedback. We evaluated the robustness of the ICA algorithm in the simulations and found it effective (see Appendix 2, available at www.jneurosci.org; and Discussion).

Comparison of synergies and associated weight matrices among frogs. To compare synergies, we adjusted the variance of component activation time series to unity. Corresponding adjustments in the mixing matrix W preserved the transformation into EMG. Thus, low-variance magnitude and noisy independent components had low weights w_ij in the mixing matrix W.

Synergies were represented as columns in W. The components in the mixing matrix W were automatically sorted from the largest to smallest projected variance by ICA. However, premotor drives will be distributed in different proportions between different reflexive behaviors. Consequently, the ordering of ICs and their drive synergies (i.e., weight matrix column) in matrix W might vary significantly between animals, depending on the proportions of behaviors exhibited: a priori, repertoires of behaviors of spinal and brainstem frogs differed.

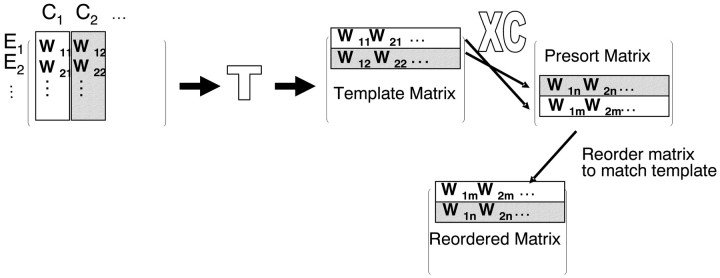
We ensured that similar muscle synergies were contained in the similar ordered weight matrix columns of different matrices, regardless of the variance associated with each data set and each frog's repertoire. For this matrix sort, we chose two matrices at a time from a pool of 16 (8 spinal EMG data and 8 brainstem EMG data). We compared the drive synergies represented in these matrices using an inner product column similarity measure. Every drive synergy (column) in the first matrix was correlated with every drive synergy (column) in the second matrix. The drive synergies (columns) that correlated most strongly were identified as representing the “same synergy.” The next best pair of correlations was identified, and so on. We also computed the average correlation between all pairs of matrices, averaging over all the synergies (columns) in a pair. We identified an individual weight matrix from the set that had the largest average correlations with all other matrices. This matrix, from a spinal animal, formed a template for subsequent resorting of all synergies in both spinal and brainstem matrices. This minimized the resorting of matrices needed. All matrices were reorganized so that drive synergies (columns) with the strongest correlations with a specific drive synergy in the template were aligned (note that this process involved first transposing matrices). This process is represented schematically in Figure 1. The resulting aligned matrices were then compared in detail.

Figure 1.

The sort process for synergies. The matrix rows represent component contribution to one of the 10 muscles studied (e.g., W11 for C1 contribution to E1). The matrix columns represent the components (C1..Cn) as synergies and their muscle compositions. Columns in W (synergies) are sorted first by projected EMG variance. Additional sorting is required to bring synergies into alignment. Matrices are first transposed. The sort then uses an inner product similarity measure between individual rows of a candidate matrix and a template matrix to build a matrix of correlations of all possible row pairings. The sort then uses this matrix to reorder the candidate matrix so the most similar rows occupy the same positions as the template matrix. The template matrix possesses the highest mean correlation with all matrices from all frogs. Finally, the matrix is again transposed.

Time-frequency analysis for characterization of primitive dilation. The more complete repertoire of richer motor patterns in the brainstem frogs might be achieved by altering (1) the composition or (2) the temporal properties (dilation or contraction) of common drives, or (3) both (Giszter et al., 2001; Giszter, 2001).

To identify the time structure of common drives, we proceeded as follows. The drives from ICA were pulsatile (Figs. 2, 3B), so we characterized the time scale of information through time-frequency analysis. This approach convolves a time–domain signal with pulse-like waveforms (wavepackets) possessing different characteristic time scales (and hence durations). The resultant transform is a series of coefficients indicating the relative strength of each pulse or wavepacket through particular moments in time and at particular time scales, or, more loosely, burst durations.

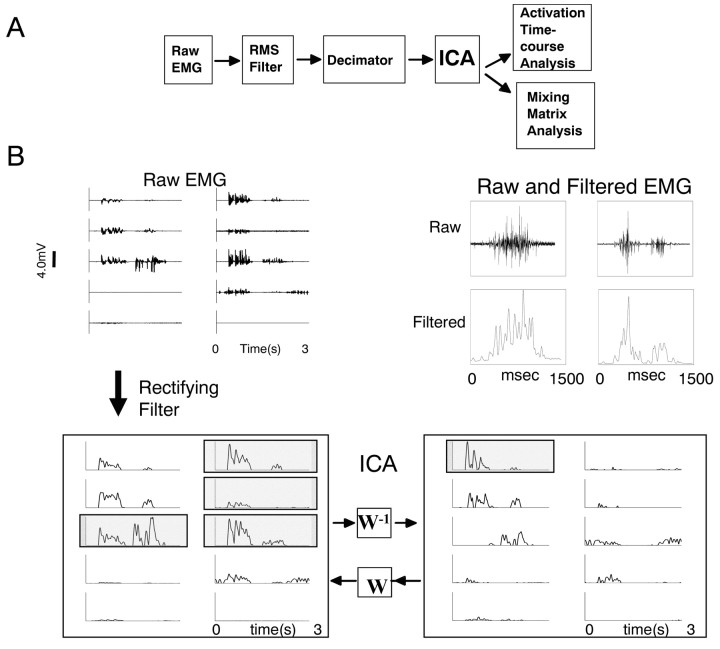
Figure 2.

A, Data processing stream. Ten-channel EMGs filtered by RMS 40-point moving average were down-sampled to 250 Hz, periods of inactivity were excised, and activity periods were concatenated. The resultant 10 × 262,144 matrix of EMG data (>1000 sec of activity) was subject to ICA. The mixing matrix and 10 activation time courses were then analyzed. B, Top left, Raw EMG. Top right, Sample raw EMG and filtered EMG on expanded ordinate and time scale. Bottom left, Rectified EMGs (E) after filtering. Bottom right, These are a linear combination of IC activations (C). W is a 10 × 10 matrix, called the mixing matrix, transforming components C into EMG E: E = WC. Some EMG traces outlined in gray at the left are similar. Much of this similarity comes from the first ICA component in the activations on the right. Muscles are numbered left 1–5 and right 6–10 from top to bottom. Component 1 projects heavily to muscles 3, 6, 7, and 8 (shaded and outlined; left). The muscles are ordered: 1, rectus anticus (RA); 2, rectus internus (RI); 3, adductor magnus (AD); 4, semimembranosus (SM); 5, gluteus (GL); 6, vastus internus (VI); 7, biceps femoris (illiofibularis) (BI); 8, sartorius (SA); 9, vastus externus (VE); 10, semitendinosus (ST).

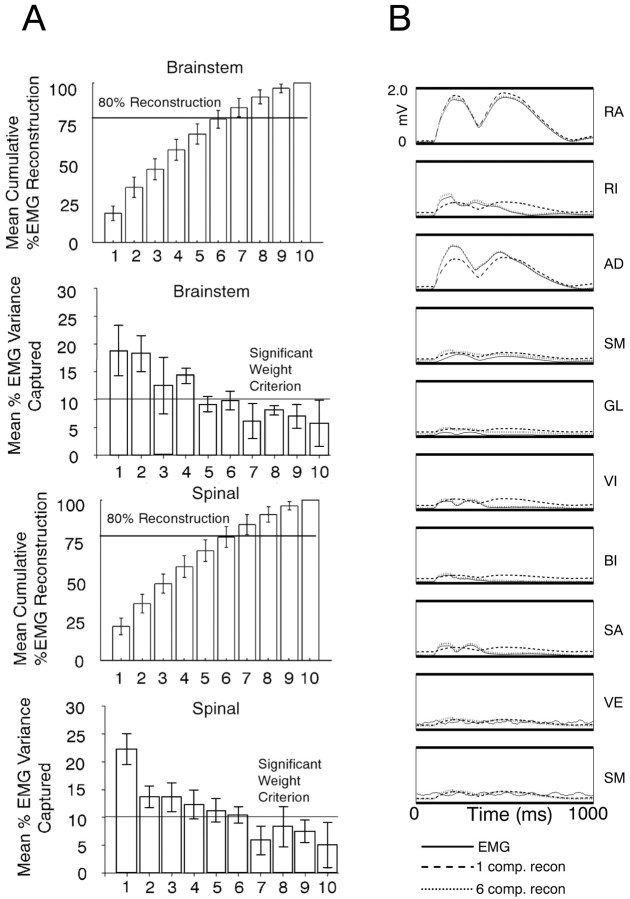
Figure 3.

Six independent components captured most variances in all frogs. A, Components were projected through the mixing matrix for approximate reconstructions of EMG recordings. The top two bar graphs show cumulative variance (above) and individual component variance (below) for the brainstem frog. Spinal frogs are shown in bottom two bar graphs. The first six components capture >80% of the variance (horizontal line) in all frogs. If one muscle equals one component, each component will contribute 10% of EMG variance. In all frogs, the variance accounted for by individual components drops below 10% (horizontal line) for components 7–10. The variance was distributed more equally between the first two components in brainstem animals, but this difference was not significant. B, Reconstruction of 1 sec and two bursts of 10-channel rectified and filtered EMG activity (solid) using only one (dashed line) or the first six independent (dotted line) components for reconstruction. Only a few components are capable of capturing nearly all the variance of this signal. In this recording segment, one component captures >85% and six components capture >95% of the original 10-channel EMG variance. The muscles are ordered: 1, rectus anticus (RA); 2, rectus internus (RI); 3, adductor magnus (AD); 4, semimembranosus (SM); 5, gluteus (GL); 6, vastus internus (VI); 7, biceps femoris (illiofibularis) (BI); 8, sartorius (SA); 9, vastus externus (VE); 10, semitendinosus (ST).

We convolved the input time series (the IC data) with frequency-band and time-limited windowed cosine packet functions as a kernel. Cosine packets capture detail at a variety of different time scales because of their construction from a dyadic filtering scheme. Cosine packet analysis (CPA) generates an over-complete set of 2^N time and frequency localized basis functions [termed in the relevant literature “time-frequency atoms” (Strang and Nguyen, 1997)] (see Fig. 6 B1), where N is the length of the time series. A subset of such atoms must be selected from the over-complete set to reconstruct a signal using cosine packets. Many different subsets of the packets can be used to perfectly reconstruct the original waveform. The question then arises: Which packets should be selected for reconstruction of a signal? The type and number of packets that reconstruct the signal are chosen according to some optimization criterion. The chosen set gives us significant information about the composition and time structure of the time series. If a dominant pulse, or burst structure, exists in the common drive, then a single or small class of wave packets will capture most of the signal variance. We used two different methods for selecting a reconstruction packet set. The first was matching pursuit (Mallat and Zhang, 1993). This identifies a small set of wavepackets ordered by their contribution to the variance of the signal. It finds first the highest variance packet and then the next, and so on, without regard to the global outcome. Thus, it is called a local or a “greedy” algorithm. The alternative method was the best-basis algorithm (Coifman and Wickerhauser, 1992). An information-based algorithm constructs the wavelet representation of signals. This finds the set of globally lowest mutual information packets and uses these as the basis for signal reconstruction. This is equivalent to the packet representation using fewest packets for reconstruction. Thus, data from both a global information-based algorithm and a more local or greedy variance-based algorithm were compared. Generally, a small number of packet types captured most of the variance of the waveform (see Fig. 6 C).

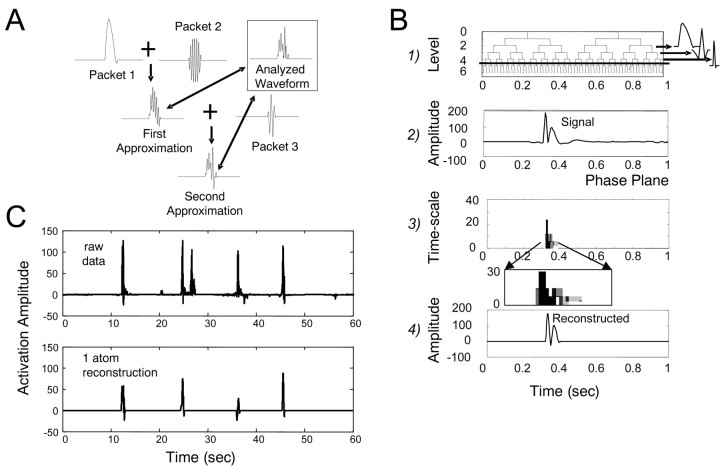
Figure 6.

Time-frequency analysis of ICA-derived time series generates a compact representation of burst and timing information in IC records. A, Synergy time series (see Figs. 1 and 2) underwent CPA. This built an approximation or a full reconstruction formed of sums of packets. B, Analysis occurs on several time scales or pulse durations. CPA repeatedly applies a set of low-pass and high-pass filters to the data. Each filter application is a node in a graph or tree (B1). In the time domain, the filter impulse response is a tapered cosine wave. A waveform is filtered with a low-pass filter (α; left branch) and a high-pass filter (β; right branch). The resultant filtered waveforms are then filtered again with other low-pass filters and high-pass filters, and so on. So, the output of filter branch α would itself be filtered, giving two nodes in the next level with net convolution filters αα (left branch) and αβ (right branch). A complete CPA of a record of N points will yield a set of 2^N packets in a tree structure occupying a range of time scales (i.e., similar to B1). Many subsets of these packets can be used to completely represent the original waveform. An example of cosine-packet decomposition and reconstruction can be seen in B2, B3, and B4. B2 shows a pulse of stereotypical synergy activity. B3 is the time-frequency representation. Each shaded cell in B3 represents the relative energy contributed to the signal by a single-packet frequency (or duration). B4 shows a reconstruction of the signal in B2 using only two packets from the tree in B1. This reconstruction captures most of the timing, scaling, and amplitude features of B2 and accounts for a substantial variance. C, A sample cosine packet decomposition performed on several seconds of IC activations made from EMGs of a spinal frog. A single type of time-frequency atom was selected with full-widths at half maximum in the range of 275 ± 12 msec, corresponding to a small subset of tree nodes in B1. These packets constructed an approximation to the original signal. In the example, the single time scale reconstruction captured >50% of the original variance. Information on pulse time was well preserved, with four of five pronounced pulses successfully reconstituted at the correct time of onset. Including adjacent time scales would capture the most variance (see Fig. 7).

We examined how particular time scales in the packet analysis contributed to the overall variance of the IC signal. We hypothesized a single time scale would capture significant variance. To test this idea, we created an approximate reconstruction of IC activations, using only the largest variance wavepackets obtained from the full basis. We incrementally added the highest variance packets until we reconstructed >80% of the variance of the original signal. Two analyses were performed on these packets: (1) a time–domain analysis of the time scale of packets as impulses; and (2) a frequency domain analysis of their spectral properties (peaks compared using F test statistics described by Bendat and Piersol, 2000). For the time–domain analysis, we examined the full width at half maximum (FWHM; i.e., a measure of duration) to classify the time scale of the selected packets/pulses. Packets were sorted into a distribution of time-frequency atoms at 20 characteristic time scales, to examine the dominant time scale of packets needed to reconstruct the EMG. In the power spectra, we examined the amplitude of peaks and steepness of the drop-off of the spectrum of packets. Reconstruction packets with higher amplitude and steeper drop-offs would indicate that the time-frequency atoms used for reconstruction possessed greater temporal consistency (less frequency jitter), compared with lower peaks and shallower spectral drop-offs. Each analysis was performed on brainstem and spinal frog data. The results of these several analyses were compared using parametric tests on the data to establish similarities and differences between the two conditions.

Results

We estimated premotor drives of spinal and brainstem frogs using ICA. The repertoire of behaviors of spinal frogs comprises primarily flexion withdrawal, crossed extensions, and wiping or scratching to body surfaces other than the head (for review, see Giszter, 1995). Wiping in the spinal frog involves primarily proximal muscles in targeting the hindlimb but both proximal and distal in wiping the back, ipsilateral leg, or forelimb. The movements show relatively simple adjustments. In contrast, the brainstem frog makes complex adjustments of these patterns and adds to the repertoire of spinal behaviors. Additions include locomotor crawling, jumps, complex wiping adjustments, and directed kicks. The additions in brainstem frogs and their adjustments all include major contributions of proximal joints and therefore proximal muscles. We focused on recordings of proximal muscles here (we had studied these extensively in previous work): bigger muscles were easier to record with confidence with less issue of cross talk, and these muscles contributed in all behaviors examined, except, perhaps, ipsilateral wipe of the calf.

We used ICA to extract independent premotor drives and examined how these drives projected to muscle activity (i.e., the component muscles) in both spinal and brainstem frogs. ICA assumes linear mixing of drives. This is appropriate for premotor drives insofar as motoneurons operate to an extent as linear summing junctions for EPSPs (but see Materials and Methods and Discussion). To us, a larger concern was feedback effects in the moving multijoint limb: the multijoint mechanical interactions and mixing attributable to homonymous and heteronymous feedback effects might present major problems. Accordingly, we tested the separability of drives in a multijoint simulation (see Appendix 2, available at www.jneurosci.org; and Materials and Methods) and confirmed the feasibility of this approach.

The Bell–Sejnowski ICA algorithm is an information-based neural network algorithm used for the blind separation of sources in signals such as the EEG and the electro-oculogram (Bell and Sejnowski, 1995; Jung et al., 2000). ICA delivers as many components as EMG channels. If a small number of independent drives underlie the EMG activity, we ought to be able to explain most of the EMG variance using a smaller number of the independent components than the full set obtained from ICA.

Application of ICA technique to characterize muscle balance in premotor drives

Our EMG electrodes provided relatively restricted pickup in our intramuscular EMG (for review, see Kargo and Giszter, 2000b). Significant high-frequency signal-dependent information was present in the original 2 kHz EMG raw data. This caused application of ICA to the raw data to often yield a mixing weight matrix W that was essentially the identity matrix (see Materials and Methods). We expected that premotor drives represented the relevant underlying physiological motor processes occurring at lower frequencies. In all analyses here, raw data were rectified and RMS filtered (Basmajian and DeLuca, 1985) with a 40-point moving average (high-frequency cutoff ∼200 Hz). To maximize data throughput to our algorithms, we then decimated the data to 250 Hz. After this filtering (see Materials and Methods), we found that substantially fewer than 10 components could be projected through the mixing matrix W to reconstruct most of the variance in the original EMG.

We recorded EMGs during an average of four sessions per frog. Records of at least 1048 sec of continuous motor activity in the EMG were used in every analysis. Before analysis, each individual EMG trace was normalized to have unit variance. The result of the analysis was a complete description of the data as a 10 × 262,144 activation matrix consisting of the derived activations of the ICs and a linear 10 × 10 “mixing” matrix (W). The IC activation matrix represented a collection of 10 time series (one per channel). Each corresponded to one of the independent drives (or sources) generating muscle activity (Fig. 2). The 10-component activation vectors and the mixing matrix W derived from ICA together completely describe the EMG data, with an appropriate combination of independent components providing perfect reconstruction of the original data. The independent components had minimal mutual information. Subsequent analysis focused on the mixing matrices and the activation time series of independent components, to examine muscle grouping and temporal structure, respectively.

Analysis of component variance contributions

The mixing matrix W from ICA represents the balance of EMG activity in the putative premotor drives (represented by ICs). We examined the properties of the mixing matrices from the entire population of frogs in the study. Each row of the square W mixing matrix contained weights describing the contribution of each different independent component to a single EMG channel. In contrast, each weight matrix column represents the synchronous synergy activated by the independent drive. Thus, weight matrix columns represent the relative weightings in the motor pools of the drive synergies as reflected in the recorded EMG.

Because each EMG record was previously normalized to unit variance and because ICA is unconcerned with simple variance per se, the drives embodied in W were potentially comparable from frog to frog. We wanted to determine which drive synergies (weight matrix columns) in matrix W were most important and whether a small number of such premotor drives (columns in W) captured most of the variance of the EMG signals within a single frog. For this, the individual and cumulative contributions to variance of each component or premotor drive were examined (Fig. 3). We considered a component interesting if it captured >10% of the variance. Usually six components were each >10% variance and cumulatively contributed 80% or more of the total variance of the signal (Fig. 3A). It is likely that the remaining components were influenced by contributions of different noise processes (see below). In some frogs, the percentage of variance accounted for by the first six components in the rectified and filtered EMG data were as high as 95% (sample-rectified EMG and reconstructed data are shown in Fig. 3B), and only in one frog did it fall below 70%. Mean variance accounted for by the first six components in spinal frogs was 80.2% with a SD in the population of 7.8%. Mean variance accounted for by the first six components in brainstem frogs was 79.9% with a SD in the population of 6.7%. These data suggest that each independent component represents a common or premotor drive that is supplied to several of the muscles from which we recorded EMG activity (Fig. 2B, EMG and ICA activations). Each activation weight (i.e., weight matrix column element) represented a drive effect on muscle and was positive for the first six extracted drives, consistent with a net excitatory drive to the motor pools and a positive rectified EMG output. Additional analysis focused specifically on these six components that accounted for ∼80% of the variance.

Identification of similar muscle groupings in different ICA

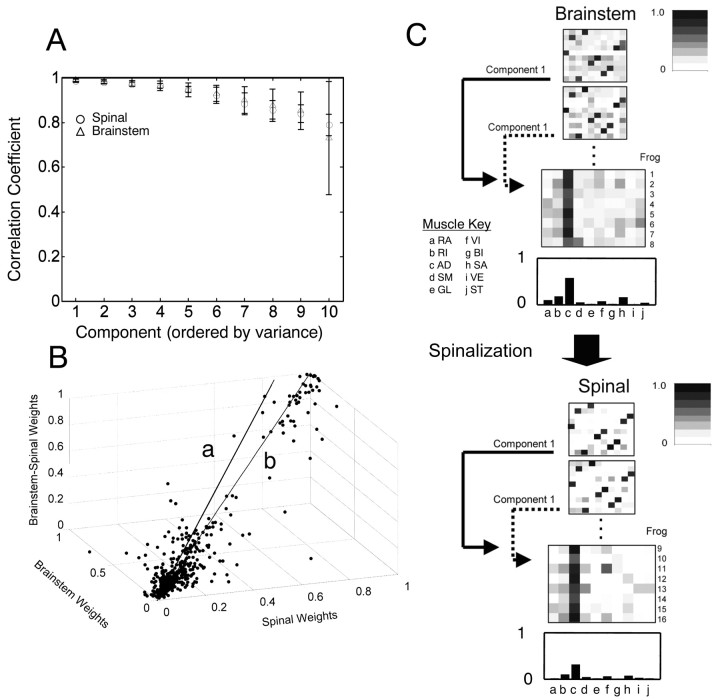
We wanted to compare the muscle groupings represented in matching drive synergies (weight matrix columns) of the mixing matrix W across animals. However, we knew a priori that repertoires of behaviors of spinal and brainstem frogs differed. To compare mixing matrices, we needed to ensure that similar muscle synergies were contained in the same weight matrix columns of different matrices. To achieve this, we sorted the matrices and components as described in Materials and Methods. We aligned similar synergies in the matrix. If matrices comprised six conserved components and four noise process components, then such sorting should only occur within, not between, these two different groups. This was usually true, and most sorting tended to be confined within the six largest components and within the four smallest. In ∼70% of the sorts, all components in the six largest components before sorting remained there after sorting. Figure 4C shows sorted (transposed) matrices graphically.

Figure 4.

Consistent muscle synergies were identified in sets of eight brainstem and eight spinal frogs' records by averaging the resorted mixing matrices (see Fig. 3 for sort). A, Mean correlations and SDs for correlation coefficients between individual synergies and the spinal template synergies are shown for all frogs. A steadily accelerating decline in the correlation between synergies occurred. The six largest synergies (reconstructing ∼80% of the signal variance) correlated with template synergies >0.9, with correlations falling off rapidly after the sixth component or synergy. Vertical bars represent SDs. B, To examine similarity among frogs, the elements of the mixing matrices from brainstem, spinal, and combined analyses were plotted a striples in a three-dimensional space. This distribution was analyzed with PCA to determine how close the points were to a unity line in this space. The first principal component was used as the best fit line to the cloud of points (line a) and was compared with the theoretical unity line (line b). The two lines are separated by only ∼3°. The fitted line was deviated slightly toward the “brainstem” axis. Similarly, brainstem weights tended to be larger than the corresponding spinal weights. Brainstem synergies focused signal energy in smaller numbers of muscles than spinal synergies. C, Grayscale illustration of weights. Each row in the matrix displayed represents a synergy. Two mixing matrices from two brainstem and two spinal frogs are shown. The grayscale patterns show the relative balances are very similar among all four matrices. Below each pair of matrices are stacked all rows of component 1 data from every spinal or brainstem frog grayscale. The average weights of this single component are shown at the bottom of each top and bottom section and are plotted as bar graphs. The muscle balance is similar between the spinal and brainstem synergies. Muscles: RA, rectus anticus; RI, rectus internus; AD, adductor magnus; SM, semimembranosus; GL, gluteus; VI, vastus internus; BI, biceps femoris (illiofibularis); SA, sartorius; VE, vastus externus; ST, semitendinosus.

We posed three questions in this data analysis: (1) How similar are synergies among spinal frogs? (2) Are similar synergies used in spinal and brainstem preparations of the same frog? and (3) How similar are synergies among all preparations of frog tested?

Correlation of spinal synergies among frogs

To test how similar the synergies were across animals, we calculated the average correlation between each drive synergy (weight matrix column) of each frog's matrix and each drive synergy (weight matrix column) of the template matrix.

We calculated a “correlation with template” statistic within the spinal frogs using the inner product. This analysis allowed us to determine the consistency of EMG weightings that were observed within synergies in different spinal frogs. All six drive synergies (weight matrix columns) in spinal frogs correlated very strongly with the matching drive synergies of the template matrix (Fig. 4A, Spinal). The across matrices correlations were large. The averaged over-synergies correlation coefficient was 0.88. The correlation coefficient r of the six largest components (from the first six components that captured most variance) were all larger than 0.9. There was very little individual variation in the muscular balances of premotor drives across spinal animals (i.e., spinal animals use a common set of premotor drives). Cross-correlation of the remaining four drives (weight matrix columns that were putative noise processes) yielded correlation coefficients that were all substantially <0.9, and the weights also showed marked increases in variance. The increase in variance indicates to us that these processes (weight matrix columns) were relatively independent and unique from animal to animal. This strongly suggests that random noise processes played a much more substantial part in these components.

Correlation of brainstem and spinal synergies within frogs

To compare brainstem synergies and spinal synergies, where possible, we paired each brainstem EMG record with a spinal EMG record of the same frog. In the remaining frogs, we made random pairings among brainstem and spinal data sets. We then concatenated these paired brainstem and spinal records into single data sets and performed an ICA analysis on each of the concatenated records. We thus obtained a set of ICA mixing matrices capturing both spinal and brainstem patterns concurrently. The mixing matrix weight values that corresponded to the six highest variance components extracted from this analysis were selected. These were then used to separately analyze and reconstruct the constituent spinal and brainstem records. Again, an average of ∼80% of spinal-only EMG variance and brainstemonly EMG variance was captured by the six most significant synergies in the mixing weight matrix derived from spinal–brainstem combined records. This indicates a high degree of similarity between extracted brainstem and spinal muscle patterns both within and even between animals. Particularly remarkable to us were results of random pairings between different animals in which stationarity of EMG pickup between the recordings was almost certainly violated in the combined analysis.

Combined brainstem and spinal synergy extraction and comparisons

Despite the tests of variance capture presented in the preceding paragraph, it remained possible that matrices might differ widely between the spinal, the brainstem, and the combined data analyses, although all of the analyses were capable of capturing significant variance

We repeated the correlation analysis for brainstem frogs. The individual correlations between synergies of each resorted brainstem weight matrix and the spinal template matrix synergies were averaged over animals. The overall average correlation of brainstem mixing matrices with the spinal template, averaged over all synergies and animals, was 0.92. The average correlation was plotted as a function of component number (Fig. 4A, Brainstem) and was similar to spinal frogs: the first six synergies (weight matrix columns) all possess the strongest average correlations with the drive synergies of the template matrix (>0.9).

We next focused analysis only on the six most consistent components. We averaged synergies to obtain the mean strength of the contribution of each synergy to the EMG of each muscle (Fig. 4C). The similarity between the largest brainstem and spinal components in both individual and average mixing matrices can be seen in the gray scale representation of weights and more clearly in the average bar graph presented for one synergy in Figure 4C. These mean mixing matrix values were then used for an analysis of individual weight significance (see below and Fig. 5).

Figure 5.

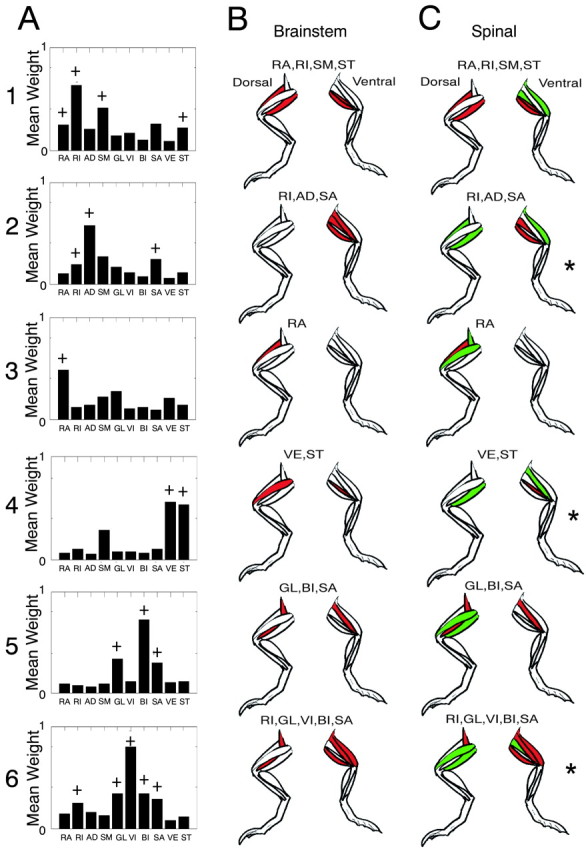
Spinal and brainstem synergies show similarity in the general component structure. A, Average weights of each of the first six components plotted as bar graphs for brainstem frogs. A standard t test assigned significance to mean values of the i, jth element of W (i.e., the synergy contribution to a muscle EMG differed significantly from the lower amplitude weights and noise processes in components 7–10). Muscles making significant contributions to synergies by these criteria are denoted in A, with a plus sign. It should be noted that this test is ad hoc. In B and C, only significant muscles by this criterion are shown (those with a plus sign in A equal the filled color in B). B, Synergies significant in averaged brainstem mixing matrices (red; see plus sign in A) are shown in dorsal and ventral views of the limbs in each panel. C, Significant spinal synergies identified from average spinal mixing matrices. Significant muscles in each synergy are shaded in red (significant in brainstem) and green (significant only in spinal). Synergies are more focused in brainstem synergy patterns. Note components 2, 4, and 6 (asterisks). A muscle in each that was recruited in the brainstem frogs was not significant using the t test criterion in the spinal frog. Muscles: RA, rectus anticus; RI, rectus internus; AD, adductor magnus; SM, semimembranosous; GL, gluteus; VI, vastus internus; VE, vastus externus; ST, semitendinosous; BI, biceps; SA, sartorius.

We also correlated the synergies in the mean mixing matrices of the spinal and brainstem data. We examined correlation between the top six matching synergy components. We found a mean (across all synergies) correlation coefficient of 0.95, indicating a very strong similarity between each of these six components in brainstem and spinal frogs.

PCA analysis of weight matrix relationships

As a final confirmation of similarity of muscular composition within corresponding drive synergies of brainstem and spinal frogs, we compared the individual weights extracted by all three different analyses for cases in which a brainstem frog underwent an additional subsequent spinalization (i.e., we compared brainstem, spinal, and combined weights in such frogs). We plotted the relationship among the values of the corresponding mixing matrix elements (i.e., elements from the same rows and columns) from each of the brainstem, spinal, and concatenated brainstem–spinal ICAs. Each element triplet (brainstem, spinal, and combined) represented the corresponding weights in each analysis. These were plotted as points in a three-dimensional parameter space (Fig. 4B). Most points appeared to fall along a straight line very near to the unit straight line, although there were some outliers. The unity line would be expected if the muscular composition of mixing weight values were nearly identical between all three analyses and conditions. We obtained an unbiased best straight line fit to the triplet matrix element data by using a principal components analysis. The first principal component extracted from the data (which accounted for ∼60% of the simple variance of the weights) yielded a line that deviated only 3° from the identity line. The line was deviated toward the brainstem axis from the theoretical unit line. This deviation, although small, may be attributable to significant brainstem weight values tending to be slightly larger than weights from the corresponding spinal-derived mixing matrices. This indicated an increased amount of signal energy focused within a smaller number of significant weights in brainstem animals' components.

Differences between spinal and brainstem frogs in significant muscle synergies

As we have noted, the first six components captured ∼80% of the entire EMG signal variance, whereas the four smallest components generally contributed <5–9% of the EMG variance separately. As such, the weights associated with the smallest four more “random” components provide a rational choice for an ad hoc random test population (brainstem frogs: mean, 0.1; SD, 0.2; spinal frogs: mean, 0.13; SD, 0.25). Nonetheless, we recognize that such weights cannot truly be considered statistically independent. We used these as a population against which to judge the significance of the weights of the other drive synergies (i.e., to judge which muscles had a significant representation in each of the first six independent components).

We used the mean mixing matrix weights obtained from the analyses in Figure 4C to evaluate the most significant muscle groupings within the synergies. We tested whether mean mixing matrix elements from the sorted six largest components (averaged over animals) differed significantly from the random test population of all of the mixing weights from the four smallest components treated as a single population. We assessed this difference using a Student's t test (α level, 0.05). Significant muscle groupings by this (ad hoc) criterion were identified in brainstem and spinal animals. These significant muscles are shown in brainstem frogs in Figure 5A. This allowed a more precise comparison of the spinal and brainstem frog modularity. In 5, B and C, the significant muscles in spinal and brainstem are indicated on cartoons of the frog anatomy, indicating the anatomical locations and agonist–antagonist relationships in coarse form. The significant muscles in the patterns of the synergies were similar between spinal and brainstem frogs (compare red-shaded muscles in Fig. 5B,C). However, very clearly, spinal frog synergies generally were composed of a greater number of significant participating muscles (a superset) compared with brainstem frog synergies (compare green-shaded muscles in Fig. 5B,C). Significant biarticular groupings of hip and knee extensor muscles (Fig. 5A, synergies 1 and 2) were found, as well as significant groupings of flexors (Fig. 5A, synergy 5).

The main similarity between brainstem and spinal synergies was the presence of two or three dominant muscles in common in each spinal and brainstem frog component synergy. Around these were gathered a supporting cast of additional significant muscles in spinal frogs. There were other significant differences in some synergies (Fig. 5C, asterisks, synergies 2, 4, and 6). In these, a muscle identified as significant in the brainstem synergy was not significant in the spinal synergy. Thus, the differences between the conditions and motor pattern formation were more than simple focusing of activity in some cases. The brainstem synergies always represented a more focused core of muscles. Perhaps this was an effect of the presence of greater inhibitory and modulatory descending influences in the spinal circuits, presumably as a result of the pontine and medullary mechanisms preserved in these preparations. The expansion of the core after spinalization usually involved more extensive co-contraction of nominal antagonists in the synergy (compare Fig. 5, B1 vs C1, with a knee extensors in added in spinal; and Fig. 5, B5 vs C5, with a dorsal hip extending and elevating muscle added in spinal).

Time-frequency analysis

Previous studies in our laboratory have found that there is a characteristic burst duration associated with the motor pattern composition and the putative activation of premotor drives in spinal frogs (Giszter and Kargo, 2000; Kargo and Giszter, 2000a; Giszter, 2001). Some preliminary data had suggested to us that this dominant timing structure might be altered in brainstem frogs to enrich the behavioral repertoire. It was therefore logical to conduct an analysis of time courses of the activations themselves. We examined the temporal structure of the extracted premotor drives in both spinal and in brainstem frogs. We used the IC activation time series data from the previous analysis and subjected these activation time courses to a time-frequency analysis. Time-frequency analysis characterizes a signal in terms of its similarity to a family of pulse-like waveforms that are localized in time and frequency (i.e., have a characteristic time scale). If the temporal structure of the extracted IC components changed in less reduced preparations (for example, if brainstem frog ICs are dilated or contracted temporally when compared with spinal frog ICs), then the comparison of their time-frequency analyses would be able to detect such a change.

We used a CPA (see Fig. 6 and Materials and Methods). We used two main optimization methods for this wavepacket analysis. The first algorithm, called matching pursuit (Mallat and Zhang, 1993), selects packets based on the variance they contribute to the original analyzed signal. Packets are selected in order of decreasing contributed variance until all signal variance is explained. The second algorithm, the best-basis technique (Coifman and Wickerhauser, 1992), uses an information-based criterion. Best-basis selects a set of packets as a basis that globally minimizes the mutual information among the set of cosine packets chosen. The results of these two sets of analyses were almost identical and will be treated as such below. The close similarity of results from both a maximum variance algorithm and a global minimum mutual information algorithm gives us confidence in these results.

Extraction of time-frequency atoms or common duration bursts

CPA delivers a collection of pulses or packets that fully reconstruct the original signal (Fig. 6A,B). Our hypothesis was that a small and relatively uniform subset of packets captured most signal variance. To test this, we classified IC-derived cosine packets in the time domain by using their duration as a measure of time scale. We used the FWHM of the central peak of each cosine packet, which should correspond with a “burst duration.” We selected enough time-frequency packets (or pulses) to account for at least 80% of activation variance from the complete basis (e.g., from a best-basis analysis). We tested the hypothesis that premotor drives in spinal animals operate at a dominant time scale, and this may differ from the time scale of premotor drives in brainstem animals. The distribution of FWHM durations was divided into 20 bins for analysis. We examined both spinal and brainstem frogs and both the single largest independent component and all of the six largest and most consistent independent components from the previous section. This analysis demonstrated that in spinal animals the greatest number of packets and the greatest amount of signal energy was concentrated at a time scale (FWHM) of ∼275 msec (Fig. 7B, bottom, Spinal: Components 1 and 1:6). Smaller amounts of signal energy were present in small peaks at shorter time scales (∼100 and 50 msec). Figure 6C shows a reconstruction achieved with only a 275 msec pulse or “atom.” This simplicity of structure in the time-frequency analysis of components was not reflected in the individual EMG channels, which showed more peaks. In particular, there was often a strong 550 msec duration peak in EMG channels, as well as the 275 msec peak. This is shown in the histogram in Figure 7A. This was presumably a result of bursts in different components causing apparent period doublings in time series of individual muscles.

Figure 7.

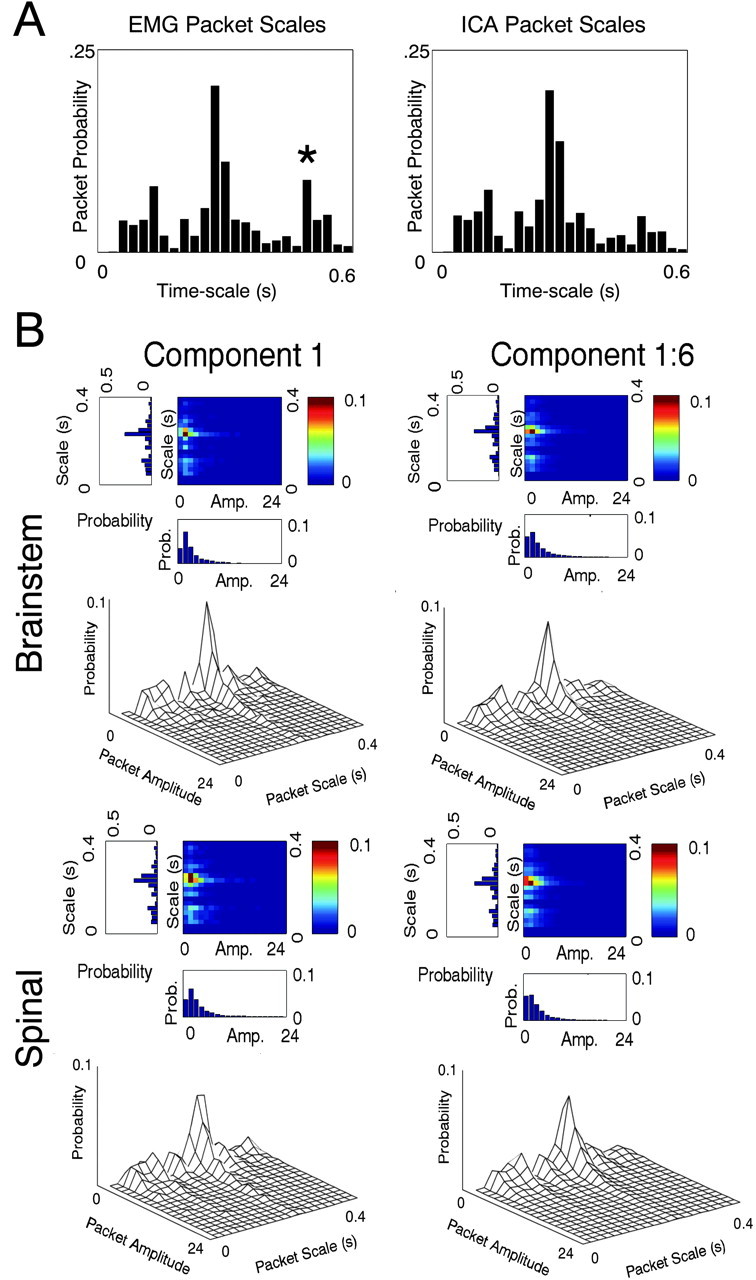
Pulses at a single dominant time scale comprise synergy activations in all frogs. A, EMGs and synergy activations computed from EMGs underwent CPA. Packets extracted were categorized by their time scale (full width at half maximum). Full widths at half maximum were subdivided into 25 equally spaced bins ranging from 1 to 600 msec duration. The packet probabilities are shown for spinal EMG and spinal synergies. These differ mainly in a peak in EMG at ∼550 msec (asterisk), which is much reduced in the synergies extracted by ICA. This difference at the 550 msec time scale was also observed in brainstem frogs. B, The amplitude of cosine packets were divided into 20 equally spaced bins ranging from 0 to 24 units (units arbitrary after normalization procedures). From these distributions, the probability of packets of particular time scales and amplitudes are plotted (mesh plot and false color temperature plot in each panel). The variance contribution of packets (data not shown) were nearly identical in form to the probability plots. Top, Brainstem frogs, synergy/component 1 (left) and synergies 1–6 (right). Bottom, Spinal frogs, synergy/component 1 (left) and synergies 1–6 (right). Packets describing the synergy (IC) contributing the most variance (left) are dominated by a single time scale of ∼275 msec in all frogs. The probability mesh plots show that brainstem frog ICs comprise greater numbers of packets at the 275 msec time scale than spinal frog ICs. The peak probability for component 1 in brainstem is at 275 msec and is 0.0819, whereas in spinal it is 0.0593. For all six components taken together (right), the brainstem peak is 0.0717 and in spinal it is 0.0623. Peak variance is captured for component 1 at 275 msec and in brainstem is 0.0492 and in spinal is 0.0338. For all six components, in brainstem the peak is 0.0434 and in spinal the peak is 0.0387.

When we examined brainstem frogs, we were forced to abandon our original speculation that packet durations in brainstem animals would be more variable. Brainstem animals demonstrated an even more consistent time scale distribution. In the first component, the number of packets in the 275 msec band increased when compared with the same band in spinal animals. This was reflected in the peak probabilities (Fig. 7B, compare brainstem peak probability of 275 msec packets 0.0819 with spinal peak probability of 275 msec packets 0.0593; and see Fig. 8A). This increase in packet frequency was also seen, although less pronounced, when all of the first six components were examined (Fig. 7B, Component 1:6, Brainstem and Spinal). Packet amplitudes also differed significantly (Kolmogorov–Smirnov test; p < 0.04). The mean amplitude of the 275 msec packets of component 1 in brainstem frogs was 2.1 units, whereas in spinal frogs it was 4.0 units. Across all six components, the mean amplitude of 275 msec packets in brainstem frogs was 2.0 units, whereas in spinal frogs it was 3 units. Thus, the 275 msec packets of spinal animals were, on average, 50–100% larger than packets in brainstem frogs. Apparently, the motor patterns of brainstem animals consisted of greater numbers of lower amplitude 275 msec band packets, and these frogs showed more temporal precision as they generated richer motor patterns.

Figure 8.

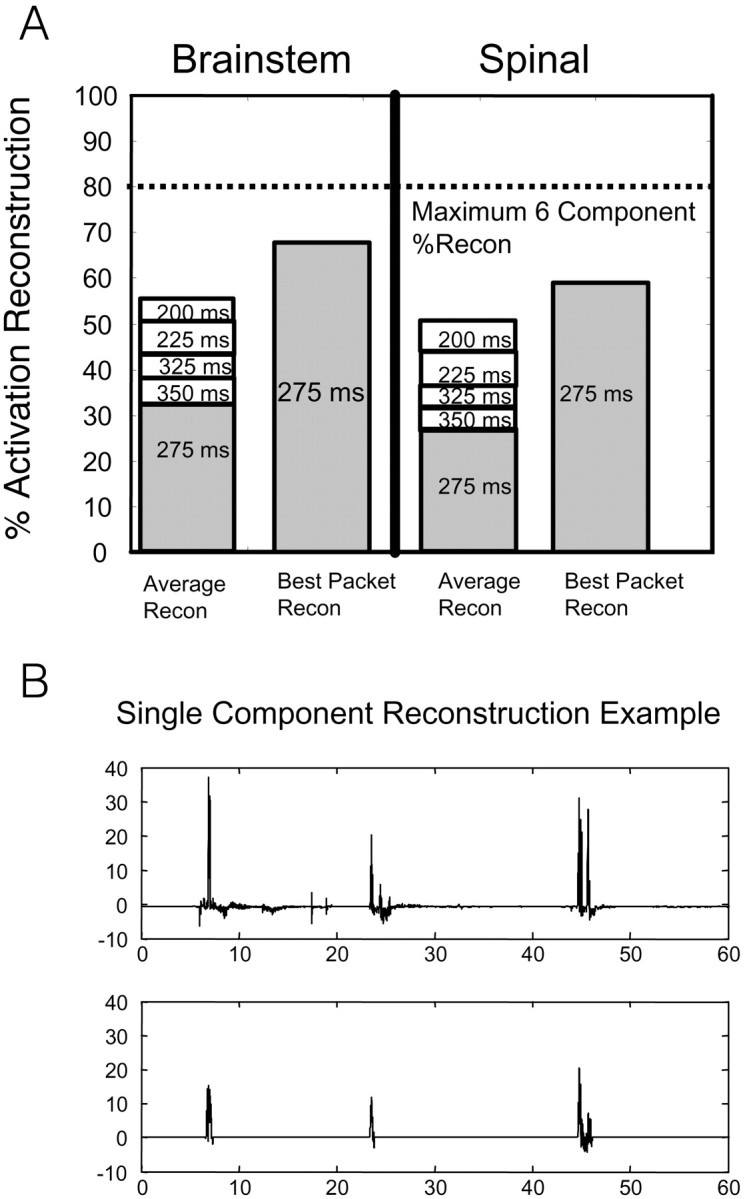
EMG reconstruction with pulses near 275 msec. Most synergy energy was at a time scale centered on 275 msec. Reconstruction for the six largest synergies was examined ∼275 msec. These synergies reconstructed >80% EMG variance (hence, 80% upper bound; dotted line). A, The variance accounted for in each 25 msec bin was assessed, and the bins from 225 to 325 msec were plotted as stacked bar graphs. This plot shows most signal energy occupied a time scale band of ∼275 msec in both spinal and brainstem frogs. Nearly half of the EMG signal energy was reconstructed by the packets between 250 and 300 msec. Differences in percentage reconstruction between spinal and brainstem populations were not significant over the bands considered. In some animals (right bars in brainstem and spinal plots), the 275 msec packet class alone captured >60% of the total EMG variance (∼80% of synergy variance). B, An example of a 275 ± 12 msec packet category successfully capturing 67% of the original activation component variance. A single channel of IC activation was selected for reconstruction using only packets with time scales falling inside the 275 msec range.

To assess the idea that relatively fixed duration or time scale pulses captured the most significant features of the premotor drive behavior in both spinal and brainstem frogs, we compared reconstructions of IC activations using packets of only particular durations clustered around the 275 msec peak duration.

We were able to achieve an average of ∼60% reconstruction of total IC activations using only five categories of packet durations (250–300 msec) (Fig. 8A) in both spinal and brainstem frogs. Note that this measure of ∼60% variance capture in total signal is equivalent to capture of ∼85% of the variance alone of the six largest components. Reconstruction of IC activations using only the dominant 275 msec time scale sometimes captured the most significant features of the pattern, as illustrated by the sample data in Figure 8B, in which a single packet type captured 67% of the signal variance of this component overall. A duration of 275 msec alone, on average, contributed ∼27% of the original activation energy in all spinal frogs. The other packets needed for 60% reconstruction in most frogs were the adjacent durations (250 msec, 300 msec, etc). Similarly, packets of 275 msec duration alone captured 30% of the variance, on average, for brainstem animals (Fig. 8A). The dominance of a single packet type indicates the presence of a preferred time course for pulses in the EMG, at ∼275 msec. Adjustments or variations of up to 50 msec in onset or offset may be indicated by the need for all five packets in most frogs.

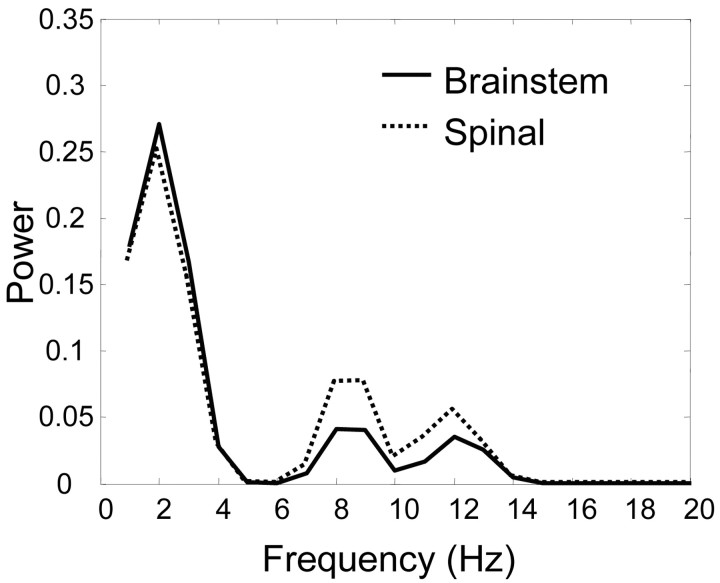
Because brainstem frogs show richer behavior, we reasoned perhaps they showed more frequency jitter or variations in their packets. To compare frequency jitter inside the dominant packets used for IC and EMG reconstructions, we calculated the average frequency spectra of 275 msec packets used for spinal or brainstem EMG reconstructions. We applied a variant of the Fisher test for the discrimination of spectra over particular frequency bands (Bendat and Piersol, 2000). The peak frequency spectra of 275 msec duration packets for both spinal and brainstem frogs were very similar, below 8 Hz (Fig. 9). However, the power spectra of spinal-derived packets fall off less rapidly at a higher frequency than do the power spectra from brainstem-derived packets. At higher frequency between 8 and 14 Hz, the frequency spectra of brainstem animals tended to contain significantly less energy than spectra from spinal frogs (α level, 0.05). This result indicates that the packets constituting premotor drives in brainstem animals possessed considerably less high-frequency jitter (i.e., more temporal regularity) than the packets constituting premotor drives in spinal animals.

Figure 9.

Brainstem frog packets possess less high-frequency jitter than spinal packets. The 275 msec scale band containing the largest number of packets and largest proportion of IC signal variance was analyzed in the spectral domain. Frequency spectra of these packets were calculated and averaged. The averaged spectra are shown. Note that the dominant time scale of brainstem and spinal packets is identical but their spectra diverge in the higher-frequency components. Significant increases (at an α level of 0.05) in spinal spectra over brainstem spectra occurred between frequencies of 8 and 14 Hz [for test, see Bendat and Piersol (2000) and Materials and Methods]. The brainstem frogs' spectra exhibit more rapid falloff of amplitude with increasing frequency content, and perhaps tighter control over the timing of packet onset and offset. Circuits present in brainstem animals but absent from spinal preparations may aid in stabilization of bursts in premotor drives.

In summary, we have identified a low-dimensional modular representation of the motor patterns in spinal and brainstem frogs centered on a few synergies and an associated burst structure. The richer behavior in the brainstem frog was achieved by using larger numbers of smoother packets (with more precision at the same average duration) and by a more focused set of premotor drives.

Discussion

Brainstem frogs show richer behavior than spinalized frogs. We found six common drives in both brainstem and spinal animals. However, brainstem frogs had more focused muscle groups than spinal equivalents. Both brainstem and spinal drives consisted of pulsed or burst-like activations. The dominant duration of bursts in all animals was ∼275 msec. The brainstem frogs' drives consisted of more such bursts, with smaller average amplitudes. Our data describe how brainstem frogs generate richer motor patterns from modular drives and relate these to force-field primitives and unit burst generation.

Assumptions of analysis

ICA assumes linear cascade mixing for combining drives. Motoneurons can be linear summing junctions (Henneman, 1990). However, various nonlinear effects occur in motoneurons (e.g., persistent inward currents effects) (for review, see Prather et al., 2001; Lee et al., 2003; Li and Bennett, 2003). Because metabotropic glutaminergic mechanisms in lower vertebrates induce motoneuron plateaus (Svirskis and Hounsgaard, 1998), even spinalized frogs could exhibit similar nonlinearities. However, these are unlikely to cause ICA to fail. More probable, these alter drive gain, recruitment gain, frequency response, and derecruitment. Summation of drives in EMG is still a reasonable approximation. However, waveforms extracted by ICA will not linearly reflect premotor synaptic drives.

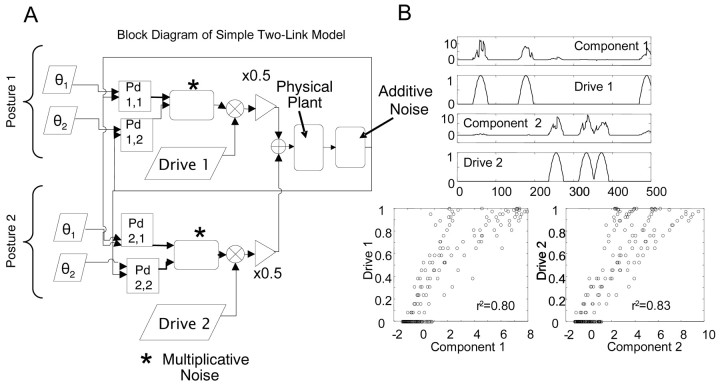
For us, multijoint mechanical interactions and recursive feedback were of more concern. Preliminary work showed ICA could separate drives in EMG (Giszter, 2001). Here, we used simulations of a two-link limb driven by multiple inputs with feedback control to test ICA with feedback (Appendix 2, available at www.jneurosci.org) (Fig. 10) (Giszter and Hart, 2003). ICA successfully extracted drives in simulation. Variance capture in frog data reconstructions here was comparable with the capture in simulation.

Figure 10.

ICA can extract independent drives in a simple two-link manipulator governed by two distinct control circuits. A, A model planar, two-link manipulator was developed. Two separate controllers [each being 2 stacked proportional derivative (Pd) controllers, one acting at each joint] competed to guide the limb to separate locations in its work space. The two stacked Pd controllers experienced common, amplitude-dependent noise sources (varied 1 to 20%), while also subject to additive sensor noise (varied 1 to 20%). Each stacked Pd controller pair was a multijoint drive and feedback (analogous to a postural or motion synergy plus feedback). Corrective forces generated by each Pd controller at each joint were multiplied by gating drive pulse trains. Pulse trains for each PD controller were random and statistically independent of one another. These output of the simulated activating controllers to the motor apparatus. The summed corrective torques here can be equated with EMG activities contributed to by several underlying premotor drives. B, ICA applied to torque records from the model. The time course of each activation can be seen below the most similar Pd controller pulse train (top). The correlation of each extracted component and the most similar pulse train was high, with r² values of 0.8 amd 0.83, respectively (bottom). The performance of ICA is dependent on the angular distance between the limb positions each controller regulates. If the limb positions are much more than a quadrant apart the performance will degrade. In the extreme limb positions >180° apart, under optimal noise conditions, we achieved r² values of ∼0.6. Other limb configurations produced better separations, with r² values of >0.95. Sensitivity to limb configuration is attributable to the intrinsic nonlinearity of the dynamics of the limb. ICA extracted good approximations of Pd drive activity over a large fraction of the work space.

Choice of information-based techniques

ICA for blind separation of sources offers advantages. Primarily, magnitude of individual channel variance (from variations in EMG pickup or gain) does not affect ICA qualitatively. ICA exploits higher-order statistics of signal information rather than variance in an attempt to minimize mutual information. Before filtering, ICA-based analysis of the raw data did not support a set of common drives but rather identified each muscle and its homonymous feedback as a unit. There may be several physiological processes desynchronizing motor units on short time scales (Maltenfort et al., 1998). We normalized EMG channel variance to generate unbiased measures of variance reconstruction in subsequent analyses, but this step was not essential. After filtering, both the significant six synergies and their activation patterns extracted by ICA here were uniformly positive. However, the algorithm did not guarantee this (see data analysis of Kargo and Nitz, 2003) and indeed other component weights were not. With lower-pass filtering we also observed negative weights. Because we could ignore pickup variations, with ICA we could directly compare extracted drives among frogs and surgical conditions. Other decomposition methods, such as principal components analysis, would need more constraints and can be biased by choice of signal gain or variance differences.

A difficulty in ICA is assigning significance to the extracted weights. All current methods are ad hoc (Duann et al., 2002). We used parametric statistics of the weights of the low amplitude components (i.e., presumed noisy and higher variance) as a test set against which to evaluate weights in the six “interesting” components.

Other approaches and results

Investigators have used PCA and factor analyses to examine modularity in both EMGs (Flanders and Herman, 1992; Davis and Vaughan, 1993; Olree and Vaughan, 1995; Poppele et al., 2002a,b) and modularity in kinematic data (Soechting and Lacquaniti, 1989; Sanger, 2000; Santello et al., 2002). Several researchers (Sepulveda et al., 1993; Saltiel et al., 2001; Ting et al., 1998; Raasch and Zajac, 1999; Tresch et al., 1999; Valero-Cuevas et al., 1998; Valero-Cuevas, 2000; d'Avella et al., 2003) have used both experimental and statistical methods, including constrained least squares fits to examine the degrees of freedom problem in motor control. All these analyses support reduction of excess degrees of freedom by motor mechanisms at segmental or other levels from the total available to a core set adequate to achieve the tasks examined.

We have presented evidence that six components (i.e., premotor drives) can explain most (>80%) of the EMG signal variance in brainstem and spinal frogs. Tresch et al. (1999) analyzed spinal flexion motor patterns and found a few synergies. Our study extended this in spinal and brainstem frogs to include different categories of behavior (walking/crawling, turning, righting, wipe/scratch, jumping, and kicking). Data resemble the results of Poppele and Lacquaniti (Poppele et al., 2002b; Ivanenko et al., 2003) in human locomotion. Four drive patterns captured most of the variance in EMG signals from human gait. A lower number of patterns could be because (1) a single category of motion was studied, and (2) their analysis used time-varying waveforms as the basis of analysis. ICA assumed linear mixing of drives but made no use of time scale or any prior assumptions about pattern. d'Avella et al. (2003) analyzed drives in EMG of intact frogs. Like Poppele, d'Avella examined “time-varying synergies.” The work by d'Avella extracted “chunks” of repeating patterns. We believe the burst or pulse activations in our study would form the “letters” in the more complex “words” in the work of d'Avella or Ivanenko.

Unit burst structures in the frog motor patterns

Our analysis was two stage: ICA, then analysis of component time series based on wavelet approaches. Flanders (2002) also used wavelets with aggregate EMG, and Lin and McKeown (2002) examined single-unit EMG. Regular bursts were detected in the drives here. Modularity similar to that observed here, comprising common duration elements, has been reported to occur in pattern generation (bursts) (Stein and Daniels-McQueen, 2002), in kinematics (kinematic strokes and segmentation) (Burdet and Milner, 1998; Doeringer and Hogan, 1998; Krebs et al., 1999), and in kinetics (torque pulses) (Vicario and Ghez, 1980).

To enrich behavior, brainstem frogs might have changed pulse/burst duration compared with spinal frogs. However, we found a common 275 msec duration wavepacket dominated both brainstem and spinal motor patterns. Compared with spinal frogs, brainstem drives showed even more pulses of 275 msec duration. The brainstem frogs' pulses were smoother: the bursts of brainstem frogs had spectra with significantly less high-frequency (>10 Hz) content.

Relating modularity here to CPGs, force-field primitives, and ontogeny of motor system

The bursts here relate to pattern generation. Grillner (Grillner, 1981; Grillner and Wallen, 1985) proposed unit CPGs associated with limb degrees of freedom. Unitary oscillators at a single joint or several different joints are fundamental features of locomotor motor control. However, the specific degrees of freedom used in pattern generation are under active investigation. Modular CPGs are often studied in fictive preparations and control groupings analyzed (Stein et al., 1998b; Stein and Daniels-McQueen, 2002). Recent results from cat fictive locomotion (Hamm et al., 1999) using coherence measures suggest motor commands are multijoint to flexors and extensors. Spinal cord pattern generation supports modular bursting that drives single-joint or multijoint muscle synergies. Our data also support multijoint burst generators.

Our data relate to the idea of motor primitives (Appendix 1, available at www.jneurosci.org). Bizzi et al. (1991), Giszter et al. (1993), and Mussa-Ivaldi et al. (1994) developed this description. Using isometric limb end point force, they constructed force-field descriptions in unparalyzed animals. Fields captured interaction of muscle recruitment, muscle force generation, and limb kinematics (Appendix 1, available at www.jneurosci.org). A motor repertoire could be organized from a few force-field primitives (Mussa-Ivaldi, 1992; Mussa-Ivaldi and Giszter, 1992; Mussa-Ivaldi and Bizzi, 2000). Small numbers of force-fields seen in cord stimulation or reflexes, suggested modular force-field primitives organized reflex behaviors. The 275 msec burst durations in data here match those observed during reflex trajectory formation and adjustment (Kargo and Giszter, 2000a). In correction responses in the study by Kargo and Giszter (2000a), a specific synergy (coactivated hip and knee flexors: iliopsoas, gluteus, iliofibularis, and sartorius) could be directly related to the kinematic correction and to an isometric force-field measurement associated with correction. Our current data build on these observations, to suggest the biomechanical force-field descriptions developed previously can be linked directly to unitary premotor burst generators from pattern generation. In data here, such synergy bursts were extracted statistically from the motor pattern but have features needed to support the properties of force-fields described in our previous work (see Appendix 1, available at www.jneurosci.org). In the studies by Kargo and Giszter (2000) and Giszter and Kargo (2000), such bursts were recruited in a controlled manner by cutaneous impact of the leg with obstacles, or were spontaneously deleted from the pattern by the spinal cord itself. In both cases, the specific synergy and burst could also be associated directly with force-fields.

Burst-like motor patterns also occur during ontogeny of motor activity. Muscles organize into oscillating groups during development. These groups elaborate more sophisticated phase patterns as development proceeds (for review, see Vinay et al., 2002). This activity may organize the neuromuscular junction, patterns of feedback, and interneuronal organization. Models have also been proposed in which developmental mechanisms build primitives for both phasic and cyclic pattern generation (Todorov and Ghahramani, 2003).

Unit bursts here could represent structural circuits of the CPG, or these could be emergent patterns of the CPG. Alternatively, they might be independent “downstream” elements recruited by CPGs. Only more detailed understanding of spinal circuitry can resolve these questions.

The basis of more complex movements

Our data address how richer motor repertoires are built from simpler building blocks. Controls might alter the composition of drives or alter durations of bursts in drives or the phases among bursts (Giszter et al., 2001). Our data emphasize the first idea. Brainstem drives used less muscles than spinal (Fig. 5), although brainstem muscle groups were similar to spinal groups. There was more co-contraction after spinalization. However, three spinal synergies also dropped one muscle from this brainstem “core” as well as adding others (i.e., there were muscles in the brainstem frog's synergies not found in corresponding spinal synergies). Muscle groupings in spinalized frogs are not an irreducible basis set for supraspinal control. Descending pathways play a crucial role in organizing modularity of spinal circuits. The interaction of brainstem and spinal circuits further sculpts synergies. Descending pathways modulate communication among spinal segments and muscles, via primary afferent depolarization (Fleshman et al., 1988; Eguibar et al., 1997) and properties of motoneuron dendrites (Hounsgaard and Kiehn, 1993; Lee et al., 2003). Loss of inhibition and modulation probably contributes to the alteration of the spinalized frog synergies and to more antagonist co-contraction. This change slows limb movement and decreases efficiency of motor patterns, consistent with a reduced repertoire.

Conclusions

Our data show spinal cord motor patterns can be considered modular, comprising characteristic drives and bursts that have minimal mutual information. These bursts are reused in multiple behaviors. Brainstem mechanisms shape the bursts, improving smoothness and reducing cocontraction. The bursts here relate to force-field descriptions obtained previously and to unit burst generators in pattern generation. Amplitude and timing control of modular unit bursts driving six synergies can account for 80% of motor pattern structure and an extensive repertoire. In summary, a simple modular motor organization of burst generators and drives may explain most of the behavioral repertoire of the frog.