Spike Synchronization in the Cortex-Basal Ganglia Networks of Parkinsonian Primates Reflects Global Dynamics of the Local Field Potentials

Abstract

Cortical local field potentials (LFPs) reflect synaptic potentials and accordingly correlate with neuronal discharge. Because LFPs are coherent across substantial cortical areas, we hypothesized that cortical spike correlations could be predicted from them. Because LFPs recorded in the basal ganglia (BG) are also correlated with neuronal discharge and are clinically accessible in Parkinson's disease patients, we were interested in testing this hypothesis in the BG, as well. We recorded LFPs and unit discharge from multiple electrodes, which were placed in primary motor cortex or in the basal ganglia (striatum and pallidum) of two monkeys before and after rendering them parkinsonian with 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine. We used the method of partial spectra to construct LFP predictors of the spike cross-correlation functions (CCFs). The predicted CCF is an estimate of the correlation between two neurons under the assumption that their association is explained solely by the association of each with the LFP recorded on a third electrode. In the normal condition, the predictors account for cortical rate covariations but not for the association among the tonically active neurons of the striatum. In the parkinsonian condition, with the appearance of 10 Hz oscillations throughout the cortex-basal ganglia networks, the LFP predictors account remarkably better for the CCFs in both the cortex and the basal ganglia. We propose that, in the parkinsonian condition, the cortex-basal ganglia networks are more tightly related to global modes of brain dynamics that are echoed in the LFP.

Introduction

Local field potentials (LFPs), mostly below 100 Hz, appear throughout the brain. Extensive electrophysiological studies have formed the current view that cortical LFPs result from synaptic activity (Eccles, 1951; Creutzfeldt et al., 1966; Elul, 1971; Klee and Rall, 1977; Mitzdorf, 1985; Eggermont and Smith, 1995a; Bedard et al., 2004). Correspondingly, the LFP fluctuations tend to have a strict phase relationship to cortical discharge: negative deflections in the LFP coincide with increases in the instantaneous firing rates of cortical neurons (Lass, 1968; Gray and Singer, 1989; Murthy and Fetz, 1996a; Donoghue et al., 1998; Destexhe et al., 1999). In addition, these fluctuations are highly correlated across distances of several millimeters in cortex (Eckhorn and Obermueller, 1993; Sanes and Donoghue, 1993; Murthy and Fetz, 1996b; Contreras et al., 1997; Bullock, 1999; Destexhe et al., 1999). Because LFPs are common to a large region of cortex and are correlated with spiking activity throughout that region, it is expected that they may be used to predict, at least in part, the neuronal correlations in cortex (Eggermont and Smith, 1995b). Because neuronal correlations elucidate collective dynamics, successfully predicting them from the LFP implies that this signal is highly informative of these dynamics (Bullock, 1997).

The theoretical account of the origin of cortical LFPs rests on the repetitious columnar structure of the cortical microanatomy (Elul, 1971; Klee and Rall, 1977; Abeles, 1982; Mitzdorf, 1985; Eggermont and Smith, 1995a). It is thus unclear whether this cortical model is applicable to other parts of the brain that lack this structure, such as the basal ganglia (BG). Nevertheless, LFPs are readily recorded from the BG of Parkinson's disease patients (Brown et al., 2001; Marsden et al., 2001; Cassidy et al., 2002) and, as in cortex, have been shown to correlate with spiking activity in these nuclei (Levy et al., 2002b). Because enhanced neuronal correlations are an established correlate of the parkinsonism (Raz et al., 1996; Hurtado et al., 1999; Levy et al., 2000, 2002a; Raz et al., 2000; Goldberg et al., 2002), we became interested in the question of whether the LFP recorded in the cortex and the BG of 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP)-treated parkinsonian primates may be used to predict this abnormal synchronization. Although answering this question cannot elucidate the sources of BG LFPs, it may highlight the importance of this signal in conveying information about collective BG dynamics. Moreover, it would justify clinically manipulating this signal for the prospect of alleviating parkinsonism (Tass, 1999; Rosenblum and Pikovsky, 2004).

The goal of the present study was to quantify in normal and parkinsonian primates to what extent spike correlations in cortex and in the BG may be predicted from the LFP. We recorded ongoing LFPs and spiking activity from multiple electrodes in the primary motor cortex (MI), striatum, or external segment of the globus pallidus of two monkeys before and after treating them with MPTP. We used partial spectra analysis (Halliday et al., 1995) to generate an LFP-predicted cross-correlation function (CCF) of the discharge of pairs of neurons (Eggermont and Smith, 1995b). This predicted CCF constitutes an estimate of the correlation between two neurons under the assumption that their association is explained solely by the association of each with the LFP. The goodness-of-fit between the predicted and observed CCFs indicates to what extent the correlations between the neurons are predicted by the ongoing LFP.

Materials and Methods

The experimental design, surgical procedures, use of accelerometers, histology, and details of the neuronal data set have been described extensively, previously (Goldberg et al., 2002). Briefly, two monkeys [monkey S, Cercopithecus aethiops (vervet), female, 3.5 kg weight; monkey Z, Macaca fascicularis, female, 2 kg weight] were trained to perform a self-initiated button-pressing task with their dominant hands. Both monkeys were rendered parkinsonian by systemic treatment with MPTP (see below). The monkeys' health was monitored by a veterinarian, and their fluid consumption, diet, and weight were monitored daily. The monkeys' care and surgical procedures were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals (1996) and with the Hebrew University guidelines for the use and care of laboratory animals in research, supervised by the institutional committee for animal care and use.

Surgical, pharmacological, and neuronal recording procedures

After training, a square recording chamber with a 27 mm side was attached to the skull under deep anesthesia in aseptic conditions. The central and arcuate sulci were within the chamber, and, in monkey S, good access to striatum and globus pallidus (GP) was available in the anterior part of the chamber. MPTP HCl (Sigma, St. Louis, MO) was injected systemically five times over a period of 4 d (0.4 mg/kg per injection, i.m.), under mild (10 mg/kg, i.m.) ketamine anesthesia. In each recording day, eight glass-coated tungsten (0.2-1.2 MΩ at 1 kHz) electrodes, confined to a 1.65-mm-inner-diameter guide tube, were inserted into the brain with a mechanical microdrive (EPS 1.28; Alpha-Omega Engineering, Nazareth, Israel). For striato-pallidal penetrations, the guide tube with the eight electrodes was first advanced ∼9 mm below the dura mater into the brain. Each electrode was then individually advanced to obtain optimal recording of single neurons. The distance along the recording track between simultaneous recording sites reached up to 4 mm but was typically 1-2 mm.

Neuronal data acquisition and analysis

We include in the analysis data from 29 cortical and 42 striato-pallidal recording sessions from 14 and 18 d, respectively, in monkey S, and 18 cortical recording sessions from 8 d in monkey Z. Cortical recordings were from the arm area of MI, pallidal recordings were from the external segment of the globus pallidus, and striatal recordings had the characteristics of the tonically active neurons (TANs) (Goldberg et al., 2002). Recording sessions typically lasted 55 min but ranged from 16 to 98 min. The output of the eight electrodes was amplified by 10⁴, bandpass filtered (1-6000 Hz, four-pole Butterworth filter), digitized at 24 kHz, and logged on a computer for off-line processing (see Fig. 1, Raw). Our analysis focused on spontaneous activity, defined as the neuronal activity during periods in which the monkey was immobile. Two uniaxial accelerometers (8630C5; Kistler, Amherst, NY) were fastened to the each of the monkey's wrists. The accelerometer on the contralateral (working) arm was used to identify periods of immobility, defined as periods in which the root mean square of the accelerometer output was below a threshold of 25 cm × sec^-2. All off-line data analysis was conducted by custom-made Matlab (The MathWorks, Natick, MA) code.

Figure 1.

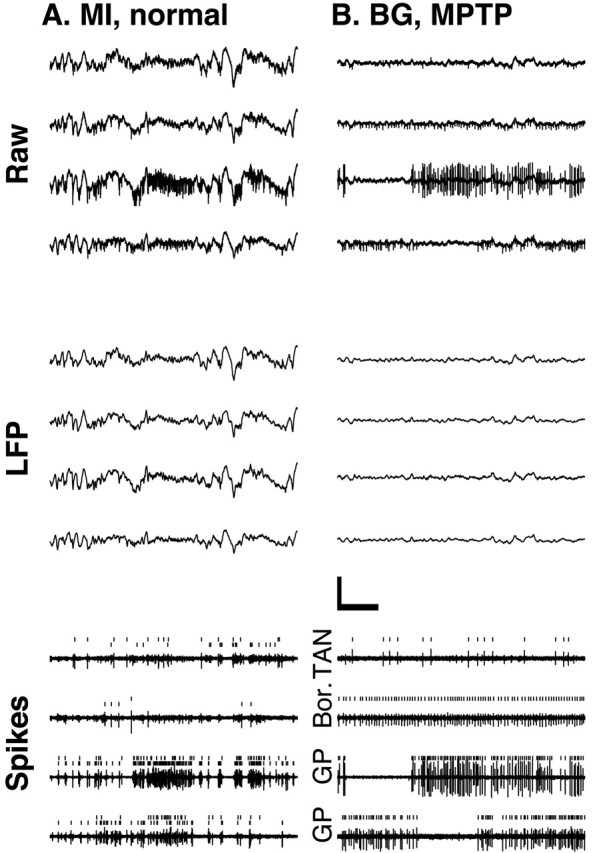
Multiple-electrode recordings from the MI and the BG. Four simultaneous 3 sec electrode traces of the extracellular recording from monkey S are shown. Raw, The output of the amplifiers, which includes both spiking activity and the slower LFPs. LFP, Digitally low-pass filtered (<150 Hz) versions of the raw traces. Calibration: 500 msec, 500 μV. Spikes, Digitally high-pass filtered versions (>500 Hz) of the corresponding raw data (arbitrary y scale). Ticks mark the spikes identified by the on-line spike sorting. Two units are shown in each MI trace. Traces in A are from MI in the normal condition. Traces in B are from the BG in the MPTP-treated condition. GP, Neuron recorded from the globus pallidus. Bor., Border cell located on the border between the striatum and the GP. TAN, A tonically active neuron of the striatum.

Spikes and CCFs. A different bandpass-filtered (0.3-6 kHz) version of the amplified analog data was fed to a template-matching device to isolate on-line the extracellular activity of one to three units per electrode (see Fig. 1, Spikes). The timing of the detected spikes was sampled at 12 kHz (MCP+, MSD2.1, AlphaMap 4.8; Alpha-Omega Engineering). Only spike trains judged to be emitted by a single cell during the real-time sorting were subjected to rate stability analysis. After stability analysis, the pairwise CCFs for cells recorded on different electrodes (Bar-Gad et al., 2001) were calculated as follows: coincidence histograms at 1 msec resolution were estimated over periods of immobility that were at least 2 sec long. The coincidence histogram was then normalized to a dimensionless CCF that tends to unity for large absolute time lags. A neuronal pair was considered significantly correlated if the square-root transformation of its CCF departed from its 95% confidence interval (CI) for a range of delay lags that was at least 8 msec long. The square-root transformation of the CCF is used because it approximately stabilizes the variance of the CCF across all delay lags (Brillinger, 1976).

LFPs and their spike-triggered averages. The analog data from the eight channels were down sampled to 400 Hz after applying an anti-aliasing low-pass (<150 Hz) finite impulse response filter (see Fig. 1, LFP). We calculated the mean value of the correlation coefficient between traces of the LFP on different electrodes by randomly choosing distinct and thus independent pairs of electrodes. The spike-triggered average (STA) of the LFP was calculated as follows: let t_s denote the spike times of a certain spike train rebinned to the sampling frequency of the LFP, and let X(t) denote the LFP recorded on a certain electrode. Using these spikes, the STA is defined as follows:

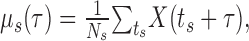1

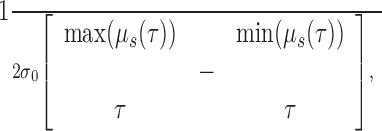
where N_s is the number of spikes in the spike train. μ_s(τ) measures the mean value of the LFP at a delay of τ from a spike emitted at time 0. The 99.9% CIs for the STA (see Fig. 2) were calculated by time reversing the LFP signal, recalculating the average for the time-reversed signal, and estimating the 3.1 SDs of the resulting waveform. These conservative CIs were chosen because they were judged visually to capture the variability of the STA. Using less conservative CIs did not change the results. We define the “spike-LFP correlation measure” (SLCM) (see Fig. 3) of the waveform of the STA μ_s(τ) as follows:

2

Figure 2.

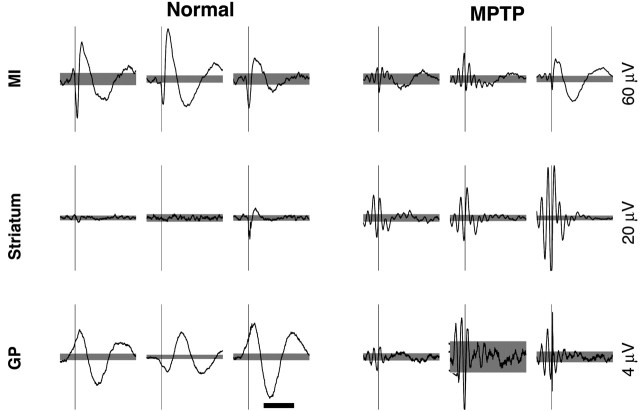
STAs of the LFP. Three examples of the STAs from each structure in both the normal and the MPTP-treated condition. Calibration: 500 msec. Thin vertical lines mark the time of the spikes. The scales of the vertical lines are given to the right of the examples. Gray background, Confidence interval of 99.9%. Examples from the primary motor cortex in the MPTP condition are taken from monkey Z. All other examples are from monkey S. In the rightmost columns in both conditions (Normal, MPTP), the spike and LFP are recorded on the same electrode.

Figure 3.

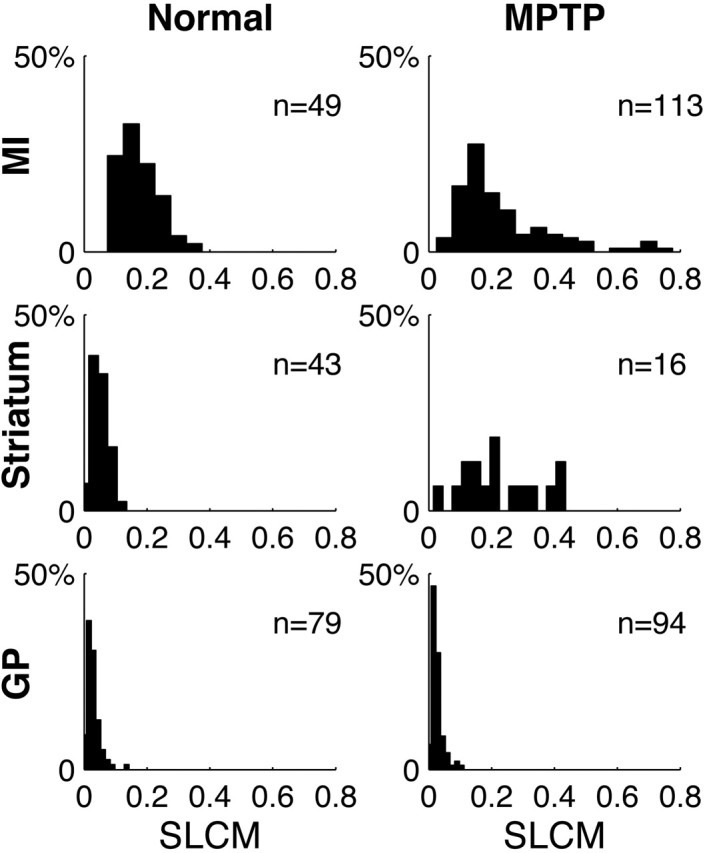
Distribution of the SLCMs between spikes and the LFP. Frequency histograms of the SLCMs from all structures in both the normal and the MPTP-treated conditions in monkey S. The number (n) of units used to generate the histogram is indicated.

where σ₀ is the SD of the LFP, and τ is between -0.5 and 1.5 sec. We divide by 2 to average the maximal positive and negative deflections.

LFP-predicted CCFs. The predicted CCF is constructed as follows. Given two spike trains and a trace of the LFP, we constructed their respective STAs, denoted μ₁(τ) and μ₂(τ). We used the LFP recorded on an arbitrarily chosen third electrode that was different from those on which the spike trains were recorded. This was done to control for the distortion of the STA waveform calculated for a unit recorded on the same electrode as the LFP (see Fig. 2, Striatum, rightmost example). Using other channels gave similar results (data not shown). Next, we calculated the Fourier transform of these two STAs, denote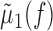d and 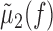, respectively, where f denotes frequency. Similarly, we calculated the power spectrum of the LFP, denoted σ²(fl), which is the Fourier transform of the autocovariance sequence of the LFP. The LFP-predicted CCF is then given by the following:

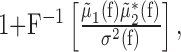3

where the asterisk denotes complex conjugation, and F^-1 is the inverse Fourier transform. The LFP-predicted CCF is the solution of a statistical model that assumes (1) a linear relationship between the firing rates of the neurons and the LFP and (2) that these firing rates are independent, given the LFP. A close correspondence between the predicted and observed CCFs means that the underlying assumptions in constructing the predictor are valid to a good approximation (Brillinger, 1983; Halliday et al., 1995). The goodness-of-fit between the observed and LFP-predicted CCFs was evaluated by calculating their Pearson's product-moment correlation coefficient, denoted c.c., and then calculating its Fisher's Z-transform:

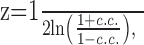4

where ln(·) is the natural logarithm (Sokal and Rohlf, 1995). Equation 3 demonstrates that the fraction by which the predicted firing rate of one neuron is modulated as a result of its association with the other behaves like the product of the quotients 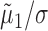and . The amplitude squared of each of these quotients relays what part of the variance of the LFP (per each frequency component) is attributable to the spiking of the corresponding neuron. In other words, these quotients are a measure of the correlation between the spiking of the neurons and the LFP. The SLCM (Eq. 2) is also a measure (in the time domain) of this correlation and can be used to estimate the amplitude of these quotients. Hence, the size of the fluctuations in the LFP-predicted CCF scales like the product of two SLCMs.

Generation of an LFP-predicted CCF was suggested previously (Eggermont and Smith, 1995b) and involved constructing from each of the two STAs and the raw LFP trace an estimator of the instantaneous rate of both neurons as a function of time. The LFP-predicted CCF was consequently generated by calculating the cross-covariance sequence of the two instantaneous rate traces. The current derivation is more straightforward in that these stages are implicit in the expression for the LFP-predicted CCF (Eq. 3) and do not need to be evaluated explicitly. In addition, we used the LFP recorded on a third electrode.

Results

The LFP is a global signal in cortex and in the BG

The LFP fluctuations are present in the ongoing activity in both cortex and the BG. Within each of these regions, the amplitude of the LFP fluctuations is quite constant across electrodes (Elul, 1971), in contrast to the amplitude of extracellularly recorded spikes (Fig. 1, Raw), which depends strongly on the distance between the electrode and the recorded neuron (Abeles, 1974; Asanuma, 1989) and on its geometry. Moreover, we found that in both cortex and the BG, the LFPs recorded simultaneously on different electrodes were remarkably similar to each other (Fig. 1, LFP). To quantify this similarity, we calculated the c.c. between the LFPs recorded on different electrodes. We found that the mean (calculated for independent pairs) of this coefficient in the normal and in the MPTP conditions ranged between 0.83 and 0.89 for pairs of electrodes in the cortex (n = 16, normal; n = 61, MPTP) and in the BG (n = 59, normal; n = 54, MPTP). Moreover, there was no significant difference between the values of the c.c.s calculated for cortical versus BG pairs or between the values before versus after MPTP treatment in either of these regions (two-tailed t tests on the Fisher Z-transformed values of the c.c.). In agreement with previous cortical studies (Eckhorn and Obermueller, 1993; Sanes and Donoghue, 1993; Murthy and Fetz, 1996b; Contreras et al., 1997; Bullock, 1999; Destexhe et al., 1999), we conclude that the LFPs recorded on a given electrode in either cortex or the BG can be taken as a signal common to all neuronal elements in its vicinity (of a few cubic millimeters).

The relationship of the LFP to spiking activity

The SD of the LFP is approximately three times larger in cortex (137 ± 30 μV; mean ± SD; n = 44 recording sites) than in either the striatum (38.7 ± 4.8 μV; n = 47) or the GP (44.5 ± 5.5 μV; n = 84). This difference was also observed in the MPTP condition (the examples in Fig. 1 are from the normal condition in MI and from the MPTP-treated condition in the BG). This finding raises the possibility that the electrodes positioned in the BG may actually be picking up an attenuated version of changes in the electrical field that are generated elsewhere, perhaps in the thalamocortical circuits (Abeles, 1982). Taken to the extreme, this suggests that the LFP recorded in the BG could be unrelated to the neuronal activity there. To determine whether neuronal discharge is related to the LFP, we calculated the waveform of the STA of the LFP fluctuations in the cortex and the BG. We found that, in the normal condition, the waveforms of STAs in the cortex and the GP were significantly different from zero at approximately the time of a spike and for >1 sec after the spike (Fig. 2, Normal). After MPTP treatment, STAs that exhibited significant oscillatory waveforms with a frequency of ∼10 Hz were observed throughout the cortex-BG network (Fig. 2, MPTP). The waveforms of the STAs calculated for a given spike train using the LFP recorded on different electrodes were highly correlated with each other (data not shown), indicating that, just as the overall LFP variability is common to the neuronal elements in its vicinity, so is the component of this variability that is correlated with neuronal discharge.

Finding significantly modulated STA waveforms in the BG indicates that, in principle, the discharge of these BG neurons is related to the LFP. To quantify the strength of this correlation, we used the ratio of the STA waveform amplitude to the SD of the LFP fluctuations, which we coin the SLCM (Eq. 2). In Figure 3, we present frequency histograms of the SLCMs in all structures in both conditions for monkey S. This figure demonstrates that the SLCMs in the GP are very small, indicating only a small correlation between GP discharge and the LFP in both the normal and the MPTP condition. In contrast, the SLCMs are large in both conditions in the cortex. The appearance of oscillatory STAs in the striatum after MPTP (Fig. 2, Striatum) is accompanied by a significant increase in the SLCMs, relative to the normal condition (p < 0.001; one-tailed Wilcoxon rank-sum test) (Fig. 3, Striatum).

The gross temporal asymmetry of the STA waveforms at approximately the time of the spike, although not a new finding, warrants some discussion. It is evident that the waveforms precede the time of spike emission by tens of milliseconds and, in this sense, are consistent with that view that the LFP represents input to the neuron. However, most of the waveform is composed of a slow oscillation that follows the spike. In cortex, this slow waveform may reflect such processes as slow afterhyperpolarizations and disfacilitation (Lorenzon and Foehring, 1992; Cowan and Wilson, 1994; Contreras et al., 1996) or even short-term synaptic depression (Varela et al., 1997). Because negative deflections in the LFP covary with increases in nearby neuronal firing rates (Gray and Singer, 1989; Eckhorn and Obermueller, 1993; Murthy and Fetz, 1996a; Donoghue et al., 1998; Destexhe et al., 1999), these prolonged STA waveforms imply that the emission of a spike is typically followed by slow changes in the local population discharge. These slow changes are therefore expected to generate a slow covariation of the firing rate in neuronal pairs, which is the topic of the next section.

Predicting spike correlations from the LFP

Consider two spike trains that are correlated with the LFP, as indicated by their respective STAs. The fact that the LFP is a signal that is common to all electrodes raises the possibility that the correlation between these spike trains can be explained by the coupling of each one to the LFP (Eggermont and Smith, 1995b). To test this possibility, we compared the observed CCF of the spike trains with a CCF that was predicted under the assumption that the neurons are correlated solely through their relationship to the LFP. The predicted CCF is generated from the two STAs and the autocovariance function of the LFP by the method of partial spectra (Eq. 3) (Brillinger, 1983; Halliday et al., 1995). A good match between the predicted and the observed CCFs indicates that the correlation between the neurons is predictable from their relationship to the ongoing LFP. It is important to note that, even if the predicted CCF exactly matches the observed one, this analysis cannot determine a causal relationship between spiking and the LFP.

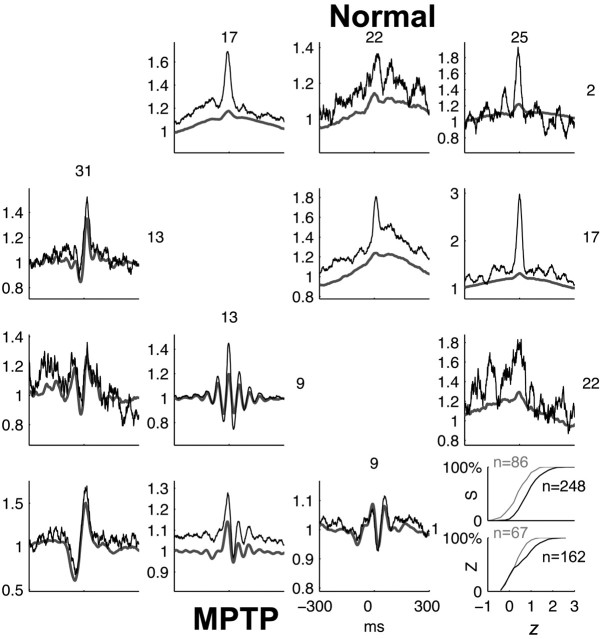
In cortex, we found that in both the normal and the parkinsonian conditions, the rate covariations in the CCFs (i.e., at large temporal scales) can be well predicted from the LFP (Fig. 4). The sharper (<80 msec wide) peak often present at approximately time 0 is only partially reconstructed (Eggermont and Smith, 1995b), which means that the neurons are correlated beyond what is predicted by their instantaneous rates alone. In the parkinsonian condition, the reconstruction of the peaks and the troughs of the oscillatory CCFs is truly remarkable (Fig. 4, MPTP). To estimate the goodness-of-fit of the LFP-predicted CCF to the observed one, we calculated Fisher's Z-transform of the c.c. between the two, denoted z. This was done only for the pairs exhibiting significant coupling (Fig. 4, inset), to avoid the confounding effect of comparing CCFs that are not significantly modulated. There was no difference in the number of significantly correlated cortical pairs in the normal and MPTP conditions in either monkey S (normal, 86 of 118, 73%; MPTP, 248 of 337, 74%) or monkey Z (normal, 67 of 136, 49%; MPTP, 162 of 326, 50%). Nevertheless, the values of z were significantly larger in the parkinsonian condition in both monkeys (monkey S, p < 10^-3; monkey Z, p < 0.05; two-tailed Wilcoxon rank-sum test), indicating that the LFP explains a larger portion of the correlations between neurons in the parkinsonian cortex than in the normal one.

Figure 4.

Comparison of predicted and observed CCFs in MI in the normal and MPTP-treated conditions. Top triangular matrix, Observed (black) and predicted (gray) CCFs of all pairs from four simultaneously recorded units in the normal condition. Bottom triangular matrix, Observed and predicted CCFs in the MPTP-treated condition. CCFs are normalized so that they tend to unity for large absolute time lags. Inset, Cumulative frequency distributions of the Fisher Z-transformed value (z) of Pearson's product-moment correlation-coefficient between the predicted and observed CCFs in the normal (gray) and MPTP-treated (black) conditions, calculated for the cases in which the observed CCFs was significantly modulated. S and Z denote the monkey. The number of neuronal pairs (n) used to generate the histogram is indicated. The significant (p < 0.05; two-tailed Wilcoxon rank-sum test) shift in the histograms indicates that the value of z is stochastically larger in the MPTP condition, implying a closer match between the predicted and observed CCF.

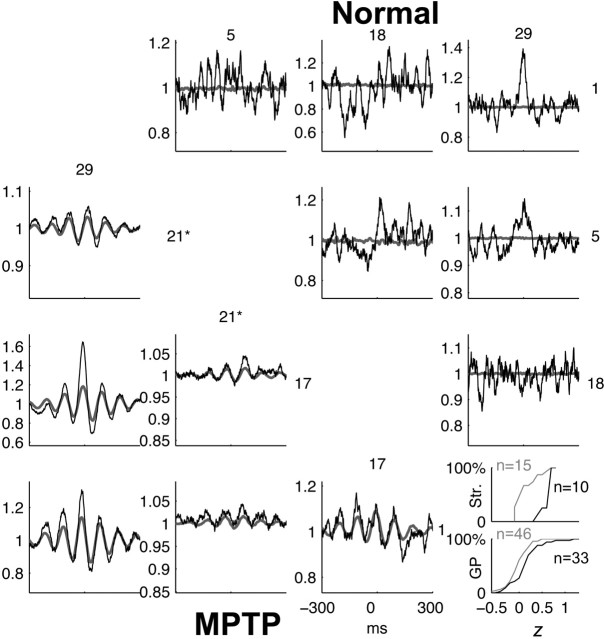
In the normal GP, the majority of recorded pairs were uncorrelated (122 of 168, 73%), with correspondingly flat LFP-predicted CCFs (data not shown), despite the fact that the waveforms of the STAs in the GP were significantly different from zero (Fig. 2). The flatness of the predicted CCF in this case is consistent with the small values of the SLCMs associated with these STAs (see Materials and Methods). In the normal striatum, 19% (15 of 79) of striatal pairs exhibit a peak in the CCF (Fig. 5, Normal) (Raz et al., 1996; Kimura et al., 2003). However, their corresponding LFP-predicted CCFs were flat, again attributable to the smallness of the SLCMs.

Figure 5.

Comparison of predicted and observed CCFs in the BG in the normal and MPTP-treated conditions. Format is the same as in Figure 4. All units are striatal TANs, except unit 21 (marked by an asterisk) in the MPTP condition, which is a GP unit. Inset, The cumulative frequency histograms are calculated separately for striatal (Str.) and GP pairs. The value of z is also stochastically larger when all BG pairs are pooled together (p < 0.001; two-tailed Wilcoxon rank-sum test), implying a closer match between the predicted and observed CCF in the MPTP condition.

After MPTP treatment, the percentage of correlated pairs in the GP decreased to 17% (33 of 197). This finding contrasts with the results from other vervets (Raz et al., 2000) and may be related to the fact that monkey S did not develop tremor (Goldberg et al., 2002; Levy et al., 2002a). In the striatum, the number of correlated pairs increased dramatically to 77% (10 of 13). The SLCMs of the striatal STAs increase with the appearance of 10 Hz oscillations, resulting in substantial oscillations in the LFP-predicted CCFs (Fig. 5, MPTP). As in cortex, (1) the predicted CCFs reconstruct the observed ones well, and (2) the values of the z in the BG increase significantly after MPTP (striatum, p < 0.001; GP, p < 0.05; two-tailed Wilcoxon rank-sum test) (Fig. 5, inset). Interestingly, the oscillations in the LFP-predicted CCF can a posteriori reveal an oscillatory component in the observed one that may be overlooked or judged insignificant otherwise (Goldberg et al., 2002). For example, consider the CCF of the striato-pallidal pair 1,21 in Figure 5 (MPTP). The 10 Hz oscillatory modulation of firing rates is <5% of the baseline rate. Nevertheless, the LFP predictor demonstrates that this weak oscillatory component is real.

Discussion

We found a high temporal correlation between LFPs recorded on electrodes that were separated by up to a few millimeters in either cortex or the BG, indicating that the LFPs constitute a signal common to large volumes of tissue (Eckhorn and Obermueller, 1993; Sanes and Donoghue, 1993; Murthy and Fetz, 1996b; Contreras et al., 1997; Bullock, 1999; Destexhe et al., 1999). By generating LFP-based predictors of the CCFs of pairs of neurons, we quantified to what extent the neuronal correlations in the ongoing spontaneous activity in cortex or the BG are explained by this global signal. We found that, in general, the slow rate covariations are predicted well by the LFP, in line with previous findings that cortical LFPs covary with neuronal firing rates (Lass, 1968; Gray and Singer, 1989; Eckhorn and Obermueller, 1993; Murthy and Fetz, 1996a; Donoghue et al., 1998; Destexhe et al., 1999). This finding suggests that the collective network dynamics reflected in the structure of neuronal correlations are primarily determined by some global mode of these dynamics (Ginzburg and Sompolinsky, 1994). This mode, in turn, is presumably reflected in the time course of the LFP fluctuations. Finally, we found that, in the MPTP condition, the prediction of the observed CCFs improved in all structures, suggesting an enhanced role of the global mode in determining neuronal correlations in parkinsonism.

As a correlation-based method, the partial spectra analysis cannot determine causality between the LFP and neuronal discharge. Moreover, by construction, the estimator is actually acausal, predicting rate covariations by using the LFP signal that both precedes and follows the spikes. In particular, this analysis cannot reveal the underlying sources of the LFP and how these influence or are influenced by neuronal discharge. Nevertheless, the successful reconstruction of neuronal correlations from the LFP is consistent with the current cortical model that assumes that this signal is representative of common and/or recurrent input to the neurons (Eccles, 1951; Creutzfeldt et al., 1966; Elul, 1971; Klee and Rall, 1977; Mitzdorf, 1985; Eggermont and Smith, 1995a; Bedard et al., 2004), possibly in the BG, as well (Updyke and Liles, 1987; Brown et al., 2001; Goto and O'Donnell, 2001; Marsden et al., 2001; Cassidy et al., 2002; Levy et al., 2002b).

Although the LFP predictor is successful at predicting the slow-rate covariations, it usually underestimates the additional short-term correlations (Eggermont and Smith, 1995b). The systematic underestimation of the narrow peaks at approximately time 0 may be a result of the linearity of our analysis. Nonlinear interactions between the output of neurons (e.g., simultaneous changes in their gain) could induce correlations between these neurons that would not be predicted from the LFP using this linear method. Alternatively, the short-term correlations may represent functional coupling between neurons that is independent of the LFP. For instance, they may reflect the activation of local cell assemblies (Abeles, 1982; Palm, 1982; Eggermont, 1990) whose activity is not reflected in the LFP. We propose that the dynamics of the TANs in the normal condition constitute an example of the latter scenario. As we have seen, the STAs and consequently the LFP-predicted CCFs are flat, even when the spike trains of these neurons are correlated (Raz et al., 1996; Kimura et al., 2003). The independence of the TAN dynamics from the LFP dynamics may result from the fact that the TANs, which are presumably the cholinergic interneurons of the striatum (Wilson et al., 1990; Aosaki et al., 1995), make up <2% of the striatal neurons (Wilson, 2003). Thus, even if the LFP fluctuations are generated in the striatum (Updyke and Liles, 1987), they may represent the neuronal activity of the medium spiny neurons (MSNs), which form the main population of striatal neurons. Furthermore, the possibility that the synaptic input to the MSNs is different from that of the TANs (Bolam et al., 2000) could explain why the discharge of the TANs is virtually uncorrelated with the LFP. Hence, our analysis is consistent with the view that the TANs form synchronized sparse assemblies of neurons that modulate the activity of the MSNs (Aosaki et al., 1995; Raz et al., 1996; Kimura et al., 2003).

This study joins numerous other studies that demonstrate the appearance of synchronized oscillatory activity within the BG of human and primate parkinsonian subjects (Nini et al., 1995; Raz et al., 1996; Levy et al., 2000, 2002b; Raz et al., 2000, 2001; Marsden et al., 2001). The global nature of the oscillations throughout the network is indicated by the facts (1) that we found similar synchronous 10 Hz oscillations in both cortex and the striatopallidal complex, (2) that these oscillations are found in the LFP fluctuations that are highly correlated across large regions of the brain, and the novel demonstration that (3) the spike synchronization is in fact predicted by the LFP. These findings support the view that implicates the whole cortex-BG-thalamus circuit in the generation of low-frequency oscillations (Magill et al., 2000; Raz et al., 2001) and does not attribute it solely to circuits internal to the BG (Plenz and Kitai, 1999).

We interpreted the improved fit in the parkinsonian condition of the LFP-predicted CCF to the observed one as resulting from an enhanced role of global network modes in determining neuronal correlations (Ginzburg and Sompolinsky, 1994). Why the MPTP insult should lead to a stronger influence of such modes is unclear. Recent modeling work addressing the onset of 5-15 Hz neuronal oscillations in the cortex-BG circuits has suggested that they may result from the destabilizing of an effective negative-feedback loop formed in these circuits as a result of the insult. In these models, the destabilization leads to the appearance of a global oscillatory mode that influences neuronal discharge throughout the circuit (Goldberg et al., 1999; Leblois et al., 2002). However, the MPTP-induced enhancement of neuronal synchronization within the cortex-BG circuits is not restricted to these high frequencies (Goldberg et al., 2002; Heimer et al., 2002) (but see Levy et al., 2002a). Moreover, we found that the improved fit of the predicted CCF to the observed one was true in cortex, even when considering the pairs of neurons that did not display any oscillatory coupling (data not shown). Thus, additional work is required to determine the mechanism by which the MPTP insult leads to more prominent global modes of brain dynamics.

Our results suggest that, during other physiological conditions characterized by exceptionally global LFPs (e.g., under anesthesia or during slow-wave sleep) (Destexhe et al., 1999), application of the current analysis will demonstrate that neuronal correlations can be primarily predicted from these signals. Indeed, a previous study conducted in the auditory cortex of anesthetized cats introduced the LFP-predicted CCF and demonstrated, as we found in awake primates, that the gross structure of the CCF is predicted from the LFP (Eggermont and Smith, 1995b). Additionally, it is likely that spike correlations can be successfully predicted from other global macrosignals as well (e.g., optical imaging) (Arieli et al., 1996). Macrosignals have the advantage of being sensitive to global modes of the network dynamics. An important demonstration of this property is present in the current analysis. We found that the presence of 10 Hz oscillations in the LFP was relatively easily and robustly demonstrated in the waveforms of the STAs in the parkinsonian condition. In contrast, it was difficult to determine the presence of an oscillatory component in the observed spike CCFs. This difference is understood when considering the details of the analysis. The coupling strength between spikes and the LFP is quantified by the SLCM. The amplitude of the LFP-predicted CCFs can be estimated as the product of the SLCM of each of the neurons with the LFP (see Materials and Methods). Thus, whereas estimating an STA whose corresponding SLCM is 0.1-0.2 may be relatively easy and may require less data, estimation of a CCF with an amplitude of this SLCM squared (i.e., 0.01-0.04), will be difficult and will require much more data. Finally, in contrast to single-unit recordings that require precise and stable placement of microelectrodes, macropotentials are easily accessible with macroelectrodes and may be more robust to electrode shifts. These properties are especially advantageous in the case of electrophysiological recordings from the BG of Parkinson's disease patients with deep-brain stimulators (Brown et al., 2001; Cassidy et al., 2002; Levy et al., 2002b).

In conclusion, the observation that the LFP quantitatively accounts for neuronal correlations, primarily in the form of rate covariations, advances our understanding of this signal by conferring it with a role of a global mode of brain dynamics (Eggermont and Smith, 1995b). The finding that this role is enhanced in parkinsonian primates underscores the potential of recording the LFPs with deep-brain electrodes and using them as a feedback signal to improve the therapeutic effect of deep-brain stimulators (Tass, 1999; Rosenblum and Pikovsky, 2004).