Whisker Vibration Information Carried by Rat Barrel Cortex Neurons

Abstract

Rats can make extremely fine texture discriminations by “whisking” their vibrissa across the surface of an object. We have investigated one hypothesis for the neuronal basis of texture representation by measuring how clusters of neurons in the barrel cortex of anesthetized rats encode the kinetic features of sinusoidal whisker vibrations. Mutual information analyses of spike counts led to a number of findings. Information about vibration kinetics became available as early as 6 msec after stimulus onset and reached a peak at ∼20-30 msec. Vibration speed, proportional to the product of vibration amplitude (A) and frequency (f), was the kinetic property most reliably reported by cortical neurons. Indeed, by measuring information when the complete stimulus set was collapsed into feature-defined groups, we found that neurons reduced the dimensionality of the stimulus from two features (A, f) to a single feature, the product Af. Moreover, because different neurons encode stimuli in the same manner, information loss was negligible even when the activity of separate neuronal clusters was pooled. This suggests a decoding scheme whereby target neurons could capture all available information simply by summating the signals from separate barrel cortex neurons. These results indicate that neuronal population activity provides sufficient information to allow nearly perfect discrimination of two vibrations, based on their deflection speeds, within a time scale comparable with that of a single whisking motion across a surface.

Introduction

Rats rely on their whisker sensory system to collect information about the surrounding environment. Among the behaviors that depend on the whisker sensory apparatus are object localization, judgment of the size and shape of objects, and comparison of the roughness or texture of surfaces (Guic-Robles et al., 1989; Brecht et al., 1997). Texture discrimination is the focus of the present work. In measuring the surface features of objects, humans and rats have approximately equivalent capacities (Carvell and Simons, 1990). In searching for neuronal codes, the leading candidates are those features of neuronal activity that vary most reliably with changes in the stimulus. Our working model is that as the rat whisks across an irregular surface such as sandpaper (see Fig. 1a), relative motion between the whisker and the surface induces a vibration along the whisker shaft with distinct texture-specific parameters (see Fig. 1b). The kinetic features of the vibration are encoded in neuronal activity (see Fig. 1c) that constitutes the brain's representation of the texture because the activity distinguishes the current stimulus from other candidates (see Fig. 1d). To test the model, the present experiments used sinusoidal whisker movements as stimuli. Although the whisker shaft vibrations induced by sweeping across surfaces are not sinusoidal, this simplified form of whisker movement is defined by just two parameters, frequency (f) and amplitude (A), and therefore allows measurement of how kinetic features are encoded under controlled conditions. A previous report suggested that neuronal firing is related to vibration velocity (Arabzadeh et al., 2003). To gain a quantitative understanding of how cortical neurons report tactile events, here we address the following questions: Which stimulus features are encoded by neuronal activity? How reliably can these stimulus features be decoded from a single trial observation of neuronal activity? How rapidly? Do different neuronal clusters across cortical columns respond differently and, if so, do their differences convey salient information? We addressed these issues by using an information theoretic approach (Shannon, 1948; Cover and Thomas, 1991) to analyze neuronal data. This approach permits a rigorous and objective quantification of how well target neurons integrating the activity in question could “decode” the stimulus (Rieke et al., 1997; Borst and Theunissen, 1999).

Figure 1.

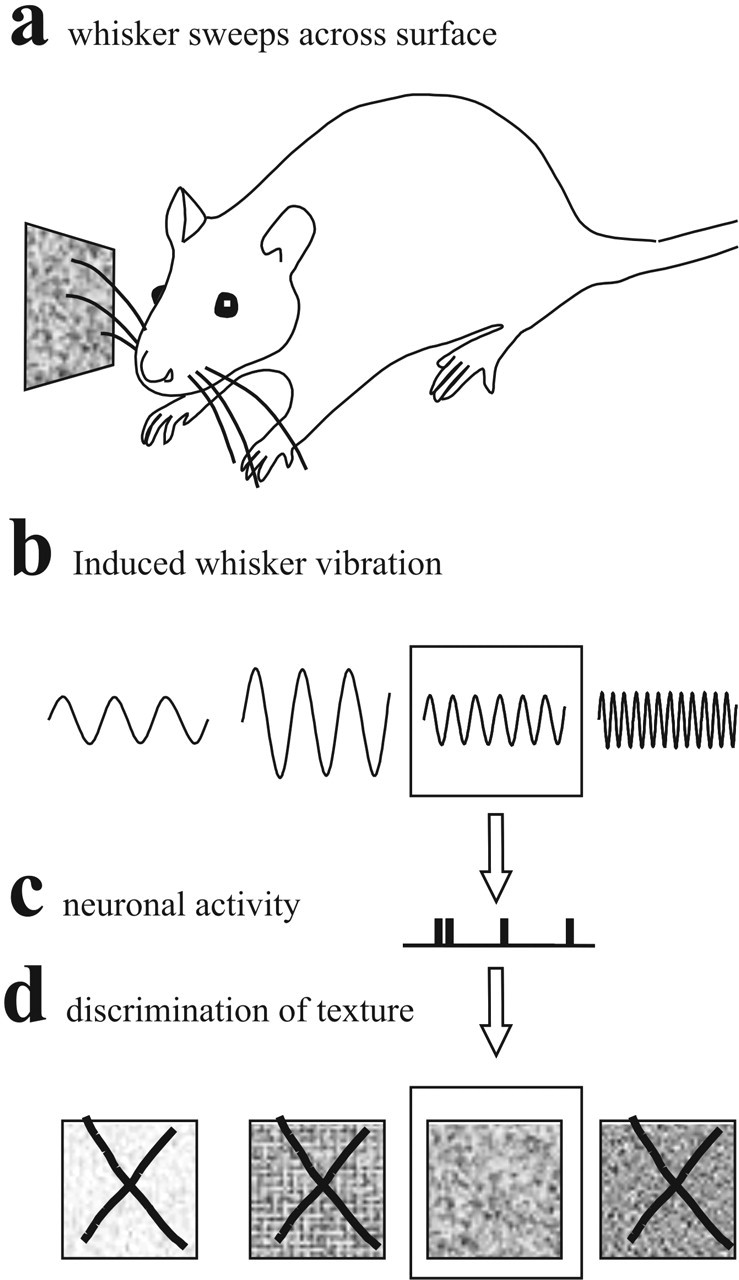
Schematic model for texture discrimination based on the proposal that the kinetic “signature” of whisker vibrations is encoded by neurons. In this scheme, vibrations take the simplest possible form, sinusoidal waveforms. See Introduction for details.

Materials and Methods

Electrophysiology. All experiments were conducted in accordance with National Institutes of Health, international, and institutional standards for the care and use of animals in research. A summary of methods is given below; for a detailed description of surgery and data acquisition, see Rousche et al. (1999) and Arabzadeh et al. (2003). Surgical anesthesia was induced by urethane (1.5 gm/kg) in five adult male Wistar rats weighing 250-350 gm. A 10 × 10 grid of 1.5-mm-long electrodes with 400 μm tip-to-tip spacing (Cyberkinetics, Salt Lake City, UT) was inserted into the vibrissa region of the left somatosensory cortex, identified according to vascular landmarks and stereotaxic coordinates (Hall and Lindholm, 1974; Chapin and Lin, 1984). The minimum and maximum depths of electrode penetrations were 700-1000 μm in all experiments. The waveforms emitted by a multiunit neural cluster of ∼3-5 neurons at each channel (Rousche et al., 1999) were selected off-line using spike-sorting programs (Cyberkinetics), and their time stamps were saved for additional analysis. Single-unit data are not presented here.

Whisker stimulation paradigm. Using thin, lightweight glass micropipettes, we made a five-rung “ladder” and attached it to a piezoelectric wafer (Morgan Matroc, Bedford, OH). We positioned the ladder on the right side of the animal's snout so that the five rungs lay just below the 20-25 whiskers in the corresponding five rows of whiskers (A-E), each whisker shaft resting lightly on the ladder ∼5 mm from the skin. Typically, the stimulus involved A1-4, B1-4, C1-5, D1-5, and E1-5. The piezoelectric wafer was driven vertically by sinusoidal voltages of varying amplitude and frequency. Each vibration began with an upward movement starting from position 0, where the position in one cycle ranged from -1/2 A to +1/2 A.

With a custom-built optic sensor, we monitored the displacement of the whisker shaft to verify that whisker movement “followed” and matched wafer movement across the full range of frequencies and amplitudes (Arabzadeh et al., 2003). Sinusoid frequency and amplitude on each trial assumed one of seven values (frequency = 19, 30, 50, 81, 131, 211, and 341 Hz; amplitude = 8, 12, 21, 33, 54, 87, and 140 μm). The resulting 49 different frequency-amplitude combinations (see Fig. 2a) were presented in pseudo-random order 100-200 times per stimulus. The vibration duration was 500 msec with a 1 sec interval between consecutive vibrations.

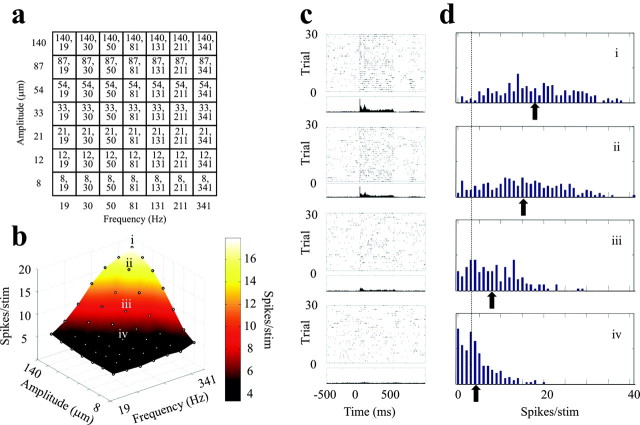
Figure 2.

Stimulus set and the characteristics of neuronal responses. a, The combination of seven frequencies (horizontal axis of grid) and seven amplitudes (vertical axis of grid) yielded the stimulus set of 49 sinusoidal vibrations. The numbers given in each element of the grid are the amplitude, frequency. b, Spike counts for each stimulus over the 0-500 msec time window (vibration onset, 0 msec) averaged over 200 trials for a neuronal cluster in barrel column D2, experiment 1. Because the frequency and amplitude scales are logarithmic, points are spaced evenly along the frequency and amplitude axes. c, Raster plots and PSTHs for the stimuli denoted i-iv in b. Dots in the top parts show spike times across 30 trials; the 200-trial PSTH (bin size, 5 msec) is aligned below the raster plot. Stimulus presentation is from 0 to 500 msec. d, Distribution of spike counts (0-500 msec) across 200 stimuli for the same four stimuli. The dotted line shows the average spontaneous activity (7 spikes/500 msec) for this neuronal cluster, and the arrows mark the average spike counts for each stimulus. Note how widely the trial-by-trial spike counts varied around the mean.

After delivery of the full stimulus set, all whiskers were cut 3 mm from their base and stimulated individually by a piezoelectric wafer with 1 Hz square pulses for 1 min. The resulting data were used off-line to determine for each electrode whether the neuronal cluster had a statistically significant response to any single whisker and, for such clusters, to identify the principal whisker and to construct barrelfield maps. Neuronal clusters that gave a statistically significant response and had a clear principal whisker were selected for analysis of responses to vibration stimuli; there were 24, 16, 37, 35, and 18 acceptable electrodes in experiments 1-5, respectively. Response onset latencies were in the range of 5-8 msec, signifying that recording sites were in a cortical layer receiving direct thalamic input.

Information theoretic analysis of spike trains. To measure how stimulus features are encoded by barrel cortex spike trains, we computed the mutual information between sensory stimuli and neuronal responses. Mutual information (Shannon, 1948) (denoted in the following simply as “information”) quantifies how well an ideal observer can discriminate between all members of the stimulus set based on the neuronal responses of a single trial. We first computed the information I({A, f};R), which can be extracted from the neuronal responses about the two sinusoid parameters, amplitude (A) and frequency (f):

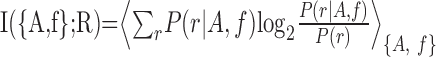1

where P(r| A, f) is the conditional probability of observing a neuronal response r given presentation of a vibration defined by an amplitude-frequency combination {A, f}, P(r) is the unconditional probability of response r [the average of P(r|A,f) across all stimuli], and <... >_{{A, f}} denotes an average across all stimuli weighted by the probability P(A, f) of presenting an (A, f) whisker vibration stimulus. In these experiments, all 49 frequency-amplitude combinations were equi-probable and thus P(A, f) = 1/49. The response of each channel was defined as the number of spikes on one trial emitted in a fixed post-stimulus time window. We thus investigate stimulus discriminability afforded by a “spike count” code only. Additional information may be obtained from the precise timing of spikes of barrel cortex neurons (Panzeri and Schultz, 2001; Panzeri et al., 2001; Petersen et al., 2001).

To explore population coding, we analyzed the information carried by (1) the neuronal clusters at single-electrode channels, (2) all recorded neuronal clusters of the array, summated together, and (3) two neuronal clusters at pairs of electrode channels. In the last case, we considered two types of information: (1) the “labeled-line” information and (2) the “pooled” information (Reich et al., 2001; Panzeri et al., 2003; Won and Wolf, 2004). The labeled-line information assumes that the decoding neuron can maintain the identity of the source, or the “label,” of each incoming spike. It is thus computed from Equation 1 by defining the response as r = (r₁,r₂), r₁ and r₂ being the number of spikes recorded at channels 1 and 2, respectively, in the selected time window. The pooled information assumes that the decoding neuron does not maintain the identity of the source of each incoming spike, instead summing all spikes. The pooled information is thus computed from Equation 1 by defining the response as r = r₁ + r_2.

A principal goal was to find out which stimulus features are encoded. Each vibration stimulus is fully defined by its joint values of A and f. Yet, the observed neuronal responses might be determined by only a smaller subset of stimulus parameters; for example, either by the features individually (i.e., A alone or f alone) or by the relationships between features (i.e., Af or A/f). An important question is whether such a simplified description reflects a “dimensionality reduction” performed by the nervous system. To address this question, we used a “stimulus grouping” approach, as outlined below (see also Fig. 4a-d). In this approach, stimuli are grouped into classes that correspond to one of the simplified descriptions outlined above. When this is done, the number of unique stimuli in the set is reduced. For frequency grouping, the 49 stimuli defined by joint values of f and A are reduced to seven groups in which all stimuli within a group have the identical value of f. Likewise, amplitude grouping yields seven groups defined by identical values of A. Grouping by identical values of the product Af or by A/f yields 13 groups. Information I(g;R) available about the stimulus set grouped in one of these ways is:

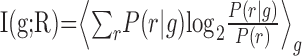2

Figure 4.

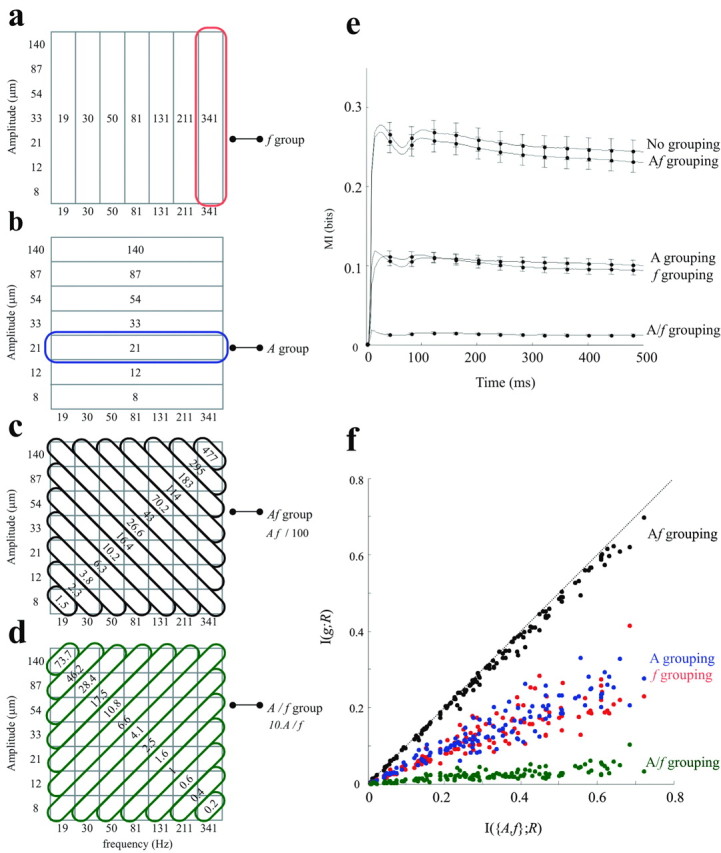
Stimulus grouping rules and their effect on information transmission. a-d, Four different stimulus grouping rules. a, Stimuli grouped into seven vertical iso-frequency bands. For the information analysis, all vibrations possessing the same frequency value were considered to be the same stimulus. The defining value is given within the band. b, Stimuli grouped into seven horizontal iso-amplitude bands. c, Stimuli grouped into 13 diagonal iso-speed bands. Within each band, the value of the product Af is given. d, Stimuli grouped into 13 diagonal A/f bands; orthogonal grouping. e, Cumulative information about the stimulus set grouped according to the features f, A, Af, and A/f plotted against the upper limit, the information about the entire set of 49 stimuli (no grouping). The data with no grouping are carried over from Figure 3d. Each curve represents the average from 130 neuronal clusters recorded in experiments 1-5. Error bars are the SEs of the mean across clusters. f, The effect of stimulus grouping on each neuronal cluster. For each neuronal cluster, the quantity of information transmitted was taken to be the maximum value of cumulative information curve. The x-axis denotes the information carried about the full stimulus set, and the y-axis denotes the information for the same neuronal cluster when stimuli were grouped according to a selected rule.

Applying the information-theoretic “data processing inequality” (Cover and Thomas, 1991), it follows that I(g;R) for any grouping rule must be less than or equal to I({A, f};R), the information about the full, ungrouped data set. I({A, f};R) can be equal to I(g;R) if, and only if, neurons respond only to the stimulus feature that characterizes the grouped responses (Cover and Thomas, 1991). Thus, comparing I(g;R) with I({A, f};R) provides a novel and objective information-theoretic metric to assess to what extent a smaller subset of stimulus parameters dictates neuronal responses (for a different approach to this problem, see Adelman et al., 2003).

The stimulus-response probabilities in the above formula are not known a priori and must be estimated empirically from a limited number, N, of experimental trials for each unique stimulus (A, f). In our data set, N was 100 (one experiment), 150 (three experiments), and 200 (one experiment). Limited sampling of response probabilities can lead to an upward bias in the estimate of mutual information (Optican et al., 1991; Panzeri and Treves, 1996; Golomb et al., 1997; Victor, 2000; Paninski, 2003). The bias magnitude depends on the number of trials per stimulus: as N increases, the estimated probabilities become more accurate, and the bias decreases. An approximate expression for the bias has been formulated (Panzeri and Treves, 1996) and can be subtracted from direct information estimations (Eq. 1), provided that N is at least two to four times greater than the number of different possible responses, R (Panzeri and Treves, 1996; Pola et al., 2003). For single channels, the number of possible responses is equal to n_max+ 1, where n_max is the maximum number of spikes observed across all trials at a single channel. In our data set, this number was <30 even for the longest time windows considered (0-500 msec after stimulus). Thus, all single-channel results were well sampled and free from bias artifact. For pairs of channels (see Fig. 5), for labeled-line information, the number of possible responses R was equal to (n_max+ 1)². We thus limited the post-stimulus window to 0-20 so that R remained of the order of 20-30. The experiment that used only 100 trials/stimulus was excluded. When computing the information obtained from pooling the spikes from all channels (see Fig. 6), the number of different responses R can be larger than the number of trials per stimulus N. To obtain unbiased estimates in this case, we reduced the dimensionality of the response space R by grouping the spike counts into up to 40 classes before applying the bias subtraction procedure.

Figure 5.

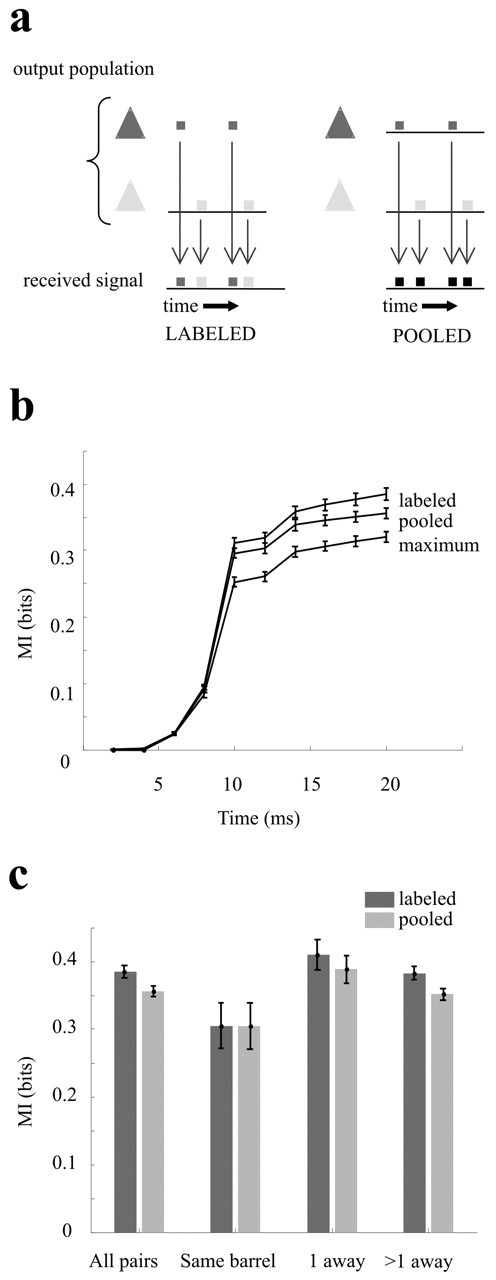
Information available based on labeled-line versus pooled decoding models. a, Schematic representation of the two decoding models. Two neurons (light and dark gray pyramids) emit spike trains. The target neurons may integrate each spike separately and conserve the label of the source neuron (left) or may pool the incoming spikes without conserving the label (right). b, Cumulative information curves averaged over all pairs (n = 276) of neuronal clusters in experiment 1. Error bars are SEM mutual information across pairs. c, Effect of relative positions of the same 276 pairs of neuronal clusters on their pooled and labeled-line information. Neuronal response is defined as spike counts in 0-20 msec after stimulus onset.

Figure 6.

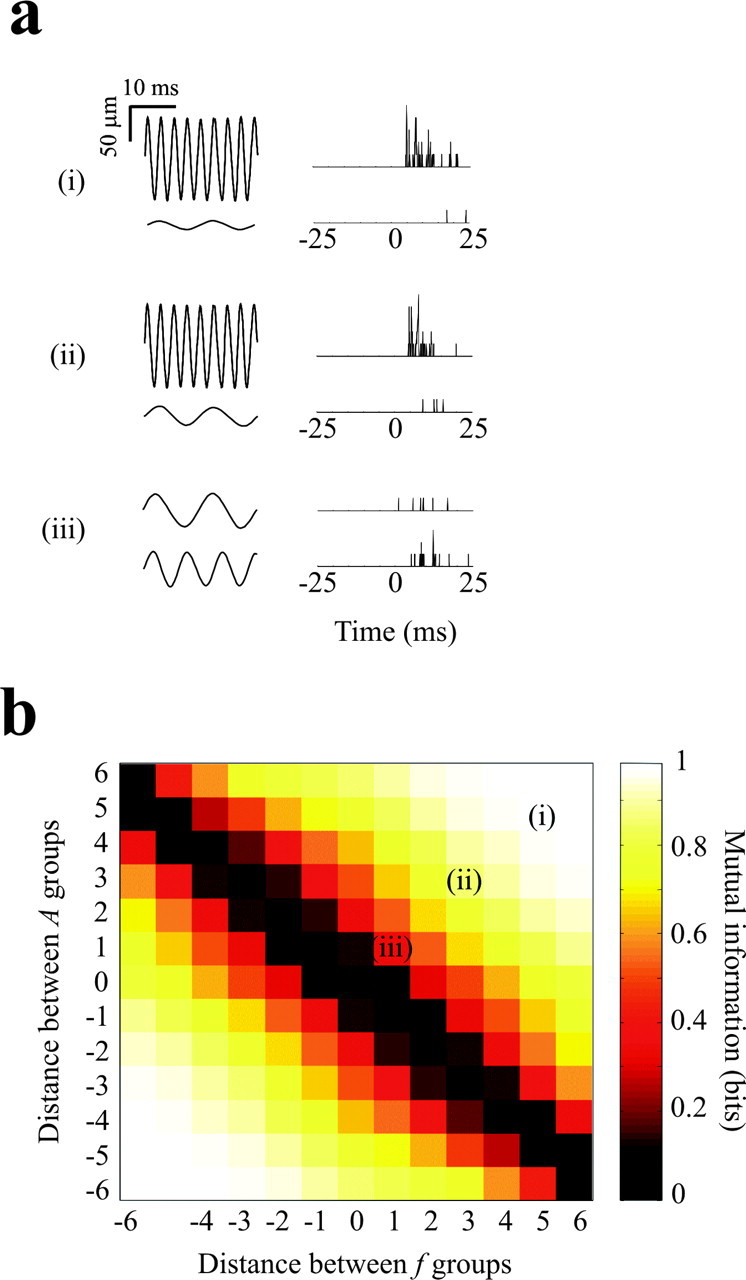
Discriminability between pairs of stimuli. a, Three pairs of sinusoidal vibrations and associated single-trial neuronal responses. Each response is the result of pooling the activity across all 37 electrodes in experiment 3. Illustrated responses were selected randomly from the 150 trials for each stimulus. b, Information carried about pairs of stimuli. To make the graph, all stimulus pairs were classified according to f₁-f₂ and A₁-A₂, in which the frequency and amplitude distances refer to steps along the selected dimension (see Fig. 4a,b). The color of each element in the graph gives the average information about all stimulus pairs with the indicated values of f₁-f₂ and A₁-A₂. Information is measured from the whole-array pooled spike count in the interval 0-25 msec after stimulus onset.

Results

Neuronal responses to sinusoidal whisker vibrations

Our hypothesis is that the encoding of whisker vibration features is the basis for the neuronal representation of texture (Fig. 1). This hypothesis is plausible only if the kinetic features of vibrations are reliably encoded by neuronal activity. Therefore, the present experiments measured cortical neuronal encoding of sinusoidal whisker movements. Sinusoidal movements are a simplified form of the whisker vibration that might occur when the whisker sweeps across a surface; if sinusoidal stimuli are not reliably encoded, then the hypothesis outlined above must be discarded. Moreover, a detailed understanding of which stimulus parameters are encoded, and by what coding mechanisms, will give us more specific predictions concerning the complex vibrations associated with whisker movement across textures.

In five experiments in urethane-anesthetized rats, a 100-microelectrode array was implanted in the middle layers (layers III or IV) of the whisker representation of the somatosensory cortex. The matrix of electrodes typically sampled ∼20 barrel columns, and each electrode recorded the activity of a small cluster of neurons. The whole grid of facial whiskers was moved together by application of a sinusoidal deflection. To explore cortical coding of the vibration, its frequency and amplitude on each trial assumed one of seven values (frequency = 19, 30, 50, 81, 131, 211, and 341 Hz; amplitude = 8, 12, 21, 33, 54, 87, and 140 μm). The resulting 49 different frequency-amplitude combinations (Fig. 2a) were presented in pseudo-random order 100-200 times per stimulus.

Figure 2b shows the response of a neuronal cluster in barrel B2 (experiment 1) to the entire set of 49 stimuli, each point of the grid associated with one frequency-amplitude combination. The z-axis refers to the spike count averaged over the 500 msec stimulus duration across 200 trials per stimulus; the color scale refers to the same measure and is interpolated between data points. The firing rate increased as either vibration amplitude (A) or frequency (f) increased. Averaged across a large number of trials, then, the firing rate was monotonically related to these physical features of the stimulus, suggesting that the neuronal activity could support discriminability among different vibrations. However, because the sensory system under natural conditions can make texture discriminations without averaging across a large number of presentations (Carvell and Simons, 1990), the more behaviorally relevant question concerns how reliably neuronal activity reports the feature of interest on a single trial. The issue of trial-by-trial variability is introduced in Figure 2c, in which responses to four stimuli are illustrated using the raster plots from 30 trials (selected randomly from 200 trials) and peristimulus time histograms (PSTHs; all 200 trials). The four stimuli are the ones denoted i-iv in Figure 2b. Although the PSTHs confirm that stimuli with higher values of A and f, on average, evoked a greater number of spikes, a significant amount of trial-by-trial variability is evident in the raster plots. To better illustrate the spike count variability, we have plotted the distribution of spike counts (0-500 msec) for all 200 trials as a histogram (Fig. 2d). The dotted line shows mean spontaneous activity measured during the 500 msec prestimulus interval, and the arrows show the average stimulus-evoked spike counts. Despite the monotonic increase in average spike count as vibration amplitude and frequency increased, there is considerable overlap between the four histograms. What was the effect of this variability in trial-to-trial spike count on stimulus representation? Below, we use mutual information measures (Shannon, 1948) to consider how reliably an ideal observer could identify the stimulus from a single-trial spike count.

Time course of information transmission

We first investigated how well a single neuronal cluster encoded vibration stimuli and over what time scale information was encoded. Figure 3a plots the mutual information (Eq. 1) about the total set of 49 stimuli carried in the spike counts of a neuronal cluster in barrel B2 (same cluster as in Fig. 2). Spike counts were measured over time windows that began at stimulus onset and ended at the time indicated on the x-axis. For example, the value at 20 msec refers to the mutual information in the spike count from 0-20 msec. We refer to this as “cumulative” mutual information. Cumulative information rose above 0, starting at 4-6 msec, and it reached a peak at ∼20-30 msec (see inset); most of the information was transmitted within this cumulative time window. There was a slight decrease in cumulative mutual information as the window reached 70-80 msec. The decrease resulted from the lower firing rate occurring after the initial response, as seen in the raster plots and PSTHs of Figure 2c. A second, smaller wave of information was transmitted between ∼100 and 150 msec. Thereafter, no additional information was present, suggesting that the spikes emitted later than ∼150 msec were either (1) non-stimulus evoked, reflecting only background activity, or (2) redundant (i.e., they did not add any extra information beyond that already provided by the early spikes).

Figure 3.

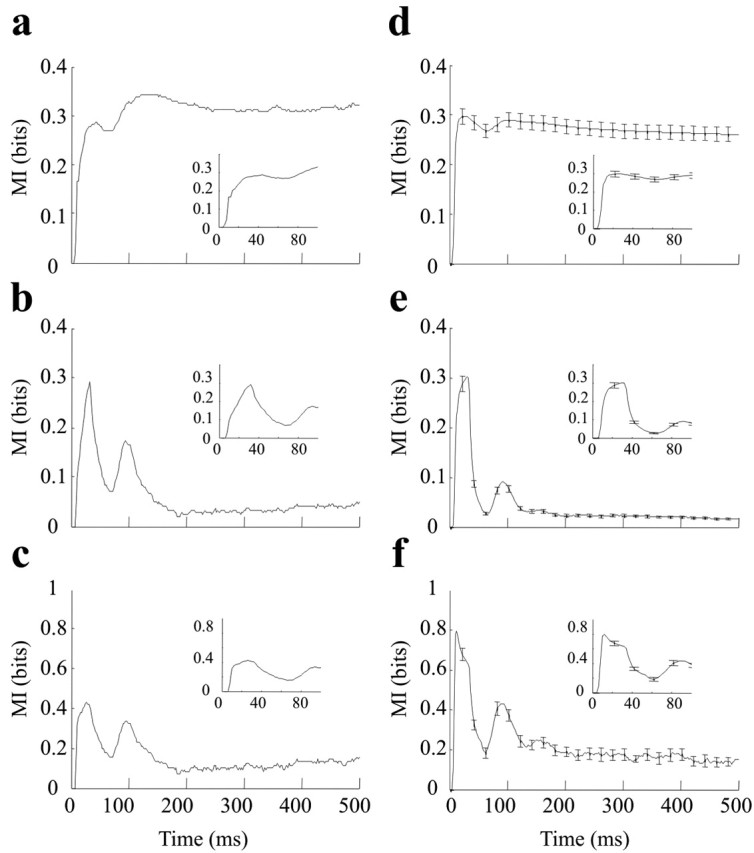
Time course of information of ∼49 stimuli carried by a single neuronal cluster (left) and by all clusters (right). a, Cumulative information: spike counts measured from stimulus onset until the time indicated on the x-axis. b, Ongoing information: spike counts measured in the 25 msec time window preceding the time indicated on the x-axis. c, Information per spike, calculated by dividing ongoing information (b) by the average number of spikes in each time window. d-f, The same plots in a-c averaged over all 130 neuronal clusters recorded in experiments 1-5. In all plots, the inset is a magnified view of the earliest part of the curve (0-100 msec).

To resolve the above ambiguity and determine how the late, “adapted,” part of the neural response encoded stimuli, we calculated mutual information based on spike counts within a sliding window of 25 msec length instead of a cumulative time window. We refer to this as “ongoing” information. Figure 3b gives the mutual information between all 49 stimuli and spike counts measured in the 25 msec window preceding the x-axis value. Two peaks of ongoing information are evident, centered at 30 and 100 msec. Thereafter, the late response (150-500 msec) was not as informative as the early response but still carried a significant amount of ongoing information. Thus, the early part of the response was more informative, but late spikes were also stimulus related. This, combined with the cumulative information results, shows that late spikes carried information that was fully redundant to that of the early spikes.

Finally, the amount of information divided by the average number of spikes in each time window provides an estimate of information per spike (Fig. 3c). From this plot, we note that the earliest spikes were the most informative, yet spikes throughout the entire response period carried information.

To study the generality of these observations across many neuronal clusters, we calculated average values across all 130 neuronal clusters recorded in five rats of the same measures shown in Figure 3, a-c. The results are given in Figure 3, d-f. The error bars show SEM. The findings made for the single-electrode cluster in Figure 3, a-c, were reproducible for different neuronal clusters and in different rats. In summary, the cumulative information (Fig. 3d) saturated very rapidly (20 msec). The ongoing information plot (Fig. 3e) indicates that activity in the later response windows remained informative, albeit less than that in the early response. The saturation in Figure 3d thus occurred because late responses were redundant. The information per spike plot (Fig. 3f) shows that late activity was less informative not only because there were few spikes but also because each spike tended to carry less information (whereas early spikes conveyed as much as 1 bit/spike of information, the later ones conveyed ∼0.2 bit/spike).

Which vibration features are encoded?

To understand vibration encoding more deeply, we tested whether cortical neurons perform a dimensionality reduction of the stimulus space. Any sinusoidal stimulus is fully defined by its joint values of A and f (Fig. 2a). Beyond characterizing neuronal response to (A, f), we also measured whether responses are selective to some smaller subset, individual stimulus features (A alone or f alone) or relationships between features (i.e., Af or A/f). We can learn precisely which of all possible features dictates neuronal activity by collapsing the complete stimulus set into groups defined by a selected feature or by a relationship between features (see Materials and Methods for details). Figure 4, a-d, shows the full stimulus set grouped by f alone, A alone, Af, and A/f. This amounts to neglecting the features not selected for; grouping by vibration frequency, for example, ignores any possible effect of vibration amplitude on neuronal output. For this reason, neuronal information about a grouped stimulus set, I({g};R), must be less than or equal to the information about the stimulus set defined by both parameters, I({A,f};R). Comparing the values of I({g};R) and I({A,f};R) quantifies how much of the total information that neurons carried about A and f is indeed related to the stimulus features described by the grouping g. Figure 4e plots I({g};R), the cumulative spike count information about f, A, Af,or A/f averaged over 130 neuronal clusters recorded in experiments 1-5. These are scaled against I({A,f};R), the “ungrouped” cumulative information shown in Figure 3d. When the stimulus set was reduced to seven frequency groups, neurons carried ∼40% as much information as the maximum. The result was identical when the stimulus set was reduced to seven amplitude groups. The >50% loss of information means that neuronal response on a single trial could not be accounted for by either feature alone as well as it could by both features together. In contrast, when the stimulus set was reduced to 13 groups defined by Af, there was only a very small loss of neuronal information (within range of error bars). This demonstrates that all the information that the neurons transmit about A and f was indeed about their product Af and that neuronal response on a single trial could be accounted for simply by the product Af as well as it could by both features together.

It is interesting to consider the effect of stimulus grouping on the efficiency of information transmission, the quantity of information neurons reported divided by the maximum information available in the stimulus set. The upper bound of information that could be transmitted by the neuronal responses is defined by the stimulus set entropy (Cover and Thomas, 1991); for equi-probable stimuli, this is the base 2 logarithm of the number of different stimuli. Reducing the stimulus set from 49 unique stimuli to 13 Af-grouped stimuli decreased its entropy from 5.6 to 3.7 bits. Because compression of the stimuli into the Af groups did not reduce the amount of information present in neuronal spike counts, the efficiency of information transmission was much higher when stimuli were considered according to Af. Thus, another way to interpret the results is that barrel cortex neurons were ∼50% more efficient in transmitting Af information than in transmitting (A,f) information.

It is interesting to note that the sum of f-grouped information and A-grouped information was ∼20% less than the information about (A,f). Thus, neurons did not encode A and f independently. If not encoded separately, A and f must have been encoded jointly, and the results obtained above show that this joint feature was the value of the product of Af. Af corresponds to a physical feature of the stimulus: it is proportional to the average speed of the sinusoidal vibration.

We also grouped the stimuli according to the feature A/f, which unlike f, A, and Af does not represent any physical quantity of the vibration. This grouping was chosen as a control for its similarity to Af grouping in terms of the two elemental features combined, the number of groups (13) and the number of unique stimuli within each group. We also refer to this as “orthogonal” grouping because in the stimulus grid, the diagonal bands grouping stimuli by A/f are orthogonal to the diagonal bands grouping stimuli by Af (Fig. 4d). Orthogonal grouping caused the loss of almost all information.

Closer examination of Figure 2b provides an explanation for these findings. This typical neuronal cluster was informative about f and A because its firing rate increased monotonically as either parameter increased. However, within a single frequency group, spike counts could vary widely as vibrations of different amplitude were collapsed together (the same observation holds for each amplitude group). The effect of collapsing dissimilar responses into a single group was to reduce information transmission. In contrast, collapsing stimuli into Af groups did not increase response variability because similar firing rates were evoked for different vibrations, so long as the product Af was constant. Thus, both the qualitative examination of the neuronal responses and the quantitative information theoretic analysis converge to the conclusion that vibration speed was the primary variable encoded by firing rate, whereas either frequency or amplitude alone were encoded in the neuronal responses in an indirect way, as a reflection of the encoding of Af.

The next analysis was aimed at detecting possible differences in coding properties between neuronal clusters. Does every neuronal cluster encode vibration speed? Are some clusters more efficient in encoding frequency than amplitude, others more efficient in amplitude than frequency? Figure 4f shows the effect of stimulus grouping on mutual information for each of 130 neuronal clusters recorded in five experiments. For each point, the x-value gives the information carried by the neuronal cluster about the full stimulus set, and the y-value gives the information about a grouped stimulus set. Thus, the distance below the diagonal line indicates the loss of information caused by grouping according to the selected feature. For every neuronal cluster, grouping the stimuli by Af (black points) caused only a minimal loss of information. Grouping the stimuli by f (red points) or by A (blue points) caused losses in information ranging from ∼30 to 70%. Orthogonal grouping of the stimuli by A/f caused huge losses in information. From this, we conclude that all neuronal clusters encoded vibration speed (Af), and none were selectively “tuned” to either frequency or amplitude alone.

Decoding the responses of multiple barrel cortex neurons

We now turn to the question of how the response of a barrel cortex neuronal population could be most efficiently decoded, or “read off,” by the target neurons. Decoding must occur for the successful transmission of information from one group of neurons to a second group. To conserve all sensory information during synaptic transmission, the target neuron must conserve the label of the spikes arriving from multiple input neurons at different sites on its dendritic tree (Fig. 5a, left). Given the biophysical difficulty in integrating each spike separately, a simple alternative to spike labeling has been proposed: spike pooling (Darian-Smith et al., 1973; Shadlen et al., 1996; Panzeri et al., 2003; Won and Wolf, 2004). In this scheme, target neurons simply sum up the activity of the afferent population (Fig. 5a, right). If the neurons in a population are tuned to similar features, and if their trial-to-trial variability (“noise”) is only weakly correlated, then pooling of their activity can average away part of the response variability of individual channels and thus lead to a population signal that is more reliable on a single trial than that carried by the most informative individual neurons (Darian-Smith et al., 1973; Zohary et al., 1994). However, pooling causes large amounts of information loss if the summed neurons are tuned to different stimulus features. Because all sampled barrel cortex neurons seem to be tuned to the same stimulus features (Fig. 4f), we would predict that the activity of neuronal clusters could be pooled without information loss. We tested the prediction directly by comparing information carried by pairs of neuronal clusters (1) when their spikes are labeled according to which neuronal cluster emitted them, and (2) when their spikes are pooled, disregarding the source of the spikes. We then asked whether the relative positions of the clusters affects their pooled information.

For each pair of neurons, three cumulative mutual information curves about the 49-stimulus set were derived: (1) labeled, (2) pooled, and (3) maximum; this last refers to the maximum information carried by one of the two clusters at each time point. The average of the curves across all possible pairs of neuronal clusters is given in Figure 5b. Comparing the labeled curve to the maximum curve, we observe that, beginning at 10 msec, the second neuron added ∼20-25% more information. When the activity of the two neurons was pooled, there was a loss of only ∼7% of the information present in the labeled activity (the upper limit for the pair of neuron clusters).

How does the relative location of the two neuronal clusters affect the outcome of pooling? Figure 5c plots the comparison between pooled and labeled information for different barrel locations. Neuronal response was defined as the spike count in a 20 msec post-stimulus time window. As in the preceding plot, there was approximately a 7% difference between the labeled and pooled information in the average of all pairs. When the neuron pair was recorded at two different electrodes in the same barrel, there was no significant difference between the information carried by pooled and labeled spikes. For neuronal clusters in non-neighboring barrels, spike pooling caused only a small loss in information.

In summary, the two analyses illustrated in Figure 5 indicate that a target population would gain additional information about vibration parameters from integrating the spikes of multiple neuronal clusters and would capture nearly all the available information without the need to label the incoming spikes according to the source neurons. If there are differences in the stimulus tuning of neurons in distant barrels, such differences do not seem to carry significant amounts of information.

Information carried about pairs of stimuli

In analysis up to this point, we have quantified the mutual information between neuronal activity and the total set of stimuli, in which the stimuli were either considered separately or grouped according to a selected feature. In contrast, behavioral tasks often do not require the discrimination among large numbers of stimuli but between just two possible stimuli (i.e., forced choice paradigm). To measure how reliably barrel cortex activity could support discrimination between pairs of stimuli, neuronal responses in experiment 3 were defined as the 0-500 msec spike counts pooled from all electrodes. Figure 6a illustrates randomly selected single-trial responses to compare the whole-array output for stimulus pairs (i), (ii), and (iii). How reliably could a “decoder” of barrel cortex output identify each stimulus in the pair? To answer this, we measured mutual information between the whole-array spike count and each possible pair of stimuli, with a possible range from 0 bits (random discriminability) to 1 bit (errorless discriminability).

Each stimulus pair was classified according to the number of groups that separated them along the frequency dimension and the amplitude dimension (Fig. 4a,b). Stimulus pairs corresponding to the top left to bottom right diagonal in Figure 6b belonged to the same Af group, the frequency difference and amplitude difference being of equal magnitude but opposite sign; such stimulus pairs were indistinguishable by spike output (0 bits of information). Each step from this diagonal represents an increase in the Af difference between the members of the pair by one additional Af group. Stimulus pairs just three steps apart in A and f could be discriminated nearly perfectly. For example, for stimulus pair (ii) in Figure 6a, the top vibration was defined as f = 341 Hz, A = 140 μm, and the bottom vibration as f = 81 Hz, A = 33 μm, such that the f difference and the A difference were both 3. The whole-array spike count carried 0.85 bits of information about all stimulus pairs with this f and A difference, as indicated by (ii) in Figure 6b. These observations confirm vibration speed, Af, as the stimulus feature that is most directly encoded by neuronal output and show that a target population decoding barrel cortex activity on a single trial could reliably classify vibrations according to their speed.

Discussion

In previous work, we measured the firing rate of barrel cortex neurons, averaged over hundreds of presentations of sinusoidal whisker vibrations. The results led us to propose that neurons encode the kinetic features of the vibration and that the firing rate is a candidate coding mechanism (Arabzadeh et al., 2003). Sensory systems, however, must support behavioral decisions by representing external events sampled for only short periods. Using the whisker system, rats can select surface textures after a small number of whisks (Guic-Robles et al., 1989; Carvell and Simons, 1990). Therefore, to support the hypothesis that encoding of vibration kinetics is the neuronal basis of texture discrimination, we examined how reliably neuronal activity reports vibration features on a single trial. Mutual information measures provide an upper bound to the coding efficiency of neurons, quantifying how reliably an ideal observer of firing rate could identify the stimulus on a single trial. Here, using information theory methods, we were able to quantitatively address some of the critical issues regarding this coding scheme.

Which stimulus features are encoded by neuronal activity?

To gain a more precise understanding of which are the most efficiently coded vibration parameters, we collapsed the complete 49-member stimulus set into groups defined by a selected feature or by a relationship between features. Information loss will be minimal if the stimuli within a group produce very similar response profiles; in that case, “mixing” stimuli across the selected group causes no greater trial-to-trial response variability than do repetitions of one single stimulus. For all the neuronal clusters in our data set, stimulus grouping by A and f produced approximately a 30-70% information loss, but grouping by Af produced only a negligible loss. Stimuli with varying frequency and amplitude could thus be combined into a single group without causing any additional variability in neuronal responses, provided that the members of the stimulus group all have the same mean speed.

Note that all the conclusions drawn here apply to the encoding of the quantity (Af)ⁿ, where n can have any positive value. The quantity (Af)² is proportional to the kinetic energy of the stimulus. We have interpreted the results in terms of Af, proportional to mean vibration speed, consistent with descriptions of the coding of velocity (for ramp and hold stimuli) by primary afferent neurons (Shoykhet et al., 2000).

The amount of information carried by neurons on a single trial might seem low compared with the entropy of the stimulus set (5.6 bits for 49 stimuli). Another way to judge neuronal coding efficiency is to consider how discriminations would be made between just two stimuli at a time. Behavioral tasks in laboratory settings usually require animals to select between two stimuli. Viewed in this way, efficiency rises dramatically because the barrel cortex spike count could support perfect discriminations between two stimuli that differed by a few steps in vibration speed.

How rapidly are stimuli discriminable in neuronal activity?

The early period of neuronal response carries the bulk of the vibration information. Information carried by the cumulative firing rate becomes available as early as 4-6 msec after stimulus onset and peaks ∼30 msec after stimulus onset. Ongoing information, that present in a sliding 25 msec window, peaks ∼30-40 msec after stimulus onset. We speculate that, in freely moving rats, textures are converted to whisker vibrations by whisker motion across the surface during whisker protraction (forward movement). If a rat whisks at 10 Hz (Harvey et al., 2001), the protraction phase of each whisk cycle will last ∼50 msec; contact with an object will be maintained for some tens of milliseconds in each whisking cycle (Sachdev et al., 2001). Our data indicate that essentially all the information about surface features induced will be present in cortical neurons on the time scale of a single forward whisk. The findings thus agree with a series of investigations of tactile, visual, and auditory sensory cortex that emphasize the fact that the earliest cortical responses can carry large quantities of stimulus information (Optican and Richmond, 1987; Tovee et al., 1993; Victor and Purpura, 1996; Buracas et al., 1998; Rolls et al., 1999; Mickey et al., 2003).

Comparison to coding of stimulus location

Previous work (Petersen and Diamond, 2000; Panzeri et al., 2001; Petersen et al., 2002) has explored characteristics of cortical population coding of stimulus location, encoding on a single trial, which of a set of possible whiskers was deflected. Here, we find that several of the coding principles generalize to whisker vibration coding. First, the temporal profile of information is similar both for the simple task of detecting which whisker was stimulated and the more complicated task of distinguishing vibrations; in both cases, most of the information in the spike count becomes available as early as 6 msec and rises until 20-30 msec. Second, in both cases, spike counts play a significant role in the coding of stimulus features (the present work has not explored whether additional information is carried by precise spike timing or spike correlations). One important comparison between coding of the identity of the stimulated whisker and the coding of vibration involves the information carried by the columnar identity of the cortical neurons, as estimated by the effect of pooling the spikes of separate neurons or neuron clusters (Panzeri et al., 2003). For both types of stimulus, pooling of the spike output of neurons from the same column has only a negligible effect on the information available to an ideal decoder. The difference emerges in the pooling of the spikes from neurons of different columns. In the case of whisker identity, such pooling leads to the loss of 25-55% of the information carried when the spikes are labeled according to the columnar location. In the case of vibration, pooling of different-column spikes leads to the loss of just 7% of the total labeled spike information. Increasing the distance between columns does not affect the amount of information lost. Whisker identity, then, is represented in a topographic framework, whereby which neuron is active and which is not carries considerable information. Vibration is represented, in our data set, in a non-topographic framework, whereby differences in the activity of different columns are not informative.

Conclusions

In primates, there are two main viewpoints concerning the neuronal mechanisms for tactile texture discrimination. One view holds that spatial signals are, by themselves, sufficient to encode most sorts of textures, including grades of roughness, because type I slowly adapting (SAI) skin receptors contain an isomorphic representation of the surface in their discharge patterns (Connor et al., 1990; Connor and Johnson, 1992; Hsiao et al., 1993; Blake et al., 1997; Yoshioka et al., 2001). A second view emphasizes the contribution of temporal signals, based on evidence that some texture tasks in humans can be solved even in the absence of spatial cues (Gamzu and Ahissar, 2001), presumably because of vibration-sensitive rapidly adapting receptors. Likewise, two viewpoints are emerging with regard to tactile texture discrimination in rodents. Recently, it has been argued that textures may be represented by a spatial code. Whisker length varies systematically across different arcs on the rat's snout (Brecht et al., 1997); as a consequence, the longer caudal ones resonate at lower frequencies than the shorter rostral ones (Neimark et al., 2003). During whisking, there could be texture-specific differences in the strength of activation of rostral or caudal whiskers. In contrast, our current work emphasizes the temporal signals that might be available in texture-induced vibrations, what we refer to as the coding of the kinetic signature of the vibration. Thus, our working hypothesis for texture representation in the rodent whisker system is closer to the primate model that focuses on temporal signals.

In summary, we used sinusoidal vibrations of the whisker shaft as simplified test stimuli, on the assumption that such stimuli contain the elemental kinetic features of which the more complex vibrations induced by textured surfaces are composed. We determined that the product Af (proportional to mean vibration speed) is the vibration parameter most reliably represented by barrel cortex neurons. A spike count code for vibration speed, which could be quickly and robustly decoded from the output of large barrel cortex populations, might act as a basic element for the discrimination of irregular surface textures. Much additional work remains to confirm vibration speed as a critical encoded feature under more natural conditions. First, sensory coding must be examined while the rat is actively whisking rather than passively receiving stimuli. A recent report pointed out that responses differ in several fundamental ways when the sensory system functions in the active versus passive modes (Szwed et al., 2003). Second, neuronal responses must be measured when the sensory system faces natural surface-induced vibrations rather than regular sinusoidal vibrations. Third, the perceptual significance of velocity coding should be evaluated. In its strictest form, velocity coding implies that all sinusoidal vibrations with equal mean speed would be perceptually indistinguishable because they would produce the same spiking output: a rat would not be able to discriminate, for example, a 131 Hz, 21 μm vibration from a 30 Hz, 87 μm vibration. If rats can be successfully trained to discriminate between such iso-speed stimuli, then we would be forced to conclude either that two iso-speed stimuli can induce different spike counts in awake, behaving rats or else that some coding mechanism beyond the firing rate is at play.