Using a Hybrid Neural System to Reveal Regulation of Neuronal Network Activity by an Intrinsic Current

Abstract

The generation of rhythmic patterns by neuronal networks is a complex phenomenon, relying on the interaction of numerous intrinsic and synaptic currents, as well as modulatory agents. To investigate the functional contribution of an individual ionic current to rhythmic pattern generation in a network, we constructed a hybrid system composed of a silicon model neuron and a heart interneuron from the heartbeat timing network of the medicinal leech. When the model neuron and a heart interneuron are connected by inhibitory synapses, they produce rhythmic activity similar to that observed in the heartbeat network. We focused our studies on investigating the functional role of the hyperpolarization-activated inward current (I_h) on the rhythmic bursts produced by the network. By introducing changes in both the model and the heart interneuron, we showed that I_h determines both the period of rhythmic bursts and the balance of activity between the two sides of the network, because the amount and the activation/deactivation time constant of I_h determines the length of time that a neuron spends in the inhibited phase of its burst cycle. Moreover, we demonstrated that the model neuron is an effective replacement for a heart interneuron and that changes made in the model can accurately mimic similar changes made in the living system. Finally, we used a previously developed mathematical model (Hill et al. 2001) of two mutually inhibitory interneurons to corroborate these findings. Our results demonstrated that this hybrid system technique is advantageous for investigating neuronal properties that are inaccessible with traditional techniques.

Introduction

Modeling and experiment have been viewed traditionally as separate, albeit complementary, fields. Neuronal models suggest new experimental directions, and experiments, in turn, suggest refinements to the models. Recent advances in technology, however, have facilitated the creation of models that operate in real time, allowing models to play a direct role in experiments (Yarom, 1991; Le Masson et al., 1999; Manor and Nadim, 2001). Numerous studies with the dynamic clamp, for example, have shown how the addition of a model conductance can affect the activity of a neuron or neuronal network (Sharp et al., 1993, 1996). Other studies have used real-time model neurons to investigate such phenomena as the role of feedback in thalamic circuits (Le Masson et al., 2002), period regulation in pacemaker networks (Nadim and Manor, 2001), and regularization of chaos in motor pattern-generating networks (Szucs et al., 2000). These approaches allow the investigator to perform experiments that would be impossible or prohibitively difficult with traditional neurophysiological techniques, while providing a biological realism and relevance not achievable through modeling alone.

Our primary focus is on understanding mechanisms of motor pattern generation. We have studied the network that paces the heartbeat of the medicinal leech (Calabrese et al., 1995). Two coupled oscillators in the third and fourth segmental ganglia generate the timing in this network. Each oscillator comprises two heart interneurons connected by reciprocal inhibitory synapses, a structure referred to as a half-center oscillator (Hill et al., 2003). These small networks produce rhythmic antiphasic bursts. When one neuron is active, it inhibits the activity of its partner; eventually, the inhibited neuron is released or escapes from inhibition and begins firing, inhibiting the first neuron. This first neuron then is released or escapes from inhibition, and the cycle repeats.

To understand the cellular mechanisms that underlie these oscillations, we have created a hybrid system consisting of a heart interneuron and a silicon neuron, a model of the heart interneuron implemented using custom microelectronic circuits (Simoni et al., 2002, 2004). The silicon neuron provides real-time operation and implements a version of the Hodgkin-Huxley formalism (Hodgkin and Huxley, 1952). This mechanistic approach to modeling facilitates investigation of biophysical properties underlying neuronal activity. When the silicon neuron and a heart interneuron are connected with reciprocal inhibitory synapses of appropriate strength, they form a hybrid half-center oscillator that produces oscillations remarkably similar to those seen in the living system.

We focused our experiments on the hyperpolarization-activated inward current (I_h), which has been shown to exert pacemaker effects in numerous vertebrate and invertebrate systems (Luthi and McCormick, 1998). By introducing changes in the maximal conductance (ḡ_h) and the activation/deactivation time constant (τ_h) of I_h, we reveal how I_h controls the period and burst duration of the heart interneurons in a heartbeat half-center oscillator. Moreover, by inducing similar changes in both model and heart interneurons, we demonstrate that the silicon neuron can serve as a replacement for a living heart interneuron; changes made to the silicon neuron can describe how similar changes in the living network affect the generation of rhythmic activity.

Materials and Methods

The silicon neuron was fabricated through an integrated-circuit brokerage service in the AMI Semiconductor (Pocatello, ID) 1.2 μm process (MOSIS, Marina del Rey, CA). It was designed to produce electrical activity similar to a leech heart interneuron by emulating its major ionic currents (Table 1) with a Hodgkin-Huxley-like formalism (Hodgkin and Huxley, 1952; Simoni et al., 2004). The silicon neuron provides emulation of several currents contained in a previously published model of an oscillator heart interneuron (Hill et al., 2001): passive leak current (I_leak); fast sodium current (I_Na); inactivating potassium current (I_K1); slow, non-inactivating potassium current (I_K2); persistent sodium current (I_P); slowly inactivating low-threshold calcium current (I_CaS); and hyperpolarization-activated inward current (I_h). The design, details, and many of the characteristics of the silicon neuron used in this study were described by Simoni et al. (2004). Parameter values of the silicon neuron were set using 16-bit, four-channel digital-to-analog converters (Analog Devices, Norwood, MA). Digital-to-analog converters were interfaced to a personal computer via PIC microcontrollers (Microchip, Chandler, AZ). A user interface and software to communicate with PIC microcontrollers was written with the Java programming language (Sun Microsystems, Santa Clara, CA). Membrane potential measurement of and current injection into the silicon neuron were accomplished by direct connection to the headstages of an Axoclamp-2A electrophysiology amplifier (Axon Instruments, Union City, CA). State variables were measured through a current preamplifier (Stanford Research System, Sunnyvale, CA). The canonical parameter values for the silicon neuron are shown in Table 1.

Table 1.

Silicon neuron current parameters

SiN current	Reversal potential Eion (V)	Maximal conductance ḡ (10−9S)	Half-activation voltage (V)	Half-inactivation voltage (V)	Activation time constant τm (sec)	Inactivation time constant τh (sec)
INa	0.045	57.0	−0.028	−0.023	0	0.005
Ip	0.030	6.0	−0.034		0.034
IK1	−0.059	70.0	−0.030	−0.020	0.01	0.5
IK2	−0.081	42.4	−0.018		0.25
ICa	0.134	2.4	−0.045	−0.050	0.086	2.5
Ih	−0.028	4.0	−0.050		2.0
Ileak	−0.060	8.0

In voltage-clamp experiments on the silicon neuron, conductances were isolated by setting all other maximal conductances to 0 nS. For all activation variables, except m_h, the membrane potential (V_m) was held at -85 mV and then stepped up to command potentials. Because I_h is hyperpolarization activated, V_m was held at 30 mV and stepped down to command potentials. For currents possessing an inactivation variable, the time constants of activation were much faster than the time constant of inactivation, which allowed us to approximate the steady-state value of the current with its peak value. In currents with only activation variables, the current at the end of the command step was taken as the steady-state value. To analyze the inactivation variables, V_m was held at various holding potentials for a time sufficient to ensure that steady-state inactivation was reached, then stepped to a command potential of 50 mV. The peak value of the current was taken as the steady-state value. Current waveforms were fit to a first- or second-order exponential to assess the value of time constants.

Mathematical modeling was performed in the GENESIS simulation environment (Bower and Beeman, 1998). Two single-compartment isopotential heart interneurons connected by mutually inhibitory synapses were modeled. Differential equations were integrated using the exponential Euler method with a time step of 10^-4 sec. For each experiment, simulation parameters were set to default values and ḡ_h was then changed. The simulation was run for 100 sec for the activity to settle, and then 400 sec of data were recorded. Details of the model structure and simulation parameters were described by Hill et al. (2001).

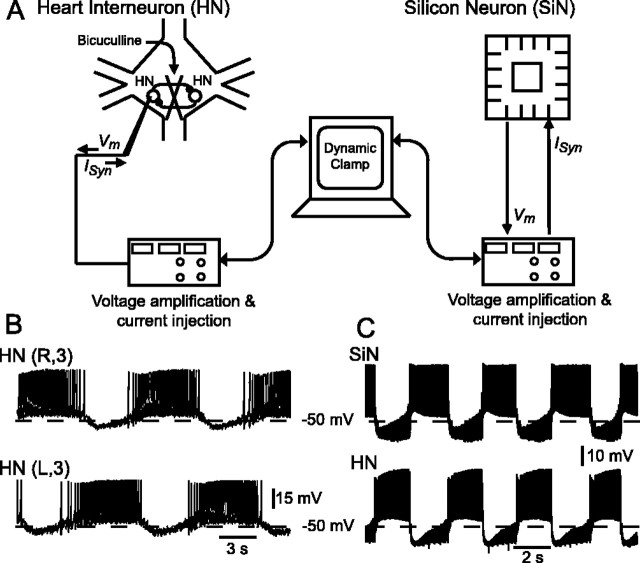
Leeches (Hirudo medicinalis) were obtained from a supplier (Leeches USA, Westbury, NY; and Biopharm, Burlington, NC) and maintained in artificial pond water at 15°C. After the animals were anesthetized in ice-cold saline, individual ganglia were dissected and pinned ventral side up in Petri dishes lined with Sylgard (bath volume, 0.5 ml). The methods for preparing and maintaining leech ganglia and for identifying heart interneurons for electrophysiological recording have been described previously (Olsen and Calabrese, 1996) (Fig. 1).

Figure 1.

Design and activity of hybrid half-center oscillator. A, Heart interneurons (HN), in an isolated ganglion preparation, were pharmacologically isolated with bicuculline. Voltage/current-clamp amplifiers were used for recording and current injection into heart interneurons and the silicon neuron (SiN). A single sharp microelectrode in discontinuous current-clamp mode was used for voltage recording and current injection into an isolated heart interneuron. Voltage recording and current injection into the silicon neuron were provided by direct connection to amplifier headstages (two-electrode current-clamp mode). Dynamic clamp provided real-time control signals to create artificial synapses between a heart interneuron and the silicon neuron. B, Activity of a living heart interneuron half-center oscillator in an isolated ganglion 3 (heart interneurons indexed by body side and ganglion number). C, Activity of a hybrid half-center oscillator.

The ganglionic sheath over the cell bodies was removed with fine microscissors or scalpels. Ganglia were superfused continuously with normal leech saline containing (in mm) 115 NaCl, 4 KCl, 1.8 CaCl₂, 10 glucose, and 10 HEPES buffer, adjusted to pH 7.4. All experiments were performed on heart interneurons in an isolated midbody segmental ganglion 3 or 4. Heart interneurons were isolated pharmacologically with 2.5 × 10^-4 m bicuculline methiodide (Sigma, St. Louis, MO) added to normal saline. In some experiments, 2 mm CsCl was added to the saline to block I_h.

Heart interneurons were penetrated with sharp microelectrodes made from borosilicate glass tubes [1 mm outer diameter, 0.75 mm inner diameter; filled with 4 m potassium acetate with 20 mm KCl (20-35 MΩ); A-M Systems, Everett, WA]. Currents were injected using discontinuous single-electrode current clamp (Axoclamp 2A; Axon Instruments, Foster City, CA). Sample rates were between 2.5 and 3 kHz. The electrode potential was monitored on an oscilloscope to ensure that it had settled between current injection cycles. Only neurons with an input resistance >60 MΩ were accepted. At the end of the experiment, microelectrodes were withdrawn from the cell, and only when the bath potential measured by the electrode was within the range ±5 mV were the data accepted.

Dynamic-clamp synapses were implemented according the following equations (Cymbalyuk et al., 2002a,b):

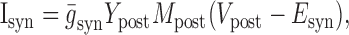1

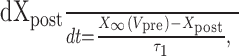2

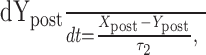3

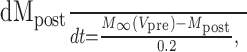4

5

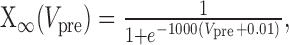6

where τ₁ = 0.002 sec, τ₂ = 0.011 sec, ḡ_syn = 500 nS, and E_syn = -0.062 V.

Dynamic-clamp I_h was implemented as follows:

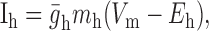7

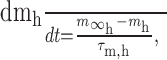8

9

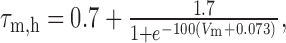10

where E_h = -0.02 V.

All dynamic-clamp calculations were performed on a dedicated real-time signal processing controller board (DS1104; DSPACE, Detroit, MI).

All experimental data were digitized and stored using pCLAMP software (Axon Instruments, Union City, CA). For both hybrid experiments and mathematical modeling, analyses of burst characteristics were performed off-line with scripts written in Matlab (MathWorks, Natick, MA). Action potentials (spikes) were detected by determining when the membrane potential rose and then fell across a threshold of -20 mV. If this sequence of two crossings occurred with an interval shorter than 1 msec, the event was taken to be spurious because of digitization error or noise and was discarded. All other such events were considered to be spikes. The time of occurrence of the spike was taken as the time when the maximum membrane potential was reached. This method was verified by eye for 630 sec of recorded data; in that data, all spikes had a width of at least 2 msec above -20 mV, and no spurious events registered as spikes. For all detected spikes in a continuous record, the mean and SD of the interspike interval (ISI) was calculated. ISIs >0.5 sec were used to mark the end of one burst and the beginning of the next burst; however, when two successive ISIs were >0.5 sec, the middle spike was considered to be spurious and was discarded. All ISIs within a burst had values within the mean ISI ± 2 SDs. We verified this method manually for 630 sec of recorded data, and it was found to be highly accurate for detecting both spikes and bursts of spikes. At least eight burst cycles were detected and analyzed per experimental trial. For each experimental trial, cycle period, burst duration, duration of the inhibited phase, and final spike frequency at burst transition was calculated. Burst period was calculated as the time between the median spike of one burst and the median spike of the next burst. Determining the cycle period in this manner minimizes period variability because of spurious spikes at the beginning and end of a burst. Burst duration was calculated as the time between the first spike of the burst and the last spike of the burst. Duration of the inhibited phase was calculated as the time between the last spike of a burst and the first spike of the next burst. The final spike frequency was defined as the instantaneous spike frequency for the last two spikes of a burst. In experiments in which the maximal conductance of the h-current (ḡ_h) was varied directly in the silicon neuron or in the heart interneuron with dynamic clamp, we measured/calculated the activation variable (m_h) and determined the percentage of the inhibited phase at which it first reached its maximal value. For heart interneurons, even when ḡ_h was set to zero or a negative value in dynamic clamp, m_h of the h-current was calculated, and this point of maximal activation was determined to estimate when endogenous h-current would activate. Values reported here are the mean and SD across experiments, except as indicated. Statistical analysis was performed by using a one-way ANOVA and a multiple comparison of means using the Bonferroni t test. A cutoff of p = 0.05 was used to evaluate statistical significance. To simplify the presentation of the multiple comparisons, comparisons to a single chosen value of the varied parameter are indicated on the figures. The chosen value of the parameter for comparison was usually the minimum value, except when varying silicon neuron (SiN) τ_h. Here, the value chosen was 0.5 sec because some of the measured characteristics varied non-monotonically with SiN τ_h, and with SiN τ_h set at 0.05 sec, these measured characteristics were at their minimum value.

Results

Properties of the isolated silicon neuron

Silicon neurons are real physical systems; they take voltages and currents as inputs and produce voltages and currents as outputs (Mahowald and Douglas, 1991; Patel and DeWeerth, 1997; Rasche and Douglas, 2000; Douglas and Rasche, 2002; Simoni et al., 2004). This approach differs from traditional mathematical modeling in that a model parameter value is represented by a voltage or current within the circuit, rather than an exact value in a numerical simulation. To assess the relationship between control voltages applied to the silicon neuron and the parameters of the emulated voltage-gated currents (Hodgkin-Huxley parameters), we measured the current-voltage relationships at the parameter inputs of the silicon neuron. These analyses produced data that a computer interface uses to translate Hodgkin-Huxley parameters to voltages that are applied to the circuit. Using this interface, we tuned the silicon neuron to the parameters derived from a mathematical oscillator heart interneuron model (Nadim et al., 1995; Hill et al., 2001). The time constants of activation and inactivation in the silicon neuron are fixed values and were set to the average values from the mathematical model (Table 1). With this set of parameters, the silicon neuron produced the desired tonic firing, but the action potentials were too wide (15 msec) and the firing frequency was too high (25 Hz). We adjusted the half-maximal activation and inactivation voltages and time constants of the fast currents to fix these discrepancies and to produce more realistic firing. This adjustment provided us with the canonical set of parameters that were used as a basis in all experiments (Table 1).

Differences between transistors can cause mismatches within the silicon neuron that can alter significantly the behavior of the circuit (Rasche et al., 1998; Patel and DeWeerth, 1999; Simoni et al., 2004). These differences come about as part of the circuit manufacturing process, and although circuit design techniques seek to minimize them, they are ultimately impossible to avoid. To assess the effects of transistor mismatch, we performed voltage-clamp analysis on the voltage-gated conductances of the silicon neuron. The results of this analysis (Fig. 2) show that the steady-state activation of the fast sodium current (m_∞Na) is nearly identical to the mathematical model, although its steady-state inactivation (h_∞Na) has a much shallower slope than its model counterpart (Fig. 2A). This difference could explain the wider spikes produced by the silicon neuron. m_∞K1 and h_∞K1 are relatively well matched, although there are both differences in slope and small offsets in the half-maximal voltages (Fig. 2B). m_∞K2, m_∞CaS, h_∞CaS, m_∞P, and m_∞h are all very similar to their mathematical model counterparts (Fig. 2C-F). The most noticeable effects of transistor mismatch are observed in the fast currents I_Na and I_K1, particularly in the slopes of h_∞Na and m_∞K1. Unfortunately, because of manufacturing limitations in the number of inputs available for the silicon neuron, the slope of all steady-state activation and inactivation curves were set as a global parameter; adjusting the slope of these curves would adversely affect the well matched slope of the other curves. Using the canonical parameters, the silicon neuron fired tonically with a spike frequency of 10-12 Hz.

Figure 2.

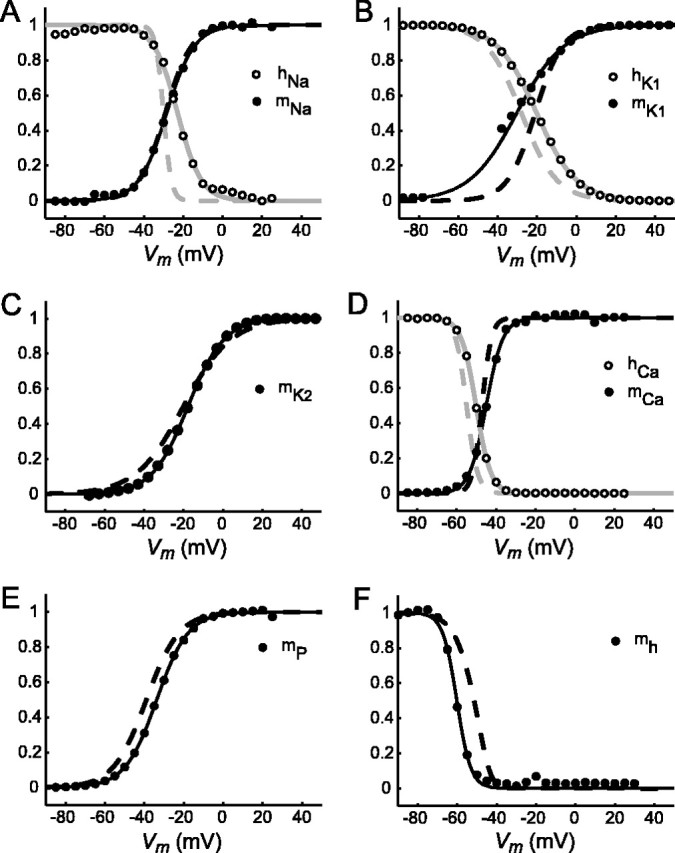
Steady-state activation and inactivation curves for the silicon neuron. The circles represent data from voltage clamp. Solid lines denote best fit of data to the activation/inactivation equations of Hill et al. (2001). The dashed lines show steady-state activation and inactivation curves for the currents of the canonical mathematical heart interneuron model. A, Fast sodium current (I_Na). B, Inactivating potassium current (I_K1). Data points from -75 to -45 mV are not shown because of large conductance/low current artifact. C, Slow, non-inactivating potassium current (I_K2). D, Slowly inactivating low-threshold calcium current (I_CaS). E, Persistent sodium current (I_P). F, Hyperpolarization-activated inward current (I_h).

Bifurcation analysis has proven to be an effective tool in analyzing transitions between different types of activity in heart interneurons (Cymbalyuk et al., 2002a). Activity in the mathematical model is sensitive to leak parameters E_leak and g_leak and produces bursting activity only in a narrow peninsula of this parameter space. This region of bursting in the parameter space E_leak versus g_leak separates areas of silence and tonic spiking (Fig. 3A, inset). To determine whether the silicon neuron behaves similarly to the mathematical model, we varied E_leak (-75 to -50 mV in steps of 2.5 mV) and g_leak (5-20 nS in steps of 1 nS) in the silicon neuron, and the resultant activity at each point was analyzed (Fig. 3A). As in the mathematical model, the silicon neuron displays bursting (Fig. 3C) in a narrow peninsula of these parameters that separates regions of silence and tonic firing (Fig. 3B). In addition, a narrow bistable region was found at the boundary between tonic firing and bursting, wherein the neuron could exhibit either tonic firing or rhythmic bursting, depending on the activity as the region was approached. Despite the differences in voltage-gated current parameters described before, these results are very similar to those from the mathematical model.

Figure 3.

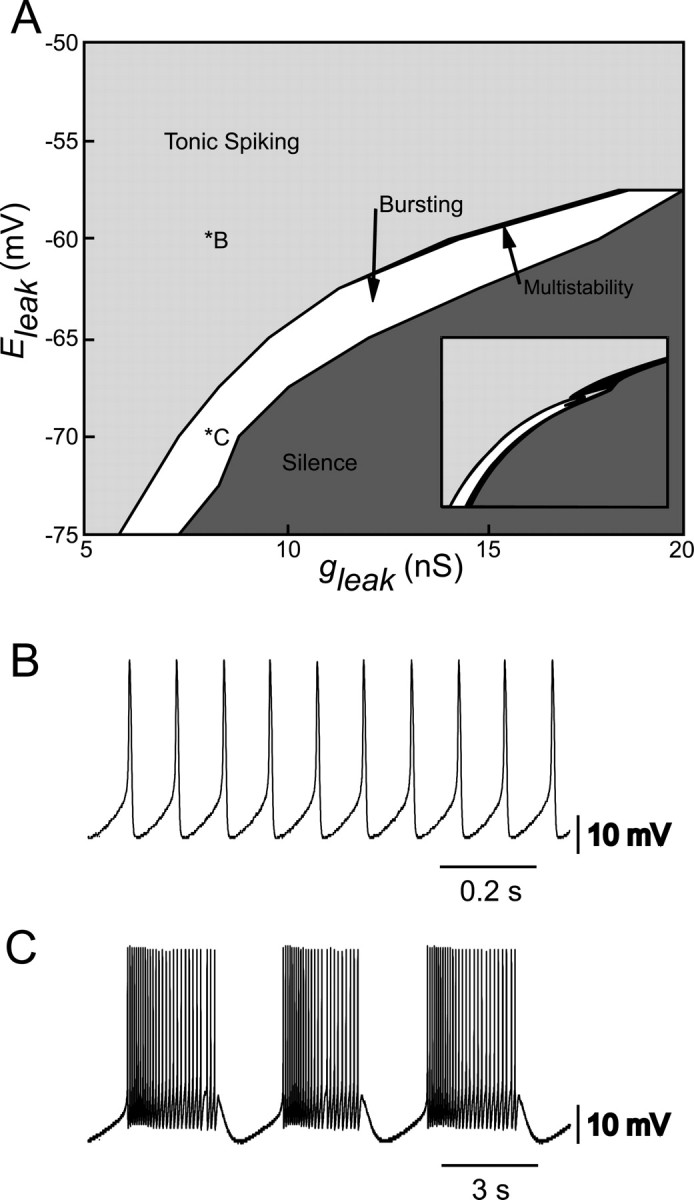
Activity of the silicon neuron depends on leak current parameters. A, Different types of activity, tonic spiking, bursting, and silence are expressed depending on the values of the leak reversal potential (E_leak) and the leak conductance (g_leak). The regions of silence and tonic spiking are separated by a region of intrinsic bursting. A small region, indicated in black (multistability), where bursting coexisted with tonic spiking was also observed. Inset, Similar activity map for the mathematical model of a heart interneuron (Cymbalyuk et al., 2002a). B, Typical activity of the silicon neuron when firing tonically. C, Typical activity of the silicon neuron when bursting intrinsically. Leak parameter values for the activity in B and C are indicated on the map in A.

Hybrid system: half-center oscillator

Dynamic clamp was used to implement artificial synaptic conductances between the silicon neuron and an intracellularly recorded oscillator heart interneuron (Cymbalyuk et al., 2002b). We discovered after several trials that cell input resistance (R_in) after sharp electrode penetration was critical to the success of establishing rhythmic bursting in the hybrid system. Poorly penetrated heart interneurons (R_in < 60 MΩ) fired at a high frequency and dominated the silicon neuron in the hybrid half-center. Moreover, the low resistance resulted in a fast membrane time constant and, therefore, poor synaptic integration. All results reported are from heart interneurons having R_in > 60 MΩ. When pharmacologically isolated in bicuculline, the heart interneurons (R_in > 60 MΩ) fired tonically with an average frequency of 10.3 ± 1.1 Hz (n = 5 trials) (Fig. 4A, bottom trace).

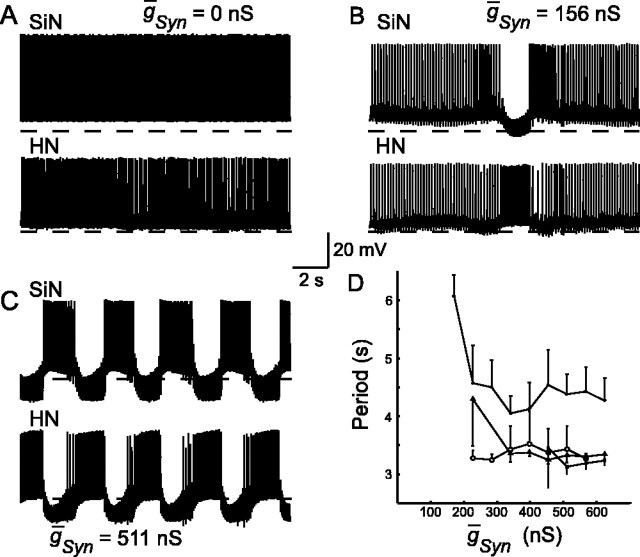
Figure 4.

Dynamic-clamp-mediated inhibitory synapses of sufficient strength transform tonic firing into rhythmic antiphasic bursting in a hybrid half-center oscillator. A, Both the silicon neuron (SiN) and the pharmacologically isolated heart interneuron (HN) fire tonically in the absence of artificial synapses (ḡ_Syn = 0 nS). B, Weak artificial synapses (small ḡ_Syn) result in sporadic lapses in activity but not rhythmic bursting. C, Strong artificial synapses (large ḡ_Syn) result in stable alternating rhythmic bursting. The dashed line in A-C indicates -50 mV. D, Results of four experiments in which ḡ_Syn was varied between 0 and 625 nS. Different symbols represent different experiments. The period of rhythmic oscillations settle to a value that remains relatively unchanged with additional variations of ḡ_Syn. The error bars indicate the SD of the period over n ≥ 8 cycles for each trial of the four individual experiments.

To determine appropriate synaptic strength for hybrid oscillations, the maximal synaptic conductance (ḡ_Syn) for both artificial synapses was varied between 0 and 625 nS in 12 equal steps for four separate preparations (Fig. 4). For low values of synaptic conductance, the two neurons continued to fire tonically, with occasional lapses in activity (Fig. 4B). Once sufficient synaptic strength had been reached, the neurons began alternating oscillations (Fig. 4C). Once stable oscillations were established, their period varied little with increasing ḡ_Syn (Fig. 4D). The oscillations ḡ_Syn = 511 nS were regular; the coefficient of variation of the period ranged from 3.7 to 11.5% with a mean of 6.8% for the four preparations (Fig. 4D). We selected 500 nS as the value of ḡ_Syn for all additional experiments.

Using canonical parameters for the silicon neuron and with ḡ_Syn set at 500 nS, rhythmic antiphasic bursting was obtained with all heart interneurons (R_in > 60 MΩ). To initiate antiphasic bursting, the synapses were activated by moving their maximal conductances from 0 to the canonical operating value (Fig. 5). Activating the synapses caused one of the neurons to be inhibited while the other continued to fire tonically. Once a neuron was inhibited, its I_h was activated; meanwhile, the spike rate of the active neuron rapidly increased and then slowly decreased because of the activation and subsequent inactivation of I_CaS. Once the spike rate in the active neuron was low enough, the inhibited neuron escaped from inhibition and began firing, inhibiting the other neuron. This process then repeated, resulting in antiphasic bursting.

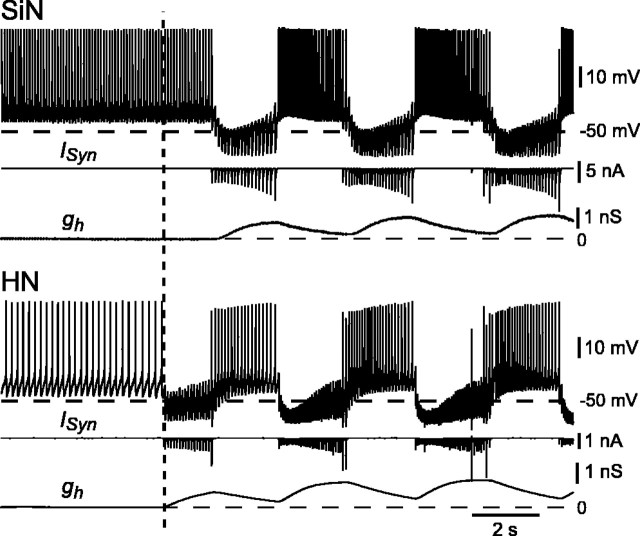
Figure 5.

Strong artificial inhibitory synapses cause an immediate transition from tonic firing to rhythmic bursting in a hybrid half-center oscillator. Membrane potential, synaptic current (I_Syn), and h-current conductance (g_h) are shown for the silicon neuron (SiN) and the heart interneuron (HN). The vertical dashed line indicates the time at which the dynamic clamp was activated to enable the mutual inhibitory synapses. When one of the neurons is inhibited, its I_h activates, driving it back toward the firing threshold. Once it begins to fire, the other neuron is inhibited, its I_h activates, driving it back toward firing threshold so that it inhibits the first neuron, and the cycle repeats.

The silicon neuron was thus suitable for investigating the role of intrinsic currents in the production and regulation of rhythmic bursting activity in a hybrid half-center oscillator. We chose to study I_h because it has been implicated as playing an important pacemaker function in a variety of systems (Luthi and McCormick, 1998). Our strategy was to vary I_h unilaterally in each member of the hybrid half-center oscillator.

Unilateral variation of ḡ_h in the silicon neuron

To assess experimentally the effects of varying ḡ_h of the silicon neuron (SiN ḡ_h), we established rhythmic antiphasic bursting between the silicon neuron and an isolated heart interneuron. In five separate experimental preparations, we varied SiN ḡ_h from 0 to 8 nS in increments of 2 nS (canonical SiN ḡ_h = 4 nS). At each interval, we assessed the cycle period, the burst duration, and the final spike frequency for each neuron. Typical activities at different values of SiN ḡ_h are shown in Figure 6A.

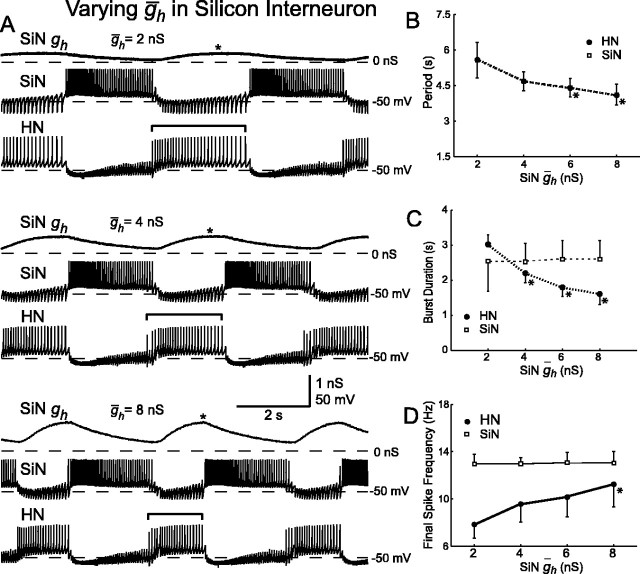
Figure 6.

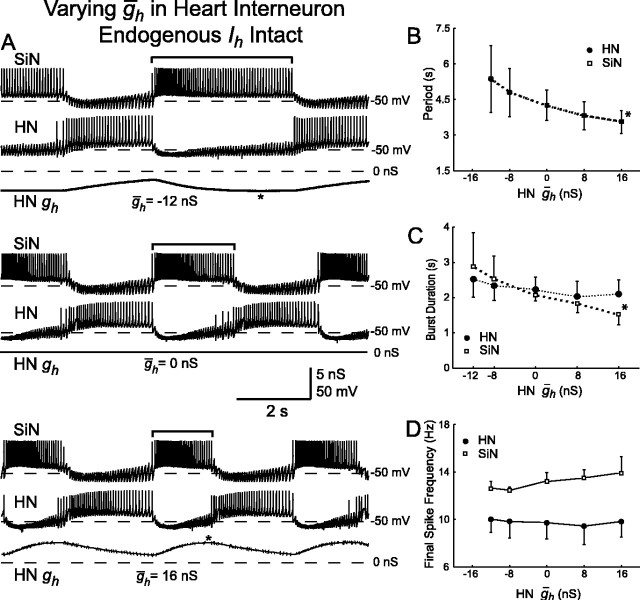
Variation of ḡ_h in the silicon neuron (SiN ḡ_h) of a hybrid half-center oscillator. A, Typical activity at three different values of SiN ḡ_h. Voltage traces for the silicon neuron (SiN) and the heart interneuron (HN) and h-current conductance (SiN g_h) for the silicon neuron are shown. As SiN ḡ_h increases, the burst duration (indicated by brackets) of the unaltered heart interneuron decreases. The asterisks indicate when during the inhibited phase h-current first reaches its maximal level of activation. B, Increasing SiN ḡ_h decreases the oscillator period. The period of the silicon neuron and the heart interneuron are the same. C, Increasing SiN ḡ_h decreases the burst duration of the heart interneuron, which is equivalent to the duration of the inhibited phase of the silicon neuron. D, Increasing SiN ḡ_h increases the final spike frequency of the heart interneuron, whereas the final spike frequency of silicon neuron remains relatively constant. In B-D, a thick line connecting data points indicates a significant effect of varying SiN ḡ_h as determined by ANOVA (p < 0.05), and asterisks indicate a significant difference (p < 0.05) between the measured value and the corresponding value when SiN ḡ_h was at its smallest value (2 nS) in pairwise comparisons.

With canonical parameter values, the cycle period was 4.7 ± 0.4 sec (mean ± SD). This period is shorter than both the average period observed in the biological system and the period of the mathematical model (8.8 and 8.6 sec, respectively), although the period is close to the low end of the range observed in the biological system (6.4 sec) (Hill et al., 2001; Cymbalyuk et al., 2002a). There are several possible factors that might explain this difference. For example, sharp microelectrode penetration of the heart interneuron causes a decrease in the membrane time constant, reducing the efficacy of spike-mediated synaptic transmission. Limitations in the silicon neuron, such as the lack of voltage-dependent time constants, or in the dynamic-clamp synapses, such as the lack of graded synaptic transmission (Hill et al., 2001), could also play a role.

With increasing SiN ḡ_h, the oscillator cycle period decreased (Fig. 6A,B); there was a statistically significant effect of varying SiN ḡ_h on the period of the system (ANOVA) (Table 2). With complete removal of I_h (SiN ḡ_h = 0), the silicon neuron was not always able to escape from inhibition (n = 2); in the cases in which it was able to escape (n = 3), the cycle period was greatly elongated (13.3 ± 1.8 sec). When SiN ḡ_h is varied, the change in the cycle period of the hybrid half-center oscillator is, mostly accounted for by the change in the duration of the inhibited phase of the silicon neuron (see Fig. 9D).

Table 2.

One-way ANOVA (p values)

Experiment	Varied neuron period	Unvaried neuron period	Varied neuron burst duration	Unvaried neuron burst duration	Varied neuron final spike frequency	Unvaried neuron final spike frequency
ḡh SiN	0.003	0.002	0.995	2.4e-6	0.997	0.027
ḡh HN	0.029	0.030	0.474	0.006	0.973	0.080
ḡh HN (w/Cs)	9.7e-9	9.7e-9	0.180	1.53e-10	0.949	8.7e-4
τh SiN	0.003	0.002	3e-7	0.068	0.828	0.170

Values in bold indicate statistical significance.

Figure 9.

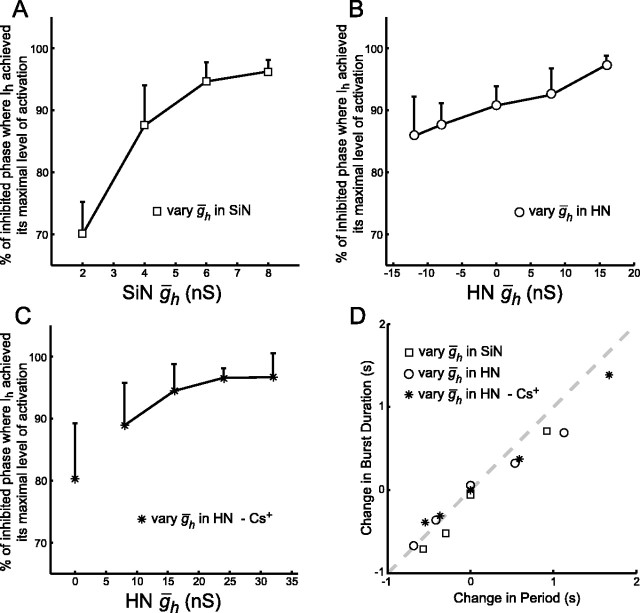
A-C, ḡ_h determines when I_h reaches its maximal level of activation during the inhibited phase of the burst cycle of a hybrid half-center oscillator. We measured this timing as the percentage of the inhibited phase at which I_h achieved its maximal level of activation. A, SiN ḡ_h varied. B, HN ḡ_h varied in the presence of endogenous I_h. C, HN ḡ_h varied with endogenous I_h blocked by 2 mm Cs⁺. The data point at HN ḡ_h = 0 nS is rather fanciful because there is no endogenous h-current and none is added or subtracted with dynamic clamp. Thus, this point is not connected to the rest by a line segment. D, Changes in the oscillator period caused by variation of ḡ_h are primarily attributable to changes in burst duration of the non-modified “neuron” (equivalent to duration of the inactive phase in the modified neuron). The change in burst duration from the canonical operating point for the non-modified neuron is plotted versus the change in the oscillator period. The dashed line indicates that all of the change in the oscillator period is attributable to change in the burst duration of the non-modified neuron. The data points all lie near this line, indicating that I_h is selectively acting to shorten the inhibited phase of the burst cycle of the oscillator.

In this hybrid half-center oscillator, the duration of the inhibited phase of one cell is approximately equal to the burst duration of the opposing cell. With canonical parameters, the burst duration of the silicon neuron and the burst duration of the heart interneuron were similar (2.5 ± 0.5 and 2.2 ± 0.3 sec, respectively). With increasing SiN ḡ_h, the burst duration of the heart interneuron decreased, corresponding to a decrease in the inhibited phase of the silicon neuron (Fig. 6A,C). The final spike frequency of the heart interneuron also increased (Fig. 6A,D). There was a statistically significant effect of varying SiN ḡ_h on the burst duration and final spike frequency of the heart interneuron but no apparent effect on these characteristics in the silicon neuron (ANOVA) (Table 2). The absence of a significant change in the burst duration of the silicon neuron indicates that variations in SiN ḡ_h selectively influence the inhibited phase of the oscillation. The increase in the final spike frequency of the heart interneuron indicates that with a higher ḡ_h the silicon neuron is able to overcome a higher frequency of inhibition from the heart interneuron and escape into its burst. Variations in SiN ḡ_h change the balance of oscillations; with higher values of SiN ḡ_h, the silicon neuron has a relatively longer burst duration (duty cycle), and with lower values of SiN ḡ_h, the heart interneuron has a relatively longer burst duration (duty cycle).

With canonical parameters, the final spike frequency is noticeably higher for the silicon neuron than for the heart interneuron; the heart interneuron is generally able to escape from a higher frequency of inhibition. This difference is most likely attributable to the difference in membrane time constants and input resistance, which determines the efficacy of dynamic-clamp synaptic currents in altering membrane potential.

At low values of SiN ḡ_h, the time point during the inhibited phase of the burst cycle at which I_h attained its maximal level of activation was well before the burst transition occurred (Fig. 6A). We expressed this time point as a percentage of the inhibited phase (see Fig. 9A-C). This observation indicates that the silicon neuron was “waiting” for a decrease in the inhibition it receives from the heart interneuron before it could begin firing. Therefore, the dynamics of spike frequency adaptation in the heart interneuron were determining the duration of the inhibited phase of the silicon neuron rather than the dynamics of I_h activation. As SiN ḡ_h increased, I_h attained its maximal level of activation at relatively later and later time points in the inhibited phase. [The absolute amount of time necessary to attain maximal activation was nearly invariant, but this maximal activation occurred at a greater percentage of the inhibited phase (see Fig. 9A).] At high values of SiN ḡ_h, I_h attained its maximal level of activation practically at the end of the inhibited phase (Fig. 6A). This observation indicates that at high values of SiN ḡ_h the dynamics of I_h activation were determining the duration of the inhibited phase of the silicon neuron rather than the dynamics of spike frequency adaptation in the heart interneuron.

Unilateral variation of ḡ_h in the heart interneuron

To vary the strength of I_h in the heart interneuron, we used dynamic clamp to create a model I_h, which could be used in conjunction with the endogenous I_h of the heart interneuron. By setting the maximal conductance of the dynamic clamp I_h, heart interneuron (HN) ḡ_h, to be greater than zero, we added to the endogenous I_h. We subtracted from the endogenous I_h by setting HN ḡ_h to negative values. Subtracting I_h in excess of the effective endogenous I_h created a positive feedback system, driving the cell to an extremely hyperpolarized state. Several cells were tested, and it was found that an artificial maximal conductance of -16 nS would almost always cause this undesirable condition to occur, but -12 nS would not; -12 nS was therefore chosen as the maximal “negative conductance.” Furthermore, the heart interneuron required a larger variation in I_h than did the silicon neuron to observe similar effects, so HN ḡ_h was varied over a larger range than in the case for the silicon neuron.

In five experiments, hybrid oscillations were established, and HN ḡ_h was varied between -12 and +16 nS. SiN ḡ_h was kept constant at the canonical value of 4 nS. Typical activity for different levels of HN ḡ_h is shown in Figure 7A. With no addition or subtraction to the endogenous I_h (HN ḡ_h = 0 nS), the cycle period of the hybrid oscillator was 4.24 ± 0.6 sec, and the burst duration of the silicon neuron (2.1 ± 0.3 sec) was similar to the burst duration of the heart interneuron (2.2 ± 0.4 sec). With increasing HN ḡ_h, the period of the system decreased (Fig. 7A,B); there was a statistically significant effect of varying HN ḡ_h on period (ANOVA) (Table 2). Moreover, with increasing HN ḡ_h, the burst duration of the silicon neuron decreased, corresponding to a decrease in the inhibited phase of the heart interneuron, and the final spike frequency of the silicon neuron increased (Fig. 7A,C,D). There was a statistically significant effect of varying HN ḡ_h on the burst duration of the silicon neuron, but the effect on final spike frequency of the silicon neuron was not statistically significant (p = 0.08; ANOVA) (Table 2). There was no apparent effect of varying HN ḡ_h on burst duration or final spike frequency in the heart interneuron (ANOVA) (Table 2).

Figure 7.

Variation of ḡ_h in the heart interneuron (SiN ḡ_h) of a hybrid half-center oscillator with endogenous I_h present. A, Typical activity at three different values of HN ḡ_h. Voltage traces for the silicon neuron (SiN) and the heart interneuron (HN) and h-current conductance (HN g_h) for the heart interneuron are shown. As HN ḡ_h increases, the burst duration (indicated by brackets) of the unaltered silicon neuron decreases. The asterisks indicate when during the inhibited phase h-current first reaches its maximal level of activation. B, Increasing HN ḡ_h decreases the oscillator period. The period of the silicon neuron and the heart interneuron are the same. C, Increasing HN ḡ_h decreases burst duration of the silicon neuron, which is equivalent to the duration of the inhibited phase of the heart interneuron. D, Increasing HN ḡ_h increases the final spike frequency of the silicon neuron, whereas the final spike frequency of the heart interneuron is relatively constant. In B-D, a thick line connecting data points indicates a significant effect of varying HN ḡ_h as determined by ANOVA (p < 0.05), and asterisks indicate a significant difference (p < 0.05) between the measured value and the corresponding value when HN ḡ_h was at its smallest value (-12 nS) in pairwise comparisons.

As observed when varying SiN ḡ_h, the change in period when varying HN ḡ_h was attributable to a change in the duration of the inhibited phase of the modified neuron (Fig. 9D). The duration of the inhibited phase of the heart interneuron, which is equivalent to the burst duration of the silicon neuron, decreased, whereas the burst duration of the heart interneuron remained relatively constant. These results are remarkably similar to the case when SiN ḡ_h, was varied; increasing HN ḡ_h caused I_h to attain its maximal level of activation at a relatively later point of the inactive phase of the burst cycle (Fig. 9B). Although the effect here is not as striking as in the SiN ḡ_h case, it is still apparent.

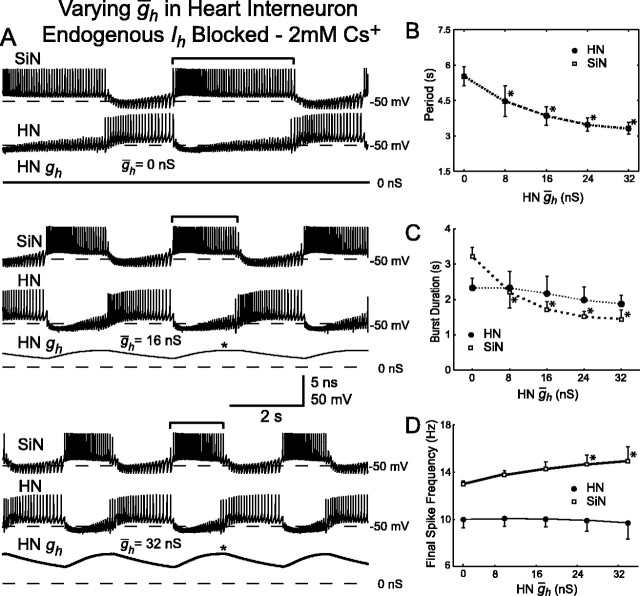
In six additional experiments, we blocked the endogenous I_h of the heart interneuron with 2 mm Cs⁺, and the dynamic clamp was then used to reintroduce a completely artificial I_h into the heart interneuron. HN ḡ_h was then varied from 0 to 32 nS in 8 nS increments. Typical activity for different levels of HN ḡ_h is shown in Figure 8A. As observed in the other experiments in which ḡ_h was varied, increasing HN ḡ_h decreased the cycle period of the system (Fig. 7A,B); there was a statistically significant effect of varying HN ḡ_h on the period (ANOVA) (Table 2). Moreover, with increasing HN ḡ_h, the burst duration of the silicon neuron decreased, corresponding to a decrease in the inhibited phase of the heart interneuron, and the final spike frequency of the silicon neuron increased (Fig. 7A,C,D). There was a statistically significant effect of varying HN ḡ_h on the burst duration and final spike frequency of the silicon neuron but no apparent effect on these characteristics in the heart interneuron (ANOVA) (Table 2). As in the previous experiments, the change in period was attributable to a change in the duration of the inhibited phase of the modified neuron (Fig. 9D). Increasing HN ḡ_h also led to an increase in the percentage of the inhibited phase at which I_h attained its maximal level of activation in the heart interneuron (Figs. 8A, 9C), which was very similar to when ḡ_h was varied in the silicon neuron.

Figure 8.

Variation of ḡ_h in the heart interneuron (HN ḡ_h) of a hybrid half-center oscillator with endogenous I_h blocked by 2 mm Cs⁺. A, Typical activity at three different values of HN ḡ_h. Voltage traces for the silicon neuron (SiN) and the heart interneuron (HN), and h-current conductance (HN g_h) for the heart interneuron are shown. As HN ḡ_h increases, the burst duration (indicated by brackets) of the unaltered silicon neuron decreases. The asterisks indicate when during the inhibited phase h-current first reaches its maximal level of activation. B, Increasing HN ḡ_h significantly decreases the oscillator period. The cycle period of the silicon neuron and the heart interneuron are the same. C, Increasing HN ḡ_h decreases the burst duration of the silicon neuron, which is equivalent to the duration of the inhibited phase of the heart interneuron. There is also a slight decrease in the burst duration of the heart interneuron. D, Increasing HN ḡ_h increases the final spike frequency of the silicon neuron, whereas the final spike frequency of the heart interneuron remains relatively constant. In B-D, a thick line connecting data points indicates a significant effect of varying HN ḡ_h as determined by ANOVA (p < 0.05), and asterisks indicate a significant difference (p < 0.05) between the measured value and the corresponding value when HN ḡ_h was at its smallest value (0 nS).

The remarkable similarity in results when ḡ_h was varied in the silicon neuron and the living heart interneuron, both with endogenous I_h present and when it was blocked by Cs⁺, demonstrates that the dynamics of dynamic clamp I_h are compatible with the intrinsic currents in the living neuron and that I_h serves a similar function in the heart interneuron and in the model neuron.

Unilateral variation of I_h in mathematical model of a half-center oscillator

To corroborate our results from the hybrid systems analysis, we investigated the effects of unilateral variation in a mathematical model of a leech heartbeat half-center oscillator (Hill et al., 2001). Previous modeling studies indicated that ḡ_h determines the final spike frequency, the firing frequency at which a heart interneuron escapes the inhibition of the other neuron in the half-center oscillator (Hill et al., 2001). However, these studies investigated only the effects of bilateral variation of parameters, not the unilateral variations that we used in our hybrid systems analysis. Using the GENESIS neural simulation environment, we varied ḡ_h of one model neuron of a model half-center oscillator from 0 to 8 nS (4 nS canonical) in 0.5 nS increments. We then assessed the resultant activity for cycle period, burst duration, duration of the inhibited phase, and final spike frequency.

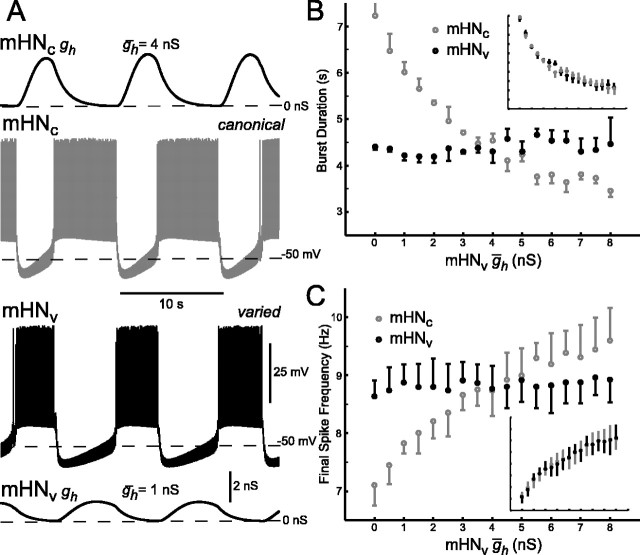
Unilateral variation of ḡ_h in the model revealed effects similar to those observed in the hybrid system (Fig. 10). Increasing ḡ_h unilaterally resulted in a decrease in the burst duration of the unmodified (constant) model cell corresponding to a decrease in the duration of the inactive phase of the modified model neuron (Fig. 10B). The burst duration of the modified model neuron, however, exhibited virtually no change. This selectivity for influencing the inactive phase of the burst was not apparent when ḡ_h was varied bilaterally (Fig. 10B, inset). Final spike frequency increased nearly linearly for the constant model neuron but remained constant for the varied model neuron (Fig. 10C). The changes in final spike frequency in the unmodified model neuron for unilateral variation of ḡ_h corresponded closely to the changes in final spike frequency observed for symmetric variation of ḡ_h (Fig. 10C, inset). These modeling results for asymmetric variation of ḡ_h further support the hypothesis developed from symmetric variation of ḡ_h in the model (Hill et al., 2001) and from our hybrid system analysis that ḡ_h sets the final spike frequency from which an inhibited neuron escapes.

Figure 10.

Unilateral variation of ḡ_h in the mathematical model of a heart interneuron half-center oscillator. A, Typical activity for an unbalanced half-center oscillator: membrane potential and h-current conductance (g_h) for both the varied (mHN_v) and the canonical (unvaried; mHN_c) model heart interneuron. B, Increasing ḡ_h causes a decrease in burst duration of the unvaried canonical “neuron,” which is equivalent to the duration of the inactive phase of the varied neuron. Varied neuron burst duration remains constant. Inset, Results for symmetric variation of ḡ_h plotted with the same axes values. C, Final spike frequency of unvaried canonical neuron increases with increasing ḡ_h. Final spike frequency of varied neuron remains relatively constant. Inset, Results for symmetric variation of ḡ_h plotted with the same axes values. The error bars indicate the SD over n ≥ 25 cycles for the individual modeling trial.

Finally, the changes in cycle period of the model half-center oscillator observed under bilateral and unilateral variation of ḡ_h are qualitatively very similar (data not shown). Essentially, the change in period for a bilateral change in ḡ_h is double that for a unilateral change in ḡ_h.

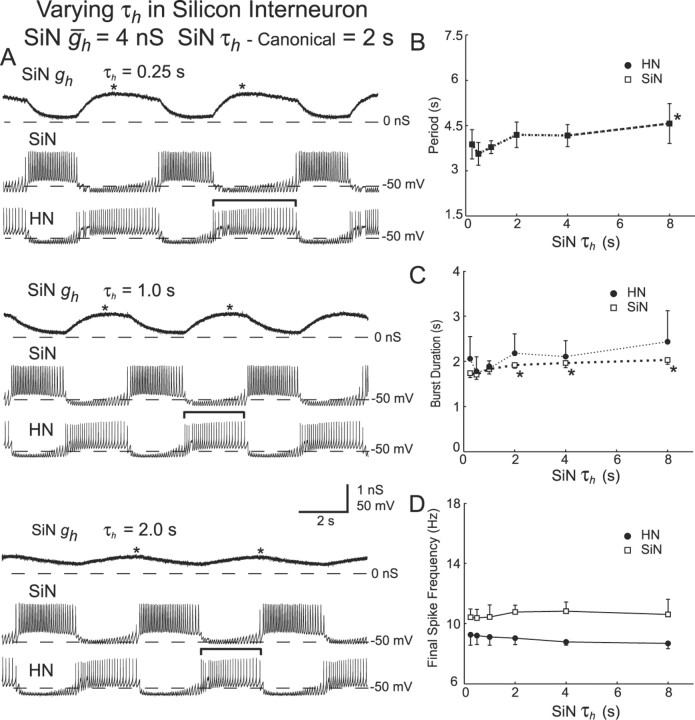
Unilateral variation of τ_h in the silicon neuron.

We assessed the effect of varying τ_h (the time constant of activation and deactivation of I_h) on the rhythmic activity of the hybrid oscillator only by varying this parameter in the silicon neuron, having demonstrated that alterations of the properties of the silicon neuron can describe similar changes in the heart interneuron.

In seven experiments, we varied τ_h of the silicon neuron (SiN τ_h) from 0.25 to 8 sec (canonical τ_h = 2 sec). Typical activity at different values of SiN τ_h is shown in Figure 11A. With canonical parameter values, the oscillator cycle period was 4.19 ± 0.42 sec, and the burst duration of the silicon neuron (1.9 ± 0.1 sec) and the heart interneuron were similar (2.1 ± 0.4 sec) (Fig. 11A). Alterations of SiN τ_h had no statistically significant effect of the final spike frequency for either cell (Fig. 11D) (ANOVA) (Table 2). There was a statistically significant effect of varying SiN τ_h on the period of the system (ANOVA) (Table 2), but this effect was complex (Fig. 11A). Between 0.5 and 8 sec, increases in SiN τ_h led to increases in period, but below 0.5 sec period decreased with increasing τ_h, although pairwise comparisons showed that this increase did not quite reach significance between SiN τ_h = 0.5 and 0.25 sec (p = 0.06). There was also no statistically significant effect of varying SiN τ_h on burst duration of the unvaried heart interneuron (p = 0.07) (ANOVA) (Table 2), although a trend in the data similar to the effect on period is apparent (Fig. 11C). Surprisingly, there was a very small, but statistically significant, effect of SiN τ_h on the burst duration of the silicon neuron (ANOVA) (Table 2; Fig. 11C); this effect reflects the slow deactivation of I_h during the burst, especially when SiN τ_h is large, that prolongs the burst. Decreasing SiN τ_h below the canonical value also led to a decrease in the percentage of the inhibited phase at which I_h attained its maximal level of activation in the heart interneuron, but no effect was noted with increases of SiN τ_h above the canonical value (Fig. 11A) (group data not shown).

Figure 11.

Variation of τ_h in the silicon neuron (SiN τ_h) of a hybrid half-center oscillator. A, Typical activity at three different values of HN ḡ_h. Voltage traces for the silicon neuron (SiN) and the heart interneuron (HN) and h-current conductance (SiN g_h) for the heart interneuron are shown. The burst duration of the unaltered heart interneuron is indicated by brackets. B, Variations in SiN τ_h have a significant effect on the cycle period. Decreasing SiN τ_h, down to 0.5 sec, causes a decrease in the cycle period. An additional decrease in SiN τ_h, however, causes an increase in the cycle period. C, Decreasing SiN τ_h decreases the burst duration of the heart interneuron and also causes a slight decrease in the burst duration of the silicon neuron. D, Variations in SiN τ_h have no significant effect on the final spike frequency of either the silicon neuron or the heart interneuron. In B-D, a thick line connecting data points indicates a significant effect of varying SiNτ_h as determined by ANOVA (p < 0.05), and asterisks indicate a significant difference (p < 0.05) between the measured value and the corresponding value when SiN τ_h was set at 0.5 sec in pairwise comparisons.

The increase in oscillator period for low values of τ_h, seen as a trend in the data of Figure 11C, was seen as a qualitatively similar effect in the mathematical model. As τ_h decreases, I_h activates faster. Up to a certain point, this means that the depolarizing current will be present at an earlier time during the inhibited phase of the burst. The duration of the inhibited phase will be shortened, and the period of oscillations will decrease. As τ_h decreases beyond a certain level, however, the activation level of I_h begins to approximate its steady-state value. The depolarizing effects of I_h move the membrane potential to a level at which I_h deactivates before the neuron reaches threshold. Thus, very little depolarizing current will be available to drive the neuron out of inhibition, and the duration of the inhibited phase will therefore increase.

Discussion

We have constructed a hybrid half-center oscillator using a living heart interneuron from the medicinal leech and a silicon model neuron. Using this hybrid half-center oscillator, we investigated the role of the hyperpolarization-activated inward current I_h in rhythm generation and the control of period and burst duration. We varied three parameters of I_h in the silicon neuron: ḡ_h (the maximal conductance of I_h) and τ_h (the time constant of I_h activation/deactivation). Using dynamic clamp, we also varied ḡ_h in the heart interneuron, both with endogenous I_h present and with endogenous I_h blocked, thereby demonstrating that the heart interneuron and the silicon neuron were functionally similar. Increasing ḡ_h increased the firing frequency of the active (unvaried) neuron at which the inhibited (varied) neuron escaped from inhibition. As a result, increasing ḡ_h decreased the duration of the inhibited phase in the varied neuron and decreased the cycle period. Varying τ_h had no effect on the spike frequency at transition; as it decreased, however, the cycle period of the hybrid oscillator initially decreased but then increased.

Validity of the hybrid neuronal network

For several years, numerous efforts have been made to construct hybrid networks for neuronal network investigations. The goal of such investigations has been to use the controllability and well defined structure of a model to better understand neuronal function, while still retaining the realism provided by living neurons. In general, these efforts have taken two different approaches. The first approach has used nonphysiological models, such as nonlinear oscillators or phenomenological model neurons, coupled with a neuron or a neuronal network (Yarom, 1991; Szucs et al., 2000). The relative simplicity of these models facilitates the study of dynamical properties; such study is extremely difficult with more complicated models. The second approach has been to use physiologically realistic, conductance-based model neurons. This approach facilitates the investigation of both the mechanisms by which activity is produced and the functional role of different conductances (Renaud-LeMasson et al., 1993; Le Masson et al., 1995, 2002; Nadim and Manor, 2001; Manor and Nadim, 2001; Derjean et al., 2003).

Our hybrid system used an analog silicon neuron that implemented a realistic conductance-based model based on the Hodgkin-Huxley formalism (Hodgkin and Huxley, 1952; Simoni et al., 2004). This mechanistic approach to modeling was necessary because we were interested in studying how intrinsic ionic currents contribute to generating rhythmic oscillatory activity. Whereas this goal could have been accomplished with a more common digital model, the silicon neuron provides several advantages in terms of scalability and power consumption that will be important in expanding the scale of the model in future hybrid systems. Although there are often many difficulties in working with silicon neurons, great care was taken to ensure that the properties of our silicon neuron were closely matched to those of the heart interneuron. Voltage-clamp analysis performed on the silicon neuron revealed that its intrinsic currents are well matched to those of a mathematical model of a heart interneuron. As a result, when the tonically firing model neuron and tonically firing biological neuron were coupled with inhibitory synapses using dynamic clamp, they produced alternating rhythmic bursting. This transformation in activity is analogous to results observed when inhibitory synaptic transmission is reversibly blocked in heart interneurons recorded by sharp microelectrode penetration (Schmidt and Calabrese, 1992; Cymbalyuk et al., 2002a).

The oscillations produced by our hybrid system were very similar to those observed in the living heart interneuron half-center oscillator. Furthermore, we demonstrated that qualitatively similar changes in cycle period, burst duration, and final spike frequency were observed when ḡ_h was varied either in the silicon neuron or in the heart interneuron. This demonstration of symmetry in observed effects between the model neuron and a heart interneuron indicates that conclusions drawn from the model can be applied confidently to the living system.

Role of I_h in heart interneuron half-center oscillators

I_h has been implicated in the generation of rhythmic activity in numerous vertebrate and invertebrate systems (Pape, 1996; Sharp et al., 1996; Luthi and McCormick, 1998; Robinson and Siegelbaum, 2003). In the thalamus, for example, the interaction of I_h with a low-threshold Ca²⁺ current leads to the generation of oscillatory bursting activity that plays an important role in sleep (McCormick and Huguenard, 1992). Additionally, it has been shown that I_h can influence or pace rhythmic activity within the inferior olive, the hippocampus, and the pre-Botzinger complex of the mammalian brain (Maccaferri and McBain, 1996; Bal and McCormick, 1997; Thoby-Brisson et al., 2000). Given the widespread distribution of I_h and its importance in the generation of rhythmic activity, it is not surprising that I_h appears to be a frequent target of modulation (Kiehn and Harris-Warrick, 1992; Harris-Warrick et al., 1995, Wang et al., 2002).

Previous modeling and physiological studies in our laboratory indicate that I_h exerts an important control on period in heart interneuron half-center oscillators (Olsen and Calabrese, 1996; Hill et al., 2001). By making unilateral changes in this analysis, we have supplemented the previous work to demonstrate the selectivity of I_h in controlling the inhibited phase of the heart interneuron burst cycle. In both the mathematical model and the hybrid system, modulation of I_h by ḡ_h and τ_h substantially affect the duration of the inhibited phase of the oscillation, with little or no effect on burst duration of the varied neuron. Thus, in addition to its role as a period regulator, I_h can also alter the balance of activity (duty cycle) in a half-center oscillator. Our results are consistent with other investigations into the functional role of I_h, which demonstrated that increasing I_h decreases cycle period and increases the duty cycle of affected cell (MacLean et al., 2003; Zhang et al., 2003). Because leech heartbeat half-center oscillators always produce equally balanced rhythmic oscillations, any modulatory process that acts on ḡ_h or τ_h would have to either act bilaterally or additionally effect some other property to maintain an appropriate balance of activity.

Overall, the results produced by experiments with the hybrid system were very similar to the results observed in simulated experiments with the mathematical model. There was, however, one prominent difference that provides some insight into the role of I_h in heart interneuron half-center oscillators. The hybrid system oscillates at a substantially shorter period than the mathematical model, although the average period of the hybrid system is close to the lower limit of periods observed in the biological oscillator (Cymbalyuk et al., 2002a). Despite this difference, the qualitative effects of ḡ_h and τ_h on period, burst duration, and final spike frequency are the same in both the hybrid system and in the mathematical model. This result not only demonstrates the validity of the hybrid system but also reveals that the qualitative effects of ḡ_h and τ_h variation are apparently independent of the cycle period. Modulatory mechanisms are often dependent on the state of the neuron (Goldman et al., 2001). Identifying mechanisms that are state independent is important because they provide a means for the network to modulate its activity regardless of other factors that may be affecting the period. For example, the heartbeat of juvenile leeches is significantly faster than that of adults (Wenning et al., 2004). Both juvenile and adult leeches could therefore use ḡ_h and τ_h to modulate their heart rate.

When ḡ_h was at canonical/normal values or smaller, we observed many cases in which I_h reached its maximal level of activation in the varied neuron long before a burst transition occurred, indicating that no transition was possible until spike frequency of the opposite interneuron declined to a low enough level to reduce inhibition in the varied neuron to the point that it could be overcome by the fully activated I_h (Figs. 6, 7, 8, 9). When ḡ_h was increased, however, I_h reached its maximal level of activation at or just before the burst transition in the varied neuron; this did not represent a change in the amount of time necessary for I_h to activate but rather the higher final frequency that could be overcome. These results indicate that time course of inactivation of the low-threshold slowly inactivating Ca²⁺ current that supports the burst (Angstadt and Calabrese, 1991; Hill et al., 2001) is critical in determining the burst duration of a heart interneuron and thus the period of a half-center oscillator, a hypothesis that may be tested in future hybrid system experiments.

In conclusion, we demonstrated that a hybrid system composed of both biological and modeled neurons can produce realistic activity, and that alterations in the properties of the model neuron accurately reflect similar alterations of the biological neuron. Furthermore, we have demonstrated how I_h can serve as a regulator of network activity, with increasing levels of I_h decreasing cycle period and increasing the duty cycle of affected neurons.