Behavioral Context and Coherent Oscillations in the Supplementary Motor Area

Abstract

Movements with similar physical characteristics can occur in various behavioral contexts, as when they are embedded in different sequences or when the expected outcomes of movements vary. Similarly, neurons in various sensory and motor structures in the brain commonly display modulations in their activity according to contextual factors, such as expected reward. Although these contextual signals must be combined with incoming sensory inputs to generate appropriate behaviors according to the animal's motivational state, the mechanisms by which these two signals are integrated remain poorly understood. The present study examined the effects of contextual factors on the magnitude of coherent oscillations in the activity of individual neurons recorded in the supplementary motor area (SMA) of monkeys during a serial reaction time task. In this task, the animal produced a predictable sequence of hand movements repeatedly according to visual instructions. The performance of the animal was influenced by the location of the rewarded target as well as the ordinal position of the movement. In contrast, the level of coherent oscillations in the activity of SMA neurons was affected only by the rewarded target location but not by the ordinal position of the movement sequence. In addition, changes in coherent oscillations were not accounted for by systematic changes in the mean firing rates. These results are consistent with the proposal that synchronous spikes might be used to control the flow of information and suggest that coherent oscillations in the SMA might encode contextual variables, such as expected reward.

Introduction

Animals can maximize their chance of survival and reproduction by selecting a course of actions that maximizes the amount of expected rewards. This process must be tuned by the animal's experience in a dynamic environment. Although the neural basis for integrating information about the animal's past behaviors, their outcomes, and incoming sensory inputs is not well understood, a number of recent studies have begun to provide some important insights. For example, many studies have now demonstrated that the location of a movement target and the amount of expected reward often influence the activity of the same individual neurons in various brain regions, including the posterior parietal cortex (Platt and Glimcher, 1999), fronto-cortical areas (Watanabe, 1996; Leon and Shadlen, 1999; Kobayashi et al., 2002; Shidara and Richmond, 2002; Roesch and Olson, 2003; Barraclough et al., 2004), the basal ganglia (Kawagoe et al., 1998), and the superior colliculus (Ikeda and Hikosaka, 2003). Therefore, how these two fundamentally different types of signals are transmitted within and across different brain areas remains an important but unanswered question. The present study examined the possibility that coherent oscillations in the neural activity might be a means to tag the signals carried by individual neurons regarding sensory inputs and corresponding motor plans with their motivational significance.

Although synchronized oscillations in neural activity have been observed in many different brain areas, their functional significance still remains controversial (Gray, 1999; Shadlen and Movshon, 1999). On the one hand, it has been proposed that spikes of multiple neurons are synchronized when individual features coded by such neurons belong to a common object (Gray, 1999; Singer, 1999; von der Malsburg, 1999). Similarly, synchronous spikes in the motor cortical areas have been proposed as a means to bind individual movement segments to produce complex movement patterns (Pfurtscheller et al., 1993; Murthy and Fetz, 1996a,b; MacKay, 1997; Riehle et al., 1997; Donoghue et al., 1998; Lebedev and Wise, 2000; Ohara et al., 2001; Baker et al., 2003). Experimental support for this hypothesis, unfortunately, has not been consistent (Lamme and Spekreijse, 1998; Thiele and Stoner, 2003). On the other hand, several studies have demonstrated that synchronized oscillations in cortical activity, especially in the gamma frequency range (30–50 Hz), might be important for controlling the flow of sensorimotor information according to various top-down factors, such as selective attention and anticipation of behaviorally relevant sensory stimuli (Cardoso de Oliveira et al., 1997; Steinmetz et al.,. 2000; Fries et al., 2001; Supèr et al., 2003). Using a wavelet cross-spectrum (Lee, 2002), a previous study found that neurons in the supplementary motor area (SMA) display robust coherent gamma frequency oscillations in their activity, but their functions were unknown (Lee, 2003). The present study shows that such coherent oscillations are affected by the spatial relationship between the individual movements and the expected location of rewarded movement target. These results suggest that coherent oscillations might contribute to the process of selecting a particular movement according to the motivational state of the animal (Averbeck and Lee, 2004).

Materials and Methods

Animal preparation and neural recording

Two male rhesus monkeys (Macaca mulatta; body weight, 6–8 kg) were used. A detailed description of the methods used to collect behavioral and single-unit data has been published previously (Lee and Quessy, 2003). Briefly, single-unit activity was recorded simultaneously from a small number of neurons in the supplementary motor area, using an Eckhorn 16-channel mictroelectrode manipulator (Thomas Recording, Giessen, Germany) and a Plexon (Dallas, TX) multi-channel acquisition processor. Electrodes were arranged in a 4 × 4 grid, and the distance between neighboring electrodes was 350 μm. All of the procedures used in the current study were approved by the University of Rochester Committee on Animal Research and conformed to the principles outlined in the Guide for the Care and Use of Laboratory Animals (National Institutes of Health publication number 85-23, revised 1985).

Behavioral task

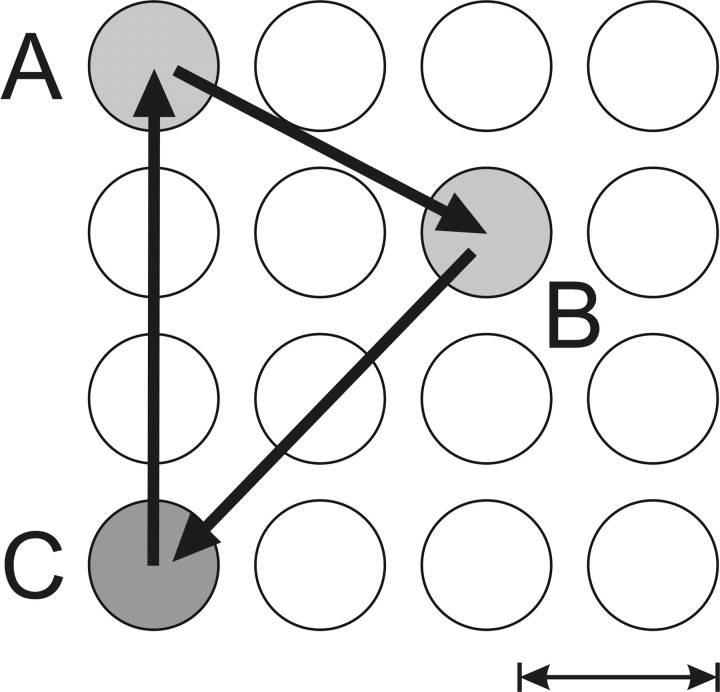
All visual stimuli were presented on a 17-inch computer screen, which was located ∼57 cm from the animal's eyes and subtended 30° and 22° visual angles horizontally and vertically, respectively. The animal was trained to capture a series of targets (red disk) presented on the monitor by moving its right hand on a touch screen, which was installed horizontally in front of the animal at its waist level. Targets were presented in a 4 × 4 grid (Fig. 1). The center-to-center distance between the neighboring target locations was 4.2°, and the radius of the target was 1.4°. The location of the touch was indicated to the animal by a feedback cursor (white disk, radius of 0.5°). In each trial, the animal was required to capture 10 successive targets to receive a drop of apple juice. The interval between the acquisition of a target and the onset of the next target (response–stimulus interval) was always 250 msec. During the majority of trials (five in a block of eight trials), targets were presented in a deterministic sequence created by cycling through three different locations three times. These locations were chosen randomly for each recording session. Denoting these three different target locations as A, B, and C, the entire sequence of target locations can therefore be expressed as C0-A1-B1-C1-A2-B2-C2-A3-B3-C3 (Fig. 1). In the remaining trials, movement sequences were systematically manipulated to distinguish the effects of sequence familiarity on behavioral performance and neural activity from other nonspecific time-dependent changes (Lee and Quessy, 2003). The results from these control trials were not included in the analysis of the present study. The movement toward the first target was also excluded because the initial hand position was not defined for it. In the following, the remaining nine movements are identified according to their targets (i.e., A1 through C3).

Figure 1.

Spatial layout of the serial reaction time task with an example triplet of target locations indicated by gray disks. The target C (dark gray) corresponds to the rewarded location. Scale bar, 5 cm.

Data analysis

Analysis of behavioral data. Reaction time was defined as the time interval between target onset and the time when the hand left the previous target, and acquisition time was defined as the interval between target onset and the time when the new target was acquired. How reaction times and acquisition times of individual movements were influenced by the location of rewarded target and the temporal proximity to the onset of rewarded movement target was analyzed with a two-way repeated measures ANOVA with the movement (A, B, C) and the cycle index for the movement triplet (1, 2, 3) as main factors. Error rate for the nth target in a given trial was computed for each recording session as the percentage of trials in which the animal failed to acquire the nth target within 1 sec from its onset after acquiring the previous target successfully. The effects of movement and cycle index on error rate were also analyzed with repeated measures ANOVA.

Wavelet cross-spectrum. The tendency for a pair of neurons to synchronize their oscillatory activities in different frequency bands was analyzed using the wavelet cross-spectrum (Lee, 2002, 2003). In a previous study, this method was used to evaluate the time course and statistical significance of coherent oscillations in individual neuron pairs (Lee, 2003). However, the pattern of activity in these neurons varies across different movements according to their direction and amplitude (Lee and Quessy, 2003). Therefore, to examine how contextual factors, such as ordinal position or temporal proximity to reward delivery, influence the magnitude of coherent oscillation, the following analysis focuses on the population average wavelet cross-spectrum (AWCS). First, spike train of neuron j in the nth trial was converted to a wavelet transform, 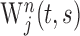, using a Morlet wavelet function (Torrence and Compo, 1998). This wavelet transform, 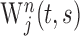, is a function of time t and scale parameter s, and its frequency is approximately the inverse of the scale parameter. Second, the wavelet cross-spectrum for a pair of neurons j and k was calculated as 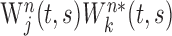, where the symbol * denotes the complex conjugate. Third, the cross-spectra for individual movements were averaged across all trials according to their target locations or ordinal positions to compute AWCS:

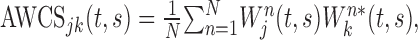where N denotes the number of trials. Because this summation is performed in the complex plane, the amplitude of the resulting cross-spectrum would be small if there is no consistent phase relationship (Lee, 2003, his Fig. 1).

Wavelet phase-locking index. Many neurons examined in this study displayed directional tuning, and therefore some of them displayed no activity during some time periods. This makes it difficult to compare the level of coherent oscillations for different movements at the level of individual neurons using wavelet coherence (Torrence and Compo, 1998), because this requires the normalization of cross-spectrum. As an alternative, this was examined at the population level using the phase-locking index (PLI) (Lee, 2003), which is defined as the following:

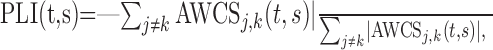where the summation was performed for all neuron pairs recorded simultaneously according to the target locations or ordinal positions of individual movements (see below), and ∥ indicates the amplitude of the cross-spectrum. The value of PLI would be 1 if the AWCS for all neuron pairs displayed the same phase relationship (i.e., zero phase), whereas it would be close to 0 if the phase difference is randomly distributed. Therefore, PLI reflects the variability in the phase difference within a population of neurons.

Because the animal repeated a triplet of movements three times before the reward delivery in each trial, there are at least two different ways in which coherent oscillations in neural activity can be influenced by the reward expectancy. One possibility is that the level of coherent oscillation increases for the movement generated toward the rewarded location (i.e., movement C), regardless of whether such a movement is actually followed by the reward or not. Another possibility is that the level of coherent oscillation increases monotonically with the ordinal position of the movement within the entire sequence in a given trial. In other words, oscillatory activity associated with a given movement might be more synchronized when it is closer to the time of reward delivery regardless of its target location. To distinguish between these two possibilities, the PLI was calculated by dividing nine movements into three groups in two different ways. In the first analysis, movements directed to the same target location (e.g., A1, A2, A3) were combined, whereas in the second analysis, three successive movements in the same cycle of a triplet (e.g., A1, B1, C1) were combined. It has been shown previously (Lee, 2003) that oscillatory activity in the SMA was strongly synchronized immediately before target onset. To determine whether reward expectancy influenced such coherent oscillations for a particular frequency range, the PLI during the 200 msec period before the target onset was averaged separately for three groups of movements as described above. The effect of reward expectancy was then quantified by the slope of a linear regression model in which the PLI in a given frequency was the dependent variable, and the index for each group (i = 1, 2, or 3) was the independent variable.

Statistical significance. A permutation test was used to test the null hypothesis that the tendency for a population of neurons to synchronize their oscillatory activities is not influenced by the reward expectancy of the animal or the ordinal position of the movement. Specifically, the average wavelet cross-spectrum was estimated separately according to the target locations or the cycle index as described above. To test whether the level of coherent oscillation is related to the rewarded target location, movements were divided into three ordered sets according to their targets (i.e., {A1, A2, A3}, {B1, B2, B3}, {C1, C2, C3}), and the order of these sets was shuffled independently for each neuron pair [e.g., ({B1, B2, B3}, {C1, C2, C3}, {A1, A2, A3}) for the first neuron pair, ({C1, C2, C3}, {A1, A2, A3}, {B1, B2, B3)] for the second, etc.]. For each shuffled data set, the PLI was computed separately for each group, and the effect of reward expectancy in the shuffled data were estimated by the slope from a linear regression model. The same procedure was used to test whether the level of coherent oscillation is related to the temporal proximity to the onset of rewarded target, except that movements were now divided into three sets according to their ordinal positions (i.e., {A1, B1, C1}, {A2, B2, C2}, {A3, B3, C3}). For both analyses, a total of 1000 shuffled data sets were generated, and the p value for the null hypothesis was calculated by the frequency of shuffles in which the observed slope was exceeded by those in the shuffled data. p values were also estimated by first fitting a normal distribution to the slopes obtained from shuffled data set. Difference between these two methods did not exceed 0.003.

Results

Effects of ordinal position on behavioral performance

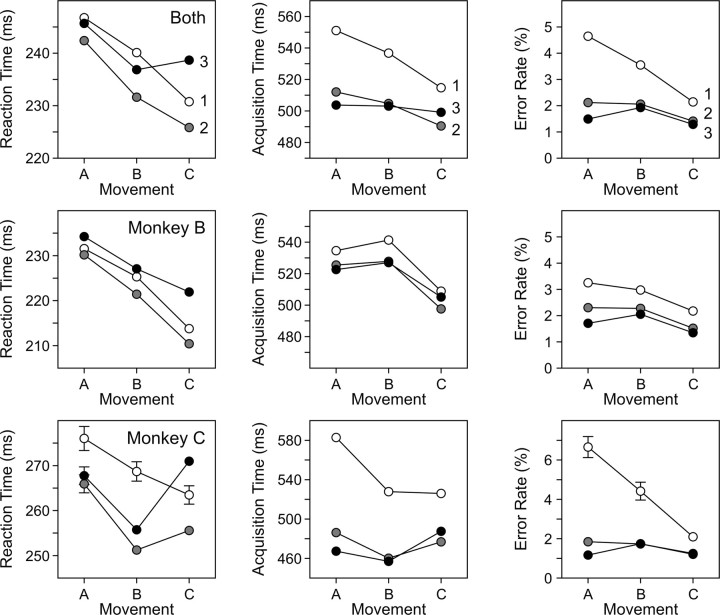
Behavioral performance of the animal changed systematically as the movement approached the rewarded target location, whether it was measured in terms of reaction time, acquisition time, or error rate (Fig. 2). The main effects of the ordinal position of a movement within a triplet and the repetition of the movement triplet (i.e., cycle index), as well as their interaction effect on both reaction time and acquisition time, were highly significant (F >13.0; p < 10^–5). This was true regardless of whether the analysis was performed separately for each animal or on the combined data. The average reaction time for the first movement in the triplet (movement A) (Fig. 2, left column) tended to be longer than those of the two remaining movements in both animals. The only exception occurred in the second animal for the last movement in the entire sequence (C3). Reaction times for individual movements in a triplet, averaged across both animals, decreased from 246 to 238 msec and to 233 msec as it approached the rewarded target location (Fig. 2, left column). Similarly, average acquisition time for each movement in the triplet, when averaged across both animals, was 518, 511, and 500 msec, respectively (Fig. 2, middle column). However, the results from the two animals differed somewhat. In monkey B, the third movement in the triplet (C) displayed the smallest acquisition times, whereas in monkey C, this occurred for the second movement (B). In contrast, the acquisition times for the first cycle of the triplet were longer than those for the last two cycles in both animals. The average acquisition times for the three successive cycles were 534, 502, and 502 msec, respectively. These results suggest that the effect of reward timing influenced the acquisition time more strongly, whereas the reaction time was predominantly affected by the rewarded target location. The overall error rate, averaged across the entire data set, was 2.3%. The main effects of the ordinal position of a movement within the triplet and the cycle number, as well as their interaction, on the error rate were also significant when the analysis was performed on the combined data set. When the same analysis was performed separately for each animal, only the effect of the cycle number was significant (F >16.5; p < 0.001). These results suggest that the cycle index affected the acquisition and error rates similarly and that the ordinal position of the movement within the triplet mostly influenced the reaction time.

Figure 2.

Effects of rewarded target location and ordinal position of the movement on behavioral performance. The results for each of three movements in a triplet (A, B, C) are shown on the horizontal axis, and the three repetitions of the triplet are shown by white, gray, and black disks (numbered 1, 2, and 3, respectively). Error bars, corresponding to 2× SEM, are shown only when the SEM is larger than the size of the symbol.

Effects of rewarded target location on coherent oscillations

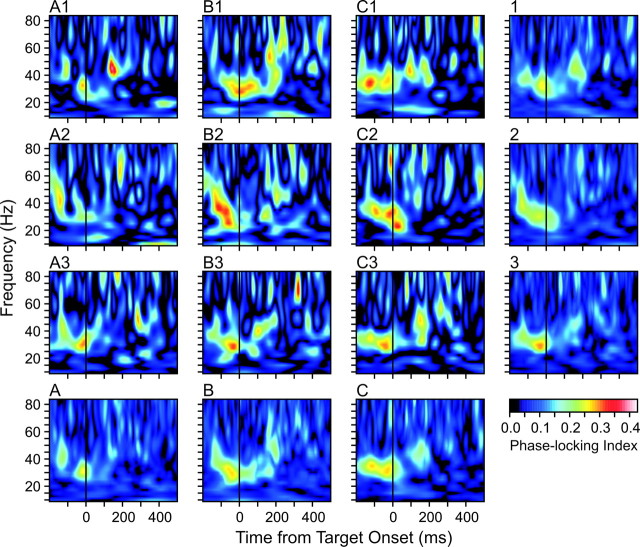
A total of 105 neurons recorded in the left SMA proper of two monkeys provided 217 simultaneously recorded neuron pairs analyzed in the present study. On average, 2373 movements were examined for each neuron pair. As reported previously (Lee, 2003), the values of the PLI in the gamma frequency range, especially in the range between 30 and 35 Hz, tended to reach their maximum values during the hold period immediately before the onset of the next target (Fig. 3). In addition, the PLI in the gamma frequency range was relatively small during the hold period before the movement starting from the rewarded location (i.e., movement A), whereas it was maximal during the hold period before the onset of rewarded target (i.e., movement C) (Fig. 3). This can be most clearly seen when the PLI was computed for individual movements according to their target locations (Fig. 3, bottom row). The PLI computed separately for each of nine movements according to their ordinal positions was more variable. Nevertheless, the same trend was found for each cycle of the movement triplet (Fig. 3, top three rows).

Figure 3.

Phase-locking index computed separately for nine movements in each trial (A1 through C3). Phase-locking index computed for the first, second, and third repetition of the triplet is shown on the rightmost column (labled 1, 2, 3), and the results for each of the three movements in the triplet are shown at the bottom (labeled A, B, C).

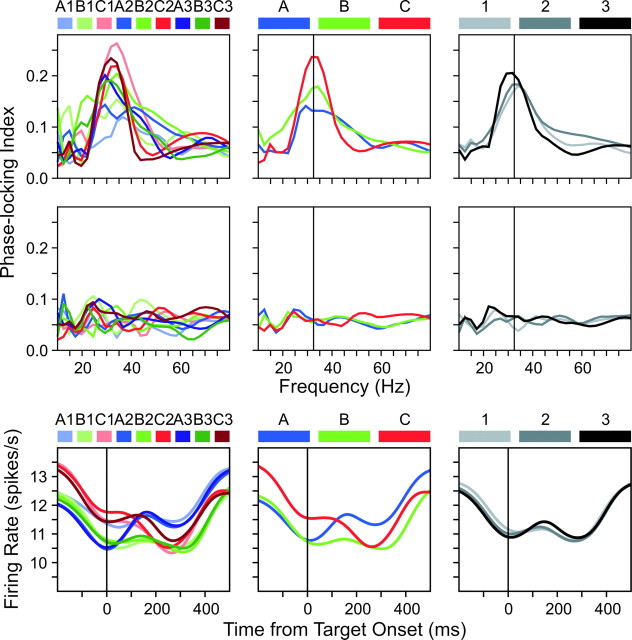
To examine more closely how the level of coherent oscillations was influenced by the location of the rewarded target, the PLI during the last 200 msec of the hold period was averaged and plotted as a function of frequency according to the ordinal positions (Fig. 4, left column) and target locations of individual movements (Fig. 4, middle column). These analyses revealed more clearly that the strength of coherent oscillation was modulated by the rewarded target location. The average value of the PLI at the frequency of 32.5 Hz for three movements in the triplet was 0.132, 0.175, and 0.237, respectively. The slope of a linear regression model in which these values were related to the movement index was 0.052/movement. A permutation test showed that this value was significantly different from zero (p = 0.017). As an additional control, the average PLI was computed for each movement in the triplet using a set of surrogate spike trains generated according to a gamma process (shape parameter k = 2) (Lee, 2003). Compared with a shift or shuffle predictor, this method provides more reliable estimates for the statistical significance of temporally correlated activity (Oram et al., 1999; Baker and Lemon, 2000; Grün et al., 2003). This analysis did not produce any systematic change in the level of coherent oscillations (Fig. 4, middle row).

Figure 4.

Top row, Average phase-locking index during the last 200 msec of the hold period plotted as a function of the frequency of coherent oscillation. Middle row, Average phase-locking index during the same period computed from the gamma surrogate spike trains (Lee, 2003). Vertical lines in the middle and right columns correspond to the frequency of 32.5 Hz used for a regression analysis. Bottom row, Population-averaged spike density functions. The results are shown separately for individual movements (left), for three movements in the triplet (middle column), and for three cycles of the triplet (right).

It should be noted that each neuron pair was examined with a different triplet of movements, which was selected randomly for each recording session. Because the number of neuron pairs examined was relatively large (n = 207), one might expect that the random variation in the spatial tuning of individual neurons would not produce a substantial change in the mean firing rate across three different movements in the triplet at the population level. However, there was a significant increase in the average activity during the last 200 msec of the hold period immediately before the onset of the target in the rewarded location (paired t test; p < 0.05). The average firing rate during the last 200 msec hold period before the onset of each target in the triplet was 11.5, 11.6, and 12.4 spikes/sec, respectively (Fig. 4, bottom row). These results suggest that the anticipation of the rewarded target produced a slight increase in the firing rate of neurons in the SMA. It was necessary, therefore, to determine whether the effect of rewarded target location on coherent oscillations might be merely a byproduct of changes in the firing rates. To test this possibility, the permutation test used to evaluate the statistical significance of changes in the coherent oscillations was repeated after controlling for the changes in the firing rates. This was accomplished by randomizing the order of three movements in a triplet only for 75% of neuron pairs selected randomly for each shuffle in a permutation test. For the remaining 25% of neuron pairs, the movements were sorted according to the average activity of the two neurons during the last 200 msec of the hold period. This percentage was chosen empirically to produce slightly larger changes in the average firing rate in the shuffled data set compared with the original data. Accordingly, the average firing rates during the same 200 msec period in the shuffled data set were 10.8, 12.1, and 12.7 spikes/sec for the three movements in the triplet, respectively. Therefore, if the observed changes in the level of coherent oscillations were entirely attributable to the small but systematic changes in the firing rates related to the rewarded target location, the result from this modified permutation test would lead to the loss of the statistical significance. Even with this new test, however, the effect described above was still significant (p = 0.045), suggesting that the changes in the level of coherent oscillations related to the rewarded target location were not merely a byproduct of changes in firing rates.

Effects of reward timing on coherent oscillations

To analyze the effect of temporal proximity of a given movement to the onset of rewarded target, wavelet cross-spectra for individual movements were averaged separately for each cycle of the movement triplet. Compared with the effect of rewarded target location, this did not reveal a strong effect on the level of coherent oscillations (Figs. 3, 4). As in the analysis described above, the effect of temporal proximity to the onset of rewarded target was quantified as a slope of the regression model relating the cycle index of the movement triplet to the average PLI computed for the last 200 msec in the hold period. The value of this slope for the frequency of 32.5 Hz was 0.020, and the maximum value of 0.028 was found for the frequency of 30.0 Hz. Permutation tests showed that neither of these values was significantly different from zero. Therefore, the level of coherent oscillations during the hold period was not related to the temporal proximity of individual movements to the onset of rewarded target.

Discussion

Reinforcement learning and representation of movement sequences

Most voluntary behaviors are generated to achieve specific goals, to either increase the chance of obtaining rewards or decrease the chance of facing penalties. In fact, economic theories can account for a wide range of choice behavior in people and animals according to the principle of utility maximization (Kagel and Roth, 1995; Kagel et al., 1995). Similarly, reinforcement learning theories have developed an array of algorithms that might be implemented by the brain (Schultz, 1998; Sutton and Barto, 1998). In these algorithms, a total amount of rewards expected from a particular action or a state of the environment, commonly referred to as value function, is updated iteratively as the animal explores the environment. During this process, rewards expected in the future are temporally discounted. As a result, if only the last movement is rewarded after a series of movements, the value functions would increase monotonically for successive movements, which might account for the performance changes observed in the present study. This situation is analogous to a fixed-ratio (FR) reinforcement schedule commonly used in operant conditioning paradigms, although the rate of response in the FR schedule remains relatively constant. However, there is often a pause in the response after a reward (post-reinforcement pause; Skinner, 1938; Griffiths and Thompson, 1973). The lack of a more systematic performance change in the FR schedule might be related to the relatively simple nature of behavioral response examined in such studies. When more complex behaviors are rewarded intermittently with a fixed ratio, the behavioral performance of the animal improves with the value function (Bowman et al., 1996; Shidara et al., 1998; Sohn and Lee, 2003), suggesting that the value function might be an important factor in determining the behavioral performance.

In reinforcement learning, value functions are defined for a particular state of the environment (referred to as state value) or a combination of a state of the environment and a particular action (referred to as action value). Therefore, the same reinforcement learning algorithms might produce different predictions, depending on the nature of state space in which the environment is represented. During the behavioral task used in the present study, animals produced the same movement triplet three times to receive a reward. This made it possible to address the question of how each of nine movements in a sequence might be represented. One possibility is that each of nine movements is represented separately with its own value function. In this case, the value function would increase monotonically after each movement, manifesting similar changes in performance. This was more or less the pattern revealed by the acquisition time and the error rate. Another possibility is that movements are represented according to their target locations. In this case, value functions would be estimated for each target location, although the animal made three separate movements to a given target location before receiving a reward. This would predict that the behavioral performance would be determined by the location of the movement target. Interestingly, reaction times displayed the pattern predicted by this second scenario, because it was more consistently influenced by the location of the movement target. These results raise the possibility that value functions might be estimated by multiple systems on the basis of different representations of individual movements in a sequence.

It is also possible that the changes in the behavioral performance observed in this study are related to chunking of individual movements in a long sequence into shorter segments (Koch and Hoffmann, 2000; Kennerley et al., 2004). In the present study, the sequence of nine movements was consistently interrupted by the reward delivery at the same target location. This might have facilitated a triplet of movements to be grouped together. Accordingly, a prolonged reaction time for the first movement in the triplet could reflect an additional processing time needed for the organization of a movement sequence. However, chunking alone does not account for the entire pattern of behavioral performance observed in this study, because accuracy and acquisition times also improved systematically during a given trial as the triplet was repeated.

Neural signals related to ordinal position and reward expectancy

Neurons in the prefrontal cortex and the basal ganglia, as well as the SMA, display modulations in their activity according to the ordinal position of a particular movement (Clower and Alexander, 1998; Shima and Tanji, 2000; Lee and Quessy, 2003). It is unknown, however, whether this effect was attributable to the repetition of a given movement or whether it was related to the temporal proximity to the expected time of reward delivery. This could not be determined because the number of remaining movements before reward was entirely determined by the ordinal position of a movement. To determine whether neural activity or behavioral performance for a movement is influenced by its ordinal position or value function, it is therefore necessary to vary the length of the movement sequence (Sohn and Lee, 2003). Therefore, it remains to be determined whether and how neural activity in these brain regions encodes value functions for individual movements in a sequence.

Despite the lack of direct evidence that value functions for individual movements in a sequence are coded in the activity of individual neurons, other features of reinforcement learning algorithms have been found in many regions of the brain. For example, reward prediction errors, often referred to as temporal difference error in reinforcement learning algorithms, are encoded by the midbrain dopamine neurons (Schultz, 1998). Similarly, activity of neurons coding the metrics of a single movement is often modulated by expected reward in various cortical and subcortical areas (Watanabe, 1996; Kawagoe et al., 1998; Leon and Shadlen, 1999; Gdowski et al., 2001; Kobayashi et al., 2002; Ikeda and Hikosaka, 2003; Roesch and Olson, 2003). Whereas most of these studies have examined how neural activity is influenced by expected rewards in a delayed response task, the activity of neurons in the prefrontal cortex (Barraclough et al., 2004) and posterior parietal cortex (Platt and Glimcher, 1999) is also modulated by the expected value of the reward during a free-choice task. Therefore, it would be important to determine the mechanisms by which these neural signals related to expected reward influence the behavioral choice of the animal.

Role of coherent oscillations in controlling cortical information flow

The results from the present study show that the level of coherent oscillations in the SMA changed systematically according to the ordinal position of the movement in a sequence. This might be related to the systematic changes in the value functions of individual movements or a process of chunking. Regardless of their functions, the result from the permutation test that preserved the observed difference in the mean firing rate showed that the difference in the level of coherent oscillations found in the present study could not be accounted for by changes in firing rates. These effects were statistically significant, but it remains unknown whether the changes in the strength of coherent oscillations found in the present study provide enough information to represent value functions reliably. Nevertheless, these results provide empirical support to the proposal that synchronous spikes, especially synchronized oscillations in the gamma frequency range, might be a means to control the cortical flow of information (Engel et al., 2001; Salinas and Sejnowski, 2001; Varela et al., 2001; Averbeck and Lee, 2004).

Synchronized oscillations described in the present study mostly occurred before the onset of movement targets (Lee, 2003). Similar results have been found in other sensory and motor cortical areas. For example, an increased level of oscillatory activity and/or synchronized spikes has been found in visual and motor cortical areas during an interval in which the animal is expecting behaviorally relevant stimuli (Cardoso de Oliveira et al., 1997; Donoghue et al., 1998). In the visual cortex, the level of synchronized spikes during the fore-period in a texture discrimination task can predict the behavioral performance (Supèr et al., 2003), and stimulus associated with reward produces higher level of coherent oscillatory activity (Salazar et al., 2004). In addition, selective attention to a particular sensory modality or a limited region of sensory space increases the extent to which the spikes of individual neurons within a given cortical area are synchronized (Steinmetz et al., 2000; Fries et al., 2001). Combined with the findings that cortical neurons are equipped with cellular and network properties to enhance their sensitivity to synchronous synaptic inputs (Galarreta and Hestrin, 1999, 2001; Gibson et al., 1999; Pouille and Scaziani, 2001; Stuart and Häusser, 2001), these results suggest that synchronized spikes might be used to control the flow of information about sensory stimuli and motor intentions according to the motivation state of the animal.