A Morphological Correlate of Synaptic Scaling in Visual Cortex

Abstract

We studied the response of dendritic spines in the thalamic-recipient zone of rat visual cortex to simple manipulations of the visual environment. We measured the morphologies of a total of 3824 spines located on the basal dendrites of 60 layer 3 pyramidal cells. As expected from previous studies, we found a significantly lower spine density in dark-reared animals at postnatal day 30 (P30) compared with light-reared controls. Additional analysis revealed that the spines in dark-reared animals were significantly shorter and more bulbous than in light-reared animals. When these two results were combined, we found that the total synaptic area per unit length of dendrite was conserved, compatible with the phenomenon of “synaptic scaling.” We also found that the increase in average spine head diameter is reversed by 10 d of light exposure (starting at P20), but surprisingly, the decrease in spine density is not. Thus, not all effects of dark rearing can be reversed by subsequent visual experience, even when the experience occurs during the third postnatal week.

Introduction

Dendritic spines are cellular compartments that contain signaling molecules important for synaptic transmission and plasticity (Koch and Zador, 1993; Harris, 1999; Nimchinsky et al., 2002). Relatively simple measurements of dendritic spines can yield direct inferences about the state of a population of synapses. The number of spines on a particular dendrite predicts the number of excitatory synapses there (Braitenberg and Schuz, 1998); spines with bigger heads have stronger synapses (Freire, 1978; Spacek and Hartmann, 1983; Harris and Stevens, 1989; Schikorski and Stevens, 1997, 2001; Nusser et al., 1998; Takumi et al., 1999; Racca et al., 2000; Matsuzaki et al., 2001, 2003; Murthy et al., 2001), and longer spines have synapses that are less mature and more modifiable (Koch and Zador, 1993; Ziv and Smith, 1996; Fiala et al., 1998; Majewska et al., 2000a,b; Yuste et al., 2000; Portera-Cailliau et al., 2003). Thus, a picture of a dendritic spine can tell us about the state of an individual synapse without sacrificing higher-level information such as the identity of the parent cell, the states of neighboring synapses, etc. In this study, we used spines to investigate how synaptic transmission in the thalamic-recipient zone of the visual cortex is modified by basic changes in the visual environment.

During normal postnatal development, visual experience contributes to a gradual maturation of the response properties of neurons in the visual cortex. Similar, but more rapid, changes occur in animals exposed briefly to light after dark rearing from birth. For example, as little as 6 hr of visual experience is sufficient for neurons in the visual cortex of dark-reared kittens to acquire normal levels of orientation selectivity and responsiveness (Buisseret et al., 1978, 1982). Very little is known about the mechanisms that underlie such experience-dependent changes in neuronal response properties; however, there is evidence that these effects require the activation of postsynaptic NMDA receptors (Bear, 1996). Because NMDA receptor activation is also necessary for the induction of long-term potentiation (LTP), it is appealing to hypothesize that visual experience induces an endogenous form of synaptic plasticity that uses the same mechanisms that underlie LTP.

Here, we used dendritic spines to interrogate the status of synaptic transmission in normally reared animals, dark-reared animals, and dark-reared animals exposed to light. Prior work on this topic, using the Golgi stain, had found that there is a rapid increase in spine density induced by light exposure in previously dark-reared mice (Valverde, 1971). We decided to revisit this finding using more modern imaging methods that would enable us to quantify the morphology, as well as the density, of dendritic spines. We also decided to investigate spines in an anatomical region where prior experience had taught us to expect a high level of activity-dependent synaptic plasticity.

Materials and Methods

Approach. Because we were interested in experience-dependent plasticity, we chose to use a preparation that would reflect as faithfully as possible the conditions inside an intact animal. For this reason, we imaged perfusion-fixed brain tissue rather than acutely prepared brain slices. The preparation of acute slices can rapidly induce a 50-90% increase in spine density (Kirov et al., 1999), and this could easily obscure the changes present in vivo. We considered live imaging in vivo, but this is restricted by optical limits to the most superficial layers of the cortex (Lendvai et al., 2000), thus making layer 4 inaccessible. However, layer 4 and deep layer 3 are of particular interest because synapses in these layers lie in the zone innervated by afferents from the thalamus (Herkenham, 1980), and this zone has been identified as a site of robust synaptic plasticity in rodents (Heynen and Bear, 2001; Sawtell et al., 2003). A number of previous studies of dendritic spine plasticity and visual experience have also looked at layer 4, but within that layer they have generally focused on the apical dendrites of layer 5 pyramidal cells (Globus and Scheibel, 1966, 1967; Valverde, 1967, 1971; Winkelmann et al., 1976, 1977). The apical dendrites of layer 5 pyramidal cells are the most densely spiny structures in the cortex (DeFelipe and Farinas, 1992) and thus probably the most easily detectable site of spine density changes. However, it is now appreciated that neurons in layer 3 are perhaps the most plastic of the cortex, exhibiting the most rapid and developmentally persistent changes in their physiological response to sensory deprivation (Daw et al., 1992; Trachtenberg et al., 2000). Therefore, we decided to quantify spines on the basal dendrites of layer 3 neurons, which are located within layer 4.

Our staining and visualization method was also chosen to take advantage of technical developments that have made more accurate quantification of spines possible than in prior studies. Most previous studies used the Golgi stain, which underreports true spine density by a factor of 3 (Feldman and Peters, 1979; Braitenberg and Schuz, 1998). This underre-porting is partly attributable to geometric consequences of the opacity of the Golgi stain. Some have attempted to resolve this problem by using geometrical methods to estimate “projected spine counts” based on Golgi data (Feldman and Peters, 1979; Larkman, 1991; Braitenberg and Schuz, 1998). We chose instead to use a more modern staining technique, namely intracellular injection of a bright fluorescent dye into lightly fixed tissue. This technique, combined with confocal microscopy and mathematical deconvolution, gives the best resolution of spiny dendrites presently possible using visible light (Vecellio et al., 2000). It may also be better suited for detection of small spines, but this conjecture needs to be confirmed with serial electron microscopy (EM).

Because this method yields three-dimensional images, we were able to avoid resorting to projected spine counts. Because of its superior resolution, we were also able to reliably quantify spine morphology without resorting to EM. As a result, we could quantify spine morphologies at a known dendritic locus, and we could obtain a sufficiently large sample for statistical tests. Each of these requirements would be difficult to meet using EM, and both together would be nearly impossible. The alternative fluorescent labeling technique of “DiOlistic” staining (Gan et al., 2000) was also considered, but we opted not to use it because we wanted reliable labeling of cells and dendrites in a very specific anatomical locus.

Subjects. Eighteen male Long-Evans black hooded rats from eight litters were used in this study. At the time of death, all animals were aged 30 d postnatal (P30). Pregnant rats were purchased from Charles River Laboratories (Wilmington, MA). Animals were housed and fed in accordance with the guidelines of the National Institutes of Health and the Brown University Animal Care and Use Committee. These animals are born with their eyes shut and do not open their eyes until the beginning of the third postnatal week (∼P15). At the end of the third postnatal week (∼P20) the animals are ready to be weaned, and at the end of the fourth postnatal week (∼P28), they develop sexually.

After birth, litters were divided into three groups: light reared (LR), dark reared (DR), and dark reared plus light exposure (DR plus LE). Animals in the LR group were raised in a normal light/dark cycle (12 hr on, 12 hr off) from birth until P30. Animals in the DR group were born into in a normal light/dark cycle, but then moved into a completely dark room at P3. (If pups are born in the dark, or moved into a dark room too soon after birth, they are rejected by their mothers and die.) DR animals were then kept in the dark until being killed at P30. Animals in the DR plus LE group were handled as with the DR group, but at P20 they were moved back into a normal light/dark cycle for 10 d before being killed at P30.

These rearing conditions were chosen based on Valverde's studies of spine density in the developing mouse (Valverde, 1967, 1971; Ruiz-Marcos and Valverde, 1969; Valverde and Ruiz-Marcos, 1969). Valverde found that a difference in spine density between LR and DR animals was first detectable at the age of eye opening (P15) and was most prominent between P20 and P30. He also found that the effect of DR plus LE was most prominent at P30, with light exposure beginning at P20. Because the developmental time course of spine formation in mouse and rat is nearly identical (Valverde, 1971; Schapiro et al., 1973), we chose to work within the same age range that Valverde found to be optimal. Furthermore, the period P20-P30 corresponds with the peak of physiological plasticity in layer 2/3 of acutely prepared slices of rat visual cortex (Kirkwood et al., 1995), and in vivo (Fagiolini et al., 1994). This period also coincides with the end of the phase of rapid synaptogenesis in the visual cortex, which occurs from approximately P10 to P20 and peaks at eye opening (Braitenberg and Schuz, 1998).

Animal killing and fixation. Rats were perfused intracardially with a fixative solution, using the method described by Peters (1970) and Hayat (1981), with slight modifications. In brief, a rat was anesthetized by intraperitoneal injection of 0.2 ml of Beuthanasia-D (active ingredient, sodium pentobarbital; Schering-Plough, Kenilworth, NJ). A small metal cannula was introduced into the heart, and the vascular system was perfused through the ascending aorta for 6.5 min with fixative solution heated to body temperature (37°C). The fixative solution consisted of 4% paraformaldehyde in 0.1 m phosphate buffer, pH 7.4. No saline prewash was used. Pressure was provided by a peristaltic pump using small-diameter tubing, with the pump speed set to produce a pressure of 150 mmHg (20 kPa) during perfusion. This protocol results in a light fixation that deteriorates over a period of days but is ideal for intracellular injection. After perfusion, the brains were removed and stored cold (4°C) in 0.1 m PBS.

Staining and histology. Sectioning and intracellular injection were performed as soon as possible after perfusion to insure optimal tissue quality for intracellular injection. The occipital pole of each hemisphere was removed in a block, immersed in PBS, and sectioned in the coronal plane at 150 μm thickness using a vibratome tissue slicer. Sections were stored cold (4°C) in PBS.

Intracellular injection was performed using a modified version of the method described by Vecellio et al. (2000). Neuronal cell bodies were visualized under differential interference contrast (DIC) optics and injected with a brightly fluorescent dye using sharp electrodes and weak negative current (Fig. 1). Sharp electrodes (tip resistance, ∼100 MΩ) were pulled using thick-wall borosilicate glass capillaries with filament (outer diameter, 1.0 mm; inner diameter, 0.58 mm; World Precision Instruments, Sarasota, FL), on a P-87 micropipette puller (Sutter Instruments, Novato, CA). Tip resistance was in the range of 80-120 MΩ, but the exact tip resistance was less important than the sharpness and straightness of the tip. The electrode was backfilled with the fluorescent dye Alexa 488 (injectable solution; Molecular Probes, Eugene, OR). The electrode shank was filled with PBS. The electrode was held by a hydraulic micromanipulator mounted on a coarse gear-driven manipulator.

Figure 1.

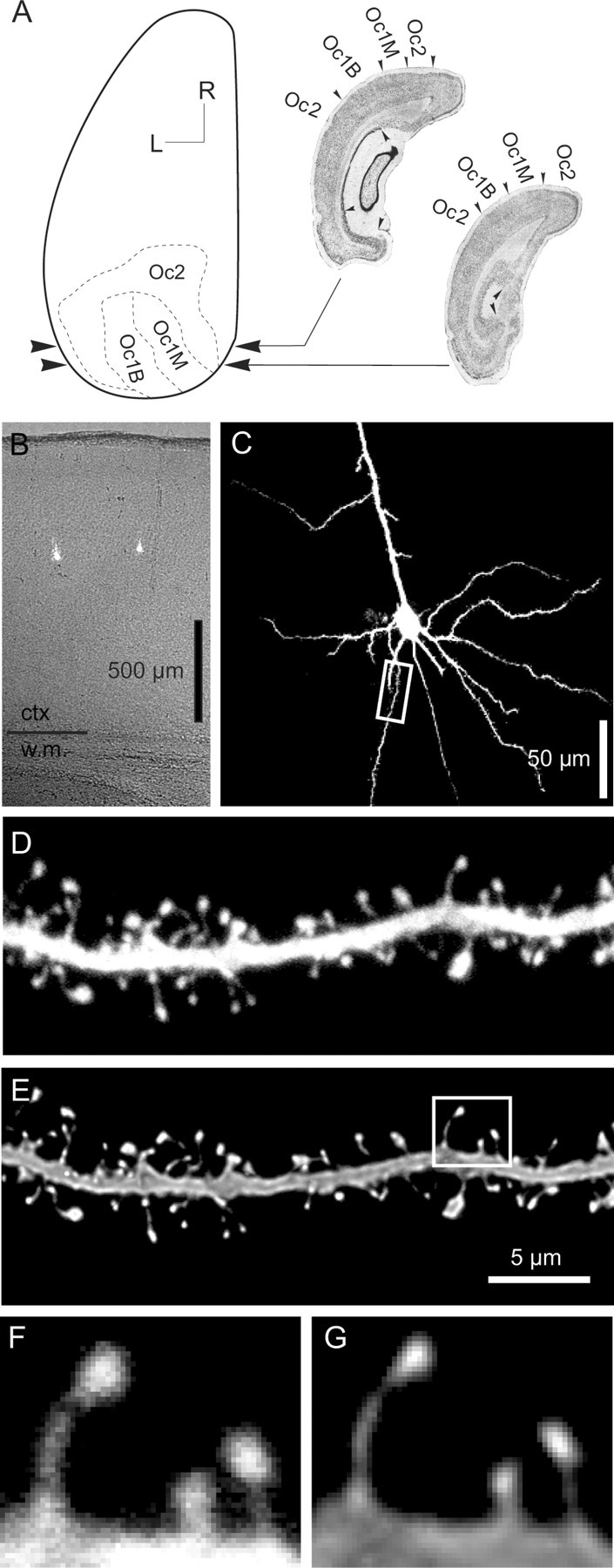
A, Topographical map of the left hemisphere of a rat brain, showing visual areas Oc2 (extrastriate cortex) and Oc1 (striate cortex, with monocular and binocular subfields Oc1M and Oc1B). The range of planes of section we used is indicated by arrowheads, and examples are shown in Nissl sections to the right of the map (redrawn from Zilles, 1985). Scale bar, 2 mm. L, Lateral, R, rostral. B, Transmitted light image of a tissue section overlaid with fluorescence image of two stained neurons. Note the white matter landmarks visible in the bottom part of the image. The cells are in lower layer 2/3 of area Oc1B. C, Maximum intensity projection (MIP) of a confocal image stack, showing a pyramidal neuron typical of those used in our study. The dendritic segment outlined with a rectangle is shown enlarged in D and E. D, E, MIP projections of a confocal image stack showing a single dendritic segment with spines before (D) and after (E) deconvolution. The spines outlined with a box are shown enlarged in F and G. F, G, Examples of spine profiles before (F) and after (G) deconvolution. The pixel resolution is 0.06 × 0.06 μm. In D and E, contrast was individually adjusted for best visibility on the printed page. In F and G, contrast was adjusted in tandem to show the redistribution of pixel intensities after deconvolution.

For DIC visualization, a fixed tissue section was placed into a small, covered, glass-bottomed culture dish (ALA Scientific Instruments, Westbury, NY), allowing illumination from below. This chamber was mounted on the stage of an upright focusing-nosepiece microscope, so that focus movements did not cause movement of the stage or electrode. The microscope was equipped for fluorescence and DIC microscopy. The microscope, stage, and electrode manipulators were isolated from vibration using an air table.

Cells chosen for injection had somata located in lower layer 3 of the binocular region of the visual cortex (Fig. 1, Zilles's area Oc1B). This zone was defined using Zilles's atlas (Zilles, 1985). The mediolateral limits were determined by means of landmarks in the white matter, and the laminar depth was determined by the equation d1/d2 = 1/3, where d1 is the distance from the cell body to the pia mater, and d2 is the distance from the white matter-layer 6 border to the pia mater. Cell bodies in this region were identified under DIC [using a 40× water-immersion lens; numerical aperture (NA), 0.8] and impaled with the electrode. A cell was filled by passing -5 to -10 nA of current in on/off cycles at 2 Hz. Filling was verified visually by checking the cell under fluorescence illumination. The current was interrupted after dendrites were well filled, and spines were visible (usually <5 min). After filling one to three cells per section, the section was removed from the chamber, washed in PBS, and postfixed by immersion in cold fix (15 min to overnight). (We saw no difference in background fluorescence with different durations of postfix.)

The postfixed tissue section was washed again in cold PBS, then immersed in several washes of Fluorsave mounting medium (Calbiochem, La Jolla, CA). Repeated immersion was used to prevent the formation of refractive index gradients in the mounted specimen. Finally, the section was mounted on a glass slide in fresh Fluorsave medium under a glass coverslip (Corning glass number 1.5; thickness, 0.17 ± 0.01 mm; Corning, Corning, NY). Slides were left for several hours at room temperature for the mounting medium to solidify, and the coverslip was then sealed with nail polish.

Confocal microscopy. Confocal image stacks were acquired using an Olympus Fluoview confocal microscope (Olympus, Melville, NY). A typical image stack consisted of 60 image planes each of 512 × 512 pixels. We used a 63× water-immersion lens (NA, 1.2), at zoom factor 8 (pixel size, 0.06 × 0.06 μm), and with z-step 0.15 μm. These settings and optics represent the highest resolution presently obtainable using light microscopy. For each stack, laser intensity and detector sensitivity were set so that the fluorescence signal from the spines occupied the full dynamic range of the detector. This meant that some pixels in the dendritic branch were saturated, but no pixels were saturated within the spines.

We determined the sampling interval in x/y/z based on the following logic. The optimal three-dimensional sampling interval of a microscope image is governed by the size of the resolvable element, which is the minimum spot size of a diffraction-limited spot of light. In fluorescence microscopy, the resolvable element can be estimated using a three-dimensional extrapolation of the Rayleigh criterion (Wallace et al., 2001). In confocal fluorescence microscopy, the true size of the resolvable element is actually approximately half of the Rayleigh unit within the image plane (the x-y plane), although in the depth axis (z-axis) it is equal to the Rayleigh unit (Vecellio et al., 2000). To adequately sample a digitized image, one must use at least two pixels per resolvable element, thus the pixel size should be half as large as the Rayleigh unit in x-y, and the z-step should be half the Rayleigh unit in z. But we also observed, in agreement with Vecellio et al. (2000), that deconvolution increases resolution in z by about twofold, so we used a z-step of one-fourth the Rayleigh unit in z. Thus, for the dye Alexa 488 (emission peak, 519 nm), with a water-immersion lens of NA 1.2, we used the sampling interval 0.06 × 0.06 × 0.15 μm in x/y/z.

Image processing and quantification. After acquisition, images were deconvolved using a blind deconvolution algorithm (Autodeblur; Autoquant, Watervliet, NY), for 10 iterations (Fig. 1 E, G).

Before quantification, all image file names were randomized by one experimenter, and a different experimenter then performed the measurements. Thus, all counts and measurements were made blind as to rearing condition.

We counted and measured spines manually, using the MetaMorph image analysis package (Universal Imaging, Brandywine, VA). Spines were counted by scrolling through the x-y planes of a three-dimensional image stack and marking spines as they came into view. All dendritic protrusions were counted as spines, and protrusions oriented into or out of the image plane were counted as soon as they first became visible, conforming to the “optical dissector” method (Howard and Reed, 1998).

We also measured the length and head diameter of each spine. We made these measurements on a two-dimensional projection of the image stack, using a bent-line tool to measure the length and a straight-line tool to measure the maximum head diameter of each spine fully contained in the image stack. Spine length was defined as the length of the bent-line going from the edge of the dendritic shaft to the tip of the spine. Spine head diameter was defined as the length of the longest straight line through the spine head, orthogonal to the axis of spine length.

We chose to measure spine head diameter because it is closely related to the surface area of the synapse, and therefore to synaptic strength. We chose to measure the total spine length, as opposed to the length of the spine neck only, because there is more uncertainty about defining the boundaries of the spine neck than those of the whole spine.

We also measured the length of each dendritic segment, in three-dimension. This was done in three steps: (1) we scrolled through x-y planes and used a bent-line tool to measure the length of the x-y projection of the segment; (2) we made an orthogonal projection of the image (using the aspect ratio correction of 1/1/2.5 for x/y/z dimensions of each pixel) and measured the z-axis deviation of the dendritic segment; and (3) we used the Pythagorean theorem to estimate the actual three-dimensional length of the segment from these two numbers.

The diameter of each dendritic segment was found on a two-dimensional projection, by taking the average of three measurements of the straight line segment orthogonal to the local length axis of the dendrite.

Stereological issues. For sampling to be unbiased, the objects being studied must constitute a uniform random sample from the natural distribution (Howard and Reed, 1998). For us, this means that any spine in the anatomical region selected for study must have an equal chance of being sampled. The anatomical region here consisted of layer 4 segments of the basal dendrites of deep layer 3 pyramidal cells. The method we used for obtaining a uniform random sample was that of marking distances along a line (Howard and Reed, 1998). If the position of the first mark is selected randomly along some interval d, then all marks made at additional intervals of d from this first mark will conform to a uniform random distribution. We applied this method first in sectioning the tissue, then in choosing the location of any cell to be studied within a section. When sectioning the tissue, we kept the section thickness constant and discarded two of every three sections. When locating a cell within a section, we chose a uniform random position along the mediolateral axis of the section. The depth of the cell body was always fixed at one-third the distance from pia to white matter.

We chose dendritic segments from the basal arbor, so that the inside edge of each segment was located 30 μm from the cell body measured along the path of the dendrite (Fig. 1C). We did not take account of dendritic branch order, but preferred instead to image dendritic segments at a fixed distance from the cell body. We chose this approach because we found determination of branch order in the basal tree to be unreliable. For example, when a basal dendrite divides into two branches, it is often unclear whether both daughter branches belong to the same branch order, because one of the daughter branches may be considerably thicker than the other and might easily be considered an extention of the “parent branch.” We chose a distance of 30 μm from the cell body because spine density is very sparse nearer to the cell body, whereas farther away, dendrites were often cut off by the edges of the tissue section.

The resolution limit of light microscopy is of the same order of magnitude as the size of the smallest dendritic spines (Harris and Kater, 1994; Wallace et al., 2001). Therefore, it is possible that we failed to detect some percentage of the total spine complement. This has been shown to be possible in an EM study by Freire (1978). However, the spines found by Freire (1978) to be undetectable did not contain active zones or postsynaptic densities, and therefore they were not capable of synaptic transmission. A loss or gain of nonfunctional synapses would not alter our interpretation of the light microscope data, but even if the undetected spines did make active synapses, the pattern of spine loss at the light microscope level would still be an index of experience-dependent plasticity. Thus, the interpretation of our results would be different, but their significance would not.

Another stereological problem arises because we used two-dimensional maximum-intensity projections of three-dimensional image stacks to make our morphology measurements. As a result of projection, there is major artifactual change in the spine length, but not in the diameter of the spine head (because of the more rounded morphology of the spine head). Furthermore, the two-dimensional projection masks spines oriented in the z-axis and therefore represents only a subset from the total population of spines on a given dendritic segment. However, because the orientation of the dendritic segment with respect to the optical axis of the microscope is chosen randomly, the subset of spines remains uniform random (Rusakov and Stewart, 1995). One downside of two-dimensional projection is that spine length will be underestimated; however, for the purpose of comparisons between groups, the true value of length is less critical. For example, if one rearing condition resulted in a higher proportion of short spines, this proportion would be preserved in the projected images.

In general, we tried to follow the stereological rules for spine analysis put forward by Rusakov and Stewart (1995), but we did depart from their protocol in two respects: (1) we did not always use the same order of dendrite, as explained above; and (2) we did not acquire all images at same detector setting, because the variability of signal intensity from preparation to preparation was too great. We decided instead that it was better to maximize dynamic range in each image and normalize the images after acquisition in contrast adjustments (as described by Vecellio et al., 2000).

Statistical analysis. Spine counts and morphological measurements were performed on five dendritic segments per animal, with four animals per rearing condition in the spine morphology study and six animals per condition in the spine density study. In general, each dendritic segment came from a different cell, although, in some cases, two segments came from the same cell. Data were analyzed using Statview (SAS Institute, Cary, NC). Normality was tested using the Shapiro-Wilk test. Because both spine density and spine morphology distributions turned out to have non-Gaussian distributions, we used the Kruskal-Wallis test, a nonparametric analog of one-way ANOVA, to test for a main effect. If we found an effect, we then used the Mann-Whitney U test as a post hoc test to look for specific changes between rearing conditions.

Results

At the time of death (P30), the weight of our animals was constant across rearing condition (one-way ANOVA; p = 0.74). The thickness of the striate cortex was also constant (one-way ANOVA; p = 0.34) (Table 1). This suggests that no large-scale developmental abnormalities or deficit in nutrition, which could alter spine distribution (Gundappa and Desiraju, 1988), were caused by our environmental manipulations.

Table 1.

Effects of deprivation and experience

	LR	DR	DR plus LE
Spine density (spines/linear micrometer)
Mean	1.81	1.53	1.54
Median	1.77	1.46	1.55
SD	0.31	0.28	0.27
Number (segments/animals)	30/6	30/6	30/6
Spine head diameter (nm)
Mean	338	353	320
Median	313	326	301
SD	112	123	107
Number (spines/segments/animals)	1419/20/4	1202/20/4	1203/20/4
Spine length (μm)
Mean	1.41	1.30	1.36
Median	1.31	1.21	1.28
SD	0.76	0.68	0.72
Number (spines/segments/animals)	1419/20/4	1202/20/4	1203/20/4
Dendritic diameter (nm)
Mean	960	854	860
SD	250	138	131
Number (segments/animals)	20/4	20/4	20/4
Animal weight (gm)
Mean	101	98	99
SD	9	16	10
Number (animals)	12	25	24
Cortical thickness (μm)
Mean	1588	1466	1641
SD	162	136	280
Numbers (animals)	6	6	6

Dendritic anatomy was apparently normal in all three conditions, although no quantification was attempted because of the number of dendrites severed by the edge of the tissue section. In all three rearing conditions, we saw the same dendritic arbor forms, from a typical pyramidal form to stellate-like forms. These dendritic morphologies correspond well with the types identified by Peters and Kara (1985) (Fig. 2).

Figure 2.

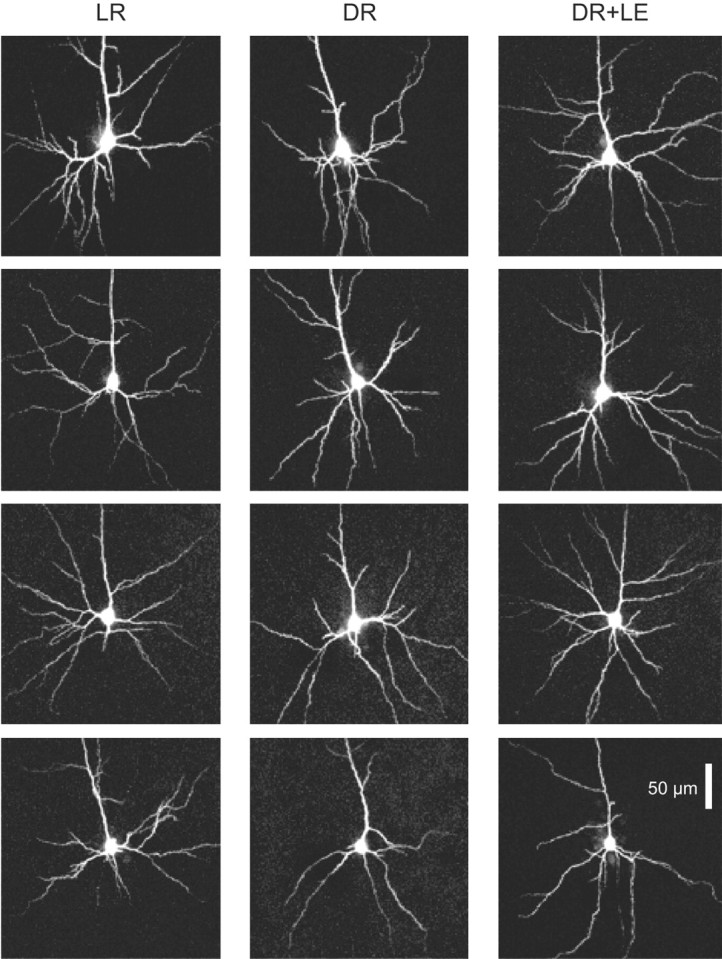
Examples of cell morphologies seen in the three rearing conditions. All images are maximum intensity projections of confocal stacks. Each column shows a set of representative cells taken from one of the three rearing conditions, ranked from most branchy (top) to least branchy (bottom). In the top row of each column is a typical “medium-sized pyramidal cell,” fitting the morphological description of Peters and Kara (1985). The remaining cells in each row resemble the “ovoid pyramidal cell” described by Peters and Kara (1985), with stellate-like dendritic anatomy in the third row, and a more sparse and shapeless dendritic arbor in the fourth row. In all three rearing conditions, the distribution of these dendritic arbor morphologies did not apparently differ.

We found a mean spine density of 1.80 spines per micrometer in LR animals, a value three times higher than that reported for the same dendritic locus using the Golgi stain (Parnavelas et al., 1973; Gundappa and Desiraju, 1988). However, those Golgi studies did not use a geometrical correction for assumed underre-porting because of the opacity of the Golgi stain. In fact, the Golgi spine count underreports the serial EM spine count by a factor of 3, according to the only existing study directly comparing Golgi and serial EM reconstructions of the same dendrite (Feldman and Peters, 1979). Therefore, our spine counts are likely to be quite close to the values determined by serial EM, although this awaits confirmation. Our visualization method does have the advantage over Golgi, that we could count all spines in three-dimension by scrolling through confocal image stacks. Spines protruding into or out of the image plane are not as frequently obscured in our image stacks as they are in Golgi-stained tissue.

We found that DR animals had a significantly lower spine density than LR controls, on the order of 15% (Figs. 3, 4). This confirms previous findings by Valverde (1971) in the apical dendrites of layer 5 pyramidal cells. However, in contrast to Valverde (1971), we did not find a return to normal spine density in DR plus LE animals (Kruskal-Wallis test, p = 0.0007; Mann-Whitney post hoc tests: LR, DR: p = 0.0027; LR, DR plus LE: p = 0.0003; DR, DR plus LE: p = 0.8556). The distribution of spine densities in DR and LR may be non-Gaussian; in DR plus LE, it is definitely non-Gaussian (Shapiro-Wilk test for normality: LR, p = 0.26; DR, p = 0.29; DR plus LE, p = 0.006; low p values in this test indicate a non-Gaussian distribution). Variability was moderately high and was not affected by rearing condition. Coefficients of variation (CV = 100σ/μ) were 17, 18, and 18%, respectively, in the LR, DR, and DR plus LE groups.

Figure 3.

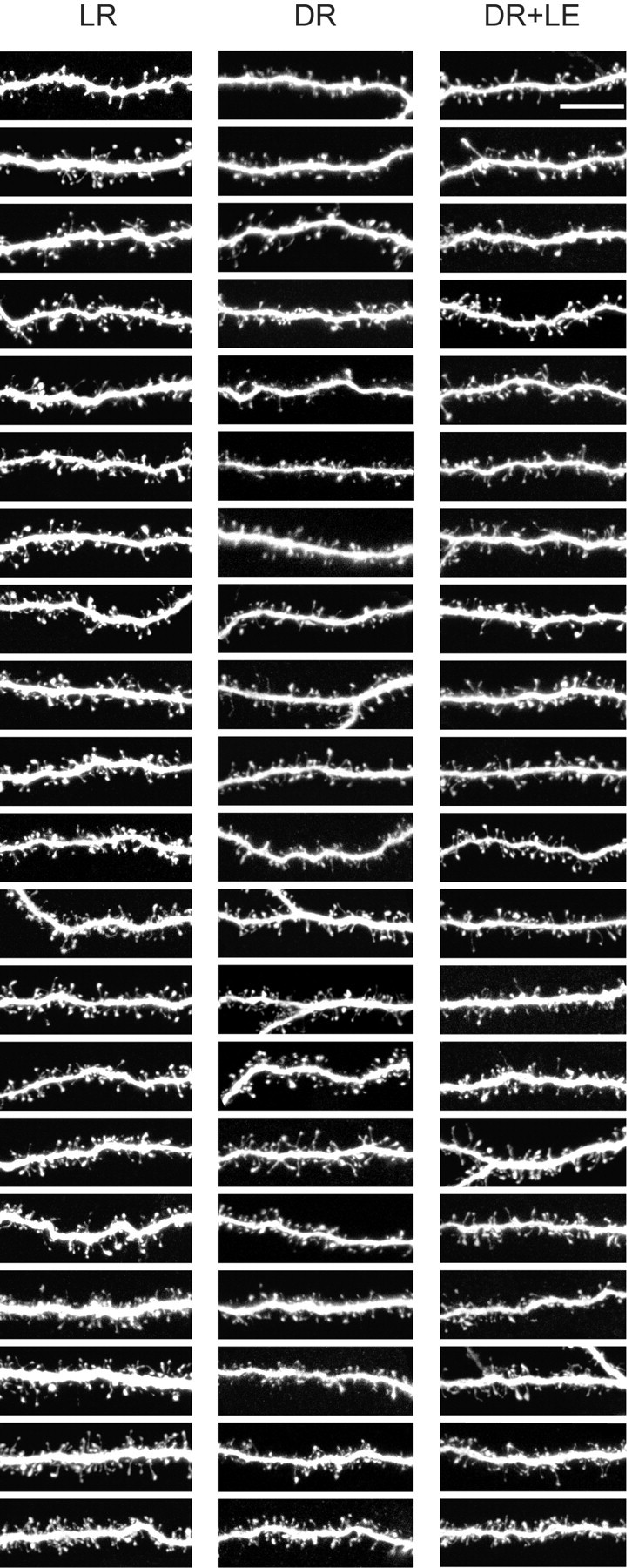
Complete raster of the images used for spine morphology quantification. (An additional 10 images per group were used for spine counts that were not used for spine morphologies.) The images are ranked within each column from least densely spiny to most densely spiny. All images are maximum intensity projections of confocal stacks, shown here as raw images (i.e., before deconvolution). Left, LR; middle, DR; right, DR plus LE. Scale bar, 10 μm.

Figure 4.

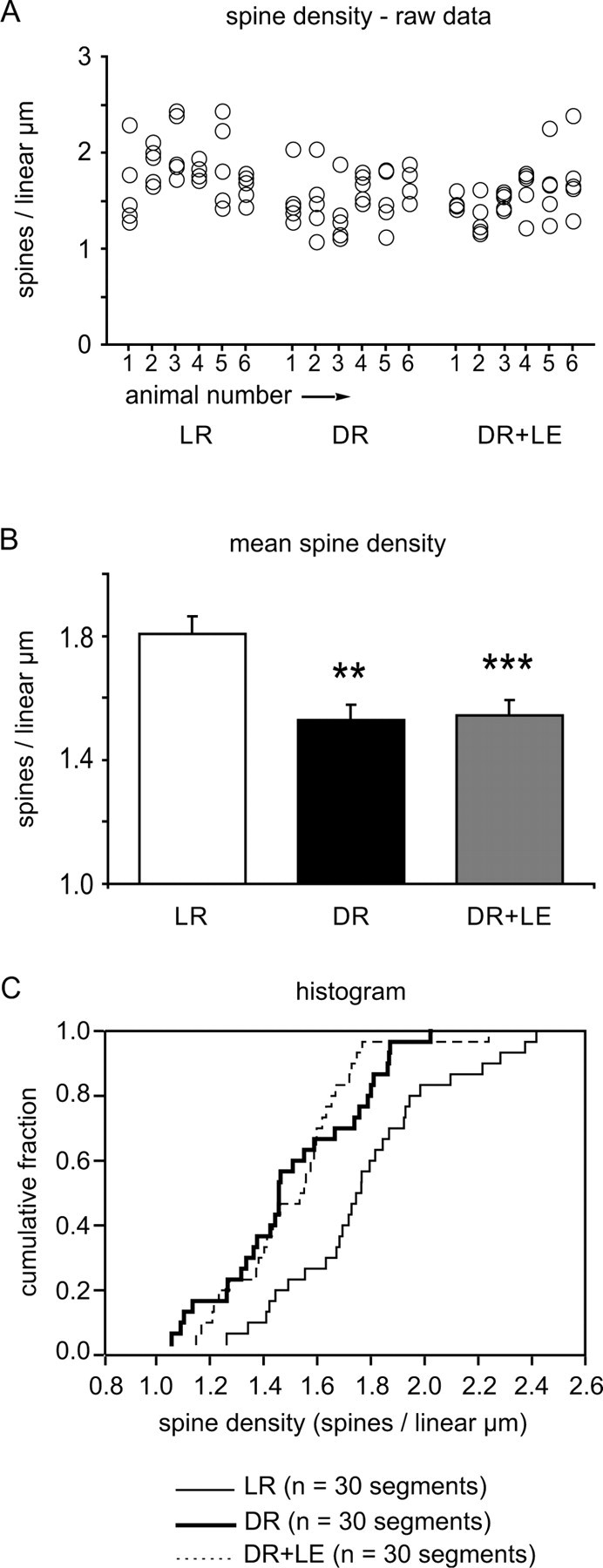
Spine density measurements. A, Raw spine density counts. Each circle represents one dendritic segment; each column represents one animal. B, Mean spine density by condition. The error bars indicate SE. Statistically significant differences from the LR condition are indicated by asterisks (^*p < 0.05; ^**p < 0.01; ^***p < 0.001). C, Cumulative probability histogram of spine density by condition.

Analysis of spine morphology (spine head diameter and spine length) revealed considerable variability. Coefficients of variation for all spines were 33, 35, and 33% for head diameter and 54, 53, and 53% for spine length in the LR, DR, and DR plus LE groups, respectively. Within-animal variability (four animals per condition) was of comparable magnitude. However, interestingly, when variability was measured within each dendritic segment, we found a significantly lower CV for spine length than head diameter in all rearing conditions. The average within-segment CV for head diameter was 31, 31, and 30%, whereas the within-segment CV for spine length was 8, 9, and 8%, for the LR, DR, and DR plus LE conditions. This means that spine length is much less variable within one dendrite than it is within the whole population. Spine head diameter, in contrast, is as variable within one segment as it is in the whole population. (These measures were computed from a subset of dendritic segments containing only four dendritic segments per animal, so that no two segments came from the same cell; thus, within-segment variability was measured rather than within-cell variability.)

It is tempting to conclude from this analysis that spine length is regulated on a dendrite-wide or cell-wide basis, as opposed to spine head diameter, which is regulated on an individual spine basis. However, sources of noise must also be considered in this interpretation. For spine length, an important source of noise is the projection of spines from three-dimension into three-dimension. The longer the spine, the more important this type of noise will be, and dendritic segments with longer spines will thus have greater within-segment variability. Therefore, low within-segment variability for spine length shows that variation in spine length stems mostly from variation between dendrites or cells. This suggests that spine length is indeed regulated on a dendrite-wide or cell-wide basis, as opposed to an individual spine basis. With spine head diameter, in contrast, our interpretation must be more cautious because the size of a spine head is of the same order of magnitude as the wavelength of light being used to visualize it. This means that photon shot noise significantly affects the imaged size of spine heads. As a result, it is hard to tell whether the high within-segment variability of spine head diameters is attributable to shot noise or to independent regulation of spine head diameter

The distributions of both spine length and spine head diameter were continuous and smooth. They were also skewed and non-Gaussian, with long upper tails (Shapiro-Wilk test; p < 0.0001 for both length and head diameter, in all conditions) (Fig. 5). The skewness of the distribution is in agreement with Schikorski and Stevens (1997), who found a similar skewed distribution of synaptic active zone sizes, but in contrast to Konur et al. (2003), who found an “approximately normal” distribution of spine head diameters. The smoothness of the distribution confirms prior reports (Vecellio et al., 2000; Konur et al., 2003) that found no evidence to support the differentiation of separate shape classes, such as “filopodia” versus “spines” (Ziv and Smith, 1996; Fiala et al., 1998), or the spine shape classes known as “stubby, mushroom, and thin” (Peters and Kaiserman-Abramof, 1970).

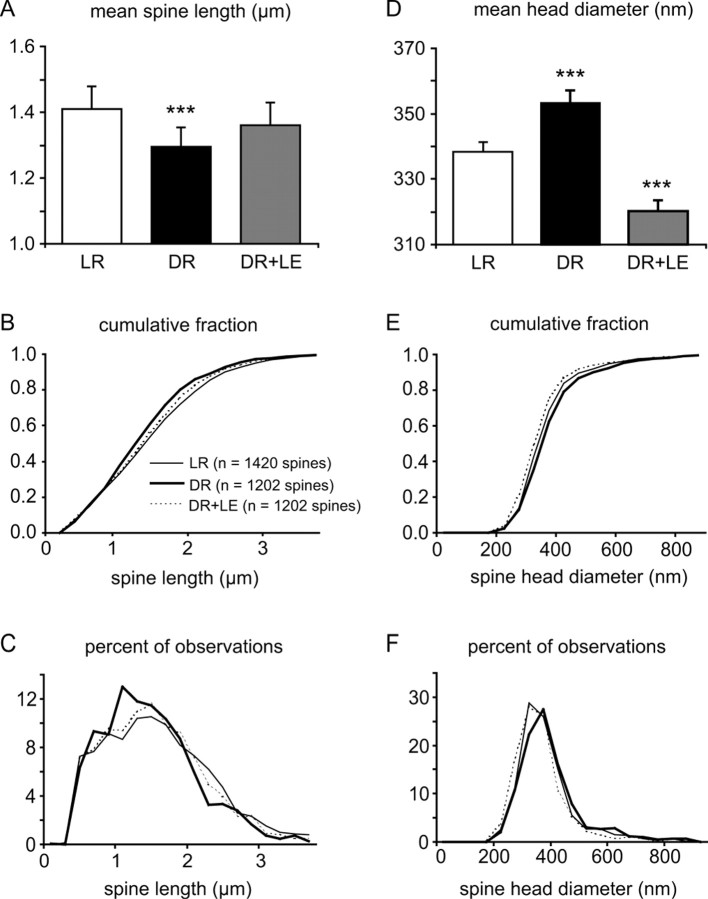
Figure 5.

Spine morphology measurements. A, D, Mean spine length and spine head diameter. The error bars indicate SE. Statistically significant differences from the LR condition are indicated by asterisks (^*p < 0.05; ^**p < 0.01; ^***p < 0.001). B, E, Cumulative probability histograms of spine morphology measurements by condition. C, F, Traditional histograms of spine morphology measurements, showing non-Gaussian distributions with long upper tails.

There was an effect of rearing condition on both spine length and spine head diameter (Kruskal-Wallis test; p = 0.0008 for spine length, p < 0.0001 for spine head diameter). Post hoc tests showed that DR plus LE animals did not have significantly longer spines than DR but did, surprisingly, have significantly smaller spine heads (Mann-Whitney U tests for spine length: DR, DR plus LE: p = 0.02; DR plus LE, LR: p = 0.16; DR, LR: p = 0.0002; Mann-Whitney U tests for spine head diameter: DR, DR plus LE: p < 0.0001; DR plus LE, LR: p < 0.0001; DR, LR: p = 0.0002) (Fig. 5).

To get a more intuitive understanding of these changes, we calculated the aspect ratio of each spine (length/width). This number would be large for long, thin spines and small for short, fat spines. We found that DR plus LE animals had a significantly larger aspect ratio than DR animals, transforming the mean spine aspect ratio from a DR-like profile toward a LR-like profile (Shapiro-Wilk tests: p < 0.0001 for each condition, indicating non-Gaussian distributions; Kruskal-Wallis test: p < 0.0001; Mann-Whitney U tests: DR, DR plus LE: p < 0.0001; DR plus LE, LR: p = 0.47; DR, LR: p < 0.0001) (Fig. 6).

Figure 6.

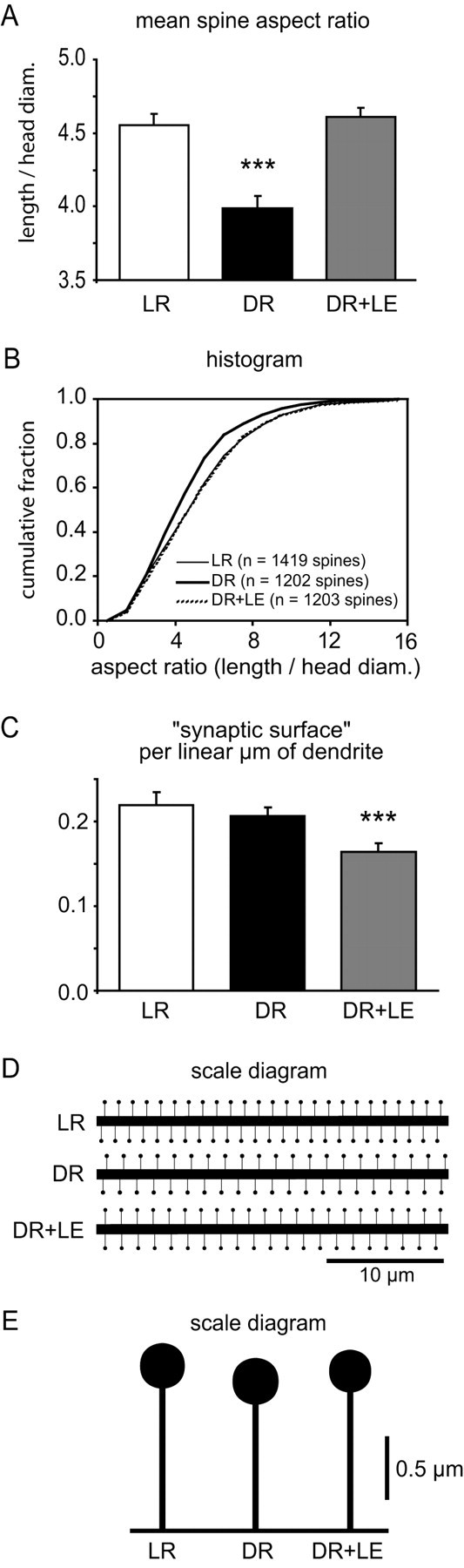
A, B, Spine aspect ratio is perturbed by DR, and this is reversed by LE. C, Total synaptic surface is preserved in DR but reduced after LE. Statistically significant differences from the LR condition are indicated by asterisks (^*p < 0.05; ^**p < 0.01; ^***p < 0.001). n = 20 segments per condition. The error bars indicate SE. D, E, Scale drawings showing mean spine density and morphology in the three experimental groups.

We thought that the opposing changes in spine head diameter and spine density could be indicative of a homeostatic regulation similar to “synaptic scaling.” Synaptic scaling (Desai et al., 2002) postulates that the total strength of synaptic input to a given neuron is homeostatically conserved, to buffer against disturbances to the output of the neuron. To see whether this was the case, we calculated the “total synaptic surface per linear microeter” for each dendritic segment in our sample. This quantity was derived by computing, for each spine, the area of a disk with a diameter that is the spine head diameter, then adding these areas together for all spines on a given dendritic segment and dividing the total area by the length of the segment. This calculation assumes that the spine head is radially symmetric, but this assumption is actually a very good predictor of true spine head characteristics measured using serial EM (Harris and Stevens, 1989). Using this calculation, we found no difference between DR and LR dendrites, compatible with the notion of synaptic scaling, but, surprisingly, DR plus LE dendrites did not scale with those of DR and LR animals (ANOVA, p = 0.0051; Bonferroni-Dunn post hoc tests: DR, DR plus LE: p = 0.015; DR plus LE, LR: p = 0.47; DR, LR: p = 0.002) (Fig. 6).

We then reasoned that spine density might be coregulated with spine head diameter on individual cells or dendrites, and this could explain the synaptic scaling we observed between the DR and LR groups. If so, then there should be a negative correlation between the spine density of a given dendritic segment and the mean spine head diameter of that segment. We found that for DR animals, this was the case, although weakly, whereas for LR animals there was no correlation (DR: correlation coefficient r = -0.587, p = 0.0065; LR: r = 0.054, p = 0.82). (In this and all other correlations we computed, substituting the square of spine head diameter yielded the same results.) This suggests that spine density and spine head diameter may be coregulated at the level of individual cells or dendrites, but only in the deprived condition, when the system is stressed as it were. In the control condition, spine head diameter seems to vary independently of spine density for individual cells or dendrites. Nonetheless, density and head diameter may be coregulated on a population level, even if they are not coregulated at the individual cell or dendrite level.

We also thought that spine length and spine head diameter might be regulated by a common mechanism, and if so, their values would be correlated in individual spines. In LR animals, we found that the Spearman rank correlation coefficient (a nonparametric analog of r) was -0.66, with p = 0.013, indicating an above-chance, but very weak negative correlation. However, in DR animals we found a Spearman coefficient of 0.014, with p = 0.62, indicating no correlation. When the data are pooled by segment, rather than pooled by condition only, the correlation disappears in LR (r = 0.15; p = 0.52) but reappears in DR (r = 0.38; p = 0.095). This again suggests that in the deprived condition, regulation may be tighter. This is generally consistent with previous reports: Harris and Stevens (1989), using serial EM, reported independent variation of spine length and spine head diameter, as did Matsuzaki et al. (2001), using two-photon images of living hippocampal slices.

Our results could be confounded by an effect of dendritic diameter, if for example thicker dendrites had more spines, as reported by Larkman (1991). To control for this possibility, we measured the mean dendritic diameter of each segment in the sample. ANOVA showed no significant difference in mean dendritic diameter between rearing conditions (p = 0.15). We also analyzed the correlation between spine density and dendritic diameter for each segment, as well as the correlation between the mean per segment of each morphological parameter and the dendritic diameter of that segment. We found, in all but one case, that neither spine density nor morphology was correlated with dendritic diameter (r < 0.26 and p > 0.25 for all measurements and all conditions). The only exception was that in LR animals there was a weak correlation between dendritic diameter and spine density (r = 0.55; p = 0.01), but not spine morphology (spine length: r = 0.25, p = 0.28; spine head diameter: r = 0.21, p = 0.37). The general lack of correlation of our measurements with dendritic diameter may be attributable to the fact that we sampled only from dendritic segments located 30 μm away from the cell body. As a result, the range of dendritic diameters represented in our sample was quite small.

Discussion

In previous work, our laboratory found that during the period P21-P28, the input/output curves for population synaptic responses in layer 3 are unchanged by dark rearing (Kirkwood et al., 1995, 1996; Quinlan et al., 1999), although DR rats at those ages show many physiological changes, including enhanced LTP and diminished long-term depression (LTD), decreased visual acuity, and larger visual cortex receptive field sizes (Fagiolini et al., 1994; Kirkwood et al., 1996). This means that the power of a set of afferent axons to excite a group of postsynaptic cells is basically unchanged by dark rearing, although the details of this connection are altered.

Turrigiano et al. (1998) found an analogous phenomenon in the analysis of spontaneous miniature synaptic currents (mEPSCs). During normal development, the frequency of mEPSCs increases, whereas the amplitude of individual mEPSCs decreases (Turrigiano et al., 1998; Desai et al., 2002). This coregulation of synapse number and synapse strength may be a form of homeostasis that ensures that the output of a postsynaptic cell remains constant despite changes to its input drive. The phenomenon has been called synaptic scaling. Interestingly, Turrigiano et al. (1998) also found that blockade of synaptic transmission or dark rearing (Desai et al., 2002) prevents the normal developmental change in mEPSCs during P14-P24. An analogous phenomenon was observed in cell cultures in which synaptic activity is blocked by the AMPA receptor blocker NBQX (1,2,3,4-tetrahydro-6-nitro-2,3-dioso-benzo[f]quinoxaline-7-sulfonamide): synapses in these cultures had more docked presynaptic vesicles, and larger synaptic active zones, than synapses in control cultures (Murthy et al., 2001).

The results we present here provide an in vivo correlate of synaptic scaling. We found that spines in DR animals are less dense, but have a larger head diameter, than in controls, indicating fewer but stronger synapses. Based on this, we predict that DR animals have decreased mEPSC frequency (compatible with decreased spine density) and increased mEPSC amplitude (compatible with increased spine head diameter). In fact, the change in mean spine head diameter that we detected translates into a change on the order of 10-50% in predicted synaptic currents in DR animals, using our estimates of synaptic surface area and available measurements of AMPA receptor conductance and density at cortical synapses (Hestrin, 1993; Nusser et al., 1998). This is a change of similar magnitude to the change in mEPSC amplitude detected by Turrigiano et al. (1998) in DR animals.

One explanation of these findings is that dark rearing causes a decrease in activity of thalamocortical afferents, which results in a loss of synapses between these afferents and their cortical partners. This loss of synapses is then balanced by a compensatory increase in the strength of remaining synapses with other, nonthalamic inputs. A problem with this hypothesis is that the effect of DR on spine density is greater than would be expected if only thalamocortical synapses were being lost. Thalamocortical synapses account for 10% of all synapses in layer 4 of rat visual cortex, and perhaps only 4% of those on the basal dendrites of layer 2/3 pyramids (Peters et al., 1979; White and Hersch, 1981; DeFelipe and Farinas, 1992). However, the spine loss we see in DR animals is 15%. One reason for this discrepancy might be that thalamocortical synapses are indeed lost, but in addition, other nonthalamocortical synapses are also lost, because of a reduction of their own sources of input.

A recent trangenic experiment supports our contention that spine number and spine size are coregulated. Hayashi et al. (2003) found that brain areas expressing a dominant-negative transgene for p21-activated kinase (PAK) show decreased spine density and increased average spine size, the same phenotype we describe here. PAK is important in regulating actin (Jaffer and Chernoff, 2002), and the susceptibility of dendritic spine morphology to manipulations of actin-regulation pathways has already received wide attention (Matus et al., 2000; Ackermann and Matus, 2003). The findings of Hayashi et al. (2004) suggest that the coregulation of spine size and spine density can occur in both directions [i.e., a primary effect on spine size (because of disruption of actin regulation) can be homeostatically balanced by a secondary effect on spine number]. It is also of interest that the spine changes in this transgenic mouse correlate with enhanced LTP and diminished LTD across a range of stimulation frequencies, similar to what has been observed in DR visual cortex (Kirkwood et al., 1996). Thus, the spine changes we observe in DR cortex could be a consequence of adjustments in the LTD/LTP modification threshold, as proposed in the Bienenstock-Cooper-Munro theory (Bienenstock et al., 1982). This type of threshold adjustment (or “metaplasticity”) can, in principle, explain the phenomenon of synaptic scaling.

DR plus LE

Having found an effect of dark rearing on spine shape and density, we investigated the effect of light exposure to DR animals, expecting to see a return toward LR anatomy. In other words, we thought that DR plus LE animals would have a higher spine density, as well as longer, thinner spines, than DR. This was partly true because spines in DR plus LE animals were longer and thinner, but surprisingly, they were not more dense. This finding seems inconsistent with the hypothesis that light exposure induces large-scale LTP-like changes in the visual cortex and also inconsistent with the principle of synaptic scaling.

We hasten to add that both LTP and synaptic scaling could be accomplished by mechanisms that are not associated with spine shape changes (Holthoff et al., 2002). However, the lack of change in spine density after light exposure may be compatible with our synaptic scaling model, if we assume that spine density changes can only be induced during an early critical period. Indeed, there are reports that spine morphology is plastic for longer than spine density (Maletic-Savatic et al., 1999; Lendvai et al., 2000). If spine morphology was still plastic in our DR plus LE group, but spine density was not (this might be the case, for example, if thalamocortical afferents had stabilized by P20 and were not able to form new synapses), then the effect we see would be perfectly compatible with the principle of synaptic scaling: increased input drive (because of light exposure) would cause a global downregulation of synaptic strength, so that output activity can remain constant. Based on this reasoning, we predict that DR plus LE animals should have the same mEPSC frequency, but smaller mEPSC amplitude, than DR animals.

The counterintuitive decrease in mean spine head diameter after light exposure might be better understood as an increased prevalence of immature spines or filopodia. This would be reflected as a change in the distribution of spine morphologies. Because the mean spine density is unchanged after light exposure, we would then expect to see the distribution of morphologies shift away from the mean in both directions (i.e., toward an increasingly bimodal distribution). However, we find that the basic shape of the distribution of spine morphologies remains consistent between all our rearing conditions (Fig. 5). This is especially clear in the distribution of spine aspect ratios, in which long, thin “filopodial” morphologies are represented as large aspect ratios (Fig. 6). (In fact, we find no evidence for discrete spine types at all. Instead there is a continuum of spine morphologies, from long and thin to short and fat.)

Another way that spine shapes could change, and new spines be created, is through a change in the spine turnover rate. There is evidence that individual spines may not be stable over the period P20-P30, but instead they may turn over in a complex dynamic manner (Okabe et al., 1999; Grutzendler et al., 2002; Trachtenberg et al., 2002; Majewska and Sur, 2003). Spine turnover may also be more rapid in synapse populations that are undergoing plasticity (Yuste and Bonhoeffer, 2001). If that is the case, then the more immature average spine morphology in DR plus LE could be attributable to a faster rate of spine turnover in that condition. If more spines are being created and destroyed, the average spine morphology appears more immature, but the total spine density remains constant.

Evidence for brief, local “critical periods”

Our hypothesis of an early critical period for spine density contradicts a previous finding by Valverde (1971). Valverde found that light exposure from P20 to P30 restores spine density of DR animals to the LR level. From this result, we know it is possible for light exposure to increase spine density in layer 4 during the same developmental period we were investigating, but this result was observed in a different dendritic locus of layer 4 (i.e., the apical dendrites of layer 5 pyramidal cells). Thus, we think that there may be a different critical period for this type of plasticity in layer 5 cells versus layer 2/3 cells, or even in basal dendrites versus apical dendrites.

There are several examples in the literature of differences in plasticity between cell types, even for closely related cells. For instance, among layer 5 pyramidal cells, the “medium” type shows greater spine loss than the “large” type in response to enucleation (Ryugo et al., 1975), dark rearing (Winkelmann et al., 1976), or monocular lid suture (Rothblat and Schwartz, 1979; Schwartz and Rothblat, 1980). These two cell populations have different axon targets (Peters and Kara, 1985) and differ considerably in terms of intrinsic physiological properties, as well as the nature and distribution of their synaptic input (Liu et al., 1991).

Even more interesting, there may be differences in the timing of plasticity between cell types. For example, the dendritic morphology of pyramidal cells in layer 3 alters in response to enucleation at P19 but gradually less so at P24 and P48 (Ruiz-Marcos and Valverde, 1970), whereas the dendritic morphology of stellate cells in layers 3 and 4 is not yet altered at P24 but is altered at P48 (Valverde, 1968).

There has also been some evidence recently that different dendritic loci within the same cell type can have differences in plasticity. For example, mice lacking the fragile X mental retardation protein show more prominent spine abnormalities on apical than on basal dendrites (Nimchinsky et al., 2001), and chronically stressed rats show dendritic changes in apical, but not basal, dendrites of hippocampal area CA3 (Watanabe et al., 1992).

We think that there may be a brief critical period, ending before P20, during which light exposure can induce new spine formation in the basal dendrites of layer 2/3 pyramidal cells. In that case, light exposure starting at P20 would have occurred too late to initiate new spine formation in DR plus LE animals, but in control animals (LR), there was enough light exposure between eye opening and P20 to induce new spine formation. This suggests that spine formation in response to visual experience is regulated by a developmental program that only needs a brief period of light exposure at the time of eye opening to be initiated.