Input-Driven Components of Spike-Frequency Adaptation Can Be Unmasked In Vivo

Abstract

Spike-frequency adaptation affects the response characteristics of many sensory neurons, and different biophysical processes contribute to this phenomenon. Many cellular mechanisms underlying adaptation are triggered by the spike output of the neuron in a feedback manner (e.g., specific potassium currents that are primarily activated by the spiking activity). In contrast, other components of adaptation may be caused by, in a feedforward way, the sensory or synaptic input, which the neuron receives. Examples include viscoelasticity of mechanoreceptors, transducer adaptation in hair cells, and short-term synaptic depression. For a functional characterization of spike-frequency adaptation, it is essential to understand the dependence of adaptation on the input and output of the neuron. Here, we demonstrate how an input-driven component of adaptation can be uncovered in vivo from recordings of spike trains in an insect auditory receptor neuron, even if the total adaptation is dominated by output-driven components. Our method is based on the identification of different inputs that yield the same output and sudden switches between these inputs. In particular, we determined for different sound frequencies those intensities that are required to yield a predefined steady-state firing rate of the neuron. We then found that switching between these sound frequencies causes transient deviations of the firing rate. These firing-rate deflections are evidence of input-driven adaptation and can be used to quantify how this adaptation component affects the neural activity. Based on previous knowledge of the processes in auditory transduction, we conclude that for the investigated auditory receptor neurons, this adaptation phenomenon is of mechanical origin.

Introduction

Many spiking neurons adapt to long-lasting stimulation. An initially high firing rate decreases over time, even though the stimulus stays constant, and eventually levels off to a steady state after a certain period, which may range from tens of milliseconds to several seconds. There is a large range of different biophysical mechanisms known to be involved in spike-frequency adaptation in different neural systems.

In many neurons, a major contribution to spike-frequency adaptation stems from output-driven components triggered by the spiking activity of the neuron itself. The spikes result in activation of calcium-dependent (Madison and Nicoll, 1984; Vergara et al., 1998; Sah and Davies, 2000) or slow voltage-dependent (Brown and Adams, 1980; Storm, 1990) potassium currents or the inactivation of sodium currents (Fleidervish et al., 1996; Vilin and Ruben, 2001; Torkkeli et al., 2001; Kim and Rieke, 2003) and lead to a negative feedback on the firing rate (Benda and Herz, 2003).

In contrast, adaptation may also contain components that are driven by the strength of the sensory or synaptic input in a feedforward way. For example, certain potassium currents may follow synaptic events or subthreshold voltage fluctuations (Trussell, 1999). Likewise, short-term synaptic plasticity can contribute to adaptation in a feedforward way (Best and Wilson, 2004). In the sensory periphery, several mechanosensitive receptor neurons are influenced by adaptation components that are driven by the sensory input. For example, as originally suggested by Matthews (1931, 1933), muscle stress relaxation contributes to adaptation in vertebrate muscle spindles and tendon organs. In the Pacinian corpuscle, the viscoelasticity of the capsule leads to a characteristic rapid adaptation (Hubbard, 1958; Loewenstein and Mendelson, 1965), and mammalian hearing systems are influenced by adaptation of the transducer currents (Ricci et al., 1998; Holt and Corey, 2000; Gillespie and Walker, 2001).

The different dependences of adaptation on the sensory input and neural output will have different effects on the coding properties of a sensory neuron. For a functional characterization of adaptation, we therefore need to identify the causal relationships between sensory input, neural activity, and the level of adaptation (cf. Nurse, 2003). This approach can be viewed as complementary to biophysically investigating the mechanisms underlying spike-frequency adaptation. Ultimately, combining biophysical and functional knowledge should yield a coherent picture of adaptation.

In this work, we aimed to uncover and analyze putative input-driven components in locust auditory receptor neurons, a model system for the mechanosensitive auditory transduction process. The study is based on in vivo recordings of spike trains in single auditory nerve fibers. So far, output-driven components have been identified as a substantial source of spike-frequency adaptation in insect mechanoreceptors (French, 1984a,b). Indications that spike-frequency adaptation in locust auditory receptor neurons is primarily output driven come from the dependence of the adaptation time constants on the firing rate of the receptors (Benda et al., 2001; Benda, 2002).

In a recent study (Gollisch et al., 2002), small differences between the spectral integration properties at stimulus onset compared with the steady state have hinted at the presence of an input-driven adaptation component, although it seemed to be covered for the most part by the more prominent output-driven adaptation. Here, we investigate this question in more detail by use of a new experimental technique that allows us to measure input-driven adaptation independently of output-driven components. To do so, we tune the intensities for different sound frequencies in such a way that the steady-state firing rate is the same. Consequently, the level of output-driven adaptation must be equal for these stimuli. Sudden switches between these sounds can now reveal input-driven components, because these need to approach a new equilibrium value after such a switch. This results in transient deflections of the firing rate, which can be observed in electrophysiological recordings of the spiking activity. The careful tuning of the sounds leads to a high sensitivity of the method allowing detection of input-driven adaptation components even when they are far smaller in effect than simultaneously present output-driven components.

As shown by our data, the induced firing-rate deflections can be used to characterize prominent features of this adaptation component such as its strength, time constants, and correlation with different stimulus and activity parameters. Similar insight is to be expected for other neurons exhibiting a mixture of input-driven and output-driven adaptation.

Materials and Methods

Electrophysiology. We performed intracellular recordings from axons of receptor neurons in the auditory nerve of adult Locusta migratoria. The tympanic hearing organ of these animals is located in the first abdominal segment above the coxa of the hindlegs. The somata of the receptor neurons are contained in the auditory ganglion on the inner side of the tympanum. Each neuron is attached to the tympanum via a short dendrite, a cilium, which protrudes from the distal tip of the dendrite, and an attachment cell, which forms the connection between the tympanum and the cilium (Gray, 1960). The receptor neurons receive their inputs via yet unidentified mechanosensory transduction channels at the cilium or dendrite. The auditory nerve contains the axons of the receptor neurons. Note that there is no synapse between the site of mechanosensory transduction and the fibers in the auditory nerve, in contrast to the mammalian inner ear.

The detailed experimental setup has been described previously (Gollisch et al., 2002). In short, the animal was waxed to a Peltier element; the head, legs, wings, and intestines were removed, and the auditory nerves were exposed. Recordings were obtained with standard glass microelectrodes (borosilicate, GC100F-10; Harvard Apparatus, Edenbridge, UK) filled with 1 mol/1 KCl, and acoustic stimuli were delivered by loudspeakers (Esotec D-260; Dynaudio, Skanderborg, Denmark) on a stereo power amplifier (DCA-450; Denon Electronic GmbH, Ratingen, Germany) ipsilateral to the recorded auditory nerve. Spikes were detected on-line from the recorded voltage trace with the custom-made on-line electrophysiology laboratory software and used for on-line calculations of firing rates and automatic tuning of the sound intensities. The measurement resolution of the timing of spikes was 0.1 msec. During the experiments, the animals were kept at a constant temperature of 30°C by heating the Peltier element. The experimental protocol complied with German law governing animal care.

Acoustic stimuli. The sounds used in this study were based on sinusoidal pure tones. For the main part of the experiments, we used stimuli that contained a switch from one constant-intensity tone to another. More precisely, each stimulus presentation of length, T, consisted of two sections of length, T/2. Each section was filled with a pure tone of frequency f₁ or f₂, respectively, played at sound intensity S₁ or S₂, respectively. At the beginning and end of each stimulus section, the intensity was linearly ramped up or down, respectively, within 0.5 msec to avoid artifacts caused by sharp intensity changes and discontinuities in the drive of the loudspeaker. We compared the responses from sound presentations for which f₁ and f₂ as well as S₁ and S₂ differed (switch stimuli) to responses from presentations for which f₁ = f₂ and S₁ = S₂ (pure stimuli). For each recording, two different sound frequencies were chosen, and all of the four resulting combinations for the first and second stimulus sections were presented alternately and repeated 20-150 times, depending on the length of the recording.

The sound intensities S₁ and S₂ were chosen so that the recorded neuron had the same (predefined) firing rate R for both tones in the steady state. Such S₁ and S₂ were found by additional tuning measurements at the beginning of each recording session. For each sound frequency, stimuli of length T/2 were presented, and the firing rate was calculated from the spike count in the last 100 msec of the presentation. The intensity S was then adjusted via an on-line analysis algorithm in the following way.

Starting at S = 50 dB sound pressure level (SPL), the intensity was increased or decreased in steps of 5 dB depending on whether the firing rate observed from two stimulus presentations was smaller or larger than the predefined firing rate R. Therefore, when both a bottom and a top bound for the required intensity were found, additional measurements for five intensities in the determined range in steps of 1 dB were repeated four to six times. The intensity corresponding to R was then calculated from a linear interpolation.

We used various sound frequencies between 1 and 15 kHz covering approximately the whole range of sensitivity of the recorded receptor neurons. The predefined firing rates for all recordings lay between 50 and 150 Hz, and experiments were performed for stimulus lengths T of 800, 1200, or 1500 msec. Between successive presentations, quiet intermissions of 700 msec (in some recordings, 1500 msec) were inserted.

Analysis of firing rates. Spikes were recorded and used to calculate the neural response for each stimulus. The time-resolved firing rate at time t after stimulus onset, R(t), was calculated by taking the inverse of the interspike interval (ISI) between the last spike before t and the next spike after t and then averaging over trials:

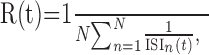where ISI_n(t) denotes the length of the interspike interval that contains the time point t in the nth trial, and N is the total number of trials.

To investigate the transient effects on the firing rate induced by the switching of tones, we analyzed firing-rate differences between switch stimuli and pure stimuli. From the firing rate R_switch(t) obtained with the switch stimulus that first contained frequency f₁ and then f₂, we subtracted the firing rate R_pure(t) of the pure stimulus containing f₂ in both sections. Analogously, we calculated the difference between the firing rates for the switch stimulus containing first f₂ and then f₁ and the pure stimulus containing only f₁. Thus, all firing-rate differences in this study were calculated for stimuli with identical second sections.

The firing-rate differences were quantified by their initial firing-rate differences, Δr, immediately after the switch and their decay time constants, τ. These were obtained by least-square fits of exponential functions (Press et al., 1992) to the time course of the firing-rate differences R_switch (t) - R_pure (t) after the switch: R_switch(t) - R_pure(t) = Δr · exp(-t/τ).

For firing-rate differences with a downward deflection, an additive constant, R_offset, was included as a third fit parameter to account for cases where the firing rate did not reach the original steady state.

For comparison, the total effect of adaptation for pure stimuli after the onset of the stimulus was quantified by the firing-rate difference between onset and steady state, ΔR, which was also obtained by fitting an exponential function to the firing rate.

Correlation analysis. We tested for correlations between the parameters describing input-driven adaptation (its strength and time constant) and parameters describing the stimulation (intensities, evoked firing rates). Correlation coefficients ρ and corresponding p values were calculated with the Matlab Statistical Toolbox (version 6.5, release 13; Math-Works, Natick, MA).

Results

Similar to many other sensory neurons, auditory receptor cells of locusts respond to prolonged external stimulation with spiking activity that contains both a tonic and a phasic component. For temperatures of ∼30°C, firing rates at stimulus onset can reach as high as 500 or even 600 Hz. Subsequently, they decrease to a steady-state level below 300 Hz. This spike-frequency adaptation takes place within the first few hundred milliseconds after stimulus onset.

Experimental characterizations of the strength and the time constants of adaptation indicate that adaptation primarily depends on the output level of neural activity, the firing rate (Benda et al., 2001; Benda, 2002). Here, we systematically test for additional input-driven adaptation components and their effects on the spiking activity of the auditory receptors by analyzing in vivo recordings of spike trains from single fibers in the auditory nerve.

An illustrative model

To clarify the idea of input-driven and output-driven adaptation, we investigate a minimal model that contains both of these mechanisms. We model the response of a sensory neuron to external input (e.g., a sensory stimulus with intensity S). In the model, the output activity (firing rate R) is a function of S and an input-driven adaptation component, A_I, as well as an output-driven component, A_O:

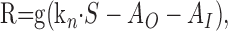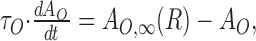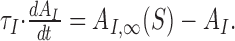The function g(x) captures the stimulus-response function of the neuron and may typically include rectification and saturation. dA_O/dt and dA_I/dt symbolize the temporal derivatives of A_O and A_I, respectively, leading to first-order differential equations that capture the build-up and decay of adaptation. Note that in this model, R is not given by a differential equation but by an instantaneous function of S, A_O, and A_I. This can be viewed as a quasistatic approximation, which is valid if the time constants of adaptation, τ_O and τ_I, are considerably longer than those governing the dynamics of R (e.g., cell membrane or synaptic time constants) (cf. Shriki et al., 2003). The first-order dynamics and the subtractive contribution of A_O and A_I as well as the instantaneous function for R are chosen merely for mathematical simplicity and are not crucial for the conclusions that we will draw from the model.

An important aspect of the model is that the dynamics of A_O and A_I depend on only the firing rate R, output of the neuron, stimulus intensity S, and input of the neuron, respectively, and that A_O and A_I take on steady-state values A_O,∞(R) and A_I,∞(S), which are only functions of R and S, respectively.

An additional important feature of the model is nonuniform tuning (i.e., the model neuron is more sensitive to some stimuli than to others). For example, the activity of an auditory neuron does not depend only on the sound intensity but also on the sensitivity of the neuron to the sound frequency of the stimulus, and a visual neuron may respond to light intensity but with an additional dependence on how well the stimulus overlaps with the spatial receptive field or spectral sensitivity of the neuron. These tuning effects are captured by the factor k_n, where the index n stands for the different applied types of stimuli; if the neuron is more sensitive to a particular stimulus, k_n will be larger.

Without losing its essential features, the above model can be solved analytically by assuming that the stimulus-response relationship, g(x), and the dependences of the adaptation components on R and S are all linear. The solutions provide insight into the dynamical behavior of the two different adaptation components. For g(x) = x, A_O,∞(R) = α·R, and A_I,∞(S) = β·R, with proportionality constants α and β, the mathematical solution is given in the Appendix.

The adaptation terms A_O and A_I have similar effects for constant stimuli. Both tend to decrease the firing rate over time until a steady state is reached. Because stimulus intensity S and output firing rate R are usually tightly coupled (for higher intensity, the firing rate is also higher), both processes tend to work in the same direction. If the time constants τ_O and τ_I are also similar, the two types of adaptation will be hard to distinguish. However, for a biophysical interpretation or for understanding the response to dynamical, fluctuating stimuli, such a distinction will be important. This raises the question how one can test, e.g., if an input-driven adaptation component such as A_I is present.

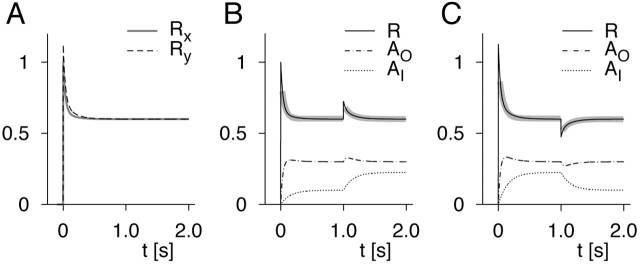
To answer this question, we investigate how the model reacts to two stimuli, x and y, for which it has different sensitivity, here modeled by using values k_x = 1 and k_y = 0.5. Figure 1 shows examples of firing rates obtained for the model with time constants τ_O = 50 msec, τ_I = 150 msec, and parameters α = 0.5 and β = 0.1. According to the steady-state equations in the Appendix, both stimuli lead to the same steady-state firing rate when the intensities are, e.g., S_x = 1 and S_y = 2.25 (Fig. 1A). Because of the difference in intensity, the contribution of A_I to the total adaptation is quite different in the two cases. Nevertheless, the time courses of the firing rates are very similar. Only a slight difference is visible during the initial firing-rate transients.

Figure 1.

Dynamics of a minimal model containing input-driven and output-driven adaptation. The firing rates and adaptation components are calculated according to the equations introduced in this paper (solutions can be found in Appendix). A, Firing rates R_x and R_y for the two stimuli under constant stimulation. The two intensities are chosen such that the firing rates in the steady state are the same for both stimuli. B, Firing rate R and the two adaptation components A_O and A_I for a stimulation where the stimulus is switched from x to y at time t = 1 sec. The thick gray curves underlying the firing rate are exponential fits to the data. C, Same as B, but at time t = 1 sec, the stimulus is switched in the other direction, from y to x.

However, when we include a switch from one of the two stimuli to the other, the A_I component is suddenly disequilibrated, because S takes on a different value. In Figure 1B, a switch from the lower intensity stimulus x to the higher intensity stimulus y leads to a pronounced upward deflection of the firing rate. This is caused by the fact that A_I is not in its steady state after the switch and needs time to approach its new equilibrium value. Conversely, a switch from the higher intensity stimulus y to the lower intensity stimulus x leads to a downward deflection of the firing rate (Fig. 1C).

Because of the temporary change of the firing rate, the adaptation component A_O also shows a small transient deflection and then resumes its original steady-state value. However, this is a secondary effect; no deflection of A_O or R would occur without the component A_I. The latter is true regardless of the exact dependence of R on A_O and A_I (e.g., subtractive or divisive) and regardless of the exact dynamics of A_O and A_I, as long as A_O is determined only by R.

The upward or downward deflection of the firing rate can be used to characterize the direction, strength, and time constant of the adaptation process A_I. At the switch, the response transient is determined primarily by the dynamics of A_I, because A_O stays near its equilibrium point all the time. However, we also see from the model that the small secondary response of A_O does not allow a complete separation of the two adaptation processes. In the model, we used time constants τ_O = 50 msec and τ_I = 150 msec. From exponential fits of the firing-rate transients after onset and switch, we obtained time constants of 53 and 71 msec for the two stimulus onsets, indicating that initially the faster and stronger adaptation component A_O dominates. After the switch, we found a time constant of 118 msec in both cases, which still reflects the mixture of the two processes. However, A_O stays near enough to its equilibrium value so that the longer time constant is revealed, and an order-of-magnitude estimate of τ_I is possible.

Experimental approach

Based on the insight gained from this minimal model, we thus proceed as follows to experimentally detect and analyze input-driven adaptation. For each recorded receptor neuron, we identified stimuli with different sound frequencies that evoke the same steady-state firing rate. This is achieved by tuning the individual sound intensities so that a predefined firing rate is reached. Because the neurons have different sensitivity for different sound frequencies, these intensities will generally be different. We then observed the firing rate when the stimulus was switched from one sound to the other. If only output-driven adaptation was present, the firing rate should stay at the constant steady-state level; in contrast, input-driven adaptation components will be disequilibrated and therefore transiently affect the firing rate.

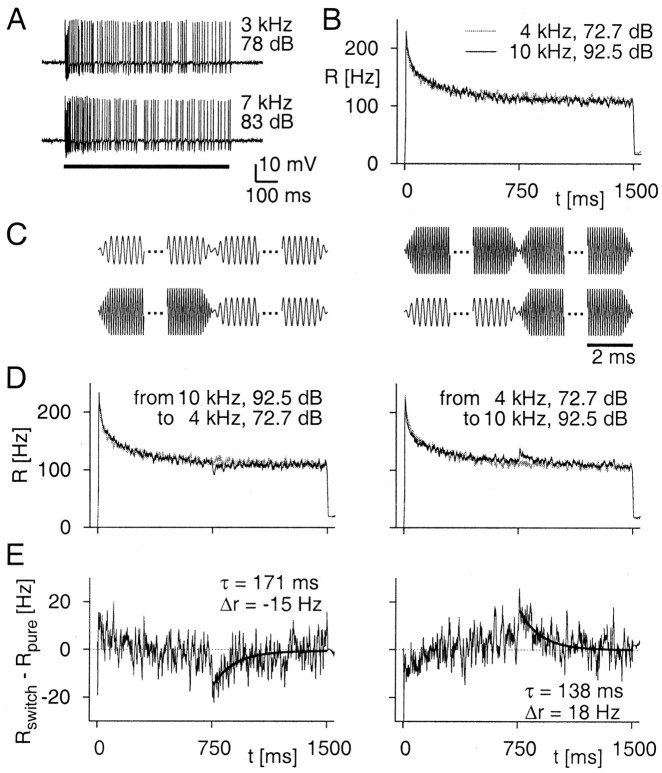
Figure 2 shows a typical sound-evoked response of an auditory nerve fiber. The firing rate is initially high and decays during the first few hundred milliseconds. No differences in spike patterns were apparent when responses for different tones that yield similar firing rates were compared (Fig. 2A). Two tones can be fine-tuned so that the evoked steady-state firing rates are indistinguishable within the measurement error (Fig. 2B). This may require substantial differences in intensity for the two tones; in the present example, the 10 kHz tone needs to be played ∼20 dB louder than the 4 kHz tone to be equally effective. The steady-state level of firing is equal for the two tones, and the initial firing-rate transients after stimulus onset are also strikingly similar. Generally, the time constants of adaptation in these cells show large variations; they are substantially higher when the cell is more strongly driven (Benda et al., 2001). The fact that equal firing rates lead to approximately equal time courses of adaptation thus indicates that the dynamics of adaptation are governed primarily by the firing rate (i.e., output of the neuron).

Figure 2.

Stimulus switches reveal input-driven adaptation, as demonstrated by data from one auditory receptor cell. A, Examples of recorded spike trains. The two traces show spike trains measured in an auditory nerve fiber during 750 msec stimulation (black bar) with pure tones of 3 and 7 kHz and intensities of 78 and 83 dB SPL, respectively. B, Instantaneous firing rates obtained from 94 repetitions of two stimuli with a duration of 1.5 sec; sound frequencies and intensities are indicated in the plot. The intensities had been tuned to reach the same steady-state firing rate. C, Schematic drawings of the applied stimuli. Shown are the two pure stimuli (top row) and the two switch stimuli (bottom row) consisting of two parts with either 4 or 10 kHz sound frequency. Only the initial and final 2 msec of each part are displayed to show the half-millisecond linear increase or decrease used for stimulus onset, offset, and the switch. D, Firing-rate transients induced by stimulus switching. At time t = 750 msec, the stimulus was switched in the way indicated by the label of the plot. A small downward deflection (black line, left panel) or upward deflection (black line, right panel) is apparent. For comparison, the gray line shows the firing rate that is obtained for the pure stimulus with sound frequency and intensity as in the second stimulus section. E, Firing-rate differences calculated by subtracting the firing rate of the pure stimulus (D, gray curve) from that of the switch stimulus (D, black curve). The deflections are fitted by exponential curves (thick black lines), and the obtained values for the initial firing-rate difference Δr and the time constant τ are indicated in the graphs.

Figure 2C shows schematic drawings of the sounds used to investigate this neuron. Four different stimuli were constructed, consisting of two parts of 750 msec filled with either 4 or 10 kHz sound frequency. The difference in amplitude indicates the different intensities at which the stimulus parts were played, although the schematic drawing is not to scale. The 4 kHz tone is shown with an amplitude 0.6 times that of the 10 kHz tone, whereas the sensitivity difference of ∼20 dB apparent in Figure 2B would yield an amplitude ratio of ∼0.1, making the 4 kHz component even smaller.

The switch from the 10 kHz tone to the lower intensity 4 kHz tone after half the stimulus duration leads to a transient decrease in firing rate (Fig. 2D, left panel). This is a sign for the presence of an input-driven adaptation component. Note that the suppression of the response after the switch from the higher to the lower intensity indicates that the level of adaptation was higher for the higher intensity stimulus. This is expected if the input intensity is what triggers this adaptation component, such as in the minimal model of the previous section.

Conversely, a switch from the lower intensity 4 kHz to the higher intensity 10 kHz tone results in a transient increase in firing rate (Fig. 2D, right panel). After the switch, the input-driven adaptation slowly builds up to its new level and, consequently, the firing rate decays back to the steady-state level. Note that the measured firing-rate transients are approximately two orders of magnitude longer than the ramps used to construct the switch (Fig. 2C). Furthermore, the pure stimuli contain the same type of ramps and show no firing-rate transients. Therefore, the short discontinuity of the stimulus intensity at the switch cannot be held responsible for causing the transients.

Also, note that the size of the firing-rate transients is small compared with the total level of adaptation. Whereas the firing rate decreased by >100 Hz after stimulus onset, the switch (despite an intensity difference of 20 dB) induced a firing-rate difference of only 20 Hz, supporting the idea that, here, input-driven adaptation is considerably weaker than output-driven adaptation. Nevertheless, this firing-rate difference after the switch can reliably be detected if the steady-state firing rates are sufficiently tuned, thus resulting in the high sensitivity of this approach.

Characterization of input-driven adaptation

To quantify input-driven adaptation, we calculated firing-rate differences between the responses to a switch stimulus, which contained a switch from one sound frequency to the other, and the responses to a pure stimulus (i.e., a stimulus with sound frequency and intensity that were constant and equaled those in the second half of the switch stimulus) (Fig. 2E). We fitted exponential curves to the firing-rate differences after the switch to obtain the initial firing-rate difference, Δr, and the decay time constant, τ. For the switch from the high-intensity 10 kHz to the low-intensity 4 kHz stimulus, the deflection is in the downward direction and, correspondingly, Δr is negative. For the switch from low to high intensity, Δr is positive.

Figure 3 shows a collection of such data from four different recorded receptor neurons. For all of these cells, the transient firing-rate deflection is clearly visible. This shows that input-driven adaptation is a general phenomenon in these neurons. Size and time constants of the effect vary considerably between cells (note the different scales on the x- and y-axes), but the direction of the firing-rate deflection has a clear relationship with the direction of the switch; switches from lower to higher sound intensity lead to upward deflections and vice versa.

Figure 3.

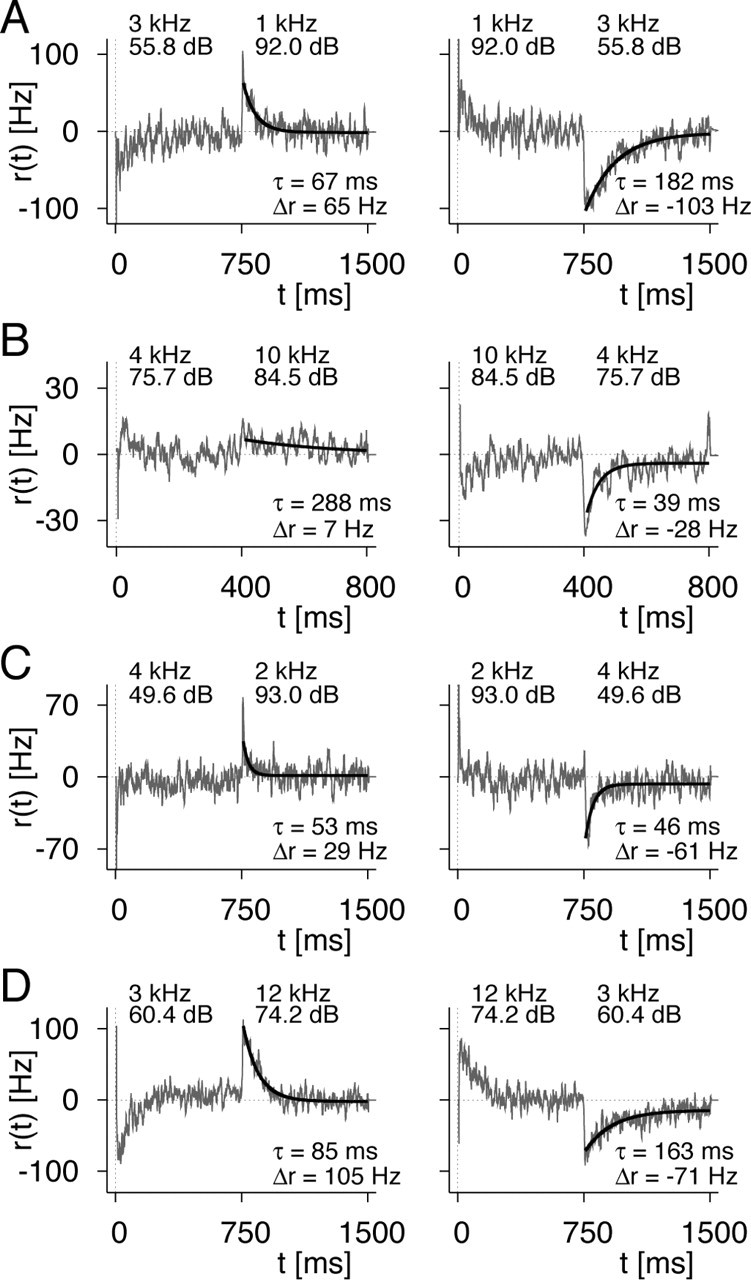
Survey of measurements of input-driven adaptation. A-D, Firing-rate differences r(t) = R_switch(t) - R_pure(t) between responses to switch stimuli and responses to pure stimuli for four cells. The stimulus switch occurred in each case after half the stimulus duration, and the parameter values shown in the plots indicate the sound frequency and intensity of the tones before and after the switch. In all experiments, both directions of switching were used, from the low-intensity to the high-intensity tone (left column) and vice versa (right column). Exponential functions (black lines) were fitted to the responses after the switch. The obtained parameters are indicated in the individual panels.

In approximately half of all of our recordings, we observed that after the switch from the higher to the lower sound intensity, the firing rate did not fully reach the original level of firing within the remaining observation time. This phenomenon is reflected in the negative asymptote of the firing-rate differences in Figure 3B-D. A possible explanation is the contribution of a much slower time scale to the recovery from input-driven adaptation. Such an effect was not seen for the build-up of input-driven adaptation. To account for this effect in the exponential fits, a constant offset was included as an additional fit parameter.

Note that the upward and downward deflections of the firing rate for the same cell do not necessarily have the same shape; the two extracted time constants may diverge considerably (Fig. 3A,B). This is in contrast to the minimal model (Fig. 1) and suggests an extension where the time constant τ_I differs for build-up and decay or explicitly depends on the intensity level, S. Because of the large cell-to-cell variability, however, the present data did not allow for a quantitative investigation of such dependence.

In some cases, the firing-rate differences after stimulus onset show a similar transient deflection as after the switch but with an opposite sign (Fig. 3D). These cases indicate that input-driven adaptation is also part of the initial total adaptation and may account for differences between tones in the time course of the firing rate after stimulus onset. Generally, however, the firing-rate differences at stimulus onset give no clear picture of input-driven adaptation (Fig. 3A-C), presumably because the dynamics are governed strongly by output-driven adaptation.

We add a note of caution for the interpretation of such data. To deduce the existence of input-driven adaptation from the switching-induced firing-rate deflections, the sound intensities need to be tuned to yield approximately the same steady-state firing rates. In the model, this was easy to achieve given the mathematical solutions (Fig. 1), but in experiments, such a tuning relies on noisy data and is never perfect. With a mismatch of steady-state firing rates, output-driven adaptation alone could in principle lead to similar deflections of the firing rates. Imagine, for example, that tone x leads to a higher firing rate than tone y. Output-driven adaptation will consequently be higher during presentation of tone x, and after the switch to tone y, the firing rate will be transiently reduced while this adaptation component decays to the steady-state level of tone y.

We can exclude this scenario by observing cases where a slight tuning mismatch is found together with a firing-rate deflection in the opposite direction to what would be expected from output-driven adaptation. In the left panel of Figure 3D, we see that although the steady-state firing rate for the 3 kHz stimulus was slightly higher than for the 12 kHz stimulus (apparent in the positive offset of the firing-rate difference in the first half of the observation), the rate increased even further after the switch to the 12 kHz stimulus. Pure output-driven adaptation would have been expected to result in a decrease of firing rate triggered by the firing-rate difference before the switch, but this is apparently overcompensated by input-driven adaptation. Thus, analyzing input-driven adaptation does not require a perfect match of steady-state firing rates, although one should be aware of possible influences from a mismatch. For additional analysis, we included only those recordings where the firing rates, measured in the 100 msec period before the switch, matched with deviations of no more than 10%. In fact, for 13 of 22 included recordings, the deviations were <3%.

Correlations of input-driven adaptation and stimulus parameters

Figure 4 summarizes the data from these 22 recordings. We analyzed the data for both switches from higher to lower intensity and vice versa. The measured firing-rate transients thus correspond to the decay and the build-up of input-driven adaptation, respectively. To distinguish more clearly between these two cases, we provide the parameters Δr and τ with indices lh for switches from lower to higher intensity and indices hl for switches from higher to lower intensity and also mark the data differently in the plots. The sound intensity in the first half of the switch stimulus is denoted by S₁ and in the second half by S₂.

Figure 4.

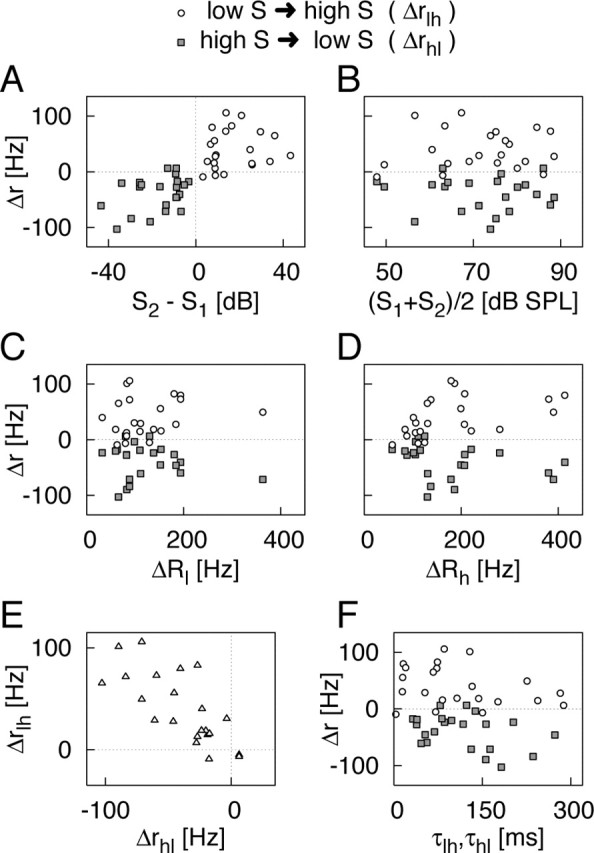
Correlation analyses of the parameters obtained from the firing-rate deflections. The initial firing-rate difference, Δr, and the decay time constant, τ, are obtained from exponential fits of the firing-rate transients after the stimulus switch. To distinguish between the two directions of the switch, the parameters are labeled Δr_lh, τ_lh for switches from lower to higher intensity, and Δr_hl, τ_hl for switches from higher to lower intensity, and the data are plotted as open circles and filled squares, respectively. The open triangles in E depict the comparison between Δτ_lh and Δτ_hl. A-F, The panels display the relationships between Δr,τ, the sound intensities S₁ and S₂, and the total level of adaptation after stimulus onset, ΔR_l for the lower intensity and ΔR_h for the higher intensity.

The direction of the firing-rate deflection is governed by the sign of S₂ - S₁; positive S₂ - S₁ (i.e., switches from lower to higher sound intensity) generally cause upward deflections of the firing rate (Δr_lh > 0) and vice versa (Fig. 4A). Consequently, we observed a strong correlation between S₂ - S₁ and the complete set of values for Δr (ρ = 0.74; p < 10^-4). To investigate whether the intensity difference has an effect on the firing-rate transient beyond determining the sign, we also analyzed the correlation between S₂ - S₁ and Δr for the two cases S₂ - S₁ > 0 and S₂ - S₁ < 0 separately. We found that for switches from higher to lower intensity (Δr_hl vs S₂ - S₁ < 0) (Fig. 4A, gray squares), the data reveal a positive correlation (ρ = 0.38; p = 0.078); the higher the intensity difference, the higher generally the difference in input-driven adaptation. For switches from lower to higher intensities (Δr_lh vs S₂ - S₁ > 0), the correlation is not significant (ρ = 0.14; p = 0.52). In contrast, we found no influence of the absolute level of intensity on the size of the firing-rate deflections (Fig. 4B), nor did the level of the steady-state firing rate systematically influence the measured effect (data not shown).

The total level of adaptation after the initial stimulus onset is denoted by ΔR_l for the lower intensity tone and by ΔR_h for the higher intensity tone. These were obtained from exponential fits to pure-stimulus responses. To investigate the contribution of input-driven adaptation to the level of total adaptation in the two cases of lower and higher intensity, we analyzed the correlation between Δr and ΔR_l and ΔR_h, respectively. Because the two switching directions lead to different signs of Δr, we analyzed Δr_lh and Δr_hl separately. We found that Δr_lh and Δr_hl are not correlated with ΔR_l (Fig. 4C) but with ΔR_h, although the correlation of Δr_hl is not quite significant (p = 0.47, p = 0.027 for Δr_lh; p = -0.30, p = 0.17 for Δr_hl) (Fig. 4D). Our conclusion is that input-driven adaptation is a substantial part of total adaptation for high-intensity tones, whereas it contributes less for low-intensity tones. This allows us to distinguish between two possible scenarios, either of which could explain the firing-rate deflections. The data supports the idea that input-driven adaptation is caused by a process that is activated at higher intensities and that reduces neural sensitivity in the high-intensity regime. In principle, the firing-rate deflections also could have been caused by an amplification process at lower sound intensity that would increase sensitivity in this regime. This hypothetical rival process would not have been expected to lead to the observed correlation of Δr with ΔR_h but rather to a correlation with ΔR_l, which is not supported by the data.

The firing-rate deflections for both switching directions of two tones measured for the same cell are of comparable size (Fig. 4E) as seen in the correlation between Δr_hl and Δr_lh (p = -0.74; p < 10^-3). This supports the idea that the same amount of input-driven adaptation builds up after the switch from lower to higher intensity as decays after the switch from higher to lower intensity.

Figure 4F shows that the time constants of the firing-rate deflections are distributed over a wide range between 10 and 300 msec. τ_lh and Δr_lh show no strong correlation (p = 0.20). However, for the shift from higher to lower intensity, the time constant τ_hl is correlated with Δr_hl (p = -0.37; p = 0.089). As we have seen from the model, time constants for the firing-rate deflections may reflect the mixture of input-driven and output-driven adaptation. The following two simple explanations of this correlation are therefore possible: (1) the strength and time constant of input-driven adaptation within a neuron are directly coupled, or (2) a larger effect of input-driven adaptation leads to a larger contribution of the corresponding time constant to the mixture reflected in the firing-rate transient. Which of these hypotheses may hold is presently undecided.

Discussion

Input-driven versus output-driven adaptation

Spike-frequency adaptation is ubiquitous in neural systems, and several biophysical mechanisms are known to contribute to this phenomenon in different neural systems. In this work, we investigated which aspects of the stimulus or the neural activity trigger adaptation in the auditory periphery of locusts. This functional characterization of adaptation is complementary to biophysical investigations of the underlying mechanisms. As a start, we distinguished between input-driven and output-driven components in the present study. Conceptually, this could be extended in the future to analyzing the dependence of adaptation on putative intermediate stages of neural processing as well as possible interactions between these components.

Many cell-intrinsic currents that contribute to spike-frequency adaptation are primarily triggered by the spiking activity of the neuron (Benda and Herz, 2003) and thus contribute to output-driven adaptation. In general, however, the correspondence between the biophysical mechanisms and the functional dependence is not always straightforward. Subthreshold activation of some potassium currents may be locally induced by synaptic events or triggered by the fluctuations of the membrane potential, thus potentially contributing to both input-driven and output-driven adaptation, depending on the specific organization of the cell under study. By the same token, output-driven adaptation need not causally depend on spiking activity, as long as the source of this adaptation component is a process that completely determines the output of the neuron. For actual mechanisms underlying output-driven adaptation, biophysical investigations, such as blocking spikes, are necessary. The functional characterization of how adaptation depends on the input and output of the neuron is of particular relevance for investigating the neurons from a signal-processing perspective.

In the present study, we specifically asked how input-driven adaptation components can be uncovered despite large contributions from output-driven adaptation. We analyzed spike-train responses recorded in vivo from auditory receptor neurons in locusts. The neural activity in these cells shows strong adaptation to prolonged acoustic stimulation and eventually settles to a steady-state firing rate under stationary stimulus conditions.

Experimental approach to detecting input-driven adaptation

The approach, which we have used to reveal input-driven adaptation components, experimentally depends on measurements of the neuronal firing rate. This is especially advantageous when intracellular recordings from the soma or dendrites are not available, and the application of biomedical agents, such as channel blockers, is difficult or impossible. The method is based on identifying intensities for different sounds that yield the same steady-state firing rate and thus the same level of adaptation as caused by the output firing rate. Switches between these sounds unmask input-driven adaptation components, which become visible as transient deflections of the firing rate.

The basic requirements of the approach are that the investigated neuron (1) receives two or more input channels that can be independently controlled, (2) combines the signals from these input channels so that they converge to the same output channel, and (3) adopts a steady-state activity that can be tuned to be equal for the different input channels. In the present example, the output was simply the firing rate, and the input channels were given by different sound frequencies for which the auditory neuron had different sensitivity. Other examples for multiple input channels are visual stimuli at different locations within the receptive field and odor constituents that lead to different dependences of the neural response on odor concentration. More generally, sensory stimulus spaces are often high dimensional, considering their possible variations in time, space, and additional components. In contrast, the relevant output signals of sensory neurons are usually considerably smaller in dimension; for stationary signals, the firing rate may suffice to describe the activity of a single neuron. This dimensional reduction in sensory coding provides a basis for identifying the required sensory input channels.

At the convergence of the input channels, the detailed information about the identity of the stimulus is lost. Any later processes in the transduction sequence cannot mediate adaptation effects that depend on input-specific attributes, such as the stimulus intensity in the present case. This may allow one to interpret these adaptation phenomena in terms of the relevant biophysical processes involved in sensory transduction (see below for discussion about the biophysical mechanism). Note that the presented approach to detecting input-driven adaptation is not restricted to analyzing primary sensory neurons. For higher-order neurons, a similar analysis may be used to reveal contributions from adaptation in the afferent pathways in contrast to cell-intrinsic adaptation mechanisms.

By measuring the firing-rate deflections, we were able to demonstrate the existence of input-driven adaptation in locust auditory receptors and to characterize the relative strength of this adaptation component and its time scales of build-up and decay in individual cells. However, because we measured the difference of adaptation for two stimuli, we did not determine the absolute level of input-driven adaptation. It thus remains an open question how much input-driven adaptation contributes to the total adaptation, as observed at stimulus onset. Performing the same experiment with more than just two tones could help answer this question, because the resulting set of firing-rate differences may suggest a certain functional dependence of the level of input-driven adaptation on the sound intensity. The limited recording time, however, currently precludes such an experiment for locust auditory receptors.

The method that we apply to detect input-driven adaptation may be viewed as a variant of the cross-adaptation technique (McBurney et al., 1972; Cobb and Domain, 2000; Heinrich and Bach, 2002). This is frequently used to investigate whether the processing of different stimuli occurs along a common pathway; if adaptation to one stimulus carries over to another, a common pathway can be assumed. Here, we modify this approach by using stimuli that are tuned to the same output level and therefore should cross-adapt each other according to pure output-driven adaptation. From the failure to completely cross-adapt, we deduce the existence of an input-driven adaptation component.

Comparison of experimental findings with the minimal model

The firing-rate deflections were well fitted by exponential functions. This is consistent with input-driven adaptation being governed by simple first-order dynamics, as were used in the minimal model. However, this is not a prerequisite of our approach. If the adaptation components would follow more complicated dynamics, the stimulus switches should also result in firing-rate transients only if input-driven adaptation is present. An in-depth analysis of the firing-rate transients may then reveal details of the adaptation dynamics.

In the model calculation (Fig. 1), we used a linear relationship between the stimulus intensity and the firing rate. A strong nonlinearity g(x) could lead to a distortion of the firing-rate transients. Input-driven adaptation could still be detected in the same way, but the extraction of time constants related to input-driven adaptation would be obstructed. In our experimental data, the following two facts indicate that the output is not affected by such strong nonlinearities, at least in the range of the observed firing-rate deflections, usually several tens of hertz: (1) the simple exponential shape of the transients, and (2) the approximate symmetry between the initial firing-rate differences for upward and downward deflections (Fig. 4E). Both are sensitive to a nonlinearity g(x) at the output stage. A future extension might combine our approach with methods that explicitly take a static output nonlinearity into account (cf. Chander and Chichilnisky, 2001).

In contrast to the model, the time courses of upward and downward deflections are not symmetric. The model could easily be extended to incorporate this observation by allowing for different time constants in the build-up and decay of input-driven adaptation or by applying an explicit dependence of the time constant on the stimulus intensity. Extended experiments could test these hypotheses by repeating the measurements with different sets of stimulus intensities for the same cell.

Asymmetries between build-up and decay of adaptation also have been observed in other systems (Smirnakis et al., 1997; Kim and Rieke, 2001). In the present case, the most striking difference between upward and downward deflections of the firing rate is that in some cells, the firing rate fails to reach the original level after a switch to lower intensity. This may be caused by a slow component present in the decay of input-driven adaptation, but its origin and possible function remain to be elucidated.

Within the minimal model, the adaptation components were, for simplicity, taken to act subtractively on the input. However, the experimental assessment of input-driven adaptation that we used in this study is independent of whether the adaptation components act in a subtractive or divisive manner. The method is thus not restricted to either of these cases; however, in contrast, we cannot distinguish between the two cases with the present data. This would require additional assessment of the gain in the different adaptational states by using nonstationary stimuli.

Biophysical mechanism

What is the biophysical mechanism behind the input-driven adaptation component? The sound stimulus is successively transformed, the sound pressure waves cause oscillations of the tympanic membrane, the animal's ear drum, which in turn leads to the opening of mechanosensory ion channels in the attached receptor neurons, and finally the induced transduction currents may trigger action potentials (Gray, 1960; Michelsen, 1971a; Hill, 1983a,b). The information about the absolute intensity is only present at the very first step of this transduction chain, the coupling of the air pressure wave to the tympanic membrane. By its resonance properties, the tympanic membrane filters the sound wave and is thereby responsible for the different sensitivities at different sound frequencies in single receptor neurons (Michelsen, 1971b; Schiolten et al., 1981). Subsequent stages of the transduction chain obtain only information about the filtered stimulus intensities and thus cannot induce an adaptation mechanism that is triggered by the absolute intensity level. We conclude that the observed adaptation process is an effect of the mechanical coupling of the stimulus to the tympanic membrane. Similar influences of mechanical structures have been described in vertebrate muscle spindles (Matthews, 1931, 1933) and the Pacinian corpuscle (Hubbard, 1958; Loewenstein and Mendelson, 1965).

The putative mechanical origin opens the possibility for a complementary characterization via the mechanical properties of the tympanum. Laser interferometry and stroboscopic illumination allow the observation of the tympanic oscillations under acoustic stimulation (Schiolten et al., 1981; Breckow and Sippel, 1985; Robert and Göpfert, 2002). Our results predict that a slight decrease in oscillation amplitude should be visible during the first few hundred milliseconds in response to constant intensity stimulation. However, the auditory ganglion, which contains the receptor-cell somata and is attached to the tympanum, also vibrates during sound stimulation (Stephen and Bennet-Clark, 1982) and thus contributes to the mechanical deformations that induce transduction. It could well be that part (or all) of input-driven adaptation is associated with this movement, which is considerably harder to observe in detail. Furthermore, the inhomogenous structure of the tympanum makes it difficult to relate such observations to individual receptor cells, because they are attached at different positions on the tympanic membrane. In this study, in contrast, we observed the effect of this adaptation component on the spiking activity of single neurons.

Possible functions of input-driven adaptation

What function may this adaptation component serve? The observed phenomenon might be a consequence of the mechanical constraints and nonlinear properties that come with the specific way of stimulus coupling. This could in fact lead to a protection of the delicate mechanical structures from damage at high sound intensities. In contrast, input-driven adaptation components in principle open up new possibilities for coding strategies, because the relative sensitivities of the neuron to different sound frequencies will change over time depending on previous intensity levels.

However, it is yet unclear what benefit would result from such a dynamical reorganization of the code. Natural stimuli for grasshoppers, such as their courtship songs, usually contain broad carrier-frequency bands (von Helversen and von Helversen, 1994; Stumpner and von Helversen, 2001). The coding properties of grasshopper auditory receptors have been shown to be particularly adapted to specific aspects of these stimuli (Meyer and Elsner, 1996; Machens et al., 2001) and to allow discrimination between slightly different songs (Machens et al., 2003). Investigating input-driven adaptation using these more complex signals may thus shed light on how this adaptation component affects neural coding.

Input-driven adaptation in other neural systems

Additional insight about the functional roles of input-driven and output-driven adaptation may result from comparisons with other sensory modalities. In fact, olfactory receptor cells have shown to be affected by adaptation mechanisms originating in somatic ion channels as well as in the ciliary transduction machinery (Narusuye et al., 2003). These mechanisms of output-driven and input-driven adaptation may have different biophysical origins compared with auditory receptor cells but could constitute analogous functional operations. Similarly, photoreceptors are influenced by several different adaptation mechanisms along the phototransduction pathway (Lamb and Pugh, 1992; Hardie and Raghu, 2001), and their relative contributions to light adaptation are of particular interest (Bownds and Arshavsky, 1995).

The approach presented in this work is not specific to the auditory system and may thus lead to similar insight in other sensory systems. For higher-order neurons, it may be applied to disentangle adaptation contributions that are caused by the activity of the investigated neuron itself and those that are inherited from previous processing steps such as short-term synaptic plasticity. As in the present study, no dendritic or somatic measurements are needed; extracellular recordings of spiking activity would suffice to identify and discriminate different (sub)cellular adaptation components.

Appendix

Solution of model equations

With the simplifying linearity assumptions g(x) = x, A_O,∞(R) = α · R, and A_I,∞(S) = β · S, the model equations read as follows:

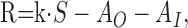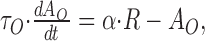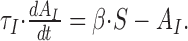This system can be solved analytically for constant input S. For initial conditions, A_O(0) = A_O,0 and A_I(0) = A_I,0, we find the following:

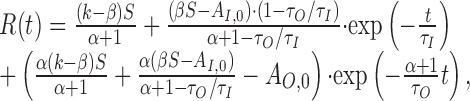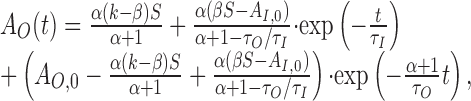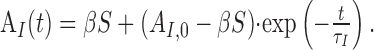Note that R(t) contains two exponential parts corresponding to the two time scales in the model. The time constant of A_O is rescaled by the factor 1/(α + 1) leading to faster dynamics as a result of the feedback between R and A_O. If the two time constants τ_O and τ_I are very similar in value, the first exponential contribution, containing the term exp(-t/τ_I), becomes very small resulting from the (1 - τ_O/τ_I) term. The firing rate at onset is then seemingly dominated by a single process. Switching between two stimuli with different sensitivity will still lead to a deflection in the firing rate revealing the input-driven adaptation component.

In the context of the present study, we need the solution for stimulus onset and after the switch. At stimulus onset, the initial conditions are given by A_O,0 = A_I,0 = 0. If the switch happens long enough after stimulus onset, the system has approximately reached its steady state, and A_O and A_I,0 can be obtained from the steady-state conditions. These are found by setting dA_O/dt = dA_I/dt = 0:

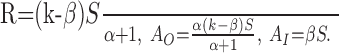Note that the values of k and S of the tone before the switch have to be inserted in these equations to obtain A_O,0 and A_I,0 as initial conditions for the system after the switch.