Longitudinal Mapping of Cortical Thickness and Brain Growth in Normal Children

Abstract

Recent advances in magnetic resonance imaging (MRI) technology now allow the tracing of developmental changes in the brains of children. We applied computer-matching algorithms and new techniques for measuring cortical thickness (in millimeters) to the structural MRI images of 45 children scanned twice (2 yr apart) between the ages 5 and 11. Changes in brain size were also assessed, showing local brain growth progressing at a rate of ∼0.4-1.5 mm per year, most prominently in frontal and occipital regions. Estimated cortical thickness ranged from 1.5 mm in occipital regions to 5.5 mm in dorsomedial frontal cortex. Gray matter thinning coupled with cortical expansion was highly significant in right frontal and bilateral parieto-occipital regions. Significant thickening was restricted to left inferior frontal (Broca's area) and bilateral posterior perisylvian (Wernicke's area on the left) regions. In the left hemisphere, gray matter thickness was correlated with changing cognitive abilities. For the first time, developmental changes in gray matter thickness, brain size, and structure-function relationships have been traced within the same individuals studied longitudinally during a time of rapid cognitive development.

Introduction

A surge of recent research has focused on brain developmental changes that occur during childhood and adolescence (Giedd et al., 1999; Sowell et al., 1999a, 2001b; Courchesne et al., 2000; Thompson et al., 2000b). Spatial and temporal patterns of normative changes in gray and white matter tissues observed thus far are consistent with the known cellular maturational changes that occur between childhood and adolescence (i.e., myelination, synaptic pruning) as well as cognitive and behavioral changes. For example, recent findings have suggested that maturation of frontal lobe gray and white matter accelerates during adolescence (Giedd et al., 1999; Sowell et al., 1999a), paralleling the increased effectiveness of executive functions (i.e., response inhibition-risk taking) that are not yet fully developed by adolescence (Spear, 2000). In contrast, it appears that the dorsal parietal cortical regions that underlie sensory and perceptual functions may develop earlier in childhood (Sowell et al., 1999b). In addition to assessing the effects of age on gray and white matter tissues within the brain, we also localized brain growth in frontal and posterior temporal cortices during childhood and adolescence (Sowell et al., 2001b). Most studies to date have been open to the criticism that they are not longitudinal. Cross-sectional samples are not sufficient to validate “change” in brain structure during maturation because of the difficulty of assembling comparable cohorts at different ages. Nonetheless, there has been a strong inclination to attribute differences between subjects primarily to differences in age.

These studies have also been open to the criticism that changes in cortical gray matter, particularly when measured as gray matter “density,” are difficult to interpret, because they can only be reported as percentage difference (or change) between one group and another. Recent advances have made it possible to estimate gray matter “thickness” in millimeters (Fischl and Dale, 2000; Jones et al., 2000; Miller et al., 2000; Kabani et al., 2001). We have recently developed similar methods by using the three-dimensional (3D) Eikonal equation (Sapiro, 2001), which automatically determines cortical thickness throughout the brain volume with submillimeter accuracy.

In this report, for the first time, we describe changes in cortical thickness in millimeters and local brain size in a sample of 45 children studied longitudinally between the ages of 5 and 11 years with ∼2 years between imaging sessions. In addition, in this report, we take the first steps toward understanding the functional-cognitive significance of structural brain maturational changes within individuals. Our previous cross-sectional studies revealed changes in gray matter and brain size between childhood, adolescence, and young adulthood. However, it was not clear whether change across a 2 year age span in young children would be detectable and statistically significant, nor whether the structural changes could be related to cognitive changes within the same individuals. We predicted a pattern of change in cortical thickness that would parallel our observations in gray matter density in the cross-sectional samples (Sowell et al., 2001b, 2003). Specifically, we hypothesized cortical thinning in the dorsal cortices of the frontal and parietal lobes, with cortical thickening in the perisylvian region.

Materials and Methods

Subjects. Forty-five children were selected from an original sample of 77 children who received cognitive and reading assessments and two magnetic resonance imaging (MRI) scans an average of 2.2 years apart between the ages of 5 and 11 (age at time 1: 5.3-9.5 years; mean, 6.7 years; SD, 1 year; age at time 2: 7.4-11.8 years; mean, 9.0 years; SD, 1 year). Twenty-three boys and 22 girls were studied; four were left-handed, and one was ambidextrous. The selected children had movement-free scans suitable for manual and automated processing. The 32 children who were excluded from the anatomical analysis because of movement artifact did not differ from the 45 children without movement artifact on measures of intelligence quotient, socioeconomic status (SES), or handedness. The children in the original sample were recruited by word of mouth and from presentations to parent groups at elementary schools. Children were excluded if they had neurological or psychiatric diagnoses, were in remedial classes, or had been tested for gifted enrollment. The objective was to obtain a sample of normal children representative of the racial and socioeconomic composition of Alachua County (Florida).

Verbal ability was estimated with the short form of the Wechsler Intelligence Scale for Children (WISC) (Wechsler, 1991) and the picture vocabulary subtest of the WJ-Cog R (Woodcock and Johnson, 1989). Dextrality was tested by offering the children items such as a hammer, pencil, and bat (Briggs and Nebes, 1975) and asking them if they always or sometimes used the same hand. A dextrality index was calculated that ranged from -1 for strongly left-handed to 1 for strongly right-handed. Parental SES was calculated from parental occupation and education (Hollingshead, 1975). Informed consent-assent was obtained from the children and their parents.

To conduct assessments of scan-rescan reliability in cortical thickness measures, we also studied three normal young adult subjects who were scanned twice with very short inter-scan intervals (all male; 24-44 years of age). Informed consent was obtained from the young adults.

MRI scan acquisition. All subjects were scanned in a Siemens 1.5 T magnet with a 3D T1-weighted protocol (Siemens AG, Erlangen, Germany). Scan parameters for the 45 children were as follows: repetition time (TR), 10 msec; echo time (TE), 4 msec; flip angle, 10°; matrix, 256 × 256 × 128; image voxel size, 0.98 × 0.98 × 1.25 mm; acquisition time, 6 min. Scan parameters for the young adults were as follows: TR, 1900 msec; TE, 4.38 msec; flip angle, 15°; matrix, 256 × 256 × 160; image voxel size, 1 × 1 × 1 mm; acquisition time, 8 min, 8 sec.

Image processing. The MR images from each individual were analyzed with a series of manual and automated procedures that included the following: (1) transforming brain volumes into a standardized 3D coordinate space (Mazziotta et al., 1995) using a 12 parameter, linear, automated image registration algorithm (Woods et al., 1993); (2) classifying images into gray matter, white matter, and CSF; (3) removing nonbrain tissue (i.e., scalp, orbits) and cerebellum and excluding the left hemisphere from the right; (4) automatically extracting the cortical surface (MacDonald et al., 1994); (5) tracing 35 sulcal and gyral landmarks on the lateral and interhemispheric surfaces of each hemisphere; (6) transforming image volumes back into their own native image acquisition space by mathematically inverting the transformation, which took them into standard space (step 1); (7) spatially registering all segmented images and brain surfaces for each individual by defining 80 standardized, manually defined, anatomical landmarks (40 in each hemisphere; the first and last points on each of 20 of the 35 sulcal lines drawn in each hemisphere) (Sowell et al., 2002, 2003); (8) spatially “time-locking” each individual's brain data acquired at time 2 to the data acquired at time 1 by manually selecting anatomical landmarks in both scans; (9) measuring cortical thickness in millimeters averaged within a 15 mm sphere attached to each cortical surface point; and (10) estimating relative local brain growth measured at each cortical surface point (Sowell et al., 2001b). The following is a more detailed discussion of the image processing procedures.

Semiautomated tissue segmentation was conducted for each volume data set to classify voxels based on signal value as most representative of gray matter, white matter, or CSF. A simple minimum distance classifier was used because it had previously been shown to provide the best results (for this T1-weighted imaging protocol) in a qualitative comparison of different tissue segmentation algorithms. A detailed discussion of the reliability and validity of the tissue segmentation protocol has been published previously (Sowell et al., 1999b).

Each individual's cortical surface was extracted using automated software (MacDonald et al., 1994) that creates a spherical mesh surface that is continuously deformed to fit a cortical surface tissue threshold intensity value (signal value, which best differentiates cortical CSF on the outer surface of the brain from the underlying cortical gray matter) from the brain volume aligned in standard international consortium for brain mapping (ICBM)-305 space (Mazziotta et al., 2001). The resulting cortical surfaces are represented as a high-resolution mesh of 131,072 triangulated elements spanning 65,536 surface points.

Image analysts (S.E.W. and E.K.), who were blind to subject gender or age, traced each of 17 sulci on the lateral brain surface [Sylvian fissure; central, precentral, postcentral, superior temporal sulcus (STS) main body; STS ascending branch; STS posterior branch; primary intermediate sulcus; secondary intermediate sulcus; inferior temporal; superior frontal; inferior frontal; intraparietal; transverse occipital; olfactory; occipito-temporal; and collateral sulci] in each hemisphere on the surface rendering of each subject's brain. An additional set of 12 sulci was outlined on each interhemispheric surface (callosal sulcus, inferior callosal outline, superior rostral sulcus, inferior rostral sulcus, paracentral sulcus, anterior and posterior segments of the cingulate sulcus, outer segment double parallel cingulate sulcus when present, parieto-occipital sulcus, anterior and posterior segments of the calcarine sulcus, and the subparietal sulcus). In addition to contouring the major sulci, a set of six midline landmark curves bordering the longitudinal fissure was outlined in each hemisphere to establish hemispheric gyral limits. Spatially registered gray-scale image volumes in coronal, axial, and sagittal planes were available simultaneously to help disambiguate brain anatomy. We developed detailed criteria for delineating the cortical lines and for starting and stopping points for each sulcus using brain surface atlases as references (Ono et al., 1990; Duvernoy et al., 1991). Raters were required to pass reliability tests where the spatial distance between their sulcal delineations averaged across six subjects was required to be within 3.5 mm of the “gold standard” delineations on the same six subjects. These criteria have been described previously along with reliability measures (Sowell et al., 2002), and complete details of the written anatomical protocol can be obtained from the authors.

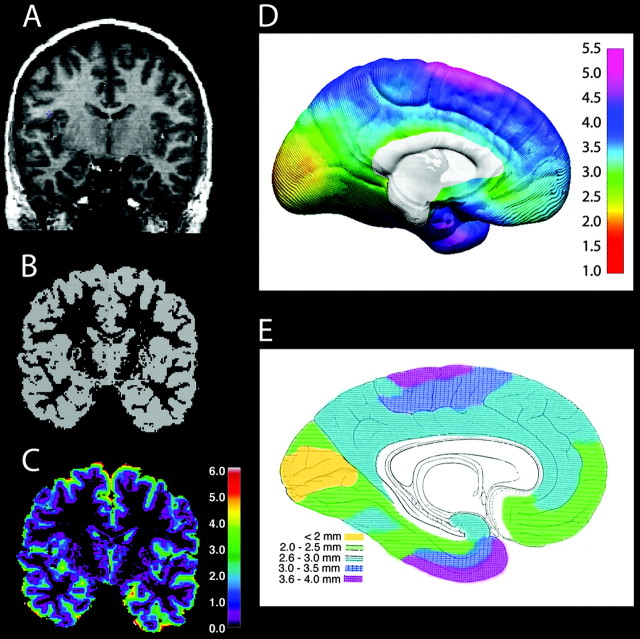
Gray matter thickness was calculated using the Eikonal Fire equation (Sapiro, 2001). Although the brain image volumes acquired for this study had voxel dimensions of 0.98 × 0.98 × 1.25 mm, we supersampled the image data to create voxel dimensions of 0.33 mm cubed. The 3D Eikonal equation was applied only to voxels that segmented as gray matter (Fig. 1), and a smoothing kernel was used to average gray matter thickness within a 15 mm sphere at each cortical surface point. This allowed us to calculate cortical thickness for each subject with a resolution much finer than the original voxel size given that the error associated with localizing anatomy on the inner and outer cortical surfaces is averaged with the unbiased error of all other voxels within the smoothing kernel. To map gray matter thickness onto the surface rendering of each subject, the coordinate for each brain surface point for each individual (anatomically matched across individuals) was mapped to the same anatomical location in their thickness volume (Fig. 1C), and the average gray matter thickness value within the 15 mm sphere was calculated. The average gray matter thickness value within the sphere was then doubled to estimate the maximum thickness at each cortical surface point.

Figure 1.

A-C, Cortical thickness maps: original T1-weighted image for one representative subject (A), tissue segmented image (B), gray matter thickness image where thickness is progressively coded in millimeters from inner to outer layers of cortex using the 3D Eikonal Fire equation (C). Note that the images were resampled to a voxel size of 0.33 mm cubed, so the thickness measures are at a submillimeter level of precision according to the color bar on the right (in millimeters). A-C are sliced at the same level in all three image volumes from the same subject. D is an in vivo average cortical thickness map created from our 45 subjects at their first scan. The brain surface is color coded according to the color bar where thickness is shown in millimeters. E, Our average thickness map can be compared with an adapted version of the 1929 cortical thickness map of Von Economo (1929). Color coding has been applied over Von Economo's original stippling pattern, respecting the boundaries of the original work, to highlight the similarities between the two maps.

Points on the cortical surfaces surrounding and between the sulcal contours drawn on each individual's brain surface were calculated using the averaged sulcal contours as anchors to drive 3D cortical surface mesh models from each subject into correspondence (Thompson et al., 2000a). This allows the creation of average surface models and the creation of maps of age effects on gray matter thickness. Given that the deformation maps (acquired during cortical surface matching) are associated with the same cortical anatomy in each subject, the local measurement of gray matter thickness (at each point over the surface of the brain) for each subject could be averaged across corresponding regions of cortex for all subjects studied (Sowell et al., 2001b; Thompson et al., 2001b). The average cortical thickness value on the medial brain surface for all 45 subjects (at time 1) is shown in Figure 1 D. We also adapted the postmortem cortical thickness map created by Von Economo (1929) by color coding it respecting his original boundaries (Fig. 1 E) to compare the average cortical thickness measures obtained with our in vivo methods. As shown, the regional correspondence between the cortical thickness maps created for children in vivo and for the postmortem data are striking. In both maps, the thickest cortex appears on the dorsal medial frontal cortex and medial temporal lobe, whereas the thinnest cortex is in the occipital lobe.

The method of measuring cortical thickness used here is based on computing the distance of the gray matter-CSF interface to the gray matter-white matter interface by building a distance field using the Eikonal Fire equation (Sapiro, 2001). Although various other approaches have been used (Fischl and Dale, 2000; Jones et al., 2000; Miller et al., 2000; Kabani et al., 2001), our approach seemed a natural and intuitive measure given that it defines thickness on the inner surface as the distance from the inner surface to the closest point on the outer surface. Given that laminar structure is not visible with MRI, we could not rely on laminar structure to define thickness, as we have done using other automated approaches in histological data (Annese et al., 2004). The agreement between the calculated thickness map and the data from Von Economo (Fig. 1) further attests to the validity of the approach.

To estimate the error in the cortical thickness measure that might simply be associated with repeated scanning, we analyzed longitudinal scans on three healthy young adults at very short intervals (∼5 min). Two subjects received two scans each, and one subject underwent short interval rescanning on three occasions ∼3 weeks apart. This individual's short-interval repeat scans were treated as three separate individuals in our error assessment analyses. Each image data set was skull stripped, tissue segmented, and inhomogeneity corrected using automated software (Shattuck et al., 2001). Surface renderings were created for each image data set (MacDonald et al., 1994) (10 image data sets, 2 for each subject), and cortical surface landmarks on the lateral brain surface identical to those described above were defined. The average absolute error in measuring cortical thickness for the individuals in the group of five subjects ranged from 0 to 1.4 mm (Fig. 2 A). We then computed the error estimate for the group average thickness maps in the larger data set (n = 45) by dividing the average absolute individual error (Fig. 2 A) by the square root of 45 minus 1 (Fig. 2 B). As shown in Figure 2 B, estimation of individual rescan reliability for cortical thickness, combined over many subjects, reveals a maximum error in the group average cortical thickness of 0.15 mm with errors being much less in most areas. Even this maximum error in the group mean cortical thickness maps, at either time point, is considerably lower than the -0.6 to 0.3 mm of maturational change that we observed over a 2 year scan interval in the 45 children studied here (Fig. 2C).

Figure 2.

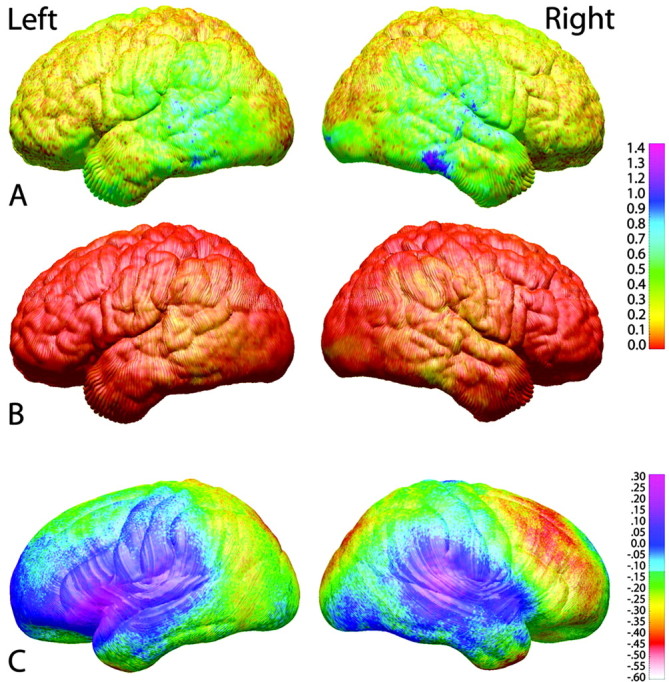
Error estimation maps. A, In the top row, a map of the average absolute value of the cortical thickness difference between short-interval scans for the five subjects is shown. The average error estimate for these subjects ranges from 0 to 1.4 mm. B, To estimate the error for each individual in the larger group of 45 subjects, we divided the average error maps by the square root of 45 minus 1. Thus, the estimated error for each of the 45 subjects ranges from 0 to ∼0.15 mm, which is considerably less than the maturational difference observed in these 45 children over a 2 year interval (C), which ranges regionally from -0.6 to 0.3 mm.

Brain growth was assessed using the “distance from the center” (DFC) measure (Sowell et al., 2001b). DFC is a measure of radial expansion calculated in millimeters from the center of the brain, approximately, at the midline decussation of the anterior commissure (i.e., x = 0, y = 0, z = 0 in Talairach coordinates) (Talairach and Tournoux, 1988) to each of the 65,536 brain surface points. We also adapted the DFC-hemisphere (DFC-H) measure to assess growth on the interhemispheric surface of the brain, where the distance from the center of the hemisphere to the surface was calculated. The coordinate from which DFC-H was measured was calculated as the center of mass of the average hemisphere of all 45 subjects at time 1 (calculated separately for the left and right hemispheres), and the same coordinate was used for the time 2 scans. The DFC-H measure was deemed more appropriate for assessing growth in midline cortical structures given that with DFC, the starting point of each measure lay on the midline (at the anterior commissure), making it difficult to assess the direction of growth along the interhemispheric surface. Thus, for the medial surface permutation and statistical maps, we used DFC-H, whereas for the lateral regions, we used the DFC measure. It should be noted that these analyses do not specify actual increases in gray or white matter alone but simply reflect radial expansion of the exterior cortical surface that is presumably caused by changes in the underlying gray and white matter.

Statistical analyses. To assess the significance of gray matter thickness change and brain growth, one-sample t tests were conducted at each brain surface point to determine whether the difference in gray matter thickness or DFC-DFC-H between time 1 and time 2 significantly differed from zero (which would be the prediction if no change in cortical thickness or brain growth had occurred). Permutation testing was conducted to correct for multiple comparisons (given that one-sample t tests were conducted at each of ∼65,000 brain surface points in each hemisphere). In these analyses, the sign of the time 1 to time 2 difference (positive or negative) for each subject was assigned randomly in each permutation, and the significance test was conducted again for the mean change (in gray matter thickness or brain size) at each cortical point with signs randomly flipped. Randomization of the sign of the computed change in each subject was conducted 10,000 times and the number of significant surface points in each random test was compared with the number of significant surface points in the real test. In other words, the threshold for assessing significance of statistical maps based on the permutation tests was determined objectively by calculating the surface area (number of surface points) of significant effects in the real one-sample t test. That surface area was used as the threshold for comparison with the random tests, and if fewer than 5% (i.e., p < 0.05) of the results from random tests reached or exceeded the surface area of the real test, the statistical map was considered significant.

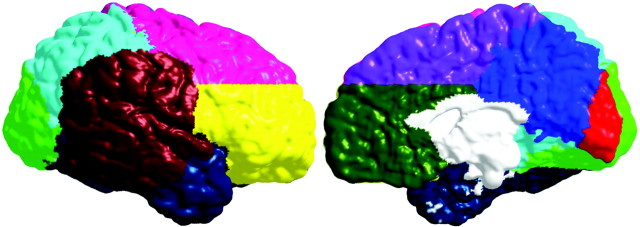
To test our regional hypotheses, anatomical regions of interest (ROIs) were used in the permutation analyses. Coarse ROIs were created for each individual from a probabilistic atlas (Evans et al., 1994) for the frontal lobe (ventral and dorsal regions separated by an axial plane passing through the intersection of the posterior extent of the inferior frontal sulcus and the precentral sulcus in each hemisphere), parietal lobe, temporal lobe, and occipital lobe. In addition to the lobar ROIs, we created a perisylvian ROI based on statistical maps from our previous study of cortical change across the human life span (Sowell et al., 2003). Essentially, this perisylvian ROI corresponded to the only brain regions where gray matter density continued to increase until ∼30 years of age in a different sample from those studied here (Sowell et al., 2003). In this region specifically, we predicted gray matter thickness increases. The ROIs for each individual were averaged to create regional masks (Fig. 3), thereby reducing the search area to specific brain regions in the permutation analyses.

Figure 3.

Regions of interest used in the permutation analyses. Lateral regions are color coded as follows: ventral frontal, yellow; dorsal frontal, pink; temporal, dark blue; occipital, green; parietal, light blue; perisylvian, brick red [created from a statistical map published previously (Sowell et al., 2003)]. Medial regions are color coded as follows: dorsal frontal, purple; ventral frontal, olive green; parietal, dark blue; occipital, red; callosal brainstem area (not tested in permutations), white.

Correlations between change in the children's raw scores on the vocabulary subtest of the WISC-R (Wechsler, 1991) and change in gray matter thickness were conducted to assess for brain-behavior relationships. Vocabulary was chosen because it is a valid measure of cognitive growth and could reasonably be expected to be associated with neural changes, particularly in the left hemisphere. Permutation analyses within the same ROIs used in the gray matter thickness and brain size analyses were used to correct for multiple comparisons in the brain-behavior analyses. Similar analyses were conducted to assess correlations in the block design subtest, which was expected to be associated with right hemisphere change. These measures were chosen because they were thought most likely to dissociate gross verbal from gross spatial cognitive abilities, which might show hemispheric differences (i.e., we predicted left hemisphere correlations for vocabulary and right hemisphere correlations for block design) in the brain-behavior analyses.

Results

Gray matter thickness

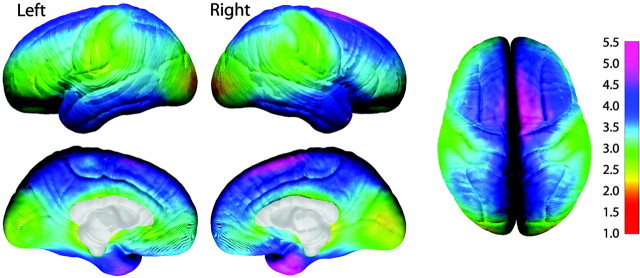
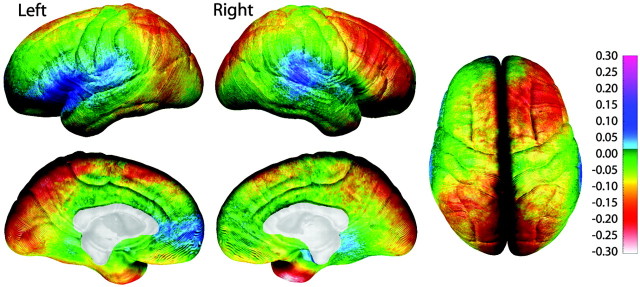
Average cortical thickness in children 5-9 years of age ranges from 1.5 to 5.5 mm (Fig. 4) over the lateral and medial brain surfaces. Longitudinal assessment of change in gray matter thickness reveals cortical thinning over large areas of right dorsolateral frontal, bilateral occipitoparietal, and anterior and posterior-inferior temporal cortices where rates of loss are on the order of 0.1-0.3 mm per year (Fig. 5). One-sample t test maps indicate that the cortical thinning as seen in Figure 5 is statistically significant in most areas (Fig. 6). Note that gray matter thickening is restricted to left anterior and posterior perisylvian regions that correspond remarkably well with traditional concepts of Broca's and Wernicke's areas. The right hemisphere homolog of Wernicke's area, but not Broca's area, also shows thickening. In these regions, children gain ∼0.05-0.2 mm of gray matter per year (Fig. 5), and these increases are also statistically significant (Fig. 6).

Figure 4.

Average cortical thickness. Shown here are left and right, medial and lateral, and top views of average cortical thickness maps for all 45 subjects at time 1. Cortical thickness is shown in color representing millimeters according to the color bar.

Figure 5.

Annualized rate of change in cortical thickness. Shown in this figure is the average rate of change in cortical thickness in millimeters according to the color bar on the right. Maximum gray matter loss is shown in shades of red, and maximum gray matter gain is shown in shades of blue.

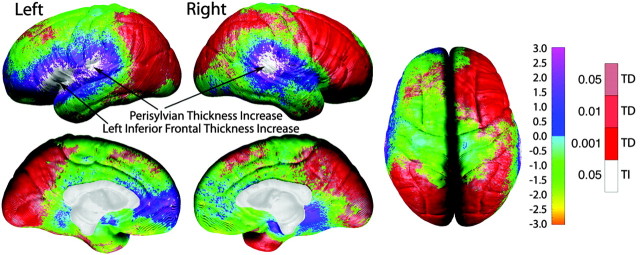
Figure 6.

One-sample t test map for gray matter thickness. These brain maps show the statistical significance of annualized change in cortical thickness measures. Color coding represents t values at each cortical surface point according to the left color bar (ranging from t = -3.0 to t = 3.0), and significant values are overlaid in shades of red [significant thickness decreases (TD)] and white [significant thickness increases (TI)] according to the color bar on the right. Arrows point to the three regions of significant gray matter thickness increases, representative of the only three regions to withstand permutation correction for multiple comparisons for thickness increase shown in Table 1.

ROI permutation results shown in Table 1 confirm the significance of changes in cortical thickness. Based on the percentage of significant surface points within the ROI (relative to the total ROI surface area), gray matter thinning is most prominent in bilateral occipital (mesial and lateral) and right lateral frontal regions, which is consistent with the appearance of the gray matter statistical maps shown in Figure 6. As predicted, based on results from previous cross-sectional studies (Sowell et al., 2001b, 2003), the left and right perisylvian regions show significant increases in gray matter thickness, and thickness increases in the left inferior frontal region are also confirmed with permutation.

Table 1.

Permutation results for gray matter thickness

	Gray matter thickness change
	Thickness increase			Thickness decrease
Region	Left	Right	Left	Right
Medial dorsal frontal	1.00	1.00	0.034 (20.6%)	0.003 (34.0%)
Medial ventral frontal	0.424	1.00	0.185	0.298
Medial occipital	1.00	1.00	0.0001 (100.0%)	0.001 (82.1%)
Medial parietal	1.00	1.00	0.005 (47.6%)	0.0002 (66.9%)
Lateral dorsal frontal	1.00	1.00	0.033 (18.3%)	0.0001 (80.5%)
Lateral ventral frontal	0.017 (18.2%)	1.00	0.225	0.0001 (77.8%)
Lateral occipital	1.00	0.818	0.0001 (80.8%)	0.0001 (66.3%)
Lateral parietal	1.00	0.638	0.001 (57.7%)	0.0001 (65.6%)
Lateral temporal	0.108	1.00	0.015 (29.6%)	0.001 (32.7%)
Perisylvian	0.012 (21.6%)	0.035 (13.7%)	0.022 (17.5%)	0.085

Positive (thickness increase) and negative (thickness decrease) results are shown separately for each ROI. The numbers presented are p values and, where significant, in parentheses are the number of surface points (i.e., surface area) within each ROI that were significant at a threshold of p = 0.05 relative to the total number of points within each ROI. Each p value represents a ratio of the number of random tests that matched or exceeded the number of significant surface points (p = 0.05) in the real test to the total number of randomizations run (i.e., 10,000).

Brain growth

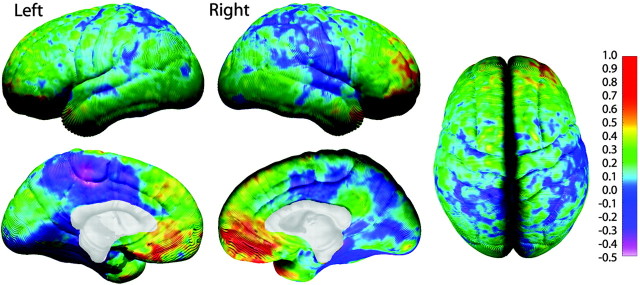
Maps of the average yearly rate of growth (Fig. 7) reveal that the brain expands at rates of up to 1 mm per year predominantly in the prefrontal cortex on both the lateral and interhemispheric surfaces. One-sample t tests were conducted at each brain surface point to determine whether the difference in DFC-H between time 1 and time 2 significantly differed from zero. The statistical maps (Fig. 8) indicate that brain growth in the frontal, anterior temporal, and occipital regions bilaterally is significant at a probability threshold of p < 0.05.

Figure 7.

Annualized rate of change in DFC (lateral surface) and DFC-H (medial surface). Brain maps showing the annualized rate of change in DFC in millimeters according to the color bar. Corpus callosum and brainstem regions have been masked out of the midline views. Note the most prominent growth shown in red where brain size increases on average 0.5-1.0 mm per year.

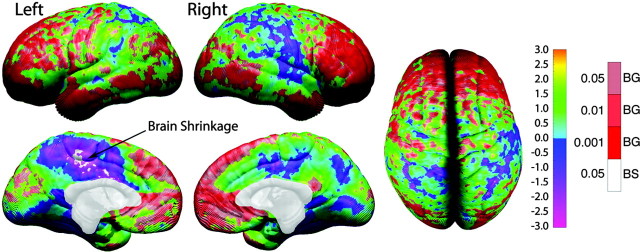
Figure 8.

One-sample t test map for radial expansion (or shrinkage). These brain maps show the statistical significance of annualized brain growth measures. Note that the color coding is inverse of that shown in Figure 6. As in both figures, we wanted to highlight the most prominent changes in red (gray matter loss for thickness but brain growth for DFC-H). Color coding represents t values at each cortical surface point according to the left color bar (ranging from t = -3.0 to t = 3.0), and significant values overlaid in shades of red [significant brain growth (BG)] and white [significant brain shrinkage (BS); according to the color bar on the right].

As shown in Table 2, permutation testing reveals that brain growth is significant in all regions except the right perisylvian, the left and right medial parietal, and the right medial occipital regions. The regions with the largest percentage of significant surface points for brain growth relative to the surface area of their ROI were the left and right lateral ventral frontal regions (67 and 77%, respectively) followed by the left and right medial ventral frontal regions (47 and 60%, respectively). Significant brain shrinkage did not occur in any of the ROIs assessed.

Table 2.

Permutation results for brain expansion and shrinkage indexed by DFC-H

Brain size change
	Growth
Region	Left	Right
Medial dorsal frontal	0.010 (23.7%)	0.023 (23.3%)
Medial ventral frontal	0.001 (47.4%)	0.0004 (59.5%)
Medial occipital	0.001 (37.5%)	0.166
Medial parietal	0.173	0.096
Lateral dorsal frontal	0.0001 (51.6%)	0.0001 (44.8%)
Lateral ventral frontal	0.0001 (67.1%)	0.0001 (77.4%)
Lateral occipital	0.0001 (43.0%)	0.0002 (36.4%)
Lateral parietal	0.009 (15.7%)	0.019 (13.8%)
Lateral temporal	0.026 (16.5%)	0.006 (22.0%)
Perisylvian	0.0002 (38.6%)	0.103

Note that in no case were the ROI permutation analyses significant for brain shrinkage between scans, and thus the negative results are not presented in the table. The numbers presented are p values and percentages exactly as described for Table 1.

Brain-behavior relationships

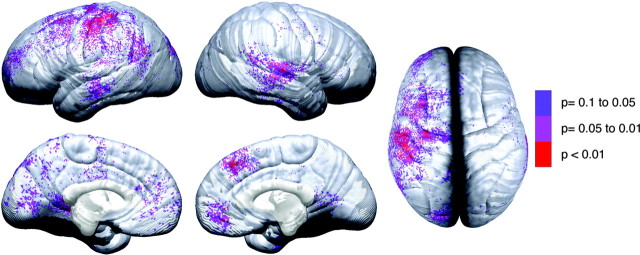
Forty-two of the children studied completed the vocabulary subtest of the Wechsler Intelligence Scale for Children, Revised (Wechsler, 1991), and 41 of the children completed the block design subtest at both scanning sessions. Results for correlations between change in vocabulary raw scores and change in gray matter thickness are shown in Figure 9. Striking hemispheric asymmetry was notable with negative correlations observed primarily in the left hemisphere. As predicted, greater gray matter thinning was associated with improved performance on the vocabulary subtest. Permutation analyses confirmed the significance of relationships between gray matter thinning and improved vocabulary scores only in the left lateral dorsal frontal (p = 0.045) and the left lateral parietal (p = 0.030) regions. Results for the block design subtest did not support our hypothesis that improvement would be correlated with right hemisphere changes. Only the left medial occipital region was significant in the ROI permutation analyses (p = 0.049) with gray matter thickening associated with improvement on the test.

Figure 9.

Brain-behavior maps for vocabulary and cortical thickness. These maps show the p value for negative correlations between change in cortical thickness (time 2 minus time 1) and change in vocabulary raw scores (time 2 minus time 1). Negative p values (i.e., regions where greater thinning was associated with greater vocabulary improvement) are represented in color according to the color bar, and regions in white were not significant. Positive correlations were not significant in the permutation analyses for any of the ROIs and are not shown here.

Discussion

Results from this study show regionally specific brain growth and cortical gray matter thickness changes within individuals studied between 5 and 11 years of age, within the relatively short time span of 2 years. Statistical maps of local brain size changes revealed the most prominent growth occurring in prefrontal cortex, as well as in temporal and occipital regions bilaterally. Gray matter thickness increases were restricted to the classical language regions of the frontal (i.e., Broca's area) and temporo-parietal cortex (Wernicke's area in the left), and more widespread thinning was observed in the right frontal and bilateral parietal and occipital association cortices. In addition, cortical thinning in the left dorsal frontal and parietal lobes is correlated with improved performance on a test of general verbal intellectual functioning.

Earlier cross-sectional studies of normative brain maturation during childhood and adolescence have led researchers to conclude that gray matter loss occurs as part of the ultimate sculpting of the brain into the fully functioning adult nervous system (Jernigan et al., 1991; Pfefferbaum et al., 1994; Reiss et al., 1996; Sowell et al., 1999b, 2001b, 2003; Courchesne et al., 2000). One longitudinal report of brain maturation has shown developmental changes in gray and white matter during childhood, but regional assessments were only made at the gross lobar level in that report (Giedd et al., 1999). Another study conducted by our group assessed changes in cortical gray matter density in 13 adolescents studied as controls for a group with schizophrenia, but the sample was relatively small, and brain size (i.e., DFC), cortical thickness, and behavioral correlates were not assessed (Thompson et al., 2001a; Gogtay et al., 2004). In the present report, we have estimated longitudinal changes in cortical thickness in millimeters during childhood, which has to our knowledge never before been accomplished in cross-sectional or serial studies in children. The striking correspondence between our cortical thickness maps and those of postmortem studies conducted nearly 90 years ago (Von Economo, 1929) strengthens our confidence in the validity of the cortical thickness estimation used here and lend confidence to the interpretation that there is regional variation in gray matter thinning and thickening during childhood.

It is interesting to note that gray matter thinning occurs at the same time and in the same locations as brain growth (i.e., frontal and parieto-occipital regions). We observed a similar relationship between growth and gray matter loss in an earlier cross-sectional sample where we used density rather than thickness to measure cortical change (Sowell et al., 2001b). In that report, we speculated that cortical gray matter density reduction could be attributable to, in part, increased proliferation of myelin into the periphery of the cortical neuropil, which would change the MR signal value from gray matter in the younger subjects to white matter in the older subjects. The same conclusions can be drawn here, essentially, that apparent cortical thinning during childhood is probably not entirely caused by a reduction in the size or number of neuron cell bodies or their synaptic processes (as might be the case in normal aging) (for a discussion, see Sowell et al., 2003) but rather by an increase in the myelin coating of fibers in the lower cortical layers. It may seem inappropriate to use the term gray matter thinning to describe myelin proliferation into the cortical neuropil. Our data and data from others using volumetric methods suggest that gray matter is replaced by white given that white matter volumes increase and gray matter volumes decline (Jernigan et al., 1991; Giedd et al., 1999; Courchesne et al., 2000). Even in histological data, the boundary between gray and white matter is not “black and white” (Annese et al., 2004). Of course, MRI cannot be used to measure cell packing, myelin per se, or synaptic density, but our maps of cortical thickness in millimeters in children scanned longitudinally further support the notion that the last vestiges of local brain growth and apparent concomitant cortical thinning during childhood primarily result from increases in myelination.

These results confirm localized thickness increases in frontal and temporal perisylvian gray matter during childhood. Our confidence in these remarkable results is strengthened by several factors. First, we predicted this effect in advance given findings from two previous cross-sectional reports (Sowell et al., 2002, 2003) and ensured correct localization of the predicted effect by creating a region of interest from a statistical map of the perisylvian region, which had shown changes in an independent sample. Second, of the 20 ROIs studied for gray matter thickness change (10 per hemisphere), only three showed a significant thickness increase within individuals between the first and second scan: left and right perisylvian regions (as predicted), and the right ventral, lateral frontal region. Notably, both anterior and posterior primary language regions in the left hemisphere, as well as the right perisylvian region show the same pattern of change, and the pattern of change in these regions is distinct from other brain regions where gray matter appears to thin. Given that language functioning has been so well localized to the perisylvian (i.e., Wernicke's area) and inferior frontal cortices (i.e., Broca's area), the cortical thickening in these regions observed here lead to speculation that there is a relationship to the fine tuning and mastery of linguistic skills that occur during the age range studied.

Relationships between gray matter thinning and change scores on two different cognitive measures supported only one of our two hypotheses; left hemisphere cortical thinning was associated with increases in vocabulary. In a previous cross-sectional study, we found negative correlations between gray matter volume in the frontal lobes bilaterally and the children's performance on a measure of verbal learning (Sowell et al., 2001a), partially consistent with the present results. Notably, we did not see positive correlations between the verbal measure and cortical change in primary language regions where gray matter changes were in the opposite direction. Performance on the vocabulary subtest may reflect more general verbal intellectual abilities, which might be expected to correlate with more diffuse left hemisphere maturation. Our predictions regarding right hemisphere correlations with the visuospatial measure were not confirmed. However, the verbal and visuospatial measures did show distinct brain-behavior patterns, suggesting that the correlations observed between cortical thickness changes and the verbal measure were not carried by more global intellectual capabilities. Although we predicted a double dissociation between left hemisphere cortical thickness and vocabulary scores on the one hand, and right hemisphere cortical thickness and performance on the block design test on the other, these predictions were not fully supported. Thus, results from the brain-behavior analyses should be interpreted with caution. Additional functional studies with cognitive tests designed to test the function of specific areas will be needed to explore changing brain behavior relationships during childhood.

In his postmortem work on the postnatal development of the human cerebral cortex, Conel (1967) noted that cortical thickness decreased between 4 and 6 years of age in 23 of 37 regions measured. Cortical thickness increased in several areas as well, although the pattern of thickness increases and decreases is difficult to compare with the cortical thickness maps created here, given that Conel did not precisely localize where along any particular sulcus or gyrus his measurements were taken. Cortical thickness measurements in Conel's 6-year-old subject ranged from 2.0 to 3.3 millimeters, whereas our average measurements ranged from 1.5 to 5.5 millimeters. Part of this discrepancy probably lies in the fact that brain shrinkage occurs postmortem during fixation (Quester and Schroder, 1997).

One research group (Fischl and Dale, 2000) has reported cortical thickness measured in vivo in normal young adults ranging between 1 and 4.5 mm. It should be noted that both ours and other research group's (Fischl and Dale, 2000) automated cortical thickness measurement algorithms depend on other algorithms used to segment gray matter, white matter, and CSF within the MR images. Different tissue segmentation algorithms use different methods for handling partial volume effects and could result in generalized over or under representation of gray matter and white matter. Our study of the reliability of cortical thickness measures in a small sample of young adults scanned at very brief intervals resulted in thickness error estimates of 0-0.15 mm, which is considerably less than the thickness change measures reported in this sample of children scanned at 2 year intervals. However, it should be noted that other factors potentially affecting cortical thickness change measures (i.e., subject placement in the scanner, temperature) can occur at somewhat longer intervals (i.e., days rather than minutes) and were not assessed in this report.

Our cortical thickness estimates were somewhat higher than those reported previously in young adults between 20 and 37 years of age (Fischl and Dale, 2000). To assess the extent to which error in tissue segmentation (i.e., overinclusion of CSF in the gray matter compartment) may have contributed to the differences in results between the two studies, we measured cortical thickness in 66 young adults between 20 and 37 years of age (E. R. Sowell, P. M. Thompson, A. W. Toga, and B. S. Peterson, unpublished data) using the same tissue segmentation algorithms as those for the children. Notably, cortical thickness in the young adults was considerably thinner than in the children and ranged from 1 to 4.5 mm, the same thickness range reported by Fischl and Dale (2000). Thus, it is likely that our in vivo thickness measures are greater than those reported by the other research group (Fischl and Dale, 2000) because of the immature state of the cortex in the children we studied.

Here, with the longitudinal samples, we actually measured gray matter thinning and brain growth within individuals studied at 2 year intervals. Additional longitudinal studies extending the age range into adolescence may be helpful in further addressing the spatial and temporal sequence of these maturational changes.

Even more exciting is the prospect of applying these techniques to the longitudinal study of learning disabled and psychiatric samples to investigate spatial and temporal alterations in the developmental changes reported here. The establishment of a normal baseline against which abnormal development can be assessed may be one of the most important contributions of this report.