Role of Spike Timing in the Forelimb Somatosensory Cortex of the Rat

Abstract

The aim of this study was to test the hypothesis that the significance of spike timing in somatosensory processing is not a specific feature of the whisker cortex but a more general characteristic of the primary somatosensory cortex. We recorded ensembles of neurons using microwire arrays implanted in the deep layers of the forelimb region of the rat primary somatosensory cortex in response to step stimuli delivered to the cutaneous surface of the contralateral body. We used a recently developed peristimulus time histogram (PSTH)-based classification method to investigate the temporal precision of the code by evaluating how changing the bin size (from 40 to 1 msec) would affect the ability of the ensemble responses to discriminate stimulus location on a single-trial basis. The information related to the discrimination was redundantly distributed within the ensembles, and the ability to discriminate stimulus location increased when decreasing the bin size, reaching a maximum at 4 msec. In our experiment, at 4 msec bin size the first spike per neuron after the stimulus conveyed almost as much information as the entire responses, so the temporal precision of the code was preserved in the first spikes. Subsequent spikes were less frequent but conveyed more information per spike. Finally, not only the trials correctly classified but also the trials incorrectly classified conveyed information about stimulus location with a similar temporal precision. We conclude that the role of spike timing in cortical somatosensory processing is not an exclusive feature of the highly specialized rat trigeminal system, but a more general property of the rat primary somatosensory cortex.

Introduction

The timing of single spikes can constitute a powerful mechanism to construct neural codes for sensory information (Bialek et al., 1991; Hopfield, 1995; deCharms and Merzenich, 1996; de Ruyter van Steveninck et al., 1997; Borst and Theunissen, 1999; Ahissar et al., 2000; Petersen et al., 2002; DeWeese et al., 2003; Ariav et al., 2003). In somatosensory processing, the role of spike timing has been studied in the barrel field cortex of the rat by using two different approaches. Ghazanfar et al. (2000) found that an artificial neural network can discriminate stimulus location from the activity of ensembles of neurons, reaching maximal performance at bin sizes between 3 and 6 msec. Panzeri et al. (2001) arrived to a similar conclusion regarding the temporal precision of the somatosensory code using a rigorous approach based on information theory applied to single neurons. These studies suggested that the timing of neuronal spikes plays an important role in the coding of stimulus location in the whisker area of the primary somatosensory cortex.

It is not clear, however, whether in the rat the importance of spike timing is a specific feature of the highly specialized whisker cortex or a more general characteristic of cortical somatosensory processing. The forelimb region of the rat somatosensory cortex is a natural target to address this issue. In fact, the rat forepaw is more similar to the human hand than the whiskers, and rats are capable of performing fine discrimination with their paws and digits (Whishaw and Pellis, 1990; Whishaw and Gorny, 1994). Importantly, the forelimb area, rather than the whiskers, is necessarily chosen in rat models studying the effects of peripheral limb amputations or spinal lesions on cortical somatosensory reorganization (Kaas et al., 1983; Kaas and Collins, 2003; Moxon and Foffani, 2003). However, the temporal precision of the neural code in the forelimb somatosensory cortex of the rat is unknown.

To address this problem, we recorded ensembles of neurons using arrays of microwires implanted into the deep layers of the rat primary forelimb cortex (five animals, 10 ensembles) in response to step stimuli delivered to the cutaneous surface of the contralateral body (10 locations on the forelimb). We used a recently developed peristimulus time histogram (PSTH)-based classification method (Foffani and Moxon, 2004) to investigate the temporal precision of the neural code by evaluating how changing the bin sizes affected the ability of the ensemble responses to discriminate stimulus location on a single-trial basis. We also compared the importance of the first spikes of the neurons to that of subsequent spikes after the stimulus for the discrimination, and we performed an error analysis to assess whether trials that were not correctly classified still carried information about stimulus location.

Materials and Methods

Experimental protocol

Surgical procedures and neuron discrimination. The surgical procedures used here have been previously described in detail (Foffani and Moxon, 2004), although here we targeted the forelimb somatosensory cortex rather than the whisker cortex. Briefly, arrays of 16 channel microwire electrodes (NB Labs, Dennison, TX) were chronically implanted with stereotaxic techniques into the forepaw region of the forelimb primary sensorimotor cortex (layer V-VI) (Fig. 1) of each hemisphere in five rats (coordinates 0.5 mm anterior to bregma and 3.5 and 4.5 mm lateral to -1.5 posterior to bregma and 3.0 and 4.0 mm lateral, atlas of Paxinos and Watson). Analog signals were filtered and amplified using Multi-Neuron Acquisition Processor (MNAP) (Plexon, Inc. Dallas, TX), and single neurons were discriminated on each electrode using commercial software Nex (Plexon, Inc.). All procedures were approved by the Institutional Animal Care and Use Committee at Drexel University and followed National Institutes of Health guidelines.

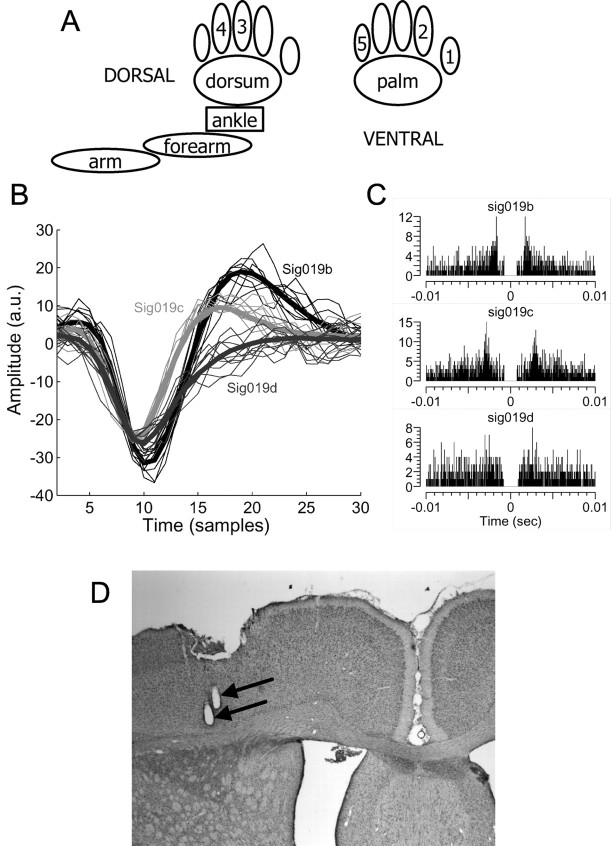
Figure 1.

Experimental procedures. A, Drawing of stimulus locations. One hundred punctuate step stimuli were delivered to each of 10 locations on both sides of the body. Namely, digit 3, digit 4, dorsal paw (dorsum), ankle, forearm, and arm were stimulated dorsally, where as digit 1, digit 2, digit 5, and ventral paw (palm) were stimulated ventrally. B, C, Example of spike sorting from an electrode (electrode 19) where three neurons (b, c, d) were discriminated. Note that electrode 19 indicates the third electrode of the 16 channel array implanted in the right cortex in a bilateral implant on one animal; electrodes 1-16 indicate the array implanted in the left cortex. B, The three cells had distinguishable spike waveforms. Thick lines represent the average wave forms (sig019b, 949 spikes; sig019c, 1980 spikes; sig019d, 1073 spikes). Thin lines are representative waveforms of single spikes (10 waveforms per neuron). C, The autocorrelograms show the expected refractory period and different patterns for the three cells. For details about the relationship between the refractory period and the autocorrelogram, see Bar-Gad et al. (2001). D, Histological confirmation of electrode placement. The photomicrograph shows an example of postmortem brain slice Nissl stained after a stimulating current had been placed down the electrodes at the end of the experiments. The black arrows indicate the location of two electrode tips in the deep layers (V-VI) of the forepaw somatosensory cortex.

Passive cutaneous stimulation (sensory maps). The animals were lightly anesthetized with Nembutal (35 mg/kg), and 10 locations on each forelimb (five digits, dorsum, palm, ankle, forearm, arm) (Fig. 1) were stimulated using a fine-tipped metal probe that moved 0.5 mm (controlled through a piezoelectric element actuated by a Grass stimulator) and simultaneously sent pulses to the MNAP to record the precise time of stimulation. Every location was stimulated 100 times with step stimuli (100-msec-long at 0.5 Hz frequency). The spike times for all discriminated neurons were recorded during the experiment along with time stamps of the onset of the stimuli. Signals were stored in Nex (Plexon), and the single-trial bin counts (i.e., single-trial rate histograms, 1 msec bin size) of all the neurons were exported to Matlab (version 6.5; The Mathworks, Natick MA) for further analysis.

Histology. To examine the position of the electrodes, postmortem brain slices were Nissl-stained to mark cell bodies. After the final recording session, rats were anesthetized, and a stimulating current was placed down the electrodes to mark the electrode tips (60 μA for 45 sec). Each rat was transcardially perfused with 0.1 m phosphate buffer then 4% paraformaldehyde in 0.1 m phosphate buffer. The brain was removed from the skull, and electrodes were extracted from the brain. The brain was stored in 4% paraformaldehyde in 0.1 m phosphate buffer overnight then transferred to a 30% sucrose solution. After 5 d, the brain was removed from solution, embedded in Tek solution, and frozen. The brains were cut into 40-μm-thick coronal sections using a cryostat and collected on slides. The tips of the electrodes were easily visualized because of the hole created by the microstimulation. Most electrodes were in layer V with some reaching layer VI (Fig. 1 D).

Data analysis

PSTH-based classification using ensembles of neurons. The responses of the ensembles of neurons to the cutaneous stimuli were used to discriminate stimulus location on a single-trial basis. For this purpose, we used a PSTH-based classification method previously described and validated (Foffani and Moxon, 2004). In brief, the method consists of creating a set of templates based on the average neural responses to the stimuli delivered to the different locations (i.e., the PSTHs) and classifying each single-trial by assigning it to the location with the “closest” template in the Euclidean distance sense. Figure 2 provides a visual interpretation of the method. For each animal, neurons recorded on the same side of the brain were considered as an ensemble, and single-trial responses to the 10 contralateral locations stimulated were included in the classification. All the analyses were performed in complete cross-validation by excluding from the templates only the trial to be classified and repeating the procedure for every trial. Complete cross-validation is particularly efficient using the PSTH-based classification method (for details, see Foffani and Moxon, 2004). For each ensemble, classification performance was evaluated by using two measures: (1) the total percentage of trials correctly classified and (2) the bits of mutual information between predicted and actual stimuli, computed from the confusion matrix of the classification (Gochin et al., 1994; Rolls et al., 1997, 1998; Panzeri et al., 1999; Laubach et al., 2000; Gruner, 2002; Franco et al., 2004). Perfect classification would lead to 100% of trials correctly classified and 3.32 bits (i.e., log₂10) of mutual information. The upward bias of the mutual information caused by finite sampling was experimentally minimized by using 10 times as many trials per location (100) as the number of locations (10). Note that the data processing inequality implies that the mutual information between predicted and actual stimuli is a lower bound for the mutual information between the neural responses and the actual stimuli (Schneidman et al., 2003).

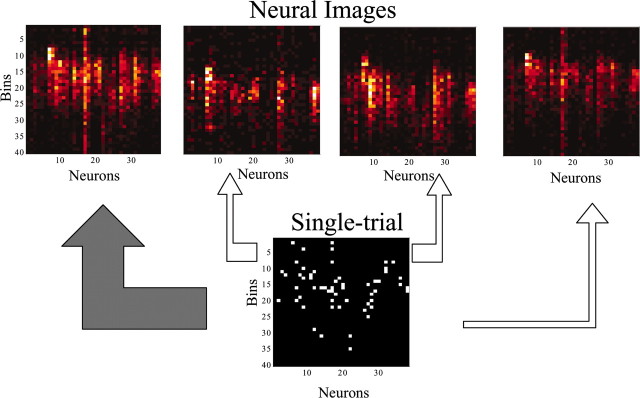
Figure 2.

Visual interpretation of the PSTH-based classification method. The “neural images” (top) represent the average responses (i.e., the PSTHs) of 38 forepaw cortical neurons to four different locations. Each column in a neural image corresponds to the PSTH of one neuron in a 40-msec-long poststimulus time window from +5 to +44 msec after stimulus onset. The window is divided into 40 bins of 1 msec. Colors are light-graded from minimal response (black) to maximal response (white). In the classification, a single trial in the testing set (bottom) is “aligned” over all the neural images (as indicated by the arrows) and assigned to the “closest” neural image in the sense of a minimum pixel-by-pixel mean squared error. In the example, the squared error between the single trial and the neural images is, from left to right, 7.11, 7.41, 7.37, and 7.23. The single trial is therefore classified to the top left neural image, as indicated by the gray arrow.

Role of spike timing. To investigate the role of spike timing and to study the temporal precision of the neural code, (1) a 40 msec poststimulus response window (+5 to +44 msec) was selected, (2) this response window was divided into bins, and (3) the classification was repeated with seven different bin sizes: 1, 2, 4, 5, 10, 20, and 40 msec. A one-way repeated measure ANOVA was performed to evaluate how changing the bin size would affect classification performance. Each ensemble of neurons was considered as a different sample (n = 10). The main factor of the ANOVA was the bin size, with seven levels (1, 2, 4, 5, 10, 20, and 40 msec). Tukey's honest significant difference test was used for post hoc comparisons. The ANOVA was separately performed using the two measures of classification performance introduced above.

First spikes and subsequent spikes. Classification performances were obtained by applying the PSTH-based classification method under two additional conditions: (1) considering only the first spike per neuron after the stimulus, and (2) considering all subsequent spikes after the first one. The classification was performed at 4 msec bin size for each ensemble of neurons. To allow proper comparison, classification performance was measured in bits of mutual information as defined above. On a single-neuron basis, for every location we also computed the mean of the first spike latency as a measure of response latency, and the SD of the first spike latency as a measure of jitter, i.e., temporal precision of the first spike. For every neuron, we also defined the maximal response latency as the latency in response to the stimulus that generated the greatest first spike latency and the minimal response latency as the latency in response to the stimulus that generated the smallest first spike latency. We then defined the latency range as the difference between the maximal response latency and minimal response latency across locations, and the optimal jitter as the minimal jitter across locations. Only trials in which a neuron exhibited at least one spike were used to estimate the latencies.

Error analysis. To evaluate whether trials incorrectly classified still contained information about stimulus location, an error analysis was performed. In addition to considering the spatial organization of the off-diagonal elements in the confusion matrix, an “error distance”, D, was defined for every trial as follows: for every discriminated trial, D equaled 1 if the trial was correctly classified, D equaled 2 if the correct location was the second choice (i.e., the Euclidean distance between the trial response and the correct template was greater than the distance between the same trial response and one other template but smaller than all the other distances), D equaled 3 if the correct location was the third choice, and so on. For trials incorrectly classified (D > 1), the discrete probability distribution function of D was estimated by counting the number of trials incorrectly classified with D = 2, D = 3,..., D = 10, and dividing each count by the total number of trials incorrectly classified. If there were no information in the mistakes, one would expect the trials incorrectly classified to be assigned randomly to any other location. In that case, the D of the trials incorrectly classified would have a discrete uniform distribution between 2 and 10. This null hypothesis was tested through a single-sample Kolmogorov-Smirnov test (Matlab function “kstest”). To investigate the temporal precision of information contained in the trials incorrectly classified, the error analysis was performed at the seven different bin sizes (see above), and the discrete probability distribution function of D in the mistakes (D > 1) was estimated for each ensemble (n = 10) at each bin size. The first value of this probability distribution function, which corresponds to the percentage of trials incorrectly classified in which the correct location was the second choice (D = 2), was submitted to a one-way repeated measure ANOVA, similar to the analysis described above for the trials correctly classified (see “Role of spike timing”). Again, the main factor of the ANOVA was the bin size, with seven levels (1, 2, 4, 5, 10, 20, and 40 msec). Tukey's honest significant difference test was used for post hoc comparisons.

Throughout the text, Pearson coefficient was used for correlations, results were considered significant at p < 0.05, and values are means ± SD unless otherwise specified.

Results

PSTH-based classification using ensembles of neurons

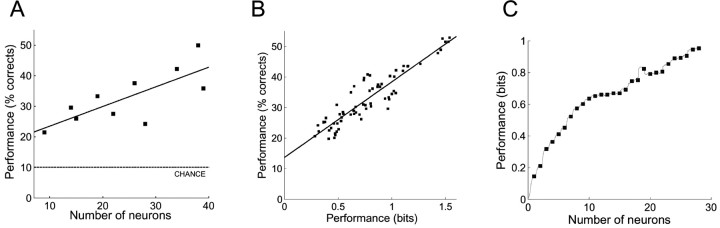
Ten different ensembles of neurons were recorded from five animals bilaterally implanted in the forelimb region of the primary somatosensory cortex. The average number of neurons per ensemble was 24 (range 9-39). The PSTH-based classification method was used to evaluate, for each ensemble, the ability of the neural responses to discriminate which location was stimulated on a single-trial basis. Classification performance was first expressed as the number of trials correctly classified divided by the total number of trials. For every ensemble of neurons, classification performance was greater than chance (10%) at all bin sizes. The maximal performance (52.9%, i.e., >5 times greater than chance) was obtained with an ensemble of 38 neurons at 2 msec bin size. The minimal performance (19.8%, i.e., about two times greater than chance) was obtained with an ensemble of nine neurons at 40 msec bin size. At all bin sizes there was a significant correlation (Pearson: r >0.71; p < 0.02) between classification performance and the number of neurons in the ensemble (Fig. 3A). Similar results were obtained when the classification performance was expressed in bits by calculating the mutual information between predicted and actual stimuli from the confusion matrix. In fact, the two measures of classification performance (percentage of trials correctly classified and bits of mutual information) were highly correlated (Pearson: r = 0.92; p < 0.0001; n = 70) (Fig. 3B). Random neuron dropping revealed a sublinear increase of classification performance when increasing the number of neurons included in the analysis, suggesting that information about stimulus location in this simple task was redundantly distributed within the ensembles (Fig. 3C).

Figure 3.

Single-trial classification of stimulus location using ensembles of neurons. A, Scatter plot of the classification performance (expressed as percentage of trials correctly classified and averaged across all bin sizes) as a function the number of neurons in the ensemble. The solid line is the best linear fit of the data, and the dotted line indicates chance classification performance (10%). The performance of the classification increases as the number of neurons increases. B, Comparison of classification performance evaluated by the percentage of trial correctly classified (y-axis) and the bits of mutual information between neural responses and stimuli (x-axis). Each point represents the performance of one ensemble at a given bin size (so there are 10 × 7 = 70 points). The two measures of performance are well correlated. C, Neuron dropping. Classification performance is plotted as a function of the neurons included in the analysis. For each number of neurons N on the x-axis, the value on the y-axis represents the bits of information at 4 msec bin size averaged over all the populations with at least N neurons. Gray points correspond to single variables, and black squares (every 10 variables) correspond to the different neurons. The maximum number of neurons used was 28. The smooth and sublinear performance increase when adding neurons reveals information redundancy within the ensembles in this simple task (Franco et al., 2004) and supports the idea of distributed processing in the somatosensory cortex (Nicolelis et al., 1998; Ghazanfar et al., 2000).

Role of spike timing

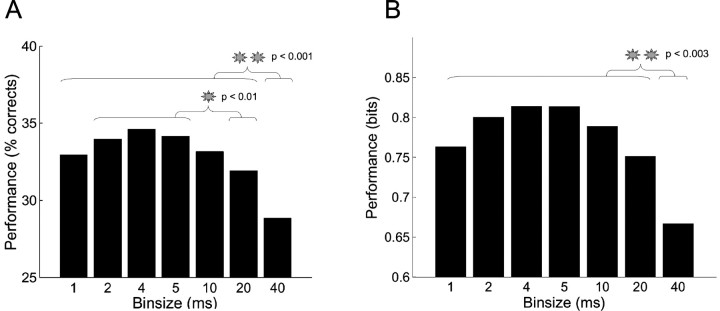
To study the role of spike timing, we used a one-way ANOVA design that tested the influence of the bin size on classification performance. The ANOVA was separately performed using either the percentage of trials correctly classified (Fig. 4A) or the bits of mutual information (Fig. 4B). In both cases, the ANOVA main effect, bin size, was significant (p < 0.000001; n = 10). Post hoc analysis revealed that classification performance at 40 msec bin size (28.75 ± 8.16% or 0.67 ± 0.32 bits) was significantly smaller than the performance at any other bin size (p < 0.003). When using the percentage of trials correctly classified, the performance at 20 msec bin size was significantly smaller than the performance at smaller bin sizes, except 1 msec (p < 0.01). On average, the maximal classification performance was reached at 4 msec bin size (34.46 ± 8.88% or 0.81 ± 0.34 bits), indicating that spike timing conveyed more information about stimulus location than the probability of spike per stimulus alone.

Figure 4.

Role of spike timing in the somatosensory code. A, B, Classification performance as a function of the bin size. The performance represents the percentage of trials correctly classified (A) and the bits of mutual information between stimuli and neural responses (evaluated from the confusion matrix) (B) averaged across 10 ensembles of neurons from five rats. The gray stars represent significant differences. The largest bin size, 40 msec, provides the poorest classification performance.

First spikes and subsequent spikes

We separately examined the contribution of the first spike per neuron after the stimulus and the contribution of subsequent spikes to the temporal precision of the code in discriminating stimulus location. In the ensembles (n = 10), the performance of the PSTH-based classification method at 4 msec bin size using only first spikes was 0.76 ± 0.27 bits, which corresponds to 94% of the performance obtained with all spikes at 4 msec. The performance using only subsequent spikes was 0.53 ± 0.33 bits, which corresponds to 65% of the performance obtained with all spikes. Interestingly, 68% of the total number of spikes were first spikes, and only 32% were subsequent spikes, which means that at 4 msec bin size subsequent spikes conveyed 48% more information per spike than first spikes. Nevertheless, first spikes alone conveyed almost as much information about stimulus location as the entire responses. The temporal precision of the code was then characterized on a single-neuron basis by calculating the mean and SD of the first spike latency for every location. Neurons (n = 244) responded to the different locations with different latencies. The latency range (i.e., the temporal difference between the location with minimal latency and the location with maximal latency for each neuron) was 12.5 ± 6.1 msec. The optimal jitter (i.e., the temporal precision of the first spikes ad measured by the minimal SD of the first spike latency across locations) was 4.1 ± 1.9 msec. Therefore the stimulus-related temporal precision of the first spikes within locations allows ensembles of neurons to discriminate latency differences between locations.

Error analysis

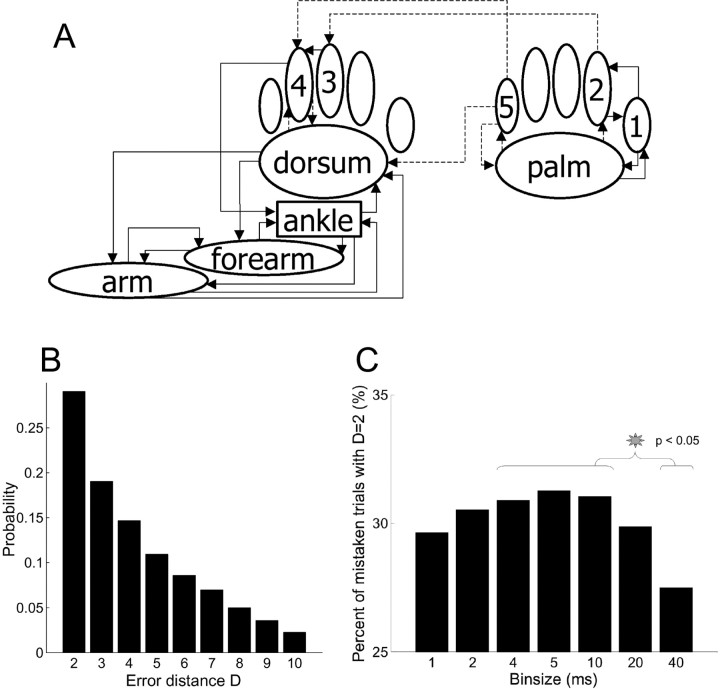
To investigate whether the trials incorrectly classified contained information about stimulus location, we performed an error analysis. First, we systematically considered the spatial organization of the selected location in the trials incorrectly classified by studying the off-diagonal elements of the confusion matrix. The “mislocalization” of the trial incorrectly classified was extremely somatotopic, in the sense that the chosen location was usually a skin site nearby the correct location (Fig. 5A).

Figure 5.

Error analysis. A, Drawing of the “mislocalizations” of trials incorrectly classified. Arrows from location a to location b indicate that at least 15% (solid lines) or 13% (dotted lines) of the trials incorrectly classified when a was contacted were assigned to b. The mislocalization was somatotopically organized, in the sense that the chosen location was usually a skin site nearby the correct location. The 24 arrows represent 47.9% of the trials incorrectly classified, compared with 26.7% (i.e., 24 of 90) as predicted by chance. B, Probability distribution function of the error distance, D, of the trials not correctly classified (D >1), including all bin sizes and all neuron ensembles. The correct location is the second choice in ∼30% of the trials incorrectly classified, the third guess in ∼20% of the trials incorrectly classified, and so on. This highly asymmetric distribution shows that even the trials incorrectly classified contain information about stimulus location. C, The percentage of trials incorrectly classified for which the correct location was the second choice (i.e., D = 2) is shown as a function of the bin size. Values represent averages across 10 ensembles of neurons. The gray star indicates significant differences. As for the trials correctly classified, the poorest performance (minimal percentage of trials incorrectly classified with D = 2) is obtained at 40 msec bin size.

To provide a more rigorous quantitative evaluation of the information present in the trials incorrectly classified we calculated, for every trial, an error distance, D, that defines how far the correct choice was from the actual one (i.e., D = 1 if the trial was correctly classified, D = 2 if the correct location was the second choice, and so forth). The probability distribution function of the error distance, D, in the trials incorrectly classified (i.e., trials with D >1) was skewed toward low values of D (Fig. 5B), suggesting the presence of information about stimulus location. In fact, when a given trial was incorrectly classified, ∼50% of the times the correct location was within the third choice (compared with 22% as predicted by chance). The one-sample Kolmogorov-Smirnov test confirmed that the probability distribution function of D in the trials incorrectly classified was significantly different from a discrete uniform distribution function, which would be expected if no information were contained in the mistakes (p < 10^-9; n = 46990, including all incorrectly classified trials for the 10 ensembles at any bin size). These results suggest that the trials incorrectly classified contained significant information about stimulus location.

Finally, the error analysis also provided additional insights into the temporal precision of the somatosensory code. We used a one-way ANOVA design that tested the influence of the bin size on the percentage of trials incorrectly classified in which the correct location was the second choice (D = 2). The ANOVA main effect, bin size, was significant (p = 0.015; n = 10). Post hoc analysis revealed that the percentage of trials incorrectly classified with D = 2 was smaller at 40 msec bin size compared with bin sizes between 4 and 10 msec (p < 0.04) (Fig. 5C). In other words, at bin sizes between 4 and 10 msec the probability distribution function of D in the trials incorrectly classified was more skewed toward D = 2, which indicates more information about stimulus location. On average, the maximum percentage of trials incorrectly classified with D = 2, that is maximum information about stimulus location, was reached at 5 msec bin size, corroborating the significant role of spike timing in discriminating stimulus location.

Discussion

The main finding of this study is that in the forelimb somatosensory cortex of the rat, spike timing conveys significant information about stimulus location on a single-trial basis. The information in our experiment was redundantly distributed within ensembles of neurons, and the ability to discriminate stimulus location increased when decreasing the bin size, reaching a maximum at 4 msec. At 4 msec bin size the first spikes of each neuron after the stimulus conveyed almost as much information as the entire responses, so the temporal precision of the code was preserved in the first spikes. Subsequent spikes were less frequent but conveyed more information per spike. Finally, not only the trials correctly classified but also the trials incorrectly classified conveyed information about stimulus location with a similar temporal precision. Overall, these results suggest that spike timing could play an important role in forelimb somatosensory processing.

The data analysis method we used to perform the single-trial discrimination of stimulus location, the PSTH-based classification method (Foffani and Moxon, 2004), was applied here for the first time to study the neural code in the forelimb somatosensory cortex. Because changing the bin size changes the total number of variables, to study the temporal precision of the code it is important that the statistical properties of the classification method have a low sensitivity to the number of variables in the dataset. The PSTH-based method uses only first-order statistics (i.e., the means), and the convergence of the estimate of the mean does not depend on the number of variables, but only on the number of trials. This property makes the PSTH-based method particularly appropriate for studying the temporal precision of the neural code (Foffani and Moxon, 2004), which was the primary objective of this study.

The PSTH-based method does not explicitly take into account information represented by correlations between neurons. However, previous studies in the whisker cortex suggested that these correlations play minor roles in the somatosensory code (Ghazanfar et al., 2000; Petersen et al., 2001) and that stimulus-dependent changes in correlation convey almost no information about stimulus location (Petersen et al., 2001), which allows a decoder that neglects correlation to extract virtually 100% of the encoded information (Panzeri et al., 2002). Nevertheless, the redundancy we found in ensembles of neurons, as revealed by the sublinear increase of information as the number of neurons increased (Franco et al., 2004), does reflect correlation between neurons as absence of “information independence” (Schneidman et al., 2003) and can be related to the “signal similarity” described in the whisker cortex (Petersen et al., 2001; Pola et al., 2003). Importantly, information theoretic redundancy should be carefully interpreted within the specific boundaries of the experiment, because it could reflect low entropy of the stimulus set chosen (Rolls et al., 1997) rather than actual redundancy in the somatosensory code. Nonetheless, our results support the idea that even with simple stimuli, and even exploiting the information conveyed by spike timing, the somatosensory code is highly distributed in large ensembles of broadly tuned neurons (Nicolelis et al., 1998; Ghazanfar et al., 2000).

Using the PSTH-based classification method, changes in performance as a function of bin size can be intuitively interpreted in relation to the PSTH profiles. Large bin sizes maximize the PSTH height but provide a poor description of the temporal information of the response. By decreasing the bin size, the entire temporal information of the responses is captured, thereby increasing classification performance. If the bin size is decreased below a critical point (intuitively below the trial-to-trial temporal precision of the spikes), then the only effect obtained is to progressively decrease the height of the PSTH, which becomes more flat and again provides a poor description of the temporal information of the response. More formally, assuming that at any bin size enough trials are available to produce reliable estimates of the PSTH, the result of over-binning is that when a single-trial spike is matched to the corresponding PSTH template, the Euclidean distance between the spike and the corresponding bin, b, in the PSTH (i.e., [1 - PSTH(b)]²) tends to 1 when the number of bins is increased (i.e., when the bin size tends to 0), independently of the bin b where the spike occurred. Experimental results are in agreement with this interpretation: in the whisker cortex, the jitter of the first spike is 2.6 msec (Panzeri et al., 2001), and deterioration of PSTH-based classification performance starts at bin sizes <2 msec (Foffani and Moxon, 2004) (see also Ghazanfar et al., 2000); in the forelimb cortex, as shown in the present study, the jitter of the first spike is larger, 4.1 msec, and deterioration of classification performance starts at larger bin sizes, <4 msec. It should be noted, however, that the results obtained with the PSTH-based method, as with any other decoder, depend on the assumptions of the method itself. Therefore, although our results indicate 4 msec as the optimal bin size for decoding information from the neural responses, they do not necessarily imply that 4 msec is the temporal precision of the forelimb somatosensory code.

Our findings in the forepaw somatosensory cortex are similar to the results previously obtained in the rat whisker cortex (Ghazanfar et al., 2000; Panzeri et al., 2001; Petersen et al., 2001; Foffani and Moxon, 2004). This similarity is somewhat surprising given the gross physical difference between the two systems. Indeed, the cutaneous surface of the forepaw, unlike the facial whiskers, is continuous. It has been shown, however, that the spatial distribution of the receptive field centers across the forepaw is organized in discrete segregates whose relative distances are in the order of our interlocation distances (Favorov et al., 1987; Favorov and Diamond, 1990; Favorov and Whitsel, 1988a,b). Further investigation is needed to understand the physiological significance of the intrasegregate variability of the neural responses. Our results suggest that the intersegregates “temporal coding” in the forepaw somatosensory cortex parallels the inter-whiskers temporal coding in the barrel field cortex. In conclusion, the data presented in this study show that the role of spike timing in cortical somatosensory processing is not an exclusive feature of the highly specialized rat trigeminal system, but a more general property of the rat primary somatosensory cortex.