Visual Feedback Control of Hand Movements

Abstract

We investigated what visual information contributes to on-line control of hand movements. It has been suggested that motion information predominates early in movements but that position information predominates for endpoint control. We used a perturbation method to determine the relative contributions of motion and position information to feedback control. Subjects reached to touch targets in a dynamic virtual environment in which subjects viewed a moving virtual fingertip in place of their own finger. On some trials, we perturbed the virtual fingertip while it moved behind an occluder. Subjects responded to perturbations that selectively altered either motion or position information, indicating that both contribute to feedback control. Responses to perturbations that changed both motion and position information were consistent with superimposed motion-based and position-based control. Results were well fit by a control model that optimally integrates noisy, delayed sensory feedback about both motion and position to estimate hand state.

Introduction

We recently reported evidence that visual feedback from the hand contributes to on-line control of reaching throughout the full extent of the movement, even for relatively fast movements (Saunders and Knill, 2003). In the current research, we used a similar method to investigate exactly what visual information is used for feedback control. Two components of visual feedback that could potentially contribute are information about the position of the hand and information about the motion of the hand. The experiments reported here test the relative contributions of these two feedback signals to control of pointing movements.

A number of control strategies could be based solely on feedback about hand position. A visual feedback controller might steer to maintain a predetermined visual path, making corrective adjustments whenever sensory feedback indicates that the position of the hand has deviated from the desired trajectory. Adaptation studies provide evidence that the motor system does attempt to maintain preferred kinematic trajectories, such as straight-line paths (Shadmehr and Mussa-Ivaldi, 1994; Wolpert et al., 1995a). Another type of model, the vector integration to endpoint (VITE) model of Bullock and Grossberg (1988), maps the difference vector between hand and target positions onto a desired hand velocity.

Motion information alone could also be used to guide hand movements. A kinematic controller that generates desired velocity changes (or acceleration changes) could use a homing strategy of keeping the visual motion of the hand directed toward the target, for example. Such a controller would rely solely on the visual motion of the hand relative to the target and would not need information about the position of the hand to generate kinematic “commands.” It would therefore be robust to small miscalibrations of visual and nonvisual coordinates and could be generalized to tasks like controlling a mouse cursor that involve an arbitrary mapping from motor to visual space. Solving the inverse dynamics problem of mapping kinematic signals to muscle activation would still require information about the pose of the hand in body-centered coordinates; however, this information is potentially available from nonvisual sources [for evidence that vision and proprioception contribute differently to kinematic planning and solving inverse dynamics, see Sober and Sabes (2003)].

Paillard (1981, 1996) has argued that both position and motion feedback contribute to controlling hand movements, but in different movement phases: a fast homing-type strategy based on visual motion is used during the initial part of movements, and a slower position-based strategy is used for final end-phase adjustments. The two-phase proposal is based on the intuition that motion acuity remains high in the periphery, whereas position acuity decreases sharply with retinal eccentricity. An optimal controller, however, would use visual information about both position and motion continuously throughout a movement, with the relative contributions of the two signals depending on their relative reliability.

To distinguish empirically the contributions of visual motion and position feedback signals to on-line control, we measured responses to dynamic perturbations of visual feedback from the hand. To perturb visual feedback from the hand during movements, we used a simple but finely calibrated virtual display system in which subjects viewed a moving virtual fingertip rather than the real fingertip. This allowed us to apply dynamic changes to the mapping from physical to visual space. We applied a number of different remappings to isolate the relative contributions of motion and position feedback for on-line control of subjects' pointing movements. Results were compared with the behavior of a feedback controller that optimally integrates delayed information about the position and velocity of the hand to continuously update internal estimates of hand state.

Materials and Methods

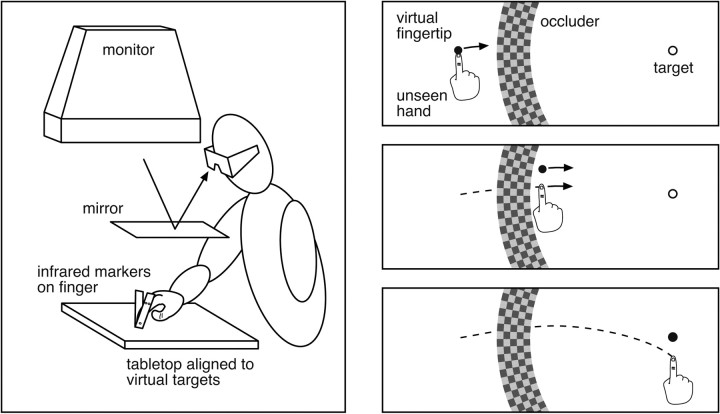
Design and conditions. Figure 1 shows a schematic of the virtual display system and an illustration of the trial sequence from the vantage point of the subject. Subjects performed a simple pointing task, with visual feedback provided by a small sphere that moved in real time with their unseen fingertip. On one-third of the trials, the mapping from physical space to visual space was changed while the virtual fingertip moved behind an occluder. The remappings varied from trial to trial, and both perturbation type and direction were randomized to prevent adaptation. The occluder served to mask the perturbation onsets, and all of the subjects reported being unaware of the perturbations when questioned after the experiment, even when told what they would have looked like. Kinematic data consisted of the three-dimensional (3D) position of a subject's fingertip sampled at 480 Hz during the movements.

Figure 1.

a, Illustration of the experimental apparatus. Subjects were presented with stereo images using shutter glasses and a monitor viewed through a mirror. The mirror prevented a view of the hand and allowed artificial visual feedback to be presented in the subjects' manual workspace. Subjects moved their fingers to visual targets that were aligned with a tabletop. An Optotrak 3020 system tracked infrared markers attached to a subject's finger, and these data were used to render a virtual sphere representing the subject's fingertip (virtual finger). b, Illustration of a trial sequence. Views showa top-down projection onto the tabletop. At the start of a trial (top panel), a target (open circle) and virtual fingertip (solid circle) appear, along with an annular-shaped occluder. The subject's task was to move the virtual fingertip to touch the target. During initial movement, the virtual fingertip coincided with the actual location of the subject's unseen finger. On perturbed trials, when the finger emerged from behind the occluder, its position and direction of motion were changed and no longer matched the actual finger (middle panel). Depending on the perturbation condition, subjects may have had to compensate for the perturbation to successfully reach the target with the perturbed virtual fingertip (bottom panel).

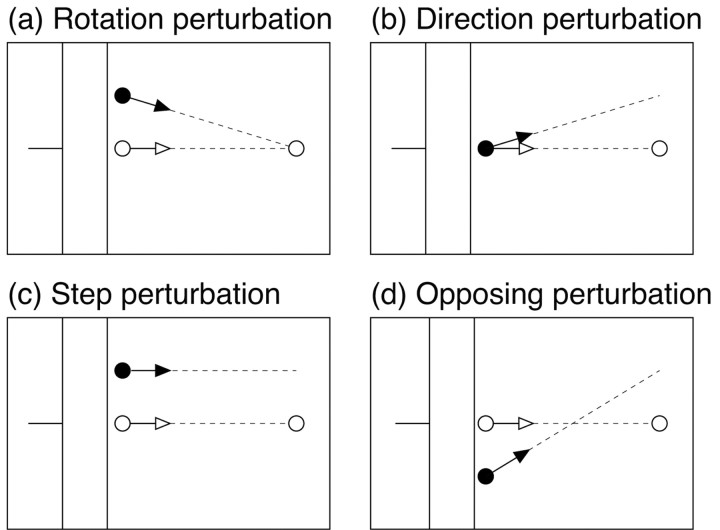
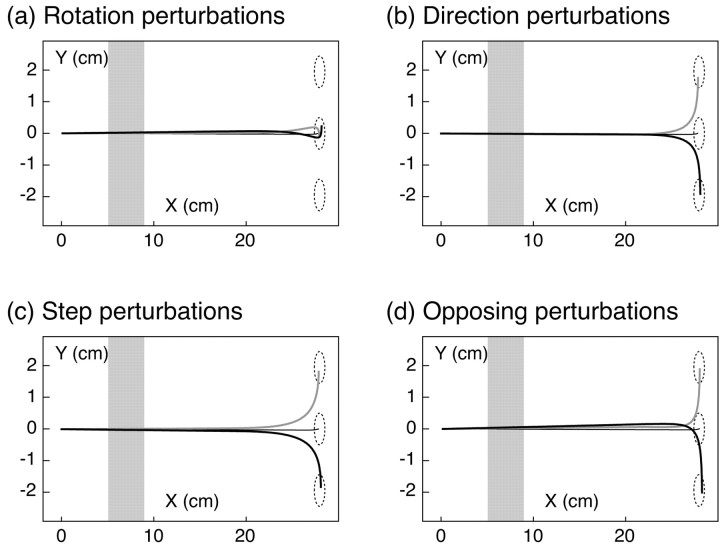
We chose four different types of perturbations to distinguish possible visual control signals. Feedback control based on the relative motion of the hand, as in a homing strategy, would be unaffected by perturbations that preserve the relationship between the movement of the visual hand and the target. Figure 2a shows an example of such a perturbation. Visual space was rotated around the target, so that the perturbed position of the finger was displaced relative to the unseen hand while leaving its motion relative to the target unchanged. We refer to this as a “rotation” perturbation.

Figure 2.

Illustration of the four perturbation types. a, Rotation perturbations: visual space was rotated around the target, such that position of the virtual fingertip was displaced relative to the unseen finger, but the direction of motion relative to the target was unchanged. b, Direction perturbations: visual space was rotated around a point just past the occluder, along the line connecting initial and target positions. The position of the virtual fingertip initially coincided with the actual finger, but its direction of motion was different. c, Step perturbations: visual space was displaced in the direction perpendicular to main axis of movement. This changed both the position of the virtual fingertip and its direction of motion relative to the target. d, Opposing perturbations: visual space was rotated around a point between the target and the emergent point. This also changed both the position and the relative motion of the virtual fingertip, but in opposite directions compared with step perturbations.

A second type of perturbation, shown in Figure 2b, altered the motion of the virtual fingertip when it emerged from behind the occluder while initially leaving its position unchanged. Because the change in movement direction was small, the discrepancy in position increased only slowly over time, so a controller that relied solely on position feedback would be expected to show only a delayed response to such perturbations relative to the rotation perturbation. We refer to this as a “direction” perturbation.

Figure 2, c and d, illustrate two other classes of perturbations that produce different initial displacements in position, either upward or downward, but the same change in relative motion as the direction perturbations. We will refer to these as “step” perturbations and “opposing” perturbations. To the extent that feedback control is based on the relative motion of the hand, these perturbations would be expected to have similar effects. On the other hand, on the basis of position feedback, these perturbations would be expected to produce responses in opposite directions.

Apparatus and display. Visual displays were presented in stereo on a computer monitor viewed through a mirror (Fig. 1), using CrystalEyes (Stereographics, San Rafael, CA) shutter glasses to present different stereo views to the left and right eyes. The left and right eye views were accurate perspective renderings of the simulated environment. Displays had a resolution of 1024 × 768 pixels and a refresh rate of 120 Hz (60 Hz for each eye's view). The stimuli and feedback were all drawn in red to take advantage of the comparatively faster red phosphor of the monitor and prevent interocular cross-talk.

The horizontal mirror prevented a view of the subject's hand. Visual feedback about hand position was provided instead by a 1-cm-diameter virtual sphere that moved in real time along with the subject's actual finger. The targets of subjects' movements were 1-cm-diameter circles rendered to be aligned with an unseen tabletop (∼55 cm from the eyes), which provided consistent haptic feedback when a subject's finger touched a target.

In addition to the target and the virtual fingertip, displays included a planar annular-shaped occluder object, rendered to appear 9 cm above the tabletop. At this height, the virtual finger passed behind the occluder on normal movements. In experiment 1, the radius and width of the occluder were set so that its cyclopean projection onto the tabletop had an inner radius of 19 cm and an outer radius of 23 cm relative to the target (projected width 4 cm), and it was positioned so that its occluded region was centered on the line connecting the finger starting location to the target. In experiment 2, occluders were positioned similarly and had the same inner radius but were extended to have an outer radius of 32 cm, so that the virtual fingertip was occluded even at the start of movements. In both experiments, the virtual finger emerged from behind the occluder at approximately the same distance from the target: 19 cm (25% of the distance to the target). The exact distance varied somewhat across trials, because it depended on finger height as well as progress toward the target.

The four types of perturbations have been described qualitatively in the previous section. The specific mappings used in these cases were chosen to equate as closely as possible three parameters: the initial position displacements (0 or ±2 cm), the change in the initial direction of the virtual finger relative to the target (0° or ±6°), and the size of the correction needed to compensate for the perturbation (0 or ±2 cm). For rotation perturbations, the visual coordinates for rendering the virtual fingertip were rotated by ±6° around the target. At a distance of 19 cm from the target, which is approximately where the virtual fingertip would have emerged from behind the occluder, this rotation produces an initial position displacement of ±2 cm. The actual amount of initial position conflict varied slightly depending on the height of the hand when it emerged from behind the occluder, but for the viewing conditions used and the small vertical movements made by subjects, the discrepancy was negligible. For direction perturbations, visual space was rotated by ±6°, but around the point 19 cm away from the target along the line connecting target and starting positions. To compensate for the rotation, the endpoint of the unseen hand would have had to be ±2 cm from the target in the y direction. If the path of the finger did not follow a straight line to the target, this rotation would have produced a slight change in the initial position of the hand, but for the modest amounts of curvature that we observed (∼2 cm from straight path), the shifts would have been very small, on the order of 0.02 cm. For step perturbations, visual space was globally shifted by ±2cminthe y-axis direction. When the hand initially became visible at a distance of 19 cm, the direction of the shifted virtual finger relative to the target was changed by ±6°, the same as in the direction perturbation condition. Finally, opposing perturbations were generated by rotating visual coordinates by 12° around a point 9.5 cm from the target (halfway between the target and near edge of the occluder). The initial position of the virtual fingertip was displaced by approximately ±2 cm, and the shift in endpoint required to compensate for the perturbation was 2 cm, in the direction of the initial displacement. The initial change in the direction of motion relative to the target for this condition was slightly smaller than in the other conditions, on average 5.9° instead of 6°. This was an unavoidable consequence of constraining the required endpoint correction to be ±2 cm, as in the other conditions.

An Optotrak 3020 system (NDI, Waterloo, Ontario, Canada) recorded the time-varying position of a subject's finger at 480 Hz. The data were used to dynamically update the position of the virtual fingertip. Subjects wore a finger splint on their right index finger, which had a triad of active infrared markers. The position of a subject's fingertip within the splint was computed from the position of the three markers attached to the splint. The optical measurements had very small latencies (<2 msec), but the speed of the graphical rendering loop imposed a significant additional latency on visual feedback, ∼42 msec for the first experiment and 25 msec in the second experiment (different graphics cards). When computing the rendered position of the virtual fingertip, we compensated for this delay by linearly extrapolating from the latest marker position, using the position from previous frames to estimate velocity. For the experiments, we used an extrapolation time of 33 msec, which we later discovered to be an underestimate of delay in the first experiment and an overestimate in the second. The inaccurate delay estimates contributed a bias in rendered finger position of up to 0.6 cm along the direction of movement at the point of average peak velocity. The bias in the perpendicular direction was much smaller, peaking at ∼0.05 cm for the average peak velocity in that direction. Linear extrapolation contributed an additional bias in the x position of the virtual finger caused by acceleration of the hand, varying between approximately –0.3 cm at the point of peak acceleration to 0.3 cm at peak deceleration. The biases in the y direction caused by extrapolation were comparatively small, ranging between approximately ±0.02 cm. Extrapolation also had the effect of amplifying the intrinsic noise in Optotrak measurements; however, even after amplification, this noise remained small (rms error = 0.016 cm).

Spatial calibration of the virtual environment required computation of the coordinate transformation from the reference frame of the Optotrak to the reference frame of the computer monitor and the location of a subject's eyes relative to the monitor. These parameters were measured at the start of each experimental session using an optical matching procedure. The backing of the half-silvered mirror was removed temporarily so that subjects could see their hand and the monitor simultaneously, and subjects aligned an Optotrak marker to a sequence of visually cued locations. Cues were presented monocularly, and matches were performed in separate sequences for left and right eyes. Thirteen positions on the monitor were cued, and each position was matched twice at different depth planes. The combined responses for both eyes were used to determine a globally optimal combination of 3D reference frame and eye position. After the calibration procedure, a rough test was performed in which subjects moved a marker viewed through the half-silvered mirror and checked that the position of a rendered dot was perceptually coincident with the marker. Calibration was deemed acceptable if deviations appeared to be <1–2 mm. Otherwise, the calibration procedure was repeated.

Procedure. The task for subjects was to move their finger back and forth to touch a series of targets presented in the virtual environment. At the start of a trial, a new target would appear on the opposite side of the workspace as the current hand position. The target onset was the cue to move. Subjects were instructed to move to touch the target in a fast and “natural” manner. On reaching the target, they were to keep their finger in place until the next target appeared. Data collection was triggered by initiation of movement and continued for 1.5 sec. Immediately after this recording period, a new target appeared and the occluder was repositioned, indicating the start of the next trial. The time between successive trials varied depending on how quickly subjects initiated movement, averaging ∼2 sec.

Subjects were instructed to try to move at about the same speed on each trial. Feedback was provided throughout the experiment to train subjects to reach the target within a range of times around a goal time of 500 msec. Subjects received positive feedback for movement durations within 75–125% of the goal time (a larger circle appeared around target) and negative feedback otherwise (“X” through target indicating too fast; no change indicating too slow). For purposes of feedback, reaching the target was defined as bringing the virtual finger to a stop (speed <0.5 mm/sec) within 1 cm of the center of the target. Before the main experiment blocks, subjects were allowed 20–40 unperturbed practice trials to familiarize themselves with the timing constraint.

The targets varied in location within two ellipses on the table, which were 10 cm wide, 16 cm tall, and separated by 28 cm. The target position for a trial was chosen relative to the end location of the previous trial. The target distance was always 28 cm (∼26° of visual angle), whereas the direction from the starting position to the target varied randomly between –15° and +15° relative to the horizontal midline of the table, subject to the constraint that the endpoint lay within the target ellipse. Occasionally, subjects moved their hands toward the center of the workspace too early (contrary to instructions), such that it was impossible to satisfy the criteria. In these cases, a random position within the opposite ellipse was chosen as target location, and the trial was discarded from analysis.

Perturbations were applied on one-third of the trials. Perturbed and unperturbed baseline trials were randomly intermixed, with the constraint that at least one baseline trial separated any two perturbed trials. This constraint was included to reduce the potential for interference across sequential perturbed trials. For the same reason, we also excluded from analysis all baseline trials that were preceded by perturbed trials. This reduced the amount of baseline trials available for analysis by half.

In experiment 1, the virtual fingertip remained visible at the end of a trial and the start of the subsequent trial. To prevent sudden jumps in figure position after a perturbed trial, the preceding remapping remained in effect until the hand passed behind the occluder, at which point the perturbation was turned off. This was not an issue for experiment 2, because the hand was not initially visible.

Before analysis, data were filtered to remove various types of irregular trials. These included trials with incomplete data caused by occluded markers, trials with mistimed recording caused by a false start, trials in which subjects began moving before the target appeared, and trials in which motion was not complete within ±40% of the goal time. Some trials contained isolated frames in which the markers were occluded from view from the Optotrak. If there were no more than four nonsequential missing frames on a trial, the trial was not excluded. Instead, the data from isolated missing frames were filled in by linearly interpolating between adjacent frames. Trials with adjacent missing frames, or with more than four isolated missing frames, were excluded from analysis.

Subjects participated in three experimental sessions on separate days. Each began with calibration of the virtual environment, followed by practice trials to familiarize a subject with the task, and then two blocks of experimental trials separated by a brief break. Subjects performed 528 trials in each experimental block. Before irregular trials were filtered (see above), this yielded a total of 264 trials per perturbation type (half positive and half negative), 1056 postperturbation trials, and 1056 baseline unperturbed trials.

Data analysis. Movements showed large variability in overall trajectories but were also very smooth, so much of the variability could be attributable to differences in initial conditions, motor plans, goal paths, etc. To derive a sensitive measure of the effect of perturbations, we temporally decorrelated the data series using linear filters fit to the data (Saunders and Knill, 2003).

We assumed that for unperturbed trials the position of the fingertip at time t was a linear function of the n previous positions:

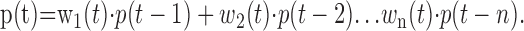(1)

The weights w₁(t), w₂(t),... w_n(t) were allowed to vary as a function of time but were assumed to be constant across trials. To align the data series temporally, we defined t = 0 to be the moment when the hand emerged from behind the occluder, so that t represents time after perturbation. Because there was variability in speed and time course of trials, the assumption of that weights are the same across trials corresponds to assuming that the weights are relatively constant over small shifts in t.

If the data series are smooth and temporally correlated, the linear model given by Equation 1 should closely fit the data and account for most of the variability across trials. Responses to perturbations can be distinguished as changes in trajectory that would not be predicted solely on the basis of the previous path. Thus, we augmented the model with an added term representing the effect of perturbations:

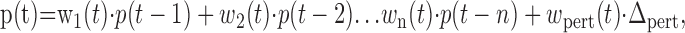(2)

where Δ_pert is +1 for positive perturbations and –1 for negative perturbations. The function w_pert(t) represents the evolving influence of the perturbation on subjects' movements and should be zero for times before subjects show any corrective response to perturbations. We refer to this function as the perturbation influence function.

For each subject, we applied linear regression to the baseline trials to estimate the autoregressive weights in equation 1). We set n = 6 for the analysis but found that the results were insensitive to the exact value for n > 6. To compute influence functions for each perturbation type [w_pert(t)], we correlated the sign of the perturbations (+1, –1) on perturbation trials with the error between the hand position at time t and the position predicted by the autoregressive model. For testing, we applied the analysis separately to the x and y components of finger position (in tabletop coordinates), but the x components yielded no significant effects, so we only report the results for the y components here.

Response latencies to the perturbations, t_resp, were derived by computing the first point in time at which the perturbation influence functions, w_pert(t), were significantly different from zero. The raw influence function was first smoothed with a one-sided (causal) exponential filter, f(t) = exp(λt) for t < 0, with λ = 25 msec, producing a time-weighted cumulative measure of the perturbation influence. The filtered result, f(t)*w_pert(t), was compared at each time t to a statistical threshold derived from resampling baseline trials, and the earliest superthreshold time was taken to be the response latency. The resampling procedure consisted of repeatedly applying the analysis to randomly chosen baseline trials (sampling with replacement) and using the results to estimate the null-model noise distribution of filtered w_pert(t).

Subjects. Five subjects participated in experiment 1, and eight subjects participated in experiment 2. All were naive to the purposes of the experiment and were paid to participate. Subjects provided informed consent in accordance with guidelines from the University of Rochester Research Subjects Review Board. Our apparatus required that subjects use their right hand, so only right-handed subjects were accepted.

Modeling. For comparison with human data, we implemented a feedback control model that optimally integrates noisy position and velocity feedback signals over time and simulated the performance of the model for the conditions of our experiments. The model was an expanded version of the feedback control system proposed by Hoff and Arbib (1993), in which the sensory front-end is augmented with a Kalman filter for integrating noisy sensory feedback with ongoing estimates of hand state. We modeled the dynamics of the hand as a linear system driven by a jerk signal (derivative of acceleration) that satisfies the minimum jerk principle, as proposed by Hoff and Arbib (1993). The system was corrupted by two independent sources of added Gaussian noise, one with SD proportional to the jerk signal and the other with a constant SD. The general form for the system dynamics is given by:

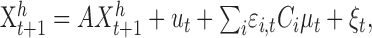(3)

where the state vector represents the two-dimensional position, speed, and acceleration of the hand in a coordinate frame aligned with the table, as well as the two-dimensional position of the target on the table (we did not simulate the small movements in the perpendicular direction that subjects show). The x-axis was taken to be in the direction of the target from the original hand position, and the y-axis was defined as the perpendicular direction within the plane of the table. ϵ_i,t is a standard normal random variable, C_i represents the proportional motor noise, and ξ_t is a constant noise source with covariance matrix Σ^ξ. The state vector is given by:

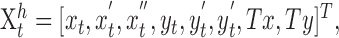(4)

where Tx and Ty represent the position of the target. The state transition matrix, A, is given by:

(5)

where ∂ is the time step used to iterate the update equations in the simulations. Given an estimate of the state of the system at time t, the minimum jerk control law is given by (Hoff and Arbib, 1993):

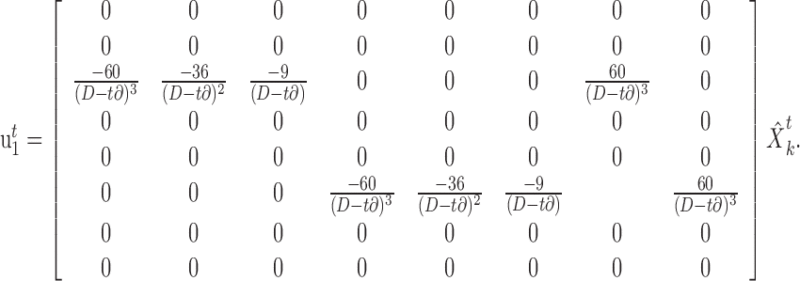(6)

To realistically model the visual feedback available to the human visual–motor system, we had to account for two properties of the visual feedback. First, the uncertainty of both position and motion information, as reflected in discrimination thresholds, varies as a function of the state of the hand. Positional acuity is inversely proportional to eccentricity; thus it is well modeled by a noise source with SD proportional to position of the hand in retinal coordinates (Levi et al., 1988; Burbeck and Yap, 1990; Whitaker and Latham, 1997). Similarly, motion acuity, in both speed and direction, varies with target speed. Motion discrimination thresholds are well fit by a model in which the velocity components in both the direction of motion and the perpendicular direction are corrupted by a mixture of proportional noise, the SD of which is proportional to the speed of the motion, and a constant noise component (Orban et al., 1985; De Bruyn and Orban, 1988). Second, estimates of position and velocity are effectively low-pass filtered by the visual system. Psychophysical sensitivity to periodic modulations in both speed and direction of motion is well fit by a model in which velocity estimates are filtered through a second-order filter with a time constant of 40 msec (Werkhoven et al., 1992). Although similar estimates are not available in the literature for position estimates, we assumed that the same filter applies to position estimates.

To incorporate the state-dependent nature of visual noise and the temporal filtering of visual feedback, we found it convenient to incorporate the sensory parameters in an augmented state vector along with the hand and target state parameters. The full state vector was:

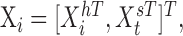(7)

where the sensory subvector is augmented by dummy variables used to implement the second-order filter:

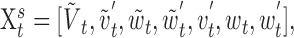(8)

with update equations:

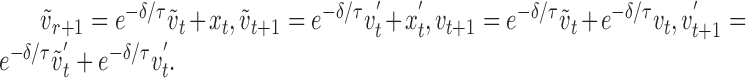(9)

Similar equations apply to the w parameters that represent the y-position and the y-component of velocity. ∂ is the time step used in the simulation to iterate the update equations, and τ = 40 msec is the time constant of the filter. The update equations (Eq. 9) are modeled by appropriate entries in an augmented update matrix A.

To accommodate the state-dependent noise in the sensory signal, the update equation for the full system takes the form:

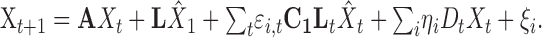(10)

The second term is the control law given in Equation 6 above, the third term represents the signal-dependent motor noise, and the fourth term represents the state-dependent noise used to model state-dependent uncertainty in the sensory estimates of position and velocity.

The sensory signal is modeled by the equation:

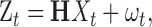(11)

where H is a matrix that simply peels off the temporally filtered, noisy estimates of position and velocity (v_t,v_t′,w_t,w_t′), and ω_t is a constant noise source with covariance matrix, Σ^ω.

The optimal, adaptive Kalman filter for this system is given by the time update equations:

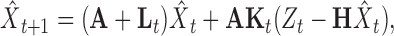(12)

where the Kalman gain matrix, K_t, is given by:

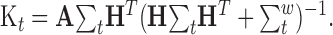(13)

Σ_t is the error covariance matrix for the state estimate at time t. The error covariance matrix is updated according to the time update equation:

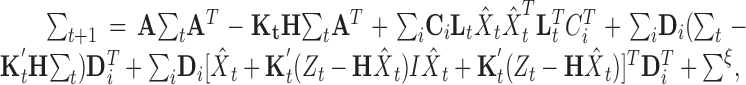(14)

where K′ is the modified Kalman gain (used to predict the state of the system at time t rather than to predict the state of the system at time t + 1, given by:

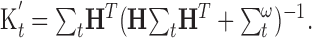(15)

The Kalman filter runs delayed by Δ msec, so the delayed state estimates are propagated forward through the state update equations using the remembered values of the motor commands, u_t, to arrive at an estimate of the current hand state.

To simulate the model, we had to set parameters for the visual noise on position and velocity. We chose values that fit with observed psychophysical data, as described below. We fit the motor noise parameters and the sensorimotor delay by hand to subjects' data.

Modeling: position noise. We used results from two-point interval discrimination studies to set the parameters for visual noise on position estimates (Burbeck, 1987; Burbeck and Yap, 1990; Whitaker and Latham, 1997). The data from these studies are consistent with a Weber fraction of 0.05 on position estimates beyond several degrees away from the fovea for stimuli viewed for 250 msec. This value is invariant to a large number of properties of the target (Burbeck, 1987; Toet and Konederink, 1988). Because subjects' finger movements were almost entirely along the axis between the starting position and the target (the x-axis), we modeled the SD of subjects' visual estimates of hand position (for 250 msec viewing) in tabletop coordinates to be:

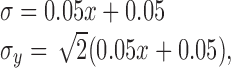(16)

where the √2 factor in the y-direction corrects for perspective foreshortening (subjects viewed the tabletop from an angle of ∼45°). The constant additive term models a minimum SD in position estimates of 0.5 mm in the center of the fovea (3′ arc) but has little impact on the behavior of the model, because the hand is outside the fovea for most of the movement. We used a small angle approximation in treating position in tabletop coordinates as proportional to visual angle. To parameterize the noise model, we multiplied the SDs by a factor of 10.2 so that a sensory version of the Kalman filter run on static stimuli for 250 msec gave estimates with the SDs listed above.

The constant of proportionality in Equation 16 determines the appropriate diagonal elements of the D_i matrices that model the state-dependent noise on position. The constant noise term is the SD of the corresponding elements of the constant noise vector, ξ. The noise on visual estimates of target position was modeled as being constant, because the target is stationary and assumed to be fixated during movement. We assumed an SD of 0.5 mm (equivalent to a visual angle of 3′ of arc).

Modeling: motion noise. Results from speed and direction discrimination studies show a somewhat more complicated behavior than position perception. Up to speeds of 64°/sec (close to the peak velocity measured in our experiments), Weber fractions for speed decrease to a minimum of 0.08 for viewing durations of 500 msec (Mateef et al., 2000). These results are consistent across a number of studies and types of stimuli (Orban et al., 1985; De Bruyn and Orban, 1988). Subjects' threshold curves are well fit by a mixed constant and proportional noise model in which the SD of visual estimates of speed is given by:

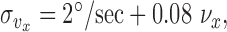(17)

where we have assumed that the speed of motion is equivalent to its velocity along the x-axis (approximately true for most of the duration of subjects' movements). Using a small angle approximation to convert this to units of distance along the table top (assuming an average viewing distance of 52 cm) gives:

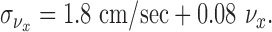(18)

Direction discrimination thresholds behave in a qualitatively similar manner to speed discrimination thresholds, but when converted into units of speed in a direction perpendicular to the path of motion, thresholds are lower by more than a factor of 8. For the SD of velocity estimates perpendicular to the direction of motion, therefore, we have:

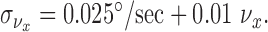(19)

Converting this to tabletop coordinates and adjusting for perspective foreshortening, we have for the SD:

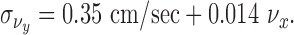(20)

Again, we approximated the principle direction of motion to be in the x direction. We scaled the parameters by constant factor of 14.3 so that a sensory version of the Kalman filter run on static stimuli for 500 msec would give velocity estimates with SDs listed above. The constants of proportionality in Equations 19 and 20 determine the appropriate diagonal elements of the D_i matrices that model the state-dependent noise on position. The constant noise terms are the SDs of the corresponding elements of the constant noise vector, ξ.

Other model parameters. The motor noise used to fit the human data were set to:

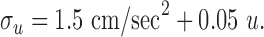(21)

The coefficient of proportionality (0.05) for the proportional noise determined the diagonal elements of the C₁ and C₂ matrices corresponding to the motor commands (the jerk signals in x and y), whereas the constant noise term determined the SD of the same elements of the constant noise vector, ξ. We simulated the model with a sensorimotor delay of 115 msec, for a duration of 750 msec, iterating the system with a time step of ∂ = 2 msec. We simulated the occluder by setting the sensory noise components of ξ to a very large number (approximating infinite noise) for the time that the fingertip was behind the occluder. Perturbations were induced at t = 270 msec. The duration of movement was set on the basis of estimates of the average time that subjects' fingers came to rest, and the time of perturbation was set on the basis of the average time after the start of movement that subjects' fingers reappeared from behind the occluder. Simulations of the small occluder and the large occluder showed little difference in performance.

Results

Responses to perturbations

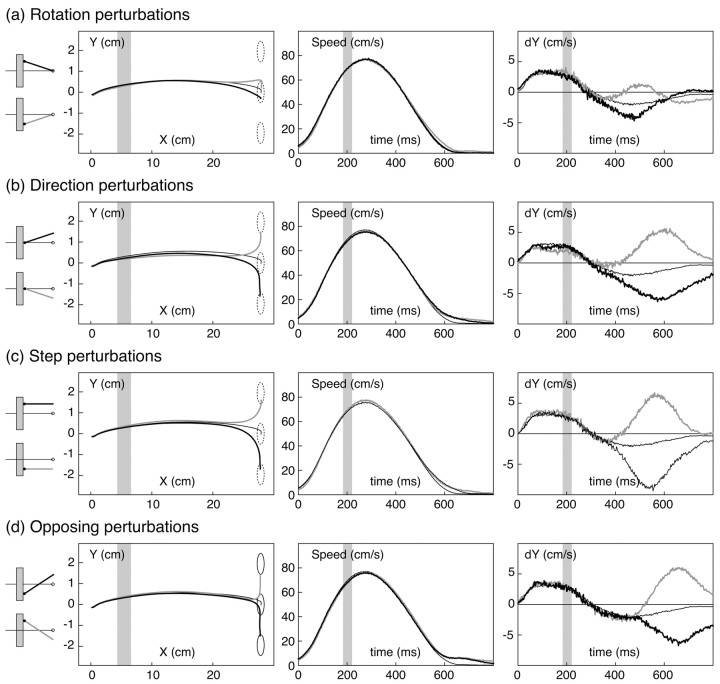
Figure 3 shows mean data for a representative subject. It is clear that all of the perturbations induced responses, including rotation perturbations, for which no correction was required. This can be seen most readily in the plots of mean y-velocity of perturbed trials, which diverge from that of unperturbed trials for all perturbation types. In the conditions that altered relative motion, subjects corrected their movements to almost fully compensate for the change in required endpoint: the average error in the final position of the virtual fingertip was 0.4 cm, corresponding to an 80% correction.

Figure 3.

Mean trajectories and kinematic data for a representative subject from experiment 1. The four sets of graphs (a–d) correspond to the four types of perturbations. Each graph plots three data series, corresponding to mean data from trials with positive perturbations (black lines), negative perturbations (gray lines), or no perturbations (thin lines). Before averaging across trials, the raw finger position data were normalized with respect to target direction and projected onto the tabletop (i.e., ignoring height from the table). The left graphs plot mean trajectories of the fingertip in x–y space on the tabletop. The three dashed circles on the graphs show the range of positions for the actual unseen fingertip that would successfully have brought the virtual fingertip to the target. Middle graphs plot (unsmoothed) finger speed as a function of time. Right graphs plot the y component of finger velocity as a function of time. The shaded regions depict when the virtual finger was hidden from view behind the occluder.

To compute a more sensitive measure of perturbation effects, we temporally decorrelated the raw data, as described in Materials and Methods. We fit an autoregressive model to predict the position of a subject's fingertip at each recorded frame of movement as a weighted sum of the preceding positions and a weighted contribution of the perturbation. The weight assigned to the perturbation at each time step provides a measure of the influence of the perturbation on subjects' movements. This is equivalent to correlating the residual of the best fitting autoregressive model with the perturbations.

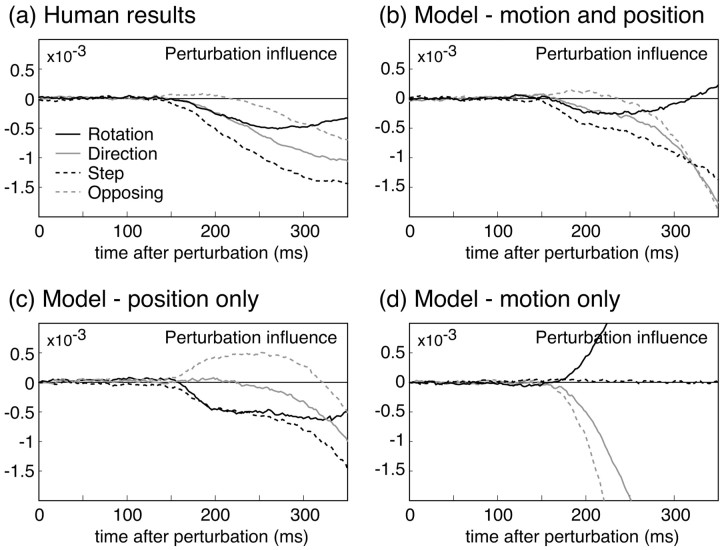
Figure 4a plots the measured perturbation influence functions as a function of time after the perturbation for the four perturbation types, averaged across subjects. All subjects showed the same qualitative pattern of results, with the only differences being in overall reaction time and magnitude of the influence functions. Rotation perturbations elicited transitory responses. For the other conditions, initial responses were in a direction appropriate for correcting for the overall effects of the perturbations. There was a consistent ordering in the overall magnitude of responses across conditions: step perturbations produced the largest effects, direction and rotation perturbations produced intermediate effects, and opposing perturbations produced the smallest effects.

Figure 4.

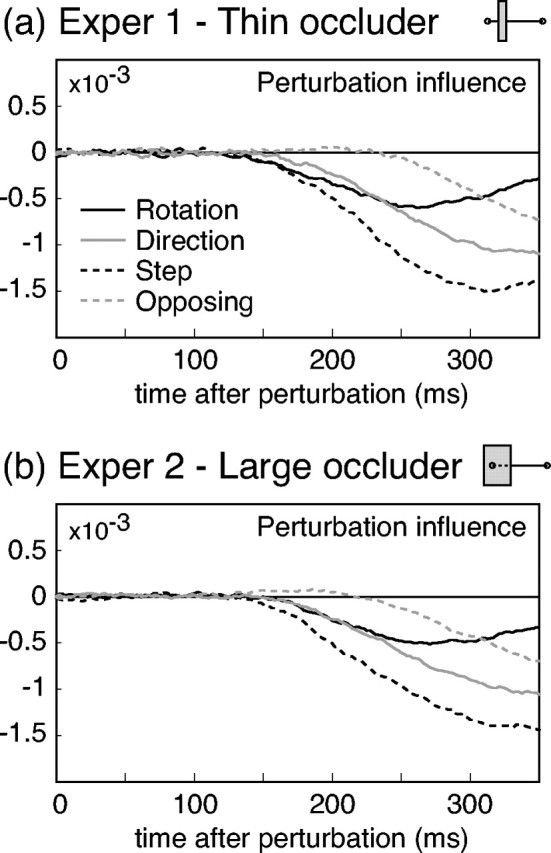
Perturbation effects. a, Results for experiment 1, in which the occluder was thin and the initial movement was visible. The four lines plot the perturbation in fluence functions for each of the four perturbation types. The raw weights derived from the regression analysis (see Materials and Methods) were smoothed by a causal exponential filter with time constant 25 msec and then averaged across subjects (n = 5). b, Results for experiment 2, in which the occluder was large and covered the entire initial movement. The plots show smoothed perturbation influence functions, averaged across subjects (n = 8), as in the previous plot.

Response latencies for each subject and condition were computed from the decorrelated time series. Rotation and step perturbations produced the fastest responses, with mean latencies of 143 msec (SD 8 msec) for rotations and 146 msec (SD 12 msec) for step perturbations. Responses to direction perturbations had slightly longer latencies, averaging 170 msec (SD 10 msec), whereas opposing perturbations produced very delayed responses, with 251 msec (SD 10 msec) mean latency.

Control for motion signal

The occluder was intended to mask the motion created by the transient jump in visual position caused by the perturbations while maintaining the naturalness of the stimulus display; however, long-range motion processes (integrating over a region ∼8° or more) could show a response to the transient jumps in three of the perturbation conditions. We controlled for this possibility in a second experiment, in which the task and perturbation types were the same as before, but the occluder was enlarged so that it covered the virtual fingertip throughout the initial movement. Under these conditions, there is no possibility of a motion cue to positional displacement. The time between the last view of the virtual fingertip on a previous trial and its reappearance from behind the extended occluder was ∼300 msec, during which the large high-contrast occluder appeared, adding a large temporal transient. If motion across the narrow occluder was a significant factor in the perturbation responses observed in experiment 1, one would expect responses in experiment 2 to be attenuated or absent.

Figure 4b shows perturbation effects in the second experiment, averaged across subjects, for the four perturbation conditions. As in the previous experiment, responses were observed for all conditions, including rotation perturbations. Overall, the magnitude of corrections and latencies of response were similar to the initial experiment. The only significant difference in results was that the response latency to rotation perturbations was slightly longer in experiment 2 (average 173 msec; SD 11 msec). This longer latency was statistically equivalent to the response latency to direction perturbations (average 176 msec; SD 7 msec). The results of experiment 2 demonstrate that subjects respond to perturbations of finger position even when motion cues to position displacement are eliminated. The near-equivalence of the effects across experiments strongly suggests that responses observed for the narrow occluder did not depend on the long-range motion cue.

Implications for control strategies

The results of the experiments strongly constrain the class of models that could account for visual feedback control of reaching movements. The data clearly contradict a model that uses only the visual motion of the hand, such as the homing strategy described in Introduction. In the rotation perturbation condition, the direction and speed of motion of the hand relative to the target are statistically the same in perturbed and unperturbed trials, yet in perturbed trials, subjects initially corrected their movements in a direction appropriate for the positional error created by the perturbation. Moreover, subjects showed very different responses to the other three perturbation conditions, despite the fact that all three conditions gave rise to equivalent relative motion errors for a significant period of time after the virtual finger reappeared from behind the occluder.

The results are also inconsistent with the hypothesis that the brain only uses positional information about the hand for feedback. The position feedback model would predict a much slower response to direction perturbations, in which position errors accrue slowly, than to any of the other three conditions. In experiment 2, however, subjects responded to these perturbations just as quickly as to rotation perturbations, which induced immediate positional errors. Control based solely on visual position would also predict similar initial responses to opposing and step perturbations, whereas observed responses in these conditions differed greatly in both strength and latency.

The response to opposing perturbations, for which the relative motion of the virtual finger initially suggests a correction in the opposite direction of that signaled by the positional error, is particularly illuminating. Subjects show a response in the correct direction, but much delayed relative to their responses to the other perturbations. They behave as if the positional and motion errors initially serve to cancel out their effects on the controller. A correction is only seen late because the positional error, by the nature of the perturbation, shrinks over time (and eventually changes direction), whereas the motion error remains constant. These observations lead to the general conclusion that visual feedback about both the position and motion of the hand contribute to on-line control of reaching movements.

An ideal observer model for feedback control of reaching movements

To understand how the brain combines motion and position feedback information for feedback control, and to relate human performance to the uncertainty that we might expect in those signals, we simulated the performance of a feedback control model that optimally integrates visual signals about the position and velocity of the hand over time. We used data from psychophysics on positional and motion acuity, as well as on temporal smoothing of visual signals, to parameterize the temporal filtering and visual noise components of the model. Such models have had recent success in accounting for perceptual estimation tasks in which subjects appear to optimally combine different sources of sensory information, and in one case feed-forward information from motor commands (Ghahramani, 1995; Wolpert et al., 1995b; Ernst and Banks, 2002; Van Beers et al., 2002).

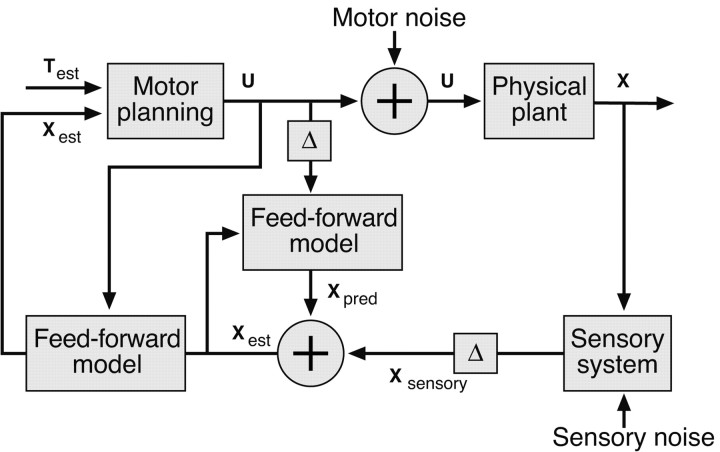
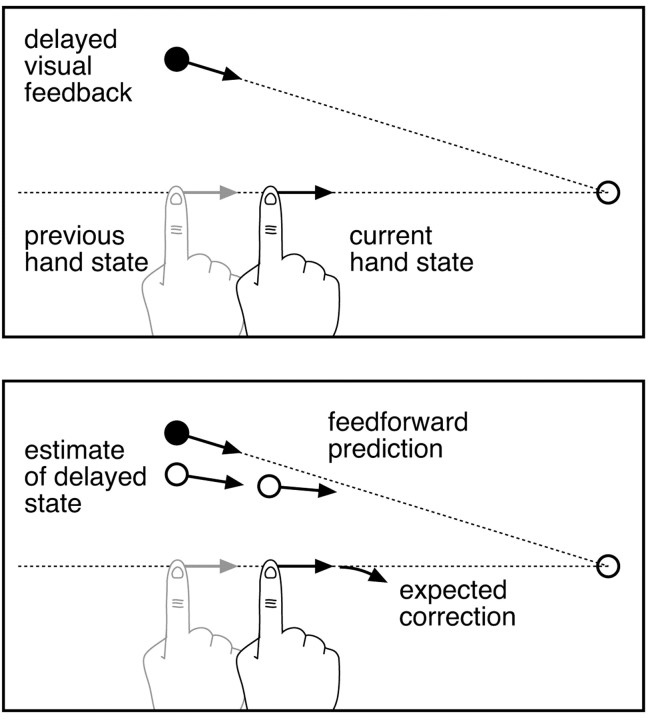
Figure 5 shows a schematic diagram of the model. The sensory component of the model is an adaptive Kalman filter that maintains a running estimate of the state of the hand using incoming sensory information and outgoing motor signals. The filter continuously updates its estimate of hand state by combining its current estimate with the information derived from new sensory (visual) signals and an estimate of the motor command that was most recently sent out to the system. To account for sensorimotor delays, the filter runs in a delayed loop, and the delayed estimates of hand state are input into a forward model that uses estimates of the motor commands sent out during the delay period to “predict” the current state of the hand from the delayed estimate (Miall et al., 1993). Figure 6 illustrates how such a system could qualitatively account for subjects' responses to rotation perturbations.

Figure 5.

Block diagram for the control model. The input to the system is the current best estimates of the state of the hand and the target position. The controller uses a minimum-jerk control law to convert these to a jerk signal (change in acceleration) to which motor noise is added before being applied to modify the motion of the hand. In the model presented here, the plant is trivial, because we assume a perfect kinematic controller. The plant simply integrates the jerk signal to change the acceleration of the hand. Delayed sensory estimates of the state of the hand are combined in an optimal way (through the Kalman gain matrix) with equivalently delayed internal estimates of the state of hand, and updated through the state update equation to generate a new estimate of the state of the hand at the next time step. The resulting sequence of state estimates are propagated forward through the state update equation, using the motor commands generated during the delay period, to generated ongoing estimates of the current state of the hand.

Figure 6.

Illustration of how the model would respond to rotation perturbations. a, The situation at the moment when the controller first has access to visual feedback, after the hand has come back into view. Because of sensory delay, the visual feedback corresponds to a previous state of the hand. b, To estimate current hand state, the new visual feedback is combined with the previous estimate of hand state (which at the moment of reappearance would correspond, on average, to the actual hand state) and propagated in time through a forward model of the system dynamics (using the motor commands sent out during the delay period). Because the perturbed visual path is rotated relative to the actual path, extrapolation would generally be inaccurate, leading to a “correction” away from the target direction.

Because we are concerned primarily with the nature of the visual feedback used to control reaching movements, we focused our modeling efforts on the sensory component of the model and used a simple minimum jerk control law to model the motor output of the system as a function of estimated hand state (Hoff and Arbib, 1993). The resulting model is equivalent to the Hoff and Arbib (1993) model, augmented with a Kalman filter to optimally integrate incoming feedback signals. Note that the control law uses internal estimates of hand position, velocity, and acceleration to generate motor commands, although the system that we model only uses visual feedback about position and velocity.

We simulated a model that incorporates state-dependent noise on the sensory feedback, with noise levels consistent with psychophysical measures of motion and position acuity in humans. The model therefore accommodates speed-dependent changes in motion discrimination thresholds and eccentricity-dependent changes in spatial acuity. We also assumed that the sensory estimates of both hand position and velocity were temporally low-pass filtered in concordance with observed psychophysical behavior (Werkhoven et al., 1992). Details are given in Materials and Methods. Parameters for the sensory filters—the noise levels for visual estimates of the direction and speed of finger movement, and the noise levels for visual position estimates—were derived from published psychophysical data as described in Materials and Methods. The only free parameters in the model were the noise terms for the control signal and the sensorimotor delay. These were set by hand to best fit subjects' data.

Figure 7 shows example mean trajectories derived from simulating the model's performance in the experiment described here. The model's corrections are all qualitatively similar to those shown by human subjects. More illuminating are the results of fitting the autoregressive model to estimate the perturbation influence functions for the model, shown in Figure 8b. The model replicates the results of all four perturbations. In particular, it replicates subjects' responses both to rotation perturbations (it shows a small, incorrect initial correction) and to opposing perturbations (it shows an apparent increase in the latency of the response to the perturbation). The model deviates somewhat from subjects' behavior at the ends of the movement. This is likely attributable to the fact that the model did not include low-pass filtering of the motor output and consequently allowed the production of physically unrealistic instantaneous changes in acceleration during final corrections.

Figure 7.

Sample mean trajectories of the model, for the same conditions as shown previously in Figure 3.

Figure 8.

Perturbation influence functions for human and model data. a, Replotting of the human data from experiment 2.b, Simulated responses of a feedback controller that optimally integrates both position and motion information to estimate hand state, to the same perturbation conditions tested in the human data (see Results for details). For each perturbation condition, we “ran” the model on many simulated trials and applied the same regression analysis to the model kinematics to derive perturbation weight functions for the model. Parameters for the simulations are given in Materials and Methods. c, Performance of the model if only feedback about hand position is used. The two notable deviations from human performance are that the model responds incorrectly to the initial positional error created by the opposing perturbation, and it responds much more slowly to the direction perturbations. d, Performance of the model if only velocity feedback is used. The model deviates dramatically from human performance. Note, however, that this model does not correspond to the homing strategy described in Results.

The performance of the model is very sensitive to the noise parameters. The response of the model to the opposing perturbations, in particular, deviates from subjects' performance when the relative levels of noise in the position and velocity signals are changed by as little as 25%. Changing the noise levels by ≥100% leads to more dramatic effects, such as significantly slowing the response to direction perturbations when the velocity noise is increased or greatly attenuating the response to the rotation perturbation when the position noise is increased. To illustrate the importance of including both position and velocity feedback, we simulated models that use only one or the other. The constrained models maintain state estimates of position, velocity, and acceleration, as required for the minimum-jerk control law, but only use visual feedback about either position or velocity. Thus, the position feedback-only model effectively uses changes in the position signal over time to update its internal estimate of velocity. The velocity feedback-only model effectively integrates the velocity feedback signal to update its internal estimate of position. As shown in Figure 8, c and d, eliminating either position of motion feedback dramatically changes the responses of the model to the perturbations and makes it impossible to fit subjects' performance. The qualitative pattern of behavior for these models is invariant to the free parameters of the model (sensorimotor delay and motor noise parameters).

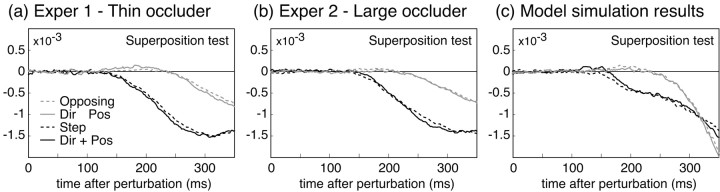
We can apply linear systems analysis to both subjects' and model performance data to glean a deeper understanding of subjects' on-line control. Were the human control system linear, the autoregressive model that we fit to the data would be the optimal predictor of measured finger position. The perturbation weight functions would also show the property of superposition: the weight functions derived from a perturbation that was the sum of two “base” perturbations would be equal to the sum of the weight functions derived separately for the base perturbations. Over the duration in which they could effect subjects' behavior, the average perturbations of any two of our perturbation classes, expressed as a function of time, were approximately linear sums of the other two (e.g., the step perturbation was equal to the sum of the rotation perturbation and the direction perturbation). Figure 9 shows that subjects' perturbation weight functions do follow the law of superposition. Similarly for the model, although it is only quasilinear (because of the state-dependent noise), the perturbation weight functions derived from the model's performance also show good superposition.

Figure 9.

Illustration of superposition on the perturbation effects. Both in the human data (a, b) and in the model data (c), responses to step perturbations were approximately the sum of responses to direction and rotation perturbations, and responses to opposing perturbations were approximately the difference of responses to direction and rotation perturbations. The results shown here are averaged across subjects. Individual subjects' data showed similar relations.

The superposition analysis shown in Figure 9 may be seen as reflecting how the relative errors in feedback about fingertip position, on the one hand, and motion, on the other, combine to generate corrective movements of the hand. When perturbations affect position and motion signals in opposite directions, as in the opposing perturbation condition, the feedback from the two signals almost exactly cancel each other for a period after the perturbation. Only when the position error shrinks does the system begin to respond to the motion error.

Discussion

Although the role of visual feedback from the hand for guiding movements has been the focus of extensive work (Keele and Posner, 1968; Carlton, 1981; Connolly and Goodale, 1999; Saunders and Knill, 2003), previous studies have addressed only basic issues of whether visual feedback contributes at various times during movements and the speed and magnitude of on-line corrections. More specific questions, like what visual control signals are used or how they are incorporated with nonvisual information, remain virtually unexplored. A novel aspect of the experiments reported here is that they distinguish different ways that visual feedback could be used. By using an interactive virtual environment, we were able to test various dynamic remappings of visual space that differentiate between classes of feedback control strategies.

The results demonstrate that visual feedback control during the fast phase of movements is not simply on the basis of the direction of hand motion relative to the target. Subjects made responses even when perturbations did not alter the relationship between hand motion and target direction, and conditions that introduced the same changes in target directional error produced different responses. To account for these effects, the feedback control mechanism must be sensitive to the conflicts between perturbed and actual hand position and not just to the direction of the hand relative to the target. The results also rule out a strategy based solely on visual position, such as steering to maintain a planned kinematic path or setting the desired instantaneous velocity based on the difference in hand and target position as in the VITE model (Bullock and Grossberg, 1988). In the case of direction perturbations, subjects responded before there was any significant conflict between actual and visually presented hand position, and perturbations that created matched positional conflicts produced different results depending on the visual direction of the hand. We conclude that both position and motion feedback signals are used for on-line control of hand movements.

As an analytical tool, we simulated the performance of a feedback controller that optimally integrates noisy visual estimates of hand position and velocity with a running estimate of hand state using a Kalman filter. We found that, with realistic assumptions about sensory noise and feedback delay, we were able to reproduce the pattern of perturbation responses observed in the human data. Moreover, the relative contributions of position and motion signals implied by the perturbation influence functions is consistent with what is known about position and motion acuity in human observers. Thus, subjects' responses to the perturbations were consistent with the noise levels to be expected in visual feedback signals.

It has been suggested previously that control based on visual position is slower than motion based-control and limited to final adjustments at the end of movements, when the hand is in central vision (Paillard, 1981, 1996; Blouin et al., 1993). Our results do not support such a qualitative distinction between the contributions of motion and position feedback signals. Responses to perturbations affecting position and direction were equally fast and in both cases would have had to begin when the hand was near peak velocity. Rather, humans appear to integrate position and velocity feedback in a manner consistent with the reliability of the signals.

The sensorimotor reaction time apparent in the influence functions shown in Figure 4 is on the order of 150–170 msec. This is somewhat slower than other estimates of reactions to large perturbations in target position (Goodale et al., 1986; Prablanc and Martin, 1992; Brenner and Smeets, 1997). Much of this difference is likely to be caused by the small size of the perturbations; however, we should note that the model showed similar apparent reaction times when the sensory delay built into the model was only 115 msec. The difference between the assumed sensory delay in the model and the appearance of significant responses to perturbations in the kinematics can be attributed to, on the one hand, the accrual over time of the influence of sensory feedback on internal state estimates in the Kalman filter, and on the other hand, to the effective low-pass properties of the minimum jerk controller, which makes smooth corrections rather than sharp ones.

Miall et al. (1993) propounded the idea that the visuomotor system uses a forward model to deal with long delays in sensory feedback. Data from adaptation studies are consistent with the hypothesis that the brain compensates for delayed estimates of hand state by propagating motor commands through a forward model of hand dynamics (Bhushan and Shadmehr, 1999). Although our experiments do not directly test this hypothesis, it is difficult to see how a system without some form of prediction could account for the results. The perturbations occurred when subjects' fingertips reappeared from behind the occluder, a point in the trajectory at which the hand was moving at near peak velocity. Given the visuomotor delay fit in the model (115 msec), subjects' fingertips would have been ∼6–9 cm closer to the target and moving much slower than indicated by the initial perturbed sensory feedback when the visual feedback would have begun to influence the movement. Without some form of compensation for the change in hand state that accrued during the sensory delay period, the system would have been unable to accurately correct for the perturbations.

The model simulated here used a simple minimum jerk control scheme, which did not take into account the dynamics of the musculoskeletal system. This model could potentially be refined by deriving an optimal dynamic control law for determining the neural control signals to send out to a model of the musculoskeletal system (Todorov and Jordan, 2002). Although this would be a significant improvement on our control model, we doubt that it would significantly impact the results relating to the weighting of feedback signals. Any reasonable control law will base its signals on the estimated state of the hand relative to the target, as does the minimum-jerk law. When the estimated hand position and velocity indicate that the hand is moving along a trajectory below the average trajectory, a controller will send a signal that includes a compensatory component. Thus, although the magnitude of instantaneous corrective responses will vary between controllers, the directions will not. The important qualitative conclusions that we have drawn should therefore generalize across a wide class of control laws.