Abstract
We investigated how V1 neurons integrate two stimulus features by presenting stimuli from a stimulus set made up of all combinations of eight different directions of motion and nine binocular disparities. We investigated the occurrence and shape of the resulting joint tuning function. Among V1 neurons, ∼80% were jointly tuned for disparity with orientation or direction. The joint tuning function of all jointly tuned neurons was separable into distinct tuning for disparity on the one hand, and orientation or direction tuning on the other. The degree of separability and the mutual information between the stimulus and the firing rates were strongly correlated. The mutual information of jointly tuned neurons when both features were decoded together was highly correlated with the mutual information when the two features were decoded separately, and the information was then summed. Jointly tuned neurons were just as good at representing information about single features as neurons tuned for only a single feature. The tuning properties of most jointly tuned neurons did not dynamically evolve over time, nor did jointly tuned neurons respond earlier than neurons tuned for only a single feature. The response selectivity of V1 neurons is low and decreases the information that a neuron represents about a stimulus. Together these results suggest that distinct stimulus features are integrated very early in visual processing. Furthermore, V1 generates a distributed representation through low response selectivity that avoids the curse of dimensionality by using separable joint tuning functions.
Keywords: striate cortex, orientation, direction, disparity, joint tuning, separability, information, binocular, motion, depth
Introduction
Our visual environment contains objects that differ in terms of many stimulus features, or dimensions, such as orientation, color, direction of motion, binocular disparity, and spatial frequency. To process information, the visual system needs to be sensitive to each of these features. Although it is well understood how these attributes are processed independently from each other, they rarely appear singly. This study aims to clarify how combinations of features are processed and integrated by the visual system.
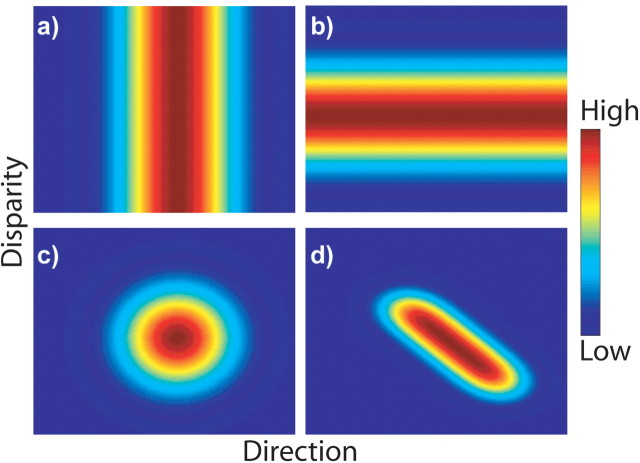
Several strategies to process and represent multiple features have been proposed. According to a simple but popular approach, each dimension is initially represented by its own exclusive pool of neurons (Treisman and Gelade, 1980; Livingstone and Hubel, 1988; Zeki, 1993). Each pool is tuned only for a single feature (see Fig. 1a,b), and the information across the different neuron pools is subsequently processed to allow for interactions across them. An alternative possibility is that the visual system integrates different features very early in processing. Lennie (1998) proposed the generation of a joint representation, where a single neuron pool represents various features and each neuron is jointly tuned for a combination of stimulus attributes (see Fig. 1c,d).
Figure 1.
Ways of representing multiple stimulus features. These maps show the firing rate of hypothetical neurons as a function of direction and disparity. Multiple stimulus features could be encoded in three different ways: by neurons that are exclusively tuned for a single stimulus feature such as only direction (a) and only disparity (b), by neurons that encode multiple stimulus features separably (c), and by neurons that encode multiple stimulus features in a nonseparable way (d).
The way in which a neuron responds to multiple stimulus features is expressed by a joint tuning function, which is the activity of a neuron in response to all combinations of stimulus features. This function can take many different shapes, giving rise to two possible representational strategies. In one strategy, multiple features are represented by a joint tuning function that is the combination (e.g., multiplication) of distinct tuning curves for each individual feature (see Fig. 1c). Such a joint tuning function is called “separable.” It has the virtue that the joint tuning is a natural extension of the tuning for each individual feature, thus simplifying the decoding of single features. Another strategy is to represent features by a joint tuning function that cannot be expressed as the combination of distinct tuning curves for individual features (see Fig. 1d). Such a joint tuning function is called “inseparable,” because the tuning for a single feature depends on the specific choice of another feature. An inseparable joint tuning function allows neurons to represent higher-level features. For example, space-time inseparability by striate cortex (V1) neurons gives rise to direction selectivity (Adelson and Bergen, 1985).
Although several groups have studied single-feature tuning curves for several stimulus attributes (Schiller et al., 1976; De Valois et al., 1982; Leventhal et al., 1995; Geisler and Albrecht, 1997; Smith et al., 1997; Grunewald et al., 2002; Prince et al., 2002a), very little research has systematically explored joint tuning by presenting stimuli made up of feature combinations. Some studies have focused on contrast, orientation, or spatial frequency (Webster and De Valois, 1985; Jones et al., 1987; Hammond and Kim, 1996; Victor and Purpura, 1998; Bredfeldt and Ringach, 2002; Mazer et al., 2002). The joint representation of these features has been modeled with the same spatial filter and thus may be a special case (Daugman, 1985; Jones and Palmer, 1987; Parker and Hawken, 1988). To extend our understanding of the representation of multiple features, Qian (1994) proposed that direction and disparity are represented jointly and this representation is separable. It is now known that some V1 neurons are jointly tuned for direction and disparity and these neurons exhibit spatiotemporal as well as disparity-temporal tuning (Anzai et al., 2001; Pack et al., 2003). At present, however, the hypothesis of Qian (1994) that direction and disparity are primarily represented jointly in V1, and that this representation is separable, still has not been tested. In contrast, it has been shown that many neurons in area medial superior temporal (MST) represent direction and disparity inseparably (Roy and Wurtz, 1990). Therefore, the present study aims to elucidate the strategy used by V1 to represent and integrate several important features: binocular disparity, direction of motion, and orientation.
Materials and Methods
Animal preparation. Two male monkeys (Macaca mulatta), aged 3-5 years, were used. All procedures were in compliance with the National Institutes of Health Guide on the Treatment of Animals and were approved by the Animal Care and Use Committees at the University of Wisconsin-Madison. All surgeries were performed under sterile conditions using general anesthesia. In one procedure, two scleral search coils (one in each eye) were implanted, craniotomies were performed, and recording cylinders were implanted over V1 (30° bevel, normal to skull; 15 mm lateral from midline, 12 mm above occipital ridge). Water intake of the animals was regulated during experimental sessions, and water intake and weight were monitored on a weekly basis to ensure the health of the animals. Usually animals were used in experimental sessions during the week, and they had ad libitum access to water on the weekends.
Experimental apparatus. All experiments were performed in a dark, sound- and radiofrequency-shielded booth (Acoustic Systems, Austin, TX). To measure eye position, the animals were placed inside an 18 inch field coil (Crist, Bethesda, MD) that induces a magnetic field. Animals were under constant supervision via an infrared camera. Behavioral control and data collection were performed using a commercially available experimental control program (TEMPO, Reflective Computing, St. Louis, MO) running on two PCS. Visual stimuli were generated by a dedicated graphics computer, running an OpenGL graphics program on a dual Processor PC.
Data collection. The animals were seated in a primate chair, facing a computer monitor, and performed a fixation task for fluid reward. In this task, animals maintained their gaze within 1° of a central spot of light for 2 sec. The head was fixed, and the eye position of both eyes was monitored using the scleral search coil technique (Judge et al., 1980). Between one and four epoxy-(Fred Haer, Bowdoinham, ME) or glass-coated (Alpha-Omega, Jerusalem, Israel) tungsten electrodes with 0.5-3 MΩ impedance at 1 kHz were independently advanced into V1 using a multi-electrode microdrive (MT and EPS, Alpha-Omega). The signal from each electrode was amplified and filtered (0.6-6 kHz), and a notch filter was applied (MCP, Alpha-Omega). Single neurons were isolated on-line using a template-matching algorithm (MSD, Alpha-Omega). The receptive field (RF) of each neuron was mapped using a pattern of dots that could be moved on a computer screen using a computer mouse.
Visual stimuli. Visual stimuli were shown on a high-speed monitor (CV 931 X, Totoku) running at 160 Hz, with a resolution of 1024 × 768. Visual stimuli consisted of moving dots that were anti-aliased, allowing for subpixel resolution. Thus, visual stimuli could be rendered with high temporal and spatial resolution. Moving dots had 0.12° diameter and appeared in yellow, red, or green. Visual disparity was generated using a red/green anaglyph system using Kodak Wratten filters: in front of the right eye was a red filter (filter number: 29), and in front of the left eye was a green filter (filter number: 61). All luminances had been adjusted so that dots of all colors (red, green, or yellow) had the same luminance when viewed through the filters (5.4 cd/m2). The cross talk between the two eyes was as follows: the luminance of green dots seen through the red filter was 0.2 cd/m2, and the luminance of red dots seen through the green filter was 0.7 cd/m2. In addition, a fixation point (diameter 0.2°) was shown in white.
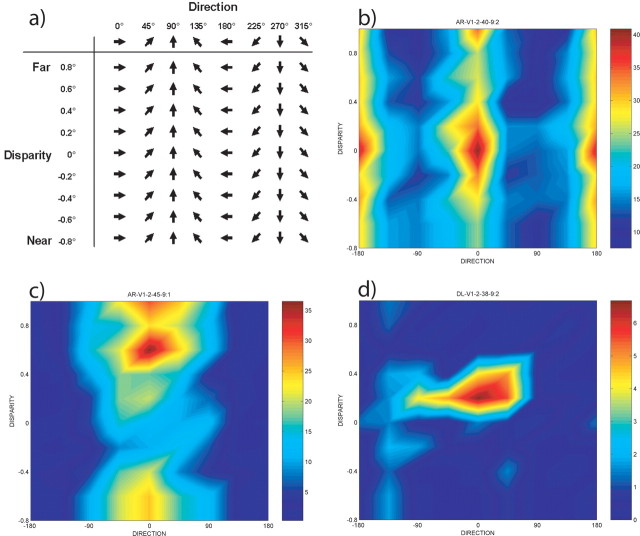
All stimuli were composed of a single set of dots moving coherently in a fronto-parallel plane. The moving dots were shown within a circular aperture, having a diameter of 5° and dot density of 40 dots per square degree. The stimuli were positioned to cover the RFs of all neurons that were being recorded. The RFs had median eccentricities of 2.2° (range 0.1°-5°) in animal A and 3.9° (range 1.8°-18.6°) in animal D. The speed of the dots was 6°/sec, and there were eight possible directions of motion spaced at 45°. The dots were shown at one of nine possible disparities, ranging from near (-0.8°) to far (0.8°) in steps of 0.2°. All (8 × 9 = 72) combinations of directions and disparities were used as visual stimuli. For control purposes, a blank stimulus was also shown, yielding a total of 73 distinct stimuli. A single visual stimulus was shown per trial, lasting 1 sec. Other than the fixation point, the screen was blank for 0.5 sec both before and after the stimulus. Trials were blocked so that within each block each stimulus was presented exactly once. Usually five blocks were run during a recording session.
Analysis. Most of the analyses were performed using Matlab (Math-works, Natick, MA), although SAS was also used for some statistical analyses (SAS Institute, Cary, NC). In each trial the firing rate was determined over the 1 sec stimulus interval. To determine tuning properties, we performed a weighted two-way ANOVA, where the weighting (by the inverse of the variance) served to homogenize the variance across stimulus conditions. We used a bootstrap analysis to determine whether a neuron that showed a significant effect of direction/orientation was actually direction selective or tuned for orientation. Throughout our analyses, the distinction between direction- and orientation-tuned neurons was maintained. To determine tuning indices, we averaged data across different repetitions of the same stimulus. For each neuron we determined the peak response P, which occurred at the preferred direction and the preferred disparity. The direction index is 1 - A/P, in which A is the response to a stimulus moving opposite to the preferred direction at the preferred disparity. The disparity index is 1 - W/P, where W is the weakest response to a stimulus moving in the preferred direction. In control analyses we also determined more traditional indices: the traditional direction index using a direction tuning curve at zero disparity and the traditional disparity index using a disparity tuning function at the preferred direction. These two traditional indices were strongly correlated with our indices. Because our indices use all of the available data, we preferred them in our analyses.
To determine whether a neuron was separable, we performed a singular value decomposition (SVD) (Peña and Konishi, 2001; Mazer et al., 2002). SVD is the decomposition of a matrix into a sum of matrices, each of which in turn is the product of separate direction and disparity tuning curves. The matrices are ordered such that the first contributes most to the sum and the last contributes the least. The weight of each matrix is called the singular value (SV). To determine whether a neuron is separable, it is enough to test that the first (and therefore strongest) but not the second SV is significantly larger than the noise level (permutation test; p < 0.05). If the second SV exceeds the noise level, a neuron is not separable. The degree of separability was further quantified using the separability index, which is obtained by squaring the first SV and dividing it by the sum of the squares of all SVs. It ranges from 12.5% (not at all separable) to 100% (completely separable).
To better understand the joint tuning function, we fit the mean firing rates to four distinct models, each of which combined single-feature tuning functions (Fig. 1) that were obtained in the optimization process. These single-feature tuning functions were nonparametric. The single-feature tuning function was made up of eight direction weights, and the disparity was made up of nine disparity weights. Fits for orientation tuning had only four orientation weights. The combination of the orientation and disparity weights could be multiplicative (12 df because there was a common gain, and each single-feature tuning function had one redundant weight), additive (12 df), or the larger of the two (winner-take-all, 13 df). We also fit a multiplicative model with an additive baseline term (13 df). The combination of direction and disparity had four additional degrees of freedom in each model. The modulation strength was determined based on the single-feature tuning functions obtained in this latter, enhanced multiplicative fit, although the trends reported are true for all of the models. (This measure is also known as the modulation depth; however, to avoid confusion with binocular disparity, we refer to it as modulation strength here.) The modulation strength related to a single-feature tuning curve was defined as the difference between the largest and smallest weights divided by their sum. Because for each neuron there were three single-feature tuning curves (orientation, direction, and disparity), there are also three distinct modulation strengths, one for each feature. For orientation-tuned neurons, we used only the orientation modulation strength, and for direction-tuned neurons, we used only the direction modulation strength. To determine the variability of a neuron, we used the relationship between the mean and variance of the firing rate (Vogels et al., 1989; Snowden et al., 1992). We performed a linear regression in log-log coordinates resulting in a slope and an offset. We refer to the slope as “response variability.”
To determine the mutual information, we used the raw, unaveraged data and binned the firing rates into six bins of variable width such that on average, each bin contained the same number of trials. We have varied the number of bins used (range, 4-12) and obtained similar results. Using the binned data, we estimated the probability distributions of the stimulus p(s), the neural response p(r), and their joint distribution p(s,r). We determined the mutual information using the following standard equation: I(S;R) = H(S) + H(R) - H(S,R), where H(X) = -∑x p(x) log2 p(x).We compensated biases in the estimation of the mutual information using extrapolation (Strong et al., 1998) and randomization procedures. In rare cases, the information estimate was negative, which was corrected by setting the information to zero. We also used a parametric technique to determine mutual information without the need for binning (Gershon et al., 1998), which yielded similar results. To determine the response selectivity (Rolls and Tovee, 1995; Vinje and Gallant, 2002), we determined the selectivity index by applying the following equation to the data from each neuron separately:
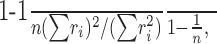 |
where ri is averaged firing rate, i indexes is different stimulus conditions, and n is the total number of stimulus conditions. The selectivity index ranges from 0% (not at all selective) to 100% (selectivity for only one stimulus).
We also determined the effect of eye movements. To do so we determined the mean fixation drift and mean vergence in each trial. We then subjected both of these measures separately to a two-way ANOVA with direction and disparity as main effects. Sessions that showed a significant effect of direction on the fixation drift and those that showed a significant effect of disparity on vergence were excluded from further analysis.
Results
Database
We performed 110 recording sessions in two animals. Of these sessions, approximately one-third were excluded from further analysis because there were systematic effects of eye movements. In these sessions, the stimulus condition affected fixation drift in 23% of sessions and vergence in 15% of sessions (some sessions showed both effects). Because V1 RFs are tiny, small but systematic changes in eye position may affect firing rates, thus potentially biasing direction and disparity tuning. To avoid any biases, we removed all neurons recorded during these sessions from the database. In the remaining 75 recording sessions, we recorded the neuronal activity of 184 neurons. Based on neuronal depth under the dura and the position of layer 4C, we estimate that most of the neurons recorded were located in the supragranular layers; however, no histological data are available to confirm this. Furthermore, because of the very large number of different stimulus conditions, no classification of neurons as simple or complex cells could be performed.
Tuning
We determined the joint tuning for binocular disparity and direction of motion of single neurons by presenting all 72 combinations of 8 directions and 9 disparities (Fig. 2a). Although the stimulus set does not contain orientations per se, orientation-selective neurons do respond to these stimuli, although they respond similarly for opposite directions of motion. The two opposite directions resulting in maximal responses are parallel to the preferred orientation of a neuron. Neurons are categorized as tuned for orientation or direction, and all further analyses are adjusted accordingly. The joint tuning function for one example neuron is shown in Figure 2b. A weighted two-way ANOVA is used to analyze the tuning properties of this neuron. This neuron is tuned for both orientation and disparity and has no interaction. A second neuron that is tuned for direction and disparity is shown in Figure 2c. Finally, Figure 2d shows a neuron that has an interaction between direction and disparity. Among the 184 single neurons that we recorded from, 150 are tuned for our stimulus set. Among these tuned neurons, only a small proportion of neurons are tuned exclusively for one stimulus feature (orientation, 8%; direction, 5%; disparity, 6%). The remaining 81% of neurons are jointly tuned and thus integrate multiple stimulus features. From this, we conclude that joint tuning for multiple stimulus features is a common property of V1 neurons.
Figure 2.
Stimulus set and example neuron. a, The joint tuning for direction and disparity was studied by presenting stimuli that varied in both direction of stimulus motion and binocular disparity. The resulting firing rates give rise to a joint tuning function, which depends on both direction and disparity. b, A map representation of the joint tuning function. Maps have been aligned such that 0° corresponds to the preferred direction. Calibration indicates firing rate calculated over the 1 sec stimulus interval. This neuron is tuned for orientation and disparity. The neuron is orientation selective because there are two (opposite) directions for which it is strongly activated. c, A neuron that is tuned for direction and disparity. d, A neuron that exhibits a significant interaction between direction and disparity. Note that direction is circular and hence wraps around.
Among the neurons that integrate multiple features, three neuron types could be distinguished. As one would expect in V1, the largest group of neurons (45%) were tuned for orientation and disparity. Furthermore, 21% were tuned for direction and disparity, and 34% had a significant interaction between direction and disparity. Unless stated otherwise, “joint tuning” refers to all three of these neuron types together. Note that the existence of an interaction in a neuron does not imply that it is not separable. For example, if direction and disparity are multiplied by a neuron, that neuron is likely to have a significant interaction, although its joint tuning function is separable.
Separability
The integration of multiple features can be accomplished in many ways. One obvious possibility is that the joint tuning function is simply a combination of separate tuning for each stimulus feature. Neurons for which the joint tuning function can be decomposed into distinct orientation and disparity tuning curves or distinct direction and disparity tuning curves are called separable. (For simplicity, we will hence forth refer to orientation/direction, meaning that for neurons tuned for orientation we used orientation, and for neurons tuned for direction we used direction.) An SVD was used to test whether V1 neurons are separable. Across our sample of jointly tuned neurons, every one was separable (permutation test; p < 0.05). The separability index quantifies the degree of separability without using a binary criterion (see Materials and Methods).
The separability index can be thought of as the proportion of the variance that is accounted for by a separable model given the data. As such, one might worry that this index may be affected by two different components: the true separability of a neuron under study, and noise in the data. Because the separability index is analogous to the R2 statistic, the noise has already been taken into account by the separability index. Still, to limit the effect of noise, we use averaged firing rates when determining the separability index. Furthermore, we directly investigated the relationship that peak response, single-feature tuning, or response variability have on the separability index using correlation analyses. We find that none of these variables that are not tied to separability are correlated with the separability index (Table 1). Thus, having eliminated potential confounding variables, we are confident that the separability index is a measure of separability.
Table 1.
Correlation of separability index with other variables
|
|
Correlation coefficient |
p value greater than |
|---|---|---|
| Response peak | 0.07 | 0.5 |
| Modulation strength (orientation) | 0.08 | 0.5 |
| Modulation strength (direction) | −0.01 | 0.9 |
| Modulation strength (disparity) | −0.02 | 0.8 |
| Response variability |
−0.08 |
0.4 |
This table shows for five distinct variables that could be related to the separability index the Spearman Rank correlation index and the corresponding p value (rounded down to the nearest decimal). As shown, none of the correlations are significant, suggesting that the separability index does not represent these other variables and instead is a true measure of separability.
In our sample of V1 neurons, the separability index was quite high (50%). Among the three neuron types, the separability index differed significantly, being largest for neurons with an interaction between direction and disparity (Kruskal-Wallis test; p < 0.01). This is consistent with a multiplicative rather than an additive combination of the two stimulus features.
Although SVD is very sensitive at detecting separability, it is not as sensitive in determining how single-feature tuning curves are combined. To study how the single-feature tuning curves are combined, we fit the data with three possible models. In the multiplicative model, the joint tuning was caused by the multiplication of separate orientation/direction and disparity tuning curves; in the additive model, the joint tuning was caused by the addition of separate tuning curves; in the winner-take-all model, the joint tuning was the larger of the separate tuning for each condition. Across our sample of neurons, we find that all three models account for the data very well, with <5% of neurons failing a χ2 goodness-of-fit test. There were only small but significant (p < 0.001) differences between the proportion of variance accounted for by each model (multiplicative, 67%; additive, 66%; winner-take-all, 62%). Our previous finding that joint tuning is separable is supported by the fact that these three models provide very good fits, and they are all separable. Adding an extra parameter to the multiplicative model for the baseline activity significantly improves the variance accounted to 69%.
We noticed that the joint tuning function for many neurons was dominated by one feature and that the other feature seemed to provide a smaller contribution (Fig. 2b,c). To find out whether this impression is generally true, we determined the strength of modulation for orientation, direction, and disparity separately using the models just described (see Materials and Methods). The strength of modulation is a measure of how much the firing rate changes as one of the features is changed. Thus, there are three modulation strengths: one for orientation, one for direction, and one for disparity. We find that for neurons tuned for orientation and disparity, the median modulation strength for orientation is 31% lower than that for disparity (Wilcoxon test; p < 0.005). For neurons tuned for direction and disparity, the median modulation strength for direction is ∼64% higher than that for disparity (Wilcoxon test; p < 0.05). This effect might be an artifact of the stimulus space. Although orientation and direction are circular and we can therefore map the entire space, the disparity is linear, and we map only a section of this space (-0.8° to 0.8°); however, because the maximum disparity is large (0.8°), which is a horizontal offset on the order of the size of a receptive field of a V1 neuron, this is unlikely to be a problem. Furthermore, the orientation modulation strength for neurons only tuned for orientation does not differ significantly from the disparity modulation strength for neurons that are only tuned for disparity (Mann-Whitney; p > 0.1). Finally, previous reports have shown that for the majority of V1 neurons, the extrema of the disparity tuning curves lie within the range that we tested (Poggio et al., 1985; Prince et al., 2002b). Thus, for jointly tuned V1 neurons, the modulation strength for direction is larger than that for disparity, which in turn is larger than that for orientation.
Mutual information
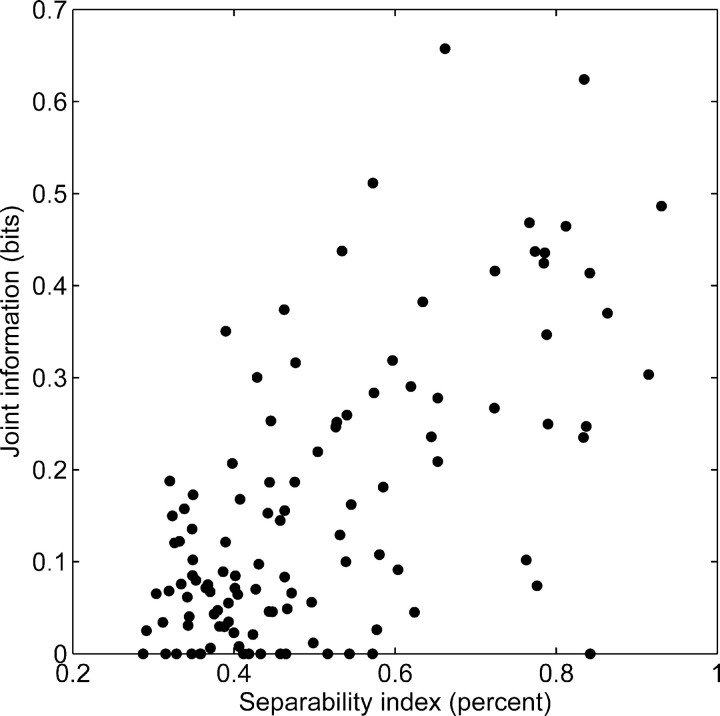
The results described thus far show that V1 neurons are separable, but this analysis leaves unclear what the benefit of separability is for a single neuron. This benefit can be gleaned from the main role of a neuron, which is to process and transmit information. Consequently, to determine whether separability is useful for neurons, we determined the mutual information between our stimulus set containing both direction and disparity and the firing rate. Because both stimulus features are included, we call this the joint information. If separability is important for neurons, then across our neuron sample the joint information and the separability index should be correlated, which we find confirmed (Spearman rank correlation rs = 0.58; p < 0.001) (Fig. 3). We noted previously that, in principle, the separability could be confounded with other variables, such as peak response, modulation strength, or response variability. Although we have already shown that these variables are not related to the separability index, we wanted to ascertain that there are no residual effects. To this end, we determined the partial correlation between the joint information and the separability index, from which potential correlations attributable to peak response, modulation strengths, and response variability are removed. This partial correlation is highly significant (rs = 0.63; p < 0.001), indicating that the relationship between separability index and joint information is truly caused by separability and not an artifact of other variables. This is a correlational analysis, without a specific causal direction; however, if one accepts that the degree of separability is a constant property of a neuron and the joint information is the outcome of processing in a specific set of trials, then our results suggest that the degree of separability enhances the ability of individual neurons to represent visual information. This makes separability a highly advantageous strategy to integrate multiple stimulus features, such as direction and disparity.
Figure 3.
Separability index and joint information. As the separability index increases, so does the information that a jointly tuned neuron represents about the stimulus. The separability index is a percentage that expresses how separable a neuron joint tuning is. Neurons that are completely separable have a separability index of 100%. Neurons that are completely inseparable have a separability index of 12.5%.
In some situations it may be of interest to access only a single stimulus feature such as direction, although a neuron is tuned for both orientation/direction and disparity. How well are individual neurons able to represent single features? To understand this, we determined the direction information, which is the information that a neuron provides about the stimulus direction while ignoring the disparity. Similarly, we determined the orientation and disparity information. Jointly tuned neurons that were orientation tuned represented ∼20% more information about disparity than about orientation (Wilcoxon test; p < 0.05); however, the theoretical maximum orientation information is only ∼60% of the maximum disparity information, because there were only four orientations and nine disparities. If we take this into account, in other words if we compare the capacity, the difference between orientation and disparity vanishes (Wilcoxon test; p > 0.2). In contrast, jointly tuned neurons that were direction tuned represented more than four times as much information about direction than about disparity (Wilcoxon test; p < 0.001), with or without taking the maximum information into account. This pattern of results is consistent with our previous results that the modulation strength for direction is larger than that for disparity, which in turn is larger than that for orientation. Having looked at the representation of individual features, we next turn to the joint representation.
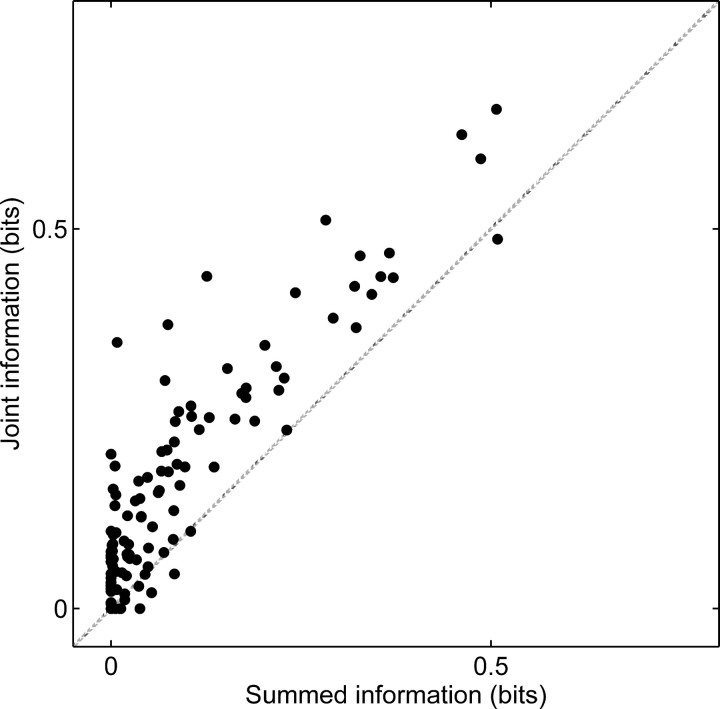
The summed information is the sum of the orientation/direction and disparity information. One of the results from information theory states that if the representation of orientation/direction and disparity is statistically independent (which is a stronger statement than separability, because separabililty is only a statement about mean firing rates, whereas independence is also a statement about higher-order statistics, such as the variance), then the joint information should equal the summed information. Otherwise, the joint information should be larger than the summed information. Across our sample of jointly tuned neurons, these two quantities are strongly correlated (rs = 0.9; p < 0.001) (Fig. 4); however, the joint information is consistently larger than the summed information (Wilcoxon test; p < 0.001). It is interesting to note that the difference (0.07 bits) is approximately constant and does not depend on how large the joint or summed information is (Fig. 4). Thus, there is a nearly constant cost associated with neurons that integrate multiple features when decoding only a single feature. As one would expect, this cost is negligible for single tuned neurons. Of course, the cost for jointly tuned neurons disappears if the other feature is known ahead of time.
Figure 4.
Comparison of decoding both stimulus features at once or one at a time. The joint information (about both direction and disparity) is strongly correlated with the summed information (the sum of the separate direction and disparity information).
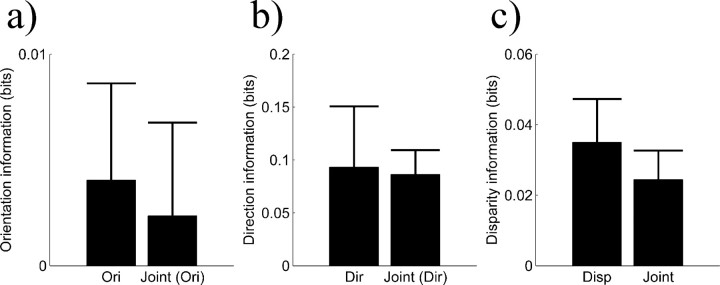
Neurons only tuned for a single feature should have, in principle, an advantage in representing a single stimulus feature. To test this, we compared the orientation/direction information of neurons tuned only for orientation or direction and of neurons jointly tuned for orientation/direction and disparity. Similarly, we compared the disparity information of disparity tuned neurons and jointly tuned neurons. Across our sample of neurons, the information represented about single stimulus features (orientation, direction, or disparity) by single tuned neurons was not significantly different from the information represented by jointly tuned neurons (Mann-Whitney test; p > 0.4) (Fig. 5). Because of the small number of neurons tuned for a single feature, the power of this test is limited; however, based on the difference between joint information and summed information of 0.07 (see above), one would expect half that difference between jointly tuned and single tuned neurons when decoding a single stimulus feature. The actual difference is considerably smaller than the expected value, suggesting that joint tuning does not adversely affect the ability to represent single stimulus features. This is a counterintuitive result, because, in principle, single tuned neurons should always have a large advantage over jointly tuned neurons when only single stimulus features are considered.
Figure 5.
Representation of single features by single and jointly tuned neurons. a, The orientation information for neurons tuned only for orientation (Ori) is not significantly different from that for jointly tuned neurons that are orientation selective [Joint (Ori)]. b, The direction information for neurons tuned only for direction (Dir) is not significantly different from that for jointly tuned neurons that are direction selective [Joint (Ori)]. c, The disparity information for disparity tuned neurons (Disp) is not significantly different from that for jointly tuned neurons (Joint). Bar height denotes median information, and error bars represent SEs.
Thus, it appears that the neurons that are only tuned for a single stimulus feature are particularly poor at representing that stimulus feature. There are three obvious explanations for this. First, the mean firing rates of neurons that are tuned for a single stimulus feature may not be spread out as much as those of jointly tuned neurons. If this is the case, then the modulation strength for single tuned neurons should be smaller than the modulation strength for jointly tuned neurons. This difference is not significant for orientation (Mann-Whitney test; p > 0.2), direction (p > 0.1), or disparity (p > 0.3). Alternatively, the mean firing rates of single tuned neurons may be higher than for jointly tuned neurons. Because the variance of the firing rate is correlated with the mean firing rate (Vogels et al., 1989; Snowden et al., 1992), this would result in higher variances; however, the opposite is the case. Single tuned neurons have lower mean firing rates than jointly tuned neurons (Mann-Whitney test; p < 0.05). Finally, it is possible that the relationship between mean and variance is steeper for singly tuned neurons than for jointly tuned neurons, resulting in noisier responses. As is customary, we performed a regression of the mean against the variance in log-log coordinates (Vogels et al., 1989; Snowden et al., 1992). This regression results in a slope and an offset. We refer to the slope as response variability. Across our sample of neurons, we find that neurons tuned for a single stimulus feature tend to have a larger response variability than jointly tuned neurons (Mann-Whitney test; p < 0.005), whereas the offset does not differ significantly (p > 0.6). In other words, when the mean is factored out, the firing rate of single feature neurons is more variable than that of jointly tuned neurons. This increased variability of single feature neurons reduces their ability to represent single feature information in a way that is comparable with the reduction of jointly tuned neurons because of their joint tuning. This reduction is of a magnitude similar to the cost of jointly representing two features. As a result, single and jointly tuned neurons represent single features equally well.
Dynamics
Neuronal responses develop over time. It is possible that the first neurons that respond are tuned for single features and neurons that integrate multiple stimulus features start responding later, for example, because of feedback mechanisms. To understand this we determined neuronal response onset latencies. On average, latencies depend on the neuron type. Neurons that are tuned for two stimulus features tend to have shorter latencies than neurons that are tuned for a single feature or show an interaction (Kruskal-Wallis test; p < 0.05) (Table 2). Therefore, jointly tuned neurons in general are not activated after single tuned neurons.
Table 2.
Response latencies as a function of neuron type
|
|
Single |
Joint |
Inter |
|---|---|---|---|
| Mean latency (msec) | 89 | 69 | 81 |
| SE (msec) |
1.7 |
0.4 |
0.8 |
Neurons that are tuned for a single feature (Single) have longer latencies than neurons that are tuned for two features (Joint) or neurons that have an interaction (Inter).
Alternatively, it might be that neurons initially are tuned for single features and that they develop tuning to multiple features over time. To test this, we determined the firing rate over the first 25 msec after response onset for neurons for which the response onset latency could be determined. We then classified the neurons as singly or jointly tuned. The proportion of these neurons that are jointly tuned is only slightly smaller over the first 25 msec (73%) than over the entire 1 sec stimulus interval (81%). This indicates what happens across the population of neurons. For individual neurons, tuning properties remain fairly constant: 86% of neurons that were jointly tuned over the first 25 msec are also jointly tuned across the entire 1 sec stimulus interval. Conversely, of the neurons that are jointly tuned over the 1 sec stimulus interval, 76% were jointly tuned during the first 25 msec. Thus, whether a neuron is singly or jointly tuned remains fairly constant across the response. Together, these analyses suggest that joint tuning arises early in the response and dynamical changes over time play a role in only a minority of neurons.
Response selectivity
Two different models have been proposed to show how a population of neurons represents stimuli. In a sparse code, the activity of a very small number of neurons represents a stimulus. In contrast, in a distributed code, most neurons are active in response to a stimulus. These two codes impose important requirements in single neuron responses. In the sparse code, a single neuron should be highly selective and thus not very responsive, whereas in a distributed code, a single neuron should only be weakly selective, and therefore active most of the time. Clearly, the selectivity of a neuron is based on properties of the joint tuning function; but which properties of this joint tuning function matter?
To answer this question we determined the selectivity index. It is an index that indicates how rarely a neuron is active (Rolls and Tovee, 1995; Vinje and Gallant, 2002). Across our sample of V1 neurons, the selectivity index is quite low (18%) and does not differ across the three jointly tuned neuron types or between singly and jointly tuned neurons (Kruskal-Wallis test; p > 0.8). The selectivity index is distinct from the separability index, but they are correlated (rs = 0.44; p < 0.001). The selectivity index is strongly correlated with the direction index (rs = 0.52; p < 0.001), meaning that direction tuned neurons are highly selective. The response selectivity is also correlated with the disparity index (rs = 0.80; p < 0.001). This is not surprising, because it measures the selectivity of a neuron. More importantly, the selectivity index is correlated with the excess fit of the multiplicative model over the additive model (rs = 0.31; p < 0.001). In other words, neurons are more selective the more multiplicative the two feature dimensions interact in the joint tuning.
If neurons use sparse coding to enhance their ability to represent visual information, then there should be a correlation between selectivity index and the joint information. In contrast, in a distributed code, there should be a negative correlation. These two quantities are not correlated (rs = -0.09; p > 0.3), thus not favoring either model. It is possible, however, that the separability index somehow masks the effect of the selectivity index. To uncover this, we performed multiple regression, using the joint information as the dependent variable and the separability and selectivity indices as independent variables. The multiple regression model is significant (p < 0.001) and accounts for 54% of the variance. We find that, as before, the separability index increases the information represented (slope = 0.8 bit per percentage separability index; p < 0.001), whereas the selectivity index decreases the information represented (slope = -0.3 bit per percentage selectivity index; p < 0.001). The decrease in the information with increasing selectivity means that a neuron that fires in response to more stimuli can represent more states that are distinct from each other than a neuron that is only active for very few stimuli.
Having used multiple regression as a way to unmask weak effects on the joint information, we extended this by adding five additional factors to the regression model: peak firing rate, all three modulation strengths, and the response variability. This leads to an increase of variance accounted to 60%. The coefficients of peak firing rate and all modulation strengths are not significant. In contrast, the coefficient for the response variability (slope = -0.0322 bit; p < 0.05) is significant. It is not surprising that the response variability should reduce the overall amount of information represented. Based on these results, we developed a final model that contained only separability index, selectivity index, and response variability. This model accounted for 58% of the variance. The slopes and significance of separability index, selectivity index, and response variability were not different from the previous model. Together, these analyses confirm that separability per se was the best predictor of the information that a neuron could represent and this predictive power could not be explained on the basis of other factors such as peak response, modulation strengths, or response variability.
More selective neurons respond to fewer different stimuli; in the extreme case, such neurons respond to only one stimulus at a specific direction and disparity. For such a neuron it would be irrelevant how it was decoded, because the joint and the summed information would be the same. On the other hand, a neuron that is very unselective (but still jointly tuned) will have responses for many feature combinations. How such a neuron is decoded (both features together or each separately) would strongly affect the result. Thus, the joint information should be larger than the summed information, as can be seen in Figure 4. Taking these considerations together suggests that the difference between the joint and the summed information, that is the cost of joint tuning, should decrease with increasing selectivity index. This is indeed the case (rs = -0.31; p < 0.001).
In conclusion, our results show that the response selectivity is low and increases to the extent that the single feature tuning curves interact multiplicatively. Increasing the response selectivity reduces the ability of a neuron to represent information. Because a distributed code requires low selectivity and a sparse code requires high selectivity, our results suggest that V1 uses a distributed code as a way to ensure fidelity of representation of the stimulus. Furthermore, our results show that the response selectivity of neurons makes it easier to access information about individual stimulus features.
Eye movements
Because V1 receptive fields are so small, one has to worry about the effects of eye movements in awake behaving monkeys (Grunewald et al., 2002). Three types of eye movements are of particular concern: fixation error, fixation drift, and vergence. To ensure that our results were not confounded by eye movements, we took several steps. First, we performed an analysis to detect systematic deviations attributable to the stimulus condition. As described previously, any experimental session with a significant effect was removed from further analysis; however, it is still possible that systematic deviations that did not reach significance affected our results. To safeguard against this, we determined the mutual information of the fixation error and the stimulus. We found that this quantity was not correlated with the joint information, which is the mutual information between neuronal firing rates and the stimulus (rs = 0.0; p > 0.9). Similarly, the mutual information between eye drift and stimulus was not correlated with the neuronal joint information (rs = -0.02; p > 0.7), nor was the mutual information between vergence and the stimulus (rs = 0.12; p > 0.2). The partial correlation between the joint information and the separability index, from which any potential linear effects caused by drift or vergence have been removed, is highly significant (rs = 0.6; p < 0.001). Finally, a partial correlation analysis showed that the relationship between the joint and the summed information was not affected by the fixation drift or vergence (rs = 0.9; p < 0.001). Thus, we conclude that the effects that we report are not artifacts attributable to eye movements but instead reflect neuronal processing.
Discussion
Joint tuning
Previous research has shown that some neurons in area V1 are tuned for multiple stimulus features (Schiller et al., 1976; De Valois et al., 1982; Leventhal et al., 1995; Geisler and Albrecht, 1997; Smith et al., 1997; Grunewald et al., 2002; Prince et al., 2002a). Such multidimensional representations have been studied by testing for single stimulus features one at a time. For example, in V1 studies it is common to first vary orientation and then spatial frequency at the preferred orientation (Schiller et al., 1976; De Valois et al., 1982; Geisler and Albrecht, 1997). Although these approaches form a good starting point, they are problematic. First, if the initial stimulus feature is chosen incorrectly, the second feature may be poorly mapped. Second, tuning curves that are obtained for only a single stimulus feature cannot detect any interactions between features. Finally, if neurons are tuned for several features, then a joint mapping will be much more sensitive in detecting tuning for each individual stimulus feature because multi-way statistics can be used. Thus, traditional experiments may have underestimated the prevalence of multi-feature tuning. In our experiments, we extensively mapped all combinations of eight directions and nine disparities. We find that 80% of neurons are jointly tuned and these neurons respond as early as singly tuned neurons. Thus, our data support the possibility that orientation, direction, and disparity are integrated early on.
Recently, several other studies have investigated tuning for motion and disparity (Anzai et al., 2001; Pack et al., 2003). The former study (Anzai et al., 2001) presented stimuli of preferred orientation and looked at the effects of spatiotemporal offsets within one eye (motion) and across eyes (motion-in-depth). Pack et al. (2003) investigated the spatiotemporal interactions of light flashes within the same eye (motion) and across eyes (disparity); however, neither study performed a joint mapping of direction and disparity. As a result, those experiments do not address joint tuning for two stimulus features other than spatial and temporal position. For example, although Anzai et al. (2001) showed that in some neurons the preferred disparity changes over time, giving rise to sensitivity to motion-in-depth, their results do not provide information about whether the preferred disparity changes at different orientations or directions of motion in a fronto-parallel plane. Separate experiments, like those described in the present study, are necessary to elucidate joint tuning.
Separability
Thus far, separability has been studied in V1 neurons for orientation, spatial frequency, and phase (Webster and De Valois, 1985; Jones et al., 1987; Hammond and Kim, 1996; Victor and Purpura, 1998; Bredfeldt and Ringach, 2002; Mazer et al., 2002). These features are represented by V1 neurons with small deviations from separability; however, these results may be a special case. Although orientation, spatial frequency, and phase are different concepts, they appear to be related because the same spatial Gabor filter (although with different parameter settings) believed to be underlying simple and complex cell responses gives rise to all of them (Daugman, 1985; Jones and Palmer, 1987; Parker and Hawken, 1988). Consequently, it is not surprising that there are only small deviations from separability between orientation and spatial frequency (Webster and De Valois, 1985; Jones et al., 1987; Hammond and Kim, 1996; Victor and Purpura, 1998; Bredfeldt and Ringach, 2002; Mazer et al., 2002). Thus, to understand the representation and integration of multiple features in general, it is essential to broaden the scope of features that are tested for separability beyond the traditional candidates.
Joint tuning for direction and disparity in V1 is of considerable interest, because many cortical areas, including V1, V2, V3, the middle temporal area (MT), and MST, respond to direction and disparity. It is not known, however, how direction and disparity are jointly represented. One notable exception is MST, a later stage of visual processing, in which many neurons have opposite preferred directions, depending on the disparity (Roy and Wurtz, 1990). Thus, the representation of direction and disparity by many MST neurons is not separable. In contrast, the present study shows that direction and disparity are represented separably by V1 neurons. To understand processing in the motion pathway going from V1 to MST via MT, it will be crucial to understand how the separable representation in V1 is converted into a nonseparable representation in MST.
Our results show that V1 neurons that are tuned for single stimulus features are noisy, represent little information, and have long latencies. Thus, these neurons appear distinct from jointly tuned neurons. It is possible that single and jointly tuned neurons are located in different cortical laminas and thus also differ on anatomical grounds. Alternatively, it is possible that singly tuned neurons may turn out to be simple cells and jointly tuned neurons are complex cells (in principle, the reverse assignment is also possible, although less likely). Unfortunately, our data do not provide precise laminar information and do not speak to the distinction between simple and complex cells. Thus, this awaits future study. Our data do argue, however, against the strong model that orientation, direction, and disparity are represented by separate populations of neurons, as shown in Figure 1, a and b (Treisman and Gelade, 1980; Livingstone and Hubel, 1988; Zeki, 1993). Instead, our results show that most V1 neurons integrate different stimulus features early on, supporting the two joint tuning models shown in Figure 1, c and d. Finally, our data provide strong support for the model that orientation, direction, and disparity are represented separably by V1 neurons. What might be the benefits of such a representation for visual processing?
Importance of separability
The importance of the present study is that it demonstrates separability for features that, by necessity, are not obtained through the same mechanisms and for which the joint representation has not yet been studied. The prevalence of separability in our data confirms a long-held assumption about the joint encoding of several variables held by theoretical and experimental neuroscientists alike. Theoretical neuroscientists appreciate separability because the mathematics of separable and multiplicative joint tuning is considerably simpler than that of nonseparable joint tuning (Vogels, 1990; Zohary, 1992; Seung and Sompolinsky, 1993; Brown et al., 1998; Zemel et al., 1998; Zhang et al., 1998). Experimentalists, in turn, assume separability when they map each stimulus feature separately, which reduces the number of trials required to understand the tuning properties of a neuron (Schiller et al., 1976; De Valois et al., 1982; Webster and De Valois, 1985; Jones et al., 1987; Geisler and Albrecht, 1997). Are there other, more general benefits to the brain for having a separable representation?
In a representation that encodes multidimensional stimuli, decoding of individual stimulus dimensions is not trivial. In general, if a population of neurons encodes multidimensional stimuli, the best way to access individual dimensions is to encode the dimensions separably. This means that tuning for different stimulus dimensions does not interact. In this case, averaging across irrelevant feature dimensions very easily retrieves each individual feature dimension (Heeger, 1987; Grzywacz and Yuille, 1990). For example, for neurons tuned for direction and disparity, averaging across disparity can specify the direction (Qian and Andersen, 1997); however, our results show that there is a cost for decoding single features in comparison to decoding all features at once. This cost is reduced with increasing response selectivity. The response selectivity is related to how single features interact to give the joint tuning function. Our results show that a multiplicative interaction increases response selectivity. Thus, although separability and response selectivity are properties of encoding, their importance is to simplify decoding of individual stimulus features.
Population coding
Having studied how a single neuron represents multiple stimulus features, we now look at how this constrains how a population of neurons represent visual information. There are two extreme possibilities. At one extreme, a small number of neurons represent each combination of specific feature values. This is called a sparse code (Barlow, 1972), and it requires neurons that are highly selective in their responses. The advantage of this code is that at any given point in time, only a small number of neurons is active; however, there is a serious disadvantage. To represent all possible combinations of many stimulus features, a very large number of neurons is necessary, growing exponentially with the number of dimensions. This is called the “curse of dimensionality” (Bellman, 1961).
On the other extreme, a large number of neurons, possibly all in a cortical area, represent a stimulus (Grossberg, 1973; Rumelhart et al., 1986; Grunewald and Lankheet, 1996). In such a representation, most neurons are active to some degree most of the time, which is why this is called a distributed code. A disadvantage of this code is the high metabolic demands of the ongoing activity (Levy and Baxter, 1996; Laughlin et al., 1998). Can such a representation overcome the curse of dimensionality? Theoretical work suggests that distributed representations can represent stimuli with high accuracy, although not requiring an exponential increase in the number of neurons if single neuron tuning curves are separable (Sanger, 1991).
Our single neuron results suggest, for several reasons, that V1 uses a distributed representation and not a sparse code. First of all, our data show that response selectivity is low, which means that many neurons are active in response to all stimuli that we used. Second, we find that neurons with lower response selectivity represent more information, just as one would expect in a distributed code. Third, our analyses demonstrate that separability enhances the information represented, consistent with theoretical work that shows that a distributed code can escape the curse of dimensionality when neurons are separable (Sanger, 1991). Because it is known that in higher cortical areas the representation is sparse (Young and Yamane, 1992), it will be important to study how the distributed representation in V1 is converted to a sparse representation in higher cortical areas. Furthermore, a distributed representation in V1 based on firing rates opens the possibility that synergistic codes, for example, interneuronal correlations of firing rates, play a role in the representation of information in V1 (Oram et al., 1998; Abbott and Dayan, 1999; Panzeri et al., 1999; Jenison, 2000). Current experiments in our laboratory are exploring this possibility.
Footnotes
This research was supported in part by the Howard Hughes Medical Institute Program for Faculty Career Development, the Whitehall Foundation, and the Wisconsin National Primate Research Center (5P51 RR 000167). We thank A. J. Mandel, C. Rypstat, K. Staszcuk, K. Beede, S. Chlosta, B. Baxter, A. Arens, and T. Zec for assistance. We thank R. L. Jenison, D. C. Bradley, and M. A. Basso for helpful comments on this manuscript.
Correspondence should be addressed to Dr. Alexander Grunewald, Departments of Psychology and Physiology, University of Wisconsin-Madison, 1202 West Johnson Street, Madison, WI 53706. E-mail: agrunewald@wisc.edu.
Copyright © 2004 Society for Neuroscience 0270-6474/04/249185-10$15.00/0
References
- Abbott LF, Dayan P (1999) The effect of correlated variability on the accuracy of a population code. Neural Comput 11: 91-101. [DOI] [PubMed] [Google Scholar]
- Adelson EH, Bergen JR (1985) Spatiotemporal energy models for the perception of motion. J Opt Soc Am [A] 2: 284-299. [DOI] [PubMed] [Google Scholar]
- Anzai A, Ohzawa I, Freeman RD (2001) Joint-encoding of motion and depth by visual cortical neurons: neural basis of the Pulfrich effect. Nat Neurosci 4: 513-518. [DOI] [PubMed] [Google Scholar]
- Barlow HB (1972) Single units and sensation: a neuron doctrine for perceptual psychology? Perception 1: 371-394. [DOI] [PubMed] [Google Scholar]
- Bellman RE (1961) Adaptive control processes: a guided tour. Princeton: Princeton UP.
- Bredfeldt CE, Ringach DL (2002) Dynamics of spatial frequency tuning in macaque V1. J Neurosci 22: 1976-1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown EN, Frank LM, Tang D, Quirk MC, Wilson MA (1998) A statistical paradigm for neural spike train decoding applied to position prediction from ensemble firing patterns of rat hippocampal place cells. J Neurosci 18: 7411-7425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daugman JG (1985) Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. J Opt Soc Am [A] 2: 1160-1169. [DOI] [PubMed] [Google Scholar]
- De Valois RL, Albrecht DG, Thorell LG (1982) Spatial frequency selectivity of cells in macaque visual cortex. Vision Res 22: 545-559. [DOI] [PubMed] [Google Scholar]
- Geisler WS, Albrecht DG (1997) Visual cortex neurons in monkeys and cats: detection, discrimination, and identification. Vis Neurosci 14: 897-919. [DOI] [PubMed] [Google Scholar]
- Gershon ED, Wiener MC, Latham PE, Richmond BJ (1998) Coding strategies in monkey V1 and inferior temporal cortices. J Neurophysiol 79: 1135-1144. [DOI] [PubMed] [Google Scholar]
- Grossberg S (1973) Contour enhancement, short-term memory, and constancies in reverberating neural networks. Stud Appl Math 52: 217-257. [Google Scholar]
- Grunewald A, Lankheet MJ (1996) Orthogonal motion after-effect illusion predicted by a model of cortical motion processing. Nature 384: 358-360. [DOI] [PubMed] [Google Scholar]
- Grunewald A, Bradley DC, Andersen RA (2002) Neural correlates of structure-from-motion perception in macaque V1 and MT. J Neurosci 22: 6195-6207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grzywacz NM, Yuille AL (1990) A model for the estimate of local image velocity by cells in the visual cortex. Proc R Soc Lond B Biol Sci 239: 129-161. [DOI] [PubMed] [Google Scholar]
- Hammond P, Kim JN (1996) Role of suppression in shaping orientation and direction selectivity of complex neurons in cat striate cortex. J Neurophysiol 75: 1163-1176. [DOI] [PubMed] [Google Scholar]
- Heeger DJ (1987) Model for the extraction of image flow. J Opt Soc Am [A] 4: 1455-1471. [DOI] [PubMed] [Google Scholar]
- Jenison RL (2000) Correlated cortical populations can enhance sound localization performance. J Acoust Soc Am 107: 414-421. [DOI] [PubMed] [Google Scholar]
- Jones JP, Palmer LA (1987) An evaluation of the two-dimensional Gabor filter model of simple receptive fields in cat striate cortex. J Neurophysiol 58: 1233-1258. [DOI] [PubMed] [Google Scholar]
- Jones JP, Stepnoski A, Palmer LA (1987) The two-dimensional spectral structure of simple receptive fields in cat striate cortex. J Neurophysiol 58: 1212-1232. [DOI] [PubMed] [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC (1980) Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Res 20: 535-538. [DOI] [PubMed] [Google Scholar]
- Laughlin SB, de Ruyter van Steveninck RR, Anderson JC (1998) The metabolic cost of neural information. Nat Neurosci 1: 36-41. [DOI] [PubMed] [Google Scholar]
- Lennie P (1998) Single units and visual cortical organization. Perception 27: 889-935. [DOI] [PubMed] [Google Scholar]
- Leventhal AG, Thompson KG, Liu D, Zhou Y, Ault SJ (1995) Concomitant sensitivity to orientation, direction, and color of cells in layers 2, 3, and 4 of monkey striate cortex. J Neurosci 15: 1808-1818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy WB, Baxter RA (1996) Energy efficient neural codes. Neural Comput 8: 531-543. [DOI] [PubMed] [Google Scholar]
- Livingstone M, Hubel D (1988) Segregation of form, color, movement, and depth: anatomy, physiology, and perception. Science 240: 740-749. [DOI] [PubMed] [Google Scholar]
- Mazer JA, Vinje WE, McDermott J, Schiller PH, Gallant JL (2002) Spatial frequency and orientation tuning dynamics in area V1. Proc Natl Acad Sci USA 99: 1645-1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oram MW, Foldiak P, Perrett DI, Sengpiel F (1998) The “Ideal Homunculus”: decoding neural population signals. Trends Neurosci 21: 259-265. [DOI] [PubMed] [Google Scholar]
- Pack CC, Born RT, Livingstone MS (2003) Two-dimensional substructure of stereo and motion interactions in macaque visual cortex. Neuron 37: 525-535. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Schultz SR, Treves A, Rolls ET (1999) Correlations and the encoding of information in the nervous system. Proc R Soc Lond B Biol Sci 266: 1001-1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker AJ, Hawken MJ (1988) Two-dimensional spatial structure of receptive fields in monkey striate cortex. J Opt Soc Am [A] 5: 598-605. [DOI] [PubMed] [Google Scholar]
- Peña JL, Konishi M (2001) Auditory spatial receptive fields created by multiplication. Science 292: 249-252. [DOI] [PubMed] [Google Scholar]
- Poggio GF, Motter BC, Squatrito S, Trotter Y (1985) Responses of neurons in visual cortex (V1 and V2) of the alert macaque to dynamic random-dot stereograms. Vision Res 25: 397-406. [DOI] [PubMed] [Google Scholar]
- Prince SJ, Pointon AD, Cumming BG, Parker AJ (2002a) Quantitative analysis of the responses of V1 neurons to horizontal disparity in dynamic random-dot stereograms. J Neurophysiol 87: 191-208. [DOI] [PubMed] [Google Scholar]
- Prince SJ, Cumming BG, Parker AJ (2002b) Range and mechanism of encoding of horizontal disparity in macaque V1. J Neurophysiol 87: 209-221. [DOI] [PubMed] [Google Scholar]
- Qian N (1994) Computing stereo disparity and motion with known binocular cell properties. Neural Comput 6: 390-404. [Google Scholar]
- Qian N, Andersen RA (1997) A physiological model for motion-stereo integration and a unified explanation of Pulfrich-like phenomena. Vision Res 37: 1683-1698. [DOI] [PubMed] [Google Scholar]
- Rolls ET, Tovee MJ (1995) Sparseness of the neuronal representation of stimuli in the primate temporal visual cortex. J Neurophysiol 73: 713-726. [DOI] [PubMed] [Google Scholar]
- Roy JP, Wurtz RH (1990) The role of disparity-sensitive cortical neurons in signaling the direction of self-motion. Nature 348: 160-162. [DOI] [PubMed] [Google Scholar]
- Rumelhart DE, McClelland JL, University of California San Diego PDP Research Group (1986) Parallel distributed processing: explorations in the microstructure of cognition. Cambridge, MA: MIT.
- Sanger TD (1991) A tree-structured algorithm for reducing computation in networks with separable basis functions. Neural Comput 3: 67-78. [DOI] [PubMed] [Google Scholar]
- Schiller PH, Finlay BL, Volman SF (1976) Quantitative studies of single-cell properties in monkey striate cortex. II. Orientation specificity and ocular dominance. J Neurophysiol 39: 1320-1333. [DOI] [PubMed] [Google Scholar]
- Seung HS, Sompolinsky H (1993) Simple models for reading neuronal population codes. Proc Natl Acad Sci USA 90: 10749-10753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith III EL, Chino Y, Ni J, Cheng H (1997) Binocular combination of contrast signals by striate cortical neurons in the monkey. J Neurophysiol 78: 366-382. [DOI] [PubMed] [Google Scholar]
- Snowden RJ, Treue S, Andersen RA (1992) The response of neurons in areas V1 and MT of the alert rhesus monkey to moving random dot patterns. Exp Brain Res 88: 389-400. [DOI] [PubMed] [Google Scholar]
- Strong SP, Koberle R, de Ruyter van Steveninck RR, Bialek W (1998) Entropy and information in neural spike trains. Phys Rev Lett 80: 197-200. [Google Scholar]
- Treisman AM, Gelade G (1980) A feature-integration theory of attention. Cognit Psychol 12: 97-136. [DOI] [PubMed] [Google Scholar]
- Victor JD, Purpura KP (1998) Spatial phase and the temporal structure of the response to gratings in V1. J Neurophysiol 80: 554-571. [DOI] [PubMed] [Google Scholar]
- Vinje WE, Gallant JL (2002) Natural stimulation of the nonclassical receptive field increases information transmission efficiency in V1. J Neurosci 22: 2904-2915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogels R (1990) Population coding of stimulus orientation by striate cortical cells. Biol Cybern 64: 25-31. [DOI] [PubMed] [Google Scholar]
- Vogels R, Spileers W, Orban GA (1989) The response variability of striate cortical neurons in the behaving monkey. Exp Brain Res 77: 432-436. [DOI] [PubMed] [Google Scholar]
- Webster MA, De Valois RL (1985) Relationship between spatial-frequency and orientation tuning of striate-cortex cells. J Opt Soc Am [A] 2: 1124-1132. [DOI] [PubMed] [Google Scholar]
- Young MP, Yamane S (1992) Sparse population coding of faces in the inferotemporal cortex. Science 256: 1327-1331. [DOI] [PubMed] [Google Scholar]
- Zeki S (1993) A vision of the brain. Boston: Blackwell Scientific Publications.
- Zemel RS, Dayan P, Pouget A (1998) Probabilistic interpretation of population codes. Neural Comput 10: 403-430. [DOI] [PubMed] [Google Scholar]
- Zhang K, Ginzburg I, McNaughton BL, Sejnowski TJ (1998) Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. J Neurophysiol 79: 1017-1044. [DOI] [PubMed] [Google Scholar]
- Zohary E (1992) Population coding of visual stimuli by cortical neurons tuned to more than one dimension. Biol Cybern 66: 265-272. [DOI] [PubMed] [Google Scholar]