Abstract
In the accessory olfactory bulb (AOB), sensory neurons expressing a given vomeronasal receptor (VR) gene send divergent projections to many glomeruli, and second-order neurons (mitral cells) link to multiple glomeruli via branched primary dendrites. We used calcium imaging and paired somadendritic patch-clamp recording to track backpropagated action potentials (APs) in rat AOB primary dendrites. In cells loaded with 150 μm Calcium Orange, somatic spikes elicited fluorescence transients over the entire primary dendritic tree, and the relative fluorescence increment ΔF/F0 increased along all branches from soma to glomeruli. Backpropagation was reliant on Na+ channels: in 1 μm TTX, somatic AP commands evoked dendritic Ca2+ transients that declined steeply with distance. In paired soma- dendritic whole-cell recordings, backpropagated APs were unattenuated up to ∼200 μm from the soma, whereas subthreshold voltage transients decayed markedly. Computational modeling indicated that the large distal Ca2+ transients are consistent with active, not passive, backpropagation. Genetic tracing in the AOB has suggested homotypic connectivity with individual mitral cell dendritic arbors projecting only to glomeruli targeted by sensory neurons expressing the same VR gene. Non-decremental, non-dichotomous backpropagation in AOB primary dendrites ensures fast, reliable communication between mitral cells and their homotypic glomeruli, binding them into functional modules in accordance with their VR-coded inputs.
Keywords: accessory olfactory bulb, mitral cells, calcium, fluorescence, dendrites, modeling
Introduction
The mammalian vomeronasal system mediates the detection of chemical signals involved in conspecific recognition and reproductive function (Halpern, 1987; Keverne, 1999; Halpern and Martinez-Marcos, 2003). Stimuli entering the vomeronasal organ activate primary sensory neurons that project to discrete glomeruli in the accessory olfactory bulb (AOB). Within the glomeruli, afferent nerve terminals make synaptic contact with primary dendritic tufts of second-order neurons (mitral cells). Axons of sensory neurons expressing a given vomeronasal receptor (VR) gene send divergent projections to many AOB glomeruli (Belluscio et al., 1999; Del Punta et al., 2002), and AOB mitral cells link to multiple glomeruli via complex, branched primary dendrites (Takami and Graziadei, 1990, 1991). Sensory neurons expressing receptors belonging to V1R or V2R gene superfamilies project to rostral or caudal subdivisions of the AOB, respectively (Herrada and Dulac, 1997; Ryba and Tirindelli, 1997; Halpern et al., 1998). Recently, genetic tracing of afferent fibers combined with dye labeling of dendrites revealed a homotypic connectivity in the AOB: individual mitral cells link primarily, or exclusively, to glomeruli targeted by sensory neurons expressing the same VR gene (Del Punta et al., 2002). This convergent dendritic topology suggests that information distributed in parallel across multiple glomeruli is collated and integrated by second-order neurons.
The multiple glomerular projections of mitral cells in the AOB contrast with a simpler architecture in the main olfactory bulb (MOB) of mammals. Olfactory sensory axons expressing a given olfactory receptor gene project to a unique pair of glomeruli in each bulb (Mombaerts et al., 1996), and each mitral cell links to one glomerulus via one (or a few) unbranched primary dendrite(s) (Price and Powell, 1970; Kishi et al., 1982; Orona et al., 1984). First-stage olfactory processing is performed by intraglomerular and interglomerular networks (Pinching and Powell, 1971; Kosaka et al., 1998; Puopolo and Belluzzi, 1998; Kasowski et al., 1999; Schoppa and Westbrook, 2002; Urban and Sakmann, 2002; Aungst et al., 2003), and the results of these computations are passed to mitral cell somata as subthreshold EPSPs conducted down the primary dendrites. Second-stage processing depends on lateral inhibition between mitral and granule cells (Rall et al., 1966; Isaacson and Strowbridge, 1998; Luo and Katz, 2001; Urban, 2002). MOB primary dendrites support reliable backpropagation of action potentials from soma to glomerulus (Bischofberger and Jonas, 1997) and forward propagation of action potentials initiated at the glomerular tuft (Chen et al., 1997). This active signaling suggests that primary dendrites play key roles in coordinating glomerular and mitral-granule networks.
Here, we examine the propagation of fast electrical signals in the complex, branched primary dendrites of rat AOB mitral cells. Using a combination of dual whole-cell patch-clamp recording and high-speed calcium imaging in slices, we demonstrate reliable global backpropagation of action potentials from soma to glomerular tufts in both rostral and caudal subdivisions of the AOB. This active dendritic signaling allows rapid coordination of the activity of divergent and convergent multiglomerular pathways in the AOB, binding them into VR-specific functional modules, homologous to MOB uniglomerular modules.
Materials and Methods
Slice preparation. Adult male Sprague Dawley rats (postnatal days 28-42, CD strain; Charles River Laboratories, Wilmington, MA) were killed by halothane anesthesia, and the olfactory bulbs were removed into an ice-cold sucrose slicing solution containing (in mm) 240 sucrose, 2.5 KCl, 10 Na-HEPES, 10 glucose, 1 CaCl2, 4 MgCl2, and 0.2 ascorbic acid, pH 7.2, bubbled with 100% oxygen. The MOB was blocked rostrally, and parasagittal slices (160 μm) including the AOB were cut with a vibrating blade slicer and allowed to recover for 1-3 hr (30-23°C) in an interface chamber with high Mg2+ artificial CSF (ACSF) (in mm): 124 NaCl, 2.5 KCl, 26 NaHCO3, 1.25 NaH2PO4, 10 glucose, 1 CaCl2, and 3 MgCl2 (equilibrated with 95% O2/5% CO2). For recording, slices were transferred to an open Plexiglas chamber, submerged, and perfused at 2 ml/min with standard ACSF (in mm): 124 NaCl, 2.5 KCl, 26 NaHCO3, 1.25 NaH2PO4, 25 glucose, 2 CaCl2, and 1.3 MgCl2 (equilibrated with 95% O2/5% CO2) at 25°C. Pharmacological agents were introduced by switching the perfusion reservoir. Tetrodotoxin (TTX) was obtained from Sigma-Aldrich (St. Louis, MO). After completion of experiments, slices were fixed overnight at 4°C in PBS with 2% glutaraldehyde. To confirm cell identity and reconstruct dendritic morphology, biocytin-loaded cells were stained with Vectastain Elite ABC kit and visualized with VIP peroxidase substrate kit (Vector Laboratories, Burlingame, CA). Slices were cleared as whole mounts in 80% glycerol, and cells were examined under a Nikon Microphot microscope with digital camera. Primary dendrites were identified by their thicker proximal diameters and projections into the glomerular layer. Finer secondary dendrites followed lateral trajectories that never intersected the glomerular layer. Assignment of mitral cells to the rostral or caudal subdivision of the AOB was based on soma location and dendritic projection (Jia and Halpern, 1997; Sugai et al., 1997; von Campenhausen et al., 1997). In some slices, we used Gi2α immunoreactivity to delimit the glomerular layer of the rostral subdivision (Shinohara et al., 1992). Avidinbiotin-peroxidase-stained slices were incubated in 3% horse serum (20 min), 1.5% horse serum plus 10 μg/ml anti-Gi2α mouse monoclonal antibody (clone L5.6; 1 hr; Lab Vision, Fremont, CA), 1.5% horse serum plus 10 μg/ml biotinylated secondary antibody (horse anti-mouse; 1 hr), and 2 μg/ml Texas Red avidin (30 min; reagents from Vector Laboratories).
Fluorometric imaging. In calcium-imaging experiments, slices were examined under an Olympus BX50-WI microscope with LUMPlan Fl/IR 60×, numerical aperture (NA) 0.90 water immersion objective (UM571). Mitral cell somata in the AOB were visualized under differential interference contrast (DIC) illumination, using a V-1070 low-light CCD video camera (Marshall Electronics, El Segundo, CA). Somatic whole-cell recordings were made with an Axopatch-1D voltage-clamp amplifier (Axon Instruments, Union City, CA) or a BVC-700 current-clamp amplifier (Dagan, Minneapolis, MN). Both amplifiers were controlled by Pulse 8.5 software (HEKA Electronik, Lambrecht, Germany). Dual somatic whole-cell recordings were obtained with the pair of amplifiers to verify that the Axopatch-1D did not significantly distort action potentials in current-clamp mode and could clamp the somatic membrane to an action potential waveform in voltage-clamp mode. Pipettes (4-8 MΩ) were filled with a K-methylsulfate-based intracellular solution containing (in mm) 122 K-CH3SO4, 5 KCl, 26 K-HEPES, 2 Mg-ATP, 0.3 Na-GTP, 1 MgCl2,4Na2-phosphocreatine, and 6.5 biocytin HCl, pH 7.2, 314 mOsm. For imaging, the pipette included the hydrophilic indicator dye Calcium Orange (150 μm; tetrapotassium salt; Molecular Probes, Eugene, OR). The dye was excited by light from a Zeiss HBO 100 W/2 Hg arc lamp, directed through an XF101-2 filter cube (525AF45 excitation filter, 560DRLP dichroic, 565ALP long-pass filter; Omega Optical, Brattleboro, VT). Lamp output was regulated by an AttoArc variable intensity control and gated by a Uniblitz electronic shutter (Vincent Associates, Rochester, NY). For fluorescence imaging, we ran a NeuroCCD-SM camera at a 1 or 5 kHz frame rate, controlled by Neuroplex 6.5 software (Red Shirt Imaging, Fairfield, CT). Repeated imaging of widely separated locations on extensive dendritic arbors was facilitated by computer-assisted microscope positioning and manual focusing. The optics were mounted on an XY platform driven by DC motors and a controller board (M227.25, C-842; Polytec PI, Auburn, MA) commanded by custom software written in LabVIEW (National Instruments, Austin, TX). Backlash in the motors was <1 μm. This system was used to calibrate and compute the distance between different sites along the dendrites. After completion of an experiment, fluorescence and DIC images of in vitro cell morphology were acquired by digitizing the video camera signal with a frame grabber board (PCI-1407; National Instruments).
Initiation of fluorometric imaging was delayed until at least 40 min after the start of whole-cell recording. To measure fluorescence, spatial averages of camera voltage at several adjacent pixels encompassing a region of interest (soma or dendrite) were computed, the background fluorescence of neighboring pixels was subtracted, and the responses to stimulation were expressed as relative stimulus-evoked changes in resting fluorescence, F0, i.e., as ΔF/F0 = (Fpeak - F0)/F0. By varying arc lamp output, we confirmed that this ratio was independent of illumination intensity. For individual responses, the value of F0 was estimated by averaging the voltage over a 20 msec interval of the prestimulus baseline, and Fpeak was the maximal average over a <100 msec sliding window bracketing the response peak. Fluorescence was recorded over 500 msec minus 1 sec poststimulus periods. Stimuli of 100 msec duration consisted of (1) one or more action potentials evoked under current clamp, or (2) voltage-clamp commands of prerecorded action potential waveforms (series resistance >90% compensated). Dual somatic whole-cell recordings were used to confirm that the voltage-clamp commands reproduced the prerecorded spike waveforms. Calcium Orange was resilient to photobleaching (Thomas et al., 2000), and shifts in F0 during the less than ∼100 msec rising phases of responses were negligible. Data analyses were performed in Origin 7.0 (OriginLab) and with custom software written in LabVIEW. Analysis results are reported as mean ± SD, except for time-windowed averages in which we used SEM. For display purposes, some ΔF/F0 traces were subjected to low-pass digital filtering (four-pole Bessel) to reduce high-frequency noise.
Dendritic patch-clamp. In dual patch-clamp experiments, mitral cell somata and dendrites were visualized under a Nikon E600FN microscope with a Leica 63×, NA 0.90 water immersion objective, infrared (IR)-DIC optics, and C2400-79H CCD camera (Hamamatsu Photonics, K.K., Hamamatsu City, Japan). Current-clamp recordings were made using two BVC-700 microelectrode amplifiers (Dagan) in bridge mode with electrode capacitance and series resistance compensation. Under IRDIC, primary dendrites were traced 100-200 μm from the soma, and distances along the somatodendritic axis were measured by a three-dimensional motion control system driving the microscope and objective (Lowe, 2002). Identity and morphology of cells were verified by staining and reconstruction of the biocytin-loaded cells. Action potential amplitudes and widths were extracted from the data using custom software to localize peaks and subtracting the voltage at pre-spike inflection points at the foot of the spike, as described previously (Lowe, 2002).
Modeling action potential backpropagation into the distal dendrite. A simple compartmental model of a generic AOB mitral cell primary dendrite was implemented in the NEURON simulation platform (Hines and Carnevale, 1997). The model was composed of five sections: a cylindrical soma, an axon initial segment, axon hillock, and a single 400-μm-long dendrite divided into proximal and distal sections, each 200 μm in length. Biophysical parameters of the model (Tables 1, 2) were chosen by assuming a homology with MOB mitral cells. To generate action potentials, voltage-dependent Na+ and noninactivating K+ conductances were inserted throughout the cell, with a higher density in the axon initial segment. These were represented by Hodgkin-Huxley-style two-state models (Hodgkin and Huxley, 1952) using the formalism of Mainen et al. (1995). We initially tested model parameters previously used to fit dual patch-clamp recordings of action potential propagation in MOB mitral cell primary dendrites (Shen et al., 1999). We retained the passive electrical properties and Na+ conductance densities of that model but needed to modify other parameters to fit our data. The model of Shen et al. (1999) incorporated fast K+ channel kinetics, with activation time constants of 0.324 msec at -30 mV and 0.033 msec at +30 mV. This is an order of magnitude faster than the kinetics measured by Bischofberger and Jonas (1997), in patches excised from the MOB primary dendrite (3.1 msec at -30 mV and 0.48 msec at +30 mV). Because of their rapid activation, we found that the fast model K+ channels opened during the upstroke of an action potential, and K+ channel blockade was predicted to boost dendritic action potential amplitude. However, application of tetraethylammoniun (TEA) does not increase the amplitude of action potential waveforms in the primary dendrite (Bischofberger and Jonas, 1997). We also found that the fast model K+ channels could strongly attenuate the spread of passive voltage transients in our simulations of the effects of TTX. Shen et al. (1999) incorporated K+ channels into their model at a density 12-fold lower than the mean value measured from excised patches (Bischofberger and Jonas, 1997). To better fit our data, we used a model of a delayed rectifier K+ conductance with slower activation kinetics (4.38 msec at -30 mV and 2.29 msec at +30 mV) (Table 2). This model could fit our dual patch-clamp recordings of action potentials from the AOB with a K+ channel density eightfold higher than the value of Shen et al. (1999). The higher density comes closer to the mean value measured from excised patches. Our slower K+ conductance does not open during the upstroke of an action potential, so the depolarizing phase of the spike depends only on the Na+ conductance. This led us to use slower Na+ channel kinetic parameters, more similar to those used by Mainen et al. (1995).
Table 1.
Model parameters
|
|
Diameter d (μm) |
Length L (μm) |
Segments |
|---|---|---|---|
| Geometric | |||
| Axon initial segment | 1.5 | 20 | 10 |
| Axon hillock | 1.5-15 | 5 | 10 |
| Soma | 15 | 25 | 1 |
| d0: 3, 2; λT: 200, | |||
| Dendrite: proximal | 150 | 200 | 200 |
| Dendrite: distal | λT: 200, 150 | 200, 450 | 200, 450 |
| Electronic | |||
| Ri: intracellular resistivity (Ω cm) | 70 | ||
| Cm: specific membrane capacitance (μF cm−2) | 1.2 | ||
|
Rm: specific membrane resistance (Ω cm2) |
|
30,000 |
|
|
|
ḡNa (S cm−2) |
ḡK (S cm−2) |
Pca (cm sec−1) |
Ca-Orange (μm) |
Endogenous buffer (mm) |
|---|---|---|---|---|---|
| Mechanism densities | |||||
| Axon initial segment | 1 | 0.015 | 0 | 0 | 0 |
| Axon hillock | 0.026 | 0.0336 | 0 | 0 | 0 |
| Soma | 0.026 | 0.0336 | 0 | 0 | 0 |
| Dendrite: proximal | 0.026 | 0.0336 | 1.8 × 10−4 | 150, 82.5-135 | 1.4 |
| Dendrite: distal |
0.026, 0 |
0.0336, 0 |
1.8 × 10−4
|
150, 82.5-135 |
1.4 |
Values of parameters used in the model cell for numerical simulation of action potential backpropagation into the apical dendrite. ḡNa and ḡK, Densities of Na+ and K+ conductance; PCa, permeability of high threshold Ca2+ channels. d0, initial dendritic diameter, at soma; λT, exponential decay length of dendritic taper. The length of the distal dendritic section was 200 μm in all modeling, except for the generation of the rise time ratio curves in Fig. 7H, where it was 450 μm. Dendritic diameter and taper was d0 = 3, λT = 200 for a standard dendrite, and d0 = 2, λT = 150 for a thin dendrite.
Table 2.
Model mechanisms
|
Na+ channel |
|
| iNa = ḡNam3h (V-ENa), ENa = 74 mV |
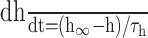 , τh = 1/(αh + βh) , τh = 1/(αh + βh) |
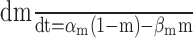
|
h∞ = 1/(1+e(V+60)/4) |
| αm = -0.08(V+76)/(e-(V+76)/3.5 - 1) | αh = 0.053(V + 62.4)/[1 - e- (V + 62.4)/8] |
| βm = 0.65(V + 34)/[e(V + 34)/4 - 1] | βh = - 0.004(V + 90)/[1 - e(V + 90)/5.6] |
| Delayed rectifier K+ channel | |
| iK = ḡKn4(V - EK), EK = - 105 mV | αn = -0.022 (V + 20)/[e-(V + 20)/12 - 1] |
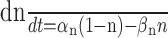
|
βn = 0.0048 (V + 8)/[e(V + 8)/19 - 1] |
| High-threshold Ca2+ channel | βm = 0.1 e-V/20 |
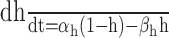
|
|
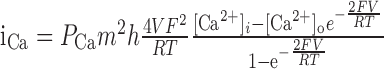
|
αh = 0.000168 e-V/36.76 |
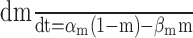
|
βh = 1/[1 + e(-V + 56.94)/18.11] |
| αm = 0.25 (-V + 35)/[e(-V + 35)/10 - 1] | [Ca2+]0 = 2 mm, [Ca2+]i (rest) = 50 nm |
| Ca-Orange (B) and endogenous buffer (S) |
|
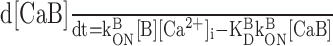
|
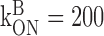 mm-1 msec-1, mm-1 msec-1, 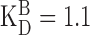 μm μm
|
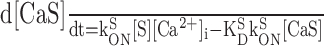
|
BT = 150 μm,  mm-1 msec-1 mm-1 msec-1
|
| [CaB] + [B] = BT, [CaS] + [S] = ST |
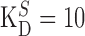 μm, ST = 1.4 mm, F = 96,485 C mol-1 μm, ST = 1.4 mm, F = 96,485 C mol-1
|
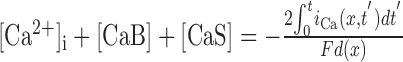
|
d(x) = d0e-x/λT, 
|
Model equations describing intrinsic membrane conductances, calcium buffers, and fluorescence. V, Transmembrane voltage; [Ca2+]i, free calcium ion concentration; [B] and [CaB], concentrations of free and calcium-bound forms of Calcium Orange; [S] and [CaS], concentrations of free and calcium-bound forms of endogenous buffer.
A transient A-type K+ conductance was reported to regulate the amplitude of backpropagating action potentials in MOB secondary dendrites (Christie and Westbrook, 2003). We did not include a transient conductance in our model because there is no evidence for it in the primary dendrite. Such a conductance might be expected to attenuate EPSPs orginating in the distal tuft (Hoffman et al., 1997), interfering with the transfer of excitatory signals from tuft to soma. However, a recent voltage-imaging study showed that primary dendrites conduct EPSPs over long distances with little attenuation (Djurisic et al., 2004).
The properties of voltage-dependent Ca2+ conductances in the dendrites of AOB mitral cells have not been determined. We decided to model these as high-threshold (N-type) Ca2+ channels. Pharmacological studies on MOB mitral cells have implicated major contributions of L- or N-type channels to the Ca2+ current (Wang et al., 1996). The N-type channels are likely to be localized to the dendrites because L-type channels appear to have no role in dendrodendritic transmission (Isaacson and Strowbridge, 1998), and the L-type channel blocker nifedipine suppresses somatic, but not dendritic, Ca2+ entry into mitral cells (Bischofberger and Schild, 1995). We adopted the Hodgkin-Huxley-style equations that were used to model an N-type Ca2+ conductance found in dendrites of hippocampal pyramidal neurons (Jaffe et al., 1994). Model parameters were modified to better approximate the high-threshold Ca2+ conductances observed in MOB mitral cells: model currents activated at approximately -30 to -20 mV, half-activation voltage was approximately -1 mV, and peak inward current occurred at approximately +2 mV; inactivation parameters were selected to yield a half-inactivation potential of -67 mV and a slope of 13.2 mV (see Fig. 7D) (Wang et al., 1996). Calcium current was calculated using the Goldman-Hodgkin-Katz equation. The density of Ca2+ conductance was chosen to produce a somatic whole-cell Ca2+ current of a few hundred picoamperes in a voltage step from -65 to 0 mV (Wang et al., 1996). With this channel density, action potential-generated ΔF/F0 increments were comparable with those measured in our experiments.
Figure 7.
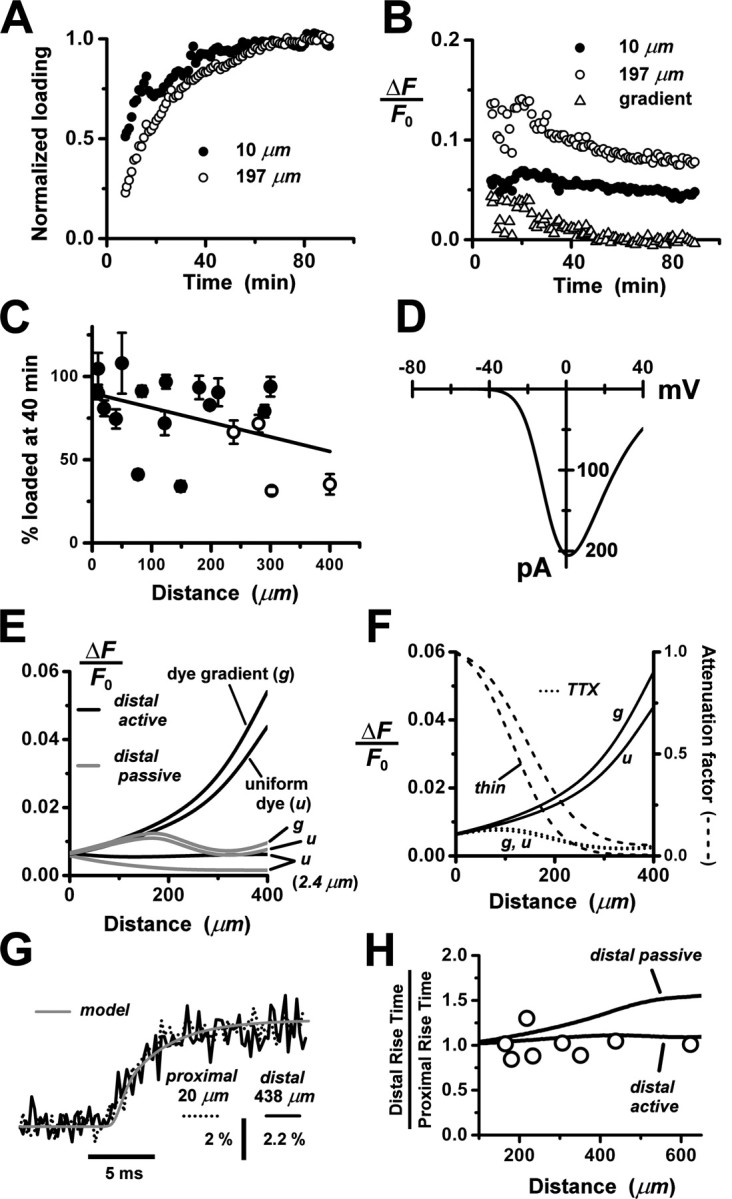
Modeling calcium transients in the AOB primary dendrite. A, Experimentally determined indicator dye-loading curves for proximal (•; 10 μm from soma) and distal (○; 197 μm from soma) locations on an AOB primary dendrite. Abscissa, Time after breakthrough into whole-cell mode; ordinate, resting fluorescence normalized to plateau fluorescence (average of points after 80 min). B, Time dependence of relative fluorescence change ΔF/F0 elicited by a single backpropagating action potential during dye loading of the dendrite in Figure 7A. Proximal and distal measurements (• and ○) correspond to the same locations as in Figure 7A. The effect of the diameter change of a tapered dendrite was estimated by taking the difference between the distal and proximal ratios after loading was complete (time, > 80 min). This difference was then subtracted from the distal data set to reveal the contribution of the dye gradient to the spatial gradient in the ratio ΔF/F0 (▴). C, Estimated percentage of loading of primary dendrites at various distances from the soma, 40 min after breakthrough into whole-cell mode. The plot shows pooled data from dendrites of 13 cells, observed for loading periods of 80-120 min. Points plotted as filled circles are percentages derived from loading curves that either attained a fluorescence plateau (indicating completion of loading) or displayed clearly convex curvature that could be fitted by an exponential function to estimate a plateau level. A plateau level could not be estimated for a few of the more distal loading curves that continued to ramp up without signs of saturation. In these cases, an upper bound on the percentage of loading at 40 min was obtained by normalizing to the final fluorescence value (○). D, Current-voltage relationship for the model N-type calcium channel used in our computations of Ca2+ dynamics. The curve is the peak value of calculated total membrane current after a voltage step from -65 mV to the abscissa value. For this calculation, a single-electrode voltage clamp was applied to the isolated soma of the mitral cell model (dendrite, axon hillock, and initial segment were detached). E, Plots of computed spatial profiles of ΔF/F0 along a model primary dendrite with a linear (135-82.5 μm) indicator dye gradient (g) or a uniform (150 μm) dye concentration (u). The dendrite is tapered (d0 = 3 μm; λT = 200 μm) in the top four curves and has a uniform diameter (2.4 μm) and uniform dye concentration in the bottom two curves. Comparing these curves shows that both taper and dye gradient contributed to the profile. For the profiles shown in black, backpropagation was active throughout the entire dendrite; for those shown in gray, it was active in the proximal half of the dendrite and passive in the distal half. Comparing these curves shows that passive backpropagation strongly reduced ΔF/F0 in the distal dendrite. F, Computed TTX attenuation of ΔF/F0 spatial profiles along a tapered model dendrite. Solid curves show control profiles for active backpropagation, with (g) or without (u) dye gradient (same as in E). Dotted curves show corresponding profiles computed with an action potential waveform voltage clamp at the soma and Na+ channel density globally set to zero to simulate action of TTX. The TTX attenuation factor (with dye gradient) was obtained by dividing the dotted curve (g) by the solid curve (g) and plotted as the top dashed curve (left ordinate scale). To illustrate the effect of dendrite diameter, the attenuation factor is also shown for a thin model dendrite (bottom dashed curve; same thin dendrite as in Fig. 6 B). G, Experimentally observed rising phases of fluorescence transients in a primary dendrite, measured near the soma (20 μm; dotted black curve) and at a distal location (438 μm; solid black curve). Data from the two locations were superimposed by rescaling amplitudes and shifting time origins. Solid gray curve, Model fit to the shape of the distal rising phase. H, Plot of ratios of distal 50% rise time (at 165-623 μm) to proximal 50% rise time (at 20-30 μm). Open circles are measured ratios (n = 7 cells; 1 cell with 2 dendritic branches), and solid curves are predictions from the model dendrite (extended to 650 μm length) with either fully active backpropagation of action potentials or passive backpropagation in the distal section (> 200 μm). The experimental 50% rise time was estimated from a monoexponential curve fit to ΔF/F0 over the initial 20 msec of the response. The model 50% rise time was taken as the difference between the time when the computed ΔF/F0 reached 50% of its value at 20 msec and the time when it was only 1% of that value.
Calcium influx into the model dendrites was buffered by 150 μm Calcium Orange, with dissociation constant KDB = 1.1 μm (Thomas et al., 2000), binding rate kONB = 200 mm-1 msec-1 (Naraghi, 1997), and a linear spatial gradient approximating measured dye gradients (see Fig. 7C). Fluorescence ratio ΔF/F0 was derived by assuming a cytoplasmic dynamic range of 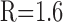 for Calcium Orange (Thomas et al., 2000). Because our aim was to calculate peak amplitudes, calcium extrusion was not modeled because decay times of responses were much slower than rise times.
for Calcium Orange (Thomas et al., 2000). Because our aim was to calculate peak amplitudes, calcium extrusion was not modeled because decay times of responses were much slower than rise times.
Dendritic sections also incorporated 1.4 mm of a uniformly distributed endogenous Ca2+ buffer with dissociation constant KDS = 10 μm and binding rate kONS = 100 mm-1msec-1, providing a buffering capacity of 140. Buffering capacities of 50-200 are typical for dendrites of pyramidal neurons (Helmchen et al., 1996; Maravall et al., 2000), and the soma and dendrites of rat MOB mitral cells have not been found to contain high levels of high-affinity calcium-binding proteins (Wouterlood and Härtig, 1995; Toida et al., 1996; Jia and Halpern, 2004). We used the principle axis (PRAXIS) method (Brent, 1976) to find endogenous buffer parameters that predicted the slow, delayed rising phase of the dendritic fluorescence transient. To assess the possible role of radial diffusion of calcium and indicator dye in determining the delayed rising phase, we modeled mass transport by partitioning dendrites into 10 annular shells and assumed diffusion coefficients of 0.6 μm2msec-1 for Ca2+ and 0.25 μm2msec-1 for Calcium Orange. We found that diffusion had a negligible effect on the fluorescence time course, in agreement with previous modeling of presynaptic boutons (Sabatini and Regehr, 1998). We only show simulation results from models without diffusion.
Dendritic tapering was modeled as an exponential function with initial diameter d0 and taper length λT. To estimate tapering of AOB primary dendrites, cells were loaded by whole-cell pipette with 1 mm Alexa Fluor 488 hydrazide (Molecular Probes), lightly fixed in glutaraldehyde (2%; 30 min), and imaged in PBS with a 63×, NA 0.9 water immersion objective, using the 488 nm argon line of a Leica TCS-2 confocal microscope. Intensity profiles orthogonal to the dendritic axis were measured with Image-Pro Plus software (Media Cybernetics, Silver Spring, MD), and diameters were extracted by fitting the profiles to the convolution of the intensity of the Gaussian beam with a dye-filled dendrite of circular cross section (Gennerich and Schild, 2002). We assumed a diffraction-limited focal volume, with 1/e2 radii rxy = 0.224 μm, rz = 0.844 μm. Primary dendritic tapering of two analyzed cells could be described approximately by exponential curves with d0 = 4 μm and λT = 150 or 360 μm. This large difference in tapers is consistent with wide variation in the dendritic geometries of AOB primary dendrites (Takami and Graziadei, 1991). In our modeling, we used a standard tapered dendrite with d0 = 3 μm, λT = 200 μm, and we also tested a thin dendrite with d0 = 2 μm, λT = 150 μm.
In all simulations, a 5 μsec time step was used to fix accurately action potential peaks.
Results
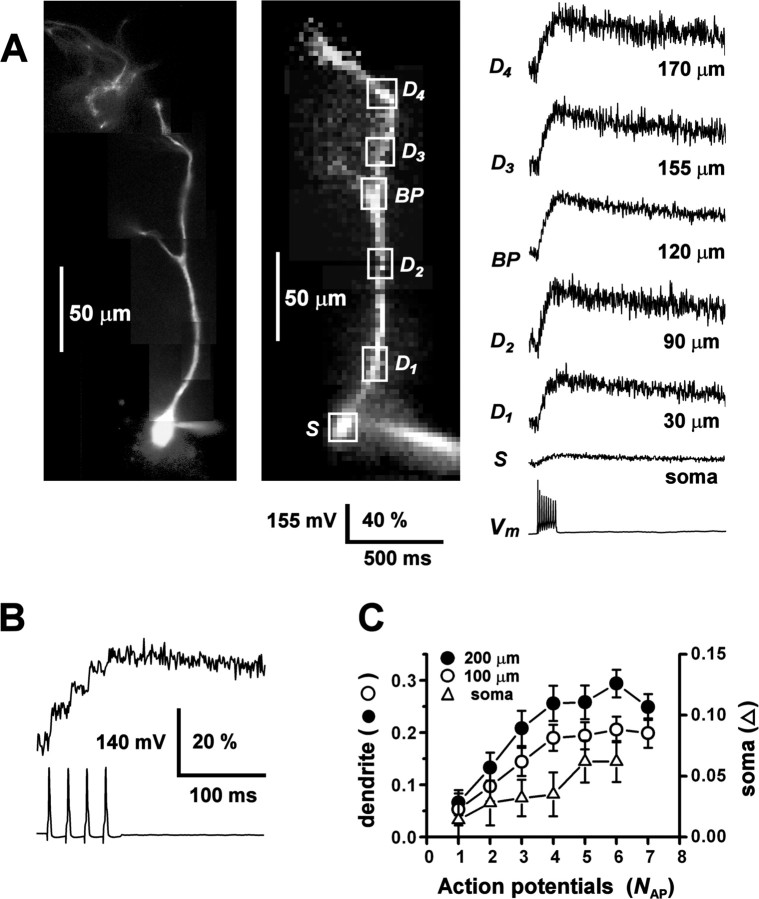
To track dendritic signal propagation in AOB mitral cells, we applied the method of fluorometric calcium imaging, using the high-affinity, visible wavelength calcium indicator Calcium Orange. In parasagittal slices, putative mitral cell somata located <50 μm below the slice surface were selected for recording on the basis of their large diameters (transverse diameter, 11.44 ± 4.56 μm; mean ± SD, n = 35) and their positions in the deeper external plexiform layer of the AOB (several hundred micrometers ventral to the glomerular layer). During whole-cell recording from the soma, input resistance was 150 ± 20 MΩ (n = 30), and membrane resting potential was -55 ± 5 mV (n = 25). Data were rejected if input resistance fell below 100 MΩ or rose above 200 MΩ. Injection of short current pulses evoked single-action potentials, and sustained current injection induced repetitive firing. Action potential discharge was followed by large fluorescence transients in the soma and dendrites. Figure 1A shows the ΔF/F0 signals measured from the soma and several locations along a primary dendrite, evoked by a train of action potentials. The amplitude of ΔF/F0 was, on average, larger in the dendrites compared with the soma (by a factor of 5.8 ± 5.0 at 100 μm; n = 18 cells), consistent with the higher dendritic surface to volume ratio. Monoexponential fits to the decaying phases of the transients yielded time constants of τ = 581 ± 338 msec for somatic responses (n = 10) and τ = 627 ± 244 msec for dendritic responses (n = 15; 100 μm from the soma). To control the number (NAP) and timing of action potentials, we also evoked spike trains by injecting series of short current pulses (0.5-3 msec, 1-2 nA) over a 100 msec interval. Figure 1B shows that the indicator dye could detect calcium increments caused by individual spikes within a train of action potentials. Amplitudes of fluorescence transients increased sublinearly with action potential number up to NAP = 5 spikes and saturated for NAP > 5 spikes (Fig. 1C). This was expected for a high-affinity dye with intracellular dissociation constant KD ∼1.1 μm (Thomas et al., 2000). To avoid dye saturation, we limited the number of spikes to NAP ≤ 4.
Figure 1.
Action potentials evoke calcium transients in AOB primary dendrites. A, An AOB mitral cell was loaded with 150 μm Calcium Orange during somatic whole-cell current-clamp recording, and a train of action potentials (Vm) was evoked by current pulse injection (100 msec, 300 pA). Left, Fluorescence image of cell acquired by video camera after the experiment. Middle, Fluorescence image of resting cell acquired by NeuroCCD imaging system. Right, Relative fluorescence transients (ΔF/F0) recorded from the soma (S) and from several regions of interest (boxes) along the primary dendrite (D1-D4) up to 170 μm from the soma, including one branch point (BP). Vertical scale bar, membrane potential Vm (millivolts) and ΔF/F0 (percentage). Dendritic traces were low-pass filtered (250 Hz) to reduce high-frequency noise. B, Expanded view of the rising phase of the ΔF/F0 response of another cell to a train of four action potentials evoked by 3 msec, 1 nA pulses, showing fluorescence increments of decreasing amplitude associated with individual spikes. The region of interest was on the primary dendrite 40 μm from the soma. C, Plot of the peak amplitude of ΔF/F0 at the soma and proximal dendrite (100 and 200 μm) of a third cell, as a function of increasing NAP, the number of action potentials in a 100 msec stimulus interval (3 msec, 1 nA pulses). Saturation of the fluorescence response occurred for NAP > 4.
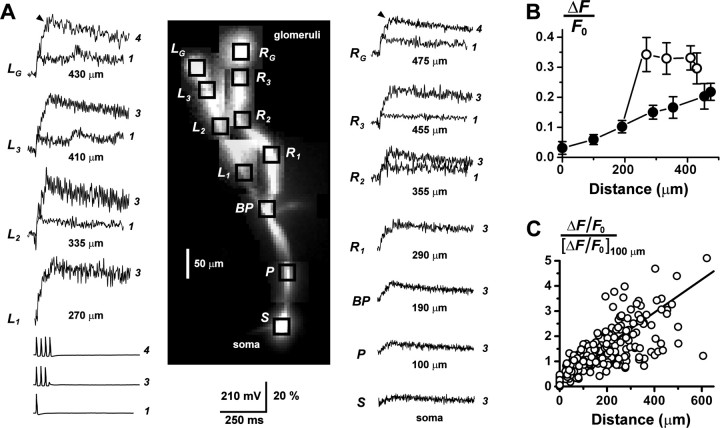
Action potential-evoked fluorescence transients were detected in the primary dendrites of all AOB mitral cells recorded (n = 47). Application of 150 μm Cd2+ to the bath solution abolished both somatic and dendritic transients (n = 6 cells), indicating that they relied on calcium entry through voltage-activated calcium channels. The extent of the imaged dendrites was variable, depending on damage and truncation during slice preparation. Ca2+ transients were detected throughout the dendrites of 47 cells (51 branches): 20 cells with 100-200 μm, 13 with 200-300 μm, and 14 with 300-625 μm length dendrites. Of 37 cells subsequently processed for biocytin staining, 9 resided in the rostral subdivision of the AOB, 14 in the caudal subdivision, and 14 could not be unambiguously assigned to either subdivision. Figure 2A shows data from a cell with two intact branches of a primary dendrite, both of which could be traced to their apical glomerular arborizations. Trains of three or four somatic action potentials were accompanied by large fluorescence transients throughout the dendritic arbor, including the apical glomerular tufts. In the distal branches and tufts, a single-action potential was sufficient to evoke a fast Ca2+ transient.
Figure 2.
Calcium signaling in multiple branches of the AOB primary dendrites. A, During whole-cell recording, two branches of the primary dendrite of an AOB mitral cell were traced to their terminal glomerular arborizations (tufts) by fluorescence imaging. Trains of three action potentials were evoked by injection of series of 3 msec, 1 nA pulses into the soma. Prominent fluorescence transients ΔF/F0 were recorded from the soma (S), proximal dendrite (P), and both left (L1-L3) and right (R1-R3) branches of the distal dendrite. At the glomerular tufts (LG and RG; 430 and 475 μm, respectively), the cell fired a fourth action potential, the timing of which is indicated by the black arrowheads just before the peaks of the traces. Overlaid are the responses to the firing of a single-action potential, recorded from the tufts and distal dendrites (> 300 μm). A single spike could evoke a large, fast Ca2+ signal in the distal compartments of the cell, showing that the large glomerular responses to spike trains did not require temporal summation of series of passively conducted voltage transients. The different amplitudes of the left and right branches may be attributable to an asymmetry in dendritic diameter. Vertical scale bar, membrane potential Vm (millivolts) and ΔF/F0 (percentage). The number of action potentials fired is indicated to the right of the traces. Dendritic branch traces were low-pass filtered (200 Hz) to reduce high-frequency noise. B, Plot of the amplitude of ΔF/F0 versus distance from the soma for the cell in A. Amplitudes were measured after discharge of three action potentials (at black arrow in the tufts). ○, Left dendrite; •, trunk and right dendrite. C, Plot summarizing the increasing trend of ΔF/F0 with increasing distance from the soma, for primary dendrites from n = 47 cells. For each cell, the ΔF/F0 profile was normalized to its value at 100 μm, and the plots from all cells were pooled. The somatic amplitude was not used here for normalization because of its greater variance. The number of action potentials that generated these responses was variable (1, 3, or 4 spikes). The approximately linear relationship between fluorescence increment and spike number for NAP < 4 (see Fig. 1C) allowed us to combine data sets with varying spike number without distorting the normalized profiles. The fitted line represents the average linear regression for the sample of all cells.
Amplitudes of ΔF/F0 in the primary dendrites increased steadily with distance from the soma (Figs. 1A, 2A,B). Peak relative amplitudes of fluorescence transients in the more distal dendritic segments and apical tufts were larger than those recorded from the soma and proximal dendritic shaft. Although some cells exhibited locally decreasing gradients in ΔF/F0 along restricted portions of dendrite, the overall trend was for ΔF/F0 to increase with distance from the soma. This trend is evident in the pooled and normalized data from the sample of 47 cells shown in Figure 2C. Linear regression of ΔF/F0 data from individual cells yielded a wide range of slopes (0.0001-0.0043 μm-1). Much of this variation was removed by normalizing data from different cells to the values at 100 μm (normalized slope, 0.0066 ± 0.0025 μm-1). The trend of increasing ΔF/F0 along the dendrite might be caused by tapering of the AOB primary dendrites, which differ from mammalian MOB primary dendrites, the diameters of which remain nearly constant from soma to glomerulus (Mori et al., 1983). Tapering increases the surface/volume ratio, and if all else were equal, ΔF/F0 would scale inversely with diameter. A concentration gradient of the indicator dye, left by incomplete loading of the dendrites, may also contribute to a positive gradient in ΔF/F0.
Seven glomerular tufts were imaged from five mitral cells (dendrite length, 300-400 μm), and all exhibited large amplitude fluorescence transients in response to somatic action potential discharge (Fig. 2A) (380 μm). Our optical system was not capable of resolving the fine branches of the glomerular arborizations, so these responses represent spatial averages over the tuft. Several morphological classes of glomerular arborization have been described (Takami and Graziadei, 1991), and the variable diameters of our imaged tufts (minor diameter: range, 15.8-65.7 μm; mean ± SD, 41.5 ± 26.2 μm) indicated that we sampled more than one such class.
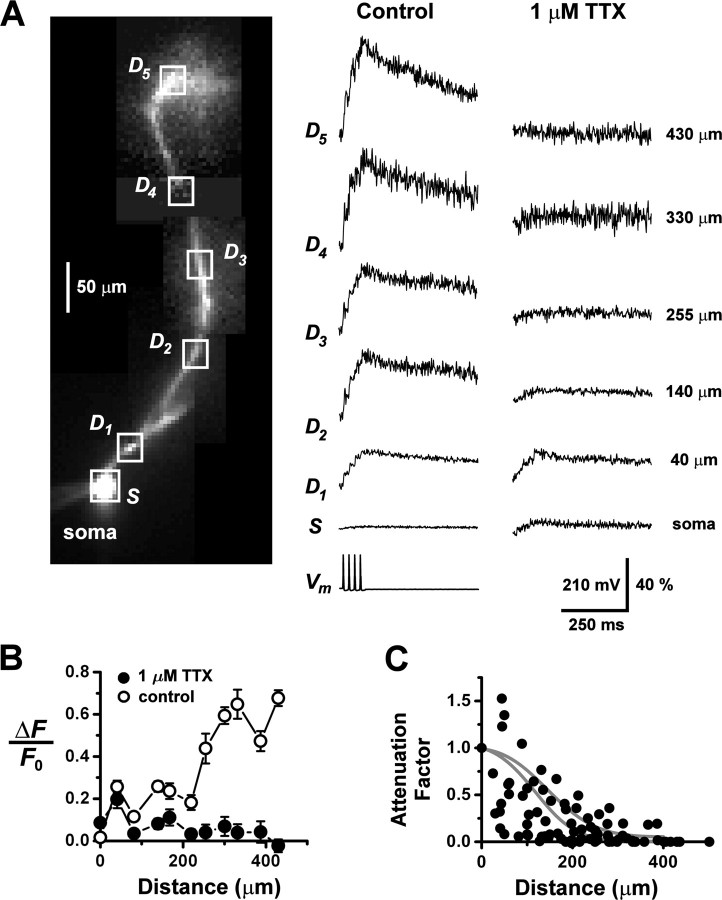
The detection of Cd2+-sensitive calcium transients in the dendrites establishes that somatic firing can depolarize the dendritic membrane sufficiently to activate calcium channels. Do these calcium transients reflect the active or passive backpropagation of action potentials into the dendrites? To address this question, we examined the role of voltage-sensitive Na+ conductances in generating the responses. Figure 3A shows a series of fluorescence signals recorded from a mitral cell, starting at the soma and ranging out to ∼430 μm along a primary dendrite. In the control series, evoked by a train of four somatic action potentials, ΔF/F0 gradually increased with distance from the soma. A second fluorescence series was recorded in response to somatic action potential voltage-clamp commands, following bath application of 1 μm TTX to block Na+ conductances. Perfusion of TTX dramatically altered the spatial profile of responses, causing the relative amplitude to decline sharply with increasing distance from the soma. For many cells, the response was almost negligible at more than ∼200 μm (Fig. 3B). In some cells, voltage-clamp commands in TTX elicited fluorescence responses that were larger at the soma and proximal dendrite compared with previous control responses recorded under current clamp. This may have been caused by drifts in series resistance or changes in calcium channels during an extended period of whole-cell recording. However, in all instances, the TTX responses exhibited a strongly decaying spatial gradient with increasing distance from the soma. To quantify the effect of TTX on the amplitude of ΔF/F0 along the dendrite, we plotted the TTX attenuation factors after spatial profiles were normalized to the soma (Fig. 3C). Monoexponential fits to attenuation data for individual cells gave an average decay length of 113 ± 80 μm (mean ± SD, n = 11 cells). Attenuation by TTX shows that calcium signal propagation in AOB primary dendrites is an active process. It requires recruitment of a regenerative Na+ current, and it cannot be sustained by a calcium spike alone.
Figure 3.
Dendritic calcium transients depend on a voltage-gated Na+ conductance. A, Under whole-cell current clamp, an AOB mitral cell fired action potentials in response to somatic current injection (train of 3 msec, 1 nA pulses) and the resulting fluorescence transients were recorded at varying distances (boxes) from the soma (left column of traces). The bath perfusion solution was then replaced with one containing 1 μm TTX to block voltage-gated Na+ channels, and the previously recorded spike train was used as a voltage-clamp command to the soma. The right column of traces shows the fluorescence transients evoked by this command, recorded at the same locations as the control responses. Dendritic traces were low-pass filtered (300 Hz) to reduce high-frequency noise. Vertical scale bar, membrane potential Vm (millivolts) and ΔF/F0 (percentage). B, A plot of the peak amplitudes of ΔF/F0 as a function of distance from the soma reveals the strong inhibitory effect of TTX on the range of propagation of Ca2+ transients along the dendrite (data from the cell shown in A). ○, Control condition; •, 1 μm TTX. C, Pooled data summarizing the effect of TTX on dendritic calcium transients (n = 11 cells). The somatic amplitudes of ΔF/F0 before and after addition of the TTX were rescaled to match each other, and the ratio of the amplitudes was computed point-wise along the dendrite. This ratio provides a measure of the attenuation of the fluorescence transients resulting from Na+ channel block. Solid gray curves indicate model calculations of the attenuation factor for a dendrite with standard taper (top curve) and a thin dendrite (bottom curve).
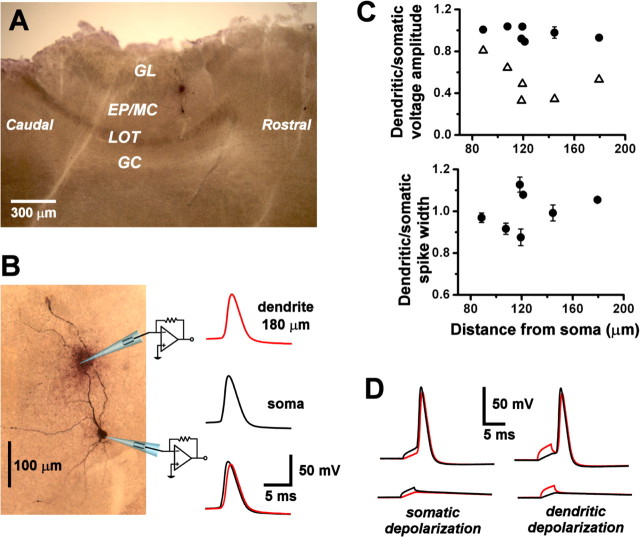
Although calcium fluorometry provides a useful probe of signal propagation in the dendrites, it does not measure membrane voltage directly. To analyze non-decremental backpropagation of action potentials, we subjected AOB mitral cells to dual whole-cell current-clamp recording from the soma and primary dendrite. In parasagittal slices, primary dendrites could be visually identified on the basis of their dorsally oriented projections toward the glomerular layer of the AOB. When a suprathreshold current pulse was injected into the soma, an action potential was recorded by both somatic and dendritic electrodes (Fig. 4A). The peak of the action potential in the soma preceded that in the dendrite, showing that the spike initiated closer to the soma and backpropagated into the dendrite. Backpropagation to sites up to ∼200 μm from the soma occurred with little or no peak voltage attenuation (attenuation factor, 0.97 ± 0.06; spike amplitude, 75 ± 8 mV; distance, 88-182 μm; n = 7 cells, 5 from rostral AOB, 1 from caudal AOB, and 1 ambiguous) and no significant broadening (spike half-width, 2.13 ± 0.40 msec; broadening factor, 1.00 ± 0.09; n = 7) (Fig. 4B). The lack of attenuation was not a passive cable property because, at the same distances, fast subthreshold voltage transients evoked by injection of short (2 msec) current pulses were substantially attenuated along the dendrite (attenuation factor, 0.42 ± 0.10; distance, 120-182 μm; n = 5) (Fig. 5A,B). When current was injected at the dendritic recording site, action potentials still initiated near the soma and backpropagated into the dendrite (Fig. 5D). Spike conduction velocity calculated from differences in peak times was 0.40 ± 0.10 msec-1 (n = 4).
Figure 4.
Action potentials backpropagate into AOB primary dendrites. A, Biocytin-labeled mitral cell, reconstructed in a whole mount of a sagittal slice of the AOB. The cell was subjected to paired whole-cell recording from the soma and from a site on a branch of primary dendrite 180 μm from the soma (marked by the darkly stained extracellular deposit). GL, Glomerular layer; EP/MC, external plexiform and mitral cell layer; LOT, lateral olfactory tract; GC, granule cell layer. B, Spontaneous action potentials were recorded under whole-cell current clamp (resting membrane potential, -48 mV). Single-action potentials initiated near the somatic recording site (middle black trace) and backpropagated to the dendritic recording site (top red trace) with almost no voltage attenuation (bottom overlaid traces). C, Top plot summarizes voltage attenuation factors (dendritic amplitude/somatic amplitude) of backpropagated action potentials (closed circles) at various distances along the primary dendrite (pooled data; n = 7 cells). Also shown are attenuation factors for subthreshold voltage transients (open triangles) induced by 2 msec, 100-350 pA current pulses (pooled data; n = 5 cells). The bottom plot summarizes broadening factors (dendritic width/somatic width) of backpropagated action potentials at various distances along the primary dendrite (pooled data; n = 7 cells). D, Left column of traces shows subthreshold voltage transients (bottom pair) and action potentials (top pair) induced by injection of 3 msec current pulses at the somatic recording site (320 pA subthreshold, 340 pA suprathreshold). Black trace, Soma; red trace, dendrite. In the right column of traces, 3 msec current pulses were injected into the dendritic recording site to produce subthreshold voltage transients (bottom pair; 300 pA) or action potentials (top pair; 400 pA). Action potentials initiated near the soma, regardless of the current injection site. The resting membrane potential was -55 mV.
Figure 5.
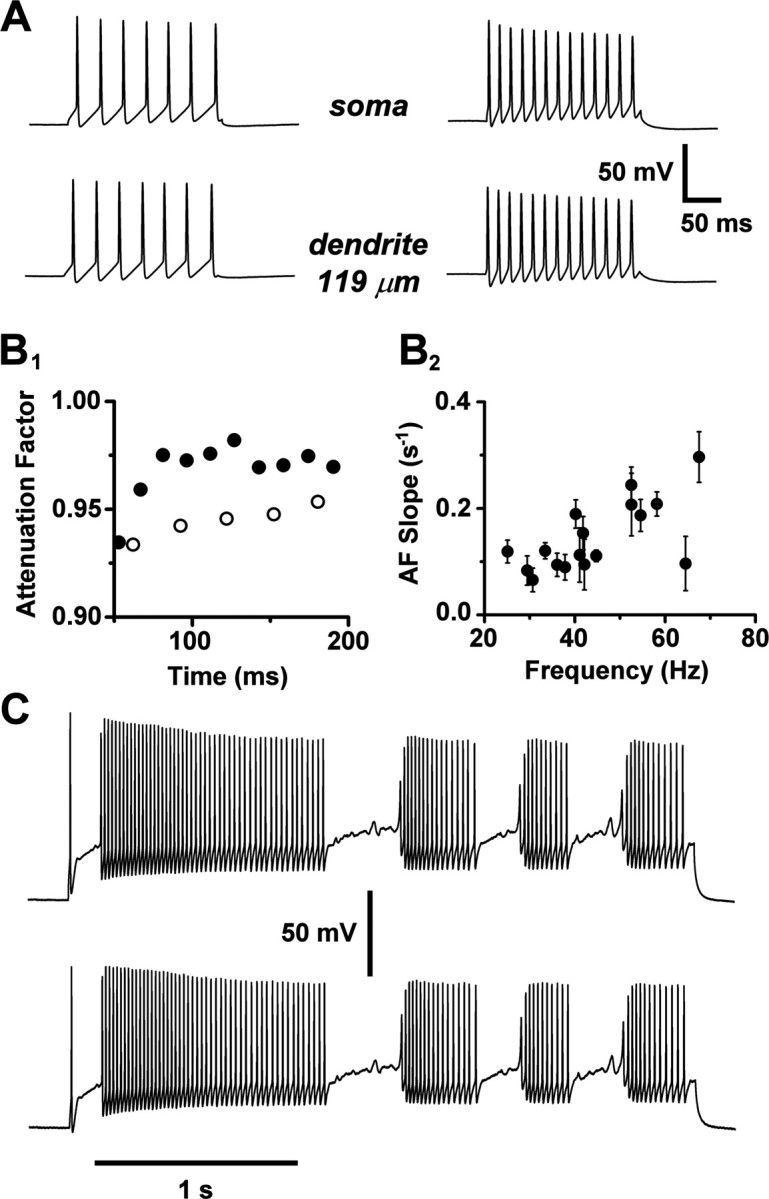
Action potential backpropagation is activity independent. A, Paired whole-cell recordings from the soma and primary dendrite (119 μm) of an AOB mitral cell firing spike trains at lower frequency (left pair of traces; 30-35 Hz) and higher frequency (right pair; 60-72 Hz). B, On the left (B1), the backpropagation attenuation factors (dendritic amplitude/somatic amplitude) for individual action potentials in A are plotted as a function of time. ○, Lower frequency; •, higher frequency. On the right (B2), the slopes of linear fits to attenuation factor versus time plots like B1 are shown over a range of firing frequencies (pooled data from n = 4 cells). C, Paired whole-cell recordings of clustered spike discharge and subthreshold membrane potential oscillations from the soma (top trace) and primary dendrite (bottom trace; 145 μm) of an AOB mitral cell (3.1 sec, 400 pA current pulse).
We have shown that single-action potentials can propagate unattenuated into the primary dendrite. However, AOB mitral cells may fire at frequencies in excess of 20 Hz during chemosensory investigation of conspecifics (Luo et al., 2003). At these frequencies, trains of action potentials in the apical dendrites of some cortical neurons experience pronounced activity-dependent attenuation (Spruston et al., 1995; Stuart et al., 1997). To test whether such phenomena occur in AOB mitral cells, we evoked spike trains of different frequencies by injecting 200 msec current pulses of various amplitudes into the soma (Fig. 5A). We found no activity-dependent attenuation over a wide frequency range of 25-67 Hz. Rather, we observed a small facilitation of the amplitudes of backpropagated spikes relative to the somatic spikes (Fig. 5B). Linear regression of the time sequences of attenuation factors of individual spikes in the trains yielded a significant positive slope of 0.15 ± 0.07 sec-1 (n = 17 trials; four cells; p < 0.001; one-tailed t test), which was positively correlated with firing rate (r = 0.66). This effect can be traced to a progressive reduction of somatic spike amplitudes, attributable perhaps to cumulative inactivation of Na+ current during steady somatic depolarization. The lack of activity-dependent attenuation confirms that dye saturation, not spike attenuation, underlies the saturation of dendritic fluorescence transients shown in Figure 1C.
Activity-independent backpropagation means that precise amplitude and time information encoded in complex spike patterns is communicated with high fidelity from soma to dendritic locations. This is illustrated in Figure 5C, where injection of a sustained current into the soma of an AOB mitral cell evoked clusters of γ-frequency (35-50 Hz) spike trains, separated by intervals of subthreshold membrane potential oscillation. The simultaneous dendritic recording confirmed that both spike clusters and oscillations were faithfully transmitted from soma to dendrite (145 μm).
The average length of AOB primary dendrites from soma to glomerular arborization is ∼400 μm (Takami and Graziadei, 1991). Our dendritic recording sites extended out to ∼200 μm, which is, on average, about halfway to the glomerular layer (Fig. 4A). The progressive tapering and divergent trajectories of AOB primary dendrites presented a technical barrier to direct patchclamp recordings from more distal dendritic sites. We therefore adopted a computational approach to assess the propagation of action potential transients into these sites. We sought to gain a semiquantitative understanding of the origins of the spatial profiles of ΔF/F0 and to evaluate their compatability with active versus passive backpropagation into the distal dendrite.
A simplified compartmental model was used to calculate voltage transients and associated calcium fluorescence profiles. A soma and axon initial segment were connected to a dendrite represented by a 400 μm tapered cable. The proximal 200 μmofthe dendrite was populated with a sufficient density of voltage-gated Na+ and K+ channels to support active backpropagation, as indicated by our paired recordings. Kinetic parameters and densities of the Na+ and K+ channels in the model were adjusted so that computed action potential waveforms fit the data obtained from paired recordings taken from soma and dendrite (Fig. 6A). In the distal 200 μm of the dendrite, active and passive conduction were compared by setting the Na+ and K+ conductance densities either equal to the proximal densities, or to zero. In Figure 6B, the computed spatial profiles of the peak voltage and half-width of model action potentials are plotted for both active and passive backpropagation in the distal dendrite (black and gray curves). Removal of active conductances from the distal dendrite resulted in a pronounced attenuation and broadening of the spikes, signaling failure of active backpropagation (Fig. 6C, voltage waveforms). We also modeled the TTX experiment of Figure 3, by setting Na+ channel density to zero throughout the cell and applying a simulated voltage waveform clamp at the soma. We again found strong decay and broadening of voltage transients along the dendrite (Fig. 6B, dotted curves; C, voltage waveforms). These effects were manifested more strongly in a thinly tapered dendrite, as expected for electrotonic decay of voltage along a cable. To show that our delayed rectifier K+ conductance did not attenuate the amplitudes of dendritic voltage transients, we modeled the effect of K+ channel block by TEA in an action potential waveform voltage-clamp experiment, setting K+ channel density to zero throughout the cell. The simulation predicted that TEA should broaden dendritic voltage transients but leave their amplitudes unaltered (Fig. 6C). This result compares favorably with data from MOB primary dendrites (Bischofberger and Jonas, 1997, their Fig. 4C).
Figure 6.
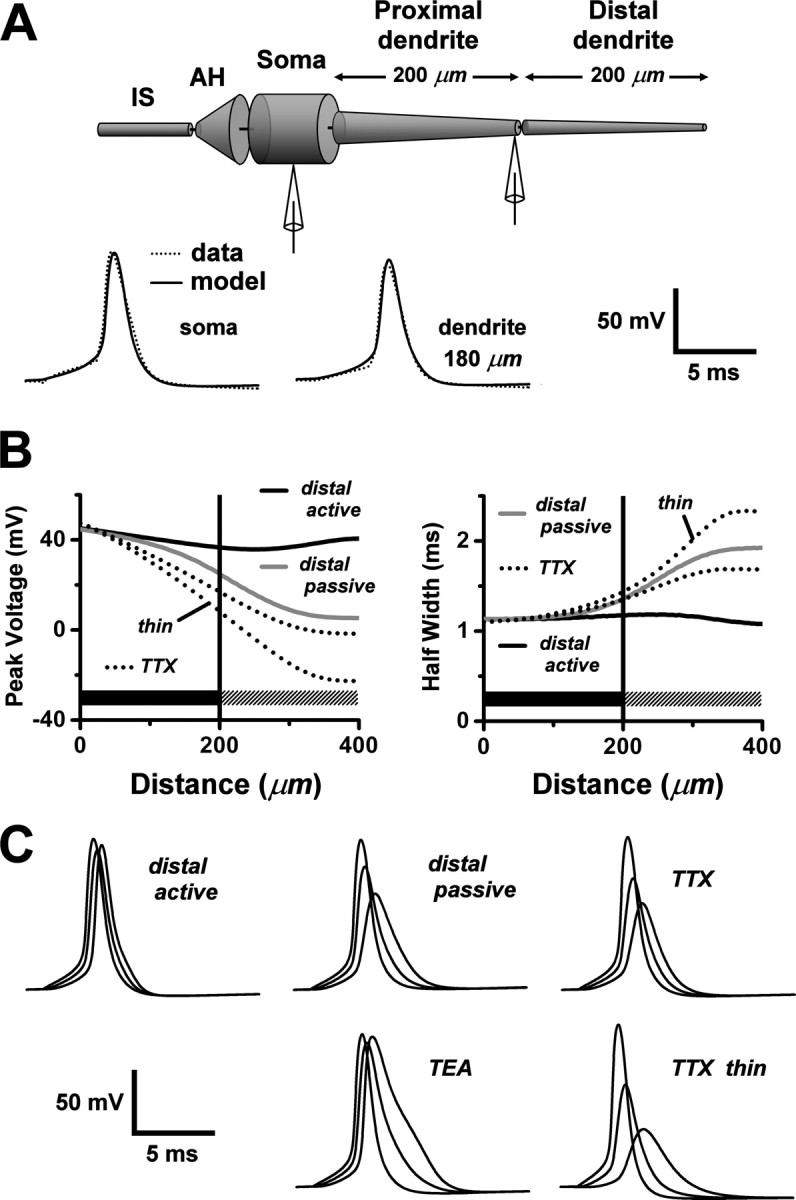
Modeling action potential backpropagation in the AOB primary dendrite. A, Top, A schematic illustration of our compartmental model of an AOB mitral cell with a single tapered primary dendrite. The distal half of the dendrite was represented as a separate section, in which the density of Na+ and K+ channels could be independently set to zero to explore the consequences of passive backpropagation. AH, Axon hillock; IS, axon initial segments. Bottom, Action potential waveforms computed from the model (solid curves) were fit to action potentials obtained from a paired soma- dendritic whole-cell recording (dotted curves; dendritic recording at 180 μm). Pipette symbols in top diagram show approximate recording locations. B, Plots, as a function of distance from the soma, of model calculations of the peak voltages (left) and half-widths (right) of voltage transients associated with action potential backpropagation under the following different conditions: (1) solid black curves: the control condition, with active backpropagation supported by Na+ and K+ channels uniformly distributed throughout the full length of the dendrite; (2) solid gray curves: passive distal dendrite, with Na+ and K+ channels retained in the proximal dendritic section (dark horizontal bars), but deleted from the distal dendritic section (> 200 μm; hatched horizontal bars); (3) unlabeled dotted curves: simulation of the TTX experiment, with Na+ channels deleted everywhere, and the somatic action potential waveform of the control condition (1) applied by single-electrode voltage clamp at the soma (electrode series resistance, 10 MΩ); and (4) dotted curves labeled “thin”: same as previous condition, but with a thin tapered dendrite (d0 = 2 μm; λT = 150 μm). C, Computed voltage transients during action potential backpropagation. Each set of three waveforms shows the voltage at the soma, middle of the dendrite (200 μm), and end of the dendrite (400 μm) (backpropagation time lag from left to right). Plots labeled “distal active,” “distal passive,” “TTX,” and “TTX thin” correspond, respectively, to conditions 1-4 in Figure 7B. In the plot labeled “TEA,” K+ channels were deleted everywhere, Na+ channels were retained as in the control condition (1), and a control somatic action potential waveform was applied by a single-electrode voltage clamp at the soma.
To model the fluorescence ratio ΔF/F0, we needed to translate voltage transients into calcium dynamics. For this purpose, an N-type voltage-gated Ca2+ channel was inserted at uniform density throughout the model dendrite, with kinetic parameters chosen to mimic the properties of high-threshold Ca2+ channels characterized in MOB mitral cells (Fig. 7D) (Wang et al., 1996). The indicator dye was modeled as a high-affinity exogenous Ca2+ buffer, binding Ca2+ in competition with an endogenous, low-affinity Ca2+ buffer. The endogenous buffer was assumed to be spatially uniform, but the indicator dye might exhibit a concentration gradient, because of incomplete loading from the pipette. This can cause the fluorescence ratio ΔF/F0 to vary along the dendrite. As dye concentration decreases away from the soma, ΔF/F0 should increase because F0 varies linearly with concentration, whereas ΔF is nearly constant. Magnitudes of dye gradients were estimated experimentally by monitoring changes in resting fluorescence (loading curves) of dendrites at various times after whole-cell breakthrough.
Figure 7A shows loading curves measured from proximal and distal locations of an AOB primary dendrite, normalized to the fluorescence plateau attained after ∼80 min (when loading was complete). During dye loading, we also monitored local changes in fluorescence accompanying single-action potentials and noticed a significant reduction in the ratio ΔF/F0 over time (Fig. 7B). The ratio leveled off after 80 min, indicating that the change was associated with the loading process. However, even after loading was complete and dye gradients had dissipated, a difference remained between ratios at proximal and distal locations. We attributed this residual difference to the effect of dendritic taper. Our loading measurements demonstrated that a dye gradient could contribute to the increasing trend of ΔF/F0 observed along the dendrite (Fig. 2C). Similar data for loading at proximal and distal sites along the same dendrite were acquired from four additional cells. Figure 7C plots percentage of loading along the dendrite at 40 min, our earliest imaging time, observed at various distances from the soma. The solid line represents a least squares fit to the data, and we used this linear dye gradient (90% of 150 μm at the soma, 55% at 400 μm) in our model.
Computed ΔF/F0 spatial profiles for a dye gradient (g) and a uniformly distributed dye (u) are compared in Figure 7E (top pair of curves). The model predicted the increasing trend of ΔF/F0, and the presence of a dye gradient boosted the ratio, in agreement with our loading measurements. Switching from a tapered model dendrite to one with uniform diameter removed the positive slope in the ΔF/F0 profile (Fig. 7E, bottom curves), showing that tapering is a major determinant of the profile. On the same graph, we show computed spatial profiles of ΔF/F0 for passive conduction into the distal dendrite (gray curves). Removal of Na+ and K+ conductances from the distal dendrite strongly attenuated the local Ca2+ influx and abolished the increasing trend of ΔF/F0. We concluded that our experimental results are inconsistent with passive backpropagation in the distal dendrite. We expect that this conclusion also applies to branched dendrites, because adding branches lowers the distal impedance, which should further attenuate distal voltage and Ca2+ transients. Therefore, the simplest model consistent with our data is one with uniformly active backpropagation through the entire dendritic arbor.
Figure 7F shows the results of a model simulation of the TTX experiment of Figure 3. The effect of TTX was mimicked by setting Na+ channel density to zero throughout the cell. The model predicted the decay of the TTX attenuation factor along the proximal dendrite, with a decay length that lies within the range of our observations. The scatter in the TTX data may be associated with experimental error, but we also considered the possibility that cell-to-cell variations in dendritic geometry might be a factor. Attenuation curves for standard and thin model dendrites are compared in Figure 7F and also plotted over the data in Figure 3C. The shorter decay distance for the thin dendrite shows that variations in cable geometry can introduce a large variance into the attenuation profile of ΔF/F0.
As an additional test of active backpropagation, we compared the rising phases of fluorescence transients recorded from the proximal and distal primary dendrite, evoked by a single-action potential initiated by somatic current injection. Passively conducted voltage transients in the distal dendrite are expected to be broadened, and the associated calcium responses may be slower than calcium responses recorded close to soma. Typical experimental rising phases of ΔF/F0 recorded from proximal and distal dendrites are rescaled and overlaid in Figure 7G. The data are clearly superimposable, with no significant slowing of the distal response. Similar data were acquired from a total of n = 8 cells. The 50% rise time at 20-30 μm from the soma was 1.84 ± 0.29 msec, and more distally along the dendrite it was 1.84 ± 0.40 msec (165-623 μm). Distal rise times were not significantly slower than proximal (p > 0.05; paired t test). We noticed that the rising phases of fluorescence transients outlasted the falling phases of action potentials that generate the calcium tail current at 25°C (Sabatini and Regehr, 1996). In our model, this slowed time course can be explained by competition between the endogenous Ca2+ buffer and the exogenous indicator dye. Initially, a fraction of the calcium is bound rapidly by a higher concentration of low-affinity endogenous buffer and is subsequently released more slowly to be rebound by the high-affinity fluorescent indicator (Sabatini and Regehr, 1998). The solid curve in Figure 7G shows that our model of this process could fit the observed rising phase.
Experimental and model results are summarized in Figure 7H, which plots the ratio of distal 50% rise time to proximal 50% rise time (open circles) at various distances along the primary dendrite. This ratio was uncorrelated with distance from the soma (r = 0.0039). The solid curves in Figure 7H are computed rise time ratios along the model dendrite, for active and passive invasion of spikes into the distal section. Eliminating active conduction in the distal section resulted in a slowing of the ΔF/F0 rising phase that deviated from experimental observation. This provides additional evidence supporting our contention that back-propagation in the distal dendrite is active, not passive.
Discussion
The branching dendritic topology and multiglomerular projections of the second-order neurons in the AOB have been known since their original description over a century ago by Ramón y Cajal (1901). More recent Golgi studies revealed the diverse ramifications expressed by the AOB primary dendrites (Takami and Graziadei, 1990, 1991). A single mitral cell may connect to a unique glomerulus, or it may send dendritic branches to as many as six glomeruli. A one-to-many connectivity was also found in afferent projections of vomeronasal sensory neurons. Axons of cells expressing one VR gene were found to target 10-30 distinct glomeruli (Belluscio et al., 1999). This mutual divergence of peripheral and central mappings to the glomerular layer is compatible with simple or complex schemes for processing vomeronasal sensory information, depending on the pattern of connectivity. The wiring plan was recently clarified by using lipophilic tracers to visualize the dendritic arbors of mitral cells connected to glomeruli receiving input from defined VR receptors (Del Punta et al., 2002). It was discovered that mitral cells communicate primarily or exclusively with glomeruli receiving input from a common VR receptor (homotypic connectivity). This convergence of distributed inputs onto second-order neurons suggests a simplified scheme in which VR-coded information is handled in a modular manner, by separate, parallel ensembles of interlinked glomeruli and mitral cells.
The physiological results presented here support the idea that the anatomical modules in the AOB correspond to functional modules. We showed that when mitral cells fire action potentials, the spikes backpropagate without attenuation into the primary dendrites. Backpropagation is active, being supported by Na+ channels. Spikes negotiate branch points without failure, propagating into all the daughter branches to reach the distal glomerular arbors. This fast signaling may assist in the precise coordination of electrical activity among mitral cells with shared glomerular projections. In the MOB, mitral cells with primary dendrites projecting to a common glomerulus display time-correlated electrical activity. Simultaneous recordings from two somata have demonstrated synchrony of low-frequency membrane potential oscillations (Carlson et al., 2000; Schoppa and Westbrook, 2001) and action potentials (Schoppa and Westbrook, 2002). This synchronization is likely to depend on intraglomerular coupling between apical dendritic tufts. It has been proposed to involve some combination of conventional fast synaptic transmission via AMPA receptors, slow spillover transmission, and electrical relays through gap junction complexes (Schoppa and Urban, 2003). Active propagation of action potentials in MOB primary dendrites ensures that synchronization signals are not delayed by capacitative filtering along the extended stretch of cable separating soma from apical tuft. A similar function could be served by active signal conduction in the more complex AOB primary dendrites.
We have shown that invasion of backpropagated action potentials elicits strong calcium transients in the primary dendritic trunks and glomerular tufts of AOB mitral cells. Similar robust calcium responses to backpropagated spikes have been reported in primary dendrites and glomerular arbors of MOB mitral cells (Isaacson and Strowbridge, 1998; Charpak et al., 2001; Debarbieux et al., 2003). The calcium influx into the primary dendritic trunks may be associated with dendrodendritic transmission between mitral cells and granule cells. Immunocytochemical (Takami et al., 1992; Quaglino et al., 1999) and electrophysiological (Reinhardt et al., 1983; Jia et al., 1999; Taniguchi and Kaba, 2001) studies indicate that the AOB contains lateral inhibitory mitral-granule circuits similar to those of the MOB. The calcium influx into the glomerular tufts may serve two important presynaptic functions: (1) it may provide the trigger for the dendrodendritic transmission between mitral cell tufts in the same glomerulus, necessary for modular coordination of activity; and (2) it may activate dendrodendritic synapses between mitral cells and juxtaglomerular cells providing a lateral inhibitory pathway between glomeruli belonging to different functional modules.
The primary dendritic architecture of mammalian AOB mitral cells resembles that of mitral cells in the MOB of non-mammalian vertebrates. In both cases, the dendrites branch and connect to multiple glomeruli (Satou, 1990; Jiang and Holley, 1992; Dryer and Graziadei, 1994). It has been suggested that these ramifying dendrites perform more complex integrative functions than the specialized uniglomerular primary dendrites in the mammalian MOB (Takami and Graziadei, 1990; Dryer and Graziadei, 1994). This may be true for the non-mammalian dendrites if they link to glomeruli receiving convergent inputs from different olfactory receptors. The dendrites in the mammalian AOB, however, link to glomeruli innervated by a common VR receptor. This pattern of connectivity would seem to preclude sensory integration by the dendritic branches. Consistent with this, activation of individual AOB mitral cells in mouse is highly specific with regard to sex and genetic strain of conspecifics (Luo et al., 2003). Our finding of uniform fast electrical and calcium signaling in all branches also favors a simple model of dendritic processing. Regenerative Na+ conductances render the primary dendrites electrically compact at both low and high conduction frequencies, making their heterogeneous, irregularly branched morphologies essentially irrelevant. We propose that homotypic connectivity segregates the AOB circuitry into VR-coded multiglomerular modules that are functionally equivalent to the olfactory receptor-coded uniglomerular modules in the MOB.
Footnotes
This work was supported by National Institute on Deafness and Other Communication Disorders Grant DC04208 to G.L. We gratefully acknowledge helpful comments and advice on this manuscript from A. Gelperin, B.M. Salzberg, and the anonymous reviewers. Invaluable technical assistance was provided by A. Ladavac.
Correspondence should be addressed to Dr. Graeme Lowe, Monell Chemical Senses Center, 3500 Market Street, Philadelphia, PA 19104-3308. E-mail: loweg@monell.org.
Copyright © 2004 Society for Neuroscience 0270-6474/04/249341-12$15.00/0
References
- Aungst JL, Heyward PM, Puche AC, Karnup SV, Hayar A, Szabo G, Shipley MT (2003) Centre-surround inhibition among olfactory bulb glomeruli. Nature 426: 623-629. [DOI] [PubMed] [Google Scholar]
- Belluscio L, Koentges G, Axel R, Dulac C (1999) A map of pheromone receptor activation in the mammalian brain. Cell 97: 209-220. [DOI] [PubMed] [Google Scholar]
- Bischofberger J, Jonas P (1997) Action potential propagation into the presynaptic dendrites of rat mitral cells. J Physiol (Lond) 504: 359-365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bischofberger J, Schild D (1995) Different spatial patterns of [Ca2+] increase caused by N- and L-type Ca2+ channel activation in frog olfactory bulb neurones. J Physiol (Lond) 487: 305-317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brent R (1976) A new algorithm for minimizing a function of several variables without calculating derivatives. In: Algorithms for minimization without derivatives, pp 200-248. Englewood Cliffs, NJ: Prentice Hall.
- Carlson GC, Shipley MT, Keller A (2000) Long-lasting depolarizations in mitral cells of the rat olfactory bulb. J Neurosci 20: 2011-2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charpak S, Mertz J, Beaurepaire E, Moreaux L, Delaney K (2001) Odorevoked calcium signals in dendrites of rat mitral cells. Proc Natl Acad Sci USA 98: 1230-1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen WR, Midtgaard J, Shepherd GM (1997) Forward and backward propagation of dendritic impulses and their synaptic control in mitral cells. Science 278: 463-467. [DOI] [PubMed] [Google Scholar]
- Christie JM, Westbrook GL (2003) Regulation of backpropagating action potentials in mitral cell lateral dendrites by A-type potassium currents. J Neurophysiol 89: 2466-2472. [DOI] [PubMed] [Google Scholar]
- Debarbieux F, Audinat E, Charpak S (2003) Action potential propagation in dendrites of rat mitral cells in vivo. J Neurosci 23: 5553-5560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Punta K, Puche A, Adams NC, Rodriguez I, Mombaerts P (2002) A divergent pattern of sensory axonal projections is rendered convergent by second-order neurons in the accessory olfactory bulb. Neuron 35: 1057-1066. [DOI] [PubMed] [Google Scholar]
- Djurisic M, Antic S, Chen WR, Zecevic D (2004) Voltage imaging from dendrites of mitral cells: EPSP attenuation and spike trigger zones. J Neurosci 24: 6703-6714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dryer L, Graziadei PP (1994) Mitral cell dendrites: a comparative approach. Anat Embryol (Berl) 189: 91-106. [DOI] [PubMed] [Google Scholar]
- Gennerich A, Schild D (2002) Anisotropic diffusion in mitral cell dendrites revealed by fluorescence correlation spectroscopy. Biophys J 83: 510-522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halpern M (1987) The organization and function of the vomeronasal system. Annu Rev Neurosci 10: 325-362. [DOI] [PubMed] [Google Scholar]
- Halpern M, Martinez-Marcos A (2003) Structure and function of the vomeronasal system: an update. Prog Neurobiol 70: 245-318. [DOI] [PubMed] [Google Scholar]
- Halpern M, Jia C, Shapiro LS (1998) Segregated pathways in the vomeronasal system. Microsc Res Tech 41: 519-529. [DOI] [PubMed] [Google Scholar]
- Helmchen F, Imoto K, Sakmann B (1996) Ca2+ buffering and action potential-evoked Ca2+ signaling in dendrites of pyramidal neurons. Biophys J 70: 1069-1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrada G, Dulac C (1997) A novel family of putative pheromone receptors in mammals with a topographically organized and sexually dimorphic distribution. Cell 90: 763-773. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT (1997) The NEURON simulation environment. Neural Comput 9: 1179-1209. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 117: 500-544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman DA, Magee JC, Colbert CM, Johnston D (1997) K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature 387: 869-875. [DOI] [PubMed] [Google Scholar]
- Isaacson JS, Strowbridge BW (1998) Olfactory reciprocal synapses: dendritic signaling in the CNS. Neuron 20: 749-761. [DOI] [PubMed] [Google Scholar]
- Jaffe DB, Ross WN, Lisman JE, Lasser-Ross N, Miyakawa H, Johnston D (1994) A model for dendritic Ca2+ accumulation in hippocampal pyramidal neurons based on fluorescence imaging measurements. J Neurophysiol 71: 1065-1077. [DOI] [PubMed] [Google Scholar]
- Jia C, Halpern M (1997) Segregated populations of mitral/tufted cells in the accessory olfactory bulb. NeuroReport 8: 1887-1890. [DOI] [PubMed] [Google Scholar]
- Jia C, Halpern M (2004) Calbindin D28k, parvalbumin, and calretinin immunoreactivity in the main and accessory olfactory bulbs of the gray short-tailed opossum, Monodelphis domestica J Morphol 259: 271-280. [DOI] [PubMed] [Google Scholar]
- Jia C, Chen WR, Shepherd GM (1999) Synaptic organization and neurotransmitters in the rat accessory olfactory bulb. J Neurophysiol 81: 345-355. [DOI] [PubMed] [Google Scholar]
- Jiang T, Holley A (1992) Some properties of receptive fields of olfactory mitral/tufted cells in the frog. J Neurophysiol 68: 726-733. [DOI] [PubMed] [Google Scholar]
- Kasowski HJ, Kim H, Greer CA (1999) Compartmental organization of the olfactory bulb glomerulus. J Comp Neurol 407: 261-274. [PubMed] [Google Scholar]
- Keverne EB (1999) The vomeronasal organ. Science 286: 716-720. [DOI] [PubMed] [Google Scholar]
- Kishi K, Mori K, Tazawa Y (1982) Three-dimensional analysis of dendritic trees of mitral cells in the rabbit olfactory bulb. Neurosci Lett 28: 127-132. [DOI] [PubMed] [Google Scholar]
- Kosaka K, Toida K, Aika Y, Kosaka T (1998) How simple is the organization of the olfactory glomerulus?: the heterogeneity of so-called periglomerular cells. Neurosci Res 30: 101-110. [DOI] [PubMed] [Google Scholar]
- Lowe G (2002) Inhibition of backpropagating action potentials in mitral cell secondary dendrites. J Neurophysiol 88: 64-85. [DOI] [PubMed] [Google Scholar]
- Luo M, Katz LC (2001) Response correlation maps of neurons in the mammalian olfactory bulb. Neuron 32: 1165-1179. [DOI] [PubMed] [Google Scholar]
- Luo M, Fee MS, Katz LC (2003) Encoding pheromonal signals in the accessory olfactory bulb of behaving mice. Science 299: 1196-1201. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Joerges J, Huguenard JR, Sejnowski TJ (1995) A model of spike initiation in neocortical pyramidal neurons. Neuron 15: 1427-1439. [DOI] [PubMed] [Google Scholar]
- Maravall M, Mainen ZF, Sabatini BL, Svoboda K (2000) Estimating intracellular calcium concentrations and buffering without wavelength ratioing. Biophys J 78: 2655-2667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mombaerts P, Wang F, Dulac C, Chao SK, Nemes A, Mendelsohn M, Edmondson J, Axel R (1996) Visualizing an olfactory sensory map. Cell 87: 675-686. [DOI] [PubMed] [Google Scholar]
- Mori K, Kishi K, Ojima H (1983) Distribution of dendrites of mitral, displaced mitral, tufted, and granule cells in the rabbit olfactory bulb. J Comp Neurol 219: 339-355. [DOI] [PubMed] [Google Scholar]
- Naraghi M (1997) T-jump study of calcium binding kinetics of calcium chelators. Cell Calcium 22: 255-268. [DOI] [PubMed] [Google Scholar]
- Orona E, Rainer EC, Scott JW (1984) Dendritic and axonal organization of mitral and tufted cells in the rat olfactory bulb. J Comp Neurol 226: 346-356. [DOI] [PubMed] [Google Scholar]
- Pinching AJ, Powell TP (1971) The neuron types of the glomerular layer of the olfactory bulb. J Cell Sci 9: 305-345. [DOI] [PubMed] [Google Scholar]
- Price JL, Powell TP (1970) The mitral and short axon cells of the olfactory bulb. J Cell Sci 7: 631-651. [DOI] [PubMed] [Google Scholar]
- Puopolo M, Belluzzi O (1998) Inhibitory synapses among interneurons in the glomerular layer of rat and frog olfactory bulbs. J Neurophysiol 80: 344-349. [DOI] [PubMed] [Google Scholar]
- Quaglino E, Giustetto M, Panzanelli P, Cantino D, Fasolo A, Sassoe-Pognetto M (1999) Immunocytochemical localization of glutamate and gamma-aminobutyric acid in the accessory olfactory bulb of the rat. J Comp Neurol 408: 61-72. [DOI] [PubMed] [Google Scholar]
- Rall W, Shepherd GM, Reese TS, Brightman MW (1966) Dendrodendritic synaptic pathway for inhibition in the olfactory bulb. Exp Neurol 14: 44-56. [DOI] [PubMed] [Google Scholar]
- Ramón y Cajal S (1901) Textura del lóbulo olfativo accesorio. Trab Lab Invest Biol 1: 141-150. [Google Scholar]
- Reinhardt W, MacLeod NK, Ladewig J, Ellendorff F (1983) An electrophysiological study of the accessory olfactory bulb in the rabbit. II. Input-output relations as assessed from analysis of intra- and extracellular unit recordings. Neuroscience 10: 131-139. [DOI] [PubMed] [Google Scholar]
- Ryba NJ, Tirindelli R (1997) A new multigene family of putative pheromone receptors. Neuron 19: 371-379. [DOI] [PubMed] [Google Scholar]
- Sabatini BL, Regehr WG (1996) Timing of neurotransmission at fast synapses in the mammalian brain. Nature 384: 170-172. [DOI] [PubMed] [Google Scholar]
- Sabatini BL, Regehr WG (1998) Optical measurement of presynaptic calcium currents. Biophys J 74: 1549-1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satou M (1990) Synaptic organization, local neuronal circuitry, and functional segregation of the teleost olfactory bulb. Prog Neurobiol 34: 115-142. [DOI] [PubMed] [Google Scholar]
- Schoppa NE, Urban NN (2003) Dendritic processing within olfactory bulb circuits. Trends Neurosci 26: 501-506. [DOI] [PubMed] [Google Scholar]
- Schoppa NE, Westbrook GL (2001) Glomerulus-specific synchronization of mitral cells in the olfactory bulb. Neuron 31: 639-651. [DOI] [PubMed] [Google Scholar]
- Schoppa NE, Westbrook GL (2002) AMPA autoreceptors drive correlated spiking in olfactory bulb glomeruli. Nat Neurosci 5: 1194-1202. [DOI] [PubMed] [Google Scholar]
- Shen GY, Chen WR, Midtgaard J, Shepherd GM, Hines ML (1999) Computational analysis of action potential initiation in mitral cell soma and dendrites based on dual patch recordings. J Neurophysiol 82: 3006-3020. [DOI] [PubMed] [Google Scholar]
- Shinohara H, Asano T, Kato K (1992) Differential localization of G-proteins Gi and Go in the accessory olfactory bulb of the rat. J Neurosci 12: 1275-1279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N, Schiller Y, Stuart G, Sakmann B (1995) Activity-dependent action potential invasion and calcium influx into hippocampal CA1 dendrites. Science 268: 297-300. [DOI] [PubMed] [Google Scholar]
- Stuart G, Schiller J, Sakmann B (1997) Action potential initiation and propagation in rat neocortical pyramidal neurons. J Physiol (Lond) 505: 617-632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugai T, Sugitani M, Onoda N (1997) Subdivisions of the guinea-pig accessory olfactory bulb revealed by the combined method with immunohistochemistry, electrophysiological, and optical recordings. Neuroscience 79: 871-885. [DOI] [PubMed] [Google Scholar]
- Takami S, Graziadei PP (1990) Morphological complexity of the glomerulus in the rat accessory olfactory bulb—a Golgi study. Brain Res 510: 339-342. [DOI] [PubMed] [Google Scholar]
- Takami S, Graziadei PP (1991) Light microscopic Golgi study of mitral/tufted cells in the accessory olfactory bulb of the adult rat. J Comp Neurol 311: 65-83. [DOI] [PubMed] [Google Scholar]
- Takami S, Fernandez GD, Graziadei PP (1992) The morphology of GABA-immunoreactive neurons in the accessory olfactory bulb of rats. Brain Res 588: 317-323. [DOI] [PubMed] [Google Scholar]
- Taniguchi M, Kaba H (2001) Properties of reciprocal synapses in the mouse accessory olfactory bulb. Neuroscience 108: 365-370. [DOI] [PubMed] [Google Scholar]
- Thomas D, Tovey SC, Collins TJ, Bootman MD, Berridge MJ, Lipp P (2000) A comparison of fluorescent Ca2+ indicator properties and their use in measuring elementary and global Ca2+ signals. Cell Calcium 28: 213-223. [DOI] [PubMed] [Google Scholar]
- Toida K, Kosaka K, Heizmann CW, Kosaka T (1996) Electron microscopic serial-sectioning/reconstruction study of parvalbumin-containing neurons in the external plexiform layer of the rat olfactory bulb. Neuroscience 72: 449-466. [DOI] [PubMed] [Google Scholar]
- Urban NN (2002) Lateral inhibition in the olfactory bulb and in olfaction. Physiol Behav 77: 607-612. [DOI] [PubMed] [Google Scholar]
- Urban NN, Sakmann B (2002) Reciprocal intraglomerular excitation and intra- and interglomerular lateral inhibition between mouse olfactory bulb mitral cells. J Physiol (Lond) 542: 355-367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Campenhausen H, Yoshihara Y, Mori K (1997) OCAM reveals segregated mitral/tufted cell pathways in developing accessory olfactory bulb. NeuroReport 8: 2607-2612. [DOI] [PubMed] [Google Scholar]
- Wang X, McKenzie JS, Kemm RE (1996) Whole cell calcium currents in acutely isolated olfactory bulb output neurons of the rat. J Neurophysiol 75: 1138-1151. [DOI] [PubMed] [Google Scholar]
- Wouterlood FG, Härtig W (1995) Calretinin-immunoreactivity in mitral cells of the rat olfactory bulb. Brain Res 682: 93-100. [DOI] [PubMed] [Google Scholar]