Abstract
Ion channels open and close stochastically. The fluctuation of these channels represents an intrinsic source of noise that affects the input-output properties of the neuron. We combined whole-cell measurements with biophysical modeling to characterize the intrinsic stochastic and electrical properties of single neurons as observed at the soma. We measured current and voltage noise in 18 d postembryonic cultured neurons from the rat hippocampus, at various subthreshold and near-threshold holding potentials in the presence of synaptic blockers. The observed current noise increased with depolarization, as ion channels were activated, and its spectrum demonstrated generalized 1/fbehavior. Exposure to TTX removed a significant contribution from Na+ channels to the noise spectrum, particularly at depolarized potentials, and the resulting spectrum was now dominated by a single Lorentzian (1/f2) component. By replacing the intracellular K+ with Cs+, we demonstrated that a major portion of the observed noise was attributable to K+ channels. We compared the measured power spectral densities to a 1-D cable model of channel fluctuations based on Markov kinetics. We found that a somatic compartment, in combination with a single equivalent cylinder, described the effective geometry from the viewpoint of the soma. Four distinct channel populations were distributed in the membrane and modeled as Lorentzian current noise sources. Using the NEURON simulation program, we summed up the contributions from the spatially distributed current noise sources and calculated the total voltage and current noise. Our quantitative model reproduces important voltage- and frequency-dependent features of the data, accounting for the 1/f behavior, as well as the effects of various blockers.
Keywords: voltage noise, current noise, biophysical modeling, coding, neural computation, PSD
Introduction
The effects of intrinsic noise in neuronal membranes have been studied for a long time, with pioneering studies by Pecher (1939), Fatt and Katz (1950, 1952), Derksen and Verveen (1966), Verveen et al. (1967), and numerous others (Fishman, 1973; Wanke et al., 1974; Fishman et al., 1975a,b; for a thorough review, see DeFelice, 1981). More recently, there has been a reinvigoration of interest in the field. Noise that is intrinsic or extrinsic to the neuron is now understood to have important effects on its information processing capabilities, changing action potential dynamics (Chow and White, 1996; White et al., 1998; Kretzberg et al., 2001b), enhancing signal detection (Wiesenfeld and Moss, 1995; Gammaitoni et al., 1998), altering the spike-timing reliability (Schneidman et al., 1998; van Rossum et al., 2003), and affecting the tuning properties of the cell (Hunter et al., 1998; Hunter and Milton, 2003; Schreiber et al., 2004).
Here, we focus on subthreshold noise caused by intrinsic, nonsynaptic noise sources, in cultured hippocampal neurons. To study the noise experimentally and theoretically, we measured power spectral densities (PSDs) of voltage and current fluctuations at the soma, in the presence of synaptic blockers 6,7-dinitroquinoxaline-2,3-dione (DNQX) and picrotoxin. The noise PSD is the variance per unit frequency. It provides an effective signature of the noise spectrum. The integrated PSD yields the root mean square (rms) noise, or σ, which is also identical to the square root of the variance. We compared these measurements with calculated power spectra resulting from stochastic fluctuations of four Markov channel subpopulations in a 1-D cable model (Johnston and Wu, 1995; Sakmann and Neher, 1995; Manwani and Koch, 1999a). We show that apparent excess noise in the form of 1/f dependency can be resolved as the sum of several Lorentzian components caused by channel gating fluctuations.
The subthreshold voltage and current fluctuations produced by channels present appropriate topics for a combined experimental and modeling approach. First, below threshold, the neurons behave in a mostly stationary manner, allowing us to obtain long traces of data without altering the properties of the neuron. Second, neuronal behavior is simpler in the absence of spikes. If our theoretical methods prove applicable here, we can extend them to spiking neurons. Third, subthreshold fluctuations are of interest in their own right. Modeling studies and experimental measurements have indicated the presence of considerable intrinsic subthreshold noise in some preparations (Manwani and Koch, 1999a; White et al., 2000; Beierholm et al., 2001). The reliability and accuracy of spike timing can be affected by subthreshold noise because it can alter spike initiation in the neuron (Softky and Koch, 1993; Schneidman et al., 1998; Fourcaud-Trocme et al., 2003; van Rossum et al., 2003). Dendritic integration (Margulis and Tang, 1998; Poirazi et al., 2003), interaction between dendro-dendritic synapses in the olfactory bulb (Shepherd, 1998) or the inferior olive nucleus (Lampl and Yarom, 1997), the operations of nonspiking neurons, such as in the retina (Shepherd, 1998) or in the visual and olfactory systems of invertebrates (de Ruyter van Steveninck and Laughlin, 1996; MacLeod and Laurent, 1996; Kretzberg et al., 2001a), are all performed in the subthreshold regime.
Materials and Methods
Cell culture. Pregnant Wistar rats were killed by inhalation of CO2 at day 18 of gestation. Embryos were removed immediately by cesarean section, and hippocampi were extracted rapidly under stereomicroscopic observation under sterile conditions, cut into 1 mm pieces, and digested with 0.25% trypsin and 0.25 mg/ml DNase (Sigma, St. Louis, MO) at 36°C for 15 min. The pieces were then rinsed gently in HBSS without Ca2+ or Mg2+ (Life Technologies, Gaithersburg, MD), washed twice in plating medium, and triturated gently in 1 ml of plating medium with five passes through the 0.78 mm opening of a tip of a P-1000 Pipetman. Suspended cells were removed with a Pasteur pipette, and the remaining pieces were triturated once more. The resulting suspensions were filtered through a 70 μm nylon mesh to remove large debris and centrifuged for 2 min at 150 × g to pellet the cells, which were resuspended by trituration as above. Cells were plated in a 150 mm2 area at the middle of 35 mm Biocoat plastic culture dishes (Becton Dickinson, Franklin Lakes, NJ) to an approximate density of 300 cells/mm2. Cultures were maintained at 36°C in a 5% CO2 incubator. The plating and feeding medium was Neurobasal with B27 supplement, with 500 μm Glutamax and 25 μm glutamate. [K+] in this medium was 5.4 mm. Two milliliters of medium with the addition of 5% horse serum (Life Technologies) were added to the bath after plating to promote glial growth. After 3 d, 0.05% 1-β-d-arabinofuranosylcytosine (Sigma) was added to the medium to inhibit additional glial growth. The following day and weekly thereafter, 0.75 ml of culture medium was removed from each dish and replaced with 1 ml of fresh medium.
Electrophysiology. Whole-cell somatic recordings were performed on 140 cells with a Multi-Clamp 700A from Axon Instruments (Foster City, CA). The soma was identified visually using phase-contrast microscopy. The extracellular solution consisted of 140 mm NaCl, 5 mm KCl, 10 mm glucose, 5 mm HEPES, 2 mm CaCl2, and 1 mm MgCl2, pH 7.4 with NaOH, with 40 μm DNQX and 40 μm picrotoxin (diluted from 200 mm solutions in DMSO) added to block AMPA/kainate and GABAA synapses. dl-2-Amino-5-phosphonovaleric acid, an NMDA channel blocker, was tested in a few trials and found to be unimportant in the subthreshold regime. The intracellular solution contained (in mm) 120 K-glucose, 20 KCl, 10 Na-phosphocreatine, 10 HEPES, 10 sucrose, 5 EGTA, 4 Mg-ATP, 0.3 Tris-GTP, and 0.1 CaCl2, pH 7.4 with KOH. The resulting reversal potentials were calculated from the Nernst equation: -85.7 ± 0.3 mV for K+ and +66.5 ± 0.3 mV for Na+. These reversal potentials were also used in the model. Spiking threshold was generally found to be ∼-55 mV, and the mean resting potential was -74 ± 4 mV (n = 88). To investigate the role of various channels, 0.5 μm tetrodotoxin (TTX; a Na+ channel blocker), 4 mm 4-aminopyridine (4-AP; a fast K+ channel blocker), 10 mm tetraethylammonium (TEA; a nonspecific K+ channel blocker), or 20 μm nifedipine (an L-type Ca2+ blocker) were applied to the bath focally by using a Picospritzer with a U-tube system (Khakh et al., 1995). Drugs were purchased from Sigma. In the TEA experiments, 10 mm sucrose was also added to the control solution to prevent osmolality changes. To block almost all K+ channels, the intracellular K+ was replaced with Cs2+. In all experiments, the access resistance ranged from 8 to 25 MΩ. Cells for which the access resistance drifted by >4 MΩ during the recording were discarded. The fast capacitance was automatically compensated by ≈6 pF in the Multi-Clamp circuit. No series resistance compensation was performed.
All averaged data are presented as mean ± SD.
Spectral methods. In the linear regime, the voltage output measured at a location x, for instance the soma, is related to the current input at another location, y, in the cell, through the following relationship:
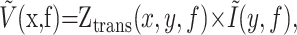 |
1 |
which reduces to Ṽ(f) = Zin(f) × Ĩ(f) for a single compartment (Koch, 1999). Ṽ(x,f) and Ĩ(y,f) are the complex Fourier transform of the time-dependent voltage, V(x,t), and current, I(y,t), respectively. Ztrans(x,y,f) is the complex transfer impedance between x and y for a signal at frequency f. Its amplitude represents the strength of propagation through the neuronal membrane. Equation 1 is essentially Ohm's law for time-dependent signals in the frequency domain. It is thought to be a good approximation for signal transmission of small perturbations in active dendritic cables (Koch, 1984).
The PSD offers an effective description of the fluctuation power for small perturbations as a function of frequency f. When linearity holds, the current and voltage PSDs, SI(f) and Sv(f), are related to each other by the following input impedance:
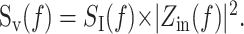 |
2 |
For any geometry in which current source densities, sI(y,f), are distributed throughout the membrane:
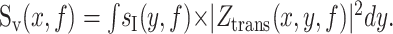 |
3 |
Thus, the voltage noise at a point, x, results from the summation of noise from current sources distributed throughout the membrane. The current fluctuations at point y propagate to point x with an amplitude given by the transfer impedance. A population of channels can contribute to the total noise through sI(y,f) and through Ztrans(x,y,f). It should also be made clear that the current trace at x, as measured under voltage clamp, is not the total current through the entire membrane. That is:
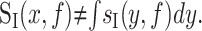 |
4 |
Rather, some current is inevitably shunted through the membrane as it propagates through the neuron. The effective current PSD is given by the following:
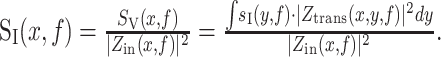 |
5 |
Equation 5 demonstrates that the impedance can also affect the noise measured under voltage clamp by affecting the propagation of current to the soma. Overall, the current PSD, SI(f), is a good indicator of the extent of fluctuations from current sources in the neuron, whereas the voltage PSD, Sv(f), better accounts for the impedance properties of the cell and may be more relevant from a computational and a voltage threshold viewpoint.
Data analysis. In these experiments, we measured Sv(f), SI(f), and Zin(f) at the soma, under the assumption of stationarity. PSDs were calculated from 2 min long traces of data under current or voltage clamp at several holding potentials (Fig. 1 A, B). In current-clamp mode, the current was adjusted to generate traces at the desired mean voltage, while the fluctuations around the holding potential were measured. In voltage-clamp mode, the voltage was clamped to the desired holding potential and the fluctuations in current were measured. Signals were led to a 1.2 kHz anti-aliasing filter, then digitized at 10 kHz.
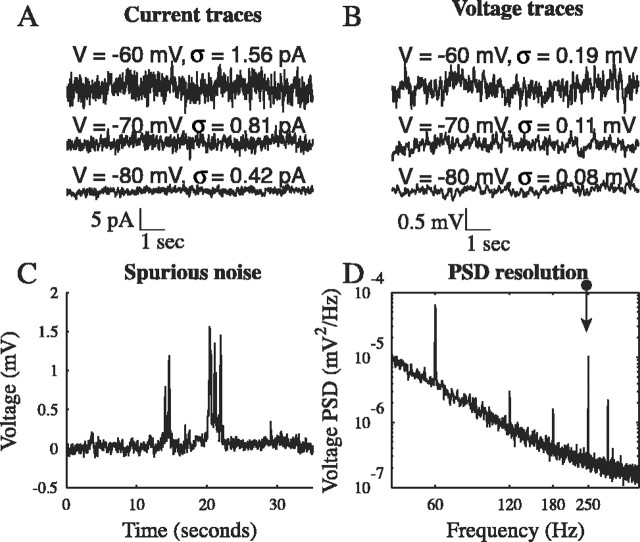
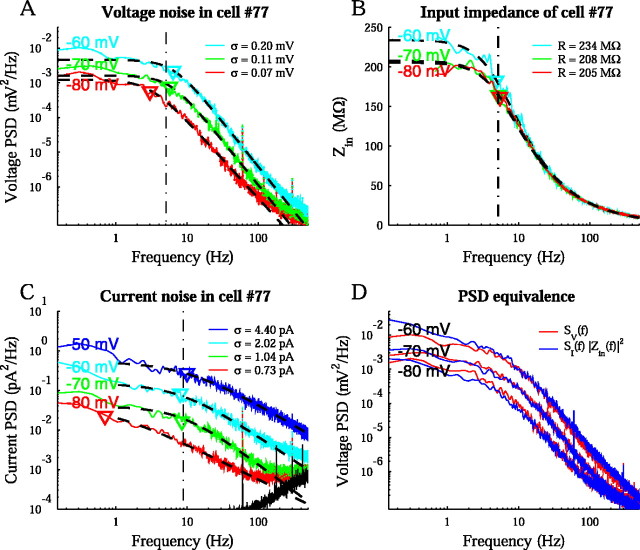
Figure 1.
Sample traces. A, Ten-second current traces are shown at three holding potentials. Current noise increased with depolarization. B, Ten-second voltage traces are shown for the same cell at the same potentials (controlled by adjusting the current). Voltage noise also increased with depolarization. The voltage traces are clearly low-pass filtered by the membrane. C, Occasional nonstationary events, such as those ∼14 and 20 sec, were removed from the traces. These likely corresponded to unblocked synaptic activity and often lasted for several seconds, although their appearance and behavior varied from cell to cell. D, For a typical PSD, power line interference (at 60 Hz and multiples) and an injected 0.5 pA, 250 Hz component (indicated by an arrow) are evident.
Occasionally, nonstationary events were observed, similar to those shown in Figure 1C, lasting up to several seconds. Their occurrence was rare and entirely random. Such events were manually removed from the trace. The removed sections corresponded to 0.67% of the total data. The source of these events was unclear. They may have been attributable to unblocked synaptic activity. They were more prevalent at hyperpolarized holding potentials, suggestive of the activity of ligand-gated Cl- channels.
Additional data processing involved high-pass filtering by removing all components below 0.1 Hz. The PSD was then calculated with the Welch method, using MATLAB (MathWorks, Natick MA). In this routine, the data were divided into 50% overlapping 5 sec Hann-windowed segments, and the power in each frequency bin was averaged across all segments, at a resolution of 0.15 Hz. Power line interference at 60 Hz and its harmonics, as well as an injected 0.5 pA, 250 Hz, sinusoidal input, could be resolved in the voltage PSD in a sample trial (Fig. 1 D).
Current and voltage PSDs were both reasonably well fit by functions of the following form, in the appropriate frequency range:
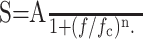 |
6 |
We use subscripts I and V to differentiate between the two cases. In Equation 6, A is the DC (f = 0) amplitude, fc is the cutoff frequency, and n is the exponent. In a log-log plot, the PSD is approximately constant, with amplitude A, for frequencies f ≪ fc, and falls off with slope -n for f ≫ fc. Deviations from Equation 6 are also expected because the measured PSDs are likely composed of several individual PSDs (see Fig. 8 A), each corresponding to a separate noise source (Manwani and Koch, 1999a). Nevertheless, a fit to this function was useful for obtaining an effective cutoff and slope in each condition.
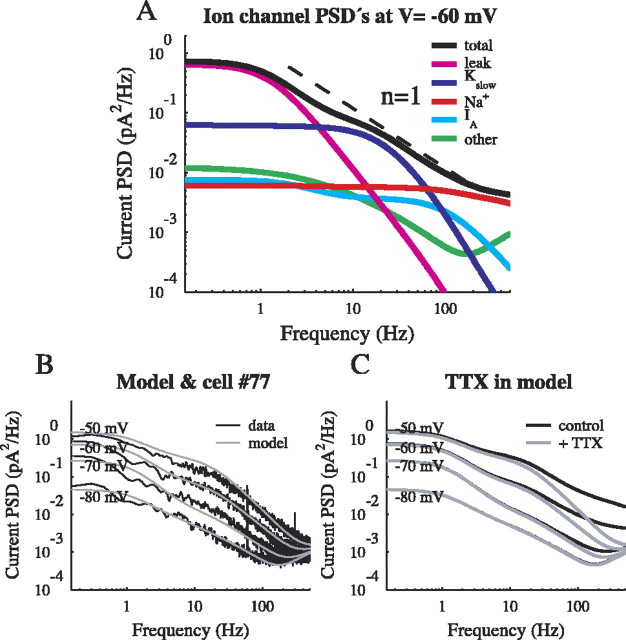
Figure 8.
The model. A, The total current PSD was described as the sum of separate Lorentzian PSDs from each channel. Although each channel gave rise to a 1/f2 component for frequencies above its cutoff, the spread of cutoff values produced a summed PSD that behaved as approximately 1/f in the range from 1 to 100 Hz. B, The current PSD is shown for the model and for the sample cell under the TTX condition at four holding potentials (-50, -60, -70, and -80 mV). Some important features are the increasing prominence of the slow K+ current (18 Hz cutoff) and the voltage-dependent increase across all frequencies. C, The effect of TTX was reproduced in the model by setting the Na+ channel density to zero, producing a decrease in PSD at frequencies >10 Hz, in agreement with the data presented in Figure 5A.
The rms noise or SD, σ, is given by the following equation:
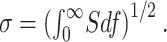 |
7 |
It is the square root of the total fluctuation power (or variance). Variances and PSDs from different noise sources are additive and suitable for percentile comparisons. In contrast, the rms is a more intuitive measure of the magnitude of the noise. In practice, σ was calculated numerically, by integrating the PSD to 500 Hz. At higher frequencies, instrumental noise was dominant and could sometimes be discerned at frequencies as low as 100 Hz. Therefore, we set 500 Hz as a reasonable integration limit to allow isolation of the biological contribution. For a Lorentzian PSD (n = 2 in Eq. 6) with fc = 10 Hz, the underestimation of σ associated with ignoring higher frequencies would be ≈1%.
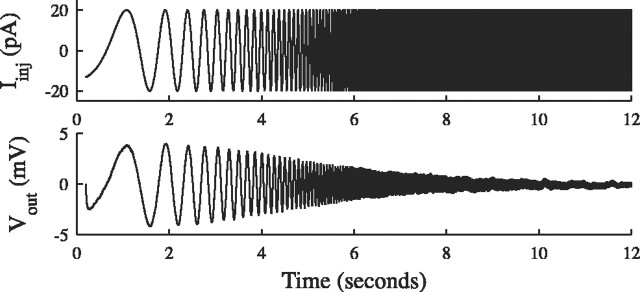
Following Gutfreund et al. (1995) (see also Hutcheon et al., 1996), the input impedance magnitude,|Zin(f)|, was calculated in current-clamp mode by injecting a 12 sec log chirp current and measuring the resulting voltage output. An example is shown in Figure 2.
Figure 2.
Determining input impedance. A 12 sec log chirp current was injected into the cell under current clamp, and the resulting output voltage, relative to the holding potential, was measured. The ratio of the Fourier transforms was the impedance Zin(f) = Ṽout(f)/Îinj (f). The input resistance was 200 MΩ in this instance.
The input impedance magnitude was well fit by the following equation:
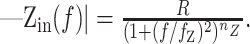 |
8 |
This particular form arises naturally from the Green's functions of passive cables of varying length (Jack et al., 1975; Tuckwell, 1988). For example, in a single compartment:
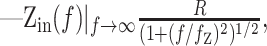 |
9 |
whereas for a semi-infinite cable:
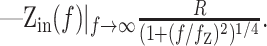 |
10 |
The amplitude and frequency dependence of the input impedance contains information about the geometry of the cell, as well as the contributing conductances from ion channels. The DC (f = 0) amplitude of Zin is the effective input resistance, R, which reflects the active and passive conductances in the cell. The frequency cutoff, fz, generally depends on the membrane time constant. R and fz are also affected by phenomenological contributions from the voltage and time dependencies of the conductances (Mauro et al., 1970; Sabah and Leibovic, 1972). The slope, nz, is determined by the geometry of the cell (Jack et al., 1975; Koch, 1984). In the control condition, the observed mean nz of 0.33 ± 0.05 (n = 59) was intermediate between the one-fourth expected for a semi-infinite cable and the one-half expected for a single compartment (Eqs. 9, 10). This illustrates that from the viewpoint of the soma, the cable effects in Equation 8 were well represented by a somatic compartment connected to an unbranched dendritic cable (a “ball-and-stick” model).
Instrumental noise was estimated experimentally by obtaining traces with the resistor-capacitator (RC) cell provided by Axon Instruments (see Fig. 5A, inset) and calculating the current PSD (see Fig. 5A, arrow). When the biological noise was low, usually at frequencies >100 Hz, the instrumental noise dominated (see Fig. 5A) This “Johnson” noise was an artifact of the non-zero access resistance (DeFelice, 1981; Sherman-Gold, 1993). The Johnson current noise in a circuit is given by the following:
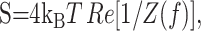 |
11 |
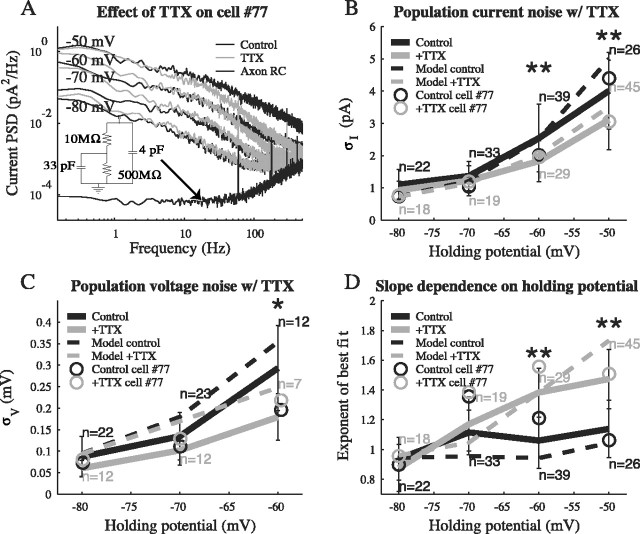
Figure 5.
The role of Na+ channels. A, Current PSDs are shown for the sample cell in Figure 4 (at -50, -60, -70, and -80 mV) before and after the addition of TTX to the bath. There is no significant difference at -70 or -80 mV. The most consistent effect across all cells occurred at frequencies >100 Hz for holding potentials of -60 and -50 mV: the noise decreased with the blockage of Na+ channels. This was in agreement with the low amplitude, yet flat noise spectrum expected from fast Na+ channels, as demonstrated by the model (Fig. 8 B, red). The amplitude decrease in this example, at -50 mV, was larger than average. The current PSD from an idealized RC cell is shown as well, indicating the presence of instrumental noise at low amplitudes and at frequencies >100 Hz. B, The mean rms current noise was compared between control and TTX trials for both the sample cell (open circle) and the population (solid curves). The difference in the rms noise became increasingly significant with depolarization (p = 0.17, 0.28, 0.0019, and 7 × 10-4; t test at -80, -70, -60, and -50 mV). C, In a t test comparison with and without TTX, the mean rms voltage noise was similarly affected by depolarization (p = 0.072, 0.068, and 0.012; t test at -80, -70, and -60 mV). Additional depolarization under current clamp evoked trains of action potentials, vitiating noise measurements. D, The slope nI, of the best fit of AI/1 + (f/fc)nI to the current PSD on double logarithmic coordinates, is shown averaged over the experimental data. Depolarization in the presence of TTX uncovered a voltage-dependent 1/f2 noise component, most likely from the slow K+ current. t test comparisons of the slope in control versus TTX trials at each holding potential yielded (p = 0.19, 0.25, 7 × 10-10, and 3 × 10-6; t test at -80, -70, -60, and -50 mV).
where kB is Boltzmann's constant and T is the temperature (DeFelice, 1981). In whole-cell measurements, it becomes (Sherman-Gold, 1993) the following:
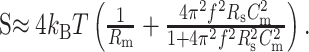 |
12 |
Rm is the membrane resistance and Cm is the membrane capacitance. Equation 12 is in excellent agreement with the experimental data depicted in Figure 5A (arrow). For reasonable values, the term on the right, arising from the access resistance, R (10 MΩ here) (see Fig. 5A, inset), dominates at higher frequencies (f > 50 Hz) and increases quadratically with frequency up to ≈3 kHz.
The model. The current fluctuations arising from Markov processes have been described (DeFelice, 1981; Johnston and Wu, 1995). Consider, for example, a simple two-state, open and closed channel with voltage-dependent rate constants. The current-voltage relationship is given by the following:
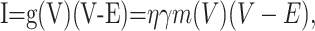 |
13 |
with η as the channel density, γ as the single-channel conductance, and E as the reversal potential. The probabilistic single gating particle, m(V), follows the kinetics below:
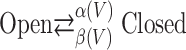 |
14 |
where α(V) and β(V) are the voltage-dependent rates of closing and opening, respectively. The PSD of current noise in this case is given by the following:
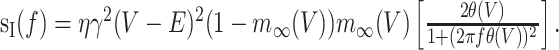 |
15 |
Here, m∞(V) = α(V)/(α/V) + β(V)) is the steady-state open-channel probability, and θ(V) = 1/(α(V) + β(V)) is the activation time constant. This analysis can be extended to more complicated kinetic schemes to calculate sI(f) for arbitrary channel kinetics (Sakmann and Neher, 1995; Hille, 2001).
Some principles about current noise attributable to Markov processes can be appreciated through Equation 15. The quadratic dependence of sI(f) on γ, the single-channel conductance, provides a good indicator of the noise that can be expected from a particular channel. For example, large conductance Ca2+-activated K+ (BK) channels, which have unit conductances near 180 pS (Kang et al., 1996), can give rise to very large current fluctuations, whereas single KA channels with a 10 pS conductance (Mainen and Sejnowski, 1998) are significantly less noisy. The power in Equation 15 depends on the steady-state open-channel probability, m∞, with the functional form (1 - m∞)m∞. This relationship is maximal for m∞ = 0.5, when the channel is equally likely to be open and closed. For many voltage-dependent channels in the subthreshold regime, m∞ < 0.5 but increases with depolarization. Therefore, (1 - m∞)m∞, and hence sI(f), also increase with depolarization. sI(f) depends linearly on θ(V), at f ≪ fc, where fc = 1/2πθ(V) is the cutoff frequency; thus, more slowly fluctuating channels give rise to larger magnitude fluctuations in this regime. This is particularly relevant when the membrane time constant imposes a natural cutoff below fc. For K+ and (under some conditions) Cl- channels, the driving force in Equation 15 also increases with depolarization, further magnifying the noise. Another important feature of Equation 15 is that it is a Lorentzian. This means that for f ≫ fc, the PSD behaves as 1/f2. When Equation 15 is fit to Equation 6, a slope of n1 = 2 is expected. In contrast, non-Markov kinetics, such as fractal kinetics (Liebovitch and Sullivan, 1987), could instead give rise to generalized 1/f behavior, with n1 ≈ 1.
Several channels, with their own characteristic current PSDs, were incorporated into the full model using NEURON (Hines and Carnevale, 1997) (Fig. 3). Equations similar to Equation 15 allowed us to analytically calculate the current PSD arising from each channel. These were then incorporated into the 1-D cable model. Using Equation 5, SI(f) and Sv(f) were calculated at the soma by integrating the contributions of each noise source in the membrane. The transfer and input impedances were obtained with the extended impedance class of NEURON (Hines and Carnevale, 1997, 2000). The effectiveness of this analytical description was previously demonstrated using Monte Carlo simulations by Steinmetz et al. (2000).
Figure 3.
Compartmental model. The model consisted of one somatic compartment, 11 dendritic compartments, and included four populations of ion channels: a fast Na+ channel (gNa), a fast K+ channel (gA), a slow K+ channel (gK), and a K+ leak channel (gleak). Shown are the conductances, g = ηγ, where η is the channel density and γ is the single-channel conductance. The channel densities and single-channel conductances are given in Materials and Methods. The membrane capacitance, Cm = 1 μF/cm2, and the axial resistance, Ra = 200 Ωcm, are shown. The steady-state space constant, λ = 840 μm, gives a dimensionless dendritic electronic length of L = 0.475.
The details of the model were as follows: a single-compartment sphere of area 800 μm2, and a single unbranched dendritic cable of length l = 400 μm and diameter 4 μm, were approximated by 11 discrete compartments. The steady-state space constant was λ = 840 μm. Hence, the dimensionless dendritic electronic length was L = 1/λ = 0.475 (Koch, 1999). The membrane capacitance was Cm = 1 μF/cm2, and the axial resistance was Ra = 200 Ωcm.
The model included solely the following channels, accounting for both active and passive behavior. (1) An inactivating Na+ channel (Mainen et al., 1995):
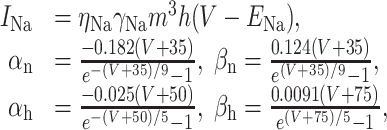 |
16 |
with m∞ = αn/(αn + βn), τm = 1/(αn + βn), h∞ = 1/(1 + e(V+65)/6.2), τh = 1/(αh + βh). (2) A fast K+ channel (Korngreen and Sakmann, 2000):
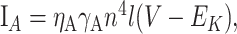 |
17 |
with n∞ = 1/(1 + e-(V + 47)/29), τn = 0.34 + 0.92e-(V + 71)2/592), l∞ = 1/1(1 + e(V + 66)/10), and τ1 = 8 + 49e-((V + 73)/23)2,, which accounts for delayed rectifier and IA. (3) A slow K+ channel (Korngreen and Sakmann, 2000), composed of two subpopulations of inactivation states, b1 and b2, with the activation time constant scaled by a factor of 0.6:
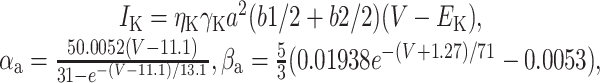 |
18 |
with a∞ = αa/αa + βa), τa = 1/(αa + βa) - 10, τb1 = 360 + (1010 + 23.7 (V + 54))e-(V + 75)2/482, τb1 = 2350 + 1380e-0.01118V - 210e-0.0306V, and b1∞ = b2∞ = 1/(1 + e(V+58)/11). (4) A two-state leak channel:
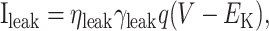 |
19 |
with open-pore probability q∞ = 0.98 and τq = 120.
The latter channel was loosely based on the KCNKØ channel (Zilberberg et al., 2000). The high conductance and the kinetics of leak channels, as described by Zilberberg et al. (2000) and Goldstein et al. (2001), indicate that they would contribute significantly to the whole-cell noise. Nevertheless, their inclusion here may be considered phenomenological. Certainly, some form of non- or weakly voltage-dependent membrane leak, with a reversal potential close to the reversal potential of K+, represents a significant portion of the subthreshold conductance. Blocking K+ channels with internal Cs+ increases the input resistance of a cell by several orders of magnitude, suggesting that the leak is indeed K+ conducting.
The single-channel conductances were γNa = 20 pS, γA = 10 pS, γK = 15 pS, and γleak = 60 pS. The channel densities, ηA = 1/μm2, ηK = 6/μm2, and ηleak = 0.012/μm2, were uniform throughout the somatic and dendritic membrane, except for Na+, for which ηNa = 12/μm2 in the soma and ηNa = 2/μm2 in the dendritic cable. The channel kinetics were obtained from available literature (Mainen et al., 1995; Korngreen and Sakmann, 2000; Zilberberg et al., 2000). The densities were chosen to match PSDs of a sample cell (77) and allow action potential generation, while maintaining the low Na+ density expected in the dendritic membrane (Mainen et al., 1995; Mainen and Sejnowski, 1998). Data from other cells were also well fit by adjusting the model parameters. Other, more sophisticated or realistic, channel distributions and geometries could give rise to similar results. We found that from the viewpoint of somatic recordings, the model was insensitive to complicated dendritic configurations, giving equivalent behavior when branching was increased, as long as the total membrane area was unchanged. However, a single unbranched cable effectively captured the dendritic input impedance load measured in the experiments. Thus, we opted for simplicity. The geometric parameters, the somatic area, cable length, and cable diameter, were chosen to obtain the high-frequency input impedance slope of 0.34, in line with the data.
In addition to biological parameters, a PSD corresponding to instrumental noise, from the access resistance and stray capacitance of the pipette electrode assembly, was included in the model, using Equation 11 and the parameters of the idealized RC cell from Axon Instruments (see Fig. 5A, inset). It was also necessary to add a baseline noise PSD to the model because even near the K+ reversal potential, some noise remained that could not be explained by the channels above. Its inclusion was done by uniformly distributing a noise source in the form of Equation 6 with amplitude A = 2.5 × 10-6 pA2/Hz, cutoff at fc = 5 Hz, and n = 1 in the membrane. This baseline noise may come from Ih, Ca2+ currents, chloride currents, or unblocked spontaneous synaptic activity. We did not attempt to block it using pharmacology because it represented a small (<1 pA) amount of current noise.
Results
Experimental results
Voltage PSDs for a typical cell are shown in log-log plots in Figure 4A. Because the cell was depolarized from the resting potential, the power increased across all frequencies. This voltage dependence was consistent with both the activation of voltage-gated conductances and an increased driving force for K+ channels. At each holding potential, the PSD was well fit by Equation 6. In this example, the power was essentially constant up to the cutoff frequency, at fc = 5.0 ± 1.8 Hz (Fig. 4A, dashed vertical line), reflecting a time constant, τ = 1/2πfc, of 32 ± 11 msec. Above that frequency, the power fell off with a mean negative slope, nv = 2.4 ± 0.2. The high-frequency slope is comparable with that seen in neocortical cells with large synaptic activity (nv ≈ 2.6) (Destexhe et al., 2003). In contrast, synaptic noise at high frequencies is mostly insensitive to holding potential, unlike the voltage-dependent changes observed here (Diba et al., 2002).
Figure 4.
Noise in a sample cell. A, The voltage PSD is shown at three holding potentials, with the rms,σ, given in the legend. The noise increased as the cell was depolarized. The best fit to SV = AV/1 + (f/fc)nV is shown with a dashed curve. Here, nV = 2.4 ± 0.2. Individual PSD cutoffs, fc, are shown by inverted triangles. The mean cutoff was at 5 ± 2 Hz, indicated by a vertical line, corresponding to a time constant, τ = 1/2π fc, of 32 ± 11 msec for the cell. B, The input impedance magnitude was well fit by R/(1 + (f/fc)2)nV, as shown with the dashed curve. The cutoff frequency, fZ = 5.2 ± 0.2 Hz, matched the cutoff of the voltage PSD, with nZ = 0.345 ± 0.005. The DC component, R, corresponded to input resistances of 205-234 MΩ. C, The current PSD is shown for the same cell at four holding potentials. It was fit to SI = AI/1 + (f/fc)nI for f > 1 Hz. The high-frequency portion of the graph was confounded by instrumental noise, shown in black and detailed in Materials and Methods, along with visible power line interference at 60 Hz. Otherwise, noise increased at all frequencies with depolarization. The mean cutoff, indicated by the vertical line, was now at 8 ± 1 Hz for three holding potentials, with an outlier at 0.7 Hz for -80 mV. D, The current and voltage PSDs are related by SI(f) = SV(f)/| Zin(f)|2 demonstrated at the holding potentials of Figure 4 A.
The input impedance magnitude of the cell was also measured and is shown in Figure 4B. It was fit to R/(1 + (f/fZ)2)nZ, demonstrating a 5.2 ± 0.3 Hz cutoff (Fig. 4B, dashed vertical line) and an exponent, nZ, of 0.345 ± 0.005. This exponent reflected an effective geometry intermediate between that of a single compartment and an infinite cable (Eqs. 8-10). The amplitude of the impedance displayed a nonlinear increase with depolarization, a consequence of voltage-dependent conductances in the membrane (Koch, 1984).
The current noise was also measured in this cell by reconfiguring the Multi-Clamp 700A circuit to voltage-clamp mode. The current PSD (Fig. 4C) showed the same general voltage dependence as the voltage PSD, increasing in amplitude at all frequencies as the cell was depolarized. However, the cutoff (dashed vertical line) differed from the values of 5.0 and 5.2 Hz seen above for the voltage PSD and input impedance. Both the current PSD, SI(f), and the input impedance, Zin(f), have their own characteristic cutoff frequencies, fc and fZ. The current PSD cutoff, fc, is a consequence of the particular fluctuating channel kinetics, as discussed for Equation 15. The impedance cutoff, fZ, on the other hand, is generally determined by the linearized conductance properties of the membrane (Koch and Poggio, 1985) and captures the low-pass filtering effects of the cell (Koch, 1999). The voltage PSD cutoff of the cell in Figure 4, then, mostly reflected fZ and the influence of the membrane time constant (see Eq. 3). Nevertheless, the effect of the current kinetics can also be seen in the -80 mV voltage PSD, which reflected the current PSD cutoff for that holding potential. The mean slope of the current PSDs, nI = 1.1 ± 0.2, was also a consequence of Equation 3. The slopes of SI(f) and Sv(f) are related by the squared slope of the impedance; inspection of Equation 5 in the log domain reveals that nI + 4nZ = nV. Equation 5 is demonstrated in Figure 4D, where SI(f) ×|Z(f)|2 is compared with SV(f) as measured at the soma. The close correspondence of these two curves establishes the linearity of noise fluctuations in this system and validates the linear treatment in the model.
To isolate the effect of Na+ channels on the noise, 0.5 μm TTX was added to the bath. In Figure 5A, the current PSD before and after the addition of TTX is shown for the sample cell. A consistent effect of TTX at depolarized holding potentials was a decrease in PSD amplitudes at frequencies above 100 Hz. This could be clearly seen in Figure 5A at -60 and -50 mV. Very little change was evident at -80 and -70 mV, as expected from the voltage dependence of Na+ channels. The small amplitude differences appearing at frequencies below 1 Hz were not consistently observed across the population (Fig. 5B).
A population comparison of the rms current noise between cells with and without TTX in the bath showed that the effect of TTX on the amplitude of the current noise became increasingly significant with depolarization (pairwise t tests at four voltage values) (Fig. 5B). At -50 mV, the difference in the rms current noise between the two conditions was 0.90 ± 1.51 pA (n = 26), representing a 40 ± 49% change in the mean current variance. The large SDs indicate that there was a great degree of cell-to-cell variability in the magnitude of the contribution from Na+ channels. In the sample cell in Figure 5A, TTX resulted in a 1.35 pA decrease in the rms current noise, corresponding to a 52% change in the variance; therefore, in that cell, Na+ channels were a large source of noise. A significant difference was also seen in the rms voltage noise at -50 mV (Fig. 5C). The rms voltage noise decreased by 0.11 ± 0.11 mV (n = 7), or 63 ± 34% of the mean variance. Thus, TTX had a larger impact on the voltage noise than on the current noise, a consequence of Na+ channel effects on the impedance (Eq. 3). Population data in Figure 5D displayed a change in slope with depolarization that was seen in the sample cell. This change was significant at -60 and -50 mV.
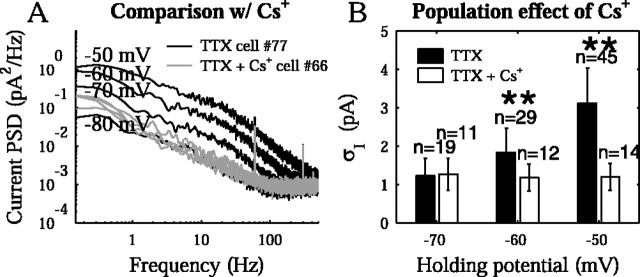
We tested the hypothesis that the remainder of the noise in the current PSDs was dominated by K+ channel fluctuations. Currents through the K+ channels were eliminated by replacing the intracellular K+ with Cs+. Because a “before” and “after” comparison with a different pipette solution was not possible, the rms current noise was examined across a population. Once internal Cs+ in the pipette blocks most of the K+ channels, the resting potential of a cell becomes strongly depolarized in distal, poorly clamped regions. This depolarization can result in regenerative Na+ and Ca2+ events that propagate partially to the soma and contribute additional noise. This necessitated the inclusion of TTX in the bath to create a controlled comparison. The results are shown in Figure 6. Blocking K+ channels indicated that K+ channels were an increasingly significant source of current noise at depolarized holding potentials. For cells at -50 mV, at least 85 ± 12% (n = 14) of the noise variance, in the presence of TTX, was attributable to K+ channels. The effect of the holding potential on the noise was also consistent with the K+ reversal potential. The remaining noise may have been attributable to various sources. Many K+ channels remain somewhat permeable to Cs+ ions and can therefore still lead to current fluctuations (Zilberberg et al., 2000). Furthermore, cultured hippocampal neurons express a large variety of ion channels (Banker and Goslin, 1998), including Ih (Maccaferri et al., 1993), ligand-gated channels (Bekkers et al., 1990; Bekkers and Stevens, 1995), spontaneously opening Cl- channels (Birnir et al., 2000), and various Ca2+ channel subtypes (Hille, 2001), each of which can give rise to current fluctuations. Some channels may become even noisier with an internal Cs+ solution because the unclamped branches at the more distal parts of the membrane will depolarize, activating voltage-gated channels. Thus, these measurements underestimate the contribution of K+ channels.
Figure 6.
The role of K+ channels in current noise. A, A sample cell with internal Cs+ in the presence of TTX, at holding potentials (-50, -60, -70, and -80 mV), is shown alongside the example cell data from Figure 5A. The voltage-dependent increase in noise does not occur with internal Cs+. B, The effect of internal Cs+ was observed through a population comparison in the presence of TTX at -70, -60, and -50 mV). Regardless of the holding potential, the rms current noise with internal Cs+ (and TTX) was 1.2 ± 0.4 pA, showing that in comparison with the standard pipette solution, the activity of channels giving rise to noise was suppressed by internal Cs+. The data showed significant differences between standard and Cs+ solutions at -50 and -60 mV (p = 2.0 and 5 × 10-10; t test).
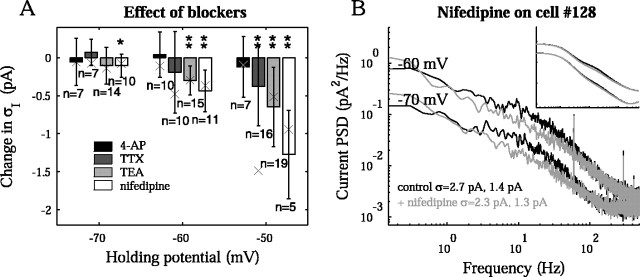
Other experiments with blockers were performed to gauge the significant channel contributions to the current noise. In Figure 7A, we plot the difference in rms current noise before and after the addition of each blocker to the bath. The same cell was used in both conditions. Results from voltage-clamp experiments were combined with current-clamp experiments rescaled by the squared impedance (Eq. 5). The TTX experiments again showed a significant decrease in rms noise at -50 mV. The addition of 4 mm 4-AP, a KA (and often KDR) channel blocker, had a dramatic effect on the fast outward current, following depolarizing voltage steps (data not shown); however, it had little effect on the subthreshold noise spectra, as expected from the kinetics and small single-channel conductance of the fast K+ channel (see also Fig. 8A, cyan KA PSD). Adding 10 mm TEA to the bath had no effect on the fast outward current but substantially reduced a slow outward current in the transient I-V curves (data not shown). It also reduced the noise as the cell was depolarized. The effect was most significant at -60 and -50 mV (p = 2 × 10-4 and 4 × 10-3; t test), with a 32 ± 16% and 37 ± 22% decrease in the variance. This was consistent with the internal Cs+ experiments because TEA blocks many types of K+ channels at the concentration used here (Hille, 2001). The addition of 100 μm nickel (n = 3), a T-type Ca2+ channel blocker, had no significant effect on the either the spectra or I-V plots, suggesting little influence from these channels in the preparation (data not shown). Experiments with 200 μm nifedipine, an L-type Ca2+ channel blocker, demonstrated significant change in the rms noise at -60 and -50 mV (p = 2 × 10-5 and 2 × 10-5; t test), with 27 ± 10% and 44 ± 17% decrease in variance. Nifedipine trials for a sample cell are also shown in Figure 7B, demonstrating some effect of the blocker on the current noise PSD. It cannot be concluded whether this was because of blockage of L-type Ca2+ channels, deactivation of Ca2+-dependent K+ channels, or some combination of the two. However, the difference in the current PSD was consistent with the PSD contribution of the slow K+ current in the model (Figs. 7B, inset; 8A, dark blue PSD).
Figure 7.
The effect of blockers on current noise. A, The mean difference in rms current noise is shown before and after the addition of various blockers on a cell at -50, -60, and -70 mV). Data were pooled from the current spectra, SI(f), and from the voltage spectra and impedance, SV(f)/|Zin(f)|2. The changes in rms noise were significantly larger than zero for TEA (p = 0.028, 2 × 10-4, and 4 × 10-3; t test), at -60 and -50 mV for nifedipine (p = 2 × 10-5 and 2 × 10-5; t test), and at -50 mV for TTX (p = 0.0056; t test), indicated by * and **. Results for the model cell are indicated with an X. To simulate the effect of each blocker, we changed the channel densities as follows: 4-AP, ηA = 0; TTX, ηNa = 0; TEA, ηK = 3, ηleak = 0.009; nifedipine, ηK = 0. B, The current PSD shape was altered by the addition of 20 μm nifedipine to the bath in a sample cell. The change is suggestive of a diminished slow K+ component in the current PSD. Compare B with inset, where the density of slow K+ channels in the model is reduced from ηK = 6 to ηK = 4 at the same holding potentials.
Modeling results
Four distinct channel populations, with their characteristic current PSDs, were incorporated in the full model. Their individual contributions to the total current PSD can be seen in Figure 8A. The densities were chosen to agree with data from the sample cell, yet the model also reproduced features that were observed in most cells. The following three experimental results were, in fact, anticipated by the model (Manwani and Koch, 1999a; Diba et al., 2002).
First, there was an increase in the noise with depolarization across the entire frequency range (Fig. 8B). This was consistent with the expected increase in the contribution of K+ channels in the model to the total noise. A large portion of the increase arose because depolarization leads to an increased driving force for K+ channels, consistent with the internal Cs+ experiments. The voltage-dependent changes in the PSD, shown in Figure 8C, gave rise to similar voltage-dependent changes in the rms noise, indicated with dashed lines in Figure 5, B and C.
Second, as seen in Figure 8, A and C, at the most depolarized holding potentials, Na+ channels were a major component of the current noise at frequencies >100 Hz. Integrated across all frequencies, Na+ channels in the model accounted for 33% of the current variance at -60 mV. Figure 8C shows that removing Na+ channels in the model replicated the effect of TTX on the sample cell (Fig. 5A).
Third, in the model, depolarization activated the slow K+ channel, which manifested itself as a Lorentzian noise component with a cutoff at fc = 18 Hz. This corresponds to an effective time constant of 8.8 msec for the slow K+ channel, dominated by the transition from the open to the fully closed state. Its PSD is shown (dark blue) in Figure 8A. Figure 8, A and C, further demonstrates that the 1/f behavior can arise from a summation of several Lorentzian components that have a range of cutoff frequencies. In the experiments with TTX, the observed slope of the current PSD increased with depolarization (Fig. 5D), indicating the emergence of a Lorentzian (1/f2) noise source. In the model, the slow K+ Lorentzian contribution becomes particularly prominent when Na+ channels are removed (compare Figs. 5A, 8C) and dominates the high-frequency spectrum as the cell is depolarized.
The kinetics of the slow K+ channel came from experiments on neocortical pyramidal cells (Korngreen and Sakmann, 2000). In our experiments, the addition of nifedipine, an L-type Ca2+ channel blocker, caused a decrease in noise at the most depolarized holding potentials and changed the shape of the current noise PSD. The contribution of the slow K+ channel seen in Figure 8A indicated agreement with the nifedipine experiments (Fig. 7B), suggesting that a Ca2+-dependent K+ current with similar kinetics may be a source of noise in the neurons. The fast K+ channel (Fig. 8A, cyan) never contributed significantly in the model because of its fast kinetics and small conductance. Blockage with 4-AP in the experiments (Fig. 7A, black) also produced no noticeable change in the noise. Other channels that did not have a significant noise contribution were excluded from the model to maintain simplicity.
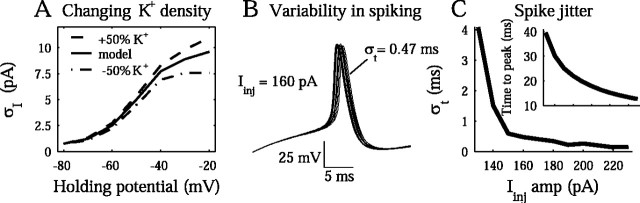
Experimentally, action potential generation prevents the measurement of intrinsic channel noise at suprathreshold voltages. However, using the model, we can make predictions of the expected rms noise at these holding potentials (Fig. 9). For example, Figure 9A indicates that at -40 mV the rms current noise is 7.7 pA, a 240% increase in the variance relative to the noise at -50 mV (σ = 5 pA). These calculations may be appropriate when the mean potential of the neuron is elevated by active input synapses. Under such conditions, it has been suggested that noise plays an important role in creating a graded spiking response and gives rise to contrast invariance tuning (Anderson et al., 2000; Mitchell and Silver, 2003).
Figure 9.
Suprathreshold model. A, The voltage dependence of the rms noise is shown for a threefold range of K+ channel densities. The leak and slow K+ channel densities are varied between (ηleak = 0.006, ηK = 3), (ηleak = 0.012, ηK = 6), and (ηleak = 0.018,ηK = 9) (channels per square micrometer). Noise increases with K+ channel density and with depolarization. B, We performed Monte Carlo simulations of a 160 pA depolarizing current pulse injection for 40 msec. Ten trials are shown in the overlap. σt indicates the SD of the temporal jitter in the resulting action potential. C, The SD in the time of the spike peak is shown from 20 trials performed at varying amplitude of the 40 msec current pulse. The timing jitter decreases with increasing input current amplitude. The mean spike peak time is plotted in the inset.
To explore the expected jitter from the fluctuating channels at voltages above the spike threshold, we performed full-scale Monte Carlo simulations of the model, in the manner described by Steinmetz et al. (2000). Briefly, this involved creating probabilistic versions of these channels and using a random number generator to determine individual state transitions in each compartment. We injected 40-msec-long current steps of varying amplitude, Iinj, at the soma to simulate various input current conditions, with 20 trials at each setting. The probabilistic nature of the channels leads to variable trial-to-trial behavior. For illustration, 10 trials at Iinj = 160 pA are superimposed in Figure 9B. The jitter in the timing of the action potentials, σt, was measured as the SD in the time of peak voltage. This rough treatment suggests that jitter of 0.2 to 4 msec might be expected as a consequence of the stochastic channels in the neurons studied here (Fig. 9C). This places inherent restrictions on a code that depends on an accurate representation of spike timing. Compensatory mechanisms in the dendrites may play an important role in overcoming the limitations of a precise temporal code (Trussell, 1999; Ariav et al., 2003; Poirazi et al., 2003).
Discussion
We measured the noise attributable to ion channels in cultured neurons from the hippocampus of embryonic day 18 rat embryos. We studied a variety of holding potentials and pharmacological conditions. The experimental results were simulated by a reduced geometric model of a neuron with four stochastic channel populations: a fast Na+ channel, a fast K+ channel, a slow K+ channel, and a K+ leak channel. We do not claim these include all the channel types that contribute to noise in the preparation. Certainly, the channels expressed in cultured hippocampal neurons are expected to be more diverse and likely include Ih; P-, N-, and Q-type Ca2+ channels; Cl- channels; and other K+ channels not accounted for here. Additionally, the kinetic properties of the channels, even the leak channel alone (Goldstein et al., 2001; Ilan and Goldstein, 2001), are more complex than our simple kinetic schemes (Vandenberg and Bezanilla, 1991; Traynelis and Jaramillo, 1998; Hille, 2001). Our model represents a highly simplified account of the channel noise in real neurons. Nevertheless, the important features of the measured noise were explained.
Contributions from individual channel types
We found that at all frequencies, the current and voltage PSDs of the noise increased with depolarization. Furthermore, the shape of the noise PSDs changed markedly at high frequencies with the addition of TTX to the bath. The model accounted for these effects of both voltage and TTX on the shape of the PSD. In particular, the model anticipated the Lorentzian behavior of the noise at depolarized holding potentials; this behavior was revealed by removal of the Na channel contribution. Na+ channels also affect the noise through the impedance term. In neocortical pyramidal cells, Na+ channels can give rise to amplifications by up to a factor of four in the impedance (Diba et al., 2002). The effects in our cells were less dramatic but may well account for some amplification of the voltage noise with depolarization. A noticeable effect from sodium channels would be expected for cells with subthreshold resonance (Hutcheon et al., 1994; Gutfreund et al., 1995). None of our cells, however, showed resonant behavior.
Some models of persistent Na+ channels have led to predictions of substantial noise in other preparations (White et al., 1998), although we saw no evidence of these channels in our experiments. Calculation of sI(f) with the persistent Na+ channel model of White et al. (1998) nevertheless confirms that, if present, such channels yield considerable noise at the holding potentials studied here.
A major source of current noise came from K+ channels, especially as the cell was depolarized. In previous analyses (Manwani and Koch, 1999a; Steinmetz et al., 2000), the K+ noise came from fast delayed-rectifier channels. At the concentration of 4-AP we used (4 mm), almost all delayed rectified potassium channels in the hippocampus would be blocked (including Kv1.1, 1.2, 1.3, 1.6, 1.8, and 2.2). The principal exception is Kv2.1 (blocked only at substantially higher concentrations of 4-AP). Of the three transient, A-type potassium channels that have been reported in the hippocampus, Kv1.4 is blocked, whereas Kv4.1 and Kv4.2 are partially blocked (Catterall et al., 2002). Our experiments with internal Cs+ indicated that the most significant noise contributions came from leak and other (slow) K+ channels. Recent studies have also demonstrated the significant potential influence of slow K+ channels on the spike-timing reliability of cortical neurons (Schreiber et al., 2004). Additionally, the large unitary conductances of BK channels, for example, indicates that they can be quite noisy (Kang et al., 1996). Our suggestion here, that leak channels may present a significant portion of the membrane noise, is novel but follows reasonably from the studies by Zilberberg et al. (2000), Goldstein et al. (2001), and Ilan and Goldstein (2001). Varying the density of the leak and slow K+ channels in our model gives rise to a range of voltage-dependent behavior in the predicted current noise, σI (Fig. 9A), indicating that a variety of noise levels can be described by these channels.
Generality of findings
Channels give rise to membrane fluctuations in a number of ways. One is through resistive Johnson noise, which is usually negligible (DeFelice, 1981; Manwani and Koch, 1999a). Another is through excess, or generalized, 1/fnoise arising from the diffusion of ions through the pores (Bezrukov and Vodyanoy, 1994; Mak and Webb, 1997) or from fluctuations in the open conductance of channels (Mercik and Weron, 2001; Siwy and Fulinski, 2002). Excess noise has been observed in some biological preparations (Fishman et al., 1975a; Neumcke, 1978) and may indeed be significant in our preparation at hyperpolarized holding potentials. In this study, we reproduced many features of the observed noise by modeling solely stochastic effects from channel open-close events. Indeed, we demonstrated that the 1/f spectral behavior seen in the control condition arises from the summation of separate Lorentzian (1/f2) components, substantiating the Markov treatment in the model.
An important source of noise we did not consider in this study is synaptic noise (Calvin and Stevens, 1968; Smetters and Zador, 1996; Manwani and Koch, 1999a; Rudolph and Destexhe, 2003). In vitro studies indicate that spontaneous synaptic release (minis) may represent a significant source of membrane fluctuations. In neocortical slices, for example, the synaptic activity from minis is generally greater than the current fluctuations from ion channels (Diba et al., 2002). In contrast, ion channels are still important for shaping the neuronal response to synaptic noise (Eq. 3). For example, in neocortical slices, Na+ channels cause significant changes in the voltage noise through the impedance term Ztrans(x,y,f), without being significant sources of current noise, sI(y,f) (Diba et al., 2002). This is, in effect, a statement of the well known amplification effect of Na+ channels on other current sources (Stuart and Sakmann, 1995; Stuart, 1999). In vivo, the activity is more marked by “noisy” firing of presynaptic neurons (Pare et al., 1998; Destexhe et al., 2001, 2003; Fellous et al., 2003), which further overwhelms the contribution from stochastic ion channels. Such network states have recently been proposed as mechanisms for gain modulation (Chance et al., 2002; Mitchell and Silver, 2003), enhanced signal detection (Ho and Destexhe, 2000; Stacey and Durand, 2001), contrast invariance tuning (Anderson et al., 2000), and more (for a thorough review, see Destexhe et al., 2003). However, this type of background activity is active and may be categorized as extrinsic to the neuron.
Variability of results
Although our main findings were consistent across the population, there was a great deal of variability from cell to cell, as evident from the large error bars in Figures 4, 5, 6, 7. In the culture, on average, 85% of the cells are the equivalent of pyramidal cells and 15% are interneurons. Whereas it can generally be assumed that recordings were from the pyramidal cells, it is possible that some of the observed variability resulted from differences in neuronal type. Besides, even within a single dish, there was large variability in cell body shape and size, extensiveness of dendritic processes, and local connectivity, which could furthermore lead to variable expression of ion channels in the cell. Unfortunately, we were not able to detect distinct classes of neurons in our data. Additionally, the age of the neurons in the culture ranged from 10 to 20 d. This represents a wide range because many processes and channel types develop over this duration. The input resistance of the cells generally decreases with age, suggesting larger membrane areas and the expression of more channels. Nevertheless, the generality of our main results, despite the apparent variability, suggests that they will be valid in other preparations as well.
Conclusion
In their theoretical studies, Manwani and Koch (1999a) and Steinmetz et al. (2000) showed that Hodgkin and Huxley-type channels, inserted in a single somatic compartment, can give rise to 1.5 mV rms voltage noise. Such large noise levels were not observed in any of the cells we looked at; the rms noise we measured rarely exceeded 0.3 mV. The predictions in these studies resulted from the large input impedances of the somatic patches (Rin = 4 GΩ). The magnitude of voltage noise scales approximately with input resistance for a constant current noise (Eq. 3). In the cells we recorded from, the input resistances were instead on the order of 100 MΩ. This indicates the importance of evaluating the input resistance or impedance in noise calculations. High input resistance membranes, such as more compact cells, thin dendrites, or electrically isolated dendritic spines, can be more susceptible to voltage fluctuations than the somatic recordings performed here.
The results here exemplify a novel quantitative model of intrinsic channel noise at the whole-cell level. As shown by Manwani and Koch (1999a), these assumptions can be extended to include synaptic noise. The linearized treatment at the root of our analysis can provide the basis for calculation of information theoretical parameters, such as the coding fraction for synaptic input to the dendritic tree (Manwani and Koch, 1999b; Steinmetz et al., 2001). An additional advantage of this framework is that it can be easily extended to other channel models distributed in reconstructed neurons. This approach allows for quantitative calculation of PSDs and rms noise in a variety of preparations, thus providing a useful tool for gauging intrinsic noise from the relevant ionic conductances.
Footnotes
This work was supported by the National Institute of Mental Health, the National Science Foundation, and a Sloan-Swartz Postdoctoral Fellowship to K.D. We are deeply indebted to Irina Sokolova and Sheri McKinney for help with the culture preparation and patch clamp. Additionally, we thank Eric Slimko, Sacha Malin, Gilad Jacobson, Yosef Yarom, and Idan Segev for valuable discussions and Michael Hines and Ted Carnevale for assistance with the NEURON simulation environment.
Correspondence should be addressed to Dr. Kamran Diba, Division of Biology 139-74, 1200 East California Boulevard, Pasadena, CA 91125. E-mail: diba@klab.caltech.edu.
Copyright © 2004 Society for Neuroscience 0270-6474/04/249723-11$15.00/0
References
- Anderson JS, Lampl I, Gillespie DC, Ferster D (2000) The contribution of noise to contrast invariance of orientation tuning in cat visual cortex. Science 290: 1968-1972. [DOI] [PubMed] [Google Scholar]
- Ariav G, Polsky A, Schiller J (2003) Submillisecond precision of the input-output transformation function mediated by fast sodium dendritic spikes in basal dendrites of CA1 pyramidal neurons. J Neurosci 23: 7750-7758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banker G, Goslin K (1998) Culturing nerve cells, Ed 2. Cambridge, MA: MIT.
- Beierholm U, Nielsen CD, Ryge J, Alstrom P, Kiehn O (2001) Characterization of reliability of spike timing in spinal interneurons during oscillating inputs. J Neurophysiol 86: 1858-1868. [DOI] [PubMed] [Google Scholar]
- Bekkers JM, Stevens CF (1995) Quantal analysis of EPSCs recorded from small numbers of synapses in hippocampal cultures. J Neurophysiol 73: 1145-1156. [DOI] [PubMed] [Google Scholar]
- Bekkers JM, Richerson GB, Stevens CF (1990) Origin of variability in quantal size in cultured hippocampal neurons and hippocampal slices. Proc Natl Acad Sci USA 87: 5359-5362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezrukov SM, Vodyanoy I (1994) Noise in biological-membranes and relevant ionic systems. In: Biomembrane electrochemistry (Blank M, Vodyanoy I, eds), pp 375-399. New York: Oxford UP.
- Birnir B, Eghbali M, Everitt AB, Gage PW (2000) Bicuculline, pentobarbital and diazepam modulate spontaneous GABA(A) channels in rat hippocampal neurons. Br J Pharmacol 131: 695-704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calvin WH, Stevens CF (1968) Synaptic noise and other sources of randomness in motoneuron interspike intervals. J Neurophysiol 31: 574-587. [DOI] [PubMed] [Google Scholar]
- Catterall WA, Chandy KG, Gutman GA (2002) The IUPHAR compendium of voltage-gated ion channels. Leeds, UK: IUPHAR Media.
- Chance FS, Abbott LF, Reyes AD (2002) Gain modulation from background synaptic input. Neuron 35: 773-782. [DOI] [PubMed] [Google Scholar]
- Chow CC, White JA (1996) Spontaneous action potentials due to channel fluctuations. Biophys J 71: 3013-3021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeFelice LJ (1981) Introduction to membrane noise. New York: Plenum.
- Derksen HE, Verveen AA (1966) Fluctuations of resting neural membrane potential. Science 151: 1388-1389. [DOI] [PubMed] [Google Scholar]
- de Ruyter van Steveninck R, Laughlin SB (1996) The rate of information transfer at graded-potential synapses. Nature 379: 642-645. [Google Scholar]
- Destexhe A, Rudolph M, Fellous JM, Sejnowski TJ (2001) Fluctuating synaptic conductances recreate in vivo-like activity in neocortical neurons. Neuroscience 107: 13-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Pare D (2003) The high-conductance state of neo-cortical neurons in vivo. Nat Rev Neurosci 4: 739-751. [DOI] [PubMed] [Google Scholar]
- Diba K, Jacobson G, Oz Y, Koch C, Segev I, Yarom Y (2002) Characteristics of subthreshold noise in neocortical pyramidal neurons. Soc Neurosci Abstr 28: 312.4. [Google Scholar]
- Fatt P, Katz B (1950) Some observations on biological noise. Nature 166: 597-598. [DOI] [PubMed] [Google Scholar]
- Fatt P, Katz B (1952) Spontaneous subthreshold activity at motor nerve endings. J Physiol (Lond) 117: 109-128. [PMC free article] [PubMed] [Google Scholar]
- Fellous JM, Rudolph M, Destexhe A, Sejnowski TJ (2003) Synaptic background noise controls the input/output characteristics of single cells in an in vitro model of in vivo activity. Neuroscience 122: 811-829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman HM (1973) Relaxation spectra of potassium channel noise from squid axon membranes. Proc Natl Acad Sci USA 70: 876-879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman HM, Poussart DM, Moore LE (1975a) Noise measurements in squid axon membrane. J Membr Biol 24: 281-304. [DOI] [PubMed] [Google Scholar]
- Fishman HM, Moore LE, Poussart DM (1975b) Potassium-ion conduction noise in squid axon membrane. J Membr Biol 24: 305-328. [DOI] [PubMed] [Google Scholar]
- Fourcaud-Trocme N, Hansel D, van Vreeswijk C, Brunel N (2003) How spike generation mechanisms determine the neuronal response to fluctuating inputs. J Neurosci 23: 11628-11640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gammaitoni L, Hanggi P, Jung P, Marchesoni F (1998) Stochastic resonance. Rev Mod Phys 70: 223-287. [Google Scholar]
- Goldstein SA, Bockenhauer D, O'Kelly I, Zilberberg N (2001) Potassium leak channels and the KCNK family of two-P-domain subunits. Nat Rev Neurosci 2: 175-184. [DOI] [PubMed] [Google Scholar]
- Gutfreund Y, Yarom Y, Segev I (1995) Subthreshold oscillations and resonant frequency in guinea-pig cortical neurons: physiology and modelling. J Physiol (Lond) 483: 621-640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B (2001) Ion channels of excitable membranes, Ed 3. Sunderland, MA: Sinauer.
- Hines ML, Carnevale NT (1997) The NEURON simulation environment. Neural Comput 9: 1179-1209. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT (2000) Expanding NEURON's repertoire of mechanisms with NMODL. Neural Comput 12: 995-1007. [DOI] [PubMed] [Google Scholar]
- Ho N, Destexhe A (2000) Synaptic background activity enhances the responsiveness of neocortical pyramidal neurons. J Neurophysiol 84: 1488-1496. [DOI] [PubMed] [Google Scholar]
- Hunter JD, Milton JG (2003) Amplitude and frequency dependence of spike timing: implications for dynamic regulation. J Neurophysiol 90: 387-394. [DOI] [PubMed] [Google Scholar]
- Hunter JD, Milton JG, Thomas PJ, Cowan JD (1998) Resonance effect for neural spike time reliability. J Neurophysiol 80: 1427-1438. [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Miura RM, Yarom Y, Puil E (1994) Low-threshold calcium current and resonance in thalamic neurons: a model of frequency preference. J Neurophysiol 71: 583-594. [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Miura RM, Puil E (1996) Subthreshold membrane resonance in neocortical neurons. J Neurophysiol 76: 683-697. [DOI] [PubMed] [Google Scholar]
- Ilan N, Goldstein SA (2001) Kcnko: single, cloned potassium leak channels are multi-ion pores. Biophys J 80: 241-253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack JJB, Noble D, Tsien RW (1975) Electric current flow in excitable cells. Oxford: Clarendon.
- Johnston D, Wu SM-S (1995) Foundations of cellular neurophysiology. Cambridge, MA: MIT.
- Kang J, Huguenard JR, Prince DA (1996) Development of BK channels in neocortical pyramidal neurons. J Neurophysiol 76: 188-198. [DOI] [PubMed] [Google Scholar]
- Khakh BS, Humphrey PP, Surprenant A (1995) Electrophysiological properties of P2X-purinoceptors in rat superior cervical, nodose and guinea-pig coeliac neurones. J Physiol (Lond) 484: 385-395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch C (1984) Cable theory in neurons with active, linearized membranes. Biol Cybern 50: 15-33. [DOI] [PubMed] [Google Scholar]
- Koch C (1999) Biophysics of computation: information processing in single neurons. New York: Oxford UP.
- Koch C, Poggio T (1985) A simple algorithm for solving the cable equation in dendritic trees of arbitrary geometry. J Neurosci Methods 12: 303-315. [DOI] [PubMed] [Google Scholar]
- Korngreen A, Sakmann B (2000) Voltage-gated K+ channels in layer 5 neo-cortical pyramidal neurones from young rats: subtypes and gradients. J Physiol (Lond) 525: 621-639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kretzberg J, Warzecha AK, Egelhaaf M (2001a) Neural coding with graded membrane potential changes and spikes. J Comput Neurosci 11: 153-164. [DOI] [PubMed] [Google Scholar]
- Kretzberg J, Egelhaaf M, Warzecha AK (2001b) Membrane potential fluctuations determine the precision of spike timing and synchronous activity: a model study. J Comput Neurosci 10: 79-97. [DOI] [PubMed] [Google Scholar]
- Lampl I, Yarom Y (1997) Subthreshold oscillations and resonant behavior: two manifestations of the same mechanism. Neuroscience 78: 325-341. [DOI] [PubMed] [Google Scholar]
- Liebovitch LS, Sullivan JM (1987) Fractal analysis of a voltage-dependent potassium channel from cultured mouse hippocampal neurons. Biophys J 52: 979-988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maccaferri G, Mangoni M, Lazzari A, Difrancesco D (1993) Properties of the hyperpolarization-activated current in rat hippocampal Ca1 pyramidal cells. J Neurophysiol 69: 2129-2136. [DOI] [PubMed] [Google Scholar]
- MacLeod K, Laurent G (1996) Distinct mechanisms for synchronization and temporal patterning of odor-encoding neural assemblies. Science 274: 976-979. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ (1998) Modeling active dendritic processes in pyramidal neurons. In: Methods in neuronal modeling: from ions to networks, Ed 2 (Koch C, Segev I, eds), pp 171-210. Cambridge, MA: MIT.
- Mainen ZF, Joerges J, Huguenard JR, Sejnowski TJ (1995) A model of spike initiation in neocortical pyramidal neurons. Neuron 15: 1427-1439. [DOI] [PubMed] [Google Scholar]
- Mak DO, Webb WW (1997) Conductivity noise in transmembrane ion channels due to ion concentration fluctuations via diffusion. Biophys J 72: 1153-1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manwani A, Koch C (1999a) Detecting and estimating signals in noisy cable structure, I: neuronal noise sources. Neural Comput 11: 1797-1829. [DOI] [PubMed] [Google Scholar]
- Manwani A, Koch C (1999b) Detecting and estimating signals in noisy cable structures, II: information theoretical analysis. Neural Comput 11: 1831-1873. [DOI] [PubMed] [Google Scholar]
- Margulis M, Tang CM (1998) Temporal integration can readily switch between sublinear and supralinear summation. J Neurophysiol 79: 2809-2813. [DOI] [PubMed] [Google Scholar]
- Mauro A, Conti F, Dodge F, Schor R (1970) Subthreshold behavior and phenomenological impedance of the squid giant axon. J Gen Physiol 55: 497-523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mercik S, Weron K (2001) Stochastic origins of the long-range correlations of ionic current fluctuations in membrane channels. Phys Rev E Stat Nonlin Soft Matter Phys 63: 051910. [DOI] [PubMed] [Google Scholar]
- Mitchell SJ, Silver RA (2003) Shunting inhibition modulates neuronal gain during synaptic excitation. Neuron 38: 433-445. [DOI] [PubMed] [Google Scholar]
- Neumcke B (1978) 1/f noise in membranes. Biophys Struct Mech 4: 179-199. [DOI] [PubMed] [Google Scholar]
- Pare D, Shink E, Gaudreau H, Destexhe A, Lang EJ (1998) Impact of spontaneous synaptic activity on the resting properties of cat neocortical pyramidal neurons in vivo. J Neurophysiol 79: 1450-1460. [DOI] [PubMed] [Google Scholar]
- Pecher C (1939) La fluctuation d'excitabilité de la fibre nerveuse. Arch Intern Physiol 49: 129-152. [Google Scholar]
- Poirazi P, Brannon T, Mel BW (2003) Arithmetic of subthreshold synaptic summation in a model CA1 pyramidal cell. Neuron 37: 977-987. [DOI] [PubMed] [Google Scholar]
- Rudolph M, Destexhe A (2003) Characterization of subthreshold voltage fluctuations in neuronal membranes. Neural Comput 15: 2577-2618. [DOI] [PubMed] [Google Scholar]
- Sabah NH, Leibovic KN (1972) The effect of membrane parameters on the properties of the nerve impulse. Biophys J 12: 1132-1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakmann B, Neher E (1995) Single-channel recording, Ed 2. New York: Plenum.
- Schneidman E, Freedman B, Segev I (1998) Ion channel stochasticity may be critical in determining the reliability and precision of spike timing. Neural Comput 10: 1679-1703. [DOI] [PubMed] [Google Scholar]
- Schreiber S, Fellous JM, Tiesinga P, Sejnowski TJ (2004) Influence of ionic conductances on spike timing reliability of cortical neurons for suprathreshold rhythmic inputs. J Neurophysiol 91: 194-205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd GM (1998) The synaptic organization of the brain, Ed 4. New York: Oxford UP.
- Sherman-Gold R, ed (1993) The axon guide for electrophysiology and biophysics laboratory techniques. Foster City, CA: Axon Instruments.
- Siwy Z, Fulinski A (2002) Origin of 1/f(alpha) noise in membrane channel currents. Phys Rev Lett 89: 158101. [DOI] [PubMed] [Google Scholar]
- Smetters DK, Zador A (1996) Synaptic transmission: noisy synapses and noisy neurons. Curr Biol 6: 1217-1218. [DOI] [PubMed] [Google Scholar]
- Softky WR, Koch C (1993) The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J Neurosci 13: 334-350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stacey WC, Durand DM (2001) Synaptic noise improves detection of subthreshold signals in hippocampal CA1 neurons. J Neurophysiol 86: 1104-1112. [DOI] [PubMed] [Google Scholar]
- Steinmetz PN, Manwani A, Koch C, London M, Segev I (2000) Subthreshold voltage noise due to channel fluctuations in active neuronal membranes. J Comput Neurosci 9: 133-148. [DOI] [PubMed] [Google Scholar]
- Steinmetz PN, Manwani A, Koch C (2001) Variability and coding efficiency of noisy neural spike encoders. Biosystems 62: 87-97. [DOI] [PubMed] [Google Scholar]
- Stuart G (1999) Voltage-activated sodium channels amplify inhibition in neocortical pyramidal neurons. Nat Neurosci 2: 144-150. [DOI] [PubMed] [Google Scholar]
- Stuart G, Sakmann B (1995) Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron 15: 1065-1076. [DOI] [PubMed] [Google Scholar]
- Traynelis SF, Jaramillo F (1998) Getting the most out of noise in the central nervous system. Trends Neurosci 21: 137-145. [DOI] [PubMed] [Google Scholar]
- Trussell LO (1999) Synaptic mechanisms for coding timing in auditory neurons. Annu Rev Physiol 61: 477-496. [DOI] [PubMed] [Google Scholar]
- Tuckwell HC (1988) Introduction to theoretical neurobiology. Cambridge, UK: Cambridge UP.
- Vandenberg CA, Bezanilla F (1991) A sodium channel gating model based on single channel, macroscopic ionic, and gating currents in the squid giant axon. Biophys J 60: 1511-1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Rossum MC, O'Brien BJ, Smith RG (2003) Effects of noise on the spike timing precision of retinal ganglion cells. J Neurophysiol 89: 2406-2419. [DOI] [PubMed] [Google Scholar]
- Verveen AA, Derksen HE, Schick KL (1967) Voltage fluctuations of neural membrane. Nature 216: 588-589. [DOI] [PubMed] [Google Scholar]
- Wanke E, DeFelice LJ, Conti F (1974) Voltage noise, current noise and impedance in space clamped squid giant axon. Pflügers Arch 347: 63-74. [DOI] [PubMed] [Google Scholar]
- White JA, Klink R, Alonso A, Kay AR (1998) Noise from voltage-gated ion channels may influence neuronal dynamics in the entorhinal cortex. J Neurophysiol 80: 262-269. [DOI] [PubMed] [Google Scholar]
- White JA, Rubinstein JT, Kay AR (2000) Channel noise in neurons. Trends Neurosci 23: 131-137. [DOI] [PubMed] [Google Scholar]
- Wiesenfeld K, Moss F (1995) Stochastic resonance and the benefits of noise—from ice ages to crayfish and squids. Nature 373: 33-36. [DOI] [PubMed] [Google Scholar]
- Zilberberg N, Ilan N, Gonzalez-Colaso R, Goldstein SA (2000) Opening and closing of KCNKO potassium leak channels is tightly regulated. J Gen Physiol 116: 721-734. [DOI] [PMC free article] [PubMed] [Google Scholar]