Abstract
The presence of various ongoing oscillations in the brain is correlated with behavioral states such as restful wakefulness or drowsiness. However, even when subjects aim to maintain a high level of vigilance, ongoing oscillations exhibit large amplitude variability on time scales of hundreds of milliseconds to seconds, suggesting that the functional state of local cortical networks is continuously changing. How this volatility of ongoing oscillations influences the perception of sensory stimuli has remained essentially unknown.
We investigated the relationship between prestimulus neuronal oscillations and the subjects' ability to consciously perceive and react to somatosensory stimuli near the threshold of detection. We show that, for prestimulus oscillations at ∼10, 20, and 40 Hz detected over the sensorimotor cortex, intermediate amplitudes were associated with the highest probability of conscious detection and the shortest reaction times. In contrast, for 10 and 20 Hz prestimulus oscillations detected over the parietal region, the largest amplitudes were associated with the best performance.
Our data indicate that the prestimulus oscillatory activity detected over sensorimotor and parietal cortices has a profound effect on the processing of weak stimuli. Furthermore, the results suggest that ongoing oscillations in sensory cortices may optimize the processing of sensory stimuli with the same mechanism as noise sources in intrinsic stochastic resonance.
Keywords: ongoing oscillations, prestimulus states, conscious perception, intrinsic stochastic resonance, magnetoencephalography, human
Introduction
Ongoing oscillations are prominent in many cortical areas, and their functional significance remains a matter of intense debate (Salmelin and Hari, 1994; Pfurtscheller and Lopes da Silva, 1999; Wiest and Nicolelis, 2003). Ongoing neuronal oscillations may be both endogenous and exogenous in origin and induce a wide range of activity-dependent processes that modify the functional connectivity of the underlying neuronal networks on many time scales (Marder, 1998). Furthermore, ongoing oscillations at stimulus onset appear to superimpose on stimulus-driven activities, resulting in a large variability of stimulus-evoked responses (Arieli et al., 1996). Altogether, one would therefore expect the ongoing activity both on short and on longer time scales to have an influence on how neuronal networks process incoming signals. Ongoing oscillations have indeed been found to influence stimulus-related activities (Nikouline et al., 2000; Fries et al., 2001; Liang et al., 2002; Makeig et al., 2002) and have been suggested to potentially play a constructive role, e.g., by “priming” representations of anticipated stimuli (Engel et al., 2001; Kenet et al., 2003) or a given sensory system (Fanselow et al., 2001). Nevertheless, the significance of ongoing oscillations for conscious perception and behavior has remained essentially unknown.
Ongoing oscillations may be particularly important in biasing the processing of stimuli at the threshold of sensation (Fanselow et al., 2001; Gong et al., 2002). One framework for understanding how the processing of such weak stimuli may benefit from ongoing oscillations is stochastic resonance (Wiesenfeld and Moss, 1995). Stochastic resonance is a phenomenon found in many nonlinear systems, including the nervous system, where moderate levels of noise in weak signals optimize the signal detection (Chialvo and Apkarian, 1993; Collins et al., 1996). Computational models of neuronal systems have revealed recently that signal detection and transmission may, in fact, also be enhanced by noise from within the system (Hô and Destexhe, 2000; Stocks and Manella, 2001), giving rise to a phenomenon termed intrinsic stochastic resonance.
We investigated the relationship between the amplitude of prestimulus oscillations and the subjects' ability to consciously perceive and react to weak somatosensory stimuli. Here we show that prestimulus oscillations may indeed enhance psychophysical performance, possibly through intrinsic stochastic resonance.
Materials and Methods
Subjects and recordings. Ongoing neuromagnetic activity was recorded from 14 subjects (23-32 years of age; one female) with 204 planar gradiometers from a 306 channel magnetoencephalography (MEG) instrument (Neuromag Elekta, Helsinki, Finland). The data were digitized at 900 Hz and resampled off-line to a sampling frequency of 300 Hz after the application of an antialiasing filter of 100 Hz. Electro-oculograms (EOGs) and thumb-movement electromyograms were recorded for artifact rejection and for the detection of subjects' responses, respectively. The study was approved by an ethical committee of the Helsinki University Central Hospital.
Experimental paradigm. The subjects were stimulated electrically on the tip of the index finger with weak 0.2 msec constant-current pulses. The stimuli were applied to the left index finger, right index finger, or simultaneously to both index fingers with equal probabilities in a semi-random order; the interval between consecutive pulses was random and uniformly distributed in the 3-4 sec interval. Four 20 min epochs were recorded for each subject, giving ∼1400 stimulus events per subject. Before the session, the intensity was adjusted separately for both fingers so that maximally 50% of the trials were detected. Subjects were instructed to sit relaxed with their eyes closed and promptly twitch the thumb of the hand(s) in which they felt the stimulus during the recording sessions.
Data analysis. The data were analyzed off-line using MATLAB (Math-Works, Natick, MA). Trials with EOG signals of >80 μV were discarded from additional analysis, which resulted in 855 ± 124 (mean ± SD) and 863 ± 123 artifact-free trials for the stimulation of the left and right finger, respectively.
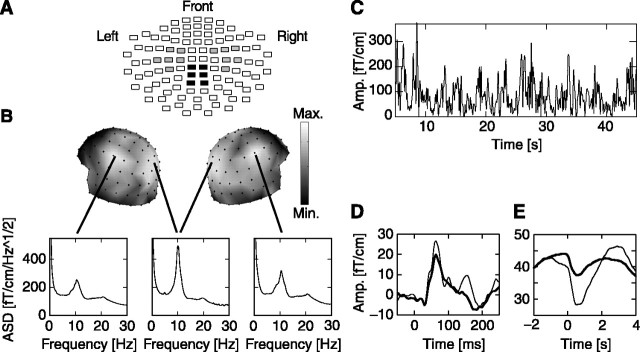
The positions of 12 channels covering sensorimotor or parietal regions are shown on a flattened view of the helmet-shaped sensor array (see Fig. 1 A). From the channel groups over the left and right sensorimotor regions, we selected for additional analyses those four channels from each hemisphere that showed the largest amplitude attenuation of 10 Hz oscillations in response to the detected stimuli, because this attenuation reflects the interaction between neuronal processing of somatic stimuli and the classical “μ rhythm” of the somatosensory and motor cortices [hence, the term “sensorimotor” (Pfurtscheller and Lopes da Silva, 1999)]. From the parietal channel group, we selected those four channels that had the largest peaks in the amplitude spectral density between 8 and 13 Hz, because the parietal 10 Hz oscillations have been linked to attention, which is crucial to the present task (Vanni et al., 1997).
Figure 1.
Dynamics of ongoing oscillations at 10 Hz. A, The positions of channels that covered the left and right sensorimotor (gray) and parietal (black) regions are shown on a flattened view of the helmet-shaped sensor array. Each rectangle represents the two joint planar gradiometers. B, The amplitude spectral density (ASD) plots of the MEG signals have distinct peaks at ∼10 Hz with local maxima over parietal and left and right sensorimotor regions (insets are computed from all of the 20 min sessions and averaged across the 4 selected channels in each region and across all subjects). Max., Maximum; Min., minimum. C, The amplitude (Amp.) envelope of 10 Hz oscillations from a representative subject and a channel over the right sensorimotor region shows that these oscillations exhibit large amplitude variability on time scales of hundreds of milliseconds to tens of seconds. D, Somatosensory-evoked fields were visible in the grand average of both detected (thin lines) and undetected (thick lines) trials (data from a representative channel over the right sensorimotor region). E, The 10 Hz oscillation amplitude attenuated transiently after stimulation for both detected and undetected trials (the average is across all trials, across selected channels and subjects, and over both hemispheres, giving a total of 7697 detected and 16,355 undetected trials).
The correlation between prestimulus oscillation amplitude and the subjects' ability to detect and react to the stimuli was estimated as follows. For a given prestimulus window (e.g., 1000 msec) and frequency band (e.g., 7-13 Hz), the trials were sorted into 10-percentile bins with respect to the mean amplitude of the oscillations. The oscillation amplitude was determined by using a wavelet filter separately for each channel, as described by Linkenkaer-Hansen et al. (2004), and then averaged across the four channels. The sorting was done by rearranging the trials separately for each subject in ascending order of prestimulus amplitudes and then grouping the first 10% of the trials in the first 10-percentile bin, the next 10% of the trials in the second 10-percentile bin, etc. This procedure is also a normalization to compensate for the intersubject variability in absolute values of oscillation amplitude. For each subject, we then calculated the fraction of stimuli that were detected (termed “hit rate”) and the mean reaction time to the detected stimuli for each of the 10 groups of trials. To normalize for the interindividual differences in hit rate [32 ± 13% (mean ± SD)] and reaction time (498 ± 82 msec), the hit rate and mean reaction time in each prestimulus-amplitude bin were determined as the percentage change relative to the mean across all bins for each subject. The sorting of hit rate and reaction time was performed for the γ (27-53 Hz), β (15-29 Hz), α (7-13 Hz), θ (3-7 Hz), and δ (1-3 Hz) frequency bands and prestimulus windows of 250, 500, 1000, 1500, 2000, and 2500 msec. Statistical tests, unless otherwise stated, were based on ANOVA.
Results
Ongoing activity is dominated by 10 Hz oscillations
Pronounced oscillatory activity at ∼10 Hz was observed bilaterally over the sensorimotor and parietal cortices (Fig. 1B). These oscillations fluctuated intermittently in amplitude (Fig. 1C), suggesting that the underlying networks were in a highly dynamic state (Linkenkaer-Hansen et al., 2001). This was also reflected in the susceptibility of the sensorimotor oscillations to the stimuli; although the weak stimuli only elicited very small somatosensory evoked fields in most subjects (Fig. 1D), both the detected and undetected stimuli induced a transient suppression of the oscillations, which peaked at ∼550 msec after the stimulus onset (two-tailed t test; p < 0.0001) (Fig. 1E). Thus, the stimulus processing perturbed the ongoing oscillations even when it did not lead to a conscious perception (Libet et al., 1967).
Dependence of psychophysical performance on 10 Hz oscillations
The large amplitude range of 10 Hz oscillations (Fig. 1C) suggests that if different amplitudes were associated with distinct functional states of the network, the oscillations could affect stimulus processing (Nikouline et al., 2000). To assess this notion at the level of psychophysical performance, we investigated the relationship between the amplitude of prestimulus 10 Hz oscillations over sensorimotor or parietal regions and the following: (1) the probability of stimulus detection (hit rate) and (2) the mean reaction time.
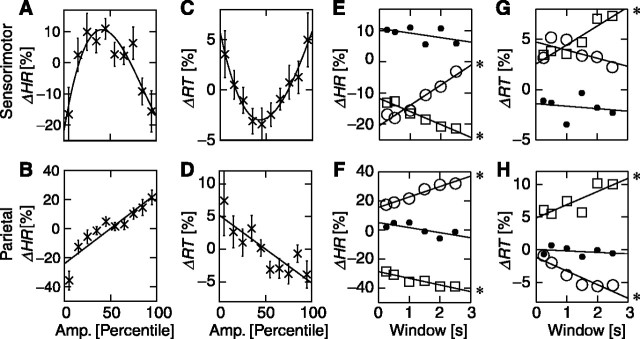
Single trials were sorted with respect to prestimulus 10 Hz oscillation amplitude separately over contralateral sensorimotor and parietal regions into 10-percentile bins. We calculated the change in hit rate and mean reaction time from the trials in each of the 10 bins relative to the mean of all trials for each subject. The results from the left- and right-finger stimulations were averaged (see Materials and Methods). Over the sensorimotor regions, hit rate and the prestimulus amplitude were clearly correlated with an optimum at intermediate amplitude values (Fig. 2A). The relationship was well described by a parabolic function (cubic fit, r2 = 0.84, p < 0.01; ANOVA) and only poorly by linear regression (r2 = 0.04; p = 0.56). The differences in hit rate between the trials with the intermediate amplitudes and the trials with the very low or high levels of activity were 28 ± 11 (mean ± SEM) and 27 ± 9 percentage points, respectively. Over the parietal region, in contrast, hit rate was positively and linearly correlated with prestimulus 10 Hz oscillations (Fig. 2B) (linear regression, r2 > 0.73, p < 0.002) with a negligible parabolic contribution (r2 = 0.14 for cubic-linear fit). In the trials with the highest levels of prestimulus activity, the hit rates were 57 ± 10 percentage points larger than during the trials with lowest levels of activity. Oscillations over both sensorimotor and parietal regions thus had a remarkably strong, albeit distinct, correlation with psychophysical performance.
Figure 2.
Evidence for linear and parabolic dependences of performance on prestimulus oscillation amplitude. For trials belonging to 10 levels of prestimulus amplitudes of 10 Hz oscillations in a prestimulus window of 1000 msec, we have plotted the change in hit rate (ΔHR) relative to the mean across all trials (see Materials and Methods for details). The best performance is seen at intermediate amplitudes of oscillations over sensorimotor regions (A) and at the largest amplitudes of oscillations over the parietal cortex (B). The difference in reaction time (ΔRT) relative to the mean across all trials also exhibited a parabolic and a linear dependence on the prestimulus amplitudes over sensorimotor (C) and parietal (D) regions, respectively. The data points indicate the grand-average mean ± SEM (n = 14). A least-squares fit to the data of a third-order polynomial is indicated by the solid lines in A and C. The hit-rate change of the first (squares), fifth (dots), and 10th (circles) amplitude bin is plotted as a function of the prestimulus-window size for sensorimotor (E) and parietal (F) channels. The same plots for the reaction time are shown in G and H. The changes in both hit rates and reaction times exhibit clear trends toward a poorer performance for small-amplitude states with increasing prestimulus time scales (squares). Conversely, the large-amplitude states show worse performance with smaller time windows (circles). These dependencies were common to the sensorimotor and parietal regions. Significant linear trends in E-H are marked with an asterisk to the right of the least-squares fitted lines. Amp., Amplitude.
Sorting the reaction times with respect to 10 Hz oscillations over sensorimotor regions revealed that the subjects responded 7 ± 3 (mean ± SEM) and 8 ± 4 percentage points faster with intermediate prestimulus amplitudes than with the very small or large amplitudes, respectively. Again, this relationship was well fit by a parabolic function (Fig. 2C) (cubic fit, r2 = 0.97, p < 0.0001; linear regression, r2 = 0.05, p = 0.52). For the 10 Hz oscillations over the parietal cortex, the reaction times were negatively and linearly correlated with prestimulus amplitudes (Fig. 2D) (linear regression, r2 > 0.73, p < 0.002) with a negligible parabolic contribution (r2 = 0.09 for cubic-linear fit). In trials with the highest levels of prestimulus activity, the reaction times were 11 ± 7 percentage points shorter than during the trials with lowest levels of activity.
It is well known that stimulation and/or movement of the index finger may influence the amplitude of ongoing 10 Hz oscillations in the sensorimotor region for up to a few seconds after the stimulus (Neuper and Pfurtscheller, 2001; Stancák et al., 2003) and thus the level of oscillatory activity in the prestimulus interval of the subsequent trial despite the (long) mean interval between finger movements of ∼11 sec (note that the mean hit rate was only 32% and the mean interstimulus interval was 3.5 sec). The analysis revealed, however, that the number of trials with a movement in the preceding trial was uniformly distributed among the amplitude bins (p = 0.98; one-way ANOVA). Thus, movement-related activities do not contribute to the nonuniform distribution of performance for different prestimulus levels of 10 Hz activity.
Time-scale dependence of prestimulus functional states
To explore the robustness of the effects shown in Figure 2A-D with respect to the selected prestimulus activity, we (1) increased the size of the prestimulus windows in steps from 250 to 2500 msec and (2) placed a constant-size 250 msec prestimulus window with gaps of 0, 250, 750, 1250, 1750, and 2250 msec to the stimulus onset.
The intermediate levels of prestimulus oscillations over sensorimotor regions were optimal for the performance and gave rise to stable hit rates and reaction times for all time windows (Fig. 2E,G). In contrast, the hit rates in percentile bins with the smallest and largest amplitudes had a strong dependence on window sizes (p < 0.001, linear regression). These correlations were similar for the reaction time, albeit less significant (p < 0.01 and p < 0.19 for smallest and largest amplitude bins, respectively). The positive trend of the largest amplitudes suggests that the detrimental effect of a large-amplitude oscillation is larger very close to the stimulus onset. This was confirmed using the sliding 250 msec prestimulus window showing decreasing hit rates with decreasing gaps between the prestimulus window and stimulus onset for the largest-amplitude bin of trials (data not shown; p < 0.05, linear regression). The decreasing performance for the smallest-amplitude trials with increasing prestimulus window duration over which the oscillation amplitude was integrated indicates that the 10 Hz oscillations carry a functionally significant memory of their past for several oscillation cycles; otherwise, the changes in hit rate would have converged to zero for increasing window sizes.
The time-window dependences of hit rate and reaction time for the first-, fifth-, and 10th-percentile groups over the parietal region were qualitatively the same as those for over the sensorimotor region (Fig. 2F,H). Thus, the fifth-percentile group was stable, whereas the first and 10th groups exhibited significant linear trends toward poorer and better performance at longer time scales, respectively (linear regressions: p < 0.05 for both the first- and 10th-percentile groups of hit rate and reaction time).
Dependence of psychophysical performance on oscillations in other frequency bands
We then analyzed the dependence of hit rate on prestimulus activity in the γ, β, θ, and δ frequency bands in the prestimulus window of -1000 to 0 msec. Over the sensorimotor region, the γ and β oscillations were associated with the largest hit rate at intermediate amplitudes (Fig. 3A,B) (cubic fits, r2 > 0.74, p < 0.03; linear regressions, r2 < 0.22, p > 0.17) and thus had a correlation with performance similar to that for the 10 Hz oscillations (compare Fig. 2A). However, the hit rate was not significantly correlated with prestimulus amplitude in δ and θ bands (Fig. 3C,D) (r2 < 0.64, p > 0.24 for all linear and cubic fits). Over the parietal region, the hit rate had a positive and linear correlation with β-oscillation amplitudes (Fig. 3F) (r2 < 0.85; p < 0.0001). The other frequency bands, however, had no systematic influence on hit rate (Fig. 3E,G,H) (r2 < 0.64, p > 0.08 for all linear and cubic fits), except the δ band, which had a minor, albeit significant, cubic trend (Fig. 3H) (r2 = 0.74; p < 0.04).
Figure 3.
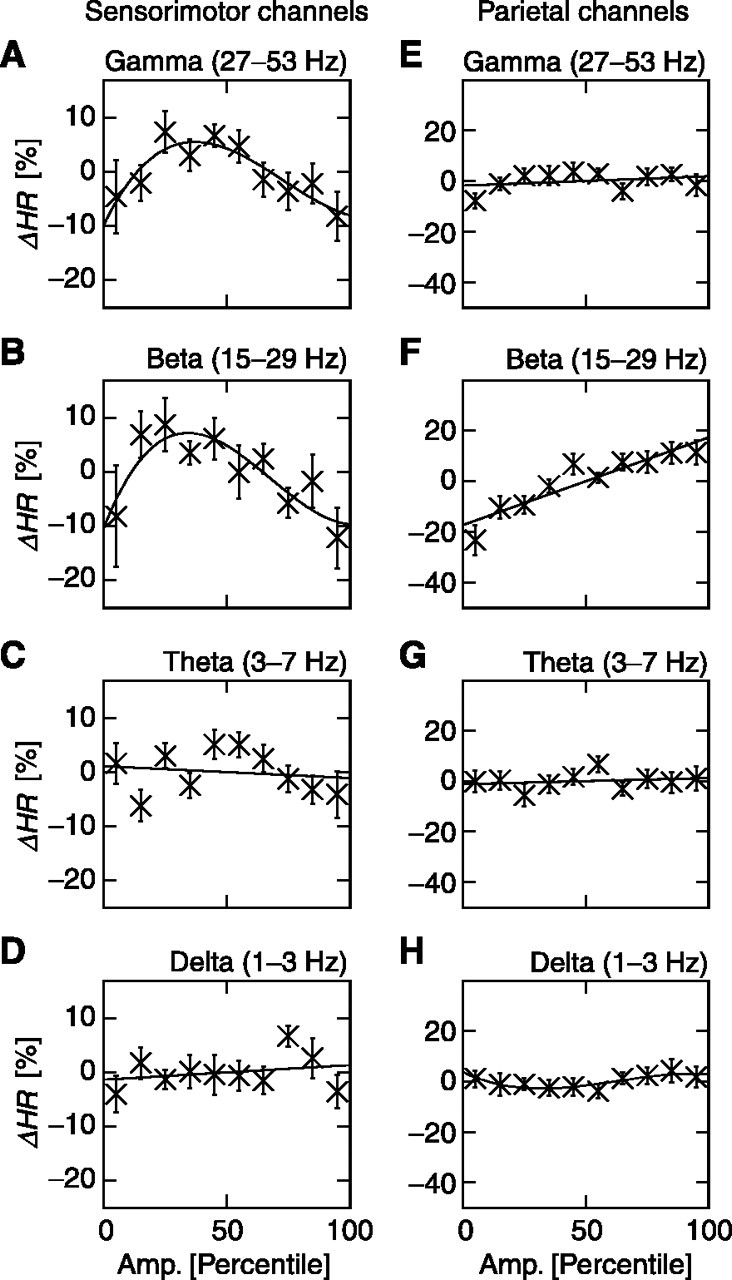
The dependence of hit rate on oscillations over the sensorimotor and parietal regions. The same plot as in Figure 2 A is shown, but for different frequency bands over the sensorimotor (A-D) and parietal (E-H) regions. ΔHR, Change in hit rate; Amp., amplitude.
Discussion
We investigated the impact of prestimulus neuronal oscillations on the hit rate and reaction time to weak somatic stimuli. The central findings of this study were that the behavioral performance was optimized by intermediate amplitudes of 10, 20, and 40 Hz oscillations over the sensorimotor regions and by maximum amplitudes of 10 and 20 Hz oscillations over the parietal region. The results indicate that these oscillations have profound and distinct effects on behavioral performance.
Stochastic resonance: a general mechanism of noise-dependent optimization of signal processing
Increasing the level of noise in a linear system decreases the output signal-to-noise ratio. In nonlinear systems, however, the signal-to-noise ratio may increase with increasing noise levels up to the point at which the noise itself begins to dominate the detection-transmission process and consequently decrease the signal-to-noise ratio. This gives rise to a parabolic relationship between signal-to-noise ratio and noise, the hallmark of stochastic resonance (Wiesenfeld and Moss, 1995). Several theoretical and modeling studies suggest that the nervous system could also use intrinsic stochastic resonance (Hô and Destexhe, 2000; Stocks and Manella, 2001).
We exploited the considerable variability in the ongoing activity to sort out the relationship between psychophysical performance and prestimulus neuronal activity in a graded manner. The unequivocal parabolic relationship between the level of sensorimotor prestimulus activity and behavioral performance suggests that sensorimotor processing exploits intrinsic stochastic resonance in which the ongoing activity plays the role of an intrinsic noise source. Ongoing activity may give rise to barrages of stimulus-unrelated synaptic inputs that are, in fact, noise in the traditional sense (Shu et al., 2003). However, endogenous neuronal activity may also “prime” a certain sensory system (Fanselow et al., 2001) or activate specific stimulus representations (Engel et al., 2001; Kenet et al., 2003). The poor behavioral performance at very low or very high levels of prestimulus activity seen in Figure 2, A and C, could therefore reflect the top-down activation of a too-small or a too-large neuronal population, respectively (Gong et al., 2002).
Prestimulus functional states are graded functions of amplitude and time
It may seem natural to suggest that it is the activity immediately at stimulus onset that influences the processing of the stimulus, as opposed to ongoing oscillations farther back in time. Recent studies, however, have shown that the autocorrelation of the amplitude envelope of ongoing 10 and 20 Hz oscillations decays slowly over tens of seconds both during rest and when the oscillations are strongly perturbed by sensory input (Linkenkaer-Hansen et al., 2001, 2004). We have shown here that activity up to at least 2-2.5 sec before stimulus onset, over both sensorimotor and parietal regions, has an influence on hit rate and reaction time (Fig. 2E-H). Hence, there appears to be a direct link between the strong autocorrelation of ongoing activity and the persistence of prestimulus activity on different time scales to influence behavioral performance. Moreover, the present results suggest that the functional state of cortical or thalamocortical networks is a graded function of both the duration and amplitude of their ongoing oscillations (Fanselow et al., 2001).
Attention and 10 Hz oscillations
The success in detecting threshold-level sensory stimuli is critically dependent on attentional resources and on successful maintenance of the neuronal representation of target stimuli in short-term memory. We found that the largest-amplitude prestimulus 10 Hz oscillations over the parietal cortex led to the best performance (Fig. 2B,D), which is in line with recent findings suggesting a role for these oscillations in working memory (Halgren et al., 2002; Jensen et al., 2002) and attention (von Stein et al., 2000; Fanselow et al., 2001; Mima et al., 2001; Yamagishi et al., 2003).
The classical interpretation of 10 Hz oscillations is that of an “idling rhythm” that would allow the networks to respond more readily than from a “cold start” (Salmelin and Hari, 1994). Our data support this notion in that very small prestimulus amplitudes in both sensorimotor and parietal regions indicate a poorer performance compared with intermediate levels of oscillations. The different correlations between performance and the amplitude of prestimulus 10 Hz oscillations over parietal and sensorimotor regions suggest, however, that the functional significance of these oscillations is more complicated than accounted for by the “idling hypothesis.”
Our results raise the possibility that the enhanced efficiency of neuronal processing implicated in attention could partly be achieved by top-down modulation of the strength of the ongoing oscillations to the optimal intermediate levels. In this scheme, the optimal performance with large-amplitude 10 Hz oscillations in the parietal region would reflect attentional effort, whereas the intermediate amplitude in the sensorimotor regions would represent the optimal filter properties of sensorimotor areas to detect the weak incoming stimuli, possibly through a mechanism of intrinsic stochastic resonance (Hô and Destexhe, 2000; Wiest and Nicolelis, 2003).
Footnotes
This work was supported by the Danish Research Agency, the Foundation of Technology (Finland), the Academy of Finland, the Helsinki University Central Hospital Research Funds, and the Juselius Foundation. We thank Titia van Zuijen for discussions and anonymous reviewers for constructive criticism.
Correspondence should be addressed to Dr. Klaus Linkenkaer-Hansen, Netherlands Institute for Brain Research, Meibergdreef 33, 1105 AZ Amsterdam, The Netherlands. E-mail: k.linkenkaer@nih.knaw.nl.
Copyright © 2004 Society for Neuroscience 0270-6474/04/2410186-05$15.00/0
References
- Arieli A, Sterkin A, Grinvald A, Aertsen A (1996) Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science 273: 1868-1871. [DOI] [PubMed] [Google Scholar]
- Chialvo DR, Apkarian AV (1993) Modulated noisy biological dynamics: three examples. J Stat Phys 70: 375-391. [Google Scholar]
- Collins JJ, Imhoff TT, Grigg P (1996) Noise-enhanced tactile sensation. Nature 383: 770. [DOI] [PubMed] [Google Scholar]
- Engel AK, Fries P, Singer W (2001) Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci 2: 704-716. [DOI] [PubMed] [Google Scholar]
- Fanselow EE, Sameshima K, Baccala LA, Nicolelis MAL (2001) Thalamic bursting in rats during different awake behavioural states. Proc Natl Acad Sci USA 98: 15330-15335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P, Neuenschwander S, Engel AK, Goebel R, Singer W (2001) Rapid feature selective neuronal synchronization through correlated latency shifting. Nat Neurosci 4: 194-200. [DOI] [PubMed] [Google Scholar]
- Gong Y, Matthews N, Qian N (2002) Model for stochastic-resonance-type behavior in sensory perception. Phys Rev E Stat Nonlin Soft Matter Phys 65: 031904(1-5). [DOI] [PubMed] [Google Scholar]
- Halgren E, Boujon C, Clarke J, Wang C, Chauvel P (2002) Rapid distributed fronto-parieto-occipital processing stages during working memory in humans. Cereb Cortex 12: 710-728. [DOI] [PubMed] [Google Scholar]
- Hô N, Destexhe A (2000) Synaptic background activity enhances the responsiveness of neocortical pyramidal neurons. J Neurophysiol 84: 1488-1496. [DOI] [PubMed] [Google Scholar]
- Jensen O, Gelfand J, Kounios J, Lisman JE (2002) Oscillations in the alpha band (9-12 Hz) increase with memory load during retention in a short-term memory task. Cereb Cortex 12: 877-882. [DOI] [PubMed] [Google Scholar]
- Kenet T, Bibitchkov D, Tsodyks M, Grinvald A, Arieli A (2003) Spontaneously emerging cortical representations of visual attributes. Nature 425: 954-956. [DOI] [PubMed] [Google Scholar]
- Liang H, Bressler SL, Ding M, Truccolo WA, Nakamura R (2002) Synchronized activity in prefrontal cortex during anticipation of visuomotor processing. NeuroReport 13: 2011-2015. [DOI] [PubMed] [Google Scholar]
- Libet B, Alberts WW, Wright EW, Feinstein B (1967) Responses of human somatosensory cortex to stimuli below threshold for conscious sensation. Science 158: 1597-1600. [DOI] [PubMed] [Google Scholar]
- Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ (2001) Long-range temporal correlations and scaling behavior in human brain oscillations. J Neurosci 21: 1370-1377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linkenkaer-Hansen K, Nikulin VV, Palva JM, Kaila K, Ilmoniemi RJ (2004) Stimulus-induced change in long-range temporal correlations and scaling behavior of sensorimotor oscillations. Eur J Neurosci 19: 203-211. [DOI] [PubMed] [Google Scholar]
- Makeig S, Westerfield M, Jung TP, Enghoff S, Townsend J, Courchesne E, Sejnowski TJ (2002) Dynamic brain sources of visual evoked responses. Science 295: 690-694. [DOI] [PubMed] [Google Scholar]
- Marder E (1998) From biophysics to models of network function. Annu Rev Neurosci 21: 25-45. [DOI] [PubMed] [Google Scholar]
- Mima T, Oluwatimihelin T, Hiraoka T, Hallet M (2001) Transient inter-hemispheric neuronal synchrony correlates with object recognition. J Neurosci 21: 3942-3948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuper C, Pfurtscheller G (2001) Evidence for distinct beta resonance frequencies in human EEG related to specific sensorimotor cortical areas. Clin Neurophysiol 112: 2084-2097. [DOI] [PubMed] [Google Scholar]
- Nikouline VV, Wikström H, Linkenkaer-Hansen K, Kesäniemi M, Ilmoniemi RJ, Huttunen J (2000) Somatosensory evoked magnetic fields: relation to pre-stimulus mu rhythm. Clin Neurophysiol 111: 1227-1233. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Lopes da Silva FH (1999) Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol 110: 1842-1857. [DOI] [PubMed] [Google Scholar]
- Salmelin R, Hari R (1994) Spatiotemporal characteristics of sensorimotor neuromagnetic rhythms related to thumb movement. Neuroscience 60: 537-550. [DOI] [PubMed] [Google Scholar]
- Shu Y, Hasenstaub A, Badoual M, Bal T, McCormick DA (2003) Barrages of synaptic activity control the gain and sensitivity of cortical neurons. J Neurosci 23: 10388-10401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stancák A, Svoboda J, Rachmanová R, Vrána J, Králík J, Tintera J (2003) Desynchronization of cortical rhythms following cutaneous stimulation: effects of stimulus repetition and intensity, and of the size of corpus callosum. Clin Neurophysiol 114: 1936-1947. [DOI] [PubMed] [Google Scholar]
- Stocks NG, Manella R (2001) Generic noise-enhanced coding in neuronal arrays. Phys Rev E Stat Nonlin Soft Matter Phys 64: 030902(1-4). [DOI] [PubMed] [Google Scholar]
- Vanni S, Revonsuo A, Hari R (1997) Modulation of the parieto-occipital α rhythm during object detection. J Neurosci 17: 7141-7147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Stein A, Chiang C, König P (2000) Top-down processing mediated by interareal synchronization. Proc Natl Acad Sci USA 97: 14748-14753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiesenfeld K, Moss F (1995) Stochastic resonance and benefits of noise: from ice ages to crayfish and SQUIDs. Nature 373: 33-36. [DOI] [PubMed] [Google Scholar]
- Wiest MC, Nicolelis MAL (2003) Behavioral detection of tactile stimuli during 7-12 Hz cortical oscillations in rats. Nat Neurosci 6: 913-914. [DOI] [PubMed] [Google Scholar]
- Yamagishi N, Callan DE, Goda N, Anderson SJ, Yoshida Y, Kawato M (2003) Attentional modulation of oscillatory activity in human visual cortex. NeuroImage 20: 98-113. [DOI] [PubMed] [Google Scholar]