On the Initiation and Propagation of Dendritic Spikes in CA1 Pyramidal Neurons

Abstract

Under certain conditions, regenerative voltage spikes can be initiated locally in the dendrites of CA1 pyramidal neurons. These are interesting events that could potentially provide neurons with additional computational abilities. Using whole-cell dendritic recordings from the distal apical trunk and proximal tuft regions and realistic computer modeling, we have determined that highly synchronized and moderately clustered inputs are required for dendritic spike initiation: ∼50 synaptic inputs spread over 100 μm of the apical trunk/tuft need to be activated within 3 msec. Dendritic spikes are characterized by a more depolarized voltage threshold than at the soma [-48 ± 1 mV (n = 30) vs -56 ± 1 mV (n = 7), respectively] and are mainly generated and shaped by dendritic Na⁺ and K⁺ currents. The relative contribution of AMPA and NMDA currents is also important in determining the actual spatiotemporal requirements for dendritic spike initiation. Once initiated, dendritic spikes can easily reach the soma, but their propagation is only moderately strong, so that it can be modulated by physiologically relevant factors such as changes in the V_m and the ionic composition of the extracellular solution. With effective spike propagation, an extremely short-latency neuronal output is produced for greatly reduced input levels. Therefore, dendritic spikes function as efficient detectors of specific input patterns, ensuring that the neuronal response to high levels of input synchrony is a precisely timed action potential output.

Introduction

Information in the brain is encoded through patterns of action potentials that occur in specific sets of neurons at specific times. Action potentials are the result of the integration of thousands of excitatory and inhibitory synapses impinging on the dendritic arborization. Despite being pivotal for signal encoding in cell-to-cell neurotransmission, the general principles and rules that neurons use to transform synaptic inputs into a specific pattern of action potentials are still poorly understood.

In CA1 pyramidal neurons, as in many other neurons, action potentials are usually generated at the soma-axon because this region has the lowest voltage threshold for spike generation (Kandel et al., 1961; Eccles, 1964; Williams and Stuart, 2002). Yet, when many inputs come synchronously to a restricted portion of the dendrites, these same neurons are also fully capable of producing a highly nonlinear form of integration through the generation of dendritically initiated spikes (Cragg and Hamlyn, 1955; Spencer and Kandel, 1961; Turner et al., 1991; Golding and Spruston, 1998; Ariav et al., 2003). Local dendritic spikes have been shown to occur in the hippocampus in vivo, in particular during behavioral states characterized by sharp wave activity (Kamondi et al., 1998), such as awake immobility and slow-wave sleep. These dendritic spikes have been suggested to function as coincidence detectors for the induction of cooperative long-term potentiation and, because of their limited propagation, create clusters of effective synapses in different dendritic domains (Häusser et al., 2000; Golding et al., 2002). This dendritic compartmentalization could theoretically lead to a significant enhancement of the storage capacity of neuronal systems (Poirazi and Mel, 2001), as in the case of CA1 apical terminal branches, that would behave as parallel processing units (Wei et al., 2001).

Despite a potentially important role for dendritically initiated spikes in synaptic integration and neuronal computation, many fundamental issues remain unresolved. We have specifically set out to characterize the basic properties and functional impact of these signals. We found that dendritic spike initiation requires highly coincident and loosely clustered synaptic input and that their generation often leads to short-latency axonal action potential output for relatively low input levels. These data suggest that dendritic voltage spikes and the resultant short-latency output represent the neuronal response to high levels of input synchrony.

Materials and Methods

Four hundred-micrometer-thick slices were prepared from 8- to 12-week-old Sprague Dawley rats as described previously (Magee, 1998), according to methods approved by the Louisiana State University Health Science Center Institutional Animal Care and Use Committee. Rats were given a lethal dose of ketamine and xylazine, perfused through the ascending aorta with an oxygenated solution just before death, and decapitated. Dendrites from CA1 pyramidal cells were visualized using an Axioskop (Zeiss, Oberkochen, Germany) equipped with infrared video microscopy and differential interference contrast (DIC) optics.

The external solution used for recordings contained (in mm) 125 NaCl, 3 KCl, 25 NaHCO₃, 1.25 NaHPO₄, 1.3 CaCl₂, 1 MgCl₂, and 25 glucose and was saturated with 95% O₂ and 5% CO₂ at 33-35°C. These [Ca²⁺]_o and [K⁺]_o were chosen because they are close to those found in the CSF of adult rats (Fisher et al., 1976; Poolos et al., 1987; Jones and Keep, 1988).

Electrophysiological recordings from distal dendrites were performed using BVC-700 amplifiers (Dagan, Minneapolis, MN) in the active “bridge” mode, filtered either at 1 or at 10 kHz and digitized at 50 kHz. Patch pipettes had a resistance of 4-6 MΩ when filled with a solution containing (in mm) 120 K-methylsulphate, 20 KCl, 10 HEPES, 0.5 EGTA, 4 NaCl, 4 MgATP, 0.3 Tris₂GTP, and 14 Na₂phosphocreatine, pH 7.25. For calcium imaging experiments, EGTA was replaced with 4K-bis-fura-2 (100 μm). The distance of the dendritic electrode from the visually identified soma was measured under DIC conditions. All the somata were within 20 μm of the cell body layer.

EPSC-shaped waveforms characterized by AMPA current kinetics (τ_rise, 0.1 msec; τ_decay, 2 msec) (Magee and Cook, 2000; Smith et al., 2003) were injected through the whole-cell electrode. The current amplitude values reported in the text always refer to the peak. Series resistance was below 15 MΩ in the experiments in which only one dendritic electrode was used to inject currents and record the voltage. In most experiments, however, a second dendritic recording pipette (at <20 μm) was used to independently monitor the membrane potential to minimize series resistance artifacts. The results obtained in these two cases were equivalent, and the data were pooled together. The voltage values were not corrected for the junction potential. In a set of experiments to determine the temporal patterns required for the generation of dendritic spikes, the neurons were stimulated using a real-time conductance injection amplifier (SM-1; Cambridge Conductance, Cambridge, UK) (Harsch and Robinson, 2000), in which the reversal potential for AMPA currents was set to 0 mV. The same amplifier was also used to inject a combination of AMPA and NMDA conductances. τ_rise and τ_decay for NMDA currents were set to 1 and 20 msec, respectively, and the voltage dependence of the block by Mg²⁺ was reproduced by the amplifier by multiplying the linear conductance equation by a Boltzmann-type nonlinearity (Harsch and Robinson, 2000) (where K₁ and K₂ were set to 0.3 and 0.06 mV, respectively). The AMPA/NMDA amplitude ratio was 2 (McDermott et al., 2003).

All the simulations were performed with the NEURON simulation program (version 5.5) (Hines and Carnevale, 1997) using its variable time step feature and the ParallelContext class on a 24-processor cluster using the parallel virtual machine system. The model and simulation files are available for public download under the ModelDB section of the Senselab database (http://senselab.med.yale.edu). The realistic model of a hippocampal CA1 pyramidal neuron has been used in previous work (Migliore et al., 2004) and included sodium, delayed rectifier, and A-type potassium currents (I_Na, I_KDR, and I_A, respectively) and a noninactivating, nonspecific cation current (I_h). In general, all conductances were based on the available experimental data for CA1 neurons. Briefly, the I_Na and I_KDR were uniformly distributed, whereas the peak conductances for I_A and I_h were linearly increased with distance from the soma (Hoffman et al., 1997; Magee, 1998) up to 500 μm. Furthermore, after additional specific experimental suggestions for CA1 neurons, the activation curves for I_Na (Gasparini and Magee, 2002) and I_h (Magee, 1998) for dendritic compartments at d μm from the soma were progressively shifted by -8^⋆(d -100)/200 mV, where 100 < d < 300. Excitatory AMPA and NMDA conductances were used to model each synaptic input. The AMPA conductance was implemented using a double-exponential function [the Exp2Syn() built-in function of NEURON], with 0.5 and 1 msec for the rise and decay time, respectively, a reversal potential of 0 mV, and a peak conductance of 0.5 nS [obtained as the conductance value needed to produce a 0.6-0.8 mV unitary EPSP at ∼300 μm (Magee and Cook, 2000)]. With these parameters, 53 synapses were required for spike initiation in the apical trunk/tuft when activated synchronously in the same location. The NMDA conductance was implemented with a custom modification (to adapt the format to the event-driven scheme used in the latest versions of NEURON) of a minimal kinetic scheme, originally based on a NEURON model fitting experimental data (Destexhe et al., 1994). A [Mg²⁺]_o of 1 mm and a reversal potential of 0 mV were assumed. To calculate the spike probability as a function of synaptic spread in space and activation times, 48-60 synapses were distributed in the main apical trunk ∼300 μm from the soma and activated within different time windows, using in both cases a uniform random distribution. A range of spatial (0-200 μm) and temporal (0-5 msec) distribution was explored. A spike probability was obtained from 30 simulations by testing for the presence of a dendritic action potential in a compartment at 300 μm. For any given combination of spatial and temporal range, synaptic locations and activation times in each simulation were chosen according to a random uniform distribution. Local synaptic background activity (high-conductance state) was implemented with the model of a fluctuating point conductance used by Destexhe et al. (2001), with average peak values for the excitatory and inhibitory conductances of 6 ± 6 nS and 29 ± 13 nS, respectively.

A Quantix 57 CCD camera (Roper Scientific, Trenton, NJ) with a 535 × 512 pixel array and single wavelength (380 nm) excitation was used for Ca²⁺ fluorescence imaging experiments. Changes in [Ca²⁺]_i associated with dendritic spikes were quantified by calculating ΔF/F, where F is the fluorescence intensity before stimulation after subtracting autofluorescence, and ΔF is the change in fluorescence during neuronal activity (Lasser-Ross et al., 1991). The autofluorescence of the tissue was measured in a region of equal size adjacent to the dye-filled neuron. The ΔF/F measurements were usually repeated three to six times and averaged. The sequential frame rate was 50-100 Hz, and pixels were binned in a 5 × 5 array.

Data are reported as means ± SEM. Statistical comparisons were performed by using Student's t test. Means were considered to be significantly different when p < 0.05.

Results

To study how synaptic inputs are integrated in CA1 pyramidal neurons in isolation from presynaptic components, we injected EPSC-shaped currents of increasing amplitude through a whole-cell electrode positioned on the distal (>250 μm) apical trunk/tuft. In the example in Figure 1A, we recorded the resulting voltage deflections [injected EPSPs (iEPSPs)] with an electrode <20 μm distant. The responses were typically subthreshold for low current intensities, whereas higher current injections (on average 3.9 ± 0.2 nA; n = 28) elicited a dendritic spike (Fig. 1B,C). As opposed to somatic action potentials, dendritic spikes showed no clear inflection point to easily define the voltage threshold for the regenerative activation of Na⁺ channels (Fig. 1B,D). However, the second temporal derivative of the voltage traces could be successfully used to determine the threshold. Two components could be recognized in these traces: the first peak was attributable to the current injection, whereas the second component was the reflection of the dendritic spike itself and was abolished in the presence of tetrodotoxin (TTX) (data not shown). We found that the inflection point for somatic spikes corresponds to the voltage value at which the second peak reaches 20% of its maximal value, so we used the same value to operationally define the voltage threshold for dendritic spikes (Fig. 1D). When measuring the voltage threshold in this way for both locations, we found that it was more depolarized for dendritic than for somatic spikes [-48 ± 1 mV (n = 30) vs -56 ± 1 mV (n = 7), respectively] (Fig. 1E). It is worth noting that the threshold for dendritic spike initiation appeared to be inversely correlated with the rate of membrane depolarization (dV/dt) preceding the spike itself (Fig. 1F). This relationship can be explained by the fact that different rates of membrane depolarization differentially affect the balance between the inward and outward currents required for spike initiation in the dendrites, as has been also shown for somatic action potentials (Azouz and Gray, 2000).

Figure 1.

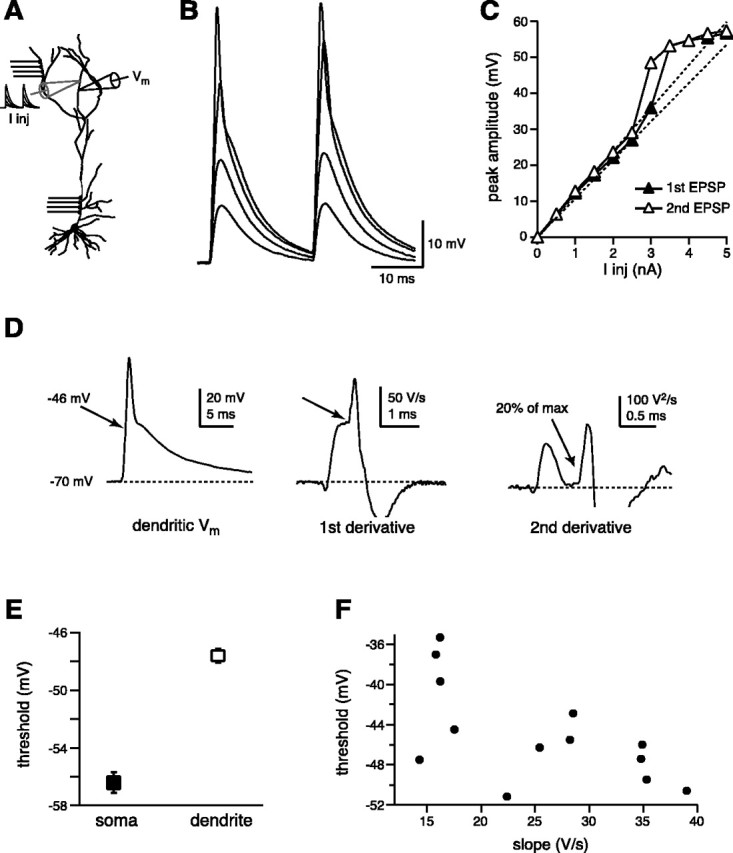
High-intensity, EPSC-shaped currents evoke dendritic spikes. A, Experimental configuration. EPSC-shaped currents of increasing intensity were injected into distal (>250 μm) dendrites of pyramidal CA1 neurons through a whole-cell electrode, and the voltage was recorded with another electrode placed 20 μm distant. B, The voltage responses were typically linear for lower current intensities, whereas the generation of a dendritic spike resulted in a nonlinear EPSP peak amplitude versus current (I-V) plot for higher current injections (C). D, The voltage threshold for dendritic spikes was defined as the voltage at which the second peak of the second temporal derivative reaches 20% of its maximal value. E, The voltage threshold for dendritic spikes, calculated at 294 ± 6 μm, was higher (-48 ± 1 mV; n = 30) than for somatic spikes (-56 ± 1 mV; n = 7). F, The voltage threshold for dendritic spikes was inversely correlated to the rate of membrane depolarization (dV/dt) preceding the spike.

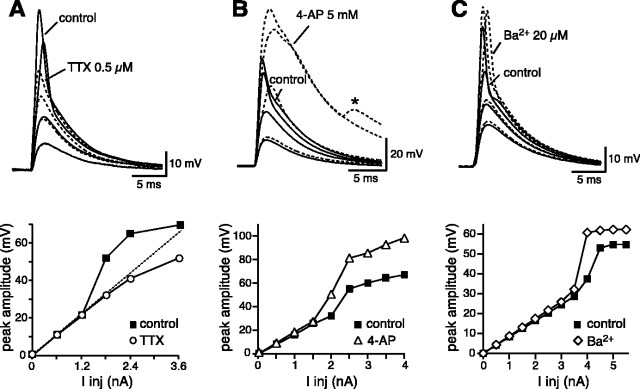
Local dendritic spikes were mediated by transient Na⁺ currents because the perfusion of TTX (0.5 μm) completely abolished the supralinearity associated with the action potentials and the current-voltage relationship actually became sublinear for high current intensities (Fig. 2A). The sublinearity was abolished by the subsequent addition of 4-aminopyridine (4-AP) (5 mm) to the bath (data not shown) (Cash and Yuste, 1999), implying that it was attributable to the activation of A-type K⁺ currents at more depolarized potentials. Transient K⁺ channels were also found to be important determinants of dendritic spikes. 4-AP (5 mm) shifted the EPSP peak amplitude versus current (I-V) plots to the left, so that a lower current intensity was required for the generation of a local spike (Fig. 2B). 4-AP also increased the amplitude of dendritic spikes (from 67 ± 1 to 93 ± 3 mV; p < 0.0001; n = 8) and decreased their voltage threshold (from -45 ± 1 to -52 ± 1 mV; p < 0.0001; n = 8). We also found that Ba²⁺, at a concentration that selectively blocks inward rectifier K⁺ channels (20 μm), shifted the I-V plots to the left and increased the amplitude of dendritic spikes (from 57 ± 2 to 61 ± 3 mV; p < 0.02; n = 8) (Fig. 2C). In this case, however, the voltage threshold was not affected (from -48 ± 1 mV in control conditions to -48 ± 1 mV in the presence of Ba²⁺; p > 0.2; n = 8). We next examined the possible involvement of Ca²⁺ channel activation on dendritic spikes by analyzing the effect of Ni²⁺ (200 μm) on different spike parameters (Magee and Carruth, 1999). We found that Ni²⁺ did not significantly affect the spike voltage threshold [-48 ± 1 mV in control conditions (n = 30) vs 47 ± 1 mV in the presence of Ni²⁺ (n = 7); p > 0.05], or the spike amplitude (65 ± 2 vs 68 ± 1 mV; p > 0.1), or the half-width (2.5 ± 0.2 vs 2.8 ± 0.2 msec; p > 0.2). These data fit well with previous reports that A-type K⁺ channels, densely expressed in the distal regions of CA1 pyramidal neurons, limit the regenerative activation of dendritic Ca²⁺ channels (Magee and Carruth, 1999). This primarily Na⁺ channel-mediated dendritic spike is different from that found in the apical tufts of CA1 pyramidal neurons in slice cultures in which a Ca²⁺ channel-dependent spiking mechanism has been reported (Wei et al., 2001). This difference could be the result of either the more prolonged form of input used in that study or to the differences in the preparation. The lack of a large Ca²⁺ spike component makes these spikes also different from the distal dendritic spikes of layer V cortical pyramidal neurons, which are thought to have only a limited amount of transient outward current (Schiller et al., 1997; Bekkers, 2000; Larkum et al., 2001; Williams and Stuart, 2002).

Figure 2.

Active currents involved in generating and shaping dendritic spikes. A, TTX (0.5 μm) blocked the generation of local dendritic spikes and eliminated the supralinearity in the I-V plot, which actually became sublinear for high current intensities. B, 4-AP (5 mm) lowered the current threshold for the generation of dendritic spikes and increased their amplitude. 4-AP also increased the amplitude of dendritic spikes (from 67 ± 1 to 93 ± 3 mV; p < 0.0001; n = 8) and decreased their voltage threshold (from -45 ± 1 to -52 ± 1 mV; p < 0.0001; n = 8). For higher current intensities, back-propagating spikes (asterisk) could be recorded. C, Ba²⁺ (20 μm) increased the amplitude of dendritic spikes and decreased the current threshold for their generation, but the voltage threshold was not affected (from -48 ± 1 mV in control conditions to -48 ± 1 mV in the presence of Ba²⁺; p > 0.2; n = 8).

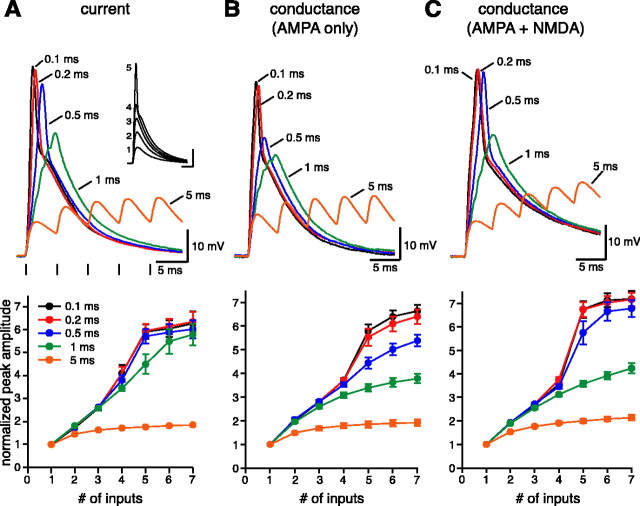
The experiments presented until now show that a great amount of current (usually ≥3 nA) is required to evoke dendritic spikes, meaning that a large number of synapses have to be activated synchronously. We therefore decided to examine the temporal requirements for the generation of dendritic spikes (i.e., what is the maximum interval of time over which the inputs can be spread and still be able to generate a dendritic action potential). For this purpose, after finding the threshold current for the generation of a dendritic spike, we divided it by 5 and injected seven of these “unitary inputs” asynchronously, at different intervals between 0.1 and 5 msec (Fig. 3A). In these conditions, a dendritic spike could be generated only when the intervals between the inputs were ≤0.5 msec (meaning that the five inputs were actually spread over ∼2 msec). For 1 msec intervals, the response tended to increase almost linearly with the number of the inputs, whereas for 5 msec intervals the summation of the unitary inputs was clearly sublinear. It is worth noting that the voltage threshold for dendritic spike initiation was inversely correlated with synaptic input synchronization (-49 ± 1 mV for the 0.1 msec interpulse interval, -45 ± 1 mV for the 0.2 msec interval, and -41 ± 2 mV for the 0.5 msec interval; n = 5), confirming the predictions from cortical neurons (Azouz and Gray, 2000).

Figure 3.

Temporal requirements for dendritic spike generation. A, For every neuron, the current required to initiate a dendritic spike was measured for a completely synchronous input (inset calibration: 10 mV, 5 msec). This level was divided in five unitary inputs that were then injected with increasing intervals from 0.1 to 5 msec. For example, in this CA1 neuron, the threshold current was 4.0 nA, and it was divided into five inputs of 0.8 nA each. With the asynchronous inputs, a dendritic spike could be evoked only for intervals ≤0.5 msec, because it appears also in the average plot. B, Dendritic spikes were evoked only for intervals ≤0.2 msec in dynamic-clamp configuration, when conductances with the characteristics of only AMPA receptors were generated. C, When AMPA and NMDA conductances were coinjected (AMPA/NMDA, 2:1), the time window for dendritic spike generation broadened to 0.5 msec. In the three average plots, the peak amplitudes were normalized to the amplitude of the elementary input for each experiment [9.3 ± 0.3 mV (n = 7) in A, 8.5 ± 0.6 mV (n = 12) in B, and 8.2 ± 1.2 (n = 8) in C].

The fact that the driving force for AMPA currents changes with the membrane potential could play a fundamental role and affect the temporal integration of the inputs, so we repeated the same experiment in dynamic-clamp configuration, generating conductances instead of injecting currents. In this case, the temporal window for spike generation was narrower, because the input summation at the 0.5 msec interval remained subthreshold and was clearly sublinear for 1 msec intervals (Fig. 3B). We then extended our analysis by considering the contribution of NMDA receptors to the temporal pattern required for dendritic spike generation, because their negative slope conductance has been hypothesized to be capable of counteracting the shunting effect of AMPA conductances (Cook and Johnston, 1999). The addition of NMDA conductances (AMPA/NMDA amplitude, 2:1) broadened the temporal requirements for spike generation, so that five inputs were again able to generate a spike when injected at 0.5 msec intervals (Fig. 3C), but it did not seem to affect the sublinear responses (1 and 5 msec intervals), probably because of the negligible activation of NMDA currents at hyperpolarized potentials. Thus, the additional voltage-dependent current provided by the NMDA conductance acts to replace the AMPA current lost as the driving force decreases during the depolarization, allowing the synaptic conductance to act as a constant current source. Interestingly, the input-output relationships for the supralinear responses (up to 0.5 msec intervals) were somewhat sigmoidal in shape, approximating the subunit functions recently used in a computational model of dendritic spiking in CA1 pyramidal neurons (Poirazi et al., 2003).

We next examined the spatial requirements for dendritic spike generation. For this purpose, we performed a set of experiments using two electrodes placed at different distances on the main apical trunk and measured the current threshold required to generate a dendritic spike when injected either through one or through both electrodes (Fig. 4A). In the example in Figure 4, in which the distance between the two electrodes was 85 μm, we found that a 4 nA current injection was required to elicit a local spike in the case of one electrode (data not shown). When the same amount of current was divided between the two electrodes, there was no regenerative response, and we had to increase the current intensity to 3 nA in each electrode to evoke a local spike in both locations (Fig. 4 A). The pooled data from n = 7 neurons show that the relative current threshold increased with the distance between the two electrodes, so that 30-50% more input current was required with ∼100 μm electrode separation (Fig. 4 B).

Figure 4.

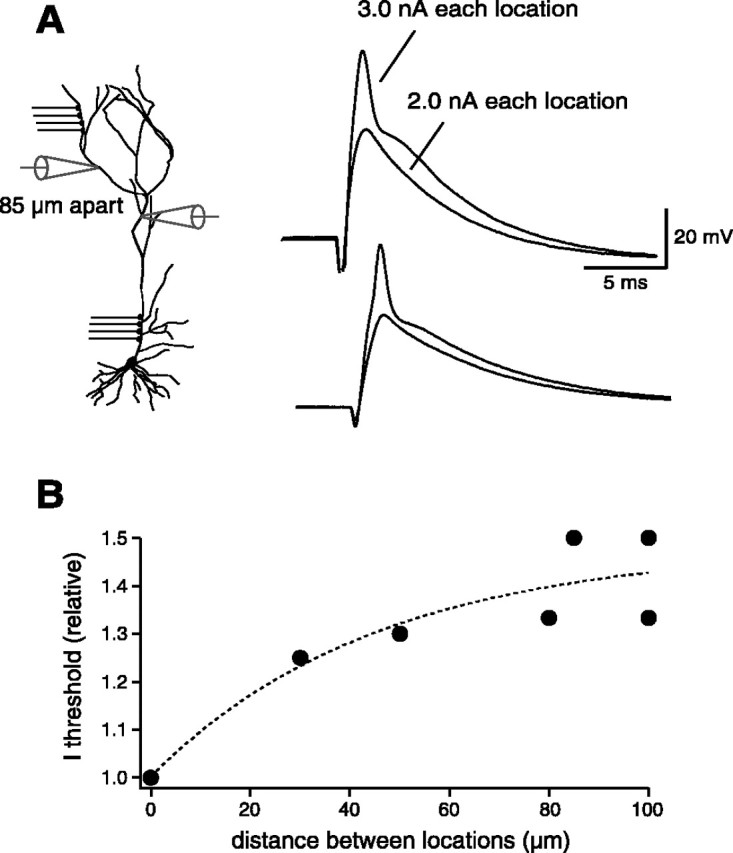
Spatial requirements for dendritic spike generation. A, Experimental configuration. Two dendritic electrodes placed at different distances (85 μm in this case) were used to inject EPSC-shaped currents and measure the current threshold to generate a dendritic spike when the current was injected through either one or both of the electrodes together. In this neuron, the current threshold was 4.0 nA for one electrode, whereas 3.0 nA had to be injected simultaneously in both of the electrodes to initiate a dendritic action potential (the total current threshold in this case was 6.0 nA). The relative current threshold was thus 1.5 times higher than in the case of the injection through one single electrode. B, Plot of the current threshold required for a dendritic spike when injected through two electrodes (normalized to the “single” current threshold) as a function of the distance between the two electrodes.

We were then interested to study the spatiotemporal requirements for dendritic spike generation in the case of dispersed synaptic inputs, a condition that most likely will occur in vivo. Because this cannot yet be achieved experimentally, we used a realistic computer model of a CA1 pyramidal neuron. To reproduce the main experimental findings on colocalized inputs (Fig. 3), five inputs in a compartment at ∼300 μm from the soma were activated at different constant intervals using current injections (Fig. 5A, left) or synaptic conductances with AMPA-only (Fig. 5A, middle) or AMPA plus NMDA (Fig. 5A, right) components. In agreement with the experiments, the model showed that colocalized synaptic inputs activated at a >1 msec interval fail to elicit a dendritic spike, that this limit is somewhat reduced (∼0.5 msec) when using AMPA-only conductances, and that the addition of an NMDA component gave results that were closer to current injections (Fig. 5A,B). We then used the model to study the effects of more heterogeneous spatiotemporal distributions of 48-60 dispersed synapses on dendritic spike generation. This range of synapses approximates the range that can be estimated from the EPSC-shaped current injections (Fig. 1). Here the total amount of current required to initiate dendritic spikes (3000-4000 pA) can be divided by the amount of current required to produce a unitary EPSP of 0.8 mV amplitude (∼60 pA unitary) to give a range of 50-66 synapses. For any given tested combination of spread in timing and space, a spike probability was obtained from 30 simulations, randomly redistributing in each simulation synaptic locations and activation times (see Materials and Methods). The results shown in the contour plots (Fig. 5C) demonstrate that there is an optimal range of temporal and spatial distributions for which the spike probability is higher. In particular, more synchronous inputs resulted in a high spike probability for a broad spatial distribution (Fig. 5C) (timing distribution, <1.6 msec). However, because synapses were activated within a larger time window (Fig. 5C) (timing distribution, >1.6 msec), a certain degree of spatial spreading (∼60 μm in our case) was more efficient than highly localized inputs in generating a dendritic spike. This effect is caused by the shunting effect of AMPA conductances and could be eliminated by the addition of the NMDA conductances (see also Fig. 3). The general conclusion from these simulations is that highly coincident (all the inputs must come in a <3 msec window) and fairly clustered (<100 μm) inputs are required for dendritic spike generation. The imposition of high-conductance state conditions (see Materials and Methods) did not affect the spike probability at near threshold input patterns (Fig. 5D). This suggests that if such a state were to occur in hippocampal CA1 pyramidal neurons, it would not significantly change the spatiotemporal requirements for dendritic spike initiation. We also extended our analysis to examine the impact of the number of synaptic inputs on the spike probability. Figure 5E shows the maximal time window during which the inputs can be spread over a distance of 50 μm (left) or 100 μm (right) as a function of the number of activated synapses, in the case of AMPA-only or AMPA plus NMDA conductances.

Figure 5.

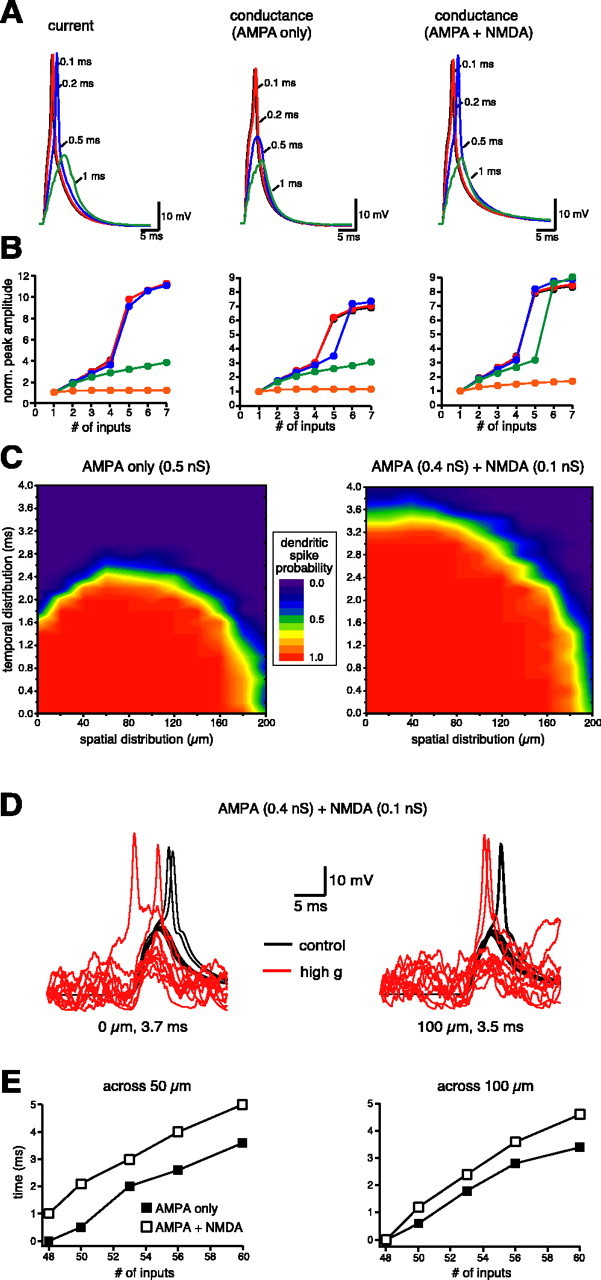
Effects of realistic spatial and temporal patterns on dendritic spike initiation. A, A multicompartment model qualitatively reproduces the experimental findings on the temporal patterns required for dendritic spike initiation in the case of five inputs (compare Fig. 3). The same temporal patterns were used to model current-clamp (left; unitary peak current, 0.23 nA) and dynamic-clamp (middle; unitary peak conductance, 5.2 nS) conditions for the case of AMPA-only or AMPA plus NMDA (right; unitary peak conductances for AMPA and NMDA of 4 and 1 nS, respectively) conductances. B, I-V plots of the EPSP spike amplitude, normalized to the amplitude of the elementary input, as a function of the number of inputs for current injections (left), AMPA-only conductances (middle), and AMPA plus NMDA conductances (right). C, Contour plots of the spike probability (calculated from 30 simulations) as a function of the spatial and temporal distribution for 53 AMPA-only (left) and for AMPA plus NMDA (ratio, 4:1; right) synapses (the minimal number needed to reach threshold in the case of AMPA-only conductances activated synchronously in the same location). D, Imposition of high-conductance conditions (see Materials and Methods) does not affect spike probability for input patterns near threshold [53 synapses given at the same location within 3.7 msec (left) or over 100 μm distance within 3.5 msec (right)]. In all cases (black, control; red, high conductance), dendritic spikes are initiated 2 of 10 times. E, Plot of the maximal time over which the synaptic inputs can be distributed as a function of the number of activated inputs over a spatial distribution of 50 μm (left) or 100 μm (right).

We then investigated the extent of propagation experienced by dendritic spikes. There are three functionally relevant variations. First, the propagation can be highly limited so that the impact of the spike is localized to a small region of the arbor (Schiller et al., 1997, 2000; Golding and Spruston, 1998; Wei et al., 2001). Second, the spike may propagate very effectively to the soma, where it then initiates an axonal action potential output with very high probability (Chen et al., 1997; Martina et al., 2000; Larkum et al., 2001; Williams and Stuart, 2002). Finally, there can be some propagation mode in between these two extremes, in which forward-propagation is weakly regenerative so that the effective invasion of the soma/axon region by the dendritic spike is easily modulated (Larkum et al., 2001).

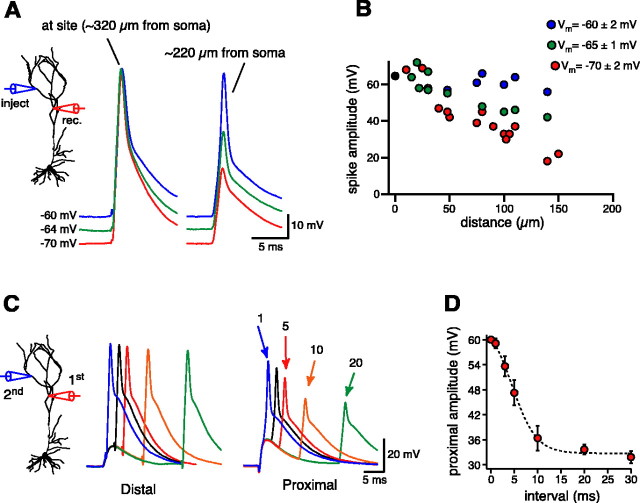
To examine how dendritically initiated spikes propagate to the soma in CA1 pyramidal neurons, we elicited them with one electrode and recorded the amplitude of the propagated signal with a second pipette located at different distances proximal to the first one (Fig. 6A). With V_m near rest (approximately -66 mV), dendritic spikes showed a limited amount of attenuation with distance, such that the amplitude recorded 100 μm proximal was approximately two-thirds of the initial amplitude (∼40 mV) (Fig. 6A,B). The propagation distance, however, was not a static feature of these regenerative events, because changes in the V_m could effectively alter the amplitude of the propagated spike. When the membrane potential was relatively hyperpolarized (approximately -70 mV), the spike amplitude began decreasing ∼20 μm from the site of injection so that it was less than half (∼30 mV) at 100 μm. In contrast, at a significantly depolarized V_m (approximately -60 mV), there was very little reduction in spike amplitude even up to 150 μm proximal to the initiation site (Fig. 6A,B). In addition to steady-state changes in the V_m, transient depolarizations, as might be expected for large EPSPs or other failed dendritic spikes, could also very effectively “boost” forward-spike propagation (Fig. 6C). The obvious difference with these voltage signals was a time dependence imposed by the time course of the transient depolarization, so that spike propagation was facilitated only up to 5 msec after the EPSP generation (Fig. 6C,D). Thus, in a situation that is reminiscent of the boosting of back-propagating action potentials, the effectiveness of forward-spike propagation could be modulated both by changes in “resting” V_m and by transient depolarization (Magee and Johnston, 1997; Bernard and Johnston, 2003).

Figure 6.

Dendritic spike propagation depends on the V_m and interactions with transient depolarizations. A, A dendritic spike was evoked by injecting EPSC-shaped currents in one electrode, and the amplitude of the propagated signal was measured at different distances (100 μm in this case). As seen in the individual traces, the extent of propagation was highly dependent on the V_m, with depolarization to approximately -60 mV removing almost all the decrement. B, Pooled data of the propagated spike amplitude as a function of the distance between the two electrodes. Near rest (-65 ± 1 mV; green circles), the amplitude was ∼40 mV at 150 μm from the initiation site, and it was decreased by hyperpolarization (red circles) and increased by depolarization (blue circles). C, A subthreshold EPSP-like depolarization was evoked with a proximal dendritic electrode (∼175 μm from the soma), whereas a dendritic spike was initiated at a more distal recording site by a second electrode (∼275 μm from the soma) with different time intervals between the current injections (0-30 msec). It can be seen from the individual traces and from the pooled data (D; distance between pipettes ranged from 80 to 140 μm; n = 4) that the transient depolarization was highly effective in boosting the propagating spike when the two events were closely timed. The amount of spike amplitude boosting followed the temporal profile of the subthreshold transient depolarization. This indicates that propagating dendritic spikes and other transient dendritic depolarizations, similar to large EPSPs or other failed dendritic spikes, could interact in a complicated manner.

In our experiments, we have observed a more robust forward-propagation of dendritic spikes than previously reported for CA1 neurons (Golding and Spruston, 1998; Magee, 1999; Golding et al., 2002). A possible explanation for this could be that in our latest recordings we used a different external solution with a 3.0 mm [KCl] and 1.3 mm [CaCl₂] (physiological solution). To test this hypothesis, we compared dendritic spike propagation (using the spike-associated Ca²⁺ influx as a measure of propagation) in the physiological solution with that in one with 2.5 mm [KCl] and 2.0 mm [CaCl₂] (low-K⁺ solution). Figure 7 shows typical examples of optical recordings obtained for different neurons in the two solutions. The average data in Figure 7D clearly show that in the physiological solution the Ca²⁺ influx decreased only slightly in the first 100 μm, whereas in the low-K⁺ solution the Ca²⁺ signal decreased substantially in the first 20-40 μm. We also found that dendritic spike initiation was depressed by switching to the low-K⁺ solution, as shown in Figure 7E. The average data in Figure 7F show that in the presence of 3.0 mm [KCl] and 1.3 mm [CaCl₂], the I-V plots for the first and the second iEPSPs were shifted to the left, meaning that lower current intensities were required to evoke a dendritic action potential in these conditions. These data confirm that both spike initiation and propagation are enhanced in the more physiological external solution. A conservative explanation for these results is that the decrease in the extracellular charge screening (∼5 mV) (Hille, 2001) and the slight depolarization associated with the 3.0 mm [KCl] and 1.3 mm [CaCl₂] solution affect the activation of voltage-gated ion channels involved in the initiation of dendritic spikes.

Figure 7.

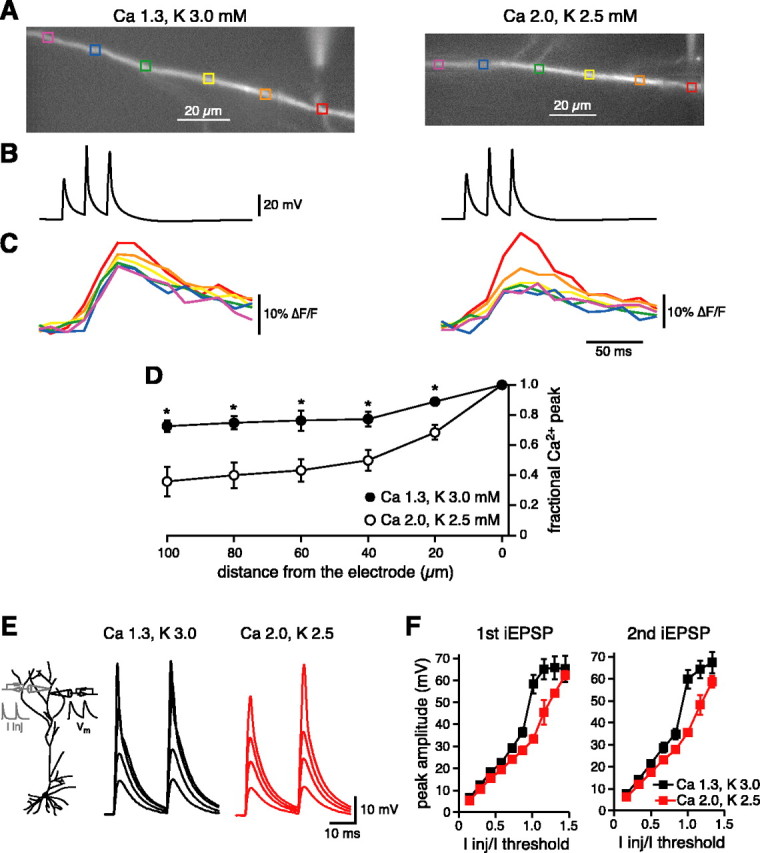
Changes in extracellular K⁺ and Ca²⁺ decrease initiation and propagation of dendritic spikes. A, Images of bis-fura-2-filled dendrites from two different CA1 pyramidal neurons in solutions containing 3.0 mm [KCl] and 1.3 mm [CaCl₂] (physiological solution; left) or 2.5 mm [KCl] and 2.0 mm [CaCl₂] (low-K⁺ solution; right). The tip of the electrode was approximately in the area delimited by the red box in A [at a distance of 320 μm (left) and 280 μm (right) from the soma]. B, Voltage responses to a 50 Hz train of EPSC-shaped currents. The stimulation intensities were 3 nA (left) and 2.5 nA (right). C, Optical recordings showing the ΔF/F associated with the dendritic spikes shown in B (average of 5 traces). D, Average data of the normalized Ca²⁺ influx associated with local dendritic spikes as a function of the distance from the recording electrode in the two different solutions (^*p < 0.01). Although in the physiological solution the Ca²⁺ influx decreased only by 27 ± 4% (n = 11) at 100 μm, in the low-K⁺ solution, the decrease was 64 ± 1% (n = 7). E, Raising [Ca²⁺]_o from 1.3 to 2.0 mm and decreasing [K⁺]_o from 3.0 to 2.5 mm depressed dendritic excitability. The membrane potential hyperpolarized (from -67 ± 1 to 69 ± 1 mV; p < 0.01; n = 16), the input resistance at steady state decreased (from 39 ± 3 to 34 ± 2 MΩ; p < 0.01; n = 16), and the temporal summation, measured as the ratio between the fifth and the first EPSP (for a 1.5 nA injection at 50 Hz), decreased (from 12 ± 3 to 7 ± 3%; p < 0.02; n = 8). Dendritic spike initiation was also reduced by the shift from the new solution to the old one because more current was required to evoke them. Also, the voltage threshold for dendritic spike initiation was more depolarized (from -44 ± 1 to 49 ± 1 mV; p < 0.002; n = 7). F, The mean current-voltage relationship for the first and the second iEPSPs is shifted to the right in the 2.0 mm Ca and 2.5 mm K solution. The current values are normalized to the current threshold necessary to evoke a dendritic spike in the physiological solution.

The final issue we wanted to investigate was the impact of dendritically initiated spikes on the somatic voltage. For this purpose, we elicited spikes with one dendritic electrode and recorded the propagated signal with a second pipette located at the soma (Fig. 8A). In most neurons (10 of 12), the initiation of a dendritic spike at potentials close to the resting V_m (-65 ± 1 mV) resulted in an axonal action potential output with a short latency (<2 msec from the start of current injection) at a threshold potential that appeared to be more hyperpolarized than normal (but see below) (Fig. 8B, C). In all neurons, ∼5 mV of hyperpolarization (to -71 ± 1 mV) inhibited forward-spike propagation to such a degree that the only obvious reflection of the dendritic spike at the soma was a sharp increase in the initial rate of rise of the somatic EPSP (Fig. 8C). The effect of V_m on spike propagation can also be appreciated in current-voltage plots of somatic responses for dendritic current injections ranging from subthreshold to suprathreshold levels (at the dendritic site) (Fig. 8D). In these recordings, the somatic depolarization profile was dependent on V_m and voltage-gated ion channel availability. In all cases, the somatic depolarization increased in a linear manner for current injections ≤2 nA. Larger injections produced a profound supralinearity when the membrane was held near a resting V_m (-65 ± 2 mV; n = 5) while a distinct sublinear profile was observed at more a hyperpolarized V_m (-71 ± 1 mV; n = 7). This sublinearity was even more pronounced in the presence of TTX (0.5 μm) (Fig. 8D). From the I-V plots, we can conclude that under favorable propagation conditions (relatively proximal initiation site, depolarized V_m or K⁺ channel blockade), the initiation of a dendritic spike produces a short-latency action potential output at significantly lower input levels (∼3.0 vs >5.0 nA) than when an evoked dendritic spike does not effectively propagate to the soma (hyperpolarized V_m).

Figure 8.

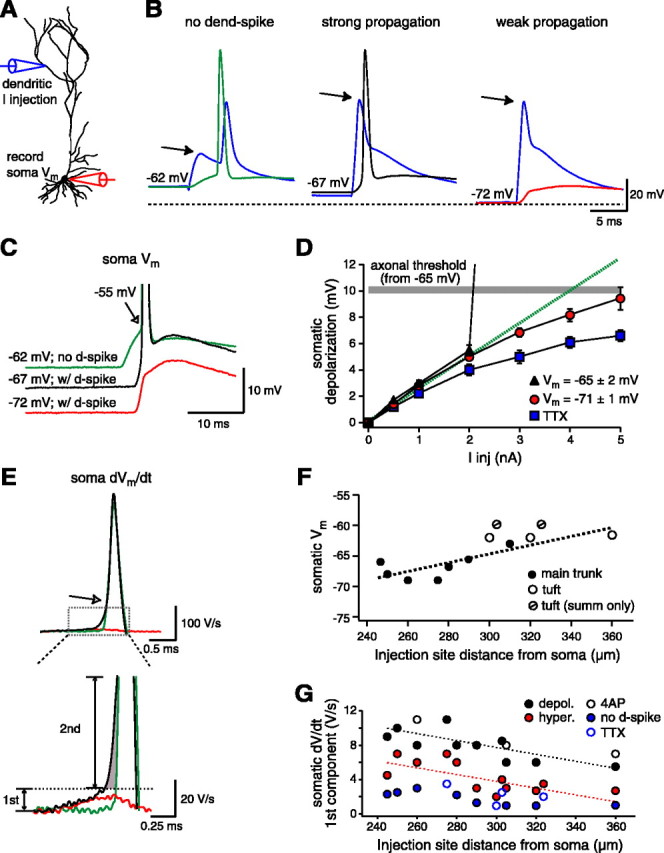
The somatic impact of dendritically initiated spikes. A, Experimental configuration. A dendritic electrode (blue traces) located 285 μm from the soma was used to inject current and record voltage, while the response at the soma was recorded with a second electrode. B, Effect of the V_m on signal propagation to the soma. Left, The injection of relatively small amounts of EPSC-shaped current (2 nA) does not evoke a dendritic spike but travels to the soma, where it provides enough slow depolarization to initiate a somatic action potential at this more depolarized V_m (-62 mV; green trace from the soma). The spike recorded in the dendritic trace is back-propagating. Middle, Larger current injections (4 nA) lead to the initiation of a dendritic spike and the subsequent generation of a short-latency somatic action potential at the normal V_m (-67 mV; black trace from the soma). Right, At hyperpolarized potentials (-72 mV; red trace from the soma), a dendritic spike is initiated by the large current injection (4 nA), but it is unable to propagate to the soma effectively enough to evoke an action potential output. C, Superimposition of the somatic recordings from B. Notice the apparently lower threshold for the spike evoked at -67 mV and the fast iEPSP rise time with the V_m at -72 mV. D, I-V plot of the depolarization recorded at the soma after dendritic current injections at the normal V_m (black triangles; n = 5), at hyperpolarized potentials (red circles; n = 7), and in the presence of TTX (blue squares; n = 4). The gray line shows the action potential threshold for slow somatic depolarizations without dendritic spikes with respect to the average V_m (-65 ± 1 mV; n = 5). E, First derivative (dV/dt) of the traces in C. The enlargement (bottom) shows the initial ramp component that is only present when a dendritic spike is evoked (black and red traces). The plot shows that this initial ramp can be further broken into two separate components: one that is larger and present only when propagation is strong enough to evoke action potential output (labeled second; black trace; shaded region), and another that is present regardless of a somatic spike (labeled first; black and red traces). F, Plot of the most hyperpolarized V_m at which a dendritic spike could still evoke a short-latency somatic output (<2 msec). Short-latency action potential output could not be evoked in two neurons when dendritic current injection initiated a spike in the apical tuft region. In these cells, action potential threshold at the soma was reached at the peak of the iEPSP (∼7 msec) and was therefore considered to be the result of summation (summ only) and not the direct result of the strong propagation of the dendritic spike. G, The amplitude of the first component of the initial dV/dt ramp depends on the distance of the injection site from the soma and other factors influencing spike propagation. The second component of the initial dV/dt ramp exhibited a similar location dependence (data not shown).

In addition to this dependence on the V_m, dendritic spike propagation also appeared to vary as a function of the distance of the initiation site from the soma. This was observed in two ways. First, the degree of hyperpolarization that would allow a propagation strong enough to produce a short-latency action potential output at the soma decreased with distance, so that the farther away dendritic spike generation occurred, the less the V_m could be hyperpolarized. In fact, a small amount of depolarization (∼3 mV) was required in two neurons in which the spike was initiated >300 μm away from the soma and, perhaps more importantly, at input sites in the apical tuft region (Fig. 8F). Second, the profile of the rate of rise of the V_m (dV/dt) during the somatic action potential was different if it followed a dendritic spike. When the somatic action potential was produced by the slow depolarization of the soma, the dV/dt showed a single large (345 ± 30 V/sec; n = 10) component (Fig. 8E, green traces) that is thought to reflect the robust invasion of the soma by an axonal action potential (Colbert and Johnston, 1996) (Fig. 8E). If, on the other hand, the somatic action potential followed a dendritic spike, a similarly large (330 ± 20 V/sec; n = 10) dV/dt profile was preceded by a slower initial ramp component (Fig. 8E, black trace). This initial slower component appears to reflect the strength of forward-spike propagation, in that it increased under conditions that improved propagation (depolarized V_m and 4-AP) (Fig. 8G) and decreased when this was weaker (hyperpolarized V_m and TTX) (Fig. 8G). The amplitude of this initial ramp component was also dependent on the initiation site so that the farther away the soma, the lower the rate of rise (Fig. 8G). Also, because of this initial component, the somatic/axonal action potentials appeared to be generated at more hyperpolarized potentials when they followed a dendritic spike (Fig. 8B,C). However, because the transition to the large “axonal” component occurred at almost exactly the same potential in both cases (approximately -55 mV), we can conclude that the output threshold voltage was not lowered by dendritic spike initiation. Thus, dendritic spike propagation in CA1 pyramidal neurons seems to be at once strong enough to easily reach the voltage threshold for axonal action potential output, all the while remaining weak enough to be sensitive to both morphological and physiological conditions.

Discussion

Summary

We have examined the basic properties and functional impact of dendritic spikes initiated in the distal apical trunk and proximal tuft regions of hippocampal CA1 pyramidal neurons, finding that: (1) the dendritic spike threshold is ∼10 mV more depolarized than at the soma; (2) dendritic Na⁺ and K⁺ channels play a role in setting the threshold and determining the shape and forward-propagation of dendritic spikes; (3) highly synchronized inputs (∼50 synapses activated within 3 msec) are required for spike initiation; (4) a moderate level of spatial clustering (all inputs arriving in ≤100 μm of the dendrite) promotes spike initiation; (5) NMDA receptors enhance spike initiation by counteracting the shunting of AMPA synaptic conductances; (6) forward-propagation of these spikes is only moderate, allowing for modulation by physiologically relevant parameters such as V_m and external ion concentration; and (7) when forward-propagation is robust, the mode of dendritic integration is significantly changed such that a short-latency action potential output is produced for lower levels of synaptic input. These data indicate that interactions between dendrite morphology, active membrane properties, and synaptic characteristics allow CA1 pyramidal neurons to respond preferentially to synchronous input with a large dendritic spike and associated Ca²⁺ influx and the generation of well-timed action potential output.

Our recordings here are limited to the distal apical trunk and proximal tuft dendritic regions. Other regions, such as basal dendrites and perhaps radial oblique branches, have also been suggested to generate local dendritic spikes (Ariav et al., 2003; Polsky et al., 2004). Given the paucity of data concerning their active and synaptic properties, it is possible that the spiking mechanisms in the radial oblique and basal dendrites are different from what we report here. However, a recent report demonstrated that basal dendritic spikes in CA1 pyramidal neurons are also primarily mediated by voltage-gated Na⁺ channels (Ariav et al., 2003) and therefore may be similar to those investigated here.

Dendritic spike initiation

We found that the voltage threshold for dendritic spike generation is almost 10 mV higher than at the soma for the most synchronous current injections. This observation confirms the widely accepted idea that the threshold for spike generation is higher in the dendrites than at the soma (Kandel et al., 1961; Eccles, 1964). This location dependence can be attributed to the different properties of the ionic channels along the somatodendritic axis. One channel population that certainly plays an important role in dendritic spiking is Na⁺ channels, because their blockade completely eliminated the spikes. The lower axonal threshold in pyramidal neurons has been attributed to an as yet unsubstantiated higher axonal channel density as well as to a hyperpolarized shift in the activation range of axonal Na⁺ channels (Colbert and Johnston, 1996; Häusser et al., 2000; Colbert and Pan, 2002). A shift in the Na⁺ channel activation curve is, however, not the critical factor in setting the dendritic spike threshold, because distal dendritic Na⁺ channels have an activation range shifted to the left compared with proximal locations (Gasparini and Magee, 2002). Instead, the key factor seems to be the distance-dependent increase in the expression of A-type K⁺ channels in CA1 pyramidal dendrites (Hoffman et al., 1997). Accordingly, we have shown that a significant block of I_A by 4-AP substantially lowered the voltage threshold for dendritic spikes. Inward rectifier K⁺ channels appear to contribute to the input resistance and thus to setting the number of inputs that are needed to elicit a dendritic action potential, but they do not affect the voltage threshold. Because dendritic Na⁺ and K⁺ channels are affected by neuromodulation and plasticity (Colbert and Johnston, 1998; Hoffman and Johnston, 1998; Gasparini and Magee, 2002; Frick et al., 2004), the initiation of dendritic spikes is likely to be modulated in a similar manner. We also found that under control conditions, there is only a minimal role for voltage-gated Ca²⁺ channels in shaping the local dendritic spikes, although these channels are activated during these large depolarizations (Fig. 7).

Because of their relatively high threshold of activation, dendritic spikes are generated only after a substantial, rapid dendritic depolarization (∼20 mV within <1 msec). To achieve this, a large amount of synaptic input (∼50 synapses) must arrive onto a fairly restricted region (<100 μm) of the apical dendrite within a short window of time (∼3 msec) (Magee and Cook, 2000). There is some relationship between the temporal and spatial requirements, so that the more inputs are clustered, the more they can be separated in time and vice versa (Fig. 5). We found that the maximal interval over which the inputs can be spread was narrower when AMPA-like synaptic conductances were injected instead of currents but that the addition of a voltage-dependent NMDA component broadened this interval so that it was comparable with that found in current-clamp conditions. Also, the decrease in spike initiation, observed when synapses are too closely clustered (Fig. 5C), was abolished by adding an NMDA component. Thus, it appears that the negative slope conductance of the NMDA component can counter the shunting effect of the AMPA conductance and broaden the spatiotemporal requirements for dendritic spike initiation by providing the net synaptic current a region of zero slope conductance (Cook and Johnston, 1999). In this situation, the relative AMPA/NMDA receptor ratio present at the synapses becomes an important parameter in determining the level of synaptic clustering that can still effectively produce dendritic spiking (Otmakhova et al., 2002). This ability to counter the shunting effect of other excitatory synaptic conductances is a relatively unappreciated function for the NMDA receptor and could represent a mechanism for many NMDA receptor-dependent phenomena (McHugh et al., 1996; Cash and Yuste, 1999; Golding et al., 2002; Ariav et al., 2003).

Dendritic spike propagation

We have shown that spikes initiated in the main apical trunk can, under normal conditions, propagate to the soma to produce an action potential output, thus greatly increasing the efficacy of the input that initiated the spike. Consequently, under the appropriate conditions, highly synchronized input results in short-latency (<2 msec) action potential output for input levels (the number of synapses activated) substantially lower than those required when dendritic spike propagation is reduced (hyperpolarized V_m or in the presence of TTX) (Fig. 8). This indicates that in these circumstances, neurons respond more to the pattern of the input than to its quantity by producing an output with timing that is closely linked to that of the input.

Nevertheless, the strength of dendritic spike propagation is still weak enough to be modulated by numerous factors, such as the distance of the generation site, the V_m, the extracellular ion concentrations, as well as anything else that changes the dendritic voltage-gated channel profile. This high level of modulation offers neurons an enormous potential for complex interactions among the various classes of excitatory and inhibitory synaptic inputs present in CA1 pyramidal neurons. In this scheme, the propagation of a dendritic spike generated in the tuft or distal apical trunk by perforant path inputs could be enhanced by properly timed Schaffer collateral input or diminished by properly timed inhibitory input to the proximal region (Lisman, 1999). Thus, both cooperative and obstructive interactions are possible during the coincident activation of different classes of inputs, as is occasionally found in other pyramidal cells (Larkum et al., 2001). Other interesting interactions could occur among propagating trunk spikes and spikes initiated in the radial oblique branches or among spikes initiated in different radial oblique branches as they reach the apical trunk. In this case, a strong multiplicative interaction would be expected if the timing among different branches is appropriate (Fig. 6) (Poirazi et al., 2003).

Finally, even when they do not propagate to the soma, dendritic spikes could amplify synaptic potentials and increase the rate of rise of the resulting somatic EPSP. This functions as an effective way to decrease spike-timing jitter and increase spike precision (Ariav et al., 2003). Thus, the exact impact of dendritic spike initiation on action potential output will depend on a complicated interaction with many other factors as the spike propagates through the dendritic arbor to the soma.

Functional impact

What is the function of dendritic spikes in CA1 pyramidal neurons? Perhaps the best way to approach this question is to consider (1) what additional features they provide a neuron, (2) what is required to produce them, (3) when they occur, and (4) what network function occurs during this time. Concerning the first issue, nonlinear phenomena such as dendritic spikes might allow neurons to respond differentially to variable spatiotemporal input patterns (Poirazi et al., 2003). Thus, highly synchronized and clustered inputs produce a large dendritic voltage spike and associated Ca²⁺ influx along with a well-timed action potential output, a signaling pattern that would not occur for less synchronous input patterns. Next, we have shown that large amounts of synchrony are required for dendritic spike generation. Such input patterns are most likely to be found during the occurrence of EEG patterns known as sharp waves (Csicsvari et al., 1999). In fact, there is some evidence that dendritic spikes are indeed produced during sharp-wave behavioral states such as awake immobility, feeding behaviors, and slow-wave sleep (Kamondi et al., 1998). Finally, it has been observed that a time-compressed reactivation of hippocampal cell assemblies occurs during these behavioral states, with the final outcome of this network activity hypothesized to be the long-term storage of preceding behaviors (Wilson and McNaughton, 1994; Kudrimoti et al., 1999). Thus, it is tempting to speculate that the additional features provided by dendritic spikes allow individual CA1 pyramidal neurons to more effectively store information both in the hippocampal circuits themselves (Golding et al., 2002) and in the downstream cortical regions (Qin et al., 1997).