Multiple Time Scales of Adaptation in Auditory Cortex Neurons

Abstract

Neurons in primary auditory cortex (A1) of cats show strong stimulus-specific adaptation (SSA). In probabilistic settings, in which one stimulus is common and another is rare, responses to common sounds adapt more strongly than responses to rare sounds. This SSA could be a correlate of auditory sensory memory at the level of single A1 neurons. Here we studied adaptation in A1 neurons, using three different probabilistic designs. We showed that SSA has several time scales concurrently, spanning many orders of magnitude, from hundreds of milliseconds to tens of seconds. Similar time scales are known for the auditory memory span of humans, as measured both psychophysically and using evoked potentials. A simple model, with linear dependence on both short-term and long-term stimulus history, provided a good fit to A1 responses. Auditory thalamus neurons did not show SSA, and their responses were poorly fitted by the same model. In addition, SSA increased the proportion of failures in the responses of A1 neurons to the adapting stimulus. Finally, SSA caused a bias in the neuronal responses to unbiased stimuli, enhancing the responses to eccentric stimuli. Therefore, we propose that a major function of SSA in A1 neurons is to encode auditory sensory memory on multiple time scales. This SSA might play a role in stream segregation and in binding of auditory objects over many time scales, a property that is crucial for processing of natural auditory scenes in cats and of speech and music in humans.

Introduction

The activity of neurons in primary auditory cortex (A1) is influenced by stimulus history. For example, when pairs of pure tones with variable interstimulus intervals are presented, the response of A1 neurons to the second tone often adapts in a frequency-specific manner if the interval is shorter than ∼200-300 msec (Calford and Semple, 1995; Brosch and Schreiner, 1997). Most studies of context-sensitivity in nonbehaving animals have reported time scales of tens to hundreds of milliseconds. A few studies have demonstrated longer time scales, on the order of seconds (Malone et al., 2002; Ulanovsky et al., 2003), and perhaps longer (Condon and Weinberger, 1991); however, none of these studies has examined explicitly the time scales involved.

Sensitivity of A1 neurons to stimulus history could be used for stream segregation or binding of auditory objects over time (Bregman, 1990; Nelken et al., 2003), which is important for processing of complex auditory scenes. This sensitivity can also be used for optimizing the coding of sounds by matching the neuronal firing to the stimulus statistics (Brenner et al., 2000; Fairhall et al., 2001) and for forming a sensory memory trace that may capture the complexity of past auditory stimulation (Näätänen et al., 2001).

Human auditory sensory memory has been shown to have a memory span of seconds, and perhaps even tens of seconds, in both behavioral studies (Cowan, 1984) and evoked-potential studies (Bottcher-Gandor and Ullsperger, 1992; Näätänen, 1992; Cowan et al., 1993). Evoked-potential studies of sensory memory are usually conducted using an oddball design, in which rare tones (“deviants”) are embedded within a sequence of common tones (“standards”), and the standard tones robustly elicit weaker responses than the deviants (Näätänen, 1992; Cowan et al., 1993). We have recently tested the sensitivity of single A1 neurons to stimulus history using the oddball design and have shown that the responses to the standard are adapted compared with the deviant and that the magnitude of this effect is inversely proportional to the long-term probability of the deviant (Ulanovsky et al., 2003). We have also shown that this stimulus-specific adaptation (SSA) is absent in the auditory thalamus for stimulus parameters for which it was strongly expressed in A1 and, furthermore, that SSA affects mostly sustained rather than onset responses, suggesting a substantial late contribution by intracortical processing. Because previous studies of evoked potentials in humans have implicated the auditory cortex in sensory memory (Näätänen and Winkler, 1999), we have proposed that SSA in single A1 neurons could contribute to auditory sensory memory (Ulanovsky et al., 2003).

Here we studied the dynamics of adaptation in A1 neurons, focusing on the various time scales involved. We characterized the effects of the detailed stimulus sequence structure on the neuronal responses, showed that SSA has both local and global aspects, and constructed a simple linear model that concisely describes these results. Finally, we showed that SSA in A1 neurons causes a bias in the neuronal responses to unbiased stimuli.

Materials and Methods

Surgery. Experiments were performed on adult cats under protocols authorized by the committee for animal care and ethics of the Hebrew University-Hadassah Medical School, as described in detail previously (Bar-Yosef et al., 2002). Anesthesia was induced by xylazine (0.1 mg, i.m.) followed by ketamine (30 mg/kg, i.m.) and maintained with halothane (0.25-1.25% as needed) mixed with oxygen and nitrous oxide (30% O₂/70% N₂O). Anesthesia level was monitored by measurement of heart rate (<150/min) and blood pressure (kept at ∼100 mmHg) measured via a cannula in the femoral artery. Expiratory CO₂ levels were kept at 3-3.5%. During data acquisition, all of the animals except one were sufficiently anesthetized so that they did not resist the respirator and were not paralyzed. The one animal that did resist the respirator was paralyzed by injection of vecuronium bromide (0.1 mg, i.v.) every 1-2 hr, as necessary.

Electrophysiology. Extracellular recordings were performed in A1 (five cats), in auditory thalamus [medial geniculate body (MGB), one cat], and in A1 and MGB simultaneously (one cat). Thalamic recordings were performed in all major subdivisions of the MGB. Recordings were done using two to four glass-coated tungsten microelectrodes (lab made, impedance of 0.2-0.6 MΩ at 1 kHz, as measured in the brain tissue), which were inserted perpendicularly to the cortical surface (when recording in A1) or dorsoventrally (when recording in MGB). Each electrode was manipulated independently using a four-electrode drive (EPS; Alpha-Omega, Nazareth Illit, Israel). The electrical signals were amplified (MCP Plus; Alpha-Omega) and filtered between 200 Hz and 6 kHz. Spike waveforms were sampled at 24 kHz and stored for off-line sorting (AlphaMap; Alpha-Omega). Single units were spike sorted on-line using template-based sorting, and in most cases they were also sorted off-line, to improve unit isolation. The on-line sorters (MSD; Alpha-Omega) supply a histogram of the squared error between the detected spike and the template, and we required these histograms to have a peak followed by a clear minimum, signifying the presence of a homogeneous class of spike shapes similar to the template. For off-line spike, sorting we used an in-house sorting program (courtesy of Prof. M. Abeles, Department of Physiology, Hebrew University), using principal components analysis of spike shapes: we computed the projections of the spike shapes onto the first and second principal components and then plotted these projections on a two-dimensional plane and manually encircled visually distinct clusters. We also verified that there were no interspike intervals shorter than the refractory period of a single unit. On average, this allowed us to isolate one well separated unit from each electrode per recording location. Well separated units were additionally selected for analysis if they had significant auditory responses (t test; p < 0.05) and had stable spontaneous firing rates (∼5% of the well separated units were discarded for being either nonresponsive or nonstationary). The responses of 158 neurons from A1 and 27 neurons from MGB conformed to these criteria and are reported here. Part of the data presented here was also used for different purposes in Ulanovsky et al. (2003).

Sound generation. Stimuli were pure tones generated digitally (AP2; Tucker-Davis Technologies, Alachua, FL), converted to analog voltage (DA3-4; Tucker-Davis Technologies), attenuated (PA4; Tucker-Davis Technologies), and switched with onset and offset ramps of 10 msec (SW2; Tucker-Davis Technologies). The sounds were presented to the animal through sealed, calibrated earphones (designed by G. Sokolich, Newport Beach, CA), with calibration performed in situ by probe microphones (Knowles Electronics, Itasca, IL) precalibrated relative to a B&K microphone.

Characterizing neurons. During the initial characterization of neurons, all stimuli were 115 msec long and presented at a rate of one per second. The microelectrodes were advanced while diotic broadband noise bursts were presented. After a unit was isolated on each electrode, the preferred aurality was determined using broadband noise rate-level functions to the right (contralateral) ear alone, left ear alone, and both ears together; the remainder of the experimental protocol was performed at the preferred aurality using pure tones only. The frequency response area (FRA) was measured using a matrix of 45 frequencies logarithmically spaced from 0.1 to 40 kHz and eight sound levels linearly spaced between 0 and 87 dB sound pressure level, and the best frequency (BF) and minimal threshold of the neuron were determined. We then presented the main auditory stimuli of our experiments.

Auditory oddball stimuli. For testing the adaptation properties of auditory neurons, we used three stimulus designs, all using pure tones of identical duration (230 msec), interstimulus interval (736 msec onset to onset), and tone level (fixed at 40 dB above minimum threshold of one of the simultaneously recorded neurons, usually the neuron that had the best on-line separation), as follows. (1) An oddball design: the deviants were embedded in a sequence of standards. We selected two frequencies, f₁ and f₂ (f₁ < f₂), with the central frequency (f₂ × f₁)^1/2 having a fixed value close to the BF of the neuron that was best separated on-line. The relative probability of f₁ and f₂ was fixed within each stimulus block (see Fig. 1 A). (2) A “switching-oddball” design: we repetitively swapped the probabilities of the two tones within the block (see Fig. 1 B). (3) A “response-curve” design: n frequencies were presented with equal probability (n = 20), as is typically done for measuring neuronal response curves (see Fig. 1C), except that the frequency range was 0.97 octaves, a narrow range that fit inside the FRA of most neurons at the tested level.

Figure 1.

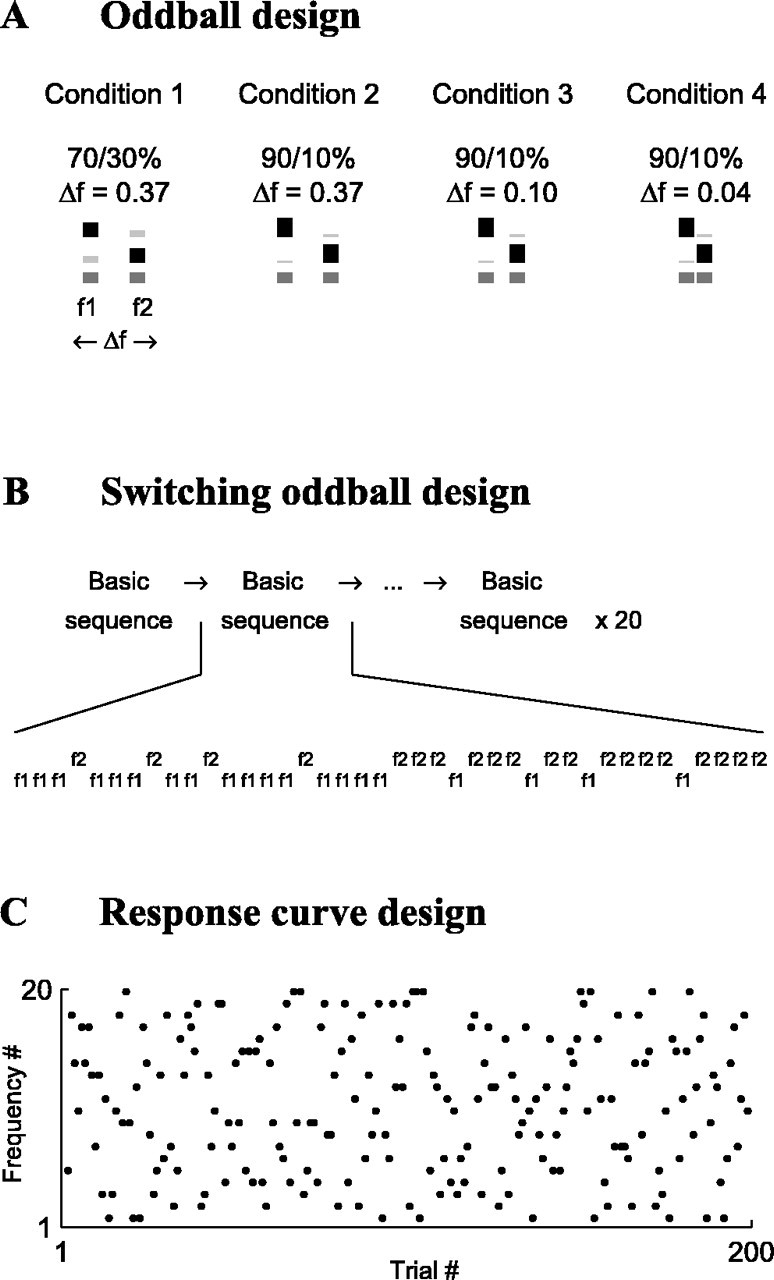
Auditory stimuli used in this study. A, The oddball design: stimuli consisted of sequences of standard and deviant tones, differing in frequency. We used three probability ratios (p = 90/10, 70/30, and 50/50%) and three frequency differences (Δf = 0.37, 0.10, and 0.04), and their combination defined four stimulus conditions. For each condition, we schematically represent here the three blocks that were used. The stimulus probability is denoted by the height of bars as well as by their darkness (standard, black; deviant, light gray; 50/50% control, dark gray), and the frequency difference Δf is denoted by the horizontal separation. B, The switching-oddball design, consisting of a basic 40 trial sequence, in which the f₁/f₂ probability ratio switched in the middle from 80/20 to 20/80% (Δf = 0.37). This frozen basic sequence, which is given at the bottom, was repeated 20 times for a total of 800 trials and was identical for all neurons. C, The response-curve design. We randomly presented 20 frequencies, 10 repetitions each, spanning a total frequency range of 0.97 octaves (each dot represents 1 stimulus trial).

For the oddball design, the frequency difference Δf = (f₂ - f₁)/(f₂ × f₁)^1/2 was set to one of three values: Δf = 0.37, 0.10, or 0.04, corresponding to frequency ratios of 0.526, 0.141, and 0.057 octaves, respectively. The probability of appearance of standard/deviant was 90/10 or 70/30%, in addition to a 50/50% control. The combination of Δf and probability of the standard/deviant defined a “stimulus condition,” and we used four different stimulus conditions (see Fig. 1 A). Each condition was composed of three blocks: in one block, frequency f₁ was standard and f₂ was deviant; in another block, f₂ was standard and f₁ was deviant; the third block served as a control (50/50%). Because of the large number of stimulus blocks, not all neurons were tested with all of the four conditions. In MGB we used only condition 3 (p = 90/10%; Δf = 0.10) (see Fig. 1 A). In each block, the tone sequences were generated as a random permutation of the total number of stimuli in the block, so for a given type of block, the number of appearances of each frequency was the same for all neurons. All blocks contained a total of 400 tones.

For the switching-oddball design, which we presented only in A1, we used blocks of 800 trials, consisting of 20 identical repetitions of a basic “frozen” sequence of 40 trials (see Fig. 1 B). In the first 20 trials of the basic sequence, the frequencies f₁/f₂ had probabilities 80/20%, and in the last 20 trials, the probabilities were swapped (see Figs. 1 B, 6 A).

Figure 6.

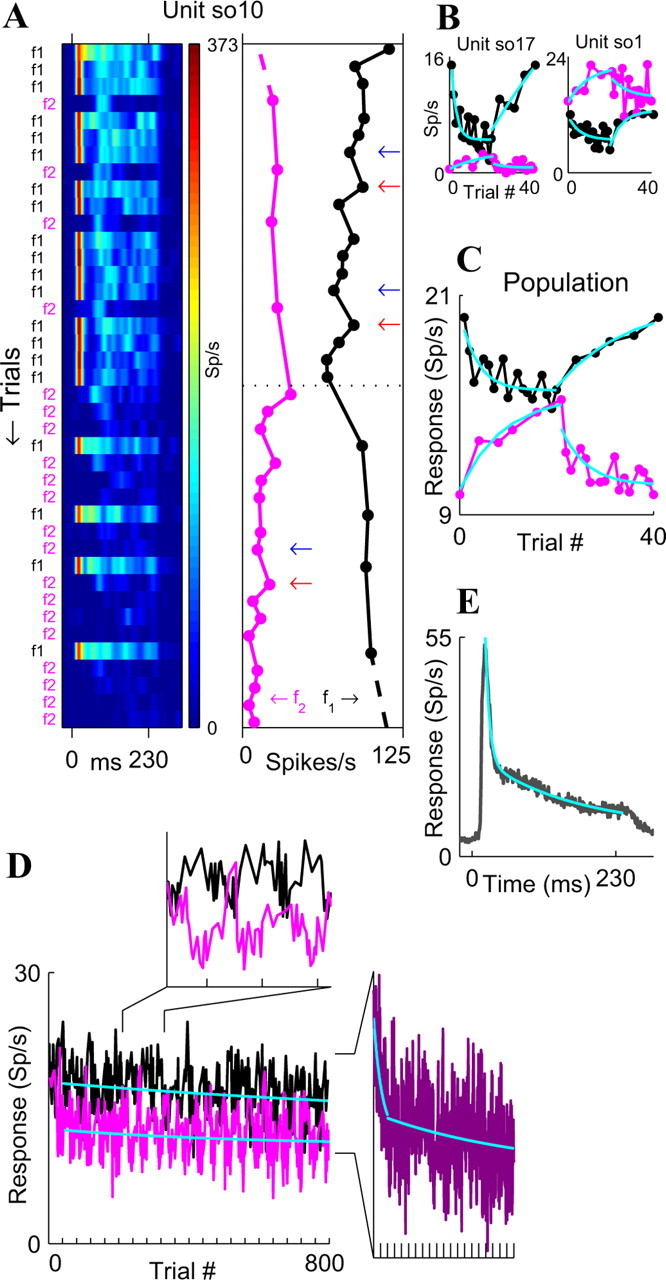
Time course of adaptation to frozen switching-oddball stimuli, showing multiple time scales of adaptation (n = 24 neurons in A1). A, Left, Responses of a single neuron to the two tones that comprise the basic 40 trial stimulus sequence (the sequence is displayed along the ordinate) (see also Fig. 1 B). The responses were averaged over the 20 repetitions of this frozen sequence and are represented as color-coded PSTHs. Right, Spikes counts for the same cell, for frequencies f₁ (black) and f₂ (magenta). Arrows mark examples of predeviant (blue) and postdeviant (red) standards. B, Average responses of two more neurons as a function of the sequential position of the stimulus within the basic 40 stimulus sequence (black, f₁; magenta, f₂), together with exponential fits (cyan). C, Exponential fits to the population mean responses (same colors as in B). We computed the mean response over all neurons and then used nonlinear least-squares fitting of exponential functions to this mean. D, Population responses to the full 800 trials, unfolding the 20 repetitions of the basic sequence (ticks at the bottom). Top inset, “Zoom in” on the responses to three consecutive repetitions of the basic sequence. Right inset, Average population response to frequencies f₁ and f₂, with separate exponential fits for trials 1-80 (steep cyan curve), for which we used the exponential computed from the p = 50% responses in Figure 5C (τ = 48.4 sec), and for trials 81-800 (shallow cyan curve). E, Mean within-tone population response in the switching-oddball design, averaged over the two frequencies for all of the trials and all neurons (gray), together with a double-exponential fit (cyan).

For the response-curve design, we presented a 200 trial block consisting of 20 frequencies (evenly spaced on a logarithmic scale) × 10 repetitions each (see Fig. 1C). The stimuli were presented randomly and spanned a narrow frequency extent, totaling 0.97 octaves, centered close to the BF of the neuron. We used the same stimulus level as for the other designs: 40 dB above minimum threshold. Because of the high stimulus level, for most neurons all of the 20 frequencies evoked significant responses (we never observed nonmonotonic neurons that were completely suppressed at high levels, although we did observe some neurons that were partially suppressed; all of the nonmonotonic neurons were included in the analysis together with the monotonic ones, because no clear differences were found in the adaptation dynamics between monotonic and nonmonotonic neurons).

Data analysis. Poststimulus time histograms (PSTHs) (see Fig. 2) were smoothed with a 10 msec Hamming window for display only, but analyses were done without smoothing. Responses were quantified by spike counts that were measured in a window of 330 msec, starting at stimulus onset and ending 100 msec after stimulus offset. To quantify the magnitude of SSA, we defined a normalized SSA index (SI) as follows:

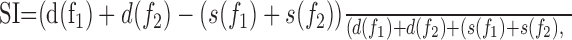where d(f₁) and s(f₁) are responses to frequency f₁ when it was deviant and standard, respectively, and similarly for f₂.

Figure 2.

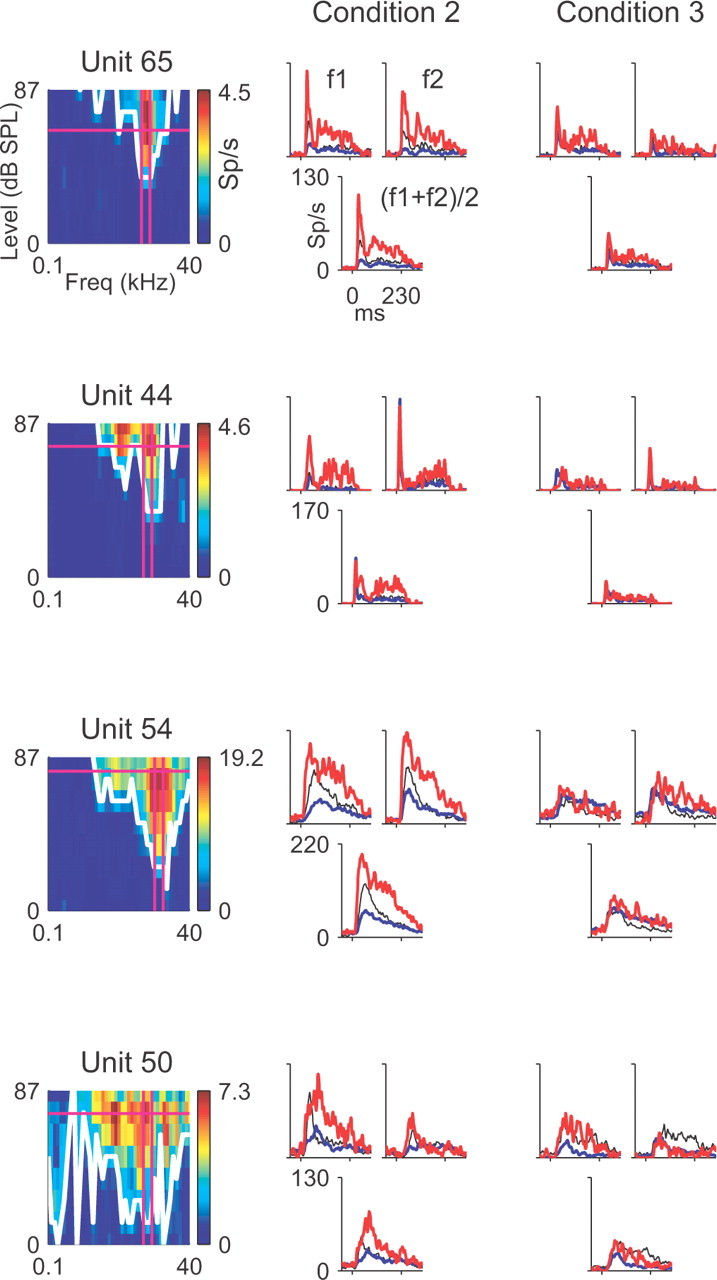
Activity of four neurons in A1 in response to the oddball stimuli. Each row corresponds to one neuron. First column, FRA (color coded) with the tuning curve (white line) and amplitude and frequencies used for the oddball stimuli (magenta; vertical lines are for Δf = 0.37). Second column, Responses to condition 2 of the oddball stimuli (p = 90/10%; Δf = 0.37), for frequency f₁ and f₂ separately, as well as the mean response to f₁ and f₂. Third column, Responses to condition 3 (p = 90/10%; Δf = 0.10). Colors denote standard (blue), deviant (red), and p = 50% control (black). The stronger response to the deviant than to the standard (red > blue), both when f₁ was the deviant and f₂ was the deviant, demonstrates the presence of SSA.

To look for a possible dependence of SI on the shape of the FRA and position of the tones with respect to the FRA, we computed the tuning curves (see Fig. 2, white lines on FRAs), defined as the lowest level for each frequency in which the response of the neuron was higher than its spontaneous firing rate +20% of the maximal overall response. We then computed the following nine parameters: (1) minimal threshold, defined as the lowest level reached by the tuning curve; (2) the difference between the level of the oddball stimuli and the minimal threshold; (3) BF, defined as the frequency at which the sum of the responses over all sound levels was maximal; (4) absolute difference, in octaves, between the BF and the central frequency (f₂ × f₁)^1/2; (5) tuning curve compactness, defined as the area of the frequency-level plane lying above the tuning curve, divided by the squared length of the tuning curve (compactness is high for compact V-shaped tuning curves and low for multipeaked tuning curves such as unit 50 in Fig. 2); (6) sharpness of tuning of the FRA at 40 dB above threshold (Q₄₀), defined as the BF divided by the FRA width at that level (the total width, including all tuning curve peaks); (7) sharpness of tuning of the FRA at 10 dB above threshold (Q₁₀); (8) average firing rate of the neuron, defined as the average of the responses to frequencies f₂ and f₁ at the 50/50% probability condition; and (9) f₂ - f₁ response difference, defined as the absolute difference in responses to frequencies f₂ and f₁ for the 50/50% probability condition, normalized by the sum of the responses as follows:

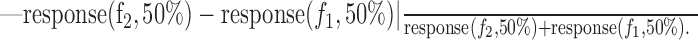We computed the correlations of SI with these nine parameters for condition 2 (p = 90/10%; Δf = 0.37) (see Fig. 1 A) and condition 3 (p = 90/10%; Δf = 0.10), yielding a total of 18 correlations.

To characterize the spike-count distributions of neurons, which tended to have prominent zero-count peaks (many “failed responses”), we fit the spike count distributions with a mixture model of a Poisson process with excess failure probability: p(n) = p_fδ₀ + (1 - p_f)Poiss(n;λ), where p(n) denotes the probability of observing n spikes and p_f is the excess probability of failures (zero counts, denoted by δ₀) over that expected from a Poisson distribution. To fit the model, the rate λ of the Poisson distribution Poiss(n;λ) was estimated as follows. First, for each neuron, we computed the average spike count using those trials that had non-zero counts only, denoting this average by λ_non-zero. Because λ_non-zero was computed without taking failures into account and because failures may happen even under the Poisson assumption, λ_non-zero is larger than the parameter λ of the Poisson component. To obtain the correct λ, we solved for λ using the relationship λ_non-zero = λ/(1 - e^-λ), which is easily derived from the Poisson distribution. The Poisson distributions that are plotted in Figure 4, A and B (solid line), are based on this λ. We then used the observed probability of zero counts, p(0), and computed p_f from the above formula for p(n), as follows:

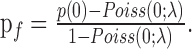Figure 4.

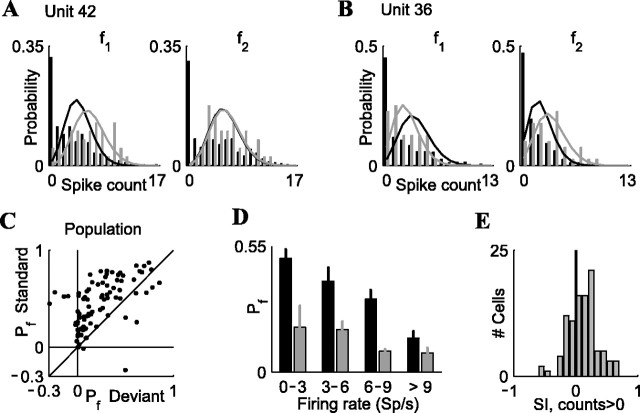
Adaptation increases the proportion of failures in the responses of A1 neurons. A, B, Spike-count distributions for two neurons (A, B), for frequencies f₁ and f₂, when they were standards (black bars) or deviants (gray bars). Solid lines, Fits of Poisson distributions, based on non-zero counts only. C, The parameter p_f indicates the observed probability of zero-counts minus predicted probability from the Poisson fits, plotted for standards against deviants. D, More failures for standards than for deviants. Population means of p_f for standards and deviants, grouped by firing rate, are shown. Note that each neuron contributes twice to this plot; for example, for the deviant it may contribute to a high firing-rate bin and for the standard it may contribute to a lower firing-rate bin. Number of neurons averaged for each bar, from left to right: 57, 38, 13, 21, 11, 6, 16, and 32. E, Adaptation index SI, computed for non-zero counts only. Data are for stimulus condition 2 (p = 90/10%; Δf = 0.37).

To characterize the time course of SSA in the oddball design, the responses to the k standard trials and the (400 - k) deviant trials were combined by their order of presentation in the sequence, averaged across all neurons, and then plotted at their original 400-trial-long time scale (see Fig. 5C,D). We then performed a nonlinear least-square fit to this population mean curve to find the best-fitting exponential function as follows: decay_size × (1 - e^-t/τ) + asymptote.

Figure 5.

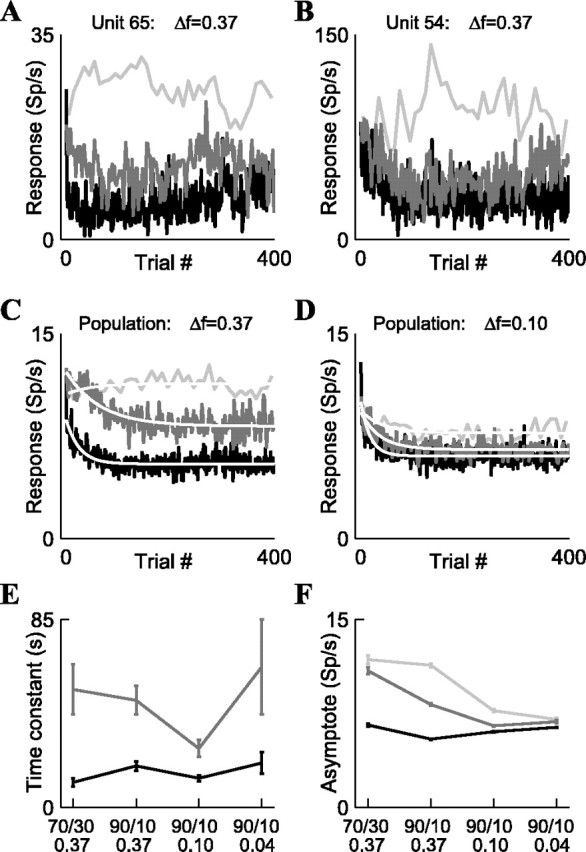
Time course of adaptation to oddball stimuli in A1 neurons. A, B, Two examples of adaptation to stimulus condition 2 (90/10%; Δf = 0.37), plotted separately for deviant (light gray), p = 50% (medium gray), and standard (black). Responses were smoothed with a three-element hamming window for display only. C, Time course of adaptation of the mean population responses for stimulus condition 2 (90/10%; Δf = 0.37); colors are the same as in A and B. The abscissa shows the average serial position of the trial inside the block; the ordinate shows the mean population firing rate (without any smoothing) together with single-exponential fits (white). D, Time course of adaptation of the mean population responses for stimulus condition 3 (90/10%; Δf = 0.10). E, Time constants of fitted exponentials for the four stimulus conditions (data for deviants are not shown because the weak adaptation made computation of these time constants very inaccurate). F, Asymptotic firing rates of the exponential fits. In all population panels, for each of the four stimulus conditions, we used all of the neurons presented with this condition: n = 30, 99, 107, and 68, respectively, for conditions 1-4 (the 4 stimulus conditions are listed from left to right in E, F).

For the switching-oddball stimuli, we performed a similar fitting procedure (for all fits, the SD of τ was derived from the least-square fitting procedure). We chose to fit the mean population responses, because the responses of individual neurons were often too noisy to allow a good fit, although many of the neurons did show clear adaptation and recovery from adaptation (see Fig. 6 A, B). Importantly, when taking those neurons where the fitting converged successfully, the median time constant was quite similar to the time constant computed by fitting the mean population response. Thus, the typical fit was quite similar to the fit of the average (see Results).

Modeling the effect of global probability and local sequence. The response of each neuron at every trial (i.e., the spike count evoked by each tone) was normalized as follows:

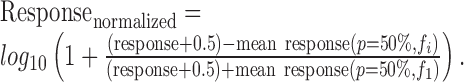Thus, the normalized responses were centered at the mean response in the 50% condition. The addition of 0.5 spikes per second to each trial was necessary for avoiding logarithms of 0 where zero counts occurred. We also tried a number of other normalizations (z-score, ratio of responses) combined with a number of transformations (log transformation, power transformation, linear transformation); they all gave similar results. For each stimulus probability, the normalized responses of all neurons were then analyzed together to determine the effects of local and global stimulus history.

Statistics. Statistical tests were considered significant when p < 0.05, except where multiple comparisons were made, in which case the significance level was adjusted appropriately. In some cases, p values are specifically stated as a measure for the strength of the effects.

Results

Adaptation of A1 neurons to stimulus statistics

When presenting oddball stimuli (Fig. 1A), A1 neurons tended to respond more strongly to the deviant stimuli, often responding more strongly to frequency f₁ when f₁ was the deviant but also more strongly to frequency f₂ when f₂ was the deviant [Fig. 2, red(f₁) > blue(f₂) and red(f₂) > blue(f₁)]. Thus, A1 neurons showed SSA.

We used an SI to quantify the adaptation strength (see Materials and Methods). SI was on average positive in all four stimulus conditions: condition 1 (n = 30 neurons), SI = 0.142 ± 0.212 (mean ± SD); condition 2 (n = 99), SI = 0.265 ± 0.223; condition 3 (n = 107), SI = 0.126 ± 0.202; condition 4 (n = 68), SI = 0.053 ± 0.126. These average SIs correspond to a response that was stronger when the tone was deviant, compared with the same tone when standard, by 33, 72, 29, and 11%, respectively, for the four stimulus conditions.

The SI values were correlated between the four stimulus conditions so that highly adapting neurons tended to have large SIs in all conditions: the average Spearman correlation between the six pairs of conditions was r_s = 0.252, and the average correlation between condition 2 (p = 90/10%; Δf = 0.37) and the other three conditions was r_s = 0.337. Although stimulus-specific changes in firing rates were found in essentially all neurons, only a few neurons (6 of 158) showed an effect of latency, whereby the latency of the onset responses was shorter for the deviant. Therefore, the analyses of neuronal responses presented here are based on spike counts, focusing on the two conditions for which we collected the most data: condition 2 (p = 90/10%; Δf = 0.37), in which the adaptation was also strongest, and condition 3 (p = 90/10%; Δf = 0.10), which elicited adaptation only in A1 and not in MGB (Ulanovsky et al., 2003).

Many neuronal properties in cortex are organized in columns. To check whether SSA is also arranged in columns, we compared the SI values for neurons recorded within the same electrode track, as opposed to neurons recorded in different tracks. Because tracks were mostly perpendicular to the cortical surface, the neurons recorded in each track approximately represent a single cortical column. Figure 3A shows the SI values for condition 3, summarizing 91 neurons recorded in 29 tracks in four cats. Included in this analysis are all neurons in tracks that had two neurons or more per track.

Figure 3.

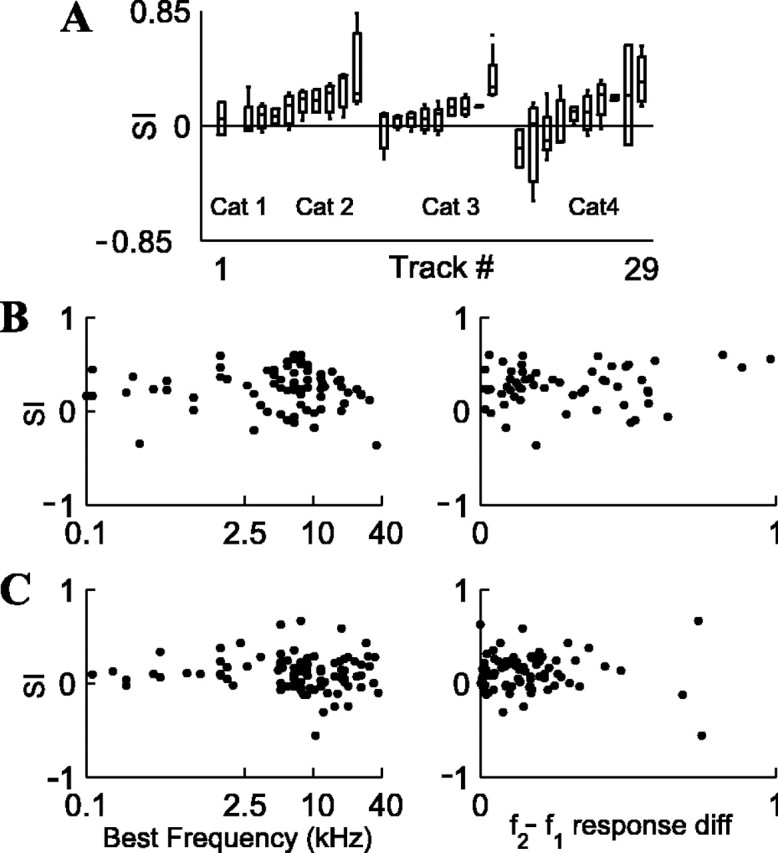
A, Adaptation columns in A1: box plots of SI values for neurons recorded along the same electrode track (29 tracks from 4 cats), sorted for each cat in ascending order of average SI. Each box plot represents the median, interquartile range, and total range of SIs along a single electrode track. Only electrode tracks with two neurons or more are shown (total n = 91 neurons). In cat 1, only a single track was recorded (track #1). Data are for p = 90/10%; Δf = 0.10. B, No correlation between the SI and the BF of the neuron (left; n = 76 neurons) or the f₂ - f₁ response difference (right; n = 56) for p = 90/10%, Δf = 0.37. C, Same lack of correlation for p = 90/10%, Δf = 0.10 (n = 90 and 81 for left and right panels, respectively).

As illustrated by Figure 3A, the between-track SI variability was larger than the within-track SI variability (one-way ANOVA, grouped by tracks; condition 3, F_(28,62) = 1.751, p < 0.05; condition 2, F_(26,64) = 1.911, p < 0.02), suggesting that well separated neurons recorded in the same cortical column tended to undergo adaptation of similar magnitude.

The track length (depth difference between the first and last recording location in each track) had an average of 444 μm, averaged across all 29 tracks, with an interquartile range of 243-654 μm and a total range of 0-1217 μm. We did not observe any clear variation of SI with absolute recording depth (data not shown), but because absolute depth was not measured accurately (unlike the relative depth along a track, which was accurate), it is possible that some systematic relationship between SI and cortical layer does exist.

Because the distances that we measured along a track were substantially shorter than the distances between tracks along the cortical surface, it could be possible that it is not columnar organization but rather absolute distance (both in depth and along the cortical surface) that determines the differences between the SIs of neurons. In this case, we would expect a correlation between the length of a track and the range of SI values (maximum SI minus minimum SI) along it; however, this correlation was not significant (r = -0.01; df = 27; NS), further indicating a columnar structure of adaptation.

The similarity of SI values along an electrode track could be an epiphenomenon of other shared properties. For example, it could be attributable to the variability between cats; however, the within-track similarity of SIs remained when we took into account the variability between cats (one-way nested ANOVA; tracks nested within cats; condition 3, F_(25,61) = 1.798, p < 0.05; condition 2, F_(23,63) = 1.584, p = 0.077).

Another possibility is that the SSA is correlated with other neuronal properties, which in turn are organized in cortical columns; however, the SI was uncorrelated with all parameters that describe the shape of the receptive fields of auditory neurons (their FRA). Figure 3, B and C, shows that the SI was uncorrelated with the BF of the neuron and with its f₂ - f₁ response difference (the absolute difference of responses to f₂ and f₁ for p = 50/50% presentation; see Materials and Methods). This lack of correlation is illustrated in Figure 2, in which all neurons showed strong adaptation despite variability in their BF (e.g., higher BF in unit 54 than in unit 65) and their f₂ - f₁ response difference (e.g., in condition 2, frequency f₁ evoked substantially stronger responses than frequency f₂ in unit 50 but not in the other units; however, the SSA was as strong as in other units. The response to f₁, when standard, was smaller not only than the response to f₁, when deviant, but also than the response to f₂, when deviant). Figure 2 also illustrates the independence of SI from the FRA bandwidth (larger bandwidth in units 54 and 50 than in units 65 and 44). Altogether, we computed the correlation of SI with the following response parameters: minimal threshold, stimulus level above threshold, BF, stimulus frequency difference from BF, tuning curve compactness, FRA sharpness at 40 dB above threshold (Q₄₀) and 10 dB above threshold (Q₁₀), average firing rate, and f₂ - f₁ response difference (see Materials and Methods for definitions). We computed these correlations for conditions 2 and 3, yielding a total of 18 correlations. None of these correlations was significant (we considered the Bonferroni-corrected p = 0.003 level, but in fact all correlations yielded p > 0.04 individually). Together, these data indicate that the tendency of an A1 neuron to undergo adaptation is independent of its tonal response properties and that SSA is a neuronal property that seems to be clustered in “adaptation columns.”

Adaptation increases the proportion of failures in the responses of A1 neurons

The strong adaptation in the firing rate for the standard could result from a decrease in the mean of the spike count distribution, preserving the shape of this distribution, or it could result from a nontrivial change in the shape of the spike count distribution. To examine this, we analyzed the full spike count distributions of the neurons, computed separately for the standard trials and for the deviant trials (Fig. 4). Figure 4, A and B, shows the spike count distributions for two neurons. These distributions have a prominent zero-count bin; this bin contains all trials in which the neuron failed to respond altogether. The excess of failures was especially large for the standard stimuli (black bars). To quantify this, we fit to the spike count distributions a mixture model of a Poisson process and a binary component as follows: p(n) = p_fδ₀ + (1 - p_f)Poiss(n;λ) (see Materials and Methods) (Fig. 4A,B, solid lines denote the Poisson component).

The parameter p_f, which quantifies the extra failure probability relative to a pure Poisson distribution, was positive in most neurons (Fig. 4C), both for the standard stimuli (91 of 99 neurons; Wilcoxon signed rank test: p < 10^-14) and for the deviant stimuli (75 of 99 neurons; Wilcoxon signed rank test: p < 10^-7). In fact, for the standard stimuli, 52% of the neurons (51 of 99) had p_f > 0.4, which means that if the probability of failures predicted from the Poisson model was, for example, 0.2, then the observed probability of failures was >0.6. This suggests that the excess failures in this model are indeed essential for describing the responses. A trial results either in a failure (with probability p_f) or in a response, and if there is a response, the spike count is approximately Poisson distributed (which also contributes to the total failure probability).

Moreover, p_f was larger for the standard than for the deviant stimulus (Fig. 4C) (86 of 99 neurons above the diagonal; Wilcoxon signed rank test: p < 10^-12). This difference in p_f could be caused by the difference in firing rates (smaller rate for the standard), or it could be caused by adaptation per se (which is stronger for the standard), regardless of the firing rate. To dissociate these two possibilities, we plotted p_f for the standard and the deviant, separated into groups of matched firing rates (Fig. 4D). Figure 4D demonstrates that p_f was reduced at higher rates (twoway ANOVA on firing rate groups × standard/deviant status; effect of firing rate groups: F_(3,186) = 5.26, p < 0.002); however, when this effect of firing-rate group is factored out, p_f was clearly higher for the standards than for the deviants (two-way ANOVA as above; effect of standards vs deviants: F_(1,186) = 12.11, p < 0.001; no significant interaction was found between standard/deviant status and firing rate: F_(3,186) = 1.3, p = 0.28, although it seems that the difference between the groups does become smaller with increased firing rate). These data suggest that in the adapted state, A1 neurons have an increased number of “failures,” regardless of firing rate.

In some extreme cases, such as frequency f₂ of the neuron in Figure 4A, the fitted Poisson distributions were essentially identical for the standard and the deviant (note overlap of black and gray solid lines). In this case, the adaptation increased the probability of failures without affecting at all the spike count distribution in those trials when the neuron did respond; however, in most neurons, the firing rate was suppressed for the standard compared with the deviant even in trials with non-zero responses, as can be seen from SI values computed for trials with non-zero responses only (Fig. 4E) (SI > 0; Wilcoxon signed rank test: p < 10^-5). Nevertheless, the SI computed for non-zero responses only was much smaller than the SI computed for all of the trials (Wilcoxon signed rank test: p < 10^-10; data not shown). Thus, adaptation had a dual effect on neuronal firing: it decreased the firing rate in those trials when the neuron did respond, but it also increased disproportionately the probability of failures.

Finally, one interpretation of these data is that the neuronal firing is determined by a two-stage mechanism. First, the neuron either responds or fails, in a Bernoulli process (or a binary process) with probability of failure P_f; second, if the neuron does respond, it responds in a Poisson manner. We propose that this is a generalization of the recently reported finding of “binary spiking” in A1 (DeWeese et al., 2003). In that case, the neuron, when responding, almost always fired a single spike. We show here that the distribution of spikes, when responding, may also be different from that suggested by DeWeese et al. (2003), although keeping the binary character of the response-failure decision.

Multiple time constants of adaptation in A1

To address the time course of cortical adaptation, we first examined how the neuronal responses develop over consecutive trials of the oddball design (Fig. 5) (see also Materials and Methods). Figure 5, A and B, illustrates the time course of adaptation of two single neurons in condition 2. These neurons adapted over time to the high-probability stimuli but showed very little adaptation, or even enhancement of the responses, to the low-probability stimuli. We were interested in computing the time constants of this adaptation and comparing them with reported time constants from human evoked potentials and sensory memory studies, which presumably reflect the activity of large neuronal populations. Because of this, and because it was difficult to compute time constants for most individual neurons attributable to variability in the responses, we report here the dynamics of the mean population responses (Fig. 5C,D).

The time course of adaptation differed with stimulus probability. For example, in condition 2 (p = 90/10%; Δf = 0.37) (Fig. 5C), there was no adaptation when the tone appeared with a probability of 10% (light gray), but when the same tone was equiprobable (dark gray), the responses adapted exponentially with a single time constant τ = 48.4 ± 6.5 sec. When the tone appeared with a probability of 90% (black), the time constant was τ = 18.7 ± 2.1 sec, with an additional faster time constant of ∼1 sec expressed as a substantial decline immediately after the first trial. For the other stimulus conditions (e.g., condition 3, p = 90/10%, Δf = 0.10) (Fig. 5D), there was some adaptation for the deviant, but otherwise the results were similar. The responses in the equiprobable condition were fit well by a single slow exponential, whereas when the tones appeared with a probability of 90%, the responses contained both a fast (∼1 sec) and a slow component.

Figure 5E displays the slow time constant for the four stimulus conditions, showing that the time constant of adaptation was consistently longer when the tones were equiprobable (probability 50%) than when the same tones appeared with a probability of 90% (χ² = 46.9; df = 4; p < 10^-8). The ratios of time constants between the 50 and 90% cases equaled 4.7, 2.6, 2.0, and 3.2 for the four stimulus conditions, being larger than the ratio of standard probabilities (90% divided by 50% = 1.8) and smaller than the ratio of deviant probabilities (50% divided by 10% = 5), indicating that the time constants were not simply proportional to the probability of either the standard or the deviant. Thus, adaptation had complex dynamics, consisting of at least two time constants, in which the slower time constant depended on the probability of the tone being faster when the tone probability was higher.

The steady-state responses also varied with the stimulus condition (Fig. 5F). The difference between the steady-state responses for a tone when rare and when common decreased as the frequency difference decreased. This was caused mostly by a decrease in the steady-state responses to the tones when rare (Fig. 5F, light gray) but also by a possible increase in responses for the same tones when common (black).

To further study the dynamics of adaptation, we presented 24 neurons in A1 with a switching-oddball design, in which we repetitively switched between two stimulus probability distributions (Figs. 1B, 6A). These stimuli consisted of frozen sequences that were identical for all neurons. The responses to the frozen sequences had at least four time constants of adaptation and recovery from adaptation (Fig. 6): (1) “one-trial effect” (τ ∼ inter-stimulus interval = 0.736 sec): responses to the standard stimulus in postdeviant trials (Fig. 6A, red arrows) were enhanced compared with predeviant trials (blue arrows). (2) “Adaptation to stimulus statistics”: neuronal responses to a stimulus adapted when it was the standard and recovered from adaptation when it was the deviant (Fig. 6A,B, examples of three neurons). When fitting exponential functions to the single-neuron responses (Fig. 6B), the time constants were quite variable among neurons, with a median time constant of τ = 6.57 sec for the adaptation (interquartile range, 2.9-17.2 sec) and τ = 14.71 sec for the recovery (interquartile range, 3.4-61.0 sec). The time course of the mean population response (Fig. 6C) was well fit by single exponentials and had time constants that were reasonably similar to the population medians: τ = 3.20 ± 1.56 sec for the adaptation and τ = 8.75 ± 5.65 sec for the recovery. Thus, in this case, the fit to the average was reasonably similar to the average of the fits. (3) “Adaptation to stimulus meta-statistics”: to reveal slower time constants, the full block of 800 trials was used (Fig. 6D). The transitions 80/20% → 20/80% → 80/20% → 20/80% → (...) resulted in a long-term presentation probability of 50/50% for the two tones. Indeed, the initial portion of the long-term curve (Fig. 6D, right inset) was well fit by the same exponential as the p = 50% responses from Figure 5C: τ = 48.4 sec [to obtain this curve, we eliminated the antiphase modulations in the responses that were caused by the probability switching (Fig. 6D, top inset) by interpolating and averaging the responses to the two frequencies as a function of location in the global sequence]. This result suggests that the neurons adapted to the long term meta-statistics of the stimuli. (4) “Very slow adaptation”: the latter portion of the curve in Figure 6D showed a very slow adaptation, with time constant τ = 630 ± 969 sec; however, this was a very small decline that, in addition, was not stimulus specific, so we will henceforth focus on time constants of up to a few tens of seconds.

Adaptation was present not only when considering responses over the time course of many trials but also during the tone presentation itself, as seen from the population PSTH (Fig. 6E). This adaptation was well fit by a double exponential, with a fast time constant describing the early adaptation of the responses (τ = 6.6 ± 0.4 msec) and a slower time constant describing the adaptation of the sustained responses (τ = 150.3 ± 29.0 msec). Together, this multitude of time constants, from τ ∼ 6.6 msec to τ ∼ 48.4 sec (and perhaps up to τ ∼ 630 sec), provides evidence that the time scales of adaptation in A1 neurons span at least four to five orders of magnitude, from milliseconds to tens and hundreds of seconds, all being present simultaneously.

Effect of short-term versus long-term stimulus history

The one-trial effect that we observed in the responses to the frozen stimuli (Fig. 6A, red and blue arrows) can be restated as follows. The response to tone A is stronger when it is preceded by a different tone, B (B→ A, or “BA sequence”), than when it is preceded by the same tone, A (AA sequence). In principle, such a one-trial effect could explain the stronger neuronal responses to the deviants relative to the standards. According to this “local-only hypothesis,” the response to stimulus A in the sequence BA (response R_BA) and the response to stimulus A in the sequence AA (response R_AA) obey the one-trial effect (that is, R_BA > R_AA), but R_BA and R_AA are fixed responses that are independent of the global probability of A. If A has a probability of 10%, however, then BA sequences occur nine times more often than AA sequences, and the average response to A is R_deviant = (0.9 R_BA + 0.1 R_AA), whereas if A has a probability of 90%, the situation is reversed, and the average response to A is R_standard = (0.1 R_BA + 0.9 R_AA). It follows that because of the one-trial effect (R_BA > R_AA), we should observe R_deviant > R_standard, as was indeed the case.

In contrast to this local-only hypothesis, the “local-plus-global hypothesis” suggests that in addition to the one-trial effect (R_BA > R_AA), the responses are also influenced by the global probability of A, so that both R_BA and R_AA are higher when A is a deviant than when A is a standard, thus further increasing the difference between R_deviant and R_standard. In other words, the hypothesis is that A1 neurons integrate the sensory input over long time periods, becoming more adapted to A when A occurs more often, so that the responses also depend on the long-term probability of stimulus A.

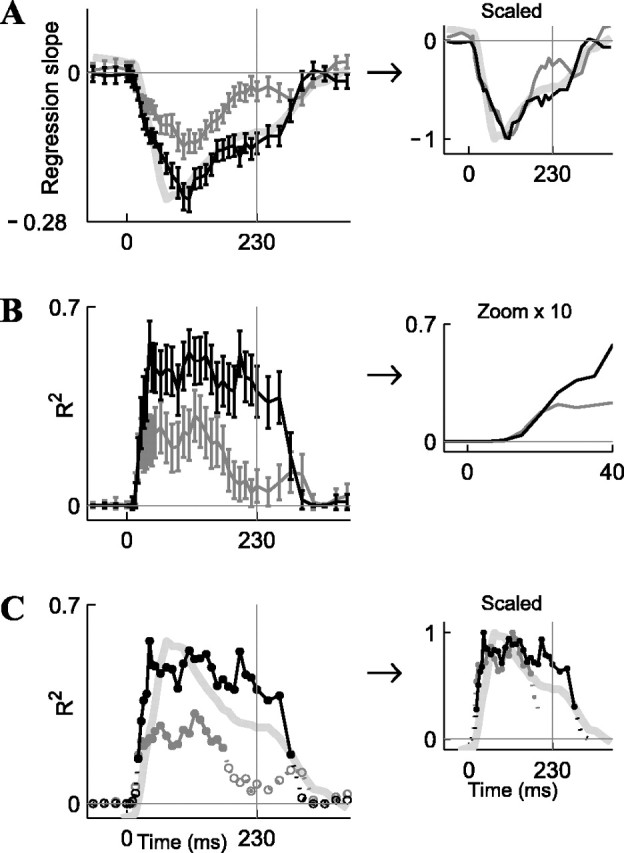
To distinguish between these two hypotheses, we analyzed the concurrent effects of the local sequence and the global probability, following the analysis method of Squires et al. (1976) that was originally applied to the P300 evoked potential. The analyses were done separately for each probability condition. We represented the stimulus at every trial by “A” (the “first-order response”), where A could be frequency f₁ or f₂, whether standard or deviant. We then associated each response with the sequence that preceded it, the “local stimulus history.” Thus, when the preceding stimulus was identical to the current stimulus, the responses were associated with the second-order sequence AA, whereas when the preceding stimulus was different from the current stimulus, the responses were associated with the second-order sequence BA. Similarly, there were four possible third-order sequences that ended with A (BBA, ABA, BAA, and AAA), eight possible fourth-order sequences (BBBA, BABA, etc.), and 16 possible fifth-order sequences (BBBBA, ABABA, etc.). We then computed the average normalized neuronal response associated with each of these sequences (see Materials and Methods for the normalization procedure), considering only sequences that occurred at least 25 times among all trials times all neurons. The averaged responses for each class were plotted in the form of “local history trees,” drawn separately for each of the five probabilities (Fig. 7).

Figure 7.

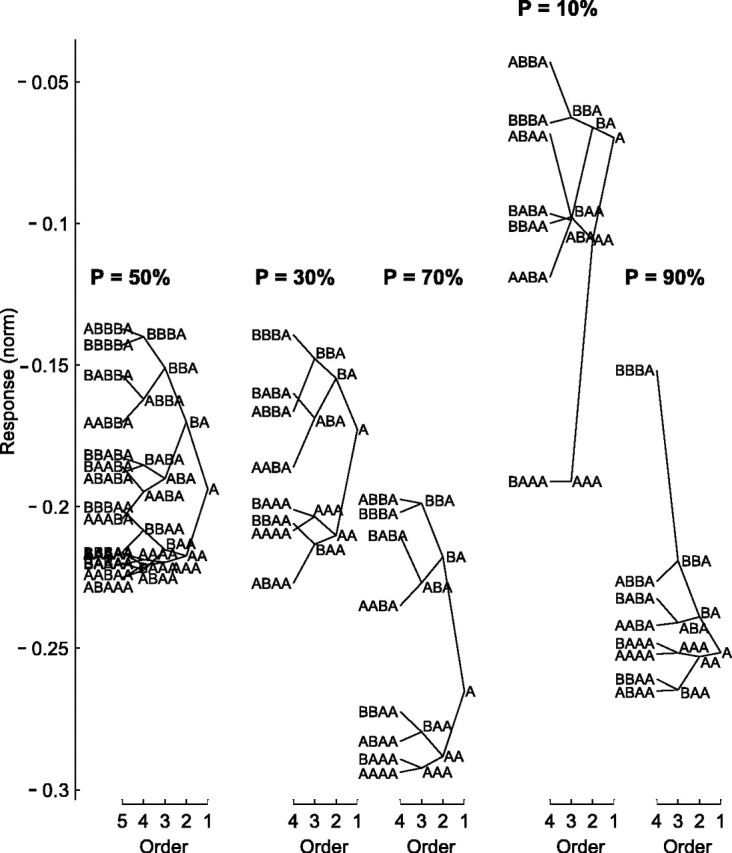
Local history trees for the responses to the oddball stimuli, for Δf = 0.37, computed separately for each of the five stimulus probabilities (p = 10, 30, 50, 70, and 90%). Ordinate, Mean normalized response to a stimulus, grouped according to the preceding stimulus sequence, starting from the stimulus (A) and ending with fourth-order sequences (e.g., BBBA) (see Results). The fifth-order sequences (e.g., BBBBA), were much less orderly and therefore were drawn only for p = 50% for illustration. Each sequence in the tree connects with two higher-order sequences (corresponding to the addition of B or A before that sequence) and one lower-order sequence. All of the plotted sequences are based on averaging of at least 25 repetitions among all trials × all neurons (the AAAA sequence for p = 10% did not meet this criterion and therefore was omitted). Trees for p = 50, 10, and 90% are based on 68 neurons; trees for p = 30 and 70% are based on 29 neurons.

As expected from both the local-only and local-plus-global hypotheses, the one-trial effect was indeed present, with response to stimulus A being stronger when preceded by B than by A (R_BA > R_AA). In fact, this one-trial effect was present in each of the five trees. Moreover, in most cases, the one-trial effect was generalized to an “n-trial effect,” whereby the response to stimulus A was stronger when it was preceded by a sequence that started with B than by the same sequence that started with A (e.g., R_BBA > R_ABA). This n-trial effect was present up to sequences of orders three to four and less pronounced for fifth-order sequences (Fig. 7) (p = 50%), suggesting a decaying “memory” for the local sequence.

The responses to local sequences, however, depended on the global probability as well. For example, in Figure 7, it is clear that R_BA(p = 10%) > R_BA(p = 30%) > R_BA(p = 50%) > R_BA(p = 70%) > R_BA(p = 90%). This is inconsistent with the prediction of the local-only hypothesis but consistent with the prediction of the local-plus-global hypothesis.

To quantify these observations, we constructed a linear model for the history sensitivity of A1 responses, similar to the model of Squires et al. (1976). We assumed that the neuronal responses to a stimulus are positively correlated with the “unexpectedness” of the stimulus, which in turn is determined by a linear combination of two factors: (1) the global probability of the stimulus, which could take here the values p = 0.1, 0.3, 0.5, 0.7, or 0.9, and (2) the memory (M) for the local abundance of this stimulus within the preceding sequence. For M, we assumed that the effect of preceding stimuli is a decaying function of serial position; specifically, we assumed that the memory for stimulus A at trial k depends in an exponentially decaying manner on the sequence of stimuli S_i that preceded it, as follows:

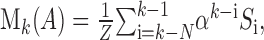where S_i = 1 for stimulus A, S_i = 0 for stimulus B, N is the order of the sequence (we used N = 5), α is a constant that determines the time course of memory decay, and Z =∑αⁱ is a normalization factor that makes M into a measure of local probability. Our prediction was that the neuronal responses would be negatively correlated with both p and M.

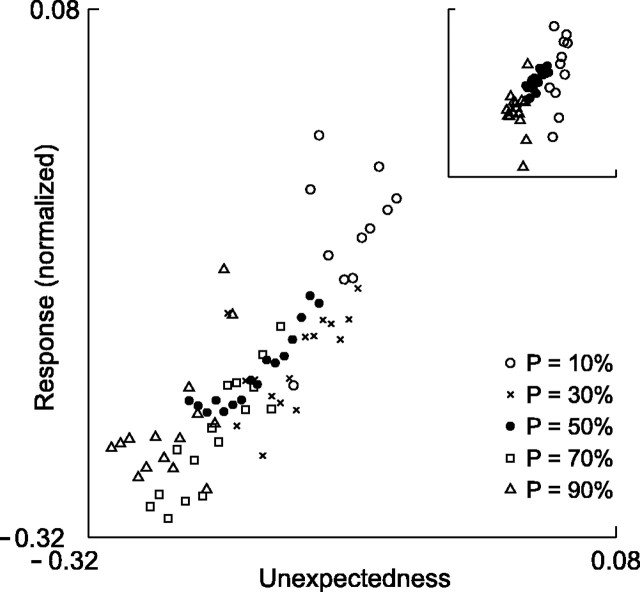
We started by fitting the model to the Δf = 0.37 data (probabilities 90/10, 70/30, and 50/50%). First, we computed the free parameter α, by finding the α that gave the most negative linear correlation between the local memory M and the averaged normalized neuronal responses (the correlation was computed over all fifth-order sequences, n = 16). The obtained value was α = 0.51, which corresponded to correlations r =-0.603, -0.897, -0.927, -0.611, and -0.398, respectively, for probabilities 90, 70, 50, 30, and 10%. This determined the time constant of the exponentially decaying memory M: τ_M = 1/(1 - α) = 2.04 trials = 1.50 sec (the quality of the fit was in fact quite insensitive to the exact value of α, with α = 0.51 yielding correlation coefficients that differed on average only by 0.01 from their individual optimal values when α was fit separately for each of the five probabilities). This value of α was used in the rest of the analyses of Δf = 0.37 data. To determine the dependence of the neuronal responses on the unexpectedness, we performed multiple linear regression of the average responses on the global probability p and local memory M (the regression was done for the 16 sequences × 5 probabilities, n = 80). This resulted in the following linear model: responses ∝ unexpectedness = -0.071 - 0.147 p - 0.099 M.

Figure 8 shows the observed responses for the five-trial sequences, plotted as a function of the unexpectedness, indicating that the data were well fit by the linear model (R² = 0.682; F = 76.0; p < 10^-16). For the Δf = 0.10 data (Fig. 8, inset), for which we had only three probabilities, p = 0.1, 0.5, and 0.9, we obtained a similar value of α (α = 0.48), and the model provided a good fit as well (R² = 0.396; F = 12.8; p < 10^-4). Thus, the concept of unexpectedness that depends on both local and global contexts is able to explain a significant amount of the variability in the data.

Figure 8.

Fitting a linear model of stimulus “unexpectedness” to A1 responses. Each dot represents the mean population response to one fifth-order local sequence, with symbol shape representing the global probability p. Main plot, Δf = 0.37. Inset, Δf = 0.10 (x-axis and y-axis limits: -0.31 to -0.12).

The coefficient of p, -0.147 ± 0.016, and the coefficient of M, -0.099 ± 0.015, were both significant, indicating that p and M contributed separately to the explained variance of the observed neuronal responses. As a consequence, the response was negatively correlated with both the global probability p and the local memory M. The factors p and M were also significant when computing single-variable regressions for Δf = 0.37 (p: R² = 0.473, F = 64.6, p < 10^-10; M: R² = 0.300, F = 30.8, p < 10^-6) and for Δf = 0.10 (p: R² = 0.341, F = 20.7, p < 0.0001; M: R² = 0.124, F = 5.7, p < 0.03). Moreover, the factors p and M were essentially independent of each other (correlation coefficient: r = 0.138; NS) because of the design of the experiment: most values of M appeared at all levels of p. Together, these data suggest the existence of multiple time scales for the influence of stimulus history, with the local history (M) and the global history (p) operating on two independent time scales. Specifically, the local history M had a time constant of two trials [τ_M = 1/(1 - α) ∼ 1.5 sec], whereas the global history may perhaps be accumulating over the long time constants observed in Figures 5 and 6 (τ_P ∼ tens of seconds).

Finally, to assess the dynamics of this linear model throughout the 230 msec duration of the tone, we repeated the above analysis using 50 msec sliding windows. Figure 9A shows the time dependence of the regression slopes, and Figure 9B shows the time dependence of the R² values. Note that the numerical values of the p regression slopes (Fig. 9A, black) and the M regression slopes (dark gray) can be compared directly, because both of these factors are probabilities. The p and M factors influenced the responses with a similar time course during their rise phase (Fig. 9A,B, insets); however, the dependence on the p and M factors differed in their falling phase (Fig. 9C). The long-term history p (black) contributed to the neuronal responses throughout the stimulus, whereas the contribution of the short-term history M (dark gray) seemed to terminate before the end of the stimulus. Thus, the encoding of different stimulus aspects terminated at different times. This finding is in contrast to the results of some studies of visual cortical neurons, which have suggested that the encoding of local and global aspects of visual stimuli start, rather than terminate, at different times (Sugase et al., 1999; Pack et al., 2001).

Figure 9.

Dynamics of the fits to the linear model of Figure 8, computed using a 50 msec sliding window. The windows were shifted by 20 msec (before and after the stimulus), 10 msec (during the stimulus), or 5 msec (during the onset responses). The abscissa denotes the centers of the 50 msec bins. The vertical lines indicate time of stimulus offset (t = 230 msec). A, Regression slopes of the model, separately for the global probability p (black) and local sequence M (dark gray). Light gray, Difference between the population response to the deviant and the standard, DS = PSTH(Deviant) - PSTH(Standard), inverted and scaled. Inset, Scaling of all three curves to the same minimum. B, Fraction of variance explained by the model R². Inset, “Zoom in” on the initial time. C, Fraction of variance explained by the model, R², showing separately the significant time bins (filled circles and solid lines) and nonsignificant time bins (empty circles and dotted lines). Light gray, DS = PSTH(Deviant) - PSTH(Standard). Inset, Scaling all three curves to the same maximum.

No sensitivity to stimulus history in thalamic neurons

For the oddball stimuli (Fig. 1A), we have demonstrated previously that in stimulus condition 3 (90/10%; Δf = 0.10), neurons in the auditory thalamus (MGB) did not show a significant difference between the responses to standards and deviants (Ulanovsky et al., 2003); however, the lack of stimulus-specific adaptation does not necessarily preclude the presence of any type of adaptation in the MGB.

In fact, adaptation does occur in MGB while a stimulus is on, on time scales of milliseconds and hundreds of milliseconds, similar to Figure 6E here (Ulanovsky et al., 2003). To study the possible presence of longer-term adaptation in MGB, we plotted the time course of neuronal responses (Fig. 10A) (compare Fig. 5D, showing data from cortex). The result demonstrates that such adaptation is not present in MGB under the current experimental conditions. Second, the local history trees for the MGB (Fig. 10B) showed the lack of a one-trial effect, at least for p = 10% and p = 90%. For these trees, response(AA) > response(BA), which is the opposite of the one-trial effect (compare with the strong effects in cortex) (Fig. 7). For p = 50%, the tree was somewhat more consistent with a one-trial effect, but the thalamic one-trial effect was very weak compared with cortex (note that the scale of the ordinate in Fig. 10B is substantially magnified compared with that of Fig. 7). Third, fitting the best linear model (Fig. 10C), as in Figure 8, resulted in a poor fit (R² = 0.050; F = 0.764; p = 0.475), and this was also true for the separate linear regressions on p and M (R² = 0.050 and 0.017, respectively). Thus, for the same stimulus parameters for which the linear model provided a good fit to the responses of A1 neurons, it failed to fit the responses of MGB neurons. These data suggest that the neuronal responses in MGB do not adapt to stimulus history on time scales of seconds or longer.

Figure 10.

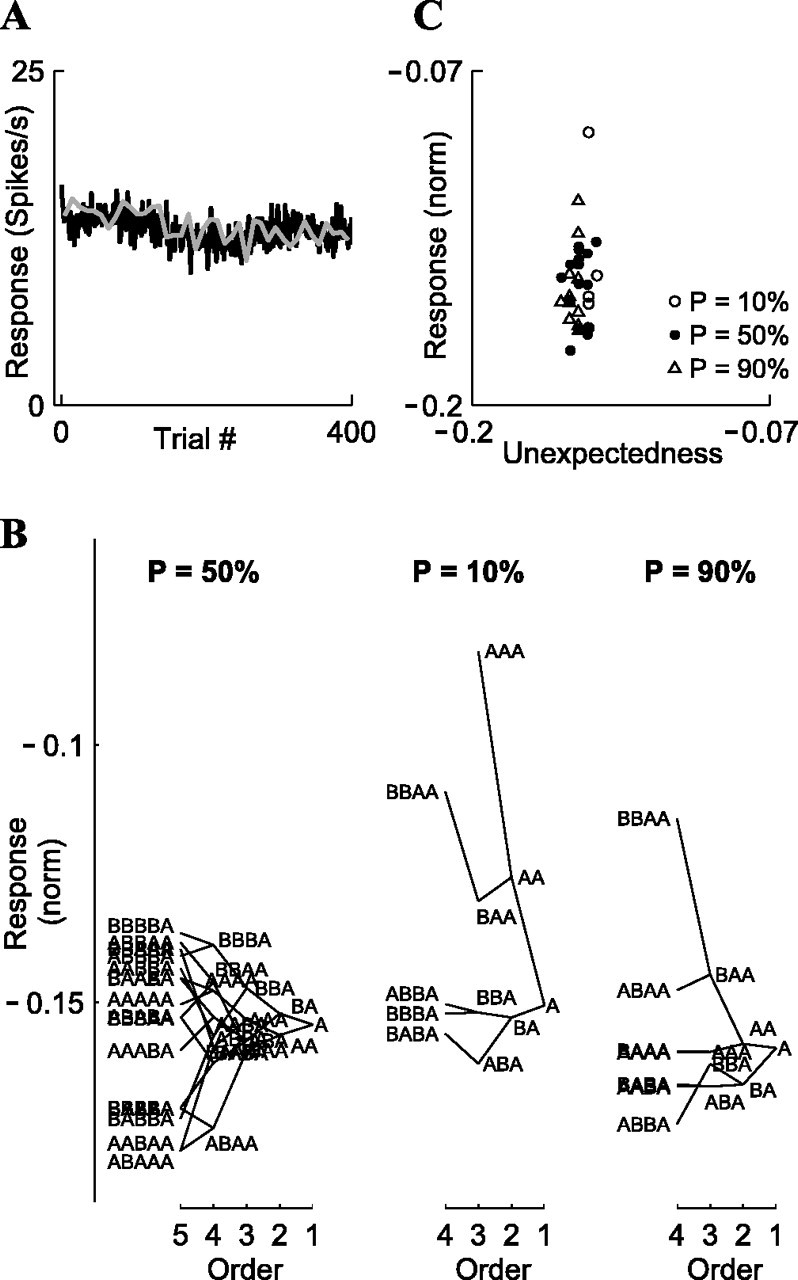
No adaptation in auditory thalamus (MGB; n = 27 neurons; p = 90/10%; Δf = 0.10). A, Time course of mean population responses to the oddball stimuli, showing no decline over trials (gray, deviant; black, standard) (compare Fig. 5D). Data for p = 50% were not plotted here, because of the smaller number of neurons (n = 17). B, Local history trees (compare Fig. 7). C, The linear model of stimulus “unexpectedness” provides a poor fit to MGB responses (compare Fig. 8). In both B and C, some dots were missing for the p = 10% and p = 90% conditions, because not all possible sequences occurred in the data.

SSA causes bias in the neuronal responses to unbiased stimuli

SSA in A1 may affect neuronal responses not only in oddball designs with two frequencies but also in more complex designs, e.g., in an equal-probability presentation of many tones, as used for example in the measurement of auditory response curves. To examine this, we measured response curves of 89 neurons in A1, using the response-curve design. We presented a stimulus ensemble consisting of 20 evenly spaced frequencies × 10 repetitions each, presented randomly and spanning a relatively small frequency extent (FE) of = 0.97 octaves (Figs. 1C,11A, dot raster illustrates the randomized stimuli). The central frequency of this ensemble was placed close to the best frequency of the neuron, the stimulus level was ∼40 dB above the threshold of the neuron, and the interstimulus interval was 0.736 sec. Thus, except for the narrow frequency range used here, the other parameters were quite similar to those used in standard tests of frequency response.

Figure 11.

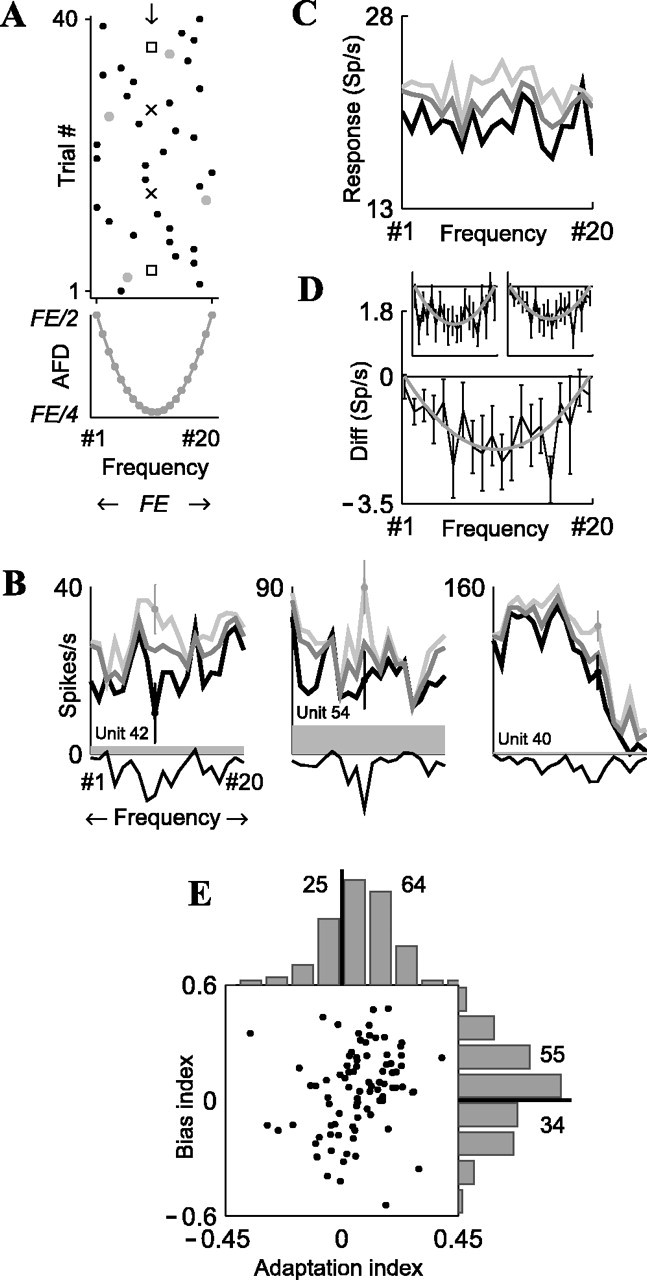
Adaptation-induced bias in neuronal response curves measured over a narrowband range of 0.97 octaves (A1; n = 89 neurons). A, Response-curve design (see also Fig. 1C). Stimuli were tones of 20 frequencies × 10 repetitions each, totaling 200 trials (dot raster illustrates the first 40 trials). Gray circles, Trials preceding the occurrences of frequency 10 (denoted by arrow). At frequency 10, the near trials (□) and the far trials (×) are marked separately (see Results for definitions). U-shaped curve, Theoretical average frequency difference (AFD) of each tone from the preceding trials. B, Three neurons in primary auditory cortex, showing for each neuron the far (light gray), full (dark gray), and near (black) response curves and the full - far difference curve (plotted below each graph). Error bars represent SEM, averaged across frequencies. Gray rectangles indicate spontaneous firing rate ± SD. C, Mean population responses for neurons with an average full firing rate of more than five spikes per second (Sp/s) (n = 42). D, Difference curve of the population responses (black), overlaid with the U-shaped average frequency difference curve (gray), demonstrating the U-shaped bias in narrowband response curves. Main plot, Full - far (n = 42 neurons); left inset, near - far (n = 42); right inset: full - far for all of the neurons (n = 89). Error bars, SEM y-axis limits for left and right insets: -7.5-1.5 and -2.25-0.45 spikes/sec, respectively. E, Scatter plot of bias index versus adaptation index. Histograms, Index distributions, together with numbers of neurons above and below 0 (black lines).

To understand the possible effect of adaptation, we consider only the one-trial effect demonstrated above, whereby the adaptation strength is correlated negatively with the frequency difference from the stimulus at the preceding trial (see also Brosch and Schreiner, 1997). For our uniformly distributed stimuli, the average frequency difference from preceding trials has a U shape (Fig. 11A, bottom), equaling FE/4 for frequencies at the center of the frequency range (“central” frequencies) (Fig. 11A, arrow) and FE/2 for frequencies at the edges of this range (“eccentric” frequencies). Because of the one-trial effect, it may be expected that adaptation should be minimal in trials preceded by dissimilar stimuli. Furthermore, Figure 11A suggests that the responses to central frequencies should adapt more strongly than the responses to eccentric frequencies, potentially creating a U-shaped bias in measured response curves.

To test the prediction that adaptation is minimal in trials preceded by dissimilar stimuli, we computed the “full” response curves of neurons (based on all 10 repetitions of each frequency), as well as response curves based on subsets of the trials: “far” curves, based on trials preceded by dissimilar stimuli (differing by > FE/4; the exact value did not affect the results much), and “near” curves, based on trials preceded by similar stimuli (differing by < FE/4). Response curves of three neurons are displayed in Figure 11B. Compared with the far condition (light gray), in which adaptation was expected to be minimal, the adaptation appeared to be stronger in the full condition (dark gray) and even stronger in the near condition (black). This adaptation was also seen in population averages (Fig. 11C) (Wilcoxon signed rank test; pooling all neurons times all frequencies: p < 10^-15 for far - full and for full - near).

To quantify the overall tendency of a neuron to undergo adaptation, we used an adaptation index, computed as the contrast between the total spike counts evoked in the far and near conditions: adaptation index = (far - near)/(far + near). The adaptation index was positive in 72% of the neurons (64 of 89 neurons; Wilcoxon signed rank test: p < 10^-5), and moreover, 24% of the neurons (21 of 89) had an adaptation index >0.1666, corresponding to a >40% increase in firing rate in the far relative to the near adaptation condition.

To test the predicted U-shaped bias in the full response curve, we compared it with the far curve (in which adaptation is minimal). The population average of the full - far difference curves (Fig. 11D) did indeed have the expected U shape, which was also similar to the U-shaped curve of the average frequency difference displayed in Figure 11A (Pearson correlation: r = 0.685, 0.467, and 0.634 for main plot, left inset, and right inset, respectively, of Fig. 11D, with df = 18, p < 0.001, p < 0.05, and p < 0.005). This effect was seen, although not very strongly, in many individual neurons (Fig. 11B, plots below each graph). To quantify this, we used a bias index, computed as the correlation of the U-shaped average frequency difference curve in Figure 11A with the full - far difference curve for each neuron. The bias index was positive on average (Fig. 11E, right histogram) (55 of 89 neurons; Wilcoxon signed rank test: p < 0.05), suggesting the presence of a U-shaped bias in most neurons.

We expect that the stronger the adaptation, the more pronounced should be the U-shaped bias. Indeed, the adaptation index (Fig. 11E, top histogram) and the bias index (Fig. 11E, right) were correlated (Fig. 11E) (Spearman correlation: r_s = 0.30; df = 87; p < 0.005), suggesting that neurons with a stronger tendency to adapt also show a stronger U-shaped bias in their response curves.

The bias was maximal at the center of the frequency range used in the experiment (Fig. 11D), rather than at the location of the peaks of the individual response curves. In fact, the peaks of the response curves were not necessarily at the center of the frequency range. The average population tuning curve was flat (Fig. 11C), suggesting uniform distribution of peak locations. This happened because we recorded simultaneously from several neurons that often had somewhat different BFs (see Materials and Methods) and hence had different peak locations for the response curves. Furthermore, no significant difference from zero was found for a centrality index, defined as the correlation of the U-shaped curve from Figure 11A with the full response curve of the neuron (Wilcoxon signed rank test: T = 1871, df = 88, p = 0.59). Thus, the observed bias (Fig. 11D) cannot be explained by strong activity-dependent adaptation at the peak of the response curve but is more likely caused by the stimulus-specific bias mechanism proposed above.

These data demonstrate that measuring response curves using unbiased sets of stimuli (randomized, equiprobable, equal amplitude) may nevertheless result in a U-shaped bias, at least when using a narrow frequency range, as we did here. This bias is largest at the middle of the frequency range used. Such bias is not expected for angular parameters such as the orientation of visual stimuli (Müller et al., 1999; Dragoi et al., 2000), where no “center” or “edges” exist (provided that the stimuli evenly cover all possible orientations); however, for other parameters for which stimulus-specific adaptation has been shown, such as spatial frequency (Saul and Cynader, 1989a) and temporal frequency (Saul and Cynader, 1989b) of visual stimuli, we would expect such an adaptation-induced U-shaped bias in neuronal responses.

Discussion

We demonstrated here multiple time scales of adaptation in A1, spanning several orders of magnitude, from milliseconds to tens and possibly hundreds of seconds. Furthermore, a simple linear model, taking into account both the local and global history of the sequence preceding a stimulus, accounted for a high proportion of the variance in the responses of A1 but not of MGB neurons.

Multiple time scales of adaptation in A1

Previous studies that examined the effect of stimulus history on neurons in A1 and primary visual cortex focused either on long-term history, using prolonged adapting stimulation (Movshon and Lennie, 1979; Saul and Cynader, 1989a; Condon and Weinberger, 1991; Dragoi et al., 2000), or on short-term history, using pairs of stimuli (Calford and Semple, 1995; Brosch and Schreiner, 1997; Müller et al., 1999).

Here we used designs in which the stimulus contained several time scales, and this allowed us to reveal several concurrent time scales of neuronal adaptation, ranging from milliseconds to tens and possibly hundreds of seconds (Figs. 5, 6). The response of cortical neurons during tone presentation is well known to adapt rapidly, and here we have shown that it can be fit with two time constants (τ ∼6.6 and τ ∼150 msec) (Fig. 6E). The adaptation time constant was progressively slower for the local sequence preceding the stimulus (τ_M ∼1.5 sec) (Fig. 8), for the stimulus statistics (τ ∼3-15 sec) (Fig. 6B,C), for the long-term stimulus metastatistics (τ ∼48 sec) (Fig. 6D), and for the very long-term 800 trial stimulus presentation (τ ∼630 sec) (Fig. 6D), although this effect was weaker than the others documented here. Thus, neurons in A1 seem to adapt to any time scale present in the stimulus.

Interestingly, previous studies in A1 have reported short time scales when using short stimuli (Brosch and Schreiner, 1997), medium time scales for medium-duration stimuli (Malone et al., 2002), and long time scales for long-stimulation designs (Condon and Weinberger, 1991). Together with our results, this indicates that the time constant of neuronal adaptation in A1 may perhaps scale with the stimulus duration, similar to the power-law scaling of adaptation observed in visual neurons of the fly (Fairhall et al., 2001) and even in isolated Na⁺ channels (Toib et al., 1998).

Finally, not all of these time constants of adaptation are stimulus specific. The longest time constant (τ = 630 sec) and the two shortest time constants (6.6 and 150 msec) are not necessarily stimulus specific but could reflect activity-dependent “fatigue.” The stimulus-specific components had time constants that ranged from τ_M ∼1.5 to τ ∼48 sec. We have shown previously that SSA also exists when shortening the interstimulus interval to 375 msec (Ulanovsky et al., 2003), and other reports have demonstrated SSA for yet shorter intervals (Calford and Semple, 1995; Brosch and Schreiner, 1997). Therefore, when considering SSA as a possible mechanism of auditory sensory memory in single neurons, we conclude that this auditory memory has a time span that lasts between a few hundred milliseconds and a few tens of seconds, depending on the stimulus. Interestingly, these numbers are very similar to the time span of auditory memory in humans, as derived from both behavioral (Cowan, 1984) and evoked-potential (Bottcher-Gandor and Ullsperger, 1992; Cowan et al., 1993) studies.

Mechanisms of adaptation

Adaptation mechanisms can be divided into two classes (Gollisch and Herz, 2004): (1) mechanisms operating at the output of the neuron, such as activation of voltage-dependent conductances (Sanchez-Vives et al., 2000a,b) or tonic hyperpolarization (Carandini and Ferster, 1997), both of which operate at the level of the somatic membrane potential and cannot be stimulus specific, and (2) mechanisms operating at the inputs to the neuron, such as synaptic depression and facilitation (Abbott et al., 1997; Tsodyks and Markram, 1997) or inhibition (Zhang et al., 2003), both of which may differentially affect different parts of the dendritic tree of the neuron and thus may be stimulus specific. Our data showed that in many neurons, the responses were enhanced for frequency f₁ when f₁ was deviant and for f₂ when f₂ was deviant (Fig. 2) (Ulanovsky et al., 2003); furthermore, the f₂ - f₁ response difference was uncorrelated with the SI (Fig. 3B,C), implying that it made no difference whether the two frequencies elicited the same initial activity. These findings argue strongly against activity-dependent adaptation and suggest a contribution by mechanisms operating at the inputs to the neuron.

Synaptic depression of thalamocortical synapses has been shown to contribute to activity-dependent adaptation in somato-sensory and olfactory cortices (Chung et al., 2002; Best and Wilson, 2004), and in principle, such depression might also account for stimulus-specific adaptation. The longer latency of SSA compared with the latency of the neuronal responses (Ulanovsky et al., 2003) suggests the involvement of intracortical processing, however, so the depressing synapses involved may be corticocortical rather than thalamocortical. Interestingly, recovery of corticocortical synapses from depression is best described by several time constants coexisting together (Varela et al., 1997), ranging between a few hundreds of milliseconds and a few tens of seconds (Tsodyks and Markram, 1997; Varela et al., 1997; Markram et al., 1998), which matches the stimulus-specific time constants described here.

Stimulus-specific changes in inhibition (Wehr and Zador, 2003; Zhang et al., 2003) could provide an alternative mechanism for SSA. A recent study (Eytan et al., 2003) demonstrated an analog of SSA in ex vivo networks of cortical neurons. Eytan et al. (2003) used an analog of the oddball design by stimulating two points in the network, one at a high rate and another at a lower rate. They found a depression in the responses to the standard and an increase for the deviant, and this selective enhancement of responses was abolished by blocking GABAergic inhibitory transmission using bicucculine. An inhibitory mechanism is consistent with recent intracellular studies in A1 (Wehr and Zador, 2003; Zhang et al., 2003), which showed that the input to A1 neurons is composed of a balanced combination of excitation and inhibition, during which the inhibitory input follows the excitatory input with some time delay. The longer delay of the inhibition may account for the longer latency of SSA; however, it remains to be seen whether such inhibition has time constants that are slow enough to account for the longer time constants of SSA demonstrated here.

Finally, both of these mechanisms would face the challenge of explaining the robust SSA evoked by frequency differences as small as Δf = 0.10 (Fig. 2) and Δf = 0.04 (Ulanovsky et al., 2003). This Δf is substantially smaller than the typical peripheral tuning width, and hence the standard and deviant tones presumably activate highly overlapping sets of inputs to MGB and A1 neurons. Therefore, a more complex network effect might be necessary to explain SSA.

SSA and sensory memory

Two components of the evoked potentials were studied extensively using the auditory oddball design: the mismatch negativity (MMN), which originates in the auditory cortex (Näätänen, 1992; Tiitinen et al., 1994; Jääskeläinen et al., 2004), and the P300, which has diffuse origins centered mostly in frontal cortex (Escera et al., 2000; Friedman et al., 2001; Ranganath and Rainer, 2003). The MMN is an early preattentive component implicated in sensory memory; the P300 is a later component, implicated in attention shift and behavioral orienting responses (Escera et al., 2000).

The relationships of MMN and P300 are currently unclear. We have suggested previously that SSA provides a detailed single-neuron correlate of MMN (Ulanovsky et al., 2003). Although the sensory processing mechanisms operating in awake behaving animals may be substantially richer than those studied here (Fritz et al., 2003; Weinberger 2004), our present results in anesthetized cats nevertheless provide an interesting link among P300, MMN, and SSA, in that they are all similarly influenced by stimulus history. Squires et al. (1976) used the same linear model as we did (Fig. 8) to describe the influence of sequence history on P300, reporting very similar results, including a similar value of the local memory parameter α (α = 0.6 in their study; α = 0.51 in ours). Although we are not aware of a study that applied the same linear model to MMN, there were several studies that demonstrated a one-trial effect for MMN (Sams et al., 1983, 1984; Jääskeläinen et al., 2004), similar to our result for SSA. In addition, several other similarities exist among SSA, MMN, and P300. The magnitude of all three increases with deviant rarity, it increases with the parametric deviance of the deviant, and they all show long time constants of seconds or tens of seconds (Näätänen, 1992; Cohen and Polich, 1997; Yago et al., 2001; Ulanovsky et al., 2003). On the basis of this, we speculate that at least some of the simpler properties of P300 may be inherited directly from the MMN, which in turn is attributable to SSA in auditory neurons.

In summary, we have shown that A1 neurons are sensitive to past auditory events for tens of seconds. The lack of such sensitivity in auditory thalamus, for the same stimulus parameters for which it was clearly present in A1, implies a function that is unique to A1. Many years of research have indicated that the performance of A1 neurons is not better than, and is probably even worse than, subcortical neurons, when comparing standard measures of sensory coding such as width of tuning curves and temporal response properties (Creutzfeldt et al., 1980; Miller et al., 2001; Joris et al., 2004). Therefore, we propose that we need to consider higher-level functions, such as sensory memory, if we want to understand the role of A1 in auditory processing.