Augmentation Increases Vesicular Release Probability in the Presence of Masking Depression at the Frog Neuromuscular Junction

Abstract

Synaptic augmentation is a short-term component of synaptic plasticity that increases transmitter release during repetitive stimulation and decays thereafter with a time constant of ∼7 sec. Augmentation has typically been observed under conditions where there is little or no depression because of depletion of synaptic vesicles from the readily releasable pool (RRP) of transmitter. We now study augmentation under conditions of pronounced depression at the frog neuromuscular junction to gain additional insight into mechanism. If augmentation reflects an increase in the size of the RRP of transmitter, then augmentation should not be present with depression. Our findings using four different experimental approaches suggested that augmentation was still present in the presence of pronounced depression: mathematical extraction of augmentation from the changes in transmitter release after repetitive stimulation, identification of augmentation with Ba²⁺, correction of the data for the measured depletion of the RRP, and identification of an augmentation component of residual Ca²⁺. We conclude that the augmentation machinery still acts to increase transmitter release when depression reduces the RRP sufficiently to mask obvious augmentation. The masked augmentation was found to increase transmitter release by increasing the probability of releasing individual vesicles from the depressed RRP, countering the effects of depression. Because augmentation and depression have similar time courses, either process can mask the other, depending on their relative magnitudes. Consequently, the apparent absence of one of the processes does not exclude that it is still contributing to short-term synaptic plasticity.

Introduction

Repetitive stimulation of synapses changes the amount of transmitter released by each nerve impulse (Magleby, 1987; Regehr and Stevens, 2001; Zucker and Regehr, 2002). Such short-term synaptic plasticity has been divided into processes of synaptic enhancement that increase transmitter release and synaptic depression (D) that decrease release. Components of enhancement include facilitation, augmentation (A), and potentiation (P), with time constants of <1 sec, ∼7 sec, and tens of seconds to minutes, respectively (Mallart and Martin, 1967; Rosenthal, 1969; Magleby and Zengel, 1976a; McNaughton, 1982; Poage and Zengel, 1993). Components of depression include very fast, fast, and slow components with time constants of recovery of <0.5 sec, ∼6 sec, and tens of seconds to minutes, respectively (Takeuchi, 1958; Magleby, 1973b; Dittman and Regehr, 1998; Wu and Betz, 1998; Stevens and Wesseling, 1999b; Wesseling and Lo, 2002)

In this report, we study the interaction between augmentation and the fast (∼6 sec) component of depression to determine whether augmentation continues to enhance transmitter release when depression dominates the response. Such studies are essential, because studies of augmentation have typically been performed under conditions where there is little or no depression. Under such conditions, Magleby and Zengel (1976b) found, with successive conditioning-testing trials, that the magnitude of augmentation continued to increase as depression was starting to develop. They argued that if depression is a depletion of the synaptic vesicles immediately available for release, then augmentation could not arise from an increase in the same pool of vesicles, because both an increase and a decrease in the same pool could not occur simultaneously. Stevens and Wesseling (1999a) directly measured the size of the readily releasable pool (RRP) of synaptic vesicles and found that the RRP was not increased when augmentation was present. Because the RRP was not increased, they concluded that augmentation was a potentiation of the vesicular release process. In contrast, Rosenmund et al. (2002) have found, for a synapse with the mammalian unc 13-2 (Munc13-2) priming protein, that augmentation arises from both an increase in the size of the RRP and also from an increase in the vesicular probability of release. If augmentation requires an increase in the size of the RRP at the frog neuromuscular junction (NMJ), then augmentation should not be present if depression reduces the size of the RRP.

To test this possibility, we now examine augmentation under conditions of pronounced depression. We find that augmentation is still present when depression is sufficiently large to mask augmentation. Mathematical analyses of the recovery from depression, application of Ba²⁺ to identify augmentation, and measurements of residual Ca²⁺ all suggested the presence of a masked augmentation. The size of the RRP was decreased when augmentation was present during depression, indicating that augmentation arises from an increase in the fraction of vesicles released from the RRP. Our findings show that augmentation is a major factor acting to sustain transmitter release in the presence of depression, and that the absence of detectable augmentation by traditional conditioning-testing techniques is not sufficient to exclude that augmentation is present and enhancing release.

Materials and Methods

Preparation, recording, and solutions. Endplate potential (EPP) amplitude was used as a measure of evoked transmitter release, as in previous studies (Fatt and Katz, 1951; Del Castillo and Katz, 1954; Magleby, 1973a; Wu and Betz, 1998). EPPs were recorded from cutaneous pectoris nerve-muscle preparations (Wu and Betz, 1996, 1998) from both northern and southern varieties of the frog Rana pipiens and also in a few experiments from the sartorius nerve-muscle preparation (Fatt and Katz, 1951). Extracellular recording of EPPs was performed with a surface electrode constructed from either a polyethylene tube or a fire-polished glass capillary tube with internal diameters of ∼0.3-0.6 mm. The surface electrode was filled with the same solution as in the bath and positioned over an endplate region to obtain a maximal positive or negative amplitude response while just lightly touching the muscle surface. Surface recording averages the response from many endplates and gives a good measure of average intracellular activity (Magleby, 1973a). Such averaging reduces the number of trials required to average quantal fluctuation. Intracellular recordings used to determine quantal content were obtained with 5-60 MΩ glass microelectrodes filled with 3 m KCl using the Geneclamp amplifier (Axon Instruments, Foster City, CA). Electrode placement at the endplates was determined by inserting the electrode along a muscle fiber until maximal EPP amplitude was achieved (Fatt and Katz, 1951). Results from previous studies indicate that postsynaptic sensitivity would be expected to remain constant for the conditions of our experiments (Magleby and Pallotta, 1981; Zengel and Sosa, 1994). Thus, the changes in EPP amplitude in our experiments reflect changes in transmitter release.

The muscle was stretched slightly and pinned into a chamber. The standard bathing solution had the following composition (in mm): 115 NaCl, 2 KCl, 2 CaCl₂, 5 MgCl₂, 2 HEPES, 5 glucose, and 0.03 choline chloride. The pH was adjusted to 7.3. The concentration of Ca²⁺ (added as CaCl₂) was changed for some experiments as indicated. Curare, which binds reversibly with postsynaptic acetylcholine receptors, was added as needed, typically 3-6 μm, to reduce the amplitudes of the EPPs sufficiently to prevent action potentials and minimize nonlinear summation of EPP amplitudes (McLachlan and Martin, 1981). Suprathreshold stimulus pulses of 0.1 msec duration were administered to the nerve through a suction electrode using an optically isolated stimulation unit. Experiments were performed at 18-21°C.

Stimulation patterns were generated by computer using custom software designed for Windows 2000-based computers, and the resulting potentials were recorded with 16 bit resolution at 10 kHz with a DT-3016 digital-to-analog and analog-to-digital (A/D) converter via the DTx-EZ OLE programming interface (Data Translation, Marlboro, MA) and stored digitally. The dynamic range of the A/D converter allowed large changes in EPP amplitude to be measured accurately. The program displayed each EPP during the conditioning-testing trials, measured each EPP amplitude, and also displayed the EPP amplitudes divided by the control EPPs. Hence, the progress of each experiment was monitored in real time. The entire record during each conditioning-testing trial was also stored in digital format for later review.

EPP amplitudes were measured as the average of the five highest sampling points minus the average value of five baseline sampling points measured before the stimulation for that EPP. When the stimulation rate was fast enough that EPPs were evoked before the full decay of a previous EPP (such as when stimulation was applied at 125 Hz to measure the readily releasable pool), the baseline was determined by extrapolating the decay of the previous EPP to the time at which the peak amplitude of the following EPP occurred. Conditioning-testing trials were evaluated for consistency throughout each trial and from trial to trial. In some trials, large erratic changes in EPP amplitude would occur. This was assumed to result from nerve failure, and these trials were discarded, as in previous studies of this type (Magleby and Zengel, 1976a).

Additional analysis was performed using Windows 2000-based computers with custom software and IGOR Pro (WaveMetrics, Lake Oswego, OR). Trials taken under the same experimental conditions from the same muscle were typically averaged together to reduce variability. In a few instances, such as for data taken at low quantal content, trials from different muscles were also averaged. To measure miniature end plate potential (MEPP) amplitude, records were recorded in axon binary format files and analyzed using the Mini Analysis program (Synaptosoft, Leonia, NJ).

Estimating the components of enhancement and depression. Estimates of the contributions of the components of enhancement and depression to transmitter release were made by assuming the following:

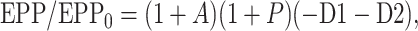Scheme1

where EPP/EPP₀ is the ratio of the EPP amplitude at time t to the EPP amplitude at time 0 before the conditioning train and D1 and D2 are fast and slow components of depression (Magleby and Zengel, 1982; Zengel and Magleby, 1982; Magleby, 1987; Stevens and Wesseling, 1999a; Dittman et al., 2000; Regehr and Stevens, 2001; Zucker and Regehr, 2002). A, P, D1, and D2 are defined as the fractional change in a testing EPP amplitude over control in the absence of the other processes such that:

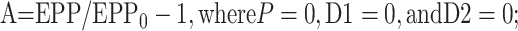1a

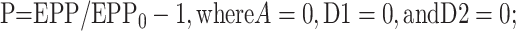1b

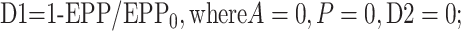1c

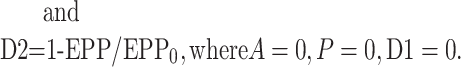1d

With this definition, a magnitude of 1.0 for augmentation or potentiation would double the size of the EPP, and a magnitude of 1.0 for depression would reduce EPP amplitude to 0. For Scheme 1, the magnitude of a component, Y, at any time, t, after the conditioning train, where Y represents A, P, D1, or D2, is described by the following:

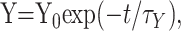2

where Y₀ is the magnitude of the component immediately following the conditioning train, and τ_Y is the time constant of decay for A and P and the time constant of recovery for D1 and D2. Estimates of the magnitude and time constant of each component after conditioning trains were obtained by fitting Scheme 1 to the testing EPP amplitudes after the conditioning trains using the Levenberg-Marquardt nonlinear least squares fitting routine in IGOR. Each fit was repeated 5-10 times using different sets of initial parameters to assure that the best parameters were obtained. This fitting process was repeated when one or more of the parameters were set to 0 and in all possible combinations of components to determine whether the data could be described with fewer than four components. Facilitation, which decays to insignificant levels in ∼1 sec (Mallart and Martin, 1967; Zengel and Magleby, 1982), was excluded from the fitting by applying the first testing EPPs ≥1 sec after the conditioning train. Fitting simulated data similar to the experimental data indicated that the components could be recovered from the simulated data with this systematic procedure, although the solutions were not always unique (see Results).

In addition to Scheme 1, three additional schemes with various combinations of additive interactions between A and P and multiplicative interactions between D1 and D2 were also used to analyze the data, and the same general conclusion was obtained: augmentation was typically present at normal quantal content, even when masked by depression. The estimates of the components presented in this study are based on Scheme 1, because this scheme generally described the data with the least error and because previous experimental findings are consistent with Scheme 1: a multiplicative interaction between augmentation and potentiation is consistent with studies under conditions of low quantal content (Magleby and Zengel, 1982; Zengel and Magleby, 1982), and an additive interaction between the components of depression is consistent with recovery from depression through parallel pathways that supply vesicles to the RRP (Kuromi and Kidokoro, 1998; Richards et al., 2000, 2003; Gandhi and Stevens, 2003; Rizzoli and Betz, 2004).

Quantal variation and other experimental error would be expected to introduce variation of the EPP amplitudes about the mean response, introducing some uncertainty in the estimated values of the time constants and magnitudes of the components. As a test of these error estimates, multiple fits of simulated data with random Gaussian errors equal to 1% of the mean EPP amplitude (an error similar to the scatter in typical experimental data about the fitted curves) gave error estimates similar to those given by the fitting routine.

Imaging. Fluorescence ratio imaging techniques were used to measure average intracellular free Ca²⁺ in motor nerve terminals during and after repetitive stimulation (Almers and Neher, 1985; Delaney et al., 1989; Suzuki et al., 2000). Ca²⁺ indicators were loaded into frog motor nerve terminals by backfilling the nerves (Peng and Zucker, 1993; Wu and Betz, 1996). The motor nerve was cut a few millimeters proximal to where it branched into the cutaneous pectoris muscle. The preparation was pinned onto a Sylgard-coated polystyrene Petri dish and covered with bathing solution. A thin annulus of Vaseline (inner diameter, ∼2 mm) was placed such that the cut end of the nerve was exposed in the center. A small drop (0.5 μl) of highly concentrated indicator dye (50 mm fura-2, bis-fura-2, or fura-2 dextran; Molecular Probes, Eugene, OR) was pipetted into the center of the Vaseline ring to immerse the nerve ending in dye. Immediately thereafter, a short section of the nerve ending was cut off with iris scissors to ensure that a route for dye diffusion was available. The dish was covered and protected from light and held at room temperature for 2-3 hr. The preparation, with the dye loading in progress, was then placed in a refrigerator overnight for experimentation the following morning. EPPs similar in size and shape to those obtained from muscles without dye loading were readily elicited.

Terminals loaded with indicator were imaged in ratio pairs with 340 and 380 nm illumination using the TILL Photonics Imaging System II (TILL Photonics, Martinsried, Germany) and a Nikon (Tokyo, Japan) Eclipse E600FN upright microscope equipped with a Nikon 60× fluorescence objective (2 mm working distance). During typical conditioning-testing trials, pairs of images were acquired with 10 msec of exposure at each wavelength, separated by a 5 msec interval. Precise timing of image acquisition in relation to nerve stimulation was accomplished by acquiring each pair of images only when the TILL Photonics system was triggered by the custom software used to stimulate the nerve. Results did not depend on the order of exposure to the 340 and 380 nm illumination. To examine slow calcium transients associated with augmentation, the image pair was taken just before stimulation to allow the greatest possible time for the fast Ca²⁺ transients to decay after the previous impulse. During the conditioning train, image pairs were acquired once every fourth EPP to reduce indicator bleaching.

The sequences of images acquired during the trials were analyzed using TILLvisION (TILL Photonics) macros and IGOR. Outlines of the terminal on each image were determined using an automated threshold routine, and the average fluorescence intensity was determined for the area within the outline, during and after the conditioning train. This procedure resulted in consistent, reliable outlines in each image frame in relationship to the nerve terminals, even if slight movement occurred in the plane of the image. Background fluorescence measured from areas of muscle with no nerve terminals was subtracted before ratios were calculated. The imaging system was calibrated by measuring florescence ratios in buffered standardized solutions from the fura-2 Ca²⁺ Imaging Calibration Kit (Molecular Probes) with concentrations ranging from 0 to 39 μm free Ca²⁺. To adjust for in situ differences in ionic strength, viscosity, and Ca²⁺ buffering by lipids and proteins, minimum and maximum ratios were decreased by 30% (Almers and Neher, 1985; Wu and Betz, 1996; Petr and Wurster, 1997), and the measured K_d was set to the reported value of the in situ measurement of Petr and Wurster (1997). Ratios were then converted to [Ca²⁺] using Equation 5 in the study by Grynkiewicz et al. (1985). We checked for saturation of the Ca²⁺ indicator by performing the same type of experiments using different dyes with different affinities. With bis-fura-2, an indicator with properties similar to fura-2 but with a lower affinity for Ca²⁺, similar changes in Ca²⁺ were observed. More importantly, the measured levels of free Ca²⁺ at the time of the apparent augmentation component of the decay of free Ca²⁺ were typically threefold to fourfold less than the peak measured Ca²⁺ immediately after the train, indicating that the indicators were well below saturation when measuring augmentation. Furthermore, estimates of the levels of free Ca²⁺ in the nerve terminal obtained by calibrating each indicator against known concentrations of Ca²⁺ demonstrated that the Ca²⁺ indicators used in this study were working well below their range of saturation when estimating the augmentation component of free Ca²⁺.

The decay of free residual Ca²⁺ was analyzed in a manner similar to the analysis of the decay of EPP amplitudes, except that only additive components were considered, such that:

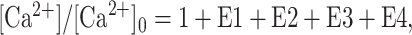3

where E1, E2, E3, and E4 are components of [Ca²⁺] that decay exponentially with time, as described by Equation 2. Typically, only two or three components of Ca²⁺ decay were evident. Because there was no apparent depression of residual Ca²⁺ as there was for transmitter release, the fits were typically well defined.

Error estimates. Unless otherwise indicated, the estimates of the parameters describing the components of decay of EPP amplitudes and residual Ca²⁺ after the trains are expressed as the estimated parameter value ± the 95% confidence interval, calculated with the Levenberg-Marquardt nonlinear least squares fitting routine in IGOR. Each decay that was fit typically represented the average of experimental responses obtained under identical experimental conditions from either the same preparation or from multiple preparations, as indicated. Averaging experimental data in this manner before fitting greatly reduces the variability arising from both quantal fluctuation and noise before the fitting process. In some cases specifically indicated, data from different preparations are fitted separately and then compared using the means ± SEMs.

Results

EPPs were recorded from frog cutaneous pectoris and sartorius muscles to examine the contribution of augmentation and depression to stimulation-induced changes in transmitter release under levels of low and normal quantal content and to examine the mechanism underlying these processes. Four approaches were used to identify, characterize, and explore mechanisms of augmentation and depression: (1) kinetic analysis of the decay of EPP amplitudes after conditioning stimulation; (2) identification of augmentation by its characteristic enhancement by Ba²⁺; (3) measurement of the decay of intracellular Ca²⁺ after repetitive stimulation; and (4) measuring changes in the RRP of transmitter during these processes. Under the conditions of these experiments, changes in EPP amplitude should give a good measure of changes in transmitter release (see Materials and Methods).

Augmentation and potentiation of transmitter release are readily observed at low quantal content when depression is negligible

Figures 1 and 2 show stimulation-induced changes in transmitter release using identical stimulation patterns for conditions of low quantal content with negligible depression (Fig. 1) (0.4 mm Ca²⁺ and 5 mm Mg²⁺) and for conditions of normal quantal content with pronounced depression (Fig. 2) (2 mm Ca²⁺ and 5 mm Mg²⁺), demonstrating the dramatic difference in response under these two conditions (Regehr and Stevens, 2001; Zucker and Regehr, 2002). For each trial, the nerve was first stimulated once every 5 sec to establish a control response. The nerve terminal was then conditioned by stimulation at 20 Hz for 240 impulses. The effect of this conditioning stimulation was monitored by testing with single stimuli at 1, 3, 6, and 10 sec after the train and then by testing once every 5 sec for 40 impulses and once every 10 sec for 30 impulses. Figure 1A presents examples of surface-recorded EPPs during a conditioning-testing trial at low quantal content, and Figure 1B presents the average EPP amplitudes for 121 such conditioning-testing trials from six different muscles. EPP amplitudes in Figure 1B are normalized to the control EPP amplitudes before the conditioning trains, represented by the first five control points, which did not change in amplitude.

Figure 1.

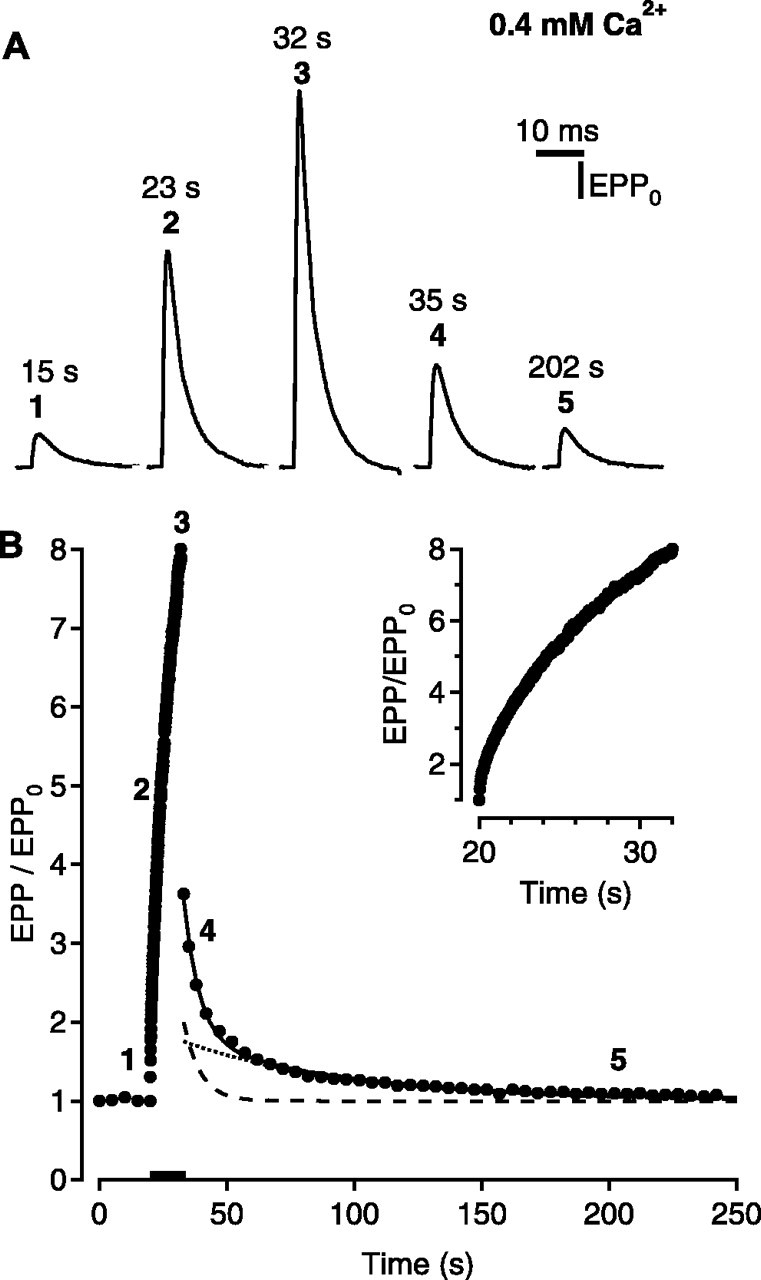
Short-term synaptic plasticity when the neuromuscular junction functions as a facilitating synapse. Low levels of Ca²⁺ (0.4 mm) were used to obtain low levels of transmitter release with minimal depression. The conditioning stimulation was 240 impulses at 20 per second, delivered during the time marked by the bar in B. A, Surface-recorded EPPs evoked before (1), during (2, 3), and after (4, 5) the conditioning stimulation. Stimulus artifacts were removed by connecting the baseline before and after the stimulus. The bold numbers for the averaged data in B indicate the times during the conditioning-testing trials when the surface EPPs were recorded. B, Plot of average EPP amplitudes (filled circles) versus time for 121 conditioning-testing trials from six experiments. The inset plots EPP amplitudes during the train. The continuous line is the predicted EPP amplitudes assuming EPP/EPP₀ = (1 + A)(1 + P) obtained by fitting with Scheme 1, where potentiation (dotted line) is given by τ_P = 64.5 ± 7.8 sec and P₀ = 0.77 ± 0.07, and augmentation (dashed line) is given by τ_A = 6.4 ± 0.6 sec and A₀ = 1.17 ± 0.10.

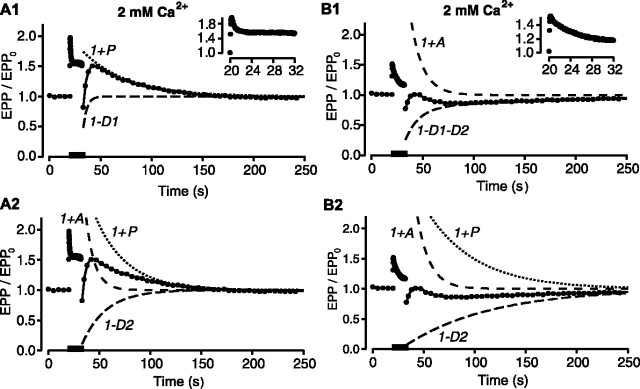
Figure 2.

Short-term synaptic plasticity when the neuromuscular junction functions as a depressing synapse. Normal levels of Ca²⁺ (2 mm) were used to give normal levels of release with high release probabilities and depression. A, B, Plots of EPP amplitudes versus time (filled circles) during conditioning-testing trials identical to those in Figure 1 for two different experiments. Insets plot EPP amplitudes during the trains. Bars indicate the time of conditioning stimulation of 240 impulses delivered at 20 per second. The components of short-term synaptic plasticity were estimated by fitting the EPP amplitudes after the trains with Scheme 1. The estimated components are plotted as dashed and dotted lines and are labeled as follows: D1, faster component of depression; D2, slower component of depression. The continuous lines are the EPP amplitudes predicted with Scheme 1 using the fitted components. Ten trials from one preparation were averaged for A, and 16 trials from another preparation were averaged for B. A1, Two components fit with potentiation (τ_P = 44.1 ± 2.1 sec; P₀ = 0.8 ± 0.03) and fast depression (τ_D1 = 3.7 ± 0.3 sec; D1₀ = 0.7 ± 0.02). A2, Three-components fit with a 56% reduction in χ² error compared with A1, with augmentation (τ_A= 10.3 ± 0.5 sec; A₀ = 2.8 ± 0.2), potentiation (τ_P= 38.5 ± 1.9 sec; P₀ = 3.8 ± 0.3), and slow depression (τ_D2 = 56.7 ± 6.0 sec; D2₀ = 1.0 ± 0.01). B1, Three-component fit with augmentation (τ_A = 11.9 ± 0.8 sec; A₀ = 2.2 ± 0.6) and fast (τ_D1 = 14.2 ± 4.6 sec; D1₀ = 0.6 ± 0.06) and slow (τ_D2 = 192 ± 32 sec; D2₀ = 0.2 ± 0.01) depression plotted as a single trace. B2, Three-component fit with a 12% reduction in χ² error compared with B1, with augmentation (τ_A = 12.3 ± 0.5 sec; A₀ = 3.1 ± 0.2), potentiation (τ_P = 48.4 ± 3.2 sec; P₀ = 2.0 ± 0.1), and slow depression (τ_D2 = 84.6 ± 4.5 sec; D2₀ = 0.94 ± 0.01).

During the conditioning train, the EPP amplitudes rapidly increased and then decayed back to control level after the train, with multiple apparent time constants, as has been reported previously (Magleby, 1979; Zengel et al., 1980; Zengel and Magleby, 1982; Regehr and Stevens, 2001; Zucker and Regehr, 2002). The immediate drop in EPP amplitude during the first second following the train is primarily attributable to the rapid decay of facilitation, which has a time course of <1 sec (Mallart and Martin, 1967; Magleby, 1973a; Zengel and Magleby, 1982; Zucker and Regehr, 2002). After the decay of facilitation, the EPP amplitudes decay with two components, augmentation and potentiation (Magleby and Zengel, 1976a). Augmentation and potentiation were estimated by fitting the decay of the EPP amplitudes after the train in Figure 1B, with Scheme 1, with depression set to 0, where the continuous line in Figure 1B is the predicted decay of the EPP amplitudes with this scheme. The decay of potentiation is shown in Figure 1B as a dotted line, with a projected magnitude immediately after the train, P₀, of 0.77 ± 0.07 and a time constant of decay, τ_P, of 64.5 ± 7.8 sec, and the decay of augmentation is shown in Figure 1B as a dashed line, with a projected magnitude immediately after the train, A₀, of 1.17 ± 0.10 and a time constant of decay, τ_A, of 6.4 ± 0.6 sec. The parameters characterizing augmentation and potentiation at low quantal content at frog NMJs obtained in this study with Scheme 1 with depression set to 0 were consistent with those reported previously (Magleby and Zengel, 1976a).

Depression dominates the response immediately after the conditioning train at normal quantal content

Examples of the two general types of response observed for stimulation-induced changes in transmitter release at normal quantal content are presented in Figure 2, A and B. In contrast to conditioning trains at low quantal content where EPP amplitudes increased monotonically eightfold during the train (Fig. 1B), at normal quantal content, EPP amplitudes increased only 1.5- to 2-fold followed by a decrease to a plateau level of 1.2-1.5 times the control level (Fig. 2A1, B1, insets). Just as at low quantal content, the immediate drop in EPP amplitude during the first second following the conditioning train was primarily attributable to the rapid decay of facilitation (Mallart and Martin, 1968). However, in contrast to the greatly increased testing EPPs measured 1 sec after the train at low quantal content, at normal quantal content, the EPP amplitudes dropped to a level that was below the control level, indicating that depression was present. From this depressed value, the testing EPP amplitudes then rose above the control level over time, suggesting that one or more of the slower decaying process that increase transmitter release during the train were obscured by depression immediately after the train, giving rise to classical posttetanic potentiation (Rosenthal, 1969; Magleby, 1973b; Zucker and Regehr, 2002). The depression may reflect a depletion of the RRP of synaptic vesicles during the train with recovery thereafter and perhaps also a decrease in the number of release sites (Takeuchi, 1958; Thies, 1965; Lass et al., 1973; Regehr and Stevens, 2001; Zucker and Regehr, 2002).

The pattern of stimulation used for the experiments in Figures 1 and 2 was designed to elicit and test for the components of augmentation, potentiation, and depression while minimizing the number of conditioning and testing stimuli required. Similar results were obtained when additional or fewer testing impulses were placed 1-15 sec after the train to test for augmentation and when the last 30 testing impulses delivered once every 10 sec were replaced with 60 impulses delivered once every 5 sec, but the additional testing impulses decreased the number of trials that could be obtained from the preparations for experiments at normal quantal content. Also performed, but not presented here, were experiments with different numbers and frequencies of stimuli during the conditioning trains. The findings from these experiments were consistent with those presented here.

Exploring the possible interplay between augmentation and depression with simulation

Because augmentation of the frequency of MEPPs is present under conditions when EPPs are depressed (Zengel and Sosa, 1994), one explanation for the apparent absence of augmentation of EPP amplitudes after the conditioning trains at normal quantal content (Fig. 2) is that augmentation is masked by depression. Because augmentation typically decays with a time constant of ∼7 sec (Magleby and Zengel, 1976a; Kamiya and Zucker, 1994; Stevens and Wesseling, 1999a), and the fast component of depression recovers with a similar time course (Takeuchi, 1958), the interplay between the decay of augmentation and the recovery of depression may be masking augmentation. This possibility is examined in Figure 3 for some expected magnitudes and time constants of each process.

Figure 3.

Simulated interplay between the effects of augmentation and depression on transmitter release. For all plots, normalized testing EPP amplitudes after a hypothetical conditioning train are simulated and plotted as continuous lines, assuming EPP/EPP0 = (1 + A)(1 - D). The components of augmentation and depression are plotted as dashed lines. A, Simulated EPP/EPP₀ with τ_D = 7 sec, D₀ = 0.5, τ_A = 7 sec, and A₀ = 0 - 1.5 in steps of 0.1. B, A special case with τ_D = 7 sec, D₀ = 0.7, τ_A = 7 sec, and A₀ = 0.7 that gives two identical mathematical solutions (continuous line). In one of these, augmentation is correctly revealed (Eq. 4), and in the other, depression completely masks augmentation (Eq. 5), giving a single faster false component of depression and no augmentation. C, An example of a case in which augmentation can mask depression, with τ_D = 7 sec, D₀ = 0.3, τ_A = 7 sec, and A₀ = 1.0. The dotted line is a simulation of EPP amplitudes with only augmentation, with τ_A = 9.1 sec, A₀ = 0.44, and no depression.

Figure 3A presents a simulation (in continuous time) of testing EPP amplitudes that would be observed after a hypothetical conditioning train in which EPP amplitude is given by the product of depression with a 6 sec time constant and a magnitude of 0.5 and augmentation with a 7 sec time constant and magnitudes that range from 0 to 1.5, such that:

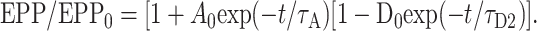4

A clear visual indication of augmentation, as indicated by a process of enhancement that decays with a time constant of ∼7 sec, did not become apparent until the magnitude of augmentation exceeded 0.6, indicating that depression can readily mask augmentation, and even when augmentation was observed, its magnitude was decreased by the depression.

When the time constants and the magnitudes of augmentation and depression are identical, then Equation 4 reduces to the following:

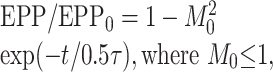5

with M₀ = A₀ = D₀ and τ = τ_A = τ_D. Thus, when A₀ = D₀ and τ_A = τ_D, Equation 5 is also a false solution to Equation 4 that indicates no augmentation and a single component of depression with a magnitude equal to the square of the magnitude of depression and with a time constant equal to one-half the actual time constant of depression. This is shown in Figure 3B, where the top dashed line is the decay of augmentation with a magnitude of 0.7 and a time constant of 7 sec, the bottom dashed line is the recovery from depression with a magnitude of 0.7 and a time constant of 7 sec, and the continuous line indicates both the true and false solutions for the testing EPP amplitudes that would be observed for this combination of augmentation and depression, as described by Equations 4 and 5, respectively. Thus, if the NMJ works as described by Equations 4 and 5, an observation of no augmentation and a component of depression with a fast time constant may simply reflect that augmentation and depression have very similar time constants and magnitudes so that depression completely masks augmentation.

The above examples in Figure 3, A and B, show that depression can mask augmentation. Figure 3C shows that augmentation can mask depression. This figure gives an example of two descriptions of the data that can be obtained when augmentation and depression have identical (or very similar) time constants, and the magnitude of depression is ≤0.3 and also considerably less than the magnitude of augmentation. The top dashed line indicates the decay of augmentation with a magnitude of 1.0 and a time constant of 7 sec, and the bottom dashed line indicates the recovery from depression with a magnitude of 0.3 with a time constant of 7 sec. The continuous line indicates the decay of EPP amplitudes that would be observed for these values of augmentation and potentiation. The dotted line, which approximates the data, indicates the EPP amplitudes that would be observed assuming that only augmentation with a magnitude of 0.46 and a time constant of 9.5 sec were present with no depression. Although the difference between the continuous and dotted lines in Figure 3C is obvious in this perfect data, for experimental data where there is facilitation at short times, quantal variation, and noise, this difference may not be apparent, leading to a possible erroneous conclusion that only augmentation with an apparent slower decay was present when, in fact, there was also significant depression. The observation that depression can slow the observed decay of augmentation is consistent with previous analysis (Qian and Delaney, 1997).

Recovering augmentation and depression from simulated data

For the simulated data in Figure 3, the magnitudes and time constants of the true components of augmentation and depression used to generate the EPP potential amplitudes were readily recovered by fitting the simulated data using the techniques described in Materials and Methods. For the case where A₀ = D₀ and τ = τ_A = τ_D, both the true and false solutions were obtained. For simulated data with variation in the EPP amplitudes resulting from added quantal fluctuation and noise and with facilitation for times <1 sec, fitting the simulated data showed that the true solutions for augmentation and potentiation were still typically obtained, but in addition, false solutions, sometimes with only one component when there should have been two, were also sometimes obtained (as in Fig. 3B,C). These false solutions for simulated data typically underestimated the magnitude of augmentation and overestimated its time constant. In a few cases in the simulated data, augmentation was completely masked by depression even when appreciable augmentation was present. However, in no case for simulated data in which the time constants of augmentation and depression were different did depression create a false component of augmentation when augmentation was not initially present.

Estimates of augmentation, potentiation, and depression at normal quantal content

Having found by simulation that it should be possible to estimate augmentation, if present, from experimental data with depression, the testing EPP amplitudes after the conditioning trains in Figure 2 obtained at normal quantal content were fitted with Scheme 1. Augmentation, potentiation, and depression estimated with Scheme 1 are plotted as dashed and dotted lines in Figure 2. The predicted EPP amplitudes using these components (continuous lines) provided excellent descriptions of the data. Figure 2, A and B, presents two types of typical responses. For each experiment, the data could be described with different combinations of components, although in each case, the second descriptions (A2 and B2) gave less error.

Figure 2A presents an example of one of the experiments in which the data could be well described either with or without a component of augmentation. The predicted EPP amplitudes (continuous line) without a component of augmentation are shown in Figure 2A1, where components of potentiation (dotted line) and depression (dashed line) could describe the data. The predicted EPP amplitudes (continuous line) with a component of augmentation are shown in Figure 2A2, where components of augmentation (top dashed line), potentiation (dotted line), and depression (bottom dashed line) gave a better description (56% decrease in χ² error). Although including an augmentation component decreased the error, both fits were excellent. Consequently, although the data in Figure 2A are consistent with augmentation being present, they do not clearly establish its presence. Four of 15 experiments were of this type.

Figure 2B presents an example of an experiment where a component of augmentation was always detected when fitting the data. Figure 2B1 shows the predicted EPP amplitudes (continuous line) with a component of augmentation (top dashed line) and two components of depression (combined into the bottom dashed line). Figure 2B2 shows the predicted EPP amplitudes (continuous line) with components of augmentation (top dashed line), potentiation (top dotted line), and depression (bottom dashed line). Both fits detected augmentation, and both fits were excellent, with the fit in B2 having slightly less error (13% decrease in χ²). Five of 15 experiments were of this type, where a component of augmentation was always detected, even though the other components were not always well defined.

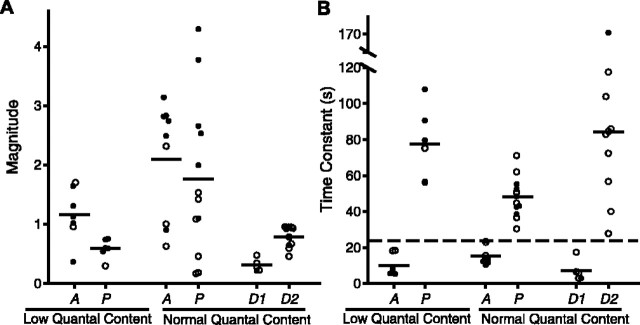
The results of 15 experiments at normal quantal content with the same stimulation pattern used in Figure 2 are summarized in Figure 4, together with the results from the experiments at low quantal content. The estimated parameters included in this figure are those associated with the fits with the smallest errors. Because components of transmitter release are typically identified by their time constants (Magleby, 1987; Regehr and Stevens, 2001; Zucker and Regehr, 2002), we used the time constants of decay to separate augmentation from potentiation. When both a fast and a slow component of enhancement were detected in the same experiment (data are plotted as filled symbols in Fig. 4), the fast component was designated as augmentation and the slower as potentiation. The slowest decay of the component designated as augmentation by this criteria was 24 sec. This value of 24 sec was then used to distinguish augmentation from potentiation when only one component of enhancement was detected. When the time constant of the single component was ≤24 sec, the component was designated as augmentation, and when the time constant was >24 sec, the component was designated as potentiation. For purposes of plotting in Figure 4, the same criteria of 24 sec was used to separate the fast and slow components of depression, because two components of depression were not observed a sufficient number of times to establish a critical time for separation. Because there are at most two of 22 points for which identity as augmentation or potentiation might be in doubt by this criteria, the conclusions of this study would not depend on the classification of these two points.

Figure 4.

Magnitudes (A) and time constants (B) of augmentation, potentiation, and depression after the conditioning train. Plotted estimates are for the best (lowest χ²) fits of Scheme 1 to EPP amplitudes evoked by testing impulses after conditioning trains delivered with the same pattern as in Figures 1 and 2. Results are presented for experiments at low quantal content obtained with low Ca²⁺ (0.4 mm) in which an enhancing response was observed and also for experiments at normal quantal content obtained with normal Ca²⁺ (2 mm) in which depression was observed. Filled symbols plot estimates of A and P when both were observed in the same experiment, and filled symbols also plot estimates of D1 and D2 when both were observed in the same experiment. Open symbols plot estimates of A or P when only a single enhancing component was observed in an experiment, and open symbols also plot estimates of D1 or D2 when only a single depressing component was observed in an experiment. Horizontal bars indicate the mean values for each column.

The mean time constant of decay of augmentation at normal quantal content (15.3 ± 1.6 sec) was slower than for data obtained at low quantal content (10.1 ± 2.2 sec) and can be compared with previous estimates at low quantal content for similar duration trains (7.2 sec; range, 4.5-9.5 sec) (Magleby and Zengel, 1976a). The mean time constant of decay of potentiation at normal quantal content (48.0 ± 3.3 sec) was faster than observed at low quantal content (77.7 ± 8.2 sec) and can be compared with previous estimates (∼65 sec) at low quantal content (Magleby and Zengel, 1976a). From Figure 4, it can be seen that the estimated time constants of the fast component of depression (7.1 ± 2.7 sec) are sufficiently close to those for augmentation to contribute to the masking of augmentation. Because errors in estimating augmentation in the presence of depression can increase the apparent time constant of augmentation (Fig. 3C) (Qian and Delaney, 1997), the true time constants of augmentation could be less than the estimated time constants, being even closer to the time constant of depression, allowing even greater masking.

The results from experiments like those in Figures 2 and 4 thus indicate that in 60% of the preparations, augmentation either was present or improved the fit at normal quantal content, even though this component was usually not obvious by visual inspection of the data. Because depression has the potential to mask the detection of augmentation, even when fitting with quantitative models (Fig. 3), it cannot be excluded that augmentation was also present in the remaining 40% of our experiments but went undetected.

Ba²⁺ identifies augmentation at normal quantal content

An important identifying characteristic of augmentation at low quantal content is that Ba²⁺ increases the magnitude of augmentation while having little affect on its time constant of decay or on potentiation (Zengel and Magleby, 1980, 1981; Zengel et al., 1980; Poage and Zengel, 1993). Thus, we examined whether the addition of Ba²⁺ to the bathing solution would increase the magnitude of the apparent component of augmentation observed in the previous section at normal quantal content. EPP amplitudes are presented during (Fig. 5A) and after (Fig. 5B) conditioning trains for experiments with 2 mm Ca²⁺ (filled circles) and after adding 2 mm Ba²⁺ (open circles). The addition of Ba²⁺ increased the enhancement of EPP amplitudes during the train (Fig. 5A) and converted the visually observed depression after the train to a large visually apparent component of augmentation (Fig. 5B). The effect of Ba²⁺ on augmentation was reversible, as shown for another experiment in Figure 5, C and D, where the numbers on the records indicate data first obtained with 2 mm added Ba²⁺ (1), then without added Ba²⁺ (2), and then again with 2 mm added Ba²⁺ (3). In five additional experiments with 2 mm added Ba²⁺, a visually obvious component of augmentation was present after the train. The time constants and magnitudes of augmentation and depression determined by fitting with Scheme 1 in the six experiments with added Ba²⁺ are shown in Figure 5, E (augmentation) and F (depression).

Figure 5.

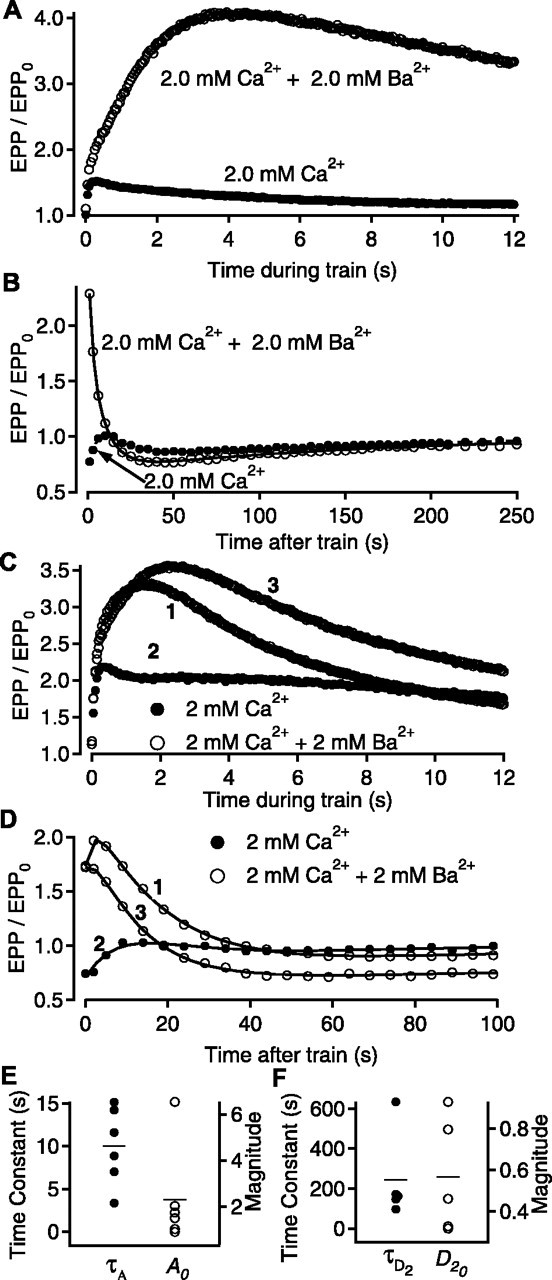
Ba²⁺ identifies augmentation at normal quantal content. A, B, Normalized EPP amplitudes are presented during (A) and after (B) conditioning trains for experiments with both 2 mm Ca²⁺ plus 2 mm Ba²⁺ (open circles) and 2 mm Ca²⁺ alone (filled circles). A clear augmentation component with Ba²⁺ was observed (continuous line, with τ_A = 8.9 ± 1.2 sec, A₀ = 1.8 ± 0.3; τ_D2 = 163 ± 22 sec, D2₀ = 0.32 ± 0.02). C, D, The enhancing effect of Ba²⁺ on augmentation was reversible. Normalized EPP amplitudes are shown during (C) and after (D) conditioning trains from a single experiment with 2 mm added Ba²⁺ (1), after washing out the Ba²⁺ (2), and after adding the Ba²⁺ again (3). The components after the train in part D: 1, τ_A = 15.5 ± 1.2 sec, A₀ = 3.2 ± 1.2, τ_D1 = 2.0 ± 0.9 sec, D1₀ = 0.14 ± 0.08, τ_D2 = 45.8 ± 12.9 sec, D2₀ = 0.44 ± 0.21; 2, τ_A 15.6 ± 1.4 sec, A₀ = 2.3 ± 0.3, τ_D1 = 27.8 ± 3.2 sec, D1₀ = 0.79 ± 0.02; and 3, τ_A = 11.3 ± 1.6 sec, A₀ = 2.4 ± 0.5, τ_D1 = 4.30 ± 3.0 sec, D1₀ = 0.10 ± 0.05, τ_D2 = 1240 ± 1150 sec, D2₀ = 0.44 ± 0.21. E, F, The time constants (filled circles) and magnitudes (open circles) for augmentation and the slow component of depression in six experiments with 2 mm Ca²⁺ plus 2 mm added Ba²⁺.

Although adding 2 mm Ba²⁺ to 2 mm Ca²⁺ greatly increased the magnitude of the visually observed component of augmentation (Fig. 5B,D), the estimated magnitudes of augmentation with added Ba²⁺ determined by fitting with Scheme 1 (except for one experiment where augmentation was 6.5) were typically less than the fitted magnitudes in the absence of added Ba²⁺, as shown by comparing the magnitudes in Figure 5E with 2 mm Ba²⁺ to those in Figure 4A, normal quantal content, without Ba²⁺. Thus, adding 2 mm Ba²⁺ to 2 mm Ca²⁺ appears to reveal augmentation in some manner not necessarily associated with a change in magnitude. A slow depression was observed in five of the six experiments with Ba²⁺ (Fig. 5F), with a fast component apparent in only one of the experiments (not plotted). Thus, Ba²⁺ may facilitate identification of augmentation at normal quantal content by reducing the fast component of depression, perhaps by preferentially releasing vesicles from the reserve rather than the RRP, as observed in chromaffin cells (Duncan et al., 2003).

As a further test of whether augmentation was present with marked depression, experiments similar to those in Figure 5 were performed but with 4 mm Ca²⁺ rather than 2 mm Ca²⁺ to further increase both transmitter release and depression. Adding 2 mm Ba²⁺ in these experiments also clearly identified a masked augmentation (data not shown).

Ba²⁺ acts specifically

To investigate the possibility that adding Ba²⁺ might reveal augmentation in some manner through a general increase in the concentration of divalent ions rather than through a specific action of Ba²⁺, we examined whether increasing the divalent concentration by adding both Ca²⁺ and Mg²⁺, rather than by adding Ba²⁺, would increase augmentation. The relative amount of Ca²⁺ and Mg²⁺ to add, to increase the total divalent ion concentration by 2 mm without changing the quantal content, was calculated with the equations by Dodge and Rahamimoff (1967). In three experiments of this type, increasing the total divalent concentration by 2 mm by adding 0.4 mm Ca²⁺ and 1.6 mm Mg²⁺ to the solution for normal quantal content containing 2 mm Ca²⁺ and 5 mm Mg²⁺ had little effect on stimulation-induced changes in EPP amplitudes during or after the conditioning trains when compared with the normal solution (data not shown). In another series of experiments, increasing the concentration of divalent ions by adding 2 mm Ca²⁺ rather than 2 mm Ba²⁺, for a total of 4 mm Ca²⁺, increased depression with no visual indication of augmentation (data not shown). Mg²⁺ typically blocks Ca²⁺ channels rather than passing through them (Hille, 2001), so replacing Ba²⁺ by mainly increasing Mg²⁺ would mainly test for the extracellular effects of increasing divalents. Replacing Ba²⁺ with Ca²⁺ would test for both extracellular and intracellular effects of divalents, because the terminal would be exposed to more extracellular Ca²⁺, and more Ca²⁺ would also enter the nerve terminal through the Ca²⁺ channels. Thus, increasing the divalent concentration by adding Ca²⁺ or by adding both Ca²⁺ and Mg²⁺ did not increase augmentation, whereas adding Ba²⁺ did, suggesting that the Ba²⁺ effect is specific, rather than acting through a general increase in divalent ion concentration.

Decay of residual Ca²⁺ includes a component with an augmentation-like time course

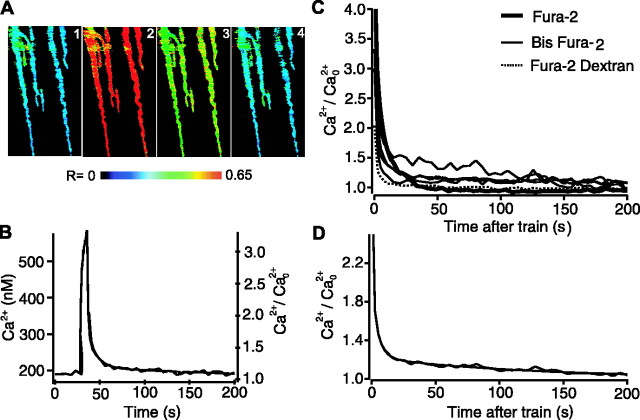
Because augmentation is associated with and requires an increase in free Ca²⁺ in nerve terminals under conditions where augmentation is obviously present (Swandulla et al., 1991; Delaney and Tank, 1994; Kamiya and Zucker, 1994; Regehr et al., 1994; Zengel et al., 1994; Rosenmund et al., 2002; Zucker and Regehr, 2002), we examined whether there is a component of free Ca²⁺ in the nerve terminal with a time course similar to augmentation under conditions like those in Figure 2 where depression would mask augmentation. Ratiometric imaging was used to estimate changes in residual Ca²⁺ in synaptic terminals of the frog NMJ during conditioning-testing trials after the terminals were loaded with fura-2 by backfilling (see Materials and Methods). Figure 6A shows pseudocolor ratio images before (A1), during (A2), and 1.75 sec (A3) and 186 sec (A4) after a conditioning train. The ratio images indicate that the free Ca²⁺ in the nerve terminal increased during repetitive stimulation and decayed thereafter, as observed previously (Almers and Neher, 1985; Delaney et al., 1989; Swandulla et al., 1991; Delaney and Tank, 1994; Kamiya and Zucker, 1994; Regehr et al., 1994; Zengel et al., 1994; Lin et al., 1998; Suzuki et al., 2000; Rosenmund et al., 2002; Zucker and Regehr, 2002)

Figure 6.

An augmentation-like component of decay of residual Ca²⁺ after conditioning trains with 2 mm Ca²⁺. A, Pseudocolor images of fura-2-loaded terminals before the conditioning train (1), just before the last impulse of the conditioning train (2), and 1.75 and 186 sec after the end of the conditioning train (3, 4). B, Residual Ca²⁺ measured from nerve terminals from a single preparation loaded with bis-fura-2 before, during, and after a conditioning stimulation (240 impulses at 20 per second). The response is the average from six consecutive trains from a single preparation. Normalized residual Ca²⁺ is shown on the right axis and was described with the sum of three exponentials starting 1 sec after the end of the conditioning train (smooth line), with time constants of 1.1 ± 1.1, 9.5 ± 4.0, and 260 ± 160 sec and magnitudes of 0.54 ± 0.25, 0.55 ± 0.20, and 0.21 ± 0.05, respectively. C, The decay of residual Ca²⁺ from six different preparations, measured with bis-fura-2, fura-2, or fura-2-dextran. D, The decay of Ca²⁺ averaged from the data in D is described by the sum of three exponentials (smooth line), with time constants of 1.8 ± 0.2, 7.8 ± 2.6, and 128 ± 15 sec and magnitudes of 1.7 ± 0.2, 0.28 ± 0.18, and 0.21 ± 0.01, respectively.

The rise and decay of free Ca²⁺ in the nerve terminal from a single preparation during and after conditioning trains with 2 mm Ca²⁺ is shown in Figure 6B (continuous line with some variability). For this experiment, the terminals were loaded with bis-fura-2. The residual Ca²⁺ after the train decayed with three exponentials, with time constants of 1.1 ± 1.1, 9.5 ± 4.0, and 260 ± 160 sec and magnitudes of 0.54 ± 0.25, 0.55 ± 0.20, and 0.21 ± 0.05, respectively (smooth continuous line). The listed 95% confidence intervals for these components indicate that three distinct components are present, because the time constants at the limits of the 95% confidence intervals are still well separated, and none of the magnitudes at the limits of the 95% confidence intervals approached zero. Of these three components, the intermediate component (τ = 9.5 sec) decayed with kinetics similar to augmentation of transmitter release.

Figure 6C presents the decay of Ca²⁺ after the train from each of six different preparations to show the range in Ca²⁺ response among preparations. Fitting each of these experiments indicated that there was a component of free Ca²⁺ that decayed with kinetics similar to augmentation. To reduce the effects of noise in the signal, the data from the individual preparations were first averaged to obtain the decay in Figure 6D and then fitted with sums of exponentials. The average decay of Ca²⁺ was described by three exponentials with time constants of 1.8 ± 0.2, 7.8 ± 2.6, and 128 ± 15 sec, with magnitudes of 1.7 ± 0.2, 0.28 ± 0.18, and 0.21 ± 0.01, respectively (smooth continuous line). As was the case for single experiments, there was an augmentation-like component of Ca²⁺ decay for the averaged data, indicated by the 7.8 sec component. This component was seen with fura-2, bisfura-2, and fura-2 dextran, suggesting that compartmentalization of indicator in internal cellular structures did not appreciably affect the results. Ca²⁺ indicators in high concentrations can slow the decay of free Ca²⁺ (Tank et al., 1995). The time constant of decay of the augmentation component of free Ca²⁺ was not significantly different (p > 0.7) when comparing fura-2-based indicators (5.6 ± 3.0 sec (mean ± SEM; n = 4; K_d, 145 nm) and bis-fura-2 indicators (4.7 ± 1.6 sec; mean ± SEM; n = 3; K_d, 370 nm), suggesting (assuming equal loading) that the Ca²⁺ indicators were not significantly slowing the decay of the augmentation component of free Ca²⁺. Thus, under conditions of normal quantal content where depression was substantial, an augmentation component of residual Ca²⁺ was observed, indicating that the residual Ca²⁺ required for the augmentation detected in our experiments was present. Augmentation-like components of residual Ca²⁺ have been observed previously in various preparations in which augmentation of transmitter release was readily observed at low quantal content (Augustine et al., 1992; Delaney and Tank, 1994; Kamiya and Zucker, 1994; Brain and Bennett, 1995; Tank et al., 1995; Lin et al., 1998).

In contrast to the depression of EPP amplitudes after trains at normal quantal content, depression of residual Ca²⁺ after trains at normal quantal content was never observed. The decay of residual Ca²⁺ in Figure 6, B and D, is qualitatively similar to the decay of EPP amplitudes in the absence of depression in Figure 1B.

Testing and correcting for depression by measuring the RRP reveals an augmentation component at normal quantal content

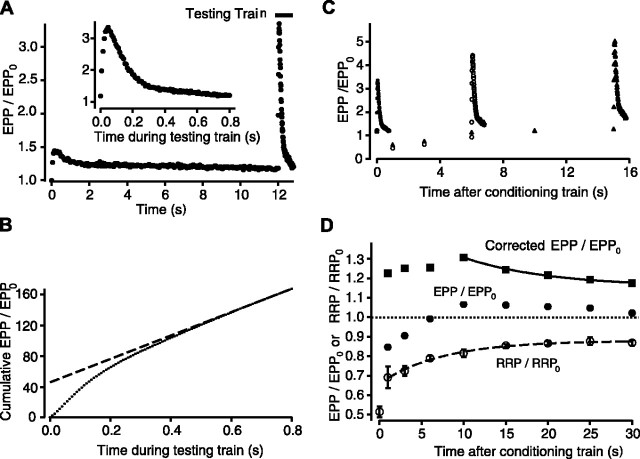
As an additional method to determine whether augmentation is present at normal quantal content in the presence of depression, we estimated depression by measuring the size of the RRP. The observed EPP amplitudes were then corrected for depression to determine whether augmentation was masked by the depression. The size of the RRP was estimated using the rundown method (Liu and Tsien, 1995; Wang and Zucker, 1998; Bollmann et al., 2000). At various times after a conditioning train, a high-frequency train of stimulation (100 impulses at 125 Hz) was applied to the nerve to substantially deplete the RRP to measure its contents. Figure 7A shows EPP amplitudes during a 12 sec conditioning train immediately followed by a high-frequency testing train to measure the size of the RRP. During the high-frequency testing train, transmitter release first increased and then decreased to a quasi steady-state level (Fig. 7A, inset). Figure 7B plots the cumulative EPP amplitudes during the high-frequency testing train as a dotted line. The approach of the cumulative EPP amplitudes to a steady-state increasing response is thought to occur when the number of vesicles released per impulse is equal to the number replenished between impulses (Bollmann et al., 2000). Because the slope of cumulative EPP amplitude versus stimulus number is proportional to the rate of refilling in the steady state, a projection of a line fit to the steady-state response intercepts the ordinate at a value approximately equal to the size of the RRP (in units of normalized EPP amplitude). In the experiment in Figure 7B, the projected size of the RRP was ∼9500 quanta (47.5 intercept × 200 quanta = 9500) if it is assumed that the normal quantal content is 200 synaptic vesicles (Katz, 1969). The method used in Figure 7B may overestimate or underestimate the size of the RRP, depending on what changes occur in the rate of refilling during the train used to test for the RRP, and because the rundown of EPP amplitudes did not reach a true steady state. If the fractional overestimation or underestimation of the RRP was similar for each determination, then the errors would cancel out, provided that estimates of the RRP were expressed as the ratio to the control RRP, as done below.

Figure 7.

Augmentation increases fractional transmitter release from the RRP. A, Plot of normalized EPP amplitudes against time for a conditioning-testing train identical to those in Figures 1 and 2, except that a testing train of 100 impulses at 125 Hz is added immediately after the conditioning train. The inset plots the normalized EPP amplitudes during this testing train on an expanded time scale. B, Cumulative normalized EPP amplitude (small filled circles) versus time during the testing train. The dashed line is a fit to the last 20 points of the testing train. The intercept of the dashed line with the ordinate provides an estimate for the size of the RRP at the end of the conditioning train. C, Three representative superimposed conditioning-testing trials in which testing trains are applied to estimate the RRP at 0 sec (filled circles), 6 sec (open circles), and 15 sec (filled triangles) after the end of the conditioning trains. Only the time after the conditioning trains is plotted. D, Plots of the observed EPP amplitudes (circles), the RRP (open circles; estimated as shown in A-C), and the EPP amplitudes corrected for depletion of the RRP (squares) (Eq. 6) against time after the conditioning train. Each point plots the average of three or more experiments. The data were fit with single exponentials plus constants, because data were not obtained beyond 30 sec to define the slow components. The dotted line plots the control EPP level in the absence of augmentation or depression. The dashed line plots the recovery of the RRP, with τ_D1 = 7.4 ± 2.5 sec, D1₀ = 0.22 ± 0.03, and a constant for D2₀ of 0.12 assuming minimal recovery of D2 during the 30 sec of plotted data. The continuous line is the estimated decay of normalized EPP amplitudes after correcting for the decrease in the RRP, with τ_A = 10.3 ± 0.8 sec, A₀ = 0.40 ± 0.21, and a constant for P₀ of 0.16 assuming insignificant decay of P₀ during the 30 sec of plotted data. This figure shows that the RRP is not increased after the train, but that EPP amplitudes (evoked transmitter release) are increased, indicating an increased fractional release from the RRP during the decay of augmentation.

To determine the time course of recovery of the RRP after a conditioning train, the size of the RRP was estimated at different times after the conditioning train, each in a separate trial, by substituting the high-frequency train for one of the testing impulses that would normally be applied. Three superimposed trials are shown in Figure 7C for estimates of the RRP at 0, 6, and 15 sec after the end of the conditioning train. In Figure 7D, estimates of the RRP from multiple trials in three experiments are plotted against time after the conditioning train (open circles). The RRP was depleted 32%, 1 sec after the train, and then recovered with a time constant of 7.4 ± 2.5 sec (between 1 and 30 sec). In these same experiments, EPP amplitudes were reduced 15% 1 sec after the train, increased above the control level at 10 sec, and then decayed (filled circles). The observed EPP amplitudes (Fig. 7D, filled circles) were corrected for the depletion of the RRP to obtain the corrected EPP amplitudes (filled squares) using the following:

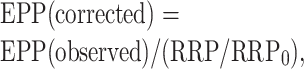6

where RRP/RRP₀ (open circles) is the ratio of the RRP at the indicated times after the train to the control RRP₀ in the absence of a train. The corrected EPP amplitudes decayed exponentially with a time constant of 10.3 ± 0.8 sec (continuous line through filled squares) from a magnitude of 1.06 ± 0.55, consistent with augmentation. This estimate of augmentation from the decay of EPP amplitudes after directly correcting for depletion of the RRP is in general agreement with the estimates of augmentation obtained by the rather different method of fitting EPP amplitudes after the conditioning trains with augmentation, depression, and potentiation (Figs. 2, 4), where augmentation had a time constant of 15.3 ± 1.6 sec and magnitude of 2.0 ± 0.3 (Fig. 4). Thus, the results in this and the previous sections suggest that augmentation is present at normal quantal content even when it is not apparent because of masking by depression.

Augmentation arises from an increased vesicular release probability from the RRP

Augmentation could arise from an increase in the number of synaptic vesicles immediately available for release (an increase in the size of the RRP) or from an increase in the probability of releasing vesicles from the RRP (an increase in the vesicular release probability; see Introduction). Ten seconds after the conditioning train in Figure 7D, transmitter release (filled circles) was ∼6% greater than the pretetanus level (i.e., there was net enhancement) despite a 19% reduction in the size of the RRP (open circles). This enhancement of release then decayed as the RRP recovered. As indicated in the previous section, correcting the enhanced release for the decreased size of the RRP gave a corrected decay of EPP amplitudes (filled squares) consistent with the decay of augmentation. These observations in Figure 7D of enhanced release from augmentation when the size of the RRP was decreased indicates that augmentation in these experiments was associated with an increase in the probability of vesicular release from the RRP, rather than from an increased size of the RRP. This conclusion is consistent with studies at lower quantal content in hippocampal neurons (Stevens and Wesseling, 1999a).

Discussion

Synaptic augmentation is a stimulation-induced component of short-term synaptic plasticity that can greatly increase the amount of transmitter release (Magleby and Zengel, 1976a; Magleby, 1987; Regehr and Stevens, 2001; Zucker and Regehr, 2002). Studies of augmentation have typically been performed under experimental conditions or in preparations where depression is not significant. Here, we extend the study of augmentation to conditions of normal quantal content (2 mm Ca²⁺) at the frog NMJ. Under these conditions, depression was observed immediately after the conditioning trains (Fig. 2), rather than the pronounced augmentation that is typically observed with low Ca²⁺ (Fig. 1).

Results from four different experimental approaches in our study suggest that augmentation can enhance transmitter release at normal quantal content, even when masked by depression. First, mathematical analysis of the recovery of EPP amplitudes after conditioning trains extracted a component of augmentation in 60% of the experiments (Figs. 2, 4). Second, the addition of Ba²⁺, which increases the magnitude of augmentation in the absence of depression (Zengel and Magleby, 1980; Zengel et al., 1980), identified augmentation by making it readily apparent (Fig. 5). Third, a component of residual Ca²⁺ was present after the train at normal quantal content with a time course similar to that of augmentation (Fig. 6), indicating that the residual Ca²⁺ required to activate augmentation (Swandulla et al., 1991; Delaney and Tank, 1994; Kamiya and Zucker, 1994; Regehr et al., 1994; Zengel et al., 1994; Rosenmund et al., 2002; Zucker and Regehr, 2002) was present under the conditions of our study. Fourth, after correcting the EPP amplitudes after the trains for the measured depletion of the RRP, augmentation was present (Fig. 7). Thus, three independent methods revealed augmentation of evoked transmitter release after conditioning trains in the presence of depression, and a fourth indicated that the residual Ca²⁺ required to activate augmentation was also present. Additional support for augmentation in the presence of depression is the observations of Zengel and Sosa (1994) of an augmentation component of increased MEPP frequency in the presence of pronounced depression (3.6 mm Ca²⁺). Thus, our findings and those of Zengel and Sosa (1994) indicate that even when pronounced depression masks augmentation, the machinery for augmentation can still function to increase transmitter release.

The observations in Figure 4A that the mean magnitudes of augmentation and potentiation are increased 1.8-fold and 3.3-fold, respectively, at normal quantal content when compared with low quantal content (p < 0.05 in each case) are consistent with augmentation and potentiation arising from the accumulation of residual Ca²⁺ in the nerve terminal (Swandulla et al., 1991; Delaney and Tank, 1994; Kamiya and Zucker, 1994; Regehr et al., 1994; Zengel et al., 1994; Regehr and Stevens, 2001; Rosenmund et al., 2002; Zucker and Regehr, 2002), because more Ca²⁺ would enter the nerve terminal with each impulse at the higher Ca²⁺ used for normal quantal content (Suzuki et al., 2000).

Our analysis on the interplay between augmentation and depression, together with the analysis of Qian and Delaney (1997), indicates that caution must be used when interpreting experimental observations when both augmentation and depression are present and have similar time courses. If the magnitude of augmentation is several times larger than the magnitude of depression, then the observed augmentation can decay with little or no indication of depression, even when depression is sufficient to reduce the observed magnitude of augmentation and increase the observed time constant of augmentation (Fig. 3C). Alternatively, if depression is sufficiently large, then the observed depression can recover after the conditioning train with little or no indication of augmentation, even though augmentation can decrease the observed magnitude and time constant of depression (Fig. 3A,B). Thus, an experimental observation of only augmentation or only depression would not exclude that the other process is present, but masked, and experimental manipulations that appear to alter the observed process could actually be working through changes in the masked process.

To avoid such potential errors in interpretation, several approaches are available. Mathematical analysis of the processes can be applied, as done in our study (Figs. 2, 4), to extract the masked process while correcting the observed processes for the changes in their observed properties attributable to the masked process. However, such extraction requires some knowledge about the properties of the processes. For our study, we assumed that depression and augmentation at the frog NMJ recover exponentially (Takeuchi, 1958; Magleby and Zengel, 1976a) and that there is a multiplicative relationship between these processes (Scheme 1). Whereas it is unlikely that these assumptions are strictly correct, (Glavinovic and Narahashi, 1988; Zucker and Regehr, 2002), our results suggest that they are sufficient to reveal augmentation.

Alternatively, direct estimates can be made of depression and then the observed augmentation corrected for depression. At the NMJ where depression is mainly caused by depletion of transmitter available for release (Takeuchi, 1958; Thies, 1965), depression can be estimated by measuring the size of the RRP. Using this approach, we found that the RRP was decreased immediately after the conditioning train and then recovered with a time constant of ∼7 sec (Fig. 7). After correcting the EPP amplitudes for the depletion of the RRP, a component of augmentation was revealed that decayed with a time constant of ∼10 sec. An assumption of an exponential recovery of the RRP was not sufficient to account for all of the observed depression immediately after the conditioning train (Fig. 7D), suggesting an additional faster depression (Dobrunz et al., 1997; Varela et al., 1997), or that factors in addition to depletion may be contributing to depression (Zucker and Regehr, 2002). A third approach that will be important to quantify dynamic changes in the components is modeling of the release process (Magleby and Zengel, 1982; Sen et al., 1996; Varela et al., 1997; Dittman et al., 2000; Matveev et al., 2002; Aristizabal and Glavinovic, 2003).

Our observation in Figure 7D of a 6% net enhancement of transmitter release 10 sec after the conditioning train when augmentation was present (filled circles), despite a 19% reduction in the size of the RRP (open circles), indicates that augmentation at normal quantal content at the frog NMJ arises from an increased probability of release of synaptic vesicles from the RRP. Augmentation at low quantal content at the frog NMJ also appears to arise from an increased vesicular release probability (Magleby and Zengel, 1976b). Thus, under both the depressing conditions of normal quantal content and the enhancing conditions of low quantal content, augmentation does not require an increase in the size of the RRP at the frog NMJ. These observations are consistent with those of Stevens and Wesseling (1999a), who found by measuring the RRP with hypertonic solutions that augmentation at low quantal content for synapses of cultured hippocampal neurons was a potentiation of the release process and not an increase in the RRP.

Recent studies by Rosenmund et al. (2002) suggest that the mechanism of augmentation may be more complex at some synapses. They examined synapses in neuronal culture with two different forms of Munc13, a component of the presynaptic active zone that is essential for the priming of synaptic vesicles to make them release ready (Augustin et al., 1999; Ashery et al., 2000; Martin, 2002). For the high Ca²⁺ (4 Ca²⁺ and 4 Mg²⁺) used in their experiments, synapses with Munc13-1 displayed depression during the conditioning trains and no augmentation after the trains, whereas synapses with Munc13-2 displayed enhancement during the trains and pronounced augmentation after the trains. For the Munc13-1 synapses, it is not clear whether the apparent absence of augmentation reflected the masking of augmentation by depression or the true lack of augmentation. For the Munc13-2 synapses, augmentation increased transmitter release sixfold, whereas the RRP was increased only 2.6-fold, suggesting that augmentation at Munc13-2 synapses reflected an increase in both the size of the RRP and the probability of vesicular release from the RRP. This dual mechanism for augmentation for Munc13-2 synapses is in contrast to our findings at the frog NMJ and those of Stevens and Wesseling (1999a) for hippocampal synapses at low quantal content where augmentation is associated with an increase in the vesicular probability of release and not with an increase in the RRP. Thus, the factors that contribute to augmentation may differ among synapses.

The demonstration of masked augmentation at the NMJ under conditions of normal quantal content has physiological implications. Skeletal neuromuscular transmission is an all-or-none process in which the EPP must depolarize the muscle fiber to threshold to generate a muscle action potential for contraction to occur. At the frog NMJ, three to five times more synaptic vesicles are released to a single nerve impulse than are required to depolarize to threshold, giving a large safety factor in the absence of repetitive stimulation (Wood and Slater, 2001). Estimates of augmentation and depression in our experiments suggest that the build up of augmentation during repetitive stimulation acts to maintain the safety factor by increasing the probability of vesicular release from the partially depleted RRP.