Receptive Field Size in V1 Neurons Limits Acuity for Perceiving Disparity Modulation

Abstract

Disparity selectivity in the striate cortex has generally been studied with uniform disparity fields covering the receptive field (RF). In four awake behaving monkeys, we quantitatively characterized the spatial three-dimensional structure of 55 V1 RFs using random dot stereograms in which disparity varied as a sinusoidal function of vertical position (“corrugations”). At low spatial frequencies, this produced a modulation in neuronal firing at the temporal frequency of the stimulus. As the spatial frequency increased, the modulation reduced. The mean response rate changed little and was close to that produced by a uniform stimulus at the mean disparity of the corrugation. In 48 of 55 (91%) neurons, the modulation strength was a lowpass function of spatial frequency. These results are compatible with a response determined only by the weighted mean of the disparities of the dots (the weights being set by the RF envelope) and suggest that there is no disparity-based surround inhibition or selectivity for disparity gradients. This simple weighting scheme predicts a relationship between RF size and the high-frequency cutoff. Comparison with independent measurements of RF size was compatible with this. All of this behavior closely matches the binocular energy model. The mean cutoff frequency, 0.5 cycles per degree, is similar to equivalent measures of decline in human psychophysical sensitivity for such depth corrugations as a function of frequency (Tyler, 1974; Prince and Rogers, 1998; Banks et al., 2004). This suggests that human cyclopean acuity for disparity modulations is limited by the selectivity of V1 neurons. This in turn is primarily limited by the RF size, because we find no sensitivity for disparity gradients or other disparity differences within the RFs.

Introduction

Stereopsis (the process of retrieving information about depth from binocular disparity) depends on the activity of disparity-selective neurons in the visual cortex. The earliest site at which such neurons occur is the striate cortex (Barlow et al., 1967; Pettigrew et al., 1968). Although several recent studies (Cumming and Parker, 1997, 1999, 2000) have shown that these neurons do not straightforwardly account for many aspects of depth sensation, it still seems likely that this early processing places some limits on stereoscopic performance (Prince et al., 2000; Cumming and DeAngelis, 2001). (In a similar way, the activation of individual photoreceptors is very indirectly linked to our perception of form but imposes limits on spatial acuity.) Here, we investigate the role played by neurons of the striate cortex in the representation of complex three-dimensional surfaces.

It is potentially misleading to study responses to surface properties using small isolated stimuli. Random dot stereograms provide a more powerful stimulus for exploring such responses. Yet, all studies of disparity selectivity in the striate cortex that have used random dot stereograms (RDS) have only explored responses to planar, fronto-parallel surfaces at different depths (DeAngelis, 2000). Conversely, typical three-dimensional scenes contain many irregular surfaces. There may therefore be some advantage to constructing receptive fields (RFs) that are selective for surfaces more complex than fronto-parallel patches. There is evidence that some extrastriate cortical areas show selectivity for three-dimensional slant (Shikata et al., 1996; Sakata et al., 1999; Tsutsui et al., 1999; Sugihara et al., 2002; Nguyenkim and DeAngelis, 2003), or for higher-order disparity features (Janssen et al., 1999). Such responses may simply be inherited from complex three-dimensional RFs in V1 (if those exist). Alternatively, the striate cortex may contain a piecewise fronto-parallel depth map, from which the responses in the extrastriate cortex are constructed. In such a scheme, the size of the patches in V1 would place limits on the spatial acuity of the three-dimensional maps in the extrastriate cortex and on the cyclopean spatial acuity of the observer.

We investigated these questions using a stimulus that simultaneously permitted us to explore the three-dimensional structure of the RF and to estimate its cyclopean acuity. The stimulus was a random dot pattern in which the disparity was a sinusoidal function of position, producing a grating in depth (“corrugation”). In principle, the linear superposition of a series of such corrugations can be used to generate any three-dimensional surface (Fourier synthesis in the disparity domain). To evaluate the significance of our findings, we also explored the responses of model neurons to disparity corrugations. These were modifications of the energy model (Adelson and Bergen, 1985; Ohzawa et al., 1990; Fleet et al., 1996), using two-dimensional RFs (Bridge et al., 2001).

These data may help to understand some of the limiting factors in the human perception of shape from disparity. Several studies have reported that human observers are unable to detect disparity modulations with frequencies above 3 cycles per degree (cpd) (Tyler, 1974, 1983; Schumer and Ganz, 1979; Howard and Rogers, 1995; Prince and Rogers, 1998; Bradshaw and Rogers, 1999). The accompanying article (Banks et al., 2004) shows that this poor acuity cannot be explained by stimulus properties but must reflect the mechanisms by which disparity is processed. Here, we explore the physiological basis for this limitation. These data are the first to examine neuronal responses to such stimuli and hence the first time that the power of Fourier analysis has been applied to the study of three-dimensional RF structures.

Materials and Methods

Animals and training. For monkeys Hg and Rb, all procedures were performed in accordance with the United Kingdom Home Office regulations on animal experimentation. For monkeys Df and Rf, all procedures complied with the Public Health Service policy on the humane care and use of laboratory animals, and all protocols were approved by the Institute Animal Care and Use Committee.

We studied neurons in the striate cortex (V1) of one female (Rb) and three male (Df, Hg, Rf) alert monkeys (Macaca mulatta). In a surgical procedure under general anesthetic, the animals were implanted with a head fixation post and scleral eye coils in both eyes (Judge et al., 1980). The monkeys were then trained to maintain fixation on binocular visual stimuli for fluid reward. A detailed description of the general methods was reported by Cumming and Parker (1999).

Single-unit recording. We recorded extracellularly with tungsten in glass microelectrodes (Merrill and Ainsworth, 1972) (monkeys Hg and Rb) and glass-coated platinum-iridium electrodes (FHC, Inc., Bowdoinham, ME) (monkeys Df and Rf), introduced transdurally into the striate cortex each day of recording. The signal was amplified (Bak Electronics, Mount Airy, MD), filtered (200 Hz to 5 kHz), digitized (32 kHz), then stored to disk (using the Datawave discovery system). Unit isolation was always checked offline. A magnetic scleral search system (C-N-C Engineering, Enfield, CT) measured the positions of both eyes. Only data from trials in which fixation was maintained (to within 0.4-l°, depending on monkey) were analyzed.

The minimum response field of each neuron was initially mapped by hand with a high-contrast bar of approximately preferred orientation. Stimuli were then centered over the minimum response field.

Stimulus presentation for electrophysiology. The visual stimuli were displayed on two EIZO (Ishikawa, Japan) Flexscan 78 monitors (for monkeys Hg and Rb) and EIZO Flexscan F980 monitors (for monkeys Df and Rf) and were viewed at a distance of 89 cm in a Wheatstone stereoscope configuration through two small mirrors. The mirrors had a diameter of 18 mm (for monkeys Hg and Rb) and 30 mm (for monkeys Df and Rf) and were positioned ∼1.5 cm in front of the animals' eyes. A workstation (Silicon Graphics, Mountain View, CA) generated the stimuli at a mean luminance of 37 or 42 cd·m ^-2, maximum contrast of 99%, and at a frame rate of 72 Hz.

The corrugation stimuli were always presented for a duration of 2 sec. For monkeys Df and Rf, the characterization of other cell properties (disparity tuning, RF location and size, spatial frequency measurements with luminance gratings) used stimuli lasting only 420 msec, separated by 100 msec, allowing four stimulus presentations within one 2 sec trial.

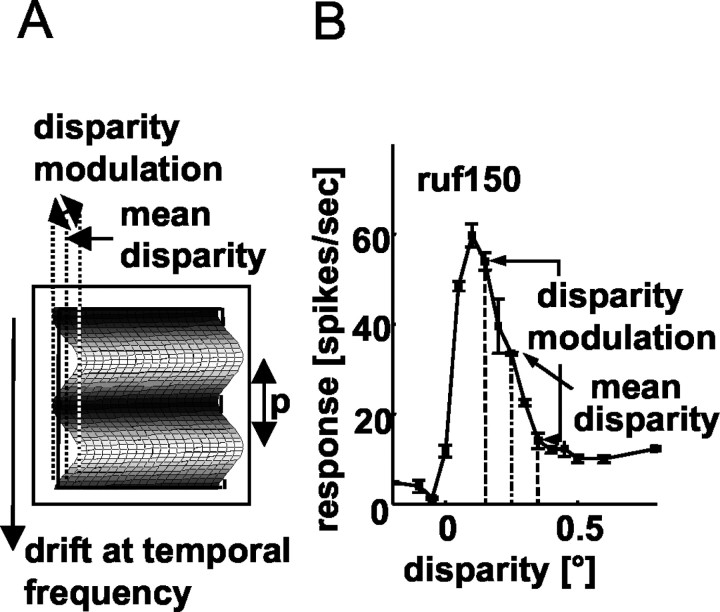
Measurements of disparity tuning functions and responses to depth-modulating corrugations. Disparity tuning was measured using circular patches of dynamic RDS. To keep mean luminance constant, the RDS consisted of equal numbers of randomly distributed black and white dots of 99% contrast (0.1 × 0.1° size and with an overall density of 50%) on a mid-gray background. A new RDS was presented in each video frame. The RDS was centered on the minimum response field and extended beyond its limits. The disparity of the central region of the RDS varied from trial to trial, while a surrounding annulus (0.5-2° wide) was kept at zero disparity. The width of the annulus was always greater than the largest disparity used, eliminating monocularly detectable changes in the stimuli and keeping variation of vergence to a minimum. If the neuron exhibited sensitivity to disparity, responses to sinusoidal modulations of disparity (corrugations) (Fig. 1A) were studied. The disparity-defined grating was drifted across the RF at a temporal frequency of 2 Hz. The corrugation had a surrounding rectangular frame at zero disparity. The total stimulus size was 5 × 5° (4° corrugation plus 1° frame) (Fig. 1A), which always extended well beyond the limits of the minimum response field. Thus, any contextual modulation by disparities within 2° of the RF center would be revealed. The corrugation was always oriented horizontally (disparity was a sinusoidal function of vertical position), so that horizontal disparities did not introduce any monocular texture gradients. In a vertically oriented corrugation, the disparity variation leads to changes in dot density, producing monocular images that contain vertical “stripes” defined by regions of high dot density. The only orientation that completely abolishes these monocular changes is horizontal. The disparity modulated between the preferred and the null disparity estimated from the disparity-tuning curve (Fig. 1B).

Figure 1.

The experimental procedure. A, Schematic representation of the stimulus (corrugation). The mean disparity and the range of disparity modulation were chosen for each cell individually according to the values obtained from the disparity-tuning curve (B) of the cell. Corrugation frequency (1/p; p = spatial period) was varied systematically in random order between trials. The planar control stimulus was presented at a disparity equal to the mean disparity of the corrugation. B, An example of the disparity-tuning curve for cell ruf150. The arrows indicate the mean disparity of the corrugation and the range for which the depth modulation of the corrugation was chosen for this cell.

The spatial frequency of the corrugation (1/spatial period) (Fig. 1A) will be referred to as “corrugation frequency.” It was varied from 0.06-4 cpd in one octave increments, presented in pseudo-random order. At all corrugation frequencies, the phase of the corrugation was chosen in such a way that the central vertical position of the corrugation was a peak (i.e., phase of 0°) at the beginning of each 2 sec trial. At the lowest corrugation frequency used, the full width of the stimulus was only one-quarter of a cycle, so the stimulus over the RF was a nearly uniform disparity with a sinusoidal modulation over time. Each stimulus condition was presented a minimum number of four times (maximum, 18 times; mean, 8.7).

We interleaved an otherwise identical planar stimulus with a constant disparity equal to the mean disparity of the corrugation. Because there was no temporal variation in the disparity of this stimulus, it allowed us to estimate the extent of temporal modulation in the neuronal firing that was unrelated to the disparity modulation of the stimulus.

Data analysis. All the neurons included in the analysis showed significant modulation of the firing rate with changes in disparity (in RDS with uniform disparity) on a one-way ANOVA (p < 0.05). An additional selection criterion was that the mean response at the preferred disparity exceeded 15 spikes/sec. The strength of disparity tuning was assessed with the disparity discrimination index (DDI) (Prince et al., 2002):

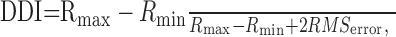1

where R_max and R_min are the highest and lowest √ rates, respectively, on the tuning curves, and RMS_error is the square root of the residual variance around the means of √ rates across all disparities.

For most neuronal data, variance increases approximately proportional to mean spike count (Dean, 1981). Using the square root of the spike counts approximately stabilizes the variance (Cumming and Parker, 2000; Bridge and Cumming, 2001; Prince et al., 2002). For this reason, we always used square roots of counts for this analysis or when fitting Gaussians to these data.

Relative modulation. The corrugation stimuli produced a sinusoidal modulation of the disparity, between the null and preferred values, at the center of the RF. The main manifestation of disparity selectivity in response to these stimuli was, therefore, a periodic modulation in firing rate at the drift frequency. We quantified this by measuring the relative modulation (RM) (Movshon et al., 1978). This is the ratio of the amplitude of the modulation at the fundamental frequency (f1; the temporal frequency of the drifting corrugation) and mean response rate (f0). The value for f1 was obtained by averaging the responses for all trials, then calculating the modulation of this mean response at the frequency f1. The same calculation, applied to responses to the planar stimulus, served as a control for the extent of modulation that was not attributable to the corrugation. To eliminate artifactual modulation related to response latency and the onset transient, the first stimulus cycle (500 msec) of each trial was discarded.

A resampling (1000 cycles) and bootstrapping method was used (Davison and Hinkley, 1997) to determine confidence intervals. RM in response to at least one corrugation of the lowest five corrugation frequencies had to be significantly higher (on the 5% level, corrected for multiple comparisons) than in response to the planar stimulus, before additional analysis of the response modulation was undertaken. This criterion did not reject any neurons that responded only to higher corrugation frequencies: all neurons that showed significant modulation at 2 or 4 cpd showed greater modulation at lower frequencies.

To quantify the amount of neuronal modulation, we measured the RM contrast: .0

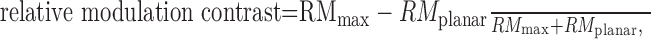2

where RM_max is the peak RM in response to the corrugation and RM_planar is the RM in response to the planar stimulus with no temporal or spatial modulation in disparity.

Corrugation frequency tuning. For most cells, we found that the extent of modulation (RM) decreased as the corrugation frequency of the disparity corrugations was increased (see Results). To describe this quantitatively, Gaussian functions were fit to RM as a function of corrugation frequency, using a nonlinear optimization algorithm based on the simplex-search method (Lagarias et al., 1998). Because these were purely descriptive functions, they were allowed to be a Gaussian function of linear or log frequency, whichever minimized the least-square deviations. The Gaussian functions had four free parameters (mean, amplitude, SD, and baseline) that, except for the mean, were constrained to values ≥0.

Gaussian fits were considered adequate if they explained >75% of the variance within the data. The high cutoff frequency was defined as the corrugation frequency at which the Gaussian dropped to two-thirds of its peak. (In a few cases, in which Gaussians fits had a mean <0, it was defined as the frequency at which the Gaussian dropped to two-thirds of the response at 0 cpd.)

Quantitative measurements of RF size. To quantify RF size, we measured responses to a thin stationary rectangle (0.24 × 5.99°) of dynamic random dots (each dot usually 0.08 × 0.08°) over a range of locations. RF size was measured monocularly for each eye and binocularly, in which case the preferred disparity of the cell was added to the display of the rectangle. In some cases, only binocular measures at the preferred disparity were obtained because the cell was lost before collecting monocular data or monocular responses were too weak to be reliable. Because we always used horizontally oriented corrugations, response modulation to corrugations provided us with information about the RF structure only along a vertical axis. We, therefore, fit Gaussian functions to the neuronal response rate as a function of the vertical position of the stimulus.

Spatial frequency-tuning measurements with gratings. The luminance structure of each RF was examined with drifting sinusoidal luminance gratings at the preferred orientation and temporal frequency. Spatial frequencies between 0.12 cpd and 16 cpd were presented a minimum of four times each. A Gaussian was fit to the mean response rate as a function of spatial frequency (in linear or logarithmic units, whichever gave the better fit).

Model. To assist the interpretation of our results, we also examined the responses of model V1 neurons to these stimuli. All simulations were run in Matlab 6 (MathWorks, Natick, MA) on either a Pentium personal computer running Linux or a Silicon Graphics Octane.

The model we used was a version of the binocular energy model (Ohzawa et al., 1990) that was described in detail by Bridge et al. (2001). In brief, two-dimensional Gabor functions were used to simulate RFs for each eye. Because the left and right subunits were generated separately, interocular differences in RF structure could be produced. Linear summation of the responses (inner product of the image and the RF) from each eye, followed by half-wave rectification then squaring, generated a binocular simple cell. Summation of four binocular simple cells (in quadrature phase pairs) produced a binocular complex cell.

To create the corrugated RDS, a random number generator was used to determine the x and y positions of the 400 dots, each subtending 0.1° of visual angle. Disparity was added by horizontally displacing dots in opposite directions in the left and right eye stimuli. Five hundred different RDS patterns were presented to the cells, and the responses to each pattern were summed. RM was calculated as described for the physiological data analysis.

Results

We recorded data from 161 isolated single units in four animals, 62 from monkey Hg, 51 from monkey Df, 36 from monkey Rf, and 12 from monkey Rb. Of 106 cells exhibiting significant disparity tuning, 25 failed to yield adequate data for examining responses to depth corrugations (some cells were lost before collecting sufficient data; for others, the stimulus was not properly matched to the disparity-selective range; one cell was excluded because it showed strong intrinsic modulation of firing close to the stimulus frequency). Of the remaining 81 neurons, 55 showed significant modulation in the firing rate when tested with disparity corrugations.

Neuronal modulation in response to sinusoidal corrugation

During presentation of these stimuli, the disparity at any point of the RF modulates sinusoidally over time. The temporal frequency of this modulation (2 Hz) is the same throughout the RF. If the response of the neuron were a linear function of the disparities of the dots covering the RF, this should result in a sinusoidal modulation of the firing rate with the same temporal frequency as the stimulus. This was exactly the pattern we observed (Fig. 2A). For quantitative analysis of this behavior, we calculated the RM, the amplitude of the modulation at the stimulus temporal frequency (f1) divided by the mean firing rate (f0). This measure is similar to the F1:F0 ratio measured in response to sinusoidal luminance gratings, which is used to differentiate simple and complex cells (Skottun et al., 1991). An important difference arises because most V1 neurons show little response to a field of uniform luminance, whereas most neurons in this study showed a substantial response to an RDS with a uniform disparity (the value of which was equal to the mean of the disparities covered by our corrugations) (Fig. 1). This has two significant consequences. First, the value of RM is rarely much larger than 1 (i.e., the neurons are not generally silenced at the null disparity). Second, fluctuations in the firing rate in the absence of any changes in disparity mean that the value of RM does not necessarily fall to zero even when there is no disparity modulation. To control for this, we also measured the response to a corrugation with a depth modulation of 0 (i.e., a planar stimulus with a constant disparity over space and time, interleaved with the modulating stimuli).

Figure 2.

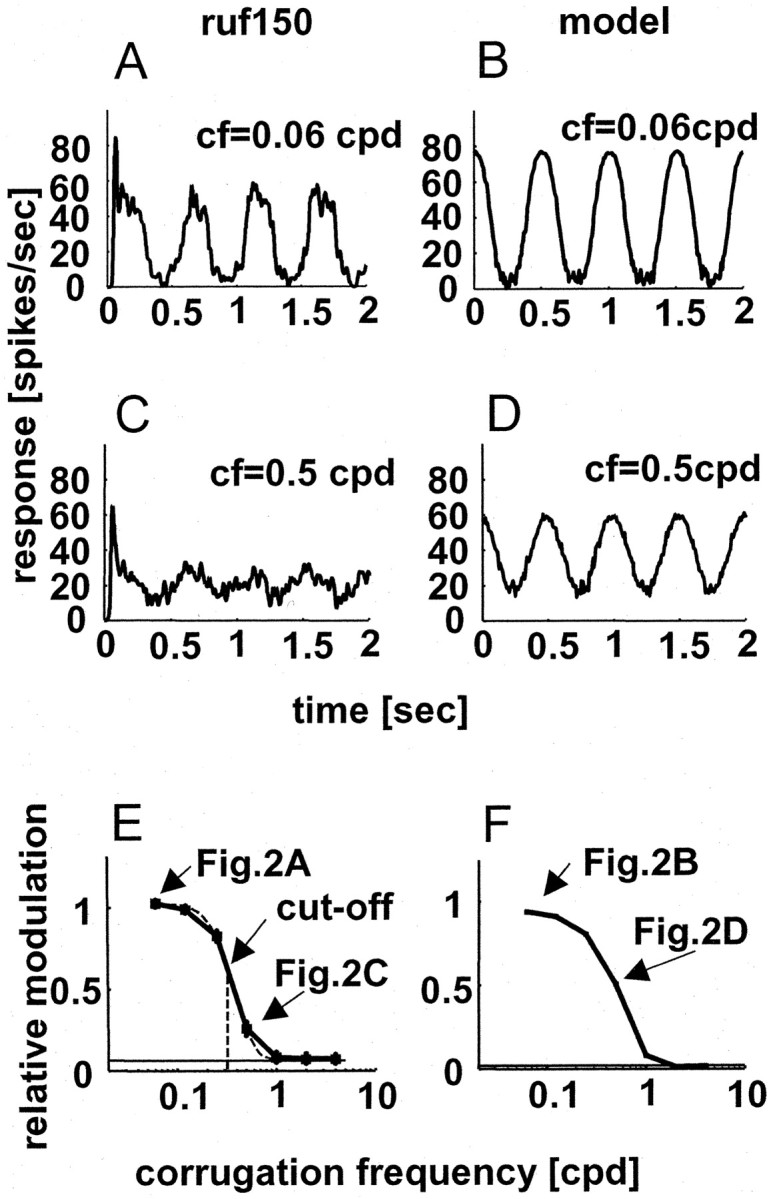
Responses of a typical neuron (A, C, E) and the energy model (B, D, F) to sinusoidal corrugations in depth. A and B show spike density functions for the response to a corrugation frequency of 0.06 cpd. C and D show responses to a corrugation frequency of 0.5 cpd. The temporal frequency was always 2 Hz. In E and F, RM is plotted as a function of the corrugation frequency. The arrows indicate the RM calculated for the data shown in A-D and the high corrugation frequency cutoff (0.32 cpd) obtained for cell ruf150 (the corrugation frequency at which the modulation falls to two-thirds of the peak). The baseline in E corresponds to the RM value in response to the planar control stimulus (no modulation).

Because the corrugations were always oriented horizontally, the monocular images defining these stimuli were all indistinguishable. In preliminary experiments, we explored responses to other orientations, and in these cases, it was necessary to examine responses to the monocular images, because these contain variations in dot density. We found that, in some cases, these density variations alone (in monocular images) were sufficient to modulate the neuronal discharge rate. For this reason, the rest of the study was limited to horizontally oriented corrugations.

Responses to disparity-modulating corrugations of different frequencies

For the lowest corrugation frequency used (0.06 cpd), there was very little variation in disparity over the extent of the RF of the neurons in this study. This stimulus resembled a traditional planar RDS, in which the disparity of the patch varied over time. The sinusoidal response modulation therefore simply reflects the selectivity of the neuron for the disparity of a fronto-parallel planar patch (and the magnitude of the modulation depends on the strength of disparity selectivity). As the modulation amplitude is kept constant and the corrugation frequency increases, spatial variation of disparity within the RF is introduced. At some frequency, this should increase RM in neurons that are selective for any spatial variation in disparity within their RF (just as the structure of a simple cell RF produces the strongest response for intermediate spatial frequency in luminance gratings). If the three-dimensional structure of the RF is planar and selective for the same disparity throughout, the response should depend on the weighted mean of the disparities (the weights being set according to the position of the dots over the RF):

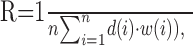3

where R denotes the instantaneous neuronal response, i corresponds to the position in the RF, d(i) corresponds to the disparity of the stimulus at this position, and w(i) corresponds to the weight of the RF envelope at this position. (This is only true for disparities limited to the linear portion of the response that lies between null and preferred disparities, as in our experiments.) Consider a hypothetical cell with a rectangular RF [i.e., disparity input has equal weights throughout the RF (w(i) = constant)]. The response then simply depends on the mean disparity, so that when the spatial period of the corrugation equals the RF width, there is no modulation in the mean disparity and, hence, no modulation in the response. For a Gaussian RF, modulation decreases as a Gaussian function of increasing corrugation frequency. Figure 2E shows the value of RM as a function of corrugation frequency for a typical neuron, and Figure 2F shows the response of our implementation of the energy model. Both the neuron and the model show a lowpass function, behaving as if the response at any time is determined by the mean of the disparities over the RF.

A second feature of responses reflecting the mean weighted disparity is that the mean firing rate should not change as a function of corrugation frequency (provided that a full number of corrugation cycles is presented for each frequency, as we did in our experiments). This was a consistent feature of the neuronal responses: only 9 of 55 (16%) cells showed a significant change in mean spike rate with corrugation frequency (5% significance on ANOVA). Even these cells showed only modest changes in the mean firing rate, and we did not observe a consistent pattern of change in mean firing with respect to corrugation frequency.

We completed tests with corrugations of several different corrugation frequencies for 55 cells that showed significant modulation for at least one frequency. The variation in RM as a function of corrugation frequency was generally well described by Gaussian functions (Fig. 2E). All Gaussian fits explained >75% of the variance in the data. These fits were then used to quantify the two main features of interest shown in Figure 2E. First, we examined whether all cells had their largest responses at low corrugation frequencies (spatially lowpass). Second, we examined the highest corrugation frequency that produced substantial modulation (high corrugation frequency cutoff, the point at which RM falls to two-thirds of the peak).

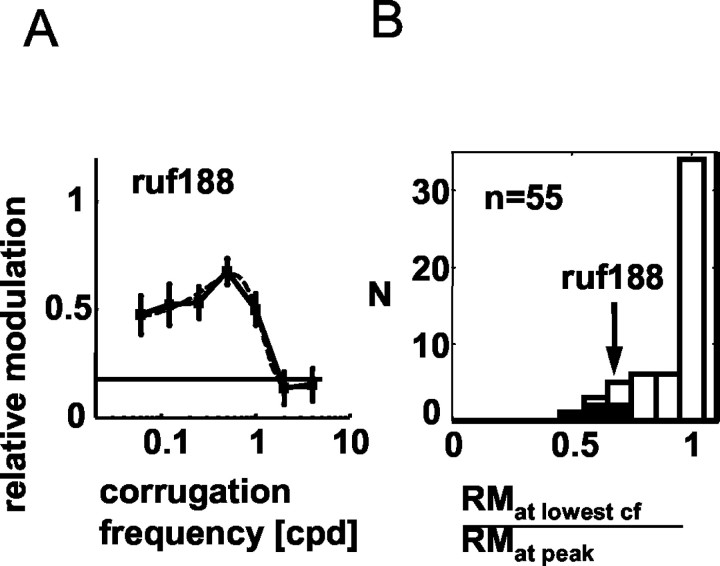
The fitted Gaussian functions were not constrained to be lowpass. Figure 3A shows an example in which the best fit had a peak at intermediate frequencies. We estimated the extent of attenuation in RM at low frequencies by comparing the RM at the lowest frequency tested with the peak value of RM. (Values for this comparison were obtained from the data, not from the fits.) The large majority of these ratios were close to 1 (>0.9 for 40 of 55 cells, 73%) (Fig. 3B). Except for one cell, all values were >0.5 and hence would be considered lowpass by the criterion of Hawken et al. (1996).

Figure 3.

Response attenuation at low frequencies was unusual. A shows RM as a function of corrugation frequency for one neuron (ruf188) with unusually marked attenuation at low frequencies. The dashed line corresponds to the Gaussian curve fitted to the data. The RM for the lowest frequency tested (0.06 cpd) was only 70% of that at the peak of the fit. This ratio, (RM at the lowest frequency tested)/(RM at peak), was used to estimate the extent of low-frequency attenuation for the population of 55 neurons (frequency histogram shown in B). The black bars correspond to the ratios of cells with statistically significant attenuation at low frequency.

The apparent reduction in RM at low frequencies for some cells may primarily be the result of random fluctuations in response. To evaluate this statistically, we compared the RM at 0.06 cpd with the largest RM observed. This was significant for 5 of the 55 cells (p < 0.05; two-tailed test corrected for multiple comparisons, by resampling). (We also used nested Gaussian fits to see whether adding a non-zero mean produced a significant improvement, with similar results, with 7 of 55 being significant.)

Thus, it seems that a small population of neurons do show significant attenuation of their response modulation at low corrugation frequencies. However, even in this selected population, the attenuation was modest (the example shown in Fig. 3A was one of the five significant cases). Thus, it does not seem to represent a specialization for processing more complex three-dimensional configurations. The phase of the responses suggested that these were not responses to surface slant: the absolute response phases were close to 0° (response peak when the preferred disparity was in the center of the RF), and there was no systematic shift in phase as a function of corrugation frequency. These features are compatible with a degree of surround suppression produced when the surround was at the same disparity as the center.

The above analyses establish that the vast majority of V1 neurons show a lowpass response to sinusoidal variations in disparity, suggesting fronto-parallel RFs. This is in agreement with previous reports of binocular interaction profiles elongated in the fronto-parallel plane (Anzai et al., 1999, their Fig. 1). The results presented here go beyond the previous report in two respects. The examples shown by Anzai et al. (1999) display elongation in the fronto-parallel plane, but their analysis did not examine this feature quantitatively or rule out slant selectivity. The quantitative analysis in the present study suggests that selectivity for a uniform disparity across the RF is a general feature of disparity-selective neurons in the striate cortex. Furthermore, the use of a reverse-correlation analysis by Anzai et al. (1999) relies on the assumption of a linear neuronal response. They used a sequence of noise stimuli in which there is no single consistent pattern of disparities, whether it be planar or sinusoidal. Thus, a detecting system that is sensitive to a consistent pattern of disparities would be inadequately stimulated by such a noise stimulus. Nonlinear responses to combinations of disparities simultaneously present in the RF could therefore not be examined. For example, a nonlinear interaction between neighboring parts of the RF might generate selectivity for slant independent of mean disparity. Such a response would be revealed by our measures with corrugations, because the stimulus contains appropriate multiple disparities. The lowpass response to the corrugations therefore allows us to exclude the possibility of nonlinear responses to combinations of disparities. It is important to stress that the lowpass response not only indicates linear summation of disparities but also that the input to this linear summation seems to show the same disparity preference at each point in the RF. Linear summation across an RF with a preferred disparity that changes across the RF would also generate bandpass responses.

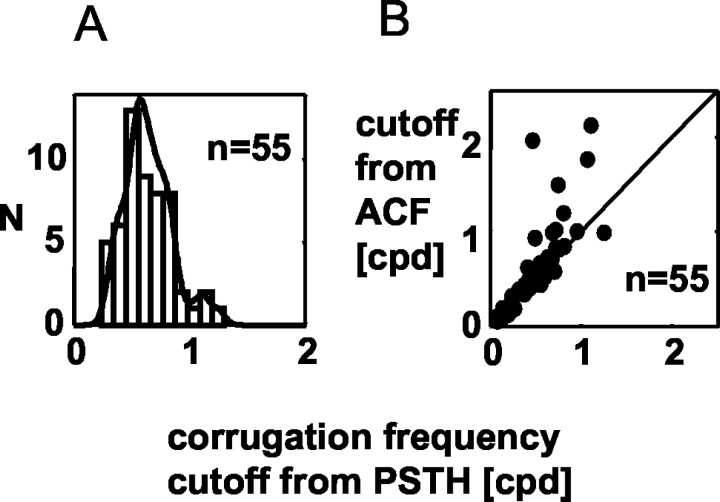
Because RM is a lowpass function of corrugation frequency for most neurons, their response can be summarized by the high corrugation frequency cutoff for the RM (Fig. 2C). We took as our measure the frequency at which the fitted Gaussian fell to two-thirds of its peak value. Figure 4A shows the distribution of this high-cut frequency for 55 cells. It tends to occur at quite low frequencies, with a mean of 0.5 cpd (±0.26 cpd; SD), much lower than typical values for luminance gratings in monkey V1 at these eccentricities (Foster et al., 1985). The highest value observed was 1.3 cpd.

Figure 4.

High corrugation frequency cutoff. A shows a frequency histogram and superimposes a smoothed density function. It is possible that, in some cases, modulation to high-frequency corrugations was underestimated because of the effects of fixational eye movements. We, therefore, reanalyzed all the data using the autocorrelation function of the spike trains to estimate periodic modulation. This is less sensitive to eye movements (see Appendix). B compares the corrugation frequency high cutoffs calculated with this autocorrelation method, with the cutoff estimated from the modulation in the peristimulus time histogram (PSTH). Despite the generally excellent agreement between the two measures, the cutoff frequency estimated from the autocorrelation functions is substantially larger in a few cases. This leads to a significant difference between the two measures across the population (p < 0.01; n = 55; paired t test).

However, this analysis is complicated by small eye movements during fixation. Changes in vertical eye position will change the phase of the sinusoid that falls over the RF center, changing the phase of the neuronal response. Significant variation in the phase of the response within and between trials leads to an underestimate of the modulation amplitude. This problem is greatest for high corrugation frequencies, because small movements constitute a larger fraction of the spatial period. This could, therefore, lead to an underestimate of the high corrugation frequency cutoff. However, the majority of the cutoff frequencies observed were too low to be explained by the observed variation in vertical eye position: the mean of the observed SDs was 0.14, 0.19, 0.21, and 0.22° for monkeys Hg, Rb, Df, and Rf, respectively. Because the measured variation in eye position overestimates the true variation (Read and Cumming, 2003), it seems that eye movements are unlikely to have compromised these measurements in more than a few neurons.

As an additional safeguard against the effect of eye movements, we reanalyzed the data using the autocorrelation function to detect periodic modulation in the firing rate, independent of phase (Schlittgen and Streitberg, 2001). The appendix shows how, with the help of the autocorrelation function, the effect of saccadic eye movements on RM is reduced. Figure 4B compares the value of high corrugation frequency cutoff for the two analysis methods. In all but a few cases, the two methods gave similar answers, confirming that the influence of eye movements on the measurement of RM was generally small. In a few cases, the autocorrelation method produces clearly larger values, suggesting that eye movements may have had a significant effect in these neurons. This leads to a weak, but significant (p < 0.01; paired t test), tendency toward higher values for the autocorrelation method (mean value, 0.61 ± 0.44 cpd; SD by the autocorrelation method).

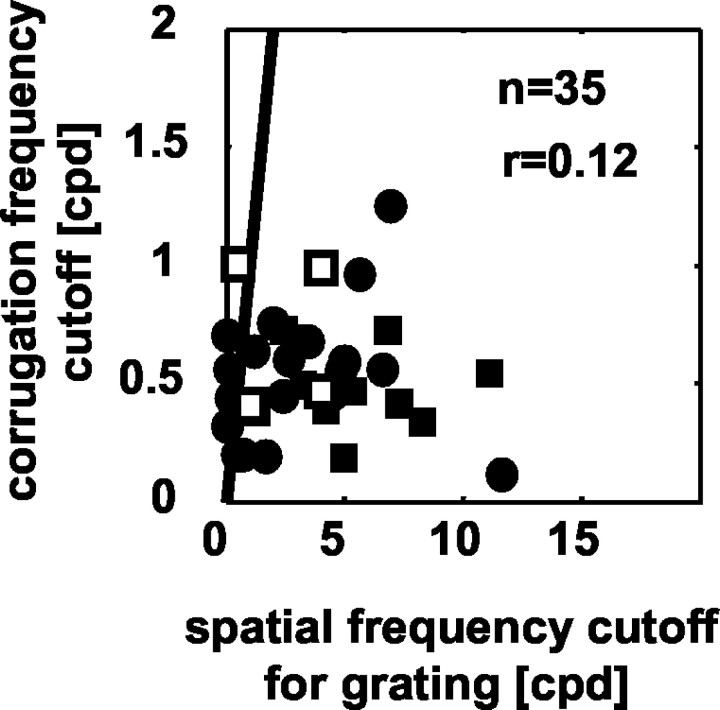
We compared the high-frequency cutoff for depth corrugations with the spatial frequency high cutoff for luminance gratings in 35 of the 55 cells. The luminance gratings were presented at the preferred orientation (20 monocular, dominant eye, 15 binocular at the preferred disparity), whereas the depth corrugations were always horizontal (0°; disparity variation always along a vertical axis). To compare these values therefore the high-cut frequency for the gratings was multiplied by cos (grating orientation), to estimate the cutoff frequency along the vertical axis. Despite the fact that this shifts the cutoff spatial frequency to lower values for the luminance gratings, these values are almost always greater than the cutoff corrugation frequency for depth modulation (Fig. 5; note the different scales on abscissa and ordinate). This indicates that the three-dimensional structure of the RF is on a coarser scale than the luminance structure. Furthermore, there is no significant correlation between these measures (r = 0.12; NS). Both of these observations follow if the luminance structure of the RF is used to calculate interocular correlation across finite regions of the two retinae (as in the energy model; see simulations below). The three-dimensional structure is determined by the area over which this is estimated, not by the luminance RF structure within it. The relationship between luminance variation and the ability to extract the three-dimensional structure is also discussed in the accompanying article (Banks et al., 2004).

Figure 5.

Comparison of high corrugation frequency cutoff values in response to corrugations (ordinate) and high spatial frequency cutoff to sinusoidal luminance gratings (abscissa). The filled symbols show data for 35 neurons, obtained monocularly for the dominant eye (circles; n = 20) or binocularly (squares; n = 15). The solid line depicts the identity. There is no significant correlation between the two properties of the neurons (r = 0.12; NS; n = 35). Open squares represent values obtained from the model using four different RFs. This illustrates that the model does not require a correlation between corrugation and spatial frequency cutoffs for these two stimuli.

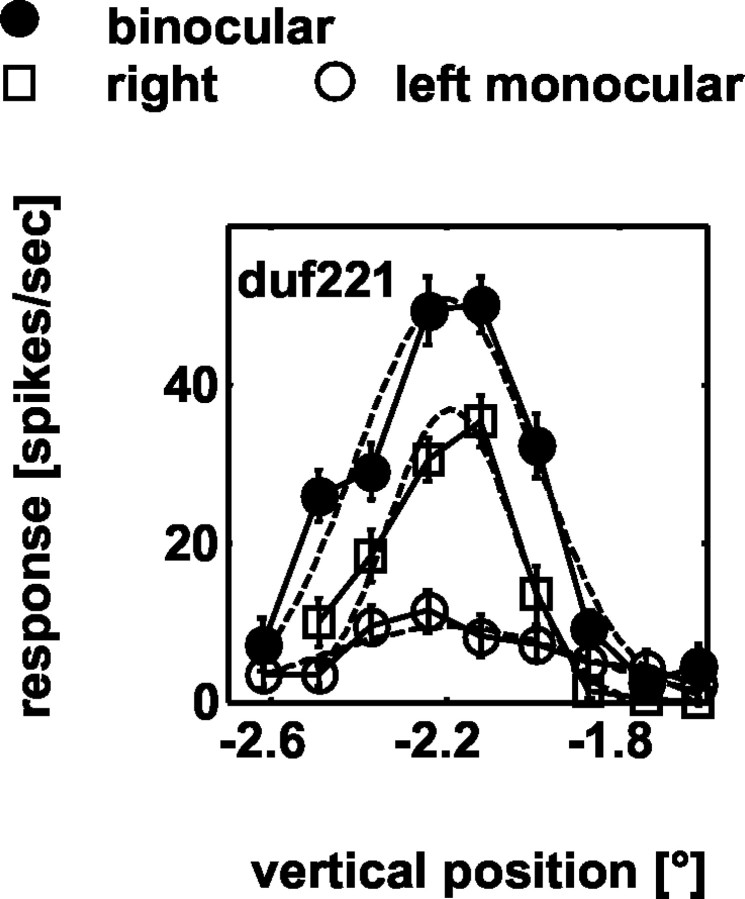
If the neurons were constructed from subunits that are all selective for the same fronto-parallel disparity (as in the energy model, producing a lowpass response), then the high corrugation frequency cutoff for disparity modulation should be determined by the RF size. We therefore obtained quantitative estimates of the vertical extent of the RF for 21 neurons. These measures used thin strips of random dot texture like those used for the depth corrugations (see Materials and Methods). Gaussian functions were fit to the response rate as a function of vertical position, and the SD was used as a measure of the half-width of the minimum response field. Data for one example neuron are shown in Figure 6. Two of these 21 neurons showed a degree of bandpass response (suggesting a center-surround organization). Their high-frequency cutoff is determined by the size of the center region. [Similarly for retinal ganglion cells, the cutoff spatial frequency is a predictor of center size of the RF (Linsenmeier et al., 1982).] Because the size of the center of the preferred disparity would have been difficult to measure independently, we excluded these two neurons from the comparison.

Figure 6.

Example data illustrating the measurement of RF height for cell duf221. The vertical position of the stimulus relative to the fovea is depicted on the abscissa and the firing rate on the ordinate. Filled circles represent the measurements in response to a binocular stimulus, open markers in response to a stimulus being presented monocularly. Gaussian functions (dashed lines) are fitted to each of the data curves.

Suppose the response rate of a neuron was given by the sum of its responses to the disparities of individual dots, weighted by the Gaussian envelope of the RF. Under these circumstances, we can use the Fourier transform of the minimum response field to predict the way in which RM varies with corrugation frequency. The Fourier transform of a Gaussian in space with an SD of σ_x is a Gaussian in the frequency domain with SD:

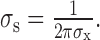4

The frequency domain counterpart of the RF envelope is the corrugation frequency-tuning width. If RM is a lowpass function of corrugation frequency (as for the vast majority of the neurons and in the energy model), the Gaussian in the frequency domain is centered around zero. In this case, frequency-tuning half-width can be estimated by the corrugation frequency cutoff.

Before examining this relationship for real neurons, note that the responses of the energy model are not necessarily given by the sum of the responses to the disparities of individual dots. Consider a display in which two dots are presented to both eyes (l₁, r₁, l₂, r₂) and each is given a different disparity (l₁ - r₁ ≠ l₂ - r₂). It is an oversimplification to consider only these two disparities, because the response of a model will also depend on the disparities produced by the other possible dot pairings (pairing l₁ with r₂, and so on). In general, model responses will depend, in a complicated way, on the disparities and positions of the dots.

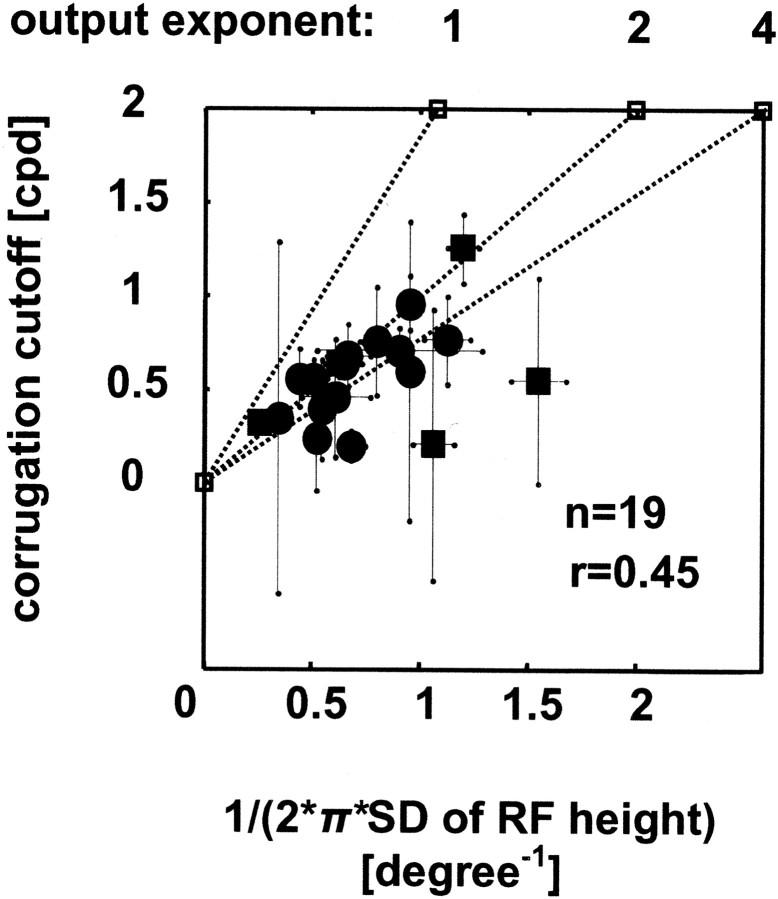
We therefore ran simulations with our implementation of the energy model (Bridge et al., 2001), measuring the minimum response field and the high corrugation frequency cutoff for corrugations in the same way as for the neurons. The behavior of the model was very similar to the naive prediction, suggesting that the complex interactions between dots do not produce any systematic change in firing when averaged over many different dot patterns. One model parameter that had an important influence on this relationship was the value of the output exponent. Although the energy model is usually described with a half-squaring output nonlinearity, this is largely for mathematical convenience. Raising the output to higher powers produces qualitatively similar results, and a number of studies have suggested that the output exponents often are >2 in real neurons (Anzai et al., 1999; Gardner et al., 1999). For model neurons, larger output exponents lead to smaller estimates of the minimum response field, whereas the cutoff frequency for depth corrugations was less affected. The relationship between the minimum response field, high-frequency cutoff, and output exponent for model neurons is shown by the dotted lines in Figure 7.

Figure 7.

The relationship between RF size (the SD of a Gaussian fit to responses like those in Fig. 6; SDrf) and high-frequency cutoff for depth corrugations (the SD of a lowpass Gaussian fit to data like those shown in Fig. 2E; SDsf). Because an inverse relationship is expected, 1/(2π^*SDrf) is plotted on the abscissa (i.e., the SD of the same Gaussian in the frequency domain). There is a significant correlation (r = 0.45; p < 0.05; n = 19). Circles and squares depict cells, for which the RF was measured monocularly in the dominant eye (n = 14) and binocularly (n = 5), respectively; the error bars correspond to SEs (by resampling). This relationship was also examined with the model (dotted lines). The model responses are shown for three different output exponents (1, 2, and 4). Note that no neuron lies significantly above the line predicted by the model with an output exponent of 2 (i.e., a half-squaring output nonlinearity). This line also represents the identity line. The output exponent of 1 refers simply to half-wave rectification, a sufficient nonlinearity to generate disparity selectivity.

Superimposed on these model data, Figure 7 compares the size of the minimum response field with the high corrugation frequency cutoff for 21 neurons. Only fits that explained >70% of the variance were used. The correlation (r = 0.45; p < 0.05) is significant, and the majority of neurons (14 of 19) lie beneath the line obtained from the model simulations (dotted line at output exponent of 2, which also represents the identity line). The points above the line do not differ significantly from it (by resampling). Cells that fall below the predicted line can readily be explained by assuming an output exponent that is >2. Across the population, there is a tendency for the high corrugation frequency cutoff to be lower than predicted by the model with an exponent of 2. This may indicate that most neurons have an output nonlinearity that is more expansive that half squaring. Alternatively, it may be that the area over which the disparity integration takes place is somewhat larger than our estimate of the minimum response field.

Although the high corrugation frequency cutoff was significantly correlated with minimum response field size, there was considerable scatter in this relationship. This may explain why we found no clear relationship between the high corrugation frequency cutoff and eccentricity (r = 0.04; n = 55; NS partial correlation with respect to monkey).

Determinants of modulation strength

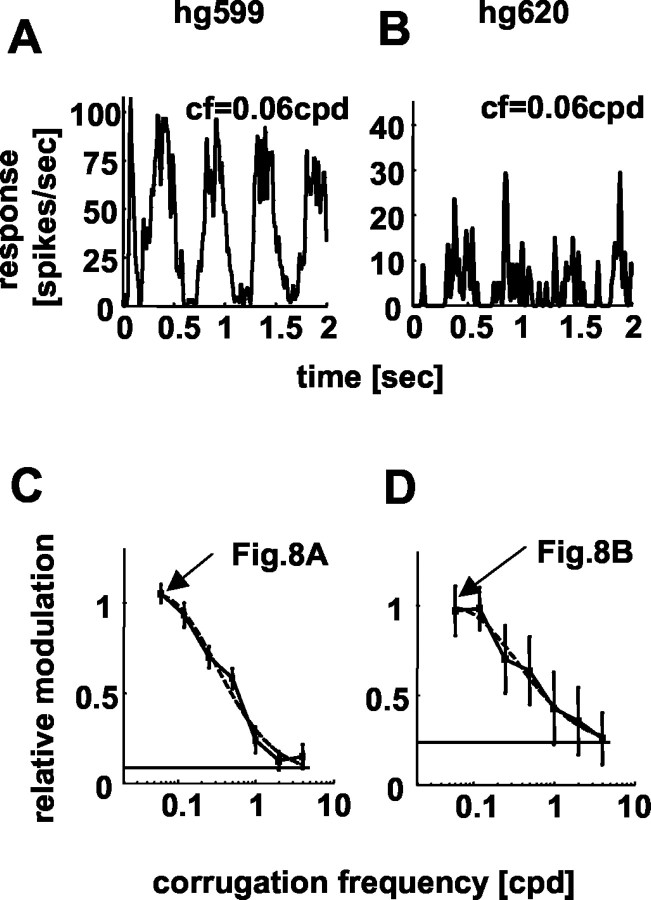
The analysis above has focused primarily on how RM varies with changes in the corrugation frequency of depth modulation. The strength of the modulation was largely ignored. In this context, it is important to note that the estimation of RM is more reliable with higher mean firing rates. Figure 8 demonstrates this for two neurons firing at a mean spike rate of 46 spikes/sec (hg599; left column) and 8 spikes/sec (hg620; right column), respectively. Both neurons produce similar values of RM. The 2 Hz modulation is, however, much clearer in the spike density function for the neuron with the higher firing rate (Fig. 8A). The responses to the planar control stimulus show no clear modulation in either cell (data not shown), but their RM values differ by a factor of 3 (baseline in Fig. 8C,D: RM, 0.08 for cell hg599; RM, 0.24 for cell hg620).

Figure 8.

Relative modulation and mean firing rate. A and B show spike density functions for two neurons, with very different mean firing rates (46 spikes/sec and 8 spikes/sec, respectively). The corrugation frequency of the disparity corrugation was 0.06 cpd, and the temporal frequency was 2 Hz. Although the values of RM are similar for both neurons (C, D), the modulation is much clearer for the neuron with the higher firing rate (A). Neurons with lower firings rates give less reliable estimates of RM. This is most clearly seen from the error bars in (C, D), which show SDs of the resampled populations.

Raw values of RM can, therefore, be a misleading guide because large values can occur at random in weakly modulating cells with low mean firing, or simply because a neuron has a tendency to periodic activity regardless of the stimulus. We therefore quantified the modulation strength with a contrast measure, the RM contrast (see Materials and Methods), that compares the modulation produced by corrugations with that produced by the planar stimulus with no disparity variation.

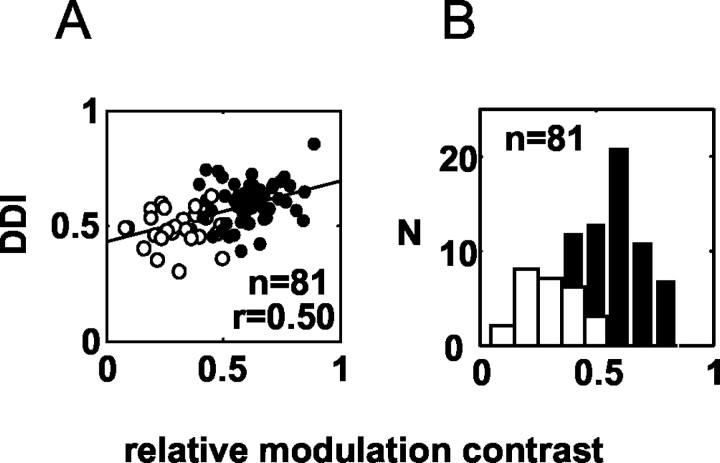
Note that when neuronal firing is weak, the value of RM for the planar control stimulus is often large, so this measure is not biased toward large values in weakly activated neurons (unlike similar measures on raw spike counts) (Prince et al., 2002). We investigated the relationship between RM contrast and two properties: retinal eccentricity and disparity selectivity (DDI) (Fig. 9). There is no significant dependence of modulation on retinal eccentricity (r = -0.0007; n = 55; NS partial correlation with respect to monkeys; data not shown). But, there is a highly significant positive correlation with the DDI (r = 0.50; p < 10^-5) (Fig. 9A).

Figure 9.

The relationship between strength of disparity tuning (measured by the DDI) and the strength of modulation induced by the corrugations (measured by RM contrast). The filled symbols represent the neurons for which the RM was significant (n = 55), and open circles indicate the neurons for which RM was not significant (n = 26). All neurons included in this plot had significant disparity tuning (n = 81). There is a strong and significant (r = 0.5; p < 10 ^-5) correlation. All neurons with a DDI >0.65 showed significant RM. B, Frequency distribution for RM contrast values for the 81 cells tested. The open and filled bars represent nonsignificant and significant modulation, respectively.

Neurons without significantly higher modulation in response to the corrugations than in response to the planar stimulus (Fig. 9A, ○) have a significantly lower DDI (mean DDI, 0.30 vs 0.61 for neurons with significant modulation; p < 10^-6; n = 81; t test). All neurons with a DDI above 0.65 show significant modulation. At first sight, this correlation is not surprising because both measures are closely dependent on the strength of disparity tuning. But, this need not be true. Consider a neuron with a response that depends primarily on the magnitude of surface slant. Such neurons could show weak disparity selectivity for planar RDS but modulate their activity strongly during presentation of depth corrugations, because these present different values of slant at different points in the cycle.

The correlation between DDI and RM contrast, especially the lack of neurons showing strong RM contrast with weak DDI, is additional evidence that there is not a population of neurons in V1 that are selective for slant but only weakly selective for disparity in planar RDS. We also studied responses in 19 neurons that were not disparity selective (ANOVA; p > 0.05), which are not shown in Figure 9. None of these showed significant modulation to the corrugations.

One potentially important source of scatter in the relationship between the strength of disparity tuning and the strength of modulation to depth corrugations may be the temporal properties of the stimulus. All of the data reported here used a stimulus temporal frequency of 2 Hz. This is well below the temporal frequency high cutoff for most neurons when examined with luminance gratings. [All of the neurons reported by Hawken et al. (1996) had temporal frequency high cutoffs >2 Hz.] However, it is possible that the temporal integration for disparity processing is over greater periods and that some neurons might have shown stronger modulation had we used lower temporal frequencies. We are currently investigating temporal integration in response to depth corrugations.

Comparisons of the physiological data with predictions from the model

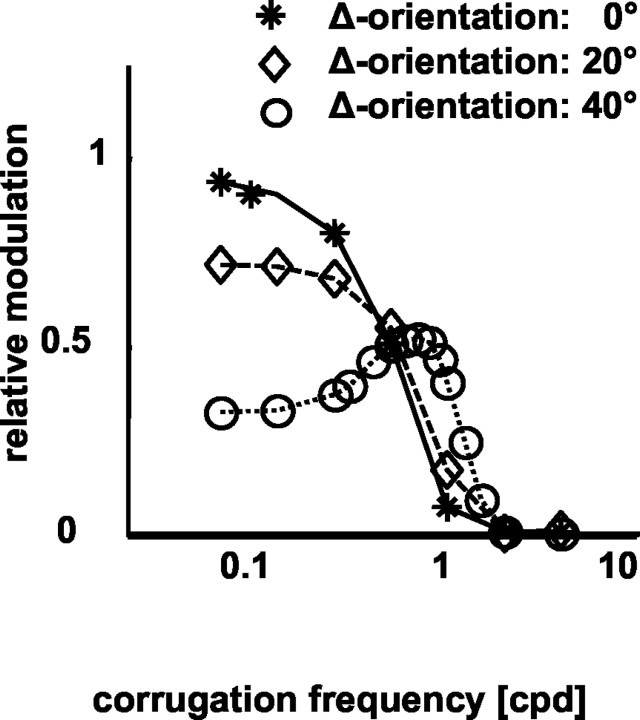
At several points, we have shown responses of model complex cells, using a model similar to the energy model for disparity-tuned complex cells implemented by Ohzawa et al. (1990) but using two-dimensional RFs (Bridge et al., 2001). These simulations showed that all of the physiological data are compatible with such a model: (1) The model responded with a sinusoidal modulation of the response at the stimulus temporal frequency (Fig. 2). (2) The strength of this modulation depended on the relationship between the corrugation frequency of the corrugation and the size of the RF, in a similar manner to that seen in the neuronal data (Fig. 7). (3) Corrugation frequency selectivity for depth corrugations is determined by RF size. Spatial frequency selectivity for contrast gratings is determined by the structure within the RF. For this reason, spatial frequency tuning for luminance contrast and corrugation frequency for depth corrugations can be manipulated separately in the model (Fig. 5, □). They are also uncorrelated in the physiological data (Fig. 5). (4) The model shows a lowpass response to depth corrugations. Interestingly, this remains true even when an orientation difference between the eyes is introduced to the model (Fig. 10). Although it has been suggested that such orientation differences might be a specialization for detecting surface slant (Blakemore et al., 1972; von der Heydt, 1978; Ninio, 1985; Mitchison and McKee, 1990; Cagenello and Rogers, 1993), within the context of the energy model, the response remains dominated by the effects of positional disparity (Bridge et al., 2001, their Fig. 7), so that the modulation at low frequencies is very similar to that at intermediate frequencies. If very large orientation differences are used [40°; much larger than those found physiologically (Bridge and Cumming, 2001)], a modest increase in response can be seen at intermediate frequencies (Fig. 10, dotted line). Thus, the lack of any bandpass response to disparity corrugations in V1 neurons is not evidence against the existence of interocular differences in preferred orientation. It is evidence against the existence of neurons primarily sensitive to surface slant.

Figure 10.

The effect of orientation differences in model neurons. Model neurons were constructed with different RF orientations in the two eyes. The response of these models to corrugations of variable corrugation frequency was then assessed, using the same protocol as we used for real neurons. RM (ordinate) obtained from model simulations is plotted against corrugation frequency (abscissa). Orientation difference between the monocular RFs (0, 20, and 40° for solid, dashed, and dotted lines, respectively) was the only parameter changed between the simulations. Note that a decline in RM at low spatial frequencies only becomes apparent for large orientation differences (40°; open circles).

Discussion

Previous studies of disparity selectivity in the striate cortex have used stimuli that correspond to planar fronto-parallel surfaces. This differs markedly from studies of responses to contrast, in which the two-dimensional structure of the stimulus (orientation, spatial frequency, etc.) is more important than its luminance. To explore the three-dimensional structure of V1 RFs, we examined responses to sinusoidal modulation of disparity in RDS. Every aspect of the response we examined could be explained as a response to the weighted mean of the disparities of the dots covering the RF (the weights being set by the RF envelope), as if the optimum disparity is the same at all locations within the RF.

First, this predicts that the response should be a sinusoidal modulation in activity, at the temporal frequency of the stimulus, exactly as we observed. Second, the extent of modulation (RM) should be greatest at low frequencies. This was the typical pattern. Third, the way in which the RM declined with increasing stimulus corrugation frequency was well described by a Gaussian function of frequency. This is the form expected if the shape of the RF envelope is also a Gaussian. Furthermore, this cutoff frequency never significantly exceeded the limit predicted from an independent measure of the RF envelope. Finally, the correlation between disparity selectivity (DDI) and the maximum value of RM indicates that there is not a subpopulation of neurons that are weakly tuned to disparity but strongly tuned for disparity gradients.

All of these properties of V1 neurons were readily matched with an implementation of the energy model (Ohzawa et al., 1990), extended to include two-dimensional RFs in each eye (Bridge et al., 2001). This therefore represents another success for the most widely accepted mechanism by which disparity selectivity arises in V1. It is important to note that, taken by themselves, the data reported here are compatible with a wide range of other models. Any model in which the response is, on average, determined by the mean disparity of the dots weighted according to their location in the RF would suffice.

The general absence of attenuation in RM at low frequencies excludes two plausible possibilities for an underlying RF structure. First, it indicates a lack of any center-surround organization in the disparity domain (i.e., any suppression from the surround does not depend on disparity, at least over the range of disparities tested here). If a region activated by one disparity was surrounded by a region where the same disparity suppressed the response, then a uniform field of dots at that disparity would produce a weaker response than a stimulus with an intermediate corrugation frequency, placing the preferred disparity at the center but not in the surround. A few neurons (5 of 55) showed weak, but significant, attenuation of their response at low corrugation frequencies. The phase of their responses was compatible with a weak center surround organization of this type. However, the attenuation was modest even in this small subpopulation, so it does not seem to be a significant feature of the response of the population of V1 neurons.

Second, the lack of low-frequency attenuation argues against a specialization for signaling slant. These depth corrugations place a time-varying slant over the RF, and because the amplitude of the corrugations was constant, the magnitude of the slant variation increased with the corrugation frequency. A neuron activated only by non-zero values of slant would cease responding at low frequencies. Note that this observation does not exclude the possibility that the activity of some neurons is weakly affected by stimulus slant. It does indicate that the effects of changes in slant are small compared with the effects of changes in mean disparity. This is a feature of the energy model, even when interocular differences in preferred orientation are incorporated (Bridge et al., 2001).

One possibility is that because we only used disparity modulations in one orientation, we might have missed a population of neurons that are selective for tilt about other axes. If this were the case, the population would have to be strongly biased away from responding to tilt around a horizontal axis to explain the lack of slant-selective responses we observed, which seems unlikely. To measure responses to different corrugation frequencies at multiple orientations would require substantially more data per neuron. Furthermore, disparity modulations presented at any other orientation introduce monocular changes to the stimulus (variation in dot density) that depend on spatial frequency and orientation. Therefore, had we found neurons that appeared slant selective only for variation in disparity along nonvertical axes, this would not have provided clear evidence for slant selectivity.

The lack of slant selectivity in V1 raises the question of how slant selectivity in extrastriate cortical areas arises. The most natural possibility is that this is derived by combining the outputs of V1 disparity-selective neurons. This allows a neuron to detect slant by means of piecewise planar (fronto-parallel) approximations. Studies of slant selectivity in extrastriate cortex have all used large enough stimuli that this explanation is entirely possible (Shikata et al., 1996; Sakata et al., 1999; Tsutsui et al., 1999; Sugihara et al., 2002; Nguyenkim and DeAngelis, 2003). Furthermore, a recent study of slant selectivity in area MT (Nguyenkim and DeAngelis, 2003) found responses to pairs of small planar patches that were commensurate with this explanation. One consequence of such an explanation is that modulations over regions as small as V1 RFs should not be detected by such neurons. That is to say that if tested with depth corrugations like those used here, this model predicts that high-frequency cutoffs for slant-selective neurons should not be higher than those reported here.

Although such responses have not been studied in extrastriate cortical areas, one can pursue the same logic all the way to psychophysical measures. If slant selectivity throughout the brain is derived from piecewise comparison of outputs from V1 neurons, then the high-frequency cutoffs reported here should limit the psychophysical observer's ability to detect disparity modulations at high corrugation frequency. Human psychophysical studies (Tyler, 1974; Schumer and Ganz, 1979; Howard and Rogers, 1995; Bradshaw and Rogers, 1999; Banks et al., 2004) have found that the acuity to detect disparity modulations is surprisingly poor (when considering the high acuity to detect luminance structure or stereo-acuity). The accompanying article (Banks et al., 2004) shows that this cannot be explained by limitations inherent to the stimulus and also argues that using piecewise frontal disparity estimates imposes a limit on the highest attainable acuity for disparity modulations. Comparing the physiological data here with psychophysical responses at similar eccentricities suggests that spatial integration of these V1 neurons is what limits performance. The neuronal data show a reduction to 66% of maximal sensitivity at a mean frequency of 0.5 cpd, at a mean eccentricity of 3.7°. If psychophysical judgments depended on these responses, a corrugation frequency of 0.5 cpd should produce thresholds 50% higher than the optimum. The two human studies that examined thresholds at these eccentricities (Prince and Rogers, 1998; Banks et al., 2004) found 50% threshold elevation at 0.5-0.6 cpd. The similarity between these values for single neurons and for human psychophysics suggests that the acuity limit for humans is determined by the frequency at which the majority of V1 neurons fail to modulate their responses. The cutoff frequency for the neurons seems in turn to be limited by the size of the RF (Fig. 7). Taken together, these observations suggest a simple physiological explanation for the observation that cyclopean acuity for depth modulations is so poor. When the period of the corrugation is smaller than the RF size, the response of neurons with adjacent RFs becomes identical, and the corrugation cannot be detected.

The properties of V1 neurons do not explain why human sensitivity to depth corrugation is reduced at frequencies lower than 0.3 cpd, because nearly all neurons showed a simple lowpass function of corrugation frequency. The reduced sensitivity to low frequencies may, therefore, reflect the consequences of processing in the extrastriate cortex. Suppose that extrastriate cortex generated a representation of relative disparity by comparing nearby subregions. At very low frequencies, there would be little difference in disparity between the subregions. Consequently, the response will be attenuated at low frequencies. Conversely, the lack of low-frequency attenuation that we report here for V1 neurons implies that they are not sensitive to disparity differences within their RFs.

It is intriguing to compare the disparity structure of V1 RFs with the way in which other parts of the visual system are organized for luminance processing. The response seems to be determined by the disparity presented over a small region, regardless of the disparities outside that area. In this way, their processing of disparity is less sophisticated than the luminance processing of retinal ganglion cells. The closest analogy seems to be with photoreceptors, the response of which to luminance shows the same simple spatial structure as the response of V1 neurons to disparity. In this sense, disparity-selective cells in V1 might be considered the photoreceptors of the “cyclopean retina” (Julesz, 1971).

Appendix

Saccadic eye movements result in instantaneous changes of phase of the periodic modulation of the spike train. We used the autocorrelation function of the spike train in an attempt to estimate the periodic modulation in firing in a way that was not sensitive to this effect of eye movements. The autocorrelation function of the spike train describes for all t how well the spike train at time t correlates with the spike train at time t + τ (i.e., it compares the spike train at t with that at t + τ). For a periodic spike train of period λ, its autocorrelation function is maximal for τ = nλ, for n = 0, 1, 2, etc. It thus is a description of the periodic modulation of the spike train, centered around 0, regardless of the phase of the spike train. Although changes in the phase of a response can affect the extent of correlation (the modulation amplitude in the autocorrelation function), this is small unless the phase changes are frequent. If a phase-shift occurs at t₁, then this affects the comparison and, consequently, the extent of correlation for the segment of the spike train: t₁ < t < t₁ + τ, whereas for t < t₁ and t > t₁ + τ it remains unaffected. Hence, for small τ, the effect of occasional phase shifts is small, and the autocorrelation function best represents the spike train cleared from the disruptions caused by saccades. Extracting the f1 component from the autocorrelation function for small τ, thus, provides an estimate of its value that is relatively unaffected by saccades. At very small values of τ, the autocorrelation function reflects the intrinsic statistics of the firing of a neuron. We, therefore, calculated the amplitude of f1 modulation in the autocorrelation function from τ = 250 msec (0.5 λ) to τ = 750 msec (1.5 λ).