A Neural Correlate of Reward-Based Behavioral Learning in Caudate Nucleus: A Functional Magnetic Resonance Imaging Study of a Stochastic Decision Task

Abstract

Humans can acquire appropriate behaviors that maximize rewards on a trial-and-error basis. Recent electrophysiological and imaging studies have demonstrated that neural activity in the midbrain and ventral striatum encodes the error of reward prediction. However, it is yet to be examined whether the striatum is the main locus of reward-based behavioral learning. To address this, we conducted functional magnetic resonance imaging (fMRI) of a stochastic decision task involving monetary rewards, in which subjects had to learn behaviors involving different task difficulties that were controlled by probability. We performed a correlation analysis of fMRI data by using the explanatory variables derived from subject behaviors. We found that activity in the caudate nucleus was correlated with short-term reward and, furthermore, paralleled the magnitude of a subject's behavioral change during learning. In addition, we confirmed that this parallelism between learning and activity in the caudate nucleus is robustly maintained even when we vary task difficulty by controlling the probability. These findings suggest that the caudate nucleus is one of the main loci for reward-based behavioral learning.

Introduction

Guided only by reward and penalty information, animals can adapt their behaviors so that maximal rewards are obtained in the long run, even in unfamiliar and stochastic environments. This reward-based behavioral learning problem has been modeled in several ways (Sutton and Barto, 1998; Breiter et al., 2001). The central learning algorithm in the reinforcement learning models changes behaviors in proportion to reward prediction errors. Some computational models have proposed that the signal transmission in the striatum is modified by synaptic plasticity for behavioral learning, while being guided by reward prediction error conveyed by midbrain dopamine neurons (Houk et al., 1995). In their pioneering work, Hollerman and Schultz (1998) have accumulated compelling evidence that dopamine neurons in the monkey midbrain encode reward prediction errors. Human imaging studies have revealed that the activity in the ventral striatum and putamen (Berns et al., 2001; Breiter et al., 2001; McClure et al., 2003; O'Doherty et al., 2003) is correlated with the reward prediction errors in classical conditioning tasks.

The dorsal striatum, which receives inputs from the dopamine neurons and constitutes loop circuits with many cerebral cortical areas, can potentially be the main locus of reinforcement learning in which behavioral changes are induced by synaptic plasticity while controlled by the reward prediction error. However, it has not yet been demonstrated that the neural activity of the dorsal striatum parallels the behavioral change or reward prediction errors during reward-based learning of new behaviors. To investigate the neural mechanism of reward-based behavioral learning (instrumental conditioning), experimental sessions should contain at least several trials of behavioral learning for a reliable correlation between behavioral changes and neural activity. In addition, the correlation would be more reliable if the rate or difficulty of learning could be quantitatively controlled by task parameters. Here, we developed a new stochastic decision task that satisfies all of these prerequisites and demonstrate that the activity of the caudate nucleus parallels the behavioral change during learning as well as the amount of short-term reward by using functional magnetic resonance imaging (fMRI).

Materials and Methods

Experimental paradigm. In a Test block of the task (Fig. 1 A), subjects were required to move a start disk (green; displayed at 0 sec) located in one of two boxes to the target box where a target disk (red; displayed 0.5 through 1.0 sec) is located by pushing the left or right button after a sound cue. Note that the start and target disk positions can overlap. All of the subjects pushed the buttons with their right-hand index or middle finger. If the green disk moved to (or stayed at) the target disk box successfully, the target box lighted up, and the subject earned a positive reward (+5 yen). Otherwise, the subject suffered the same amount of penalty (-5 yen). The accumulated reward was displayed above the boxes and was updated after each button push. Successive trials were initiated using the final disk position of the previous trial as a start disk position, with a randomly selected target disk position.

Figure 1.

Experimental design. A, Visual displays, button pushing, and their timing in the stochastic decision task. B, C, Graphical explanation of transition rule (rule 2). The two circles denote the two (left or right) positions of the disk. The arrows and attached numbers represent disk movements and their corresponding probabilities when the displayed button is selected.

The disk movement was stochastically dependent on the selected button according to the transition rules described below (rules 1-4). For example, in rule 2, the left button push (Fig. 1 B) moved the disk to the right with a probability of 0.8 and to the left with a probability of 0.2, regardless of whether the disk was initially located at the left or right. Conversely, the right button push (Fig. 1C) moved the disk to the left with a probability of 0.8 and to the right with a probability of 0.2. Therefore, in rule 2, the optimal behavior for the right target, for example, as in Figure 1 A, was to push the left button.

One transition rule consists of two 2 × 2 matrices corresponding to a left or right button push, respectively. Each element of the matrices shows the disk movement probability for a given start and target position in the following format as displayed in the first matrix in rule 1: (1) first row, starting from left, (2) second row, starting from right, (3) first column, moving to left, and (4) second column, moving to right.

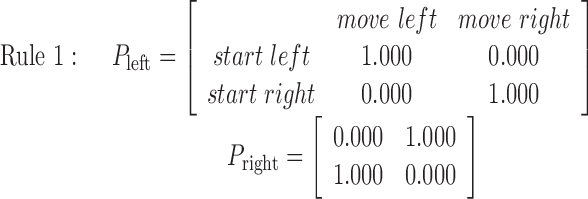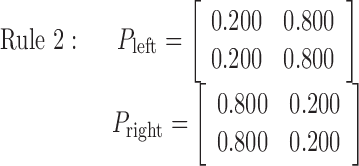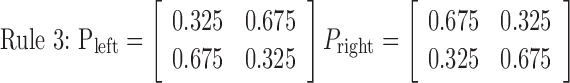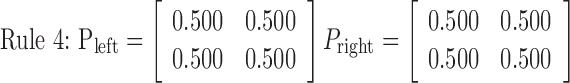Rule 1 is deterministic, consisting of probabilities 0 and 1, and always moves the disk in the same way. Rules 2, 3, and 4 are increasingly more stochastic with dominant probabilities of 0.8, 0.675, and 0.5, respectively. Therefore, rules 1, 2, and 3 became more difficult to learn in this order. Rule 4, with equal 0.5 probabilities, is completely random, so no effective learning was possible. An essential and attractive property of the current task is that the task difficulty is controlled by only one parameter (i.e., the dominant probability in a principled way). Because preparatory experiments found that previous exposition to rule 4 sometimes deteriorates subsequent learning in other rules and increased differences among subjects, rules 1-4 were used in this fixed order in scanning sessions for all of the subjects without explicit instructions concerning task difficulty. As expected, actual learning became slower in this order.

One Test block included 12 trials. In a Control block, the subjects were required to push the same buttons as in the preceding Test block after a visual instruction given as the green disk position. There was no reward or penalty given in the Control block. The Test and Control blocks were interleaved. One session for each transition rule included 15 Test/Control blocks containing 180 Test trials and lasted for 24 min (4 sec × 12 trials × 2(Test + Control) × 15 blocks). The subjects were told that the disk would move in a stochastic but systematic manner according to the pushed button and were encouraged to earn as much monetary reward as possible, which was actually given to them in addition to the basic compensation.

Explanatory variables. Four explanatory variables were derived from subject behaviors. The short-term reward (SR) denotes the amount of money (yen) obtained in one term, defined as one-half of a block (six trials). The accumulated reward (AR) denotes the amount of money accumulated up to the current term in each transition rule.

The learning rate index (LRI) quantifies the change in button push behavior from one term to the next. Because the subject's behavior in the ith term can be described by how often button b was pushed when start s and target t are provided (s, t, and b take a value of either left or right), we represent it as probabilities P_i(b|s,t). Therefore, the differences in button push behaviors can be captured by a distance measure between the two corresponding probabilities. The KL distance (Cover and Thomas, 1991) defined below is the most standard measure of distance between two probabilities p and q, where the summation is taken for all of the possible events to calculate expectation. The KL distance formally represents how much information (bits) is lost when a probabilistic distribution p is compressed by another distribution q instead of p. It takes a non-negative value and equals 0 only if p and q are identical:

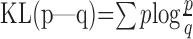The LRI of the ith term representing behavioral change in the adjacent ith and (i + 1)th terms is a straightforward application of the KL distance between the two sets of probabilities P_i+1(b|s,t) and P_i(b|s,t). If a given transition rule is learnable for a subject (rules 1-3), the subject is expected to change behavior a lot at the beginning of learning, but not to change it much at the later stage of learning. In this case, LRI is expected to look like an exponentially decaying learning curve, which approximately reflects how much synaptic plasticity takes place for behavioral changes.

The learning convergence index (LCI) represents a memory consolidation process for optimal decision-making. Because the progress in learning can be measured by how close the current button push behavior is to the final one, LCI was defined as a similarity index between the current and final button push behaviors. Because a negated value of the KL distance between P_i(b|s,t) and P_final(b|s,t) represents a similarity of behaviors in the ith and final term, we defined the LCI of the ith term by normalizing the negated KL distance between 0 and 1. Therefore, LCI becomes 0 when the current button push behavior is maximally distant from the final one and approaches 1 as the current behavior becomes more similar to the final one, in other words, as the optimal (except rule 4) behavior is acquired.

The correlation coefficient between two explanatory variables for one subject was highest at 0.68 between LCI and SR and <0.41 for any other combination. The mean and SD over subjects between LCI and SR were 0.61 and 0.07, respectively. The multicolinearity among the explanatory variables was evaluated by the variance inflation factor (VIF) (Chatterjee and Price, 1977). The VIF of one variable is 1/(1 - R ²), where R is a multiple correlation coefficient of the given variable fitted by the remaining variables. Typically, the statistical result is assumed unreliable if VIF > 10. In our experiment, the maximum value of VIF for all of the subjects was 2.21.

MRI acquisition and analysis. Eight healthy adults (24-33 years of age; two females, six males; all right-handed) participated in the experiment. The informed consent of the participants was obtained beforehand, and the protocol was approved by the ethics committee of Advanced Telecommunications Research Institute. MRI scanning was done with a 1.5 tesla Marconi scanner. For each subject, 480 scans ([Test (8 scans) + Control (8 scans)] × 15 × 2) of Bold images (repetition time, 6 sec; echo time, 55 msec; flip angle, 90°; field of view, 192 mm; resolution, 3 × 3 × 3 mm) were acquired for the first two rules. Each fMRI session contained four preliminary dummy scans corresponding to six Control trials to allow for T1 equilibration effects. After a break, the same procedure was repeated for the other two rules. High-resolution structure images were also acquired for each subject. The data were analyzed by statistical parametric mapping (SPM99) (Friston et al., 1995). Before the statistical analysis, we conducted motion correction and nonlinear transformation into the standard space of the Montreal Neurological Institute coordinates as implemented in SPM99. These images were smoothed with a 6 mm full-width half-maximum isotropic Gaussian kernel. The transformation into the Talairach coordinates (Talairach and Tournoux, 1998) was done by affine transformation after the entire analysis was completed.

Regression analysis was conducted on all of the fMRI data of the four rules. In addition to LRI, LCI, SR, and AR, we added four binary variables (each representing one rule). The regression results were masked with the Test-Control contrasts obtained for all of the rule sessions (p < 0.05, corrected), under the assumption that all of the learning-related brain activities are included in Test-Control. During Control blocks, LRI, LCI, and SR were set to 0, and AR was set to the AR of the preceding Test condition. AR-correlated voxels in Figure 3A-C were for only the rule 4 condition (Elliot et al., 2000), because the monotonic increases in AR for the other rules may absorb physiological and mechanical noises.

Figure 3.

Results from the correlation analysis. A, B, C, The numbers attached to the brain loci are defined in Table 1. The red, green, blue, and yellow regions denote the voxels correlated with LRI, LCI, SR, and AR, respectively. The color scaling of the t value is shown in the bar graphs. A voxel correlated with two variables is represented as a mosaic of the two colors with black outline. The frontal sections highlight the Talairach coordinates of the left caudate nucleus (A), left lateral cerebellum (B), and right orbitofrontal cortex (C), with thin horizontal and vertical lines. D, Three-dimensional distribution of voxels correlated with LRI and SR within a rectangular parallelepiped (-18 < x < -9; -12 < y < 6; -3 < z < 24), where x, y, and z represent the Talairach coordinates. CNH, CNB, and GP denote the head and body of the caudate nucleus and the globus pallidus, respectively. P denotes the peak voxel correlated with LRI whose location is (-9, -3, 0). The most ventral voxel correlated with LRI was located in the plane of z = -3. E, Bold signal increase averages and SDs over 11 voxels and eight subjects.

Results

Behavioral Data

Figure 2 shows how the reward acquisition and button push behaviors changed during the Test blocks for the least (A) and most (B) successful subjects in terms of total monetary reward, as well as the average of the eight subjects (C). The SR continued to increase during the entire session for rules 1-3. The horizontal lines in the top row of Fig. 2C show theoretical maximum values for SR that can be expected for optimal button pushing (30, 18, 10.5, and 0 yen for rules 1-4, respectively). ARs increased almost monotonically for rules 1-3 and exhibited increasingly smaller positive slopes for rules 1-3 but did not increase for rule 4. SRs in the final terms were not significantly different from the above theoretical maximum values (p > 0.4). Correspondingly, ARs in the final terms (excluding rule 4) were significantly larger than zero (p < 0.0001). These observations demonstrate that learning certainly took place for rules 1-3.

Figure 2.

Behavioral results of learning. Shown are data from the least successful subject (A), the most successful subject (B), and the average and SDs of all eight subjects (C). The time courses of SR, AR, LRI, and LCI are shown from top to bottom.

In the deterministic task (rule 1), the LRI decreased to 0 and the LCI approached 1 within 10 terms for all of the subjects. In the moderately stochastic task (rules 2 and 3), the decrease in LRI and the increase in LCI became gradually slower than for rule 1. In the random task (rule 4), LRI and LCI tended to continuously fluctuate until the very final stage. Figure 2C indicates that the average LRI across subjects was large at early terms and decreased as learning progressed, while individual subjects sometimes did not change their behaviors for the first few trials and their LRI started from 0 (Fig. 2A, rule 3). All of the subjects reported in retrospective inquiries that they tried in vain to discover the rules between the button push and the disk movement even for rule 4, and four of them reported that they eventually fixed their behavior. These observations indicate that learning difficulty was effectively controlled by the stochastic parameter.

fMRI study

Subtraction analysis

We first determined which brain areas were more strongly activated in the Test condition than in the Control condition for each transition rule (p < 0.05, corrected for multiple comparisons in rules 2-4; p < 0.001, uncorrected in rule 1). Rule 1 induced activation only in the bilateral intraparietal sulcus, bilateral superior parietal cortices, and left cerebellum. In addition to these areas, rules 2 and 3 strongly activated the basal ganglia, right cerebellum, bilateral premotor, bilateral orbitofrontal, bilateral superior parietal, bilateral occipital, and right prefrontal cortices, as well as the supplementary motor area (SMA). In rule 4, in addition to the above areas, the brain activity extended to the left prefrontal cortex, right amygdala, and right superior temporal lobule. Although these neural activities were generally strongest in rule 4, signal intensity in the caudate nucleus, the globus pallidus, and the orbitofrontal cortex were rather constant, that is, t values for rules 2-4 were 6.05, 5.47, and 5.80 in the left caudate nucleus, 7.09, 6.93, and 6.10 in the left globus pallidus, and 7.52, 7.24, and 7.34 in the left orbitofrontal cortex, respectively.

Regression analysis

To further investigate the brain structures found in the subtraction, we performed a multivariate regression analysis of fMRI data with LRI, LCI, SR, and AR. The threshold for LRI, LCI, and AR was p < 0.05, corrected for Test-Control volume, and that for SR was p < 0.001, uncorrected. Table 1 and Figure 3 summarize the brain areas revealed by the analysis. LRI had significant correlations with activity in the bilateral caudate nucleus, globus pallidus, orbitofrontal, prefrontal, and occipital cortices, right parietal, premotor, and temporal cortices, and cerebellum. LCI exhibited significant correlations with activity in the bilateral dorsal premotor, parietal, supplementary motor area, and left cerebellum. SR was correlated with activity in the left caudate nucleus, bilateral occipital, and parietal cortices. AR had correlations with activity in the bilateral prefrontal, premotor, parietal, and occipital cortices, supplementary motor area, and right orbitofrontal cortex.

Table 1.

The stereotactic coordinate and the peak t value within brain regions correlated with LRI, LCL, SR, and AR

	Learning rate			Learning convergence			Short-term reward			Accumulated reward
ROI	Stereotactic coordinates	t value	Stereotactic coordinates	t value	Stereotactic coordinates	t value	Stereotactic coordinates	t value
1 LSP					−38, −79, 30	5.48	−22, −64, 52	13.14
2 RSP	23, −70, 36	6.86			34, −76, 35	4.34	26, −64, 47	7.41
3 LIP			−11, −73, 38	7.54
4 RIP			10, −73, 38	7.54
5 LPM			−32, 3, 53	7.54			−35, 5, 48	11.69
6 RPM	19, 20, 27	6.49	28, 0, 53	7.72			23, 0, 55	9.80
7 SMA			−6, −9, 47	5.74			−3, −3, 47	9.17
8 LPF	−30, 43, 7	7.21					−37, 32, 12	10.58
9 RPF	31, 49, 13	8.64					23, 46, 13	11.21
10 LOF	−40, 43, −6	6.94
11 ROF	30, 43, −6	7.26					23, 43, −1	19.79
12 LCN	−0, −3, 0	6.70			−16, −3, −18	3.79
13 RCN	12, 3, 10	5.87
14 LGP	−14, −9, 2	6.08
15 RGP	12, −3, 5	5.40
16 LCB			−30, −59, −35	5.74
17 RCB	34, −73, −25	7.13
18 RST	41, −32, −2	7.47					52, −53, 8	8.56
19 LOC	−25, −94, 8	6.09			−27, −64, 2	4.60	−19, −76, 22	12.65
20 ROC	26, −85, −5	6.19			26, −59, 2	4.20	15, −70, 23	8.82

The regions of interest (ROIs) were superior parietal cortex (SP), intraparietal sulcus (IP), dorsolateral premotor cortex (PM), supplementary motor area (SMA), prefrontal cortex (PF), orbitofrontal cortex (OF), caudate nucleus (CN), globus pallidus (GP), cingulate cortex (CC), cerebeller cortex (CB), amygdala (AM), superior temporal lobule (ST), and occipital cortex (OC). L, Left; R, right.

Figure 3A shows that the activity of the caudate nucleus significantly correlated with LRI and SR. The caudate activity was stronger on the left side probably because subjects used their right hand. In Figure 3A, it is also observed that activity of the globus pallidus was correlated with LRI, and activity of the dorsal premotor cortex and SMA was correlated with LCI and AR. Importantly, the contiguous voxels correlated with both LRI and SR in the entire brain were located only in the dorsolateral bank of the lateral ventricle. Simultaneous correlation with LRI and SR is computationally essential for reinforcement learning loci, because synaptic plasticity (LRI related) should be induced by reward prediction errors (SR related). Furthermore, three-dimensional reconstructions of these LRI- and SR-correlated voxels (Fig. 3D) were in good agreement with the three-dimensional shapes of the caudate nucleus head and body, as well as the globus pallidus. In the caudate nucleus, the correlation with LRI was stronger in the ventral region and the correlation with SR was confined to the dorsal part. In addition, the activity of the left lateral cerebellum was correlated with LCI (Fig. 3B), and that of the orbitofrontal and prefrontal cortices was correlated with LRI and AR (C).

Bold signal trends in the ventral caudate nucleus

The essential role of the ventral caudate nucleus in reward-based behavioral change was also confirmed by a direct assessment of neural activity that was measured as a Bold signal increase in each Test block compared with the subsequent Control (baseline) block. This analysis was conducted separately for each transition rule (rules 1-4). The activity in the ventral part of the left caudate nucleus (11 voxels marked by asterisks in Fig. 3D) around the peak (marked by P in Fig. 3D) of LRI correlation exhibited a tendency to decrease during the tasks with all of the rules except rule 4. The rate of decrease (the negative slope of the regression using all of the data from the eight subjects) became smaller with greater randomness of probability (Fig. 3E) (-0.022, -0.014, -0.007, and -0.006 for rules 1-4, respectively). These slopes were significantly negative (<0) for rules 1-3 (p < 0.05). Furthermore, the average regressions for individual subjects, considering intersubject variance, confirmed that the slopes of rule 1 and rule 2 were significantly <0 (p < 0.005) and also significantly less than the slope of either rule 3 or rule 4 (p < 0.005). Correspondingly, there was also a decrease in LRI (Fig. 2) with similar dependence on the randomness of probability (rules 1-4). The curve fitting by exponential functions was statistically significant (rules 1-3; p < 0.05) and also logical, because LRI is positive by definition and approaches 0. The exponential decay rates for rules 1-4 were -0.134, -0.111, -0.031, and 0.009, respectively. Thus, the analysis of Bold signal trends confirmed that there was parallelism between the decrease in activity of the caudate nucleus and that in behavioral change (LRI) for the four different levels of learning difficulty (rules 1-4). More specifically, the decrease in the Bold signal in the caudate nucleus as well as the decrease in the magnitude of changes in button-push behaviors between the two neighboring terms were statistically significant for only rules 1-3, in which learning was possible, and their negative slopes became smaller as learning became more difficult (rule 1 > rule 2 > rule 3 > rule 4).

Discussion

The most important finding in our study was that activity in the ventral part of the caudate nucleus exhibited a strong correlation with the magnitude of behavioral change during learning (instrumental conditioning). Bold signal analysis revealed parallelism between the decrease in caudate nucleus activity and that in LRI in wide variations in task difficulty (rules 1-4). Among possible cognitive elements that can be captured by LRI, our first concern is the behavioral change in the context of the reinforcement learning theory (Sutton and Barto, 1998), assuming that behavioral change is guided by reward prediction errors. Experimental evidence is now accumulating on the roles played by midbrain dopamine neurons and the ventral striatum in representing reward prediction error. Monkey neurophysiological studies demonstrated that dopamine neurons in the monkey midbrain encode reward prediction errors (Hollerman and Schultz, 1998). Human imaging studies using reward (classical conditioning) tasks revealed that activity in the ventral striatum (Berns et al., 2001; Breiter et al., 2001) and putamen (McClure et al., 2003; O'Doherty et al., 2003) is correlated with the reward prediction error. In the context of reward-based behavioral learning, computing a subject's reward prediction error is difficult, and no attempt has ever been made to estimate it. Therefore, we took a behavior-based approach and computed LRI only from subjects' behaviors without making any additional assumptions. In the framework of the reinforcement learning theory, LRI is expected to reflect synaptic plasticity responsible for behavioral change, which is a product of the reward prediction error, inputs for behavior generation, and an adaptively changing learning coefficient. Therefore, LRI and reward prediction error may be correlated but could be significantly different from each other. Our results suggest that the caudate nucleus plays an important role in behavioral learning guided by reward prediction error, which is sent from the midbrain, as proposed in several computational models (Houk et al., 1995; Montague et al., 1996).

It is probable that LRI-correlated brain activity also involves higher cognitive functions, such as inference and hypothesis testing about the task structure, although the stochastic decision task was originally designed with the simple reinforcement learning theory as the guiding principle. Because we expect that more random tasks (rules 3 and 4) are more likely to invoke these cognitive functions than simple tasks (rules 1 and 2), it is noteworthy that, in the subtraction analysis, the activity in the cerebral cortical areas, including the dorsolateral prefrontal cortex, tended to increase in accordance with the task difficulty (rules 2-4). This may suggest that these cortical areas were partly involved in such higher cognitive learning more than the caudate nucleus. Related to the caudate activity correlation with LRI, Parkinson patients were reported to have difficulty in learning a probabilistic decision-making task (Knowlton et al., 1996).

It was also remarkable that no overlapping correlation was found between LCI and LRI, both of which are learning-related variables. As learning proceeds, LRI decreases, while LCI increases and saturates. Therefore, LRI and LCI may well correspond to initial nonroutine learning with attention and later routine behavior with less attention, respectively (Fig. 2C, LRI and LCI). In the reinforcement learning interpretation, we note that LRI corresponds to synaptic plasticity responsible for behavioral changes, and LCI corresponds to memory consolidation for optimal behaviors. The LRI-correlated caudate activity is consistent with reports that the anterior striatum was active and essential when a monkey learned a new motor sequence (Miyachi et al., 1997, 2002). LCI-correlated activity was found in the bilateral dorsal premotor and intraparietal cortices, SMA, and left lateral cerebellum. The dorsal premotor cortex and SMA exhibited additional correlation with AR. This may indicate that these areas are involved in the intermediate phase of learning by selecting an appropriate action on the basis of the previous experience of rewards. This view is consistent with the following human imaging studies. In a positron emission tomography study, the precision of the subjects' recall of a stimulus sequence was correlated with the dorsal premotor cortex and supplementary motor area activity (Honda et al., 1998). An fMRI study also reported activation of the SMA and precuneus in the intermediate and late stages of motor sequence learning, respectively (Sakai et al., 1998). It is also interesting that the locus for the LCI-correlated activity in the left lateral cerebellum was close to that involved in learning novel tool use (Imamizu et al., 2000) and possibly related to the visuomotor transformation (internal model) that routinely maps a visual input to an appropriate selection of behavior. This interpretation is also supported by the subtraction analysis showing that only the parietal cortex and cerebellum were activated in rule 1, in which the learning converged rapidly.

The results concerning reward variables (SR and AR) were in good agreement with previous studies. Primarily, the dorsal part of the caudate nucleus (Kawagoe et al., 1998) and orbitofrontal cortex (Elliot et al., 2000) were correlated with SR and AR, respectively. The small overlapped activation in the caudate nucleus by SR and LRI can be explained by the difference in temporal characteristics of LRI and SR; LRI represents a low-frequency decaying component, whereas SR represents a high-frequency fluctuating component attributable to stochasticity in the reward schedule.