Continuous Time Causal Mediation Analysis

Abstract

While causal mediation analysis has seen considerable recent development for a single measured mediator (M) and final outcome (Y), less attention has been given to repeatedly measured M and Y. Previous methods have typically involved discrete-time models that limit inference to the particular measurement times used, and do not recognize the continuous nature of the mediation process over time. To overcome such limitations, we present a new continuous time approach to causal mediation analysis that uses a differential equations model in a potential outcomes framework to describe the causal relationships among model variables over time. A connection between the differential equations models and standard repeated measures models is made to provide convenient model formulation and fitting. A continuous time extension of the sequential ignorability assumption allows for identifiable natural direct and indirect effects as functions of time, with estimation based on a two-step approach to model fitting in conjunction with a continuous time mediation formula. Novel features include a measure of an overall mediation effect based on the ‘area between the curves’, and an approach for predicting the effects of new interventions. Simulation studies show good properties of estimators and the new methodology is applied to data from a cohort study to investigate sugary drink consumption as a mediator of the effect of socioeconomic status on dental caries in children.

1. INTRODUCTION

Mediation analysis seeks to determine the extent to which the effect of an exposure or intervention on a health outcome is due to its effect on one or more causally intermediate variables (or mediators). A goal of such an analysis is to illuminate the mechanisms through which the exposure or treatment affects the health outcome. An important related application is in the development of more effective, acceptable, and cost-effective interventions.

Recently, mediation analysis has been formulated using a potential outcome (causal model) framework. The resulting methodology, referred to as causal mediation analysis, provides, and elucidates the basis for, causally interpretable mediation (direct and indirect) effects. Causal mediation analysis for a single mediator has been addressed, for example, by Robins and Greenland (1992)¹, Albert (2008)², and Imai et al. (2010)³. Recent developments have involved more complex situations, including multiple (non-causally-ordered) mediators^4,5, causally ordered mediators^6–8, and a repeatedly measured mediator⁹. Most of these methods involve versions of the mediation formula¹⁰ or the G formula¹¹; an alternative approach uses a natural effect model in conjunction with inverse weighting¹². In addition, though not based on a potential outcomes framework, structural equation model^13,14 and related (e.g., cross-lagged model¹⁵; and state space model¹⁶) methods for mediation analysis, possibly utilizing repeated measures, have been offered. An approach using linear mixed effects model has also been proposed¹⁷.

Causal mediation analysis, and causal modelling in general, has predominantly relied on discrete time models. The prototypical mediation model is represented by the causal diagram (technically, a directed acyclic graph, or DAG¹⁸) given in Figure 1 (left). Here, we suppose that the exposure (X), mediator (M) and final outcome (Y) are measured at times t₁, t₂, and t₃, respectively, with t₁ < t₂ < t₃. For example, this model might describe the direct effect of a behavioral intervention on body mass index (BMI) in children and its indirect effect via diet change¹⁹. A discrete causal mediation model for longitudinal data (repeated measures of X, M, and Y, with the subscript indicating the time point) is represented in Figure 1 (right).

Figure 1.

Discrete mediation models (left: single measurement, right: repeated measures)

There has been increasing recognition that conventional (discrete time) mediation models are inadequate for explaining, or providing predictions related to, many social/behavioral and biological processes in health, which may often be seen as evolving in continuous time²⁰. Aalen et al. (2014)²¹, for example, showed in simulation studies that the use of a discrete mediation model, when the true model is continuous, can seriously distort estimates of mediation effects, thus, imply a null or small mediation effect, when in fact a large effect is present, or vice versa. In contrast to discrete time models, continuous time models (as represented in Figure 2) represent the underlying processes which are considered as existing prior to the selection of measurement times.

Figure 2.

Mediation in continuous time

Aside from the possible distortion induced, discrete time models for mediation/path analysis involving continuous time processes have a number of other shortcomings. One is that inferences are restricted to the particular measurement times used, a consequence being that different measurement times imply different questions and are apt to produce different conclusions. In addition, discrete time models are generally ill–equipped to handle longitudinal data with unbalanced measurement times, that is, where subjects have different measurements times. A further limitation is that discrete time models become increasingly cumbersome as the number of repeated measures increases. Some work to address these issues within the SEM framework, for example, using latent trend variables, has been done²².

Unfortunately, there has been little development of causal models for the continuous time context. Most of this work has been directed at determining the causal effect of a treatment varying over time rather than mediation analysis per se^23–26. Recently proposed methods for mediation analysis in continuous time have been based on ordinary differential equations models^21,27. However, these methods are not based on a causal (in particular, potential outcomes) model and thus do not provide clear implications for causal inference. Also, they deal with contexts in which a differential equations model can be directly specified. This may not be the case in many health areas, including those involving psychosocial factors, in which continuous time mediation analysis may be of interest.

In this paper, we develop a novel causal approach to mediation analysis that recognizes model variables as continuous processes over time. We begin by presenting a new causal differential equations (CDE) model. Using differential equations involving potential outcomes, the model is flexible in allowing a variety of variable types. We relate this model to standard regression models for longitudinal data, thus allowing intuitive and familiar approaches to data fitting as part of a continuous time mediation analysis. We further show how this approach allows one to extend the notion of mediation to that of ‘partial mediation’ whereby the mediator is activated over part, but not all, of the time range of interest. We apply the new approach to a longitudinal cohort study of dental caries in early childhood and conclude with a discussion of its advantages and limitations along with directions for future research.

2. CONTINUOUS TIME MEDIATION MODEL

2.1. Model

We introduce what we refer to as the causal differential equation (CDE) model, beginning with the following general form:

$$d{V}_t^{\left(k\right)}\left(A\right)/dt=g_k\left[t,{\overline{V}}_t\left(A\right)\right]$$ (1)

where V_t^(k)(A) is the potential outcome of the kth response variable (k=1,…,K) at time t ∈ [0, T] under (possibly time-varying) intervention A; ${\stackrel{-}{\mathit{V}}}_t\left(A\right)={\stackrel{-}{\mathit{V}}}_t\left({\stackrel{-}{A}}_t\right)$ is the history of $\mathit{V}=(V^{\left(1\right)}\dots ,V^{\left(K\right)})\prime$, a column vector of the model variables, under intervention A, up to time t; and g_k is a specified function for the kth variable. Note that the V^(k) may be expected or latent versions of the corresponding observed variables. This model may be supplemented by assumed probability distribution functions for the variables.

The CDE model yields an (instantaneous) causal effect of an intervention, A¹, versus another intervention, A⁰, at some time t, expressed as the following difference in potential outcomes for some variable, V (dropping the superscript (k) for now),

$$\frac{d{V}_t\left(A^1\right)}{dt}-\frac{d{V}_t\left(A^0\right)\mathrm{ }}{dt}={\text{lim}}_{\Delta \to 0}[{\{V}_{t+\Delta }\left({\stackrel{-}{A}}_{t+\Delta }^1\right)-V_t\left({\stackrel{-}{A}}_t^1\right)\}-{\{V}_{t+\Delta }\left({\stackrel{-}{A}}_{t+\Delta }^0\right)-V_t\left({\stackrel{-}{A}}_t^0\right)\}]/\Delta$$ (2)

In other words, expression (2) represents the difference in the instantaneous change in the potential outcome of variable V at time t, due to intervention A¹ versus intervention A⁰.

For concreteness, and applicability to our later causal mediation problem (in our dental data example), we will focus on the following special case of the CDE model:

$$\frac{d{\tilde{M}}_t\left(A\right)}{dt}=g_M[{t,X}_t^M,\mathrm{ }{\mathit{L}}^{\mathit{M}};\alpha ]$$ (3)

$$\frac{d{\tilde{Y}}_t\left(A\right)}{dt}=g_Y[{t,\mathrm{ }X}_t^Y,{\tilde{M}}_t\left(A\right),{\mathit{L}}^{\mathit{Y}};\beta ]$$ (4)

where ${\tilde{Y}}_t$ and ${\tilde{M}}_t$ denote individual-level expected values of the outcome and the mediator, respectively, at time t; $X_t^Y$ and $X_t^M$ are functions indicating the exposure level (affecting Y and M, respectively) at t; A is the ‘intervention’ (effectively defined by $X_t^Y$ and $X_t^M$); L^M and L^Y are vectors of baseline covariates, possibly including latent variables (e.g., random effects) predicting M and Y, respectively; and α and β are vectors of unknown parameters (which may sometimes be dropped in the notation).

By integrating both sides of the above differential equation, we obtain the following integral equations:

$${\tilde{M}}_t\left(A\right)\mathrm{ }={\tilde{M}}_0\left(A_0\right)+{\int }_0^t{g}_M[{s,X}_s^M,{\mathit{L}}^{\mathit{M}}]ds$$ (5)

$${\tilde{Y}}_t\left(A\right)={\tilde{Y}}_0\left(A_0\right)+{\int }_0^t{g}_Y[s,X_s^Y,{\tilde{M}}_s(A),{\mathit{L}}^{\mathit{Y}}]ds$$ (6)

Since $X_t^M,\mathrm{ }{X}_t^Y,$ and ${\tilde{M}}_t\left(A\right)$ are generally functions of time, t, it will be helpful to define the following composite functions:

$$h_A^M\left(t\right)\equiv {g_M[t,X}_t^M,{\mathit{L}}^{\mathit{M}}],\mathrm{ }{h}_A^Y(t)\equiv g_Y[{t,X}_t^Y,{\tilde{M}}_t{(X}_t^M),{\mathit{L}}^{\mathit{Y}}].$$ (7)

If $h_A^M\left(t\right)$ and $h_A^Y\left(t\right)$ are continuous over t ∈ [0, T], we obtain the models,

$${\tilde{M}}_t\left(A\right)=H_A^M\left(t\right)=G_M[{t,X}_t^M,{\mathit{L}}^{\mathit{M}}]$$ (8)

$${\tilde{Y}}_t\left(A\right)=\mathrm{ }{H}_A^Y\left(t\right)=G_Y[t,X_t^Y,{\tilde{M}}_t\left(A\right),{\mathit{L}}^{\mathit{Y}}]$$ (9)

where $H_A^M\left(t\right)$ and $H_A^Y\left(t\right)$ are the antiderivatives of $h_A^M\left(t\right)$ and $h_A^Y\left(t\right)$, respectively, and G_M and G_Y are functions (of the indicated arguments) yielding the composite functions ($H_A^M$ and $H_A^Y$).

As a simple example, the differential equations,

$$\frac{d{\tilde{M}}_t\left(A\right)}{dt}={\alpha }_2\mathrm{e}\mathrm{x}\mathrm{p}({\alpha }_0+{\alpha }_1{x}^{\prime }+{\alpha }_{2}t)$$

$$\frac{d{\tilde{Y}}_t\left(A\right)}{dt}=\left[{\beta }_2+{\beta }_3{\alpha }_2\text{exp}\left({\alpha }_0+{\alpha }_{1}x\prime +{\alpha }_{2}t\right)\right]\cdot \text{exp}\left[{\beta }_0+{\beta }_{1}x+{\beta }_{2}t+{\beta }_3{\tilde{M}}_t\left(A\right)\right]$$

with $X_t^Y=x$ and $X_t^M=x\prime$ (i.e., both fixed over time), correspond to the integral equations,

$${\tilde{M}}_t\left(A\right)=\mathrm{e}\mathrm{x}\mathrm{p}[{\alpha }_0+{\alpha }_1{x}^{\prime }+{\alpha }_{2}t\text{]}$$

$${\tilde{Y}}_t\left(A\right)=\text{exp}\left[{\beta }_0+{\beta }_{1}x+{\beta }_{2}t+{\beta }_3{\tilde{M}}_t\left(A\right)\right].$$

We may wish to directly model the integral, as opposed to the differential, equations, that is, G_M and G_Y rather than g_M and g_Y. Particularly for health and behavioral data, it may be easier to specify a model of the expected values rather than derivatives of the expected values. This will be the emphasis of the present paper, in which we use suitable longitudinal models for the G_M and G_Y functions. However, the integral equations ((5) and (6)) motivate a new class of longitudinal models that handles certain extensions such as that of the next section. In other contexts, available scientific theory may allow direct specification of the CDE (i.e., g_M and g_Y functions).

2.2. Extension for Treatment Discontinuities

We wish to extend (8) and (9) to allow for $h_A^M\left(t\right)$ and/or $h_A^Y\left(t\right)$ being discontinuous. Such discontinuities may result from discontinuous changes in exposure or treatment over time. In fact, we will focus on the case of discontinuities in $X_t^Y$ and/or $X_t^M$ while the functions g_Y and g_M are continuous. For mediation analysis, this extension will enable, for example, an assessment of mediation through a treatment implemented over part - but not all - of the time range. Thus, we now make the relaxed assumption that $h_A^M\left(t\right)$ and $h_A^Y\left(t\right)$ are piecewise continuous over [0,T] (thus, $H_A^M\left(t\right)$ and $H_A^Y\left(t\right)$ piecewise differentiable) and construct models based on (5) and (6). Supposing that $h_A^Y\left(t\right)$ has d discontinuity points, t₁,..,t_d in (0,T) (so that $H_A^Y\left(t\right)$, the piecewise antiderivative of $h_A^Y\left(t\right)$, is piecewise differentiable for the resulting intervals) we write,

$${\tilde{Y}}_t\left(A\right)={\tilde{Y}}_0\left(A\right)+{\sum }_{j=0}^{d}I(t>t_j)G_Y\left[s,X_s^Y,{\tilde{M}}_s\left(A\right),L^Y\right]|{}_{t_j}^{ t_{j+1}^{*}}$$ (10)

where t₀ ≡ 0, t_d+1 ≡ T, $t_j^{\mathrm{*}}=\text{min}\left(t,\mathrm{ }{t}_j\right)$, I(t > t_j) =1 if t > t_j, I(t > t_j) =0 otherwise, and $G_Y\left[t,X_t^Y,{\tilde{M}}_t\left(A\right),{\mathit{L}}^{\mathit{Y}}\right]=h_A^Y\left(t\right)$ is the antiderivative of $g_Y[{t,X}_t^Y,{\tilde{M}}_t{(X}_t^M),{\mathit{L}}^{\mathit{Y}}]$ for any constant $X_t^Y$ and $X_t^M$.

Each ${\tilde{M}}_t\left(A\right)$ term would be expressed in a similar way using the piecewise differentiable function $H_A^Y\left(t\right)$ and a partition based on discontinuities in $h_A^M\left(t\right)$. Namely, when $h_A^M\left(t\right)$ has r discontinuity points, t_M,1,…, t_M,r in (0,T), we would have,

$${\tilde{M}}_t\left(A\right)={\tilde{M}}_0\left(A\right)+{\sum }_{j=0}^{r}I(t>t_{M,j})G_M\left[s,X_s^M,L^M\right]|{}_{t_{M,j}}^{ t_{M,j+1}^{*}}$$ (11)

where t_M,0 ≡ 0, t_M,r+1 ≡ T, $t_{M,j}^{\mathrm{*}}=\text{min}\left(t,\mathrm{ }{t}_{M,j}\right)$, and $G_M\left[t,X_t^M,{\mathit{L}}^{\mathit{M}}\right]=h_A^M\left(t\right)$ is the antiderivative of $g_M[{t,X}_t^M,{\mathit{L}}^{\mathit{M}}]$ for any constant $X_t^M$.

To illustrate the above expressions, we consider a couple of simple examples also of interest for our later application.

Example 1. Suppose a person is exposed but the mediator set as if not exposed over the entire time interval, [0,T]. This intervention, denoted as A^1,0, can be described in previous notation as follows:

$$A^{\mathrm{1,0}}\equiv {\{X}_t^Y=1,\mathrm{ }{X}_t^M=0;\mathrm{ }t\in [0,T]\}\equiv \{X^Y=1,\mathrm{ }{X}^M=0\}$$

resulting in potential outcomes, ${\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)={\tilde{Y}}_t(X^Y=1, X^M=0)$, for t ∈ [0, T]; note that we may drop the subscript t in the notation in the case of a constant exposure status.

Because there are no discontinuities for this intervention, we can use expression (9) (a special case of (10)) along with (8) (a special case of (11) to get,

$$\widetilde{Y_t}\left(A^{\mathrm{1,0}}\right)=G_Y\left[{\mathrm{ }t,X}^Y=1,{\tilde{M}}_t\left(X^M=0\right),{\mathit{L}}^{\mathit{Y}}\right]$$

for t ∈ [0, T], with

$${\tilde{M}}_t\left(X^M=0\right)=G_M\left[{t,\mathrm{ }X}^M=0,{\mathit{L}}^{\mathit{M}}\right]$$

Example 2. Consider a person who is exposed but whose mediator is set as if exposed until time t₁ < T, and then as if not exposed starting at time t₁. This intervention will be denoted as $A^{1,t_1}\equiv {\{X}_t^Y=1, X_t^M=(1\left[0,t_1\right), 0[t_1,T\left]\right)\}$.

As there is no discontinuity in $X_t^Y$ we have,

$${\tilde{Y}}_t\left(A^{1,t_1}\right)=G_Y[t,X_t^Y,{\tilde{M}}_t(A^{1,t_1}),{\mathit{L}}^{\mathit{Y}}]$$

for t ∈ [0, T]. However, there is a discontinuity in $X_t^M$, so we use (11) to get,

$${\tilde{M}}_t\left(A^{1,t_1}\right)=G_M\left[t^{*},X_{t^{*}}^M=0, L^M\right]+I(t>t_1)G_M\left[s,X_s^M=1,L^M\right]|{}_{t_1}^t$$

where t* = min(t, t₁), t ∈ [0, T].

We note that the theory up to this point allows exposure processes, $X_t^Y$ and $X_t^M$, to be continuous in each interval. However, our focus will generally be on the case of a binary exposure as is applicable in our data example.

2.3. Mediation Estimands

Mediation (that is, natural direct and indirect) effects may be formulated as appropriate contrasts (for example, differences or ratios) of expected potential outcomes of Y. For example, the natural indirect effect of X_t on ${\tilde{Y}}_t$ through ${\tilde{M}}_t$ could be expressed as the difference in expected potential outcomes of ${\tilde{Y}}_t$ under the two interventions, $A^1={\{X}_t^Y=1, X_t^M=1; t\in [0,T]\}$ and $A^{\mathrm{1,0}}={\{X}_t^Y=1, X_t^M=0; t\in [0,T]\}$ respectively, keeping in mind that the relevant part of an intervention for the outcome ${\tilde{Y}}_t$ occurs up to time t. This contrast may be written as,

$${I_t\left(A^{\mathrm{1,0}}\right)=E\{\tilde{Y}}_t\left(A^1\right)\}-{E\{\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)\}$$

$$={\int }_{\mathit{l}}^{}\left\{{\tilde{Y}}_t\left(A^1\right)-{\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)\right\}{f}_L\left(l\right)d{\mu }_{\mathit{L}}\left(\mathit{l}\right)$$ (12)

where f_L denotes the joint density function of the baseline covariate vector, L, obtained as the union of L^Y and L^M. The estimand I_t(A^1,0) thus represents an indirect effect of exposure X (continuously maintained at level 1 versus level 0) on $\tilde{Y}$ at time t though mediator $\tilde{M}$, considered as a process, up to time t.

The corresponding natural direct effect, which also involves the intervention $A^0\equiv {\{X}_t^Y=0, X_t^M=0; t\in [0,T]\}$, is,

$${D_t\left(A^{\mathrm{1,0}}\right)=E\{\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)\}-{E\{\tilde{Y}}_t\left(A^0\right)\}$$

$$={\int }_l^{}\left\{{\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)-{\tilde{Y}}_t\left(A^0\right)\right\}{f}_L\left(l\right)d{\mu }_{\mathit{L}}\left(\mathit{l}\right).$$ (13)

The preceding two effects yield the decomposition, T_t = D_t(A^1,0) + I_t(A^1,0), where $T_t{=E\{\tilde{Y}}_t\left(A^1\right)\}-{E\{\tilde{Y}}_t\left(A^0\right)\}$ is the total exposure effect at time t.

Alternative versions of these effects are obtained by defining the intervention, $A^{\mathrm{0,1}}={\{X}_t^Y=0,\mathrm{ }{X}_t^M=1;\mathrm{ }t\in [0,T]\}$. We then have $I_t\left(A^{\mathrm{0,1}}\right)={E\{\tilde{Y}}_t\left(A^{\mathrm{0,1}}\right)\}-{E\{\tilde{Y}}_t\left(A^0\right)\}$ and ${D_t\left(A^{\mathrm{0,1}}\right)={E\{\tilde{Y}}_t\left(A^1\right)\}-E\{\tilde{Y}}_t\left(A^{\mathrm{0,1}}\right)\}$, which comprise the alternative decomposition, T_t = D_t(A^1,0) + I_t(A^1,0). The discussion in Albert et al. (2018)⁸ is relevant to the choice of estimands/decomposition.

As an extension alluded to in the previous section, we may wish to consider the indirect effect of exposure through the mediator over a reduced portion of the time period, thus a ‘partial’ indirect effect. For example, the intervention $A^{1,t_1}$ involves exposed individuals where the effect of the exposure on the mediator is removed starting at some time t₁. A corresponding indirect effect may be defined as,

$${I_t\left(A^{1,t_1}\right)=E\{\tilde{Y}}_t\left(A^1\right)\}-{E\{\tilde{Y}}_t\left(A^{1,t_1}\right)\}.$$ (14)

This estimand is relevant to contexts, such as in our data example, where the start of the (future) intervention would correspond to stopping the exposure. An alternative estimand may be of interest when the intervention would involve initiation of exposure or treatment. Another possibility is an intervention that stops (rather than starts) at some time t₁.

The above estimands at any given time t have a cross-sectional interpretation. We may also wish to assess the overall direct and indirect effects over the time range of interest. A useful summary measure is the ‘area between the curves’ (ABC). Specifically, this is the area between the curves given by the plots of the expected value of $\tilde{Y}$ versus time for the two interventions implied by an indirect effect of interest. For example, the ABC for the total indirect effect (that is, corresponding to an intervention affecting M over the whole time range) is given by

$$ABC\left(A^{\mathrm{1,0}}\right)={\int }_0^T\left[{E\{\tilde{Y}}_t\left(A^1\right)\}-{E\{\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)\}\right]dt.$$ (15)

Alternative versions are defined in an obvious manner, for example, $ABC\left(A^{\mathrm{0,1}}\right)={\int }_0^T\left[{E\{\tilde{Y}}_t\left(A^{\mathrm{0,1}}\right)\}-{E\{\tilde{Y}}_t\left(A^0\right)\}\right]dt$. The ABC measure is easily generalized for ‘partial’ indirect effects using (14); namely, we define, $ABC\left(A^{1,t_1}\right)={\int }_0^T\left[{E\{\tilde{Y}}_t\left(A^1\right)\}-{E\{\tilde{Y}}_t\left(A^{1,t_1}\right)\}\right]dt$.

Alternative scales for natural direct and indirect effects may be used. A popular alternative to the mean difference scale given above is the mean ratio scale. For example, ratio-scale analogs to the mediation estimands, (12) and (13), are as follows:

$${I_t^r\left(A^{\mathrm{1,0}}\right)=E\{\tilde{Y}}_t\left(A^1\right)\}/{E\{\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)\}$$

$${D_t^r\left(A^{\mathrm{1,0}}\right)=E\{\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)\}/{E\{\tilde{Y}}_t\left(A^0\right)\}$$

and we obtain a decomposition of the total (ratio scale) effect at time t as ${T_t^r\equiv E\{\tilde{Y}}_t\left(A^1\right)\}/{E\{\tilde{Y}}_t\left(A^0\right)\}=I_t^r\left(A^{\mathrm{1,0}}\right)\bullet D_t^r\left(A^{\mathrm{1,0}}\right)$. The alternative versions for the ratio scale are denoted in obvious notation as $I_t^r\left(A^{\mathrm{0,1}}\right)$ and $D_t^r\left(A^{\mathrm{0,1}}\right)$ and provide the alternative decomposition, $T_t^r=I_t^r\left(A^{\mathrm{0,1}}\right)\bullet D_t^r\left(A^{\mathrm{0,1}}\right)$. In models in which the alternative forms are equal we may write, for example, $I_t^r=I_t^r\left(A^{\mathrm{1,0}}\right){=I}_t^r\left(A^{\mathrm{0,1}}\right)$; further, we may drop the subscript when the effect is constant over time, for example, D^r = D^r(A^1,0) = D^r(A^0,1).

For the area between the curves, a natural definition corresponding to the ratio scale, while maintaining the interpretation as an area, is based on the log-transformed expected values, for example, ${\text{ABC}}^r\left(A^{\mathrm{1,0}}\right)={\int }_0^T\left[\mathrm{l}\mathrm{o}\mathrm{g}{E\{\tilde{Y}}_t\left(A^1\right)\}-{\mathrm{l}\mathrm{o}\mathrm{g}E\{\tilde{Y}}_t\left(A^{\mathrm{1,0}}\right)\}\right]dt$, and similarly for the alternative version denoted as ABC^r(A^0,1). These definitions are readily generalized to the interventions starting at time t₁, for example,${ABC}^r\left(A^{1,t_1}\right)={\int }_0^T\left[\mathrm{l}\mathrm{o}\mathrm{g}{E\{\tilde{Y}}_t\left(A^1\right)\}-{\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{ }E\{\tilde{Y}}_t\left(A^{1,t_1}\right)\right]dt$. In the case where $I_t^r\left(A^{\mathrm{1,0}}\right){=I}_t^r\left(A^{\mathrm{0,1}}\right)$ for t ∈ [0, T], we use the abbreviated notation, ABC^r = ABC^r(A^1,0) = ABC^r(A^0,1).

For the indirect effects (including ABCs) for either scale we may also define mediation (or indirect effect) proportions. For instance, the indirect effect proportions (for intervention A and at time t) for the difference and ratio scales are defined as I_t(A)(prop) ≡ I_t(A)/(D_t(A) + I_t(A)) and $I_t^r\left(A\right)\left(\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\right)\equiv \mathrm{l}\mathrm{o}\mathrm{g}\left(I_t^r\left(A\right)\right)/{\{\mathrm{l}\mathrm{o}\mathrm{g}(I}_t^r\left(A\right){)+\mathrm{l}\mathrm{o}\mathrm{g}(D}_t^r\left(A\right)\left)\right\}$, respectively. Similarly, for areas between the curves we define proportions on the difference and ratio scales as, for example, $\text{ABC}\left(A^{1,t_1}\right)\left(\text{prop}\right)=\text{ABC}\left(A^{1,t_1}\right)/\text{ABC}\left(A^0\right)$ and ${\text{ABC}}^r\left(A^{1,t_1}\right)\left(\text{prop}\right)={\text{ABC}}^r\left(A^{1,t_1}\right)/{\text{ABC}}^r\left(A^0\right)$, where $\mathrm{A}\mathrm{B}\mathrm{C}\left(A^0\right)\equiv {\int }_0^T\left[{E\{\tilde{Y}}_t\left(A^1\right)\}-{E\{\tilde{Y}}_t\left(A^0\right)\}\right]dt$ and ${\text{ABC}}^r\left(A^0\right)\equiv {\int }_0^T\left[\text{log}{E\{\tilde{Y}}_t\left(A^1\right)\}-\text{log}{E\{\tilde{Y}}_t\left(A^0\right)\}\right]dt$.

2.4. Identification and Inference

The estimands given above involve expected values of ${\tilde{Y}}_t\left(A\right)$ for various interventions, that is, particular specifications of A. We will demonstrate the identifiability of these expected potential outcomes by showing that they can be written as functions of (estimable) association model parameters under certain assumptions. Our approach is an extension of the mediation formula approaches of Pearl (2001)²⁸ and Imai et al., 2010³ (see also Albert and Nelson, 2011⁶, and Daniel et al., 2015⁷).

Our assumptions are as follows, starting with a continuous version of the standard consistency assumption:

Assumption 1. Consistency:

$$\begin{gathered} {\tilde{Y}}_t\left(x,m\right)={\tilde{Y}}_t\text{ if }{X}_t=x\text{ and }{\tilde{M}}_t=m,\text{ and} \\ {\tilde{M}}_t\left(x^{\prime }\right)={\tilde{M}}_t\text{ if }{X}_t=x^{\prime } \end{gathered}$$

for all x, x′, m and t ∈ [0, T]. That is, the potential outcomes for ${\tilde{Y}}_t$ and ${\tilde{M}}_t$ where the levels of the causal variables are set to those observed (for a given individual), are equal to the observed (or actual latent) values for ${\tilde{Y}}_t$ and ${\tilde{M}}_t$, respectively.

We also assume a continuous time version of the sequential ignorability assumption:

Assumption 2. Sequential ignorability in continuous time:

$$\{{\tilde{Y}}_t(x,m),{\tilde{M}}_t(x\text{'})\}\coprod X_t|L=l$$ (16)

$${\tilde{Y}}_t(x,m)\coprod {\tilde{M}}_t(x\text{'})|X_t=x\text{'},L=l.$$ (17)

for all x, x′, m, and l, and any t ∈ [0, T].

Expression (16) states that potential outcomes for $\tilde{Y}$ and $\tilde{M}$ at a given time, t, are independent of the observed exposure (X) at time t, given the baseline variables L; similarly, (17) states that potential outcomes for $\tilde{Y}$ and $\tilde{M}$ at time t are independent given X_t and L. In other words, it is assumed that there are no unobserved confounders among the model variables (X, M, and Y) at any time. An accompanying assumption is that of positivity, that is, P(X_t = x|L = l) > 0 and $P\left({\tilde{M}}_t\left(x\right)=m\text{|}{X}_t=x, L=l\right)>0$, for x = 0, 1, and m and l in their respective support sets. While this sequential ignorability assumption may appear to be strong (as it often is considered to be in the discrete time case), we note that the vector of baseline confounders (L) may include latent variables, as utilized in our data example discussed later.

In Web Appendix A, we show, given the above assumptions, that the expected potential outcome for a constant intervention can be expressed using the following version of the mediation formula:

$${E\{\tilde{Y}}_t\left(x,{\tilde{M}}_t\left(x^{\prime }\right)\right)\}={\int }_l^{\mathrm{ }}{\int }_m^{\mathrm{ }}E\left\{{\tilde{Y}}_t|X=x,{\tilde{M}}_t=m,L=l\right\}{f}_{{\tilde{M}}_t|\mathrm{ }X=x^{\prime },\mathrm{ }L=l}\left(\left.m\right|x^{\prime },l\right)f_L(l\left)d{\mu }_{{\tilde{M}}_t}\right(m\left)d{\mu }_L\right(l)$$ (18)

for t ∈ [0, T]. More general (including discontinuous) intervention functions require additional assumptions. Web Appendix A also shows for such cases that expected potential outcomes for Y can be identified under the causal differential equations model, that is, (5)-(9).

Estimation of the expected potential outcomes using the continuous time mediation formula (18) is done in conjunction with association models for M and Y. As a concrete example, we consider the following model used for the dental data described in the next section:

$${\tilde{M}}_{ij}\equiv E\{M_{ij}|t_{ij},x_i,c_i,u_i^M\}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}[{\alpha }_0+{\alpha }_1{x}_i+{\mathit{\alpha }}_2{\mathit{c}}_{\mathit{i}}\text{+}{u}_i^M]}{{\left[1+\mathrm{e}\mathrm{x}\mathrm{p}\{-{\alpha }_3{t}_{ij}\}\right]}^{1/{\nu }_M}}$$ (19)

$${\tilde{Y}}_{ij}\equiv E\{Y_{ij}|t_{ij},x_i,c_i,{{\tilde{M}}_{ij},u}_i^Y\}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}[{\beta }_0+{\beta }_1{x}_i+{\mathit{\beta }}_2{\mathit{c}}_{\mathit{i}}+{\beta }_3\mathrm{l}\mathrm{o}\mathrm{g}({\tilde{M}}_{ij})+u_i^Y]}{{\left[1+\mathrm{e}\mathrm{x}\mathrm{p}\{-({\beta }_4{t}_{ij}+{\beta }_5{t}_{ij}\bullet {\mathrm{l}\mathrm{o}\mathrm{g}(\tilde{M}}_{ij}))\}\right]}^{1/\nu }}$$ (20)

Equations (19) and (20) are nonlinear regression models based on the generalized logistic function²⁹; for convenience, we refer to them as generalized logistic models. Although (19) and (20) have specific forms pertaining to our data example, variations (for example, including other interaction terms, a time-dependent exposure, X, and different measurement times for Y and M) are possible. We also utilize natural continuous-time extensions of models (19) and (20). Thus we write ${\tilde{M}}_{it}$ and ${\tilde{Y}}_{it}$ to refer to expected values for M and Y, respectively, for individual i at any given time t.

Note the important role of the random effects in (19) and (20) in increasing the plausibility of the sequential ignorability assumptions (in particular, (17)). From the DAG on the right-hand side of Figure 1, it is apparent that previous observations of the mediator (M) represent confounders of the relationship between M and Y at a later time. We assume that the random effects explain any associations (further, any casual relationships) among the repeated measures for M, and likewise for Y. The assumed causal model is thus represented in Figure S1 (Supporting Information, Appendix A). We see for this DAG (under the nonparametric structural equation model (NPSEM) interpretation¹⁸) that assumptions (16) and (17), with u^M and u^Y included in L, are satisfied.

The association models for M and Y may be fit jointly, but we consider a computationally faster two-step approach, making the additional assumption of independent $u_i^M$ and $u_i^Y$. A Monte Carlo approach is used in lieu of integration over ${\tilde{M}}_t$ in the mediation formula. Note, as indicated above, that the baseline covariate vector, L, is considered to include both the observable baseline variables and random effects; that is, L = (c, u^M, u^Y). The algorithm for estimation of expected potential outcomes is as follows:

1. Fit association models for M and Y.

   1. Step 1: Fit (e.g., via maximum likelihood) the M model (19) based on an assumed distribution for M and the data: repeated responses, M_ij, the observed exposure (x_i) and baseline covariates (c_i) for i = 1 ,…,N, j = 1,…,n_i. Obtain predicted values for the $u_i^M$ yielding predicted values for ${\mathrm{l}\mathrm{o}\mathrm{g}(\tilde{M}}_{ij})$ (denoted as ${\widehat{M}}_{ij}$) for each individual i and time t_ij.
   2. Step 2. Fit the Y model (20) under an assumed distribution for Y using Y_ij (the repeated measures) x_i, c_i and ${\widehat{M}}_{ij}$ for i = 1 ,…,N, j = 1,…,n_i.
      We thus obtain estimates of regression parameters (the α’s and β’s from (19) and (20), respectively) as well as the random effects variances, with estimates denoted with hats (e.g., ${\widehat{\sigma }}_M^2$).

2. For a given intervention, compute estimated expected potential outcomes via the mediation formula.

   Do the following over a grid of values of time, t ∈ [0, T], by some small interval size δ:

   For a specified intervention, A (say with ${X_t^Y=x,X}_t^M=x\prime$), and time, t, do the following independently for each person i = 1 to N (with covariate vector c_i):

   1. draw ${\widehat{u}}_i^M\mathrm{ }$from $N(0,{\widehat{\sigma }}_M^2)$ and (independently) ${\widehat{u}}_i^Y$ from $N(0,{\widehat{\sigma }}_Y^2)$;
   2. compute predicted value (denoted as ${\widehat{M}}_{it}\left(A\right)$) of ${\mathrm{l}\mathrm{o}\mathrm{g}(\tilde{M}}_{it}\left(A\right))$ given ${\widehat{u}}_i^M$ and c_i with x_i = x′ and time t using continuous time version of (19) with estimates plugged in for parameters;
   3. compute predicted value (denoted as ${\widehat{Y}}_{it}\left(A\right)$) of ${\tilde{Y}}_{it}\left(A\right)$ given ${\widehat{u}}_i^Y,\mathrm{ }{\widehat{M}}_{it}\left(A\right)$, and c_i, with x_i = x and time t using continuous time version of (20) with estimates plugged in for parameters;
   4. An estimate of the marginal effect is obtained by summing over i; namely, ${\widehat{E}\{\tilde{Y}}_t\left(A\right)\}={\sum }_{i=1}^N{\widehat{Y}}_{it}\left(A\right)$.

To reduce Monte Carlo error, one may ‘clone’ the sample (or other ‘reference group’) using a chosen multiplier as suggested in previous work^7,8. The above describes the approach for fixed $X_t^M$ and $X_t^Y$ (which would be similar for continuous but not fixed exposures). For discontinuous $X_t^M$ and $X_t^Y$ the above steps can also be implemented where the appropriate ${\widehat{Y}}_{it}\left(A\right)$ and ${\widehat{M}}_{it}\left(A\right)$ are used based on expressions (10) and (11). Web Appendix B provides an illustrative derivation of formulae for expected potential outcomes for a discontinuous intervention, namely, $A^{1,t_1}$ (defined in Section 2.2), in the context of the generalized logistic model.

The estimated potential outcomes are then used to obtain estimated mediation effects for a chosen scale. We note that for the ratio scale, in contrast to the difference scale, we have $D_t^r\left(A^{\mathrm{0,1}}\right)=D_t^r\left(A^{\mathrm{1,0}}\right)$ and $I_t^r\left(A^{\mathrm{0,1}}\right)=I_t^r\left(A^{\mathrm{1,0}}\right)$, which obtains when there is not an X by M interaction in the Y model. Further, in the present model, the ratio-scale direct effect is fixed over time (and given by exp(β₁)), thus, denoted simply as D^r, while the indirect effect (written as $I_t^r$) varies over time due to the inclusion of the M by t interaction term. Once indirect effects are computed over a grid of times, the area between the curves (ABC) corresponding to a given type of indirect effect of interest may be obtained using the trapezoid method.

Confidence intervals for the specified direct and indirect effects (at any given time) can be obtained via bootstrap resampling. In particular, we use the bootstrap percentile method to obtain 95 percent confidence intervals.

3. SIMULATION STUDY

We conducted a simulation study to evaluate properties of our mediation effect estimates. Our main scenario roughly mimics the dental data (to be presented and analyzed in Section 4) based on the generalized logistic model described above. However, using the same model we also wish to learn the implications of varying the number of observed measurements per person.

We simulated data using models (19) and (20), with both Y and M as negative binomial, X as Bernoulli, and a single baseline covariate C as normally distributed. As C represents a confounder it is involved in the generation of X (using a logistic regression model). Random effects for M and Y (namely, u^M and u^Y) were generated independently from normal distributions. A time variable, t, was also included. Models (19) and (20) were then used to generate M (as a function of specified t and generated x, c, and u^M) and Y (as a function of t, x, c, u^M, and u^Y). A total sample size of 200 was used. The number of measurements per person (equally spaced in the time interval [0, 40]) were 3, 6, and 11. The parameter values used in the simulations are provided in Web Appendix C, Table S1. Five hundred independent replicates (datasets) were generated and analyzed as described below.

We included both ratio and difference scale mediation effect estimators. The method and formulae are given in Section 2. A multiplier of 10 (‘cloning’ the sample) was used to reduce Monte Carlo error. Bootstrap (percentile method) 95 percent confidence intervals were obtained using 300 bootstrap samples (sampling data vectors corresponding to subjects in each dataset). Occasionally, generated values (usually in combination with extreme estimates from certain bootstrap samples) would result in a large (nonevaluable) argument for the exponential function or power operation, which we remedied through truncation of the relevant argument. In addition, some datasets resulting in non-convergence in the fit of either the M or Y model resulting in exclusions. From the 500 replicates minus the exclusions (the numbers of which were recorded), the statistics listed below were computed.

The true values for each estimand were obtained by applying the continuous time mediation formula (18) using the true values for the regression parameters, the empirical distribution of the covariates for the given dataset, and drawing random effects (in a Monte Carlo approach) from their true distributions (yielding generated ${\mathrm{l}\mathrm{o}\mathrm{g}(\tilde{M}}_{it}\left(A\right))$ for given A, c_i, and t). Note that the generated (empirical) covariate distribution for a dataset was considered as the true covariate distribution and dataset-specific true values were used in computing the biases and coverage probabilities. For each scenario, we computed (averaging over replications): bias (average estimate minus the true value), relative bias (average ratio of the bias and the true value), standard error of the bias, coverage (percent of 95% confidence intervals that cover the true value) and power (percent of 95% confidence intervals that do not cover 0).

Tables 1 and 2 provides the simulation results for the ratio-scale estimands. Note that on the ratio scale the (natural) direct effect is constant over time and the two versions for each effect (e.g., D(A^1,0) and D(A^1,0) are equal.

Table 1.

Simulation estimated bias, relative bias, and standard error of bias (based on 500 replicates mimicking the dental data, n=200) for mediation (natural direct (D) and indirect (I)) effects on ratio scale; subscripts (20 and 40) indicate times for indirect effects; m indicates the number of (equally spaced) measurements for simulated data. Note: all 500 replicates were used for m = 6 and 11; one resulted in non-convergence (499 were used) for m = 3

		Bias			Rel Bias			SE Bias
Estimand	True╲	m = 3	6	11	m = 3	6	11	m = 3	6	11
Dr	1.350	0.068	0.036	0.022	0.051	0.026	0.017	0.021	0.015	0.012
$I_{20}^r$	1.653	−0.033	0.003	−0.018	−0.018	0.003	−0.009	0.013	0.012	0.011
$I_{40}^r$	1.279	0.060	0.053	0.038	0.048	0.042	0.031	0.009	0.008	0.007
ABCr	13.403	−0.480	−0.821	−0.578	−0.030	−0.057	−0.037	0.237	0.189	0.175
$I_{20}^r$(prop)	0.625	0.107	0.028	0.027	0.174	0.047	0.045	0.056	0.034	0.010
$I_{40}^r$(prop)	0.449	0.220	0.140	0.065	0.445	0.315	0.157	0.321	0.051	0.026
ABCr (prop)	0.598	−0.368	0.060	0.032	−0.650	0.102	0.055	0.483	0.021	0.011

Table 2.

Simulation estimated coverage and power (based on 500 replicates mimicking the dental data, n=200, from percentile method 95% confidence intervals, 300 bootstrap samples) for mediation (natural direct (D) and indirect (I)) effects on ratio scale; subscripts (20 and 40) indicate time points for indirect effects; m indicates the number of measurements. All 500 replicates used for m = 6 and 11; 499 used for m = 3

	Coverage (%)			Power (%)
Estimand╲	m = 3	6	11	m = 3	6	11
Dr	0.954	0.948	0.952	0.164	0.254	0.286
$I_{20}^r$	0.948	0.924	0.942	0.862	0.978	0.982
$I_{40}^r$	0.948	0.932	0.932	0.808	0.958	0.978
ABCr	0.920	0.916	0.942	0.794	0.916	0.972
$I_{20}^r$(prop)	0.970	0.958	0.946	0.575	0.864	0.952
$I_{40}^r$(prop)	0.990	0.972	0.958	0.415	0.654	0.782
ABCr(prop)	0.972	0.958	0.946	0.589	0.826	0.918

From Table 1, we see that relative biases are low (less than 6%) for direct and indirect effect (including ABC) estimates even with as few as 3 time points. Proportions (including that for the ABC) tend to be less stable and have high (simulation estimated) relative biases (up to 65%) and high standard error of bias at m=3. However, these biases are reduced considerably with higher m. The estimated relative biases for the ABC proportion are 10.2% and 5.5% for 6 and 11 time points, respectively.

Table 2 provides simulation results for coverage and power for the same (ratio-scale) estimands. Coverage is found to be good (at least 92%) even for m = 3, though coverage for indirect effect proportions are somewhat conservative for smaller m. Closer to nominal (95%) coverage is found for m = 6 and this is closer still for m=11. Power for all estimands is seen to increase with increasing m, particularly in going from 3 to 6 time points.

The equalities noted above for the alternative versions for the ratio-scale estimands do not hold on the difference scale; consequently, there are a greater number of distinct difference-scale estimands. Nevertheless, the overall conclusion for these (see results provided in Web Appendix C, Tables S2, S3) are generally consistent with those of the ratio scale.

4. DATA EXAMPLE

The data for the present example are from a longitudinal study of dental caries in a cohort of very low birth weight (VLBW) and normal birth weight (NBW) children followed from birth³⁰. In this study 468 child-caregiver dyads (234 VLBW; 234 NBW) were enrolled and assessed at child ages 8, 18, and 36 months on oral health outcomes, as well as behavioral and demographic variables, including socioeconomic status (SES).

A secondary finding of this study was that there is a relationship between SES and dental caries as measured by the number of decayed, filled and missing teeth (DMFT). As an exploratory question, we sought to learn the extent to which the effect of SES (considered as a fixed binary variable, 1 for low SES, 0 for high SES) on DMFT is mediated by the child’s consumption of sugary drinks. The latter was obtained via a caregiver questionnaire which included questions about frequency of the child’s consumption of such sugary drinks as soft drinks and juice. The caregiver was asked to respond to each question on a five-level Likert scale (1=none to 5=very often). We calculated a sugary drink score (denoted as SDRK) as the mean score over the relevant questions. A table of descriptive statistics for the model variables is provided in Web Appendix D (Table S4). The analysis was based on 440 child-caregiver dyads that had complete data for the included covariates (noted below) and at least one measurement (over the three time points) each of SDRK and DMFT. Similar results (not shown) were obtained using the complete cases (n=195).

Although SDRK and DMFT were measured at only three time points, these measurements are considered as realizations of underlying (latent) continuous time processes. We therefore wished to determination the extent of mediation as a function of age and to assess the overall mediational effect over the age range of interest.

For the longitudinal association models for M (SDRK) and Y (DMFT) we used the generalized exponential models given by (19) and (20), respectively. For both models, the vector of baseline covariates, c, included birth group (1 for very low birth weight group, 2 for normal birth weight group), and sex (1 for male, 0 for female). Both Y and M were assumed to be distributed as negative binomial.

The generalized logistic model is appropriate for the dental data in part because it describes the means for M and Y (conditional on the covariates and random effects) as monotonically increasing over time, as would be expected for sugary drink use and DMFT in young children. Initial models for M and Y included time by SES (t × X) interactions in the numerator; however, these terms did not appear to improve the model fit based on AIC (and were not found to be statistically significant) and were dropped from the models.

The estimates (with standard errors) for the M and Y model parameters are given in Table 3. Figure 3 shows the predicted means of potential outcomes for DMFT, including those corresponding to the total indirect and partial indirect effects as a function of time (t, age in months). The natural direct and indirect effects were computed on both the difference and ratio scales. Estimates and 95% confidence intervals for mediation effects on the ratio scale are provided in Table 4. Bootstrap percentile confidence intervals were based on 499 bootstrap samples, with possible exclusions due to non-convergence. A multiplier of 10 (‘cloning’ the sample) was used to reduce Monte Carlo error in the mediation formula computations. Results on the mean difference scale (for which there a larger number of estimands) are provided in Web Appendix D (Table S5).

Table 3.

Estimates, standard errors, and p-values (Wald test) of parameters in generalized logistic models for M (SDRK) and Y (DMFT) fit to dental data

M Model				Y Model
Parameter	Estimate	SE	p-value	Parameter	Estimate	SE	p-value
α0 (Int)	0.18	0.28	0.53	β0 (Int)	−2.50	0.81	0.002
α1 (SES)	0.77	0.15	<0.001	β1 (SES)	0.69	0.46	0.13
α21 (Birth)	0.22	0.14	0.12	β21 (Birth)	0.29	0.37	0.44
a22 (Sex)	−0.077	0.14	0.59	β22 (Sex)	−0.046	0.37	0.90
a3 (Time)	0.17	0.027	<0.001	β3 (SDRK)	1.15	0.38	0.003
kM (Disp)	0.38	0.080	<0.001	β4 (Time(t))	0.21	0.057	<0.001
νM (Damp)	0.12	0.023	<0.001	β5 (t × SDRK)	−0.057	0.022	0.012
σM (SD)	0.57	0.11	<0.001	k (Disp)	1.64	0.67	0.015
				ν (Damp)	0.047	0.023	0.047
				σY (SD)	2.85	0.92	0.002

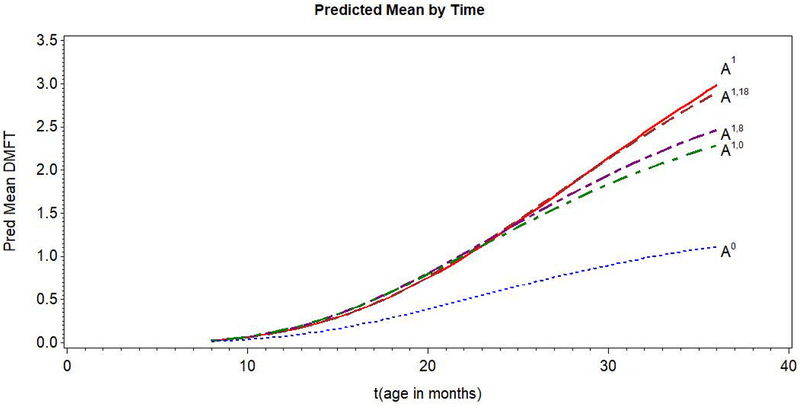
Figure 3.

Plot of mean predicted DMFT by age of child (t) using the generalized logistic model, (18) and (19), for alternative interventions (indicated by different A’s).

Table 4.

Results for analysis of dental data – inference for mediation (natural direct (D) and indirect (I)) estimands on mean ratio scale. Estimates and, for indirect effects, proportions are given along with bootstrap percentile method 95% confidence intervals (499 bootstrap samples generated, 489 used). Subscripts indicate time (age in months) for (cross-sectional) indirect effects. ABC (area between the curves) provides overall indirect effect for specified intervention (starting at indicated time)

Estimand	Est	95% CI	Prop.	95% CI
Dr	2.05	(1.02, 4.19)	-	-
$I_8^r$	0.98	(0.53, 1.61)	−0.03	(−4.35, 1.87)
$I_{18}^r$	0.91	(0.72, 1.76)	−0.14	(−0.88, 0.85)
$I_{36}^r$	1.31	(1.04, 2.11)	0.27	(0.03, 0.93)
ABCr(A1,0)	0.64	(−6.27, 16.39)	0.03	(−0.38, 0.89)
ABCr(A1,8)	0.01	(−4.40, 11.83)	0.0007	(−0.26, 0.56)
ABCr(A1,18)	−0.03	(−0.63, 1.58)	−0.002	(−0.03, 0.08)

As an example, we see from Table 4 that the (time independent) ratio-scale estimate of the natural direct effect (and 95% confidence interval (CI)) is 2.05 (1.02, 4.19). Thus, at any given time over the observed time range, there is an estimated factor increase of 2.1 in mean DMFT for low SES versus high SES when the mediator, SDRK, takes values as if everyone were high (or low) SES. The ratio-scale estimates of the natural indirect effect (and 95% CI), at 18 and 36 months, respectively, are 0.91 (0.72, 1.76) and 1.31 (1.04, 2.11). The latter result indicates an estimated 1.3 factor increase in mean DMFT at 36 months of age if everyone were high (equivalently, low) SES, and SDRK (over the whole time range) were at the level each person would have if low SES versus the level each person would have if high SES. The corresponding estimated mediation proportions (95% CIs) are −0.14 (−0.88, 0.85) and 0.27 (0.03, 0.93) for 18 and 36 months respectively. Thus, an estimated 27 percent of the effect of SES on DMFT at 36 months is through SDRK (considered continuously up to that time); from the 95% confidence interval this is seen to be nominally statistically significant at the 0.05 α level.

The estimated mediation proportions on the difference scale (see Web Supporting Information, Appendix D, Table S5) are similar overall, and the conclusions regarding statistical significance are the same for both scales. Our contention is that the ABCs based on the difference scale are more meaningful than those of the ratio scale as the former corresponds to areas based on means (as in Figure 3) rather than log means. For the ABC on the difference scale, in particular ABC(A^1,0), corresponding to a total mediation effect, the estimated proportion (95% CI) is 0.19 (−0.16, 0.94). The lack of statistically significance for the ABC, in contrast to the indirect effect at 36 months, may be due to the greater variability of the former; also the proportion is lower (for A^1,0, 0.19 versus 0.37 (difference scale)), presumably due to the lower (and even negative) estimated indirect effects at younger ages.

For partial mediation where the mediator is affected (by a future intervention) starting at 8 months, the estimated overall mediation proportion (ABC – difference scale, 95% CI) is 0.11 (−0.16, 0.70). If instead the intervention begins at 18 months the estimated ABC proportion (95% CI) is 0.01 (−0.053, 0.18). Thus an estimated 11% (1%) of the effect of SES on DMFT up to age 36 months is due to SDRK at 8 (18) months and later. As expected, these proportions are smaller than that of the complete mediation situation (where an intervention affecting SDRK starts at birth) and are also not statistically significant. However, it is interesting that starting the intervention affecting SDRK at 18 months (to a lesser extent, 8 months) provides a dramatic reduction in the predicted mediation proportion relative to starting the intervention at time 0 (birth).

For comparison, we also analyzed these data using a roughly analogous discrete time approach (Bind et. al., 2016).³¹ Note that this approach provides estimates of overall natural direct and indirect effects, assumed as constant over the measurement times. This is in contrast to our continuous time approach which considers natural direct and indirect effects as functions of time. We found that results from the discrete time approach are consistent with those of the continuous time approach, in the sense that the former gives estimates that are similar to those found from the continuous time approach at around the midpoint of the time range for the data. Details and further discussion are given in the Web Supporting Information, Appendix F.

To critically evaluate a particular data analysis using the proposed continuous time mediation analysis approach, it will be important to carefully consider the assumptions of the method. In the Web Supporting Information, Appendix E, we provide an elaborated discussion of key assumptions, both causal and for the association model, and discuss their plausibility for the dental data. For the untestable continuous time sequential ignorability assumption, just as with the established discrete version, it will be desirable in practice to perform a sensitivity analysis. Unfortunately, a sensitivity analysis expressly designed for the continuous time mediation model is not yet available. However, a rough approach is possible using a recently developed sensitivity analysis method for a discrete time causal mediation analysis with outcomes (Y and M) following generalized linear models.³² The results of the sensitivity analysis suggest that the conclusion of a statistically significant natural direct effect is sustained, while conclusions regarding natural indirect effects change, over a plausible range of sensitivity parameter values. Further details are provided in the Web Supporting Information, Appendix G.

5. DISCUSSION

In this paper we present an approach to causal mediation analysis for longitudinal data using continuous time models. In particular, we introduce a causal (potential outcome based) differential equations (CDE) model to account for underlying mediator (M) and final outcome (Y) processes that are continuous over time. We consider an easily integrable class of functions so that expected outcomes can be related to standard (albeit nonlinear) longitudinal regression models. Extension to wider classes of functions for differential equations models will be of interest for the future.

Our methodology is in the spirit of the mediation formula approach for estimation of natural direct and indirect effects; identification of these effects is obtained under a continuous time version of the commonly used sequential ignorability assumption. We specified nonlinear longitudinal regression (association) models based on the generalized logistic function for both the mediator (M) and final outcome (Y). A two-step approach to estimation of the association model parameters is proposed for computational ease. Alternative association models may be considered and it is possible that results will be sensitive to model misspecification. Thus, the use of model diagnostics and criticism is an important preliminary step. Nonparametric or semiparametric models will be of interest to better assure robustness of results.

While it may appear that the CDE model is not involved in the constant exposure case once the longitudinal models (such as (19) and (20)) are specified, in fact this model still provides the underpinning for the mediation process and resulting inference (which becomes clearer in the discontinuous exposure case). For example, the predicted values for Y at some time t are not entirely determined by the current values for X and M (that is, $\mathrm{l}\mathrm{o}\mathrm{g}\left(\tilde{M}\right)$) as seems to be specified by (19) and (20); rather those predicted values are dependent on the exposure history (in the present case, exposure being constant at the indicated levels, x and x′ for Y and M, respectively) from time 0, as revealed by the CDE (or its integral form).

As elaborated in Section 2.4, using the ratio scale in the context of the generalized logistic model, provides intuitive estimators of natural direct and indirect effects, in which time-independence (or dependence) follows directly from the specification of the corresponding association models (that is, the inclusion or not of certain interaction terms). Thus, a recently expressed criticism of the mediation formula methodology³³, namely the complicated and unintuitive nature of interaction effects, is circumvented in this case.

In addition, the selected association models use random effects to explain correlations among repeated measures. The random effects for the mediator and final outcome are assumed to be independent in our two-stage modelling approach. Another limitation is that individual trajectories are fixed conditional on the random effects, constraining the dynamic potential of the model. Thus, while our use of random effects allows for some randomness in outcome trajectories, the current model may not be adequate for certain types of causal relationships, for example, where there are lagged effects. On the other hand, at least in our example, we believe that the lack of a lag is plausible as we are describing the relationship among the underlying processes; for example, average (smoothed) sugary drink usage may have an immediate, albeit infinitesimal, effect on the underlying dental caries process. In future work, we will seek to expand the flexibility of the approach by employing stochastic differential equations to describe mediation in the context of dynamic changes over time.

Our simulation studies showed good properties of the estimators, indicating that the two-step approach works reasonably well. This is true despite the approach not accounting for measurement error due to the use of estimated ${\mathrm{l}\mathrm{o}\mathrm{g}(\tilde{M}}_{it}\left(A\right))$ in the Y model. There is the potential for more refined approaches, for example, using joint modeling, though computational challenges would need to be overcome. Our simulations also show the potential for gains in precision with increasing numbers of (equally spaced) measurements. We found the method to be useful in a dental data example despite the relatively small number of (three) time points. The data used in our example and a SAS macro to implement the method are provided in the Web Supplementary Information.

Novel features of our continuous time method include the use of the ‘area between the curves’ (ABC) as a measure of the overall mediation effect. In addition, we are able to consider alternative (‘partial’) mediation effects corresponding to interventions that affect the mediator starting (or stopping) at selected post-baseline times. In this way, the continuous time methodology allows for prediction of effects of more refined and realistic future interventions. Further variations of conceived interventions, for example, with additional starts and/or pauses of treatment, may be readily implemented.