Metabolic kinetic modeling provides insight into complex biological questions, but hurdles remain

Abstract

Metabolic models containing kinetic information can answer unique questions about cellular metabolism that are useful to metabolic engineering. Several kinetic modeling frameworks have recently been developed or improved. In addition, techniques for systematic identification of model structure, including regulatory interactions, have been reported. Each framework has advantages and limitations, which can make it difficult to choose the most appropriate framework. Common limitations are data availability and computational time, especially in large-scale modeling efforts. However, recently developed experimental techniques, parameter identification algorithms, as well as model reduction techniques help alleviate these computational bottlenecks. Opportunities for additional improvements may come from the rich literature in catalysis and chemical networks. In all, kinetic models are positioned to make significant impact in cellular engineering.

Introduction

Metabolic networks are highly integrated networks that are regulated in sophisticated ways. Because of this complexity, strategies for metabolic engineering are often non-intuitive, and engineering questions are often best addressed by metabolic models. Constraint-based models (CBMs), based on stoichiometry, have been widely successful over the last 15 years at guiding engineering efforts without the need for mechanistic detail [1]. However, CBMs cannot capture the relationship between flux, enzyme expression, metabolite levels, and regulation that is possible with kinetic models (Box 1) [2^•]. Although computationally costly, kinetic models are more predictive and are especially appropriate when there is not an obvious objective function for optimization or when exploring dynamic effects [3]. However, within kinetic modeling, it can be difficult to determine where to start due to the great wealth of published frameworks. Here we highlight the questions that are well suited for kinetic models and the various hurdles to their use.

Box 1. Type of question informs the type of model used.

CBMs are more appropriate for some types of questions:

Flux distribution (during growth):

What does the intracellular flux distribution look like?

Growth rate:

How might the ratio of media components Y1 and Y2 affect growth?

Knockouts (during growth):

Which enzyme(s) should be knocked out to increase flux through pathway P?

Maximum theoretical yield (MTY):

How does the MTY of product X change if I change media composition?

Kinetic models are better suited for others:

State prediction:

Which enzyme(s) should I overexpress to increase production of metabolite X?

Knockouts (during non-growth):

Which enzyme(s) should be knocked out to increase flux through pathway P during non-growth conditions?

Metabolic stability:

Will incorporating heterologous pathway P limit productivity due to metabolic instability? How much can I overexpress enzyme E without losing stability?

Regulatory interactions:

Is there an allosteric interaction between enzyme E and metabolite X?

Questions addressed by recent kinetic modeling frameworks

Recent kinetic modeling frameworks primarily seek to answer four types of questions: those involving (1) metabolic state prediction and engineering strategies, (2) identification of unmodeled phenomena, (3) metabolic stability, and (4) kinetic variation. The relative strengths of each framework are shown in Table 1.

Table 1.

Applicability of mechanistic and data-driven metabolic modeling and inference frameworks

Key: [] = N/A [*] = Low [**] = Medium [***] = High		Applicability of framework in providing insights regarding:						Resource availability
		Metabolic engineering strategies		Regulatory structure inference
	Framework name	Rate-limiting steps	State prediction	Metabolite-level	Transcriptional	Metabolic stability	Kinetic variation	Experimental	Computational	Scalability	Recent applications
Mechanistic, targeted	EM-RA	**	***	*		***	**	***	**	**	[16,17•]
	ABC-GRASP	***	***	**		**	**	***	*	*	[5]
	ORACLE+ IMCA	***	*		*	*	**	**	***	**	[8]
	ORACLE+ iSCHRUNK	***	*			*	**	***	***	**	[7]
	MASS	*	*			*	***	**	***	***	[18,20]
Data-driven, untargeted	LiP-SMap			***				**	***	***	[12••]
	Fuhrer [13]			**	**			*	***	***	[13]
	Kochanowski [14•]				***			*	***	***	[14•]
	SIMMER			***				*	***	***	[11]
	Costello [57••]	***	***	*	*			*	**	***	[57••]

Metabolic state prediction and engineering strategies

Most kinetic modeling frameworks are designed to address questions involving prediction of metabolic states or rate-limiting steps, as these questions are central to metabolic engineering efforts. As kinetic parameters of individual enzymes are rarely known or are uncertain, many frameworks rely on exploring a range of parameters and selecting a subset that are consistent with experimental observations. Using the parameters derived from model training, network kinetics can be analyzed and predictions made for potential engineering strategies. The Ensemble Modeling (EM) paradigm is widely used because it requires minimal data and can accommodate large uncertainties in kinetic parameters [4]. EM explores parameters that are thermodynamically consistent with models that collectively describe dynamic and steadystate behavior. Because many parameters might be equally consistent with experimental data, the range of parameters effectively captures prediction uncertainty (i.e. a small range means low uncertainty, and a large range means high uncertainty). ABC-GRASP is similar in concept to EM but uses a wider range of kinetics and uses probability distributions, rather than discrete parameter sets [5]. However, these features can add a large computational cost relative to EM.

The ORACLE framework incorporates Metabolic Control Analysis (MCA) to succinctly characterize steady-state behavior and predict rate-limiting steps [6]. Recently, two extensions to the ORACLE framework were developed that significantly expand its utility. iSCHRUNK uses machine learning tools on the final set of kinetic parameters to further reduce uncertainty [7]. In another work, inverse MCA (IMCA) was integrated into ORACLE to incorporate the effects of transcriptional regulation on enzyme expression, which affects steady-state behavior [8]. However, validating predicted enzyme expression rate against measured mRNA concentration changes was challenging, potentially due to the low correlation between mRNA and enzyme expression levels [9].

Regulatory structure inference

While kinetic modeling can be used to test the presence/absence of structures in the network and regulation [5,8], only a small fraction of the possibilities can typically be explored due to computational limitations. Two notable exceptions include a method where dynamic metabolite data were used to systematically test a large set of putative allosteric interactions [10] and another method where Michaelis–Menten rate laws with variable allosteric terms were fit to an -omics dataset on a reaction-by-reaction basis [11].

Recently, however, numerous untargeted experimental strategies which do not require kinetic modeling have also been developed [12^••,13,14^•]. For example, LiP-SMap detects allosteric interactions by analyzing the difference in the protease cleavage sites of proteins when bound to a given metabolite [12^••]. Another study used high-throughput metabolomics data from a single-gene knockout library to infer gene-metabolite relationships [13]. Finally, a library of fluorescent transcriptional reporters was used to quantify the activity of metabolic promoters in Escherichia coli, and their activity was correlated with metabolome response to identify metabolites involved in transcriptional regulation [14^•]. These experimental methods can be used to identify regulatory mechanisms that can be incorporated into kinetic models.

Metabolic stability

Metabolic pathways are stabilized during evolution, so cells are typically robust to perturbations to native enzyme concentrations. However, the addition of heterologous pathways may not result in similar steady-state stability. While frameworks predicting metabolic states can assess steady-state stability indirectly, Ensemble Modeling for Robustness Analysis (EMRA) directly calculates the likelihood of a perturbation causing metabolic instability [15]. Recently, EMRA was used to assess the stability of cell-free systems, which are not optimized via evolution [16]. EMRA was also used to show how incorporation of kinetics and stability constraints further constrains the Maximum Theoretical Yield as predicted by FBA [17^•].

Kinetic variation

While there is variability in the metabolome and proteome among cell strains, it is thought that variation in the kinetome – the space of kinetic rate constants in metabolism – correlates better with genetic variation [18]. The MASS (Mass Action Stoichiometric Simulation) framework can perform large-scale analysis of kinetic variation [19]. Because MASS assumes mass action kinetics (e.g. Rate = k₁[A][B]), a population of thermodynamically consistent rate constant sets can be efficiently computed and studied. While mass action kinetics is an oversimplification of many metabolic reactions, comparison of the fitted rate constants can reveal loci of important variation between systems, for example, in red blood cells from different patients [18] as well as metabolic response to specific drugs [20].

Hurdles to large-scale quantitative predictions

While kinetic models can address complex biological questions, data limitations can result in large uncertainties in predictions, and large models can result in computational intractability. Here, we discuss these hurdles, focusing on recent developments to overcome them.

Challenges in experimental measurements used to train kinetic models

The most important type of data for kinetic models is structure. At a minimum, structure includes all reactions relevant to the system but may also include regulatory interactions and cell growth. While most reaction networks are well-defined, promiscuous enzyme activity and heterologous pathways can have unforeseen effects. Tools such as BNICE [21], Pickaxe [22], Retropath2.0 [23], and novoStoic [24] can elucidate these reactions through comparison to known reaction chemistry [25].

Because kinetic models ultimately depict system properties as a function of kinetic parameters, there have been several efforts in constructing ‘bottom-up’ models of metabolism where one uses directly measured or predicted kinetic properties of enzymes in model parameterization. While much progress has been made, using in vitro enzyme properties can cause unrealistic model behavior without the manual curation of regulatory effects [26,27]. Recent efforts [28] have shown that Michaelis–Menten rate law approximations using kinetic data can replace detailed rate laws; however, as enzyme kinetic information remains sparse, this approach is only valid for a small number of well-characterized reactions.

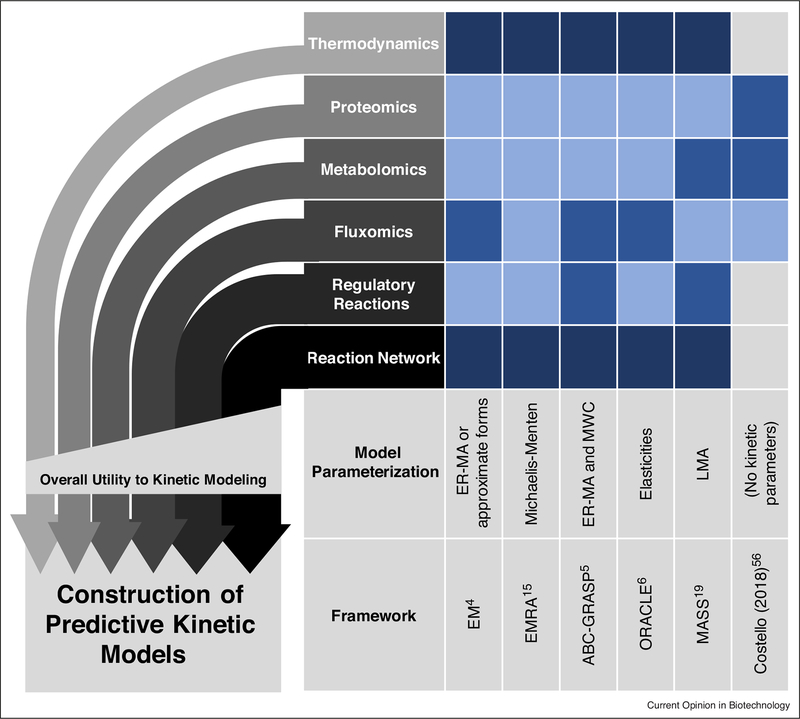
More commonly, -omics measurements are used to train kinetic models. However, different kinetic modeling frameworks utilize different types of -omics data to varying degrees (Figure 1); therefore, data types readily available for a given project should be taken into consideration when deciding on a kinetic modeling framework.

Figure 1.

Different data types have varying value to kinetic modeling frameworks.

-omics types are required to varying levels by different model frameworks (darkest boxes indicate data type is required, less dark boxes indicate data type is used to a high degree in practice, lighter blue boxes indicate data type can be used, light gray boxes indicate data type is not used) [4,5,6,15,19,57^••]. While all the -omics data types shown have utility in kinetic modeling, modeling results are usually most sensitive to variation in those near the bottom (e.g. variation in network structure). Thus, those data types generally provide more utility to kinetic modeling efforts and should be prioritized. Note that while regulatory reactions provide much value to kinetic modeling, they are not always incorporated, either because they are unknown or because they cannot be incorporated easily using a given framework. Data-driven models, while requiring very large amounts of data, may not require knowledge of the reaction network or regulatory interactions at all [57^••].

ABC-GRASP, Approximate Bayesian Computation – General Reaction Assembly and Sampling Platform; EM, Ensemble Modeling; EMRA, Ensemble Modeling for Robustness Analysis; ER-MA, Elementary Reaction Mass Action; LMA, Law of Mass Action; MASS, Mass Action Stoichiometric Simulation; MWC, Monod-Wyman-Changeux; ORACLE, Optimization and Risk Analysis of Complex Living Entities.

Flux data are arguably the most difficult to obtain. Nevertheless, fluxes are generally the most important property to measure, as most frameworks, including ORACLE, EM, ABC-GRASP, and MASS, require an accurate intracellular reference flux distribution. ¹³C tracer studies elucidate aspects of intracellular metabolism, while uptake and secretion fluxes are obtained by measuring changes in extracellular metabolite concentrations.

Measurements of intracellular metabolomics are also useful for parameter inference, but they are difficult to obtain. Metabolomics can refer to either relative or absolute concentrations of metabolites. While relative measurements – which do not require internal standards and are higher throughput – can typically be incorporated in rate laws, absolute metabolomics are required to accurately implement thermodynamic constraints [29]. Reaction thermodynamics strongly control fluxes for most reversible reactions and thus help to ensure feasibility in kinetic models [11]. For a thorough review of metabolomics methods, see Ref. [30].

Proteomics, while a low-throughput measurement, can be directly incorporated into most kinetic modeling frameworks. This is especially true in the case of highly irreversible reactions in which fluxes are often sensitive to enzyme concentration [11]. Relative proteomics are currently higher throughput than absolute measurements, although label-free absolute proteomics methods have made recent advances [31].

Parameter identifiability

Usually, experimental datasets measure too few conditions or not enough fluxes/metabolites/proteins at a given condition to resolve all parts of a network, that is, those parameters lack identifiability with the data provided. Methods for determining parameter and structural identifiability are complex and previously reviewed [32]. However, model solutions containing many feasible model parameterizations, including aspects of the network that are non-identifiable, are typically sufficient to answer design hypotheses, even if individual members of the solution contain loosely fit parameters [33]. We especially want to highlight recent modeling efforts that result in a distribution of parameters, rather than just one optimal set, and provide impactful insight into system behavior despite lacking a sufficient amount of data for direct parameter identification [15,16,34,35]. In general, kinetic models are best positioned to identify overall changes in system behavior rather than individual parameter values, as different sets of kinetic parameters can give rise to the same overall behavior.

Most kinetic models are written as large systems of stiff ordinary differential equations (ODEs) that are computationally expensive to solve. However, optimization tools such as Markov Chain Monte Carlo (MCMC) [36], genetic [37], and particle swarm [38,39] algorithms can decrease computational burden. For example, a parallelizable scatter search method was developed [38]. This method initiates multiple threads of a search algorithm, and the combination of these results is then communicated between parallel threads to better search the solution space. Additionally, a genetic algorithm (GA) step was added to the traditional EM framework to identify a single parameter set rather than an ensemble [37]. However, the lack of an ensemble makes it challenging to gauge uncertainty as there is no dispersion in one model, so several GA searches should be deployed in parallel. Furthermore, while the GA step more efficiently searches the parameter space, it often results in lower overall computational efficiency due to parameter tuning and overhead costs. Thus, these tools may not always reduce computational burden. However, other techniques that reduce the parameter sampling space directly by, for example, imposing reference flux states, reaction thermodynamic limits, and local stability constraints often reduce computational burden [4,16,29,34,40,41^•]. While these strategies efficiently search and constrain the kinetic parameter space, directly reducing the number of kinetic parameters can also improve computational tractability.

Model reduction

The goal of model reduction is to reduce the number of kinetic parameters while maintaining predictive power. Although reduction techniques are often applied after parameter estimation [42–45], here we highlight a priori model reduction methods applicable to most kinetic modeling efforts.

1. Model scope - selecting the appropriate amount of detail to include before using post-parameter estimation reduction techniques [42–45] is an ill-defined process. Too much detail leads to an impractical amount of time spent on model reduction (due to large computational costs), while too little detail may not capture observed effects at all.

2. Rate expression - the type of rate expression determines the number of parameters required. Approximate rate laws, such as lin-log kinetics, are model-reducing as they use fewer kinetic parameters [46]. However, they typically invoke assumptions whose validity should be checked [2^•,47]. This natural trade-off should be considered during initial model development [28,48].

3. Conservation analysis - biological networks inherently contain conserved moieties, such as the total pool of ATP, ADP, and AMP. These conserved groups are considered independent variables in many kinetic modeling approaches and increase the stiffness of ODE systems, increasing solve time. Because it is difficult to manually identify all conserved moieties, a tool that performs conservation analysis on biological networks was developed [49]. We have found that using this method decreases computation time.

4. Lumping - lumping techniques, such as a condensing a linear pathway into a single reaction, can greatly shrink the parameter space [50,51]. Often, optimization methods are used to identify potential lumping schemes throughout the network [26,52].

Use of appropriate model reduction techniques can greatly reduce the resources required to interrogate large-scale biological networks [43]. Conservation analysis, in particular, is easy to implement [49] and would provide value to most kinetic modeling efforts.

Conclusions

While we have reviewed the types of questions addressed by recent kinetic modeling frameworks, comparative studies need to be done in order to further characterize similar kinetic frameworks, similar to comparisons done for CBM frameworks [53]. In addition, it is important to survey modeling efforts in other fields, such as heterogeneous catalysis [54–56], and especially efforts that take advantage of the increasing availability of -omics data, particularly fluxomics, intracellular metabolomics, and proteomics [57^••]. Improving parameter estimation and model reduction techniques will allow tractable simulations for large-scale kinetic models while the discussed structural inference techniques can best inform model structure. As metabolic networks are large, complicated, and highly-coupled, sophisticated modeling frameworks will be essential in predicting system-level behavior.