Fractal dimension of cerebral white matter: A consistent feature for prediction of the cognitive performance in patients with small vessel disease and mild cognitive impairment

Abstract

Patients with cerebral small vessel disease (SVD) frequently show decline in cognitive performance. However, neuroimaging in SVD patients discloses a wide range of brain lesions and alterations so that it is often difficult to understand which of these changes are the most relevant for cognitive decline. It has also become evident that visually-rated alterations do not fully explain the neuroimaging correlates of cognitive decline in SVD. Fractal dimension (FD), a unitless feature of structural complexity that can be computed from high-resolution T₁-weighted images, has been recently applied to the neuroimaging evaluation of the human brain. Indeed, white matter (WM) and cortical gray matter (GM) exhibit an inherent structural complexity that can be measured through the FD.

In our study, we included 64 patients (mean age ± standard deviation, 74.6 ± 6.9, education 7.9 ± 4.2 years, 53% males) with SVD and mild cognitive impairment (MCI), and a control group of 24 healthy subjects (mean age ± standard deviation, 72.3 ± 4.4 years, 50% males). With the aim of assessing whether the FD values of cerebral WM (WM FD) and cortical GM (GM FD) could be valuable structural predictors of cognitive performance in patients with SVD and MCI, we employed a machine learning strategy based on LASSO (least absolute shrinkage and selection operator) regression applied on a set of standard and advanced neuroimaging features in a nested cross-validation (CV) loop. This approach was aimed at 1) choosing the best predictive models, able to reliably predict the individual neuropsychological scores sensitive to attention and executive dysfunctions (prominent features of subcortical vascular cognitive impairment) and 2) identifying a features ranking according to their importance in the model through the assessment of the out-of-sample error.

For each neuropsychological test, using 1000 repetitions of LASSO regression and 5000 random permutations, we found that the statistically significant models were those for the Montreal Cognitive Assessment scores (p-value = .039), Symbol Digit Modalities Test scores (p-value = .039), and Trail Making Test Part A scores (p-value = .025). Significant prediction of these scores was obtained using different sets of neuroimaging features in which the WM FD was the most frequently selected feature.

In conclusion, we showed that a machine learning approach could be useful in SVD research field using standard and advanced neuroimaging features. Our study results raise the possibility that FD may represent a consistent feature in predicting cognitive decline in SVD that can complement standard imaging.

Highlights

• •White matter fractal dimension is altered in small vessel disease patients with MCI.
• •White matter complexity's decrease consistently predicts worse cognitive performance.
• •Fractal dimension may be a new marker of white matter damage in small vessel disease.

1. Introduction

Mild cognitive impairment (MCI) defines a clinical status in which cognitive deficits are present but their severity, although clinically recognizable, does not impact on the personal autonomy in activities of daily living, and thus does not reach the level of dementia. Various dementia subtypes are preceded by an MCI stage (Gauthier et al., 2006). Small vessel disease (SVD) is recognized as a major cause of stroke and dementia (Rensma et al., 2018), and has been shown to be frequently associated with a cognitive impairment mainly characterized by deficits of attention and executive function (O'Brien et al., 2003; Pantoni, 2010). Neuroimaging plays today a crucial role in defining the presence of SVD in patients with cognitive decline in whom it may be the sole pathological process or coexist with degenerative processes (Pantoni, 2010). Efforts have been made to harmonize the neuroimaging definition of macroscopic lesions underlying SVD on conventional MRI, including recent small subcortical infarcts, white matter hyperintensities (WMH), lacunes, enlarged perivascular spaces (EPVS), cerebral microbleeds, and atrophy (De Guio et al., 2016; Wardlaw et al., 2013). A consensus paper reporting neuroimaging standards for research in SVD also recognized the importance of new MRI techniques to evaluate the different expressions of SVD (Wardlaw et al., 2013). However, it remains unclear, at present, which are the neuroimaging features that better predict clinical features, particularly cognitive status. Additionally, both subcortical and cortical changes are today accepted as features of SVD, but their respective role in terms of clinical correlates is not yet established. Also, the evaluation of different SVD features in a single patient is not easy and rather demanding in terms of time and use of MRI techniques.

During the last 20 years, quantitative assessment of brain volume using isotropic high-resolution T₁-weighted MR images has been largely applied to evaluate macroscopic structural alterations occurring in both aging and neurological diseases (Toga and Thompson, 2002). However, volume assessment does not capture the inherent structural complexity of the cerebral white matter (WM) and the cortical gray matter (GM). This complexity may be investigated using fractal geometry, which describes the complexity of objects that show, in a proper range of spatial scales, self-similarity, i.e., a geometrical property of objects composed of subunits and sub-subunits similar to the whole shape (Mandelbrot, 1967, Mandelbrot, 1982). The fractal dimension (FD) is a compact, unitless, geometric shape feature which represents how much the object fills the space (Tolle et al., 2003) and yields a single quantitative index of the structural complexity of an object (Zhao et al., 2016). The FD of cerebral WM and cortical GM can be computed using high-resolution T₁-weighted images commonly employed in SVD and therefore does not require additional MRI acquisitions.

Both cerebral WM and cortical GM exhibit fractal properties in a statistical sense (Bullmore et al., 1994; Free et al., 1996; Kiselev et al., 2003; Majumdar and Prasad, 1988; Zhang et al., 2006). The WM and GM FD values have been found positively associated with cognitive performance in aged subjects (Mustafa et al., 2012) and the GM FD also with the Alzheimer's Disease Assessment Scale-Cognitive (ADAS-cog) scale in Alzheimer's disease patients (King et al., 2010). Along this line, it is reasonable to assume that the WM FD and GM FD, as measurements of the structural complexity of the brain, might represent a potentially useful feature also in SVD.

The aims of this study were to assess whether the FD of cerebral WM and/or of cortical GM computed using high-resolution isotropic T₁-weighted MR images are valuable predictors of cognitive performance in patients with SVD and MCI, and if they are complementary to other standard neuroimaging features and to WM and GM volumes. We employed a machine learning strategy based on LASSO (least absolute shrinkage and selection operator) regression applied on several neuroimaging features in a nested cross-validation loop. This approach was aimed at 1) choosing the best predictive models, able to reliably predict the individual neuropsychological scores sensitive to attention and executive dysfunctions (prominent features of subcortical vascular cognitive impairment) and 2) identifying a features ranking according to their importance in the model through the assessment of the out-of-sample error, that is a measure of how accurately a model is able to predict values for unseen data.

2. Materials and methods

2.1. Participants

In this study, we included 76 patients with evidence of MCI and WM T₂-weighted imaging hyperintensities of presumed vascular origin of moderate or severe extension who were enrolled in one (Florence) of the VMCI-Tuscany study centers and who were object of a previous report (Pasi et al., 2015). Twelve patients were excluded because FreeSurfer segmentations were not satisfactory after manual editing and re-running up to three times (see Section 2.4.2 White and gray matter volumes sub-section below). Final analyses were thus performed on 64 patients. The mean (± standard deviation (SD)) age and years of education were 74.6 ± 6.9 and 7.9 ± 4.2 years, respectively; 34 patients (53%) were males.

A control group composed of 24 healthy control subjects (12 men and 12 women, mean age ± standard deviation 72.5 ± 4.7 years) was included in the study. No significant difference in age (t-test, p = .07) and in sex proportion (χ² test, p = .97) was present between the patient and control groups. Healthy controls had no familial or personal history of neurologic or psychiatric disorders, and underwent a neurologic examination that showed no abnormalities. They were assessed with Mini Mental State Examination (MMSE) and their score corrected for age and education level (mean 29.03 ± 1.14, range 26.2–30) resulted within the normal range for the Italian population (Measso et al., 1993). Finally, their MRI showed no (in 6 subjects) or mild (in 18 subjects) brain WMH on T₂-weighed fluid-attenuated inversion recovery (FLAIR) images (according to the modified version of the Fazekas scale (Pantoni et al., 2005)) without lacunes. Patients and controls underwent the same imaging protocol on the same scanner, but evaluation of some standard neuroimaging features of SVD (i.e., cerebral microbleeds, enlarged perivascular spaces, and quantitative WM lesion load) was available only for the patient sample as part of the Vascular MCI-Tuscany Study protocol (see Section 2.2Vascular MCI-Tuscany Study neuropsychological evaluation and Section 2.3MRI examination sub-sections below).

2.2. Vascular MCI-Tuscany study neuropsychological evaluation

The Vascular MCI-Tuscany Study is a 3-center, prospective, observational study aimed at evaluating the determinants of the transition from vascular MCI to dementia in patients with SVD. The study methodology has been reported in details elsewhere (Poggesi et al., 2012). The study was conducted in accordance with the Helsinki Declaration and was approved by the local Ethics Committee. Each patient gave a written informed consent. To be included, patients had to have: 1) MCI according to Winblad et al. criteria (Winblad et al., 2004), operationalized in agreement with Salvadori et al. (Salvadori et al., 2016); and 2) evidence on MRI of moderate-to-severe WMH on FLAIR T₂-weighed images in agreement with a modified version of the Fazekas scale (Pantoni et al., 2005). Study inclusion and MRI analysis were based on the same MRI scans.

According to the study protocol, at baseline, each patient underwent a comprehensive neuropsychological evaluation by means of the VMCI-Tuscany neuropsychological battery, that is an extensive tool specifically developed for patients with SVD and MCI (Salvadori et al., 2015). The VMCI-Tuscany neuropsychological battery includes both global cognitive functioning tests and second-level tests covering different cognitive domains. For the purpose of this study, among the cognitive tests of the VMCI-Tuscany neuropsychological battery, we selected those which are sensitive to attention and executive dysfunctions, because these are prominent features of subcortical vascular cognitive impairment (O'Brien et al., 2003). The cognitive tests selected were:

• •Montreal Cognitive Assessment (MoCA), a 10-min cognitive screening tool (Conti et al., 2015; Nasreddine et al., 2005) suggested by the NINDS-CSN (National Institute for Neurological Disorders and Stroke and the Canadian Stroke Network) to harmonize standards for the evaluation of vascular cognitive impairment, because it includes several items assessing executive functions, attention and concentration (Hachinski et al., 2006). Total score range is 0–30; higher scores represent better performance.
• •Visual Search, for focused attention, a digit cancellation task with a time limit (Della Sala et al., 1992). The score (range 0–50) is the number of corrected targets crossed out; higher scores represent better performance.
• •Symbol Digit Modalities Test (SDMT), for sustained attention, a symbol substitution task with a time limit (Nocentini et al., 2006). The score (range 0–110) is the number of correct answers; higher scores represent better performance.
• •Trail Making Test (TMT), Part A, for psychomotor speed, a visual scanning and tracking task in which participants are asked to connect in order a sequence of 25 numbers (Giovagnoli et al., 1996). The score is the time in seconds required to complete; higher scores represent worse performance.
• •Color Word Stroop Test, for selective attention and response inhibition, requires the participants to selectively process the color features of written words, while continuously blocking out the processing of reading (Caffarra et al., 2002b). The interference effect is evaluated by means of execution time in seconds; higher scores represent worse performance.
• •Immediate copy of the Rey-Osterrieth Complex Figure (ROCF); despite this test is commonly used for the assessment of visuo-spatial abilities, there is growing consensus on the fact that its complexity requires an integrative cognitive approach, and its reproduction involves also planning and organizational strategies that are related to executive functions (Caffarra et al., 2002a; Elderkin-Thompson et al., 2004; Freeman et al., 2000; Salvadori et al., 2018; Shin et al., 2006). The score (range 0–36) is based on the presence and accuracy of 18 units of the figure; higher scores represent better performance.

For the neuropsychological tests, we used the available normative data that are based on healthy Italian adult samples national norms to calculate demographically-adjusted scores by means of the regression equations extracted by normative studies (Caffarra et al., 2002a; Caffarra et al., 2002b; Conti et al., 2015; Della Sala et al., 1992; Giovagnoli et al., 1996; Nocentini et al., 2006). Since age and level of education resulted significantly associated with the performance in all the selected cognitive tests, a factor of correction was applied. For the visual search test, also sex was found to be a statistically significant factor, and the corresponding correction was then calculated and applied (Nocentini et al., 2006).

2.3. MRI examination

All subjects were examined on a clinical 1.5 T system (Intera, Philips Medical System, Best, The Netherlands) equipped with 33 mT/m maximum gradient strength and a 6-channel head coil. After the scout image, sagittal 3D T₁-weighted turbo gradient echo [repetition time (TR) = 8.1 ms, echo time (TE) = 3.7 ms, flip angle = 8°, inversion time = 764 ms, field of view (FOV) = 256 mm × 256 mm, matrix size = 256 × 256, 160 contiguous slices, slice thickness = 1 mm] images were acquired for WM and cortical GM segmentation.

The MR examination protocol included an axial T₂-weighted FLAIR sequence (TR = 11,000 ms, TE = 140 ms, inversion time (TI) = 2800 ms, flip angle = 90°, FOV = 250 mm × 250 mm, matrix size = 280 × 202, 40 contiguous slices, slice thickness = 3 mm, interslice gap = 0.6 mm) and an axial T2*-weighted gradient-echo sequence [TR = 696 ms, TE = 23 ms, flip angle = 18°, FOV = 250 mm × 200 mm, matrix = 252 × 160; 22 slices; slice thickness = 5 mm; interslice gap = 1 mm; number of excitations (NEX) = 2].

All images were visually assessed by an experienced neuroradiologist in order to identify possible artifacts. After this visual quality control, all images were used for further processing.

2.4. Neuroimaging feature extraction

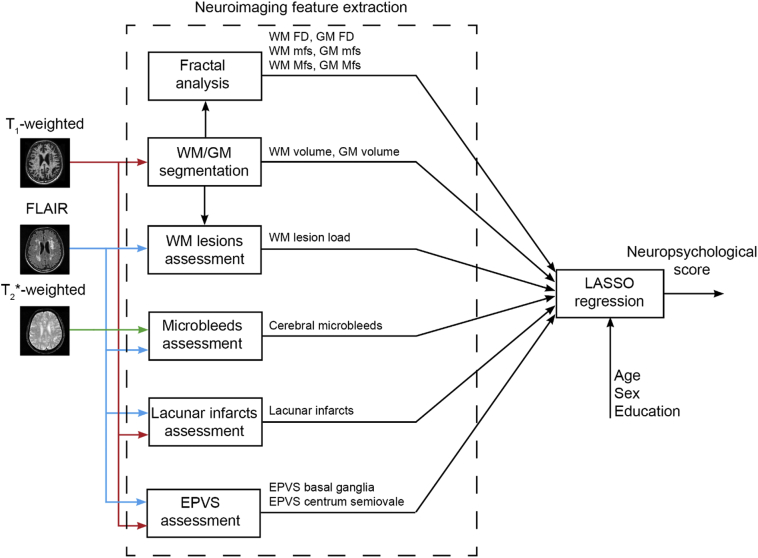
A general overview of the neuroimaging feature extraction procedure is shown in Fig. 1.

Fig. 1.

Overview of the neuroimaging feature extraction procedure for LASSO (least absolute shrinkage and selection operator) regression. We fitted a separate regression model for each neuropsychological test. WM and GM volumes are normalized to the estimated intracranial volume (EPVS = enlarged perivascular spaces, FD = fractal dimension, FLAIR = Fluid-attenuated inversion recovery, GM = gray matter, Mfs = maximum fractal scale, mfs = minimum fractal scale, WM = white matter). Demographic variables (age, sex and level of education) have been inserted as additional predictors to model possible residual effects in the patient population.

2.4.1. Standard neuroimaging features of small vessel disease

For the purposes of the present study, we decided to focus on the main MRI SVD-related markers, i.e., white matter hyperintensities, lacunes, enlarged perivascular spaces, and cerebral microbleeds, that were evaluated according to the conventional and quantitative MRI methods applied within the Vascular MCI-Tuscany Study. While lacunes, EPVS and cerebral microbleeds have been conventionally evaluated according to standard visual rating approaches centrally performed by an experienced neurologist, the WMH have been quantitatively expressed as the lesion load.

Lacunar infarcts were defined as cavities 3 to 10 mm in diameter mostly ovoid/spheroid, and were categorized as 0 = (absent), 1 = (1–3), 3 = (>3).

Microbleeds were defined as small, rounded or circular, well-defined hypointense lesions within brain tissue ranging from 2 to 10 mm in diameter; the Microbleed Anatomical Rating Scale (MARS) was used to assess the total number of microbleeds (Gregoire et al., 2009).

Enlarged perivascular spaces were defined as small, sharply delineated structures of cerebrospinal fluid intensity on imaging that followed the orientation of the perforating vessels, ran perpendicular to the brain surface, and were < 3 mm wide. EPVS have been assessed in the basal ganglia and centrum semiovale, and were coded as 0 = (absent), 1 = (≤10), 2 = (11−20), 3 = (21–40), and 4 = (≥40).

A single observer outlined the T₂-hyperintense WM lesions on FLAIR images of all patients with SVD and MCI using a semiautomated segmentation technique based on user-supervised local thresholding (Jim 5.0, Xinapse System, Leicester, UK; www.xinapse.com/Manual/). We thus defined the WM lesion load as the total lesions volume normalized by the individual cerebral WM volume (see Section 2.4.2 White and gray matter volumes sub-section below).

2.4.2. White and gray matters volumes

Cortical reconstruction and volumetric segmentation was performed with the FreeSurfer image analysis suite v. 5.3, which is documented and freely available (http://surfer.nmr.mgh.harvard.edu/). The technical details of these procedures are described in prior publications (Fischl, 2012). All the FreeSurfer outputs were visually inspected for defects: all planes (coronal, sagittal and axial) were examined to evaluate segmentation and surfaces reconstruction errors. We applied the correction procedures proposed by the FreeSurfer developers, consisting of both editing of brain and WM masks and adding control points and re-running of the FreeSurfer pipeline (https://surfer.nmr.mgh.harvard.edu/fswiki/FsTutorial/TroubleshootingData). The manual editing of a single operator and re-running was carried out up to three times to assure that all defects were corrected (McCarthy et al., 2015).

Volumes of cerebral WM, cortical GM and estimated intracranial volume (eTIV) were also computed. To reduce the effect of brain size, both WM and GM volumes were normalized to eTIV.

2.4.3. White and gray matter fractal analysis

We investigated both the FD of the cerebral WM and of the cerebral cortical GM. Among different methods to compute the FD, we chose the box counting algorithm, which is a fairly direct and reliable method to analyze fractal objects (Esteban et al., 2007; Mustafa et al., 2012; Zhang et al., 2006). Briefly, a grid composed of 3-D cubes of side r has been overlapped to the brain region of interest (WM or cortical GM) and the number of intersections N(r) between the grid and the brain region has been counted (Falconer, 2005). This process was iterated for different r values, with a uniform distribution in a logarithm scale (r = 2^k voxels, where k = 0, 1, …, 8 in this work). As suggested by Goñi and colleagues (Goñi et al., 2013), 20 random offsets with a uniform distribution were placed on the origin of the 3-D grid and the mean value of all the intersections (one for each offset value) has been calculated to extract a single N(r) for each r value. Then, we plotted N(r) against r in a bi-logarithm plane and the FD has been calculated as the absolute value of the slope of the linear regression. This linear relationship in the bi-logarithm plane is equivalent to a power law N(r) = K r^{– FD} in the natural scale, where FD, the fractal dimension, is the exponent (with a negative sign) and K is the prefactor (Mandelbrot, 1982).

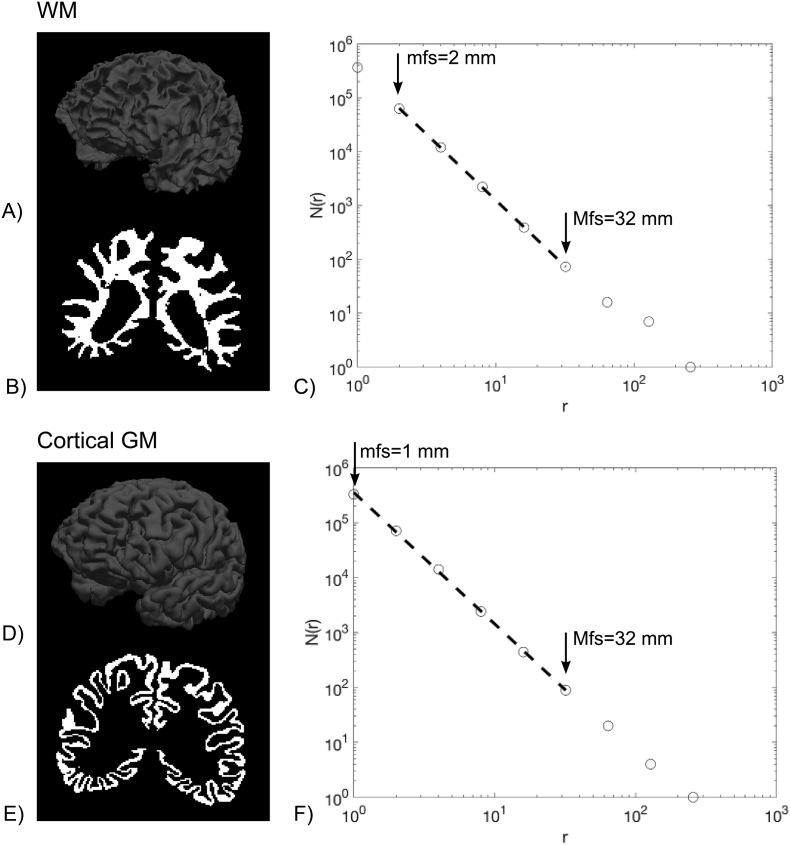
Generally, a brain structure shows its fractal properties in an interval of spatial scales, which is unknown a priori. Therefore, in this study, we applied an automated selection of spatial scales, for each brain region, looking for the interval in which the linear regression exhibits the best fit, as determined by the highest coefficient of determination (adjusted for the number of data points) R²_adj using the same approach adopted previously (Marzi et al., 2018). Both the minimum fractal scale (mfs) and the maximum fractal scale (Mfs) of WM and cortical GM have been also considered as potential predictors of cognitive scores. An example of a WM and a cortical GM segmentation mask in one patient with SVD and MCI is shown in Fig. 2.

Fig. 2.

Example of a WM and a cortical GM segmentation mask in one patient with SVD and MCI. A) A 3-D view of the GM/WM interface surface; B) A coronal slice of the WM volume mask; C) The log-log plot of N(r) counts vs. cube side r (mm) is shown for the cerebral WM volume mask. The regression line, which showed the highest R²_adj (0.9999) and a sign changed slope (i.e., FD) equal to 2.4530, is also superimposed. The WM mfs was 2¹ = 2 mm and the WM Mfs was 2⁵ = 32 mm; D) A 3-D view of the pial surface; E) A coronal slice of the GM volume mask; F) The log-log plot of N(r) counts vs. cube side r (mm) is shown for the cortical GM volume mask. The regression line, which showed the highest R²_adj (0.9996) and a sign changed slope (i.e., FD) equal to 2.4429, is also superimposed. The GM mfs was 2⁰ = 1 mm and the GM Mfs was 2⁵ = 32 mm.

To assess the accuracy of our method for the computation of the FD using an automated selection of the spatial scales, the proposed implementation has been preliminarily applied to binary synthetic volumetric images with known FD, obtaining a percentage relative error < 3% (see Supplementary Appendix and Supplementary Table 1). The FD computation was implemented in custom scripts developed in C++ and Bash languages and in MATLAB environment (R2018a, MathWorks, Natick, MA, USA) under a Linux operating system.

2.5. Descriptive statistics and between-group analysis

Descriptive analyses were carried out to characterize the sample in terms of socio-demographic, cognitive scores and neuroimaging features. We also compared WM and GM volumes, fractal dimensions and minimum and maximum scales between healthy controls and patients using a Mann Whitney test corrected for multiple comparisons with the Holm-Bonferroni procedure (to control the family-wise error rate) using a corrected significance p-value <.05.

2.6. LASSO regression

We fitted a separate regression model for each neuropsychological test. In particular, we studied the potential of all neuroimaging features (see Fig. 1) in predicting cognitive adjusted scores using the least-square linear regression with regularization by the L¹-norm (LASSO regression method) (Hastie et al., 2013). In detail, we determined the fitted regression coefficients β^ by minimizing the residual sum of squares plus a penalty term proportional to the L¹-norm of the coefficients:

${\beta }^{^}\left(\alpha \right)=arg\underset{\beta }{min}\left(\frac{1}{2N}\parallel y-X\beta {\parallel }_2^2+\alpha \parallel \beta {\parallel }_1\right)$,where α is a positive weighting parameter on the L¹ penalty, X the vector of explanatory variables (neuroimaging and demographic features), ∥∥₁the L¹-norm, ∥∥₂ the L²-norm and N the number of samples (patients) used for fitting. The α penalty weights the degree of sparsity, so that higher values of α enforce sparsity in the regression coefficients, i.e., drive more coefficients in the model to be exactly zero. In this way, the regression fit and feature selection are carried out at the same time.

For each model, in order to reduce the possibility of overfitting and for hyperparameter (α weight) optimization, the regression task was performed in a nested 10-fold cross-validation (CV) loop (Mueller and Guido, 2017). In this procedure, for each fold of the outer 10-fold CV, the training set is used for an inner 10-fold CV in order to evaluate the performance of the inner classifier while varying the α penalty term in the set {h × 10^p, 1}, where h = {1, 2, …, 9} and p = {−4, −3, −2, −1}. Once α value that minimized the out-of-sample prediction error (Hastie et al., 2013) has been found in the inner CV, the model with that α value is re-trained on the outer training set and tested on the test set kept out from the outer CV. This procedure is repeated for each fold of the outer CV. Before each training of the LASSO regression (both in the inner and in the outer CV), each feature was standardized with reference to the training set only. Test set data were not used in any way during the learning process, thus preventing any form of peeking effect (Diciotti et al., 2013). Performance was quantified in terms of the Pearson correlation coefficient between predicted and actual values of the neuropsychological test computed on the test set of the outer CV.

Since the selected features may vary depending on how the data are split in each fold of the CV, for each neuropsychological test, we repeated the nested CV procedure 1000 times recording the frequency that each feature was selected and the sign of the regression coefficient estimates from each fold of the round of the outer CV. In fact, the frequency of selection of a feature indicates to what extent that feature is more likely to be included in the model and the 1000 repetitions allow investigating a robust statistical association between neuropsychological scores and features. Average and standard deviation of the results from all repetitions (correlation coefficients r between real and predicted labels in the test set of the outer CV) were computed to get a final model assessment score.

For each neuropsychological test, statistical significance of prediction performance was determined via permutation analysis – recommended especially when the sample size is small (Noirhomme et al., 2014). Thus, for each neuropsychological test, 5000 new models were created using a random permutation of the labels (i.e., neuropsychological scores), such that the explanatory variables were dissociated from its corresponding neuropsychological score, to simulate the null distribution of the performance measure against which the observed value was tested (Nichols and Holmes, 2002). Correlations were considered significant if the p-value computed using permutation tests was <0.05.

We used own code developed in Python programming language (release 3.7.1, available at https://www.python.org/) for data analysis. In particular, the linear regression model was implemented by using the LassoCV function of the scikit-learn module (version 0.20.1).

3. Results

The computational analyses performed for the extraction of advanced neuroimaging features were carried out on a Dell PowerEdge T620 workstation equipped with two 8-core Intel Xeon E5–2640 v2, for a total of 32 CPU threads, and 128 GB RAM, using the Oracle Grid Engine batch-queuing system. For each subject, the processing time required approximately 30 min for the quantification of WM lesions volume, 9 h of a single core CPU time (with additional ~5 h after each manual editing) for FreeSurfer segmentation, and about 2 min for the calculation of both WM FD and GM FD. The total computation time for the 1000 nested CV loop and 5000 random permutations for all neuropsychological tests was about 3 h on a single core of a Linux workstation equipped with a 4-core (8 threads) INTEL i7-7700K CPU and 64 GB RAM.

3.1. Descriptive statistics and between-group analysis

Distributions of the neuropsychological tests mean and SD adjusted scores, and percentages of patients with an abnormal performance in each test are shown in Table 1. Four patients did not complete the TMT-A and one the immediate copy of the ROCF. Percentage of abnormal performance in all tests ranged from 39 to 47%, except for the Rey–Osterrieth Complex Figure, with an abnormal performance in 78% of patients.

Table 1.

Distributions of the neuropsychological tests adjusted scores and of percentages of patients with an abnormal performance.

Neuropsychological test	Number of patients	Patients with an abnormal performance (%)	Mean (standard deviation)	Min, max
Montreal cognitive assessment	64	28 (44%)	20.6 (4.5)	11.95, 29.29
Visual search	64	27 (42%)	31.8 (8.5)	14.3, 50.17
Symbol digit modalities test	64	27 (42%)	36.9 (9.6)	22.02, 59.04
Color word stroop test	64	30 (47%)	38.5 (28.7)	−3.45, 155.09
Trail making test - part A	60	25 (39%)	62.3 (46.4)	3.77, 202.2
Rey–osterrieth complex figure (immediate copy)	63	49 (78%)	22.9 (8.3)	4, 36

Descriptive statistics of neuroimaging features and available comparisons between healthy subjects and patients with SVD and MCI have been reported in Table 2. All features extracted using fractal analysis (minimum scale, maximum scale, and FD) of both WM and cortical GM in patients have also been listed in the Supplementary Table 2.

Table 2.

Descriptive statistics of neuroimaging features [mean (SD), minimum and maximum values], and comparisons between healthy subjects and patients with SVD and MCI.

		Feature	Healthy subjects (N = 24)	Patients with SVD and MCI (N = 64)b	P-value (corrected)
Standard features	Visual rating	Lacunar infarcts (categorical)c	0	2.09 (0.81) [1–3]	NA
		Microbleeds (number)	–	1.27 (3.71) [0–18]	NA
		EPVS basal ganglia (categorical)°	–	1.72 (0.77) [0–4]	NA
		EPVS centrum semiovale (categorical)°	–	1.77 (0.77) [1–3]	NA
	Quantitative	WM lesion load (unitless)	–	0.07 (0.05) [0.01–0.20]	NA
Volumes		GM volume (unitless)	0.24 (0.02) [0.21–0.28]	0.23 (0.02) [0.20–0.27]	0.002 (0.015)a
		WM volume (unitless)	0.30 (0.02) [0.25–0.32]	0.29 (0.02) [0.24–0.34]	0.040 (0.161)
Fractal analysis		GM FD (unitless)	2.4407 (0.0203) [2.4010–2.4819]	2.4359 (0.0167) [2.3969–2.4746]	0.097 (0.120)
		GM mfs (mm)	1.83 (0.64) [1–4]	2.13 (0.50) [2–4]	7 × 10−4(0.006)a
		GM Mfs (mm)	31.3 (3.27) [16–32]	31.5 (2.81) [16–32]	0.412 (0.412)
		WM FD (unitless)	2.4874 (0.0311) [2.4135–2.5297]	2.4650 (0.0341) [2.3960–2.5316]	0.002 (0.015)a
		WM mfs (mm)	1.67 (0.48) [1–2]	1.48 (0.50) [1–2]	0.070 (0.120)
		WM Mfs (mm)	16.67 (3.27) [16–32]	20.25 (7.12) [16–32]	0.011 (0.054)

EPVS = enlarged perivascular spaces, FD = fractal dimension, GM = gray matter, Mfs = maximum fractal scale, mfs = minimum fractal scale, N = number of participants, NA = not applicable, SD = standard deviation, WM = white matter. WM and GM volumes are normalized to the estimated intracranial volume.

^aSignificant at a Mann Whitney test corrected for multiple comparison with the Holm-Bonferroni procedure (to control the family-wise error rate) using a corrected significance p-value <.05.

^bExcept for microbleeds, where N = 63.

^c0 = (absent), 1 = (1–3), 3 = (>3).° 0 = (absent), 1 = (≤10), 2 = (11–20), 3 = (21–40), 4 = (≥40). - = not measured.

As compared to healthy controls, the group of patients with SVD and MCI showed significantly reduced WM FD and GM normalized cortical volume and increased minimum spatial scale of GM.

3.2. LASSO regression

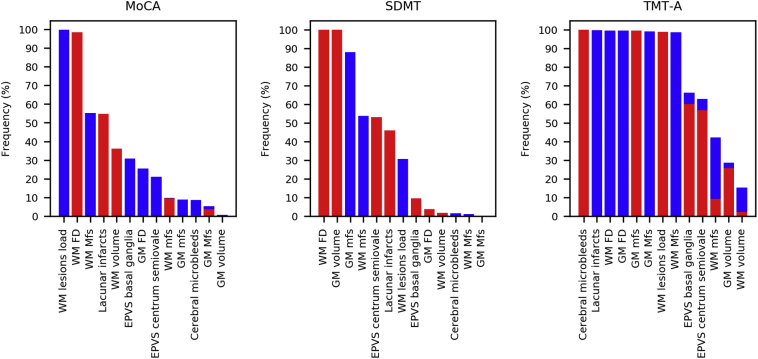
In Table 3, the results obtained for all LASSO regression models are displayed. We found that the statistically significant models were those for MoCA (r = 0.321, p-value = .039), SDMT (r = 0.324, p-value = .039) and TMT-A (r = 0.354, p-value = .025). Significant prediction above-chance of these scores was obtained using different sets of neuroimaging features. A ranking of all neuroimaging features according to the LASSO feature selection frequency is shown in Fig. 3. The average frequency, among significant models (MoCA, SDMT and TMT-A scores), with which each feature was selected (regression coefficient different from zero) across all outer CV folds in 1000 repetitions of LASSO regression is shown in Fig. 4. The WM FD was the most frequent feature consistently selected in the significant models.

Table 3.

Mean and standard deviation of the Pearson coefficient of correlation r between the LASSO predicted values of the test set of the outer CV and the actual values using 1000 repetitions of the nested 10-fold CV. P-values indicate the probability that the empirical r score could arise by chance. They have been computed using 5000 permuted-data CV scores simulating the null distribution.

Neuropsychological test	Mean r (SD)	p-value
MoCA	0.321 (0.079)	0.039⁎
Visual search	0.106 (0.091)	0.318
SDMT	0.324 (0.073)	0.039⁎
TMT-A	0.354 (0.094)	0.025⁎
Stroop	0.222 (0.082)	0.106
ROC-F immediate copy	0.295 (0.090)	0.090

MoCA, montreal cognitive assessment; ROC-F, Rey–Osterrieth complex figure; SD, standard deviation; SDMT, symbol digit modalities test; TMT-A, trail making test - part A.

^⁎Significant at the permutation-test using a significant p-value <.05.

Fig. 3.

Ranking of LASSO-based neuroimaging feature selection. For each significant model, the frequency with which each feature was selected (coefficient different from zero) across all outer CV folds in 1000 repetitions of LASSO regression is shown. The features have been reordered based on the occurring average frequencies. Red bars indicate the frequency with which the corresponding coefficient was positive (direct association with the neuropsychological scores) – whereas blue bars, the frequency with which the corresponding coefficient was negative (inverse association with the neuropsychological scores).

Fig. 4.

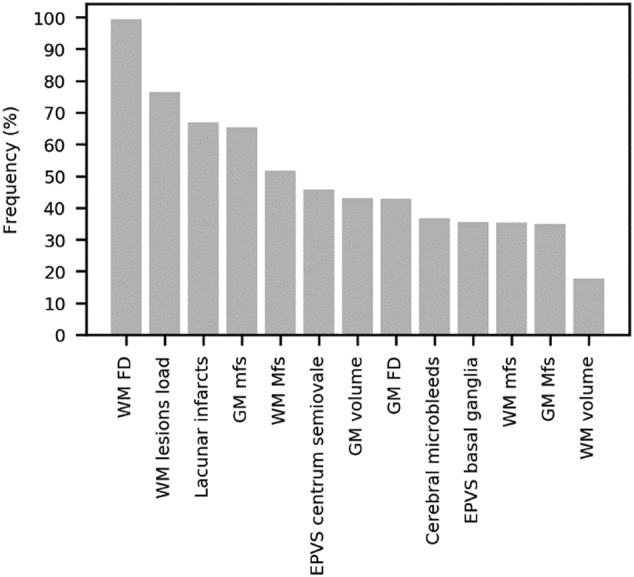
The average frequency among MoCA, SDMT and TMT-A tests with which each neuroimaging feature was selected (coefficient different from zero) across all outer CV folds in 1000 repetitions of LASSO regression among MoCA, SDMT and TMT-A tests is shown.

Finally, Table 4 shows the neuroimaging features selected with frequency > 80% based on 1000 repetitions of the nested CV along with the direction (positive/negative) of the most frequent sign of the corresponding regression coefficient. The WM FD was the only feature consistently selected in all three models.

Table 4.

Neuroimaging features selected with frequency > 80% based on 1000 repetitions of the nested cross-validation along with the direction (positive/negative) of the most frequent sign of the regression coefficient have been reported. For each neuropsychological test, the score interpretation has been also indicated.

Neuropsychological test	Cognitive scores interpretation (worst to best performance)	Relevant features
MoCA	Low to high values	WM FD (+), WM lesions load (−)
SDMT	Low to high values	WM FD (+), GM volume (+), GM mfs (−)
TMT-A	High to low values	Cerebral microbleeds (+), Lacunar infarcts (−), WM FD (−), GM FD (−),GM mfs (+), GM Mfs (−), WM lesions load (+), WM Mfs (−)

MoCA, montreal cognitive assessment; SDMT, symbol digit modalities test; TMT-A, trail making test - part A.

(+): a positive direction of the regression coefficient sign indicating a direct association.

(−): a negative direction of the regression coefficient sign indicating an inverse association.

4. Discussion

4.1. Potentials of WM FD in predicting cognitive performance in patients with SVD and MCI

In this study of patients with SVD and MCI, we used the capability of machine learning in predicting neuropsychological scores on tests sensitive to attention and executive dysfunctions. We found that WM FD was, on average, the feature most consistently selected for predicting neuropsychological scores among the statistically significant models. The WM FD was significantly reduced in patients with SVD and MCI as compared to healthy controls. Also, among the significantly predicted scores, we observed that the trend of the relationship between the WM FD and cognitive performance is univocal. Accordingly, a decrease in WM FD, i.e., a reduction of structural complexity of WM, was associated with a worsening in cognitive performance. It is conceivable that cognitive impairment observed in patients with subcortical WM damage associated with SVD derives from the effect of a diffuse cortical-subcortical disconnection syndrome rather than from a localized mere tissue loss. Of note, in our study, the WM volume was a negligibly selected feature - the latest in feature ranking. We submit the hypothesis that FD represents a marker of global disarrangement of the WM in SVD patients. These pieces of evidence are in line with a previous study in healthy subjects in which individuals with reduced WM FD had lower intelligence scores and more age-related cognitive decline (Mustafa et al., 2012).

As compared to healthy controls, the group of patients with SVD and MCI also showed a significantly higher minimum spatial scale of the cortical GM, automatically determined by the fractal analysis. Consistently, in the patient group, the GM mfs increased when cognitive performance was worsened. A recent study analyzed the minimum and maximum spatial scales in healthy subjects (Krohn et al., 2019). Although ours and Krohn et al. studies differ for some methodological and pre-processing differences, we observed a similar preference of the automatic selection of spatial scales for smaller minimal scales and shorter interval lengths (number of data points employed in the selected scale range). Indeed, in the patient sample, the most frequent combinations were, for WM, mfs = 1 mm and interval length = 5 data points and mfs = 2 mm and interval lenght = 4 data points, while, for GM, mfs = 2 mm and interval length = 5 data points (see Supplementary Table 2). However, further studies are needed to investigate the impact of each disease condition on the spatial scales. In our patient sample, we hypothesize that the behavior of the GM mfs might reflect an initial disruption of the cortical GM – which is known to be present in this patient population (Wardlaw et al., 2013), and is also in line with the reduced GM normalized cortical volume – at a finer spatial scale.

4.2. WM FD as a feature of structural complexity

The WM FD assumes a fractional value between 2 and 3, capturing the structural complexity of a highly complex object which fills the space more than a smooth surface (2-dimensional), but less than a filled volumetric structure (3-dimensional). In our study, we observed a mean FD of cerebral WM of 2.4650 in patients with cerebral SVD and MCI that was significantly lower than that observed in healthy controls. The WM FD has been also computed in other neurological diseases. Esteban et al. demonstrated that the cerebral WM FD was lower in patients with multiple sclerosis as compared to controls (Esteban et al., 2007; Esteban et al., 2009). In another study, the FD of the cortical GM/WM interface was significantly reduced in patients with epilepsy (Cook et al., 1995). Multifractal properties of WM abnormalities in healthy elderly subjects have also been recognized in T₂-weighted images (Takahashi et al., 2009), also in in relation to early-stage atherosclerosis (Takahashi et al., 2006).

Similarly to the FD of the cortical ribbon (King et al., 2010), the value of the WM FD may depend not only on volumetric changes of subcortical WM, but also on volumetric changes of basal ganglia and lateral ventricles. This is due to the fact that both FDs (of cortical ribbon and WM) are affected by alterations of the GM/WM interface. Ventricular enlargement of lateral ventricles has been described in patients with SVD (Jokinen et al., 2012). We are not aware of studies reporting basal ganglia volume loss in SVD even though this possibility might exist.

4.3. FD as a complementary feature in the SVD research field

Our results suggest that the WM FD might be a marker of cognitive performance in patients with SVD and MCI. This result has potentially relevant implications. In fact, FD is a measurement that can be computed in the field of SVD research using standard high-resolution T₁-weighted imaging and does not require further dedicated acquisitions. We observed that also other features obtained from quantitative neuroimaging procedures (e.g., WM lesion load) provided predictive value beyond what is available from visual rating of standard features in SVD, which are likely to be easier and less expensive to assess.

Besides WM FD, neuroimaging features frequently selected (> 80%) in our sample of SVD MCI patients included WM lesions load, GM volume, GM mfs, cerebral microbleeds, GM FD, lacunar infarcts, WM Mfs and GM Mfs. Of note, the degree of importance of these features varied across different neuropsychological scores. Overall, the results suggest that the models for prediction of MoCA and SDMT scores are sparser as compared to that obtained for TMT-A. As expected, due to the inherent complexity of the behavioral measurement of cognitive performance, the obtained results also support the view that more than one neuroimaging feature is needed to reliably predict cognitive scores in this patient population and that, in general, different sets of features may be required to predict different scores. This is in accordance with the fact that these features quantify complementary aspects of SVD-related modifications occurring in the brain. In particular, the joint analysis through the FD and brain volumes might provide greater prediction abilities than the use of each measurement separately (King et al., 2009). In fact, it is well known that the FD and volume examine and quantify different structural aspects, thus generally being complementary to each other (Farahibozorg et al., 2015; Free et al., 1996; King et al., 2009).

Taken together, our data suggest that different neuroimaging tools should be used when evaluating the cerebral cortex and the subcortical WM to obtain significant outcomes.

4.4. Methodological considerations

We explored predictive abilities of a wide set of standard and advanced neuroimaging features with a machine learning approach (using the out-of-sample error), in line with the goals of achieving the clinical diagnosis on an individual basis. This approach is different from the conventional linear regression analysis applied to the entire data set in which the possibility of overfitting may not be negligible. In particular, we used LASSO regression in order to perform, at the same time, a multivariate linear regression and feature selection.

Considering the exploratory nature of our study, mainly aimed at evaluating the possible role of WM FD as an additional MRI marker potentially associated with cognitive performance in SVD, we repeated the same model of analysis on several cognitive tests to explore the consistency of the associations across 1) different measurements within the same cognitive domain and 2) several rounds of a nested CV loop (1000 repetitions). In particular, we chose a 10-fold CV because it offers a favorable bias-variance trade-off (Hastie et al., 2013; Lemm et al., 2011) and is also adequate for model selection (Breiman and Spector, 1992). Fitting all neuropsychological scores simultaneously into a single comprehensive model could also be carried out, but it would probably require a larger dataset in order to learn the different and complex pattern of associations among neuropsychological scores and neuroimaging features.

We considered the main standard features in SVD research in order to take into account important explanatory variables in the models, such as the WM lesion load (accounting for lesions extent), cerebral microbleeds, EPVS, and lacunes. WM and GM volumes have been introduced in the analysis to further consider the impact of macroscopic structural alterations, such as brain atrophy, on cognitive performance. The effect of age, sex, and education has been accounted for using neuropsychological scores corrected according to normative data and using demographic variables as predictors in the models to account for potential residual effects in the patient population. We used both standard and advanced neuroimaging features; in particular, we adopted an algorithm for the estimation of the FD using an automated selection of the spatial scales (Marzi et al., 2018), which showed good accuracy on synthetic structures.

We feel that the fact that both mfs and Mfs vary across patients with SVD and MCI does not limit the between-scan comparability. In fact, each patient has been studied in his/her optimal range of spatial scales, automatically determined according to the maximization of a best-fit regression. Moreover, spatial scales are 1-D measurements like cortical thickness and we feel that spatial scales should not be normalized, following recommendations suggested for cortical thickness (Ad-Dab'bagh et al., 2005; Schwarz et al., 2016). However, future studies should examine this aspect in more detail.

4.5. Limitation and future developments

We enrolled a rather small number of patients. Therefore, our results need to be confirmed in other studies using independent and larger samples. The number of included patients also restricted the possibility of performing analyses with a larger number of neuropsychological tests assessing also different cognitive domains, and with a larger set of neuroimaging features. We thus decided to limit our analyses to tests known to assess cognitive functions that are mainly affected in patients with subcortical vascular disease and using a limited number of features. Admittedly, a more extensive neuropsychological evaluation could offer a more complete appreciation of the respective role of the WM FD and other neuroimaging features in outlining cognitive deficits in patients with SVD.

Our results suggest that, in a sample of patients with SVD and MCI, a set of neuroimaging features (in which the WM FD was the most relevant) predicts cognitive performance and we feel that this is important per se for the SVD research field. At present, we are not able to assess if such significant predictions are due to the SVD and/or MCI condition. This could be investigated in future studies in which a sample of patients with SVD only, a sample of patients with MCI only, and a group of healthy controls will be examined using the same MRI scanner and protocols and the same neuropsychological battery. A larger sample group of healthy subjects would be also valuable for a deeper investigation of possible associations of mfs and Mfs with aging or cognition.

Future studies using longitudinal patient evaluations will investigate whether WM FD might represent an earlier marker of WM damage.

Finally, in our study, we computed the FD of the general structure of the WM. Future studies may explore the structural complexity of the WM surface and WM skeleton. In particular, the skeleton retains peculiar characteristics of the WM morphology (Liu et al., 2003) with a reduced influence of atrophic changes of WM or surrounding brain regions which may increase the variance of the FD estimates in the sample population (Krohn et al., 2019). A joint FD analysis of WM general structure, surface and skeleton may thus more completely characterize the structural complexity of WM in both normal aging and neurological diseases (Zhang et al., 2007).

5. Conclusions

We showed that a machine learning approach could be useful in SVD using standard and advanced neuroimaging features. Our study results raise the possibility that FD may represent a consistent feature in predicting cognitive decline in SVD that can complement standard imaging and clinical features in SVD.

The following are the supplementary data related to this article.

Supplementary Table 1

Theoretical Hausdorff-Besicovitch FD and FD measured through the algorithm using automated selection of spatial scales. Adjusted coefficients of determination R_adj² are also reported, showing the excellent fit of the regression lines in the log-log plane.

Supplementary Table 2

WM and GM FD, minimum spatial scale, maximum spatial scale and coefficient of determination adjusted for the number of data points (R²_adj) computed using the automated selection of spatial scales are shown for patients with SVD ad MCI.

Supplementary material

Funding sources

The VMCI-Tuscany study was funded by Tuscany region. Salvadori was supported by a project funded by Tuscany region and Health Ministry under Grant Aimed Research Call 2010 (Bando Ricerca Finalizzata 2010, Grant number: RF-2010-2321706, ClinicalTrials.gov Identifier: NCT02033850). We thank the nonprofit organization Associazione per la Ricerca sulle Demenze (ARD) ONLUS (Department of Neurology, Luigi Sacco Hospital, Milan, Italy) for supporting dissemination costs.

Declaration of Competing Interest

None.