Processivity, Velocity, and Universal Characteristics of Nucleic Acid Unwinding by Helicases

Abstract

Helicases are components of the cellular replisome that are essential for unwinding double-strand nucleic acids during the process of replication. Intriguingly, most helicases are inefficient and require either oligomerization or assistance from other partner proteins to increase the processivity of unwinding in the presence of the replication fork, which acts as a barrier to progress. Single-molecule force spectroscopy has emerged as a promising experimental technique to probe how relieving this barrier on the helicase can allow for increased efficiency of unwinding. However, there exists no comprehensive theoretical framework to provide unique interpretations of the underlying helicase kinetics from the force spectroscopy data. This remains a major confounding issue in the field. Here, we develop a mathematical framework and derive analytic expressions for the velocity and run length of a general model of finitely processive helicases, the two most commonly measured experimental quantities. We show that in contrast to the unwinding velocity, the processivity exhibits a universal increase in response to external force, irrespective of the underlying architecture and unwinding kinetics of the helicase. Our work provides the first, to our knowledge, explanation to a wide array of experiments and suggests that helicases may have evolved to maximize processivity rather than speed. To demonstrate the use of our theory on experimental data, we analyze velocity and processivity data on the T7 helicase and provide unique inferences on the kinetics of the helicase. Our results show that T7 is a weakly active helicase that destabilizes the fork ahead by less than 1 k_BT and back steps very frequently while unwinding DNA. Our work generates fundamental insights into the force response of helicases and provides a widely applicable method for inferring the underlying helicase kinetics from force spectroscopy data.

Significance

How helicases effectively unwind double-stranded nucleic acids is not well understood. The dynamics of helicases is often probed by varying the barrier to nucleic acid unwinding in force spectroscopy experiments. To analyze such experimental data, here, we develop a general model of finitely processive helicases with arbitrary step size and interaction range and predict a universal response of processivity to force. We demonstrate the utility of our model by analyzing experiments on the T7 helicase and uniquely identifying T7 as a weakly active helicase that back steps frequently in the presence of the replication fork. Our results suggest that by mimicking force effects, oligomerization or interaction with partner proteins lead to increased helicase processivity, but not necessarily the unwinding velocity.

Introduction

Helicases are enzymes that play an important role in almost every aspect of RNA and DNA metabolism (1, 2, 3, 4, 5, 6, 7). This class of molecular motors utilizes free energy from ATP or dTTP hydrolysis to translocate directionally over single-strand (ss) nucleic acids (8, 9, 10). In this respect, they are similar to other motors like kinesin and myosin, which also predominantly exhibit directional motion on microtubules and actin filaments, respectively (11, 12). In addition, some helicases can also couple ss translocation with unwinding of double-strand (ds) nucleic acids, thus playing a crucial role in cellular functions like replication, recombination, and DNA repair. The “processive, zipper-like” ds unwinding activity was first demonstrated by Abdel-Monem et al. (13) in Escherichia-coli-based DNA helicase in 1976. Interestingly however, most helicases cannot unwind double strands of nucleic acids by themselves and require either oligomerization or assistance from other partner proteins to increase the efficiency of processive unwinding (14, 15, 16). The fundamental principles governing this collaborative improvement of unwinding efficiency have not been fully elucidated.

A helicase that uses energy from ATP or dTTP hydrolysis to destabilize the ss-ds nucleic acid junction is considered to be “active.” On the other hand, a helicase that utilizes the thermal fraying of the ds and opportunistically steps ahead when the downstream site is open is referred to as “passive” (2). Considerable effort has been devoted to classifying various helicases into these two categories because this description provides an intuitive idea of the mechanism of nucleic acid unwinding and could explain why many helicases are inefficient at unwinding nucleic acids by themselves (17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27). Earlier work used bulk kinetic assays or analysis of crystal structures to classify the activity of helicases (18, 19, 20), whereas more recent studies have primarily resorted to single-molecule experiments coupled with theoretical frameworks to establish the mode of unwinding of various helicases (23, 24, 25, 26, 28, 29, 30).

Although ascertaining whether a helicase is active or passive is difficult and remains a controversial question for a number of helicases, we recently used this description in a quantitative framework to predict some surprisingly universal characteristics, which are independent of the dsDNA sequence (31). By generalizing the original mathematical framework introduced by Betterton and Jülicher (32, 33, 34), we predicted that the processivity of active and passive helicases should always increase in response to external forces applied equally to the two complementary single strands of dsDNA or dsRNA in the hairpin geometry (31). This intriguing prediction was later validated in the Pif1 and RecQ helicases (35, 36). Unlike the processivity, the velocity of unwinding, however, shows no such universal behavior and exhibits a variety of responses to external force depending on whether the helicase is active or passive (31). In our earlier work, we solved for the velocity and processivity of a helicase (with both the step size and interaction range equal to one basepair) taking the sequence of DNA into account using numerically precise solutions. Here, we use a physically motivated approximation scheme to derive analytical expressions for both the velocity and processivity of a model that also accounts for a general step size and interaction range. Similar models accounting for a nonzero step size and interaction range have been used to study the velocity of unwinding using numerical simulations, without the benefit of easy to use analytical expressions (26, 37). These expressions allow us to demonstrate the universality of the nature of the response of processivity to force, enabling us to draw far-reaching conclusions on the evolution of helicases to optimize the number of basepairs that are unwound.

The analytic results derived here also allow us to analyze single-molecule experimental data on helicases more precisely than attempted before by simultaneously analyzing the velocity and processivity of a particular helicase instead of merely the velocity. As in our earlier work (31), our focus here remains on the hairpin geometry of the dsDNA or dsRNA in which equal amounts of force are applied in opposite directions on the complementary strands. In the framework introduced by Betterton and Jülicher (32, 33, 34) (and its variants), force or sequence dependence of the unwinding velocity had previously been fit to experimental data to determine the nature of T7, T4, and NS3 helicases (23, 24, 25, 26). However, Manosas et al. (37) pointed out that the multiparameter fit of the Betterton and Jülicher (32, 33, 34) model to velocity data is not robust, with different parameter sets fitting the data equally well. More disturbingly, the various best-fit parameter sets suggest completely different unwinding mechanisms and fail to provide any conclusive results for the fitting parameters. This is especially problematic when parameters like the step size and the potential backstepping rate have not been characterized experimentally for a particular helicase and need to be estimated from fits of the theory to data. As a consequence, the literature on helicases is rife with contradictory claims about the mechanism of action of a specific helicase. For instance, steady-state and pre-steady-state kinetic assays (38) as well as studies of crystal structures (18) determined that NS3 helicase is passive, whereas a single-molecule experiment coupled with a mathematical analysis suggested that NS3 is active (23). Similarly, the T7 helicase was deemed to be an active helicase in two previous works (24, 26), whereas simple physical arguments suggested that T7 is passive (37). Here, we show that our theory, which is used to simultaneously analyze velocity and processivity data, can be used to robustly obtain the values of all the parameters associated with the unwinding activity of a helicase. Using data on the T7 helicase as a case study, we use our theory to explain both the force response of velocity and processivity, and in the process, we quantitatively show that T7 is very weakly active. Further, we recapitulate a number of independent experimental results on T7, thus confirming that the model is a good description of the helicase. Our theory also shows that an externally applied force, which in vivo could be generated by binding of ss partner proteins, results in an increase in processivity in all helicases, regardless of whether they are active or passive. This important finding prompts us to propose that helicases may have evolved to optimize processivity rather than speed.

Materials and Methods

Theoretical model for nucleic acid unwinding helicases

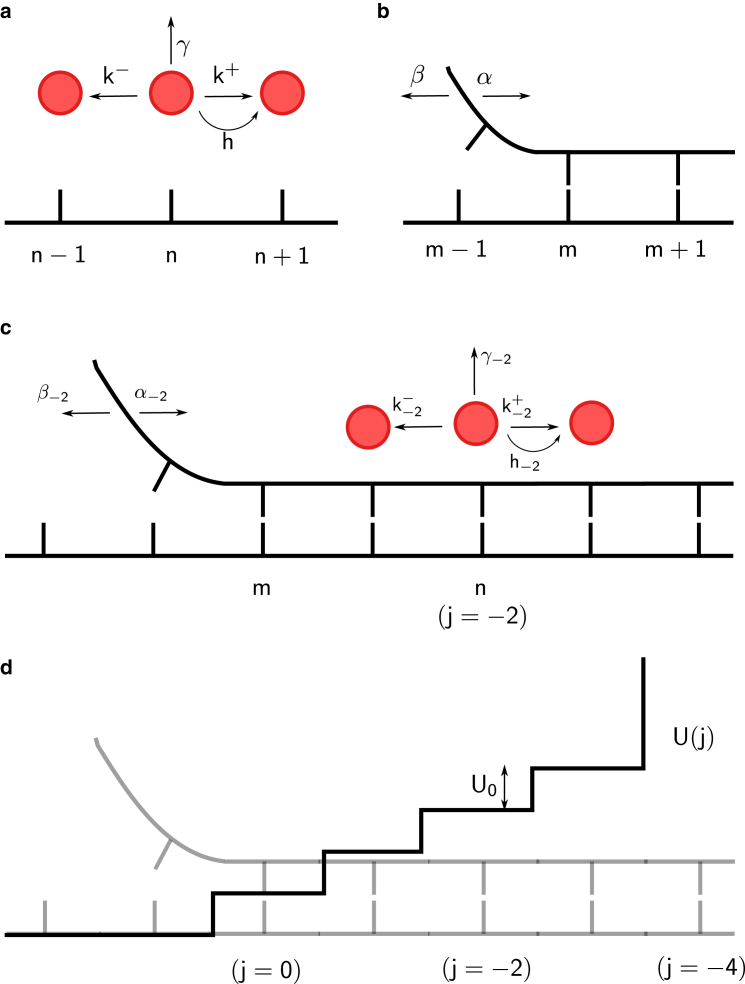
The model, shown in Fig. 1, is a generalization of the one introduced by Betteron and Jülicher (32, 34) that accounts for the finite processivity of the helicase and allows for an arbitrary step size and a general interaction range between the helicase and the ds. Fig. 1 a shows the helicase (red solid circles) as it translocates on the ss nucleic acid strand (depicted as a bold black line). The position of the helicase on the nucleic acid track is denoted by n. The helicase can exhibit pure diffusion and hence can step to the right or left with equal rate k⁺ = k⁻ = k. When the NTP hydrolyzes, the helicase moves forward at a rate h where h > k, thus resulting in a net forward rate h + k, whereas the backward rate is k. If the mechanical step size of the helicase is s, then every time the motor steps forward or backward it does so by s nucleotides, resulting in an average velocity along the ss given by V_ss = sh. The helicase could also disengage from the nucleic acid track with a dissociation rate, γ.

Figure 1.

Model of nucleic acid unwinding by a helicase. (a) Single-strand (ss) stepping kinetics of the helicase are shown. (b) Double-strand (ds) thermal “breathing” is shown. (c) Modification of stepping kinetics of the helicase and breathing rates of the ds are shown. (d) The interaction potential that causes the modification of rates in (c) is shown. To see this figure in color, go online.

Fig. 1 b represents the ss-ds junction at position m. The basepair at the junction can rupture at a rate α (increasing m to m + 1), whereas a new basepair can form (decreasing m to m − 1) at rate β such that α/β = exp(−ΔG), where ΔG is the stability of the particular ds basepair. All energies in this article are in units of k_BT.

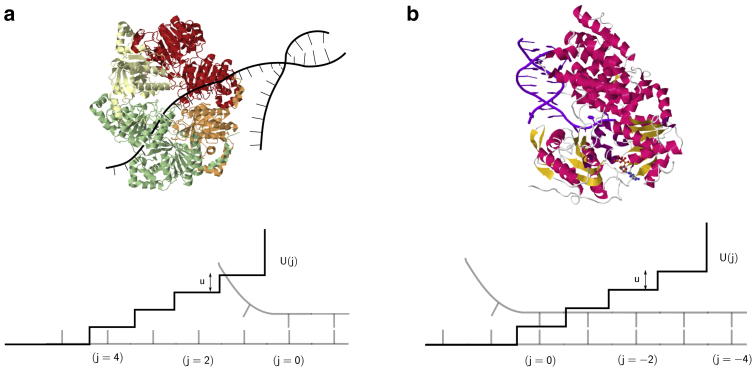
Fig. 1 c shows how the rates change when the helicase and the junction approach each other. Modifications of the original rates occur because of the interaction potential U (j), a particular example of which is shown in Fig. 1 d. As the helicase and junction approach each other, they interact. As a result, the helicase has to perform extra work, which is U₀ per basepair to step forward. This energy is provided from the hydrolysis of ATP. We follow the description in (33) and define$j\equiv m-n$ to be the difference in the positions of the junction and the helicase. The rates are modified depending on j, and this is indicated by the value of j as a subscript. For example, h₋₂ denotes the modified forward-stepping rate when j = −2 (Fig. 1 c). The motivation for allowing negative values of j and hence a potential as shown in Fig. 1 c comes from helicases like PcrA and NS3 (see Fig. 2 b). These helicases seem to physically interact with downstream basepairs of the ds (19, 23), possibly distorting and destabilizing a number of bases beyond the junction. Therefore, for a general scenario, we let the helicase interact with the ds over a range r of basepairs, after which a hard wall exists at j = −r. For ring helicases like T7, which encircle one strand of the DNA while excluding the other (39, 40), destabilization is not likely to happen by physical overlap with bases downstream of the junction (see Fig. 2 a) but might occur because of electrostatic interactions (41). For such helicases, j would always be positive with a hard wall at j = 0. Note that the exact position of the potential does not matter: a shifted potential with the first step at j = 4 and hard wall at j = 0 (Fig. 2 a) would give identical results for the velocity and processivity as the potential shown in Fig. 2 b. Hence, this model for the interaction range of the helicase is general. The short-range potential is chosen to have a constant step height U₀ and is defined as follows:

$$U\left(j\right)=\{\begin{array}{ll}\infty \hfill & j\le -r\hfill \\ \left(1-j\right)U_0\hfill & -r<j\le 0\hfill \\ 0\hfill & j>0.\hfill \end{array}$$ (1)

Figure 2.

Different scenarios for the interaction potential between the helicase and double strand (ds). (a) Crystal structure of T7 helicase (Protein Data Bank (PDB): 1E0J) and a cartoon of dsDNA are shown. The helicase encircles one strand and excludes the other, suggesting that the interaction with the junction must happen from a distance, presumably because of electrostatic forces. (b) Shown is the crystal structure of the PcrA helicase bound to dsDNA (PDB: 3PJR), showing the overlap of the helicase domains with bases beyond the junction. Shown below both the figures are the corresponding interaction potentials U(j). Identical expressions for the unwinding velocity and run-length result for both the potentials. To see this figure in color, go online.

The unwinding process in reality is likely governed by a number of additional energy scales besides U₀, for example, the interaction of the helicase with its partner proteins. However, our primary aim in this work is to model the interaction of the helicase with the ds-ss junction, which we assume to be most simply described by one energy scale. The validity of this simple assumption can of course only be tested after analyzing a variety of experimental data and verifying that inferred parameters are physically realistic. The results, as discussed below, show that this simple model is indeed sufficient to explain many aspects of force spectroscopy data on helicases. The nucleic acid breathing rates are modified because of this interaction as follows:

$$\begin{array}{l}{\alpha }_j=\alpha e^{-\left(f-1\right)\left(U\left(j\right)-U\left(j+1\right)\right)},\\ {\beta }_{j+1}=\beta e^{-f\left(U\left(j\right)-U\left(j+1\right)\right)},\end{array}$$ (2)

such that $\left({\alpha }_j/{\beta }_{j+1}\right)=e^{-\left(\mathit{\Delta }G-U_0\right)}$ for all values of j. In Eq. 2, f is a number between 0 and 1, representing the fractional position of the free-energy barrier between basepair open and basepair closed states from the open state. Nucleic acid opening takes the system from state j to state j + 1, whereas closing takes the system from j + 1 to j. Hence, the exponents in Eq. 2 involve the term U(j) − U(j + 1). The rates of the helicase also get modified because of the interaction and change as follows:

$$\begin{array}{l}{k}_j^{+}=k{e}^{-f\left(U\left(j-s\right)-U\left(j\right)\right)}\\ h_j=h{e}^{-f\left(U\left(j-s\right)-U\left(j\right)\right)}\\ k_{j-s}^{-}=k{e}^{-\left(f-1\right)\left(U\left(j-s\right)-U\left(j\right)\right)}\\ {\gamma }_j=\gamma e^{U\left(j\right)}.\end{array}$$ (3)

With a step size s, the helicase cannot move to the right if j ≤ s − r, and hence $k_j^{+}=h_j=0$ for all j ≤ s − r. Equation 3 shows that as long as the helicase and the ss-ds junction are separated by a distance j > s, the forward rates are independent of $U_0$: $k_j^{+}=k$ and h_j = h. For the backward rate, $k_j^{-}=k$ as long as j > 0. Notice that the exponents in Eq. 3 contain the term U(j − s) − U(j) because the helicase jumps s nucleotides every time it steps forward or backward.

Force effects on transition rates

To model the effect of a constant external force F applied directly to the ds junction in the unzipping direction, the ds opening and closing rates change from α_j, β_j to ${\alpha }_j^F$, ${\beta }_j^F$ such that

$$\begin{array}{c}\frac{{\alpha }_j^F}{{\beta }_{j+1}^F}=\frac{{\alpha }_j}{{\beta }_{j+1}}{e}^{\mathit{\Delta }{G}_F}\\ =e^{-\left(\mathit{\Delta }G-U_0-\mathit{\Delta }{G}_F\right)}\\ \equiv b{e}^{U_0},\end{array}$$ (4)

where we defined $b\equiv e^{-\left(\mathit{\Delta }G-\mathit{\Delta }{G}_F\right)}$, and ΔG_F is the destabilizing free energy of the basepair at the junction because of the constant external force F. Assuming a freely jointed chain (FJC) model for the ssDNA segments, the expression for ΔG_F is given as follows (42):

$$\mathit{\Delta }{G}_F=2\frac{L}{l}\text{log}\left(\frac{1}{Fl}\text{sinh}\left(Fl\right)\right),$$ (5)

where L is the contour length per base and l is the Kuhn length. In writing Eq. 4, we assume that all of the external force F is transmitted through the single strands and destabilizes the basepair at the junction. For ring-shaped helicases like T7, which encircle one strand while excluding the other (39, 40), this model is a very good description. However, this may not be an accurate description of other helicases like the NS3 in which the domains surround both the strands of the nucleic acid, and the junction may be protected to some extent from external forces (5). For such helicases, a more careful analysis is needed and is left for future work.

With the model thus defined, we need to solve for the velocity and the processivity of the helicase as it unwinds the ds nucleic acid. The velocity is defined as the average number of bases per unit time that the helicase moves to the right in a binding event. For the processivity, multiple definitions have been proposed (34). The mean binding time $\langle \tau \rangle$, the translocation processivity $\langle \delta n\rangle$, which gives the average distance moved by the helicase in a binding event, and the unwinding processivity $\langle \delta m\rangle$, which gives the distance moved by the ss-ds junction during a single binding event of the helicase, are used as measures of helicase processivity. As shown numerically in (34), the latter two definitions of processivity are almost identical when the helicase attaches close to the ss-ds junction. Because this is the physically relevant situation, as we argued previously (31), we will not differentiate between $\langle \delta n\rangle$ and $\langle \delta m\rangle$ in this work and refer to both as the run length or processivity.

Results

Unwinding velocity and run length: solution of the model

To solve for the velocity and run length of a finitely processive helicase, we first note that α and β are larger by orders of magnitude (43, 44, 45) than any rate describing the kinetics of the helicase. Therefore, even before the helicase takes a single step (backward, forward, or detach), the ss-ds junction would have opened and closed multiple times. As a result, the probability P_j of observing the helicase and junction at a separation j would have reached a steady-state distribution long before the helicase moves. Because there is a hard wall at j = −r, there is no probability current between j and j + 1 in this steady state for any value of j. This, along with the normalization condition, ${\sum }_j{P}_j=1$, allows us to solve for P_j as follows:

$$P_j=\{\begin{array}{ll}0\hfill & j\le -r\hfill \\ b^{r+j-1}{e}^{\left(r+j-1\right)U_0}{P}_{-r+1}\hfill & -r<j\le 1\hfill \\ b^{r+j-1}{e}^{r{U}_0}{P}_{-r+1}\hfill & j>1\hfill \end{array},$$ (6)

where

$$P_{-r+1}={\left[\frac{b^{1+r}{e}^{r{U}_0}}{1-b}+\frac{{\left(b{e}^{U_0}\right)}^{1+r}-1}{b{e}^{U_0}-1}\right]}^{-1},$$ (7)

where b, as defined before, is given by $\left(\alpha /\beta \right)e^{\mathit{\Delta }{G}_F}$. The two-body problem of the helicase and junction can now be recast in terms of a one-body problem involving only the helicase, moving with renormalized rates that we denote with a tilde (${\tilde{k}}^{+}$, ${\tilde{k}}^{-}$, $\tilde{h}$ and $\tilde{\gamma }$); ${\tilde{k}}^{+}$ is given by ${\tilde{k}}^{+}={\sum }_j{k}_j^{+}{P}_j$, and similar expressions describe all the other renormalized rates. Performing the sums, the final lengthy expressions for ${\tilde{k}}^{+}$, $\tilde{h}$, ${\tilde{k}}^{-}$, and $\tilde{\gamma }$ are given in Appendix A. Notice that although $k_{+}=k_{-}=k$, the helicase-junction interaction causes the renormalized rates to become different, hence ${\tilde{k}}^{+}\ne {\tilde{k}}^{-}$.

The unwinding velocity is given as follows:

$$v_{\text{unw}}=s\left(\tilde{h}+{\tilde{k}}^{+}-{\tilde{k}}^{-}\right).$$ (8)

For s = 1 and r = 1, v_unw reduces to

$$v_{\text{unw}}^{\mathrm{1,1}}=\frac{e^{-\left(f-1\right)U_0}\left(1+b\left(e^{f{U}_0}-1\right)\right)\left(b\left(h+k\right)-k\right)}{1+b\left(e^{U_0}-1\right)}.$$ (9)

The expression for one-step active unwinding derived by Betterton and Jülicher (Eq. 27 in (33)) reduces to our expression in Eq. 9 when all the rates associated with the helicase are neglected compared to α and β.

The mean attachment time of the helicase $\langle \tau \rangle$ is given by the inverse of the renormalized detachment rate as follows:

$$\langle \tau \rangle =\frac{1}{\tilde{\gamma }}.$$ (10)

The processivity is given by $\langle \delta m\rangle =v_{\text{unw}}\langle \tau \rangle$. Using Eqs. 8 and 10, we obtain the equation as follows:

$$\langle \delta m\rangle =\frac{s\left(\tilde{h}+{\tilde{k}}^{+}-{\tilde{k}}^{-}\right)}{\tilde{\gamma }}.$$ (11)

For s = 1 and r = 1, $\langle \delta m\rangle$ reduces to the expression as follows:

$${\langle \delta m\rangle }^{\mathrm{1,1}}=\frac{e^{-f{U}_0}\left(1+b\left(e^{f{U}_0}-1\right)\right)\left(b\left(h+k\right)-k\right)}{\gamma }.$$ (12)

Equations 8, 10, and 11 along with Eq. 16 are the important results in this article. Note that by defining $k^{-}\equiv k$ and $k^{+}\equiv k+h$ in Eqs. 9 and 12, we obtain the same model used in our previous work (31).

Universal force response of the unwinding processivity

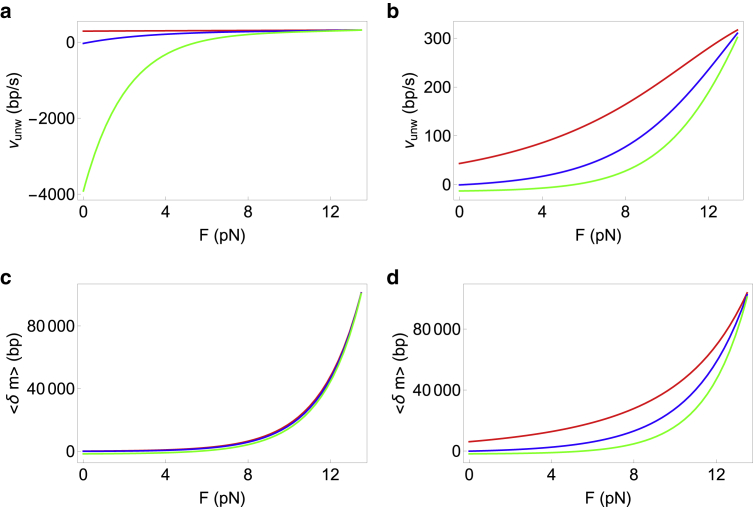
In our earlier work (31), we showed numerically that the unwinding velocity and processivity show contrasting responses to external force. We analyzed a model with a step size of one basepair and an interaction potential with a one-basepair range. Below, we first revisit the earlier model to highlight the basic results and show quantitatively the differences between the responses of velocity and processivity to force. We then point out the effects of increasing the step size and the interaction range of the helicase.

For s = 1 and r = 1, the expressions for velocity and processivity are given by Eqs. 9 and 12, respectively. As in our previous work, we choose ΔG_F = FΔX for illustrative purposes. Choosing this simple form instead of the more accurate model based on the FJC (Eq. 5) does not qualitatively change any of the results (31). We will look at the limit k = 0 to simplify all the analytic expressions. For the more general case of nonzero k, as long as $k\ll h$, all the results are valid. Helicases are believed to satisfy this criterion (37), which is supported by our fitted values (discussed below) from data on the T7 DNA helicase.

Setting ΔG_F = FΔX and differentiating Eq. 9 with respect to F, we obtain the following expressions for passive (U₀ = 0) and optimally active (f = 0, U₀ = ΔG) helicases. Note that optimally active helicases are ones in which $f\to 0$ and U₀ ≥ ΔG.

$$\frac{d{v}_{\text{unw}}^{\mathrm{1,1}}}{dF}=\{\begin{array}{cc}{e}^{-\mathit{\Delta }\text{G}+F\mathit{\Delta }\text{X}}h\mathit{\Delta }\text{X}& \left(\text{passive}\right)\\ \frac{e^{2\mathit{\Delta }\text{G}+F\mathit{\Delta }\text{X}}h\mathit{\Delta }\text{X}}{{\left(e^{\mathit{\Delta }\text{G}}+e^{F\mathit{\Delta }\text{X}}\left(-1+e^{\mathit{\Delta }\text{G}}\right)\right)}^2}& \left(\text{optimally}\text{active}\right).\end{array}$$ (13)

The equation above shows that for a passive helicase, the slope of the velocity-force curve is not only always positive; it increases exponentially with F (Fig. 3 a, orange curve). On the other hand, for an optimally active helicase, the expression for the slope has the term e^FΔX both in the numerator as well as the denominator, with a higher power of F in the denominator, implying that the increase in velocity with force will be much less rapid than an exponential. As can be seen from Fig. 3 a, the curves (red and blue) have the opposite curvature compared to the passive helicase (orange curve). In contrast, the force-dependent behavior of the processivity shows a universal increase, which can be seen as follows:

$$\frac{d{\langle \delta m\rangle }^{\mathrm{1,1}}}{dF}=\{\begin{array}{cc}\frac{e^{-\mathit{\Delta }\text{G}+F\mathit{\Delta }\text{X}}h\mathit{\Delta }\text{X}}{\gamma }& \left(\text{passive}\right)\\ \frac{e^{-\mathit{\Delta }\text{G}+F\mathit{\Delta }\text{X}}h\mathit{\Delta }\text{X}}{\gamma }& \left(\text{optimally}\text{active}\right).\end{array}$$ (14)

Figure 3.

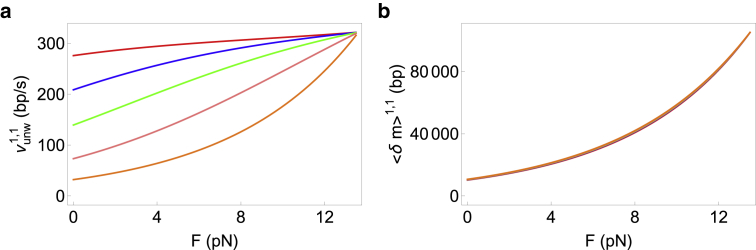
Response of (a) velocity and (b) processivity to external force for a helicase with a 1-bp step size and a 1-bp interaction range. $h=322s^{-1}$ and ΔG = 2.25 k_BT for all curves in both panels. The interaction potential U₀ decreases from the top to the bottom curve as follows: 5 k_BT (red), 3 k_BT (blue), 2 k_BT (green), 1 k_BT (pink), and 0 k_BT (orange). The bottom-most curve (orange) therefore corresponds to a passive helicase, whereas the top two (red and blue) curves correspond to optimally active helicases. The velocity curves are plots of Eq. 9, whereas the processivity curves are plots of Eq. 12. To see this figure in color, go online.

Equation 14 shows that the slopes are identical for both passive and optimally active helicases and increase exponentially with force. This is very clearly illustrated in Fig. 3 b in which all the curves almost superpose.

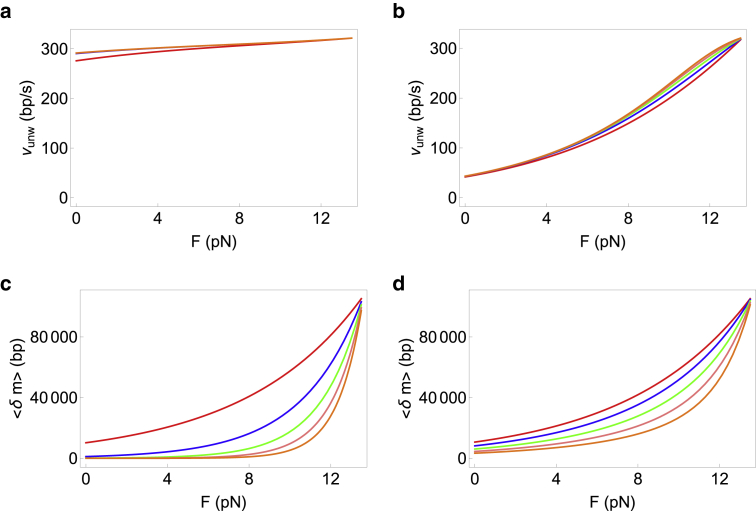
For a general step size and interaction range of the helicase, the full expressions for unwinding velocity (Eq. 8) and processivity (Eq. 11) are complicated; hence, we only show a few representative plots in Figs. 4 and 5 for a variety of step sizes and interaction ranges. Fig. 4 shows that increasing the range of interaction (keeping the step size fixed) affects the velocity and processivity in different ways. At a given force, while the velocity of unwinding increases when the range is increased (Fig. 4, a and b), the processivity decreases (Fig. 4, c and d). However, the universal behavior obtained in our previous work (31) remains valid: the unwinding velocity can increase or remain almost constant with force depending on whether the helicase is active or passive. The processivity on the other hand always increases with external force. Fig. 5 shows the effect of increasing the step size while keeping the interaction range fixed for optimally active (Fig. 5, a and c) as well as very weakly active (Fig. 5, b and d) helicases. At a given value of force, both the velocity and processivity decrease with increase in the step size. For an optimally active helicase, the decrease in velocity is rapid, becoming strongly negative at low forces (Fig. 5 a). The reason for this phenomenon is that the backstepping rate increases with U₀ (more active helicase). The helicase-junction interaction leads to the helicase imparting a force on the junction (=U₀ divided by the basepair distance). This in turn causes an opposite force from the junction on the helicase. This opposing force is larger for larger U₀, thereby leading to larger effective backstepping rates as U₀ increases. For larger step sizes (3 bp for the green line in Fig. 5 a), the helicase needs more bases open downstream simultaneously and hence is less likely to step forward. Coupled with a larger backstepping rate, the net effect is negative unwinding velocities of the helicase.

Figure 4.

Effect of increasing the interaction range of the helicase on the unwinding velocity and processivity at a fixed step size. The step size in all panels is fixed at 1 bp, ΔG = 2.25 k_BT for all curves and $h=322s^{-1}$; thus V_ss = 322 bp/s. The interaction ranges going from the top to the bottom curves are 1 bp (red), 2 bp (blue), 3 bp (green), 4 bp (pink), and 5 bp (orange). (a and c) Optimally active helicase with U₀ = 5 k_BT and f = 0.01 is shown. (b and d) Very weakly active helicase with U₀ = 0.3 k_BT and f = 0.01 is shown. To see this figure in color, go online.

Figure 5.

Effect of increasing the step size of the helicase on the unwinding velocity and processivity while keeping the interaction range fixed. The interaction range in all panels is fixed at 3 bp, ΔG = 2.25 k_BT for all curves and $h=\frac{322}{s}{s}^{-1}$, thus V_ss = 322 bp/s. The step sizes going from the top to bottom curves are 1 bp (red), 2 bp (blue), and 3 bp (green). (a and c) Optimally active helicase with U₀ = 5 k_BT and f = 0.01 is shown. (b and d) Very weakly active helicase with U₀ = 0.3 k_BT and f = 0.01 is shown. To see this figure in color, go online.

To summarize, our analysis in this section shows that irrespective of the step size, interaction range, active or passive nature of the helicase, the unwinding processivity should always increase with force. The unwinding velocity however does not exhibit the same universal increase with external force.

Unwinding mechanism of the T7 helicase

Simultaneous fitting of DNA unwinding velocity and run-length data

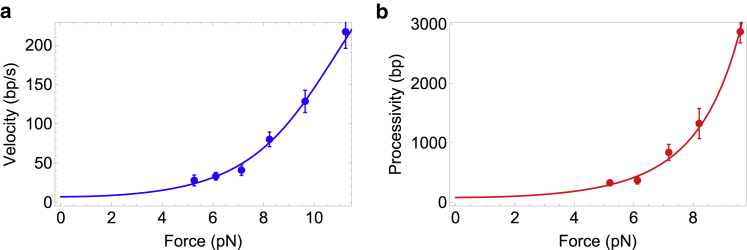
Because fitting only the expression for the unwinding velocity to experimental data proves to be insufficient for estimating physically reasonable parameters, we reasoned that fitting the theory to the available data to the two observables simultaneously should significantly limit the parameter space and allow for better extraction of the important parameters of the system. Using the velocity given in Eq. 8 and the processivity given in Eq. 11, we use our theory to analyze data from the T7 helicase.

We first observe that the velocity as a function of force has the following parameters: U₀, k, f, s, r, and h. It follows from Eq. 11 that the processivity has one extra parameter, the dissociation rate γ associated with the mean binding time of the helicase (31, 46). However, γ is a quantity that is measured in bulk experiments (47, 48), whereas the relation V_ss = sh allows us to use the experimentally determined value of V_ss to eliminate another free parameter. Thus, the number of free parameters left to be determined from fitting to experimental data is five: U₀, k, f, s, and r. To test our method, we fitted velocity and processivity data from single-molecule experiments on the T7 helicase (Figs. 6B and S6, respectively, of (26)). Kim et al. (47) reported γ = 0.002 s⁻¹ at 18°C. Because the single-molecule experiment was performed at 25°C, we used the rough estimate that around room temperature, a number of chemical rates increase by about a factor of 2–3 for every 10°C increase (49) to estimate γ at 25°C. We therefore used γ = 0.003, 0.004, and 0.005 s⁻¹. We used h = 322/s (s is the step size) because the ss velocity was measured to be 322 bp/s (26), which seems not inconsistent with the bulk result of 132 bp/s at 18°C (47). We took ΔG = 2.25 because the DNA sequence had 48% GC content (supporting material of (25)). Both the bulk- and single-molecule experiments were performed at 2 mM dTTP concentration.

For the force-dependent destabilization of the ds given in Eq. 5, the parameters L and l need to be chosen carefully to reproduce the critical force F_c observed in the experiment. F_c (the force where ΔG = ΔG_F) was observed to be around 13.6–13.7 pN for the dsDNA sequence we have analyzed in this work (Fig. 6B of (26)). The usual values chosen for L and l are 0.56 and 1.5 nm, respectively (42). However, F_c for this choice of parameters (and ΔG = 2.25) is ∼15 pN, so we chose L = 0.63 nm and l = 1.5 nm to reproduce the observed critical force. To check the robustness of our results, we also tried a different parametrization L = 0.56 and l = 1.95 nm, which results in F_c = 13.6 pN. Both these parametrizations produce nearly identical results; thus, we show results with only the first one (Tables 1 and 2).

Table 1.

Fitting to Only Velocity Data

Step Size s (bp)	Interaction Range r (bp)	χ2
1	20	3.04
2	10	1.65
2	20	1.72
2	50	1.74
3	3	2.3
3	4	2.8

Shown are just a few fits, obtained by varying s and r, from all those that are similar. The definition of similar is that the worst fit should be 0.5 times as likely as the best fit according to the AICc (see text for details).

Table 2.

Fitting Simultaneously to Velocity and Run-Length Data

Step Size s (bp)	Interaction Range r (bp)	χ2
2	5	4.69a
2	6	5.23

Compared to Table 1, the parameter space with similar fits to the data has been drastically reduced. The definition of similar is exactly the same as that used in Table 1.

^aThis is the best fit among all the similar fits. The parameters for this fit along with errors are U₀ = 0.69 ± 0.02, f = 0.19 ± 0.04, k = 0.6 ± 0.4. Clearly, each parameter can be robustly estimated.

Quality of fits

The simultaneous fitting of velocity and processivity data was performed by fixing the step size s and the interaction range r (because these parameters can only be discrete numbers) and using Eqs. 8 and 11 to compute the χ² metric (weighted sum of the squared deviations between the model result and data). Minimization of the χ² metric to obtain the best-fit parameter values for U₀, f, and k was performed using the FindMinimum function in Wolfram Mathematica 11.2. This procedure was repeated for many combinations of s and r values. The results of the simultaneous fitting procedure are shown in Fig. 6. Tables 1 and 2 show the quality of fits (χ²) for a variety of parameter sets with “similar” fits. To quantitatively define similarity of fits, we used the Akaike Information Criterion (AICc) (50) defined as follows:

$$\text{AICc}={\chi }^2+2p+\frac{2p\left(p+1\right)}{N-p-1},$$ (15)

where N is the number of data points and p the number of free parameters. The usefulness of this criterion is that the quality of the two sets of fits can be quantitatively compared: if two model fits have AICc values of a₁ and a₂, respectively, with a₁ < a₂, then model 2 has a likelihood $\text{exp}\left(\left(a_1-a_2\right)/2\right)$ of being the true interpretation of the data relative to model 1. Using this interpretation, we show in Tables 1 and 2 all fits that are at least 0.5 times as likely as the best fit among that set. Table 1 shows the result of fitting to only velocity data; multiple parameter regions can fit the velocity data with similar quality of fits. Table 2 shows results of our simultaneous fitting procedure. Clearly, Table 2 shows that the simultaneous procedure allows a much narrower range of parameters to produce similar fits. In addition, the errors on the parameters are small, allowing all parameters to be extracted with great robustness. The best-fit parameters are U₀ = 0.69 ± 0.02 k_BT, f = 0.19 ± 0.04, k = 0.6 ± 0.4 s⁻¹, s = 2 bp, and r = 5 bp.

Figure 6.

Simultaneous fitting of velocity and run-length data. The filled circles with error bars are experimental data for the T7 helicase from (26). The line in (a) is Eq. 8 fitted to velocity data, whereas the line in (b) is Eq. 11 fitted to processivity data. The best-fit parameters are given in Table 2. To see this figure in color, go online.

Comparison with experiments on T7 unwinding of DNA under zero-force conditions

An earlier bulk experiment (51) and a more recent single-molecule experiment based on fluorescence resonance energy transfer (52) on T7 DNA were carried out under conditions of zero external force. Using an “all-or-none” assay at 18°C, five DNA sequences (average GC content of 37%) were unwound with T7 in (51), resulting in an average unwinding velocity of 15 bp/s. Approximately consistent with these results, the unwinding velocity at 23°C of T7 on a 35% GC sequence was found to be 8 bp/s (52). Fig. 6 a shows our model prediction for the unwinding velocity at zero force: v_unw = 7.1 bp/s. Keeping all the parameters fixed at the values shown in Table 2 but reducing ΔG to 1.9 to correspond to a DNA sequence comprising roughly 37% GC basepairs, our model predicts an unwinding velocity of 18 bp/s at zero force. Taking into account that our analysis is based on an experiment performed at a slightly higher temperature (25°C) compared to either of these two zero-force experiments, our results are consistent with the two previous works.

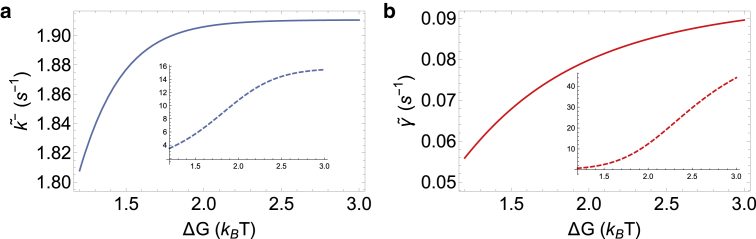
Predictions for sequence dependence of detachment and backstepping rates of T7 while unwinding dsDNA at zero force

The sequence dependence of the detachment rate of a helicase is an aspect that can be directly measured in experiments (23, 53) and can be an indicator of whether the helicase is active or passive. By fixing the parameters in our model to the best-fit values of Table 2 and changing only ΔG, we can predict how the detachment and backstepping rate of T7 will depend on the sequence composition while unwinding DNA. The results of this analysis are shown in Fig. 7. As is evident, neither the detachment rate nor the backstepping rate are very sensitive to ΔG, because the helicase is only very weakly active. Interestingly, this is akin to the observations made in a previous experiment on the DnaB helicase (53) for which it was shown that for sequences with 50–100% GC composition, the detachment rate was almost constant. Because both DnaB and T7 are very similar in structure and sequence, belonging to the superfamily-4 group of helicases, our results suggest that the ring helicases of the superfamily-4 group might all use a similar weakly active mechanism for unwinding DNA.

Figure 7.

Predictions for sequence dependence of T7 detachment and backstepping rates while unwinding dsDNA. (a) The backstepping rate while unwinding $\left(k_{-}^{\text{'}}\right)$ hardly changes as a function of the sequence stability as a result of the helicase being only weakly active. (b) Similarly, the detachment rate while unwinding $\left(k_d^{\text{'}}\right)$ changes by only a factor of 1.5 with change in ΔG. The insets in both figures show the hypothetical situation of a highly active T7, with U₀ = 2.0 k_BT. Both the backstepping and detachment rate show much more sensitivity to ΔG under highly active circumstances. To see this figure in color, go online.

Discussion

T7 is weakly active

From the best-fit parameters in Table 2, we infer that the T7 helicase is a weakly active helicase, destabilizing the ds junction by about 0.69 k_BT per base. The value of U₀ obtained here is different from the $\left(1-2\right)$ k_BT estimate reported earlier in (24, 26). Both these works analyzed only velocity data; the former looked at sequence dependence, whereas the latter examined the force dependence of velocity. It was originally pointed out (37) and verified by us specifically for T7 in this work (Table 1), that analyzing only the velocity data using the multiparameter Betterton and Jülicher (32, 33, 34) model is not sufficient for robust parameter estimates. There are other differences as well between our model and the ones used previously (24, 26). The parameter f was fixed to 0.05 in both those earlier studies, whereas we allow it to vary, given that f is a physical quantity, which could take on any value between 0 and 1. We also have the extra parameter k, which gives the rate of pure diffusion. The presence of this parameter allows for back steps, which was neglected in the previous studies. It is important to include this parameter, especially in light of recent experiments that directly observed back stepping (27, 52). Interestingly, in a previous work analyzing DnaB kinetics in the hairpin geometry (54), the interaction potential was estimated to be 0.5 ± 0.1 k_BT, which is almost identical to our finding for the T7 helicase. Although this result on DnaB was obtained by fixing the step size to 1 bp (see more on the DnaB step size later) and suffered from a number of the parameter estimation issues discussed above, the overall conclusion from our work as well as (54) seems to be that ring helicases like T7 and DnaB are weakly active.

Step size of T7

Our prediction of a step size of 2 bp (two bases advanced for each dTTP hydrolyzed) is in agreement with certain previous experimental results. Using a pre-steady-state analysis, it was found that one dTTP molecule is consumed for every 2–3 basepairs translocated by T7 on an ssDNA (47). A crystal structure of the DnaB helicase bound to ssDNA showed that the step size of DnaB is 2 bp (55). DnaB and T7 are both members of the superfamily-4 group of helicases, with very similar sequence and structure in the C-terminal domains (22, 56). These results suggest that the step size of T7 while unwinding dsDNA may also be 2–3 bp, under the assumption that ss translocation and ds unwinding occur with the same step size. A recent single-molecule FRET-based unwinding assay using T7 observed stochastic pauses after every 2–3 bp of G-C-rich DNA unwound (52). However, the waiting times of these pauses were γ-distributed rather than exponentially distributed, suggesting the presence of hidden steps within those pauses. Although the results do not prove a direct association of these hidden steps with dTTP consumption, it would not be surprising if the helicase has a distribution of step sizes with shorter steps of 1 bp while unwinding G-C bases. Because our model does not distinguish between the step size during translocation, unwinding, or for different sequences, it is likely that our result of 2 bp per dTTP consumed is a reflection of the average step size over the entire ds sequence of the DNA being unwound. Further experiments, including determination of crystal structures, would be able to shed more light on this interesting conundrum. Indeed, recent cryogenic electron microscopy structures of the T7 replisome clearly suggest that the helicase advances by two nucleotides per step as it encircles a DNA strand in a spiral “lock washer” form (57), thereby providing strong support for our model prediction.

Interaction range of T7

The interaction range of ∼5 bases that we obtain from our fits is physically reasonable given the structure of the T7 ring helicase and its mode of binding to dsDNA. While the DNA strand excluded from the T7 ring is negatively charged, the C-terminal face of T7 is also negatively charged (41). Replacement of the charged residues on the C-terminal by uncharged ones leads to a reduction in efficiency of complementary strand displacement (58). These results strongly suggest that the moderately weak (0.69 k_BT per base) interactions between the helicase and DNA that we predict are electrostatic in nature. Given that the Debye-Hückel screening length is ∼1 nm in physiological salt concentrations (59), the range of electrostatic interaction of the helicase should be a few nanometers. Our prediction of five bases (∼1.7 nm) therefore is physically reasonable. Notice that fitting to only velocity data would predict an interaction range greater than 20 bp, which would be unphysically large.

The ∼5 bp interaction range that emerges from fitting the data also serves as postpriori justification of the FJC model used to describe force effects on the nucleic acid strands. The persistence length of ssDNA is in the same range, ∼1–3 nm depending on the salt concentration. Because our interest here was in analyzing the hairpin geometry where the force applied acts on the two complementary single strands of the hairpin, an FJC model with a Kuhn length of 1.5 nm is a reasonable model to use.

Backstepping rate of T7 while unwinding or translocating

The backstepping rate of helicases is usually very difficult to measure directly because of the lack of sufficient resolution in single-molecule experiments. Hence, the backstepping rate is usually assumed to be negligible compared to the forward-stepping rate or neglected completely (37). Using the parameters extracted from our fits to T7 data (given in Table 2), we now show that although this assumption is valid when the helicase translocates on ssDNA, the backstepping probability is orders of magnitude larger while unwinding dsDNA. Note that in this discussion and throughout this article, we set the ATP concentration at 1 mM, which is roughly the physiological concentration of ATP. Experiments are usually performed at ATP concentrations of 1 mM or higher. If the ATP concentration is made very low in an experiment, naturally the backstepping probability will be substantially larger (27) until it approaches $50\text{\%}$ at 0 ATP, implying no directionality associated with the motion of the helicase.

The ratio of forward- to backward-stepping rates while translocating is (h + k)/k, hence using k = 0.6 and h = V_ss/s = 161, this ratio turns out to be 269. This result is interesting and suggests that T7 back steps approximately as frequently as some of the other processive molecular motors like kinesin, which also has similar values for this ratio in the absence of external force (60). The backstepping probability at every step is given by k/(k + (h + k)), which is a mere $0.3\text{\%}$ for the T7 parameters given in Table 2. However, when the helicase unwinds dsDNA, the rates change, and the modified backstepping probability is given by $\widetilde{k^{-}}/\left(\widetilde{k^{-}}+\left(\tilde{h}+\widetilde{k^{-}}\right)\right)$. For the same parameter set, this works out to be 26%, almost two orders of magnitude larger than the backstepping probability while translocating. Our prediction regarding this enhanced backstepping probability while unwinding is similar to the observations in a recent experiment on the XPD helicase in which it was shown that at 1 mM ATP, the backstepping probability is about 10% (27). Our analysis therefore suggests that XPD, which belongs to superfamily 2, may not be unique in this respect; the superfamily-4 helicase T7 also seems to back step with relatively large probability while unwinding dsDNA. Further experiments on helicases belonging to the same superfamily are needed to probe the extent of back stepping.

Universal nature of force response of helicase processivity, oligomerization, and partner proteins

Helicases often cannot unwind ds nucleic acids by themselves but require partner proteins like ss binding proteins or oligomerization to increase the efficiency (14, 15, 16). We use efficiency to mean that the helicase is highly processive. Although the mechanistic reasons for the increase in efficiency is likely to vary for individual helicases, our work suggests the possibility of a single physical principle underlying this effect. Our theory shows that the increase in processivity in response to external force should hold for all helicases. In particular, unlike the unwinding velocity, the processivity increases with external force irrespective of the active or passive nature of the helicase. This prediction has recently been validated in two different helicases Pif1 and RecQ (35, 36). Because the external force destabilizes the ds and decreases the free energy of the basepairs at the junction, we predict that any perturbation that results in reduction of basepair stability should result in universal effects, similar to the force response of helicases. There is strong evidence that partner proteins, like ss binding proteins, melt nucleic acids by reducing the stability of basepairs (see a more detailed discussion in (31)). Similar effects may be achieved by oligomerization of helicase monomers. A recent study on the UvrD helicase showed that dimerization leads to a closed conformation of the 2B subdomain of the leading UvrD monomer (16), a conformation that contacts the junction duplex and presumably destabilizes it (61, 62). This implies the possibility that a universal underlying principle governs the response of helicases in the presence of force, partner proteins as well as oligomerization. An immediate prediction of this theory is that a weakly active helicase like T7 should exhibit increased velocity and processivity in the presence of partner proteins. This phenomenon has indeed been observed previously, but not explained (63, 64). On the other hand, partner proteins should increase only the processivity of an active helicase like NS3. This prediction is borne out as well in experiments (65). It is rare to find universal behavior, especially on the nanometer scale representing motors including helicases. That this seems to be the case for helicases is remarkable. The universal increase of processivity with force, regardless of the nature of the helicase also suggests that this class of motors may have evolved to optimize processivity rather than speed.

Conclusions

Whether a particular helicase unwinds ds nucleic acids using an active or passive mechanism has been a subject of much debate. Here, we derived analytic expressions for both the velocity and processivity of generic unwinding helicases and showed that only by simultaneously using velocity and run-length data can the active/passive nature of a helicase, and thus the unwinding mechanism, be discerned. Simple expressions for the processivity or run length of helicases were previously unavailable; thus, our work should prove useful in the future analysis of helicase unwinding trajectories. Our results also quantitatively predict that the processivity should show a universal increase with force unlike the velocity, which has implications for in vivo unwinding of nucleic acids by the replisomal complex. This result seems to be borne out in a variety of experiments, and further work will help in verifying these predictions. Finally, we have also quantitatively shown that the backstepping rate of the T7 helicase while unwinding double strands is orders of magnitude larger than the backstepping rate while translocating on ss nucleic acid. Although we analyze only average velocities here, analyzing and interpreting helicase unwinding velocity distributions will be important in the future by combining our work here with results we have derived earlier on the stochastic effects of motor velocities (60). The full distributions could reveal interesting details of helicase heterogeneity that remain inaccessible to models analyzing just averages.

Author Contributions

S.C., C.J., and D.T. designed and performed research and wrote the manuscript.

Editor: Anatoly Kolomeisky.

Appendix A

The full expressions for ${\tilde{k}}^{+}$, $\tilde{h}$, ${\tilde{k}}^{-}$, and $\tilde{\gamma }$ are given as follows:

$$\begin{array}{c}\frac{{\tilde{k}}^{+}}{k^{+}}=\frac{\frac{b^{r+s}{e}^{r{U}_0}}{1-b}+\frac{e^{-fs{U}_0}\left(y^{1+r}-y^s\right)}{y-1}+\frac{b^r{e}^{\left(r-fs\right)U_0}\left(z^s-z\right)}{z-1}}{\frac{b^{1+r}{e}^{r{U}_0}}{1-b}+\frac{y^{1+r}-1}{y-1}},\\ \frac{\tilde{h}}{h}=\frac{\frac{b^{r+s}{e}^{r{U}_0}}{1-b}+\frac{e^{-fs{U}_0}\left(y^{1+r}-y^s\right)}{y-1}+\frac{b^r{e}^{\left(r-fs\right)U_0}\left(z^s-z\right)}{z-1}}{\frac{b^{1+r}{e}^{r{U}_0}}{1-b}+\frac{y^{1+r}-1}{y-1}},\\ \frac{{\tilde{k}}^{-}}{k^{-}}=\frac{\frac{b^r{e}^{r{U}_0}}{1-b}+\frac{e^{\left(1-f\right)s{U}_0}\left(y^{1+r-s}-1\right)}{y-1}+\frac{e^{\left(1-f\right)\left(s-1\right)U_0}{y}^{1+r-s}\left(z^{s-1}-1\right)}{z-1}}{\frac{b^{1+r}{e}^{r{U}_0}}{1-b}+\frac{y^{1+r}-1}{y-1}},\\ \frac{\tilde{\gamma }}{\gamma }=\frac{e^{r{U}_0}\left(y-1\right)}{b\left(1+b^r{e}^{r{U}_0}\left(y-1\right)-\left(b-1\right)e^{U_0}{y}^r\right)-1},\end{array}$$ (16)

where $y\equiv b{e}^{U_0}$ and $z\equiv b{e}^{f{U}_0}$.