Quantifying the Local Mechanical Properties of Cells in a Fibrous Three-Dimensional Microenvironment

Abstract

Measurements of the mechanical response of biological cells are critical for understanding injury and disease, for developing diagnostic tools, and for computational models in mechanobiology. Although it is well known that cells are sensitive to the topography of their microenvironment, the current paradigm in mechanical testing of adherent cells is mostly limited to specimens grown on flat two-dimensional substrates. In this study, we introduce a technique in which cellular indentation via optical trapping is performed on cells at a high spatial resolution to obtain their regional mechanical properties while they exist in a more favorable three-dimensional microenvironment. We combine our approach with nonlinear contact mechanics theory to consider the effects of a large deformation. This allows us to probe length scales that are relevant for obtaining overall cell stiffness values. The experimental results herein provide the hyperelastic material properties at both high (∼100 s⁻¹) and low (∼1–10 s⁻¹) strain rates of murine central nervous system glial cells. The limitations due to possible misalignment of the indenter in the three-dimensional space are examined using a computational model.

Significance

Current techniques to externally probe the mechanical properties of adherent cells are typically limited to flat two-dimensional substrates. Because two-dimensional substrates are not representative of the cellular microenvironment found in tissues, adherent cells often express unrealistic morphologies or phenotypes when grown on flat substrates. We demonstrate a, to our knowledge, novel experimental setup that allows the probing of the mechanical properties of adherent cells grown in a fibrous scaffold at length scales that are relevant for future diagnostic techniques in studies of disease and injury. Using optical trapping and nonlinear contact mechanics formulations, we can perform indentation testing on cells at precise locations to obtain their regional hyperelastic mechanical properties while they exist in a more favorable three-dimensional environment.

Introduction

With three-dimensional (3D) culture systems, cell surface receptors can become spatially organized in a biologically relevant configuration, allowing cells to receive the mechanical cues and cell-cell communications that can be lost with cultures grown on flat plastic and glass substrates (1, 2, 3). Differences in cell morphology and phenotype in 3D cultures have been shown across various cell types, such as chondrocytes (4), hepatocyes (5, 6), epithelial cells (7), and astrocytes (8, 9). Given the same stiffness substrate, a different cell morphology can result in different cell stiffness (10).

Conventional techniques for the mechanical testing of cells, such as atomic force microscopy (AFM) or scanning force microscopy, require cells to be grown on a flat substrate so that the cell surface can be vertically indented with an AFM probe tip of a selected geometry. Previous efforts to probe the mechanical properties of cells in a more native environment have used computational modeling to estimate the elastic properties of heterogeneous samples containing cells embedded in a 3D extracellular matrix (ECM) (11, 12) by measuring an overall “apparent stiffness.” A computational model is used to decouple the Young’s modulus of the cell from the overall apparent stiffness, with the assumption that the ECM is a well-characterized and homogeneous matrix surrounding a perfectly spherical cell. Such approaches cannot be readily applied to local cell compartments or nonspherical cells.

Another technique in which the mechanical properties of cells can be probed in a 3D scaffold environment is through intracellular particle-tracking microrheology—a technique in which spherical particles are internalized by the cell, and the movement of the particles is tracked over time (13, 14, 15, 16, 17). Previous studies have utilized microrheology to obtain mechanical properties of cells grown in a 3D scaffold (18, 19, 20), but these measurements do not incorporate the effects of plasma membrane tension, which has a major contribution to stiffness measurements (21, 22). Active microrheology can also provide mechanical properties of 3D tissue in vivo (23, 24, 25). Although these examples allow one to probe the mechanical properties of cells in a native environment, it is limited in its applicability in the determination of local mechanical properties of individual cellular compartments.

Here, we present a technique using an optically trapped silica bead to perform indentation testing on central nervous system (CNS) murine cells grown in an electrospun scaffold (Fig. 1, A–E). Although optical trapping has previously been employed for indentation testing (26), previous studies have not applied this technique to probing cells in a 3D scaffold environment. Optical trapping utilizes a highly focused laser beam to trap particles (e.g., silica beads) in 3D space with a precisely measured amount of force. A priori calibration measurements are performed to find the forces required to perturb the bead from its equilibrium position in the center of the trap. In contrast to some indentation tests in which the cell and substrate remain stationary while being subjected to surface deformation from a rigid indenter, our approach uses the precise translation of the cell into the optically trapped bead (which is loosely “fixed” at the specific x, y, and z location of the trap center). Upon translating the scaffold, the cell collides with the bead, and the extent of bead deflection is proportional to the force that tries to restore the bead back to its equilibrium position. Through measuring the amount of force acting at the cell surface and the amount of indentation at the cell surface, it is possible to obtain the mechanical response of specific cellular compartments. Our technique is applied to processes of glial cells, which possess a polygonal morphology (instead of their characteristic stellate morphology) when grown on two-dimensional (2D) substrates (27, 28).

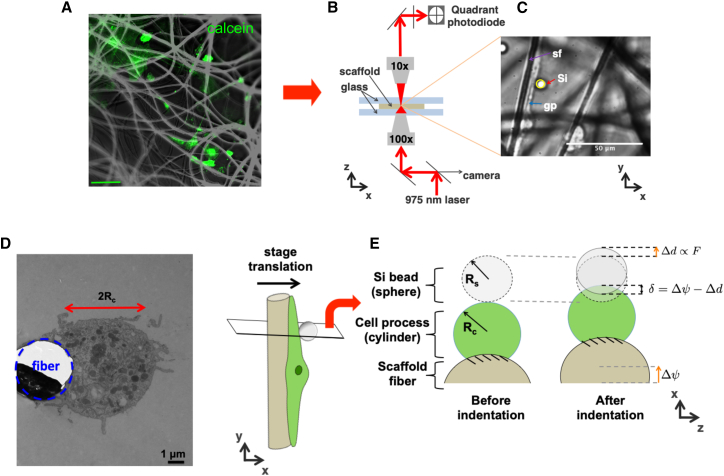
Figure 1.

Schematic for OT indentation setup. (A) Cells are grown for 7–10 days in an electrospun PVDF scaffold to grow cellular processes. Cells are stained in calcein to help differentiate cells from the scaffold fibers. Scale bars, 50 μm. (B) Scaffolds with cells are inverted onto coverslips with silica bead solution. Specimens are clamped into a translational piezoelectric stage at the focal point of the trapping laser. A quadrant photodiode at the back focal plane is used to detect deflection of the 975 nm laser, thereby providing x, y, and z changes of bead displacement. (C) Shown is an example image of glial process (gp) grown along a scaffold fiber (sf). An optically trapped streptavidin-coated silica bead (Si) is brought into contact with the biotinylated surface of the cell. (D) TEM shows the cross-sectional view of the scaffold fiber outline (blue circle) and glial cellular process (diameter of 2R_c). TEM images verify that the cells indeed have a cylindrical morphology. (E) The specimen stage is translated in the direction perpendicular to the fiber (+x direction in the example, depicted with orange arrows). The cross-sectional view depicts the scaffold translation (Δψ), measured bead deflection (Δd), and cell indentation (δ = Δψ − Δd). The bead deflection (Δd) is related to force through prior calibration of the OT. To see this figure in color, go online.

Materials and Methods

Indentation analysis

By simultaneously measuring the force applied (F) to the membrane, along with the extent of indentation (δ), mathematical relationships derived from contact mechanics can be used to obtain the cellular mechanical properties. Fig. 1 E shows a schematic of the indentation depth calculation. The specimen stage is translated in the x and y directions, and the scaffold containing the cells is also translated in the direction toward an optically trapped bead. The cell then collides with the optically trapped bead, causing a small deflection of the bead (Δd) from the center of the focused laser spot. As shown in Fig. 1 B, bead translation is measured through tracking changes to the transmitted laser path with a back focal plane quadrant photodiode (PDQ80A; Thorlabs, Newton, NJ). The distance of stage translation is denoted as Δψ, where Δψ_i = Δψ_x or Δψ_y, depending on the cell specimen orientation. Stage translation was measured with a piezo driven NanoMax stage (MAX311D; Thorlabs) in closed loop mode with strain gauge readers (TSG101; Thorlabs). Although the theoretical resolution of the piezo stage was 5 nm, we could only verify the accuracy of the scaffold translation to within 25 nm (more details on measuring the stage compliance are provided in the Supporting Materials and Methods). Because the internal strain gauges of the stage provide positional feedback, the movement of the stage becomes nonlinear (slowing down as it approaches its final position). The indentation depth (or displacement, δ) from the cell surface is then, simply, the following:

$${\delta }_i=\mathit{\Delta }{\psi }_i-\mathit{\Delta }{d}_i.$$ (1)

Here, the usage of Δd_i refers to the translation of the bead from the optical trap (OT) center in the i^th direction (the direction of stage translation). We assume that the silica bead is rigid and does not undergo deformation (only translation from the OT center). In other words, Δψ_i and Δd_i are both rigid body translations of the scaffold fiber and bead, respectively. The force applied to the cell is therefore determined from the bead deflection by the following: F_i = k_iΔd_i, where k_i is the known calibrated stiffness of the OT calibrated in the i^th direction (for the x, y, and z directions). Because of the high stiffness of the scaffold fibers (29), we can assume that the fiber remains rigid during the indentation testing (see Supporting Materials and Methods for calculations).

Because biological materials often undergo large deformations (δ/R_c > 0.05, where R_c is the local cell radius) and demonstrate a strain-stiffening behavior (30, 31), it is desirable to obtain material parameters that can describe the cell as a hyperelastic material. A commonly used hyperelastic model for soft materials is the incompressible Mooney Rivlin model (32), described by the strain energy density function:

$$W_{MR}=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right),$$ (2)

where I₁ and I₂ are the first and second invariants of the Cauchy-Green tensors. C₁₀ and C₀₁ are empirically determined material constants. For the case of infinitesimal strains, C₁₀ and C₀₁ are stiffness parameters that are related to the elastic modulus (E) by E = 4(1 + v)(C₁₀ + C₀₁). Here, we will define a nondimensional ratio of the material parameters $\kappa =\left(C_{10}\right)/\left(C_{10}+C_{01}\right)$. For the case of C₀₁ = 0 (κ = 1) in Eq. 2, the dependence on the second invariant is eliminated, and the material response exhibits less strain stiffening.

In our experiments, deformation is observed at short timescales (<1 s). During this time frame, we can ignore changes in cellular volume and assume the cell behaves in an incompressible manner (33, 34, 35, 36), which allows us to assume that v = 0.5. The Mooney Rivlin model was originally a phenomenological model used to capture the experimentally observed strain-stiffening behavior of rubber-like materials (32, 37). Although several hyperelastic models exist to capture the large deformation behavior of incompressible rubber (e.g., the neo-Hookean, Mooney Rivlin, and Ogden models), it is common to use these models to describe elastomers and soft biological materials (38).

To utilize the indentation test data to obtain the hyperelastic material properties of the Mooney Rivlin model, we utilize the following hyperelastic indentation force-displacement formulation:

$$F_{MR}\left(\delta ,R_s,R_c\right)=F_c\left(\delta ,R_s\right){\mathit{\Omega }}_{ellip}\left(\frac{R_s}{R_c}\right){\mathit{\Omega }}_{MR}\left(\frac{\delta }{R_s},\frac{R_s}{R_c}\right),$$ (3)

where F_c is the force-displacement relationship for a classical Hertz formulation for a circular contact area (39), and Ω_ellip is a correction factor that accounts for the ellipticity in contact area that occurs between a sphere and cylinder (40, 41, 42). Let R_s refer to the radius of the spherical indenter, whereas R_c refers to the cylindrical radius of the cell. Ω_MR is a corrective function that depends on R_s/R_c, δ/R_s, and the nondimensional ratio of the material properties, κ. The analytical expressions for Ω_MR and Ω_ellip are given in the Supporting Materials and Methods.

Fabrication of electrospun scaffolds

We created 3D polymer scaffolds by electrospinning polyvinylidene fluoride (PVDF) directly onto glass coverslips. PVDF solution was prepared to a final PVDF concentration of 15% w/w by adding PVDF pellets to dimethylformamide and acetone (1:1 ratio). Random fibrous mats were collected on coverslips taped to a grounded metal collector plate located 12–13 cm from the electrospinning syringe tip. Electrospinning was performed at a voltage of 10–12 kV at 3–5 mL/h flow rate from the syringe. The resulting PVDF fiber diameters were 1–4 microns, and the final overall scaffold thicknesses ranged between 50 and 150 microns. Scaffolds were thin and porous to allow sufficient spacing for unobstructed transmission of the trapping laser. After gluing the edges of the scaffolds to the underlying glass, coverslips were placed in six-well culture plates. Before introducing cell cultures, the wells containing the coverslips were UV-sterilized and immersed in 1× phosphate-buffered saline (PBS) at 37°C in an incubator overnight (43).

Cell culture

For primary mixed glia culture, cortices of mouse pups (The Jackson Laboratory, Bar Harbor, ME) P3-6 were isolated and plated on the poly-L-lysine-coated T-75 culture flasks in Dulbecco’s Modified Eagle Media/F12 50:50 media (15-090-CV; Corning, Corning, NY) with 10% fetal bovine serum and 1% antibiotics as per our previous protocol (44). The primary glia culture was maintained with a media change every 3–4 days. After 14 days of culture, glial cells were isolated by shaking the flask at 180 rpm × g at 37°C overnight. Cells were maintained for at least 3–4 days at 5% CO₂ and 37°C incubation before seeding cells into the electrospun scaffold at a density of 1 × 10⁶ cells per 100 μL of media. Once cells were added to the scaffolds at a high density, the scaffolds were incubated for 30 min for better attachment before adding more media. Once seeded on the cell scaffolds, cells were given 7–10 days to grow processes before performing indentation experiments. The glial cells grew processes along the length of the electrospun fibers, consistent with previous reports (9, 45). 2 h before the indentation experiments, media from the scaffold culture plate was removed and washed once with 1× PBS. Cell surfaces were biotinylated with EZ-link Sulfo-NHS-Biotin at a final concentration of 2 mM (number (#) 21217; Thermo Fisher Scientific, Waltham, MA). Cells were then washed three times with 100 mM Glycine-PBS (#VW1479-02; VWR, Radnor, PA) to remove excess biotin. Finally, cells were incubated in 500 nM of Calcein-AM (#C1430; Life Technologies, Carlsbad, CA) in plain Dulbecco’s Modified Eagle Media/F12 50/50 media to ensure cells were alive during mechanical testing as well as to help distinguish cellular processes from the scaffold fibers to determine the cell process diameters. Cell sizes ranged from ∼30 to 100 μm in overall diameter (including processes). Transmission electron microscopy (TEM) was used to ensure that the cell processes exhibited a circular profile.

OT setup

A 975 nm laser operating at 200 mW at the back aperture of a Nikon 100× oil immersion objective (NA = 1.25) was used to optically trap 5-micron diameter streptavidin-coated silica beads (Bangs Laboratories, Fishers, IN). Trap stiffness was calibrated in the x, y, and z directions through power spectrum drop-off calibration (46, 47). The trap stiffness in the x, y, and z directions was found to be k_x = 34.9 pN/μm, k_y = 34.2 pN/μm, and k_z = 24.1 pN/μm. Back focal plane detection of the transmitted laser light was obtained with a quadrant position detector (#PDQ80A; Thorlabs). Beads were optically trapped in the vicinity of a cell of interest and gently pressed against the cell surface for 3–5 min to ensure a sufficient bond between the streptavidin-coated bead and biotinylated cell surface. Only cell processes within the first ∼80 μm from the bottom coverslip were selected because the OT is unable to operate at larger depths. At the (x, y) location of the bead, the z depth was scanned throughout the scaffold thickness to ensure that the optical path was unobstructed for the transmitted laser light.

A three-axis high precision piezo actuator specimen stage (NanoMax stage; Thorlabs) was translated in the direction perpendicular to the long axis of the cell process (and its supporting PVDF fiber). In practice, the scaffold fibers were roughly aligned (rotated about the z axis) perpendicular to the loading direction by gently tapping the edges of the specimen stage holder. Images of the cell and scaffold fiber orientation were taken and analyzed with FIJI to ensure that the scaffold fibers were within 20° of the x and y axis of stage translation. Calibration was performed to ensure that translation of the actuator resulted in the same amount of translation of the scaffold (see Supporting Materials and Methods). Position data of the trapped bead as well as the X and Y strain gauge position data from the actuator stage was recorded with a National Instruments Data Acquisition system (USB-6212, Austin, TX) and custom LabVIEW program. A sampling rate of 36 kHz was sufficient to capture bead deflection during the 600 nm movement of the specimen stage over 50 ms. In practice, this is a force-controlled indentation experiment because the force history is most easily controlled with precise stage translation achieved using strain gauge feedback (48).

Although the setup uses a near-infrared laser to reduce thermal damage to the samples, previous work has demonstrated that a high laser power (>100 mW) can have non-negligible effects on trap calibration because the localized heat can increase the thermal motion of the bead and decrease the viscosity of the medium (49). Assuming a power of 200 mW is delivered to the sample, there is an expected temperature increase of 1–4°C (49), which varies as a function of the bead distance from the bottom coverslip (2.5–80 microns). In the future, the power spectrum drop-off calibration technique utilized in this study could be improved by accounting for changes to viscosity as a function of these thermal effects.

Electron microscopy

TEM was used to ensure that the cell processes exhibited a circular profile (i.e., cylindrical morphology). TEM samples were fixed with 2.5% glutaraldehyde and 3 mM magnesium chloride in 0.1 M sodium cacodylate (SC) for 1 h. Cells were washed in 0.1 M SC, 3 mM magnesium chloride (CaCl2), and 3% sucrose buffer in three 10 min rinses and incubated (on ice and in the dark for 1 h) in reduced 1% osmium with 0.8% potassium ferrocyanide in 0.1 M SC. This was followed by three 0.1 M maleate buffer rinses and en bloc stained with 2% uranyl acetate (0.22 μm filtered, 1 h, dark) in 0.1 M maleate buffer. Cells were dehydrated in a graded series of ethanol before embedding in EPONATE 112 resin (Ted Pella, Redding, CA). Samples were incubated at 37°C for 2–3 days before moving to a 60°C oven overnight. Regions of interest were selected, and sections picked up on 2 × 1 mm copper slot grids (Ted Pella). Sections were triple stained with 1% tannic acid (aqueous) (Mallinckrodt Pharmaceuticals, St. Louis, MO), aqueous 2% uranyl acetate (Polysciences, Warrington, PA), and 0.04% lead citrate (aqueous filtered). Samples were imaged on a Philips CM120 TEM with a 16-bit, eight megapixel AMT XR80 CCD.

Alignment effects

The cell is easily aligned in the x-y plane because this is observable by the camera. However, alignment of the bead along the z direction was not possible by visual inspection. We utilize measurements of the tangential force (z direction shown in Fig. 1 E) to relate to the “misalignment offset” (referred to as α in Fig. 2 A). A computational model was used to quantify the extent to which α would affect the force-displacement curves. Details of the computational model are provided in the Supporting Materials and Methods. TEM showed approximately circular cross sections for the cells (Fig. 1 D), which justified modeling the experiment as a rigid sphere in contact with a soft cylindrical cell (Fig. 2 A). Because errors due to α would likely be dependent on the ratio of R_s/R_c, simulations were performed to encompass the values of R_s/R_c (in the range of 0.6–10) observed in the experiments.

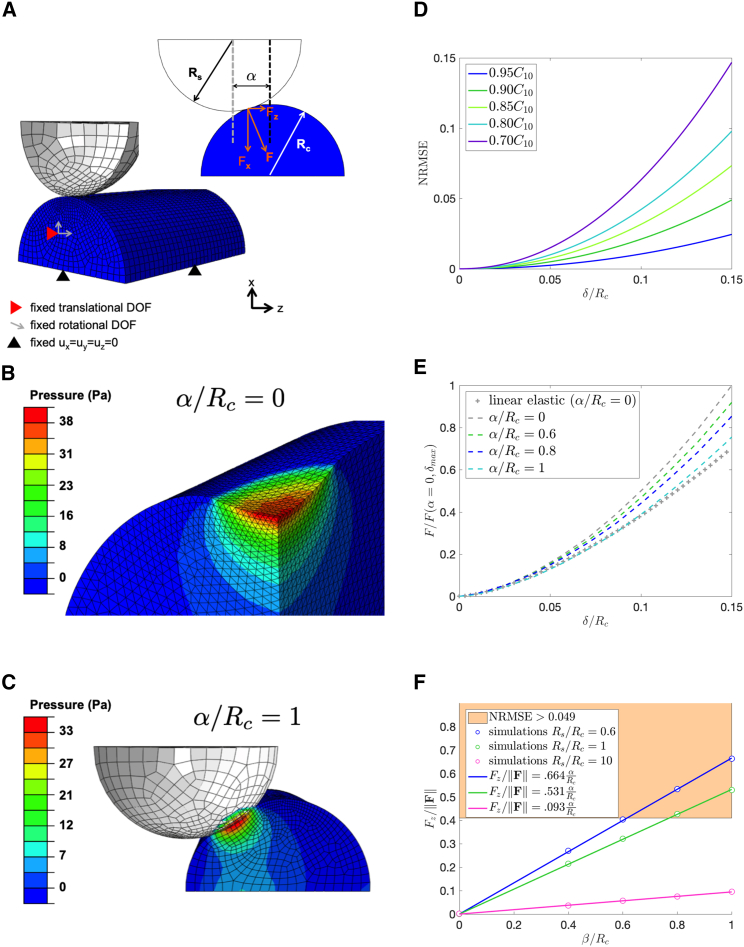
Figure 2.

Effects of indentation misalignment. (A) Shown is a schematic of the finite element model dimensions and boundary conditions. R_s is the radius of the spherical indenter, R_c is the radius of the cellular process, and α is the perpendicular distance that quantifies the offset of the indenter from the centerline of the specimen. (B) Shown is a finite element simulation of resulting pressure distribution when α = 0. (C) Pressure distribution when α/R_c = 1 shows a decrease in peak pressure at the point of contact. (D) Shown is the plot of normalized root mean-square error (NRMSE) of the force obtained by varying the value of C₁₀ in a simplified Mooney Rivlin material (C₀₁ = 0) under indentation. The x axis is a nondimensional measure of indent depth. An NRMSE value greater than 0.049 is associated with >10% error in the material stiffness. (E) Shown is the normalized force versus nondimensional displacement for various amounts of offset in the case of R_s/R_c = 1. (F) Computational models provide a measure of tangential force (F_z) to force magnitude for various amounts of offset for different values of R_s/R_c. The shaded area of the plot encompasses the region where the NRMSE > 0.049. A threshold of $F_z/\Vert \mathbf{F}\Vert =.41$ results in an experiment being deemed unreliable for obtaining material properties. To see this figure in color, go online.

Finite element simulations were performed with the commercial package Abaqus (Dassault Systèmes) to obtain the force-displacement relationships for each combination of R_s/R_c and α. A rigid spherical indenter was prescribed a normal displacement of 0.75 μm into a hyperelastic cylindrical specimen using a frictionless contact. Although the prescribed displacement conditions in the experimental setup are different (because the scaffold is translated into the bead during the experiments), the resulting force-displacement behavior from the model is equivalent to the experiment. The purpose of the computational model was not to capture the bead deflection from the OT center but rather the effects of misalignment on the total force and indentation depth (δ) at the cell surface. For each value of R_s/R_c, individual simulations were performed with varying amounts of α (α/R_c = 0, 0.4, 0.6, 0.8, 1).

A mesh convergence study was initially performed to obtain the minimum necessary element size at the contact interface. Several simulations were performed with the smallest element size at the center of contact varying between 2.5 × 10⁻⁵ and 5 × 10⁻⁴ mm. It was observed that all simulations (including the coarsest mesh) were able to accurately capture the theoretical force-displacement curves for a linear elastic material at small strains, although a minimum element size of 1 × 10⁻⁴ mm was necessary for the convergence of the total internal energy.

To reduce computational costs, a symmetric plane was enforced transverse to the cylinder length. Effects from the free boundary end were avoided by making the total length of the cylindrical specimen in the model at least twice the length of the major axis of the elliptical contact area. The bottom face of the model was given a fixed displacement boundary condition (u_x = u_y = u_z = 0). In reality, a smaller surface area would adhere to the PVDF fiber, as shown in the TEM image of Fig. 1, allowing for more expansion in the out-of-plane directions. Here, we are exclusively interested in the relative effect of misalignment and therefore not largely concerned with replicating the wide range of possible cell adhesion boundary conditions.

Because biological materials often undergo large deformations (δ/R_c > 0.05) and demonstrate a strain-stiffening behavior (30, 31), it is desirable to obtain material parameters that can describe the cell as a hyperelastic material. A commonly used hyperelastic model for soft materials is the incompressible Mooney Rivlin model, as described previously with the strain energy density function in Eq. 2. Because we are only interested in using the model to quantify the effects of misalignment, C₀₁ was set equal to zero, so that Eq. 2 reduces to a simpler strain energy density function (the neo-Hookean strain energy for hyperelastic materials).

To obtain bounds for the experimental data, we calculated the normalized root mean-square errors (NRMSE) due to various amounts of α. The normalized NRMSE is calculated by the following:

$$\text{NRMSE}=\frac{RMSE}{F\left(\alpha =0,{\delta }_{max}\right)},$$ (4)

where

$$\text{RMSE}=\sqrt{\frac{{\text{Σ}}_T{\left(F\left(\alpha \right)-F\left(\alpha =0\right)\right)}^2}{T}}.$$ (5)

The summation in the second expression is performed at T values (sample points) of normalized indentation depth δ/R_c. Note that the root mean-square error is normalized by the forces of a perfectly aligned sphere at the maximum indentation depth (F(α = 0, δ_max)).

Because errors due to α would likely depend on the ratio of R_s/R_c, simulations were performed to encompass the values of R_s/R_c (in the range of 0.6–10) observed in the experiments. As shown in the pressure distribution contour plots of Fig. 2, B and C, as one increases the misalignment offset, the cell experiences smaller stresses.

Fig. 2 D shows that for α = 0, the NRMSE value greater than 0.049 is associated with >10% error in the estimated material stiffness, C₁₀. This provides a threshold for an acceptable NRMSE value. Fig. 2 E shows a comparison of normalized force-displacement curves for various values of α alongside the theoretical curve for a linear elastic material when R_s/R_c = 1. The NRMSE plots for R_s/R_c = 0.6 and R_s/R_c = 10 can be found in the Supporting Materials and Methods.

Note that an offset value of α/R_c = 1 corresponds to forces that are of similar magnitude to a linear elastic approximation (with no offset) as shown in Fig. 2 E. Because a 10% error in moduli resulted in an NRMSE of 0.049, we used the computational model to provide the range at which NRMSE >0.049. The NRMSE threshold was found to be exceeded when the ratio of tangential force (F_z) to force magnitude $\left(\Vert \mathbf{F}\Vert \right)$ was greater than 0.41 as seen by the shaded region in Fig. 2 F. Any experiments with measured forces of $F_z/\Vert \mathbf{F}\Vert >0.41$ were therefore discarded because they could generate significant errors in the determination of moduli.

Limitations

One limitation of our experiment is that the indentation formulation requires a relatively rigid scaffold. Although one could use the indentation formulation for scaffold fibers with a Young’s modulus ≥30 MPa, the experimental boundary conditions are changed in the presence of softer scaffold fibers. Using a softer material for the scaffold fibers could potentially result in fiber bending during indentation, thereby changing the observed values for δ.

It is well known that cells exhibit different mechanical properties depending on the stiffness of their underlying substrate (10, 50, 51, 52). This experiment provides a more realistic morphology, but the underlying substrate is not the same as in vivo conditions, which could alter the cytoskeletal structures and mechanical properties of the cell. The cells also do not interact with the electrospun scaffolds in the same way as a native ECM (degradation, deposition, etc.), which could also influence the cellular phenotypes and mechanical properties (53). Nevertheless, it allows us to probe glial cellular processes, a morphological feature that is nearly lost when glial cells are grown on flat 2D substrates (27, 28, 54).

The OT setup presented here is capable of high resolution. However, it is limited by the maximum force (∼20 pN) and maximum allowable deflection (∼600 nm) of the trap. With the particular laser beam intensity and silica beads used in our experiment, the maximum allowable deflection limited us to probing only the first 600 nm from the cell membrane surface. It is uncertain if the majority of our results only reflect the actin cortex, although we did see evidence of variation in stiffness values within the first 300 nm. It should also be noted that, even though our results show nearly homogeneous values of stiffness for the first 600 nm of indentation, there could be a higher limit (>600 nm) that also shows relative homogeneity. The smallest processes probed in our experiments were roughly 700 nm in diameter, but this setup can be used to probe smaller processes (as small as 270 nm), as defined by the Rayleigh criterion: $d=\left(1.2\lambda \right)/\left(2N.A.\right)$ (where d is the minimum resolved feature size, λ ≈ 550 nm, and N.A. = 1.25 in our experimental setup).

Although we did not distinguish between glial cell types during the experiment, we performed immunostaining on fixed specimens to have an idea of the cell type populations present in our scaffolds (see Supporting Materials and Methods). Although astrocytes were the most prevalent in the cell cultures, the experimental results contain a mix of these cell types, and thus no conclusions should be drawn regarding differences between specific cell type and properties. In future work, it is possible to use fluorescent labeling with our experimental setup to establish relationships between cell types and the nonlinear mechanical properties.

The experimental setup presented in this study could be modified to observe viscoelastic behavior and simultaneously perform in situ visualization of cytoskeletal components during indentation. Based on previous literature, it is possible that indentation with our experimental setup would result in cytoskeletal depolymerization, thereby causing hysteretic behavior (55, 56). By modifying the experiment to incorporate cyclic loading over time, one might expect to see additional irreversible effects, such as overall softening in the mechanical response.

Results

Parameter fitting

Because the determination of the initial contact point is important for the characterization of the force-displacement relationship (57), we utilized streptavidin-coated silica beads adhered to biotinylated cell membrane surfaces. This allows us to specify that the bead is in contact with the cell membrane when δ = 0. The biotin itself is incorporated into the glycocalyx layer (or “cellular brush”) surrounding the cell membrane. In reality, the first 10–50 nm of the indentation is probing the cellular brush, which can be accounted for using a “brush model” during indentation analysis (58, 59). For the cells in this study, the thickness of the cellular brush is negligible, and is within the error in tracking the positional data of the bead (which was found to be ∼20 and 30 nm in the x and y directions, respectively). Error in the experiments was dominated by noise in bead movement due to Brownian movement as well as nearby molecules being drawn into the OT during the experiment. The uncertainty in the OT stiffness was less influential than fluctuations in bead movement (more details within Supporting Materials and Methods).

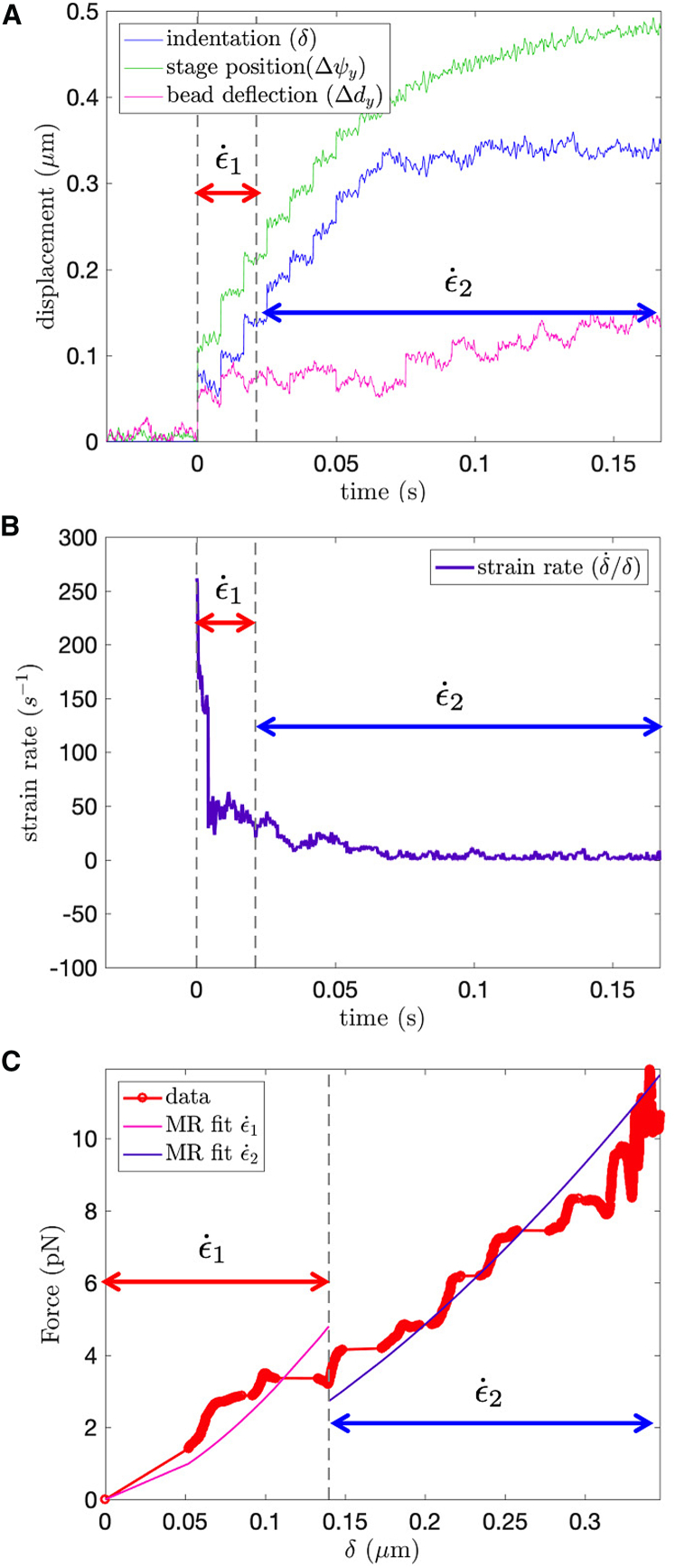
The strain rate was calculated using the conventional definition of indentation velocity over indentation depth $\left(\dot{\mathrm{ϵ}}=\dot{\delta }/\delta \right)$ (60). Across all experiments, an initial “jump” in the displacement of the piezo stage resulted in a high apparent initial strain rate, whereas the slower approach to the final position resulted in a slower strain rate (Fig. 3 A). The initial and strongly varying regime has substantially higher strain rates $\left({\dot{\mathrm{ϵ}}}_1\approx 50-400{\mathrm{s}}^{-1}\right)$ than the later low strain rate regime $\left({\dot{\mathrm{ϵ}}}_2\approx 2-40{\mathrm{s}}^{-1}\right)$ as shown in in Fig. 3 B, but the second strain rate regime has an essentially constant strain rate and thus provides a better measure of material behavior. The end of the first strain rate regime typically occurred when the instantaneous strain rate first dropped below 30 s⁻¹. This is based on the premise that brain tissue has shown significantly different material properties between strain rates of 30 and 60 s⁻¹ (61). The desired material properties can be fitted separately for the two strain rate regimes (denoted as ${\dot{\mathit{ϵ}}}_1$ and ${\dot{\mathit{ϵ}}}_2$ in Fig. 3 C).

Figure 3.

Depiction of force-displacement relationship obtained from a single experiment. (A) The piezo stage initially jumps (green line) to a large displacement during ${\dot{\mathrm{ϵ}}}_1$, resulting in a large jump in indentation depth (blue line). The piezo stage then slows down to its final position during ${\dot{\mathrm{ϵ}}}_2$. (B) The average initial strain rate $\left({\dot{\mathrm{ϵ}}}_1\right)$ is at least one order of magnitude larger than the second strain rate $\left({\dot{\mathrm{ϵ}}}_1\right)$. The time at which the strain rate transitions from high (>100 s⁻¹) to low (<20 s⁻¹) is calculated for each test. Strain rate is defined as $\dot{\delta }$/δ. (C) The displacement at which the strain rate transitions is found so that a hyperelastic force-displacement curve is fit to each strain rate regime. To see this figure in color, go online.

The desired hyperelastic constants, C₁₀ and κ, were found for the two strain rate regimes. The resulting force-displacement curve is separately fit to a Mooney Rivlin model for each of the two strain rate regimes by minimizing the squared error between the theoretical curve and experimental data. The hyperelastic constant C₁₀ ranged from 1 to 20 Pa across all experiments and strain rates, whereas κ ranged from 0.17 to 0.75 (note that κ = 1 corresponds to a neo-Hookean hyperelastic material). Because of the soft nature of the glial cells, the hyperelastic model was necessary because indentation strains ranged from ${\delta }_{max}/R_c\subset \left[0.08,0.86\right]$.

It should be noted that for large indentation strains (where the indentation strain can be defined as δ/R_c), the force-displacement relationship becomes less accurate because of substrate interactions. In the case of large indentation strains, the cell will experience restriction of deformation in the loading direction and possibly more strain along the length of the cylinder (due to incompressibility). Furthermore, the type of boundary condition (i.e., “full-adhered” versus “no adhesion”) at the cell-fiber or cell-substrate interface will have a greater influence on the response. In reality, a combination of full-adhesion and no-adhesion modeling should be used to obtain material properties for different regions of the cell based on the presence of focal adhesions (62). Our previous work with the analysis of the hyperelastic indentation model shows that for relatively large cells (R_s/R_c ∼1), the hyperelastic formula is accurate until an indentation strain of 0.45. For smaller cells (R_s/R_c ∼20), the hyperelastic indentation model loses accuracy because of substrate effects for indentation strains greater than 0.25 (63). For the experiments presented in this study, the size ratios R_s/R_c ranged from 0.8 to 14.8. Because the mean indentation strain was 0.40 across all experiments, this indicates that in some cases (R_s/R_c ≥ 10), the effects of the substrate interaction may introduce additional uncertainty in extracting stiffness values from the force-displacement curves.

Effect of strain rate

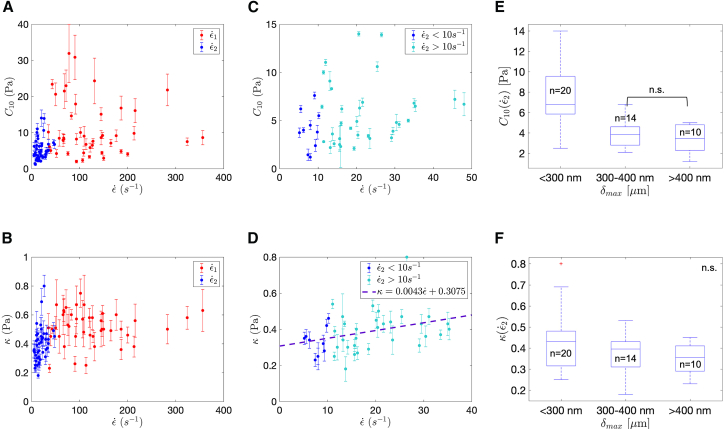
Fig. 4, A and B show the parameters C₁₀ and κ as functions of strain rate for both strain rate regimes. Because the strain rates vary within the strain rate regime, the reported strain rate values in Fig. 4, A and B were computed as the mean value of strain rate within their respective time intervals. At the high strain rate regime $\left({\dot{ϵ}}_1\right)$, the strain rate varies significantly, and therefore, the reported strain rate values are less meaningful. For this reason, the remaining plots (Fig. 4, C–F) show the parameters as a function of rate in the second strain rate regime $\left({\dot{ϵ}}_2\right)$.

Figure 4.

Summary of experimental results across all specimens. (A) Comparison of the obtained material parameter C₁₀ across the varying calculated strain rates (n = 44 for each strain rate). The higher strain rate regime (red) showed a stiffer response (paired sample two-tailed t-test, p-value$\ll 0.05$). (B) Shown is the comparison of the parameter κ across the varying calculated strain rates (n = 44 for each strain rate). The second strain rate regime (blue) showed lower κ values, indicating a more nonlinear response (paired sample two-tailed t-test, p-value$\ll 0.05$). (C) A closer look at stiffness values for the second strain rate regime is shown. For ${\dot{\mathrm{ϵ}}}_2<10s^{-1}$, stiffness values were lower (one-tailed t-test, p-value <0.05). (D) A closer look at κ for the second strain rate regime is shown. For ${\dot{\mathrm{ϵ}}}_2<10s^{-1}$, κ values were lower (one-tailed t-test, p-value <0.05). (E) No significance (n.s.) was found for stiffness when the maximum indentation depth exceeded 300 nm (multiple comparison Bonferroni test, p-value $\ll 0.05$). (F) No significance was found for κ as a function of maximum indentation (multiple comparison Bonferroni test, p-value $\ll 0.05$). To see this figure in color, go online.

The force-indentation curve for ϵ₂ is fitted through a minimization of the RMSE for values only within the ϵ₂ regime. In other words, the fitting of the ϵ₂ curve is path independent–it assumes that the forces start at zero. However, it is possible that the behavior is affected by the initial strain history in ϵ₁. By comparing the mechanical response of a given strain rate in ϵ₁ to the response (for the same given strain rate) in ϵ₂, it is possible to learn more about inelastic effects (i.e., the path-dependent behavior of the material response). Although only a small number of tests demonstrated the same strain rate response (at 50 s⁻¹ in Fig. 4, A and B), one can see a similar response in the stiffness between the ϵ₁ and ϵ₂ regimes. These results suggest that the material response is path independent, but more experiments would need to be performed at various indentation depths to draw further conclusions.

A paired sample two-tailed t-test was performed on the values of C₀₁ and κ between the high and low strain rate regimes (Fig. 4, A and B). It was found that both C₀₁ and κ were significantly higher at high strain rates (p-value $\ll 0.05$). Note that the higher values of κ correspond to a response that is more similar to a linear elastic material.

Within the second strain rate regime (Fig. 4, C and D), it is also observed that C₁₀ and κ increase at higher strain rates $\left(\dot{\mathit{ϵ}}>10{\mathrm{s}}^{-1}\right)$. When comparing the lowest strain rates (<10 s⁻¹) to the higher strain rates (>30 s⁻¹), the stiffness C₁₀ increases approximately by a factor of 2. A one-tailed t-test showed that C₁₀ is lower for $\dot{\mathrm{ϵ}}<10{\mathrm{s}}^{-1}$ (p-value = 0.041). A stiffer cellular response is expected at higher strain rates because cross-linkers in the cytoskeleton have sufficient time to rearrange during slowly applied forces (64, 65, 66). At higher strain rates, there is not enough time for cross-link rearrangement, and the cytoskeletal networks (e.g., actin networks) behave more rigidly (64, 65). At lower strain rates, κ was also significantly lower (t-test, p-value = 0.045), meaning that the response deviated farther from linear elastic theory. A summary of the measured cell properties for various strain rates is shown in Table 1. Note that the large SD from the mean values in the range of 30–360 s⁻¹ is mostly attributed to the fact that the ϵ₁ regime consists of a wide range of strain rates. Although we used a hyperelastic formulation to obtain material properties, the values of the approximate elastic moduli are provided to compare with previous reports on cell mechanical properties (which often provide the shear or elastic modulus under the assumption of linear elasticity or viscoelasticity).

Table 1.

Material Properties of Cells in 3D Scaffolds with Respect to$\dot{\mathrm{\epsilon }}$ in This Study

Strain Rate	Mean C10(Pa)	Mean κ	∗E (Pa)	EH (Pa)	Sample Size
0–10 s−1	4.039 ± 2.0	0.33 ± 0.08	74 ± 18	43.4 ± 23	n = 10
10–30 s−1	5.7 ± 3.9	0.40 ± 0.13	85 ± 31	52.7 ± 35	n = 28
30–360 s−1	10.3 ± 7.4	0.51 ± 0.11	122 ± 66	87.0 ± 61	n = 50

Results are presented as the mean value with SDs. Elastic moduli values (^∗E) are given by the small strain approximation, ^∗E = 4(1 + v)(C₁₀ + C₀₁), assuming v = 0.5. The variable E_H is the Young’s modulus found by fitting the force-displacement data to the classical Hertzian relationship.

Stiffness and maximum indentation depth

To understand where heterogeneities due to cytoskeletal constituents might occur along the indentation depth, a statistical comparison was performed between the maximum indentation depth locations (δ_max) and the material properties. Fig. 4, E and F compares material properties for the lower strain rates $\left({\dot{ϵ}}_2\right)$ with δ_max. A one-way analysis of variance test followed by Bonferroni’s multiple comparison test showed a significant difference (p-value$\ll 0.05$) in stiffness between δ_max < 300 nm and the two other groups (δ_max = 300–400 nm and δ_max > 400 nm). We did not see any correlation between κ and the maximum indentation depth δ_max (Fig. 4 F). Our results suggest that differences in stiffness can occur within the first 300 nm of the surface; however, the majority of cells showed similarly low stiffness values at large maximum indentation depths (Fig. 4 E). The mean maximum force (F_max) across all experiments was ∼10 ± 3.5 pN, whereas the mean maximum indentation depth (δ_max) was ∼320 ± 100 nm. Individual cell process diameters ranged from 0.7 to 11.8 μm, and final indentation depths ranged from 130 to 550 nm (slightly below the maximum allowable bead deflection of the OT).

We expected to see more variation in the mechanical response of cells at large indentation depths because the cytoskeleton underneath the actin cortex would presumably vary across specimens. However, our results suggest that most glial cells showed similar stiffness values at indentation depths >300 nm. Previous studies suggest that the actin cortex can be heterogeneous because of various structural types (e.g., mesh network versus fiber bundles) within subregions of individual cells (67). Although we were not able to visually observe the subcellular actin structures in situ, our results support the idea that variations in the mechanical properties of the actin cortex exists between cells—an observation that has been noted in previous literature (67, 68, 69).

Discussion

Nonlinearity in mechanical response

To determine the extent of nonlinearity demonstrated in the experimentally found parameters (Table 1), the previously described computational model was used to obtain the maximum principal stress and maximum principal logarithmic strain found at the center of the contact area (Fig. 5). The model used a stiffness value of C₁₀ = 5 Pa (the average value found from the experiments across all strain rates), along with the average values of κ (κ = 0.3 at lower strain rates, κ = 0.5 at higher strain rates). In this example (which only shows results for the case of R_s/R_c = 1), the response begins to show deviation from the linear elastic model for maximum principal strains ≥0.08. An 18% maximum principal logarithmic strain results in ∼15% difference in stress between κ = 0.3 and the linear elastic case. Fig. 5 shows that the approximation of κ = 1 matches the linear elastic solution for a maximum principal logarithmic strain ≤0.15.

Figure 5.

Using an average of the experimentally found parameters (C₁₀= 4 Pa), the computational model was used to evaluate the maximum principal stress versus maximum principal strain. The range of κ found in our experiment (κ = 0.3–0.5) differs from the linear elastic formulation case for the maximum principal strain ≥0.08. Here, κ is the nondimensional parameter from the Mooney Rivlin (MR) model. The solution approaches linear elasticity when κ = 1. Stress is normalized by either the Young’s modulus E (elastic case) or ^∗E = 4(1 + v)(C₁₀ + C₀₁) (MR case) with the assumption of v = 0.5.

Comparison to previous literature

Even within the same cell type, different types of experimental testing procedures can result in elastic moduli that vary 1000-fold because of the extent of deformation, the rate of deformation, the geometry of the probe, the location probed in the cell, and the extracellular microenvironment (70). For glial cells, the measured Young’s modulus reported in literature varies by several orders of magnitude (100 Pa–100 kPa) (71, 72, 73, 74).

A comparison of the elastic moduli found for different CNS cells in previous literature is shown in Table 2. The most comprehensive experiment on mechanical properties of CNS cells was performed by Lu et al., in which the Young’s modulus of glial cell processes was found to be between 0.1 and 1 kPa (with softer moduli corresponding to lower frequencies of vibratory loading) (71). Using an approximation of E = 4(1 + v)(C₁₀ + C₀₁) and ν = 0.5, the Young’s modulus extracted from our curve fitting (^∗E) varies from 74 to 122 Pa (depending on the loading rate). Although previous literature does not list the properties as a function of strain rate, the approximate Young’s moduli we found (^∗E) at the higher strain rates are similar to the majority of previous studies (∼100 Pa). Our results for stiffness during the slow strain rate regime are closer to the reported experimental values of glial scar CNS tissue (E = ∼50 Pa) found with a large spherical indenter (∼100 μm) at slower indentation velocities (5–10 μm s⁻¹) (75).

Table 2.

Comparison of Material Properties of CNS Cells Grown on 2D Substrates

Study	Cell Type and Region	Approximate Elastic Modulusa	Method
Moeendarbary et al. (75)	neocortex slice	50–500 Pa	AFM
Lu et al. (71)	astrocyte process	90–150 Pa	AFM
Ayala et al. (72)	astrocyte process	108 Pa	optical tweezers
Lu et al. (53)	astrocyte process	200 Pa	AFM
Lu et al. (71)	astrocyte soma	300 Pa	AFM
Lu et al. (71)	neuron process	320 Pa	AFM
Elkin et al. (83)	organotypic slice	135–380 Pa	AFM
Bernick et al. (33)	neuron soma	204 Pa	AFM
Iwashita et al. (84)	neuron soma	230 Pa	AFM
Urbanski et al. (85)	freshly excised tissue	250 Pa	AFM
Grevesse et al. (86)	neuron soma	1050 Pa	magnetic tweezers
Grevesse et al. (86)	neuron process	7000 Pa	magnetic tweezers
Spedden et al. (36)	neuron soma	550 Pa	AFM
Miller et al. (73)	astrocyte process	57,000 Pa	AFM
Lee et al. (74)	astrocyte soma	142,000 Pa	AFM

^aFor cases in which only a shear modulus is reported, the Young’s modulus was approximated by using v = 0.5. For vibratory loading, the elastic storage modulus at the lowest available frequency was cited.

In addition to the lack of strain rate data in the literature, differences between our results and the literature could also be attributed to the fact that the references in Table 2 use different measurement techniques as well as different force-indentation relationships for finding the material parameters (70). In Table 2, we also show the calculated values of E_H for our experiments, which assumes a linear elastic half space (as opposed to the hyperelastic cylindrical formulation used to approximate C₁₀, κ, and hence, C₀₁). The calculation of E_H uses the classical Hertz formulation, given in Eq. S2. Note that the material properties shown in Table 2 are primarily for cells grown on 2D substrates (with the exception of the experiments on neocortex slices, organotypic slices, and freshly excised tissue).

Conclusion

In conventional cell indentation experiments, a small spherical probe or pyramidal tip is used, which often reflects the stiffness of local cytoskeletal components but not the overall cell stiffness (76). By using a larger spherical indenter (R_s ∼ R_c), the length scale probed in this study is useful for studying the overall mechanical properties of cells in future diagnostic methods for disease and injury. Our approach also allows one to probe large indentation depths (δ_max/R_c) while still measuring the cell mechanical properties over the desired region of interest.

By obtaining positional data during the indentation of optically trapped beads with cells grown in scaffolds, we have developed a method to obtain local mechanical properties of cells grown in a 3D environment. To our knowledge, this is a novel use of indentation via optical trapping and provides a way to measure the local properties of adherent cells in a 3D environment. Through a computational model, we also provide experimental bounds on the required alignment when indenting cylindrical bodies with a spherical indenter. In the future, it is possible to use this technique to evaluate new biomaterials by comparing the mechanical properties of cells within different fibrous 3D substrates. Although we performed our experiments with CNS glial cells, future studies can also use this approach to probe the strain rate dependent and nonlinear properties of various adherent cell types in a more native environment.

Author Contributions

A.D., K.T.R., and A.V. designed research. A.D., L.R., and S.O. performed research. A.D., L.R., S.O., S.H.K., and A.V. contributed new reagents and analytic tools. A.D., L.R., and K.T.R. analyzed data. A.D., K.T.R, L.R., S.O., S.H.K., and A.V. wrote the article.

Editor: Jochen Guck.

Supporting Citations

References (77, 78, 79, 80, 81, 82) appear in the Supporting Material.