Surface and Bulk Stresses Drive Morphological Changes in Fibrous Microtissues

Abstract

Engineered fibrous tissues consisting of cells encapsulated within collagen gels are widely used three-dimensional in vitro models of morphogenesis and wound healing. Although cell-mediated matrix remodeling that occurs within these scaffolds has been extensively studied, less is known about the mesoscale physical principles governing the dynamics of tissue shape. Here, we show both experimentally and by using computer simulations how surface contraction through the development of surface stresses (analogous to surface tension in fluids) coordinates with bulk contraction to drive shape evolution in constrained three-dimensional microtissues. We used microelectromechanical systems technology to generate arrays of fibrous microtissues and robot-assisted microsurgery to perform local incisions and implantation. We introduce a technique based on phototoxic activation of a small molecule to selectively kill cells in a spatially controlled manner. The model simulations, which reproduced the experimentally observed shape changes after surgical and photochemical operations, indicate that fitting of only bulk and surface contractile moduli is sufficient for the prediction of the equilibrium shape of the microtissues. The computational and experimental methods we have developed provide a general framework to study and predict the morphogenic states of contractile fibrous tissues under external loading at multiple length scales.

Significance

Cell aggregates have been serving as a model for in vitro studies of morphogenesis. The equilibrium configurations of aggregates display analogies with liquid drops as a manifestation of surface tension. We study to what extent these conclusions can be extended to fibroblast-populated three-dimensional collagen gels, another classical model for morphogenesis and wound healing. Using microelectromechanical systems and robotics technology along with computational modeling, we demonstrate that surface stresses that emerge from spatially distributed collective cellular contractility play a key role in the shaping of engineered fibrous microtissues. The presented biomimetic three-dimensional model and the experimentally validated computational modeling framework facilitate the discovery of the biophysical principles of self-assembly and self-healing for tissue engineering and regenerative medicine.

Introduction

Tissue morphogenesis, the shaping of tissues, is a critical process during development and repair. During development, coordinated cell movement and rearrangement, deposition and assembly of extracellular matrix (ECM), and asymmetric cellular contractility morph the embryo into a coherent body that consists of compartmentalized organs and tissues with characteristic shapes and well-defined boundaries (1). When tissues are injured, these embryonic processes are partially recapitulated, which leads to a reconstruction process (2). Whereas much research has focused on understanding the signaling pathways involved in wound closure (3, 4, 5), little is known about the mesoscale physical principles of multicellular organization required to restore the architecture of three-dimensional (3D) tissues during repair.

In fibrous tissues, fibroblasts physically interact with the surrounding nonlinear elastic and viscoelastic ECM (6, 7, 8). These interactions are studied in vitro by encapsulating cells within 3D biopolymer hydrogels such as collagen and fibrin (9, 10, 11, 12). Once the scaffold is polymerized, cells adhere to and pull on the fibers, resulting in the contraction of the hydrogel (13, 14, 15, 16). Pioneering research suggested a central role for traction forces in closing skin wounds (17, 18, 19). With the invention of microengineered wound healing models, it has been experimentally confirmed that epidermal tissue repair is regulated by cellular forces (20, 21).

Construction of 3D tissue architecture, however, is not solely driven by bulk tissue contraction. Wound-activated closure of topological defects resembles morphogenetic events associated with embryogenesis (2, 22, 23). Embryonic tissues are best modeled as viscous liquid drops whose shape is governed by the minimization of free surface energy (24, 25, 26, 27). Similarly, 3D cell aggregates show fluid behavior at longer timescales (28, 29, 30, 31). Surface stresses of even synthetic soft materials that are in thermodynamic equilibrium are strong enough to deform solid bodies in their bulk (32, 33). Surface stress of solids becomes equivalent to surface tension of liquids when stress is constant and the surface behavior is isotropic. Although surface stresses are important drivers for shaping living and synthetic materials, theoretical and computational studies of fibrous tissues have so far been focused on mechanical anisotropy and nonlinear elasticity and have neglected the surface effects (34, 35, 36, 37, 38).

Given its role in shaping embryonic tissues, we hypothesize that in addition to bulk contraction, cell-derived surface stresses also play a crucial role in the formation and restoration of shape in fibrous tissues, specifically at small length scales. Recent work has shown that fibroblasts accumulate at the periphery of reconstituted collagenous microtissues, which leads to formation of a heterogenous architecture containing a collagen-rich core that is sparsely populated by cells and a fibronectin-rich shell with high fibroblast density (39, 40). We postulate that the spatially heterogenous force generation and matrix remodeling within fibrous tissues can be represented in the continuum scale through the introduction of surface stresses. We employed microfabricated tissue gauge technology with robot-assisted surgical and optochemical manipulation to test this hypothesis and investigate how tissue shape evolves during self-healing of wounded fibrous microtissues. Building on an energetically motivated equilibrium theory, we developed a computational framework that consists of a novel, to our knowledge, constitutive model coupling active and passive elasticity with bulk and surface energy components. Finite-element simulations of the model recapitulated the shape response of microtissues to various surgical interventions, therefore confirming that cell-derived surface stresses play a major role in the closure of wounds and restoration of shape in fibrous microtissues. Our results also indicate that surface contractile stresses may act together with bulk contraction in sculpturing the form or drive tissue morphogenesis in opposing directions, depending on the boundary conditions.

Materials and Methods

Device fabrication

Tissue gauges were fabricated as described previously (21, 41). Briefly, polydimethylsiloxane (PDMS, Sylgard 184; Dow-Corning, Midland, MI) substrates were molded from SU-8 masters. The devices were then sterilized in 70% ethanol, followed by ultraviolet exposure for 15 min. Before cell seeding, the devices were treated with 0.02% Pluronic-F127 solution (Sigma-Aldrich, St. Louis, MO) for 10 min at room temperature.

Cell culture

NIH-3T3 fibroblasts (Sigma-Aldrich) were cultured in Dulbecco’s modified Eagle’s medium GlutaMAX (LifeTechnologies, Carlsbad, CA) supplemented with 10% fetal bovine serum (LifeTechnologies) and 1% penicillin-streptomycin (LifeTechnologies). Cells were passaged every 2–3 days using trypsin 0.25% EDTA (LifeTechnologies) and not kept longer than 20 passages. All experiments were done with cells that tested negative for mycoplasma.

Microtissue model

One million cells were suspended in 2 mg ⋅ mL⁻¹ liquid neutralized collagen type I from rat tail (Corning BV Life Sciences, Corning, NY) and seeded in the device. The entire assembly was centrifuged to drive cells into the chambers containing the cantilevers. Excess solution was then removed, leaving only the chambers filled with liquid. The device was centrifuged once again in an inverted configuration to move the cells closer to the cap of the cantilevers before polymerization. A few hours after polymerization, we observed the spontaneous contraction of the collagen matrix by the cells. Cantilevers incorporated within each chamber spatially constricted the contraction of the collagen matrix.

Large-scale tissue formation

Boundary conditions were set by pinning dissection pins (Fine Science Tools, Foster City, CA) inside the wells of a 24-well plate (1.9 cm²) coated with PDMS. Wells were sterilized with ethanol and ultraviolet treatment. To prevent cell adhesion, devices were incubated in 0.02% Pluronic-F127 solution (Sigma-Aldrich) for 10 min at room temperature. One million 3T3 cells suspended in 2 mg ⋅ mL⁻¹ liquid neutralized collagen type I from rat tail were seeded into the wells. The tissues spontaneously formed within 24 h.

Robotic micromanipulation

A compact six-degrees-of-freedom robotic system was constructed from piezoelectric stick-slip actuators that have submicron positioning precision. The design is based on an ophthalmic microsurgery platform introduced elsewhere (42). The system was teleoperated over a fully motorized Nikon Ti Eclipse (Nikon Instruments, Tokyo, Japan) microscope, which provided real-time visual feedback (Fig. S1). A 3D-printed adaptor enabled the use of a wide range of actuated and nonactuated instruments for performing operations such as implantation of microstructures, making incisions, and cutting tissue parts (Video S1). Actuation of the tools was driven by a stepper motor (Haydon Kerk Pittman, Milford, NH) controlled by an Arduino microprocessor. Full-thickness incisional wounds were generated using a dissection pin (Fine Science Tools), and microscissors (Alcon, Fort Worth, TX) were used for cutting the boundaries of the microtissues. Microimplants were fabricated from glass substrates and PDMS elastomer. Glass capillaries were filled with uncured PDMS using capillary action and subsequently heated for curing. Microimplants were inserted into the microtissues using microtweezers (Alcon).

Cytotoxic photoconversion

Medium containing 20 μM blebbistatin (in dimethyl sulfoxide; Sigma-Aldrich) was added to the culture medium 2 h after wounding the microtissues. Predefined regions of the tissues were exposed to blue light (460 nm, coolLED pE-4000; coolLED, Andover, UK) using a programmable digital micromirror device (Andor, Belfast, UK) through a Plan Apo λ 10× objective mounted on the microscope. Light exposure was pulsed five times for 3 s with 30 s periods. Light intensity was adjusted between 1 and 100 μWcm⁻² depending on the size of selected region (0.06–0.9 mm²). After light exposure, the medium containing the inhibitor was exchanged with fresh culture medium.

Microscopy and quantitative image analysis

For wide field imaging, microtissues were labeled with Hoechst 33342 (Thermo Fisher Scientific, Waltham, MA) to visualize the nuclei of the cells. Phase-contrast and fluorescent images were captured every hour for 20 h with an ORCA-Flash4.0 digital CMOS camera (Hamamatsu, Hamamatsu City, Japan) and a Plan Fluor 10× objective mounted on the microscope equipped with a live-cell incubator (Life Imaging Services, Switzerland). Time-lapse images were segmented using a semiautomated processing software in ImageJ for the quantification of gap and tissue size. Closure rate and curvature were measured by a custom script written in MATLAB (The MathWorks, Natick, MA). The script calculated the slope of the line that fitted gap size data recorded over time. For curvature measurements, the script accepted the location of the micropillars as the reference to define the global center point and the axis of symmetry. The outlines of the microtissues were digitally reconstructed by selecting points along the boundaries every 25 μm. The curvature was calculated from the radius of the circle that fitted those points. Symmetry was defined as the ratio of the average distance between the points that define the left and right boundaries/the symmetry axis.

Confocal and multiphoton microscopy

Microtissues were fixed with 4% formaldehyde, permeabilized with 0.2% Triton X-100, and blocked in 10% goat serum for 1 h at room temperature. Samples were subsequently incubated with antibodies against fibronectin (ab2413; Abcam, Cambridge, UK) and collagen (AB755P; Merck Millipore, Burlington, MA) overnight at 4°C and detected with goat anti-rabbit Alexa-647 (1:100; Thermo Fisher Scientific) conjugated antibodies. Fluorescently labeled microtissues were imaged using an inverted confocal microscope (LSM 700; Zeiss, Oberkochen, Germany) equipped with a 20× objective. Nonlabeled collagen type I was visualized by second-harmonic imaging microscopy. Images were taken with an upright Leica DM 6000 CFS microscope (Wetzlar, Germany) equipped with a 20× water immersion objective and HeNe laser source (excitation 800 nm, second-harmonic light detection with a 400/15 cutoff filter). Representative images are z-projections of three to five images.

Viability assay

For staining live and dead cells, the Viability/Cytotoxicity Assay Kit (Biotium, Fremont, CA) was applied according to the manufacturer’s protocol. Briefly, a staining solution of 2 μM calcein acetoxymethyl as living cell stain (green) and 4 μM ethidium homodimer III as dead cell stain (red) was prepared in phosphate-buffered saline. Microtissues were incubated for 40 min in the staining solution, washed three times, and resuspended in phosphate-buffered saline solution.

Statistical analysis

All values were given as mean ± SEM or shown as box plots. The central mark within the box indicates the median, and the borders are the first and third quartiles. Whiskers were shown as dashed lines. Statistical significance was calculated with unpaired Student’s t-test. p-Values greater than 0.05 were considered to be statistically not significant.

A new equilibrium theory for contractile microtissues

The main constituents of the experimental model are collagen fibers, fibroblasts, and culture medium. The solid collagen network was modeled as a two-dimensional (2D) foam-like material with high compressibility, whereas the fluid component was not explicitly modeled. Contraction of the tissue on its surface and in the bulk were driven by isotropic packing of the constituent collagen fibers. We refer the reader to (43) for the general theory on the curvilinear kinematics of the surface and the volume of a 2D soft body and (44) for the specific considerations implemented in this work. We adopted the same notation in the following formulation.

We consider a continuum body that takes the material (or reference) configuration ${\mathrm{ℬ}}_0$ in the fully relaxed state and spatial (or current) configuration ${\mathrm{ℬ}}_t$ at time t > 0 under loading. The spatial and material coordinates x and X are connected through an invertible deformation map x = ϕ(X). We can define the deformation gradient as F = Gradϕ(X) through this map. The Jacobian determinant J = det(F) defines the volumetric change of a material volume element dV to a spatial volume element dv. The boundary of the body is defined by a network of smooth curves ${\mathcal{C}}_0^{\kappa }\left(\mathbf{X}\right)$ in the material configuration, with κ = 1, n_curv, where ${\mathcal{C}}_0=\cup {\mathcal{C}}_0^{\kappa }\left(\mathbf{X}\right)=\partial {\mathrm{ℬ}}_0$. The intersections of n_curv curves define n_poin points ${\mathrm{P}}_0^{\pi }$ with π = 1, n_poin. The curve deformation gradient is defined as $\tilde{\mathbf{F}}=\widetilde{\text{Grad}}\varphi \left(\mathbf{X}\right)=\lambda \mathbf{t}\otimes \mathbf{T}$, where λ = dl/dL denotes curve stretch and tangents T to boundary $\partial {\mathrm{ℬ}}_0$ are convected by the deformation to $\mathrm{t}=\left(\tilde{\mathbf{F}}\cdot \mathbf{T}\right)/\tilde{\mathbf{F}}\cdot \mathbf{T}$. Boundary line elements dL of ${\mathcal{C}}_0=\partial {\mathrm{ℬ}}_0$ are mapped to elements dl of ${\mathcal{C}}_t=\partial {\mathrm{ℬ}}_t$ through the curve Jacobian $\tilde{J}=\widetilde{\text{det}}\tilde{\mathbf{F}}=\left|\tilde{\mathbf{F}}\cdot \mathbf{T}\right|/\left|\mathbf{T}\right|$. In the 2D setting, the curve Jacobian equals the curve stretch $\lambda =\tilde{J}$.

After the definition of the bulk and surface kinematics of the system, we move to the energetic considerations. We made the assumption that there were no internal dissipation mechanisms such as diffusion, viscoelasticity, or any dissipation that may stem from the chemical cycle associated with the contraction of fibroblasts. As a result, all deformations are fully recoverable. We postulate that the system can be described through a bulk potential energy U₀ = W₀ + V₀ per material unit volume in ${\mathrm{ℬ}}_0$ and a surface potential energy u₀ = w₀ + v₀ per material surface length in $\partial {\mathrm{ℬ}}_0$. The internal contributions can be defined as W_o(F; X) and $w_o\left(\tilde{\mathbf{F}};\mathbf{X}\right)$, whereas the external contributions can be defined as V_o(ϕ; X) and v_o(ϕ; X). Note that W_o(F; X) and $w_o\left(\tilde{\mathbf{F}};\mathbf{X}\right)$ are equivalent to the bulk and surface components of the Helmholtz free energy because our material is nondissipative and perfectly elastic. We restricted the surface potential energy to be isotropic, and thus, w₀ is independent of T. The passive elasticity of the collagen network along with the active contraction of encapsulated fibroblasts provides the bulk potential energy, whereas the surface potential energy stems from the active contraction of fibroblasts residing on the surface of the tissue at equilibrium. The formation of surface stresses is a manifestation of underlying biological processes, including the migration of cells toward the surface and the local rearrangement of the fibronectin matrix though cell-induced forces.

The total potential energy functional I(ϕ) is defined as

$$I\left(\varphi \right)={\int }_{{\mathrm{ℬ}}_0}{U}_o\left(\mathbf{F},\varphi ;\mathbf{X}\right)dA+{\int }_{{\mathcal{C}}_0}{u}_o\left(\tilde{\mathbf{F}},\varphi ;\mathbf{X}\right)dL.$$ (1)

An equilibrated configuration is obtained by minimizing this functional considering all admissible deformations δϕ. By adding the constraint that the first variation must be equal to zero δI(ϕ) = 0, we obtain a weak form statement as

$${\int }_{{\mathrm{ℬ}}_0}\mathbf{P}:\text{Grad}\delta \varphi dA+{\int }_{{\mathcal{C}}_0}\tilde{\mathbf{P}}:\widetilde{\text{Grad}}\delta \varphi dL={\int }_{{\mathrm{ℬ}}_0}{\mathbf{b}}_0\cdot \delta \varphi dA+{\int }_{{\mathcal{C}}_0}{\tilde{\mathbf{b}}}_0\cdot \delta \varphi dL.$$ (2)

The two-point bulk and surface Piola stress tensors are given by

$$\mathbf{P}={\partial }_{\mathbf{F}}{U}_0\text{and}\tilde{\mathbf{P}}={\partial }_{\tilde{\mathbf{F}}}{u}_0,$$ (3)

where we define the operator ${\partial }_{\left(\cdot \cdot \right)}(\cdot )=\partial (\cdot )/\partial \left(\cdot \cdot \right)$. The partial derivative of the bulk potential energy is taken with respect to the deformation gradient, whereas the partial derivative of the surface potential energy is taken with respect to the surface deformation gradient. The body forces and tractions are given by

$${\mathbf{b}}_0=-{\partial }_{\varphi }{U}_0\text{and}{\tilde{\mathbf{b}}}_0=-{\partial }_{\varphi }{u}_0.$$ (4)

Following the derivation presented in (44), we can finally arrive at a set of localized force balance equations.

To relate the stress at any material point to deformation, we have to consider constitutive laws for the mechanical components. We consider an internal surface energy $w_0\left(\tilde{J}\right)$ that captures the contribution of cellular contractility at the tissue surface and a bulk internal energy given by $W_0\left(I_1,J\right)=W_0^p\left(I_1,J\right)+W_0^a\left(J\right)$. The bulk internal energy consists of a passive term that captures the permanent elasticity of the collagen network, including compressibility effects, and an active term that represents the bulk contractility of fibroblasts. The internal surface energy component must recapitulate the empirical results, including the minimization of surface area and associated reduction of boundary curvature that resembles fluids retaining constant surface tension. On the other hand, the deformations are restricted by the solid nature of the bulk material and the given boundary conditions. This leads to the choice of a specific internal surface energy that is constant per unit deformed surface length, described as

$$w_0\left(\mathbf{F}\right)=\gamma \tilde{J},$$ (5)

where γ is an equilibrium value that corresponds to the energy per unit area for the equilibrated tissue. We will refer to γ as the contractile surface modulus because it represents the level of cellular contractility on the surface at the equilibrium state. The Piola surface stress tensor from (Eq. 3) is obtained as

$$\tilde{\mathbf{P}}=\gamma \tilde{\mathbf{F}}/\tilde{J}$$ (6)

and the Cauchy surface stress tensor as

$$\tilde{\mathbf{\sigma }}=\tilde{\mathbf{P}}{\tilde{\mathbf{F}}}^T/\tilde{J}=\gamma \tilde{\mathbf{I}},$$ (7)

where Ĩ is the surface unit tensor. The implication of (Eq. 7) is that the surface Cauchy stress is constant and isotropic, thus resembling surface tension of liquids. The active part of the bulk energy is chosen to be

$$W_0^a\left(J\right)=\eta J.$$ (8)

Active bulk energy is a function of the volume change of the bulk J based on the assumption that the contractile action of the cells is locally relative to the volumetric deformation. The bulk contractile modulus, η, represents the equilibrium value of cellular contractility in the bulk of the tissue. The passive elasticity follows a compressible neo-Hookean model:

$$W_0^p\left(I_1,J\right)=\frac{\mu }{2}\left(I_1-3-2lnJ\right)+\frac{\lambda }{2}{\left(1-J\right)}^2,$$ (9)

where μ and λ are the shear and bulk modulus of the tissue and I₁ = tr(C) = tr(F^TF) is the first principal invariant of the right Cauchy-Green deformation tensor. Finally, the Piola stress tensor from Eq. 3 is derived as

$$\mathbf{P}=\frac{\mu }{2}\left[\mathbf{I}:\left(2\mathbf{F}-2{\mathbf{F}}^{-T}\right)\right]+\left[\lambda \left(1-J\right)+\eta \right]J{\mathbf{F}}^{-T}.$$ (10)

The proposed equilibrium theory allows the consideration of cell-derived surface and bulk contraction. The displacement field is calculated with respect to an initial state, which corresponds to an undeformed and stress-free tissue. Mechanical stresses and tractions can be extracted from the model. Loading can be imposed either by defining nonzero contraction moduli γ and η—which correspond to the surface and bulk terms, respectively—or through the application of external forces.

Results

Shape evolution of fibroblast-populated collagen microtissues

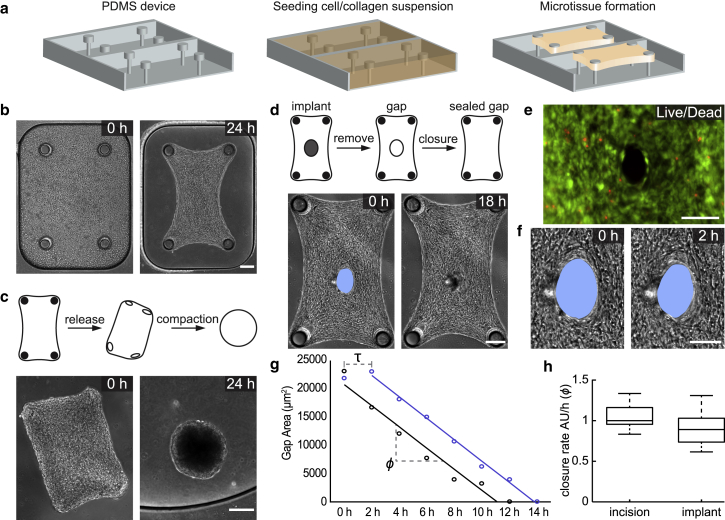
To systematically study the effect of mechanical perturbations on tissue morphology, we generated arrays of 3D constrained microtissues consisting of NIH-3T3 fibroblasts encapsulated in a type I collagen matrix that were suspended inside microwells over multiple PDMS cantilevers (Fig. 1 a). Fibroblasts compacted the collagen matrix and formed 3D microtissues around the caps of the cantilevers in each well (Fig. 1 b; Video S2). We utilized a compact dexterous robotic micromanipulation system for the execution of well-defined mechanical interventions (Fig. S1). The system allowed us to perform microsurgical operations with high precision in a repeatable fashion. The release of the microtissues from the cantilevers resulted in bulk contraction and formation of spherical tissues with a diameter of 356 ± 18 μm within 24 h (Fig. 1 c; Video S3). A similar globular equilibrium shape was attained when the tissues were engineered inside wells that did not contain cantilevers. The deviation from the rectangular shape that was defined by the geometry of the surrounding well was a clear indication that surface stresses governed the shape. There is no other physical mechanism described by the theory of nonlinear elasticity that can drive this morphological change other than the development of surface stresses.

Figure 1.

Engineered 3D fibrous microtissues display fluid-like behavior. (a) A schematic of the device and tissue engineering workflow is given. Fibroblasts suspended in a collagen type I solution form microtissues constrained between flexible cantilevers. (b) Representative images showing the initial and final shapes during the course of microtissue contraction are given. (c) Representative images showing the morphological evolution of microtissues released from the cantilevers are given. Free-floating microtissues contract further until they attain a spherical form. (d) Representative images showing the spontaneous closure of damage-free gaps generated using a microfabricated implant are given. (e) Cell viability staining of the gap area (live, green and dead, red) right after the removal of the implant is shown. Scale bars, 100 μm. (f) Temporal sequence of micrographs of the gap area showing the immediate start of closure is given. Scale bars, 100 μm. (g) Graph showing the time course of the gap area for two different microtissues with gaps generated by surgical incision (blue) or removal of the implant (black) is given. Unlike physically damaged tissues, tissues with damage-free gaps do not show an initial lag phase (denoted by τ) because of opening and smoothing of the wound edge. Both types of gaps close overnight with comparable closure rates (ϕ), which is defined as the slope of the fitted line. (h) Box plots showing relative closure rates (n = 10) are given. The median of the closure rate of incision wounds is taken as the reference and normalized to 1. Scale bars, 150 μm unless defined otherwise. To see this figure in color, go online.

To further investigate the role of surface stresses in boundary restoration, we made full-thickness microsurgical wounds in the center of the microtissues and monitored the tissue’s response. Within minutes after the incision was made, the gap widened further (Fig. S2). Over the following few hours, the rough wound edge was smoothed by the alignment and elongation of the cells along the circumferential boundary of the gap, and the wounds closed within 24 h. Cell viability assays indicated that cells were physically injured by the cutting procedure (Fig. S2). To investigate whether physical injury is required for closure, we inserted microscale implants using robotic micromanipulation into the center of the microtissues during gelation and carefully removed the implants to avoid damage to the cells residing at the interface (Fig. 1 d). Removal of the implants after overnight culture generated damage-free gaps, as indicated by the live/dead assay (Fig. 1 e). Over the course of the next 24 h, the gap progressively closed while maintaining its shape and position (Fig. 1 f; Video S4). Temporal analysis of the gap area showed a constant rate of closure (1146 ± 249 μm² h⁻¹) throughout the process until the gap closed. The delay, τ, that was observed in the course of healing of incision wounds due to smoothing of boundaries was not present, which consequently resulted in a faster closure (Fig. 1 g). The closure rates of damage-free gaps and incision wounds were comparable to each other (Fig. 1 h). Together, these results indicate that physical injury is not required for closure of fibroblast-populated collagen microtissues and therefore suggest that closure is mechanically driven.

Finite-element simulations capture shaping and reshaping of microtissues

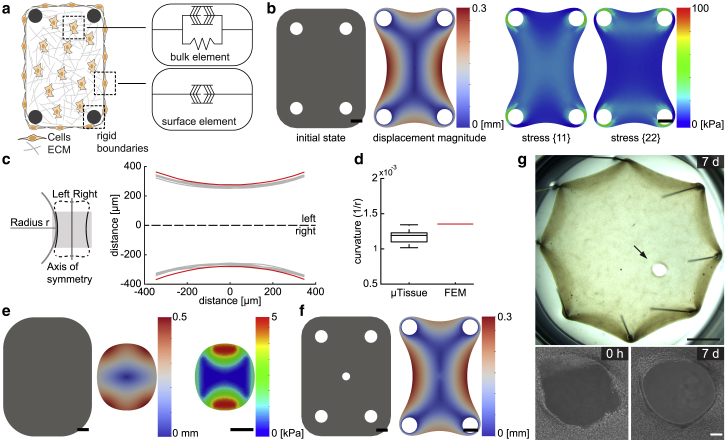
Motivated by the experimental observations, we postulate that active stresses generated by the cell contractility on the free surfaces drive the evolution of tissue shape at small scales and developed an equilibrium theory that captures the fundamental features of loading-dependent contractility of microtissues at finite strain. We implemented the weak form given in Eq. 2, along with the constitutive equations given in Eqs. 6 and 10, in the open-source platform FEniCS (45, 46). The bulk and surface contractile moduli η and γ are the only loading conditions applied during simulations (Fig. 2 a). In other words, no external mechanical force is applied other than the reaction forces. When the contractile moduli are set to zero, the material is considered to be at the reference (undeformed) state. Experimentally, this reference state corresponds to the initial state of the tissue right after the gelation of collagen matrix and before the application of forces by encapsulated fibroblasts. The reference configuration for the finite-element simulations is chosen to represent the geometry shown in Fig. 1 b (left). Because our proposed model is based on an equilibrium theory, the simulation results are not sensitive to the point in time when the damage is induced, and the only meaningful option for the induction of damage is the mapping of the location and geometry of the damaged region in the reference state. The model then simulates the final equilibrated shape of the microtissues. For numerical stability, the values of η and γ were ramped from zero to their prescribed values during the simulations. Boundaries were clamped at the experimentally measured positions of the cantilevers, and no load was applied on the outer surface. The cantilevers were considered rigid because for the chosen material composition and cantilever design, we did not observe deformation during the experiments. Because the simulations are based on an equilibrium theory, only the final equilibrated state is captured for a given set of boundary conditions.

Figure 2.

Predicted microtissue shapes resemble empirical observations. (a) Schematic description of the energy-based microtissue model is shown. The active contractile component in the bulk represents the contractile activity of the fibroblasts embedded in the matrix. This component acts in parallel with the passive elastic element that represents the tissue stiffness. The active contractile component at the surface is a representation of the contractile activity of the fibroblasts residing on the surface. Cantilevers are modeled as rigid boundaries. (b) Finite-element simulations are shown. (Left) The initial shape, in which η and γ are set to zero, and the equilibrium shape, in which η and γ are set to their calibrated values, are shown, and (right) the distribution of principal stress is shown. The color bars indicate displacement magnitude in mm and stress in kPa, respectively. Scale bars, 150 μm. (c) Schematic description for the measurement of curvature is shown. (Right) The full set of reconstructed microtissue boundaries (gray, n = 6) are shown along with the prediction of the simulation (red). (d) A box plot showing curvature calculated from experimental data (black, n = 10) and simulations (red) is given. (e) Finite-element simulation of a free-floating microtissue is shown. The shape of the untethered microtissue at the initial undeformed state and at the equilibrium state are shown, along with the stress map at the equilibrium state. (f) Finite-element simulation of a microtissue with a central hole that is 50 μm in diameter is shown. The displacement magnitude shows closure of the hole at the equilibrium state. (g) Gap closure in centimeter-scale tissues is shown. Incisional wounds that are larger than 500 μm do not close after a week, whereas wounds smaller than 100 μm spontaneously close overnight. Upper panel shows a stereo microscope image of a fibroblast-populated collagen tissue engineered around eight pins in a well plate. Scale bars, 2 mm. Lower panel shows temporal sequence of phase-contrast images of the wound area. Scale bars, 150 μm. To see this figure in color, go online.

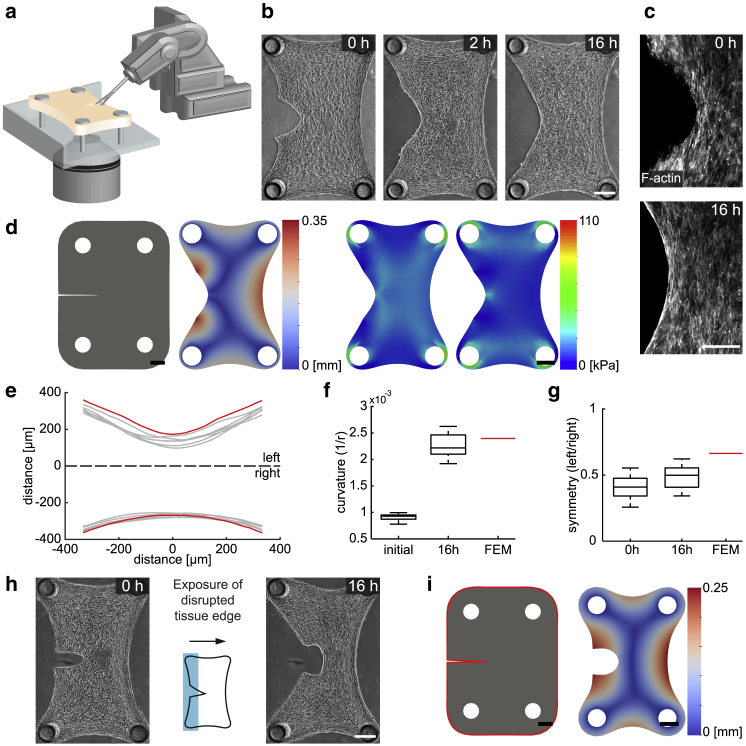
The elastic modulus and the Poisson’s ratio were taken as E = 18.33 kPa and ν = 0.3, respectively (41, 47, 48, 49). The shear and bulk modulus μ and λ were uniquely defined using the elastic modulus and Poisson’s ratio. Experimental measurements were then used to calibrate the bulk and surface contractile moduli, which were determined to be η = 11 kPa and γ = 1.83 mN mm⁻¹. The calibration was performed by fitting the parameters according to the equilibrated shape of the contracted tissue (Fig. 1 b, right) and the equilibrated shape of the tissue after the disruption of the periphery (Fig. 4 b, rightmost). First, bulk and surface activation were tuned to match the tissue shape at the equilibrated state before cutting. A representative example is shown in Fig. 1 b. The parameters were tuned a second time to match the tissue shape after a single cut had been made at the periphery, as shown in Fig. 4 b. Shear and bulk modulus were kept constant while bulk and surface activation were independently varied until the predicted shapes matched the experimental results.

Figure 4.

Surface stresses drive restoration at the tissue periphery. (a) A schematic illustration of the cutting of tissues using the actuated microscissors mounted on the robotic platform is given. (b) Temporal sequence of micrographs showing the morphological changes after the cut is shown. (c) Immunofluorescence optical section of a microtissue showing the filamentous actin is given. The cellular contractility at the periphery smooths the rough edges. (d) Finite-element simulations of a microtissue with a thin notch on its side are shown. Displacement map (left) and simulated distribution of principal stress (right) are shown at the equilibrium state. (e) The full set of reconstructed microtissue boundaries 16 h after surgical intervention (gray, n = 6) are shown along with the prediction of the simulation (red). (f) A box plot showing curvature at the operated side of the microtissue (n = 12) is given. The red line shows the predicted curvature. (g) A box plot showing the symmetry of microtissues with respect to the longitudinal axis (n = 12) is given. The red line shows the predicted symmetry. (h) Phototoxic inactivation of cells at the disrupted boundary is shown. Representative images are from before and 16 h after treatment. The schematic shows the exposed area (shaded in blue). (i) Finite-element simulation of a cut microtissue is shown. The surface contractile modulus on the periphery of the microtissue is set to zero throughout the simulation (highlighted in red). Scale bars, 150 μm. To see this figure in color, go online.

The model recapitulated the empirical shapes of engineered microtissues at the steady state (Fig. 2 b). Although the bulk free energy resulted in the compaction of the bulk tissue with passive elasticity, the surface energy drove minimization of the surface area. The latter eliminated abrupt changes in curvature throughout the boundaries. To quantify tissue morphology, we measured the curvature κ of the outline at the long sides of the tissue (Fig. 2 c). The radius r was measured by fitting a curve along the tissue contour within the highlighted central region (Fig. 2 d). The simulated form of the microtissue is slightly less compacted but shows a higher curvature. The match between the computational and experimental results is not limited to the chosen 4-post geometry. The model captured the morphological evolution of other symmetric and asymmetric cantilever configurations (Fig. S3).

The model provided the distribution of mechanical stresses within individual microtissues (Fig. 2 b). The results were qualitatively comparable with the predictions of biochemomechanical models, including the alignment of predicted principal stress and the generation of large gradients of intratissue stress that propagate away from the cantilevers (41). A quantitative comparison would be misleading because the previously established models remain in the small-deformation regime. Another prediction of the model was that in accordance with experimental results, unconstrained microtissues compact close to a spherical form (Fig. 2 e). The 2D simulation resulted in the planar projection of an ellipsoid shape, an ellipse that is very close to a circle. Here, surface stresses of the solid smooth the edges and tend to minimize the surface area, as shown in the right panel in Fig. 2 e. The deviation from the rectangular shape that was defined by the geometry of the surrounding well was a clear indication that surface stresses governed the shape. Once again, there is no other physical mechanism described by the theory of nonlinear elasticity that can drive this morphological change other than the development of surface stresses.

To recapitulate the closed-contour wounds, a circular hole was formed in the center of the microtissue with a diameter comparable to that of the experimental assays (Fig. 2 f). This topology defined the initial state before contraction. The rest of the boundary conditions and the values of the three calibrated parameters (elastic modulus, bulk, and surface contractile moduli) were all kept the same. The gaps shrunk in size by several orders of magnitude at the equilibrium state, which effectively indicated closure. Taken together, modeling free energy as the superposition of a surface and a bulk component introduced predictive power to capture morphogenic evolution of tissues after mechanical perturbations that were previously inaccessible for soft tissue models.

Elastocapillary length and boundary restoration

After discovering the dominant role of surface stresses in shaping microscale fibrous tissues, we sought to investigate whether our observations are universal or specific to a certain length scale. Elastocapillary length l_s dictates the regime in which surface effects are relevant for a specific solid material (32, 33). This number is defined as the ratio of surface stress that is given by the surface stress over shear modulus, l_s = Y/G, where Y is analogous to γ in the case of isotropic constant surface stress. For metals, l_s can be very small, on the order of picometers. For extremely soft materials such as microgels with loosely cross-linked polymer chains or biological tissues, l_s ranges from ∼10 nm up to ∼1 mm. The material properties of the microtissues studied in this work define an elastocapillary length of l_s = 80 μm. The size of the surgically induced wounds were within this length scale, and thus the surface stresses were expected to be dominant. We asked whether wounds with an order of magnitude larger sizes would spontaneously close. To test this idea, we formed centimeter-scale tissues and inflicted wounds that were scaled up with the same ratio (Fig. 2 g). After an initial smoothing process around the wound edge, the gaps stayed open even after a week. These results show that although the initial geometry and the type of the wounds were similar in the microscale and mesoscale tissues, there exists a scaling factor driving the wound closure event. We conclude that the elastocapillary length scale associated with the development of surface stresses must be the dominant factor. Although this deduction does not explain the underlying biological mechanisms behind the development of surface stresses, it suggests that there are such mechanisms that drive the development of surface stresses that do not explicitly appear in our continuum theory.

Activity of the fibroblasts at the wound edge is indispensable for closure

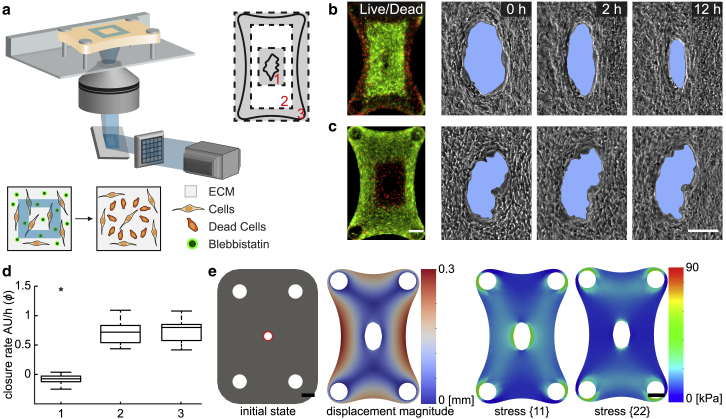
The model allows us to selectively disable surface effects while keeping the bulk contraction active. We asked whether we could stop the cellular activity at the wound edge without manipulating the cells residing away from the area and compare the experimental results with simulations. Previous work has shown that exposure of blebbistatin-treated cells to blue light (390–490 nm) causes a strong phototoxic effect that leads to a dose-dependent cell death (50). We utilized the photosensitivity of this small molecule inhibitor of myosin II for selectively deactivating cells within predefined regions of the microtissues. Projection of blue light (460 nm) on subregions of the microtissue was performed using a programmable digital mirror display (Fig. 3 a). The duration and power of blue light exposure was optimized to deliver 100% cell death within the treated area while preserving viability throughout the rest of the microtissue (Fig. S4). Illumination with green light (525 nm) had no effect on blebbistatin-treated cells, which confirmed that the response was due to wavelength-specific optochemical conversion (Fig. S4).

Figure 3.

Deactivation of surface effects in the experiments and simulations. (a) Schematic illustration of the method for the spatiotemporally controlled photoconversion of blebbistatin and local killing of cells is shown. A programmable digital micromirror display system is used for projecting blue light on predefined regions of the sample. The culture medium is supplemented with blebbistatin before exposure. Three areas are selected for the treatment: 1) the wound edge, 2) the region between the wound edge and the outline, and 3) the peripheral region. Cell viability staining (live, green and dead, red) and temporal sequence of wound area for microtissues that went through a treatment in (b) area 3 and (c) area 1 are shown. Scale bars, 100 μm. (d) A box plot showing relative closure rates of microtissues that went through treatment in three different regions (n = 12) is given. Closure rates were measured 10 h after light exposure. The median of incision gap closure without any treatment is the reference control and corresponds to 1. Statistical analysis: unpaired Student’s t-test, ^∗P ≤ 0.05. (e) Finite-element simulation of a microtissue with a central hole is shown. The surface contractile modulus is set to zero around the hole throughout the simulation (highlighted in red). Displacement (left) and stress distribution (right) at the equilibrium state are shown. Scale bars, 150 μm. To see this figure in color, go online.

Three distinct regions were targeted for phototoxic treatment: the outer boundary of the tissue, wound edge, and the area in between (Fig. 3 a). After killing of the cells at the periphery, we observed a macroscale compaction due to the relaxation of surface stresses at the outer boundary of the tissue (Fig. 3 b). The coupling of mechanical activity among distant cell groups stems from the surrounding 3D fiber network. The initial compaction, on the other hand, did not influence the overall closure rate (Fig. 3 d). Likewise, targeting the cells residing between the tissue boundary and the wound edge showed no significant change in closure kinetics compared to the control. On the other hand, deactivating the cells at the wound edge within a 0.2 × 0.3 mm² area in the center halted the closure process (Fig. 3 c). The wound edge stayed rough, and there was no tissue movement toward the gap area within the first 18 h (Video S5). After the migration of surrounding cells into the area, the gap started to close, thus suggesting that cells residing at the wound edge are indispensable for closure.

To verify that build-up of stress gradients and plastic deformation of collagen matrix during tissue formation did not play an important role in the observed behavior, we introduced the microsurgical wounds and illuminated confined areas immediately after cell seeding, before the microtissue started to contract. We confirmed that gaps introduced at this stage closed over the course of tissue formation. As expected, deactivating the cells at the wound edge completely halted the closure process (Fig. S5). For the other two cases that involve killing cells outside the wound area, we did not observe a change in the closure rate. Imaging of collagen, fibronectin, and cytoskeleton at the tissue boundary showed that the killing of cells at the periphery resulted in the elimination of surface stresses, which was manifested as the lack of F-actin and matrix alignment, as well as a much sparser cell-fibronectin layer (Fig. S5). Taken together, these results indicate that cells at the boundary are responsible for the closure of holes via generation of surface stresses in fibrous tissues.

To recapitulate the effect of phototoxic treatment at the wound edge in the computational model, we eliminated the surface stresses around the circular gap. The simulation results showed that circular holes formed in the middle of the tissues stayed open, and even enlarged further according to the tissue geometry (Fig. 3 e). The enlargement was expected because the geometry of the hole was solely controlled by the bulk contraction. The relatively high levels and the distribution pattern of stress around the hole at the equilibrium state showed that the tissue behaved as a sheet with a central hole under biaxial loading in the absence of surface stresses. The build-up of stress around the hole resulted in observable decrease in the stress at the periphery and around the cantilevers. Taken together, these results indicate that cells at the boundary are responsible for the closure of holes via generation of surface stresses in fibrous tissues.

Shape restoration at the tissue periphery

The restoration process may depend on the stress at the wounded side and the geometry created by the damage, which are essentially determined by the location of the surgical intervention. So far, we have only studied the restoration of closed-contour defects contained within the boundaries of the microtissues. Open-contour wounds that are generated at the tissue border would present a different stress distribution and thus may lead to a different restoration process. To study this condition, a single cut was performed using a robotically operated microscissor at the periphery of the microtissues (Fig. 4 a). Within minutes after the disruption of the tissue boundary, the opening was extended because of the elimination of surface stresses. In the following 6 h, the concave edges on both sides of the cut were pulled toward the main body, which resulted in a smooth curve (Fig. 4 b; Video S6). Again, this is a unique mechanical response that cannot be explained or captured in a way other than the development of surface stresses. We observed patterns of filamentous actin around the periphery that correlated with the degree of mechanical stress (Fig. 4 c). Immediately after making the incision, F-actin staining showed disorganized filaments at the boundary, which became organized as a single tension line after 16 h and remained the same over days. We mimicked the microsurgical operation in the model by forming a slit on the side of the tissue as an initial condition. The simulated form at the equilibrium state resembled the steady-state shape of the cut microtissues (Fig. 4 d).

The restoration process led to the formation of a smooth convex periphery between the cantilevers in time (Fig. 4 e). The tissue contraction at the wound edge decreased the overall tissue width along the cut line and increased the curvature of the manipulated periphery compared to the initial state. The increase in curvature was quantitatively captured by the computational model (Fig. 4 f). We defined the longitudinal axis passing through center of the tissue as the axis of symmetry. The tissue shape with respect to this axis was asymmetric even after 2 days postdamage, which showed that unlike closed-contour wounds, there was no internal mechanism that would drive expansion of the boundaries at the wounded side (Fig. 4 g).

The geometric evolution at the boundary suggested that surface contraction drives not only the closure of closed-contour wounds but also defects at the tissue periphery. We next investigated whether it was the contractile activity of the cells residing at the wound edge that was responsible for the remodeling of the dissected tissue parts. Killing the cells around the outer surface using phototoxic treatment significantly affected the restoration process and resulted in the formation of a cavity with an ellipsoidal shape (Fig. 4 h). The generation of this geometry was a clear indication of the absence of surface stresses on the cut region. To recapitulate the effect of phototoxic treatment, we eliminated the surface stresses around the tissue in the model. The simulation results mirrored the empirical observations in which the bulk contraction led to formation of a cavity at the cut location (Fig. 4 i). Taken together, these results show that the disruption of the external boundary of the microtissue leads to further remodeling, during which surface stresses drive recovery of a smooth outline.

Discussion

During embryonic development or in 3D in vitro cell aggregate cultures, surface tension can drive morphological transitions such as viscous spreading, cell sorting, and fusion of microtissues (27, 51, 52, 53). In these biological systems, the surface tension is determined by intercellular adhesion and cortical tension (29). Here, our results suggest that surface stresses also drive the shaping and restoration of fibrous microtissues, a mechanism that was recently proposed to shape engineered bone-mimicking microtissues (54). Thus, the role of surface stresses in tissue morphogenesis is not restricted to embryonic and epithelial tissues but can be extended to fibrous tissues, as well.

Traditional modeling approaches follow local rearrangements inside fibrous microtissues and focus on how contractile forces drive tissue reorganization (35, 36). Whereas these models captured the anisotropy and heterogeneity of a cell-compacted collagen gel, they cannot explain the macroscopic shape changes that we observed in our experiments. Introducing surface stresses through a novel, to our knowledge, and simple constitutive model did capture the observed experimental shape changes and confirmed the assumption that underlying micromechanical processes in the vicinity of the surface are effectively captured in the continuum scale. The following question arises: what generates surface stresses in engineered collagen microtissues? Recent work has shed light on how fibroblasts encapsulated inside collagen gels migrate toward and self-organize at the surface of the microtissues. The compaction of the collagen network coincides with the assembly of an extended and fibrillar fibronectin mesh surrounding the bulk tissue (39). Gradients of fibronectin conformations generated from the core to the periphery guide migration of fibroblasts to the tissue surface (40). As a result, the spatial organization of cells and ECM generates a biphasic core-shell architecture, a compressible collagen tissue with low cell density surrounded by a dense fibronectin-cell composite. The fibronectin matrix provides the overall cohesion for the microtissue and the effective transmission of forces between different layers.

In our computational model, the contraction of the collagen gel is driven by the bulk contraction modulus η, whereas the surface contractile modulus γ represents the loading generated by the fibroblast activity (i.e., migration, contractility, and fibronectin remodeling) at the surface. The magnitude of γ = 1.83 mN mm⁻¹ is significantly higher than the surface tension values reported in the literature for epithelial monolayers and embryonic tissues (51, 55, 56, 57, 58). These articles refer either to 3D cell clusters interacting primarily with cell-cell contacts (51) or epithelial monolayers patterned on isotropic, linear elastic surfaces (55, 56, 57, 58), whereas surface stresses in our experimental model are generated through fibroblast-ECM interactions on the surface of a compressible and plastically deformable solid. It is important to note that active tensile modulus of an epithelial monolayer spans two orders of magnitude across cell types (ranging from 0.58 ± 0.26 to 180 ± 65 nN mm⁻¹), and it depends on the activity state of the cells, as well as the composition of the underlying collagen matrix (57, 58). Fibroblasts in our microtissue model may build up significantly higher stresses on the tissue surface because fibrous networks impart complex mechanical characteristics due to nonlinear stiffening in response to loading and differential rigidity in axial versus transverse directions with respect to fiber orientation (59). Furthermore, experiments with free-floating, fibroblast-populated collagen lattices have shown that after the compaction of the gel, fibroblasts within the outermost region begin to differentiate into myofibroblasts, which is associated with the generation of stress fibers and the ability to sustain a larger contractility (60). As a result, significant tensile stresses may develop in the outer region of the contracted gel while cells reorient and compact the collagen. Mechanical modeling of these constructs suggested that the outermost region experiences a tensile circumferential stress and the innermost region experiences a compressive stress (61). These observations are in accordance with our findings (see Fig. S6), and we postulate that the increased density of fibroblasts at the surface, changes in their phenotype that leads to elevated contractility, and the remodeling of the fibronectin matrix together lead to a high tensile circumferential stress, which appears as a high γ-value in our model.

The presented modeling paradigm complies with the results of recent experiments with very soft gels, which showed that the relative importance of surface stress and bulk elasticity is a matter of length scale. Furthermore, interfacial stresses can deform solid bodies in their bulk at microscale (32, 33). The model required fitting of only two parameters for the prediction of the equilibrium shape of free-standing and constrained microtissues with arbitrary initial geometry. During the simulation of surgical cuts, we observed a deviation from the empirical data, as the perturbed boundary did not become a smooth line (Fig. 4 d). This issue may be addressed with the incorporation of additional physical properties of collagen networks such as anisotropy and plasticity (62, 63, 64). Furthermore, a more accurate constitutive law can be derived for cell-driven surface contractility in viscoelastic solids. The constitutive relation prescribed on the tissue surface follows Eq. 7, which leads to a constant surface stresses much like a fluid. To move further, a strain-dependent surface stress can be introduced, which will mitigate the issue of surface stresses increasing uniformly over the whole surface and allow for local changes of surface stress. The modeling of these nonlinear properties would also allow the simulation of intermediate morphological states during self-repair and prediction of the effect of multiple consecutive surgical operations.

To conclude, through experimental and theoretical developments, this study confirms that contractile collagen microtissues develop surface stresses and correlates them to underlying biological mechanisms. The developed surface stresses have a significant effect on the morphological response after damage and follow an elastocapillary length scale. It also provides new, to our knowledge, experimental tools and a novel computational framework to examine how cells coordinate shaping after mechanical perturbations. The robotic manipulation methods introduced here provide high throughput, precision, and repeatability, which together facilitate data acquisition and testing of the predictive power of computational models. Extension of the work to study the shaping of fibrous tissue constructs with multiple cell types of different contractile activity and spatial distribution would be of fundamental relevance to developmental biology and regenerative medicine. In natural tissues, the activation of cells is not constant but regulated by the mechanical properties of the surrounding tissue. These nonlinear effects can be incorporated into the computational model to provide insights into their contribution to tissue mechanics. The model can be further validated with the experimental measurement of surface and bulk stresses in fibrous tissues.

Author Contributions

M.S.S. designed the study. E.M. performed experiments. B.L. and N.B. developed computational models and performed simulations. J.E. contributed technology. E.M. analyzed experimental data. E.M., J.E., N.B., and M.S.S. wrote the manuscript. N.B. and M.S.S. supervised the project.