The impact of balloon-expandable transcatheter aortic valve replacement on concomitant mitral regurgitation: a comprehensive computational analysis

Abstract

The aortic and mitral valves function in a reciprocal interdependent fashion. However, the impact of transcatheter aortic valve replacement (TAVR) on the aortic–mitral continuity and severity of mitral regurgitation (MR) are poorly understood. In this study, a comprehensive engineering analysis was performed to investigate the impact of TAVR on MR severity and left heart dynamics in a retrospective patient case who harbours bicuspid aortic valve stenosis and concomitant functional MR. The TAVR procedure was computer simulated using a balloon-expandable valve, and the impact of three implantation heights on aortic–mitral coupling, MR severity and device performance were analysed. The accuracy and predictability of the computer modelling framework were validated with pre- and post-operative echo data. The highest deployment model resulted in higher stresses in the native leaflets, contact radial force and stent recoil, while the midway implantation model gave better haemodynamic performance and MR reduction in this patient case. Although the regurgitant volume decreased (less than 10%) for the three deployment configurations, no significant differences in MR severity improvement and mitral leaflet tethering were found. Acute improvement in MR was (i) due to the mechanical compression of the stent against the aortic–mitral curtain, (ii) due to an immediate drop in the ventricular pressure and transmitral pressure gradient. Albeit a single real clinical case, it is our hope that such detailed engineering computational analysis could shed light on the underlying biomechanical mechanisms of TAVR impact on MR.

1. Introduction

The aortic (AV) and mitral (MV) valves are coupled via a common fibrous continuity known as the aortic–mitral curtain or intervalvular fibrosa [1]. As a result, the physiological function of either of these two valves involves the complementary function of the other [2]. A better understanding of the aortic–mitral structural coupling and the ability to accurately assess the biomechanical changes in different treatment scenarios is important, especially in the context of heart valve intervention planning and post-procedural assessment, where these changes will have an impact not only on valve dynamics but also on left ventricular (LV) function. A prime example of aortic–mitral functional complexity is during the treatment of severe aortic stenosis (AS) in the presence of secondary significant mitral regurgitation (MR).

The prevalence of moderate-to-severe concomitant MR in patients undergoing transcatheter aortic valve replacement (TAVR) ranges from 20% to 33% [3], with significant impact on prognosis [4,5]. Albeit, MR is inherently left untreated in this setting, and its severity may decrease, remain unchanged or even increase following the procedure [6,7]. As existing clinical data on the direction and magnitude of MR severity following TAVR have demonstrated conflicting evidence and constitute a current clinical dilemma, a quantitative engineering analysis of the underlying synchronized reciprocal behaviour and biomechanical AV-LV-MV coupling during and after TAVR can potentially provide the basis for an individualized treatment approach and better procedural planning.

Patient-specific cardiac computer modelling can provide unique insights into valve function and disease states, as well as allow for exploration within a range of treatment options that cannot be performed via in vitro, animal and human studies alone [8]. For instance, Gao et al. [9] simulated MV dynamics over half of the cardiac cycle using a computational LV-MV model developed from cardiac magnetic resonance imaging. More recently, Caballero et al. simulated AV-LV-MV dynamics over the entire cardiac cycle under physiological and degenerative MR states [10,11]. While these computational studies have addressed some key challenges in modelling the complex biomechanical coupling between the heart valves and the blood flow in the left heart (LH), to the best of our knowledge, no patient-specific fluid–structure interaction (FSI) computational models have been developed to analyse the effect of TAVR on aortic–mitral coupling and MR severity for patients with severe AS and concomitant MR.

The aims of this study are therefore: (1) to develop a robust patient-specific LH model with severe AS in the presence of significant functional MR, and validate the pre-TAVR LH dynamics with clinical echo data, (2) model the TAVR procedure and analyse the influence of stent implantation height on aortic–mitral structural coupling, and (3) simulate and validate the post-TAVR LH dynamics with the goal to investigate the effect of TAVR on MR severity. We believe that this work offers a detailed engineering analysis that could shed some light on the structural and haemodynamic impact of TAVR on concomitant MR. Further development of such computer models could support better evaluation and prediction of interventional treatments, and ultimately improve patient outcomes.

2. Material and methods

2.1. Patient information

A 71-year-old male patient with a mean aortic annulus diameter of 23 mm was referred for TAVR at Hartford Hospital (Hartford, CT). Pre-TAVR echo examination revealed classical low-flow, low-gradient severe AS, a bicuspid AV (BAV) with eccentric coaptation between the non-coronary leaflet and fused left and right coronary leaflets, with no raphe between them (Sievers type 0 L/R) [12]. Mild aortic insufficiency was detected. Moderate-to-severe functional MR was also found, with restricted posterior mitral leaflet (PML) motion and reduced leaflet coaptation, resulting in a posteriorly directed regurgitant jet. The LV wall thickness was normal, but the chamber was mildly dilated with severe global hypokinesis with regional variation. The left atrium (LA) was dilated despite a normal antero-posterior diameter. A 26 mm first-generation Edwards SAPIEN valve was successfully deployed via transapical approach. Moderate-to-severe MR was still present after TAVR.

2.2. Patient-specific left heart model

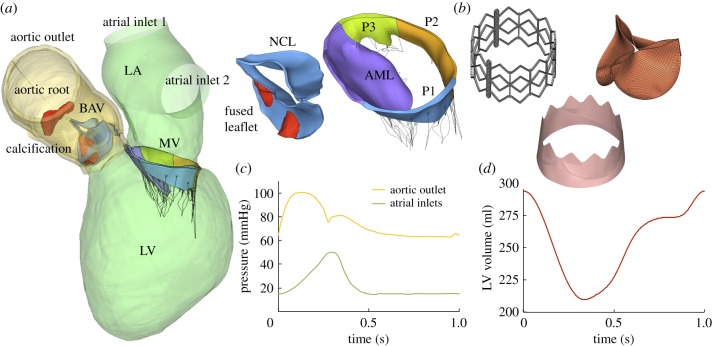
The patient-specific LH model was created from the pre-TAVR cardiac multislice computed tomography (MSCT) images after obtaining approval from the Institutional Review Board. The MSCT images, acquired with a GE LightSpeed 64-channel volume CT scanner, had an in-plane resolution of 0.82 × 0.82 mm and a slice thickness of 0.625 mm. Ten phases of the cardiac cycle were collected using an ECG-gated sequence. DICOM images were imported into Amira-Avizo (Thermo Fisher Scientific, MA) and 3D Slicer (www.slicer.org) software to segment the cardiac structures, which included the ascending aorta, aortic root, BAV, calcification, MV, chordae, LV and LA endocardial walls. HyperMesh software (Altair Engineering, Inc., MI) was then used to create a high-quality finite-element (FE) mesh. Figure 1a shows the patient-specific LH model. Two calcific deposits were found in the fused leaflet, as well as one in the coronary ostia close to the right coronary artery. Image segmentation and mesh generation techniques have been previously described in detail elsewhere [10,13].

Figure 1.

(a) Patient-specific LH model reconstructed from the MSCT images, (b) balloon-expandable TAV model, (c) aortic and LA pressure waveforms and (d) LV volume waveform. (Online version in colour.)

An anisotropic hyperelastic material model, based on Holzapfel et al. [14,15], was adopted to characterize the mechanical response of most cardiac tissues, while the isotropic hyperelastic Ogden material model [16] was used to characterize the mechanical properties of mitral chordae and aortic–mitral curtain. Material parameters were determined by fitting in-house multiprotocol biaxial and uniaxial testing data of human cardiac tissues. Details on the implementation of the constitutive models as well as material parameter fitting can be found in the electronic supplementary material.

2.3. Balloon-expandable transcatheter aortic valve model

A generic balloon-expandable TAV model, based on a 26 mm first-generation Edwards SAPIEN device was used in this study [17]. As seen in figure 1b, the TAV consists of three components: stainless steel stent, skirt and bovine pericardium leaflets. The generic TAV leaflet geometry and material parameters used in this study were obtained from previous studies [18–20]. In this model, the attachment line of the leaflets to the stent is curved from the commissures downwards to the leaflet cusps, having a scallop leaflet shape similar to that of the Edwards SAPIEN valve design. More details on the balloon-expandable TAV model can be found in the electronic supplementary material.

2.4. FE modelling of transcatheter aortic valve replacement procedure

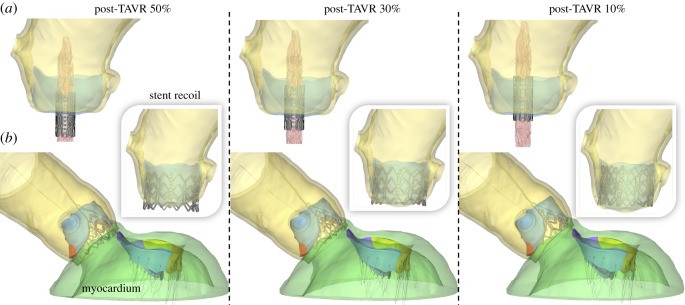
The TAVR procedure was simulated in the patient-specific LH model through four major simulation steps [17,21]. To accurately evaluate the impact of TAVR on MR severity, the patient-specific myocardium surrounding the aortic root, aortic–mitral curtain, MV and proximal LV/LA endocardial walls was also reconstructed from the MSCT images and integrated in the LH model, as seen in figure 2b.

Figure 2.

(a) Crimped stent geometry at the three deployment heights, (b) LH models with myocardium after TAVR deployment and stent recoil. (Online version in colour.)

2.4.1. Step 1: stent crimping

Initially, the nominal stent was positioned coaxially within the aortic root and centred into the aortic annulus. The crimped stent and balloon geometries were obtained by applying a radial displacement on two cylindrical-surface sheaths. The stent was crimped to an exterior diameter of 8 mm (24 Fr catheter), as seen in figure 2a, and positioned in a way that the TAV commissures had the same orientation as the native aortic sinuses. The BAV leaflets were pre-opened with a cone-shaped catheter to simulate the effect of the insertion of the delivery system across the AV.

To quantify the impact of TAV deployment height on LH dynamics and MR severity, the axial positioning of the stent with respect to the aortic annulus plane was parametrized to replicate three clinical deployment configurations: (1) midway, denoted as post-TAVR 50%. The conventional manufacture's recommendation for the Edwards SAPIEN system is to position the mid-point (i.e. 50 : 50) of the stent at the aortic annulus plane [22]. (2) Post-TAVR 30%, defined as a slightly higher device implantation, with 30% of the stent located below the aortic annulus. (3) Post-TAVR 10%, defined as a high device implantation, with only 10% of the stent located below the aortic annulus plane. The aortic annulus plane was defined as the virtual plane formed by joining the points of basal attachment of the BAV leaflets [22].

2.4.2. Step 2: balloon inflation

The mechanical response of the fluid-filled balloon expansion was modelled by the surface-based fluid cavity method, capable of simulating the coupling between the deformation of the balloon and the fluid inside [17]. The balloon was pressurized for 0.25 s until it was fully inflated. This method was initially calibrated to ensure a correct nominal stent size after balloon inflation.

2.4.3. Step 3: stent recoil

The internal pressure of the balloon was decreased over a time period of 0.25 s. Therefore, the stent recoiled and stabilized, and the native BAV leaflets adopted a more natural open position.

2.4.4. Step 4: transcatheter aortic valve leaflet and skirt positioning

The TAV leaflets and skirt were not included during the stent deployment procedure, but were added after stent recoil. Their effect on the biomechanical interaction between the stent and the native aortic tissue has been shown to be negligible [23] The TAV leaflets were mounted in the deformed stent using a virtual assembly method [24]. Briefly, the nodes lying on the leaflet attachment and along the commissures were mapped onto the stent frame through a set of non-uniform imposed displacements, ensuring an appropriate final leaflet position.

During TAVR modelling, the ascending aorta and myocardium were constrained at their distal ends allowing only rotational degrees of freedom. The balloon was constrained at its distal and proximal ends in order to mimic the bond to the catheter and avoid rigid body motion. The kinetic energy was monitored to ensure that the ratio of kinetic energy to internal energy remained under 10%. The resulting deformed LH models after stent recoil were used to assess post-TAVR LH dynamics using FSI modelling.

2.5. FSI modelling of pre- and post-transcatheter aortic valve replacement left heart dynamics

A fully coupled FSI numerical approach that combines smoothed particle hydrodynamics (SPH) for the blood flow and nonlinear FE analysis for the heart valve structures was implemented in this study. FSI simulation set-up was performed as described in previous works [10,11]. Briefly, time-dependent pressure boundary conditions were applied at the two atrial inlets (pulmonary veins) and at the aortic outlet of the pre- and post-TAVR LH models. As seen in figure 1c, a pathological atrial pressure waveform was prescribed at the inlets, with an elevated V-wave due to the regurgitant volume in the atrial cavity during systole [25]. To match the patient's clinical data, the mean diastolic atrial pressure value was adjusted to be 12 mmHg, while the peak systolic and diastolic aortic pressure values were set to 100 mmHg and 63 mmHg, respectively.

Endocardial wall motion was imposed as a time-dependent nodal displacement boundary condition based on the 10 cardiac phases from the MSCT images. A detailed description of the cardiac wall motion modelling procedure can be found in previous publications [10,13]. Figure 1d shows the time-varying LV volume change waveform obtained from the FSI model. Pressure boundary conditions and cardiac wall motion were kept the same for the pre- and post-TAVR LH models, simulating immediate post-operative LH dynamics, without considering the cardiac remodelling mechanisms that occur over time after TAVR. The patient's heart rate was approximately 60 bpm, corresponding to a cardiac cycle of 1 s. Note that FSI simulations begin at early systole, resembling the isovolumetric contraction phase. Two cardiac cycles were conducted and the results from the second cycle were analysed herein. SPH particle sensitivity [13,26] and FE mesh sensitivity [27] studies were previously performed. All FE and SPH-FE simulations were performed using Abaqus/Explicit.

2.6. Data analysis

2.6.1. Fluid parameters

The regurgitant volume in the MV (RV_MV) and the AV (RV_AV) were obtained from the pre- and post-TAVR FSI models by integrating the negative MV systolic flow rate curve and negative AV diastolic flow rate curve over time, respectively. The RV was defined as the sum of the valve closing and the leakage volumes. Similarly, the stroke volume in the MV (SV_MV) and the AV (SV_AV) were obtained by integrating the positive MV diastolic flow rate curve and positive AV systolic flow rate curve over time, respectively. MR severity was graded using the regurgitant fraction criterion [28], RF_MV = RV_MV/LVSV, where LVSV is the total SV of the LV (SV_AV + RV_MV). AV effective orifice area was calculated as $\mathrm{EO}{\mathrm{A}}_{\mathrm{AV}}=\mathrm{MSF}/51.6\sqrt{\mathrm{\Delta }P}$, where MSF is the root mean square systolic flow rate, and ΔP is the mean systolic pressure gradient [29].

2.6.2. Structural parameters

The three stent deployment configurations were analysed and compared during the TAVR procedure in terms of peak $({\mathrm{S}}_{\mathrm{I}}^{\mathrm{MAX}})$ and average $({\mathrm{S}}_{\mathrm{I}}^{\mathrm{AVRG}})$ maximum principal stress values in the BAV leaflets, sinus, calcification and MA, contact radial force between the stent and aortic root, and stent deformation. To facilitate comparison between different models and avoid the bias caused by local high stress concentration, only the 99-percentile values of the peak stress were evaluated [30]. Moreover, leaflet annular regions were not included in the average stress calculation in order to avoid boundary effects. The contact radial force between the recoiled stent and surrounding cardiac tissues was calculated as $\mathrm{RF}={\sum }_{i=1}^{n_s}r{f}_{i,\mathrm{post}}$, where n_s is the total number of nodes in the stent, and rf_i,post is the radial contact force at each stent node after recoil. Stent deformation was evaluated by quantifying stent eccentricity and recoil. Stent eccentricity, which assesses the conformity of the stent deformation after recoil, was calculated as the ratio of the maximum stent diameter to minimum stent diameter. Stent recoil was determined as (D_min expanded − D_min recoiled)/D_min expanded, where D_min is the minimum stent diameter during fully balloon expansion and stent recoil. These two metrics were calculated at three different cross-sections of the stent (i.e. bottom, middle and top) with the mean value reported.

Additionally, post-TAVR tissue mechanics were evaluated by the average maximum principal stress values calculated in the BAV/TAV leaflets and MV leaflets during peak diastolic and systolic pressure, respectively. Chordae forces (F_chordae) at peak systole were also reported. The force experienced by a particular chordae group was calculated as the sum of vectors representing the tension in each individual chorda attached to that chordae group.

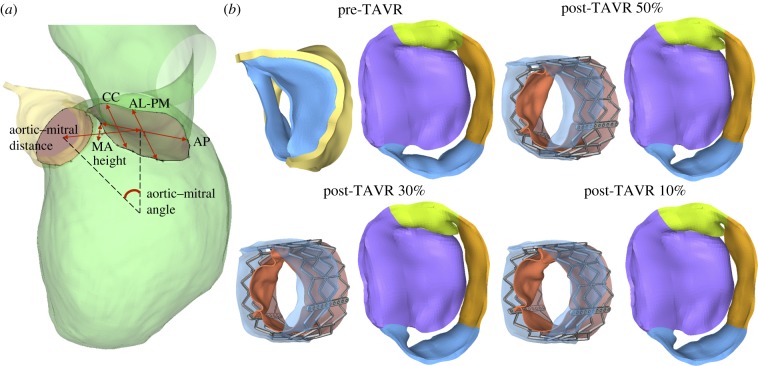
2.6.3. Aortic–mitral geometrical parameters

Aortic–mitral structural coupling during TAVR was evaluated in terms of the geometrical parameters shown figure 4a. The following measurements were obtained during systole: (a) aortic annulus and MA areas, (b) antero-posterior (AP) distance, defined as the distance between mid-anterior and mid-posterior MA points, (c) anterolateral–posteromedial (AL-PM) distance, (d) inter-commissural (CC) distance, (e) MA height, defined as the maximum vertical distance between the highest and lowest points of the saddle-shaped MV, (f) aortic–mitral angle, defined as the angle between the planes of the MA and the aortic annulus, (g) aortic–mitral distance, defined as the centroid distance between the MA and the aortic annulus, (h) aortic annulus motion, defined as the longitudinal excursion of the aortic annulus during the TAVR procedure, and (i) anterior and posterior MA motion, defined as the posterior displacement of the MA during the TAVR procedure.

Figure 4.

(a) Aortic–mitral geometrical parameters, (b) aortic–mitral coupling at peak systole. (Online version in colour.)

3. Results

3.1. Pre-transcatheter aortic valve replacement left heart dynamics

Table 1 displays the computed haemodynamic parameters of the patient-specific LH model throughout the cardiac cycle before TAVR. Numerical measurements are compared to the patient's available pre-TAVR echo data. Generally, there is good quantitative agreement between the simulation results and the clinical data, which demonstrates that the SPH-FE FSI modelling framework can accurately simulate the patient-specific LH pathological dynamics. FSI simulation of BAV function revealed the classical low-flow low-gradient AS found clinically, with an EOA_AV less than 1 cm², mean systolic pressure gradient less than 40 mmHg, and decreased LV ejection fraction (LVEF) less than 50%. Similarly, FSI simulation of MV function demonstrated moderate-to-severe MR, which was consistent with the patient's clinical echo examination.

Table 1.

Pre-TAVR LH haemodynamics and echo comparison.

	pre-TAVR FSI	pre-TAVR Echo
SVAV (ml)	46.28	43
RVAV (ml)	9.34	—
SVMV (ml)	74.64	—
RVMV (ml)	37.59	—
RFMV (%)	44.82	—
MR severity (RFMV)	moderate-to-severe	moderate-to-severe
LVEF (%)	28.55	25
AV peak gradient (mmHg)	34.82	34
AV mean gradient (mmHg)	23.97	20
AV peak velocity (m s−1)	2.82	2.9
EOAAV (cm2)	0.77	0.67
E wave (m s−1)	0.79	0.9
A wave (m s−1)	0.54	0.6
E/A	1.47	1.5
MR peak gradient (mmHg)	118.59	—
MR peak velocity (m s−1)	5.42	—

3.2. Transcatheter aortic valve replacement-in-BAV biomechanics

Figure 2a shows the crimped stent geometry at the three deployment heights, while figure 2b shows the final deformed geometries after balloon deflation and stent recoil. No severe leaflet overhanging or potential risk for coronary obstruction was observed. The shortest distance between the coronaries and the native leaflets was found to be 7.5 mm for the post-TAVR 10% case, which was between the left coronary ostia and the fused leaflet free edge. No evident gaps between the recoiled stent and the native annular tissue were observed in the post-TAVR LH models, which was later confirmed in the FSI blood flow simulations by the absence of paravalvular leak (PVL).

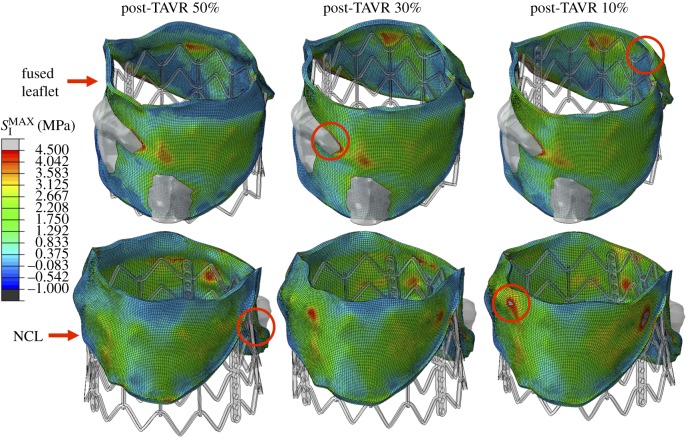
The stress distribution on the native BAV leaflets after stent recoil is presented in figure 3. Similar stress distribution patterns were observed for the three implantation configurations, where peak values were located in regions in contact with the higher portion of the stent for the post-TAVR 30% and 10% models, and in the leaflet-root attachment region close to the commissures for the post-TAVR 50% case, as shown by the red circles in figure 3. Another leaflet region that experienced high stress values was the leaflet belly region in contact with the large calcification deposit due to the stiffer material properties. For the aortic root, high stress values were found at the leaflet-root attachment lines, especially in the fused leaflet commissures.

Figure 3.

Stress distribution (MPa) in the BAV leaflets after stent recoil. Red circles denote regions of peak stress values. A maximum stress value threshold of 4.5 MPa was applied such that higher stress values were displayed in grey, facilitating comparison between models. (Online version in colour.)

As presented in tables 2 and 3, the highest deployment model (post-TAVR 10%) resulted in higher peak stress values in the leaflets, sinus and calcification regions. The highest peak stress in the anterior MA, however, was found for the midway implantation model (post-TAVR 50%), a direct result of a larger aortic–mitral curtain tissue in contact with the stent. The contact radial force between the recoiled stent and surrounding cardiac tissues is listed in table 2. The post-TAVR 10% model gave the highest contact force, with a value of 108 N, while the post-TAVR 50% case gave the lowest contact force, with a value of 98 N. Stent eccentricity and recoil values are also presented in table 2. All three stents showed a similar eccentricity, maintaining a nearly uniform circular pattern. Stent recoil, however, was lower for the midway implantation model (3.3%) than for the highest implantation model (6.2%).

Table 2.

TAVR-in-BAV biomechanical parameters after stent recoil.

	post-TAVR 50%	post-TAVR 30%	post-TAVR 10%
${\mathrm{S}}_{\mathrm{I}}^{\mathrm{MAX}}(MPa)$
native BAV leaflets	2.75	2.93	3.15
sinus	2.11	2.16	2.34
calcification	1.88	1.95	2.02
anterior MA	0.151	0.064	0.036
posterior MA	0.012	0.024	0.014
${\mathrm{S}}_{\mathrm{I}}^{\mathrm{AVRG}}(MPa)$
native BAV leaflets	0.74	0.88	1.01
sinus	0.31	0.31	0.3
contact radial force (N)	98.13	104.09	107.79
stent eccentricity	1.05	1.08	1.07
stent recoil (%)	3.30	5.75	6.17

Table 3.

Aortic–mitral geometrical parameters during systole. Percentage variations with respect to the pre-TAVR LH model are reported in parenthesis.

	pre-TAVR	post-TAVR 50%	post-TAVR 30%	post-TAVR 10%
aortic annulus area (cm2)	4.93	5.13	5.00	4.94
MA area (cm2)	11.40	10.97	11.04	11.10
AP distance (mm)	35.53	33.29	34.30	34.41
AL-PM distance (mm)	39.54	40.97	40.58	40.66
CC distance (mm)	31.14	31.18	30.80	30.94
MA height (mm)	6.00	5.10 (−15)	6.18 (3)	6.49 (8)
aortic–mitral angle (°)	123.05	116.88 (−5)	112.81 (−8)	111.23 (−10)
aortic–mitral distance (mm)	28.46	27.48	27.06	26.97
aortic annulus motion (mm)	—	3.87	3.15	2.82
anterior MA motion (mm)	—	3.28	2.31	1.92
posterior MA motion (mm)	—	1.00	0.76	0.48

3.3. Transcatheter aortic valve replacement impact on mitral regurgitation: structural dynamics

We found an important reduction in the MA height from pre- to the post-TAVR 50% model (15%); however, as the stent implantation height increased, the MA height increased instead; up to 8% for the post-TAVR 10% case. Additionally, the aortic–mitral angle decreased between 5% and 10% following TAVR, with a smaller systolic angle in the highest implantation model than in the midway implantation model. Although the MA area (approx. 3.2%), AP distance (approx. 4.3%) and aortic–mitral distance (approx. 4.5%) decreased in all post-TAVR models, there were no evident changes when comparing these before and after TAVR. Similarly, both AL-PM distance (approx. 3%) and aortic annulus area (approx. 2%) had a slight tendency to increase after TAVR. In regards to the aortic annulus motion, it was found that this anatomical structure was displaced approximately 3.3 mm towards the LVOT during TAVR, and this motion seemed to decrease as the stent implantation height increased. Moreover, the anterior MA was also displaced approximately 2.5 mm posteriorly during TAVR, again, this motion decreased as the implantation height increased. Finally, figure 4b shows the aortic–mitral complex before and after TAVR during peak systolic flow. Although it is evident that the regurgitant orifice area decreased in all post-TAVR models, MR was still present. Moreover, the post-TAVR 50% model exhibited the smallest regurgitant orifice area, which was later confirmed by the quantification of the RV_MV.

3.4. Transcatheter aortic valve replacement impact on mitral regurgitation: fluid dynamics

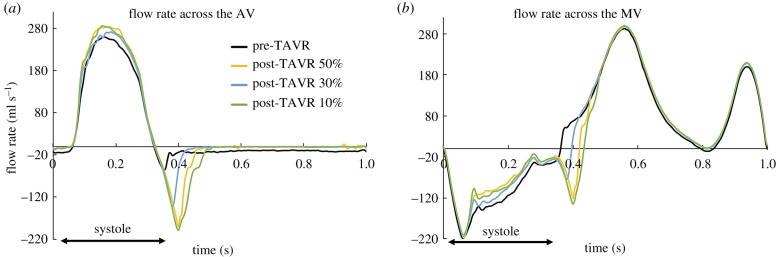
Figure 5 shows the flow rate waveforms across the AV an MV throughout the cardiac cycle for the pre- and post-TAVR LH models. The negative aortic flow at end-systole (figure 5a) indicates the retrograde blood flow into the LV during AV closure, while the negative systolic mitral flow (figure 5b) indicates the backflow of blood into the LA due to MV leaflet closing and MR. Diastolic inflow rates (positive) across the MV were approximately the same for all models, since LV size and motion remained unchanged immediately post-TAVR. As expected, the pre-TAVR LH model had the lowest peak aortic flow and forward SV (SV_AV), as seen in figure 5a. Following TAVR, correction of the AV obstruction led to an immediate reduction in the LV systolic pressure, which decreased the pressure gradient across the AV and MV, and therefore led to a reduction in the RV_MV and an increase in the SV_AV.

Figure 5.

Flow rate (ml s⁻¹) across the (a) AV and (b) MV throughout the cardiac cycle. (Online version in colour.)

As shown in table 4, improved LV function and haemodynamic success of the procedure was found in all post-TAVR LH models, as confirmed by the reduction of MR and AV/MR peak velocities, and by the increase in the EOA_AV. The greater degree of MR improvement (10%) was for the post-TAVR 50% model; which, based on the RF_MV criterion, can now be classified as moderate MR. When compared with the pre-TAVR model, the degree of MR severity remained unchanged for the post-TAVR 30% and 10% models.

Table 4.

Pre- and post-TAVR LH haemodynamics and post-TAVR echo comparison.

	pre-TAVR	post-TAVR 50%	post-TAVR 30%	post-TAVR 10%	post-TAVR echo
SVAV (ml)	46.28	52.24	49.11	51.94	48
RVAV (ml)	9.34	11.43	7.21	15.39	—
SVMV (ml)	74.64	74.54	76.93	72.72	—
RVMV (ml)	37.59	33.84	34.8	35.89	32
RFMV (%)	44.82	39.32	41.48	40.87	—
MR severity (RFMV)	moderate-to-severe	moderate	moderate-to-severe	moderate-to-severe	moderate-to-severe
LVEF (%)	28.55	29.30	28.56	29.90	30
AV peak gradient (mmHg)	34.82	22.64	24.12	23.88	16.6
AV mean gradient (mmHg)	23.97	11.98	12.54	12.53	8.4
AV peak velocity (m s−1)	2.82	1.74	1.73	1.70	2.0
EOAAV (cm2)	0.77	1.20	1.12	1.17	1.4
E wave (m s−1)	0.79	0.80	0.83	0.88	0.87
A wave (m s−1)	0.54	0.54	0.57	0.58	0.54
E/A	1.47	1.48	1.47	1.51	1.6
MR peak gradient (mmHg)	118.59	114.09	110.87	112.76	108
MR peak velocity (m s−1)	5.42	4.92	4.91	4.93	5.2

When comparing the pre- and post-TAVR aortic flow rate waveforms shown in figure 5a, a notable change in the onset time of BAV/TAV closure was found. The TAV device had a distinct slower closure and higher closing volume compared to the native BAV leaflets, with the highest RV_AV obtained for the post-TAVR 10% model. Pre-procedural mild aortic regurgitation, found clinically in the patient's echo examination, was also detected in the pre-TAVR computational model, as shown by the negative diastolic aortic flow (figure 5a). Aortic regurgitation was resolved following TAVR, both in the real clinical case and in the FSI simulations. Moreover, the absence of PVL in all post-TAVR LH models matched the post-operative echo findings.

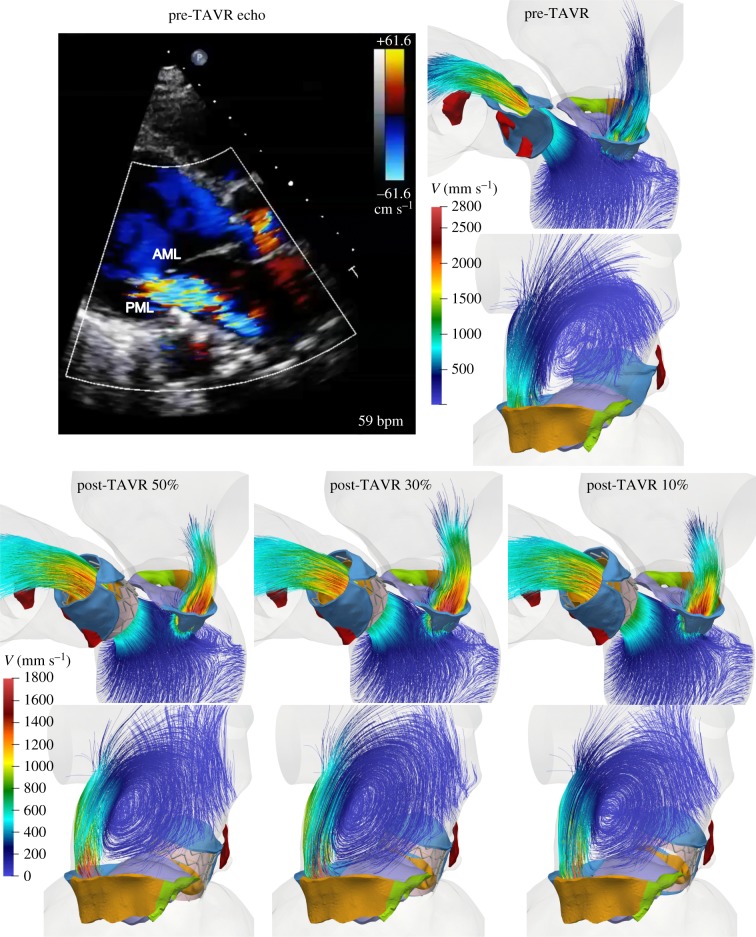
Additionally, figure 6 shows the intraventricular velocity streamlines coloured by velocity magnitude during peak systole. Due to the restricted PML motion, the pre-TAVR model displayed a posteriorly directed regurgitant jet, which qualitatively matched the Doppler colour echo image shown in figure 6. The regurgitant jet structures were similar between pre- and post-TAVR states, with an eccentric ‘wall-hugging' jet that impinged the postero-lateral atrial wall. The strength and velocity of the jet, however, decreased after the procedure, with a similar MR peak velocity for all post-TAVR models (table 4).

Figure 6.

Pre-TAVR Doppler colour echo image, and pre- and post-TAVR FSI velocity streamlines showing regurgitant jet structures at peak systole. Note the different velocity scales between pre- and post-TAVR models. (Online version in colour.)

Overall, when compared to the patient-specific post-TAVR echo data, numerical results corresponded well to the echo measurements (table 4), which demonstrate the accurate predictive capabilities of our patient-specific modelling methodology, that is, the simulated TAVR procedure using the FE analysis, followed by the simulated post-TAVR LH dynamics using the FSI analysis. Nevertheless, some differences between the echo and FSI data were found, especially regarding the AV pressure gradients. These differences, which will be later discussed, are in line with the inherent uncertainties in the echo flow recordings and the image-based computer simulations.

3.5. Post-transcatheter aortic valve replacement left heart tissue mechanics

Table 5 presents the average stress values calculated for the BAV/TAV leaflets and MV leaflets during peak diastolic and systolic pressure, respectively. It was found that the average stress in the AML was at least 20% lower following TAVR, potentially due to the morphological changes caused by the posterior displacement of the anterior MA during the procedure. Due to the restricted motion of the PML observed clinically, the average stress in the PML did not show significant changes between pre- and post-TAVR states. Although the average stress in the AML was generally higher than in the PML before and after TAVR, it was found that the peak mitral leaflet stresses were actually located at the tethered PML chordae insertion regions, near the leaflet free-edge and basal chordae locations.

Table 5.

Post-TAVR LH tissue parameters. Percentage variations with respect to the pre-TAVR model are reported in parenthesis.

	pre-TAVR	post-TAVR 50%	post-TAVR 30%	post-TAVR 10%
${\mathrm{S}}_{\mathrm{I}}^{\mathrm{AVRG}}(MPa)$
BAV/TAV	0.076	0.151 (99)	0.161 (112)	0.149 (96)
AML	0.126	0.090 (−29)	0.101 (−20)	0.102 (−19)
PML	0.082	0.082 (0)	0.079 (−4)	0.076 (−7)
Fchordae (N)
AML marginal	1.14	0.95 (−17)	0.92 (−19)	0.86 (−24)
AML strut	2.04	3.23 (59)	3.13 (54)	3.05 (50)
AML basal	3.84	2.47 (−36)	2.90 (−25)	2.84 (−26)
PML marginal	6.13	6.95 (13)	6.50 (6)	6.05 (−1)
PML basal	7.33	5.58 (−24)	6.05 (−18)	6.24 (−15)

Since this patient had a postero-lateral regurgitant gap with PML tethering near the anterior papillary muscle (PM), the LH models experienced high PML chordae forces when compared to AML chordae tensions. There was an imbalanced force distribution between the two PM, with anterior PM force being higher than posterior PM force. Due to the anatomical changes in the MV and the mitral apparatus force redistribution following TAVR, AML strut tension increased at least 50%, while AML marginal and basal chordae tensions decreased between 17% and 36%. Similarly, PML basal tension decreased at least 15%, while PML marginal chordae showed no evident changes in their tension. It is important to note, however, that the total AML and PML chordae tensions were largely unchanged during pre- and post-TAVR states, and between the different three deployment models, which suggest that mitral leaflet tethering was not improved immediately after TAVR, but that there was a force redistribution between the different components of the mitral apparatus, in particular concerning changes in tension between marginal, basal and strut chordae.

4. Discussion

The main contribution of the present study was a comprehensive analysis of TAVR impact on aortic–mitral coupling, MR severity and LH dynamics in a rigorously developed and validated patient-specific cardiac computational model. Specifically, this work presented an engineering mechanics study that

• (1)Integrated cardiac tissue mechanics and blood flow modelling using an FE and fully coupled FSI framework which allowed for an accurate assessment and validation of a real TAVR clinical case with BAV, low-flow low-gradient AS, and functional MR.
• (2)Investigated the impact of stent deployment height on TAVR–host tissue interaction and found that for this particular patient, the highest deployment model resulted in higher stresses in the native tissues, contact radial force and stent recoil.
• (3)Quantified that during TAVR, due to mechanical compression of the stent against the aortic–mitral curtain, the anterior MA was displaced posteriorly while the aortic annulus was displaced towards the LVOT.

Moreover, the new knowledge learned from a clinical perspective includes the following:

• (1)Following TAVR, no significant differences in MR severity improvement (less than 10%) and PML tethering were noted with a generic balloon-expandable TAV at the three implantation heights.
• (2)In general, the midway implantation model gave better TAV performance haemodynamic measures and MR reduction.
• (3)The biomechanical mechanism of immediate MR evolution after TAVR is multifactorial. Acute changes in MR severity are (i) due to the mechanical compression of the stent against the aortic–mitral curtain, (ii) due to an immediate drop in the LV pressure and transmitral pressure gradient.

4.1. Clinical validation and predictive performance

To the best of our knowledge, this is the first validated patient-specific computational model that simulated the LH dynamics before and after TAVR during the entire cardiac cycle. Comparison between simulation results and available pre- and post-procedural echo data demonstrated good quantitative agreement and predictive capabilities, with some computed variables agreeing better with the echo measurements than others. First, it is generally noted that differences in terms of the SV_AV, RV_MV, LVEF, E wave, A wave, E/A ratio and MR peak gradient and velocity were mostly below 10% (tables 1 and 4). It is also noted that the errors in the estimation of the AV peak and mean gradients for the pre-TAVR model, and of the AV peak velocity and EOA_AV for the pre- and post-TAVR models were below 20%. As with any image-based computational model, there exist sources of geometric and numerical uncertainties. In this study, for example, the generic TAV model used does not completely match the design of the first-generation Edwards SAPIEN valve clinically implanted in the patient. Moreover, it is important to be aware of the inherent limitations and variability in the measurement of haemodynamic variables using echo [31]. Echo examination is highly dependent on the experience of the operator, the technical quality of the study and on the patient's acoustic window [32].

4.2. Transcatheter aortic valve replacement-in-BAV

Patient-specific modelling of TAVR in a BAV patient under various procedural scenarios provided quantifiable information about device anchoring and the interaction between the stent, the aortic–mitral curtain and the native valve. The highest deployment model (post-TAVR 10%) led to higher peak stresses in the BAV leaflets, sinus and calcification, as well as higher contact radial force, stent recoil and average leaflet stress. These results are in agreement with an FE study by Bianchi et al. [33] that found that after stent recoil the high deployment model resulted in higher leaflet and sinus stresses, as well as higher contact forces than the midway deployment model. In our study, the peak stresses were generally found in the leaflet region in contact with the upper stent struts, in the leaflet-root attachment lines, and in the transition region between calcification and leaflet tissue. Altogether, these results could indicate a higher risk for tissue damage and potential for aortic root injury or rupture for the highest stent positioning, as compared to a slightly lower or midway implantation configuration. This is especially important in the BAV space, as rates of annular rupture have been reported in some series to be as high as 5.3% using the balloon-expandable SAPIEN XT valve [34]. Moreover, under BAV disease, the TAV is usually implanted higher (+4 mm above the annulus) and anchored at the tightest part of the BAV commissures, with an often higher final implantation depth due to the anchoring effect of the calcification [35]. Future parametric studies that investigate the effect of additional implantation strategies and parameters, as well as the influence of newer-generation TAV design in the BAV population would be useful to draw more definite conclusions.

Device apposition and, therefore, a correspondent measure of stent anchoring can be approximated by measuring the contact radial force, pressure or area between the stent and its surrounding tissue [21,36]. Previous in vitro and computational studies have aimed to improve the understanding of the relationship between radial force and TAVR performance [37,38]. Up to now, however, the value of this critical force for TAVR-in-BAV was unknown. Our simulation results showed that the radial force for the three implantation models ranged between 205 and 230 N, and 98 and 108 N during fully stent expansion and after stent recoil, respectively. These forces, which increased as the implantation height increased, are markedly higher than the radial forces for a tricuspid AV reported by Egron et al. [38] and Wang et al. [21] between 100 and 150 N during fully stent expansion. This difference in contact radial force between BAV and tricuspid AV anatomies may be important clinically, since TAV oversizing is common in TAVR-in-BAV in order to prevent significant PVL, especially with the older-generation TAV models.

While radial dilatation is usually desired for proper device anchoring and to avoid dislocation of the implant, an excess in radial force may also lead to impairment of the conduction system, leading to the left bundle branch or even complete atrioventricular conduction block. Indeed, PVL and high pacemaker implantation rates have been one of the main limitations of TAVR-in-BAV [39], with reported pacing rates of up to 25.5% for the balloon-expandable TAV [40]. It has been postulated that the higher incidence of cardiac conduction disorders and permanent pacemaker implantation rates in TAVR-in-BAV are related with difficulty in valve positioning and asymmetric expansion due to the irregular leaflet shape, heavy calcification and the inability to achieve a coaxial position during valve deployment [40]. For the patient-specific case studied herein, a symmetrical expansion of the TAV stent was obtained, as supported by a stent eccentricity value close to one for the three deployment models (table 2). This positive outcome can be explained by the less complex BAV type present in this patient, which was Sievers type 0 L/R without aortic root dilatation. The absence of a raphe and excessive bulky calcification, especially in the LVOT, allowed an apparently safe stent positioning with a circular uniform expansion, with no post-operative PVL found in this patient, agreeing with the clinical findings.

4.3. Effect of transcatheter aortic valve replacement on mitral regurgitation severity

Following TAVR, several clinical studies have found the aetiology and severity of MR to have varying effects on short- and long-term mortality [7,41,42]. Less is known, however, on the changes in MR severity post-TAVR, with single-centre and multicentre registry studies often giving conflicting results [6,7,41,43]. Given the paucity of high-quality data on this topic, the American Heart Association's guidelines and the European Society of Cardiology have opted not to make recommendations on concomitant MR treatment in patients undergoing TAVR. Nevertheless, with the previous knowledge of physiological aortic–mitral reciprocal behaviour [44], some echo studies have aimed to identify the structural changes in the aortic–mitral complex that may influence MR degree following TAVR [43,45,46]. Although these imaging studies have greatly enhanced our understating of the aortic–mitral coupling in this setting, the use of 2D/3D echo only allows a semi-quantitative analysis of the AV-MV anatomy and coupled function. Taking into account the fast-paced developments in transcatheter valve therapies, there is a need for more robust quantitative methods for objective and accurate assessment of AV-MV coupled dynamics. The patient-specific computational model developed in this study provided a quantitative engineering analysis of the relationship between MR severity and the 3D structural changes of the aortic–mitral continuity throughout the cardiac cycle following TAVR in a virtual human beating heart.

In agreement with previous echo studies [45,46], our analysis showed that during the TAVR procedure the MA height decreased in the post-TAVR 50% model compared with the pre-TAVR model. Interestingly, with a higher stent implantation configuration, we found that the MA height increased instead; up to 8% for the post-TAVR 10% model. The aortic–mitral angle also decreased, with a narrower angle in the highest implantation model than in the midway implantation model. Narrower distances between the centre of the aortic and mitral annuli matched changes in the aortic–mitral angle. The reports by Shibayama et al. [43] and Vergnat et al. [46] are also consistent with the present study, showing that the MA area, AP distance and AL-PM distance did not significantly change after TAVR. A critical finding of this study was that during TAVR, the aortic annulus was displaced longitudinally approximately 3.3 mm towards the LVOT, while the anterior MA was displaced approximately 2.5 mm posteriorly, with this motion decreasing as the implantation height increased. Particularly, the posterior displacement of the anterior MA suggests an actual mechanical effect of the TAV stent on the aortic–mitral curtain. Although the acute effects of afterload reduction cannot be entirely excluded, mechanical compression is likely a contributor to the small MR reduction seen after TAVR using a balloon-expandable valve. It remains to be seen whether the use of a self-expanding stent frame, which has a different radial force and a more prominent protrusion into the LVOT results in more or less structural perturbations to the aortic–mitral continuity. This is the subject of a study we are currently undertaking.

Immediate LV pressure reduction secondary to a reduction in afterload was an additional mechanism for the early improvement in MR. In this study, however, while the RV_MV decreased in all post-TAVR models, no significant differences were reported, in part due to the lack of PML tethering improvement (table 5). Overall, resolution of BAV flow obstruction led to a sharp drop in the LV systolic pressure, and subsequently, a lower transmitral pressure gradient (table 4); which in turn reduced the driving force of the MR. Both the peak and mean pressure gradients across the AV were similarly reduced among all post-TAVR models, with a trend toward slightly better TAV performance haemodynamic metrics and reduction of the RV_MV for the midway implantation model (post-TAVR 50%). Although not studied herein, reduction in MR severity in the late post-procedural period may be secondary to a regression of myocardial hypertrophy and positive remodelling of LV shape, especially in functional MR [47].

4.4. Limitations

Several limitations should be taken into consideration when interpreting our findings. First, in this study only one patient-specific anatomy was examined, and as such the specific results regarding the TAVR biomechanics and its impact on MR severity cannot be assumed to represent the entire population. However, the validity of the results stands due to their comparative nature. In the future, we plan to extend this modelling framework to a larger cohort of patients and newer-generation commercially TAV types. Second, while, on one side, cardiac tissues were realistically described as hyperelastic and anisotropic, on the other side, patient-specific cardiac tissue material properties were not available. Thus, the mechanical response of the tissues was defined from an extensive human tissue database obtained from in-house multiprotocol biaxial and uniaxial tests. Third, since this study did not consider the zero stress–free configuration of the aortic wall, a rigid body constraint was assigned to the aortic root/ascending aorta wall elements during the pre- and post-TAVR FSI simulations; however, deformable tissue properties were attributed during the TAVR FE simulations. For the same reason, aortic wall pre-stress state was neglected during the TAVR FE analysis. This assumption, which will be tacked in a future study, could lead to uncertainties on the computed stresses as well as in the tissue compliance [48–50]. The pre-stress assumption of the native leaflets might have a small impact on the solution since the transvalvular pressure is very small during TAV deployment. Fourth, post-operative MSCT images were not available, thus it was not possible to compare the deformed TAV stent geometries from the simulations with post-TAVR clinical images. However, the current study still enabled us to compare different implantation configurations and evaluate the impact of stent depth on several clinically relevant parameters. Finally, the current SPH-FE FSI modelling framework involves a high computational cost. The FE TAVR simulations required approximately 3 days to run while the pre- and post-TAVR FSI simulations required approximately 5 days to run one cardiac cycle in an Intel Xeon E5-2670 cluster. As a result, the present modelling methodology cannot be used in a clinical setting and currently, is only suitable for a research environment. Nevertheless, among other advantages, SPH is easy to parallelize. The ability to run both FE and SPH codes on GPUs will significantly reduce the running time in the near future and avoid the need for a computer cluster [51,52].

5. Conclusion

In this work, we performed a comprehensive computational engineering analysis to investigate the impact of TAVR on MR severity, aortic–mitral coupling, TAVR-in-BAV device performance, and pre- and post-TAVR LH dynamics in a retrospective real clinical case. Our results demonstrated that the biomechanical mechanism of MR evolution after TAVR is clearly multifactorial. The structural coupling of the AV-MV is a relationship that undergoes measurable changes following TAVR as the balloon-expandable stent compresses the aortic–mitral continuity. Moreover, we showed that correcting the AS abruptly reduces LV systolic pressure, which results in a lower transmitral systolic pressure gradient, which in turn reduces the pathological retrograde flow through the MV. In conclusion, albeit a single real clinical case, this study offered a detailed engineering analysis that could shed light on the underlying mechanisms of TAVR impact on MR. Further development and validation of the computational modelling techniques in a large cohort of patients could eventually enable the use of such techniques for an individualized treatment approach and ultimately support improved clinical outcomes.

Data accessibility

All relevant data are within the paper and as electronic supplementary material.

Authors' contributions

A.C. contributed to conceptualization, formal analysis, investigation, methodology, project administration, validation, visualization, writing—original draft, writing—review and editing. W.M. contributed to investigation, writing—review and editing. R.M. contributed to resources, writing—review and editing. W.S. contributed to conceptualization, funding acquisition, investigation, project administration, resources, supervision, writing—review and editing. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

W.S. is a co-founder and serves as the Chief Scientific Advisor of Dura Biotech. He has received compensation and owns equity in the company. The remaining authors have nothing to disclose.

Funding

This work was supported in part by the NIH HL127570 grant. A.C. was, in part, supported by a Fulbright-Colciencias Fellowship.