Mathematical modelling of the restenosis process after stent implantation

Abstract

The stenting procedure has evolved to become a highly successful technique for the clinical treatment of advanced atherosclerotic lesions in arteries. However, the development of in-stent restenosis remains a key problem. In this work, a novel two-dimensional continuum mathematical model is proposed to describe the complex restenosis process following the insertion of a stent into a coronary artery. The biological species considered to play a key role in restenosis development are growth factors, matrix metalloproteinases, extracellular matrix, smooth muscle cells and endothelial cells. Diffusion–reaction equations are used for modelling the mass balance between species in the arterial wall. Experimental data from the literature have been used in order to estimate model parameters. Moreover, a sensitivity analysis has been performed to study the impact of varying the parameters of the model on the evolution of the biological species. The results demonstrate that this computational model qualitatively captures the key characteristics of the lesion growth and the healing process within an artery subjected to non-physiological mechanical forces. Our results suggest that the arterial wall response is driven by the damage area, smooth muscle cell proliferation and the collagen turnover among other factors.

1. Introduction

Cardiovascular diseases (CVDs) are the leading cause of mortality in the world. In Europe, 3.9 million deaths a year are attributed to CVDs, with coronary heart disease (CHD) and stroke the primary culprits [1]. CHD is characterized by the development of atherosclerotic plaque, consisting of deposits of cholesterol and other lipids, calcium and macrophages, within the arterial wall. This causes a progressive reduction in the lumen available for the blood flow (stenosis), hardening and loss of elasticity of the arterial tissue.

The use of endovascular devices such as stents and balloons to treat advanced atherosclerotic lesions is now commonplace in the clinic. However, one of the major limitations of these interventions is the development of restenosis [2–7]. Restenosis is understood to comprise three main mechanisms: elastic recoil (in the short term), vessel remodelling and neointimal hyperplasia (in the longer term). The first and second mechanisms are typical in the case of balloon angioplasty, whereas stent deployment usually promotes the formation of neointimal hyperplasia, associated with smooth muscle cell (SMC) migration and proliferation and extracellular matrix (ECM) deposition [7]. Coronary revascularization now generally involves the use of a stent in more than 70% of cases, leading to reduced restenosis rates in comparison to balloon angioplasty alone. With the advent of drug-eluting stents (DES), the incidence of restenosis has been dramatically reduced to approximately less than 10–12% of all angioplasties [8]. However, DES do not completely remove this problem. Since the precise mechanisms behind restenosis after stenting, so-called in-stent restenosis (ISR), are still not fully understood, it therefore remains a significant clinical challenge to predict which patients will develop ISR.

Experimental studies have established a strong correlation between the level of arterial injury caused by the device and the following neointimal thickness and lumen diameter reduction at the stented area [9,10]. Novel stent designs and stent-deployment protocols that minimize induced vascular injury are therefore needed. However, the optimum stent design and the ideal drug release strategy still remain in question despite technological advances [11].

Complementary to the wide variety of experimental studies, computational analysis has emerged as a useful method for designing new medical devices in order to minimize ISR. In the last two decades, many computational models of stent deployment have been developed to study the stress–strain level that the device induces within the arterial wall [12–15]. Several mathematical and numerical models have also been developed to try to understand drug release from stents and subsequent redistribution in the arterial tissue [16–20]. Less attention, however, has been directed to modelling the biological response to treatment.

In recent years, mechanobiological models have emerged to relate mechanics to the complex biological response. These have primarily made use of discrete agent-based models (ABMs) or cellular automata (CA) methods, in some cases combining with finite-element analysis. For example, Zahedmanesh et al. developed an ABM to investigate the dynamics of SMCs in vascular tissue engineering scaffolds [21] and an ABM of ISR which allows a quantitative evaluation of the ECM turnover after stent-induced vascular injury [22]; Boyle et al. demonstrated that nonlinear growth could be simulated with a cell-centred model [23] and simulated ISR by modelling a combination of injury and inflammation with SMCs represented as discrete agents [24,25]; and Keshavarzian et al. [26] developed a mechanobiological model of arterial growth and remodelling. Evans et al. [27] highlighted the importance of using a multiscale approach to describe computationally the main physical and biological processes implicated in ISR, introducing the concept of the complex autonoma (CxA) models, based on a hierarchical aggregation of coupled CA and ABMs. Tahir et al. [28] focused on the initial phase after stenting and developed a cellular Potts model from which they hypothesized that deeper stent deployment allows easier migration of SMCs into the lumen. Most recently, Zun et al. [29] presented a three-dimensional multiscale model of ISR with blood flow simulations coupled to an agent-based SMC proliferation model and demonstrated qualitative agreement with in vivo porcine data. In the aforementioned examples, discrete models attempted to represent individual cells in the form of a lattice governed by a set of rules, in contrast to the continuum approach where the evolution of populations of cells and other species such as growth factors (GFs) are described through partial differential equations (PDEs).

In terms of continuum models, Rachev et al. [30] proposed a theoretical continuum model to describe the main mechanisms of the coupled deformation and stress-induced arterial tissue thickening observed at the regions close to an implanted stent, comparing the results obtained with experimental data documented in the available literature [31]. However, this phenomenological model does not take into account, for example, the mechanisms implicated in the SMC proliferation or the ECM synthesis. Other continuum mathematical biological models typically comprise a series of coupled diffusion–reaction equations for describing the biological interaction between several species. Such models have been developed to describe phenomena such as neointimal hyperplasia formation [32], atherosclerotic plaque formation [33–36], fibrotic tissue formation surrounding medical implants [37,38] and, more recently, ISR [39] and arterial physiopathology [40]. In contrast to discrete models where cell behaviour is usually described by a set of rules, continuum models offer a mechanistic description, featuring physical parameters which may in principle be measured. In addition, continuum models often have a lower computational cost than ABMs, and naturally allow for modelling diffusion of species and coupling with the mechanical aspects of the problem.

In this paper, we develop a model that allows us to simulate the restenosis process following the insertion of a stent into a coronary artery. The key novelty of our model is that it adopts a continuum approach to describe the sequence of events following damage to the arterial wall, and is therefore formulated in terms of densities/concentrations of a number of important species. This is advantageous because it allows us to assess how the evolution of the various species affects the overall healing process, and more importantly, how variations in the associated parameters and initial conditions influence the process. Diffusion–reaction equations are used for modelling the mass balance between biological species in the arterial wall. The main species considered to play a key role in the process are SMCs, endothelial cells (ECs), matrix-degrading metalloproteinases (MMPs), GFs and ECM. The parameters used in the model to define the biological interaction between the different species have been adapted from experimental data available in the literature. Unlike any of the existing continuum models, we are able to simulate the time-course response of six different biological species involved in ISR after the initial mechanical damage, while at the same time simulating tissue growth. Our primary aim is to gain insight into the physical mechanisms of tissue remodelling post-stenting. Simulating patient-specific cases is beyond the scope of this work: historically, mathematical and computational models in the stents domain have been formulated in idealized scenarios to gain insight before moving onto more realistic patient-specific geometries. With this in mind, we employ a simplified geometry. Notwithstanding, we do compare our results to clinical data and use our model to assess the impact of geometric variations on the final outcome through consideration of a series of commercial stents as well as different inter-strut distances and levels of strut embedment, thereby enabling us to relate our findings to stent design.

2. Governing equations and model assumptions

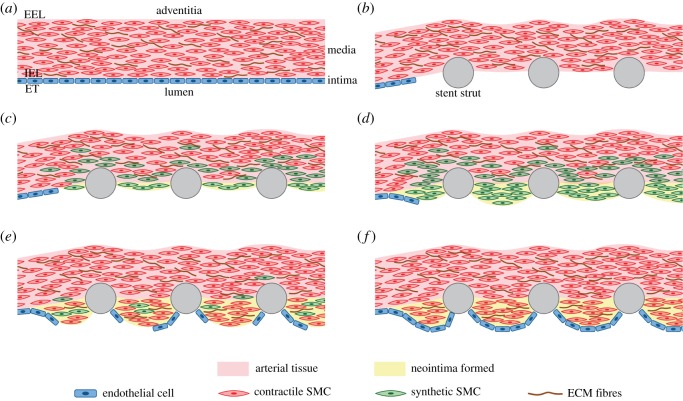
ISR is an immeasurably complex multiscale system involving a large number of species and an intricate cascade of biological processes (figure 1). Indeed, much of the biology is still unknown. Due to its complexity, in this model we include only what we believe are the predominant species and processes. Specifically, we consider three types of cells (contractile and synthetic SMCs and ECs) and three extracellular components (GFs, MMPs and ECM). We consider the following behaviour: cell types can proliferate, migrate, differentiate and die (apoptosis) while the extracellular components can be produced or degraded. Since the processes considered take place predominantly in the intima and media layers, in the following model the arterial wall refers to these layers, with the adventitia considered as the outer boundary. Furthermore, blood flow in the lumen and plasma filtration in the tissue have not been included. We refer the reader to §5 for a full discussion of the limitations of this work.

Figure 1.

Schematic of ISR. In summary, prior to stent deployment, SMCs exist in a quiescent and contractile phenotype predominantly in the media layer of the tissue and ECs populate the uninjured arterial wall (a). After stent deployment (b), endothelial denudation, atherosclerotic plaque compression (often with dissection into the media and occasionally adventitia), and unphysiological stretch of the entire artery occur [7]. Platelets are then deposited at the injured area and GFs are released. Local increases in stationary mechanical strain, which occurs following stenting, lead to up-regulation of MMP by SMCs and degradation of collagen in the ECM. Endothelial damage and denudation, among multiple factors, lead to the phenotype switch of medial SMCs from a contractile to a synthetic state [3]. Synthetic SMCs proliferate in response to GFs [24] first in the media and then these begin to migrate towards the injured area (c,d). Simultaneously, ECs migrate from the lateral edge of the damaged blood vessel surface [2] (e). Moreover, synthetic SMCs secrete ECM components, such as collagen and proteoglycans, which constitute the neointimal lesion [24]. Between two and three weeks after the stenting procedure, synthetic SMCs begin to revert to the contractile phenotype [2]. Neointima typically increases up to three months after the procedure, with little change to six months and a gradual reduction between six months to three years [6] (e,f). (Online version in colour.)

2.1. Material model

An isotropic hyperelastic constitutive model based on a Yeoh strain energy function (SEF) [41] was considered to describe the stress–strain response of the arterial wall. We assume the same mechanical response for the intima and the media layer. Assuming incompressibility of the tissue, the Yeoh SEF can be written as

$$\mathit{\Psi }=c_{10}(I_1-3)+c_{20}{(I_1-3)}^2+c_{30}{(I_1-3)}^2,$$ 2.1

where c₁₀ = 17.01 kPa, c₂₀ = −73.42 kPa and c₃₀ = 414.95 kPa are the hyperelastic material constants and I₁ is the first strain invariant of the Cauchy–Green deformation tensor. The coefficients of the hyperelastic model were identified from fitting the experimental results obtained from Holzapfel et al. [42] in specimens of human coronary arteries for the media layer in the circumferential direction using the software for calibration of hyperelastic material models (HyperFit, www.hyperfit.wz.cz).

The stent is modelled as an elasto-plastic material with a Young’s modulus of E = 200 GPa, Poisson’s ratio of ν = 0.28 (representative of biomedical grade stainless steel alloy 316L) and plasticity described by isotropic hardening J₂ flow theory with the tensile stress–strain curves taken from the literature, including a yield strength of 264 MPa and an ultimate tensile strength of 584 MPa at an engineering plastic strain of 0.247 [15].

2.2. Initial estimation and evolution of the damage

Although not completely elucidated, the stimulus triggering the cascade of inflammatory events leading to neointimal formation appears to come from the endothelial damage caused immediately after balloon dilatation and stent placement [43]. We do not explicitly account for all of the mechanical factors that initiate the process which leads to vessel injury and endothelial dysfunction. Following Zahedmanesh et al. [22], we assign a level of injury to the arterial wall, d, in a continuous range from 0 to 1. Due to the absence of reliable mechanical data in the literature on the stress–strain levels known to cause arterial injury, the experimental data of in vitro tensile tests up to failure of 13 human left anterior descending coronary arteries [42] were used to obtain a qualitative estimation of the damage in the tissue. In particular, we define a piecewise linear function to prescribe the initial arterial damage as a function of von Mises stress, σ_vm, calculated by a finite-element (FE) simulation of the stent expansion:

$$d_0=\{\begin{array}{cc}0& \mathrm{if}\hspace{0.17em}{\sigma }_{\mathrm{vm}}\le {\sigma }_{\mathrm{vm},\inf }\\ \frac{{\sigma }_{\mathrm{vm}}-{\sigma }_{\mathrm{vm},\inf }}{{\sigma }_{\mathrm{vm},\sup }-{\sigma }_{\mathrm{vm},\inf }}& \text{if}\hspace{0.17em}{\sigma }_{\mathrm{vm},\inf }<{\sigma }_{\mathrm{vm}}<{\sigma }_{\mathrm{vm},\sup }\\ 1& \text{if}\hspace{0.17em}{\sigma }_{\mathrm{vm}}\ge {\sigma }_{\mathrm{vm},\sup },\end{array}$$ 2.2

where d₀ is the initial damage in the tissue due to the stent placement. This function assigns a value of zero for the damage in areas of the arterial wall in which von Mises stress is lower than σ_vm,inf and a value of 1 for the damage in those regions in which von Mises stress exceeds σ_vm,sup (figure 2).

Figure 2.

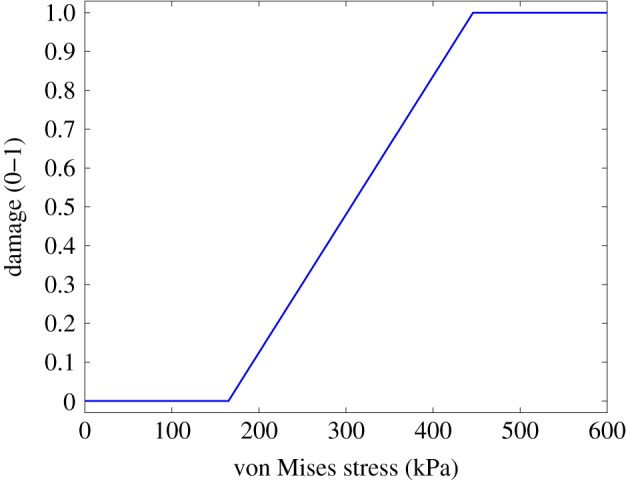
Initial damage as a function of von Mises stress in the arterial wall. In this work, the value selected for the inferior limit of the von Mises stress is 165 kPa, corresponding to three times the value of the physiological circumferential tension calculated by Laplace’s Law, for a given blood pressure of 100 mmHg (13.3 kPa). For the superior limit of the von Mises stress, a value of 446 kPa was chosen, based on the mean value of the ultimate tensile stresses for the media layer in the circumferential direction reported by Holzapfel et al. [42]. (Online version in colour.)

Moreover, damage, d, is assumed to decrease continuously with time at a rate directly proportional to the MMP concentration, c_mmp [24]. The damage evolution equation is therefore

$$\frac{\mathrm{\partial }d}{\mathrm{\partial }t}=\underset{\begin{array}{c}\mathrm{Degradation}\end{array}}{\underbrace{-k_{\mathrm{deg},d}\hspace{0.17em}d{c}_{\mathrm{mmp}}}},$$ 2.3

where d is a continuous function of space and time, d(r, z, t), to describe the damage level, k_deg,d is the degradation rate of damage and c_mmp(r, z, t) is the concentration of MMP. Equation (2.3) may be considered as a simple description of healing.

2.3. Species evolution

2.3.1. Growth factors

After mechanical arterial injury, platelets, leucocytes and SMCs, among others, release several types of GFs: platelet-derived GF (PDGF), epidermal GF (EGF), insulin-like GF (IGF), transforming GF (TGF) and fibroblast GF (FGF) [2,3,5,7]. However, since their specific roles in the inflammatory phase are not completely understood [2], the term GF includes the combined action of all of them. Denoting the concentration of GFs in the arterial wall by c_gf(r, z, t), and assuming an initial value of c_gf,0 [44], their behaviour is modelled as follows:

$$\begin{array}{r}\frac{\mathrm{\partial }{c}_{\mathrm{gf}}}{\mathrm{\partial }t}+\underset{\begin{array}{c}\mathrm{Random}\hspace{0.17em}\mathrm{motion}\end{array}}{\underbrace{\mathrm{\nabla }\cdot (-D_{\mathrm{gf}}\mathrm{\nabla }{c}_{\mathrm{gf}})}}=\underset{\begin{array}{c}\mathrm{Production}\end{array}}{\underbrace{k_{\mathrm{prod},\mathrm{gf}}\hspace{0.17em}d(1-\frac{c_{\mathrm{gf}}}{c_{\mathrm{gf},\mathrm{th}}})}}\\ -\underset{\begin{array}{c}\mathrm{Degradation}\end{array}}{\underbrace{k_{\mathrm{deg},\mathrm{gf}}(c_{\mathrm{gf}}-c_{\mathrm{gf},0})}}.\end{array}$$ 2.4

We are assuming that the GFs experience random motion (i.e. diffusion). Although the diffusion coefficient, D_gf, may in general depend on position, we take it here to be constant [32]. The right-hand side of equation (2.4) considers a dynamic balance between degradation and production. GF production is assumed to follow logistic growth: the concentration increases proportionally to the production rate, k_prod,gf, and level of damage, d, until some threshold value, c_gf,th, is reached. To simplify the mathematical model, we consider that vascular damage is the only trigger of GF production. Degradation, on the other hand, is assumed to occur at a constant rate, k_deg,gf, and in proportion to the ‘distance’ from the initial value.

2.3.2. Matrix-degrading metalloproteinases

Human MMPs are a family of 26 members of zinc-dependent proteolytic enzymes which are considered to be the normal and physiologically relevant mediators of ECM degradation [45,46]. Given that MMP-2 cleaves a wider range of ECM constituents [22], the term MMP specifically refers to MMP-2 in this model. ECs, SMCs, fibroblasts and infiltrating inflammatory cells are able to produce MMPs. In this work, we assume that mechanical damage resulting from stenting upregulates MMP production only by SMCs [46], while at the same time MMP is reduced at a constant rate [24]. The MMP evolution equation is defined as follows:

$$\begin{array}{rl}\frac{\mathrm{\partial }{c}_{\mathrm{mmp}}}{\mathrm{\partial }t}& +\underset{\begin{array}{c}\mathrm{Random}\hspace{0.17em}\mathrm{motion}\end{array}}{\underbrace{\mathrm{\nabla }\cdot (-D_{\mathrm{mmp}}\mathrm{\nabla }{c}_{\mathrm{mmp}})}}\\ & =\underset{\begin{array}{c}\mathrm{Production}\end{array}}{\underbrace{(k_{\mathrm{prod}1,\mathrm{mmp}}{c}_{\mathrm{csmc}}+k_{\mathrm{prod}2,\mathrm{mmp}}{c}_{\mathrm{ssmc}})d(1-\frac{c_{\mathrm{mmp}}}{c_{\mathrm{mmp},\mathrm{th}}})}}\\ & -\underset{\begin{array}{c}\mathrm{Degradation}\end{array}}{\underbrace{k_{\mathrm{deg},\mathrm{mmp}}(c_{\mathrm{mmp}}-c_{\mathrm{mmp},0})}},\end{array}$$ 2.5

where c_mmp is the concentration of MMPs, D_mmp is the diffusion coefficient to simulate the random movement of MMP molecules, k_prod1,mmp and k_prod2,mmp are the production rates of MMPs by contractile and synthetic SMCs, respectively, and k_deg,mmp is the constant degradation rate of MMPs. The parameter c_mmp,0 represents the initial concentration of MMP in the tissue [47], while c_mmp,th is the threshold MMP concentration.

2.3.3. Extracellular matrix

The ECM is the non-cellular component of the arterial wall that provides physical scaffolding for the cellular constituents and is responsible for cell–matrix interactions [48], playing a crucial role in the development of the pathogenesis of restenosis. In particular, ECM components are involved in the regulation of SMC phenotype: degradation of ECM after stenting promotes the transition of SMCs from a quiescent/contractile to an active/synthetic phenotype, whereas its synthesis leads to the opposite [49]. In this work, the behaviour of ECM has been directly related to the behaviour of collagen which constitutes the major component of mature restenotic tissue [7]. For this reason, collagen is assumed to be the only component of the ECM in our model. Collagen is secreted by synthetic SMCs [2] and degraded at a rate proportional to the amount of MMPs [7,24], so its behaviour can be defined as follows:

$$\begin{array}{rl}\frac{\mathrm{\partial }{c}_{\mathrm{ecm}}}{\mathrm{\partial }t}& =\underset{\begin{array}{c}\mathrm{Production}\end{array}}{\underbrace{k_{\mathrm{prod},\mathrm{ecm}}{c}_{\mathrm{ssmc}}(1-\frac{c_{\mathrm{ecm}}}{c_{\mathrm{ecm},\mathrm{th}1}})}}\\ & -\underset{\begin{array}{c}\mathrm{Degradation}\end{array}}{\underbrace{k_{\mathrm{deg},\mathrm{ecm}}(c_{\mathrm{mmp}}-c_{\mathrm{mmp},0})(1-\frac{c_{\mathrm{ecm},\mathrm{th}2}}{c_{\mathrm{ecm}}})}},\end{array}$$ 2.6

where c_ecm(r, z, t) is the concentration of collagen, which is produced at a rate k_prod,ecm and degraded at a degradation rate k_deg,ecm. The initial concentration of collagen is c_ecm,0 [47]. We assume that the natural synthesis of collagen is equal to the age-related degradation rate, therefore these terms have not been taken into account in this equation. Moreover, we assume that ECM kinetics are dominated by production and degradation and that random motion of ECM is negligible.

2.3.4. Contractile smooth muscle cells

SMCs are the most prominent cell type found in intimal hyperplasia. In our model, SMCs can exist in one of two phenotypes: contractile or synthetic. Before stent implantation, SMCs are in a quiescent/contractile phenotype (do not proliferate or synthesize matrix) within the uninjured tissue. We can define the behaviour of the contractile SMCs as

$$\frac{\mathrm{\partial }{c}_{\mathrm{csmc}}}{\mathrm{\partial }t}=\underset{\begin{array}{c}\mathrm{Differentiation}\hspace{0.17em}\\ \mathrm{from}\hspace{0.17em}\mathrm{cSMC}\hspace{0.17em}\mathrm{to}\hspace{0.17em}\mathrm{sSMC}\end{array}}{\underbrace{-k_{\mathrm{diff},\mathrm{csmc}}{c}_{\mathrm{csmc}}{K}_{\mathrm{ssmc},\mathrm{ecm}}}}+\underset{\begin{array}{c}\mathrm{Differentiation}\hspace{0.17em}\\ \mathrm{from}\hspace{0.17em}\mathrm{sSMC}\hspace{0.17em}\mathrm{to}\hspace{0.17em}\mathrm{cSMC}\end{array}}{\underbrace{k_{\mathrm{diff},\mathrm{ssmc}}{c}_{\mathrm{ssmc}}{K}_{\mathrm{csmc},\mathrm{ecm}}}},$$ 2.7

where c_csmc(r, z, t) is the contractile SMC concentration, k_diff,csmc is the differentiation rate from contractile SMCs to synthetic SMCs, k_diff,ssmc is the differentiation rate from synthetic SMCs to contractile SMCs and K_csmc,ecm and K_ssmc,ecm (figure 3) are functions defined to modulate the SMC differentiation as a function of the ECM concentration:

$$K_{\mathrm{ssmc},\mathrm{ecm}}=-({\mathrm{e}}^{-((c_{\mathrm{ecm},\mathrm{th}}/c_{\mathrm{ecm}})-1)-|(c_{\mathrm{ecm},\mathrm{th}}/c_{\mathrm{ecm}})-1|}-1)$$ 2.8

and

$$K_{\mathrm{csmc},\mathrm{ecm}}=-({\mathrm{e}}^{-((c_{\mathrm{ecm}}/c_{\mathrm{ecm},\mathrm{th}})-1)-|(c_{\mathrm{ecm}}/c_{\mathrm{ecm},\mathrm{th}})-1|}-1).$$ 2.9

Figure 3.

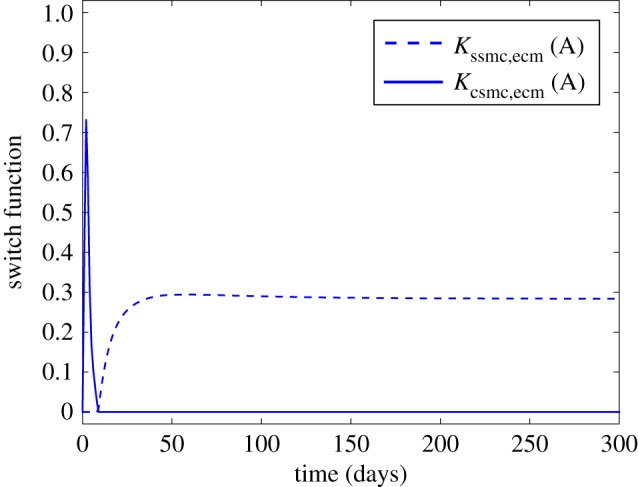
Behaviour of the switch functions defined by equations (2.8) and (2.9). (Online version in colour.)

In this model, contractile SMCs may differentiate into synthetic SMCs and vice-versa. The function K_ssmc,ecm contributes to the emergence of the synthetic phenotype, so when c_ecm < c_ecm,th the function K_ssmc,ecm takes positive values, SMCs are activated and switch to a synthetic phenotype starting to migrate, proliferate and synthesize ECM, while if c_ecm ⩾ c_ecm,th then K_ssmc,ecm is equal to zero (no differentiation). On the other hand, K_csmc,ecm contributes to the emergence of the contractile phenotype, so when c_ecm ⩽ c_ecm,th then K_csmc,ecm is zero and if c_ecm > c_ecm,th the function K_csmc,ecm takes a positive value and synthetic SMCs switch back to the contractile phenotype. At the beginning of the simulation c_ecm = c_ecm,th so K_ssmc,ecm and K_csmc,ecm are both equal to zero. We assume that contractile SMCs are initially present only in the media, and at a density of c_csmc,0 [50]. Random motion is not taken into account for this cell type since contractile SMCs are considered quiescent and do not migrate. Moreover, contractile SMCs are considered unresponsive to GFs [2].

2.3.5. Synthetic smooth muscle cells

The synthetic SMC evolution equation is as follows:

$$\begin{array}{rl}\frac{\mathrm{\partial }{c}_{\mathrm{ssmc}}}{\mathrm{\partial }t}& +\underset{\begin{array}{c}\mathrm{Random}\hspace{0.17em}\mathrm{motion}\end{array}}{\underbrace{\mathrm{\nabla }\cdot (-D_{\mathrm{ssmc}}\mathrm{\nabla }{c}_{\mathrm{ssmc}})}}=\underset{\begin{array}{c}\mathrm{Differentiation}\hspace{0.17em}\\ \mathrm{from}\hspace{0.17em}\mathrm{cSMC}\hspace{0.17em}\mathrm{to}\hspace{0.17em}\mathrm{sSMC}\end{array}}{\underbrace{k_{\mathrm{diff},\mathrm{csmc}}{c}_{\mathrm{csmc}}{K}_{\mathrm{ssmc},\mathrm{ecm}}}}\\ & -\underset{\begin{array}{c}\mathrm{Differentiation}\hspace{0.17em}\\ \mathrm{from}\hspace{0.17em}\mathrm{sSMC}\hspace{0.17em}\mathrm{to}\hspace{0.17em}\mathrm{cSMC}\end{array}}{\underbrace{k_{\mathrm{diff},\mathrm{ssmc}}{c}_{\mathrm{ssmc}}{K}_{\mathrm{csmc},\mathrm{ecm}}}}+\underset{\begin{array}{c}\mathrm{Proliferation}\end{array}}{\underbrace{k_{\mathrm{prolif},\mathrm{ssmc}}(c_{\mathrm{gf}}-c_{\mathrm{gf},0})}}\\ & -\underset{\begin{array}{c}\mathrm{Apoptosis}\end{array}}{\underbrace{k_{\mathrm{apop},\mathrm{ssmc}}{c}_{\mathrm{ssmc}}}},\end{array}$$ 2.10

where c_ssmc(r, z, t) is the synthetic SMC concentration, D_ssmc is the diffusion coefficient of synthetic SMCs in order to simulate the migration process, k_prolif,ssmc is the proliferation rate of synthetic SMCs in response to GFs and k_apop,ssmc is the apoptosis rate at which synthetic SMCs die. The initial density of synthetic SMCs in the arterial wall, c_ssmc,0, is assumed to be equal to zero [38].

2.3.6. Endothelial cells

Along with SMCs, ECs constitute the main cell type within the vasculature. ECs perform a wide variety of significant functions, e.g. cell migration and proliferation, remodelling, apoptosis and the production of different biochemical substances [51], as well as the control of vascular function [52]. Moreover, most of the mechanical responses to flow in the arterial wall, such as shear stress and stretch, directly affect ECs indicating that these cells have specific mechanotransducers capable of transforming mechanical forces into biological responses. A thin single layer of ECs forms the endothelium, which in normal conditions, besides being a permeability barrier between the blood flow and the arterial wall, promotes vasodilatation and suppresses intimal hyperplasia by inhibiting inflammation, thrombus formation and SMC proliferation and migration [53]. However, at sites of injury caused by the stent, the endothelium is denuded [7]. This de-endothelization is considered to be one of the most important mechanisms contributing to restenosis [54]. In this work, it is assumed that the endothelium is denuded between stent struts, considering that only a small amount of cells survive in this region. The behaviour of the ECs may be modelled as

$$\frac{\mathrm{\partial }{c}_{\mathrm{ec}}}{\mathrm{\partial }t}+\underset{\begin{array}{c}\mathrm{Random}\hspace{0.17em}\mathrm{motion}\end{array}}{\underbrace{\mathrm{\nabla }\cdot (-D_{\mathrm{ec}}\mathrm{\nabla }{c}_{\mathrm{ec}})}}=\underset{\begin{array}{c}\mathrm{Proliferation}\end{array}}{\underbrace{k_{\mathrm{prolif},\mathrm{ec}}{c}_{\mathrm{ec}}(1-\frac{c_{\mathrm{ec}}}{c_{\mathrm{ec},0}})}},$$ 2.11

where c_ec(r, z, t) is the density of the endothelial cells, D_ec is the diffusion coefficient of the ECs to simulate their migration from the lateral edge of the damage blood vessel surface [2] and k_prolif,ec is the EC proliferation rate. ECs can exist only in the intima or subendothelial spaces (SES). The initial concentration of ECs is assumed to be near to zero at sites where the SES is injured and c_ec,0 [55] at the intact SES. In order to ensure a tractable mathematical model, the equation which governs the behaviour of the ECs is assumed to be independent of the rest of the presented coupled PDEs.

2.4. Tissue growth

We follow the continuum framework for growth of biological tissue developed by Garikipati et al. [56] to describe the tissue growth that leads to restenosis. This formulation considers mass transport and mechanics coupled due to the kinematics of volumetric growth. Accordingly, the balance of mass in the system must satisfy

$$\frac{\mathrm{\partial }{\rho }_o^i}{\mathrm{\partial }t}={\mathit{\Pi }}_i-\mathrm{\nabla }\cdot {\mathit{M}}_i,$$ 2.12

where the index i is used to indicate an arbitrary species; ${\rho }_o^i$ are the concentrations of the species as mass per unit volume in the reference configuration; Π_i are the sources/sinks related to migration, proliferation, differentiation and apoptosis of the cells and synthesis and degradation of the substances; and M_i are the mass fluxes of the i arbitrary species. The operators $\mathrm{\nabla }(\bullet )$ and $\mathrm{\nabla }\cdot (\bullet )$ denote the gradient operator and the divergence of a vector in the reference configuration, respectively. The total material density of the tissue (ρ_o) is the sum of all the individual species concentrations (${\rho }_o^i$), i.e. ${\rho }_o=\sum _i{\rho }_o^i$. These densities, ${\rho }_o^i$, evolve if local volumetric changes take place as a result of mass transport and inter-conversion of species. That implies that the total density in the reference configuration, ρ_o, also changes with time, i.e. as species concentration increases, the material of a species swells, and conversely, shrinks as concentration decreases [56]. Assuming that these volumetric changes are locally isotropic, we can define the following growth deformation gradient tensor: ${\mathit{F}}_g^i=({\rho }_o^i)/({\rho }_{\mathrm{orig}}^i)\mathit{I}$, where ${\rho }_{\mathrm{orig}}^i$ represents the original density of a species in the reference configuration and I is the isotropic tensor of second order. Taking this into consideration, under the small strain hypothesis we can write

$$\mathrm{\nabla }\cdot {\mathit{v}}^{\mathit{i}}=\frac{{\rho }_o^i}{{\rho }_{\mathrm{orig}}^i},$$ 2.13

where v is the velocity of the material points [36]. Since the primary components of restenotic tissue are ECs, SMCs and collagen (here represented by ECM), we neglect volume contributions from the other species. Therefore, the isotropic growth that leads restenosis can be finally determined as

$$\mathrm{\nabla }\cdot \mathit{v}=\frac{\mathrm{\partial }\mathrm{\Delta }{c}_{\mathrm{ec}}}{\mathrm{\partial }t}{V}_{\mathrm{ec}}+\frac{\mathrm{\partial }\mathrm{\Delta }{c}_{\mathrm{smc}}}{\mathrm{\partial }t}{V}_{\mathrm{smc}}+\frac{\mathrm{\partial }\mathrm{\Delta }{c}_{\mathrm{ecm}}}{\mathrm{\partial }t}\frac{1}{{\rho }_{\mathrm{ecm}}},$$ 2.14

where Δc_ec, Δc_smc and Δc_ecm are the variations of concentrations of ECs, both contractile and synthetic SMCs and ECM, respectively, with respect to the initial concentration of these species before the restenosis process initiation. The parameters V_ec and V_smc are the volume of an EC and an SMC, respectively, and ρ_ecm is the collagen density (table 3). To calculate the volume of the individual cells, the shape of the ECs is assumed to be spherical [22] and the SMC shape is assumed to be ellipsoidal or spindle-shaped [57]. Therefore, the volume of each cell type may be estimated as follows:

$$V_{\mathrm{ec}}=\frac{4}{3}\pi r_{\mathrm{ec}}^3$$ 2.15

and

$$V_{\mathrm{smc}}=\frac{4}{3}\pi r_{\mathrm{smc}}^2{l}_{\mathrm{smc}},$$ 2.16

where r_ec is the typical radius of an EC, and r_smc and l_smc are the typical radius and the length of an SMC, respectively as shown in table 3. This growth process has been defined following the method described for the development of atherosclerotic plaque in [36] and the fibrosis process after the implantation of an inferior vena cava filter in [38], respectively.

Table 3.

List of parameters related to the biological model.

parameter	description	value	reference
rates
kdeg,d	damage degradation	0.5 m3 mol−1 s−1	estimated
kprod,gf	GF production	8 × 10−13 mol m−3 s−1	estimated
kdeg,gf	GF degradation	1.27 × 10−6 s−1	[24–65]
kprod1,mmp	MMP production by cSMC	3 × 10−26 mol cell−1 s−1	adapted from [22]
kprod2,mmp	MMP production by sSMC	6 × 10−26 mol cell−1 s−1	adapted from [22]
kdeg,mmp	MMP degradation	4.63 × 10−6 s−1	[24]
kprod,ecm	ECM production by sSMC	2.157 × 10−11 g cell−1 s−1	[36]
kdeg,ecm	ECM degradation	2 × 103 s−1	estimated
kdiff,csmc	cSMC differentiation	5 × 10−7 s−1	[23–36]
kdiff,ssmc	sSMC differentiation	2.314 × 10−6 s−1	[23]
kprolif,ssmc	sSMC proliferation by GF	$2.5\times {10}^{13}\hspace{0.17em}\text{cell}\hspace{0.17em}{\text{mol}}^{-1}\hspace{0.17em}{\text{s}}^{-1}$	estimated
kapop,ssmc	sSMC apoptosis	2.2 × 10−10 s−1	[66]
kprolif,ec	EC proliferation	10−6 s−1	adapted from [67]
diffusion coefficients
Dgf	GFs	2.6 × 10−11 m2 s−1	[32]
Dmmp	matrix metalloproteinases	1.2 × 10−12 m2 s−1	[68]
Decm	ECM	neglected	[36]
Dcsmc	cSMCs	neglected	[36]
Dssmc	synthetic smooth muscle cells	1.85 × 10−13 m2 s−1	[69]
Dec	ECs	8 × 10−14 m2 s−1	[32]
initial concentrations
cgf,0	GF initial concentration	3.48 × 10−7 mol m−3	[44]
cmmp,0	MMP initial concentration	3.83 × 10−7 mol m−3	[47]
cecm,0	ECM initial concentration	6.67 mol m−3	[47]
ccsmc,0	cSMC initial concentration	$3.16\times {10}^{13}\hspace{0.17em}\text{cell}\hspace{0.17em}{\text{m}}^{-3}$	[50]
cssmc,0	sSMC initial concentration	$0\hspace{0.17em}\text{cell}\hspace{0.17em}{\text{m}}^{-3}$	[38]
cec,0	EC initial concentration	$5\times {10}^{11}\hspace{0.17em}\text{cell}\hspace{0.17em}{\text{m}}^{-3}$	[55]
threshold values
cgf,th	GF threshold concentration	10 × cgf,0	estimated
cmmp,th	MMP threshold concentration	10 × cmmp,0	estimated
cecm,th	ECM threshold	cecm,0	[38]
cecm,th1	ECM superior threshold	1.5 × cecm,0	estimated
cecm,th2	ECM inferior threshold	0.1 × cecm,0	estimated
growth model
rec	EC radius	17.87 μm	[22]
rsmc	SMC radius	3.75 μm	[57]
lsmc	SMC length	115 μm	[57]
ρecm	ECM density	1 g ml−1	[47]

3. Computational model

3.1. Model geometry

A two-dimensional axisymmetric geometry corresponding to an idealized representation of a straight stented coronary artery segment is considered in all simulations (figure 4a). The baseline computational geometry (table 1) is similar to that introduced by Mongrain et al. [16], also employed by Vairo et al. [18] and modified by Bozsak et al. [19] to study the stent drug release and redistribution in the arterial wall. In order to be able to relate our findings to stent design, we also assess the impact of geometric variations on the final outcome. Specifically, we consider geometrical parameters for three commercial stents, Resolute (Medtronic), Xience (Abbott Vascular) and Biomatrix (Biosensors), whose strut dimensions were obtained from Byrne et al. [59], as well as varying the numbers of struts (n_s), inter-strut spacing (ISS), expansion diameter and level of strut embedment. In total, 9 different geometrical configurations are simulated, as summarized in table 2.

Figure 4.

(a) Baseline model geometry. The arterial wall is modelled as a multilayer structure distinguishing two different domains: intima and media layer. The adventitia is not modelled as a distinct layer but rather as a boundary condition at the outer surface of the media. The initial luminal radius, r_l, and the thickness of each wall layer, δ_j, in the unloaded geometry of the vessel are listed in table 1, based on typical physiological values found in the literature. The stent implanted in the arterial wall is represented by 10 circular struts each of 0.125 mm radius, r_s, half-embedded in the tissue and located 0.7 mm centre-to-centre distance, w_s, simulating a small lesion of 7 mm. We note that the problem is actually symmetrical about the r-axis, i.e. half way between the 5th and 6th struts. (b) Details of the FE mesh of the computational model. (Online version in colour.)

Table 1.

List of parameters related to the geometry of the baseline model.

parameter	description	value (mm)	reference
rl	lumen initial radius	1.2	[58]
δses	intima thickness	0.01	[19]
δm	media thickness	0.5	[17]
rs	strut radius	0.125	[16]
ws	interstrut distance	0.7	[16]

Table 2.

List of cases simulated to relate our findings to stent design. The last column refers to the ratio of the lumen diameter after stent expansion to the lumen diameter before stent expansion.

case	stent model	strut shape	strut size (μm)	ISS (mm)	ns	Emb. config. (%)	ratio
0	baseline model	circular	250	0.7	10	50	1.1
1	Resolute (Medtronic)	circular	91	0.7	10	50	1.1
2	Xience (Abbott)	square	81	0.7	10	50	1.1
3	Biomatrix (Biosensors)	square	120	0.7	10	50	1.1
4	baseline model	circular	250	1.4	5	50	1.1
5	baseline model	circular	250	1.0	7	50	1.1
6	baseline model	circular	250	0.5	14	50	1.1
7	baseline model	circular	250	0.7	10	25–75	1.1
8	baseline model	circular	250	0.7	10	50	1.2

3.2. Boundary conditions

The following boundary conditions were applied to the arterial wall mechanical model: (a) at the lumen–arterial wall interface, Γ_et,i and Γ_et,d, a constant pressure of 100 mmHg is used to simulate in vivo physiological conditions and (b) a displacement of 0.2 mm of the stent struts domain, Ω_s, against the wall is prescribed in order to achieve an extra dilatation of the vessel that is usual in stenting techniques. For the biological species evolution, flux and concentration continuity at the SES–media interface, Γ_iel, is prescribed. A zero flux boundary condition, $-\mathit{n}\cdot (-D_{\hspace{0.17em}j}\mathrm{\nabla }{c}_{\hspace{0.17em}j})=0$, where n is the unit normal vector to the corresponding exterior boundary and j denotes each layer of the arterial tissue, was applied at the following boundaries: lumen–wall interface, struts–wall interface, Γ_s, arterial wall inlet, Γ_j,inlet, and outlet, Γ_j,outlet, and outer surface of the media, Γ_eel, in case of GFs, MMPs, ECM and SMCs or SES–media interface in case of EC. All computational boundaries and domains are shown in figure 4 for the baseline model.

3.3. Numerical methods

The commercial software package COMSOL Multiphysics 5.3 (COMSOL AB, Burlington, MA, USA) was used to create the computational geometry and to solve numerically, by means of the finite element method (FEM), the mechanobiological model detailed in §2, which is composed of three coupled systems: (1) a steady system which simulates the mechanical expansion of the stent used for the estimation of the level of damage within the tissue, (2) a transient PDE system which simulates the temporal evolution of the biological species in the arterial wall and, finally, (3) a stationary mechanical analysis to simulate the tissue growth that leads to restenosis. The computational domains (stent struts, intima and media) were meshed using quadratic Lagrange triangular elements, resulting in an overall fine mesh with approximately 150 000 elements (figure 4b). A mesh sensitivity analysis was carried out in order to investigate the model mesh independence, testing a series of meshes with different mesh densities. Mesh independence was obtained when there was less than 2% change in the mean concentration of the biological species within the arterial wall for successive mesh refinements. The time-advancing scheme used in the transient problem was a backward differentiation formula with variable order of accuracy varying from one to five and variable time stepping. Both stationary and transient problems were solved using a direct linear solver (MUMPS) with relative and absolute tolerance assigned at 10⁻⁴ and 10⁻³, respectively.

3.4. Model parameters

Reference values of the parameters included in the governing equations are summarized in table 3. They correspond to the rates of production, degradation, proliferation and differentiation, the diffusion coefficients of the biological species, the initial concentrations and the threshold values taken into account. Wherever possible, the model input parameters were derived directly from experimental data available in the literature, but in some cases estimation was necessary to ensure that the evolution of the species was broadly consistent with the time-course of restenosis described in some experimental studies [2,3,5,7].

3.5. Sensitivity analysis

A sensitivity analysis of the 28 parameters indicated in table 1 was performed in order to evaluate the effect of varying each input parameter involved on the evolution of the restenosis process and to test the robustness of the results of the computational model. This is of particular importance because of the absence of a complete set of experimental data and the variability seen in many of the parameters. Computations were carried out for four different values for each parameter apart from the reference value, RV, which is shown in table 3. The first two values were considered ± half the reference value of the selected parameter and the other two were given by increasing and decreasing by one order of magnitude, as can be seen in table 4.

Table 4.

List of cases with the corresponding parameter values computed in the sensitivity analysis. (*) Note that due to the reference value of c_ssmc,0 in case 22 being equal to zero, the strategy for varying parameters had to be adjusted. Points A and C are located close to a central stent strut in the media and in the denuded SES between struts, respectively. Points B and D are situated far away from the stented area in the media and SES, respectively.

case	parameter	unit	RV/10	RV/2	RV	2 RV	10 RV
01	kdeg,d	m3 mol−1 s−1	0.05	0.25	0.5	1	5
02	kprod,gf	mol m−3 s−1	8 × 10−14	4 × 10−13	8 × 10−13	1.6 × 10−12	8 × 10−12
03	kdeg,gf	s−1	1.27 × 10−7	6.35 × 10−7	1.27 × 10−6	2.54 × 10−6	1.27 × 10−5
04	kprod1,mmp	mol cell−1 s−1	3 × 10−27	1.5 × 10−26	3 × 10−26	6 × 10−26	3 × 10−25
05	kprod2,mmp	mol cell−1 s−1	6 × 10−27	3 × 10−26	6 × 10−26	1.2 × 10−25	6 × 10−25
06	kdeg,mmp	s−1	4.63 × 10−7	2.31 × 10−6	4.63 × 10−6	9.26 × 10−6	4.63 × 10−5
07	kprod,ecm	g cell−1 s−1	2.15 × 10−12	1.07 × 10−11	2.15 × 10−11	4.31 × 10−11	2.15 × 10−10
08	kdeg,ecm	s−1	2 × 102	1 × 103	2 × 103	4 × 103	2 × 104
09	kdiff,csmc	s−1	5 × 10−8	2.5 × 10−7	5 × 10−7	10−6	5 × 10−6
10	kdiff,ssmc	s−1	2.31 × 10−7	1.15 × 10−6	2.31 × 10−6	4.62 × 10−6	2.31 × 10−5
11	kprolif,ssmc	cell mol−1 s−1	2.5 × 1012	1.25 × 1013	2.5 × 1013	5 × 1013	2.5 × 1014
12	kapop,ssmc	s−1	2.2 × 10−11	1.1 × 10−10	2.2 × 10−10	4.4 × 10−10	2.2 × 10−9
13	kprolif,ec	s−1	10−7	5 × 10−7	10−6	2 × 10−6	10−5
14	Dgf	m2 s−1	2.6 × 10−12	1.3 × 10−11	2.6 × 10−11	5.2 × 10−11	2.6 × 10−10
15	Dmmp	m2 s−1	1.2 × 10−13	6 × 10−13	1.2 × 10−12	2.4 × 10−12	1.2 × 10−11
16	Dssmc	m2 s−1	1.85 × 10−14	9.26 × 10−13	1.85 × 10−13	3.7 × 10−13	1.85 × 10−12
17	Dec	m2 s−1	8 × 10−15	4 × 10−14	8 × 10−14	1.6 × 10−13	8 × 10−13
18	cgf,0	mol m−3	3.48 × 10−8	1.74 × 10−7	3.48 × 10−7	6.96 × 10−7	3.48 × 10−6
19	cmmp,0	mol m−3	3.83 × 10−8	1.91 × 10−7	3.83 × 10−7	7.66 × 10−7	3.83 × 10−6
20	cecm,0	mol m−3	0.667	3.335	6.67	13.33	66.7
21	ccsmc,0	cell m−3	3.16 × 1012	1.58 × 1013	3.16 × 1013	6.32 × 1013	3.16 × 1014
22*	cssmc,0	cell m−3	0 (RV)	3.16 × 1012	1.58 × 1013	3.16 × 1013	—
23	cec,0	cell m−3	5 × 1010	2.5 × 1011	5 × 1011	1·1012	5 × 1012
24	cgf,th	mol m−3	3.48 × 10−7	1.74 × 10−6	3.48 × 10−6	6.96 × 10−6	3.48 × 10−5
25	cmmp,th	mol m−3	3.83 × 10−7	1.91 × 10−6	3.83 × 10−6	7.66 × 10−6	3.83 × 10−5
26	cecm,th	mol m−3	0.667	3.335	6.67	13.33	66.7
27	cecm,th1	mol m−3	1	5	10	20	100
28	cecm,th2	mol m−3	0.067	0.333	0.667	1.333	6.67

4. Results and discussion

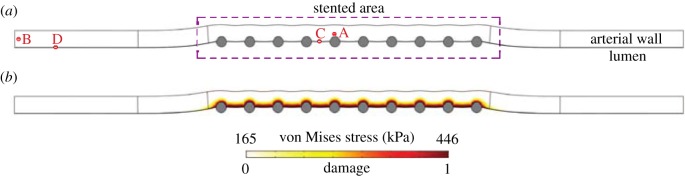
The cascade of events occurring within the arterial wall after the stenting procedure and the consequent response of all the biological species are detailed in this section. The level of damage, local concentrations of GFs, MMPs and ECM and local densities of the SMCs and ECs have been evaluated over time at different points of the computational domain, shown in figure 5a, in order to show the restenosis evolution and the stability of the model. Points A and C are located close to a central stent strut in the media and in the denuded SES between struts, respectively. Points B and D are situated far away from the stented area in the media and SES, respectively. Moreover, in order to study the evolution of the solute dynamics in the stented domain, where the behaviour of the system will be more affected by the level of damage in the tissue, the distribution of all the species at five different times of the simulation is shown.

Figure 5.

(a) Deformed computational geometry and (b) von Mises stress distribution and corresponding quantification of the initial damage in the arterial wall. Points A and C are located close to a central stent strut in the media and in the denuded SES between struts, respectively. Points B and D are situated far away from the stented area in the media and SES, respectively. (Online version in colour.)

4.1. Quantification of damage

The deformed baseline computational geometry is shown in figure 5a. The final radii after deployment in the stented and unstented domain were 1.7 mm and 1.5 mm, respectively. Moreover, the total wall thickness was reduced to approximately 0.4 mm in the stented area. Figure 5b displays the von Mises stress distribution in the arterial wall. The scaling of the stress and the corresponding quantification of the initial damage has been performed is detailed in §3.2.

4.2. Damage evolution for the baseline model

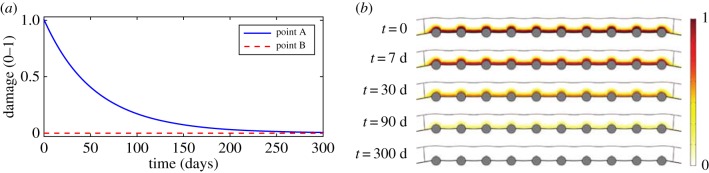
The local evolution of damage at points A and B is shown in figure 6a. At point B, the level of damage is equal to zero at every time, demonstrating that the model does not evolve over time in regions distant from the device. For this reason, local concentrations of substances and local densities of cells at points located far away from the damage caused by the stent remain approximately constant with time. At point A, the level of damage in the tissue decays exponentially with time until the healing process is complete. Figure 6b shows the distribution of the damage in the stented domain over time. Initially, the highest level of damage is found close to the stent struts and to the regions between the struts, where the endothelium has been denuded. As time proceeds, damage decreases continuously to zero in the radial and longitudinal directions towards the adventitial boundary and the unstented domain, respectively. The literature suggests that wound healing is variable in duration. Comparing with our results it can be observed that, from day 90, damage is essentially negligible across the entire baseline computational domain, indicating that the healing process is largely complete in agreement with the classical healing response documented in Forrester et al. [2]. This healing process is mainly governed by the evolution of the concentration of MMP as observed in equation (2.3) coupled with the remaining diffusion–reaction equations.

Figure 6.

Local evolution of the damage over time at two different points within the media (a) and distribution of damage in the stented area of the arterial wall at five different times after stent implantation (b). Point A and point B are located close to a central stent strut and far away from the effect of the stent in the media, respectively. (Online version in colour.)

4.3. Evolution of the species for the baseline model

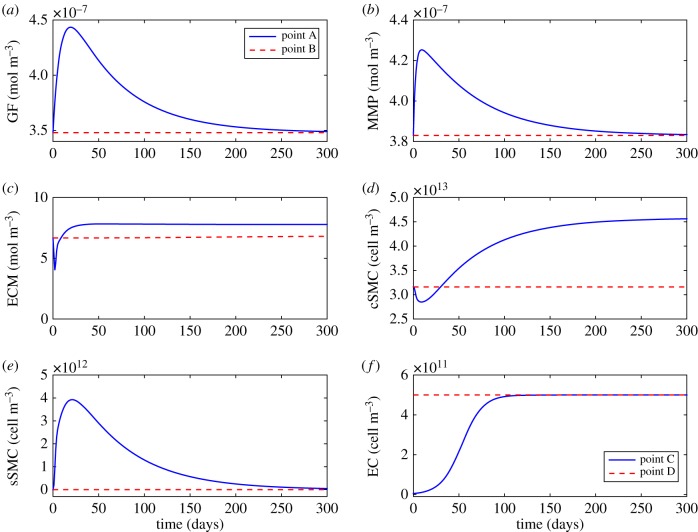
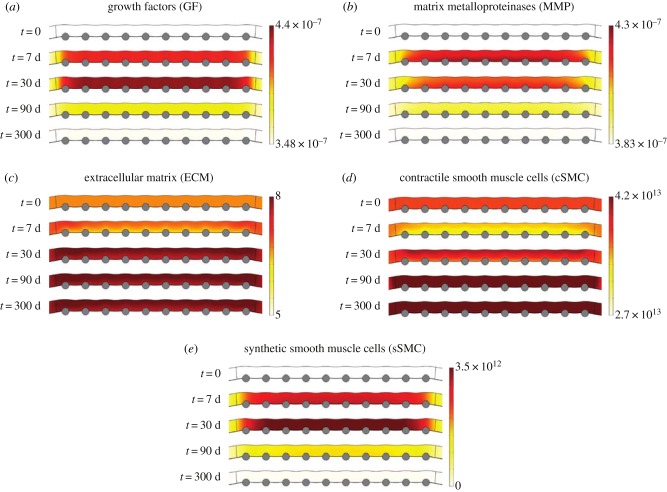
The results for the GF evolution are shown in figures 7a and 8a. At damaged vascular sites (point A), the local concentration of GFs initially increases abruptly peaking approximately between two and three weeks after stent implantation. Following this peak, the concentration decays exponentially over time returning to the physiological baseline value, contributing to the stabilization of the synthetic SMCs, in agreement with the temporal sequence of GF expression documented in Forrester et al. [2]. As the GF production depends directly on damage (equation (2.4)), at points far from the stented area (point B), the concentration of GFs does not vary over time.

Figure 7.

Time-varying local concentration/density profiles of (a) GFs, (b) MMPs, (c) ECM, (d) contractile SMCs, (e) synthetic SMCs and (f) ECs at two different points within the arterial wall. Points A and C are located close to a central stent strut in the media and in the denuded SES between struts, respectively. Points B and D are situated far away from the stented area in the media and SES, respectively. (Online version in colour.)

Figure 8.

(a–e) Evolution of the distribution of all biological species in the media layer of the arterial wall at different times of the simulation. The substance concentration and cell density are shown in mol m⁻³ and cell m⁻³, respectively. (Online version in colour.)

Figures 7b and 8b show the evolution over time for the MMPs. At the beginning of the simulation the initial concentration of MMP is set to a homeostatic value of 3.83 × 10⁻⁷ mol m⁻³ [47]. The local concentration of MMP at point A starts increasing, mainly due to its production by the synthetic SMCs, until reaching its maximum value at day 9, which is consistent with the time course of expression of MMP-2 observed by Bendenck et al. [60]. As MMP synthesis depends directly on the level of damage in the tissue, which continues decreasing over time, the effect of the degradation term of equation (2.7) is greater than the effect of the production term and, therefore, the concentration of MMPs starts decreasing until reverting to its normal physiological levels [61].

The collagen variation over time is shown in figures 7c and 8c. At early times post-deployment, the local concentration of ECM at point A is degraded as a consequence of the increase of MMPs until reaching a minimum value of 4.02 mol m⁻³ after 2 days. From this point, its concentration starts increasing over time, mainly because of the differentiation of the contractile SMCs and the proliferation of the synthetic SMCs, producing neointimal thickening in the weeks after injury [7] until an equilibrium value of approximately 7.8 mol m⁻³ is reached at approximately day 50.

Figures 7d, 8d and 7e, 8e illustrate the evolution of the contractile and synthetic SMCs, respectively. At the beginning of the process, the local density of the contractile SMCs at point A decreases due to the differentiation into a synthetic phenotype until reaching a minimum value of $2.85\times {10}^{13}\hspace{0.17em}\text{cell}\hspace{0.17em}{\text{m}}^{-3}$ one to two weeks after the stenting procedure. Meanwhile, the synthetic SMCs are immediately activated and start proliferating in the media [3]. The local density of synthetic SMCs increases to a value of $3.92\times {10}^{12}\hspace{0.17em}\text{cell}\hspace{0.17em}{\mathrm{m}}^{-3}$ between two and three weeks after injury [3], coinciding in time with the peak in the concentration of GFs and demonstrating that locally produced GFs are a major stimulus for SMC migration and proliferation, in agreement with Forrester et al. [2]. After this time, synthetic SMCs begin to revert back to the contractile phenotype. This process continues over several months and is paralleled by a change in the ECM [2]. It can be noted that the evolution in the concentration of the ECM components, mainly collagen, plays a key role in SMC differentiation, as discussed in §2.3.3, since when the ECM concentration is sufficiently low, synthetic SMCs appear, and when it is sufficiently high, contractile SMCs appear.

ECs only exist within the intima and their behaviour is governed mainly by proliferation and migration. The time-varying local density profiles of this cell type are shown in figure 7f. It can be seen that at points where the endothelium has been denuded by the stent (i.e. point C), ECs start proliferating at the beginning of the restenotic process. Between days 100 and 150, they cease proliferation, reaching, at approximately day 180, an equilibrium density of $5\times {10}^{11}\hspace{0.17em}\text{cell}\hspace{0.17em}{\text{m}}^{-3}$ [55] along the length of the SES, corresponding to homeostatic conditions and in agreement with the temporal response described by Forrester et al. [2]. It can be considered then that the endothelium has been completely restored. However, after this time restenotic events continue since both SMC proliferation/migration and ECM deposition do not necessarily cease at this time.

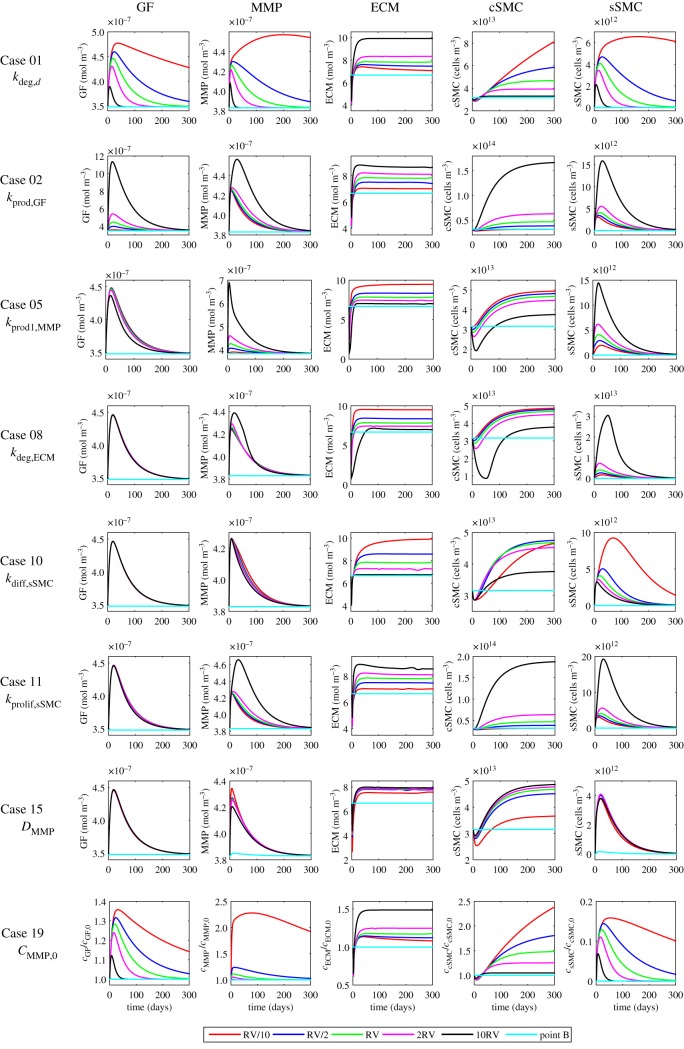
4.4. Sensitivity analysis

The results for the sensitivity analysis performed involving those parameters that have the greatest influence on the behaviour of the system are shown in figures 9 and 10. The discussion is included in the electronic supplementary material.

Figure 9.

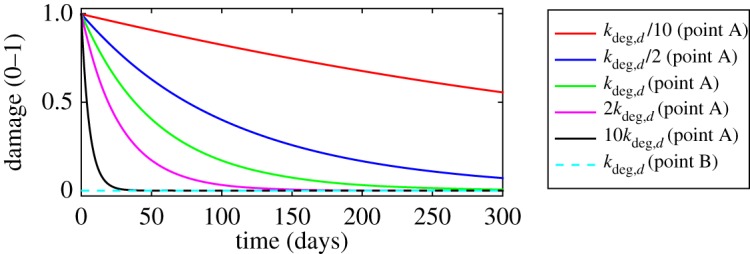
Influence of varying damage degradation rate on the evolution of the damage. Refer to the electronic supplementary material for a discussion. (Online version in colour.)

Figure 10.

Key results from the sensitivity analysis. The plots show the effect of varying several parameters on the concentration of GFs, MMPs and ECM as well as the density of contractile and synthetic SMCs for eight different cases. Computations were carried out for four different values for each parameter apart from the reference value, RV, which is shown in table 3. The values of 2RV and RV/2 were considered ± half the RV of the selected parameter; 10RV and RV/10 were given by increasing and decreasing by one order of magnitude the RV (table 4). The results shown for point B correspond exclusively to the RV (baseline model). Refer to the electronic supplementary material for a discussion. (Online version in colour.)

4.5. Tissue growth

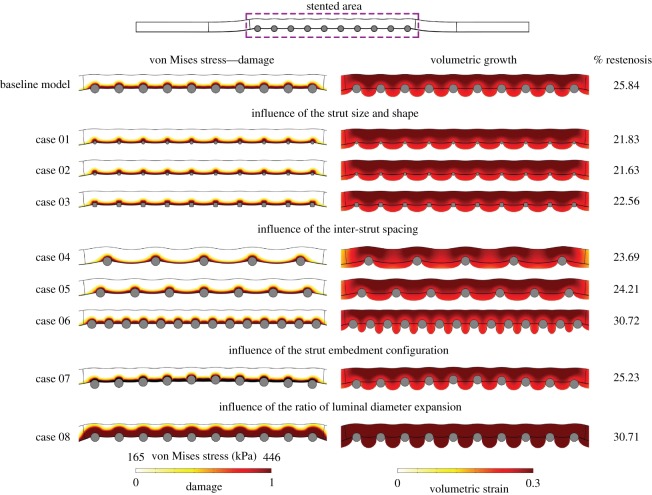
The volumetric growth of new tissue into the lumen of the vessel in response to the mechanical injury caused by the medical device after 300 days is shown in figure 11, for the baseline model. It should be noticed that the restenotic tissue grows considerably between struts. The degree of occlusion can be measured in terms of the diameter or area of restenosis [62]. In this work, the change in the cross-sectional area of the model is used as a measure of measuring arterial restenosis. The percentage of stenosis is calculated as (1 − A_r/A_ref) · 100, where A_r and A_ref are the area of the lesion and of the reference site, respectively. Therefore, the resulting degree of restenosis after 300 days is approximately 25% for the baseline set of parameters simulated in broad agreement with the clinical data presented in Nobuyoshi et al. [63].

Figure 11.

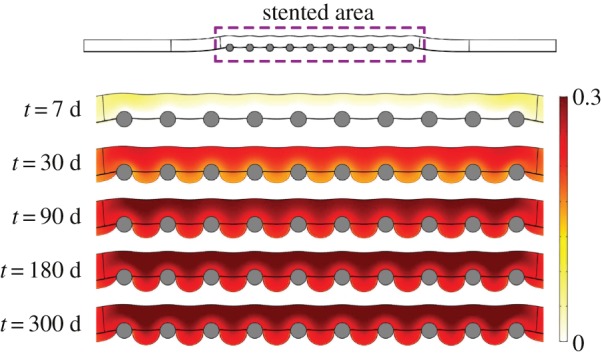
Evolution of the volumetric growth at different times of the simulation for the baseline model. (Online version in colour.)

4.6. Impact of geometric variations on tissue growth

In figure 12, we consider the impact of different geometric configurations on the % restenosis for the various cases considered in table 2. The model produces different levels of restenosis depending on the geometric parameters, and our results are in qualitative agreement with clinical observations. Specifically, the results of our simulations show that % restenosis:

• —increases with increasing strut diameter;
• —decreases with an increase in inter-strut spacing;
• —increases with an increase in lumen expansion diameter;
• —depends on the strut embedment configuration.

Figure 12.

The impact of different geometric configurations (table 2) on von Mises stress distribution and volumetric growth after 300 days. (Online version in colour.)

5. Limitations

We would like to emphasize that there are a number of limitations in this work, as we now discuss.

5.1. Validation

Whilst the continuum approach that we have adopted is advantageous in that it allows us to assess how the evolution of the various species affects the overall healing process, the disadvantage is that it is extremely difficult to measure spatiotemporal cellular densities and GF concentrations experimentally. Certainly, we are not aware of how such validation may be obtained in vivo. In short, we do not believe that the data currently exist to validate the predictions of the model at the level of individual concentrations/densities in space and in time. Therein lies the major advantage of the continuum model proposed here, i.e. the ability to simulate the evolution of species which we cannot get insight into from in vivo experiments. Notwithstanding, we have compared our results to restenosis data (at the tissue level) and have shown that our model is in broad agreement with what is seen in the clinic.

5.2. Flow modelling

We acknowledge that there is a known link between the level of shear stress and restenosis. Indeed, most haemodynamics models that assess different stent designs and patient-specific geometries set out to predict quantities such as wall shear stress (WSS), oscillatory shear index and time-averaged WSS, because these can be related to clinical outcome. Keller et al. [64], for example, investigated the correlation between mechanical and fluid stresses and the magnitude of restenosis, and found that while a linear correlation is not obtained when these stimuli are considered separately, there is a closer correlation when the combined action of these stimuli is considered. While such correlations are useful for providing insight into the influence of force on restenosis, what is less clear is precisely how the transmission of fluid forces affects the behaviour of the cells and other species involved in the healing response. The most sophisticated model of restenosis to date [29] does include the effects of flow, but in in an indirect way. Specifically, Zun et al. assume that neointimal growth is dictated by nitric oxide (NO) production, which is governed by average WSS. Therefore, Zun et al. calculate WSS from a steady laminar flow simulation and pass this to their biological solver, where the level of NO dictates the ensuing biological response through a set of rules. In the absence of data resolving the underlying physics of how the transmission of force generated by flow affects the healing process in vivo, the influence of flow has been neglected in the present analysis. Certainly, the force generated by flow would influence the parameters of our model: in this sense, the sensitivity analysis could be seen to indirectly incorporate the effects of varying flow.

5.3. Geometry

Concerning the geometry of the FE model, a two-dimensional axisymmetric geometry corresponding to an idealized representation of a straight segment of a healthy coronary artery has been considered in this study. This could be improved using more realistic geometries of the artery, such us coronary arteries with curvature, bifurcations, the presence of atherosclerotic plaque or derived directly from three-dimensional patient-specific geometries. However, such models would considerably increase the cost of the numerical simulations and are left for future work.

5.4. Damage modelling

In this work, following the approach presented by Zahedmanesh et al. [22], the modelling of the initial damage in the tissue after stenting is considered in a very simple way, which is based on the ultimate tensile stress–stretch response for each layer of human coronary arteries [42]. However, to our knowledge, there is no experimental data published in the literature which directly relate the levels of stress–strain due to stent deployment to the arterial wall injury and the sequence of events associated such as GF and MMP production, synthesis, number of proliferating SMCs, etc.

5.5. Model parameters and biological species

The biological parameters involved in this model were obtained from a wide range of in vivo and in vitro experiments from the published literature on different blood vessels from human and animal models. However, due to the important structural and functional differences between arteries [48], these parameters could vary from artery-to-artery, species-to-species and patient-to-patient, or even from one lesion to another in the same patient. Additionally, some of these parameters have had to be estimated to be consistent with the time course of the restenosis process found in different studies [2–5,7]. Moreover, all the parameters have been taken as constant and uniform through the whole artery, but in fact they are very likely to change during the process. Finally, only the most important biological species have been taken into account. Other species involved in the coronary restenosis process such as platelets, monocytes, different classes of GFs (PDGF, EGF, IGF, TGF, FGF), mesenchymal cells, fibroblasts, collagen subtypes, proteoglycans, fibronectin, etc., have been grouped or omitted. Moreover, only the main biological processes have been considered in this model. Other processes such as activation and migration of the mesenchymal stem cells, release of GFs by fibroblasts or ECM synthesis by ECs were not included.

6. Conclusion

A mathematical and computational model which successfully captures the main characteristics of the restenosis process after stent implantation in a healthy coronary artery has been presented in this work. A continuum approach has been taken into account for modelling the behaviour of the different biological species involved in ISR, resulting in a PDE system of several coupled diffusion–reaction equations, solved numerically by means of the FEM. Mechanical damage, which is quantitatively estimated as a function of the von Mises stress levels obtained in the arterial wall after a FE simulation of the stent expansion, is considered as the stimulus needed to start the process.

Our results confirm that ISR depends on multiple factors, with the ECM dynamics and SMC proliferation the primary contributors to its pathogenesis. In addition to this, the sensitivity analysis carried out for the different model parameters, as well as providing information on the stability of the model, provides us with an understanding of how changes in one parameter will affect the behaviour of the whole system. The value of k_deg,d has a significant impact on the healing rate. Moreover, it was shown that the rates of production, degradation, differentiation and proliferation taken into account highly affect the local levels of concentration/density of the species involved in the process and the temporal response of the system. The apoptosis rate of synthetic SMCs, diffusion coefficients and initial conditions also influence the evolution of the model, although to a lesser extent.

In conclusion, in spite of the simplifications and limitations we have discussed, the model developed is able to capture some of the underlying mechanisms and patterns of ISR. Moreover, the results obtained are in good agreement with clinical hypotheses relating to ISR occurrence. Therefore, this model can be considered as a step forward to a better understanding of this phenomenon.

Data accessibility

The data associated with this paper consist of the mathematical models and their numerical solution as detailed in the text.

Authors' contributions

Conceived and designed the study: M.A.M., S.M. and E.P. Development of mathematical model: J.E., M.A.M., S.M. and E.P. Computational implementation of model: J.E. Writing, review and editing: J.E., M.A.M., S.M. and E.P.

Competing interests

We declare we have no competing interests.

Funding

The authors gratefully acknowledge funding provided by the Spanish Ministry of Economy, Industry and Competitiveness under research project number DPI2016-76630-C2-1-R and grant no. BES-2014-069737.