Abstract
External beam radiation therapy is a widespread treatment for prostate cancer. The ensuing patient follow-up is based on the evolution of the prostate-specific antigen (PSA). Serum levels of PSA decay due to the radiation-induced death of tumour cells and cancer recurrence usually manifest as a rising PSA. The current definition of biochemical relapse requires that PSA reaches nadir and starts increasing, which delays the use of further treatments. Also, these methods do not account for the post-radiation tumour dynamics that may contain early information on cancer recurrence. Here, we develop three mechanistic models of post-radiation PSA evolution. Our models render superior fits of PSA data in a patient cohort and provide a biological justification for the most common empirical formulation of PSA dynamics. We also found three model-based prognostic variables: the proliferation rate of the survival fraction, the ratio of radiation-induced cell death rate to the survival proliferation rate, and the time to PSA nadir since treatment termination. We argue that these markers may enable the early identification of biochemical relapse, which would permit physicians to subsequently adapt patient monitoring to optimize the detection and treatment of cancer recurrence.
Keywords: prostate cancer, prostate-specific antigen dynamics, external beam radiation therapy, mathematical oncology
1. Introduction
Prostate cancer (PCa) is a major health burden among ageing men worldwide [1]. External beam radiation therapy (EBRT) is a feasible treatment for patients of all ages and PCa risk groups [1–3]. In EBRT, radiation is delivered from an outside beam aiming at disrupting the DNA in the tumour cells’ nuclei, which forces them to undergo programmed cell death due to excessive DNA damage accumulated from both radiation and the previous genetic alterations that generate and support PCa [4]. EBRT requires a precise planning of the radiation dose quantity, distribution over the prostate organ and temporal delivery [1,2]. Classical EBRT plans deliver a total dose of 74–80 Gy in 2 Gy fractions. Moderately hypofractionated plans (60–66 Gy delivered in 3 Gy fractions) are also used after recent clinical trials that have shown that they are non-inferior to conventional EBRT [1]. Neoadjuvant and adjuvant androgen deprivation therapy (ADT) may improve EBRT performance, but can also provoke bothersome side effects (e.g. low libido, impotence, anaemia, osteoporosis, depression). Hence, combination of EBRT with ADT is only recommended for intermediate-risk PCa (four to six months) and mandatory for high-risk tumours (two to three years) [1]. Local recurrence after EBRT can be managed with radical prostatectomy, cryoablation, brachytherapy and high-intensity focused ultrasound, while patients with advanced PCa are usually prescribed ADT, chemotherapy or a combination of both [1,2].
Patient monitoring after conclusion of EBRT largely relies on prostate-specific antigen (PSA) levels [1,2], which is a common biomarker whose levels in blood tend to rise during PCa [1,2]. Radiation-induced tumour cell death causes PSA to decrease after EBRT, so a continued rise in PSA may be indicative of PCa recurrence due to thriving cancerous cells surviving radiation therapy. However, PSA may also be affected by natural background fluctuations (e.g. diet, lifestyle), a continuous smooth increase due to prostate enlargement caused by benign prostatic hyperplasia (BPH), and sudden rises due to ceasing ADT or to the so-called PSA bounce (a transient rise of at least 0.1 to 0.5 ng ml−1 usually within 24 months after EBRT [5,6]). Therefore, physicians require robust criteria to identify when a rise in PSA corresponds to a PCa recurrence. Initially, biochemical relapse after EBRT was defined as three consecutive rises of PSA after the minimum post-EBRT PSA value registered for a given patient (PSA nadir) [1,2]. Currently, a superior criterion defines biochemical relapse as an increase larger than 2 ng ml−1 over PSA nadir [1,2], which correlates better with clinical recurrence and patient survival. The former three-point rule is still used as a warning sign in patient monitoring.
However, these criteria of biochemical relapse detection require PSA to reach a minima and start increasing, which may result in delays in the application of further treatments. Also, this relapse measure does not inform about the expected PCa prognosis. The definition of early markers of PCa recurrence and malignancy would enable physicians to successfully control the disease with an appropriate salvage treatment. This is the purpose of multiple studies aimed at analysing PSA dynamics after EBRT. A high value of PSA nadir, a short time to reach PSA nadir after EBRT termination and short PSA doubling time (or high PSA velocity) during biochemical relapse have been correlated with metastatic disease and reduced patient survival [6–10]. While these studies focus on long-term PSA dynamics, only a few investigations have focused on analysing the PSA evolution shortly after EBRT conclusion. A rising PSA trend, high PSA levels or a rapid PSA decline shortly after EBRT have been linked with poorer prognosis and patient survival [11–13]. To gain further insight, post-EBRT PSA dynamics has also been quantitatively described by fitting mathematical formulae to PSA longitudinal data in different patient cohorts [14–18]. PSA decline after EBRT in cured patients is usually described with an exponential decay (possibly added to a constant or a slowly increasing linear term accounting for benign growth), while a bi-exponential formula best represents the PSA decrease and posterior rise in biochemically relapsing patients [14–16]. This bi-exponential formula has also been leveraged in all cases, such that parametrization using PSA data for cured patients will cause the rising branch to vanish [17,18]. Still, the choice of the mathematical formula in the vast majority of quantitative studies on PSA dynamics only relies on the empirical observation of PSA temporal trends following EBRT and does not account for the underlying tumour dynamics, which is ultimately regulating the PCa recurrence.
Here, we present a patient-specific mathematical formulation of PSA dynamics based on biological mechanisms describing tumour response to radiation. Mechanistic mathematical modelling of cancer and response to treatments have improved the understanding of tumour growth and can assist physicians in clinical decision-making on a personalized basis [19–23]. Some mechanistic modelling studies have explored the connection between tumour and PSA dynamics in untreated PCa growth [24–27], under hormonal therapy [28–32], and after radical prostatectomy [33,34]. Radiation effects is a rich topic in the literature of computational modelling of cancer [20–23,35–39]. Several mathematical models have been proposed to describe radiation effects on tumour cells (e.g. cytotoxic action, cell-cycle arrest, promotion of apoptosis). The linear-quadratic model is arguably the most widely used formulation [20–22,35–37,40,41]. However, the linear-quadratic model inherently assumes a relatively fast response to radiotherapy and hence this paradigm works better in rapidly growing tumours (e.g. glioblastoma multiforme). For slowly growing tumours, such as low-grade glioma or PCa, the late response to radiation requires to account for repopulation of tumour cells, i.e. the underlying tumour dynamics [23,42,43]. Although previous modelling efforts have explored alternative formulations of radiation effects on PCa [42–45], mechanistic mathematical descriptions of the complete evolution of prostatic tumour growth and PSA after the delivery of radiotherapy are lacking. Our mathematical formulation addresses this challenge with minimal assumptions on radiation effects.
2. Methods
2.1. Patients
Anonymized patient data were obtained from Centro Oncológico de Galicia (COG, A Coruña, Spain). Ethics approval was obtained from Comité Autonómico de Ética da Investigación de Galicia (Santiago de Compostela, Spain). Informed consent was not required for the patient data used in this study.
A total of 1588 men diagnosed with localized PCa confirmed at COG (stage T1 to T2, Gleason score less than 8) and treated with EBRT in this institution between 2009 and 2015 were considered for inclusion in the study. Inclusion criteria were first-line treatment of EBRT delivered only at COG and more than 2 years of PSA monitoring with at least 5 PSA values after conclusion of EBRT. Exclusion criteria were a previous neoplastic disease prior to PCa, any other treatment for PCa (e.g. ADT, radical prostatectomy, radiotherapy, chemotherapy) and EBRT without radical intent.
A total of 71 patients satisfied the inclusion criteria and did not qualify for any of the exclusion criteria. EBRT was either conventional (64 patients, 2 Gy/dose) or hypofractionated (seven patients, 3 Gy/dose). In both cases, the original EBRT plan consisted of series of five daily doses delivered on weekdays followed by two days of rest during the weekend. For simplicity, in this preliminary study, we pooled all patients together without differentiating radiation plans. Seven patients experienced biochemical relapse (either three consecutive increasing values of PSA or an increase of more than 2 ng ml−1 over PSA nadir), of which four had reported evidence of PCa recurrence. We will refer to those patients who did not show biochemical recurrence after EBRT as cured patients. Table 1 summarises the characteristics of the patient cohort. Additionally, 43 cured patients and three biochemically relapsing patients had T1 cancer, whereas 21 cured patients and four biochemically relapsing patients had T2 cancer.
Table 1.
Characteristics of the patient cohort. IQR, interquartile range.
| characteristic | all patients (n = 71) |
cured patients (n = 64) |
relapsing patients (n = 7) |
||||||
|---|---|---|---|---|---|---|---|---|---|
| median | IQR | range | median | IQR | range | median | IQR | range | |
| clinical | |||||||||
| Pd (ng ml−1) | 6.8 | (4.9, 9.1) | (0.6, 25.4) | 6.6 | (4.9, 8.9) | (0.6, 18.9) | 10.1 | (5.6,14.7) | (3.8,25.4) |
| Gleason score | 6 | (6, 7) | (4, 7) | 6 | (6, 7) | (4, 7) | 6 | (6, 7) | (6, 7) |
| age at EBRT (yr) | 76 | (73, 78) | (63, 82) | 76 | (73, 78) | (63, 82) | 74 | (71, 78) | (68, 80) |
| radiation | |||||||||
| total dose (Gy) | 76 | (74, 76) | (60, 78) | 76 | (74, 76) | (60, 78) | 76 | (76, 76) | (76, 78) |
| doses | 38 | (37, 38) | (20, 39) | 38 | (37, 38) | (20, 39) | 38 | (38, 38) | (38, 39) |
| EBRT duration (mo) | 1.9 | (1.8, 2.1) | (0.9, 3.9) | 1.9 | (1.8, 2.1) | (0.9, 3.9) | 2.0 | (2.0, 3.5) | (1.9, 3.7) |
| PSA history | |||||||||
| number of PSA values | |||||||||
| total | 9 | (7, 10) | (6, 15) | 9 | (8, 10) | (6, 15) | 8 | (7, 9) | (6, 10) |
| pre-EBRT | 1 | (1, 2) | (1, 7) | 1 | (1, 2) | (1, 7) | 1 | (1, 2) | (1, 2) |
| post-EBRT | 7 | (6, 8) | (5, 12) | 7 | (6, 8) | (5, 12) | 6 | (5, 8) | (5, 9) |
| follow-up time (mo) | |||||||||
| total | 56.8 | (51.7, 59.4) | (38.3, 69.5) | 56.7 | (51.4, 59.3) | (40.8, 69.5) | 58.2 | (54.3, 61.1) | (38.3, 66.4) |
| pre-EBRT | 8.9 | (6.3, 13.6) | (2.2, 27.8) | 9.0 | (6.3, 13.6) | (2.2, 27.8) | 8.9 | (7.4, 15.2) | (5.3, 20.8) |
| post-EBRT | 43.4 | (36.9, 47.8) | (27.9, 59.7) | 42.7 | (37.0, 48.5) | (27.9, 59.7) | 43.5 | (37.6, 46.7) | (29.2, 53.6) |
2.2. Mathematical models
2.2.1. General formulation
Serum PSA P(t) is generally assumed to be proportional to the prostatic tumour mass and it is known to approximately follow an exponential trend in time [1,2,24–26]. Hence, if we denote the number of tumour cells by N(t), then
| 2.1 |
where ρ is a proportionality constant, τn is the characteristic time of net proliferation, and N0 = N(t0) and P0 = P(t0) are the population of tumour cells and serum PSA at a time t0, respectively.
EBRT for PCa consists of nd radiation doses delivered at times . We will assume that all doses are equal, which applies to our patient cohort. After the delivery of the k-th radiation dose at time tk, we assume that a fraction of tumour cells is irreversibly damaged and undergoes cell death after a characteristic time τd, while the remaining fraction of tumour cells Sk(t) survives and continues to grow with a characteristic time of net proliferation τs.
The dynamics of and Sk(t) are given by the following set of ordinary differential equations,
| 2.2a |
| 2.2b |
for each interval tk ≤ t < tk+1 and where , , and Rd is the dose-dependent fraction of surviving cells after the delivery of the k-th radiation. We do not assume any specific formulation for Rd, such as in most literature of computational modelling of radiation effects [20–22,35–37,40,41]. Instead, we directly compute Rd from PSA data, making the model more flexible and easier to parametrize. As each patient always receives the same dose per session, it suffices to compute one value of Rd per patient. The solutions to equations (2.2) are
| 2.3a |
| 2.3b |
for tk ≤ t < tk+1.
Let Dk(t) be the accumulated population of irreversibly damaged tumour cells due to the radiation doses already delivered for tk ≤ t < tk+1. Its dynamics satisfies the equation
| 2.4 |
where D0(t) = 0. Then, the population of total cancerous cells after the k-th radiation dose Nk(t) and the corresponding serum PSA concentration Pk(t) can be computed as
| 2.5a |
| 2.5b |
where
| 2.6a |
| 2.6b |
for tk ≤ t < tk+1.
Using equations (2.6) recursively stepwise from the first radiation dose, we obtain the following explicit formulas for the population of proliferative and damaged tumour cells
| 2.7a |
| 2.7b |
for tk ≤ t < tk+1 and where and . Hence,
| 2.8 |
for tk ≤ t < tk+1 and where we have used that P0 = ρ N0.
2.2.2. Periodic-dose model
In the particular case in which the radiation doses are equispaced in time, tk = t1 + (k − 1)τr. Then, equation (2.7b) simplifies to
| 2.9 |
and hence we may rewrite equation (2.8) as
| 2.10 |
for tk ≤ t < tk+1 (see details in electronic supplementary material, annex S2).
2.2.3. Single-dose model
Alternatively, we may assume that the whole radiation treatment is delivered at a certain time tD. Then, S(t) and D(t) are given by
| 2.11a |
| 2.11b |
where RD is the fraction of surviving cells after the total treatment dose, and . By using equations (2.5) we get
| 2.12 |
2.2.4. Non-dimensional parameters and prediction of prostate-specific antigen nadir
After the completion of radiotherapy, i.e. for , the evolution of PSA will be given by equation (2.8), which for simplicity we will denote by P(t):
| 2.13 |
Let us define the non-dimensional counterparts of P and time t, respectively, as and . Then, we may rewrite equation (2.13) in non-dimensional form as
| 2.14 |
where we have introduced two non-dimensional parameters
| 2.15a |
| 2.15b |
While α may represent the efficacy of the radiation plan, β controls the dynamics of the tumour cell populations and PSA after radiation (see §4.1). Thus, these parameters may hold predictive value, which will assess in this work.
Following a similar procedure, we may also obtain the expressions of α and β for both the periodic-dose model
| 2.16 |
and the single-dose model
| 2.17 |
Additionally, the derivative of equation (2.14) with respect to provides the non-dimensional PSA velocity
| 2.18 |
According to their definition α, θ2 and β, are positive quantities. When αθ2/β > 1, then decreases for at least some time after radiotherapy. Then, we can compute the time to PSA nadir, tn, by solving for and substituting the definition of θ2 (see §2.2.1), yielding
| 2.19 |
Hence, the time to PSA nadir Pn since the completion of EBRT at time is given by .
2.2.5. Model selection for analysis and further assumptions
Radiation plans may experience delays due to treatment side-effects, holidays, machine routine maintenance or machine failures. The reported values of EBRT duration in table 1 suggest that these interruptions were common in our patient cohort. In addition, the information about EBRT in our patient dataset consists of the dates of treatment initiation and termination, the radiation dose, and the number of doses. This input information is not compatible with an accurate use of our general model (§2.2.1), which would require the exact dates of EBRT sessions. Thus, in this work, we will focus our analysis on the periodic-dose model (§2.2.2) and the single-dose model (§2.2.3). The possible difference in results between both models, if any, would be related to treatment duration effects. Electronic supplementary material, table S1 summarizes the main quantities in all models. Electronic supplementary material, annex S1, table S2 and figure S1 show that the periodic-dose model is virtually equivalent to the general formulation, and we will analyse the single-dose model as a feasible simplification of both the general and periodic-dose models.
We will further assume that EBRT does not change the proliferation rate of surviving cells, so that τn = τs and θ1 = 1. This assumption is common in the literature [21–23], contributes to the simplicity of our models, and facilitates parametrization, especially in those patients with a limited number of PSA values before EBRT. Additionally, we choose t0 = 0 and we will assume that tD is the date of EBRT initiation in the single-dose model.
2.3. Statistical methods
We leveraged nonlinear least squares using the trust-region method to estimate the parameters of our models in a patient-specific manner. Table 2 shows the initial values for the algorithm, the lower bounds and the upper bounds used to fit the single and the periodic-dose models for each patient. We assessed the goodness of fit with the sum of squared errors (SSE), the R2, the adjusted R2 with respect to the degrees-of-freedom in error () and the root mean squared error (RMSE).
Table 2.
Initial values and bounds for models’ parameters. P(1) is the first PSA value available for each patient.
| parameter | initial value | lower bound | upper bound |
|---|---|---|---|
| P0 (ng ml−1) | P(1) | 0 | 50 |
| Rd | 0.9 | 0 | 1 |
| RD | 0 | 1 | |
| τs (mo) | 50 | 0.5 | 500 |
| τd (mo) | 2 | 0.5 | 500 |
We used the Wilcoxon rank-sum test (WRST) to identify potential markers of biochemical relapse by analysing whether model parameters, non-dimensional parameters, PSA nadir and time to PSA nadir since EBRT completion differed between cured and biochemically relapsing patients. We also tested the goodness-of-fit statistics to analyse whether the estimation of PSA dynamics was more accurate in either patient subgroup. Additionally, we compared the values of model parameters and model-derived quantities obtained with each PSA dynamics formulation. We defined in the periodic-dose model and R = RD in the single-dose model to compare the values of Rd and RD, respectively. This study was performed both globally by using the WRST and patient-wise by using the Wilcoxon signed-rank test. We used the same tests to compare the goodness-of-fit statistics produced by each mathematical model, and hence to determine whether one of them provided a superior fit. The level of significance was set at 5% for all statistical tests.
We constructed the receiver operating characteristic (ROC) curves of the quantities that changed significantly between cured and biochemically relapsing patients to assess their ability to classify patients in either group. We iteratively varied a threshold for each of these quantities independently across the whole range of values provided by each model. Threshold stepping was determined as the difference between the maximum and the minimum value divided by 1000. For each threshold, we computed sensitivity, specificity and accuracy. We also computed the area under the ROC curve (AUC) by using the trapezoidal rule and the optimal performance point by using Youden’s index.
Calculations were performed in Matlab (Release R2017b, The Mathworks, Inc., Natick, MA, USA). Parameter estimation was performed with the Curve Fitting Toolbox. Statistical tests were run with the Statistics and Machine Learning Toolbox. We also computed the 95% confidence bounds for each model fit with the Curve Fitting Toolbox.
3. Results
3.1. Model fitting
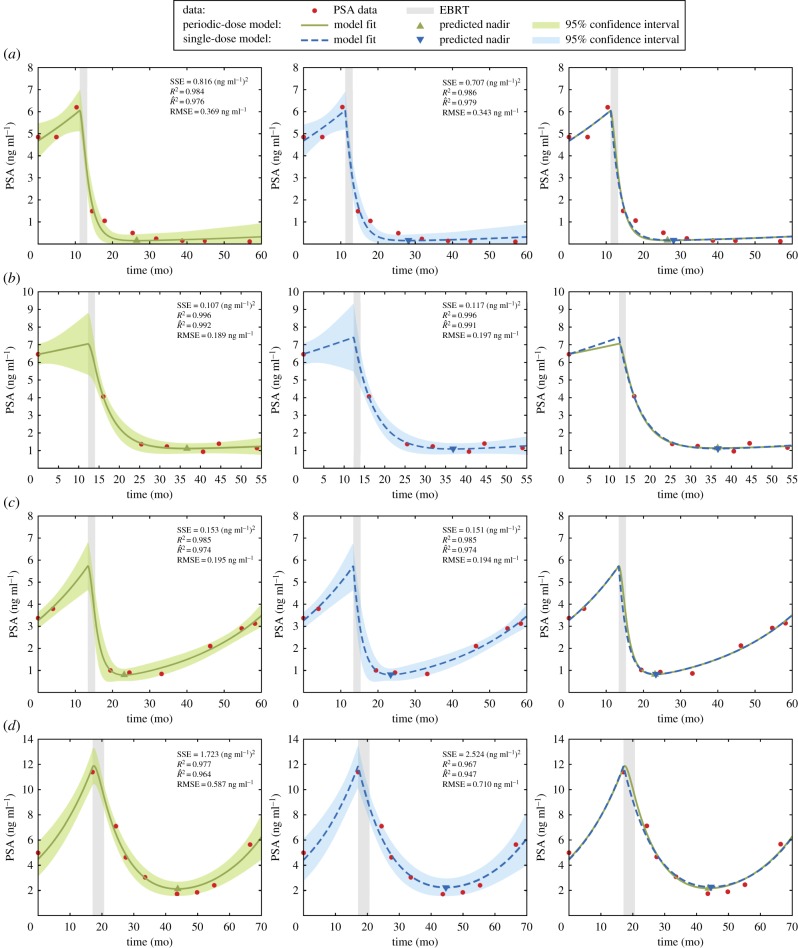
The periodic-dose model and the single-dose model succeeded in fitting individual patient PSA data. Figure 1 portrays the results for both models corresponding to two cured patients and two patients with biochemical relapse. Table 3 shows that model fitting was extraordinarily precise with both PSA dynamics models for the vast majority of patients. We observed that superior fitting results were obtained when several PSA data were distributed in an approximately even manner right before and after EBRT (see electronic supplementary material, figure S2). Conversely, few pre-EBRT PSA values or few post-EBRT PSA measurements close to treatment termination could hinder the accurate reproduction of PSA dynamics (see electronic supplementary material, figure S3). High fluctuations in PSA data always worsened the goodness of fit (see electronic supplementary material, figure S4).
Figure 1.
Curve fitting results for two cured patients (a,b) and two patients with biochemical recurrence (c,d) using both the periodic-dose model (solid green line) and the single-dose model (dashed blue line). For each patient, each row shows, respectively, the fit provided by the periodic-dose model, the fit obtained with the single-dose model, and a comparison of the fits computed with either model. The shaded areas along the model fits in the first two subfigures of each row depict the corresponding 95% confidence interval of the model fit. PSA values are depicted as red bullets and the duration of EBRT is shaded in light grey. (Online version in colour.)
Table 3.
Goodness-of-fit statistics in the patient cohort. The last column provides the p-values of the two-sided WRSTs searching for significant differences in these statistics between the subgroups of cured and biochemically relapsing patients. The level of significance was set at p < 0.05. IQR, interquartile range.
| statistic | all patients (n = 71) |
cured patients ( n= 64) |
relapsing patients (n = 7) |
WRST |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| median | IQR | range | median | IQR | range | median | IQR | range | p-values | |
| periodic-dose model | ||||||||||
| SSE (ng ml−1)2 | 0.15 | (0.06, 0.81) | (0.00, 68.23) | 0.15 | (0.05, 0.68) | (0.00, 68.23) | 1.27 | (0.16, 1.69) | (0.04, 6.79) | 0.121 |
| R2 | 1.00 | (0.98, 1.00) | (0.69, 1.00) | 1.00 | (0.98, 1.00) | (0.69, 1.00) | 0.99 | (0.98, 1.00) | (0.98, 1.00) | 0.401 |
| 0.99 | (0.97, 1.00) | (0.51, 1.00) | 0.99 | (0.98, 1.00) | (0.51, 1.00) | 0.98 | (0.97, 0.99) | (0.96, 1.00) | 0.293 | |
| RMSE (ng ml−1) | 0.19 | (0.12, 0.42) | (0.01, 3.72) | 0.18 | (0.12, 0.38) | (0.01, 3.72) | 0.50 | (0.21, 0.82) | (0.14, 1.06) | 0.063 |
| single-dose model | ||||||||||
| SSE (ng ml−1)2 | 0.15 | (0.04, 0.70) | (0.00, 68.24) | 0.14 | (0.04, 0.57) | (0.00, 68.24) | 1.19 | (0.16, 2.24) | (0.04, 6.09) | 0.112 |
| R2 | 1.00 | (0.99, 1.00) | (0.70, 1.00) | 1.00 | (0.99, 1.00) | (0.70, 1.00) | 0.99 | (0.99, 1.00) | (0.97, 1.00) | 0.284 |
| 0.99 | (0.98, 1.00) | (0.52, 1.00) | 0.99 | (0.98, 1.00) | (0.52, 1.00) | 0.98 | (0.97, 0.99) | (0.95, 1.00) | 0.228 | |
| RMSE (ng ml−1) | 0.19 | (0.11, 0.37) | (0.01, 3.72) | 0.17 | (0.09, 0.35) | (0.01, 3.72) | 0.49 | (0.21, 0.81) | (0.14, 1.01) | 0.063 |
We did not identify any significant difference between the goodness-of-fit statistics for cured and biochemically relapsing patients with any of the two PSA dynamics models in two-sided WRSTs (table 3). Nevertheless, we observed that our models tended to reproduce PSA dynamics with slightly superior accuracy for the cured patients of this cohort (table 3). The goodness-of-fit statistics of each model did not globally differ neither in the whole cohort nor in any patient subgroup according to two-sided WRSTs (table 4). However, two-sided Wilcoxon signed-rank tests identified significant differences in the accuracy of the fit obtained with each model for each patient (table 4). Corresponding one-sided Wilcoxon signed rank tests showed that the single-dose model produced lower SSE (p = 1.62 × 10−4) and RMSE (p = 2.20 × 10−4), as well as higher R2 (p = 1.08 × 10−4) and (p = 1.19 × 10−4). We observed the same results for the subgroup of cured patients (table 4), where one-sided tests also demonstrated that the single-dose model rendered lower SSE (p = 3.62 × 10−4) and RMSE (p = 4.72 × 10−4) as well as higher R2 (p = 2.32 × 10−4) and (p = 2.38 × 10−4). No model was found to provide a significantly superior accuracy in the subgroup of biochemically relapsing patients (table 4).
Table 4.
p-values obtained for the two-sided statistical tests to search for significant differences in goodness-of-fit between the periodic-dose and single-dose models. Results are shown for the whole cohort and for the subgroups of cured and biochemically relapsing patients. The significance level was set at p < 0.05. Significant p-values in bold.
| statistic | patients |
||
|---|---|---|---|
| all (n = 71) | cured (n = 64) | relapsing (n = 7) | |
| Wilcoxon signed-rank tests | |||
| SSE | 3.20 × 10−4 | 7.15 × 10−4 | 0.297 |
| R2 | 2.14 × 10−4 | 4.58 × 10−4 | 0.297 |
| 2.35 × 10−4 | 4.70 × 10−4 | 0.297 | |
| RMSE | 4.35 × 10−4 | 9.32 × 10−4 | 0.297 |
| Wilcoxon rank-sum tests | |||
| SSE | 0.642 | 0.618 | 0.805 |
| R2 | 0.689 | 0.715 | 0.620 |
| 0.680 | 0.673 | 0.710 | |
| RMSE | 0.665 | 0.629 | 0.805 |
3.2. Model-based predictors of biochemical relapse
The values of the parameters P0, Rd or RD, τs and τd obtained with the periodic-dose model and the single-dose model are summarized in table 5. We also used them to compute each model’s non-dimensional parameters (α, β), PSA nadir (Pn), and time to PSA nadir since EBRT termination (Δtn) for each patient, also reported in table 5. P0 was typically close to the first PSA value available for each patient, but it was not necessarily coincident (figure 1). The estimation of Rd, RD and τd provided values inside the parametric domain defined in table 2 for the vast majority of patients. However, we obtained τs ≈ 500 (upper bound) for many patients, especially with the periodic-dose model. This situation only occurred for cured patients, for whom larger values of τs are expected. Indeed, both large τs and very small remnant proliferative tumour cell populations after EBRT lead to similar results, i.e. no tumour regrowth for the time scales studied leads to some uncertainty in the parameter values. However, this fact did not compromise the accuracy of the model fitting to the data (see table 3; electronic supplementary material, figure S5).
Table 5.
Distribution of model parameters, non-dimensional parameters, PSA nadir, and time to PSA nadir since EBRT termination obtained with the periodic-dose and the single-dose models. The last column provides the p-values of the two-sided WRSTs searching for significant differences in these statistics between the subgroups of cured and biochemically relapsing patients. The level of significance was set at p < 0.05. Significant p-values were highlighted in bold. IQR, interquartile range.
| quantity | all patients (n = 71) |
cured patients (n = 64) |
relapsing patients (n = 7) |
WRST |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| median | IQR | range | median | IQR | range | median | IQR | range | p-values | |
| periodic-dose model | ||||||||||
| P0 (ng ml−1) | 5.9 | (4.7, 9.0) | (0.5, 25.3) | 5.9 | (4.7, 8.7) | (0.5, 24.6) | 10.1 | (4.9, 12.5) | (3.3, 25.3) | 0.213 |
| Rd | 0.92 | (0.89, 0.93) | (0.50, 0.96) | 0.92 | (0.89, 0.93) | (0.50, 0.96) | 0.90 | (0.84, 0.92) | (0.81, 0.94) | 0.251 |
| τd (mo) | 2.9 | (1.9, 3.9) | (0.5, 13.7) | 2.9 | (1.9, 4.0) | (0.5, 13.7) | 2.4 | (2.1, 3.1) | (0.5, 9.2) | 0.623 |
| τs (mo) | 498.0 | (37.4, 500) | (5.0, 500) | 500 | (62.1, 500) | (9.2, 500) | 23.9 | (11.5, 33.9) | (5.0, 42.5) | 8.77 × 10−4 |
| β (× 10−2) | 1.42 | (0.60, 5.00) | (0.14, 91.38) | 1.18 | (0.57, 4.03) | (0.14, 91.38) | 8.58 | (5.77, 44.20) | (2.02, 51.65) | 1.23 × 10−3 |
| α (× 101) | 2.78 | (1.51, 6.87) | (0.55, ∞) | 2.67 | (1.49, 6.50) | (0.55, ∞) | 6.92 | (2.63, 227.72) | (1.50, 401.43) | 0.099 |
| Pn (ng ml−1) | 0.4 | (0.2, 0.6) | (0.0, 2.7) | 0.4 | (0.2, 0.6) | (0.0, 2.7) | 0.4 | (0.4, 0.8) | (0.2, 2.2) | 0.193 |
| Δtn (mo) | 19.2 | (13.0, 23.6) | (2.7, 133.4) | 19.7 | (13.9. 24.4) | (3.2, 133.4) | 11.1 | (8.4, 18.1) | (2.7, 23.1) | 0.025 |
| single-dose model | ||||||||||
| P0 (ng ml−1) | 5.9 | (4.7, 9.0) | (0.5, 25.4) | 5.9 | (4.7, 8.7) | (0.5, 24.6) | 10.1 | (4.9, 12.5) | (3.3, 25.4) | 0.213 |
| RD (× 10−2) | 4.5 | (1.6, 7.0) | (0.0, 18.9) | 4.5 | (1.7, 7.0) | (0.0, 18.9) | 1.6 | (0.3, 4.9) | (0.0, 8.6) | 0.130 |
| τd (mo) | 3.2 | (2.1, 4.5) | (0.5, 13.7) | 3.3 | (2.1, 4.7) | (0.5, 13.7) | 2.7 | (2.4, 3.4) | (0.5, 10.5) | 0.569 |
| τs (mo) | 152.6 | (34.3, 500) | (5.0, 500) | 499.0 | (56.7, 500) | (9.2, 500) | 23.8 | (11.4, 32.9) | (5.0, 41.3) | 9.40 × 10−4 |
| β (× 10−2) | 1.96 | (0.74, 6.18) | (0.14, 93.25) | 1.50 | (0.68, 5.05) | (0.14, 93.25) | 9.85 | (6.65, 49.96) | (2.02, 60.50) | 1.72 × 10−3 |
| α (× 101) | 2.13 | (1.34, 6.19) | (0.43, ∞) | 2.12 | (1.32, 5.79) | (0.43, ∞) | 5.97 | (2.24, 158.15) | (1.06, 351.03) | 0.130 |
| Pn (ng ml−1) | 0.4 | (0.2, 0.6) | (0.0, 2.6) | 0.3 | (0.2, 0.6) | (0.0, 2.6) | 0.4 | (0.4, 0.8) | (0.2, 2.3) | 0.135 |
| Δtn (mo) | 20.9 | (13.8, 25.9) | (2.0, 170.0) | 21.7 | (14.9, 26.2) | (2.8, 170.0) | 11.6 | (8.7, 18.9) | (2.0, 23.8) | 0.022 |
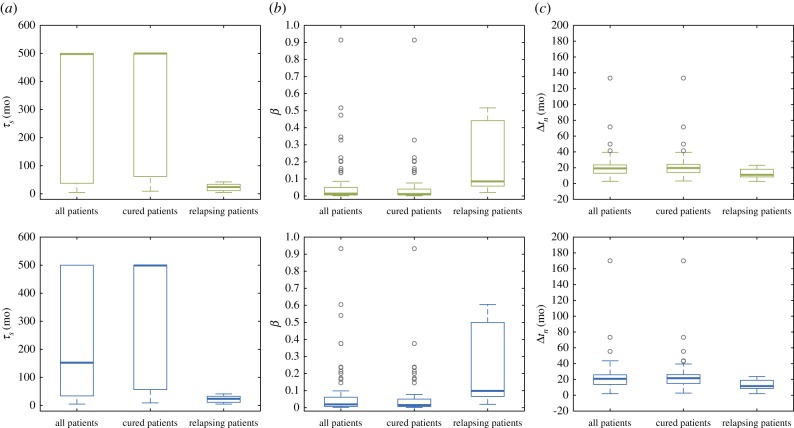
For the periodic-dose model, two-sided WRSTs identified τs, β and Δtn to be significantly different between cured and biochemically relapsing patients (table 5). The matching one-sided tests revealed that biochemically relapsing patients had smaller τs (p = 4.39 × 10−4), larger β (p = 6.17 × 10−4) and shorter Δtn (p = 0.0123). For the single-dose model, we also found τs, β and Δtn to significantly differ between cured and biochemically relapsing patients in two-sided WRSTs (table 5). Again, the corresponding one-sided tests showed that biochemically relapsing patients exhibited shorter τs (p = 4.70 × 10−4), higher β (p = 8.61 × 10−4) and smaller Δtn (p = 0.0111). Figure 2 depicts the boxplots corresponding to the values of τs, β and Δtn obtained with the periodic-dose model and the single-dose model for the whole cohort, cured patients and biochemically relapsing patients. These boxplots show how τs, β and Δtn cluster around different values in cured and biochemically relapsing patients. Among the other quantities of interest, the non-dimensional parameter α was close to the significance threshold for both models, as well as RD and Pn in the single-dose model.
Figure 2.
Boxplots of the potential patient classifiers identified in the statistical analysis: (a) the characteristic time of tumour cell proliferation τs, (b) non-dimensional parameter β = τd/τs and (c) the time to PSA nadir since EBRT termination Δtn. The first and the second row correspond to the results obtained with the periodic-dose model (green) and the single-dose model (blue), respectively. Outliers are depicted as hollow grey circles. (Online version in colour.)
Except for P0, the two-sided Wilcoxon signed-rank tests showed that the values of the remainder parameters, the non-dimensional parameters, the PSA nadir, and the time to PSA nadir obtained with either PSA dynamics model for each patient were significantly different within the whole cohort and the subgroup of cured patients (table 6). Corresponding one-sided tests in the whole cohort revealed that the single-dose model provided smaller R (p < 1 × 10−6), τs (p = 5.47 × 10−5), α (p < 1 × 10−6) and Pn (p = 0.004) as well as larger τd (p < 1 × 10−6), β (p < 1 × 10−6) and Δtn (p < 1 × 10−6). Within the subgroup of cured patients, one-sided Wilcoxon signed-rank tests also revealed that the single-dose model produced lower values of R (p < 1 × 10−6), τs (p = 2.23 × 10−5), α (p < 1 × 10−6) and Pn (p = 1.58 × 10−4) as well as larger values of τd (p < 1 × 10−6), β (p < 1 × 10−6) and Δtn (p < 1 × 10−6). Within the subgroup of biochemically relapsing patients, only R, τd, β and α were found to significantly vary with either model for each patient in two-sided Wilcoxon signed-rank tests (table 6). Corresponding one-sided tests showed that the single-dose model produced lower values of R (p = 0.023) and α (p = 0.008) as well as larger values of τd (p = 0.016) and β (p = 0.016). However, the global comparison of the values provided by either model using two-sided WRSTs did not find any significant difference neither within the whole cohort nor within any of the patient subgroups (table 6).
Table 6.
p-values obtained for the two-sided statistical tests to search for significant differences in model parameters, non-dimensional parameters, PSA nadir, and time to PSA nadir since EBRT completion between the periodic-dose and single-dose models. Results are shown for the whole cohort and for the subgroups of cured and biochemically relapsing patients. The significance level was set at p < 0.05. Significant p-values are in bold.
| quantity | patients |
||
|---|---|---|---|
| all (n = 71) | cured (n = 64) | relapsing (n = 7) | |
| Wilcoxon signed-rank tests | |||
| P0 | 0.563 | 0.288 | 0.297 |
| R | <1 × 10−6 | <1 × 10−6 | 0.047 |
| τd | <1 × 10−6 | <1 × 10−6 | 0.031 |
| τs | 1.08 × 10−5 | 4.39 × 10−5 | 0.078 |
| β | <1 × 10−6 | <1 × 10−6 | 0.031 |
| α | <1 × 10−6 | 1.12 × 10−6 | 0.016 |
| Pn | 8.12 × 10−3 | 3.13 × 10−4 | 0.078 |
| Δtn | <1 × 10−6 | <1 × 10−6 | 0.109 |
| Wilcoxon rank-sum tests | |||
| P0 | 1.000 | 0.994 | 0.902 |
| R | 0.677 | 0.673 | 0.805 |
| τd | 0.170 | 0.180 | 0.456 |
| τs | 0.633 | 0.585 | 0.902 |
| β | 0.281 | 0.238 | 0.710 |
| α | 0.308 | 0.320 | 0.710 |
| Pn | 0.941 | 0.918 | 0.805 |
| Δtn | 0.372 | 0.359 | 0.805 |
3.3. Receiver operating characteristic curves
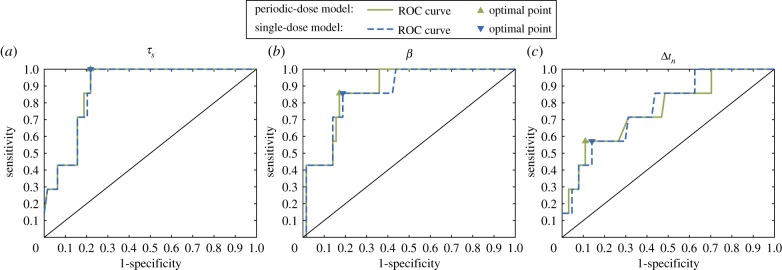
Figure 3 shows the ROC curves for the three quantities that were significantly different between the groups of cured and biochemically relapsing patients: τs, β and Δtn. The AUC and optimal performance point obtained for each quantity and model are shown in table 7. The two ROC curves for each classifier were very similar and provided comparable AUC values and optimal points of performance, especially for τs. This suggests the insensitivity in the accuracy of these classifiers with respect to the choice of mathematical model to fit PSA data.
Figure 3.
ROC curves for the different patient classifiers identified in the statistical analysis: (a) the characteristic time of tumour cell proliferation τs, (b) the non-dimensional parameter β = τd/τs and (c) the time to PSA nadir since EBRT termination Δtn. (Online version in colour.)
Table 7.
Analysis of ROC curves.
| classifier |
|||
|---|---|---|---|
| measure | τs | β | Δtn |
| periodic-dose model | |||
| AUC | 0.887 | 0.875 | 0.759 |
| optimal point | |||
| threshold | 42.6 mo | 5.15 × 10−2 | 11.2 mo |
| specificity | 78.1% | 82.8% | 89.1% |
| sensitivity | 100% | 85.7% | 57.1% |
| accuracy | 80.3% | 83.1% | 85.9% |
| single-dose model | |||
| AUC | 0.885 | 0.865 | 0.768 |
| optimal point | |||
| threshold | 41.6 mo | 6.19 × 10−2 | 11.8 mo |
| specificity | 78.1% | 81.3% | 85.9% |
| sensitivity | 100% | 85.7% | 57.1% |
| accuracy | 80.3% | 81.7% | 83.1% |
The shape of the ROC curves, the AUC, and the balance between optimal sensitivity and specificity showed that τs and β rendered almost equally outstanding results and that both performed better than Δtn, which only showed a fairly satisfactory behaviour. Parameter τs provided the highest AUC and optimal sensitivity. While β provided a slightly lower AUC than τs, it also showed a better trade-off between sensitivity and specificity at optimal performance point. Δtn was found to provide the highest optimal specificity, but the corresponding optimal sensitivity and AUC were remarkably lower with respect to those of τs and β. All potential classifiers showed similar accuracy at optimal performance point. However, as the prevalence of biochemical relapse was low in our cohort (seven out of 71 cases), the accuracy of classifiers was largely driven by the specificity, almost regardless of sensitivity (table 7). Hence, Δtn was also found to provide a slightly higher accuracy at optimal performance point.
4. Discussion
4.1. A robust formulation of prostate-specific antigen dynamics offering new insights in radiation effects on prostate cancer
Our models always lead to an explicit bi-exponential formula of PSA dynamics relying on the coupled dynamics of the radiation-induced irreversibly damaged tumour cell fraction and the surviving tumour cell population. Consequently, we provided a biophysical meaning for the parameters appearing in the empirical biexponential formulations [14–18]. Both models achieved a highly remarkable accuracy in the fitting of patient’s PSA longitudinal data in our cohort (table 3). We observed that even a limited amount of PSA data can provide an excellent fit with both models as long as (i) sufficient PSA values are evenly distributed closely around EBRT and (ii) they do not exhibit large fluctuations (see electronic supplementary material, figures S2–S4). Despite its apparent simplicity, our results show that the single-dose model suffices to accurately describe PSA dynamics before and after EBRT, even providing superior fittings than the more complex periodic-dose model (tables 3 and 4). This also means that the single-dose model is an excellent surrogate for the general model in equation (2.8), which is virtually equivalent to the periodic-dose model (see electronic supplementary material, figure S1 and table S2). This extraordinary balance between simplicity and accuracy is an appealing feature that facilitates forthcoming research on PSA dynamics and its actual clinical use.
By formally analysing our models, we found that the evolution of PSA after EBRT is characterised by only two non-dimensional parameters: α and β (see §2.2.4). The non-dimensional parameter α controls the magnitude of PSA decay due to EBRT, i.e. the amount of PSA eliminated due to radiation-induced tumour cell death. Large values of α are related to low values of Rd (equations (2.15a) and (2.16)) or RD (equation (2.17)) what means that radiation successfully eliminates tumour cells. Thus, α accounts for the efficacy of EBRT. As β = τd/τs, this non-dimensional parameter controls the coupled dynamics of the irreversibly damaged and surviving cell fractions that ultimately translates into the observable temporal trends of PSA after EBRT. Because τd < τs (see table 5), larger values of β indicate post-radiation tumour dynamics to be mostly driven by proliferation of the surviving fraction, while lower values of β point out towards a dominance of radiation-induced tumour cell death.
Interestingly, the efficacy of EBRT was better in biochemically relapsing patients, who showed larger α and lower surviving fractions (Rd or RD) than cured patients, even though these observations were statistically not significant (table 5). A dramatic decay of PSA following EBRT has also been linked to PCa recurrence in the literature [13]. We observed that biochemically relapsing patients showed smaller τs (table 5), i.e. tumours proliferated faster, which may explain this counterintuitive phenomenon: programmed cell death is triggered before cell division in case of major genetic damage [4], so fast proliferation accelerates the elimination of tumour cells affected by radiation, which translates in a dramatic decrease in total tumour cell number and thus PSA. This mechanism has also been proposed to explain the poorer prognosis of diffuse low-grade glioma patients who experience a rapid tumour volume decrease following radiotherapy using both a clinical and mathematical approach [23,46]. As α was not significantly different between biochemically relapsing and cured patients, the latter may also experience a steep PSA decay after EBRT. Hence, we require a larger cohort to validate this mechanism in PCa.
4.2. Potential patient classifiers based on tumour dynamics and identified through prostate-specific antigen dynamics
This study resulted in three classifiers that showed great potential to identify biochemically relapsing patients: a short characteristic time of tumour cell proliferation τs, a large non-dimensional parameter β, and an early time to PSA nadir since EBRT termination Δtn (tables 6 and 7). Indeed, both β and Δtn are inherently controlled by τs. As τd does not vary much between cured and relapsing patients, large β values are also a consequence of a small τs (see §4.1). Then, large β promotes an early PSA nadir (see equation (2.19)), which correlates with PCa recurrence and worse survival rates [8,9]. The additional dependence of Δtn on α, which does not significantly vary between cured and biochemically relapsing patients, might explain the comparatively worse performance of Δtn as a patient classifier in ROC analysis with respect to τs and β.
We believe that τs holds a promising, robust prognostic value for PCa both before and after EBRT. An elevated tumour cell proliferation rate (i.e. short τs) has been correlated with increased aggressiveness of PCa in terms of a high Gleason Score [47], which is a crucial clinical variable in clinical management of PCa that has been linked to a higher probability of PCa local recurrence and distant metastases [2,7,8]. While Gleason Score is normally determined from histopathological assessment of biopsy samples, τs would enable to non-invasively monitor Gleason Score and to justify further biopsies when model estimations suggest a more aggressive cancer than the baseline, diagnostic biopsy. Moreover, the PSA doubling times and velocity on the rising branch in biochemically relapsing patients can be approximated as DT ≈ τs ln2 and vP ≈ (P/τs) for all models in §2.2. Hence, small values of τs would render short doubling times and high velocities of PSA increase, which have been associated to poor prognosis in PCa recurrence [6–8,10]. Our estimation of τs in biochemically relapsing patients (table 5) agrees with previously reported tumour doubling times [48], PSA relapsing doubling times [7,10], and time to PSA nadir since EBRT termination [9]. Parameter τs also enables to estimate pretreatment PSA doubling times and velocity, whose prognostic value is controversial [49]. Our model provides a robust and systematic procedure to estimate these dynamic variables, which may facilitate the assessment of their role as PCa prognostic markers.
4.3. Limitations and future developments
Our study presents several limitations. The patient cohort featured a limited number of patients experiencing biochemical relapse, which makes it difficult to accurately identify and assess patient classifiers. Our results need to be tested in larger independent cohorts, in which we could also explore the correlations between common PCa clinical characteristics and model parameters, non-dimensional parameters and PSA nadir estimation. While our models were rather robust against PSA fluctuations, a larger cohort would also contribute to reduce their effect on statistical analysis. We could further reduce the impact of these fluctuations by using robust nonlinear least-square methods, which associate a weight to each PSA value that tends to zero as it deviates from the average trend. Furthermore, we are using biochemical relapse as a surrogate for PCa recurrence. Ideally, our PSA dynamics models should be tested to identify clinically confirmed PCa recurrence after EBRT. We plan to specifically update our cohort with patients for whom such evidence is available to conduct further research with our PSA formulations. Hence, we could also characterize local recurrence and distant metastases using model-based markers.
Despite our methods could only approximate τs ≈ 500 (upper bound) for some cured patients, we believe that this is a minor limitation for four reasons: (i) large τs is expected in cured patients, so τs = 500 mo might be an acceptable approximation; (ii) model fitting was not compromised (see electronic supplementary material, figure S5); (iii) τs plays a little role in post-EBRT dynamics of cured patients; and (iv) τs = 500 produces small β and large Δtn, contributing to classify the patient as cured. Multiple pre-EBRT PSA values, robust nonlinear least-squares fitting and problem non-dimensionalization could facilitate the accurate estimation of τs with our models.
We assumed that the proliferation rate of tumour cells did not vary after EBRT, i.e. τn ≈ τs. While this is a common assumption [21–23], recent studies suggest that radiation may also affect tumour proliferation [22,50]. To explore this phenomenon in PCa patients undergoing EBRT, we would need to estimate both τn and τs, which requires multiple PSA data both before and after EBRT. Additionally, our models do not differentiate between the PSA produced by PCa and BPH. We could add a term to equations (2.1) and (2.5b) to include the BPH contribution PBPH(t) to the tumour-generated PSA levels, i.e. P(t) = ρ N(t) + PBPH(t) and P(t) = ρ (S(t) + D(t)) + PBPH(t). For times t < 10 years, we may approximate PBPH(t) with a linear term or another exponential [26,51]. This simple model update would enable a more accurate determination of τs and model fitting. We also plan to explore alternative radiobiological definitions for Rd and RD to refine the modelling of radiation effects [20–22,35–37,40–43]. By introducing an explicit dependence of Rd and RD on the radiation dose one could pursue more sophisticated optimal EBRT plans [52].
PSA is currently the cornerstone of clinical decision-making during follow-up after local radical radiotherapy for PCa, so we focused our models on this biomarker. Emerging urine and blood tests are showing a promising performance in PCa diagnosis (e.g. PCA3, prostate health index, four kallikrein panel) and they may complement or even substitute PSA in the future [1,53]. Circulating tumour cells have also been shown to contribute to the diagnosis of advanced PCa. However, these tests are not recommended yet for routine screening due to the limited and sometimes inconsistent reported data. Once these biomarkers become routine, their corresponding dynamics could be coupled with our model to explore their joint performance to identify biochemically relapsing patients.
Personalised volumetric data of prostate and tumour could further refine the estimation of PSA production by both benign and malignant tissue [24,25]. Multiparametric magnetic resonance is an emerging imaging technique that provides a wealth of anatomic data and is increasingly used to diagnose and monitor mild PCa during active surveillance protocols. In this context, the underlying tumour dynamics model could be refined, e.g. by using a phase-field or Fisher–Kolmogorov model and linking the variable identifying tumour growth with PSA production [22,24]. Initial tumour geometry and parameter selection can then be determined by combining longitudinal PSA and imaging data [19–22,24]. However, tumour volume is not measured in routine monitoring of patients after radiotherapy and longitudinal imaging follow-up for each patient would be required besides the standard PSA data. Thus, extending our models to include volumetric data will inevitably require a specific research monitoring protocol featuring an adequate image acquisition plan.
4.4. Towards patient-specific prostate-specific antigen monitoring plans and early detection of prostate cancer recurrence
Our mathematical models can help in the early identification of biochemically relapsing patients. This requires a good parameter identification, for which we recommend collecting at least three pre-EBRT PSA values and no less than four post-EBRT PSA values. This would translate in measuring PSA every three to six months before and after EBRT, which is compatible with current clinical guidelines. This recommendation stems from the results of this study, but we plan to determine the minimal data that enables an optimal prediction of PSA dynamics with our models in forthcoming studies. Likewise, we also plan to compare observed PSA data with simulated PSA trends corresponding to alternative treatment plans, which may help to determine the window of curability and best timing for EBRT.
These initial PSA data would allow a first evaluation of the patient’s risk of relapse. Later, as further PSA data are gathered, the physician can update the prognostic variables to provide more accurate patient-specific predictions. Moreover, the predicted PSA dynamics can suggest an adequate frequency of new PSA tests to accurately parametrize our models, for instance, with shorter time intervals to precisely capture the decay following EBRT, confirm the date of nadir, and characterize a potential rising branch in relapsing patients, or longer time intervals to confirm the plateau or benign linear growth in cured patients. Hence, physicians could design a personalized PSA monitoring plan adapted to the unique PSA dynamics of each patient and informed by the underlying tumour evolution, instead of the fixed conventional recommendations currently provided by clinical guidelines.
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Ethics
Anonymised patient data were obtained from Centro Oncológico de Galicia (COG, A Coruña, Spain). Ethical approval was obtained from Comité Autonómico de Ética da Investigación de Galicia (Santiago de Compostela, Spain). Informed consent was not required for the patient data used in this study.
Data accessibility
This work did not generate data other than those presented in the article and the electronic supplementary material.
Authors' contributions
G.L., V.M.P-.G., L.A.P.-R., A.M., A.R. and H.G. conceived and designed the research, structured and analysed the results, and participated in the preparation and editing of the manuscript. G.L., V.M.P-.G., A.R. and H.G. developed the mathematical models and defined the analytical methods. G.L. performed the computations and created the displays.
Competing interests
We have no competing interests.
Funding
G.L. and H.G. were partially supported by the European Research Councilthrough the FP7 Ideas Starting Grant program (Contract # 307201). G.L. and A.R. were partially supported by Fondazione Cariplo—Regione Lombardia through the project ‘Verso nuovi strumenti di simulazione super veloci ed accurati basati sull’analisi isogeometrica’, within the program RST—rafforzamento. V.M.P-.G. work was partially supported by the Ministerio de Economía y Competitividad/FEDER, Spain (grant no. MTM2015- 71200-R) and Junta de Comunidades de Castilla-La Mancha (grant no. SBPLY/17/180501/000154).
References
- 1.Mottet N, van den Bergh RCN, Briers E, Bourke L, Cornford P, Santis MD. et al. 2018. EAU-ESTRO-ESUR-SIOG guidelines on prostate cancer. European Association of Urology. Available from: https://uroweb.org/guideline/prostate-cancer/.
- 2.Wein AJ, Kavoussi LR, Novick AC, Partin AW, Peters CA. 2012. Campbell-Walsh urology: expert consult premium edition: enhanced online features and print, 4-Volume Set. 10th edn. Elsevier Saunders.
- 3.Gray PJ, Lin CC, Cooperberg MR, Jemal A, Efstathiou JA. 2017. Temporal trends and the impact of race, insurance, and socioeconomic status in the management of localized prostate cancer. Eur. Urol. 71, 729–737. ( 10.1016/j.eururo.2016.08.047) [DOI] [PubMed] [Google Scholar]
- 4.Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. 2007. Molecular biology of the cell, 5th edn New York, NY: Garland Science. [Google Scholar]
- 5.Pinkawa M, Piroth MD, Holy R, Fischedick K, Schaar S, Borchers H, Heidenreich A, Eble MJ. 2010. Prostate-specific antigen kinetics following external-beam radiotherapy and temporary (Ir-192) or permanent (I-125) brachytherapy for prostate cancer. Radiother. Oncol. 96, 25–29. ( 10.1016/j.radonc.2010.02.010) [DOI] [PubMed] [Google Scholar]
- 6.Freiberger C, Berneking V, Vögeli TA, Kirschner-Hermanns R, Eble MJ, Pinkawa M. 2017. Long-term prognostic significance of rising PSA levels following radiotherapy for localized prostate cancer–focus on overall survival. Radiat. Oncol. 12, 98 ( 10.1186/s13014-017-0837-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zelefsky MJ, Ben-Porat L, Scher HI, Chan HM, Fearn PA, Fuks ZY, Leibel SA, Venkatraman ES. 2005. Outcome predictors for the increasing PSA state after definitive external-beam radiotherapy for prostate cancer. J. Clin. Oncol. 23, 826–831. ( 10.1200/JCO.2005.02.111) [DOI] [PubMed] [Google Scholar]
- 8.Zumsteg ZS. et al. 2015. The natural history and predictors of outcome following biochemical relapse in the dose escalation era for prostate cancer patients undergoing definitive external beam radiotherapy. Eur. Urol. 67, 1009–1016. ( 10.1016/j.eururo.2014.09.028) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ray ME. et al. 2006. PSA nadir predicts biochemical and distant failures after external beam radiotherapy for prostate cancer: a multi-institutional analysis. Int. J. Radiat. Oncol. Biol. Phys. 64, 1140–1150. ( 10.1016/j.ijrobp.2005.07.006) [DOI] [PubMed] [Google Scholar]
- 10.Bates AT, Pickles T, Paltiel C. 2005. PSA doubling time kinetics during prostate cancer biochemical relapse after external beam radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 62, 148–153. ( 10.1016/j.ijrobp.2004.09.048) [DOI] [PubMed] [Google Scholar]
- 11.Cheung R, Tucker SL, Kuban DA. 2006. First-year PSA kinetics and minima after prostate cancer radiotherapy are predictive of overall survival. Int. J. Radiat. Oncol. Biol. Phys. 66, 20–24. ( 10.1016/j.ijrobp.2006.04.028) [DOI] [PubMed] [Google Scholar]
- 12.Cavanaugh SX, Kupelian PA, Fuller CD, Reddy C, Bradshaw P, Pollock BH, Fuss M. 2004. Early prostate-specific antigen (PSA) kinetics following prostate carcinoma radiotherapy: prognostic value of a time-and–PSA threshold model. Cancer 101, 96–105. ( 10.1002/cncr.20328) [DOI] [PubMed] [Google Scholar]
- 13.Shi Z, Pinnock CB, Kinsey-Trotman S, Borg M, Moretti KL, Walsh S, Kopsaftis T. 2013. Prostate-specific antigen (PSA) rate of decline post external beam radiotherapy predicts prostate cancer death. Radiother. Oncol. 107, 129–133. ( 10.1016/j.radonc.2013.03.030) [DOI] [PubMed] [Google Scholar]
- 14.Zagars GK, Pollack A. 1997. Kinetics of serum prostate-specific antigen after external beam radiation for clinically localized prostate cancer. Radiother. Oncol. 44, 213–221. ( 10.1016/S0167-8140(97)00123-0) [DOI] [PubMed] [Google Scholar]
- 15.Cox RS, Kaplan ID, Bagshaw MA. 1994. Prostate-specific antigen kinetics after external beam irradiation for carcinoma of the prostate. Int. J. Radiat. Oncol. Biol. Phys. 28, 23–31. ( 10.1016/0360-3016(94)90137-6) [DOI] [PubMed] [Google Scholar]
- 16.Hanlon AL, Moore DF, Hanks GE. 1998. Modeling postradiation prostate specific antigen level kinetics: predictors of rising postnadir slope suggest cure in men who remain biochemically free of prostate carcinoma. Cancer 83, 130–134. () [DOI] [PubMed] [Google Scholar]
- 17.Vollmer RT, Montana GS. 1999. The dynamics of prostate-specific antigen after definitive radiation therapy for prostate cancer. Clin. Cancer Res. 5, 4119–4125. [PubMed] [Google Scholar]
- 18.Taylor JM, Yu M, Sandler HM. 2005. Individualized predictions of disease progression following radiation therapy for prostate cancer. J. Clin. Oncol. 23, 816–825. ( 10.1200/JCO.2005.12.156) [DOI] [PubMed] [Google Scholar]
- 19.Weis JA, Miga MI, Arlinghaus LR, Li X, Abramson V, Chakravarthy AB, Pendyala P, Yankeelov TE. 2015. Predicting the response of breast cancer to neoadjuvant therapy using a mechanically coupled reaction–diffusion model. Cancer Res. 75, 4697–4707. ( 10.1158/0008-5472.CAN-14-2945) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang CH. et al. 2009. Prognostic significance of growth kinetics in newly diagnosed glioblastomas revealed by combining serial imaging with a novel biomathematical model. Cancer Res. 69, 9133–9140. ( 10.1158/0008-5472.CAN-08-3863) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Corwin D, Holdsworth C, Rockne RC, Trister AD, Mrugala MM, Rockhill JK, Stewart RD, Phillips M, Swanson KR. 2013. Toward patient-specific, biologically optimized radiation therapy plans for the treatment of glioblastoma. PLoS ONE 8, 1–9. ( 10.1371/journal.pone.0079115) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lima EABF, Oden JT, Wohlmuth B, Shahmoradi A, Hormuth DA, Yankeelov TE, Scarabosio L, Horger T. 2017. Selection and validation of predictive models of radiation effects on tumor growth based on noninvasive imaging data. Comput. Methods Appl. Mech. Eng. 327, 277–305. ( 10.1016/j.cma.2017.08.009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pérez-García VM, Bogdanska M, Martínez-González A, Belmonte-Beitia J, Schucht P, Pérez-Romasanta LA. 2015. Delay effects in the response of low-grade gliomas to radiotherapy: a mathematical model and its therapeutical implications. Math. Med. Biol.: A J. IMA 32, 307–329. ( 10.1093/imammb/dqu009) [DOI] [PubMed] [Google Scholar]
- 24.Lorenzo G, Scott MA, Tew K, Hughes TJR, Zhang YJ, Liu L, Vilanova G, Gomez H. 2016. Tissue-scale, personalized modeling and simulation of prostate cancer growth. Proc. Natl Acad. Sci. USA 113, E7663–E7671. ( 10.1073/pnas.1615791113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Swanson KR, True LD, Lin DW, Buhler KR, Vessella R, Murray JD. 2001. A quantitative model for the dynamics of serum prostate-specific antigen as a marker for cancerous growth: an explanation for a medical anomaly. Am. J. Pathol. 158, 2195–2199. ( 10.1016/S0002-9440(10)64691-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vollmer RT. 2010. Dissecting the dynamics of serum prostate-specific antigen. Am. J. Clin. Pathol. 133, 187–193. ( 10.1309/AJCP3CJR3IDRCFEO) [DOI] [PubMed] [Google Scholar]
- 27.Farhat A, Jiang D, Cui D, Keller ET, Jackson TL. 2017. An integrative model of prostate cancer interaction with the bone microenvironment. Math. Biosci. 294, 1–14. ( 10.1016/j.mbs.2017.09.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hirata Y, Bruchovsky N, Aihara K. 2010. Development of a mathematical model that predicts the outcome of hormone therapy for prostate cancer. J. Theor. Biol. 264, 517–527. ( 10.1016/j.jtbi.2010.02.027) [DOI] [PubMed] [Google Scholar]
- 29.Jackson TL. 2004. A mathematical investigation of the multiple pathways to recurrent prostate cancer: comparison with experimental data. Neoplasia 6, 697–704. ( 10.1593/neo.04259) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ideta AM, Tanaka G, Takeuchi T, Aihara K. 2008. A mathematical model of intermittent androgen suppression for prostate cancer. J. Nonlinear Sci. 18, 593–614. ( 10.1007/s00332-008-9031-0) [DOI] [Google Scholar]
- 31.Jain HV, Clinton SK, Bhinder A, Friedman A. 2011. Mathematical modeling of prostate cancer progression in response to androgen ablation therapy. Proc. Natl Acad. Sci. USA 108, 19 701–19 706. ( 10.1073/pnas.1115750108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Morken JD, Packer A, Everett RA, Nagy JD, Kuang Y. 2014. Mechanisms of resistance to intermittent androgen deprivation in patients with prostate cancer identified by a novel computational method. Cancer Res. 74, 3673–3683. ( 10.1158/0008-5472.CAN-13-3162) [DOI] [PubMed] [Google Scholar]
- 33.Vollmer RT, Humphrey PA. 2003. Tumor volume in prostate cancer and serum prostate-specific antigen: analysis from a kinetic viewpoint. Am. J. Clin. Pathol. 119, 80–89. ( 10.1309/UNAQJTFPB1RQBQD4) [DOI] [PubMed] [Google Scholar]
- 34.Truskinovsky AM, Partin AW, Kroll MH. 2005. Kinetics of tumor growth of prostate carcinoma estimated using prostate-specific antigen. Urology 66, 577–581. ( 10.1016/j.urology.2005.03.085) [DOI] [PubMed] [Google Scholar]
- 35.Lewin TD, Maini PK, Moros EG, Enderling H, Byrne HM. 2018. The evolution of tumour composition during fractionated radiotherapy: implications for outcome. Bull. Math. Biol. 80, 1207–1235. ( 10.1007/s11538-018-0391-9) [DOI] [PubMed] [Google Scholar]
- 36.Rockne R. et al. 2010. Predicting the efficacy of radiotherapy in individual glioblastoma patients in vivo: a mathematical modeling approach. Phys. Med. Biol. 55, 3271–3285. ( 10.1088/0031-9155/55/12/001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Powathil GG, Adamson DJA, Chaplain MAJ. 2013. Towards predicting the response of a solid tumour to chemotherapy and radiotherapy treatments: clinical insights from a computational model. PLoS Comput. Biol. 9, 1–14. ( 10.1371/journal.pcbi.1003120) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Leder K, Pitter K, LaPlant Q, Hambardzumyan D, Ross B, Chan T, Holland EC, Michor F. 2014. Mathematical modeling of PDGF-driven glioblastoma reveals optimized radiation dosing schedules. Cell 156, 603–616. ( 10.1016/j.cell.2013.12.029) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Scott JG. et al. 2017. A genome-based model for adjusting radiotherapy dose (GARD): a retrospective, cohort-based study. Lancet Oncol. 18, 202–211. ( 10.1016/S1470-2045(16)30648-9) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.O’Rourke SFC, McAneney H, Hillen T. 2008. Linear quadratic and tumour control probability modelling in external beam radiotherapy. J. Math. Biol. 58, 799–817. ( 10.1007/s00285-008-0222-y) [DOI] [PubMed] [Google Scholar]
- 41.Bodgi L, Canet A, Pujo-Menjouet L, Lesne A, Victor JM, Foray N. 2016. Mathematical models of radiation action on living cells: from the target theory to the modern approaches. A historical and critical review. J. Theor. Biol. 394, 93–101. ( 10.1016/j.jtbi.2016.01.018) [DOI] [PubMed] [Google Scholar]
- 42.Kal HB, Gellekom MPRV. 2003. How low is the α/β ratio for prostate cancer? Int. J. Radiat. Oncol. Biol. Phys. 57, 1116–1121. ( 10.1016/S0360-3016(03)01455-X) [DOI] [PubMed] [Google Scholar]
- 43.Wang JZ, Li XA. 2005. Impact of tumor repopulation on radiotherapy planning. Int. J. Radiat. Oncol. Biol. Phys. 61, 220–227. ( 10.1016/j.ijrobp.2004.09.043) [DOI] [PubMed] [Google Scholar]
- 44.Marrero CS, Aubert V, Ciferri N, Hernández A, de Crevoisier R, Acosta O. 2017. Towards an integrative computational model for simulating tumor growth and response to radiation therapy. In 13th Int. Conf. on Medical Information Processing and Analysis, vol. 10572. p. 1057216.
- 45.Yamamoto Y. et al. 2016. Tumour and immune cell dynamics explain the PSA bounce after prostate cancer brachytherapy. Br. J. Cancer 115, 195–202. ( 10.1038/bjc.2016.171) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pallud J. et al. 2012. Dynamic imaging response following radiation therapy predicts long-term outcomes for diffuse low-grade gliomas. Neuro Oncol. 14, 496–505. ( 10.1093/neuonc/nos069) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tretiakova MS. et al. 2016. Prognostic value of Ki67 in localized prostate carcinoma: a multi-institutional study of >1000 prostatectomies. Prostate Cancer Prostatic Dis. 19, 264–270. ( 10.1038/pcan.2016.12) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Berges RR, Vukanovic J, Epstein JI, CarMichel M, Cisek L, Johnson DE, Veltri RW, Walsh PC, Isaacs JT. 1995. Implication of cell kinetic changes during the progression of human prostatic cancer. Clin. Cancer Res. 1, 473–480. [PMC free article] [PubMed] [Google Scholar]
- 49.Vickers AJ, Savage C, O’Brien MF, Lilja H. 2009. Systematic review of pretreatment prostate-specific antigen velocity and doubling time as predictors for prostate cancer. J. Clin. Oncol. 27, 398–403. ( 10.1200/JCO.2008.18.1685) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hormuth DA, Weis JA, Barnes SL, Miga MI, Quaranta V, Yankeelov TE. 2018. Biophysical modeling of in vivo glioma response after whole-brain radiation therapy in a murine model of brain cancer. Int. J. Radiat. Oncol. Biol. Phys. 100, 1270–1279. ( 10.1016/j.ijrobp.2017.12.004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lieber MM, Rhodes T, Jacobson DJ, McGree ME, Girman CJ, Jacobsen SJ, St. Sauver JL. 2010. Natural history of benign prostatic enlargement: long-term longitudinal population-based study of prostate volume doubling times. BJU Int. 105, 214–219. ( 10.1111/j.1464-410X.2009.08719.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Henares-Molina A, Benzekry S, Lara PC, García-Rojo M, Pérez-García VM, Martínez-González A. 2017. Non-standard radiotherapy fractionations delay the time to malignant transformation of low-grade gliomas. PLoS ONE 12, 1–19. ( 10.1371/journal.pone.0178552) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Filella X, Fernández-Galan E, Bonifacio RF, Foj L. 2018. Emerging biomarkers in the diagnosis of prostate cancer. Pharmacogenomics Per. Med. 11, 83–94. ( 10.2147/PGPM.S136026) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This work did not generate data other than those presented in the article and the electronic supplementary material.