Modelling the ballistic-to-diffusive transition in nematode motility reveals variation in exploratory behaviour across species

Abstract

A quantitative understanding of organism-level behaviour requires predictive models that can capture the richness of behavioural phenotypes, yet are simple enough to connect with underlying mechanistic processes. Here, we investigate the motile behaviour of nematodes at the level of their translational motion on surfaces driven by undulatory propulsion. We broadly sample the nematode behavioural repertoire by measuring motile trajectories of the canonical laboratory strain Caenorhabditis elegans N2 as well as wild strains and distant species. We focus on trajectory dynamics over time scales spanning the transition from ballistic (straight) to diffusive (random) movement and find that salient features of the motility statistics are captured by a random walk model with independent dynamics in the speed, bearing and reversal events. We show that the model parameters vary among species in a correlated, low-dimensional manner suggestive of a common mode of behavioural control and a trade-off between exploration and exploitation. The distribution of phenotypes along this primary mode of variation reveals that not only the mean but also the variance varies considerably across strains, suggesting that these nematode lineages employ contrasting ‘bet-hedging’ strategies for foraging.

1. Introduction

A ubiquitous feature of biological motility is the combination of stereotyped movements in seemingly random sequences. Capturing the essential characteristics of motion thus requires a statistical description, in close analogy to the random-walk formulation of Brownian motion in physics. A canonical example is the ‘run-and-tumble’ behaviour of E. coli bacteria, in which relatively straight paths (runs) are interspersed by rapid and random reorientation events (tumbles) [1]. The random walk of E. coli can thus be characterized by two random variables (run length and tumble angle) and two constant parameters (swimming speed and rotational diffusion coefficient), and detailed studies over decades have yielded mechanistic models that link these key behavioural parameters to the underlying anatomy and physiology [2–5]. Random-walk theory has been fruitfully applied also to studies of eukaryotic cell migration in both two [6–8] and three [9] dimensions.

Can a similar top-down approach be fruitfully applied to more complex organisms—for example, an animal controlled by a neural network? Animal behaviour is both astonishing in its diversity and daunting in its complexity, given the inherently high-dimensional space of possible anatomical, physiological and environmental configurations. It is, therefore, essential to identify appropriate models and parametrizations to succinctly represent the complex space of behaviours—a non-trivial task that has traditionally relied on the insights of expert biologists. In this study, we ask if one can achieve a similar synthesis by an alternative, physically motivated approach [10]. We seek a quantitative model with predictive power over behavioural statistics, and yet a parametrization that is simple enough to permit meaningful interpretations of phenotypes in a reduced space of variables. As an example, we focus on the motile behaviour of nematodes, which explore space using a combination of random and directed motility driven by undulatory propulsion.

The nematode Caenorhabditis elegans has long been a model organism for the genetics of neural systems [11,12], and recent advances in imaging have made it feasible to record a large fraction of the worm’s nervous system activity at single-cell resolution [13–15]. These developments raise the compelling possibility of elucidating the neural basis of behavioural control at the organism scale, but such endeavours will require unambiguous definitions of neural circuit outputs and functional performance. The worm’s behavioural repertoire [16,17] is commonly characterized in terms of forward motion occasionally interrupted by brief reversals [18–20], during which the undulatory body wave that drives its movement [21] switches direction. In addition, worms reorient with a combination of gradual curves in the trajectory (weathervaning) [22,23] and sharp changes in body orientation (omega-turns [19] and delta-turns [24]). These elementary behaviours are combined in exploring an environment [22,25]. Environmental cues such as chemical, mechanical or thermal stimuli [26] lead to a biasing of these behaviours, guiding the worm in favourable directions [22,25,27]. Finally, in practical terms, the worm’s small size (approx. 1 mm in length), moderate propulsive speed (approx. 100 μm s⁻¹) and short generation time (approx. 2 days) allow a considerable fraction of its behavioural repertoire to be efficiently sampled in the laboratory [18,28]. An influential example of such an analysis is the ‘pirouette’ model proposed by Pierce-Shimomura & Lockery [25] which describes the worm’s exploratory behaviour as long runs interrupted occasionally by bursts of reversals and omega turns that reorient the worm, in close analogy to the run-and-tumble model of bacterial random walks [1]. Later work by Iino et al. identified that worms also navigate by smoother modulations of their direction during long runs (weathervaning) [22], and Calhoun et al. have suggested that C. elegans may track the information content of environmental statistics in searching for food [29], a motile strategy that has been termed ‘infotaxis’ [30]. A recent study by Roberts et al. [20] analysed high (submicrometre)-resolution kinematics of C. elegans locomotion and developed a stochastic model of forward–reverse switching dynamics that include the short-lived (approx. 0.1 s) pause states that were identified between forward and reverse runs.

Importantly, while these previous studies have illuminated different modes of behavioural control, they were not designed to obtain a predictive model of the trajectory statistics and thus a succinct parametrization of C. elegans motility remains an important open problem. A quantitative parametrization capturing the repertoire of C. elegans’ behavioural phenotypes would facilitate data-driven investigations of behavioural strategies: for example, whether worms demonstrate distinct modes of motility (characterized by correlated changes in parameters) over time, or in response to changes in environmental conditions [28,31–33]. Variation in the obtained parameters among individuals can inform on the distribution of behavioural phenotypes within a population, and reveal evolutionary constraints and trade-offs between strategies represented by distinct parameter sets [34].

Caenorhabditis elegans is a member of the Nematoda phylum, one of the largest and most diverse phylogenetic groups of species [35,36]. Despite the diversity of ecological niches these animals inhabit [35], comparisons of nematode body plans have revealed a remarkable degree of conservation, even down to the level of individual neurons [37]. This combination of highly conserved anatomy and ecological diversity makes nematode motility a compelling case for studies of behavioural phenotypes. Anatomical conservation suggests it might be possible to describe the behaviour of diverse nematodes by a common model, and identifying the manner in which existing natural variation is distributed across the parameter space of the model could reveal distinct motility strategies resulting from optimization under different environmental conditions.

In this study, we develop a simple random walk model describing the translational movements of a diverse collection of nematode species, freely moving on a two-dimensional agar surface. In addition to providing a quantitative and predictive measure of trajectory dynamics, the parameters of our model define a space of possible behaviours. Variation within such a space can occur due to changes in individual behaviour over time (reflecting temporal variation in the underlying sensorimotor physiology, or ‘mood’), differences in behaviour among individuals (reflecting stable differences in physiology, or ‘personality’) and differences between strains and species (reflecting cumulative effects of natural selection). By quantitative analyses of such patterns of variation, we seek to identify simple, organizing principles underlying behaviour.

2. Results

2.1. Nematodes perform random walks off-food with a broad range of diffusivities across strains

In order to identify conserved and divergent aspects of motility strategies, we sampled motile behaviour over a broad evolutionary range. We selected a phylogenetically diverse collection of nematodes with an increased sampling density closer to the laboratory strain C. elegans (figure 1a; electronic supplementary material). To sample individual variation, we recorded the motility of up to 20 well-fed individuals per strain and each individual for 30 min on a food-free agar plate at 11.5 Hz with a resolution of 12.5 μm px⁻¹ (see electronic supplementary material).

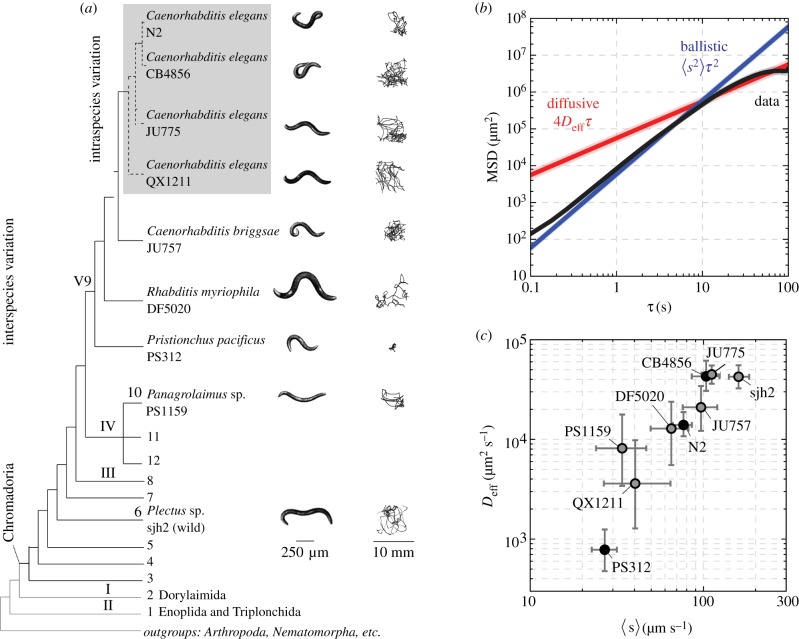
Figure 1.

Nematodes perform random walks off-food with a mean speed and effective diffusivity that varies across strains. (a) Phylogenetic tree with the strains used in this study. The bold numbers are the major clades of Nematoda. The grey box indicates genetically distinct wild isolates of C. elegans. A representative worm image and 30 min trajectory are shown to the right. (b) The average mean-squared displacement, MSD, across N2 individuals is shown in black. For comparison, we show the MSD expected from ballistic (blue) and diffusive (red) dynamics. The motility transitions from a ballistic to diffusive regime within a time scale of tens of seconds. Shaded regions indicate a 95% confidence interval. (c) Mean speed 〈s〉 and effective diffusivity D_eff (mean and 95% confidence intervals) for each strain, calculated from fits of the MSD as in (b). Across strains, both 〈s〉 and D_eff vary by orders of magnitude. (Online version in colour.)

We measured the centroid position x(t) and calculated the centroid velocity v(t), using image analysis techniques (electronic supplementary material, figure S11). We chose the centroid as the measure of the worm’s position because it effectively filters out most of the dynamics of the propulsive body wave. There was considerable variation in the spatial extent and degree of turning visible in the trajectories both within and across strains (figure 1a; electronic supplementary material, S2).

As previously seen in C. elegans [38], the measured mean-squared displacement,

$$⟨{[\mathrm{\Delta }x(\tau )]}^2⟩\equiv ⟨{|\mathit{x}(t+\tau )-\mathit{x}(t)|}^2⟩,$$ 2.1

revealed a transition from ballistic to diffusive motion within a 100 s time scale (figure 1b; electronic supplementary material, S3). Over short times, the worm’s path was relatively straight, with the mean-squared displacement scaling quadratically with the time lag τ and speed s as 〈s²〉τ² (i.e. a log–log slope of 2). Over longer times, the slope decreased with τ reflecting the randomization of orientation characteristic of diffusion, and an effective diffusivity D_eff was extracted by fits to 〈[Δx(τ)]²〉 = 4D_effτ (see electronic supplementary material). On the time scales at which the worms start encountering the walls of the observation arena, the slope of the mean-squared displacement decreased yet further, which has been shown to be a property of confined random walks [39]. Nonetheless, we have confirmed that the decay of the velocity autocorrelation function is not significantly affected by the confinement, and is consistent with a ballistic to diffusive transition (electronic supplementary material, figure S1). This analysis revealed that the visible differences in the spatial extent of these 30 min trajectories stem from variation by nearly an order of magnitude in speed and two orders of magnitude in diffusivity (figure 1c; electronic supplementary material, tables S1 and S2).

2.2. The random walk of nematodes can be decomposed into speed, turning and reversal dynamics

The broad range of observed speeds and diffusivities suggest that these diverse nematodes have evolved a variety of strategies for spatial exploration. To gain further insights into the manner in which such contrasting behaviours are implemented by each strain, we sought to extract a minimal model of the nematodes’ random walk by further decomposing the trajectory statistics of all nine measured strains. In this and the following three subsections, we illustrate our analysis and model development with data from three contrasting strains: CB4856 and PS312, which demonstrated two of the most extreme phenotypes, and the canonical laboratory strain N2 (see electronic supplementary material for equivalent data for all strains).

The translational motion of the worm can be described by the time-varying centroid velocity v(t) which can in turn be decomposed into speed s(t) and direction of motion (hereafter referred to as its ‘bearing’) ϕ(t):

$$\mathit{v}(t)=\frac{\text{d}\mathit{x}(t)}{\text{d}t}=s(t)\hspace{0.17em}[\cos \varphi (t),\sin \varphi (t)].$$ 2.2

To account for head–tail asymmetry in the worm’s anatomy, we additionally define the body orientation (ψ(t); hereafter referred to simply as ‘orientation’) by the angle of the vector connecting the worm’s centroid to the head (figure 2a). The centroid bearing is related to this orientation of the worm by

$$\varphi (t)=\psi (t)+\mathrm{\Delta }\psi (t),$$ 2.3

where the difference Δψ(t) is a measure of the alignment of the direction of movement with the worm’s body orientation (hereafter referred to simply as ‘alignment’). We found for all strains that the distribution of Δψ(t) was bimodal with peaks at 0° and 180° (figure 2c; electronic supplementary material, S7A). These match the forward and reverse states of motion described in C. elegans [18,19].

Figure 2.

The random walk of nematodes is composed of speed, turning and reversal dynamics. (a) We describe the motility of the worm by the time-varying quantities s(t) (speed; black), ψ(t) (orientation; red) and Δψ(t) (alignment; green) which measures the difference between the alignment of the velocity ϕ(t) (blue) and ψ(t). (b) One-minute examples of speed, orientation and velocity alignment time series for individuals from three exemplar strains. (c) The probability distribution of Δψ(t) reveals bimodality corresponding to forward and reverse motion. Shaded regions indicate a 95% confidence interval. (Online version in colour.)

Each of the three components of the worm’s motility (speed, orientation and alignment) varied considerably over time and in qualitatively different ways between strains (figure 2b). For example, the three strains shown in figure 2b differed not only in their average speed but also in the amplitude and time scale of fluctuations about the average speed. Similarly, the statistics of orientation fluctuations about the drifting mean also differed visibly between strains. Finally, transitions between forward and reverse runs were far more frequent in PS312 when compared with N2 and CB4856. Given the apparently random manner in which these motility components varied over time, we proceeded to analyse the dynamics of each of these three components as a stochastic process.

2.3. Speed dynamics

Speed control has not been extensively studied in C. elegans, but it is known that worms move with a characteristic speed that is influenced by stimuli [26]. When intervals corresponding to transitions between forward and reverse runs were excluded from the time series, we found that the autocorrelation in speed fluctuations decayed exponentially over a few seconds (figure 3a; electronic supplementary material, S5A), a time scale similar to the period of the propulsive body wave. These dynamics are naturally captured by an Ornstein–Uhlenbeck process [40], which describes random fluctuations arising from white noise (increments of a diffusive Wiener process, dW_t [40]) with magnitude $\sqrt{2D_s}$ that relax with time scale τ_s back to an average value, μ_s = 〈s〉:

$$\text{d}s(t)={\tau }_s^{-1}[{\mu }_s-s(t)]\hspace{0.17em}\text{d}t+\sqrt{2D_s}\mathrm{d}{W}_t.$$ 2.4

Numerical integration of this equation closely reproduced the observed speed distributions during runs (electronic supplementary material, figure S5B).

Figure 3.

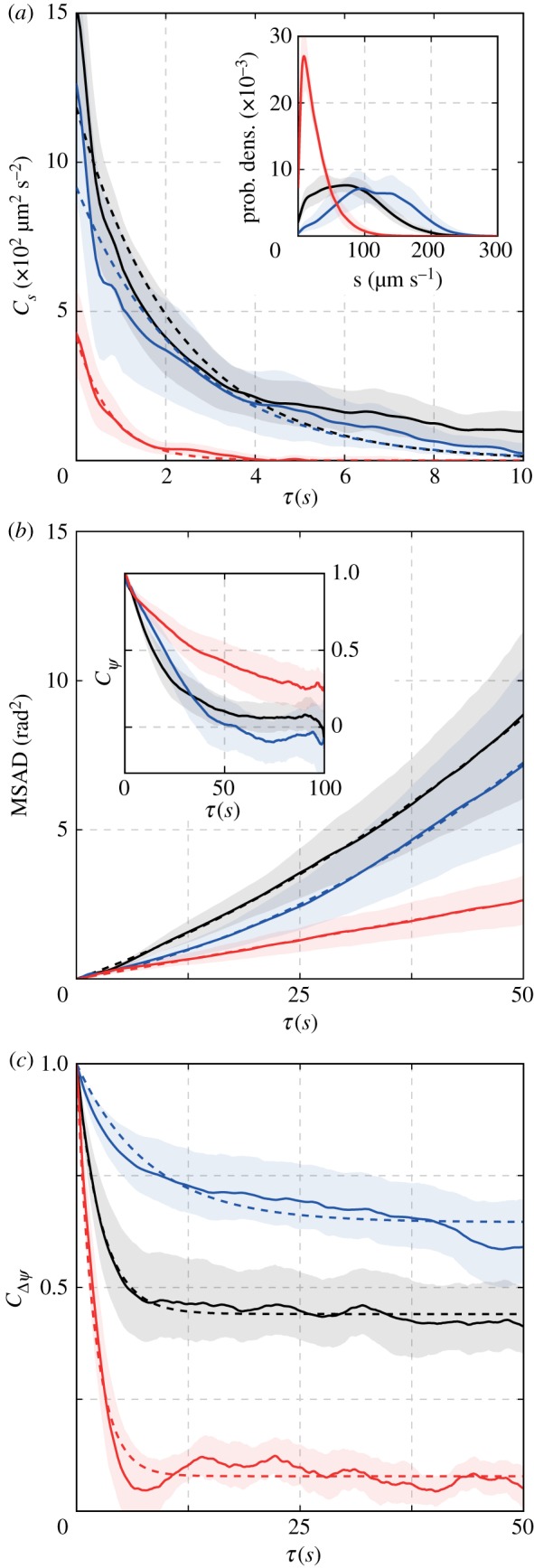
Statistical characterization of the motility dynamics. (a) The autocorrelation of the speed indicated that fluctuations decayed exponentially over a few seconds. (a, inset) Speed distributions for three exemplar strains. (b) The mean-squared angular displacement (MSAD) increased quadratically. (b, inset) The orientation autocorrelation function did not decay exponentially, with some worms demonstrating significant undershoots below zero. (c) The velocity alignment autocorrelation decayed exponentially over tens of seconds to a positive constant. In each plot, the ensemble averages for all individuals from the strains are shown with solid lines and trends are shown with dashed lines. Shaded regions indicate a 95% confidence interval. (Online version in colour.)

2.4. Diffusive turning with drift

The orientation ψ(t) captures turning dynamics that are independent of abrupt changes in bearing ϕ(t) due to reversals. To change orientation, C. elegans executes a combination of large, ventrally biased [41] sharp turns [18,24] and gradual ‘weathervaning’ [22], both of which contribute to randomization of orientation over time. This random walk in orientation was not purely diffusive: the orientation correlation $C_{\psi }(\tau )=⟨\cos [\psi (t+\tau )-\psi (t)]⟩$ does not decay exponentially (figure 3b inset; electronic supplementary material, S6B), and the mean-squared angular displacement, MSAD(τ) = 〈[ψ(t + τ) − ψ(t)]²〉, increases nonlinearly with time (figure 3b; electronic supplementary material, S6A).

We found that this nonlinear MSAD of ψ(t) could be well fitted by a quadratic function of the time delay τ: $\text{MSAD}(\tau )=k_{\psi \mathrm{rms}}^2{\tau }^2+2D_{\psi }\tau$, corresponding to a diffusion-and-drift model with root-mean-square (rms) drift magnitude $k_{\psi \mathrm{rms}}$ and angular diffusion coefficient $D_{\psi }$ (see electronic supplementary material for derivation). A non-zero drift magnitude $k_{\psi \mathrm{rms}}\ne 0$ indicates that in addition to purely random (diffusive) changes in orientation, there is an underlying bias (i.e. directional persistence) in the worms’ turning over 100 s windows, consistent with previous studies in larger arenas [23].

These observations lead to a simple model for the orientation dynamics that combines drift (approximated as a deterministic linear process over a 100 s window) with stochastic diffusion:

$$\text{d}\psi (t)=k_{\psi }\hspace{0.17em}\text{d}t+\sqrt{2D_{\psi }}\hspace{0.17em}\text{ d}{W}_t,$$ 2.5

where we set the drift magnitude $k_{\psi }=k_{\psi \mathrm{rms}}$ and dW_t represents increments of a Wiener process [40].

We note that while this model described well the orientation dynamics within 100 s windows, over longer time scales additional dynamics may be relevant. The magnitude of $k_{\psi }$ in our data (approx. 1° s⁻¹) was similar to that of weathervaning excursions reported for C. elegans navigating in salt gradients [22].

2.5. Forward and reverse runs

The observation that motion during runs switched abruptly between forward and reverse states (with Δψ ≈ {0°, 180°}, respectively; figure 2b,c; electronic supplementary material, S7A) suggested that reversals could be described as a discrete stochastic process. The manner in which reversals contribute to randomization of bearing over a time lag τ is captured by the autocorrelation function of Δψ(t), C_Δψ(τ) ≡ 〈cos (Δψ(t + τ) − Δψ(t))〉. We found that C_Δψ(τ) decayed nearly exponentially to a non-zero baseline (figure 3c; electronic supplementary material, figure S7C). This is the predicted behaviour for the autocorrelation function of the simplest of two-state processes (a ‘random telegraph process’):

$$P(T_{\mathrm{fwd}}>t)=\exp \left(\frac{-t}{{\tau }_{\mathrm{fwd}}}\right)$$ 2.6

and

$$P(T_{\mathrm{rev}}>t)=\exp \left(\frac{-t}{{\tau }_{\mathrm{rev}}}\right),$$ 2.7

in which the distributions of forward and reverse run intervals (T_fwd and T_rev) are completely determined by a single time constant (τ_fwd and τ_rev, respectively). The random telegraph process yields an autocorrelation function that decays exponentially as $C_{\mathrm{\Delta }\psi }(\tau )=C_{\mathrm{\Delta }\psi }(\mathrm{\infty })+(1-C_{\mathrm{\Delta }\psi }(\mathrm{\infty })){\mathrm{e}}^{-\tau /{\tau }_{\mathrm{RT}}}$ to a minimum value C_Δψ(∞) ≡ ((τ_fwd − τ_rev)/(τ_rev + τ_fwd))² with a time scale ${\tau }_{\mathrm{RT}}\equiv {({\tau }_{\mathrm{fwd}}^{-1}+{\tau }_{\mathrm{rev}}^{-1})}^{-1}$ [42]. Results obtained from fitting the autocorrelation function are consistent with those obtained from the distribution of time intervals between detected switching events (electronic supplementary material, figure S7). In principle, the forward and reverse states could be characterized by differences in motility parameters of our model other than these transition times, as forward and reverse motion are driven by distinct command interneurons in C. elegans [43,44]. However, we found that run speeds were nearly identical between forward and reverse runs (electronic supplementary material, figure S8). While we expect that this symmetry will be broken under some specific conditions, such as the escape response [45], the strong speed correlation between the two states motivates the assumption, adopted in our model, that reversals change only the bearing (by 180°) and the propensity to reverse direction, represented in our model by the time constants τ_fwd and τ_rev.

2.6. A model with independent speed, turning and reversals captures the ballistic-to-diffusive transition in nematode motility

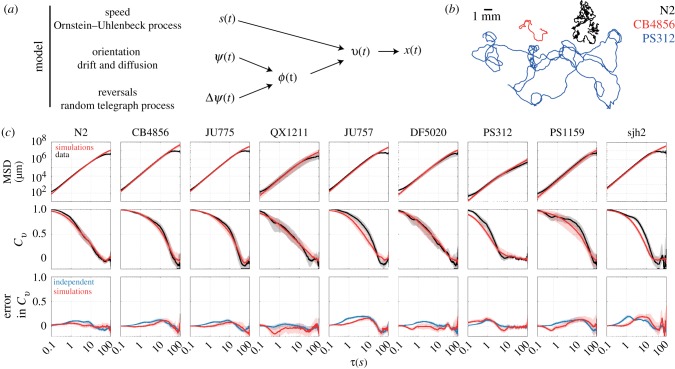
Given that the dynamics of the worm’s speed, turning and reversals could be described as simple stochastic processes, we asked whether combining them as independent components in a model of the worms’ random walk could sufficiently describe the observed motility statistics (figure 4a). We simulated trajectories of worms by numerically integrating equations (2.4)–(2.7) for the speed, orientation and reversal dynamics, respectively, which yields the worm’s velocity dynamics through equations (2.2) and (2.3), with Δψ(t) equal to 0° during forward runs and 180° during reverse runs. Simulations of this model using parameters fitted to individual worms produced trajectories that qualitatively resembled real trajectories and varied considerably in their spatial extent (figure 4b).

Figure 4.

A model consisting of independent speed (Ornstein–Uhlenbeck process), turning (drift and diffusion) and reversal dynamics (random telegraph process) quantitatively captures nematode motility. (a) Summary of the model. (b) Simulated trajectories for the three exemplar strains. (c) Statistical comparison of the data (black) and simulations (red), ensemble averaged across individuals for each strain. (c, top) The mean-squared displacement (MSD) was closely reproduced in all cases. (c, middle) The normalized velocity autocorrelation, C_v(τ)/C_v(0) (VACF), was less well captured. (c, bottom) The relatively small errors in the simulated VACF (red) can be traced to the assumption of independence in the dynamics of the speed, orientation, and velocity alignment (blue). Shaded regions indicate a 95% confidence interval. (Online version in colour.)

Next, we quantitatively assessed the performance of the model in reproducing the statistics of the observed trajectories over the time scale of 100 s, within which all strains completed the transition from ballistic to diffusive motion (figure 4c). We found that the model based on independent speed, turning and reversal dynamics closely reproduced not only the diffusivity of each strain but also the time evolution of the mean-squared displacement (〈[Δx(τ)]²〉) across the ballistic-to-diffusive transition (figure 4c, top). A closer inspection of the dynamics across this transition is possible by examining the velocity autocorrelation function (C_v(τ)), the time integral of which determines the slope of the mean-squared displacement through $(\text{d}/\text{d}t)⟨{[\mathrm{\Delta }x(\tau )]}^2⟩=2{\int }_0^{\tau }\mathrm{d}{\tau }^{\prime }{C}_{\mathit{v}}({\tau }^{\prime })$, a variant of the Green–Kubo relation [46,47]. The transition from ballistic to diffusive motion is characterized by the manner in which the normalized velocity autocorrelation C_v(τ)/C_v(0) decays over the time lag τ from unity (at τ = 0) to zero (as τ → ∞). We found that C_v(τ) varied considerably across strains, not only in the overall ballistic-to-diffusive transition time, but also in the more detailed dynamics of the autocorrelation decay over time (figure 4c, middle). Salient features, such as the transition time, of the measured velocity autocorrelation functions C_v,obs were reproduced closely by the simulated velocity autocorrelation functions C_v,model, but there were also subtle deviations in the detailed dynamics for a number of strains.

Given our model’s simplifying assumption that dynamics for s(t), ψ(t) and Δψ(t) are independent stochastic processes, we asked whether the remaining discrepancies between the simulated and measured velocity autocorrelation dynamics could be explained by violations of this assumption of independence. As a model-free assessment of the degree of non-independence, we first calculated the predicted velocity autocorrelation for the case that the dynamics of all three components are independent, C_v,indep(τ) = C_s(τ)C_ψ(τ)C_Δψ(τ), where C_s(τ), C_ψ(τ) and C_Δψ(τ) are the autocorrelation functions of the measured data for each of the components (see electronic supplementary material for derivation). We then compared the differences C_v,obs − C_v,indep (blue curve in figure 4c, bottom) and C_v,obs − C_v,model (red curve in figure 4c, bottom). Indeed, there were subtle differences both on shorter (approx. 1 s) and longer time scales (approx. 10 s). However, these errors for the simulated model were very similar to, or less than, those for the model-free prediction from the data under the assumption of independence (i.e. $C_{\mathit{v},\mathrm{obs}}-C_{\mathit{v},\mathrm{model}}\lesssim C_{\mathit{v},\mathrm{obs}}-C_{\mathit{v},\mathrm{indep}}$). These results demonstrate that modelling s(t), ψ(t) and Δψ(t) as independent stochastic processes provides a very good approximation to trajectory statistics across the ballistic-to-diffusive transition. The relatively subtle differences between the data and model arise primarily in instances where this assumption of independence between the three motility components breaks down. Consistent with these conclusions, inspection of cross-correlation functions computed from the data revealed that correlations between s(t), ψ(t) and Δψ(t) are largely absent, with only weak correlations between speed (s) and reversals (Δψ) in a subset of strains (electronic supplementary material, figure S9).

2.7. Variation of exploratory behaviour across species

The results presented in the previous sections demonstrate that a random-walk model with seven parameters describing independent speed, turning and reversal dynamics provides a good approximation of the worms’ motile behaviour over the approximately 100 s time scale spanning the ballistic-to-diffusive transition. The model parameters thus define a seven-dimensional space of motility phenotypes in which behavioural variation across strains and species can be examined. If components of behaviour were physiologically regulated or evolutionarily selected for in a coordinated manner, we would expect to find correlated patterns in the variation of these traits.

We fitted our model to the trajectory statistics of each individual worm and built a phenotype matrix of $106\hspace{0.17em}\text{worms}\times 7$ behavioural parameters (summarized in electronic supplementary material, tables S2–S4). The correlation matrix for these seven parameters, figure 5a, demonstrates that the strongest correlation were the forward and reverse state lifetimes (τ_fwd, τ_rev), followed by those describing speed and forward state life times (μ_s, τ_fwd). More broadly, there were extensive correlations among the model parameters, not only within the parameters of each motility component (speed, orientation and reversals) but also between those of different components.

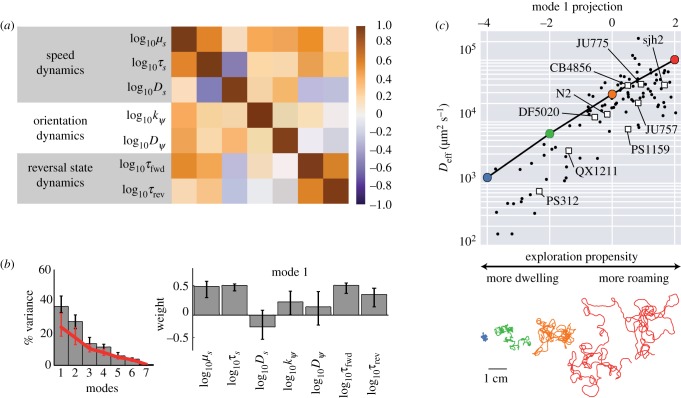
Figure 5.

Motility parameters co-vary along an axis controlling exploratory behaviour. (a) Correlation matrix of the behavioural parameters across the whole dataset. (b, left) Fraction of variance captured by each mode and the amount expected for an uncorrelated dataset (red line). (b, right) The components of the top eigenvector. (c) The effective diffusivity (top) and a 30 min trajectory (bottom, colours match points on graph) from simulations in which the projection onto the top eigenvector was varied; the principal mode can be used as an effective phenotype from a more dwelling to a more roaming behaviour. The projections and effective diffusivity of the measured trajectories are shown as black points, and the average of each strain is shown as a square. Mode projections are obtained by the dot product of the seven-dimensional vector of parameters obtained for each trajectory, and the principal eigenmode. (Online version in colour.)

We looked for dominant patterns in the correlations using principal component analysis [48] (figure 5b), uncovering a single dominant mode of correlated variation (figure 5b, left). Dominant modes are obtained by diagonalizing the correlation matrix. The eigenvalues of the correlation matrix capture the amount of variance of the variables that can be accounted by linear correlation, and therefore the magnitude of these eigenvalues organize the eigenvectors in terms of explained variance. For more details of the principal component analysis, see electronic supplementary material. This principal mode (mode 1), capturing nearly 40% of the total variation, described significant correlations among all the parameters except for D_s and $D_{\psi }$ (figure 5b, right; electronic supplementary material, table S5). We did not attempt to interpret higher modes since, individually, they either did not significantly exceed the captured variance under a randomization test (mode 3 and higher; see electronic supplementary material, and figure 5b, left) or were found upon closer inspection to be dominated by parameter correlations arising from fitting uncertainties (mode 2).

We used numerical simulations to determine the effects on motile behaviour of varying parameters along the principal mode. The measured trajectory phenotypes projected onto this mode fall in the range {− 4, 2}: the mode projections are not evenly distributed around the average phenotype at the origin. We performed simulations for parameter sets evenly sampled along this range, which largely reproduced the observed variation in the measured diffusivities D_eff as a function of the projection along the first mode. The agreement was particularly good at higher values (>−1) of the mode projection, but at lower values we noted a tendency for the D_eff from simulations to exceed that of the data. The latter discrepancy can be explained by elements of behaviour not captured by our model (see Discussion). Nevertheless, as illustrated by simulated trajectories (figure 5c, bottom), trajectories became more expansive as the mode projection increased, as did D_eff by nearly two orders of magnitude over the tested range. This suggested that the principal mode indicates exploratory propensity (figure 5c), and we confirmed that it is indeed more strongly associated with changes in D_eff than expected for randomly generated parameter sets (electronic supplementary material, figure S10). Interestingly, this mode of variation we found across individual phenotypes is reminiscent of ‘roaming’ and ‘dwelling’ behavioural variability that has been shown within individuals across time, in C. elegans [28,32] as well as other organisms [49,50].

2.8. Specialized and diversified behavioural strategies across strains

The principal behavioural mode discussed in the preceding section was identified by analysing variation across all individual worms measured in this study, coming from diverse strains and species that differ in their average behaviour (see electronic supplementary material, tables S2–S4). How does the variability among individuals of a given strain compare to differences between the average phenotypes of strains/species? On the one hand, each strain might be highly ‘specialized’, with relatively small variation within strains as compared to that across strains. On the other hand, strains might implement ‘diversified’ strategies in which genetically identical worms vary strongly in their behaviour. To address these two possibilities, we analysed the distribution of individual phenotypes within each strain, as well as that of the set of averaged species phenotypes.

For each measured individual, we computed the projection of its motility parameter set along the principal behavioural mode and estimated strain-specific distributions of this reduced phenotype (figure 6; electronic supplementary material, table S6). In principle, any detail in the shape of these distributions could be relevant for evolutionary fitness, but here we focused our analysis on the mean and standard deviation, given the moderate sampling density (less than or equal to 20 individuals per strain). Furthermore, we computed the principal-mode projection of the average phenotype of each species to define an interspecies phenotype distribution (figure 6).

Figure 6.

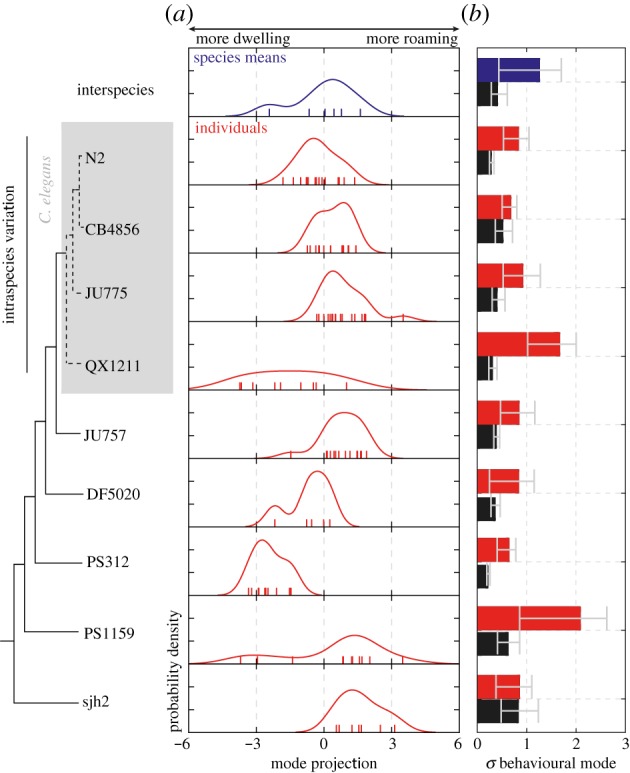
Variation of model parameters reveal specialized and diversified behavioural strategies across strains. (a) Distribution of the average phenotype for each species (interspecies variation, blue) or individuals within a strain (red). Note that the variation of individual phenotypes in some strains (e.g. QX1211, PS1159) is comparable in magnitude to that of interspecies variation. Observations are indicated with coloured ticks. (b) Comparison of the width of the phenotype distributions (coloured bars), quantified as the bootstrapped standard deviation of the data points in (a), with the uncertainty in the determination of the phenotype (black bars), quantified as the standard deviation of individual phenotype determinations over bootstrapped 100 s time windows. Error bars correspond to 95% confidence intervals across bootstrap samples. (Online version in colour.)

Strains varied considerably in both the position and breadth of their phenotypic distributions along the principal behavioural mode. Remarkably, variation across individuals within each strain was comparable in magnitude to that for the set of average phenotypes across species (figure 6). Some strains were specialized towards roaming or dwelling behaviour, such as CB4856 and PS312, respectively, with a strong bias in their behaviour and comparatively low individual variability. Others, such as QX1211 and PS1159, appeared more diversified with an intermediate average phenotype and higher individual variability. These considerable differences in phenotype distributions across strains reveal the evolutionary flexibility of population-level heterogeneity in nematodes, and suggest a possible bet-hedging mechanism for achieving optimal fitness in variable environments [51,52].

In assessing such variability of phenotypes, it is essential to ask how uncertainty in the determined parameters (obtained from model fits) contributes to the observed variability in phenotypes. We, therefore, computed the contribution of uncertainties in the individual phenotype determination by bootstrap resampling of the 100 s windows of each individual’s recorded trajectory (see electronic supplementary material). The uncertainties thus computed reflect contributions from both parameter uncertainties in curve fitting of data, as well as temporal variability in an individual’s parameters over time scales longer than the window size (100 s). With the exception of two strains (sjh2 and CB4856), this measure of uncertainty accounted for less than half of the individual variation within each strain (figure 6b). These findings support the view that the phenotypic variation estimated in the current analysis largely represented stable differences in individual behaviour.

3. Discussion

We have presented a comparative quantitative analysis of motile behaviour across a broad range of strains and species of the nematode phylum, ranging from the laboratory strain C. elegans N2 to Plectus sjh2 at the base of the chromadorean nematode lineage. Despite the vast evolutionary distances spanned by strains in this collection [53], we found that a behavioural model described by only seven parameters could account for much of the diversity of the worms’ translational movement across the approximately 100 s time scale spanning the ballistic-to-diffusive transition. This simple model provides a basis for future studies aiming to capture more detailed aspects of nematode behaviour, or to connect sensory modulation of behaviour to the underlying physiology. More generally, our results demonstrate how quantitative comparisons of behavioural dynamics across species can provide insights regarding the design of behavioural strategies.

3.1. The minimal model: what does it capture, and what does it miss?

We focused on a high-level output of behaviour—translational and orientational trajectory dynamics—and sought to build the simplest possible quantitative model that could capture the observed behavioural statistics. We found that a model with only three independent components—(1) speed fluctuations that relax to a set point on a time scale of a few seconds, (2) orientation fluctuations with drift and (3) stochastic switching between forward and reverse states of motion—describes well, overall, the trajectory statistics of all tested nematode species across the ballistic-to-diffusive transition (figure 4).

Notably, we have not included explicit representations of some reorientation mechanisms that have been studied in the past, such as the deep turns (omega- and delta-turns) [18,24], or the combination of such turns with reversals (pirouettes) [25]. In our data, we find that the timings of the initiation and termination of reversals, which would both count as runs in the pirouette description, follow exponential distributions with similar time constants as previously reported for the pirouette run distribution. While omega and delta turns must indeed be mechanistically distinct from gradual turns, we have chosen here not to explicitly model their occurrence since orientation changes in our trajectory data were adequately described by a continuous diffusion–drift process (figures 3b; electronic supplementary material, S6A). It is possible, however, that explicit representations of pirouettes and/or omega turns would be important in other experimental scenarios, e.g. those that include navigation in the presence of gradient stimuli.

In our model, ‘roaming’ and ‘dwelling’ were not assigned discrete behavioural states (as was done e.g. in [28,31,32]), but instead emerged as a continuous pattern of variation among motility parameters describing the worm’s random walk. However, robust extraction of motility parameters required pre-filtering of trajectory data that likely biased them towards more ‘roaming’ phenotypes (see electronic supplementary material), which we believe account for the noted tendency of model simulations to overestimate D_eff that was more pronounced for trajectories at the ‘dwelling’ end of the spectrum (figure 5c).

In its current form, our simple model does not account for possible correlations between the dynamics of the three motility components (speed, orientation and reversals). Indeed, at least weak correlations do exist between the components (electronic supplementary material, figure S9). Comparisons of simulated versus measured trajectories demonstrated that the effects of such correlations on the motility statistics are small but detectable (figure 4c). The differences were most significant for the velocity-autocorrelation dynamics on an approximately 10 s time scale, and were similar to those for model-free predictions obtained by combining component-wise correlation functions under the assumption of independence. Discrepancies on this intermediate time scale occurred most often in fast-moving strains that frequently approached the repellent boundary. Therefore, we suspect that the discrepancy arises from a stereotyped sequence, such as the escape response [45], that introduces temporal correlations between speed changes, turning and reversals.

While here we have focused on the transition to diffusive motion, some recent experiments suggest that C. elegans might engage in superdiffusive behaviour on time scales longer than 100 s [23,33]. Superdiffusive behaviour could arise from non-stationarities in motile behaviour, such as the roaming/dwelling transitions on time scales of several minutes [32]. Another mechanism for superdiffusion is directed motility [23] in response to external stimuli such as chemical or thermal gradients. In such environments, nematodes are known to use at least two distinct mechanisms for navigation [22,25] and the model here could be extended by studying the dependence of motility parameters on environmental statistics.

Information about the body shape can be incorporated to build a more complete behavioural model that also includes dynamics hidden by centroid behaviour [38,54]. Indeed, work by Brown et al. showed that a rich repertoire of dynamics can be identified as temporal ‘motifs’ in the postural time series of C. elegans and used to classify mutants with high discriminatory power [55]. We have found that all of the species tested here can also be described with a common set of postural modes (not shown), suggesting future directions on the evolutionary space of postural dynamics.

3.2. The exploratory behavioural mode: variability and its physiological basis

While we found that a single behavioural model could be used to characterize nematode motility across the chromadorean lineage, the parameters of the model varied extensively from strain to strain. Quantitatively, about 37% of the variation corresponded to a correlated change in the parameters underlying the timing of forward and reverse runs and the dynamics controlling speed and turning (figure 5b). We find that this principal mode of variation is associated with strong changes in exploratory propensity, as characterized by D_eff (figure 5c). This pattern of parameter variation drove a change from low-speed short runs to high-speed long runs, resembling the canonical descriptions of roaming and dwelling in C. elegans [32].

Roaming and dwelling are thought to represent fundamental foraging strategies reflecting the trade-off between global exploration and local exploitation of environmental resources [56]. Recent work has suggested that such archetypal strategies can be recovered by quantitatively analysing the geometry of phenotypic distributions in parameter space [31,34]. The motility phenotypes we found in the present study were biased along one principal dimension, with the extremes corresponding to roaming and dwelling behaviours. This observation compels us to suggest that an exploration–exploitation trade-off is the primary driver of phenotypic diversification in the motility of chromadorean nematodes in the absence of stimuli. Interestingly, a recent study on the motility of a very different class of organisms (ciliates) yielded a similar conclusion [50]: across two species and different environments, the diversity of motility phenotypes was found to be distributed principally along an axis corresponding to roaming and dwelling phenotypes. The emergence of roaming/dwelling as the principal mode of variation in such disparate species underscores the idea that the exploration–exploitation trade-off is a fundamental constraint on biological motility strategies.

A surprising finding in our study was that, for a majority of strains, the extent of behavioural variability across individuals within a strain was comparable to that for variation of phenotypes across species (figure 6). In slowly changing environments, the most evolutionarily successful species are those that consistently perform well in that environment. This can be achieved by evolving a specialized, high fitness phenotype that varies little among individuals (such as with PS312 and sjh2). However, increased phenotypic variability among individuals can improve fitness in more variable environments if some individuals perform much better in each condition—a so-called bet-hedging strategy [51,52]. The large variability we observed among individual phenotypes within each strain might reflect such a bet-hedging strategy in nematode exploratory behaviour.

The observation that the variation among genetically identical individuals can be comparable to that between disparate species raises the intriguing possibility that there exist conserved molecular and/or physiological pathways driving diversification of spatial exploration strategies. Analogous variation in exploratory behaviour was also detected in an analysis of non-stationarity in the behaviour of wild-type and mutant C. elegans under various nutritional conditions [31]. Physiologically, protein kinase G (PKG) signalling and DAF-7 (TGF-β) signalling from the ASI neuron are thought to be major mechanisms controlling roaming and dwelling in C. elegans [28,31]. PKG signalling is also involved in controlling foraging in Drosophila and other insects as well as many aspects of mammalian behaviour [57,58]. Flavell et al. also elucidated a neuromodulatory pathway involving serotonin and the neuropeptide pigment dispersing factor controlling the initiation and duration of roaming and dwelling states [32].

Perturbations to the molecular parameters of such pathways underlying global behavioural changes might provide a mechanism for the observed correlated variations at the individual, intra- and inter-species levels. The identification of such conserved pathways affecting many phenotypic parameters is of fundamental interest also from an evolutionary perspective, as they have been proposed to bias the outcome of random mutations towards favourable evolutionary outcomes [59,60]. Our simple model provides a basis for future investigations to uncover conserved mechanisms that generate behavioural variability, by defining a succinct parametrization of behaviour that can be combined with genetic and physiological methods.

Data accessibility

Trajectory data and scripts used to process, analyse and build the figures can be obtained from https://figshare.com/articles/Helms2019/7770953.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by NWO/FOM and the Paul G. Allen Family Foundation.