Anomalous water dynamics in brain: a combined diffusion magnetic resonance imaging and neutron scattering investigation

Abstract

Water diffusion is an optimal tool for investigating the architecture of brain tissue on which modern medical diagnostic imaging techniques rely. However, intrinsic tissue heterogeneity causes systematic deviations from pure free-water diffusion behaviour. To date, numerous theoretical and empirical approaches have been proposed to explain the non-Gaussian profile of this process. The aim of this work is to shed light on the physics piloting water diffusion in brain tissue at the micrometre-to-atomic scale. Combined diffusion magnetic resonance imaging and first pioneering neutron scattering experiments on bovine brain tissue have been performed in order to probe diffusion distances up to macromolecular separation. The coexistence of free-like and confined water populations in brain tissue extracted from a bovine right hemisphere has been revealed at the micrometre and atomic scale. The results are relevant for improving the modelling of the physics driving intra- and extracellular water diffusion in brain, with evident benefit for the diffusion magnetic resonance imaging technique, nowadays widely used to diagnose, at the micrometre scale, brain diseases such as ischemia and tumours.

1. Background

Brain tissues are heterogeneous systems containing numerous compartments (glia cells, neurons, myelin sheaths and extracellular space) of different shape and size separated by impermeable and semipermeable membranes. The major tissue constituent is water (greater than 70%) and physiological differences in water content are commonly found between brain regions, reflecting the differences in cell packing [1].

Water plays a key role in all life processes, among them the regulation of the ion concentration gradients across the membranes needed for the conduction of the nerve impulse [2]. Water molecules, interacting with cell membranes during their random motion, can also be used as a tool to probe tissue structure at microscopic scale, and thus to provide unique information on the functional architecture of the tissue. This is why research over the last 30 years has focused on the development of the diffusion magnetic resonance imaging (dMRI) technique which uses water diffusion as probe for revealing and characterizing a number of brain pathologies on the micrometric scale (ischemia, tumours, etc.) [3–6].

While motion in bulk water is random, the diffusion process is isotropic and the displacement probability is normally distributed, water diffusion in the brain is not a purely random process. Tissue microstructure provides barriers and creates compartments that limit molecular movement, leading to anisotropic diffusion patterns [7].

A typical dMRI diffusion measurement requires a few tens of milliseconds (approx. 50 ms). During this time, the water molecules diffuse within a distance which is of the order of micrometres (from Einstein's diffusion equation $⟨x^2⟩=2D{T}_{\mathrm{d}},$ with $⟨x^2⟩$ the mean free quadratic displacement, T_d the diffusion time and D the water diffusion coefficient, known to be approx. 10^–3 mm² s^–1 in brain tissue at body temperature) [3]. On the other hand, approximately 90% of cellular elements in the brain are smaller than or of the order of 1 µm: lipids 3–5 nm, cell membrane 10 nm, proteins 5–10 nm, ribosomes 20–30 nm, mitochondria 0.5–1 µm, axons 1–3 µm [8], dendrites 0.9 µm on average, ending up to characteristic cell body sizes of 1–10 µm, occupying only 12% of the cortex volume [9]. Thus, intrinsic cellular heterogeneity is generally not resolved by dMRI: the measured diffusion coefficient is an average over the heterogeneous cellular structure at this scale. Indeed, the overall signal observed with dMRI in an image volume element (voxel), at millimetre resolution, results from the integration of all the microscopic (micrometre) displacements of the water molecules present in this voxel. Thus, in order to bridge the gap between the micrometre and the millimetre length scales, it is essential to model the physics piloting water diffusion. In this context, deviations from a pure Gaussian-like water diffusion profile, characteristic for bulk water, have so far been systematically observed. A number of different approaches have been proposed in the literature [10], such as:

• 1)Mono-exponential decay [10], which allows determining an apparent diffusion coefficient (ADC), a phenomenological parameter largely used as biomarker for the diagnostics of pathologies such as stroke.
• 2)Bi-exponential behaviour assigned to the superimposition of the signals arising from two water diffusion pools [11,12], with slow exchange between them, during the diffusion measurement time T_d. The pools belong or not to different physical compartments (intra- and extracellular).
• 3)Deviation from Gaussian behaviour in terms of an excess of kurtosis, a mathematical tool that models heterogeneities in the diffusion process [13,14]. Even though such approach does not directly offer biophysical insight, it allows estimation of some empirical parameters related to tissue characteristics that might change with disease progression [15].
• 4)Characterization as anomalous diffusion in terms of a stretched exponential model [16]. It is particularly sensible to pathological alteration like human gliomas due to their higher degree of histological heterogeneity with respect to the normal brain tissue [17]. However, a formal link between the anomalous exponent and the biological environment characteristics has not yet been clarified.

Using neutron scattering (NS) technique, a space-resolved spectroscopy technique, the probed distance is reduced to the sub-micrometre regime, i.e. to the scale of the macromolecular separation. From the elementary building blocks of the cell (proteins, membranes, etc.) [18] to bacteria and in vivo cells [19,20], NS spectroscopy has proven to be unique in pinpointing proton dynamics at atomic scale in biological compounds regardless of the macromolecular complexity involved. In particular, the so-called incoherent NS spectroscopy has contributed with important experimental results to a better understanding of molecular dynamics in biological systems, especially of water dynamics in different biological environments. The technique provides information on atomic molecular dynamics on the picosecond to nanosecond time scale, which is essential to biological function. Indeed, thermal neutrons provide wavelengths of a few angstroms, which correspond to interatomic distances. In addition, the neutron–matter interaction has no damaging effects, making neutrons an ideal probe for the study of the dynamical properties of biological samples. The NS technique sheds light on proton dynamics averaged over all the nuclei present in the sample, weighted by the corresponding scattering cross section and the amount of a specific atom. The NS signal is especially sensitive to hydrogen nuclei, due to its large incoherent cross section, thus perfectly suited for water dynamics.

Within NS, quasi-elastic neutron scattering (QENS) in particular allows one not only to distinguish populations with different dynamics but also to inform on specific motion the H experience, providing a detailed characterization in terms of spatial and diffusion properties. Moreover, QENS is able to describe in detail translational and rotational movements of the H belonging to different water pools as shown in a recent paper from our group [21], where the dynamical properties of water from different living cells were compared.

In this paper, we present detailed insight into water dynamics in bovine brain tissue obtained through complementary dMRI and QENS experiments. For an easier reading of the paper, the basic concepts of dMRI and NS techniques are reported in appendix A.

2. Methods

2.1. Tissue extraction and sample preparation

Fresh post-mortem bovine brains were obtained from the slaughterhouse and the brain tissue extracted at the Department of Animal Medicine, Production and Health of the University of Padova (Italy). The brains were removed in two parts: the cerebellum and the cerebrum, then separated at the junction of the pons and the cerebral peduncle. A small block (0.5 cm × 0.5 cm) of the right hemisphere (RH) was extracted from the cerebrum and frozen at −160°C in liquid nitrogen vapour and divided in two prior to the dMRI and NS experiments.

2.2. Diffusion magnetic resonance imaging experiments

dMRI measurements of RH tissue at room temperature were performed at the MRI Facility of Grenoble (IRMaGe, France) using a 4.7 T Biospec 47/40 USR system (Bruker, Ettlingen, Germany), capable of delivering gradient strengths of 600 mT m⁻¹ in 120 µs, and a volume transmit/receive coil. T2 (transverse relaxation time) control scans were performed using a Carr Purcell Meiboom Gill sequence (64 spin-echoes between 5 and 320 ms, TR = 2000 ms, field of view = 70 × 70 mm², matrix = 128 × 96, slice thickness = 3 mm, two averages).

Diffusion-weighted images were acquired using a spin-echo, echo-planar, sequence (TE = 23.2 ms, δ = 7 ms, T_d = 11 ms, TR = 2000 ms, same geometry as that of the T2 sequence above, matrix = 64 × 48, two averages). Twelve reference images (b = 0.5 s mm⁻², where b is the diffusion weighting factor) were followed by diffusion-weighted images. Forty-eight values of b, varying between 100 and 9400 s mm⁻², were applied in each of the three gradient orientations (a total of 144 diffusion-weighted images). The total scan time was about 14 h.

2.3. Neutron scattering experiments

50 µm thick slices of RH were cut at −20°C using a cryotome (Thermo Scientific, Shandon Cryotome SME Cryostat, France) at the histological laboratory of the Biomedical Facility of the European Synchrotron Radiation Facility (ESRF, Grenoble, France). The thickness of the tissue slices was chosen in order to limit neutron absorption from water. The sample was closed in a vacuum-tight pure aluminium flat sample holder.

A first neutron diffraction experiment was realized at room temperature on the cold neutron three-axis spectrometer IN14 at the Institut Laue Langevin (ILL), Grenoble. The instrument was used in elastic mode with wavelength λ = 4.2 Å. The monochromatic beam was obtained by diffracting the incident cold neutron beam on a vertically focused PG002 monochromator. A N₂-cooled Be-filter was installed before the sample to suppress higher-order contamination from the monochromator. 10′ collimation before and after the sample ensured an accessible region of momentum transfer Q down to 0.06 Å^–1.

A second neutron diffraction experiment was performed at room temperature on the small momentum transfer diffractometer D16 at ILL. To enhance the coherent signal, the tissue was left equilibrating in D₂O atmosphere for 30 min. As the coherent scattering cross section of D is larger than that of its natural isotope H (σ_cD = 5.6 barn; σ_cH = 1.76 barn), this isotope exchange enhances the diffraction contrast. The instrument was operating with the MILAND ³He position-sensitive detector. The monochromator was set to deliver a wavelength λ = 4.75 Å with Δλ/λ = 0.01 full width at half maximum (FWHM) and the sample-to-detector distance was set to 950 mm. Data were (a) corrected for detector efficiency, (b) normalized to incident neutron flux and (c) integrated vertically in the range −1.2° < 2 θ_vert < 2.8°.

QENS experiments were carried out at room temperature on the high-resolution time-of-flight spectrometer IN5 at the ILL. For the present work, we chose the instrument set-up configuration at λ = 10 Å, corresponding to an energy resolution of δE ∼ 10 µeV FWHM (which is equivalent to 10^–10 s) and Q < 1.1 Å^–1 (equivalent to 6 Å). Consecutive short QENS scans were acquired (15 min each) and compared before binning. During the measured lapse of time (2 h), the scattering signal was stable, meaning that no variation was observed in proton dynamics. Data correction was achieved by normalization of the raw data to the neutron flux, subtraction of the background given by the spectrum of an empty cell, and finally normalization to a vanadium spectrum, providing the relative detector efficiency and the instrument resolution.

Based on previous elastic NS and QENS results on dependence of water dynamics in RH upon the variability of experimental conditions [22,23], we are confident in the experimental approach used in this study.

3. Results

3.1. Diffusion magnetic resonance imaging experiments

The signal decay (SI) of the RH versus b, normalized to the signal measured at b = 0.5 s mm⁻² (SI₀) and averaged (arithmetic mean) over the three orthogonal directions (x, y and z), is shown in figure 1; for comparison, the signal of deionized water (Milli-Q) is reported, in which no effects of confinement are expected. The curves represent the fits using the diffusion models: mono-exponential decay (1), bi-exponential decay (2), excess of kurtosis (3) and stretched exponential (4) (see appendix A for details). The resulting diffusion coefficients are reported in table 1. In the region at high b values, discrepancies are clearly observed and the (1) and (4) theoretical signals deviate considerably from the experimental curve.

Figure 1.

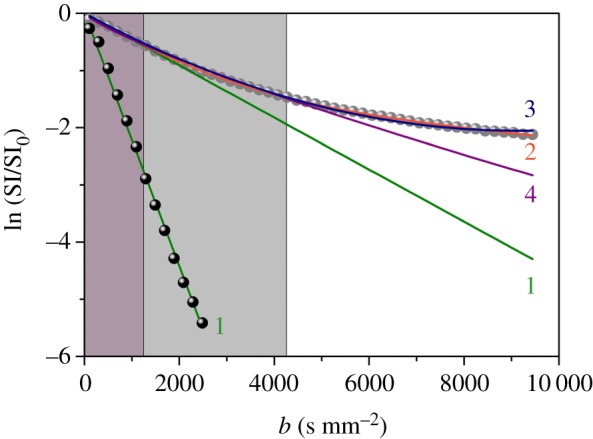
Signal decay of the RH (grey symbols) and free Milli-Q water (black symbols), normalized to the signal decay at b = 0.5 s mm⁻² and averaged over three orthogonal gradient directions. The curves represent the fits using different diffusion models: mono-exponential decay (1, equation (A 1)), bi-exponential decay (2, equation (A 2)), kurtosis excess (3, equation (A 3)), stretched exponential decay (4, equation (A 5)). The grey areas represent the regions where the mono-exponential (dark grey) and the stretched exponential (light grey) fits reproduce the experimental data with good agreement. (Online version in colour.)

Table 1.

Fitting parameters of RH evaluated using the different models and fitting regions (b_max). Units for ADC, D_fast, D_slow, D and DDC are expressed in [10⁻³ mm² s⁻¹], while b_max is expressed in [s mm⁻²]. Errors are reported in brackets.

	bi-exp [bmax = 9400]			kurtosis [bmax = variable]			stretched-exp [bmax = 4200]
mono-exp [bmax = 1300] ADC	fslow	Dfast	Dslow	bmax	D	K	DDC	γ
0.42 (0.01)	0.241 (0.007)	0.610 (0.008)	0.078 (0.003)	2000	0.48 (0.02)	0.7 (0.3)	1.9 (0.3)	0.79 (0.02)
				3000	0.49 (0.01)	0.85 (0.08)
				5000	0.491 (0.004)	0.86 (0.01)
				7600	0.467 (0.003)	0.774 (0.005)
				9400	0.448 (0.004)	0.730 (0.004)

While the free Milli-Q water is accurately described in terms of a mono-exponential decay, with ADC = 2.3(1)1 × 10⁻³ mm² s⁻¹, confirming the absence of confinement effects, the signal of the RH is best fitted, over the whole b range accessible, with a bi-exponential function. The mono-exponential decay fits the data for b values below 1300 s mm⁻², where the signal is less sensitive to confinement effects [24]. Considering the estimated ADC (0.4 × 10⁻³ mm² s⁻¹, table 1) and the T_d used in this work (11 ms), the averaged diffusion distance $⟨x^2⟩$, i.e. the distance travelled by the water molecules within the given diffusion time, is estimated from Einstein's equation to be 4 µm, thus of the order of cell body sizes in brain.

In figure 2a, we report the residues of the RH fit, defined as the discrepancy between the fit and the experimental data, in the framework of the kurtosis model, using different fitting ranges. It is clear that the kurtosis model only reproduces the ln(SI/SI₀) behaviour relatively well for b_max < 5000 s mm⁻², whereas the bi-exponential fit describes the data over the whole b-range (figure 2b). We, therefore, assume, as the best hypothesis, the presence of confinement effects and we conclude the coexistence of two water populations characterized by different degrees of interaction with the ‘barriers'. The size of each population (f_fast/slow) may be estimated by the bi-exponential fit. In RH (table 1), 76% (f_fast = 1 − f_slow) of the water molecules behave as ‘free-like', while the remaining 24% are influenced by confinement effects with a diffusion coefficient reduced by one order of magnitude. On the other hand, the free-like water molecules of the tissue show a diffusion coefficient which is much smaller than the one found in bulk water, accurately fitted using a mono-exponential decay (table 1).

Figure 2.

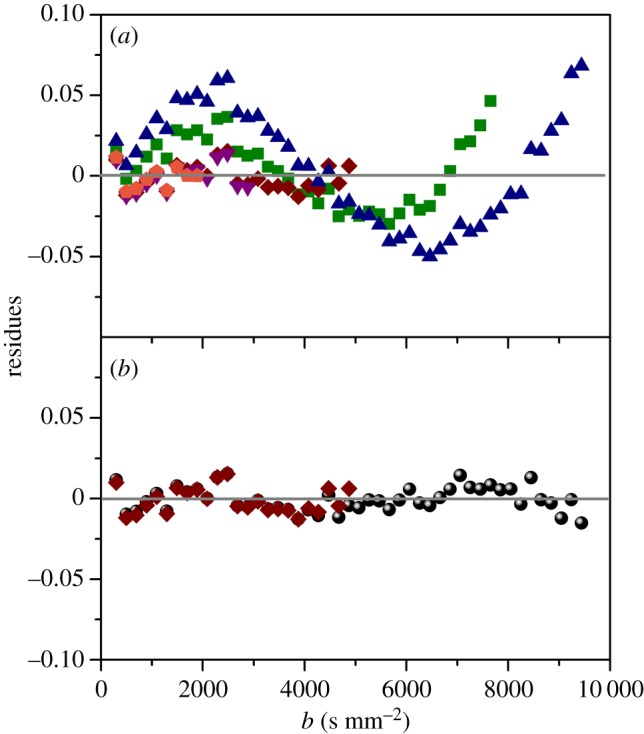
(a) Residues of the RH calculated from the fit using the kurtosis model. The different symbols represent the fits using b_max = 2000 s mm⁻² (pentagons), 3000 s mm⁻² (down triangles), 5000 s mm⁻² (diamonds), 7600 s mm⁻² (squares) and 10000 s mm⁻² (triangles). (b) Comparison between the residues estimated using the kurtosis (with b_max = 5000 s mm⁻², diamonds) and the bi-exponential (circles) models. (Online version in colour.)

3.2. Neutron scattering experiments

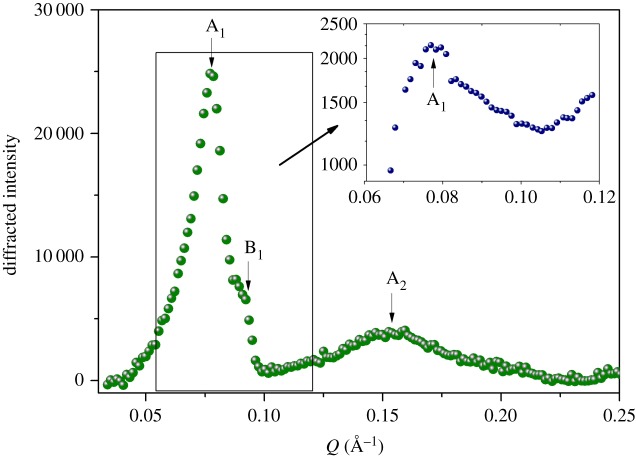
Neutron diffraction experiments were performed on RH to evaluate the level of tissue structuration. In figure 3, we report the diffraction patterns of RH measured on D16 and on IN14 (inset) at ILL. Both experiments reveal a mean diffraction peak A₁ at Q = 0.077 Å⁻¹. This peak is more prominent after H–D exchange on D16, as well as the not-resolved feature observed at B₁ position (Q = 0.092 Å⁻¹), appearing as a broad shoulder in the IN14 spectrum.

Figure 3.

Diffraction patterns of RH measured at 300 K on D16 and IN14 (inset) at ILL. (Online version in colour.)

The first main peak (A₁) can be identified as the strong second diffraction order (corresponding to repeat distance d = 160 Å) commonly observed for the structure of the lamellar myelin sheath [25–28]. Peak A₂ (Q = 0.148 Å⁻¹) corresponds to a fourth-order reflection, while the arrow at B₁ shows the poorly resolved additional first/second-order Bragg peak at Q = 0.092 Å⁻¹ (d = 68 Å).

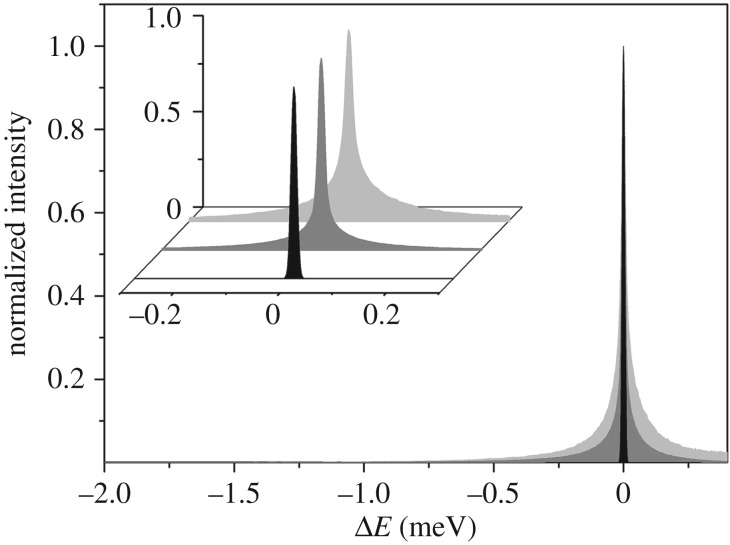
In figure 4, we report the normalized QENS spectra of RH measured on IN5, integrated over the range of Q = 0.33–0.96 Å⁻¹. To avoid static contribution, the low Q-value spectra (less than or equal to 0.26 Å⁻¹) were not included here, or in what follows, as they are affected by the before mentioned Bragg peaks. For comparison, the same spectrum is reported for the bulk water measured at the same experimental conditions. The RH yields a much broader peak than the resolution of the instrument, indicating relaxational motions falling within the time scale accessible on IN5. From the average composition of the RH tissue, we estimate the incoherent scattering signal from the water to be approximately 80% of the total intensity. Therefore, the main contribution to the QENS spectra is attributed to water diffusion.

Figure 4.

Q-summed (0.33–0.96 Å⁻¹) incoherent scattering intensity of RH (dark grey) and bulk water (light grey) measured on IN5 at 300 K. The instrumental resolution is shown in black. Inset: zoomed area. (Online version in colour.)

The Q-dependent QENS data were fitted, in the energy range from −3.0 to 0.1 meV, using equation (A 9), which allows the simultaneous fit of all the collected spectra (see appendix A). Figure 5 shows an example of a QENS-fitted spectrum at the reference value of Q = 0.69 Å⁻¹. The best-fit parameter values are reported in table 2. While the bulk-water diffusion coefficients, D, estimated through NS and dMRI agree, for water in the RH tissue they do not. Although the existence of two water pools observed at the micrometre scale is confirmed at the atomic scale, differences are found in the slow/fast population sizes. The effect of pools' exchange, too slow for NS to be detected, contrarily to dMRI, may partially account for it. Moreover, the D values observed with neutrons are significantly higher than those observed with dMRI. This discrepancy may be explained by looking at the variation of the line-width of the translational diffusive contribution as a function of Q² (figure 6). After a linear variation in the low Q region, the curves deviate from Fick's law, tending asymptotically to constant value 1/τ_fast/slow, where τ is the residence time. The deviation at high Q from free long-range diffusion is a sign of partial confinement, and the non-zero residence time suggests the interaction of the water molecules with the cellular components.

Figure 5.

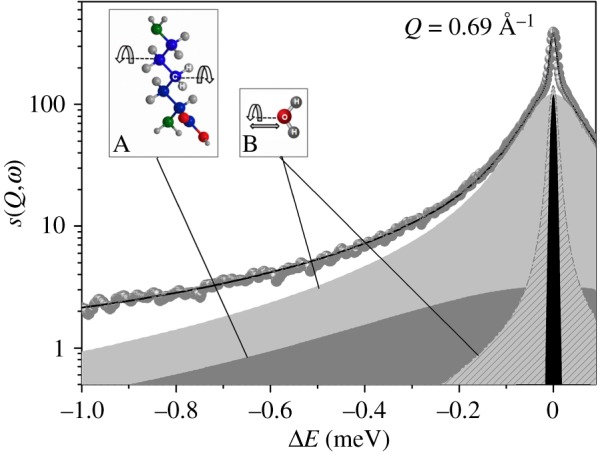
Example of a QENS spectrum at Q = 0.69 Å⁻¹ measured on IN5 at 300 K. Symbols = experimental data; solid line = total fit; black = elastic peak; dark grey = broad Lorentzian S_CH2(Q,ω); light grey = bulk-like water (fast) component; grey pattern = restricted water (slow) component. Both fast and slow components are convolutions of translational and rotational diffusion scattering functions. Inset A: typical rotational motion of CH₂ groups observed in protein amino acids and lipids; inset B: rotational and translational motions experienced by water molecules. (Online version in colour.)

Table 2.

Values of the parameters, obtained fitting QENS spectra with equation (A 7). Units for D_Tfast, D_Tslow, D_Rfast and D_Rslow, are expressed in [10⁻³ mm² s⁻¹], while τ_fast and τ_low are expressed in [ps] and Γ_CH2 in [meV]. The associated errors (in brackets) have been estimated using the Minuit minimization algorithm and the Minuit processor MINOS.

	f	pfast	pslow	pCH2	DTfast	DRfast	τfast	DTslow	DRslow	τslow	ΓCH2
RH	0.040 (0.002)	0.736 (0.002)	0.123 (0.002)	0.100 (0.002)	2.5 (0.01)	2.3 (0.2)	1.8 (0.1)	0.20 (0.02)	1.10 (0.05)	6.7 (0.3)	0.39 (0.02)
bulk watera					2.5	2.3	0.9
bulk waterb					2.3		1.1

^aDiffusion coefficient of bulk water determined experimentally from a scan of pure water (D_w) measured at 300 K on IN5 at the same energy resolution.

^bDiffusion coefficient of bulk water found in the literature [50] for T = 298 K.

Figure 6.

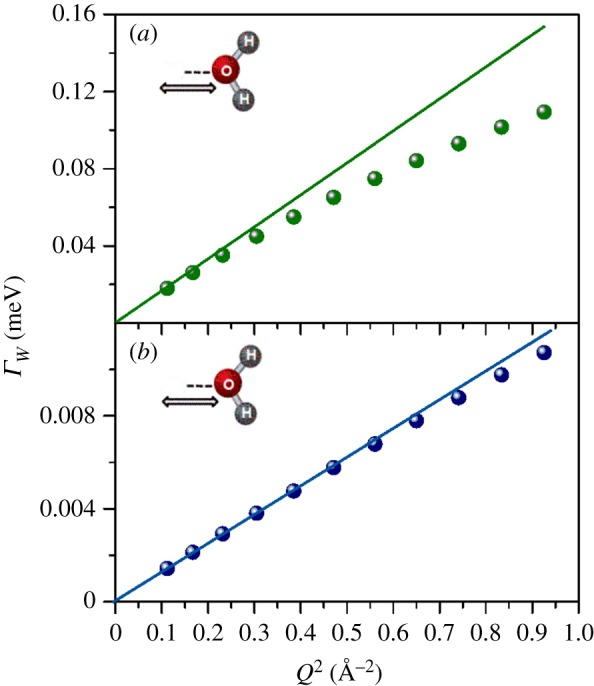
FWHM of the translational motion for bulk-like (a) and confined (b) water components, as a function of Q². Fick's Law functions (solid lines), describing the bulk-free Gaussian-like diffusion processes, have been reported in both graphs. (Online version in colour.)

4. Discussion

The reduction of the ADC in brain tissue compared with free-water diffusion has often been tentatively explained in terms of high viscosity, macromolecular crowding and restriction effects in the intracellular space, and tortuosity effects for water diffusion in the extracellular space [29]. Experimental evidence, however, has demonstrated the opposite [30–32], suggesting that the cellular components responsible for the reduced diffusion coefficient in biological tissues are much smaller than the diffusion length currently used in dMRI [33,34].

At high b values, molecules that experience more restricted diffusion dominate the dMRI measurement because the signal from the less restricted molecules has been attenuated. Conversely, at low b values, the dMRI signal contains both restricted and free contributions [35]. Combined oscillating gradient spin-echo and standard pulse gradient spin-echo sequence [36] suggest that water dynamics at short diffusion times (approx. 2–4 ms) is mainly affected by the local intrinsic viscosity [15,16,36,37], while at longer diffusion times (approx. 10–30 ms) it is predominantly affected by the presence of obstacles [38]. Moreover, Yeh and co-workers [39] have shown that D_fast/slow are not affected by cell swelling (i.e. an increase in extracellular tortuosity or intracellular restriction effects), suggesting that the decrease of the ADC is mainly driven by variations in the fast and slow volume fractions.

Our results confirm that the b-dependent dMRI signal attenuation in RH cannot be correctly described by a single exponential decay. Among the diffusion models tested in figure 1, we consider the bi-exponential signal decay as closest to the experimental data.

The problem with the bi-exponential model is to assign a biological/physiological nature to the two water pools. The most straightforward interpretation would be to associate the slow and fast water pools to the intra- (F_intra) and extracellular (F_extra) water fractions, respectively. However, the natural distribution of water in tissue is known to be the opposite (F_intra ∼ 80% and F_extra ∼ 20%) [40,41]. Furthermore, theoretical and experimental findings support the idea that both slow and fast water pools may coexist in the intracellular compartment [42–44]. Therefore, we suggest that the slow diffusion process can rather be attributed to water molecules interacting with the cell membranes and associated cytoskeleton structures, while the fast diffusion component arises from the remaining, less restricted water found in both intra- and extracellular spaces.

Table 3 reports a list of D_fast and D_slow values from the literature [11,12,33,45–48] and those obtained experimentally in this work using the bi-exponential decay model. The results we obtained from dMRI post-mortem reveal diffusion coefficients which are smaller than in vivo values, but consistent with previous post-mortem estimates [49]. It must also be noted that in the case of oocytes (female germ cells) the presence of a strong intracellular lipid signal might bias the image data obtained at very high b values. Indeed, the ¹H signal from a given voxel at high b values may originate from lipid protons rather than from water protons [45]. Even though a specimen-specificity may partially explain the difference in D_fast and D_slow (bovine versus human and rat), we believe that the discrepancy can be interpreted in terms of:

• —Brain tissue decomposition. Indeed, after somatic death brain tissue experiences autolysis, which, along with bacterial degradation, also causes tissue degradation affecting the tissue's structure (this is particularly true for white matter (WM)) and diffusion properties [49].
• —Tissue composition. In our case, both the dMRI and the neutron measurements were performed on slices of cerebral RH regardless of their grey matter (GM)–WM composition. In other words, our regions of interest include portions of GM as well as WM. This has an important averaging effect, since WM diffusion properties differ considerably from those of GM with a decreased slow diffusion coefficient (table 3). Thus, it is plausible that our averaged values are lower compared to in vivo samples in which the GM portion was isolated for the investigation.
• —Temperature effect. The enhancement of water mobility induced by temperature increase is known. Here, while dMRI and QENS experiments were performed at room temperature (25°C), human and rat diffusion coefficients (table 3) have been estimated at 37°C.

Table 3.

Fast (D_fast) and slow (D_slow) diffusion coefficients referenced in the literature [7,10,42–44] and estimated using the bi-exponential decay model. Units for D_fast, and D_slow, are expressed in [10⁻³ mm² s⁻¹]. The ranges represent minimum and maximum values. For comparison, data extracted from the present experiment are also reported. GM, grey matter; WM, white matter.

	fslow	Dfast	Dslow
human WM (in vivo)	0.29–0.42	0.66–1.68	0.02–0.26
human GM (in vivo)	0.25–0.51	0.93–1.74	0.19–0.47
rat GM (in vivo)	0.17–0.33	0.82–0.9	0.17–0.26
Xenopus laevis oocytes	0.11	1.06	0.16
bovine (present exp.)	0.241	0.610	0.078

On the other hand, our dMRI diffusion coefficients (table 1) are three to four times lower than those found with QENS measurements. The time scale of the dMRI measurements (tens of milliseconds) is sufficiently long to allow significant interaction between water molecules and cellular constituents, whereas obstructive effects influence less D measured by NS (time scale of sub-nanoseconds) as smaller distances are covered. This difference confirms that the cellular components responsible for the reduced diffusion coefficients have to be much smaller than the diffusion length used in dMRI.

The QENS analysis revealed two populations of water: a major fraction (86%, percentage relative to total water) which shows fast dynamical properties, similar to those of bulk water, and a minor fraction (14%) which displays significantly slower dynamics.

From our point of view, the existence of the two water pools cannot be explained in terms of:

• —Anisotropic effects leading to populations with different diffusion properties. Indeed, unlike the dMRI measurements, the neutron experiments provide information averaged over all directions of the whole tissue sample. It would indeed be of interest to model WM and GM independently and to evaluate how the anisotropy of water diffusion in WM, assessed using a diffusion tensor approach with at least six diffusion directions, relates to diffusion properties at the molecular level. However, investigation of anisotropy using neutrons would require the use of oriented samples such as myelin fibres.
• —WM–GM specificity. The diffusion coefficients estimated for the slow/fast proton dynamics are considerably different from those observed in pure WM and GM (table 3).

From QENS results (table 2), the fast water contribution in RH is characterized by a translational diffusion coefficient, D_Tfast, very close to the one of bulk water, D_w. The residence time is found to be higher than that of bulk water. The higher residence time reflects the longer time the protons spend interacting with heterogeneities in the internal cerebral structure. This is not surprising, as a similar behaviour has been observed in Escherichia coli (E. coli) and red blood cells [19,20,51]. The rotational diffusion coefficient, D_Rfast, for the fast water component is in agreement with the same value measured for bulk water. We conclude, therefore, that the fast water pool has a diffusion rate typical for bulk water but with a different residence time, reflecting interactions with cellular boundaries in RH.

The translational and rotational diffusive contributions of the slow water dynamics show a strong reduction in water mobility. In particular, the translational diffusion coefficient, D_Tslow, strongly deviates from bulk water and the associated residence time suggests even stronger interactions with cell membranes and other cellular components.

Even though cell biodiversity suggests a dependence of water dynamics upon cell-specific functions and intra- and extracellular environments, our results are in agreement with NMR studies [52] in which 85% of cell water in E. coli show bulk-like dynamical behaviour, while the dynamics of the remaining 15% is retarded by a factor of approximately 15 due to the direct interaction of this cell water with the biomolecular surfaces. However, it is worth noting that the application of NMR spectroscopy to brain tissue requires specific sample preparation (far from physiological conditions), resulting in tissue powder in solution, which might affect the results. New technologies based on solid-state NMR spectroscopic techniques are rapidly emerging.

We, therefore, suggest a picture where two water pools coexist in both intra- and extracellular compartments within brain tissue. These pools are characterized by different diffusion properties and driven by different degrees of interaction with the cellular constituents, mainly membranes. Their distribution in terms of density and spatial arrangement determines the diffusion properties. Moreover, unlike dMRI, where the protons bound to macromolecules (of the order of 5–15% of the total) cannot be differentiated (displaying T2 values too small), QENS allows us to evidence a dynamical contribution from the CH₂ groups of proteins and lipids by identifying a Q-independent rotational motion with a typical broadening of a few 10⁻¹ meV (table 2).

5. Conclusion

The combined use of dMRI and QENS techniques in the RH of bovine brain reveals the existence of two water populations characterized by different dynamical behaviours. The origin of dynamical heterogeneity observed with dMRI (which investigates motions on the micrometre/millisecond space/time scales) can be traced to the different cellular constituents that act as obstacles to the diffusing water molecule. QENS gives access to the incoherent scattering function S_inc(Q, ω) which depends on both the momentum transfer Q and the energy transfer ω. It is, therefore, a space-resolved spectroscopy permitting one to characterize in a unique way the two dynamical water populations. Moreover, QENS investigates motions occurring on the much shorter angstrom/picosecond space/time scales. When observed at such scales, the water translational dynamics appears to be essentially ‘jump-like' and its heterogeneity to be due to water molecules interacting with the cell membranes. Such approach allows for a much more precise description of water dynamics in brain tissue.

Appendix A

A.1. Diffusion magnetic resonance imaging

The standard dMRI procedure uses pulsed magnetic field gradients to determine the mean-squared displacement $(⟨r^2⟩)$, and ADC, of an ensemble of some molecular species over a diffusion time Δ. In the typical diffusion experiment, the magnetic field gradients are applied in pairs, with the first pulse encoding the position of the probe molecules in the phase of the nuclear spin magnetization, and the second pulse acting to reverse the effect of the first to ‘re-phase' the magnetization. The dMRI experiment detects molecular displacement during the diffusion time, Δ, between the gradient pulses, because magnetization that arises from spins that move during Δ is not perfectly re-phased by the second gradient pulse. Incoherent motion of different molecules due to diffusion results in destructive interference between the phases of signals from different spins with an overall reduction in the amplitude of the dMRI signal. In conventional dMRI, the diffusion displacement distribution of water molecules is assumed to be Gaussian. The signal intensity, SI(b), in a free medium, in a voxel and in the presence of non-zero diffusion weighting gradient along certain direction, is [10]

$$\mathrm{SI}(b)=\mathrm{S}{\mathrm{I}}_0{\mathrm{e}}^{-b\mathrm{ADC}},$$ A 1

where SI₀ is the signal intensity with no diffusion weighting, and b is the diffusion weighting factor with

$$b={\gamma }^2{G}^2{\delta }^2\left(\mathrm{\Delta }-\frac{\delta }{3}\right),$$ A 2

where G is the magnitude of the applied diffusion gradient pulses and δ is the duration of the pulses. When δ is not negligibly smaller than Δ, the diffusion time for the experiment can be written as

$$t_d=\mathrm{\Delta }-\frac{\delta }{3},$$ A 3

reflecting a measure of the time over which the diffusion process is being observed.

dMRI is sensitive to the averaged behaviour of the entire probe molecule population within the selected volume element and thus provides an estimate of the mean displacement distance of the total population. The advantage is that water is approximately 1000-fold more abundant than the next most abundant molecular species in the brain, and therefore the dMRI signal is largely dominated by the water contribution.

A.1.1. Diffusion models

(1) Mono-exponential decay

The signal decays as

$$\frac{\mathrm{SI}(b)}{\mathrm{S}{\mathrm{I}}_0}={\mathrm{e}}^{-bADC},$$ A 4

where ADC provides information on the tissue microstructure.

(2) Bi-exponential decay

The signal decays as the combination of the Gaussian-like diffusion signals arising from two water pools, one fast and the other slow

$$\frac{\mathrm{SI}(b)}{\mathrm{S}{\mathrm{I}}_0}=(1-f_{\mathrm{slow}}){\mathrm{e}}^{-b{D}_{\mathrm{fast}}}+f_{\mathrm{slow}}{\mathrm{e}}^{-b{D}_{\mathrm{slow}}},$$ A 5

where (1 − f_slow) and f_slow represent the relative fractions of the fast and slow contributions to the total signal intensity.

(3) Kurtosis approach

The deviation from Gaussianity is described as an excess of kurtosis K, a mathematically dimensionless parameter

$$\ln \frac{S(b)}{S_0}\approx -bD(t)+\frac{1}{6}{b}^2{D}^2(t)K(t).$$ A 6

The upper limit of the validity of equation (A 6) is given by $b\le 3/DK,$ corresponding to the convergence for the expansion of the equation.

(4) Anomalous diffusion: stretched exponential decay

The signal decay is described by a stretched exponential behaviour

$$\frac{S(b)}{S_0}=\exp (-\mathrm{DDC}\times b^{\gamma }),$$ A 7

where DDC is the distributed diffusion constant and the stretching exponent γ (0 < γ < 1) is linked to the heterogeneity of the medium in which the spins diffuse.

A.2. Neutron scattering

In NS experiments, neutron particles with well-defined incoming wavenumber are scattered on the samples, changing thereby their incoming kinetic energy and directions by the amounts

$$\mathrm{\Delta }E=E_f-E_i=\frac{h^2\hspace{0.17em}}{8{\pi }^2{m}_n}(k_f^2-k_i^2)\hspace{0.17em}=\hslash \omega \hspace{0.17em}Q=k_f-k_i,$$ A 8

where E_i/f and k_i/f are the energy and wavevector of incident/scattered neutrons, with ω their angular frequency. Thus, ΔE and Q are the energy and momentum transfer to the sample, respectively. The neutron intensity I(Q,ω), i.e. the number of neutrons scattered into the detector at certain energy transfers and directions, is directly proportional to a correlation function, called the scattering function S(Q,ω), which can be further separated into a coherent and incoherent part, i.e. S(Q,ω) ∼ S_coh(Q,ω) + S_inc(Q,ω).

S(Q,ω) is the mathematical Fourier-transform of the time-dependent pair correlation function G(r,t). In the coherent case, G(r,t) describes the interaction (correlation) of two sample particles, in our case hydrogen, separated by the distance r as a function of time t. The incoherent scattering depends only on the correlation between the positions of the same hydrogen at different time (self-diffusion) [53].

When ΔE = 0, the scattering process is called elastic NS, the energy exchanged is within the experimental resolution. QENS corresponds to energy transfers until approximately 2 meV; this scattering process gives information about motions of individual atoms (averaged over the whole molecule) which occur on a time scale of about 10⁻¹⁰–10⁻¹² s (translational and rotational molecular motions). The inelastic scattering corresponds to energy transfers greater than 2 meV, and is affected to molecular vibrational excitations and the creation of phonons. The elastic peaks appears for protons moving very slowly with respect to the time scale associated with the spectrometer's resolution, appearing as immobile. A typical QENS spectrum appears as a broadening of the elastic peak, while very fast protons, with respect to the energy resolution, contribute as a flat background in the QENS region.

At room temperature, the QENS experimental data reported here are fitted using an equation which takes into account free and restricted water dynamics described in terms of a model based on the coupling between translational (T) and rotational (R) motions [54]. The translational model used is the jump-diffusion model and the rotational model used is the continuous rotational diffusion on a circle. The equation used to fit the data is the following:

$$\begin{array}{rl}I(Q,\omega )\approx & \hspace{0.17em}[\hspace{0.17em}f\cdot \delta (\omega )+p_{\mathrm{fast}}\cdot S_{\mathrm{fast}}(Q,\omega ,D_{T\mathrm{fast}},{\tau }_{\mathrm{fast}},D_{R\mathrm{fast}})\\ & +p_{\mathrm{slow}}\cdot S_{\mathrm{slow}}(Q,\omega ,D_{T\mathrm{slow}},{\tau }_{\mathrm{slow}},D_{R\mathrm{slow}})\\ & +p_{\mathrm{CH}2}\cdot S_{\mathrm{CH}2}(Q,\omega ,{\mathit{\Gamma }}_{\mathrm{CH}2}(Q))]\otimes R(Q,\omega ),\end{array}$$ A 9

where f is the elastic fraction. R(Q,ω) is the instrumental resolution, while S_fast(Q,ω) and S_slow(Q,ω) are the total scattering intensities arising from the bulk-like (fast) and restricted (slow) diffusive water populations, respectively. D_Tfast/slow and D_Rfast/slow are translational and rotational diffusion coefficients, and τ_fast/slow are the residence times, i.e. the time a proton spends in a given position. S_CH2(Q,ω) is an additional contribution, arising from H not belonging to water molecules thus belonging to membranes, proteins and other cellular components. It is related to faster relaxation described by a large and Q-independent Lorentzian with a width Γ_CH2. A similar Q-independent broadening has been found in lipid [55,56] and in lipid–protein [57] systems and has been ascribed to a two-site jump rotational motion characteristic of CH₂ groups. p_fast, p_slow and p_CH2 are the fractions of atoms experiencing the three different dynamics, with (f + p_CH2 + p_fast + p_slow = 1).

A.2.1. Diffusion models

(1) Translational model: jump-diffusion model

The simplest motion occurring in a bath of particles with very low interactions is the Brownian motion in which the diffusion is assumed to occur via infinitely small, elementary jumps [53]. Assuming a time exponential decay, the energy spectrum of the scattered neutrons exhibits the shape of a Lorentzian function, whose HWHM (Γ_B) varies as a function of the momentum transfer Q. The scattering law is

$$S_B^T\hspace{0.17em}(Q,\omega )\approx \frac{{\mathit{\Gamma }}_B}{{\omega }^2+{({\mathit{\Gamma }}_B)}^2}$$ A 10

and

$${\mathit{\Gamma }}_B=D_w{Q}^2,$$ A 11

where D_w is the translational diffusion coefficient (Fick's Law). Thus, NS provides a rather direct determination of the diffusion coefficient. However, when the strength of the particle interactions increases, a deviation from Brownian's law arises, the HWHM tending to a constant for larger Q-values. This behaviour can be explained by introducing two characteristic times: the jump time τ_j during which the particle diffuses and the residence time τ_w during which it remains in the immediate vicinity of any point r and does not diffuse. In this model τ_j ≪ τ_w. In other words, for a time τ_w, an atom remains on a given site, vibrating around a centre of equilibrium and building up a thermal cloud. After this time, the atom moves rapidly to another site, in a negligible jump-time τ_j. The length of the jump vector between two sites is assumed to be much larger than the dimension of the thermal cloud. This model, called jump-diffusion model, leads to scattering law

$$\hspace{0.17em}\hspace{0.17em}{S}^T(Q,\omega )\approx \frac{{\mathit{\Gamma }}_{\mathrm{fast}/\mathrm{slow}}\hspace{0.17em}}{{\omega }^2+{({\mathit{\Gamma }}_{\mathrm{fast}/\mathrm{slow}})}^2\hspace{0.17em}},$$ A 12

where the jump-diffusion broadenings Γ_fast/slow obey the relation

$$\hspace{0.17em}\hspace{0.17em}{\mathit{\Gamma }}_{\mathrm{fast}/\mathrm{slow}}\frac{D_{\mathrm{Tfast}/\mathrm{slow}}{Q}^2}{1+{\tau }_{\mathrm{fast}/\mathrm{slow}}{D}_{\mathrm{Tfast}/\mathrm{slow}}{Q}^2}.$$ A 13

At small Q-values, this relation reduces to Brown's Law, i.e. $\hspace{0.17em}{\mathit{\Gamma }}_{\mathrm{fast}/\mathrm{slow}}={\mathit{\Gamma }}_B$. At large Q-values, the quasi-elastic broadening deviates from the Γ_B, ${\mathit{\Gamma }}_{\mathrm{fast}/\mathrm{slow}}$ reduce to constant values 1/τ_fast/slow; the τ_fast/slow parameter is the average residence time:

$${\mathit{\Gamma }}_{\mathrm{fast}/\mathrm{slow}}=\frac{1}{{\tau }_{\mathrm{fast}/\mathrm{slow}}}.$$ A 14

(2) Rotational model: continuous rotational diffusion on a circle

This model describes the reorientation motion of a molecule, which rotates randomly on a spherical surface [58]. The scattering law associated with this type of motion is the following:

$$\begin{array}{rl}& S^R(Q,\omega )\\ & =j_0^2(Qa)\delta (\omega )+\sum _{t=1}^{+\mathrm{\infty }}(2t+1)j_t^2(Qa)\frac{1}{\pi }\frac{t(t+1)D_R}{{\omega }^2+t^2{(t+1)}^2{D}_R^2},\end{array}$$ A 15

where $j_t^2(Qa)$ is a Bessel function of the first kind and order t, and a is the radius of a circle, namely the radius of the rotation. In this case, we fix the a value at 0.98 Å, which is the O–H distance in a water molecule. In this work, the sum in equation (A 15) ranges from t = 1 to t = 3; more orders did not change the convergence of the function and they are negligible.

Data accessibility

Data are accessible from osf.io/a3vp2.

Authors' contributions

F.N. conceived, designed and coordinated the study, performed the experiments, co-analysed the data and wrote the manuscript. C.D. performed the experiments, co-analysed the data and helped draft the manuscript. J.P. performed the experiment and critically revised the manuscript. C.S. provided the brain samples. B.D., J.O. and M.B. helped during the neutron experiment and critically revised the manuscript. G.L. helped during the sample preparation for neutron experiment. I.P. and A.C. critically revised the manuscript; E.L.B. led the dMRI experiment.

Competing interests

We declare we have no competing interests.

Funding

The MRI facility IRMaGe is partly funded by the French program ‘Investissement d'Avenir' run by the French National Research Agency, grant Infrastructure d'avenir en Biologie Santé—ANR-11-INBS-0006.