Interaction specificity of clustered protocadherins inferred from sequence covariation and structural analysis

Significance

The more than 50 clustered protocadherin isoforms impart neuronal identity to prevent self-synapses. This is accomplished via highly specific homodimers of the first 4 extracellular cadherin (EC) domains between neuronal processes. Using molecular dynamics, we found that individual EC domain interactions are weak and dynamic, suggesting the complex is held together by polyvalency. Using evolutionary couplings—a computational technique that identifies interacting amino acids in a protein—we found that interacting residue pairs with strong coupling scores were in contact more frequently and across more simulations than weak pairs. We built a statistical model of specificity that predicts the relative likelihood that any 2 isoforms interact and identify residues contributing strongly to specificity to reprogram protein–protein interactions.

Abstract

Clustered protocadherins, a large family of paralogous proteins that play important roles in neuronal development, provide an important case study of interaction specificity in a large eukaryotic protein family. A mammalian genome has more than 50 clustered protocadherin isoforms, which have remarkable homophilic specificity for interactions between cellular surfaces. A large antiparallel dimer interface formed by the first 4 extracellular cadherin (EC) domains controls this interaction. To understand how specificity is achieved between the numerous paralogs, we used a combination of structural and computational approaches. Molecular dynamics simulations revealed that individual EC interactions are weak and undergo binding and unbinding events, but together they form a stable complex through polyvalency. Strongly evolutionarily coupled residue pairs interacted more frequently in our simulations, suggesting that sequence coevolution can inform the frequency of interaction and biochemical nature of a residue interaction. With these simulations and sequence coevolution, we generated a statistical model of interaction energy for the clustered protocadherin family that measures the contributions of all amino acid pairs at the interface. Our interaction energy model assesses specificity for all possible pairs of isoforms, recapitulating known pairings and predicting the effects of experimental changes in isoform specificity that are consistent with literature results. Our results show that sequence coevolution can be used to understand specificity determinants in a protein family and prioritize interface amino acid substitutions to reprogram specific protein–protein interactions.

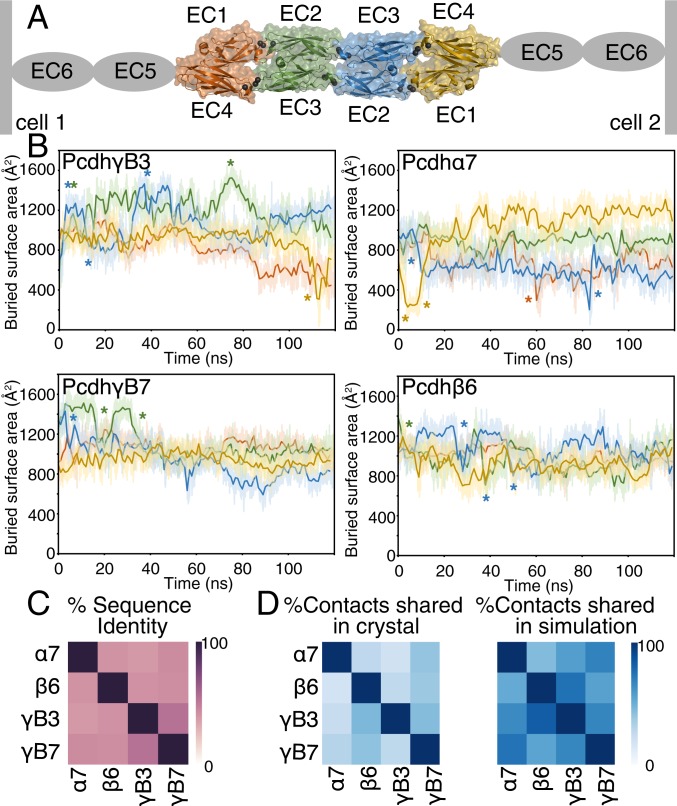
Clustered protocadherins (Pcdhs) are a large protein family that play roles in vertebrate nervous system development, including neuronal survival, axon targeting, neuronal arborization, and dendritic self-avoidance (1–9). Dendritic self-avoidance, wherein dendritic arbors are pruned when 2 dendrites from the same neuron come in contact, is mediated by formation of a clustered Pcdh assembly between 2 dendrites (5, 10). This assembly consists of specific homodimers formed in trans across 2 cellular membranes, engaging the first 4 extracellular cadherin (EC) repeat domains in an antiparallel arrangement (Fig. 1A). In addition to these trans interfaces, ECs 5 and 6 interact between protocadherins on the same neuron (cis), resulting in a zipper-like lattice (11). The trans homodimers are highly specific such that no cross interactions are observed in even the most similar isoforms (12–14). The trans EC1-4 interaction is also found in nonclustered Pcdhs (15–17), indicating the importance of this adhesive interface in cognitive function. Given the many isoforms per vertebrate genome, including 53 in the human genome, we sought to understand how specificity is achieved in this large interface.

Fig. 1.

Clustered Pcdhs have diverse and dynamic interfaces. (A) The clustered Pcdh dimer is an antiparallel complex where EC1 of the first protomer interacts with EC4 of the other protomer (orange and yellow) and EC2 interacts with EC3 (blue and green). Each simulation thus provides 2 examples of each type of interaction. (B) The BSA of the EC1/EC4 and EC2/EC3 interactions varies throughout the simulations for each simulated isoform (PcdhγB3 EC1-4, PcdhγB7 EC1-4, Pcdhβ6 EC1-4, and Pcdhα7 EC1-5). Instances of rapid interface BSA changes (>400 Ų in under 5 ns) are indicated with an asterisk in the corresponding color. (C) Percent identity of EC1-4 of the 4 clustered Pcdhs studied here. (D) Percentage of interface residue contacts shared between structures (Pcdhα7, 5dzv; Pcdhβ6, 5dzx; PcdhγB3, 5k8r; PcdhγB7, 5szp) and between structures and MD simulations. Each structure shares a mean of 32% of its contacts with other structures, and a mean of 47% of its contacts with other isoforms in simulation.

Structures of Pcdh trans dimers (11, 15, 18–20) have revealed idiosyncratic characteristics of individual dimer structures, like the lack of EC1/EC4 interaction in the PcdhγA1 and PcdhγA8 structures (20) and the small EC2/EC3 interface in PcdhγB3 (15). Based on the variety of interfaces found in the existing crystal structures (15, 18–20), it is possible that every isoform achieves specificity by adopting a different static interface conformation, or that isoforms sample a distribution of conformations, with different combinations of interface residues determining preference for self-interaction. Understanding Pcdh interaction specificity requires disentangling these scenarios by considering both interface conformations and residue–residue interaction preferences.

Prior computational work has sought to understand the evolution of specificity of the Pcdh trans interaction, finding positive selection on the trans interface (21), and suggesting that the EC2/EC3 interface plays a greater role in specificity between closely related protocadherins (10, 15). However, this computational framework could not analyze residue dependencies at the interface, or be used to predict specificities for new mutations or combinations of protocadherins. Recent computational methods based on residue coevolution have proven useful for understanding the structure and function of protein complexes (22, 23). These methods use undirected graphical models of protein sequences to find statistical dependencies between pairs of residues (24–26), successfully predicting correct protein–protein interaction pairings for families with many paralogs (27, 28), informing specificity reprogramming experiments (29, 30) and predicting the effect of mutations on protein function (31). Therefore, these generative models of residue dependencies may allow for characterization of residues important to specificity in the clustered Pcdh family, and prediction of interaction probability of all possible isoform pairs.

To better understand the structural and dynamical determinants of Pcdh interaction specificity, we use molecular dynamics (MD) simulations and crystal structures to show that isoforms adopt a range of conformations and to identify interacting residue pairs. We build a statistical model using evolutionary couplings (24, 25) to analyze specificity of all possible trans isoform interactions and infer which domains are important for interaction and specificity. This work provides insight into the molecular origins of specificity within the clustered Pcdh family and demonstrates that models based on sequence coevolution and MD simulations can be used to guide reprogramming of protein–protein interaction specificity.

Results

Structures and MD Show That Pcdh trans Interfaces Sample a Distribution of Conformations.

The trans interface of clustered Pcdhs is specific for self-interaction (12, 13) (Fig. 1A). Clustered Pcdh paralogs share only 40% residue identity at their interfaces (Fig. 1C). Crystal structures of many Pcdh isoform dimers (15, 18–20) revealed idiosyncratic features of individual isoforms, raising the possibility that different isoforms adopt different conformations in vivo, resulting in molecular specificity. For example, PcdhγA1 (in 1 of 2 dimers) and PcdhγA8 (20) lack EC1/EC4 contacts, and PcdhγB3 EC2-3 has a surprisingly small interface (15). Pairs of different isoform static structures share a mean of 32% of their interface residue contacts, with only 14 contact pairs shared between all 4 analyzed isoforms (Fig. 1D). We thus used MD simulations to test whether distinct features of individual isoforms result from static conformational differences, or from a dynamic interface crystallized in different conformations.

We performed 120-ns all-atom MD equilibrium simulations of 4 different EC1-4 homodimers from different Pcdh subfamilies to distinguish the above hypotheses: PcdhγB3, PcdhγB7, Pcdhβ6, and Pcdhα7 (SI Appendix, Table S1). Overall, the complexes did not dissociate over the course of simulation (SI Appendix, Fig. S1A and Fig. 1B). While root-mean-squared deviation (RMSD) is not an appropriate metric to determine convergence for the full Pcdh complex due to its large size and the flexibility of the hinge regions between EC repeats (32), overall RMSD remained stable and below ∼8 Å for all structures. Moreover, the RMSD of individual ECs ranged from 2 to 3 Å, showing local equilibrium (SI Appendix, Fig. S2). Also, the overall buried surface area (BSA) of each isoform was stable: The average BSA was 4,400 ± 400 Ų for PcdhγB3, 4,500 ± 300 Ų for PcdhγB7, 4,200 ± 300 Ų for Pcdhβ6, and 3,500 ± 200 Ų for Pcdhα7.

At an individual EC interaction level, fluctuations in BSA suggest these interactions are weak. Between individual EC domain dimers, which average 700 to 1,300 Ų in BSA, fluctuations in BSA can be more than 400 Ų over the course of a few nanoseconds (Fig. 1B and SI Appendix, Table S2). For example, 1 EC1/EC4 dimer of Pcdhα7 fluctuates in BSA from 1,000 Ų at the start of the simulation to ∼200 Ų at 6 ns then to 1,200 Ų around 35 ns (Fig. 1B). In another example, our previously published PcdhγB3 structure has a particularly small BSA for the EC2/EC3 interface (15). In our simulations, each EC2/EC3 interface increases in BSA from ∼600 to ∼1,200 Ų in the first 6 ns. The presence of HEPES at this interface did not cause the small interface, as structures with less or no HEPES were identical (overall RMSD over 3,210 atoms: 0.890 and 0.785 Å, respectively) (SI Appendix, Fig. S3), suggesting this structure is a conformation sampled by PcdhγB3 in solution. The larger BSA of the equilibrated PcdhγB3 structure is similar to that of other simulated clustered Pcdhs (SI Appendix, Fig. S1B). In fact, this was generally true of all simulations: the proportion of shared interface sites across the simulations is higher than that across the crystal structures alone (Fig. 1D), indicating that simulations can define interface residues representative of a protein family.

Although the MD simulations are not necessarily equilibrated, the fluctuations suggest that if these individual EC interactions were found in isolation they would be low affinity, consistent with the observation that EC1-3 constructs do not dimerize in solution (14, 18). These fluctuations in BSA agree with other simulations that find sharp decreases in BSA as prerequisites to protein complex dissociation (33). Overall, our simulations indicate that each isoform can sample a range of interface conformations, and that the available crystal structures represent only a snapshot of these conformational possibilities. Furthermore, simulations can improve consistency when defining interface residues in a protein family.

Highly Coevolving Residue Pairs Are in Frequent Contact in Simulations.

Computational methods based on residue coevolution have been useful in understanding the structure of Pcdhs, predicting the EC1/EC4 interaction and that the trans dimer architecture exists in nonclustered Pcdhs, both findings later confirmed experimentally (15, 16, 18, 34). Coevolving residue pairs identify interprotein contacts (22, 23) but can correspond to positions only in contact in certain conformations (35–37). Given the dynamic nature of the Pcdh interface and the above observation that crystal structures represent only a snapshot of possible conformations, we analyzed how often highly coevolving interface residues in the Pcdhs (15, 18) are in contact across simulations and over time.

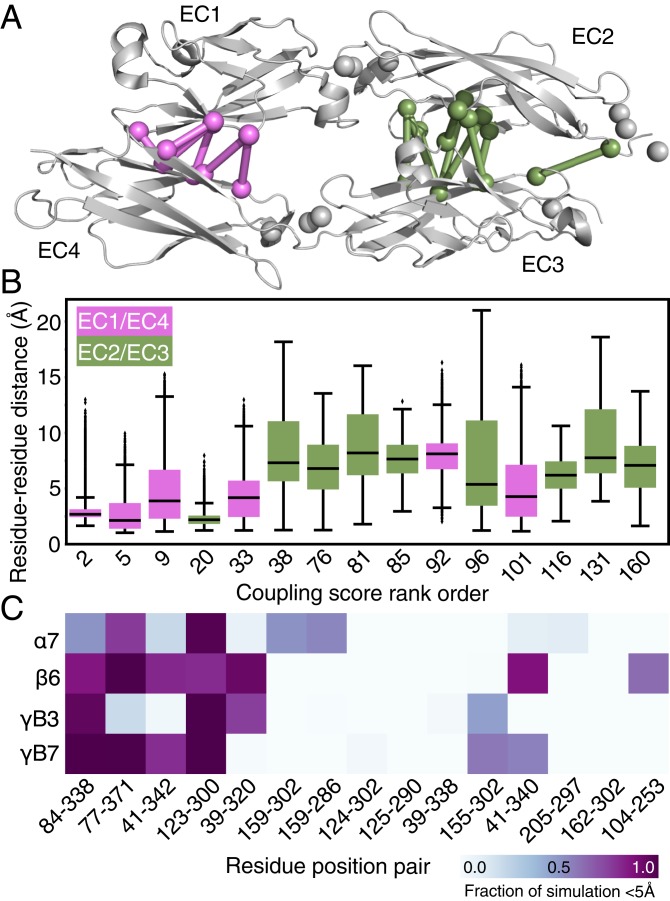
In our sequence coevolution analysis, the set of top 200 coevolving pairs includes mostly intramolecular contacts and 15 intermolecular pairs (SI Appendix, Fig. S4). We calculated the residue–residue distance of these 15 coevolving intermolecular pairs (Fig. 2A) over the course of the MD simulations. Of note, each simulation provides 2 (semi)independent observations for each residue pair due to the 2-fold symmetry of the dimer. In general, pairs with higher coevolution scores are more frequently in contact across more simulations than weaker pairs (Fig. 2B), consistent with the observation that lower-scoring pairs are less predictive of physically interacting residues (22, 23).

Fig. 2.

Evolutionary coupling scores of intermolecular pairs correlate with residue–residue interactions in simulations. (A) Clustered Pcdh half-dimer of EC1-2 and EC3-4 showing coevolving residue pairs across the EC1/EC4 (pink) and EC2/EC3 (green) interface. (B) Box plots of residue–residue distances for top 15 intermolecular pairs for all 4 simulations. Boxes are colored based on their location on the EC1/EC4 (pink) or EC2/EC3 (green) interface. (C) Heatmap of the fraction of time the top 15 intermolecular coevolving pairs are within 5 Å for the 4 simulations.

A closer examination of the top 15 intermolecular pairs reveals diverse trajectories during simulations (Fig. 2C). For the most highly coevolving pairs, the residues are in close contact most of the time in most simulations. For example, the 84 to 338 and 123 to 300 pairs (based on PcdhγΒ3 numbering in SI Appendix, Fig. S5) remain at ∼4 Å throughout all but 1 simulation (SI Appendix, Fig. S6). For some lower-scoring pairs, the residues are in close proximity in some simulations but further in others, e.g., the 159 to 302 pair residue–residue distances fluctuate between 6 and 18 Å in most simulations but stay consistently close in the Pcdhα7 interface. Other lower scoring pairs fluctuate widely in all simulations and rarely if ever come into contact, such as the 39 to 338 pair.

Model Parameters Reveal Biochemical Interactions Underlying Interface Specificity.

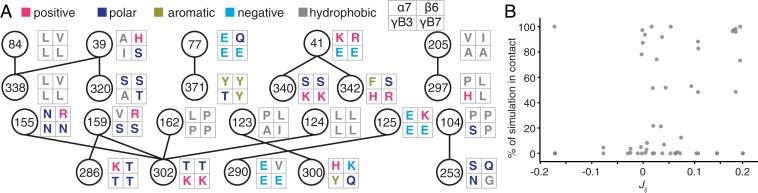
Coevolving pairs are calculated using an undirected graphical model, which has parameters for single-site biases and pairwise residue preferences for all sites (24–26). The pairwise residue preferences can capture biochemical relationships between amino acids (38). We asked whether the pairwise residue preferences, termed J_ij matrices, can shed light on the biochemical nature of interactions in the interface and inform which residues stay in contact during simulations.

We observe a weak correlation between the pairwise residue preference (J_ij value) of a particular residue pair in a particular isoform, and the fraction of the simulation that this pair spends in contact (Pearson’s r = 0.30, P < 0.05, n = 56; Fig. 3B) The top-scoring pairs, 84–338, 77–371, and 41–342, are a hydrophobic interaction, a charged-aromatic interaction, and a salt bridge, respectively (Fig. 3A). These interactions are conserved in their biochemical nature even though the particular residues have undergone substitution. Further down the list of top-scoring intermolecular coevolving pairs, the biochemical nature of the interaction becomes less apparent. For instance, the 124 to 302 pair appears to be an interaction between the hydrophobic position 124 and the charged or polar position 302. These could be due to noise in parameter inference or could indicate positions that are rapidly diversifying and inhabiting repulsive states to achieve specificity. Consistent with this latter hypothesis, these lower-scoring pairs are found predominantly on EC2/EC3, which has been identified as a region of rapid diversifying selection (21). Extreme J_ij value residue pairs for EC1/EC4 are concentrated in biochemically similar regions (e.g., 84 to 338 and 77 to 371), while significant residue pair J_ij values for EC2/EC3 pairs are broadly distributed in biochemically diverse pairs (SI Appendix, Fig. S7).

Fig. 3.

Coevolving residue pairs reveal biochemical interactions across clustered Pcdh interface. (A) The top 15 coevolving pairs and the amino acids found at these positions for the 4 simulations. (B) Weak correlation is seen between the pairwise residue preferences (J_ij values) and the fraction of the simulation these residues pairs were in contact (within 5 Å).

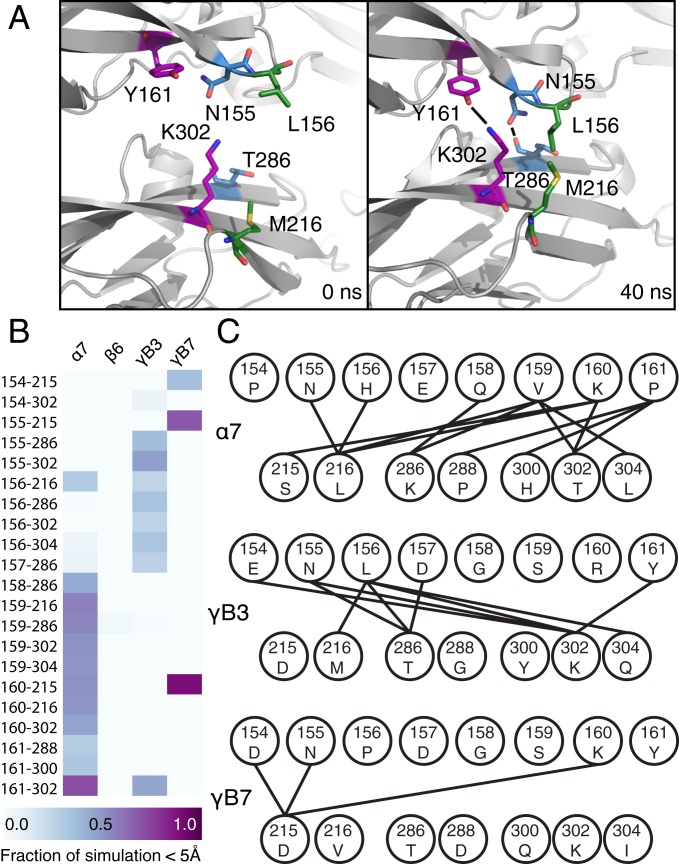
The dynamics and structural heterogeneity of residue pair interactions in EC2/EC3 may explain why coevolving pairs on this interface have lower scores. Four of the top 15 coevolving pairs cluster in the β4–β5 loop of EC2, which interacts with EC3. During simulations of the PcdhγB3 EC1-4 interface, conformational changes in this loop leads to an increased interface BSA during the first 6 ns of simulation (SI Appendix, Fig. S1B), including the formation of hydrogen bonds between Y161 and K302, and N155 and T286, and a van der Waals interaction between L156 and M216 (numbering based on SI Appendix, Fig. S5 and Fig. 4A). The corresponding interresidue distances vary in a coordinated fashion as the loop fluctuates between the disengaged state seen in the structure and an engaged state where the loop interacts directly with EC3 (SI Appendix, Fig. S8). The heterogeneity of the EC2 β4–β5 loop is echoed in its diverse conformations in other clustered Pcdh structures (SI Appendix, Fig. S9). Pcdhα7 and PcdhγB7 (unlike Pcdhβ6) also use the EC2 β4–β5 loop to interact with EC3 but use a distinct set of amino acid interactions (Fig. 4B). These interactions are biochemically diverse, including hydrogen bonds and electrostatic and van der Waals interactions (Fig. 4C). For all 3 isoforms, the interactions are dynamic and go through binding and unbinding events (SI Appendix, Fig. S8). Isoform differences in how the EC2 β4–β5 loop interacts with EC3 may explain the biochemical diversity of the coevolving residue pairs at this interface and the relative low strength of these couplings.

Fig. 4.

Structural heterogeneity and sequence diversity of EC2 β4–β5 loop contribute to isoform specificity. (A) The EC2 β4–β5 samples conformational space in the PcdhγB3 simulation, forming several interactions with EC3 (numbering based on SI Appendix, Fig. S5). (B) Residue–residue interactions (shown as a heatmap of the fraction of the simulation pairs within 5 Å) of the EC2 β4–β5 loop (positions 154 to 161) with EC3 (positions 215, 216, 286, 288, 300, 302, and 304) differ between isoforms. (C) The differences in interacting residue pairs reflect diverse biochemical interactions of this loop with EC3.

SEI Describes Pcdh Specificity Distributions.

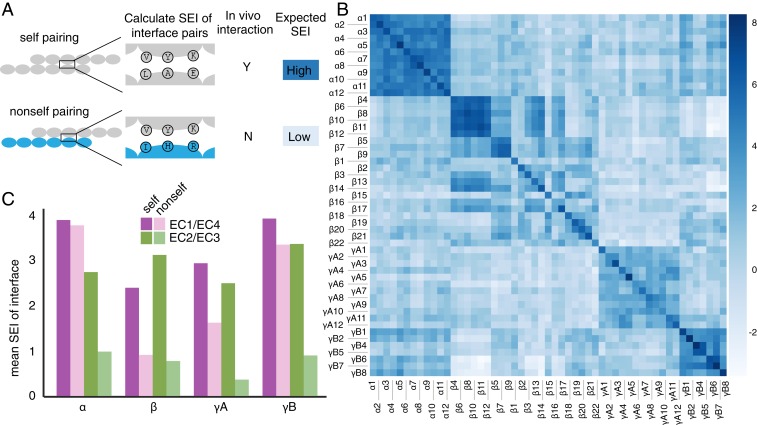
We used evolutionary couplings and simulation data to build a model of clustered Pcdh interaction specificity (Methods and SI Appendix). We assess the propensity for any 2 Pcdhs to interact by summing the pairwise residue preferences for all interface residue pairs, producing a score that we call the statistical energy of interaction (SEI) (Methods and Fig. 5A). A higher SEI indicates a higher propensity for interaction.

Fig. 5.

Statistical energy of interaction supports experimental evidence for self-interaction and divergent roles of EC2/EC3 and EC1/EC4 interfaces. (A) SEI for every possible pairing of Pcdhs was calculated by summing the energy contribution of each interacting residue pair at the interface. Based on prior work (27, 28), we expect to observe high statistical energy for self pairings, which interact in vivo (12, 13), and low statistical energy for nonself pairings. (B) Statistical energy for all possible combinations of isoforms. (C) Mean statistical energy of every self and nonself pairing for the EC2/EC3 and EC1/EC4 interface, measured within all subfamilies of clustered Pcdhs in mouse.

Our statistical model allows us to compare covariation-based determinants of specificity between all isoforms to discern the relative likelihood of interaction. For the α, β, and γ Pcdh subfamilies in mouse, the SEI of a sequence with itself (a self pairing) is higher than the SEI of a sequence with a different isoform (a nonself pairing; Fig. 5B). This is generally consistent with previous cell aggregation experiments in which clustered Pcdhs only form homodimers (12, 13). While these studies observed no nonself interaction in their experiments, our model finds that in some cases the SEI for nonself pairs is as high as for a self pairing, e.g., between β4 and β6. This could be due to particulars of the cell aggregation assay or suggest that some in vivo determinants of specificity are not fully captured by our model.

We compared the contribution of each domain–domain interface to the overall SEI. The nonself Pcdh pairs of the mouse α, γB, and γA subfamilies have a lower SEI in the EC2/EC3 interface than in the EC1/EC4 interface, indicating that the EC2/EC3 interface contributes more to specificity of these isoforms (Fig. 5C and SI Appendix, Fig. S10). The α subfamily has nearly identical SEI between EC1/EC4 self and nonself interfaces, suggesting this interaction has little discriminatory power in the α subfamily. This finding extends our previous analysis (14) that found that the EC2/EC3 interface tends to contribute more to specificity than the EC1/EC4 interface. The difference in SEI between EC2/EC3 and EC1/EC4 nonself pairs may be due to having mutations between self and nonself EC2/EC3 pairs compared to EC1/EC4 pairs, which negatively correlates with the SEI (SI Appendix, Fig. S11).

The SEI model allows us to predict how particular mutations may alter interaction specificity by recalculating SEI using individual coupling terms from the mutant sequence. Previous work has tested chimeric constructs in cell aggregation assays to understand how specificity is encoded in the clustered Pcdh family (14), and our model correctly predicts the phenotype of the majority of these mutants (SI Appendix, Fig. S12). On closer inspection of the Pcdhα7/Pcdhα8 pair, the SEI of Pcdhα8 EC1/EC4 nonself pairs are lower than the nonself EC1/EC4 pairs in other α isoforms (SI Appendix, Fig. S10). Coincidentally, the Pcdhα7/Pcdhα8 EC2/EC3 SEI is nearly identical to the self SEI scores, suggesting that, within this pair, EC1/EC4 provides more discrimination than EC2/EC3. This agrees with literature results (14) but remains an exception to the trend that EC2/EC3 provide more discriminatory power in the α, γB, and γA subfamilies.

Our model parameters are inferred only from natural sequences, and therefore self pairings, which may bias the model against nonself pairings. To avoid this possible bias, we implemented an iterative pairing algorithm that allows the isoforms to find favorable nonself pairings, if such pairings exist (23, 24) (SI Appendix, Fig. S13). The algorithm reproduces self pairings for 74% of all sequences in the alignment, averaged across 5 replicates, after iteration to convergence. This is on par with accuracy of partner detection for other proteins pairs performed by related algorithms (23, 34) and supports the use of our model built from natural sequences. When the EC1/EC4 and EC2/EC3 interactions were paired in isolation, we found that the accuracy of matching was less than when the whole interface was used, indicating that both interfaces act in combination to achieve full specificity of the interface.

Our model allows us to compute a SEI score for all pairs of clustered Pcdhs that generally agrees with experimental findings about specificity of Pcdh isoforms. Importantly, it also allowed us to dissect contributions of various interface components at an overall and subfamily level. We observed lower mean SEI at EC2/EC3 nonself interfaces than at EC1/EC4 nonself interfaces, indicating that the EC2/EC3 interface tends to be more involved in specificity.

Discussion

The highly specific antiparallel Pcdh interface that forms between neurons is required for many roles in neuronal development. Our results address the determinants of specificity in this interaction by simulating the dynamics of the Pcdh interface and modeling the contributions of each residue pair to interaction specificity.

Our MD simulations of clustered Pcdh dimers reveal that individual EC interactions sample a range of conformations in every isoform. The variations in BSA for individual EC interactions suggest that the individual interactions are weak, and the overall stability of a Pcdh dimer is established by the polyvalent nature of these individual EC interactions. This type of cooperative binding is widespread in biology and plays roles in multisubunit protein machine assembly, signaling at the membrane, and signaling between cells (39–41). The dynamic nature of clustered Pcdh complexes and the cooperativity of individual EC interactions likely play a role in interaction specificity, motivating us to incorporate these simulations in our statistical model of specificity.

The MD simulations allowed us to observe how coevolving residue pairs across a protein interface vary over time. Overall, we found that higher scoring pairs are closer together throughout the simulations and across multiple homologs, demonstrating a relationship between the strength of an interaction and the coupling score of a residue pair. This result extends previous empirical results showing that coevolving pairs are more likely to be close in 3D (22, 23), and that evolutionary couplings can correspond to multiple incompatible conformations (35–37). We also find that residue–residue distances vary between isoforms, suggesting that coevolving pairs may be important for the stability of only a subset of proteins. Thus, our MD results illustrate that coevolving pairs can represent residue interactions that are present in the ensemble of conformations sampled by the collection of homologous proteins that are present in the coevolutionary model. This knowledge could inform further developments to benchmark structure prediction using coevolution data.

By analyzing the correlation between evolutionary couplings and the behavior of residue pairs in simulations, we have shed light on the role of coevolving residue pairs in the specificity of clustered Pcdh interactions. Generally, the most strongly coevolving pairs are found between EC1 and EC4, and these pairs are frequently in contact. The biochemical nature of these interactions is consistent between isoforms, indicating that they serve a conservative role in the Pcdh interactions. Coevolving pairs between EC2/EC3 are less frequently in contact and their biochemical character changes between isoforms, suggesting these interactions are rapidly diversifying and metastable so that they can flexibly occupy new specificity space.

We constructed a model of interaction specificity from sequence data, using residue pairs found to interact in our simulations. We used this model to evaluate pairs of individual EC interfaces, allowing us to determine the relative likelihood of an interaction. We found that the difference in statistical energy of interaction (ΔSEI) supports literature results that the Pcdh interface is specific for self-interaction. Nonself pairings of the EC2/EC3 interface have lower SEI than nonself EC1/EC4 pairings for the α, γΑ, and γB subfamilies, indicating that the EC2/EC3 interface has a greater contribution to specificity. There are some differences between subfamilies as noted previously (15, 20), with the β and γA subfamilies having nearly equal contributions to specificity from both interfaces.

The extent to which protein–protein interactions avoid cross talk with paralogs is dependent on the evolutionary consequences of having promiscuous interactions. To avoid spurious signaling, bacterial 2-component systems have strict specificity encoded in a small number of residues (42, 43). Promiscuous intermediates have been derived experimentally for bacterial toxin–antitoxin and PDZ domains (44, 45), although these sequences likely have not been visited evolutionarily. The work presented here suggests a strategy used by clustered Pcdhs to ensure specificity and yet allow new specificities to easily arise through evolution. Small changes in individual EC affinity caused by a small number of mutations can alter the affinity of the whole dimer through the cooperativity of the individual EC interactions. This strategy may explain the pervasiveness of this interface for cell–cell adhesion in nervous system development.

Methods

Detailed procedures for all methods are provided in SI Appendix.

Statistical Interaction Energy Model of Clustered Pcdh Specificity.

We used evolutionary couplings to build a model of clustered Pcdh interactions. Previous studies used the statistical energy of an evolutionary couplings model to identify interacting histidine kinase-response regulator pairs (27, 28) and to predict the effects of mutations on protein function (31). For our model, only the interface residue pairs determined by our MD approach were used. The interaction energy between 2 sequences (σ^A, σ^B) is the sum of the individual coupling terms (J_ij) between the interface residues of the 2 sequences:

$$SEI\left({\sigma }^A,{\sigma }^B\right)=\hspace{0.17em}{\displaystyle \sum _{\begin{array}{c}\text{interface}\hspace{0.17em}\left(i,j\right)\\ \text{contacts}\end{array}}}{J}_{ij}\left({\sigma }_i^A,{\sigma }_j^B\right).$$

The J_ij term is the matrix of pairwise residue preferences for all possible amino acids in positions i and j (31). The change in SEI(σ) is used to predict whether the interaction will become more or less favorable. See SI Appendix for further explanation. See Datasets S1–S3 for interface residues, residue pairs, and an alignment of mouse isoforms.