A large-scale analysis of task switching practice effects across the lifespan

Significance

In modern life, we engage with many sources of information concurrently. To do this, we must continuously switch between different tasks, but this comes at a cost to performance, especially in older adults. Using a large dataset from an online cognitive-training platform, we develop a computational model of task switching that defines distinct latent measures of activating the relevant task, deactivating the irrelevant task, and making a decision. This model shows that, although task practice can improve task-switching performance, persistent costs remain even after extensive practice, and more so in older adults. We show that, with extensive task practice, older people can become functionally similar to less-practiced younger people.

Abstract

An important feature of human cognition is the ability to flexibly and efficiently adapt behavior in response to continuously changing contextual demands. We leverage a large-scale dataset from Lumosity, an online cognitive-training platform, to investigate how cognitive processes involved in cued switching between tasks are affected by level of task practice across the adult lifespan. We develop a computational account of task switching that specifies the temporal dynamics of activating task-relevant representations and inhibiting task-irrelevant representations and how they vary with extended task practice across a number of age groups. Practice modulates the level of activation of the task-relevant representation and improves the rate at which this information becomes available, but has little effect on the task-irrelevant representation. While long-term practice improves performance across all age groups, it has a greater effect on older adults. Indeed, extensive task practice can make older individuals functionally similar to less-practiced younger individuals, especially for cognitive measures that focus on the rate at which task-relevant information becomes available.

As we are increasingly engaging with multiple devices concurrently, and continuously shifting between different input sources and output platforms, it is becoming more important to understand the cognitive costs of switching from executing one task to another. How long does it take to switch between tasks? Can practice overcome the challenges of task switching? If so, how much practice is needed, and does this vary across the lifespan? A large body of research has sought to identify the cognitive processes underlying task switching by using a number of theoretical perspectives (1, 2), behavioral paradigms (3), and levels of measurement and analysis (4). Computational models of task switching are based on a variety of modeling approaches, including cognitive architectures (5), neural networks (6), and evidence-accumulation models (7, 8).

We propose a probabilistic computational model of task-switching using cognitive-training data (9) from Lumosity, an online training platform. Such online gaming platforms have supported the investigation of skill learning and cognition at unprecedented scales (10–12), as part of a trend to use naturally occurring large-scale datasets to develop and test theories of cognition (13, 14). Such data provide the significant advantage of selecting different samples of users according to demographic characteristics, levels of engagement, and training histories.

Here, we investigate task switching in 3 distinct samples of users who trained on Lumosity’s task-switching paradigm: a large adult-lifespan sample who trained for up to 60 sessions each; a sample of the most active users who trained for thousands of sessions; and a sample of older adults with at least 1,000 sessions. While previous studies have examined aging effects on task-switching performance (15–17) as well as practice effects (15, 17–21), the interaction between age and extensive practice remains poorly understood. The large user sample and range of practice in the Lumosity data enables detailed characterization of changes in task-switching behavior with aging, practice, and their interaction. The sample of extremely practiced users allows direct investigation of a key question in aging research: Can extensive practice make an older person functionally similar to a younger person?

Our computational model decomposes task switching into a number of underlying cognitive processes and details how these processes change over trials within an experimental session, as well as with practice across multiple sessions. The model is consistent with recent theoretical perspectives of cognitive control (22) that distinguish between controlled acts (e.g., responding to a particular stimulus) and acts of control (e.g., instantiating a particular task). The model instantiates the response process using evidence accumulation, similar to previous models of task switching (7, 15). However, it also introduces additional task-switching control processes that have their own temporal dynamics, operating between decisions (in the order of seconds) and across practice (in the order of minutes, hours, or days). Separating the task-switching dynamics of the control process from the temporal dynamics of the response mechanism makes it possible to compare cognitive performance across age groups on a number of latent cognitive characteristics, including the ability to perform the basic tasks, the rate of switching between tasks, and the degree to which the relevant task can be activated and the irrelevant task suppressed.

A Computational Model

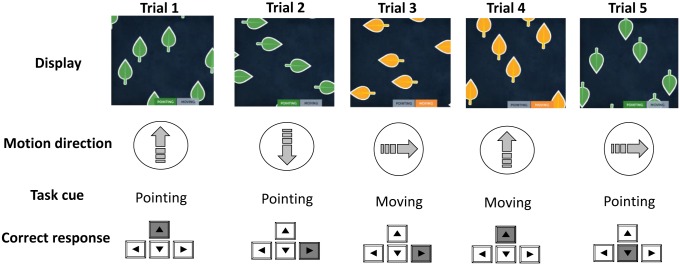
Before describing the task-switching model, we note a few constraints imposed by the particular experimental paradigm. In this task (Fig. 1), stimuli are represented along 2 visual dimensions (pointing and moving), and each visual dimension has 4 feature values (up, down, left, and right). A task cue (i.e., the words pointing or moving that are also mapped to leaf color: green or orange) indicates which stimulus dimension should be used to determine the response. For example, if the leaves are pointing up and moving down, the correct response would be up if the task cue is pointing, and down if the task cue is moving. The experimental paradigm intermittently alternates between the 2 task cues (pointing and moving), and each task run includes a variable number of trials.

Fig. 1.

Illustration of a task-switching sequence of 5 trials (top row). Each display shows a set of leaves with 2 main perceptual features: the pointing direction (as shown in the displays) and the movement direction (large arrow in second row). The task cue (pointing or moving; third row) is indicated by the color of the leaves as well as a label at the bottom of the display. Users have to respond with the direction of the cued dimension. The correct response (left, right, up, or down) is indicated by the highlighted key (bottom row). Trials 1 and 4 are congruent trials: The leaves point and move in the same direction. Trials 2, 3, and 5 are incongruent trials: The leaves point and move in different directions. In this sequence, trials 3 and 5 require a task switch.

This task is akin to the standard explicit cuing task—i.e., an explicit task cue is presented on each trial—with no preparation interval—i.e., there is no delay between the onset of the cue and the perceptual display. Therefore, the model is designed to account for the dynamics of task activation in the absence of any opportunity for advance preparation prior to target onset. Further, unlike most task-switching paradigms, the paradigm involves 4 (not 2) response alternatives per task, so we have extended the response model to account for more than 2 responses.

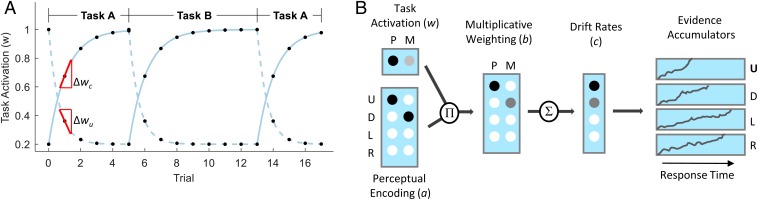
The model is illustrated in Fig. 2B. The perceptual information along the pointing and moving directions is encoded separately. Changes in task cue lead to temporal changes in task activation for the cued task (currently relevant) and the uncued task (previously relevant, now irrelevant). The activation of the cued task and deactivation of the uncued task takes time. The temporal dynamics of task activation are illustrated in Fig. 2A. The perceptual information for each dimension is weighted by the task activation for the corresponding dimension (Fig. 2B). The information is then combined across dimensions to produce the evidence (drift rates) for each individual response. Evidence accumulators—one for each response—race to determine the response choice and the response time. We apply Bayesian inference to estimate model parameters for each individual user (SI Appendix, SI Text).

Fig. 2.

(A) Illustration of the changes in task activation for the cued task (solid lines) and the uncued task (dashed lines) over trials when alternating between 2 tasks. Markers show the task activations at particular trials, and lines show the activation between trials, to illustrate the underlying dynamics. The model predictions are based on the following parameter settings: $g$ = 0.9, $h$ = 1.6, $u=0.2$, and $v=1$. The speed of task switching is assessed as the slope $\mathrm{\Delta }w$ of the task-activation function at the first switch trial, separately for cued and uncued tasks. (B) Illustration of processing in an incongruent trial with leaves pointing up and moving down. The cued dimension in this example trial is pointing, and the correct response corresponds to the up direction. The activation of perceptual features ($a$) is weighted by task activation ($w$), and the resulting weighted activations ($b$) are summed across dimensions to produce the drift rates for the 4 response alternatives ($c$). The evidence accumulator for the U (up) response reaches the decision threshold first and determines the response choice and response time. D, down; L, left; M, moving; P, pointing; R, right; U, up.

We describe the model in 4 sections: 1) the dynamics of task activation within and between runs; 2) how practice alters the task-activation dynamics; 3) a simple model for encoding perceptual information, relating this to congruency effects; and 4) the response process which uses an evidence-accumulation model to account for response time and accuracy.

Task Activation Dynamics.

Preparation for a new task takes time and involves a number of acts of cognitive control involving memory (loading the new task into memory) and attention (diverting attention to perceptual dimensions relevant to the new task), as well as setting up the rules to map stimuli to responses (1, 22). The model summarizes these changes in a single latent construct, task activation. Consistent with the notion of task-set reconfiguration (1), it takes time for the activation of the relevant task to increase. Similarly, consistent with the notion of task-set inertia (2), it takes time to decrease the activation of the irrelevant task.

We use $w_{cued,i}$ and $w_{uncued,i}$ to represent the activations of the cued and uncued tasks at trial $i$. Changes in task activation across trials are described by the difference equation:

$$w_{d,i}=w_{d,i-1}+\left(\text{asymptote}-w_{d,i-1}\right)\cdot \text{rate}.$$ [1]

The asymptote takes different values for the cued and uncued task ($\text{asymptote}=v$ and $\text{asymptote}=u$, respectively).

Generally, Eq. 1 predicts that task activation starts at a baseline value, increases to an asymptote, and decreases again to a baseline value. The timing of these changes coincides with changes in the task cue, as illustrated in Fig. 2A. For example, having switched from a run of trials on task B back to task A, activation of the cued task (A) starts near baseline $u$ and increases toward asymptote $v$. At the same time, activation for the uncued task (B, that is now irrelevant) starts near baseline $v$ and decreases to value $u$. Therefore, $u$ represents the residual task activation that persists, even after several trials have occurred after a task switch.

In addition, we also allow for different values of the rate parameter for the cued and uncued task ($\text{rate}=h$ and $\text{rate}=g$, respectively). The separation of rate parameters for cued and uncued tasks allows the model to capture asymmetries in the underlying dynamics of cognitive control. For example, there might be differences in the time to load vs. unload tasks from memory, or differences in the time to engage attention to a new dimension and disengage from the old dimension. In the illustration, given the particular parameters, the task dynamics show an asymmetry in the rates with a relatively fast change for the uncued task and a somewhat slower change for the cued task.

Based on these rate parameters, we derive a measure of task-switching speed by the slope of the task-activation function assessed at the first trial after a switch, for both the cued and uncued tasks ($\mathrm{\Delta }{w}_c,\mathrm{\Delta }{w}_u$ in Fig. 2A; SI Appendix, SI Text). This measure allows comparisons of task-switching speed across individuals with different baseline and asymptotes.

Effect of Practice.

Practice may affect a number of processing stages (e.g., perceptual or response). We assume that the main effect of practice is to change task-activation levels—i.e., increase activation for the cued task, decrease activation for the uncued task, or both. We will assume that both baseline and asymptotic task activation change as a function of the number of practiced sessions ($j$) according to exponential growth functions:

$$\begin{array}{c}{v}_j={\tau }_v+\left({\gamma }_v-{\tau }_v\right)\left(1-e^{-{\delta }_v\left(j-1\right)}\right)\hfill \\ u_j={\tau }_u+\left({\gamma }_u-{\tau }_u\right)\left(1-e^{-{\delta }_u\left(j-1\right)}\right).\hfill \end{array}$$ [2]

In this notation, $\tau$, $\gamma$, and $\delta$ are intercept, asymptote, and rate parameters, respectively, and the subscript denotes the specific variable associated with these parameters. For example, the asymptotic activation for the cued task ($v$) starts at ${\tau }_v$ and after extended practice reaches asymptote ${\gamma }_v$.

Another dimension of practice involves the rate at which asymptotic task-activation levels are achieved. Practice could speed up the activation of the cued task and/or the deactivation of the uncued task, allowing better separation between tasks after fewer trials in a run. In the model, practice can affect the rate of change in activation levels in a similar way as for the asymptotic levels above, but in logarithmic units:

$$\begin{array}{c}\text{log}\hspace{0.17em}{g}_j={\tau }_g+\left({\gamma }_g-{\tau }_g\right)\left(1-e^{-{\delta }_g\left(j-1\right)}\right)\hfill \\ \text{log}\hspace{0.17em}{h}_j={\tau }_h+\left({\gamma }_h-{\tau }_h\right)\left(1-e^{-{\delta }_h\left(j-1\right)}\right).\hfill \end{array}$$ [3]

Perceptual Model.

Let $x_l$ represent the feature value shown along dimension $l$—e.g., $x\in \left\{up,down,left,right\right\}$. Let $a_{k,l}$ represent the perceptual evidence for feature $k$ along visual dimension $l$—that is, the internal perception of the features. To simplify the perceptual model, we assume that the perceptual evidence can take only 2 distinct values: ${\varphi }_c$ for features which correctly match the physical stimulus (i.e., $x_l=k$) and ${\varphi }_o$ for incorrectly matching features ($x_l\ne k$).

The parameters ${\varphi }_c$ and ${\varphi }_o$ determine the perceptual evidence for correct and incorrect feature values, regardless of whether dimension $l$ is cued or uncued. The task cue that is presented on each trial determines which visual dimension should be used to determine the response. Ideally, only the cued dimension should be used to determine the response, but we will assume that the evidence from the uncued (but previously cued) task dimension will partially contribute, depending on its task activation. Task activation combines with the perceptual evidence in a multiplicative fashion—perceptual evidence can contribute to a response only when there is some task activation for the corresponding dimension. The multiplicative combination of perceptual evidence and task activation is conceptually similar to compound-cuing models (23) as well as gating mechanisms in connectionist models of cognitive control (24).

The perceptual evidence for feature $k$ of dimension $l$ is given by $b_{k,l}=a_{k,l}\times w_c$ for the cued task and by $b_{k,l}=a_{k,l}\times w_u$ for the uncued task. The task activations $w_c$ and $w_u$ determine how much the perceptual evidence from the cued and uncued dimensions will be differentiated, respectively. If $w_u>0$, there is some “leakage” of perceptual evidence from the wrong dimension that will contribute to the response. To complete the perceptual model, we assume that the perceptual evidence is added across dimensions for each response direction. Let $c_k$ represent the perceptual evidence for response $k$. In the model, $c$ is simply the sum of the perceptual evidence weighted by task activation: $c_k=b_{k,1}+b_{k,2}$. Because the activations are summed across dimensions, the activation is higher in a congruent trial relative to an incongruent trial, as there is additional perceptual evidence from the uncued dimension. Response congruency effects therefore depend on the task activation for the uncued dimension.

Decision Process.

Choices and response times during perceptual decision making have been modeled by stochastic accumulator models of many types (25–27). Previous task-switching modeling studies have primarily used the diffusion decision model (7, 8, 16) that is restricted to modeling 2-choice tasks. As our paradigm involves 4 response choices, we used simple race models which effectively model perceptual decisions of multiple responses (e.g., ref. 28).

In the race model, we associated a separate evidence accumulator with each of the 4 responses. The evidence for each accumulator started at zero and accumulated for each alternative until one of the accumulators reached a response threshold (Fig. 2B). The winning accumulator determined the response choice, as well as the response time. Evidence accumulation followed a diffusion process—a continuous random walk. Each accumulator had an average “drift rate” at which evidence increased, and this was set by the perceptual evidence for that response ($c_k$). The distribution of times to reach threshold was inverse Gaussian (or “Wald”) distribution (25). This distribution was parameterized by the drift rate ($c_k$), the response threshold ($\alpha$), and the variance of the Wiener process ($\sigma$). We made standard assumptions about contaminant data and the time taken for motor and perceptual processes (see SI Appendix for details).

Results

Response Time and Accuracy.

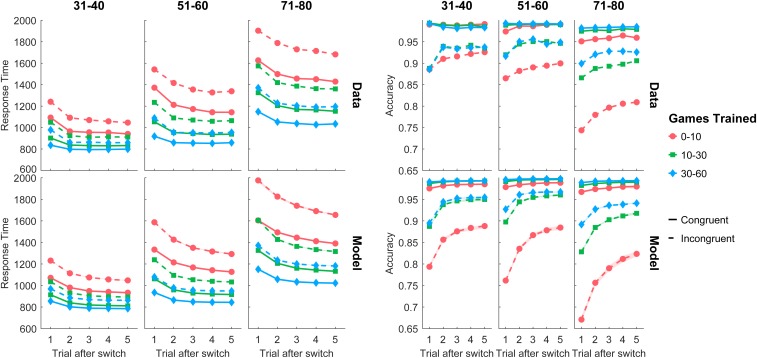
Fig. 3 shows the observed and model-predicted response times and accuracy as a function of the number of trials after a task switch, practice, and congruency for 3 of the 6 age groups. In each plot, trial 1 is a switch trial (e.g., the cued task changed from B to A), whereas trials 2–5 are task-repeat trials (e.g., task A was repeated). SI Appendix, Figs. S1 and S2 show the results separately for all age groups, as well as results of a posterror slowing analysis. Responses were slowest immediately after a task switch and sped up over several repeat trials.* Practice sped up overall response times and reduced response speedup after the second trial in a run. However, even extended practice did not eliminate response slowing for the switch trial (see also ref. 19). A similar pattern held for accuracy: It was lowest for the switch trial and gradually increased as the run progressed and with practice, especially for incongruent trials (congruent trials had accuracy near ceiling). All age groups showed qualitatively similar effects for response time and accuracy. The older age groups had generally slower response times and lower accuracy, but also showed more pronounced improvements with practice.

Fig. 3.

Average response time and accuracy for observed data (Upper) and model predictions (Lower) for the first 5 trials following a task switch, broken down by age group (columns), levels of practice (colors), and congruency (solid line, congruent; dashed line, incongruent). Shaded areas for model predictions represent 75% credible intervals. Runs extending beyond 5 trials were included in the modeling, but are not shown here.

With a relatively small set of parameters, the model captured all of the qualitative trends in response time and accuracy data, and many of the quantitative trends, albeit with some deviations—e.g., for low practice, the model underpredicted accuracy for incongruent trials.

Latent Cognitive Processing in Well-Practiced Task Switching.

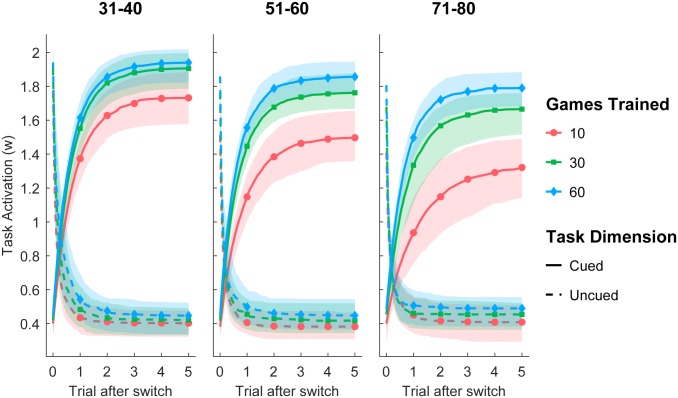
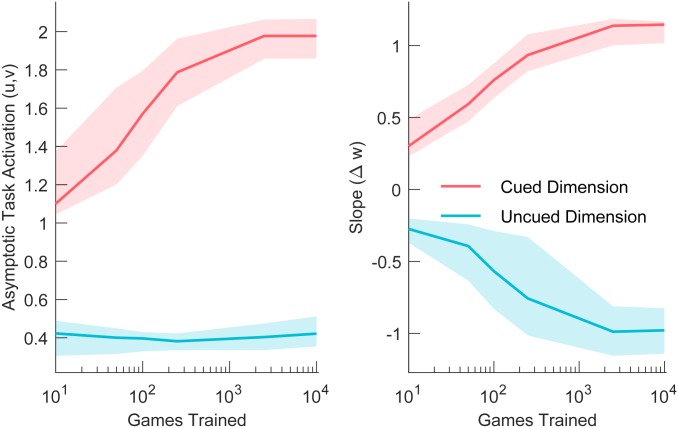
To better understand how the model captures empirical trends, we examined the inferred model parameters. Fig. 4 shows the task activations $w_c$ and $w_u$ as a function of number of trials after a task switch, by age and practice. Practice increased the asymptotic task activation for the cued, but did not affect the uncued task dimension. Fig. 5 shows that, for the highly practiced sample, the asymptotic task activation ($u,v$) for the cued task dimension increased with long-term practice (see SI Appendix, Figs. S3–S5 for additional results), but there was no corresponding decrease for the uncued task dimension, even after 10,000 sessions. This implies that irrelevant information continued to interfere even after extensive practice. The slopes ($\mathrm{\Delta }{w}_c,\mathrm{\Delta }{w}_c$) of the task-activation function show that practice increased the rate of change in task activations approximately symmetrically for the cued and uncued dimensions: Less time was needed to disengage from the perceptual dimension that is no longer relevant and to engage the relevant perceptual dimension.

Fig. 4.

Inferred dynamics of task-activation levels ($w$) for cued and uncued tasks for 3 age groups. Lines represent the mean across participants. Shaded areas represent 75% percentiles of the posterior mean across individual participants.

Fig. 5.

Effect of long-term practice on asymptotic task activation for cued and uncued task dimensions (Left) and the average slope of the task-activation function during the first trial (Right).

The estimated model parameters indicate that a number of cognitive processes change with age. One effect is a general decrease in speed of information processing, as captured by task-activation levels that directly affected the drift rates of the decision process. This is consistent with aging theories proposing general slowing of cognitive operations (29), as well as theories invoking cognitive control deficits impacting the ability to update task relevant context (30). Older age groups also make more cautious decisions, as reflected by higher decision thresholds, slower nondecision times, and larger variability in the evidence-accumulation process (SI Appendix, Fig. S6), consistent with previous findings (16, 31, 32).

The Effect of Practice on Performance Differences across Age Groups.

Fig. 3 shows that the older groups at higher practice levels performed functionally similarly to younger groups at lower practice levels, suggesting that some age differences can be overcome by training. However, age effects on response time and accuracy can be contaminated by speed/accuracy trade-offs or nondecision time components, such as motor-response times that are unrelated to task switching. To better understand age differences in performance, we assessed the speed of task switching through the slope of the activation function for cued tasks ($\mathrm{\Delta }\left(w_c\right)$).

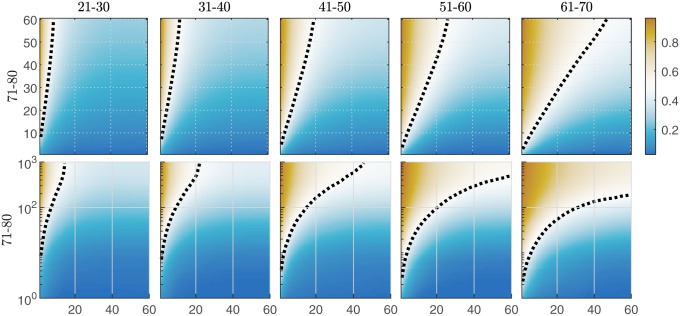
Fig. 6 shows the analysis of relative performance of younger users who trained up to 60 sessions against older (71–80 y old) users who trained up to 1) 60 sessions (Upper) and 2) 1,000 sessions (Lower). The plots show the probability that a randomly sampled older individual outperforms a randomly sampled younger individual. The key finding is indicated by the plot regions that are not blue: In many cases, older individuals outperformed younger individuals who had received the same (Fig. 6, Upper) or less (Fig. 6, Lower) training. The amount of training required for this to occur increased with the difference between the age groups being compared. In addition to comparing pairs of individuals, we also compared older individuals against the median performance of the youngest age group. This led to results similar to those shown in Fig. 6. For example, all 36 71- to 80-y-old individuals with 1,000 practice sessions performed better than the median performance of 21- to 30-y-old individuals after one practice session. This number decreased to 17 of 36 (roughly equivalent performance) when the 21- to 30-y-old individuals trained for 15 sessions. Only 11 of 36 71- to 80-y-old individuals at 1,000 practice sessions outperformed 21- to 30-y-old individuals at 60 practice sessions. Therefore, the majority of older individuals were able to match or exceed the performance of younger individuals, but only when younger individuals were relatively unpracticed. The amount of additional training that older people need to reach performance equivalent to younger age groups diminished with smaller age differences.

Fig. 6.

Performance comparison as a function of practice for the older (vertical axes) and the younger (horizontal axes) age groups. Dark orange colors indicate practice levels where the majority of older individuals are outperforming the younger individuals; dark blue colors indicate the opposite. Dashed lines show the practice levels resulting in equal odds of an older individual outperforming a younger individual. Upper compares users with training data up to 60 games. Lower compares the performance of older users with training data up to 1,000 games (36 per age group) against younger users with training data up to 60 games. The performance metric is the speed of task switching ($\mathrm{\Delta }\left(w\right)$).

Other latent measures that also assess task-switching performance, such as the asymptotic task activation ($u$, that assesses the degree to which the cued task can be activated) and the drift rates ($c$, that assesses information processing speed), produced similar results (SI Appendix, Figs. S7 and S8).

General Discussion

We present a probabilistic model for task switching that separates a control process that governs task activation from an evidence-accumulation process that governs each individual decision. We propose simple temporal dynamics across trials that determine the task activation of both cued and uncued tasks. In a very large adult-lifespan dataset with multiple task sessions, we showed that practice increased both the maximum amount of task activation for the cued task and the rate at which that maximum is reached. However, even after extensive practice, residual activation of the uncued task remained unaffected by practice or age. This explains why the model predicts that response congruency effects are not impacted by practice or age, consistent with previous empirical findings (33), as the benefit for congruent trials is directly related to the additional boost of activation from the uncued dimension.

This model provides latent parameters that can differentiate between the relative contribution of level of activation of the relevant vs. the irrelevant task on the cost of switching (34). These parameters were differently impacted by aging: Older groups showed a reduced level of cued task activation, even after multiple repeat runs, especially at low practice levels. In the particular task-switching paradigm studied in this paper, the cue was presented simultaneously with the target. An important direction for future research is to extend the task-switching model to account for cuing effects (35) when the task cue is presented before the target and the task cue is partially informative of the upcoming task.

Overall, our findings show that task switching in this particular paradigm can be substantially improved by practice across all age ranges. Many cognitive-training studies have shown that task-specific performance in a number of cognitive domains, such as perceptual speed, working memory (36), and task switching (15, 17–21), can improve with practice. Here, we show that extensive, self-motivated task-switching practice can partially mitigate aging effects on task-switching processes. With extensive task practice, older people can become functionally similar to less-practiced younger people, in this specific task.

Attempts to demonstrate transfer of cognitive training to structurally dissimilar tasks have been challenging (37, 38), possibly in part because of our poor understanding of the latent factors that underlie the learning process (34). By specifying the underlying cognitive changes that explain how people improve on task switching, this paper provides a promising direction to investigate transfer to other executive-control tasks, at a latent cognitive level.

Materials and Methods

Lumosity Data.

We performed a retrospective analysis of gameplay data for a sample of users who played “Ebb and Flow,” a task-switching game on the Lumosity platform that is designed to test the ability to switch between 2 tasks (see SI Appendix, SI Text for details on procedure). The original deidentified dataset provided by Lumosity included the gameplay history and raw data at the individual trial level for 194,695 users spanning a period from December 18, 2012 to October 31, 2017. Our user sample spent a mean of 2.5 y on the platform and included 54% females and 42% males (5% did not specify gender).

The analyses are based on 3 different samples of users. The first sample included a large set of users, but limited the total amount of practice considered. We selected 1,000 users who played at least 60 gameplays and restricted the data to only the first 60 gameplays of each user. This guaranteed that the dataset had a full learning history of 60 gameplays to avoid potential dropout confounds (10). We sampled an equal number of users across 6 age groups: 21–30, 31–40, 41–50, 51–60, 61–70, and 71–80. Overall, this data sample of 1,000 users contained 46,470 gameplay events and 2,881,161 trials.

The second sample included a small set of users with the most extensive history of practice in our Lumosity data sample. This included 15 users who practiced between 3,000 and 13,733 games over 1.5–4.5 y. The full practice history of these users was included (25,522 gameplay events and 1,778,052 trials).

The third sample included a small, randomly selected set of older users who practiced for at least 1,000 games (n = 36 users per age group: 61–70 and 71–80 y old). We restricted their gameplay history to the first 1,000 games. Overall, this data sample of 72 users contained 52,693 gameplay events and 3,339,430 trials.