Introduction to Quantitative Susceptibility Mapping and Susceptibility Weighted Imaging

Abstract

Quantitative Susceptibility Mapping (QSM) and Susceptibility Weighted Imaging (SWI) are MRI techniques that measure and display differences in the magnetization that is induced in tissues, i.e. their magnetic susceptibility, when placed in the strong external magnetic field of an MRI system. SWI produces images in which the contrast is heavily weighted by the intrinsic tissue magnetic susceptibility. It has been applied in a wide range of clinical applications. QSM is a further advancement of this technique that requires sophisticated post-processing in order to provide quantitative maps of tissue susceptibility. This review explains the steps involved in both SWI and QSM as well as describing some of their uses in both clinical and research applications.

Introduction

Susceptibility Weighted Imaging (SWI) and Quantitative Susceptibility Mapping (QSM) generate image contrast from differences the magnetization that is induced in tissues, i.e. their magnetic susceptibility, when placed in the strong external magnetic field of an MRI system. Differences in tissue susceptibility help identify materials in which the susceptibility is negative, such as diamagnetic calcification, and highly positive such as paramagnetic haemorrhage,^1,2 or paramagnetic exogenous contrast agents like gadolinium or superparamagnetic iron oxide nanoparticles (SPIONs).^3–6 The methods can also give information on elevated iron content and myelin content and venous blood oxygen saturation.^1,2,7–9

SWI combines magnitude and phase information to qualitatively display tissue magnetic field variations, while QSM quantifies the underlying magnetic susceptibilities that create these field variations. The quantitative nature of QSM allows for longitudinal monitoring of disease progression, across subjects, and potentially imaging centres whilst limiting observer bias. However, QSM requires a series of sophisticated post-processing steps which are based on understanding the relationship between magnetic susceptibility, magnetic field and MR signal, which will be described below.

What is magnetic susceptibility?

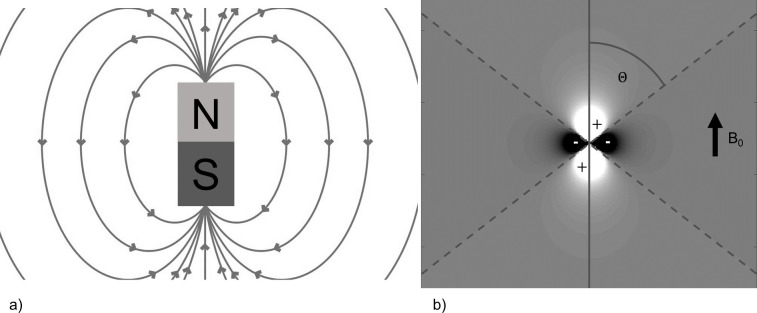
Magnetic susceptibility ($\chi$) is a material property that describes the response of an object to being placed within a magnetic field. When brought into the static magnetic field of an MRI scanner with magnetic flux density ${\mathrm{B}}_0$ and magnetic field intensity $H$, a material gains a magnetization ($M$), defined as the quantity of magnetic dipole moment per unit volume, proportional to its magnetic susceptibility, i.e. $M=\chi H$.^10,11 Paramagnetic materials have a positive susceptibility value that leads to their magnetic moments being aligned parallel to $B_0$ , whilst diamagnetic materials have a negative susceptibility and their magnetic moments align anti parallel to $B_0$.^10,11 This tissue magnetization leads to the generation of a magnetic field. Figure 1 shows the field generated by a magnetic unit dipole, i.e. a microscopic bar magnet. Note that this dipole field becomes zero at an angle of 54.7° to the direction of $B_0$ . This is often referred to as the “magic-angle” and is responsible for the spurious increase in ${\mathrm{T}}_2$ relaxation time and hence signal when highly structured tissues such as tendons happen to be aligned at this angle to the direction of $B_0$.¹² Since there are a huge number of magnetic dipoles in a given tissue, the field at any point within a given region of interest (ROI) is made up of contributions from all surrounding dipoles.¹³ The total tissue dipole field $\mathrm{\Delta }B\left(x,y\right)$ generated within an ROI, can be described by a mathematical operation called convolution, represented by the mathematical operator $\otimes$, between the susceptibility values within the ROI, known as the susceptibility map $\left(\chi \right(x,y\left)\right)$, and the unit dipole field, also referred to as the unit dipole kernel $\left(d\right(x,y\left)\right)$, scaled by the static magnetic field strength $B_0$ ^10,13–15:

Figure 1.

(a) Magnetic field lines of a magnetic dipole (b) Magnitude of the magnetic dipole field in the direction of ↑ B₀. The values along the magic angle (${\displaystyle \mathrm{\Theta }={\text{54.7}}^{\circ }}$) are zero and there are lobes of positive and negative field strength, indicated as areas of relative hyper- and hypointensity respectively.

$${\displaystyle \mathrm{\Delta }B=B_0\left(\chi \otimes d\right)}$$

By applying a Fourier Transform, we can change $\chi (x,y)$, $d(x,y)$, and $\mathrm{\Delta }B\left(x,y\right)$ into $X\left(k\right)$, $D\left(k\right)$, and $\mathrm{\Delta }B\left(k\right)$, which correspond to a decomposition into their spatial frequencies $k$. This is like the relationship between MRI raw data acquired in k-space to which an inverse Fourier transform is applied to reconstruct MR images. This relationship simplifies the mathematics since a convolution in image space corresponds to a multiplication in k-space. Therefore, we can Fourier transform all the variables, and simply multiply them in Fourier space:

$${\displaystyle \mathrm{\Delta }B\left(k\right)=B_0\left(\mathrm{X}\left(k\right)D\left(k\right)\right)}$$

This means that field map can be calculated by applying the inverse Fourier transform ^10,13–15:

$${\displaystyle \mathrm{\Delta }B\left(x,y\right)=IFFT\left(\mathrm{\Delta }B\left(k\right)\right)}$$

In other words, the field map depends on the magnitude and orientation of the static magnetic field and the shape, value and distribution of the susceptibility sources.

Susceptibility effects in MRI

In addition to these field inhomogeneities created by the material, there are also inhomogeneities in the static, i.e. MR system, magnetic field ($B_0$) and those due to the interactions between neighbouring spins (spin–spin interactions). These magnetic field inhomogeneities cause the protons to precess at different frequencies and therefore mutually dephase with time. This results in an exponential decay of the MR signal with a time constant given by $T_2^{*}$ . The spin–spin interactions are usually characterized by the $T_2$ relaxation time whilst the additional susceptibility and $B_0$ inhomogeneity differences can be characterized by a relaxation time known as $T_2^{`}$ . Together their relaxivities, i.e. their reciprocal values, add to give the $T_2^{*}$ value, i.e.

$$\frac{1}{T_2^{*}}=\frac{1}{T_2}+\frac{1}{T_2^{`}}$$

A gradient echo pulse sequence can be used to acquire multiple gradient echoes following the initial radiofrequency excitation pulse. This allows us to sample the $T_2^{*}$ decay at different echo times and the $T_2^{*}$ relaxation time can be calculated by fitting an exponential decay to the measured signals:

$${\displaystyle S\left(t\right)=S_o{e}^{-\frac{t}{T_2^{\ast }}}}$$

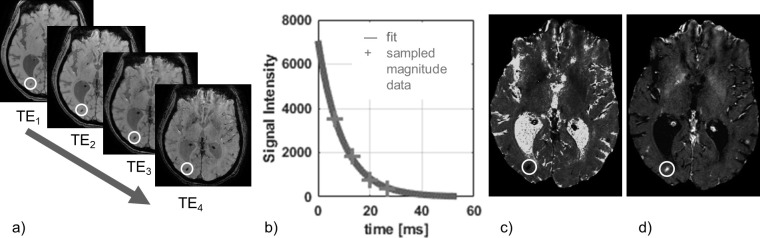
A map of $T_2^{*}$ -values, or its reciprocal $R_2^{*}=1/T_2^{*}$ , provides a quantitative measure of the amount of dephasing caused by all field inhomogeneities (Figure 2).

Figure 2.

This figure illustrates T ₂ ^*/R ₂ ^*-mapping: (a) Magnitude images of the brain acquired at four increasing echo times; the signal intensity in areas with a large susceptibility variation (in this example haemorrhage) decreases more rapidly than in the rest of the brain as indicated by the circle. (b) The time constant T ₂ ^* is estimated by fitting an exponential decay to the magnitude signal intensity variation of every voxel over time; here we consider a sample from a high SNR ROI to illustrate the exponential shape of the signal decay. (c) The curve fitting results in a map of T ₂ ^*, where the haemorrhage appears hypointense. (d) Sometimes a map of its reciprocal R ₂ ^* is used instead, where the haemorrhage appears hyperintense. ROI,region of interest; SNR, signal-to-noise-ratio.

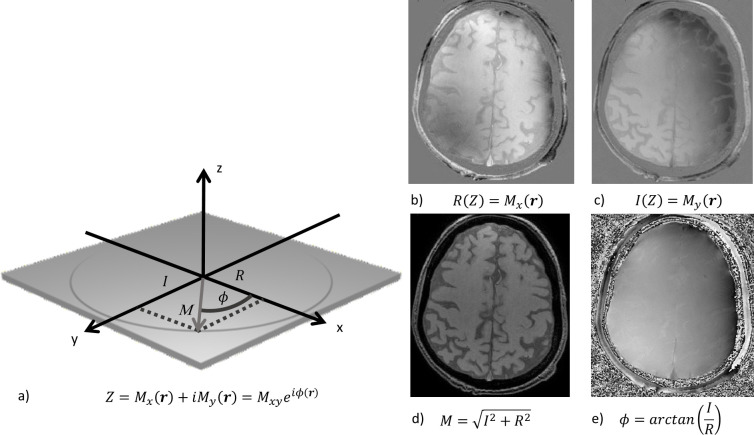
However, this $T_2^{*}$ -mapping method only considers the magnitude of the MRI signal. Raw MRI data, is acquired as a complex-valued signal, i.e. each voxel has real and imaginary components from which the signal magnitude and phase angle can be calculated (Figure 3). In most MRI, only the magnitude image is reconstructed, and the phase information is discarded. However, when properly processed, the phase of the signal contains very useful information. The phase primarily arises from the average field inhomogeneity measured within a voxel ($\mathrm{\Delta }B\left(x,y\right))$) due to susceptibility effects, whereas spin–spin interactions ($T_2$) have a negligible effect.¹⁶ The phase of the MR signal increases linearly with time (t) with a slope proportional to $\mathrm{\Delta }B\left(x,y\right)$ . Whilst the $T_2^{*}$ -value indicates the presence of local dephasing, the size of the phase shift and its sign yields more information about $\mathrm{\Delta }B\left(x,y\right)$ , and therefore about the underlying material susceptibility.¹ SWI combines both magnitude and phase data, which allows for a distinction between materials with different susceptibilities, e.g. between paramagnetic iron in haemorrhage and diamagnetic calcification.

Figure 3.

(a) The signal from the precessing proton spins which is acquired by the MR receiver is represented as a complex number with real (R) and imaginary (I) components from which a pixel-by-pixel signal magnitude and phase can be calculated. (b) Reconstruction of the real component of the magnetization. (c) Reconstruction of the imaginary component of the magnetization.(d) The calculated magnitude signal. (e)The calculated phase signal.

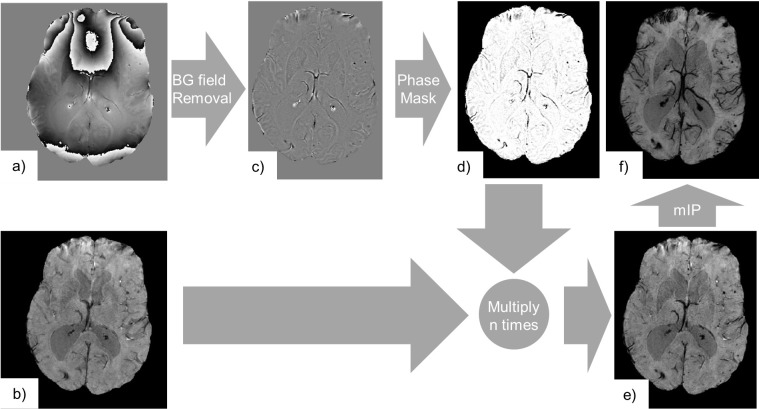
SWI requires pre-processing of the data, as shown in Figure 4. The phase data is high-pass filtered to remove the slowly varying (across the image) background field, originating, e.g. from air tissue interfaces. This background phase can potentially obscure the phase information from the desired local susceptibility sources.⁷ The filtered phase data is used to create a mask to selectively reduce the signal intensity from paramagnetic or diamagnetic susceptibility sources. In order to emphasize negative phase shifts, e.g. those created by deoxyhaemoglobin in deoxygenated blood, the mask is set to one in voxels containing a positive phase value and negative phase values are then normalized to be within the range of zero to one:

Figure 4.

SWI consists of the processing of complex gradient echo MRI data, i.e. its phase (a) and magnitude components (b). Here, we used the fourth echo from a multi echo gradient echo acquisition (TE = 26.7 ms, TR = 32.0 ms, voxel size = 0.65×0.65×1.4 mm³). The phase (a) is high-pass filtered in order to remove the background phase (c). Contrast is generated by variations in the magnetic field generated by local susceptibility sources only. We can note that paramagnetic materials (haemorrhage, venous blood) appear as negative phase shifts, while diamagnetic materials (calcification) appear as positive phase shifts. The filtered phase data is further processed to generate a phase mask (d) that only darkens areas where the phase shift is negative. The magnitude image is subsequently multiplied n times (here n = 4) in order to generate the SWI (e). The phase mask was chosen to suppress signals from negative phase shifts only, so that the visibility of both haemorrhages and the venous vasculature was enhanced. A mIP may be employed to further emphasize paramagnetic venous vasculature across the stack of slices (f). mIP,minimum intensity projection; SWI, Susceptibility Weighted Imaging; TE, echo time; TR, repetition time.

$${\displaystyle Mask\left(x,y\right)=\{\begin{array}{l}\frac{\pi +\varphi \left(x,y\right)}{\pi };if\varphi \left(x,y\right)\le 0\\ 1;if\varphi \left(x,y\right)>0\end{array}}$$

The mask is subsequently multiplied n times with the magnitude image:

$$SWI=Mag\times Mas{k}^n$$

The number of multiplications is chosen to optimize the contrast-to-noise ratio (CNR) in SWI and may be chosen depending on the magnitude of the phase shift within the structures of interest and therefore the echo time (n = 4 is commonly chosen). To improve the visualization of the venous vasculature a minimum intensity projection (mIP) through the stack of slices may be employed.⁷

Both $T_2^{*}$ weighted images, quantitative $T_2^{*}$ mapping, and SWI depict variations in magnetic field inhomogeneity, which are non-local, which means that they extend beyond the region of the susceptibility change, causing blooming artifacts that depend on tissue geometry and orientation. QSM can remove these effects by directly displaying the underlying material properties which are independent of the external field.^11,16

Quantitative Susceptibility Mapping

QSM requires several image processing steps to extract the tissue susceptibility from the phase information. These steps are described below and illustrated in Figure 5. Firstly, $\mathrm{\Delta }B$ is estimated from the phase of a gradient echo acquisition. Secondly, field inhomogeneities generated by sources outside the ROI are eliminated, so that finally an inversion operation is performed to derive the susceptibility map.

Figure 5.

QSM consists of the processing of complex gradient echo MRI data, i.e. its phase (a) and magnitude components (b). Here, we used a multiecho gradient echo acquisition (TE₁ = 6.5 ms, echo spacing = 6.744 ms, #echoes = 4, TR = 32.0 ms, voxel size = 0.65×0.65×1.4 mm³). A map of field inhomogeneities ΔB is estimated from the phase data (c). Subsequently contributions from background fields are removed to extract a map of field inhomogeneities generated by susceptibility sources inside the ROI only, ${\displaystyle \mathrm{\Delta }{B}_{int}}$ (d). A dipole field inversion operation is performed on $\mathrm{\Delta }{B}_{int}$ to calculate the susceptibility map $\chi$ (e). ROI, region of interest; QSM, Quantitative Susceptibility Mapping; TE, echo time; TR, repetition time.

From phase to field

As described above, the phase of the MR signal increases linearly with time:

$${\displaystyle \varphi \left(t\right)={\varphi }_0-2\pi \gamma \mathrm{\Delta }Bt}$$

$t$is the echo time, ${\displaystyle {\varphi }_0}$ the initial phase offset at the centre of the excitation pulse ($t=0$), and $\gamma$ is the gyromagnetic ratio.^17,18 The slope of the phase variation is proportional to the field inhomogeneity in the direction of $B_0$, $\Delta B$, which can be estimated for each voxel (Figure 6). In a multiecho gradient echo acquisition this can be done using a least-square algorithm, that weights data-points from early echoes more heavily than from later echoes because of their higher signal-to-noise ratio (SNR).^17–19 Other implementations have also successfully estimated the phase from a single echo.^2,17 It is important to carefully choose the reconstruction algorithm that generates the phase information, in particular when combining information from multiple coil elements in order to avoid artifacts and preserve relevant phase information. An excellent review of the technical considerations can be found in.²⁰

Figure 6.

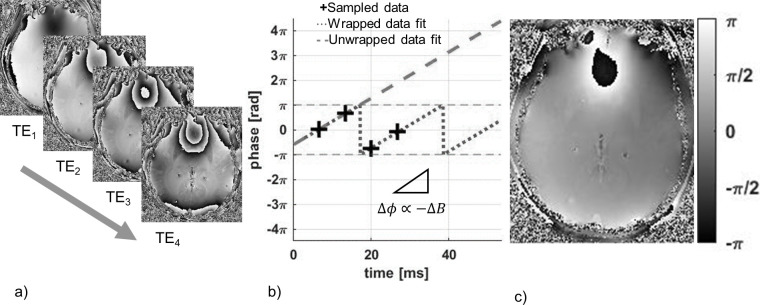
In order to estimate $\mathrm{\Delta }B$, the variation of the phase images (a) acquired from four increasing echo times (6.50, 13.24, 19.99, 26.73 ms) are monitored over time. By fitting a linear function to the multiecho phase data, phase wraps between subsequent echoes can be estimated and removed to estimate the slope of the phase variation over time and the corresponding value of ΔB (b). This is done for every voxel in the acquisition in order to generate a map of temporally unwrapped ΔB values scaled by a factor of $\gamma 2\pi \mathrm{\Delta }TE$ (c).

In other parts of the body, the linear relationship between ${\displaystyle \varphi }$ and $\Delta B$ does not hold anymore and the signal can be more accurately described by:

$$S\propto \left(W+F{e}^{-i2\pi \mathrm{\Delta }{f}_{chem}TE}\right)e^{-i2\pi \gamma \Delta BTE}$$

This equation incorporates the signal from fat which differs in precession frequency from water by ${\mathrm{\Delta }f}_{chem}$ . Therefore, water–fat separation techniques can be used to estimate the fat fraction and $\Delta B$ within each voxel.²¹

Since phase is an angle it can only be represented in the range $[-\pi ,\pi )$. However, the actual phase shift may be greater than this range due to, for example, large susceptibility differences or large echo spacings. The phase can then become “wrapped” or “aliased” into this $[-\pi ,\pi )$ range. This phase wrapping can be corrected by the use of algorithms that add an integer multiple $k$ of $2\pi$ to the acquired phase ${\displaystyle {\varphi }_w}$ :

$${\displaystyle {\varphi }_{uw}={\varphi }_w+k2\pi }$$

First, the aliasing between echoes is removed in the temporal domain. Phase wraps in between echoes are removed during the estimation of $\mathrm{\Delta }B$ and a scaled version of $\mathrm{\Delta }B$, i.e. ${\displaystyle \mathrm{\Delta }\varphi =2\pi \gamma \mathrm{\Delta }TE\mathrm{\Delta }B}$ is estimated. The remaining phase wraps are corrected by spatial phase unwrapping algorithms (Figure 7).¹¹

Figure 7.

The map of $\mathrm{\Delta }B$ values scaled by a factor of $\gamma 2\pi \mathrm{\Delta }TE$ (a) includes phase wraps that are outlined by dashed lines. Phase unwrapping algorithms identify these areas and add integer multiples of $2\pi$ ($k2\pi$) onto them. Here, bright areas indicate phase shifts of $2\pi$, dark areas $-2\pi$ and the rest is equal to zero (b). In the resulting unwrapped field map, all of the wrapping artifacts have been removed (c).

Subsequently, a mask is applied in order to select a ROI that contains an area of sufficient SNR, since noise on the phase image can lead to severe errors when estimating $\mathrm{\Delta }B$ and then propagate.²²

Background field removal

The map of field inhomogeneities measured inside the ROI ($B_{total}$) is made up of fields generated from magnetized susceptibility sources located inside ($B_{int}$) and outside the ROI ($B_{ext}$). For instance, large susceptibility differences between air/tissue and air/cortical bone create large, spatially slowly varying, fields that extend into the brain, which may obscure the comparatively small $B_{int}$ generated by local changes in susceptibility that we wish to investigate. In order to extract the susceptibility map, it is important to consider only $B_{int}$ , and remove $B_{ext}$.²³

A great deal of the research activity associated with QSM is based upon methods for background field removal and the associated algorithms are heavily mathematical. A detailed discussion is therefore beyond the scope of this article. Instead, we will highlight some of the principles applied in frequently used techniques. An excellent review that illustrates the underlying physical and mathematical principles in more detail can be found in Schweser et al.^16,24

The algorithms generally make assumptions about the mathematical properties of $B_{ext}$ and $B_{int}$ to separate them. The simplest approach, often applied in SWI, assumes that $B_{ext}$ varies at a much lower spatial frequency than $B_{int}$ and can be removed by applying a high pass filter to $B_{total}$ . While this removes slowly varying field components of $B_{ext}$ some of its components may remain and some desired components of $B_{int}$ may be suppressed.^{7,11,23,25,26} One improved method is geometry-dependent artifact correction, in which magnitude images are segmented into areas of air and tissue. After assigning susceptibility values to the segments, a calculation can be performed to estimate the field induced by the air–tissue interface.²⁷

$B_{ext}$can be better characterized as a mathematical entity known as a harmonic function^13,28–30 or by the observation that $B_{ext}$ and $B_{int}$ are approximately orthogonal to each other within the ROI.³¹ The Sophisticated Harmonic Artifact Reduction (SHARP) algorithm makes use of the spherical mean value (SMV) property of harmonic functions.²⁹ This method improves the separation of $B_{ext}$ and $B_{int}$ but results in a shrinking of the area of the ROI since the algorithm cannot be applied near the edges of the ROI (Figure 8a). Other methods, based on the SMV property, that aim to improve the SHARP algorithm have also been proposed.^32,33 Another method using the Laplacian Boundary Value algorithm makes use of another mathematical property of harmonic functions in order to set up a system of partial differential equations that can be solved in order to estimate $B_{int}$ and $B_{ext}$.³⁰ The solution of this problem requires that $B_{ext}$ is much larger than $B_{int}$ at the boundary and violations of the boundary conditions may lead to artifacts on the estimate of $B_{int}$ originating at the ROI boundary (Figure 8b).³⁰

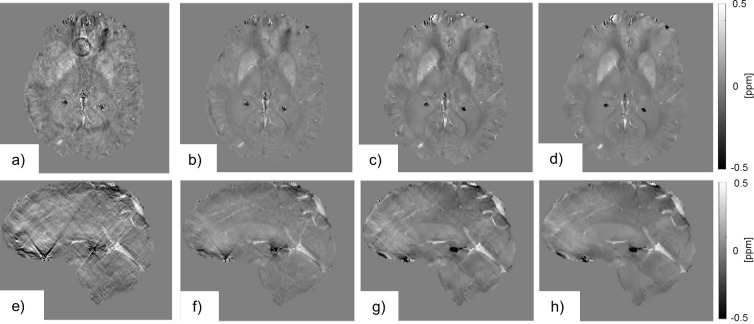
Figure 8.

This figure shows the differences between the internally $B_{int}$ (a–c) and externally generated field inhomogeneities $B_{ext}$ (d–f), as estimated by the algorithms SHARP (a, d), LBV (b, e), and PDF (c, f). $B_{ext}$ (d–f) is a large, slowly varying field component, that obscures the small local $B_{int}$ (a–c). Due to different assumptions for the boundary conditions of the Background Field Removal algorithms we can see that there are some differences near the boundary indicated by the black circles on the LBV and PDF images. Furthermore, we can see that the field estimated by SHARP is reduced due to erosion (a, d). LBV, Laplacian boundary value; PDF,Projection onto Dipole Field; SHARP, Sophisticated Harmonic Artifact Reduction.

An alternative approach is the Projection onto Dipole Fields (PDF) method, which estimates the susceptibility distribution within the field of view but outside the ROI, to estimate $B_{ext}$ . A minimization problem can be formulated based on $B_{int}$ and $B_{ext}$ being orthogonal to each other. Since this assumption is valid only to within close proximity of the boundary, it may cause some minor boundary artifacts but performs well inside the ROI (Figure 8c).³¹

Dipole field inversion

We have previously explained that the local field inhomogeneity can be estimated as $\mathrm{\Delta }B\left(k\right)=B_0\left(\mathrm{{\rm X}}\left(k\right)D\left(k\right)\right)$. This equation can be solved and the susceptibility map estimated by deconvolving $B_{int}$ with the inverse of the dipole kernel, which corresponds to a division in k-space: ${\displaystyle \mathrm{X}\left(k\right)=\frac{1}{B_0}\left(\frac{B\left(k\right)}{D\left(k\right)}\right)}$.

However, $D\left(k\right)$ in the direction of $B_0$ is defined as:

$$D\left(k\right)=\frac{1}{3}-\frac{k^2}{k_z^2}fork\ne 0$$

The spatial frequencies where $D\left(k\right)=0$ are located at the magic angle β =±54.7° relative to $B_0$ forming a cone surface. Estimating the values of ${\displaystyle \mathrm{X}\left(k\right)}$ for these spatial frequencies, is difficult to solve, since $\frac{1}{D\left(k\right)}$ results in a divide-by-zero which is undefined. Furthermore, the values of $D\left(k\right)$ decrease in the proximity to the zero-cone-surface and the division by such small values amplifies noise in this region of $\mathrm{{\rm X}}\left(k\right)$, degrading the quality of the QSM.^11,26,34 Furthermore, D(0) is either undefined³⁵ or defined to be zero^16,36 so that there is a lack of knowledge about the resulting $\mathrm{{\rm X}}\left(0\right)$. The calculated susceptibility values are therefore relative rather than absolute and need to be referenced to specific tissue regions, such as cerebrospinal fluid or white matter.³⁷

To overcome this magic angle problem, the most accurate solution in terms of image quality, SNR, and CNR is provided by imaging the subject from multiple orientations. This approach, known as Calculation Of Susceptibility through Multiple Orientation Sampling (COSMOS) acquires images at least three times, each image rotated by a sufficiently large angle. In cerebral QSM, e.g. the patient must tilt their head. Therefore, the zero-value cones from at most two orientations overlap in the same location, so that at least one acquisition always provides the missing information. Whilst very accurate, it is not feasible in clinical applications because it requires significant patient compliance and an increase in acquisition time by a factor of three.³⁴

Instead, a variety of different approaches have been proposed to limit the number of scans to a single acquisition. A detailed discussion of the highly mathematical algorithms that are used is beyond the scope of this article and further information can be found in Wang and Liu and Schweser et al.^11,16 Instead, we will review some of the principles of commonly used techniques.

Some approaches attempt to solve the problem in k-space and others by using image space. In order to solve the problem in k-space, the inverse filter $1/D\left(k\right)$ is regularized by replacing the values close to the position of the zero cone surface, where $\left|D\left(k\right)\right|$ is smaller than a certain threshold, on $1/D\left(k\right)$ with zero³⁸ or with a constant value (Figure 9a,b,e,f).²⁶ The advantage of this method is the relatively low complexity and high time efficiency. However, it is limited by its image quality. If the threshold value is too small then the noise on $\mathrm{\Delta }B$ is amplified and results in cone-shaped streaking artifacts on $\chi (x,y)$. A higher threshold value widens the modified region in k-space, limiting noise amplification and streaking artifacts, while simultaneously decreasing the contrast in $\mathrm{\chi }(x,y)$, which leads to an underestimation of the susceptibility differences.^26,38

Figure 9.

The figure shows the susceptibility maps generated by different dipole field inversion algorithms in axial (a–d) and sagittal (e–h) view. The susceptibility maps estimated using the TKD algorithm with a low threshold value (a, e) exhibits the characteristic streaking artifacts. By increasing the threshold value, we can see an improvement in image quality, but the contrast is reduced along with the streaking artifact (b, f). The MEDI algorithm is able to improve image quality even further, (c, g) and (d, h). By varying the regularization parameter, the susceptibility map gets smoother while the contrast is reduced (d, h). MEDI, Morphology Enabled Dipole Inversion; TKD, Truncated K-space Division.

Image space-based approaches estimate susceptibility maps by finding a solution that minimizes the difference between the measured $\mathrm{\Delta }B$ and the estimated $B_0(\chi \otimes d)$, so that they do not need to solve the divide-by-zero problem. Typically, a regularization term is added to minimize streaking artifacts using prior information. An example is the Morphology Enabled Dipole Inversion (MEDI) algorithm. It assumes that tissue compartments found on magnitude images have relatively uniform susceptibility values. The added regularization minimizes all edges that are present on the susceptibility map but not the magnitude image. This aims at eliminating streaking artifacts or noisy voxels.^35,36,39,40 It is important to carefully choose the amount of regularization to suppress artifacts sufficiently while avoiding an overly smooth susceptibility map with underestimated susceptibility values (Figure 9c,d,g,h).

Clinical applications

SWI and QSM have been applied to numerous pathologies, such as neurodegenerative, oncological, and cardiovascular. While most of the initial susceptibility-contrast applications have been developed for cerebral imaging, as shown in Figure 10, further development has shown a lot of promise in the rest of the body. In the following, we will describe several susceptibility-based applications to show their promise and the potential improvements that could be offered by QSM.

Figure 10.

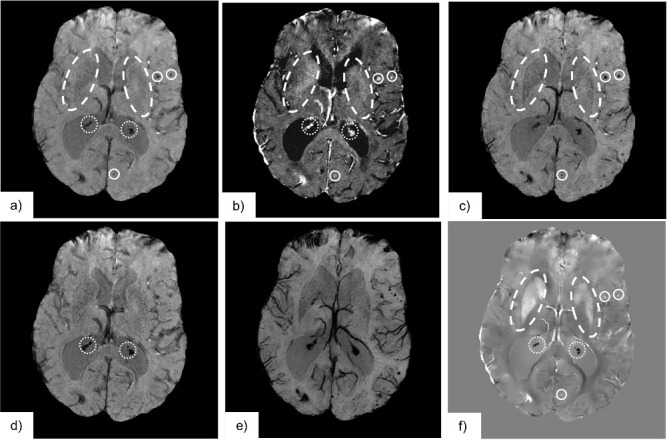
The following demonstrates the application of the discussed susceptibility-based contrast to image anatomy and pathology in the brain: (a) T ₂ ^*-weighted images indicate all susceptibility differences as hypointensities, such as calcifications (diamagnetic, $\mathrm{\chi }\S amp;lt;0$, indicated by the dotted region), haemorrhages (paramagnetic, $\mathrm{\chi }\S amp;gt;0$, indicated by the solid line region), iron rich structures (Putamen and Globus Pallidus, paramagnetic, $\mathrm{\chi }\S amp;gt;0$, indicated by dashed line region) and deoxygenated blood in the venous vasculature (paramagnetic, $\mathrm{\chi }\S amp;gt;0$) (b) R₂ ^*-mapping, the reciprocal of the T ₂ ^*-value, shows all the above as signal hyperintensities. (c) A susceptibility-weighted image employing a phase mask to reduce signal intensity for negative phase shifts only darkens areas of paramagnetic susceptibility. We have indicated the iron rich structures, haemorrhages, and veins. (d) A susceptibility-weighted image employing a phase mask to reduce signal intensity for positive phase shifts only emphasizes areas of diamagnetic susceptibility. We have indicated the calcifications by the dotted region. (e) A minimum intensity projection of the stack of susceptibility weighted images (c) improves visualization of the venous vasculature. (f) The susceptibility map is able to differentiate between regions where $\chi$ has negative and positive values, as areas of hypo- and hyperintensities, respectively.

Cerebral imaging

Variations in cerebral myelin and iron concentration, which are more diamagnetic and paramagnetic than water respectively are dominant sources of susceptibility contrast. QSM-detected iron concentrations correlate well with relaxation rate mapping MRI techniques, previously published post-mortem iron values, X-ray fluorescence, inductively coupled plasma mass spectrometry and are consistent with histological analysis.^37,41,42 When compared to traditional contrast weightings, T ₂ ^*-mapping, and SWI, QSM provides a superior CNR⁴³ while providing a quantitative measurement of iron and myelin without dependence of orientation or geometry of the ROI and non-local effects.^9,42,44 The resulting, highly detailed, anatomical maps of the brain have shown many structures consistent with histology, which other MRI techniques could not display.^37,44,45 The imaging of cerebral substructures may improve patient specific neurosurgical planning, for example to find targets for deep brain stimulation.^37,43,45 While utility of susceptibility based contrast weightings has been demonstrated,⁴⁶ it has been suggested that QSM may further improve results due to the high quality of the anatomical maps.^37,43

Accurate and quantitative anatomical mapping of brain tissue may also serve to identify and track changes of cerebral tissue. Multiple sclerosis is associated with demyelination and cerebral iron accumulation. An increase in iron levels has been shown using T ₂ ^*-mapping⁴⁷ and SWI.⁴⁸ QSM is more sensitive than T ₂ ^*-mapping⁹ to tissue changes caused by the disease, since iron accumulation and demyelination both increase magnetic susceptibility relative to the surrounding tissue while having opposing effects on the T ₂ ^*-value, i.e. iron accumulation shortens T ₂ ^* whilst demyelination prolongs T ₂ ^*.^9,49 Therefore, QSM is suitable to detect early stages of the disease which are associated with demyelination in addition to iron accumulation^9,50,51 and has been used to directly compare healthy and diseased tissue at various stages.^50,52 Susceptibility-based imaging has detected changes in demyelination and iron accumulation and has also been shown to correlate with disease duration and clinical disability.^47,53 Mapping of transverse relaxation rates, phase imaging and SWI, have also been used to find elevated iron levels in the brains of patients with Parkinson's disease (PD)^54,55 and Alzheimer’s disease.⁵⁶ These techniques have allowed for monitoring significant variations in iron levels over the course of PD^57,58 and were used to correlate iron levels with disease severity in terms of motor symptoms, suggesting its use as a biomarker for disease progression.^59–61 In both PD^62–64 and ^65,66Alzheimer’s disease patients, QSM has shown to be feasible as a means to quantify iron levels.

Cerebral haemorrhage

Haemorrhages contain different blood products, such as deoxyhaemoglobin, methaemoglobin, and/or haemosiderin, which are paramagnetic.^2,67 Susceptibility-based techniques have a higher lesion contrast and sensitivity that leads to improved detection of cerebral haemorrhages when compared to conventional and magnitude-based techniques and/or CT.^68,69 QSM provided quantitative susceptibility measures and more accurate blood product volume estimates,^70–72 and has made the differentiation of haemorrhages from veins easier.⁷³ Haemorrhages, accompany a variety of medical conditions such as stroke,⁷¹ cerebral cavernous malformations,⁷⁰ and Traumatic Brain Injury (TBI).⁷³ QSM has allowed for accurate quantitative assessment of lesion size, frequency, location, and/or iron content which could improve the understanding of the role of haemorrhages in these conditions, assess their role as a biomarker for disease severity or determine treatment response.^70–73 Studies using SWI, e.g. have suggested that microbleeds could serve as an indicator of the severity of injury, because coma scores correlated with higher occurrence and volume of haemorrhages.⁶⁹

Blood oxygenation and venography

Due to deoxyhaemoglobin being paramagnetic, SWI is frequently used to image cerebral venous vascular networks.⁷ QSM removes non-local effects and sequence/scanner dependencies from the venograms,^25,74 while also providing quantitative estimates of oxygen saturation in venous blood vessels due to the linear relationship between susceptibility and deoxyhaemoglobin content.^25,74–76 From the susceptibility values, sometimes in combination with flow measurements, different values such as oxygen extraction by tissue or the cerebral metabolic rate of oxygen can be estimated^75,76 so that normal physiological levels of deoxyhaemoglobin⁷⁴ could be monitored along with changes following CO₂ inhalation⁷⁶ or caffeine administration.⁷⁵ In clinical applications QSM has been used to evaluate local venous oxygen saturation in stroke patients.⁷⁷

Mapping changes in blood oxygen levels dynamically may yield information about cerebral functional activity. This has been widely applied in blood oxygen level dependent (BOLD) contrast-based functional Magnetic Resonance Imaging (fMRI), which relies on the T ₂ ^*-effect on magnitude images.⁷⁸ Recent studies have used the phase information to generate susceptibility maps at multiple time points, that could display neuronal activity more directly while removing geometry dependence and non-local effects.^79–81

Susceptibility-based contrast in neuro-oncology

Susceptibility-based imaging has also demonstrated promise in neuro-oncology. SWI has shown to enhance tumour visibility,⁸² image small vessels and micro-haemorrhages with high sensitivity,⁸³ differentiating them better from calcifications, necrosis and artifacts⁸⁴ than conventional multicontrast MR protocols. Appearances have correlated well with pathology.^82,83 The resulting images have been used to grade tumours,⁸³ distinguish between types of tumours⁸⁵ and metastases,⁸⁶ which is promising for initial cancer screening, cancer diagnosis, continued monitoring, and for deciding on a treatment strategy.^83–86 QSM improved differentiation between blood deposits and calcifications,⁸⁷ which may help in characterizing tumours and monitoring treatment responses.

Susceptibility-based contrast outside the brain

QSM has also been demonstrated to be feasible in MR imaging outside the brain. SWI and QSM have both been used to detect calcifications in breast tissue^21,88 and QSM has shown promise in prostate cancer imaging.^89,90 Changing iron concentration in the liver may give more information about liver disease. Therefore, SWI has been used for staging liver fibrosis which is associated with increased iron content and collagen deposition,^91,92 and for identifying iron deposits in siderotic nodules in cirrhotic livers.⁹³ QSM has been used to monitor liver iron concentration since it has shown good correlation with T ₂ ^*-mapping and biomagnetic liver susceptometry.^94,95

Due to the linear relationship between contrast agent concentration and susceptibility, QSM also serves as an ideal tool to detect and quantify contrast agent uptake, such as paramagnetic gadolinium-based contrast agents and (ultrasmall) superparamagnetic iron oxide ((U)SPIO) particles. Gadolinium-based contrast agents have been used to perform cerebral perfusion imaging using QSM and to create dynamic three-dimensional susceptibility maps.^3,4 SPIOs and USPIOs have been used to measure inflammation in the liver and spleen⁵ and monitor micro-vasculopathy for example in cerebral amyloidosis,⁶ where it was suggested to be more sensitive for vascular leakage in vivo, than dynamic contrast-enhanced (DCE) imaging.⁶

Conclusion

QSM and SWI combine gradient echo-based imaging data with prior knowledge about the relationships between magnetic susceptibility, magnetic fields, and MRI signals to display detailed information about the magnetic susceptibility of tissues. This allows for an accurate mapping of the brain architecture, the venous vasculature and for detecting and differentiating between haemorrhages and calcification. Furthermore, it has shown promise in functional imaging of blood oxygenation levels and contrast agent uptake, as well as, longitudinal imaging of structural changes such as iron accumulation or demyelination. SWI is gaining importance in cerebral applications and increasingly finding applications in other body areas. For QSM, there is a large amount of well validated software available online and QSM has shown its promise in a wide range of research settings. The direct mapping of tissue properties may offer new insights in disease development and diagnostics.